A discrete adjoint gradient approach for equality and inequality constraints in dynamics

Abstract

The optimization of multibody systems requires accurate and efficient methods for sensitivity analysis. The adjoint method is probably the most efficient way to analyze sensitivities, especially for optimization problems with numerous optimization variables. This paper discusses sensitivity analysis for dynamic systems in gradient-based optimization problems. A discrete adjoint gradient approach is presented to compute sensitivities of equality and inequality constraints in dynamic simulations. The constraints are combined with the dynamic system equations, and the sensitivities are computed straightforwardly by solving discrete adjoint algebraic equations. The computation of these discrete adjoint gradients can be easily adapted to deal with different time integrators. This paper demonstrates discrete adjoint gradients for two different time-integration schemes and highlights efficiency and easy applicability. The proposed approach is particularly suitable for problems involving large-scale models or high-dimensional optimization spaces, where the computational effort of computing gradients by finite differences can be enormous. Three examples are investigated to validate the proposed discrete adjoint gradient approach. The sensitivity analysis of an academic example discusses the role of discrete adjoint variables. The energy optimal control problem of a nonlinear spring pendulum is analyzed to discuss the efficiency of the proposed approach. In addition, a flexible multibody system is investigated in a combined optimal control and design optimization problem. The combined optimization provides the best possible mechanical structure regarding an optimal control problem within one optimization.

1 Introduction

The direct differentiation and the adjoint variable approach represent two principal analytical methods employed for sensitivity analysis in the context of optimization. The direct differentiation method [13] facilitates implementation via straightforward differentiation of system equations, constraints, and cost functions with respect to optimization variables. Despite this, the direct differentiation yields a tremendous computational effort for large-scale optimization problems. Alternatively, the adjoint variable method [13] determines design sensitivities as the solution of adjoint variable equations deduced from variations of the system equations. This avoids the necessity for direct computation of state sensitivities and can dramatically reduce the computational effort required for large-scale optimization problems when adjoint variable equations and algorithms are properly formulated.

The computation of gradients in optimization problems includes the adjoint method with a long history in optimal control theory [24]. Adjoint gradients, e.g., applied for trajectory planning, have already been presented in 1975 by Bryson and Ho [4]. The adjoint gradients have become more and more important in various optimization problems in engineering, e.g., in design optimization [32] or multibody dynamics [7, 10], since the applications have become larger in dimension. Therefore, an efficient calculation of gradients has become essential. Sensitivity analysis has wide-ranging applications in science and engineering, including optimization, parameter identification, data assimilation, optimal control, uncertainty analysis, and experimental design. Current trends in neural networks benefit from solvers capable of building efficient gradient computation for training machine-learning embedded cost functionals in high dimensions [36]. Johnston and Patel stated in [17] that adjoint methods are used both in control theory and machine learning to efficiently compute gradients of functionals. Recent publications discuss the adjoint method in multibody dynamics for various applications, e.g., in a feedback–feedforward control to compute the input control signal and corresponding trajectory predicted by a model [27]. In the work by Schneider and Betsch [38], the choice of a mechanical Hamiltonian and the incorporation of constraints is discussed, and a new approach that preserves the variational structure of the problem is introduced. Moreover, an adjoint sensitivity analysis using a QR decomposition in [16] shows how the adjoint variable method can be applied to multibody systems whose system equations are initially set up in differential–algebraic form but solved in minimal coordinates.

For optimization in complex, large-scale optimization problems, a discrete version of the adjoint method with neat features in terms of stability and accuracy has been proposed recently by various authors [3, 6, 21]. In the discrete adjoint method, the adjoint differential equations are replaced by algebraic equations by introducing a finite-difference scheme for the adjoint system directly from the numerical time-integration method. The method provides exact gradients of the discretized cost function subjected to the discretized equations of motion. The equations of motion of the multibody system and adjoint equations may either be separately discretized from their representations as differential–algebraic equations, or the equations of motion of the multibody system may be discretized first, and the discrete adjoint equations are then derived directly from the discrete multibody equations, tracing back to [4]. It has been emphasized, e.g., by Callejo et al. [6], that the adjoint method is one of the most efficient methods to evaluate sensitivities for problems involving numerous design parameters and relatively few objective functions. The latter paper has presented a discrete version of the adjoint method, which can be applied to the dynamic simulation of flexible multibody systems not only by using an ad hoc backward integration solver but leads to a straightforward algebraic procedure that provides the desired design sensitivities of rigid and flexible multibody systems. Moreover, in [3], the discrete adjoint method is discussed in different time-marching schemes, including backward difference formulas, Newmark and Adams–Bashforth–Moulton methods. In [25], a discrete adjoint sensitivity analysis considering a Newmark family integrator is presented. In Lauß et al. [21], the discrete adjoint equations for the computation of gradients of a cost function are derived using the Hilbert–Hughes–Taylor (HHT) solver to solve the system equations. The great advantage of this approach is that the cost function can also depend on the accelerations, thus allowing the use of measured data from acceleration sensors in the optimization procedure in a straightforward manner.

Flexible multibody formulations must be included in optimization problems when the cost function includes elasticity or deformation of mechanical systems. When dealing with flexible multibody systems with large deformations or large rotations, the absolute nodal coordinate formulation (ANCF) [40] is advantageous because the formulation does not use rotational degrees of freedom. Using these ANCF elements for flexible bodies, a gradient-based adjoint optimization approach has been presented by Held and Seifried [15]. There, a criterion accounts for the deformation energy of the flexible body. A recent work [44] presents an optimization approach that exploits the adjoint variable method in combination with the flexible natural coordinates formulation for obtaining the sensitivity information. A comprehensive literature review in [12] presents various gradient-based optimization methods, especially in the design optimization of flexible multibody systems. The latter-mentioned review paper discusses the main goals in the design optimization of flexible multibody dynamics and reviews concepts and applications in this field. Over 160 publications in the bibliography give a comprehensive overview of optimization algorithms, types and formulations, and sensitivity analysis. Optimal control and design optimization are discussed in various publications, but there is a gap in the literature on optimization or sensitivity analysis that combines optimal control and design optimization of multibody systems.

This paper significantly enhances optimal control and design optimization problems for flexible multibody systems. Promising results in a preliminary paper by Lichtenecker et al. [22] have shown an efficient optimal control strategy for highly flexible robotic systems based on the adjoint gradient computation method. Furthermore, flexible multibody systems, e.g., soft robots, allow new potential for performing various tasks. Soft robots have not yet fully demonstrated their capabilities, as nature is still clearly superior to them in some areas, particularly evolutionary improved motion and control. Future research should address critical challenges and focus on understanding the fundamental principles that govern the design, modeling, and control of soft robots, as stated in Hawkes et al. [14] and Della Santina et al. [9]. Improving the performance of mechanical systems, like soft robots, requires sophisticated optimization strategies to fulfill the high demands of current and future product requirements. In general, two problem formulations can be considered to describe various optimization applications: structural optimization of mechanical components and/or finding an optimal control for dynamical systems [43]. The focus of this paper is on the combination of both problems. A combined gradient computation for highly efficient optimal control while optimizing the structural components of a mechanical system within the same computation is presented.

To this end, a discrete adjoint gradient computation considering equality and inequality constraints is developed, which will be able to incorporate, e.g., final conditions and/or stress restrictions in design optimizations. With this novel approach, a sensitivity analysis of constraints with respect to optimization variables using discrete adjoints is possible, and a combined optimal control and optimal design of a mechanical system is realized. Three examples will show the application of the proposed discrete adjoint gradient approach: (1) an academic example of a one-mass oscillator in a sensitivity analysis, (2) an energy optimal control problem of a nonlinear spring pendulum, and (3) a combined optimal control and optimal sizing problem of a flexible two-arm robot using the ANCF for describing large deformations.

2 Problem description

The increasing industrial relevance of high-end solutions that fulfill a wide range of requirements demands the consideration of novel approaches at an early stage of virtual product development. For instance, finding an optimal control of a flexible multibody system under consideration of final constraints is essential to perform a manipulation according to predefined tasks [22]. In addition, innovative lightweight design requires novel approaches in the field of structural optimization [28]. The performance of mechanical systems, either in optimal control problems and/or structural optimization problems, can be increased by optimization.

An optimization problem aims to find a set of optimization variables $\mathbf{z} = \mathbf{z}^{*} \in \mathbb{R}^{z}$ to minimize a defined cost function $J$ with respect to constraints. A standard nonlinear programming (NLP) problem can be formulated by

$$\begin{aligned} & \underset{\mathbf{z}}{\text{min}}~J(\mathbf{z}) \end{aligned}$$

(1)

$$\begin{aligned} & \text{s.t.} \\& \mathbf{z}_{\mathrm{min}} \leq \mathbf{z} \leq \mathbf{z}_{ \mathrm{max}} \end{aligned}$$

(2)

$$\begin{aligned} & \hat{\mathbf{g}} = \mathbf{0} \end{aligned}$$

(3)

$$\begin{aligned} & \hat{\mathbf{h}} \le \mathbf{0}, \end{aligned}$$

(4)

wherein (2) imposes lower and upper bounds of optimization variables. Equality and inequality constraints are denoted by $\hat{\mathbf{g}}\in \mathbb{R}^{p}$ and $\hat{\mathbf{h}} \in \mathbb{R}^{q}$, respectively. To address an optimal control problem with the above NLP formulation, it is necessary to transform the original infinite-dimensional optimization problem into a finite-dimensional one by using a direct transcription method. In general, transcription methods are categorized into shooting methods and collocation methods. A widely used method is the direct single-shooting method, where only the control is parameterized. The reader is referred to [2] for a detailed description of transcription methods. The NLP problem can be treated by well-known algorithms, e.g., the sequential quadratic programming (SQP) approach or the interior point (IP) method [33]. An optimal point $\mathbf{z}^{*}$ fulfills the Karush–Kuhn–Tucker (KKT) conditions [18, 19], which are necessary first-order optimality conditions for direct optimization methods.

In this paper, the constraints $\hat{\mathbf{g}}=\hat{\mathbf{g}}(\mathbf{x},\boldsymbol{\xi})$ and $\hat{\mathbf{h}}=\hat{\mathbf{h}}(\mathbf{x},\boldsymbol{\xi})$ depend on system parameters $\boldsymbol{\xi} \in \mathbb{R}^{l}$ and on state variables $\mathbf{x} \in \mathbb{R}^{n}$ due to a time-dependent control $\mathbf{u} \in \mathbb{R}^{m}$ of a mechanical system. Thus, evaluating the (in)equality constraints requires the evolution of the system response. The dynamics of mechanical systems can be described with ordinary differential equations (ODE)

$$ \dot{\mathbf{x}} = \mathbf{f}(\mathbf{x},\mathbf{u},\boldsymbol{\xi}), \quad \mathbf{x}(0) = \mathbf{x}_{0}.$$

(5)

For the numerical computation of the state variables, the ODE can be formulated by a temporal discretization as

$$\begin{aligned} \mathbf{x}_{i+1} = \tilde{\mathbf{f}}(\mathbf{x}_{i},\mathbf{x}_{i+1}, \mathbf{u}_{i},\mathbf{u}_{i+1},\boldsymbol{\xi}), \quad i\in \{0, \ldots ,N-1\}, \end{aligned}$$

(6)

with the given initial state $\mathbf{x}_{0}$. The evolution of the state variables $\mathbf{x}_{1},\, \ldots ,\,\mathbf{x}_{N}$ is influenced by the time integrator used, the control variables $\mathbf{u}_{0},\, \ldots ,\,\mathbf{u}_{N}$, and the set of parameters $\boldsymbol{\xi}$. The discrete ODE (6) represents a general form for an explicit or implicit one-step time integrator, such as a Runge–Kutta scheme [5]. The time domain $t \in [t_{0},\,t_{\mathrm{f}}]$ is discretized with $N$ uniform intervals leading to a constant time-integration step size $\Delta t$; see Fig. 1(a). Consequently, the micro (integration) time mesh is defined by $t_{i} = \Delta t\,i$, $i \in \{0,\,\ldots ,\,N\}$, with $t_{0}=0$ and $t_{N}=t_{\mathrm{f}} = \Delta t \, N$.

Fig. 1

Time domain and index scale: $(a)$ is the time domain for time integration, $(b)$ is the $i$-index scale for time integration, and $(c)$ is the $j$-index scale for the evaluation of constraints

This paper considers equality constraints at the final time $t_{\mathrm{f}}$, while inequality constraints must be satisfied on a macro (inequality) time mesh; see Fig. 1(c) for the according index scale of the macro time mesh. The macro time mesh $\hat{t}_{j} = \Delta T \, j$, $j \in \{0,\,\ldots ,\,M\}$ is defined by $M$ time intervals between inequality constraints leading to the inequality step size $\Delta T = t_{\mathrm{f}} / M$. The circumflex $\hat{(\cdot )}$ denotes the evaluation of a variable $(\cdot )$ regarding the macro time mesh. The number of chosen time-integration points $e\, \in \mathbb{N}$ divides the inequality step size $\Delta T$ into the integration step size $\Delta t$ by defining the time-integration step size $\Delta t = \Delta T / e$. For the case $M=N$, one defines inequality constraints at the micro time mesh in each time integration. Figure 1 illustrates the time domain, including the time-integration steps and the arrangement of (in)equality constraints. For example, an equality constraint can be a particular configuration of a mechanical system at the final time $t_{\mathrm{f}}$. In contrast, an inequality constraint ensures that the acceleration is within a defined limit at the macro time mesh $\hat{t}$.

For the sake of convenience, the constraints $\hat{\mathbf{g}}$ and $\hat{\mathbf{h}}$ are concatenated into a general set of nonlinear constraints by $\mathbf{c}^{\mathsf{T}} = \bigl(\hat{\mathbf{g}}^{\mathsf{T}},\, \hat{\mathbf{h}}^{\mathsf{T}} \bigl) \in \mathbb{R}^{p+q}$. The equality constraints $\hat{\mathbf{g}} = \mathbf{g}_{N}$ represent an evaluation of $p$ implicit time-dependent functions $\mathbf{g} = \mathbf{g}(\mathbf{x}(t),\boldsymbol{\xi}) \in \mathbb{R}^{p}$ at the final time $t_{\mathrm{f}}$, while the inequality constraints $\hat{\mathbf{h}}$ are a concatenation of $r$ functions $\mathbf{h} = \mathbf{h}(\mathbf{x}(t),\boldsymbol{\xi}) \in \mathbb{R}^{r}$ evaluated at the macro time mesh. The size of the concatenated inequality constraints is $q=r(M+1)$; see the $j$-index scale for inequality constraints in Fig. 1. However, inequality constraints have to be defined in the $i$-index scale to be in accordance with a time integration of the ODE at the micro time mesh, i.e., inequality constraints are defined in the $i$-index scale with $i=ej$. The general set of constraints is formulated in the $i$-index scale by

$$ \mathbf{c} = \mathbf{B}_{1} \mathbf{g}_{N} + \sum _{j=0}^{M} \mathbf{B}_{2,j} \mathbf{h}_{e j}. $$

(7)

Boolean matrices $\mathbf{B}$ map the (in)equality constraints into the combined set of constraints, i.e.,

$$ \mathbf{c}^{\mathsf{T}} = ( \underbrace{g_{1,N},\, \ldots , \,g_{p,N}}_{\hat{\mathbf{g}}^{ \mathsf{T}}},\, \underbrace{h_{1,0},\, \ldots , \,h_{r,0},\, \ldots ,\, h_{1,N},\, \ldots , \,h_{r,N}}_{ \hat{\mathbf{h}}^{\mathsf{T}}} ), $$

(8)

in which the first subscript denotes the row and the second subscript denotes the corresponding time in the $i$-index scale of $\mathbf{g}$ and $\mathbf{h}$, respectively.

The constraint formulation in (7) allows a straightforward derivation of discrete adjoint gradients for sensitivity analysis and gradient-based optimizations. In gradient-based optimization algorithms, first-order gradients are crucial to compute a local minimum of an optimization problem. The accuracy of the gradient computation influences the convergence and robustness of optimization algorithms. In addition, the computational effort to solve an optimization problem depends on the runtime required to compute gradients. This paper addresses accurate and efficient first-order sensitivity analysis with particular emphasis on gradients of the constraint formulation in (7). One approach that meets both requirements is the adjoint method [26, 29]. This paper employs a discrete version of the adjoint method to derive first-order gradients of constraints. The proposed discrete adjoint approach replaces the finite-difference approach, usually the default of optimization toolboxes.

3 Sensitivity analysis

This section proposes a novel discrete adjoint approach to sensitivity analysis with emphasis on gradients of the constraint formulation in (7). The sensitivities are computed for a discrete set of optimization variables $\mathbf{z}$, i.e., the sensitivity analysis is defined by $\mathrm{d} \mathbf{c} / \mathrm{d} \mathbf{z}$. The adjoint method is an efficient method to compute gradients since the computational effort to compute the so-called adjoint variables does not depend on the number of optimization variables [6, 11, 31]. The discrete adjoint method constructs a finite-difference scheme for the adjoint variables directly from the time-integration method to solve the governing equations [21]. In this paper, the computation of the discrete adjoint gradients is formulated for governing equations in the form of (6). However, the discrete adjoint gradient computation can be easily adapted to deal with different one-step time integrators, as shown for an explicit and an implicit Euler method.

3.1 Discrete adjoint method for one-step time integrators

The goal of the adjoint gradient method is to avoid the expensive computation of state sensitivities $\mathrm{d} \mathbf{x} / \mathrm{d} \mathbf{z}$ by introducing adjoint variables. Following the fundamental work by Bryson and Ho [4], the constraint (7) is extended by the discrete state equations (6) leading to

$$\begin{aligned} \bar{\mathbf{c}} = \mathbf{B}_{1} \mathbf{g}_{N} + \sum _{j=0}^{M} \mathbf{B}_{2,j} \mathbf{h}_{e j} + \sum _{j=0}^{M-1}\left [\sum _{i=e j}^{e\left (j+1\right )-1}\mathbf{R}_{i+1} \left (\mathbf{x}_{i+1} - \tilde{\mathbf{f}}_{i,i+1}\right ) \right ], \end{aligned}$$

(9)

for any choice of the adjoint variables $\mathbf{R}_{1},\,\ldots ,\mathbf{R}_{N} \in \mathbb{R}^{(p+q) \times n}$ in the case where the discrete state equations are satisfied. For the sake of easier reading, the temporal discretized right-hand side of the ODE is defined by $\tilde{\mathbf{f}}_{i,i+1} :=\tilde{\mathbf{f}}(\mathbf{x}_{i}, \mathbf{x}_{i+1},\mathbf{u}_{i},\mathbf{u}_{i+1},\boldsymbol{\xi})$, $i\in \{0,\ldots ,N-1\}$. The constraint (9) is extended by introducing a double sum to account for the system dynamics. The inner sum considers the time intervals between two inequality constraints $]\hat{t}_{j},\,\hat{t}_{j+1}[$, $j \in \{0,\,\ldots ,\,M-1\}$ and the outer sum considers exactly the time instances $\hat{t}_{j}$, $j \in \{0,\,\ldots ,\,M\}$ at which inequality constraints must be satisfied; see scales in Fig. 1. However, the additional zero terms do not influence the constraints $\mathbf{c}$ in the case where the state equations are satisfied and, therefore, the gradients of $\mathbf{c}$ are equal to the gradients of $\bar{\mathbf{c}}$. The following derivation of discrete adjoint gradients is based on the extended constraints $\bar{\mathbf{c}}$.

Before deriving the gradients of $\bar{\mathbf{c}}$ by a discrete adjoint approach, the boundaries of the state variables $\mathbf{x}_{N}$ and (in)equality constraints $\mathbf{g}_{N}$ and $\mathbf{h}_{N}$, respectively, must be extracted from (9) to derive terminal conditions for the differential equations of the adjoint variables. Performing an index shift of the inner $i$-sum in (9) results in an extraction of the boundaries

$$ \begin{aligned}\bar{\mathbf{c}} =\,& \mathbf{B}_{1} \mathbf{g}_{N} + \mathbf{B}_{2,M} \mathbf{h}_{N} + \sum _{j=0}^{M-1}\left [\sum _{i=e j + 1}^{e \left (j+1 \right ) - 1} \mathbf{R}_{i} \left (\mathbf{x}_{i} - \tilde{\mathbf{f}}_{i-1,i}\right ) \right . \\&\left . + \mathbf{R}_{e j} \mathbf{x}_{e j} - \mathbf{R}_{e \left (j+1 \right )} \tilde{\mathbf{f}}_{e \left (j+1\right )-1,e \left (j+1 \right )} \vphantom{\sum _{i=e j + 1}^{e \left (j+1\right ) - 1}} + \mathbf{B}_{2,j} \mathbf{h}_{e j} \right ] - \mathbf{R}_{0} \mathbf{x}_{0} + \mathbf{R}_{N} \mathbf{x}_{N}. \end{aligned}$$

(10)

Note that (9) and (10) are equal despite different formulations. Moreover, note that the subscripts $ej$ and $e(j+1)$ in (10) are a result of the performed index shift, and the related terms are evaluated in the $j$-sum at the macro time mesh; see Fig. 1.

The derivation of discrete adjoint gradients is based on the calculus of variations. The first-order variation of (10) in terms of $\delta \mathbf{x}_{i}$, $\delta \mathbf{x}_{i-1}$, $\delta \mathbf{u}_{i}$, $\delta \mathbf{u}_{i-1}$, and $\delta \boldsymbol{\xi}$ is given by

$$ \begin{aligned}\delta \bar{\mathbf{c}} = & \mathbf{B}_{1} \left ( \frac{\partial \mathbf{g}_{N}}{\partial \mathbf{x}_{N}}\delta \mathbf{x}_{N} + \frac{\partial \mathbf{g}_{N}}{\partial \boldsymbol{\xi}}\delta \boldsymbol{\xi} \right ) + \mathbf{B}_{2,M} \left ( \frac{\partial \mathbf{h}_{N}}{\partial \mathbf{x}_{N}}\delta \mathbf{x}_{N} + \frac{\partial \mathbf{h}_{N}}{\partial \boldsymbol{\xi}}\delta \boldsymbol{\xi}\right ) \\& + \sum _{j=0}^{M-1}\left [\sum _{i=e j + 1}^{e \left (j+1\right ) - 1} \mathbf{R}_{i} \left (\delta \mathbf{x}_{i} - \frac{\partial \tilde{\mathbf{f}}_{i-1,i}}{\partial \mathbf{x}_{i-1}} \delta \mathbf{x}_{i-1} - \frac{\partial \tilde{\mathbf{f}}_{i-1,i}}{\partial \mathbf{u}_{i-1}} \delta \mathbf{u}_{i-1} - \frac{\partial \tilde{\mathbf{f}}_{i-1,i}}{\partial \mathbf{x}_{i}} \delta \mathbf{x}_{i} \right .\right . \\& \left . \left .\left . - \frac{\partial \tilde{\mathbf{f}}_{i-1,i}}{\partial \mathbf{u}_{i}} \delta \mathbf{u}_{i} - \frac{\partial \tilde{\mathbf{f}}_{i-1,i}}{\partial \boldsymbol{\xi}} \delta \boldsymbol{\xi} \right ) + \mathbf{R}_{e j} \delta \mathbf{x}_{e j} + \mathbf{B}_{2,j} \left ( \frac{\partial \mathbf{h}_{e j}}{\partial \mathbf{x}_{e j}}\delta \mathbf{x}_{e j} + \frac{\partial \mathbf{h}_{e j}}{\partial \boldsymbol{\xi}}\delta \boldsymbol{\xi} \right ) \vphantom{\sum _{i=e j + 1}^{e \left (j+1\right ) - 1}} \right . \right . \\& \left .- \mathbf{R}_{e \left (j+1\right )} \left ( \frac{\partial \tilde{\mathbf{f}}_{e \left (j+1\right )-1,e \left (j+1\right )}}{\partial \mathbf{x}_{e \left (j+1\right )-1}} \delta \mathbf{x}_{e \left (j+1\right )-1} + \frac{\partial \tilde{\mathbf{f}}_{e \left (j+1\right )-1,e \left (j+1\right )}}{\partial \mathbf{u}_{e \left (j+1\right )-1}} \delta \mathbf{u}_{e \left (j+1\right )-1} \right .\right . \\ & \left .\left . + \frac{\partial \tilde{\mathbf{f}}_{e \left (j+1\right )-1,e \left (j+1\right )}}{\partial \mathbf{x}_{e \left (j+1\right )}} \delta \mathbf{x}_{e \left (j+1\right )} + \frac{\partial \tilde{\mathbf{f}}_{e \left (j+1\right )-1,e \left (j+1\right )}}{\partial \mathbf{u}_{e \left (j+1\right )}} \delta \mathbf{u}_{e \left (j+1\right )} \right .\right . \\ & \left .\left . + \frac{\partial \tilde{\mathbf{f}}_{e \left (j+1\right )-1,e \left (j+1\right )}}{\partial \boldsymbol{\xi}} \delta \boldsymbol{\xi}\right ) \right ] - \mathbf{R}_{0} \delta \mathbf{x}_{0} + \mathbf{R}_{N} \delta \mathbf{x}_{N}. \end{aligned}$$

(11)

In this paper, the focus lies on a combined sensitivity analysis with respect to the system parameters $\boldsymbol{\xi}$ and a discrete set of control grid nodes $\bar{\mathbf{u}}$. Following Lichtenecker et al. [22], the continuous control function is formulated with $\mathbf{u} = \mathbf{C}\mathbf{\bar{u}}$, where $\mathbf{C}$ is a time-dependent interpolation function. The variables of interest in the sensitivity analysis are combined in the vector $\mathbf{z}^{\mathsf{T}} = \left (\boldsymbol{\xi}^{\mathsf{T}}, \, \bar{\mathbf{u}}^{\mathsf{T}} \right )$ and can be used as optimization variables in gradient-based optimization problems. Note that the optimization variables $\mathbf{z}$ can consist of system parameters, e.g., the stiffness of a spring of a mechanical system and/or a parameterization of the control.

To derive a variation of the constraints with respect to the optimization variables $\mathbf{z}$, the variations $\delta \boldsymbol{\xi}$ and $\delta \mathbf{u}$ in (11) can be obtained in terms of $\delta \mathbf{z}$ with

$$\begin{aligned} \delta \boldsymbol{\xi} =& \mathbf{B}_{3} \delta \mathbf{z}, \end{aligned}$$

(12)

$$\begin{aligned} \delta \mathbf{u} =& \mathbf{C}\delta \bar{\mathbf{u}} = \mathbf{C} \mathbf{B}_{4}\delta \mathbf{z}, \end{aligned}$$

(13)

respectively. The Boolean matrices $\mathbf{B}$ map the combined set of optimization variables to system parameters and control grid nodes. Substituting (12) and (13) into (11) and reformulating leads to

$$ \begin{aligned}\delta \bar{\mathbf{c}} = & \sum _{j=0}^{M-1}\left [\sum _{i=e j + 1}^{e \left (j+1\right ) - 1} \left [\left ( \mathbf{R}_{i} - \mathbf{R}_{i} \frac{\partial \tilde{\mathbf{f}}_{i-1,i}}{\partial \mathbf{x}_{i}} - \mathbf{R}_{i+1} \frac{\partial \tilde{\mathbf{f}}_{i,i+1}}{\partial \mathbf{x}_{i}} \right )\delta \mathbf{x}_{i} \right .\right . \\&\left . \left . - \mathbf{R}_{i}\left ( \frac{\partial \tilde{\mathbf{f}}_{i-1,i}}{\partial \mathbf{u}_{i-1}} \mathbf{C}_{i-1}\mathbf{B}_{4} + \frac{\partial \tilde{\mathbf{f}}_{i-1,i}}{\partial \mathbf{u}_{i}} \mathbf{C}_{i}\mathbf{B}_{4} + \frac{\partial \tilde{\mathbf{f}}_{i-1,i}}{\partial \boldsymbol{\xi}} \mathbf{B}_{3} \right )\delta \mathbf{z} \right ] \right . \\&\left . + \left ( \mathbf{R}_{e j} + \mathbf{B}_{2,j} \frac{\partial \mathbf{h}_{e j}}{\partial \mathbf{x}_{e j}} - \mathbf{R}_{e j + 1} \frac{\partial \tilde{\mathbf{f}}_{e j,e j + 1}}{\partial \mathbf{x}_{e j}} \right ) \delta \mathbf{x}_{e j} \right . \\&\left . - \mathbf{R}_{e \left (j+1\right )}\left ( \frac{\partial \tilde{\mathbf{f}}_{e \left (j+1\right )-1, e \left (j+1\right )}}{\partial \mathbf{u}_{e \left (j+1\right )-1}} \mathbf{C}_{e \left (j+1\right )-1}\mathbf{B}_{4} + \frac{\partial \tilde{\mathbf{f}}_{e \left (j+1\right )-1, e \left (j+1\right )}}{\partial \mathbf{u}_{e \left (j+1\right )}} \mathbf{C}_{e \left (j+1\right )}\mathbf{B}_{4} \right .\right . \\&\left .\left .+ \frac{\partial \tilde{\mathbf{f}}_{e \left (j+1\right )-1, e \left (j+1\right )}}{\partial \boldsymbol{\xi}} \mathbf{B}_{3} \right )\delta \mathbf{z} + \mathbf{B}_{2,j} \frac{\partial \mathbf{h}_{e j}}{\partial \boldsymbol{\xi}} \mathbf{B}_{3} \delta \mathbf{z} \vphantom{\sum _{i=e j + 1}^{e \left (j+1\right ) - 1}} \right ] \\& + \left ( \mathbf{B}_{1} \frac{\partial \mathbf{g}_{N}}{\partial \boldsymbol{\xi}} + \mathbf{B}_{2,M} \frac{\partial \mathbf{h}_{N}}{\partial \boldsymbol{\xi}} \right ) \mathbf{B}_{3} \delta \mathbf{z} + \left (\mathbf{B}_{1} \frac{\partial \mathbf{g}_{N}}{\partial \mathbf{x}_{N}} + \mathbf{B}_{2,M} \frac{\partial \mathbf{h}_{N}}{\partial \mathbf{x}_{N}} + \mathbf{R}_{N} \right ) \delta \mathbf{x}_{N}. \end{aligned}$$

(14)

Equation (14) implies the relation between $\delta \mathbf{x}$ and $\delta \mathbf{z}$. The optimization variables $\mathbf{z}$ influence the state variables $\mathbf{x}$ and, therefore, the variation of state variables should be interpreted as [6, 23]

$$\begin{aligned} \delta \mathbf{x} = \frac{\mathrm{d} \mathbf{x}}{\mathrm{d} \mathbf{z}} \delta \mathbf{z}. \end{aligned}$$

(15)

The total derivatives of state variables with respect to optimization variables are obtained by solving the matrix differential equations

$$\begin{aligned} \frac{\mathrm{d} \dot{\mathbf{x}}}{\mathrm{d} \mathbf{z}} = \frac{\partial \mathbf{f}}{\partial \mathbf{x}} \frac{\mathrm{d} \mathbf{x}}{\mathrm{d} \mathbf{z}} + \frac{\partial \mathbf{f}}{\partial \mathbf{u}} \frac{\partial \mathbf{u}}{\partial \mathbf{z}} + \frac{\partial \mathbf{f}}{\partial \boldsymbol{\xi}} \frac{\partial \boldsymbol{\xi}}{\partial \mathbf{z}}. \end{aligned}$$

(16)

This system is defined by taking the total derivative of (5) with respect to the optimization variables and, therefore, the dimension of the system depends on the number of optimization variables. The solution of the matrix differential equations is obtained by applying a temporal discretization, where the computational effort to solve (16) can become expensive in the case of a large number of optimization variables. Using the state sensitivities (16) with (15) in (14), first-order gradients of the constraint formulation in (7) can be obtained without the need for the adjoint variables. This approach is called direct differentiation. However, the goal of the proposed discrete adjoint gradient approach is to avoid the direct computation of the state sensitivities $\mathrm{d} \mathbf{x} / \mathrm{d} \mathbf{z}$. To this end, the discrete adjoint variables in (14) are defined such that the brackets multiplied with $\delta \mathbf{x}$ are zero. Hence, the discrete adjoint variables are obtained by the matrix differential equations

$$\begin{aligned} \mathbf{R}_{N} =& -\mathbf{B}_{1} \frac{\partial \mathbf{g}_{N}}{\partial \mathbf{x}_{N}} - \mathbf{B}_{2,M} \frac{\partial \mathbf{h}_{N}}{\partial \mathbf{x}_{N}} , \end{aligned}$$

(17)

$$\begin{aligned} \mathbf{R}_{i} =& ~\mathbf{R}_{i+1} \frac{\partial \tilde{\mathbf{f}}_{i,i+1}}{\partial \mathbf{x}_{i}} + \mathbf{R}_{i} \frac{\partial \tilde{\mathbf{f}}_{i-1,i}}{\partial \mathbf{x}_{i}}, \quad \forall i\in \{ej+1,\,\ldots ,\,e \left (j+1\right ) - 1\}, \end{aligned}$$

(18)

$$\begin{aligned} \mathbf{R}_{e j} =& - \mathbf{B}_{2,j} \frac{\partial \mathbf{h}_{e j}}{\partial \mathbf{x}_{e j}} + \mathbf{R}_{e j + 1} \frac{\partial \tilde{\mathbf{f}}_{e j, e j + 1}}{\partial \mathbf{x}_{e j}}, \quad \forall j\in \{1,\,\ldots ,\,M-1\}. \end{aligned}$$

(19)

Equation (17) imposes the terminal condition of the adjoint variables at the final time $t_{N}$. The computation of the adjoint variables is performed in a backward manner starting from $\mathbf{R}_{N}$ and proceeding with the adjoint system (18). It has to be emphasized that (18) is defined within the macro time mesh $]\hat{t}_{j},\,\hat{t}_{j+1}[$, $j \in \{0,\,\ldots ,\,M-1\}$. The discrete adjoint variables at the macro time mesh $\hat{t}_{j}$, $j \in \{1,\,\ldots ,\,M-1\}$ are determined by the intermediate condition in (19). The adjoint system and the intermediate condition are applied alternately in the backward integration to solve the discrete adjoint variables.

Once the discrete adjoint variables are computed by (17)–(19), the terms related to $\delta \mathbf{x}$ vanish in (14) and, therefore, the variation of the extended constraints simplifies to

$$\begin{aligned} \delta \bar{\mathbf{c}} = \underbrace{\left \{\ldots \right \}}_{ \frac{\mathrm{d} \bar{\mathbf{c}}}{\mathrm{d} \mathbf{z}}} \delta \mathbf{z}, \end{aligned}$$

(20)

where the variation $\delta \mathbf{z}$ is factored out. The simplified variation leads to first-order gradients of constraints with respect to optimization variables given by

$$ \begin{aligned}\frac{\mathrm{d} \bar{\mathbf{c}}}{\mathrm{d} \mathbf{z}} = & \sum _{j=0}^{M-1} \left [\sum _{i=e j + 1}^{e \left (j+1\right ) - 1} \mathbf{R}_{i} \left (- \frac{\partial \tilde{\mathbf{f}}_{i-1,i}}{\partial \mathbf{u}_{i-1}} \mathbf{C}_{i-1}\mathbf{B}_{4} - \frac{\partial \tilde{\mathbf{f}}_{i-1,i}}{\partial \mathbf{u}_{i}} \mathbf{C}_{i}\mathbf{B}_{4} - \frac{\partial \tilde{\mathbf{f}}_{i-1,i}}{\partial \boldsymbol{\xi}} \mathbf{B}_{3}\right ) \right . \\& \left . + \mathbf{B}_{2,j} \frac{\partial \mathbf{h}_{e j}}{\partial \boldsymbol{\xi}} \mathbf{B}_{3} - \mathbf{R}_{e \left (j+1\right )}\left ( \frac{\partial \tilde{\mathbf{f}}_{e \left (j+1\right )-1, e \left (j+1\right )}}{\partial \mathbf{u}_{e \left (j+1\right )-1}} \mathbf{C}_{e \left (j+1\right )-1}\mathbf{B}_{4} \right .\right . \\ & \left .\left . + \frac{\partial \tilde{\mathbf{f}}_{e \left (j+1\right )-1, e \left (j+1\right )}}{\partial \mathbf{u}_{e \left (j+1\right )}} \mathbf{C}_{e \left (j+1\right )}\mathbf{B}_{4} + \frac{\partial \tilde{\mathbf{f}}_{e \left (j+1\right )-1, e \left (j+1\right )}}{\partial \boldsymbol{\xi}} \mathbf{B}_{3} \right )\right ] \\ & + \left ( \mathbf{B}_{1} \frac{\partial \mathbf{g}_{N}}{\partial \boldsymbol{\xi}} + \mathbf{B}_{2,M} \frac{\partial \mathbf{h}_{N}}{\partial \boldsymbol{\xi}} \right ) \mathbf{B}_{3}. \end{aligned}$$

(21)

The discrete adjoint gradient computation for the constraint formulation in (7) is obtained by (21). Note that the computation of discrete adjoint gradients is based on the solution of the adjoint system, whose size does not depend on the number of optimization variables. The gradient computation using direct differentiation requires the solution of (16), which depends on the number of optimization variables. Therefore, the adjoint-based sensitivity analysis is computationally efficient, especially when dealing with optimization problems with a large number of optimization variables.

Employing the discrete adjoint gradient (21), e.g., within an optimization procedure, requires the specific formulation of the right-hand side vector $\tilde{\mathbf{f}}$. The chosen time integrator to solve the forward dynamics implies the backward integration of the discrete adjoint variables. Moreover, sensitivities of the forward time integrator are recognized in the computation of the discrete adjoint variables. To use the proposed discrete gradient approach, the sensitivities of the chosen forward time integrator need to be defined.

3.2 Application to the explicit Euler method

The explicit Euler method is an iterative solution scheme to approximate the state variables of the ODE in (5) by

$$\begin{aligned} \mathbf{x}_{i+1} = \underbrace{\mathbf{x}_{i} + \Delta t\,\mathbf{f}(\mathbf{x}_{i},\mathbf{u}_{i},\boldsymbol{\xi})}_{ \tilde{\mathbf{f}}(\mathbf{x}_{i},\mathbf{u}_{i},\boldsymbol{\xi})}. \end{aligned}$$

(22)

Using the above time-integration scheme in the discrete adjoint sensitivity analysis, the explicit right-hand side vector $\tilde{\mathbf{f}}$ has to be defined in the general form $\tilde{\mathbf{f}}_{i,i+1} :=\tilde{\mathbf{f}}(\mathbf{x}_{i}, \mathbf{u}_{i},\boldsymbol{\xi})$. The computation of the discrete adjoint variables requires the derivatives of $\tilde{\mathbf{f}}$ with respect to the state variables $\mathbf{x}$ given by

$$\begin{aligned} \frac{\partial \tilde{\mathbf{f}}_{i,i+1}}{\partial \mathbf{x}_{i}} = \mathbf{I} + \Delta t\, \frac{\partial \mathbf{f}_{i}}{\partial \mathbf{x}_{i}} \quad \text{and} \quad \frac{\partial \tilde{\mathbf{f}}_{i-1,i}}{\partial \mathbf{x}_{i}} = \mathbf{0}, \end{aligned}$$

(23)

where $\mathbf{f}_{i} = \mathbf{f}(\mathbf{x}_{i},\mathbf{u}_{i}, \boldsymbol{\xi})$ and $\mathbf{I}$ denotes the identity matrix. In addition, the discrete adjoint gradient computation requires the derivatives of $\tilde{\mathbf{f}}$ with respect to $\mathbf{u}$ and $\boldsymbol{\xi}$ given by

$$\begin{aligned} \frac{\partial \tilde{\mathbf{f}}_{i-1,i}}{\partial \mathbf{u}_{i}} = \mathbf{0} ,\quad \frac{\partial \tilde{\mathbf{f}}_{i-1,i}}{\partial \mathbf{u}_{i-1}} = \Delta t\,\frac{\partial \mathbf{f}_{i-1}}{\partial \mathbf{u}_{i-1}} \quad \text{and} \quad \frac{\partial \tilde{\mathbf{f}}_{i-1,i}}{\partial \boldsymbol{\xi}} = \Delta t\,\frac{\partial \mathbf{f}_{i-1}}{\partial \boldsymbol{\xi}}, \end{aligned}$$

(24)

respectively.

3.3 Application to the implicit Euler method

Similar to the explicit Euler method, the implicit Euler method is an iterative solution scheme to approximate the state variables of the ODE in (5) by

$$\begin{aligned} \mathbf{x}_{i+1} = \underbrace{ \mathbf{x}_{i} + \Delta t\,\mathbf{f}(\mathbf{x}_{i+1},\mathbf{u}_{i+1},\boldsymbol{\xi})}_{ \tilde{\mathbf{f}}(\mathbf{x}_{i},\mathbf{x}_{i+1},\mathbf{u}_{i+1}, \boldsymbol{\xi})}. \end{aligned}$$

(25)

Using the above time-integration scheme in the discrete adjoint sensitivity analysis, the implicit right-hand side vector $\tilde{\mathbf{f}}$ has to be defined in the general form $\tilde{\mathbf{f}}_{i,i+1} :=\tilde{\mathbf{f}}(\mathbf{x}_{i}, \mathbf{x}_{i+1},\mathbf{u}_{i+1},\boldsymbol{\xi})$. The computation of the discrete adjoint variables requires the derivatives of $\tilde{\mathbf{f}}$ with respect to the state variables $\mathbf{x}$ given by

$$\begin{aligned} \frac{\partial \tilde{\mathbf{f}}_{i,i+1}}{\partial \mathbf{x}_{i}} = \mathbf{I} \quad \text{and} \quad \frac{\partial \tilde{\mathbf{f}}_{i-1,i}}{\partial \mathbf{x}_{i}} = \Delta t\,\frac{\partial \mathbf{f}_{i}}{\partial \mathbf{x}_{i}}. \end{aligned}$$

(26)

In addition, the discrete adjoint gradient computation requires the derivatives of $\tilde{\mathbf{f}}$ with respect to $\mathbf{u}$ and $\boldsymbol{\xi}$ given by

$$\begin{aligned} \frac{\partial \tilde{\mathbf{f}}_{i-1,i}}{\partial \mathbf{u}_{i}} = \Delta t \, \frac{\partial \mathbf{f}_{i}}{\partial \mathbf{u}_{i}},\quad \frac{\partial \tilde{\mathbf{f}}_{i-1,i}}{\partial \mathbf{u}_{i-1}} = \mathbf{0} \quad \text{and} \quad \frac{\partial \tilde{\mathbf{f}}_{i-1,i}}{\partial \boldsymbol{\xi}} = \Delta t \, \frac{\partial \mathbf{f}_{i}}{\partial \boldsymbol{\xi}}, \end{aligned}$$

(27)

respectively.

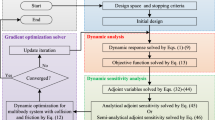
3.4 Procedure for the use of the discrete adjoint gradients

This section summarizes the sensitivity analysis using the proposed discrete adjoint gradient approach within an optimization problem. The focus is to compute first-order gradients of the constraint formulation in (7) with respect to optimization variables, i.e.,

$$\begin{aligned} \frac{\mathrm{d} \mathbf{c}}{\mathrm{d} \mathbf{z}}\Big|_{\mathbf{z}= \mathbf{z}^{(k)}}, \end{aligned}$$

evaluated at the $(k)$th iteration in a gradient-based optimization. The use of the proposed discrete adjoint gradient approach can be summarized by the following steps:

• 1. Set up an optimization problem in the form of (1)–(4) and select an NLP software package to solve the optimization problem, e.g., IPOPT [45].

• 2. Compute the derivatives by symbolic differentiation for the discrete adjoint approach:

  • a) Compute the derivatives of (in)equality constraints $\mathbf{g}$ and $\mathbf{h}$ with respect to $\mathbf{x}$ and $\boldsymbol{\xi}$, respectively, by symbolic differentiation.

  • b) Select a numerical time-integration solver and compute the derivatives of $\mathbf{f}$ with respect to $\mathbf{x}$, $\mathbf{u}$, and $\boldsymbol{\xi}$ by symbolic differentiation. Additionally, define the derivatives of the solver-specific right-hand side vector $\tilde{\mathbf{f}}$, e.g., as shown in Sect. 3.2 and Sect. 3.3 for the explicit and the implicit Euler method, respectively.

• 3. Compute the first-order gradients of the constraints using the discrete adjoint approach:

  • a) Compute the state variables $\mathbf{x}$ influenced by the set of optimization variables $\mathbf{z}^{(k)}$ with the chosen time-integration scheme.

  • b) Compute the discrete adjoint variables by solving the matrix differential equations (17)–(19) backward in time.

  • c) Compute the sensitivities of the constraint formulation in (7) using the discrete adjoint gradient approach (21).

• 4. Provide the cost function, constraints, and the respective first-order gradients via an interface to the chosen NLP software package. The Hessian of the cost function and the constraints are usually computed internally by the software package.

• 5. Repeat Steps 3 and 4 until the KKT conditions are satisfied and an optimal solution $\mathbf{z}^{*}$ is found.

As aforementioned in the second step, derivatives with respect to $\mathbf{x}$, $\mathbf{u}$, and $\boldsymbol{\xi}$ are computed by symbolic differentiation. Considering a complicated mechanical system with many state variables, the governing equations become extensive and difficult to solve. For such systems, the effort to derive system derivatives by symbolic differentiation is enormous or not feasible in a reasonable time. The following section discusses the symbolic differentiation when a mechanical system is formulated with flexible bodies.

4 Flexible multibody formulation

The governing equations of multibody systems with rigid and flexible bodies are described by the second-order differential equations

$$ \mathbf{M}(\mathbf{q},\boldsymbol{\xi}) \ddot{\mathbf{q}} = \mathbf{Q}(\mathbf{q},\dot{\mathbf{q}},\mathbf{u},\boldsymbol{\xi}), $$

(28)

where $\mathbf{M}$ is the mass matrix, $\mathbf{q}$ denotes the generalized coordinates and $\mathbf{Q}$ is the generalized force vector. In this paper, the generalized force vector

$$\mathbf{Q} = \mathbf{Q}_{\mathrm{u}} + \mathbf{Q}_{\mathrm{d}} + \mathbf{Q}_{\mathrm{g}} - \mathbf{Q}_{\mathrm{k}} $$

(29)

consists of the term associated with the control $\mathbf{Q}_{\mathrm{u}}$, the viscous damping for joint friction $\mathbf{Q}_{\mathrm{d}}$, the gravity $\mathbf{Q}_{\mathrm{g}}$, and the elasticity $\mathbf{Q}_{\mathrm{k}}$. The second-order differential equations are transformed into

$$ \dot{\mathbf{x}}= \mathbf{f} = \underbrace{ \begin{pmatrix}\mathbf{I} & \mathbf{0} \\\mathbf{0} & \mathbf{M}^{-1}\end{pmatrix}}_{\boldsymbol{\mathcal{M}^{-1}}} \begin{pmatrix}\mathbf{v} \\\mathbf{Q}\end{pmatrix},$$

(30)

wherein the state variables are expressed by $\mathbf{x}^{\mathsf{T}}=\left (\mathbf{q}^{\mathsf{T}},\, \mathbf{v}^{ \mathsf{T}}\right ) \in \mathbb{R}^{n}$ with the generalized velocities $\dot{\mathbf{q}}=\mathbf{v}$. In this paper, effects due to the elasticity of flexible bodies are considered by a nonlinear finite-element-based formulation using the ANCF as proposed by Omar and Shabana [34]. This standard ANCF element has been tested extensively in the literature and employed in structural-optimization problems, e.g., [15, 41]. The ANCF was developed to solve large-deformation problems in multibody dynamics [40]. Since the ANCF does not use rotational degrees of freedom, the formulation does not necessarily suffer from singularities arising from angular parameterizations. An essential advantage of the ANCF is that the mass matrix is constant with respect to the generalized coordinates, i.e., $\mathbf{M} = \mathbf{M}(\boldsymbol{\xi})$. For a detailed description of the flexible multibody formulation, the reader is referred to [34].

Employing the proposed discrete adjoint approach to study constraint sensitivities requires first-order derivatives of the governing equations with respect to the states, the control, and the set of parameters; see the procedure provided in Sect. 3.4. In this paper, the system derivatives are computed by using symbolic differentiation for efficient computation in the sensitivity analysis.

Modeling a mechanical system with a large number of structural elements results in an extensive system of governing equations. Therefore, the effort to derive the system derivatives by symbolic differentiation is enormous or not feasible in a reasonable time. Instead of directly computing the derivatives of the governing equations in (30), one can derive the global system derivatives based on the symbolic differentiation of a single structural ANCF element. The element-based derivatives are then assembled to compute the global system derivatives. Therefore, the computation of symbolic differentiations is very efficient and independent of the number of structural elements. To this end, the global mass matrix is defined by the local mass matrix of an element with superscript $(e)$

$$\begin{aligned} \mathbf{M} =\sum _{(e)} \mathbf{T}_{1}^{(e)^{\mathsf{T}}}\mathbf{M}^{(e)} \mathbf{T}_{1}^{(e)}, \end{aligned}$$

(31)

where the element specific Boolean transformation matrix $\mathbf{T}_{1}^{(e)}$ maps a global variable to its local representation. Similarly, the global generalized force vector reads

$$\begin{aligned} \mathbf{Q} = \sum _{(e)} \mathbf{T}_{1}^{(e)^{\mathsf{T}}} \mathbf{Q}^{(e)}, \end{aligned}$$

(32)

and the local state variables are given by

$$\begin{aligned} \mathbf{x}^{(e)} = \begin{pmatrix}\mathbf{q}^{(e)} \\\mathbf{v}^{(e)}\end{pmatrix} =\begin{pmatrix}\mathbf{T}_{1}^{(e)} & \mathbf{0} \\\mathbf{0} & \mathbf{T}_{1}^{(e)}\end{pmatrix}\begin{pmatrix}\mathbf{q} \\\mathbf{v}\end{pmatrix} = \tilde{\mathbf{T}}_{1}^{(e)} \mathbf{x}. \end{aligned}$$

(33)

In addition, the local control and the local set of parameters are defined by

$$\begin{aligned} \mathbf{u}^{(e)} = \mathbf{T}_{2}^{(e)} \mathbf{u} \quad \text{and} \quad \boldsymbol{\xi}^{(e)} = \mathbf{T}_{3}^{(e)} \boldsymbol{\xi}, \end{aligned}$$

(34)

respectively, with Boolean transformation matrices. The element-based formulations in (31)–(34) are used in the proceeding section to derive global first-order derivatives based on local representations.

4.1 Element-based derivatives for an efficient implementation of the proposed approach

The computation of the discrete adjoint equations in (17)–(19) and the discrete adjoint gradient in (21) requires the system derivatives with respect to the state variables $\partial \mathbf{f} / \partial \mathbf{x}$, the control $\partial \mathbf{f} / \partial \mathbf{u}$, and the set of parameters $\partial \mathbf{f} / \partial \boldsymbol{\xi}$. As aforementioned, an essential advantage of the ANCF is that the mass matrix does not depend on the generalized coordinates, i.e., the derivatives with respect to the state variables vanish. The constant mass matrix leads to a simplification of the derivatives of the first-order state equations (30) with respect to the state variables by

$$\begin{aligned} \frac{\partial \mathbf{f}}{\partial \mathbf{x}} = \boldsymbol{\mathcal{M}}^{-1}\begin{pmatrix}\mathbf{0} & \mathbf{I} \\\frac{\partial \mathbf{Q}}{\partial \mathbf{q}} & \frac{\partial \mathbf{Q}}{\partial \mathbf{v}}\end{pmatrix}. \end{aligned}$$

(35)

To derive element-based derivatives, the derivatives of the global generalized force vector can be formulated with (32) as follows:

$$\begin{aligned} \frac{\partial \mathbf{Q}}{\partial \mathbf{x}} = \sum _{(e)} \mathbf{T}_{1}^{(e)^{\mathsf{T}}} \frac{\partial \mathbf{Q}^{(e)}}{\partial \mathbf{x}^{(e)}} \underbrace{\frac{\partial \mathbf{x}^{(e)}}{\partial \mathbf{x}}}_{ \tilde{\mathbf{T}}_{1}^{(e)}}. \end{aligned}$$

(36)

The symbolic differentiation of the global generalized force vector $\mathbf{Q}$ for all elements simplifies to the symbolic differentiation of the local generalized force vector $\mathbf{Q}^{(e)}$ for one element. The derivatives of the global generalized force vector are assembled by using the element-specific Boolean transformation matrices $\mathbf{T}_{1}^{(e)}$ and $\tilde{\mathbf{T}}_{1}^{(e)}$. Thus, the computational effort for symbolic differentiations is tremendously reduced and independent of the number of elements.

In addition, the derivatives of the first-order state equations (30) with respect to the control are given by

$$\begin{aligned} \frac{\partial \mathbf{f}}{\partial \mathbf{u}} = \boldsymbol{\mathcal{M}}^{-1} \begin{pmatrix}\mathbf{0} \\\frac{\partial \mathbf{Q}}{\partial \mathbf{u}}\end{pmatrix}, \end{aligned}$$

(37)

where the derivatives of the generalized force vector with respect to the control are formulated with

$$\begin{aligned} \frac{\partial \mathbf{Q}}{\partial \mathbf{u}} = \sum _{(e)} \mathbf{T}_{1}^{(e)^{\mathsf{T}}} \frac{\partial \mathbf{Q}^{(e)}}{\partial \mathbf{u}^{(e)}} \underbrace{\frac{\partial \mathbf{u}^{(e)}}{\partial \mathbf{u}}}_{ \mathbf{T}_{2}^{(e)}}. \end{aligned}$$

(38)

Finally, the derivatives of the first-order state equations (30) with respect to the set of parameters read

$$\begin{aligned} \frac{\partial \mathbf{f}}{\partial \boldsymbol{\xi}} =\begin{pmatrix}\mathbf{0} \\\frac{\partial \left (\mathbf{M}^{-1}\mathbf{Q}\right )}{\partial \boldsymbol{\xi}}\end{pmatrix} = \begin{pmatrix}\mathbf{0} \\\frac{\partial \mathbf{a}}{\partial \boldsymbol{\xi}}\end{pmatrix}, \end{aligned}$$

(39)

with the generalized accelerations $\mathbf{a} = \mathbf{M}^{-1}\mathbf{Q}$. The derivatives of the generalized accelerations with respect to the set of parameters are difficult to compute because the mass matrix and the generalized force vector are functions of the parameters. The element-based formulation of the generalized accelerations is given by

$$\begin{aligned} \mathbf{M} \mathbf{a} = \mathbf{Q} \Rightarrow \sum _{(e)} \mathbf{T}_{1}^{(e)^{\mathsf{T}}}\mathbf{M}^{(e)} \underbrace{\mathbf{T}_{1}^{(e)} \mathbf{a}}_{\mathbf{a}^{(e)}} = \sum _{(e)} \mathbf{T}_{1}^{(e)^{\mathsf{T}}} \mathbf{Q}^{(e)}. \end{aligned}$$

(40)

The matrix–vector product $\mathbf{M}^{(e)} \mathbf{a}^{(e)}$ is reformulated to avoid the direct derivative of the mass matrix with respect to the parameters as a sum of vector-scalar products, leading to

$$\begin{aligned} \sum _{(e)} \mathbf{T}_{1}^{(e)^{\mathsf{T}}}\sum _{c}\mathbf{M}^{(e)}_{c} a^{(e)}_{c} = \sum _{(e)} \mathbf{T}_{1}^{(e)^{\mathsf{T}}} \mathbf{Q}^{(e)}, \end{aligned}$$

(41)

where the subscript $c$ denotes the column of the mass matrix and the row of generalized accelerations, respectively. The derivatives of the element-based formulation with respect to $\boldsymbol{\xi}$ read

$$\begin{aligned} \sum _{(e)} \mathbf{T}_{1}^{(e)^{\mathsf{T}}} \sum _{c} \Bigg( \frac{\partial \mathbf{M}^{(e)}_{c}}{\partial \boldsymbol{\xi}^{(e)}} \underbrace{\frac{\partial \boldsymbol{\xi}^{(e)}}{\partial \boldsymbol{\xi}}}_{ \mathbf{T}_{3}^{(e)}} a^{(e)}_{c} + \mathbf{M}^{(e)}_{c} \frac{\partial a^{(e)}_{c}}{\partial \boldsymbol{\xi}} \Bigg) = \sum _{(e)} \mathbf{T}_{1}^{(e)^{\mathsf{T}}} \frac{\partial \mathbf{Q}^{(e)}}{\partial \boldsymbol{\xi}^{(e)}} \mathbf{T}_{3}^{(e)} . \end{aligned}$$

(42)

By reformulation of the dyadic product of an element

$$\begin{aligned} \sum _{c}\mathbf{M}^{(e)}_{c} \frac{\partial a^{(e)}_{c}}{\partial \boldsymbol{\xi}} = \mathbf{M}^{(e)} \frac{\partial \mathbf{a}^{(e)}}{\partial \boldsymbol{\xi}} = \mathbf{M}^{(e)} \mathbf{T}_{1}^{(e)} \frac{\partial \mathbf{a}}{\partial \boldsymbol{\xi}}, \end{aligned}$$

(43)

the derivatives of the global acceleration are computed by substituting (43) into (42) and using (31)

$$\begin{aligned} \frac{\partial \mathbf{a}}{\partial \boldsymbol{\xi}} = \mathbf{M}^{-1} \sum _{(e)} \mathbf{T}_{1}^{(e)^{\mathsf{T}}} \left ( \frac{\partial \mathbf{Q}^{(e)}}{\partial \boldsymbol{\xi}^{(e)}} \mathbf{T}_{3}^{(e)} - \sum _{c} \frac{\partial \mathbf{M}^{(e)}_{c}}{\partial \boldsymbol{\xi}^{(e)}} \mathbf{T}_{3}^{(e)} a^{(e)}_{c} \right ). \end{aligned}$$

(44)

Note that the derivatives are time-dependent functions, but the inverse of the global mass matrix only needs to be computed once for the numerical evaluation since the mass matrix is constant for the ANCF.

The element-based derivatives in (36), (38), and (44) are computed by symbolic differentiation and used to assemble the global derivatives required for the proposed discrete adjoint gradient computation. In this paper, the formulation of the flexible multibody and all required symbolic differentiations are written in the computer algebra system toolbox SymPy [30], which is written in pure Python. In addition, the analytical expressions are compiled ahead of (simulation) time with Numba [20] to efficiently evaluate the derived terms. Both packages are available under an open-source license.

5 Numerical examples

This section discusses three examples to demonstrate the use and advantages of the proposed discrete adjoint gradient approach. In the first example, the sensitivity analysis of an academic one-mass oscillator is analyzed. This example provides a deep insight into the proposed approach and discusses the role of the discrete adjoint variables. The second example studies the energy optimal control problem of a nonlinear spring pendulum to discuss the efficiency of the proposed approach. The third example analyzes a combined optimal control and design problem of a Selective Compliance Assembly Robot Arm (SCARA) in a rest-to-rest motion. The bodies of the robot are modeled with flexible components, where the ANCF discussed in Sect. 4 is used to examine the effects due to elasticity. Explicit and implicit integration schemes are applied to demonstrate the versatility of the proposed approach to different time integrators, with a particular focus on the computation of adjoint variables. In addition, all examples are used to verify the proposed discrete adjoint gradients using numerical computed gradients via the finite-difference method.

5.1 Sensitivity analysis of a one-mass oscillator

As a first example, the proposed discrete adjoint gradient approach in Sect. 3 is applied to the sensitivity analysis of an academic one-mass oscillator to demonstrate the proposed procedure in Sect. 3.4 and to discuss the role of the discrete adjoint variables. The mechanical system consists of a mass $m$, a linear damping parameter $d$, and a linear spring parameter $c$. The mass is driven by a time-dependent control $u$. The state equations are given by a linear first-order differential system

$$\dot{\mathbf{x}} = \mathbf{f}(\mathbf{x},u) = \begin{pmatrix}v \\\frac{1}{m}(u - dv - cx) \end{pmatrix} , $$

(45)

wherein the state variables are expressed by $\mathbf{x}=\left (x,\,v\right )^{\mathsf{T}}$ with the position $x$ and velocity $v$ of the mass. The control variable is formulated as proposed in [22] with $u = \mathbf{C} \hat{\mathbf{u}}$, where $\mathbf{C}$ is a time-dependent cubic spline interpolation function and $\hat{\mathbf{u}}=\left (\hat{u}_{0},\ldots ,\hat{u}_{M}\right )^{ \mathsf{T}}$ is a set of control grid nodes. The grid nodes are defined at the uniformly distributed macro time mesh $\hat{t}_{j}$, $j \in \{0, \, \ldots , \, M\}$ within the time interval $[t_{\mathrm{0}},\,t_{\mathrm{f}}]$.

This example examines sensitivities of the inequality constraint $h = f - f_{\mathrm{max}} \le 0$ regarding the reaction force $f = c~x + d~v$ ($r=1$ time-dependent function) with respect to the grid nodes $\hat{\mathbf{u}}$. Hence, the variables of interest in the sensitivity analysis are defined by $\mathbf{z} = \hat{\mathbf{u}}$. The reaction force is evaluated at the macro time mesh $\hat{t}_{j}$, resulting in the concatenated vector $\hat{\mathbf{h}} = (\hat{h}_{0},\, \ldots ,\,\hat{h}_{M} )^{ \mathsf{T}}$. The reaction force depends on the state variables, which are time integrated under the influence of the control. Therefore, a change in the control grid nodes leads to a change in the reaction force. A graphical illustration of the dependencies is shown in Fig. (2), where the change of the control grid node $\delta \hat{u}_{1}$ leads to a change of $\delta \hat{f}_{1}$ and $\delta \hat{f}_{2}$.

Fig. 2

Influence of changing a control grid node on the reaction force: (a) continuous control function with grid nodes, (b) reaction force due to the control in (a)

The sensitivity analysis uses the following set of parameters: the mass $m = 1 \text{ kg}$, the damping coefficient $d = 0.5\text{ Ns/m}$, the stiffness $c = 1\text{ N/m}$, the constant time-integration step size $\Delta t = 0.001\text{ s}$, and the final time $t_{\mathrm{f}} = 2\text{ s}$. In addition, the control $u$ is discretized by three grid nodes ($M=2$ uniform distributed intervals in the time interval $[t_{\mathrm{0}},\,t_{\mathrm{f}}]$) set to $\hat{\mathbf{u}} = \left (10,\,6,\,2\right )^{\mathsf{T}}$. The initial conditions of the state variables are defined by $\mathbf{x}_{0} = \mathbf{0}$, i.e., the initial reaction force is zero.

5.1.1 Discrete adjoint gradient computation

The sensitivities of $\mathrm{d} \hat{\mathbf{h}} / \mathrm{d} \mathbf{z}$ are obtained by using the proposed discrete adjoint gradient in (21), which includes the discrete adjoint variables $\mathbf{R}$ defined in (17)–(19). Referring to the procedure in Sect. 3.4, the first step of the adjoint gradient computation is the symbolic differentiation of constraints. In this example, the reaction force is interpreted as an inequality constraint, and the derivative with respect to the state variables is given by $\frac{\partial h}{\partial \mathbf{x}} = \left (c,\,d\right )$. Derivatives with respect to $\boldsymbol{\xi}$ are not defined since the state equations are not parameterized. The second step of the adjoint gradient computation is the symbolic differentiation of the state equations. The derivatives with respect to the state variables and the control are represented by

$$ \frac{\partial \mathbf{f}}{\partial \mathbf{x}}= \begin{pmatrix}0 & 1 \\-\frac{c}{m} & -\frac{d}{m}\end{pmatrix} :=\mathbf{A} \quad \text{and}\quad \frac{\partial \mathbf{f}}{\partial u}= \begin{pmatrix}0 \\\frac{1}{m} \end{pmatrix} ,$$

(46)

respectively. Note that the simple structure of the linear state equations leads to constant system derivatives and, therefore, no forward integration is required to evaluate the derivatives.

The computation of the discrete adjoint variables is performed in a backward manner in which the final value defined in (17) is given in this example by

$$\begin{aligned} \mathbf{R}_{N} = - \begin{pmatrix}0 & 0 \\0 & 0 \\c & d\end{pmatrix}, \end{aligned}$$

(47)

where the derivative of the reaction force with respect to state variables is recognized. The explicit Euler method is used to solve the forward dynamics, and, therefore, the specific sensitivity of the right-hand side $\tilde{\mathbf{f}}$ is required, as shown in Sect. 3.2. Substituting (46) and (23) into (18) leads to the algebraic equations of the discrete adjoint variables. Starting from $\mathbf{R}_{N}$ and proceeding with

$$\mathbf{R}_{i} = \mathbf{R}_{i+1}\left (\mathbf{I} + \Delta t \mathbf{A}\right ), $$

(48)

the discrete adjoint variables are computed in a backward manner. Note that (48) is defined within the macro time mesh $]\hat{t}_{j},\,\hat{t}_{j+1}[$, $j \in \{0, \, \ldots , \, M-1\}$. The discrete adjoint variables at the macro time mesh $\hat{t}_{j}$, $j \in \{1, \, \ldots , \, M\}$ are determined by the intermediate condition in (19) given by

$$\mathbf{R}_{ej} = \mathbf{R}_{ej+1}\left (\mathbf{I} + \Delta t \mathbf{A}\right ) - \mathbf{B}_{2,j} \left (c,\,d\right ). $$

(49)

After computing the adjoint variables backward in time, the sensitivity of the inequality constraints $\hat{\mathbf{h}}$ with respect to the grid nodes $\hat{\mathbf{u}}$ can be evaluated by the proposed formulation in (21).

5.1.2 Interpretation

Figure 3 represents the evolution of each component of the adjoint variables $\mathbf{R}$. The adjoint variables $\mathbf{R} \in \mathbb{R}^{(p+q) \times n}$ consists of six components with $p=0$, $q = r(M + 1)=3$, and $n=2$. It can be observed that the adjoint variables are not necessarily smooth functions due to the intermediate condition in (49). The intermediate condition computes the adjoint variables in the same manner as in (48) and initializes the adjoint variables for the time interval $]\hat{t}_{0},\,\hat{t}_{j}]$ in addition. The gradient computation of $\mathrm{d} \hat{h}_{j} / \mathrm{d} \hat{\mathbf{u}}$ evaluated at the time $\hat{t}_{j}$ is not influenced by the system dynamics in the time interval $]\hat{t}_{j},\,\hat{t}_{M}]$ and, therefore, $\mathbf{R}_{j,\bullet} = \mathbf{0}$ in this interval for all • columns of the adjoint variables. To be more precise, the system dynamics of the gradient computation for $\hat{h}_{j}$ is only taken into account for the time interval $]\hat{t}_{0},\,\hat{t}_{j}]$, i.e., the adjoint variables for the time interval $]\hat{t}_{j},\,\hat{t}_{M}]$ are zero and do not influence the gradient. This effect is seen in the second row of the adjoint variables visualized in Fig. 3. Here, the gradient computation of $\mathrm{d} \hat{h}_{1} / \mathrm{d} \hat{\mathbf{u}}$ evaluated at the time $\hat{t}_{1} = 1\text{ s}$ is not influenced by the system dynamics in the time interval $]\hat{t}_{1},\,\hat{t}_{2}]$ and, therefore, the adjoint variables $R_{1,0}$ and $R_{1,1}$ are zero in this time interval. However, the discrete adjoint sensitivities are compared with the sensitivities computed by the finite-difference method to verify the proposed approach and its implementation. The sensitivity analysis results obtained by both approaches are in good agreement.

Fig. 3

Time evolution of the discrete adjoint variables

5.2 Energy optimal control of a nonlinear spring pendulum

The second example is focused on the energy optimal control of a nonlinear spring pendulum, as depicted in Fig. 4, inspired by the example studied in [1]. The aim is to compute a control to manipulate the mechanical system from an initial to a final state. The example studied in [1] is adapted with an additional inequality constraint during the maneuver to test the proposed discrete adjoint gradient approach. The mechanical system consists of three degrees of freedom $\mathbf{q} = (r_{\mathrm{x}},\, r_{\mathrm{y}},\, r_{\mathrm{z}})^{ \mathsf{T}}$ describing the position vector of a mass $m$ formulated in the inertial Cartesian coordinate system. The mass is connected to the ground by a spring $c$, and the strain is formulated by using a Green–Lagrangian-type strain measure

$$ \varepsilon = \frac{1}{2 l_{0}^{2}}\left (\mathbf{q}^{\mathsf{T}} \mathbf{q} - l_{0}^{2}\right ), $$

(50)

wherein $l_{0}$ denotes the strain-free spring length. The mass matrix $\mathbf{M}$ of the mechanical system is defined by using the kinetic energy

$$T = \frac{1}{2} \dot{\mathbf{q}}^{\mathsf{T}} \underbrace{m \mathbf{I}}_{\mathbf{M}} \dot{\mathbf{q}}, $$

(51)

where $\mathbf{I}$ is the identity matrix. Forces introduced due to the gravitational acceleration $g$ and the deformation of the spring are defined by

$$\mathbf{Q}_{\mathrm{nl}} = \left ( \frac{\partial V}{\partial \mathbf{q}}\right )^{\mathsf{T}}. $$

(52)

The potential energy of the mechanical system reads

$$V = m g r_{\mathrm{z}} + \frac{1}{2} c l_{0}^{2} \varepsilon ^{2}, $$

(53)

where the first term corresponds to gravity and the second to the deformation of the spring. Note that the force term $\mathbf{Q}_{\mathrm{nl}}$ is nonlinear due to the nonlinear Green–Lagrange strain measure in (50). In addition, the mass is driven by a time-dependent control $\mathbf{u} = (u_{\mathrm{x}},\, u_{\mathrm{y}},\, u_{\mathrm{z}})^{ \mathsf{T}}$ and the corresponding force in the inertial Cartesian coordinate system is defined by the principle of virtual work as $\mathbf{Q}_{\mathrm{u}} = \mathbf{u}$. The state equations are given by a nonlinear first-order differential system

$$\dot{\mathbf{x}} = \mathbf{f}(\mathbf{x},\mathbf{u}) = \begin{pmatrix}\mathbf{v} \\\mathbf{M}^{-1}\left (\mathbf{Q}_{\mathrm{u}} - \mathbf{Q}_{ \mathrm{nl}}\right ) \end{pmatrix} , $$

(54)

wherein the state variables are expressed by introducing the velocity $\dot{\mathbf{q}} = \mathbf{v}$ of the mass by $\mathbf{x}=\left (\mathbf{q},\,\mathbf{v}\right )^{\mathsf{T}}$. In this example, the control is formulated as proposed by Lichtenecker et al. [22] with $\mathbf{u} = \mathbf{C} \bar{\mathbf{u}}$, where $\mathbf{C} \in \mathbb{R}^{3 \times 3k}$ is a time-dependent cubic spline interpolation matrix and $\bar{\mathbf{u}}^{\mathsf{T}} = \left (\hat{\mathbf{u}}_{\mathrm{x}}^{ \mathsf{T}},\,\hat{\mathbf{u}}_{\mathrm{y}}^{\mathsf{T}},\, \hat{\mathbf{u}}_{\mathrm{z}}^{\mathsf{T}} \right ) \in \mathbb{R}^{3k}$ is a set of concatenated control grid nodes regarding the control functions. Each control is discretized with $k$ grid nodes defined at a uniformly distributed time mesh within the time interval $[t_{\mathrm{0}},\,t_{\mathrm{f}}]$.

Fig. 4

Nonlinear spring pendulum in a general configuration

According to the example studied in [1], the following set of parameters is used: the mass $m = 1\text{ kg}$, the stiffness $c = 0.6 \text{ N/m}$, the strain-free spring length $l_{0} = 5 \text{ m}$, and the gravitational acceleration $g = 9.81 \text{ m/s}^{2}$. The state variables $\mathbf{x}$ are time-integrated using the explicit Euler scheme on the micro time mesh in the interval $[t_{\mathrm{0}},\,t_{\mathrm{f}}]$, where the final time is $t_{\mathrm{f}}=5 \text{ s}$ with a constant time-integration step size $\Delta t = 0.001 \text{ s}$. The initial state variables are defined by $\mathbf{x}_{0} = (-2,\,-5,\,-5,\,-3,\,0,\,0)^{\mathsf{T}}$.

5.2.1 Optimization problem

The energy optimal control problem of mechanical systems has been studied by various authors with different formulations of the cost function. In this example, the energy optimal control problem is formulated by minimizing the signal energy required to manipulate the mechanical system. The signal energy is defined as the integrated quadratic control in the time interval $[t_{0},\,t_{\mathrm{f}}]$. To address the energy optimal control problem, the concatenated set of grid nodes is used to define optimization variables, i.e., $\mathbf{z}=\bar{\mathbf{u}} \in \mathbb{R}^{3k}$.

The energy optimal control problem yields the NLP problem formulated as a direct single shooting by

$$\begin{aligned} & \underset{\mathbf{z}}{\text{min}}~J = \frac{1}{2} \int _{t_{0}}^{t_{ \mathrm{f}}} \mathbf{u}^{\mathsf{T}}\mathbf{u} \,\mathrm{d}t = \frac{1}{2} \mathbf{z}^{\mathsf{T}} \underbrace{\int _{t_{0}}^{t_{\mathrm{f}}} \mathbf{C}^{\mathsf{T}}\mathbf{C}\,\mathrm{d}t}_{ \boldsymbol{\mathcal{A}}} \, \mathbf{z} \end{aligned}$$

(55)

$$\begin{aligned} & \text{s.t.} \\ & \mathbf{z}_{\mathrm{min}} \leq \mathbf{z} \leq \mathbf{z}_{ \mathrm{max}} \end{aligned}$$

(56)

$$\begin{aligned} & \mathbf{q}_{N} = \mathbf{q}_{\mathrm{f}} \end{aligned}$$

(57)

$$\begin{aligned} & \dot{\mathbf{q}}_{N} = \mathbf{0} \end{aligned}$$

(58)

$$\begin{aligned} & \hat{\mathbf{l}} / l_{\mathrm{max}} \le 1 \end{aligned}$$

(59)

$$\begin{aligned} & \mathbf{x}_{i+1} = \tilde{\mathbf{f}}(\mathbf{x}_{i},\mathbf{u}_{i}), \end{aligned}$$

(60)

where the control in (55) is formulated with $\mathbf{u} = \mathbf{C} \mathbf{z}$. The position $\mathbf{q}_{N}$ and velocity $\dot{\mathbf{q}}_{N}$ are prescribed at the fixed final time $t_{\mathrm{f}}$. The final position of the mass is defined according to [1] by $\mathbf{q}_{\mathrm{f}}=\left (2,\,-10,\,-4\right )^{\mathsf{T}}$. In addition, the optimization problem concerns normalized inequality constraints regarding the spring length $l = \sqrt{\mathbf{q}^{\mathsf{T}} \mathbf{q}}$. The inequality constraints are considered at the uniformly distributed macro time mesh $\hat{t}_{j}$, $j \in \{0, \, \ldots , \, M\}$ within the time interval $[t_{\mathrm{0}},\,t_{\mathrm{f}}]$. Evaluating the spring length $(M+1)$ times leads to the concatenated vector $\hat{\mathbf{l}} \in \mathbb{R}^{M+1}$ with $M = 500$. The defined inequality constraints forces the mass to a position within a sphere with radius $r = l_{\mathrm{max}}$ centered on the inertial Cartesian coordinate system with $l_{\mathrm{max}} = 12 \text{ m}$. Lower and upper bounds of the optimization variables are taken into account with $-5.5 \text{ N}\le \hat{u} \le 5.5\text{ N}$. As an initial guess, the optimization variables are set to $\mathbf{z} = \mathbf{0}$.

For efficient numerical computation, the NLP is solved with IPOPT 3.14.12 [45] (HSL MA97 to solve linear subproblems). The cost function, constraints, and the respective first-order gradients are provided to IPOPT via an interface. The first-order gradients of the cost function (55) can be easily computed by symbolic differentiation

$$\frac{\mathrm{d} J}{\mathrm{d} \mathbf{z}} = \mathbf{z}^{\mathsf{T}} \boldsymbol{\mathcal{A}}, $$

(61)

where the symmetric property of $\boldsymbol{\mathcal{A}}$ due to the block diagonal matrix $\mathbf{C}$ is utilized. The first-order gradients of the constraints (57)–(59) are computed following the proposed procedure in Sect. 3.4, implemented in Python.

5.2.2 Optimization results

Each control is discretized with $k=10$ grid nodes leading to $z=30$ optimization variables. Figure 5 shows the time evolution of the state variables obtained for the energy optimal control. The results are in accordance with the defined equality constraints in (57) and (58) at the final time. Figure 6 visualizes the obtained energy optimal control history and the inequality constraint regarding the spring length. It can be observed that the control variables are within the lower and upper bounds, while the inequality constraint in (59) is active. Similar to the previous example, the discrete adjoint gradients of the constraints are compared with the gradients computed by the finite-difference method to verify the proposed approach and its implementation. The sensitivity analysis results obtained by both approaches are in good agreement.

Fig. 5

Time evolution of the state variables obtained for the energy optimal control problem

Fig. 6

Optimal control history for the energy optimal control problem and the resulting spring length

To demonstrate the efficiency of the proposed discrete adjoint gradient approach, the NLP problem is solved by providing gradients of the constraints to IPOPT once using the finite-difference method and once using the discrete adjoint gradient approach. The runtimes required for converged solutions are given in Table 1. The comparison is performed with $k = 10$ and $k = 20$ grid nodes for each control. The proposed discrete adjoint approach outperforms the finite-difference method in terms of runtimes. Employing the discrete adjoint gradient approach, the change in the runtime required for $k = 10$ and $k = 20$ is small. In contrast, the runtime required for the finite-difference method depends strongly on the number of grid nodes. Note that the number of grid nodes $k$ influences the number of optimization variables $z = 3k$ and, therefore, the runtime for the finite-difference method. The number of iterations to fulfill the KKT conditions is equal for both approaches, which demonstrates the correct implementation of the discrete adjoint gradient approach.

Table 1 Runtime comparison of two different approaches to provide first-order gradients of constraints to IPOPT for converged solutions

5.3 Optimal control and design of a flexible SCARA

The third example focuses on the combined optimal control and structural optimization problem for flexible multibody systems. The idea of coupling both optimization tasks is promising to obtain the best possible mechanical structure concerning an optimal control problem. Engineers usually do not address the combined structural optimization and optimal control problem; the two challenges are typically considered independently. In addition, multibody systems with flexible components are usually underactuated, and the optimal control problem becomes more complicated than fully actuated systems [39]. Lichtenecker et al. studied in [22] the time-optimal control problem of a SCARA with flexible components. A similar system configuration is used in this example to employ the proposed discrete adjoint approach for the sensitivity analysis of a combined optimal control and structural optimization problem. Thus, a combined set of discrete adjoint gradients is used to efficiently and accurately compute first-order gradients to speed up the runtime in a direct optimization method.

Inspired by the example studied in [35], the two-arm robot depicted in Fig. 7 is analyzed in the combined optimization problem. The SCARA is driven by two controls, $u_{1}$ and $u_{2}$, in which the control variables are formulated by cubic splines similar to the previous example. In application to industrial robots, smooth trajectory planning is essential and has been presented using cubic splines, e.g., in [8, 37].

Fig. 7

SCARA in a general undeformed configuration

Each arm is divided into two ANCF elements, and an additional mass is attached to the tool-center point (TCP). Moreover, a stress marker is attached to each structural element to determine the equivalent stress $\sigma _{\mathrm{V}}$ while the robot performs a task. The material properties of the structural elements are set to $E=3\text{e}9 \text{ N/m}^{2}$ and $\rho = 1300\text{ kg/m}^{3}$ for the Young’s modulus and the density, respectively. The length of both arms is $l_{1}=l_{2}=1\text{ m}$ and the viscous damping coefficient in the revolute joints is set to $d_{1} = d_{2} = 0.2 \text{ Nm}\,\text{s/rad}$. The width of the structural elements is set to $w^{(e)}=0.002 \text{ m}$. In addition, the system is affected by the gravity field, and an additional mass $m_{\mathrm{E}} = 1 \text{ kg}$ is attached to the TCP. The state variables $\mathbf{x}$ are integrated using the implicit Euler scheme on the micro time mesh in the interval $[t_{0},\,t_{\mathrm{f}}]$, where the final time is $t_{\mathrm{f}}=2 \text{ s}$ with a constant time-integration step size $\Delta t = 0.001 \text{ s}$.

5.3.1 Optimization problem

Structural-optimization problems can be treated with so-called weakly and fully coupled methods [42]. Weakly coupled methods are based on equivalent static loads, while fully coupled methods incorporate the system dynamics into the optimization process. This example focuses on extending fully coupled methods to embed the optimal control of flexible multibody systems. Considering an optimal control problem and a structural optimization problem leads to a combined set of optimization variables, including the control parameterization and design parameter of the multibody system. In this example, the structural elements are parameterized by the height $h^{(e)}$, while the width $w^{(e)}$ and the length $l^{(e)}$ are set to constant values. The set of design parameters regarding the multibody system depicted in Fig. 7 is defined by $\boldsymbol{\xi}^{\mathsf{T}} = \left ( h^{(1)},\,h^{(2)},\,h^{(3)}, \,h^{(4)} \right )$. The optimal control problem of flexible multibody systems requires smooth control functions to reduce vibrations. In this example, a continuity requirement up to $\mathcal{C}^{2}$ of the control is enforced, similar to the previous example in Sect. 5.2, by a cubic spline interpolation. Both continuous control functions $u_{1}$ and $u_{2}$ are discretized with $k=21$ grid nodes at a uniformly distributed time mesh within the time interval $[t_{0},t_{\mathrm{f}}]$. The discretization of the control leads to the set of grid nodes $\bar{\mathbf{u}}^{\mathsf{T}} = \left (\hat{\mathbf{u}}_{1}^{ \mathsf{T}},\,\hat{\mathbf{u}}_{2}^{\mathsf{T}} \right )$. Concatenating the parameterization of the multibody system and the control leads to the combined set of optimization variables $\mathbf{z}^{\mathsf{T}} = \left ( \boldsymbol{\xi}^{\mathsf{T}},\, \bar{\mathbf{u}}^{\mathsf{T}} \right )$.

Minimizing the mass of mechanical systems is a common approach in structural optimization to enable innovative lightweight designs. In this paper, the mass minimization yields the NLP problem formulated as direct single shooting by

$$\begin{aligned} & \underset{\mathbf{z}}{\text{min}}~m=\rho \sum _{(e)} w^{(e)}~h^{(e)}~l^{(e)} \end{aligned}$$

(62)

$$\begin{aligned} & \text{s.t.} \\& \mathbf{z}_{\mathrm{min}} \leq \mathbf{z} \leq \mathbf{z}_{ \mathrm{max}} \end{aligned}$$

(63)

$$\begin{aligned} & \mathbf{r}_{\mathrm{TCP},N} = \mathbf{r}_{\mathrm{f}} \end{aligned}$$

(64)

$$\begin{aligned} & \dot{\mathbf{r}}_{\mathrm{TCP},N} = \mathbf{0} \end{aligned}$$

(65)

$$\begin{aligned} & \hat{\boldsymbol{\sigma}}_{\mathrm{V}} / \sigma _{\mathrm{Vmax}} \le 1 \end{aligned}$$

(66)

$$\begin{aligned} & \mathbf{x}_{i+1} = \tilde{\mathbf{f}}(\mathbf{x}_{i},\mathbf{x}_{i+1}, \mathbf{u}_{i},\mathbf{u}_{i+1},\boldsymbol{\xi}), \end{aligned}$$

(67)

with special attention to position and velocity constraints of the TCP, $\mathbf{r}_{\mathrm{TCP},N}$, and $\dot{\mathbf{r}}_{\mathrm{TCP},N}$, respectively, at the fixed final time $t_{\mathrm{f}}$. The final position of the TCP is defined by $\mathbf{r}_{\mathrm{f}}=\left (1,\,1\right )^{\mathsf{T}}$. In addition, the optimization problem concerns normalized inequality constraints regarding the equivalent stress $\sigma _{V}$ of the four markers attached to the structure. All four markers are evaluated at the macro time mesh $\hat{t}_{j}$, $j \in \{0, \, \ldots , \, M\}$ with $M = 100$ leading to the concatenated equivalent stress vector $\hat{\boldsymbol{\sigma}}_{\mathrm{V}}$. The upper limit of the equivalent stress is $\sigma _{\mathrm{Vmax}} = 1.1\text{e}7 \text{ N/m}^{2}$. Lower and upper bounds of the optimization variables are taken into account with $0.002 \text{ m}\le h^{(e)} \le 0.02\text{ m}$ and $-5\text{ Nm} \le \hat{u} \le 5\text{ Nm}$, respectively. Regarding the initial conditions of the state variables, the robot is defined in the undeformed configuration, where both arms are hanging vertically downward with generalized velocities equal to zero.

In terms of initializing the NLP problem, a two-stage procedure is utilized with decoupling of the optimization variables. The first stage solves an optimal control problem with a constant height of the structural elements, i.e., the optimization variables $\mathbf{z}=\bar{\mathbf{u}}$ consists of the grid nodes. The aim is to identify a control with a defined set of parameters $\boldsymbol{\xi}$ that manipulates the robot from the initial configuration so that the TCP satisfies the constraints (64) and (65) at the final time. As an initial guess for this first-stage optimization, the control grid nodes are set to $\hat{u} = 0\text{ Nm}$ and the constant height of the elements is defined by $h^{(e)}=0.02 \text{ m}$. The preoptimized set of control grid nodes $\bar{\mathbf{u}}^{*}$ and heights of the elements $h^{(e)}$ are employed as an initial guess to the combined optimization problem.

For efficient numerical computation, the NLP is solved with IPOPT 3.14.12 [45] (HSL MA97 to solve linear subproblems). The cost function, constraints, and the respective first-order gradients are provided to IPOPT via an interface. The first-order gradients of the cost function (62) can be easily computed by symbolic differentiation, while the first-order gradients of the constraints (64)–(66) are computed following the proposed procedure in Sect. 3.4, implemented in Python.

5.3.2 Optimization results

Figure 8 shows the obtained control history for both controls. It can be observed that the control is within the lower and upper bounds, while the stress constraint in (66) is active. Applying the optimal control to the SCARA leads to the position and velocity of the TCP as shown in Fig. 9. Note there are no acceleration constraints defined at the final time in this example. It can be observed that the equality constraints in (64) and (65) are fulfilled at the final time. Figure 10 visualizes the final sizing of the structural elements. The final sizing provides a structure in which the height of the structural elements becomes smaller towards the TCP; thus, the bending stiffness also becomes smaller towards the TCP. The initial mass of the robot $m_{\mathrm{init}}=0.1040 \text{ kg}$ is reduced by the final design to $m^{*}=0.0450 \text{ kg}$, which corresponds to a reduction of 56.7% regarding the initial mass. With the final design and the corresponding control, the SCARA undergoes a large deformation during manipulation. However, the results are in accordance with the constraints posed in (63)–(67) and provide a local minimum of the robot’s mass. Snapshots of the robot’s motion are illustrated in Fig. 11.

Fig. 8

Optimal control history of a flexible two-arm robot for a rest-to-rest maneuver

Fig. 9

Time evolution of the position and velocity of the TCP obtained for the optimal control and design problem

Fig. 10

Final sizing of the flexible two-arm robot

Fig. 11

Snapshots of the robot’s motion history

It has to be mentioned that normalizing inequality constraints is essential since the numerical value of the equality constraints in (64) and (65) are relatively small compared to those of the inequality constraint in (66). Without normalizing, the optimization would not converge to a local minimum. Similar to the previous examples, the discrete adjoint gradients are verified by applying the finite-difference method. The sensitivity analysis results obtained by both approaches are in good agreement. The proposed discrete adjoint gradient approach is an efficient technique to incorporate a large number of optimization variables, and the computational effort is less than using the finite-difference method. A comparison of the runtimes required to compute first-order gradients of the constraints is performed to demonstrate the efficiency of the proposed discrete adjoint gradient approach. The gradients are computed with the optimal set of optimization variables $\mathbf{z}^{*}$ ten times in a row. The average runtime required for the finite-difference method is $t_{\mathrm{FDM}} = 592.4 \text{ s}$, while the average runtime required for the discrete adjoint method is $t_{\mathrm{DAM}} = 52.2 \text{ s}$. The proposed approach reduces the computational time by 91.2% regarding the finite-difference method. The high computational time in the finite-difference method is because the number of state equations to be solved depends on the number of optimization variables. It has to be emphasized that the computation of gradients is required at each iteration of the NLP solver package, which encourages the use of the proposed discrete adjoint gradient method to improve computational efficiency.

6 Conclusion

This paper discusses adjoint-based sensitivity analysis for dynamic systems in gradient-based optimization problems. Deriving adjoint gradients is mathematically more laborious than simply computing finite differences for numerical gradients. However, the significant time advantage when using adjoint gradients for the sensitivity analysis justifies the considerable preprocessing effort. This paper presents a novel discrete adjoint gradient approach to incorporate (in)equality constraints. Moreover, the paper shows the application of different time-integration schemes, highlighting their efficiency and applicability to large-scale problems. Three numerical examples are investigated to show the application of the proposed discrete adjoint gradient approach. The sensitivity analysis of an academic example discusses the role of the discrete adjoint variables. The energy optimal control problem of a nonlinear spring pendulum studies the efficiency of the proposed approach. In addition, the proposed discrete adjoint gradients are utilized in a coupled optimal control and optimal design problem in flexible multibody dynamics.