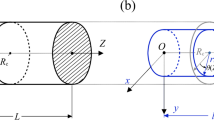
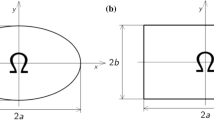
Abstract
Hill’s linear isotropic hyperelastic material models based on the one-parameter (\(r\)) Itskov family of strain tensors (including the Hencky, Pelzer, and Mooney strain tensors generating the H, P, and M material models, respectively) were used to obtain exact solutions of the simple torsion problem for circular cross-section rods from the H, P, and M materials. The “exact” solutions available in the literature for the problem of generalized torsion of cylindrical rods with free edges in the axial direction were analyzed. The objectives of the present study are to develop and implement new formulations of these material models in the commercial MSC.Marc nonlinear FE software and to verify these formulations using the above-mentioned exact solutions. Computer simulations of the simple and generalized torsion of cylindrical specimens were carried out using three material models (H, P, and M) and the standard Mooney–Rivlin model. The results of computer simulations of the resultant moment and the resultant axial force (in the problem of simple torsion) or axial elongation (in the problem of generalized torsion) were compared with exact solutions. For the simple torsion problem, the solutions obtained by the two methods are similar, but for the problem of generalized torsion, these solutions are similar only for sufficiently small values of the torsion parameter. We explain the discrepancy for sufficiently large values of the torsion parameter by the fact that the so-called “exact” solutions cease to be exact because of the assumptions made by other authors in obtaining these solutions. We assume that for all values of the torsion parameter, our numerical solutions are close to the true exact solutions. Computer simulations showed that the Pelzer material model is similar in performance to the Mooney–Rivlin model.












Similar content being viewed by others
Notes
A similar generalization of Hooke’s law can be performed for any pair of conjugate Eulerian stress and strain tensors \(\mathbf{s}\) and \(\mathbf{e}\) (cf. Korobeynikov 2019).
In our classification, this material model is more briefly called the H material model.
Since material models from the HLIH family based on the Itskov family of strain tensors belong to the family of SPH isotropic hyperelastic material models (cf. Korobeynikov 2019), below the family of these material models will be called for brevity the family of SPHr isotropic hyperelastic material models (cf. Korobeynikov et al. 2022).
Hereinafter, \(\mathcal{T}^{2}_{\text{sym}}\subset \mathcal{T}^{2}\) denotes the set of all symmetric second-order tensors.
The number \(m\) (\(1\leq m\leq 3\)) will be called the eigenindex.
Some authors call this family of strain tensors the Seth–Hill family of strain tensors (see, e.g., Curnier and Rakotomanana 1991).
In Curnier and Rakotomanana (1991), this family is termed the rubber family.
In Curnier and Zysset (2006), this family is termed the metric family.
See Appendix A in Korobeynikov et al. (2022) for details. Hereinafter, the notation \(\sum _{i\neq j=1}^{m}\) denotes the summation over \(i,j=1,\ldots , m\) and \(i\neq j\), and this summation is assumed to vanish when \(m=1\).
See Korobeynikov 2019, Eq. \((79)_{4}\).
This dependence was obtained with retention of terms up to the second order in the torsion parameter \(\bar{\gamma}\).
In particular, these HLIH materials include St. Venant–Kirchhoff material (with \(m=2\)).
We introduce the parameters \(E\) and \(\nu \) for isotropic hyperelastic materials with Hill’s linear relations, which are related to the Lamé parameters \(\lambda \) and \(\mu \) by the equalities
$$\lambda =\frac{E \nu}{(1+\nu )(1-2\nu )},\quad \mu = \frac{E}{2(1+\nu )}. $$In the literature on linear elasticity theory, the material parameters \(E\) and \(\nu \) are called Young’s modulus and Poisson’s ratio.
To integrate the equations of quasistatic motion, we use an adaptive time step with prescribed values \(\epsilon _{U}=\epsilon _{F}=0.01\) (the quantities \(\epsilon _{U}\) and \(\epsilon _{F}\) are the relative tolerances for the displacements and internal forces when using the Newton–Raphson iterative procedure).
The relative differences \(d_{M}\) and \(d_{N}\) are simultaneously the relative errors for the solutions of the same problem only for the M-R model. For the remaining (H, P, and M) material models, the quantities \(d_{M}\) and \(d_{N}\) correspond to the relative differences in the resultant moment and compressive force obtained by solving different problems (see Remark 5).
The literature “exact” solutions (37) and (41) of the problem of generalized torsion in the form of the dependence \(\varepsilon (\bar{\gamma})\) were actually obtained under some assumptions on the relative smallness of the torsion parameter \(\bar{\gamma}\); therefore solutions obtained by computer simulation (shown by dotted curves in Fig. 12) without any assumptions on the relative smallness of this parameter can be considered close to the present “exact” solutions.
References
Adamov, A.A.: Comparative analysis of the two-constant generalizations of Hooke’s law for isotropic elastic materials at finite strains. J. Appl. Mech. Tech. Phys. 42(5), 890–897 (2001). https://doi.org/10.1023/A:1017969215735
Anand, L.: On H. Hencky’s approximate strain-energy function for moderate deformations. J. Appl. Mech. 46(1), 78–82 (1979). https://doi.org/10.1115/1.3424532
Anand, L.: Moderate deformations in extension-torsion of incompressible isotropic elastic materials. J. Mech. Phys. Solids 34(3), 293–304 (1986). https://doi.org/10.1016/0022-5096(86)90021-9
Anssari-Benam, A.: On a new class of non-Gaussian molecular-based constitutive models with limiting chain extensibility for incompressible rubber-like materials. Math. Mech. Solids 26(11), 1660–1674 (2021). https://doi.org/10.1177/10812865211001094
Anssari-Benam, A., Horgan, C.O.: On modelling simple shear for isotropic incompressible rubber-like materials. J. Elast. 147(1), 83–111 (2021). https://doi.org/10.1007/s10659-021-09869-x
Anssari-Benam, A., Horgan, C.O.: Extension and torsion of rubber-like hollow and solid circular cylinders for incompressible isotropic hyperelastic materials with limiting chain extensibility. Eur. J. Mech. A, Solids 92, 104443 (2022). https://doi.org/10.1016/j.euromechsol.2021.104443
Anssari-Benam, A., Bucchi, A., Saccomandi, G.: On the central role of the invariant I2 in nonlinear elasticity. Int. J. Eng. Sci. 163, 103486 (2021). https://doi.org/10.1016/j.ijengsci.2021.103486
Anssari-Benam, A., Bucchi, A., Horgan, C.O., Saccomandi, G.: Assessment of a new isotropic hyperelastic constitutive model for a range of rubberlike materials and deformations. Rubber Chem. Technol. 95(2), 200–217 (2022). https://doi.org/10.5254/rct.21.78975
Anssari-Benam, A., Bucchi, A., Saccomandi, G.: Modelling the inflation and elastic instabilities of rubber-like spherical and cylindrical shells using a new generalised neo-Hookean strain energy function. J. Elast. 151(1), 15–45 (2022). https://doi.org/10.1007/s10659-021-09823-x
Bahreman, M., Darijani, H.: New polynomial strain energy function; application to rubbery circular cylinders under finite extension and torsion. J. Appl. Polym. Sci. 132(13), 41718 (2015). https://doi.org/10.1002/app.41718
Bathe, K.J.: Finite Element Procedures. Prentice Hall, New Jersey, Upper Saddle River (1996)
Batra, R.C.: Comparison of results from four linear constitutive relations in isotropic finite elasticity. Int. J. Non-Linear Mech. 36(3), 421–432 (2001). https://doi.org/10.1016/S0020-7462(00)00057-3
Batra, R.C.: Elements of Continuum Mechanics. AIAA, Reston (2006)
Bažant, Z.P.: Finite strain generalization of small-strain constitutive relations for any finite strain tensor and additive volumetric-deviatoric split. Int. J. Solids Struct. 33(20–22), 2887–2897 (1996). https://doi.org/10.1016/0020-7683(96)00002-9
Bažant, Z.P.: Easy-to-compute tensors with symmetric inverse approximating Hencky finite strain and its rate. J. Eng. Mater. Technol. 120(2), 131–136 (1998). https://doi.org/10.1115/1.2807001
Beatty, M.F.: Topics in finite elasticity: Hyperelasticity of rubber, elastomers, and biological tissues – with examples. Appl. Mech. Rev. 40(12), 1699–1734 (1987). https://doi.org/10.1115/1.3149545
Beex, L.A.A.: Fusing the Seth–Hill strain tensors to fit compressible elastic material responses in the nonlinear regime. Int. J. Mech. Sci. 163, 105072 (2019). https://doi.org/10.1016/j.ijmecsci.2019.105072
Bertram, A.: Elasticity and Plasticity of Large Deformations, 4th edn. Springer, Cham (2021)
Billington, E.W.: Constitutive equation for a class of isotropic, perfectly elastic solids using a new measure of finite strain and corresponding stress. J. Eng. Math. 45(2), 117–134 (2003). https://doi.org/10.1023/A:1022151106085
Blaise, B.B., Bien-aimé, L.K.M., Betchewe, G., Marckman, G., Beda, T.: A phenomenological expression of strain energy in large elastic deformations of isotropic materials. Iran. Polym. J. 29(6), 525–533 (2020). https://doi.org/10.1007/s13726-020-00816-6
Bonet, J., Wood, R.D.: Nonlinear Continuum Mechanics for Finite Element Analysis, 2nd edn. Cambridge University Press, Cambridge (2008)
Bruhns, O.T., Meyers, A., Xiao, H.: Hencky’s elasticity model with the logarithmic strain measure: a study on Poynting effect and stress response in torsion of tubes and rods. Arch. Mech. 52(4–5), 489–509 (2000)
Chiskis, A., Parners, R.: Linear stress-strain relations in nonlinear elasticity. Acta Mech. 146(1), 109–113 (2001). https://doi.org/10.1007/BF01178798
Ciarletta, P., Destrade, M.: Torsion instability of soft solid cylinders. IMA J. Appl. Math. 79(5), 804–819 (2014). https://doi.org/10.1093/imamat/hxt052
Crisfield, M.A.: Non-linear Finite Element Analysis of Solids and Structures, vol. 2. Advanced Topics. Wiley, Chichester (1997)
Curnier, A.: Computational Methods in Solid Mechanics. Kluwer, Dordrecht (1994)
Curnier, A., Rakotomanana, L.: Generalized strain and stress measures: critical survey and new results. Eng. Trans. 39(3–4), 461–538 (1991)
Curnier, A., Zysset, P.: A family of metric strains and conjugate stresses, prolonging usual material laws from small to large transformations. Int. J. Solids Struct. 43(10), 3057–3086 (2006). https://doi.org/10.1016/j.ijsolstr.2005.06.015
Darijani, H.: Conjugated kinetic and kinematic measures for constitutive modeling of the thermoelastic continua. Contin. Mech. Thermodyn. 27(6), 987–1008 (2015). https://doi.org/10.1007/s00161-014-0393-2
Darijani, H., Naghdabadi, R.: Hyperelastic materials behavior modeling using consistent strain energy density functions. Acta Mech. 213(3), 235–254 (2010). https://doi.org/10.1007/s00707-009-0239-3
Darijani, H., Naghdabadi, R.: Constitutive modeling of solids at finite deformation using a second-order stress–strain relation. Int. J. Eng. Sci. 48(2), 223–236 (2010). https://doi.org/10.1016/j.ijengsci.2009.08.006
Darijani, H., Naghdabadi, R.: Kinematics and kinetics modeling of thermoelastic continua based on the multiplicative decomposition of the deformation gradient. Int. J. Eng. Sci. 62, 56–69 (2013). https://doi.org/10.1016/j.ijengsci.2012.07.001
Darijani, H., Naghdabadi, R., Kargarnovin, M.H.: Hyperelastic materials modelling using a strain measure consistent with the strain energy postulates. J. Mech. Eng. Sci. 224(3), 591–602 (2010). https://doi.org/10.1243/09544062JMES1590
De Souza Neto, E.A., Peric, D., Owen, D.J.R.: Computational Methods for Plasticity: Theory and Applications. Wiley, Chichester (2008)
Destrade, M., Gilchrist, M.D., Motherway, J., Murphy, J.G.: Slight compressibility and sensitivity to changes in Poisson’s ratio. Int. J. Numer. Methods Eng. 90(4), 403–411 (2012). https://doi.org/10.1002/nme.3326
Destrade, M., Horgan, C.O., Murphy, J.G.: Dominant negative Poynting effect in simple shearing of soft tissues. J. Eng. Math. 95(1), 87–98 (2015). https://doi.org/10.1007/s10665-014-9706-5
Doyle, T.C., Ericksen, J.L.: Nonlinear elasticity. In: Dryden, H.L., von Karman, T. (eds.) Advances in Applied Mechanics, vol. 4, pp. 53–115. Academic Press, New York (1956). https://doi.org/10.1016/S0065-2156(08)70371-5
Duka, E.D., England, A.H., Spencer, A.J.M.: Bifurcation of a solid circular elastic cylinder under finite extension and torsion. Acta Mech. 98(1), 107–121 (1993). https://doi.org/10.1007/BF01174297
Dya, T., Blaise, B.B., Betchewe, G., Bien-aimé, L.K.M., Beda, T., Alidou, M.: Characterization of pure torsion of a rubber-like cylinder using a hyperelastic model. Eur. Phys. J. Plus 137(5), 531 (2022). https://doi.org/10.1140/epjp/s13360-022-02737-0
Falope, F.O., Lanzoni, L., Tarantino, A.M.: Finite torsion of compressible circular cylinders: An approximate solution. J. Elast. 151(2), 187–217 (2022). https://doi.org/10.1007/s10659-022-09928-x
Farahani, K., Bahai, H.: Hyper-elastic constitutive equations of conjugate stresses and strain tensors for the Seth–Hill strain measures. Int. J. Eng. Sci. 42(1), 29–41 (2004). https://doi.org/10.1016/S0020-7225(03)00241-6
Fazekas, B., Goda, T.J.: Constitutive modelling of rubbers: Mullins effect, residual strain, time-temperature dependence. Int. J. Mech. Sci. 210, 106735 (2021). https://doi.org/10.1016/j.ijmecsci.2021.106735
Gent, A.N.: Elastic instabilities in rubber. Int. J. Non-Linear Mech. 40(2–3), 165–175 (2005). https://doi.org/10.1016/j.ijnonlinmec.2004.05.006
Gent, A.N., Hua, K.C.: Torsional instability of stretched rubber cylinders. Int. J. Non-Linear Mech. 39(3), 483–489 (2004). https://doi.org/10.1016/S0020-7462(02)00217-2
Gilchrist, M.D., Murphy, J.G., Rashid, B.: Generalisations of the strain-energy function of linear elasticity to model biological soft tissue. Int. J. Non-Linear Mech. 47(2), 268–272 (2012). https://doi.org/10.1016/j.ijnonlinmec.2011.06.004
Green, A.E., Shield, R.T.: Finite extension and torsion of cylinders. Philos. Trans. R. Soc. Lond. Ser. A, Math. Phys. Sci. 244(876), 47–86 (1951). https://doi.org/10.1098/rsta.1951.0015
Green, A.E., Spencer, A.J.M.: The stability of a circular cylinder under finite extension and torsion. J. Math. Phys. 37(1–4), 316–338 (1958). https://doi.org/10.1002/sapm1958371316
Hackett, R.M.: Hyperelasticity Primer, 2nd edn. Springer, Cham (2018)
Hashiguchi, K., Yamakawa, Y.: Introduction to Finite Strain Theory for Continuum Elasto-Plasticity. Wiley, Hoboken (2013)
Haupt, P.: Continuum Mechanics and Theory of Materials, 2nd edn. Springer, Berlin (2002)
Hencky, H.: The elastic behavior of vulcanized rubber. Rubber Chem. Technol. 6(2), 217–224 (1933a). https://doi.org/10.5254/1.3547545
Hencky, H.: The elastic behaviour of vulcanized rubber. J. Appl. Mech. 1(2), 45–53 (1933b). https://doi.org/10.1115/1.4012174
Hill, R.: On constitutive inequalities for simple materials – I. J. Mech. Phys. Solids 16(4), 229–242 (1968). https://doi.org/10.1016/0022-5096(68)90031-8
Hill, R.: Aspects of invariance in solid mechanics. In: Yih, C.S. (ed.) Advances in Applied Mechanics, vol. 18, pp. 1–75. Academic Press, New York (1979). https://doi.org/10.1016/S0065-2156(08)70264-3
Holzapfel, G.A.: Nonlinear Solid Mechanics: A Continuum Approach For Egineering. Wiley, Chichester (2000)
Horgan, C.O.: A note on a class of generalized neo-Hookean models for isotropic incompressible hyperelastic materials. Int. J. Non-Linear Mech. 129, 103665 (2021). https://doi.org/10.1016/j.ijnonlinmec.2020.103665
Horgan, C.O., Murphy, J.G.: A generalization of Hencky’s strain-energy density to model the large deformations of slightly compressible solid rubbers. Mech. Mater. 41(8), 943–950 (2009). https://doi.org/10.1016/j.mechmat.2009.03.001
Horgan, C.O., Murphy, J.G.: On the modeling of extension-torsion experimental data for transversely isotropic biological soft tissues. J. Elast. 108(2), 179–191 (2012). https://doi.org/10.1007/s10659-011-9363-0
Horgan, C.O., Murphy, J.G.: Reverse Poynting effects in the torsion of soft biomaterials. J. Elast. 118(2), 127–140 (2015). https://doi.org/10.1007/s10659-014-9482-5
Horgan, C.O., Murphy, J.G.: Poynting and reverse Poynting effects in soft materials. Soft Matter 13, 4916–4923 (2017). https://doi.org/10.1039/C7SM00992E
Horgan, C.O., Saccomandi, G.: Simple torsion of isotropic, hyperelastic, incompressible materials with limiting chain extensibility. J. Elast. 56(2), 159–170 (1999). https://doi.org/10.1023/A:1007606909163
Horgan, C.O., Smayda, M.G.: The importance of the second strain invariant in the constitutive modeling of elastomers and soft biomaterials. Mech. Mater. 51, 43–52 (2012). https://doi.org/10.1016/j.mechmat.2012.03.007
Horgan, C.O., Murphy, J.G., Saccomandi, G.: The complex mechanical response of anisotropic materials in simple experiments. Int. J. Non-Linear Mech. 106, 274–279 (2018). https://doi.org/10.1016/j.ijnonlinmec.2018.05.025
Hossain, M., Steinmann, P.: More hyperelastic models for rubber-like materials: consistent tangent operators and comparative study. J. Mech. Behav. Mater. 22(1–2), 27–50 (2013). https://doi.org/10.1515/jmbm-2012-0007
Itskov, M.: On the application of the additive decomposition of generalized strain measures in large strain plasticity. Mech. Res. Commun. 31(5), 507–517 (2004). https://doi.org/10.1016/j.mechrescom.2004.02.006
Itskov, M.: Tensor Algebra and Tensor Analysis for Engineers (with Applications to Continuum Mechanics), 5th edn. Springer, Cham (2019)
Janmey, P.A., McCormick, M.E., Rammensee, S., Leight, J.L., Georges, P.C., MacKintosh, F.C.: Negative normal stress in semiflexible biopolymer gels. Nat. Mater. 6(1), 48–51 (2007). https://doi.org/10.1038/nmat1810
Kanner, L.M., Horgan, C.O.: On extension and torsion of strain-stiffening rubber-like elastic circular cylinders. J. Elast. 93(1), 39–61 (2008). https://doi.org/10.1007/s10659-008-9164-2
Kellermann, D.C., Attard, M.M.: An invariant-free formulation of neo-Hookean hyperelasticity. J. Appl. Math. Mech./Z. Angew. Math. Mech. 96(2), 233–252 (2016). https://doi.org/10.1002/zamm.201400210
Korobeynikov, S.N.: Objective tensor rates and applications in formulation of hyperelastic relations. J. Elast. 93(2), 105–140 (2008). https://doi.org/10.1007/s10659-008-9166-0
Korobeynikov, S.N.: Families of continuous spin tensors and applications in continuum mechanics. Acta Mech. 216(1–4), 301–332 (2011). https://doi.org/10.1007/s00707-010-0369-7
Korobeynikov, S.N.: Basis-free expressions for families of objective strain tensors, their rates, and conjugate stress tensors. Acta Mech. 229(3), 1061–1098 (2018). https://doi.org/10.1007/s00707-017-1972-7
Korobeynikov, S.N.: Objective symmetrically physical strain tensors, conjugate stress tensors, and Hill’s linear isotropic hyperelastic material models. J. Elast. 136(2), 159–187 (2019). https://doi.org/10.1007/s10659-018-9699-9
Korobeynikov, S.N., Larichkin, A.Y., Rotanova, T.A.: Hyperelasticity models extending Hooke’s law from small to moderate strains and experimental verification of their scope of application. Int. J. Solids Struct. 252, 111815 (2022). https://doi.org/10.1016/j.ijsolstr.2022.111815
Le Saux, V., Marco, Y., Bles, G., Calloch, S., Moyne, S., Plessis, S., Charrier, P.: Identification of constitutive model for rubber elasticity from micro-indentation tests on natural rubber and validation by macroscopic tests. Mech. Mater. 43(12), 775–786 (2011). https://doi.org/10.1016/j.mechmat.2011.08.015
Lectez, A.-S., Verron, E., Huneau, B.: How to identify a hyperelastic constitutive equation for rubber-like materials with multiaxial tension–torsion experiments. Int. J. Non-Linear Mech. 65, 260–270 (2014). https://doi.org/10.1016/j.ijnonlinmec.2014.06.007
Luehr, C.P., Rubin, M.B.: The significance of projection operators in the spectral representation of symmetric second order tensors. Comput. Methods Appl. Mech. Eng. 84(3), 243–246 (1990). https://doi.org/10.1016/0045-7825(90)90078-Z
Marc Users Guide, A.: MARC Users Guide. Vol. A. Theory and Users Information. MSC.Software Corporation, Newport Beach (CA) (2015). MSC.Software Corporation
Marc Users Guide, D.: MARC Users Guide. Vol. D. User Subroutines And Special Routines. MSC.Software Corporation, Newport Beach (CA) (2015). MSC.Software Corporation
Marc Users Guide, B.: MARC Users Guide. Vol. B. Element Library. MSC.Software Corporation, Newport Beach (CA) (2015). MSC.Software Corporation
Martin, R.J., Ghiba, I.D., Neff, P.: A non-ellipticity result, or the impossible taming of the logarithmic strain measure. Int. J. Non-Linear Mech. 102, 147–158 (2018). https://doi.org/10.1016/j.ijnonlinmec.2018.02.011
Miehe, C., Lambrecht, M.: Algorithms for computation of stresses and elasticity moduli in terms of Seth–Hill’s family of generalized strain tensors. Commun. Numer. Methods Eng. 17(5), 337–353 (2001). https://doi.org/10.1002/cnm.404
Mihai, L.A., Goriely, A.: Positive or negative Poynting effect? The role of adscititious inequalities in hyperelastic materials. Proc. R. Soc. A, Math. Phys. Eng. Sci. 467(2136), 3633–3646 (2011). https://doi.org/10.1098/rspa.2011.0281
Mihai, L.A., Goriely, A.: Numerical simulation of shear and the Poynting effects by the finite element method: An application of the generalised empirical inequalities in non-linear elasticity. Int. J. Non-Linear Mech. 49, 1–14 (2013). https://doi.org/10.1016/j.ijnonlinmec.2012.09.001
Mihai, L.A., Goriely, A.: How to characterize a nonlinear elastic material? A review on nonlinear constitutive parameters in isotropic finite elasticity. Proc. R. Soc. A, Math. Phys. Eng. Sci. 473(2207), 20170607 (2017). https://doi.org/10.1098/rspa.2017.0607
Mihai, L.A., Budday, S., Holzapfel, G.A., Kuhl, E., Goriely, A.: A family of hyperelastic models for human brain tissue. J. Mech. Phys. Solids 106, 60–79 (2017). https://doi.org/10.1016/j.jmps.2017.05.015
Misra, A., Lekszycki, T., Giorgio, I., Ganzosch, G., Müller, W.H., dell’Isola, F.: Pantographic metamaterials show atypical Poynting effect reversal. Mech. Res. Commun. 89, 6–10 (2018). https://doi.org/10.1016/j.mechrescom.2018.02.003
Mokhireva, K.A., Svistkov, A.L.: A new approach to describe the elastic behavior of filled rubber-like materials under complex uniaxial loading. Int. J. Solids Struct. 202, 816–821 (2020). https://doi.org/10.1016/j.ijsolstr.2020.07.005
Murphy, J.G.: Linear isotropic relations in finite hyperelasticity: Some general results. J. Elast. 86(2), 139–154 (2007). https://doi.org/10.1007/s10659-006-9088-7
Murphy, J.G.: The stability of thin, stretched and twisted elastic rods. Int. J. Non-Linear Mech. 68, 96–100 (2015). https://doi.org/10.1016/j.ijnonlinmec.2014.05.018
Nedjar, B., Baaser, H., Martin, R.J., Neff, P.: A finite element implementation of the isotropic exponentiated Hencky-logarithmic model and simulation of the eversion of elastic tubes. Comput. Mech. 62(4), 635–654 (2018). https://doi.org/10.1007/s00466-017-1518-9
Neff, P., Ghiba, I.D., Lankeit, J.: The exponentiated Hencky-logarithmic strain energy. Part I: Constitutive issues and rank-one convexity. J. Elast. 121(2), 143–234 (2015). https://doi.org/10.1007/s10659-015-9524-7
Ogden, R.W.: Non-linear Elastic Deformations. Ellis Horwood, Chichester (1984)
O’Shea, D.J., Attard, M.M., Kellermann, D.C.: Anisotropic hyperelasticity using a fourth-order structural tensor approach. Int. J. Solids Struct. 198, 149–169 (2020a). https://doi.org/10.1016/j.ijsolstr.2020.03.021
O’Shea, D.J., Attard, M.M., Kellermann, D.C., Sansour, C.: Nonlinear finite element formulation based on invariant-free hyperelasticity for orthotropic materials. Int. J. Solids Struct. 185–186, 191–201 (2020b). https://doi.org/10.1016/j.ijsolstr.2019.08.010
Panov, A.D., Shumaev, V.V.: Using the logarithmic strain measure for solving torsion problems. Mech. Solids 47(1), 71–78 (2012). https://doi.org/10.3103/S0025654412010062
Penn, R.W.: Volume changes accompanying the extension of rubber. Trans. Soc. Rheol. 14, 509–517 (1970). https://doi.org/10.1122/1.549176
Peyraut, F., Feng, Z.Q., He, Q.C., Labed, N.: Robust numerical analysis of homogeneous and non-homogeneous deformations. Appl. Numer. Math. 59(7), 1499–1514 (2009). https://doi.org/10.1016/j.apnum.2008.10.002
Pietrzak, G.: Continuum mechanics modelling and augmented Lagrangian formulation of large deformation frictional contact problems. PhD thesis, LMA, DGM, EPFL, Lausanne (1997)
Plešek, J., Kruisová, A.: Formulation, validation and numerical procedures for Hencky’s elasticity model. Comput. Struct. 84(17–18), 1141–1150 (2006). https://doi.org/10.1016/j.compstruc.2006.01.005
Poživilová, A.: Constitutive modeling of hyperelastic materials using the logarithmic description. PhD thesis, CTU, Prague (2002)
Rivlin, R.S.: Large elastic deformations of isotropic materials. VI. Further results in the theory of torsion, shear and flexure. Philos. Trans. R. Soc. Lond. Ser. A, Math. Phys. Sci. 242(845), 173–195 (1949). https://doi.org/10.1098/rsta.1949.0009
Rivlin, R.S.: The solution of problems in second order elasticity theory. J. Ration. Mech. Anal. 2, 53–81 (1953)
Rivlin, R.S., Saunders, D.W.: Large elastic deformations of isotropic materials VII. Experiments on the deformation of rubber. Philos. Trans. R. Soc. Lond. Ser. A, Math. Phys. Sci. 243(865), 251–288 (1951). https://doi.org/10.1098/rsta.1951.0004
Saleeb, A.F., Chang, T.Y.P., Arnold, S.M.: On the development of explicit robust schemes for implementation of a class of hyperelastic models in large-strain analysis of rubbers. Int. J. Numer. Methods Eng. 33(6), 1237–1249 (1992). https://doi.org/10.1002/nme.1620330609
Schwarz, A., Steeger, K., Igelbüscher, M., Schröder, J.: Different approaches for mixed LSFEMs in hyperelasticity: Application of logarithmic deformation measures. Int. J. Numer. Methods Eng. 115(9), 1138–1153 (2018). https://doi.org/10.1002/nme.5838
Simo, J.C., Hughes, T.J.R.: Computational Inelasticity. Springer, Berlin (1998)
Steinmann, P., Hossain, M., Possart, G.: Hyperelastic models for rubber-like materials: Consistent tangent operators and suitability for Treloar’s data. Arch. Appl. Mech. 82(9), 1183–1217 (2012). https://doi.org/10.1007/s00419-012-0610-z
Šulc, P., Kopačka, J., Pešek, L., Bula, V.: Hyperelastic proportional damping for numerical non-conservative dynamic models of hard rubbers under large deformations. Int. J. Non-Linear Mech. 137, 103823 (2021). https://doi.org/10.1016/j.ijnonlinmec.2021.103823
Talebi, S., Darijani, H.: A pseudo-strain energy density function for mechanical behavior modeling of visco-hyperelastic materials. Int. J. Mech. Sci. 208, 106652 (2021). https://doi.org/10.1016/j.ijmecsci.2021.106652
Thiel, C., Voss, J., Martin, R.J., Neff, P.: Shear, pure and simple. Int. J. Non-Linear Mech. 112, 57–72 (2019). https://doi.org/10.1016/j.ijnonlinmec.2018.10.002
Truesdell, C., Noll, W.: The non-linear field theories of mechanics. In: Flügge, S. (ed.) Encyclopedia of Physics, vol. III/3, pp. 1–602. Springer, Berlin (1965). https://doi.org/10.1007/978-3-642-46015-9
Truesdell, C., Toupin, R.: The classical field theories. In: Flügge, S. (ed.) Principles of Classical Mechanics and Field Theory. Encyclopedya of Physics, pp. 226–858. Springer, Berlin (1960). https://doi.org/10.1007/978-3-642-45943-6_2
Upadhyay, K., Subhash, G., Spearot, D.: Thermodynamics-based stability criteria for constitutive equations of isotropic hyperelastic solids. J. Mech. Phys. Solids 124, 115–142 (2019). https://doi.org/10.1016/j.jmps.2018.09.038
Valanis, K.C.: The Valanis–Landel strain energy function elasticity of incompressible and compressible rubber-like materials. Int. J. Solids Struct. 238, 111271 (2022). https://doi.org/10.1016/j.ijsolstr.2021.111271
Valanis, K.C., Landel, R.F.: The strain-energy function of a hyperelastic material in terms of the extension ratios. J. Appl. Phys. 38(7), 2997–3002 (1967). https://doi.org/10.1063/1.1710039
Valiollahi, A., Shojaeifard, M., Baghani, M.: Closed form solutions for large deformation of cylinders under combined extension-torsion. Int. J. Mech. Sci. 157–158, 336–347 (2019). https://doi.org/10.1016/j.ijmecsci.2019.04.053
Volokh, K.Y.: Comments and authors’ reply on “Linear stress-strain relations in nonlinear elasticity” by A. Chiskis and R. Parners, (Acta Mech. 146, 109–113, 2001). Acta Mech. 146(3), 109–113 (2004). https://doi.org/10.1007/s00707-004-0146-6
Wang, D., Wu, M.S.: Poynting and axial force-twist effects in nonlinear elastic mono- and bi-layered cylinders: Torsion, axial and combined loadings. Int. J. Solids Struct. 51(5), 1003–1019 (2014). https://doi.org/10.1016/j.ijsolstr.2013.11.027
Wineman, A.: Some results for generalized neo-Hookean elastic materials. Int. J. Non-Linear Mech. 40(2–3), 271–279 (2005). https://doi.org/10.1016/j.ijnonlinmec.2004.05.007
Wineman, A.S., McKenna, G.B.: Determination of the strain energy density function for compressible isotropic nonlinear elastic solids by torsion – normal force experiments. In: Carroll, M.M., Hayes, M.A. (eds.) Nonlinear Effects in Fluid and Solids, pp. 339–353. Plenum Press, New York (1996)
Wu, H.C.: Continuum Mechanics and Plasticity. Chapman & Hall/CRC Press, Boca Raton (2005)
Xiao, H.: Hencky strain and Hencky model: Extending history and ongoing tradition. Multidiscip. Model. Mater. Struct. 1(1), 1–52 (2005). https://doi.org/10.1163/1573611054455148
Xiao, H., Chen, L.S.: Hencky’s elasticity model and linear stress–strain relations in isotropic finite hyperelasticity. Acta Mech. 157(1), 51–60 (2002). https://doi.org/10.1007/BF01182154
Xiao, H., Chen, L.S.: Hencky’s logarithmic strain and dual stress–strain and strain–stress relations in isotropic finite hyperelasticity. Int. J. Solids Struct. 40(6), 1455–1463 (2003). https://doi.org/10.1016/S0020-7683(02)00653-4
Xiao, H., He, L.H.: A unified exact analysis for the Poynting effects of cylindrical tubes made of Hill’s class of Hookean compressible elastic materials at finite strain. Int. J. Solids Struct. 44(2), 718–731 (2007). https://doi.org/10.1016/j.ijsolstr.2006.05.019
Xiao, H., Yue, Z.F., He, L.H.: Hill’s class of compressible elastic materials and finite bending problems: Exact solutions in unified form. Int. J. Solids Struct. 48(9), 1340–1348 (2011). https://doi.org/10.1016/j.ijsolstr.2011.01.016
Yaya, K., Bechir, H.: A new hyper-elastic model for predicting multi-axial behaviour of rubber-like materials: formulation and computational aspects. Mech. Time-Depend. Mater. 22(2), 167–186 (2018). https://doi.org/10.1007/s11043-017-9355-y
Zhong, D., Xiang, Y., Yin, T., Yu, H., Qu, S., Yang, W.: A physically-based damage model for soft elastomeric materials with anisotropic Mullins effect. Int. J. Solids Struct. 176–177, 121–134 (2019). https://doi.org/10.1016/j.ijsolstr.2019.05.018
Zubov, L.M.: Direct and inverse Poynting effects in elastic cylinders. Dokl. Phys. 46(9), 675–677 (2001). https://doi.org/10.1134/1.1409001
Acknowledgements
The support from Russian Federation government (Grant No. P220-14.W03.31.0002) is gratefully acknowledged.
Author information
Authors and Affiliations
Contributions
S.N.K. wrote the main manuscript text, T.A.R. got exact solutions and performed FE simulations, and A.Yu. Larickin performed FE simulations and prepared all figures. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Korobeynikov, S.N., Larichkin, A.Y. & Rotanova, T.A. Simulating cylinder torsion using Hill’s linear isotropic hyperelastic material models. Mech Time-Depend Mater (2023). https://doi.org/10.1007/s11043-023-09592-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11043-023-09592-1