Modeling of a homogeneous isotropic half space in the context of multi-phase lag coupled thermoelasticity

Abstract

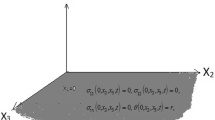
A two-dimensional multi-phase lag model in the context of generalized thermoelasticity is established for an isotropic half-space medium. A vector-matrix differential equation is obtained from the governing equations using normal mode analysis. The eigenvalue approach is applied to obtain the solutions. The temperature-dependent displacements, stresses, strains are calculated numerically and represented graphically to show the accuracy of the solution under mechanical and thermal loads.

Appendix 1

$$\begin{aligned} M_{11}=&aC_{12}+\omega ^{2}-\Omega ^{2},\quad M_{12}=M_{13}=M_{14}=0,\quad M_{15}=-iaC_{11},\quad M_{16}=1, \\ M_{21}=& M_{25}=M_{26}=0,\quad M_{22}= \frac{a^{2}+\omega ^{2}+\Omega ^{2}}{C_{21}},\quad M_{23}=- \frac{ia}{C_{21}},\quad M_{24}=-\frac{iaC_{22}}{C_{21}}, \\ M_{31}=&M_{35}=M_{36}=0,\quad M_{32}=ia \frac{\gamma ^{2}T_{0}}{\rho ^{2}C_{1}^{2}C_{E}}, \\ M_{33}=&a^{2}\frac{K_{22}}{K_{11}}+ \frac{\omega ^{2}\Bigg(\overline{R}+\tau _{0}\omega +\sum _{n=1}^{N}\frac{\tau _{q}^{n+1}}{(n+1)!}\omega ^{n+1}\Bigg)}{\frac{K_{11}}{\rho C_{E}C_{1}^{2}}\Bigg(1+\sum _{n=1}^{N}\frac{\tau _{\theta}^{n}}{n!}\omega ^{n}\Bigg)}, \, \\ M_{34}=& \frac{\gamma ^{2}T_{0}}{\rho ^{2}C_{1}^{2}C_{E}} \frac{\omega ^{2}\Bigg(\overline{R}+\tau _{0}\omega +\sum _{n=1}^{N}\frac{\tau _{q}^{n+1}}{(n+1)!}\omega ^{n+1}\Bigg)}{\frac{K_{11}}{\rho C_{E}C_{1}^{2}}\Bigg(1+\sum _{n=1}^{N}\frac{\tau _{\theta}^{n}}{n!}\omega ^{n}\Bigg)}\\ C_{11}=&C_{22}=\frac{\lambda +\mu +\frac{P}{2}}{\lambda +2\mu},\quad C_{12}=C_{21}= \frac{\mu -\frac{P}{2}}{\lambda +2\mu}\\ C_{41}=&\frac{\lambda +2\mu +\rho}{\rho c_{1}^{2}},\quad C_{42}= \frac{\lambda +P}{\rho c_{1}^{2}},\quad C_{51}= \frac{\mu -\frac{P}{2}}{\rho c_{1}^{2}},\quad c_{52}= \frac{\mu +\frac{P}{2}}{\rho c_{1}^{2}}\\ A=&\left ( \textstyle\begin{array}{c@{\quad}c} L_{11} & L_{12} \\ L_{21} & L_{22} \end{array}\displaystyle \right ) \qquad L_{11}=\left ( \textstyle\begin{array}{c@{\quad}c@{\quad}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array}\displaystyle \right ) \qquad L_{12}=\left ( \textstyle\begin{array}{c@{\quad}c@{\quad}c} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\displaystyle \right ) \\ L_{21}=&\left ( \textstyle\begin{array}{c@{\quad}c@{\quad}c} M_{11} & M_{12} & M_{13} \\ M_{21} & M_{22} & M_{23} \\ M_{31} & M_{32} & M_{33} \end{array}\displaystyle \right ) \qquad L_{22}=\left ( \textstyle\begin{array}{c@{\quad}c@{\quad}c} M_{14} & M_{15} & M_{16} \\ M_{24} & M_{25} & M_{26} \\ M_{34} & M_{35} & M_{36} \end{array}\displaystyle \right ) \end{aligned}$$

$$\begin{aligned} \textstyle\begin{array}{c@{\quad}c@{\quad}c} f_{11}=M_{11}+\lambda M_{14}-\lambda ^{2} & f_{21}=M_{21}+\lambda M_{24} & f_{31}=M_{31}+\lambda M_{34} \\ f_{12}=M_{12}+\lambda M_{15} & f_{22}=M_{22}+\lambda M_{25}-\lambda ^{2} & f_{32}=M_{32}+\lambda M_{35} \\ f_{13}=M_{13}+\lambda M_{16} & f_{23}=M_{23}+\lambda M_{26} & f_{33}=M_{33}+ \lambda M_{36}-\lambda ^{2} \end{array}\displaystyle \end{aligned}$$

$$\begin{aligned} R_{1i}(x) =& [-C_{41}\lambda _{i}(delta_{1})_{\lambda =\lambda _{i}}+iaC_{42}( \delta _{2})_{\lambda =-\lambda _{i}}-(\delta _{3})_{\lambda = \lambda _{i}}]e^{-\lambda _{i}x},\ i=1,2,3 \\ R_{2i}(x) = &[iaC_{41}(\delta _{2})_{\lambda =-\lambda _{i}}-C_{42} \lambda _{1}(\delta _{1})_{\lambda =-\lambda _{i}}-(\delta _{3})_{ \lambda =-\lambda _{i}}]e^{-\lambda _{i}x},\ i=1,2,3 \\ R_{3i}(x) = &[-C_{51}\lambda _{i}(\delta _{2})_{\lambda =-\lambda _{i}}+iaC_{52}( \delta _{1})_{\lambda =-\lambda _{i}}]e^{-\lambda _{i}x},\ i=1,2,3 \end{aligned}$$

$$\begin{aligned} z_{1} &= \sigma _{0}e^{i\omega t} \\ z_{2}& = T_{0}e^{i\omega t} \end{aligned}$$

$$\begin{aligned} S_{ij} =& R_{ij}(0),\quad i=1,4,\quad j=1,2,3 \\ S_{5k} =& R_{5k}(x),\quad k=1,2,3 \end{aligned}$$

$$D_{1}= \begin{vmatrix} z_{1} & S_{12} & S_{13} \\ z_{2} & S_{42} & S_{43} \\ 0 & S_{52} & S_{53} \end{vmatrix} \quad D_{2}= \begin{vmatrix} S_{11} & z_{1} & S_{13} \\ S_{41} & z_{2} & S_{43} \\ S_{51} & 0 & S_{53} \end{vmatrix} $$

$$D_{3}= \begin{vmatrix} S_{11} & S_{12} & z_{1} \\ S_{41} & S_{42} & z_{2} \\ S_{51} & S_{52} & 0 \end{vmatrix} \quad D= \begin{vmatrix} S_{11} & S_{12} & S_{13} \\ S_{41} & S_{42} & S_{43} \\ S_{51} & S_{52} & S_{53} \end{vmatrix} $$