Skip to main content
SpringerLink
Log in

Modelling of a Three Dimensional Thermoelastic Half Space with Three Phase Lags using Memory Dependent Derivative

  • Original Paper
  • Published:
International Journal of Applied and Computational Mathematics Aims and scope Submit manuscript

Abstract

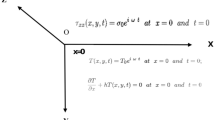
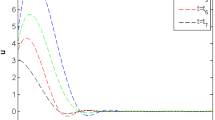
A mathematical model for a three dimensional isotropic half-space has been formulated to inspect lagging behaviours due to the presence of phase lags in context of memory dependent derivative, as an extension of several existing thermoelastic models like- Green-Naghdi-III, Lord Shulman, and Fourier’s Law etc. The analytical and procedural work has been done in integral transform domain preceded by eigenvalue approach to find the solution from the governing equations. Numerical computations and graphical representation of distribution of non-dimensional stress components, temperature with the effect of three phase lag, kernel function and time-delay has been performed with the help of the efficient mathematical software.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

Abbreviations

x i :

Space variables

\( \lambda ,\mu \) :

Lame’s Constant

u i :

Displacement components

\( \tau \) :

Relaxation Time

\( C_{E} \) :

Specific heat at constant strain

\( \tau_{q} \,,\tau_{v} \,,\tau_{T} \) :

Three-phase-lag

t :

Time variable

\( \rho \) :

Density of the material

\( T_{0} \) :

Reference temperature chosen such that \( \left| {\frac{{T - T_{0} }}{{T_{0} }}} \right| \) ≪ 1

\( \varepsilon = \tfrac{{\gamma^{2} T_{0} }}{{\rho C_{E} (\lambda + 2\mu )}} \) :

Thermal coupling parameter

σ ij :

Stress Components

ω :

Time delay

K (t, ξ):

Kernel function

References

  1. Biot, M.A.: Thermoelasticity and irreversible thermodynamics. J. Appl. Phys. 27(3), 240–253 (1956)

    Article  MathSciNet  MATH  Google Scholar 

  2. Hetnarski, R.B., Ignaczak, J.: Generalized thermoelasticity. J. Therm. Stress. 22(4), 451–476 (1999)

    MathSciNet  MATH  Google Scholar 

  3. Lord, H.W., Shulman, Y.: A generalized dynamical theory of thermoelasticity. J. Mech. Phys. Solids 15(5), 299–309 (1967)

    Article  MATH  Google Scholar 

  4. Ranjit, S.D., Sherief, H.H.: Generalized thermoelasticity for anisotropic media. Q. Appl. Math. 33(1), 1–8 (1980)

    Article  MathSciNet  MATH  Google Scholar 

  5. Sherief, H.H., Anwar, MdN: Problem in generalized thermoelasticity. J. Therm. Stress 9(2), 165–181 (1986)

    Article  Google Scholar 

  6. Ozisik, M.N., Tzou, D.Y.: On the wave theory in heat conduction. ASME J. Heat Transf. 116(3), 526–535 (1994)

    Article  Google Scholar 

  7. Green, A.E., Lindsay, K.A.: Thermoelasticity. J. Elast. 2(1), 1–7 (1972)

    Article  MATH  Google Scholar 

  8. Hetnarski, R.B., Ignaczak, J.: Soliton-like waves in a low temperature nonlinear thermoelastic solid. Int. J. Eng. Sci. 34(15), 1767–1787 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  9. Kosinski, W., Cimmelli, V.A.: Gradient generalization to inertial state variables and a theory of super fluidity. J. Theor. Appl. Mech. 35, 763–779 (1997)

    MATH  Google Scholar 

  10. Green, A.E., Naghdi, P.M.: A re-examination of the basic postulates of thermomechanics. Proc. R. Soc. Lond. Ser. A (1991). https://doi.org/10.1098/rspa.1991.0012

    Article  MATH  Google Scholar 

  11. Green, A.E., Naghdi, P.M.: On undamped heat waves in an elastic solid. J. Ther. Stress. 15(2), 253–264 (1992)

    Article  MathSciNet  Google Scholar 

  12. Green, A.E., Naghdi, P.M.: Thermoelasticity without energy dissipation. J. Elast. 31(3), 189–208 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  13. Chandrasekhariah, D.S.: Hyperbolic thermoelasticity: a review of recent literature. Appl. Mech. Rev. 21(12), 705–729 (1998)

    Article  Google Scholar 

  14. Tzou, D.Y.: A unified field approach for heat conduction from macro- to micro-scales. J. Heat Transf. 117(1), 8–16 (1995)

    Article  Google Scholar 

  15. Tzou, D.Y.: Experimental support for the lagging behavior in heat propagation. J. Thermophys. Heat Transf. 9(4), 686–693 (1995)

    Article  Google Scholar 

  16. Roy Choudhuri, S.K.: On a thermoelastic three-phase-lag model. J. Therm. Stress. 30(3), 231–238 (2007)

    Article  Google Scholar 

  17. Wang, J.L., Li, H.F.: Surpassing the fractional derivative: concept of the memory-dependent derivative. Comput. Math Appl. 62, 1562–1567 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  18. Ghosh, D., Lahiri, A.: A Study on the generalized thermoelastic problem for an anisotropic medium. J. Heat Transf. 140(9), 094501 (2018)

    Article  Google Scholar 

  19. Belman, R., Kalaba, R.E., Lockett, J.: Numerical inversion of the laplace transform. American Elsevier, New York (1956)

    Google Scholar 

  20. McPhedran, R.C., McKenzie, D.R.: The Conductivity of Lattices of Spheres I. The Simple Cubic Lattice. Royal Sciety Publishing, London (1978)

    Book  Google Scholar 

  21. Sclater, J.G., Parsons, B., Jaupart, C.: Oceans and continents similarities and differences in the mechanisms of heat loss. J. Geophys. Res. 86, 11535–11552 (1981)

    Article  Google Scholar 

  22. Turcotte, D.L., Schubert, G.: Geodynamics–applications of continuum physics to geological problems. Wiley, New York (1982)

    Google Scholar 

  23. Ezzat, M.A., El Karamany, A.S., Fayik, M.A.: Fractional order theory in thermoelastic solid with three-phase lag heat transfer. Arch. Appl. Mech. 82(4), 557–572 (2012)

    Article  MATH  Google Scholar 

  24. Sarkar, N., Mondal, S.: Transient responses in a two-temperature thermoelastic infinite medium having cylindrical cavity due to moving heat source with memory-dependent derivative. J. Appl. Math. Mech. 99(6), e201800343 (2019)

    MathSciNet  Google Scholar 

  25. Abbas, I.A.: A GN model based upon two-temperature generalized thermoelastic theory in an unbounded medium with a spherical cavity. Appl. Math. Comput. 245, 108–115 (2014)

    MathSciNet  MATH  Google Scholar 

  26. Atwa, S.Y., Sarkar, N.: Memory-dependent magneto–thermoelasticity for perfectly conducting two-dimensional elastic solids with thermal shock. J. Ocean Eng. Sci. (2019). https://doi.org/10.1016/j.joes.2019.05.004

    Article  Google Scholar 

  27. Lofty, K., Sarkar, N.: Memory-dependent derivatives for photothermal semiconducting medium in generalized thermoelasticity with two-temperature. Mech. Time Depend. Mater. 21(4), 519–534 (2017)

    Article  Google Scholar 

  28. Abd-alla, A.N., Abbas, I.A.: A problem of generalized magnetothermoelasticity for an infinitely long, perfectly conducting cylinder. J. Therm. Stress. 25(11), 1009–1025 (2002)

    Article  Google Scholar 

  29. Abbas, I.A.: A problem on functional graded material under fractional order theory of thermoelasticity. Theor. Appl. Fract. Mech. 74, 18–22 (2014)

    Article  Google Scholar 

  30. Abbas, I.A., Abo-Dahad, S.M.: On the numerical solution of thermal shock problem for generalized magneto-thermoelasticity for an infinitely long annular cylinder with variable thermal conductivity. J. Comput. Theor. Nanosci. 11(3), 607–618 (2014)

    Article  Google Scholar 

  31. Abbas, I.A., Youssef, H.M.: A nonlinear generalized thermoelasticity model of temperature-dependent materials using finite element method. Int. J. Thermophys. 33(7), 1302–1303 (2012)

    Article  Google Scholar 

  32. Abbas, I.A., Youssef, H.M.: Two-temperature generalized thermoelasticity under ramp-type heating by finite element method. Meccanica 48(2), 331–339 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  33. Ghosh, D., Lahiri, A., Kumar, R., Roy, S.: 3D thermoelastic interactions in an anisotropic elastic slab due to prescribed surface temperature. J. Solid Mech. 10(3), 502–521 (2018)

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Jadavpur University, Kolkata, 700 032, India

    Debkumar Ghosh & Abhijit Lahiri

  2. Department of Geology, Asutosh College, 92 S. P.Mukherjee Road, Kolkata, 700 026, India

    Ashis Kumar Das

Authors
  1. Debkumar Ghosh
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ashis Kumar Das
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Abhijit Lahiri
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Debkumar Ghosh.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

$$ A = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ {M_{51} } & {M_{52} } & {M_{53} } & {M_{54} } & {M_{55} } & {M_{56} } & {M_{57} } & {M_{58} } \\ {M_{61} } & {M_{62} } & {M_{63} } & {M_{64} } & {M_{65} } & {M_{66} } & {M_{67} } & {M_{68} } \\ {M_{71} } & {M_{72} } & {M_{73} } & {M_{74} } & {M_{75} } & {M_{76} } & {M_{77} } & {M_{78} } \\ {M_{81} } & {M_{82} } & {M_{83} } & {M_{84} } & {M_{85} } & {M_{86} } & {M_{87} } & {M_{88} } \\ \end{array} } \right] $$
$$ \underrightarrow v = \left[ {U_{1} \,U_{2} \,U_{3} \,\,\varTheta \,\,U_{1}^{\prime } \,U_{2}^{\prime } \,U_{3}^{\prime } \,\,\varTheta^{\prime}} \right]^{T} $$
$$ \begin{aligned} &M_{51} = A_{11} ,M_{52} = 0,M_{53} = 0,M_{54} = 0,M_{55} = 0, \hfill \\ &M_{56} = A_{12} ,M_{57} = A_{13} ,M_{58} = A_{14} , \hfill \\ &M_{61} = 0,\,\,M_{62} = B_{11} ,\,M_{63} = B_{12} ,\,M_{64} = B_{13} \,,M_{65} = B_{14} ,M_{66} = 0,\,\,\,M_{67} = 0\,,\,\,\,\,\,M_{68} = 0 \hfill \\ &M_{71} = 0,\,\,M_{72} = C_{11} ,\,M_{73} = C_{12} ,\,M_{74} = C_{13} ,\,M_{75} = C_{14} ,M_{76} = 0,\,\,M_{77} = 0\,,\,\,\,M_{78} = 0 \hfill \\ &M_{81} = 0,\,\,M_{82} = D_{11} ,\,M_{83} = D_{12} ,\,M_{84} = D_{13} ,\,M_{85} = D_{14} ,M_{86} = 0,\,M_{87} = 0\,,\,\,M_{88} = 0 \hfill \\ \end{aligned} $$
$$ \begin{aligned} A_{11} = s^{2} + \varepsilon_{3} \left( {\psi_{2}^{2} + \psi_{3}^{2} } \right), \hfill \\ A_{12} = - i\,\varepsilon_{1} \,\psi_{2} , \hfill \\ A_{13} = - i\,\varepsilon_{1} \,\psi_{3} , \hfill \\ A_{14} = 1 + \frac{{\varepsilon_{3} \,\nu \,G}}{\omega }, \hfill \\ \end{aligned} $$
$$ \begin{aligned} B_{11} = \frac{{s^{2} + \psi_{2}^{2} }}{{\varepsilon_{3} }}, \hfill \\ B_{12} = \frac{{\varepsilon_{1} \,\psi_{2\,} \psi_{3} }}{{\varepsilon_{3} }} \hfill \\ B_{13} = \frac{{i\,\psi_{2} }}{{\varepsilon_{3} }}\left( {1 + \frac{{\varepsilon_{3} \,\nu \,G}}{\omega }} \right), \hfill \\ B_{14} = - \frac{{i\,\varepsilon_{1} \,\psi_{2} }}{{\varepsilon_{3} }}, \hfill \\ \end{aligned} $$
$$ \begin{aligned} C_{11} = \frac{{\varepsilon_{1} \,\psi_{2\,} \psi_{3} }}{{\varepsilon_{3} }}, \hfill \\ C_{12} = \frac{{s^{2} + \psi_{3}^{2} + \varepsilon_{3} \psi_{2}^{2} }}{{\varepsilon_{3} }}, \hfill \\ C_{13} = \frac{{i\,\psi_{3} }}{{\varepsilon_{3} }}\left( {1 + \frac{{\varepsilon_{3} \,\nu \,G}}{\omega }} \right), \hfill \\ C_{14} = - \frac{{i\,\varepsilon_{1} \,\psi_{3} }}{{\varepsilon_{3} }}, \hfill \\ \end{aligned} $$
$$ \begin{aligned} D_{11} = \frac{{\varepsilon_{12} }}{{\varepsilon_{9} }},\,\, \hfill \\ D_{12} = \frac{{\varepsilon_{13} \,}}{{\varepsilon_{9} }},\,\,\, \hfill \\ D_{13} = \frac{{\varepsilon_{10} \,}}{{\varepsilon_{9} }},\,\, \hfill \\ D_{14} = \frac{{\varepsilon_{14} \,}}{{\varepsilon_{9} }}\,\, \hfill \\ \end{aligned} $$
$$ \begin{aligned} \beta_{1} = i\,\varepsilon_{4} \,\psi_{2} \hfill \\ \beta_{2} = i\,\varepsilon_{4} \,\psi_{3} \hfill \\ \beta_{3} = - \left( {1 + \frac{{\varepsilon_{3} \,\nu \,G}}{\omega }} \right), \hfill \\ \beta_{4} = i\,\psi_{2} , \hfill \\ \beta_{5} = i\,\psi_{3} , \hfill \\ \beta_{6} = i\,\varepsilon_{2} \,\psi_{2} , \hfill \\ \beta_{7} = i\,\varepsilon_{2} \,\psi_{3} , \hfill \\ \end{aligned} $$
$$ \begin{aligned} \varepsilon_{1} = \frac{\lambda + \mu }{\lambda + 2\mu };\varepsilon_{2} = \frac{\mu }{\lambda + 2\mu };\varepsilon_{3} = \frac{1}{{c_{0} \eta^{2} }};\,\,\varepsilon_{4} = \frac{\lambda }{\lambda + 2\mu }; \hfill \\ \varepsilon_{5} = \frac{{T_{0} \,\gamma^{2} }}{{k\,\,\eta \,\,\left( {\lambda + 2\mu } \right)}};\,\,\varepsilon_{6} = \frac{{k\,c_{0}^{4} \,\eta^{2} \,\tau_{T} }}{{k\,^{*} }};\,\,\,\varepsilon_{7} = \frac{{c_{0} \,\eta \,\,\tau_{v}^{*} }}{{k\,^{*} }};\,\,\, \hfill \\ \varepsilon_{8} = \frac{k}{{k\,^{*} }};\,\,\varepsilon_{9} = \left( {1 + \frac{{\tau_{\theta } \,\,G}}{\omega }} \right)\left( {1 + \varepsilon_{6} \,s^{2} + + \varepsilon_{7} \,s} \right);\,\,\, \hfill \\ \end{aligned} $$
$$ \begin{aligned} \varepsilon_{10} = \varepsilon_{8} \left( {s + \frac{{\tau_{q} \,s\,G}}{\omega } + \frac{{\tau_{q}^{2} \,s^{2} \,G}}{2\,\omega }} \right) + \varepsilon_{9} \left( {\psi_{2}^{2} + \psi_{3}^{2} } \right);\,\, \hfill \\ \varepsilon_{11} = \varepsilon_{5} \,\varepsilon_{8} \left( {s + \frac{{\tau_{q} \,s\,G}}{\omega } + \frac{{\tau_{q}^{2} \,s^{2} \,G}}{2\,\omega }} \right); \hfill \\ \end{aligned} $$
$$ \begin{aligned} \varepsilon_{12} = i\,\psi_{2\,} \varepsilon_{5} \,\varepsilon_{8} \left( {s + \frac{{\tau_{q} \,s\,G}}{\omega } + \frac{{\tau_{q}^{2} \,s^{2} \,G}}{2\,\omega }} \right);\,\,\, \hfill \\ \varepsilon_{13} = i\,\psi_{3\,} \varepsilon_{5} \,\varepsilon_{8} \left( {s + \frac{{\tau_{q} \,s\,G}}{\omega } + \frac{{\tau_{q}^{2} \,s^{2} \,G}}{2\,\omega }} \right); \hfill \\ \end{aligned} $$

\( \begin{aligned} & d_{1} = (h_{24} h_{13} - h_{14} h_{23} )(h_{22} h_{33} - h_{32} h_{23} ) - (h_{34} h_{23} - h_{24} h_{33} )(h_{12} h_{23} - h_{22} h_{13} ), \\ & d_{2} = (h_{34} h_{23} - h_{24} h_{33} )(h_{11} h_{23} - h_{21} h_{13} ) - (h_{24} h_{13} - h_{14} h_{23} )(h_{21} h_{33} - h_{31} h_{23} ), \\ & d_{3} = (h_{12} h_{21} - h_{11} h_{22} )(h_{21} h_{34} - h_{31} h_{24} ) - (h_{22} h_{31} - h_{21} h_{32} )(h_{11} h_{24} - h_{14} h_{21} ), \\ & d_{4} = (h_{11} h_{23} - h_{21} h_{13} )(h_{22} h_{33} - h_{32} h_{23} ) - (h_{12} h_{23} - h_{22} h_{13} )(h_{21} h_{33} - h_{31} h_{23} ), \\ \end{aligned} \),

$$ \begin{aligned} h_{11} = M_{51} - \lambda^{2} \,\,,h_{12} = \lambda M_{56} \,\,,h_{13} = \lambda M_{57} \,\,,h_{14} = \lambda M_{58} \hfill \\ h_{21} = M_{65} \,\,,h_{22} = M_{62} \, - \lambda^{2} \,,h_{23} = M_{63} \,\,,h_{24} = M_{64} \hfill \\ h_{31} = \lambda M_{75} \,,h_{32} = M_{72} \,\,,h_{33} = M_{73} \, - \lambda^{2} \,,h_{34} = \lambda M_{74} \hfill \\ h_{41} = \lambda M_{85} \,\,,h_{42} = M_{82} \,\,,h_{43} = M_{83} \,\,,h_{44} = M_{84} - \lambda^{2} \hfill \\ \end{aligned} $$
$$ R_{1i} = \left( { - \lambda_{i} \,d_{1i} + \sum\limits_{k = 1}^{3} {\beta_{k} \,d_{(k + 1)i} } } \right)e^{{ - \lambda_{i} x_{1} }} ,,i = 1(1)4 $$
$$ R_{2i} = \left( { - \lambda_{i} \,\,\varepsilon_{4} \,d_{1i} + \beta_{4} \,d_{2i} + \beta_{2} \,d_{3i} + \beta_{3} \,d_{4i} } \right)e^{{ - \lambda_{i} x_{1} }} ,i = 1(1)4 $$
$$ R_{3i} = \left( { - \lambda_{1} \,\varepsilon_{4} \,d_{1i} + \beta_{1} \,d_{2i} + \beta_{5} \,d_{3i} + \beta_{3} \,d_{4i} } \right)e^{{ - \lambda_{i} x_{1} }} ;,i = 1(1)4 $$
$$ R_{4i} = \left( {\beta_{6} \,d_{1i} - \varepsilon_{2} \,\lambda_{i} \,d_{2i} } \right)e^{{ - \lambda_{i} x_{1} }} ,i = 1(1)4 $$
$$ R_{5i} = \left( {\beta_{7} \,d_{1i} - \varepsilon_{2} \,\lambda_{i} \,d_{3i} } \right)e^{{ - \lambda_{i} x_{1} }} ,i = 1(1)4 $$
$$ R_{6i} = \left( {\beta_{7} \,d_{2i} + \beta_{6} \,d_{3i} } \right)e^{{ - \lambda_{i} x_{1} }} ,i = 1(1)4 $$
$$ R_{7i} = d_{4i} \,e^{{ - \lambda_{i} x_{1} }} i = 1(1)4 $$
$$ \begin{aligned} l_{1j} = R_{1j} (0),\,\,\,\,l_{4j} = R_{4j} (0),\,\,\,\,l_{5j} = R_{5j} ,\,\, \hfill \\ \,l\,_{7j} = R_{7j} (0),\,\,\,\,where\,j = 1,2,3,4 \hfill \\ \end{aligned} $$
$$ and\,\,A_{i} = \frac{{D_{i} }}{\Delta }\,,i = 1,2,3,4 $$
$$ \begin{aligned} D_{1} = \left[ {\begin{array}{*{20}c} 0 & {l_{12} } & {l_{13} } & {l_{14} } \\ 0 & {l_{42} } & {l_{43} } & {l_{44} } \\ 0 & {l_{52} } & {l_{53} } & {l_{54} } \\ {r^{*} } & {l_{72} } & {l_{73} } & {l_{74} } \\ \end{array} } \right],D_{2} = \left[ {\begin{array}{*{20}c} {l_{11} } & 0 & {l_{13} } & {l_{14} } \\ {l_{41} } & 0 & {l_{43} } & {l_{44} } \\ {l_{51} } & 0 & {l_{53} } & {l_{54} } \\ {l_{71} } & {r^{*} } & {l_{73} } & {l_{74} } \\ \end{array} } \right], \hfill \\ D_{3} = \left[ {\begin{array}{*{20}c} {l_{11} } & {l_{12} } & 0 & {l_{14} } \\ {l_{41} } & {l_{42} } & 0 & {l_{44} } \\ {l_{51} } & {l_{52} } & 0 & {l_{54} } \\ {l_{71} } & {l_{72} } & {r^{*} } & {l_{74} } \\ \end{array} } \right],D_{4} = \left[ {\begin{array}{*{20}c} {l_{11} } & {l_{12} } & {l_{13} } & 0 \\ {l_{41} } & {l_{42} } & {l_{43} } & 0 \\ {l_{51} } & {l_{52} } & {l_{53} } & 0 \\ {l_{71} } & {l_{72} } & {l_{73} } & {r^{*} } \\ \end{array} } \right],\Delta = \left[ {\begin{array}{*{20}c} {l_{11} } & {l_{12} } & {l_{13} } & {l_{14} } \\ {l_{41} } & {l_{42} } & {l_{43} } & {l_{44} } \\ {l_{51} } & {l_{52} } & {l_{53} } & {l_{54} } \\ {l_{71} } & {l_{72} } & {l_{73} } & {l_{74} } \\ \end{array} } \right] \hfill \\ \end{aligned} $$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ghosh, D., Das, A.K. & Lahiri, A. Modelling of a Three Dimensional Thermoelastic Half Space with Three Phase Lags using Memory Dependent Derivative. Int. J. Appl. Comput. Math 5, 154 (2019). https://doi.org/10.1007/s40819-019-0731-y

Download citation

  • Published:

  • DOI: https://doi.org/10.1007/s40819-019-0731-y

Keywords

Search

Navigation