Importance Weighting in Hybrid Iterative Ensemble Smoothers for Data Assimilation

Abstract

Because it is generally impossible to completely characterize the uncertainty in complex model variables after assimilation of data, it is common to approximate the uncertainty by sampling from approximations of the posterior distribution for model variables. When minimization methods are used for the sampling, the weights on each of the samples depend on the magnitude of the data mismatch at the critical points and on the Jacobian of the transformation from the prior density to the sample proposal density. For standard iterative ensemble smoothers, the Jacobian is identical for all samples, and the weights depend only on the data mismatch. In this paper, a hybrid data assimilation method is proposed which makes it possible for each ensemble member to have a distinct Jacobian and for the approximation to the posterior density to be multimodal. For the proposed hybrid iterative ensemble smoother, it is necessary that a part of the mapping from the prior Gaussian random variable to the data be analytic. Examples might include analytic transformation from a latent Gaussian random variable to permeability followed by a black-box transformation from permeability to state variables in porous media flow, or a Gaussian hierarchical model for variables followed by a similar black-box transformation from permeability to state variables. In this paper, the application of weighting to both hybrid and standard iterative ensemble smoothers is investigated using a two-dimensional, two-phase flow problem in porous media with various degrees of nonlinearity. As expected, the weights in a standard iterative ensemble smoother become degenerate for problems with large amounts of data. In the examples, however, the weights for the hybrid iterative ensemble smoother were useful for improving forecast reliability.

1 Introduction

In many geoscience applications, parameters of high-dimensional models must be estimated from a limited number of noisy data. The data are often only indirectly and non-linearly related to the parameters of the model. Consequently, the parameters of the model are usually underdetermined, and estimation of a single set of model parameters that satisfy the data is not sufficient to characterize the solution of the inverse problem.

Although powerful methods for quantifying uncertainty in high-dimensional model spaces with Gaussian uncertainty are available (Martin et al. 2012), and powerful Monte Carlo methods are available for non-Gaussian low-dimensional model spaces, it is still a challenge to quantify uncertainty for situations where the model dimension is large and the posterior distribution is non-Gaussian. In that case, approximate sampling methods must typically be used. A relatively standard approach to approximate sampling is through the minimization of a stochastic cost function. The method is known by various names including geostatistical inversing (Kitanidis 1995), randomized maximum likelihood (Oliver et al. 1996), randomized maximum a posteriori (Wang et al. 2018), and randomize-then-optimize (Bardsley et al. 2014). In these methods, a realization from an approximation to the posterior distribution is generated by minimizing the weighted squared distance of the posterior sample to a realization from the prior and the squared distance between the actual data and the perturbed simulated data. The method provides exact sampling when the prior distribution is Gaussian and the relationship between data and model parameters is linear. When the posterior distribution is non-Gaussian but unimodal, it is possible to weight the realizations from minimization such that the sampling is exact (Oliver et al. 1996; Oliver 2017; Bardsley et al. 2014, 2020; Wang et al. 2018), although computation of weights in high dimensions may be difficult.

The actual posterior landscape for distributed-parameter geoscience inverse problems is difficult to ascertain, although there are known to be features of subsurface flow models that result in multimodal posterior distributions: uncertain fault displacement in a layered reservoir (Tavassoli et al. 2005), uncertain rock type location in a channelized reservoir (Zhang et al. 2003), layered non-communicating reservoir flow with independent uncertain properties (Oliver et al. 2011), and non-Gaussian prior distributions for log-permeability (Oliver and Chen 2018). For relatively simple transient single-phase flow problems, in which the prior distribution of log-permeability is multivariate normal, the posterior distribution appears to be multimodal in low-dimensional subspaces, but appears to be characterized by curved ridges in higher-dimensional subspaces (Oliver and Chen 2011).

Sampling the posterior distribution correctly for subsurface flow models is difficult when there are hundreds of thousands to millions of uncertain parameters whose magnitudes must be inferred from the data. The Markov chain Monte Carlo (MCMC) methods are usually considered the gold standard for sampling from Bayesian posteriors. Because of the high computational cost of evaluating the likelihood function for subsurface flow models, however, MCMC is seldom used for subsurface models. For a two-dimensional single-phase porous flow problem in which only the permeability field is uncertain, an MCMC method with transition proposals required hundreds of thousands of iterations to generate a useful number of independent samples (Oliver et al. 1997). For a porous flow model with a more complex posterior but only three uncertain parameters, a population MCMC approach demonstrated good mixing properties and provided good results, but at substantial cost (Mohamed et al. 2012). In order to reduce the cost of the likelihood evaluation, Maschio and Schiozer (2014) replaced the flow simulator by proxy models generated by an artificial neural network. An iterative procedure combining MCMC sampling and artificial neural network (ANN) training was applied to a reservoir model with 16 uncertain attributes.

Iterative ensemble smoothers, on the other hand, have been remarkably successful at history matching large amounts of data into reservoir models with hundreds of thousands of parameters. Based loosely on the ensemble Kalman filter (Evensen 1994), which is routinely used for numerical weather prediction, iterative ensemble smoothers use stochastic gradient approximations for minimization, so that solutions of the adjoint system are not necessary. The downside of this is that the methodology must approximate the cost function as a quadratic surface. Consequently, the method is not well suited to arbitrary posterior landscapes.

When the posteriori probability density function (pdf) has multiple modes of any type, minimization-based simulation methods will almost certainly sample occasionally from local minima of the cost function that contribute very little to the probability mass in the posterior. These samples are usually, but not always, characterized by large data mismatch after minimization. In the case of an exceptionally large data mismatch, it is common practice to omit poorly calibrated model realizations when computing mean forecasts and uncertainty quantification. It is much more difficult to decide how to treat realizations with intermediate data mismatches, or realizations in general when the unweighted distribution is known to be only approximate. Importance weighting of realizations to correct for the approximate sampling is the principled approach to uncertainty quantification in these cases.

It has been shown that a standard class of importance-weighted particle filters are degenerate in high dimensions even when the so-called optimal proposal is used (Snyder et al. 2015; van Leeuwen et al. 2019). The optimal proposal is defined as the one that minimizes the variance of weights for particle filters that are based only on the new observations and the particles generated at a previous step (Doucet et al. 2000). For updating schemes that are not limited to the use of the prior ensemble of particles, the weights need not be degenerate. Ba et al. (2022) demonstrated that the weights in a properly weighted randomized maximum likelihood (RML) scheme are not necessarily degenerate, even when the problem is nonlinear. And it is known that linear inference problems can be sampled exactly using the minimization methods, in which case all weights are identical. When the problem has many modes, however, the local minimizer is attracted to modes with small probability mass, and the weights may become degenerate simply because the weights on small local minima should be small. Weights can also become degenerate when they are inaccurately computed because of approximations in the gradient.

van Leeuwen et al. (2019) identify four approaches to reducing the variance in weights for particle filters. The minimization approach (RML) used in this paper can be considered to belong to the category in which particles are pushed from the prior into regions of high posterior probability density. For inverse problems with Gaussian priors on model parameters and linear observation operators, after minimization, the particles are distributed as the target distribution, so weighting is not required. When the posterior is multimodal, however, the problem of weighting can be relatively complex, as each particle in the prior potentially maps to multiple particles in the proposal density, each with a different weight. Ba et al. (2022) computed low-rank approximations to the particle weights for a single-phase porous media flow problem using the adjoint system for the flow simulator, but adjoint systems are not always available, and the cost can be prohibitive. In this paper, we show how approximate weights can be easily computed when an ensemble Kalman-based approach is used to solve an inverse problem.

In this paper, we develop an importance weighting approach to the problem in which the relationship between observations and model parameters is sufficiently nonlinear that the posterior distribution for model parameters is multimodal. Although importance weighting in particle filters is a standard approach for dealing with nonlinearity in small data assimilation problems, we apply it to problems with relatively large numbers of model parameters and data. We show that this can be done in a hybrid iterative ensemble smoother approach for which gradients required for minimization are computed using a combination of analytical and stochastic gradients. The method is applied to a two-phase porous media flow problem with multimodal posterior pdf. In order to be useful for large problems, we improve an earlier approach through the use of circulant embedding of the covariance matrix to allow matrix multiplication in large models. Finally, we demonstrate that the weights computed using a hybrid or ensemble Kalman-like approach are noisy approximations of the true weights and that denoising the weights improves model predictability.

2 Methodology

Consider the following generic forward model for prediction of u given $\varvec{\theta }$,

$$\begin{aligned} {{\mathcal {B}}} (\varvec{\theta },u)=0, \quad \text {in}\quad \Omega , \end{aligned}$$

which for example could be a system of partial differential equations (PDEs) characterizing a physical problem. In the parameter estimation problem, the task is to quantify the unknown parameter $\varvec{\theta }$ given some limited observations of u on parts of the domain $\Omega$. The relationship between model parameters and observations is given by the widely used model

$$\begin{aligned} {\varvec{d}}^o= {g}( {\varvec{m}}(\varvec{\theta })) + \varvec{\epsilon }, \end{aligned}$$

where $g(\cdot )$ is the generic observation operator and ${\varvec{m}}(\cdot )$ is the model operator mapping the unknown $\varvec{\theta }$ to the space of an intermediate variable, such as the hierarchical model, transformation of permeability, and composite observation, including the three cases of Sect. 2. In a finite-dimensional parameter space, $\varvec{\theta } \in {{\mathbb {R}}}^{N_\theta }$, ${\varvec{m}}(\varvec{\theta })\in {{\mathbb {R}}}^{N_m}$, and ${\varvec{d}}^o\in {{\mathbb {R}}}^{N_d}$. Assume that $\varvec{\epsilon } \in {{\mathbb {R}}}^{N_d}$ is independent of $\varvec{\theta }$ and $\varvec{\epsilon } \sim \textrm{N}({\varvec{0}},{\varvec{C}}_d)$. Given a prior Gaussian distribution $\textrm{N}(\varvec{\theta }^\text {pr}, {\varvec{C}}_\theta )$, we expect to generate samples $\varvec{\theta }^i$, $i=1,\ldots ,N_e$, from the posterior distribution

$$\begin{aligned} \pi _{\Theta } (\varvec{\theta } | {\varvec{d}}^o) = \frac{\pi _{\Theta D} ({\varvec{d}}^o, \varvec{\theta })}{\pi _D ({\varvec{d}}^o)} \propto \exp (-Q(\varvec{\theta })), \end{aligned}$$

with the negative log posterior function

$$\begin{aligned} Q(\varvec{\theta })=\frac{1}{2}(\varvec{\theta }- \varvec{\theta }^\text {pr})^T{\varvec{C}}_\theta ^{-1} (\varvec{\theta }-\varvec{\theta }^\text {pr}) +\frac{1}{2}(g({\varvec{m}}(\varvec{\theta })) -{\varvec{d}}^o)^T{\varvec{C}}_d ^{-1} (g({\varvec{m}}(\varvec{\theta }))-{\varvec{d}}^o). \end{aligned}$$

In general, the normalization constant $\pi _D({\varvec{d}}^o)$ is unknown, but independent of $\varvec{\theta }$. For simplicity, ${\varvec{m}}(\varvec{\theta })$ is denoted as ${\varvec{m}}$.

In this paper, we apply ensemble Kalman-like approximations to the randomized maximum likelihood (RML) method (Kitanidis 1995; Oliver et al. 1996; Chen and Oliver 2012) for data assimilation. The RML method draws samples $({\varvec{\theta }^i}', {\varvec{\delta }^i}')$ from the Gaussian distribution

$$\begin{aligned} q_{\Theta '\Delta '}(\varvec{\theta }',\varvec{\delta }')= & {} q_{\Theta '}(\varvec{\theta }') \, q_{\Delta '}(\varvec{\delta }') = \frac{1}{(2\pi )^{\frac{N_\theta +N_d}{2}}|{\varvec{C}}_\theta |^{1/2}|{\varvec{C}}_d|^{1/2}}\nonumber \\{} & {} \times \exp \Big (-\frac{1}{2}(\varvec{\theta }'\! -\!\varvec{\theta }^\text {pr})^T{\varvec{C}}_\theta ^{-1} (\varvec{\theta }'\!-\!\varvec{\theta }^\text {pr}) -\frac{1}{2}(\varvec{\delta }'-{\varvec{d}}^o)^T {\varvec{C}}_d^{-1}(\varvec{\delta }' (\varvec{\delta }'-{\varvec{d}}^o)\Big ), \nonumber \\ \end{aligned}$$

(1)

for given $\varvec{\theta }^\text {pr}$ and ${\varvec{d}}^o$. The ith approximate posterior sample is then generated by computing the critical points of the cost functional

$$\begin{aligned} Q_i(\varvec{\theta }) = \frac{1}{2}(\varvec{\theta }-{\varvec{\theta }^i}') ^T{\varvec{C}}_\theta ^{-1} (\varvec{\theta } -{\varvec{\theta }^i}')+\frac{1}{2}({g}({\varvec{m}}) -{\varvec{\delta }^i}')^T{\varvec{C}}_d^{-1} ({g}({\varvec{m}})-{\varvec{\delta }^i}'). \end{aligned}$$

(2)

The critical points are obtained by solving $\nabla _\theta Q_i(\varvec{\theta }) =0$ for $\varvec{\theta }$. In general, the maxima and stationary points contribute little, and the Levenberg–Marquardt method with a Gauss–Newton approximation of the Hessian is used for the minimization.The ith increment in the iteration is written as

$$\begin{aligned} \delta \varvec{\theta }_l\!=\!\frac{{\varvec{\theta }^i}' \!-\!\varvec{\theta }_l}{1\!+\!\lambda _l}\!-\!{\varvec{C}}_\theta {\varvec{G}}_l^T\Big [(1\!+\!\lambda _l){\varvec{C}}_d \!+\!{\varvec{G}}_l{\varvec{C}}_\theta {\varvec{G}}_l^T\Big ]^{-1} \bigg [\Big (g({\varvec{m}}_l) \!-\! {\varvec{\delta }^i}'\Big )\!-\!\frac{{\varvec{G}}_l(\varvec{\theta }_l \!-\!{\varvec{\theta }^i}')}{1\!+\!\lambda _l}\bigg ],\nonumber \\ \end{aligned}$$

(3)

where ${\varvec{G}}_l=(\nabla _{\theta _l}(g^T))^T$, and $\lambda _l$ is the Levenberg–Marquardt regularization parameter for the $\ell$th iteration.

The ensemble Kalman approximation of the RML is asymptotically exact for Gauss-linear data assimilation problems and adopts an average sensitivity computed from the ensemble samples to approximate the downhill direction (Chen and Oliver 2012), which results in inaccurate sensitivity when the problem is highly nonlinear. To improve the accuracy of the sensitivity matrix for individual realizations, the hybrid ensemble method is introduced. (The hybrid method can refer to many different approaches. Here, we refer to approaches that use gradients that are computed partially from the ensemble and partially by direct differentiation.) Through proper forms such as Eq. (6) and Eq. (7) in the hybrid ensemble method, some derivatives are computed analytically and others are approximated from the ensemble. Consequently, instead of a single common gain matrix applied to all realizations, the gain matrix of each sample in hybrid ensemble methods is different. In a naïve implementation, the computational cost will be very high for large models. We take advantage of the block-circulant structure of the prior model covariance matrix or its square root to reduce the cost substantially, applying circulant embedding for fast multiplication of Toeplitz matrices.

For posterior distributions with multiple modes, the approximate samples from minimization-based simulation methods will almost certainly converge to local minima, some of which contribute very little to the probability mass in the posterior. These samples may result in large data mismatch after minimization. Importance weights of approximate samples from the proposal distribution are used to correct the sampling. To compute the importance weights, it is necessary to compute the proposal distribution for RML samples. Solving $\nabla _\theta Q(\varvec{\theta })=0$ leads to a map from $(\varvec{\theta }, \varvec{\delta })$ to $(\varvec{\theta }', \varvec{\delta }')$ in Ba et al. (2022),

$$\begin{aligned} \left\{ \begin{aligned}&\varvec{\theta }'=\varvec{\theta } +{\varvec{C}}_\theta {\varvec{G}}^T{\varvec{C}}_d^{-1}\big ( g({\varvec{m}})-\varvec{\delta }\big )\\&\varvec{\delta }'=\varvec{\delta }. \end{aligned}\right. \end{aligned}$$

(4)

Based on the map of Eq. (4) and the original notation, the distribution of the transformed variables is given by

$$\begin{aligned} \begin{aligned} p_{\Theta \Delta }(\varvec{\theta },\varvec{\delta })&:=n(\varvec{\theta }')^{-1} q_{\Theta '\Delta '}(\varvec{\theta }',\varvec{\delta }')J(\varvec{\theta }, \varvec{\delta })\\&= n(\varvec{\theta }')^{-1} q_{\Theta '}\Big (\varvec{\theta } +{\varvec{C}}_\theta {\varvec{G}}^T{\varvec{C}}_d ^{-1} \big (g({\varvec{m}})-\varvec{\delta } \big )\Big )q_{\Delta '}(\varvec{\delta } )J(\varvec{\theta }, \varvec{\delta }), \end{aligned}\end{aligned}$$

(5)

where $n(\varvec{\theta }')$ is the total number of critical points of Eq. (2), and $J(\varvec{\theta },\varvec{\delta })$ denotes the Jacobian determinant associated with the map $(\varvec{\theta },\varvec{\delta })\rightarrow (\varvec{\theta }',\varvec{\delta }')$. In the following, we assume that the map is locally invertible, that is, $J\ne 0$ everywhere. The form of $J(\varvec{\theta },\varvec{\delta })$ is provided by

$$\begin{aligned} J(\varvec{\theta },\varvec{\delta })=\bigg |I +{\mathcal {D}}\Big ({\varvec{C}}_\theta {\varvec{G}}^T {\varvec{C}}_d^{-1} \big (g({\varvec{m}})-\varvec{\delta }\big )\Big )\bigg |, \end{aligned}$$

where ${\mathcal {D}}(\cdot )$ is the gradient operator for ${\varvec{C}}_\theta {\varvec{G}}^T{\varvec{C}}_d^{-1} \big (g({\varvec{m}})-\varvec{\delta }\big )$ with respect to $\varvec{\theta }$.

When importance sampling is implemented for highly nonlinear problems, the variance in the log-weights will generally not be small. This is because the RML proposal density is not identical to the target density, and the ensemble samples are only approximations of the samples that would be obtained from exact computation of minima. Because of the approximations, the actual spread in computed importance weights will be larger than it should be. Denoising of importance weights has been shown to be effective at improving the weights (Akyildiz et al. 2017). For the ensemble methods based on RML, denoising will be performed when the variance of weights is large.

2.1 Example Applications

The weighting of critical-point samples in the RML method depends on the magnitude of the data mismatch at the critical points and on the Jacobian of the transformation from the prior density to the proposal density. When standard iterative ensemble smoothers are applied for data assimilation, the Jacobian is identical for all samples. If a hybrid data assimilation method is applied, however, there is the possibility for each ensemble member to have a distinct Jacobian and for the posterior distribution of particles to be multimodal. In order to apply a hybrid method iterative ensemble smoother, it is necessary that a part of the transformation from the prior Gaussian random variable to the data be analytic. Examples might include transformation from a latent Gaussian random variable to permeability followed by a system of partial differential equations mapping permeability to state variables in porous media flow, or a Gaussian hierarchical model for variables followed by a similar transformation from permeability to state variables

$$\begin{aligned} {\varvec{G}} = (\nabla _\theta (g^T))^T = {\varvec{G}}_m (\nabla _\theta ( {\varvec{m}}^T))^T= {\varvec{G}}_m {\varvec{M}}_\theta , \end{aligned}$$

(6)

where ${\varvec{G}}$ is the sensitivity matrix of the forward operator g with respect to the latent Gaussian random variable $\varvec{\theta }$, ${\varvec{G}}_m$ is the gradient of the forward operator with respect to the log-permeability ${\varvec{m}}$, and ${\varvec{M}}_\theta$ is the gradient of the log-permeability m with respect to $\varvec{\theta }$.

2.1.1 Hierarchical Gaussian

For a hierarchical Gaussian model in which hyper-parameters, $\varvec{\beta }$, of the prior model covariance such as the principal ranges and the orientation of the anisotropy are uncertain, we might use the non-centered parameterization (Papaspiliopoulos et al. 2007) to express the relationship between the observable Gaussian variable ${\varvec{m}}$ (e.g., log-permeability) and the model parameters ${\varvec{z}}$ (latent Gaussian variables) and $\varvec{\beta }$ as

$$\begin{aligned} {\varvec{m}}= {\varvec{m}}_\text {pr}+ {\varvec{L}}(\varvec{\beta }) {\varvec{z}}, \end{aligned}$$

where ${\varvec{L}}$ is a square root of the model covariance matrix ${\varvec{C}}_m={\varvec{L}} {\varvec{L}}^T$. In this application, the sensitivity of the observable variable ${\varvec{m}}$ to the latent variables ${\varvec{z}}$ and $\varvec{\beta }$ is nonlocal,

$$\begin{aligned} {\varvec{M}}_\theta = \begin{bmatrix} {\varvec{L}}&(\nabla _\beta {\varvec{L}}) {\varvec{z}}\end{bmatrix}. \end{aligned}$$

In a hybrid iterative ensemble smoother (IES), the sensitivity of production data to permeability and porosity, ${\varvec{G}}_m$, would be estimated using the ensemble of predicted data and the ensemble of model perturbations.

2.1.2 Transformation of Permeability

In some applications of data assimilation to subsurface characterization, it is desirable to generate prior realizations of the permeability field with non-Gaussian structure, that is, continuous channel-like features of high permeability embedded in a low-permeability background. A property field with these characteristics can be obtained by applying a nonlinear transformation to a correlated Gaussian field, that is, ${\varvec{m}} = f(\varvec{\theta })$, where $\theta \sim \textrm{N}(\varvec{\theta }^\text {pr}, {\varvec{C}}_\theta )$. Unlike the hierarchical example, in which the sensitivity matrix ${\varvec{M}}_\theta$ had dimensions $N_m \times N_m$ and was potentially full, the sensitivity of ${\varvec{m}}$ to $\varvec{\theta }$ for simple variable transformation will generally be diagonal.

2.1.3 Composite Observation Operators

For some types of subsurface data assimilation problems, the observation operator might be separable into two parts, one of which can be treated analytically, while the other might be a complex function of the parameters, determined by the solution of a partial differential equation. An example is the observation of acoustic impedance in a seismic survey. The state of the reservoir u (i.e., the pressure and saturation) is a function of permeability and porosity, which are denoted as $u(\varvec{\beta }_1)$. The acoustic impedance, Z, is related to the state of the reservoir and other reservoir properties through a rock physics model, which may have several additional uncertain parameters, $\varvec{\beta }_2$. Let $\varvec{\theta }=(\varvec{\beta }_1,\varvec{\beta }_2)$. The composite relationship is written loosely as

$$\begin{aligned} Z(\varvec{\theta }) = Z(u(\varvec{\beta }_1),\varvec{\beta }_2). \end{aligned}$$

The sensitivity of acoustic impedance to the permeability and porosity can be decomposed using the chain rule as

$$\begin{aligned} {\varvec{G}} = (\nabla _\theta (Z^T))^T = (\nabla _{u,\beta _2} ( Z^T))^T (\nabla _{\beta _1}( u^T))^T= {\varvec{G}}_{u,\beta _2} {\varvec{U}}_{\beta _1}, \end{aligned}$$

(7)

in which case the sensitivity of impedance to the state variables and parameters of the rock physics model, ${\varvec{G}}_{u,\beta _2}$, can be computed analytically, and the sensitivity of the state variables to permeability and porosity, ${\varvec{U}}_{\beta _1}$, can be estimated stochastically as in an iterative ensemble smoother.

2.2 Data Assimilation Based on Ensemble Methods

In practice, iterative ensemble smoothers are often an effective approach for solving large-scale geoscience inverse problems. These methods are based on the Kalman filter (Evensen 1994), which uses a low-rank approximation of the covariance matrix to replace the full covariance and avoids the need to compute adjoints of the objective functions as might be required in an extended Kalman filter. To improve the efficiency of updating the unknown parameters, a so-called smoother method using all the data simultaneously is generally adopted for parameter estimation problems. However, most parameter estimation problems are nonlinear, and a single update in which all data are simultaneously assimilated is not sufficient. For history matching, iteration is required of a smoother application. Iterative ensemble smoothers (IES) and their variants include two general approaches: multiple data assimilation (MDA) (Reich 2011; Emerick and Reynolds 2013) and IES based on randomized maximum likelihood (RML) (Chen and Oliver 2012). The iterative ensemble smoother form of the RML uses an average sensitivity to approximate the Hessian matrix. For the strongly nonlinear problems, the ensemble average sensitivity will provide a poor approximation of the local sensitivity. To partially rectify this problem, a hybrid RML-IES method has been proposed to improve the estimate of the local sensitivity; some gradients are computed analytically and others are approximated from the ensemble (Oliver 2022).

2.2.1 Iterative Ensemble Smoother

For the RML method, the computation of the gradient of the objective function with respect to the parameters is necessary. In many high-dimensional problems, the computation of derivatives is difficult. The iterative ensemble smoothers utilize ensemble realizations to approximate the first- and second-order moments, which avoids the need to compute derivatives directly. Using an iterative ensemble smoother method (Chen and Oliver 2013), the update step (Eq. (3)) for the ith ensemble member at the lth iteration can be approximated as

$$\begin{aligned} \varvec{\theta }_{l+1}^i \!=&\,\,\varvec{\theta }_l^i \!-\frac{1}{1\!+\!\lambda _l}\Xi _{\theta _l}(\Xi _{\theta _l})^T{\varvec{C}}_\theta ^{-1} ( \varvec{\theta }_l^i \!-\!{\varvec{\theta }^i}') \!-\!\Xi _{\theta _l}(\Xi _{d_l})^T \Big ((1\!+\!\lambda _l){\varvec{C}}_d+\Xi _{d_l} (\Xi _{d_l})^T\Big )^{-1}\nonumber \\&\times \Big (g({\varvec{m}}_l)-{\varvec{\delta }^i}' -\frac{1}{1+\lambda _l}\Xi _{d_l}(\Xi _{\theta _l})^T{\varvec{C}}_\theta ^{-1} (\varvec{\theta }_l^i-{\varvec{\theta }^i}')\Big ), \end{aligned}$$

(8)

where

$$\begin{aligned}\left\{ \begin{aligned}&{\Xi _{\theta _l}}=\frac{1}{\sqrt{N_e-1}}(\varvec{\theta }^1_l, \ldots ,\varvec{\theta }^{N_e}_l)\Big ({\varvec{I}}_{N_e} -\frac{1}{N_e}{\varvec{1}}_{N_e}{\varvec{1}}_{N_e}^T\Big ),\\&{\Xi _{d_l}}=\frac{1}{\sqrt{N_e-1}}\Big (g({\varvec{m}}^1_l), \ldots ,g({\varvec{m}}^{N_e}_l)\Big )\Big ({\varvec{I}}_{N_e} -\frac{1}{N_e}{\varvec{1}}_{N_e}{\varvec{1}}_{N_e}^T\Big ),\\&{{\varvec{\delta }^i}'\sim \textrm{N}({\varvec{d}}^o,{\varvec{C}}_d), \quad {\varvec{\theta }^i}' \sim \textrm{N}(\varvec{\theta }^\textrm{pr},{\varvec{C}}_\theta )}. \end{aligned} \right. \end{aligned}$$

Here, $N_e$ is the number of model realizations in the initial ensemble. The ensemble realizations are used to approximate the gradient of the forward operator g with respect to $\varvec{\theta }$. The update in Eq. (8) is restricted to the space spanned by the initial ensemble, and the number of degrees of freedom available for calibration of the model to data is $N_e-1$. To avoid the tendency for ensemble collapse with large amounts of data, localization is almost always used in high-dimensional problems. Additionally, for highly nonlinear problems, the sensitivity of data to model parameters estimated from the ensemble in Eq. (8) is a poor approximation to the local sensitivity, which often results in failure to converge to local minima.

2.2.2 Hybrid Iterative Ensemble Smoother

For the hybrid IES, instead of using an ensemble stochastic approximation of the sensitivity matrix ${\varvec{G}}$, the derivative of ${\varvec{m}}$ with respect to $\varvec{\theta }$ is computed analytically, and the chain rule is used to compute ${\varvec{G}}$ as

$$\begin{aligned} {\varvec{G}} = {\varvec{G}}_{m} \cdot \left( \nabla _{\theta } \big ({\varvec{m}}^T \big )\right) ^T = {\varvec{G}}_m {\varvec{M}}_\theta . \end{aligned}$$

(9)

Then, the update equation (Eq. (3)) can be written as

$$\begin{aligned} \begin{aligned} \varvec{\theta }_{l+1}&=\varvec{\theta }_l -\frac{1}{1+\lambda _l} (\varvec{\theta }_l-\varvec{\theta }') -{\varvec{C}}_{\theta }{\varvec{M}}_{\theta }^T(\Xi _{m_l}) ^{-T}(\Xi _{d_l})^{\text {T}} \\&\quad \times \Big ((1+\lambda _l){\varvec{C}}_d+(\Xi _{d_l})(\Xi _{m_l}) ^{-1} {\varvec{M}}_{\theta }{\varvec{C}} _\theta {\varvec{M}}_{\theta }^T(\Xi _{m_l})^{-T}(\Xi _{d_l})^{T}\Big )^{-1} \\&\quad \times \Bigg (g({\varvec{m}}_l)-\varvec{\delta }' -\frac{1}{1+\lambda _l}(\Xi _{d_l})(\Xi _{m_l})^{-1}{\varvec{M}}_{\theta } ( \varvec{\theta }_l-\varvec{\theta }' ) \Bigg ), \end{aligned} \end{aligned}$$

(10)

where ${\Xi _{m_l}}$ is defined similarly to ${\Xi _{\theta _l}}$, and ${\varvec{M}}_{\theta }=(\nabla _{\theta } ({\varvec{m}}^{\text {T}} ))^{\text {T}}$. The gain matrix for each sample is different because the sensitivity matrix ${\varvec{M}}_\theta$ is evaluated at the model realization—not estimated from the ensemble of realizations. The main challenge with straightforward application of a hybrid IES methodology is the cost of forming and multiplying by the matrix ${\varvec{M}}_\theta$ for all realizations (Oliver 2022).

Unlike the ensemble Kalman-based methods that take advantage of low-rank approximations of the covariance matrices, in the hybrid IES, the Toeplitz or block Toeplitz structure of the covariance matrix for stationary Gaussian random fields is utilized. It is then possible to efficiently compute the matrix–vector products using the fast Fourier transform after embedding the Toeplitz matrix in a circulant matrix (Appendix A).

2.3 Weighting of Model Realization

The RML method of sampling the posterior is only exact if the relationship between the data and the model parameters is linear. For many nonlinear problems, however, it is necessary to weight the samples to approximate the posterior distribution, in which case the computation of the gradient of the objective function is necessary. To avoid the need to compute ${\varvec{G}}$ directly, ensemble-based methods offer an alternative. However, exact sampling using RML requires computation of additional critical points and weighting of solutions (Ba et al. 2022). The importance weight for the kth RML sample is

$$\begin{aligned} \omega _k\propto \frac{\pi _\Theta (\varvec{\theta }^k)\pi _\Delta (\varvec{\delta }^k|\varvec{\theta }^k)}{p_{\Theta \Delta }(\varvec{\theta }^k,\varvec{\delta }^k)}, \end{aligned}$$

(11)

where $\pi _{\Theta }(\varvec{\theta })$ is the prior, and the likelihood $\pi _{\Delta }(\varvec{\delta }|\varvec{\theta })$ and the proposal density $p_{\Theta \Delta }(\varvec{\theta },\varvec{\delta })$ are provided by Eq. (5). Ba et al. (2022) showed that in high-dimensional nonlinear cases where it is not feasible to sample all critical points, it is possible to randomly sample a single critical point for each prior realization. If the critical point is sampled uniformly from the set of all critical points, the factor $n(\varvec{\theta }')$ in Eq. (5) should be set to 1.

Introducing the quantities,

$$\begin{aligned} \begin{aligned} J(\varvec{\theta },\varvec{\delta })&\approx |{\varvec{I}}_{N_\theta }+{\varvec{C}}_\theta {\varvec{G}}^T{\varvec{C}}_d^{-1} {\varvec{G}}|\\ {\varvec{V}}(\varvec{\theta })&= {\varvec{C}}_d+{\varvec{G}} {\varvec{C}}_\theta {\varvec{G}}^{\text {T}} \\ \varvec{\eta }(\varvec{\theta })&= g({\varvec{m}}) -{\varvec{d}}^o- {\varvec{G}} (\varvec{\theta }-{\varvec{\theta }}^\text {pr}). \end{aligned} \end{aligned}$$

To simplify notation, the proposal density Eq. (5) which appears in the denominator of Eq. (11) can be written as

$$\begin{aligned}{} & {} p_{\Theta \Delta }(\varvec{\theta },\varvec{\delta }) \nonumber \\{} & {} \quad = \overbrace{A_0\, \exp \left[ -\frac{1}{2} \left( \varvec{\theta } -{\varvec{\theta }}^\text {pr} \right) ^{\text {T}} {\varvec{C}}_\theta ^{-1} \left( \varvec{\theta } -{\varvec{\theta }}^\text {pr} \right) - \frac{1}{2} \left( g({\varvec{m}}) - {\varvec{d}}^o \right) ^{\text {T}} {\varvec{C}}_d^{-1} \left( g({\varvec{m}}) - {\varvec{d}}^o \right) \right] }^{\pi _{\Theta }(\varvec{\theta }) }\nonumber \\{} & {} \qquad \times \overbrace{A_1\, |{\varvec{V}}|^{1/2} \exp \left[ -\frac{1}{2 } \left( \varvec{\delta }- g({\varvec{m}}) - {\varvec{V}}^{-1} \varvec{\eta }({\varvec{m}}) \right) ^{\text {T}} {\varvec{V}} \left( \varvec{\delta } - g({\varvec{m}}) - {\varvec{V}}^{-1} \varvec{\eta }(\varvec{\theta }) \right) \right] }^{\pi _{\Delta }(\delta |\theta ) }\nonumber \\{} & {} \qquad \times A_2\, |{\varvec{V}}|^{-1/2} \exp \left[ \frac{1}{2} \varvec{\eta }(\varvec{\theta })^{\text {T}} {\varvec{V}}^{-1} \varvec{\eta }(\varvec{\theta }) \right] \, J(\varvec{\theta },\varvec{\delta }), \end{aligned}$$

(12)

where $A_0$, $A_1$, and $A_2$ are all normalization constants, independent of $\varvec{\theta }$ and $\varvec{\delta }$.

Because the first two lines in Eq. (12) cancel terms in the numerator of Eq. (11), the importance weight for sample k is

$$\begin{aligned} \omega \propto |{\varvec{V}}|^{1/2} \exp \left[ -\frac{1}{2} \varvec{\eta }(\varvec{\theta })^{\text {T}} {\varvec{V}}^{-1} \varvec{\eta }(\varvec{\theta }) \right] J^{-1}(\varvec{\theta },\varvec{\delta }), \end{aligned}$$

(13)

where second derivatives of ${\varvec{G}}$ at the critical point have been neglected.

2.3.1 Importance Weights for the IES

Although the IES method is based on RML, the application to multimodal distributions is limited, as all samples share a common estimate of ${\varvec{G}}$ estimated from the ensemble of realizations

$$\begin{aligned} \begin{aligned} {\varvec{G}}{\varvec{C}}_\theta {\varvec{G}}^T&\approx \Xi _d \Xi _d^T\\ {\varvec{G}}&\approx \Xi _d\Xi _\theta ^{T} {\varvec{C}}_\theta ^{-1} \\ {\varvec{C}}_\theta {\varvec{G}}^T&\approx \Xi _\theta \Xi _d^{T}. \end{aligned} \end{aligned}$$

(14)

Because ${\varvec{V}}(\varvec{\theta })$ and $J(\varvec{\theta },\varvec{\delta })$ are the same for all samples, the computation of weights can be simplified. Neglecting the common multiplying constant, the IES approximation to the importance weight is

$$\begin{aligned} \omega \propto \exp \left[ -\frac{1}{2} \varvec{\eta }(\varvec{\theta })^{\text {T}} {\varvec{V}}^{-1} \varvec{\eta }(\varvec{\theta }) \right] . \end{aligned}$$

The only difference in weights is a result of differences in the term $\varvec{\eta }(\varvec{\theta })$, which requires computation of ${\varvec{G}}$ from Eq. (14). For most practical problems, the ensemble size is smaller than the dimension of $\varvec{\theta }$, so the pseudo-inverse is used to approximate the inverse of prior covariance matrix ${\varvec{C}}_\theta ^{-1}$.

2.3.2 Importance Weights for the Hybrid IES

The hybrid IES is also based on the RML method of sampling, but uses a different gain matrix for each sample while still avoiding the need for solving the adjoint system. For exact sampling from the posterior in strongly nonlinear problems, the computation of weights is unavoidable. To compute the weights $\{\omega _i\}_{i=1}^{N_e}$ of samples generated by the hybrid IES, the analytic sensitivity matrix ${\varvec{M}}_\theta$ is used, which is $N_m\times N_\theta$. The derivative ${\varvec{G}}_m$ of the objective function with respect to the intermediate variable ${\varvec{m}}$ can be approximated by the ensemble samples. Finally, the computation of weights in Eq. (13) can be performed by the following forms

$$\begin{aligned} \begin{aligned} {\varvec{G}}{\varvec{C}}_\theta {\varvec{G}}^T&\approx \Xi _d\Xi _m^{-1} {\varvec{M}}_\theta {\varvec{C}}_\theta {\varvec{M}}_\theta ^T \Xi _m^{-T} \Xi _d^T \\ {\varvec{G}}&\approx \Xi _d \Xi _m^{-1} {\varvec{M}}_\theta \\ {\varvec{C}}_\theta {\varvec{G}}^T&\approx {\varvec{C}}_\theta {\varvec{M}}_\theta ^T \Xi _m^{-T} \Xi _d^T. \end{aligned} \end{aligned}$$

The dimensions of $\Xi _m$ are $N_m\times N_e$. Thus, the pseudo-inverse of $\Xi _m$ is used in the computation of ${\varvec{G}}$. For each sample, the terms of Eq. (13) are different. When ${\varvec{M}}_\theta$ or ${\varvec{C}}_\theta$ has the Toeplitz properties, circulant embedding described in Appendix A is used to reduce the computational cost of the matrix multiplication.

2.4 Excess Variance of Importance Weights

For highly nonlinear sampling problems, the variance in the log-weights should be expected to be large, since the RML proposal density is not identical to the target density. On the other hand, the actual spread in computed importance weights is larger than it should be for a number of reasons, including the fact that the minimization method used for computation of samples is approximate. The iterations are generally stopped before actual convergence, and the gradient is approximated from a low-rank ensemble. A different initial ensemble would result in a different final estimate of ${\varvec{G}}$, ${\varvec{V}}$, and $\det {\varvec{V}}$. All of these will result in variability in the computation of weights, and the non-normalized log-weights will consequently have a large spread. If the so-called noisy log-weights are used directly to compute weighted forecasts, almost all the weight will fall on a single model realization.

For large Bayesian inverse problems of the type encountered in the geosciences, the likelihood is often difficult to evaluate, and noisy approximations to the likelihood must instead be used (Dunbar et al. 2022). When the likelihood is noisy, however, the transition kernel in MCMC, or equivalently the weighting of particles in importance sampling, will be affected by the noise (Alquier et al. 2016; Acerbi 2020). This noise must either be removed or be otherwise accounted for if the sampling is to be efficient. The problem of sampling with noisy importance weights has been reviewed by Akyildiz et al. (2017), who showed that denoising can be an effective approach. In the application to weighting of RML samples, the errors appear primarily in the evaluation of the proposal density, not in the evaluation of the likelihood as in most previous studies. Because the importance weights are ratios of likelihood to proposal density, however, the effect of noise in either term on the weight is similar.

2.4.1 A Model for Noise in the Log-Weights

For simplicity, we denote the logarithm of the weights on the particles as $\omega$, so that

$$\begin{aligned} \omega = -\frac{1}{2} \log \det {\varvec{V}} - \frac{1}{2} \varvec{\eta }^{\text {T}} {\varvec{V}}^{-1} \varvec{\eta }, \end{aligned}$$

where

$$\begin{aligned} {\varvec{V}} = {\varvec{C}}_d + {\varvec{G}} {\varvec{C}}_\theta {\varvec{G}}^{\text {T}} , \end{aligned}$$

and

$$\begin{aligned} \varvec{\eta } (\varvec{\theta }) = g(\varvec{\theta }) - {\varvec{d}}^o - {\varvec{G}} (\varvec{\theta } - \varvec{\theta }^{\textrm{pr}}). \end{aligned}$$

For a nonlinear problem, the sensitivities ${\varvec{G}}$ at the minimizer will be variable, and since ${\varvec{G}}$ and the data mismatch enter quadratically in $\omega$, we expect the so-called true distribution of log-weights to be approximately chi-square. We additionally assumed a Gaussian model for the distribution of errors in the computed log-weights, which we also refer to as noise in the weights.

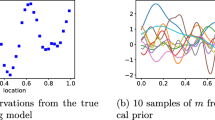
We can obtain an empirical characterization of the computational error by generating a number of realizations of the computed value of $\omega$ for the same prior sample $\varvec{\theta }'$ but with different ensembles of realizations used for computation of ${\varvec{G}}$. We did this for realizations of the monotonic transform of log-permeability by generating 16 independent ensembles of 199 realizations and augmenting each ensemble with another realization that was then common to each ensemble. Figure 1a shows the evolution of the log-weight on the single realization that was common to all 16 ensembles. The minimization was stopped when the iterations reached the terminated condition. (The particle that was common to all ensemble members stopped updating by iteration 10 in all ensembles, where the iteration number just contains the iteration that the mean of data mismatch is smaller than the last iteration.) Figure 1b shows the distribution of final values of $\omega$ (blue) and the Gaussian fit to the distribution of final values (red curve).

Fig. 1

The distributions of log-weights for the monotonic log-permeability transform

Estimating reasonable parameters in the chi-square model of the true distribution for large weights is more difficult than estimating the errors in the computation, partly because we do not have an empirical distribution of log-weights without computational noise. We instead used a trial-and-error approach in which the observed distribution of log-weights was compared with a Monte Carlo distribution of noisy samples from a chi-square distribution whose parameters were tuned to match the observed distribution. Figure 1c compares the distribution of RML-computed realizations with the realizations from the modeled distribution of noisy large weights.

The posterior distribution for noisy log-weights (Eq. (15)) is modeled as the product of a Gaussian likelihood model and a chi-square prior distribution,

$$\begin{aligned} P(\omega | \omega ^o) \propto P(\omega ^o | \omega ) P(\omega ) \end{aligned}$$

or

$$\begin{aligned}{} & {} P(\omega | \omega ^o) \propto {\left\{ \begin{array}{ll} \exp \left( - \frac{(\omega -\omega ^{o})^2}{2\sigma _o^2}\right) \left( \frac{\omega -\omega ^\text {pr}}{\sigma _\text {pr}} \right) ^{\nu /2-1} \exp \left( - \frac{\omega -\omega ^\text {pr}}{2 \sigma _\text {pr} } \right) \quad &{} \textrm{for} \quad \omega > \omega _\text {pr} \\ 0 \quad &{} \textrm{for} \quad \omega \le \omega _\text {pr}. \end{array}\right. } \end{aligned}$$

(15)

Once the parameters of the distribution have been estimated, the denoised weights are estimated by computing the maximum a posteriori values of the individual weights; that is, for each “observed” weight, we compute the maximizer of Eq. (15) to obtain the denoised weight.

For the monotonic log-permeability transform, with $\sigma _o = 16.9$, $\sigma _\text {pr} = 6$, and $\nu = 4$, we obtain the denoised log-weights shown in red in Fig. 2a. The effective sampling efficiency $N_{\textrm{eff}}/N_e = 97.8/1600 \approx 0.109$, based on Kong’s estimator Eq. (16),

$$\begin{aligned} N_{\text {Eff}}=\frac{1}{\sum _{k=1}^{N_e}\omega _k^2}, \end{aligned}$$

(16)

where $\sum _{k=1}^{N_e}\omega _k=1$.

Fig. 2

The distributions of log-weights after denoising (red colors)

The spread in the weights for the case with non-monotonic transform of log-permeability is much larger than in the case with monotonic permeability transform. First, the computation of weights appears to be less repeatable: Fig. 2a shows the evolution of non-normalized log-weights for the same sample when included in 16 otherwise independent ensembles. The spread of the final values for the common particle (Fig. 2b) is approximately five times as large for the non-monotonic case ( $\sigma _o = 95.3$) as for the monotonic case ($\sigma _o = 16.9$). Presumably, the additional variability is a result of greater variability in ${\varvec{G}}$ and the presence of more local minima. Additionally, the prior spread of log-weights appears to be larger, again because of multiple minima and the fact that the proposal distribution is farther from the target distribution in this case. For the non-monotonic log-permeability transform, with $\sigma _o = 95.3$, $\sigma _\text {pr} = 13$, and $\nu = 3$, we obtain the denoised log-weights shown in red in Fig. 2b. The effective sampling efficiency $N_{\textrm{eff}}/N_e = 27.2/1600 \approx 0.017$, based on Kong’s estimator Eq. (16).

3 Applications of Weighting to Assimilation of Flow Data

In this section, two data assimilation methods (hybrid IES and IES) are applied to a two-dimensional, two-fluid-phase flow, incompressible problem with permeability transforms, ${\varvec{m}}=f(\varvec{\theta })$, of varying degrees of nonlinearity: a monotonic log-permeability transform and a non-monotonic transform. Here, ${\varvec{m}}$ and $\varvec{\theta }$ are the same size, which leads to a diagonal ${\varvec{M}}_\theta$. For the two applications, the uncertain permeability field in the porous medium is estimated by assimilation of a time series of water rate observations at nine producing wells.

The state, u, of an incompressible and immiscible two-phase (aqueous (w) phase and oleic (o) phase) flow system is determined by the pressure p(x, t) and saturation s(x, t), which in this example are governed by

$$\begin{aligned} \left\{ \begin{aligned} -\nabla \cdot ( K\lambda _{*}(s)\nabla p)&=q,\\ \phi \frac{\partial s}{\partial t}+\nabla \cdot (f_{*}(s) v)&=\frac{q_w}{\rho _w}\quad \text {in} \quad \Omega \times [0,T] \end{aligned}\right. , \end{aligned}$$

(17)

with the boundary condition

$$\begin{aligned} v\cdot {\textbf{n}}=0\quad \text {on} \quad \partial \Omega \times [0,T], \quad s(x,0) = 0 \quad \text {in}\quad \Omega =[0,2]\times [0,2], \end{aligned}$$

where $\phi$ denotes the rock porosity, the source term q models sources and sinks, the fractional-flow function $f_*(s)$ measures the fraction of the total flow, $\lambda _*(s)$ is the mobility of the phase, K denotes the absolute permeability (assumed to be isotropic), $q_w$ denotes the w phase source, and $\rho _w$ denotes the density of the w phase. Since we only inject water and produce whatever reaches our producers, the source term for the saturation equation becomes

$$\begin{aligned} \frac{q_w}{\rho _w} = \max (q,0) +f(s)\min (q,0). \end{aligned}$$

To close the model, we must supply expressions for the w phase and o phase

$$\begin{aligned} \begin{aligned} v_i&= -K\lambda _{*i}\nabla p,\quad q = \frac{q_w}{\rho _w}+\frac{q_o}{\rho _o},\quad s_w+s_o=1,\\ p_w&=p_o,\quad v=v_w+v_o,\quad \lambda _{*i}(s) = \frac{k_{ri}}{\mu _i},\quad i=w,o. \end{aligned} \end{aligned}$$

(18)

In Sect. 3.1, the hybrid IES methodology is compared with the IES methodology for the flow problem with a monotonic log-permeability transform. In Sect. 3.2, a similar comparison is made, but for the flow problem with a non-monotonic log-permeability transform, which has a multimodal posterior distribution of the model parameters. In both cases, the latent variable $\varvec{\theta }$ is assumed to be multivariate Gaussian with covariance

$$\begin{aligned} C_\theta (x,y)=\sigma _\theta ^2 \left( 1-\frac{x^2+y^2}{\rho ^2}\right) \exp \left( -\frac{x^2+y^2}{\rho ^2}\right) , \end{aligned}$$

(19)

where x and y are the lags in the two spatial dimensions, and $\rho$ is a measure of the correlation range. The permeability field for the data-generating model is a draw from a prior model with the range parameter for the correlation length $\rho =1.1$ and standard deviation 0.8 for the monotonic and non-monotonic transforms. The true data-generating permeability values are as shown in Fig. 3. Figure 4 displays the corresponding water rate observations from the nine producing wells for both permeability transforms. To compare the results from the standard IES and hybrid IES, the ensemble size $N_e =200$ for both methods.

Fig. 3

The “true” log-permeability fields used to generate production data and forecasts. Black dots show locations of producing wells

Fig. 4

Noisy observations of water cut in nine producing wells

The observation locations are distributed on a uniform $3 \times 3$ grid of the domain $[0.1, 1.9] \times [0.1, 1.9]$ as shown in Fig. 3 (black dots). The noise in the observations is assumed to be Gaussian and independent with standard deviation 0.02. The forward model (Eq. (18)) is solved by the two-point flux approximation (TPFA) scheme, which is a cell-centered finite-volume method (Aarnes et al. 2007). For the two test cases, the forward model is defined on a uniform $41 \times 41$ grid with time step $\Delta t=0.1$. The dimension of the discrete parameter space is 1,681.

3.1 History Matching with a Monotonic Permeability Transform

To create a reservoir data assimilation test problem that is nonlinear but not obviously multimodal, a permeability transform was used that has characteristics similar to rock facies distributions, that is, regions with relatively uniform permeability and fairly sharp transitions between those regions. In some cases, the region occupied by the high-permeability facies is isolated and can be modeled well by a monotonic transformation of a Gaussian variable to log-permeability. To illustrate the effect of this type of nonlinearity on weighting in data assimilation, the transformation

$$\begin{aligned} m = \tanh \big (4\theta +2 \big ) + \tanh \big (4\theta -2\big ) \end{aligned}$$

(20)

is applied, where m and $\theta$ (scalars) denote the values of log-permeability and the latent Gaussian random variable in a cell, respectively. For the hybrid IES method, the gradient ${\varvec{M}}_\theta$ of log-permeability ${\varvec{m}}$ with respect to the Gaussian parameter $\varvec{\theta }$ is necessary. The analytic derivative is given by

$$\begin{aligned} \frac{\textrm{d}m}{\textrm{d}\theta } = 8 - 4 \tanh ^2 \big (4 \theta +2 \big ) - 4\tanh ^2 \big (4\theta -2\big ). \end{aligned}$$

With this transformation, values of $\theta <1$ are assigned $m \approx -2$, and values of $\theta > 1$ are assigned $m \approx 2$. The discretized form of the sensitivity ${\varvec{M}}_\theta$ is diagonal with

$$\begin{aligned} {\varvec{M}}_\theta = \begin{bmatrix} \frac{\textrm{d}m_1}{\textrm{d}\theta _1} &{}\quad 0 &{}\quad \ldots &{}\quad 0 \\ 0 &{}\quad \frac{\textrm{d}m_2}{\textrm{d}\theta _2} &{}\quad &{}\quad 0 \\ \vdots &{}\quad &{}\quad \ddots &{}\quad \vdots \\ 0 &{}\quad 0 &{}\quad \ldots &{}\quad \frac{\textrm{d}m_{N_\theta }}{\textrm{d}\theta _{N_\theta }} \end{bmatrix}, \end{aligned}$$

while the covariance operator ${\varvec{C}}_\theta$ of Eq. (19) is dense but block-Toeplitz (Zimmerman 1989; Dietrich and Newsam 1997). Multiplication by ${\varvec{M}}_\theta$ is trivial, but the product ${\varvec{C}}_\theta \bigl ({\varvec{M}}_\theta ^T (\Xi _{m_i})^{-T} \bigr )$ is computed using the Toeplitz property of ${\varvec{C}}_\theta$ as described in Appendix A.

Fig. 5

Model realizations for monotonic transformation of log-permeability using the IES and hybrid IES. (The same prior ensemble is used for both methods)

When the hybrid IES is applied to this problem, the gain matrices are potentially different for each realization, so it should be expected that some realizations will converge to local minima with small probability mass if the posterior has multiple modes. The samples with the largest weights are likely to be similar, however. Figure 5 shows the log-permeability fields for the first four prior realizations (top row) and corresponding posterior realizations of log-permeability values for both methods (middle row). The variability in the posterior realizations is smaller than the variability in the prior realizations, but still fairly large. The log-permeability values of the four posterior realizations from the hybrid IES with the largest weights (Fig. 5a (bottom row)) are much more similar, indicating that for this problem, importance weighting for the hybrid IES is beneficial in selecting realizations from the posterior that are similar to the true model.

Fig. 6

The weights versus misfits for the monotonic log-permeability transform using the IES (top row) and hybrid IES (bottom row). Blue points show computed weights

In contrast, when the IES is used for data assimilation with the same prior ensemble of realizations, the first four posterior realizations obtained from the IES (Fig. 5b (top row)) are similar to the four realizations with the largest weights (Fig. 5b (bottom row)). As the same gain matrix is used for all samples generated from the standard IES, the variability among posterior approximate realizations is smaller for the IES than for the hybrid IES, and unlike the situation with the hybrid IES, the unweighted and weighted posterior means obtained using the standard IES are almost identical (not shown).

For nonlinear problems such as this, it would be reasonable to expect the approximate posterior realizations with largest weights to have small data mismatch with observations. To investigate this hypothesis, a cross-plot of the weights versus squared data misfits generated using the IES (top row) and hybrid IES (bottom row) is shown in Fig. 6. Although the weights for the hybrid IES method are clearly correlated with squared data misfit, and the models with largest data misfit always have very small weights, there is considerable variability in weights even for small data misfit. The more important observation is that the nonlinearity in $g(\cdot )$ increases the variability in weights, and the mean of the squared misfit (369) using the hybrid IES is substantially larger than the expected value for samples from the posterior (270), while the weighted mean is 330.

Since the IES method generated less variability in the posterior realizations, the spread of weights in the IES method is expected to be smaller than the spread of weights in application of the hybrid IES. In fact, however, the spread of weights is quite large and almost independent of the data mismatch (Fig. 6 (top row)). This appears to be a result of errors in computation of ${\varvec{G}}$, an underestimate of the magnitude of ${\varvec{V}}$, and the degeneracy inherent in weighting of optimal proposals based purely on an ensemble of particles.

Because the range of the covariance of the permeability field is relatively large compared to the domain of interest, the observation locations are spatially distributed, and the production data from all wells are matched fairly well by the weighted and unweighted samples (Fig. 7). The posteriori means of the log-permeability fields (not shown) look similar to the truth, except that the truth is somewhat “rougher.”

Fig. 7

The posterior predictions of wells 1, 2, and 6 using the unweighted and weighted hybrid IES for the monotonic transform. Black points show true observations

The justification for data assimilation or history matching of subsurface models is generally to provide accurate assessments of future reservoir behavior. Figure 7 show the quality of the match to observed data and the predictability of future performance of the unweighted and weighted posterior ensembles at three representative wells. For this case, the differences in predictability between the weighted and unweighted realizations are small, although the prediction interval is narrower for the weighted hybrid IES, due in part to the small effective sample size.

For a Gauss-linear inverse problem, there should be no correlation between the weight on a sample from the posterior and the data mismatch—in fact, for this case, the weights should be uniform when a minimization-based sampling approach is used. For the nonlinear two-dimensional porous flow example with a monotonic log-permeability transform, the log-weights did correlate with data mismatch when the standard IES method was used for data assimilation ($r=-0.416$) and when the hybrid IES method was used ($r=-0.647$). In both cases, the quality of the data mismatch provided some information on the weighting that should be applied to a particle.

3.2 History Matching with Non-monotonic Permeability Transform

In this section, the problem of history matching and uncertainty quantification for permeability fields with a low-permeability “background” and connected high-permeability “channels” are considered. Again, soft thresholding of the Gaussian random variables is used to generate regions with relatively sharp transition to a different facies. The non-monotonic permeability transform is given by

$$\begin{aligned} m = 2 \tanh \big (4 \theta +2 \big ) + \tanh \big (2-4 \theta \big )-1, \end{aligned}$$

(21)

where $\theta$ is again the prior Gaussian random variable. The corresponding derivative of log-permeability with respect to the Gaussian latent variable, required for the hybrid IES, is then

$$\begin{aligned} \frac{\textrm{d}m}{\textrm{d}\theta } = 4 - 8 \tanh ^2 \big (4 \theta +2 \big ) + 4\tanh ^2 \big (2-4 \theta \big ). \end{aligned}$$

The true data-generating log-permeability field for this test problem is shown in Fig. 3c, and water cut observations for the nine producing wells are plotted in Fig. 4b. Although the data are not noticeably different from the data in the monotonic case (Fig. 4a), the presence of the channel facies makes the problem slower to converge to a mode and more likely to converge to a mode with small probability mass.

Fig. 8

Model realizations for a non-monotonic transform of log-permeability using the IES and hybrid IES

For the non-monotonic transform case, the variability of posterior realizations from the hybrid IES is larger than in the monotonic transform case, as illustrated by the first four prior realizations and corresponding posterior realizations (Fig. 8a). In this case, the differences are due to the use of the analytic sensitivity ${\varvec{M}}_\theta$ in the hybrid IES, which allows realizations to converge to different local minima. The posterior realizations with the largest importance weights (Fig. 8a (bottom row)) show reasonable similarity to the true field. When the IES method was used for data assimilation, the first four posterior realizations (Fig. 8b (top row)) and the four realizations with the largest weights (Fig. 8b (bottom row)) were almost identical. The lack of diversity results in the unweighted and weighted posterior means being very similar when a standard IES is used. Importance weighting has very little effect for the IES method on this problem. The effective sample size of the IES for the two cases is low, however, because the posterior spread has been underestimated (Chen and Oliver 2017; Ba and Jiang 2021).

Fig. 9

Model realizations with the smallest weights for non-monotonic transformations using the IES (top row) and hybrid IES (bottom row)

In addition to the greater diversity in the realizations compared to the monotonic case, the importance weights and the data mismatch are also much more diverse for the non-monotonic transform (Fig. 10) when the hybrid IES is used. In the non-monotonic case, the expected mean of the data misfit part of the log-likelihood is still 270 (half the number of observations). Figure 10 shows, however, that the data misfits of most posterior samples are concentrated in the interval [1, 000, 6, 000]. The posterior mean of unweighted data misfits is 3,794—approximately 14 times the expected value. The posterior mean of data misfits for weighted realizations, on the other hand, is 617, which is still larger than expected but much smaller than the mean for the unweighted realizations.

Fig. 10

The non-normalized log-weights versus misfits for the non-monotonic transform using the IES and hybrid IES. Blue points show computed log-weights

Fig. 11

The true log-permeability (left) and the unweighted and weighted posterior means using the hybrid IES (middle) and IES (right) for the non-monotonic transform

Weighted and unweighted mean log-permeability fields for the non-monotonic permeability transform are shown in Fig. 11. The middle and bottom rows of Fig. 11 show mean values of log-permeability at location (x, 1.75) for two different sets of results using different convergence trajectories (i.e., different values for the multiplier of $\lambda$ in Levenberg–Marquardt minimization). The unweighted mean for the hybrid IES bears limited similarity to the true field and shows little connectivity of the high-permeability facies. This is a result of averaging with many dissimilar realizations that are not all well calibrated. The weighted mean looks much more like the truth, as it puts more weight on samples with higher probability mass. The effect of importance weighting is perhaps more obvious in the posterior distribution of predictions of water cut. The spread in the unweighted predictions is large, even during the history-matched period (Fig. 12 (left column)) and much larger than expected given the observation error. On the other hand, the quality of the weighted posterior realizations (right column) is excellent, except for well 1. The main problem with the weighted ensemble appears to be that the spread is too small, resulting from the small effective sample size.

Fig. 12

The posterior predictions for wells 1, 2, and 6 using the unweighted and weighted hybrid IES for the non-monotonic transform. Black points show true observations

For the more highly nonlinear two-dimensional porous flow example with non-monotonic log-permeability transform, the correlation between the importance log-weight and data mismatch was very high ($r=-0.813$) when the hybrid IES was used for data assimilation, and the data mismatch after calibration could serve as a useful tool for eliminating samples with small weights. For the standard IES, however, the approximated weights were clearly not accurate, and the correlation between log-weight and data mismatch was correspondingly small ($r=-0.087$). In this case, the data mismatch would not have provided a useful proxy for weighting.

3.3 History Matching Using the Hybrid IES

The hybrid IES algorithm is somewhat more complex than the standard IES. A naïve implementation would be very costly for realistic geoscience problems because of the additional matrix–vector operations required to compute the update step. Additionally, the weights computed from the hybrid IES are only an approximation of the weights computed in the randomized maximum likelihood method, and the weights will be noisy as a result. The following subsections address solutions to these issues.

3.3.1 Efficiency of the Update Step in the Hybrid IES

Timing experiments showed that the cost of the proposed method for computing the update step using fast Fourier transform (FFT) (see Appendix A) was substantially decreased compared with the straightforward approach used by (Oliver 2022). The computational complexity of the hybrid method stems from the need to perform $N_e$ minimizations using individual gradient estimates and the cost to generate $N_e$ prior ensemble members from a high-dimensional parameter space. The covariance matrix is generally dense and large in the discretized space. While the sampling step from the prior distribution contributes to the cost of the hybrid IES, the cost is dominated by minimization of the objective function. For the two-phase flow example, the cost to generate 200 prior samples is about 0.054 s (timing should be considered illustrative, but for reference, all results were obtained on a computer with an $\text {i7-5500U@2.40GHz}\times 4$ processor with 7.5 GiB memory and a 64-bit operating system). The run time is approximately 31,000 times faster when using the FFT with nonnegative definite minimal embeddings compared with a method that uses the Cholesky decomposition and matrix multiplication, as shown in Table 1. Note that the increase in cost for the non-monotonic case is a result of the varying number of iterations required for the minimizer to converge for the different settings. In the case of the hybrid IES method, the cost to generate the $N_e$ hybrid gradient is dominated by the cost to perform $N_e$ matrix–vector multiplications with different cost functions. Hence, the computational complexity for the hybrid IES can be expected to be greater than the cost for the standard IES method. For the weighted hybrid IES, there is an additional cost incurred in the computation of the weights. Although several of the terms in the weights can be obtained at low cost through the ensemble approximations that were used for the Hessian, the $N_e$ times matrix multiplications are necessary to compute the weights. When FFT was applied to compute hybrid gradients, the cost of computing ${\varvec{C}}_\theta {\varvec{M}}_\theta ^T(\Xi _m)^{-T}$ was reduced from 0.18 s to 0.089 s for each sample relative to the case in which the matrix–vector multiplication did not use FFT (i.e., the FFT method was twice as fast).

All computational costs, including the cost of minimization, could be reduced through careful modification of the algorithms. In particular, the efficiency of the weighted hybrid IES could be improved by tempering the objective function at early iterations to avoid convergence to local minima with small weights.

Table 1 Computational cost of the hybrid IES (units = second)

3.3.2 Effect of Denoising Weights on Predictability

Unweighted posterior realizations generated by minimization of a stochastic cost function are often described as well history-matched, but differences in the quality of the match to data between some realizations and observations are too large in practice to be explained by observation error. To investigate the potential benefit of weighting the samples and of different degrees of denoising, we compute the accuracy of probabilistic predictions beyond the history-matching period for data assimilation using the hybrid IES. (Optimal weighting was not investigated for the standard IES, as weighting was not useful for the non-monotonic log-permeability case.) For this investigation, observations used in history matching end at $t=60$, and predictions are evaluated at $t=70$ for all nine producers using the “log score” (Good 1952; Gneiting and Raftery 2007). The logarithmic score evaluates the probability of the outcome given a probability density function (pdf) empirically defined by the ensemble of predictions. The log score rewards both accuracy and sharpness of the forecasts. A higher log score signifies better probabilistic prediction,

$$\begin{aligned} \mathrm{{Log}}S(P,u) = - \log ( \mathrm p(u) ), \end{aligned}$$

where a Gaussian approximation of p has been used.

The effective sample size and the log score of the forecasts were computed at $t= 70$ for all nine wells for a range of degrees of regularization of weights. Regularization of log weights was accomplished by applying a power transformation with exponents between 0 and 1 to the computed weights. The effective sample size (ESS) is affected by the degree of regularization—the ESS is 200 if equal weighting is used (i.e., if a power transformation with a very small exponent is applied). When the exponent is close to 1, one ends up using the weights as computed without denoising or regularization. Figure 13a shows predictability scores for a range of degrees of regularization using the hybrid iterative smoother with the monotonic permeability transform. Figure 13b shows corresponding results for the non-monotonic permeability transform. The solid black curves in both cases show the log score, which is somewhat small for both cases when the effective sample size is small, even though only the so-called best realizations are used for the forecast. The poor predictability for small effective sample size is a result of the small spread in the ensemble, so that even small inaccuracy of the prediction is highly improbable. As the effective sample size increases, the predictability initially increases rapidly because of the increase in the spread, but when the exponent of the power transform is decreased sufficiently, the predictability gradually decreases as more so-called bad samples are added. The impact of bad samples is smaller in the monotonic case than in the non-monotonic case because the root-mean-square error (RMSE) in the worst samples is smaller in the monotonic case.

Fig. 13

Evaluation of optimal regularization of weights for forecast predictability using the hybrid IES

Figure 14 compares unweighted predictions with weighted predictions and denoised weighted predictions for one of the wells (producer 4) in both two-dimensional porous flow examples. For producer 4, the agreement between the forecast from the data-generating model and weighted forecasts is nearly perfect, although the quality of the agreement at some other wells is lower. Better forecast predictability as measured by the log score is obtained using denoised importance weights, as described in Sect. 2.4.1, although in both examples (monotonic and non-monotonic log permeability transforms) the correct level of denoising was difficult to determine.

Fig. 14

The posterior distribution of forecasts conditioned to data to $t=60$ using the hybrid IES method. The black dots show the observed data

Although the effect of denoising is quantitatively different for the monotonic and non-monotonic permeability transforms, in both cases the best predictability is obtained when the weights are regularized such that the effective sample size is intermediate between the ESS for unweighted samples and the ESS for the weights computed using Eq. (13).

4 Landscape of the Posterior

The efficiency of the hybrid iterative smoother for sampling the posterior was relatively low in the flow example with the non-monotonic permeability transformation. For an ensemble size of 200, the effective sample size after denoising was approximately 5.5. The small size makes probabilistic inference difficult—even though the mean weighted forecasts were generally accurate, the estimates of the uncertainty often were not. In order to obtain an effective ensemble size of approximately 40 after weighting, it would be necessary to use an initial ensemble size of approximately 1,600. As the efficiency of the randomized maximum likelihood sampler using the Broyden-Fletcher-Goldfarb-Shanno (BFGS) algorithm for minimization with the gradient computed from the adjoint system was similar to the efficiency of the hybrid IES for a similar problem (Ba et al. 2022), it seems likely that the low efficiency is a result of the roughness of the posterior landscape rather than a problem with minimization.

The efficiency of sampling algorithms depends strongly on the landscape of the pdf to be sampled and on the goal of the sampling. If the objective is simply to sample in the neighborhood of the maximum a posteriori point, then using exact gradients is not always beneficial, especially if the log posterior is characterized by multiple scales—a smooth, long-range feature that is approximately quadratic and shorter-range fluctuations to the surface (Plecháč and Simpson 2020). If the posterior pdf is characterized, however, by a small number of nearly equivalent modes, then ensemble methods may fail to converge (Oliver and Chen 2018; Dunbar et al. 2022). In the numerical example with non-monotonic transformation of the log-permeability, the IES converged to the maximum a posteriori (MAP), but failed to sample other local minima. In order to clarify the behavior, the fitness landscape was evaluated in the neighborhood of the true data-generating model and over a larger region.

Fig. 15

The fitness landscape for the non-monotonic porous flow problem

The dimension of the model space is too large to visualize the landscape of the posterior directly. Instead, two illustrations of the fitness landscape for the non-monotonic log-permeability transform case were created by selecting three realizations of the model parameters to define a subspace of the model space. From three realizations, an orthonormal basis was constructed, and the log-likelihood function on a grid containing the three realizations was evaluated. In the first plot of the fitness landscape (Fig. 15a), the subspace contains both the true model, $\theta _{\textrm{true}}$, and the negative of the true model, $-\theta _{\textrm{true}}$. (Both are equally probably before conditioning to the data.) A third realization with relatively low weight was included to provide an independent basis vector needed for the two-dimensional subspace. In this case, there is a fairly large energy barrier separating the modes containing $\theta _{\textrm{true}}$ and $-\theta _{\textrm{true}}$ and a smaller barrier separating $\theta _{\textrm{true}}$ from $\theta _0$. In Fig. 15b, the subspace contains the truth and two realizations with large posterior weights. Again, each realization appears to lie in a separate mode of the likelihood, although that cannot be verified without examining the surface in higher dimensions. In any case, the posterior landscape is complex, and accurate gradients may be of limited usefulness if the goal is to locate the global minimum.

5 Summary and Conclusions

Iterative, ensemble-based data assimilation methods for sampling the posterior distribution are based on minimization of stochastic objective functions. These methods of sampling are approximate when the mapping from parameters to observations is nonlinear. To correct the sampling, importance weighting can be used. It is, however, generally difficult or costly to compute the importance weights if derivatives are computed from the adjoint system. On the other hand, the cost is relatively low for ensemble-based methods which avoid the need for adjoints. It was shown that standard products from hybrid iterative ensemble smoothers could be used to compute approximations to the importance weights. The weights computed in this way are noisy—largely because of low-rank stochastic approximations of derivatives. Denoising of the importance weights increased the effective sample size, decreased the RMSE in the estimate of the posterior model mean, and increased the predictability of future reservoir behavior.

Although the IES method converged more quickly than the hybrid IES in the numerical test problem with a multimodal posterior, the posterior realizations from the IES appear to be samples from a single mode. In some cases, the IES sampled from the mode with the highest probability, so that while the uncertainty was underestimated, the fit to data was good. In other cases, however, the IES samples were centered on a mode with lower mass and the fit was not as good. The posterior mean model for the multimodal problems using the IES was very sensitive to the choice of minimization parameters. Weighting was not effective in this case because the posteriori distributions of samples were not from the critical points of the stochastic cost function. We did not evaluate the possibility of combining multiple posterior ensembles from the IES, but it seems likely that the weighted results from a large number of ensembles would provide a better representation of the posterior.

Finally, it was noted that the posterior landscape of the inverse problem for the two-dimensional, two-phase immiscible flow appears to be multimodal when the permeability field is generated from a transformation that creates channel-like features of high permeability in a low-permeability background. The characteristics of the posterior distribution have implications for the types of data assimilation methods that can be expected to provide reasonable assessment of the uncertainty. For the flow problem with “channel-like” geology, it appeared that the standard IES may be capable of generating an ensemble of well-calibrated models, but the spread in that case was artificially small. The hybrid IES method provided an ensemble of models with much greater variability, but weighting of the calibrated realizations was necessary for posterior inference, and the effective ensemble size was much smaller than the actual ensemble size.

Appendices

Appendix A: Fast Matrix–Vector Multiplication

To accelerate the update step in the hybrid IES in large inverse problems, we apply circulant embedding for fast multiplication of Toeplitz matrices. Assuming that the forward model is defined on a uniform $(n_x+1)\times (n_y+1)$ grid, the dimensions of the corresponding covariance matrix are $(n_x+1)^2\times (n_y+1)^2$, which is extremely large in typical geoscience data assimilation applications. If the prior model covariance function is stationary and the model variables are defined on a two-dimensional regular, equispaced grid, the covariance matrix ${\varvec{C}}_\theta$ is symmetric level-2 block-Toeplitz. To reduce the storage and the computation cost, the embedding Toeplitz covariance is applied to circulant matrices. Circulant matrix–vector products can then be computed efficiently by fast Fourier transform (FFT) (Zimmerman 1989; Dietrich and Newsam 1997). A circulant matrix $\check{{\varvec{C}}}$ is a Toeplitz matrix that has its first column $\check{{\varvec{c}}}$ periodic. A Toeplitz matrix ${\varvec{C}}_\theta$ can always be augmented to generate a circulant matrix $\check{{\varvec{C}}}$. This process is called embedding, which can be written as

$$\begin{aligned} {\varvec{C}}_\theta = {\mathcal {M}}^\dag \check{{\varvec{C}}} {\mathcal {M}}( {\mathcal {H}}(\varvec{\xi })) = {\mathcal {M}}^\dag {\mathcal {F}}^{[-2]} \Big ({\mathcal {F}}^{[2]}(\check{{\varvec{c}}}) {\mathcal {F}}^{[2]}(\check{\varvec{\xi }})\Big ), \end{aligned}$$

where the operation ${\mathcal {M}}({\mathcal {H}}(\cdot ))$ injects and embeds $\varvec{\xi }$ into $\check{\varvec{\xi }}$, and ${\mathcal {F}}^{[2]}$ is evaluated by the FFT. Under the assumption of stationarity, the random field Y(x, y) has correlation function r(x, y) that depends only on the separation of variables.

Let $h_x$ and $h_y$ be constants denoting, respectively, the horizontal and vertical mesh size of a two-dimensional rectangular domain formed by the points $(x_i,y_j)$, where

$$\begin{aligned}\left\{ \begin{aligned}&x_i=ih_x,\quad 0\le i\le n_x\\&y_j=jh_y,\quad 0\le j\le n_y. \end{aligned}\right. \end{aligned}$$

The ordering of the grid nodes is done from left to right, bottom to top. Thus, the correlation matrix ${\varvec{R}}$ is block-Toeplitz (Zimmerman 1989; Dietrich and Newsam 1997), which is symmetric and uniquely characterized by the first block row

$$\begin{aligned} ({\varvec{R}}_0,{\varvec{R}}_1,\ldots ,{\varvec{R}}_{n_y}), \end{aligned}$$

with ${\varvec{R}}_j$ being the square of dimension $n_x+1$. Based on the node ordering, ${\varvec{R}}_j$ has first row and first column entries, respectively, given by

$$\begin{aligned} {r(ih_x,jh_y)}_{i=0}^{n_x} \quad \text {and} \quad {r(-ih_x,jh_y)}_{i=0}^{n_x}. \end{aligned}$$

The blocks ${\varvec{R}}_j$ are symmetric only if the correlation function has the special form r(|x|, |y|). When ${\varvec{R}}_j$ is Toeplitz for $j \ge 1$, it is uniquely characterized by its first row and first column which are written as

$$\begin{aligned} (r_{0j},r_{1j},\ldots ,r_{n_xj})\quad \text {and} \quad (r_{0j},r_{-1j},\ldots ,r_{-n_xj})^T. \end{aligned}$$

The minimal circulant embedding of ${\varvec{R}}_j$ that ensures that the embedding matrix has an even dimension (for FFT computation) is then given by the square circulant matrix ${\varvec{S}}_j$ of dimension $2(n_x + 1)$, for which the first row is

$$\begin{aligned} (r_{0j},r_{1j},\ldots ,r_{n_xj},\phi _j,r_{-n_xj},\ldots ,r_{-1j}). \end{aligned}$$

(A1)

The circulant embedding of Toeplitz matrices can be constructed by Eq. (A1). Once constructed, the circulant embedding is used to quickly generate samples from the prior and to evaluate products such as ${\varvec{C}}_\theta {\varvec{G}}^T$, which would otherwise be infeasible.

Appendix B: List of Symbols

List of Symbols

$N_\theta$:

Number of model parameters

${N}(\cdot ,\cdot )$:

Gaussian distribution

$N_d$:

Dimension of observational space

$C_\textrm{m}$:

Covariance matrix of Gaussian prior for m

$C_d$:

Covariance matrix of $\epsilon$

$N_m$:

Number of intermediate variable

$C_\theta$:

Covariance matrix of Gaussian prior for $\theta$

$\beta$:

Hyparameter or other reservoir properties

$\theta _l^i$:

ith sample for the lth iteration

${\mathcal {B}}$:

Generic forward model operator

$\theta ^{\text {pr}}$:

Mean of Gaussian prior

$\pi _D(d^{\textrm{o}})$:

Normalization constant

$Q(\theta )$:

Negative log likelihood function

$\pi _\Theta (\theta |d^{\textrm{o}})$:

Posterior distribution

$\pi _{\Theta \Delta } (\theta ,\delta )$:

Target distribution

$q_{\Theta '\Delta '} (\theta ',\delta ')$:

Proposal distribution of $(\theta ',\delta ')$

$p_{\Theta \Delta } (\theta ,\delta )$:

Proposal distribution of $(\theta ,\delta )$

$\kappa _{ri}$:

Relative permeability of phase i

$\theta$,$\delta$:

Samples of target distribution

$\theta '$,$\delta '$:

Samples of Gaussian $q_{\theta '\Delta '} (\theta ',\delta ')$

Z:

Composite observation operator

f:

Nonlinear transform from $\theta$ to m

$n(\theta ')$:

Total number of critical points

G:

Differential operator of g wrt $\theta$

$G_m$:

Differential operator of g wrt m

p(u):

Predictive distribution of u

${\check{C}}$:

Circulant matrix augmented by $C_\theta$

$P(\omega ^o|\omega )$:

Likelihood function of weights

$M_\theta$:

Differential operator of m wrt $\theta$

$I_N$:

N-dimensional identity matrix

$P(\omega |\omega ^o)$:

Posterior distribution of weights

$\textrm{Bold letter}$:

Vector or matrix of corresponding letter

$\textrm{Unbold letter}$:

Analytic representation or scalar

$N_e$:

Number of samples

$N_{\text {eff}}$:

Effective sample size

m:

Intermediate variable

$d^o$:

Observations

w:

Weights

$\epsilon$:

Observation error

l:

Iteration index

J:

Jacobian determinant

$\sigma _o$:

Standard deviation of $\omega ^o$

V, $\eta (\theta )$:

Auxiliary variables

u(x):

Model state

p(x, t):

Pressure

s(x, t):

Saturation

$\Omega$:

Spatial domain

L:

Square root of $C_M$

$\omega ^o$:

Observation of weights

$P(\omega )$:

Prior of weights

$h_x$,$h_y$:

Mesh size

$n_x$,$n_y$:

Number of grid nodes

g:

Observation operator

$\mu _{i}$:

Viscosity of phase i

$\Xi _\theta$:

Ensemble deviation for $\theta$

$1_{N}$:

N-dimensional one-vector

$\Xi _m$:

Ensemble deviation for m

$\Xi _d$:

Ensemble deviation for d

C:

Covariance operator

${\check{c}}$:

First column of ${\check{C}}$

$\sigma$:

Standard deviation of C

$\lambda _l$:

lth Regularization parameter

$\rho$:

Correlation length of C

$\delta \theta _l$:

Increment for the lth iteration

$\nu$:

Freedom of Chi-square prior for $\omega$

$\sigma _\text {pr}$:

Standard deviation of prior for $\omega$