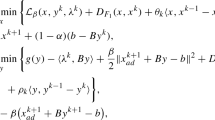An Adaptive Alternating Direction Method of Multipliers

Abstract

The alternating direction method of multipliers (ADMM) is a powerful splitting algorithm for linearly constrained convex optimization problems. In view of its popularity and applicability, a growing attention is drawn toward the ADMM in nonconvex settings. Recent studies of minimization problems for nonconvex functions include various combinations of assumptions on the objective function including, in particular, a Lipschitz gradient assumption. We consider the case where the objective is the sum of a strongly convex function and a weakly convex function. To this end, we present and study an adaptive version of the ADMM which incorporates generalized notions of convexity and penalty parameters adapted to the convexity constants of the functions. We prove convergence of the scheme under natural assumptions. To this end, we employ the recent adaptive Douglas–Rachford algorithm by revisiting the well-known duality relation between the classical ADMM and the Douglas–Rachford splitting algorithm, generalizing this connection to our setting. We illustrate our approach by relating and comparing to alternatives, and by numerical experiments on a signal denoising problem.

1 Introduction

By now, the alternating direction method of multipliers (ADMM) is a well-studied and applied splitting algorithm. In particular, it is applied to the problem

where $f:{\mathbb {R}}^n\rightarrow {]-\infty ,+\infty ]}$ and $g:{\mathbb {R}}^m\rightarrow {]-\infty ,+\infty ]}$ are proper, lower semicontinuous and convex functions, and $M\in {\mathbb {R}}^{m\times n}$. The ADMM can be traced back to 1975 in the studies of Glowinski and Marroco [26], and of Gabay and Mercier [23]. It was revisited in the early 1980s in [21, 22]. The ADMM has been successfully applied to a wide range of statistical and learning problems such as sparse regression, signal and image processing, and support vector machines, to name a few. An extensive survey on the ADMM and its applications can be found in [10].

The ADMM can be viewed as an enhanced version of the method of multipliers in the case where the objective function is separable. The augmented Lagrangian associated with (${\mathcal {P}}$) is the function

$$\begin{aligned} L_{\gamma }(x,z,y)=f(x)+g(z)+\langle y, Mx-z\rangle +\frac{\gamma }{2}\Vert Mx-z\Vert ^2, \end{aligned}$$

(1)

where $\gamma \ge 0$ is the penalty parameter and $y\in {\mathbb {R}}^m$ is the Lagrange multiplier. By employing the method of multipliers, one solves (${\mathcal {P}}$) by iteratively minimizing $L_{\gamma }(x,z,y)$ over the (primal) variables x and z while updating the Lagrange multiplier y (the dual variable). However, this requires to minimize the Lagrangian jointly in x and z. In order to avoid this situation, the ADMM takes advantage of the separability of the objective function and splits the minimization procedure into two separate steps, one for each variable. Specifically, by fixing a positive penalty parameter $\gamma$, the iterative step of the ADDM for solving (${\mathcal {P}}$) is

$$\begin{aligned} x^{k+1}&={\mathop {{{\,\mathrm{argmin}\,}}}\limits _{x\in {\mathbb {R}}^n}} L_\gamma (x,z^k,y^k), \end{aligned}$$

(2a)

$$\begin{aligned} z^{k+1}&= {\mathop {{{\,\mathrm{argmin}\,}}}\limits _{z\in {\mathbb {R}}^m}} L_\gamma (x^{k+1},z,y^k), \end{aligned}$$

(2b)

$$\begin{aligned} y^{k+1}&=y^k+\gamma (Mx^{k+1}-z^{k+1}). \end{aligned}$$

(2c)

Convergence of this scheme is well established in the case where f and g are convex, see, e.g., [10, § 3.2]. In nonconvex cases, it has been studied, e.g., [28, 30, 41, 42], under various combinations of assumptions which include, in particular, a Lipschitz continuity assumption on the gradient of f and/or g.

In the present study, we consider the case where f is strongly convex and g is weakly convex such that the objective of (${\mathcal {P}}$) is convex on the constraint. We introduce an adaptive alternating direction method of multipliers (aADMM) for which we incorporate a flexible range of penalty parameters adapted to the convexity constants of the functions f and g. To this end, we revisit the well-known relation between the classical ADMM and the Douglas–Rachford (DR) splitting algorithm [18, 31]. This duality relation was first observed in [22, § 5.1] and later revisited by other authors, see, e.g., [1, Appendix A] or [6, Remark 3.14]. A more detailed discussion regarding the ADMM is available in [20] while [34] is a recent survey on equivalences and other relations between splitting algorithms. We provide an analogous relation between our aADMM and the recent adaptive Douglas–Rachford (aDR) algorithm [3, 16]. We then employ this relation in order to derive convergence of our aADMM from the convergence of the aDR.

We point out (see Remark 4.1) that in our strongly-weakly convex setting, the functions f and g in problem (${\mathcal {P}}$) can be augmented into convex functions which transform the problem into a convex one, admissible for the classical ADMM, with the same minimizers, optimal values and computational difficulty level. However, the ADMM for the augmented problem corresponds to a Douglas–Rachford algorithm which is not in direct duality relations with the original strongly-weakly problem. Consequently, this theoretical aspect is lacking. Instead, we preserve and analyze the original problem. Our approach does yield a natural duality relation with a corresponding aDR algorithm which is instrumental in our convergence analysis. An additional benefit of our approach is that we relax and improve previously imposed assumptions on the strongly-weakly convex scenario such as in [33, 44] (see Remarks 5.1 and 5.2). Finally, although augmentation is a viable option in the strongly-weakly convex setting, application of the adaptive algorithms to the original problem has its own merit and by now was studied in a number of recent publications such as [2, 3, 16, 17, 25, 27, 32, 44, 45], to name a few.

Our main result is Theorem 5.1, where we provide convergence of the aADMM. Moreover, in order to show how our framework generalizes and relaxes the framework of the classical convex ADMM, we incorporate in our convergence analysis the relaxed assumptions regarding the convexity of f and g while not imposing further on top of the traditional constraint qualifications of the ADMM. To this end, we revisit and incorporate in our analysis some of the most commonly imposed assumptions and conditions on the classical ADMM. For the sake of accessibility and convenience, we summarize and unify our analysis with these classical conditions into an integrated tool in Corollary 5.1 for the aADMM and, in particular, in Corollary 5.2 for the classical ADMM.

Finally, we illustrate computational aspects of both approaches (our aADMM and the classical ADMM on an equivalent modified problem) by numerical experiments on a signal denoising problem with a weakly convex regularization term.

The remainder of the paper is organized as follows. In Sect. 2, we recall basic definitions and preliminary results. In Sect. 3, we recall notions of generalized monotonicity and the convergence of the adaptive Douglas–Rachford algorithm. In Sect. 4, we introduce our adaptive ADMM, we analyze some of its basic properties and we discuss conditions and constraint qualifications. The convergence of the scheme is established in Sect. 5. In Sect. 6, we conduct numerical experiments on a signal denoising problem with a weakly convex regularization term. Finally, we conclude our discussion in Sect. 7.

2 Preliminaries

Throughout, $\langle \cdot ,\cdot \rangle$ denotes the inner product in ${\mathbb {R}}^n$ with induced norm $\Vert \cdot \Vert$ defined by $\Vert x\Vert =\sqrt{\langle x,x\rangle },\ x\in {\mathbb {R}}^n$. We set ${\mathbb {R}}_+:=\{r\in {\mathbb {R}}: r\ge 0\}$ and ${\mathbb {R}}_{++}:=\{r\in {\mathbb {R}}: r>0\}$. Let $M\in {\mathbb {R}}^{m\times n}$. Then ${\text {ran}}M$, $\ker M$ and $\Vert M\Vert$ denote, respectively, the range, the null space and the matrix 2-norm of M. Let $C\subseteq R^n$ be a set. The closure, the interior and the relative interior of C are denoted by ${\text {cl}}C$, ${\text {int}}C$ and ${\text {ri}}C$, respectively. We denote by $A:{\mathbb {R}}^n\rightrightarrows {\mathbb {R}}^n$ a set-valued operator that maps any point $x\in {\mathbb {R}}^n$ to a set $A(x)\subseteq {\mathbb {R}}^n$. In the case where A is single-valued, we write $A:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^n$. The graph, the domain, the range, the set of fixed points and the set of zeros of A, are denoted, respectively, by ${\text {gra}}A$, ${\text {dom}}A$, ${\text {ran}}A$, ${\text {Fix}}A$ and ${\text {zer}}A$, i.e.,

$$\begin{aligned} {\text {gra}}A:=\left\{ (x,u)\in {\mathbb {R}}^n\times {\mathbb {R}}^n : u\in A(x)\right\} ,\quad {\text {dom}}A:=\left\{ x\in {\mathbb {R}}^n : A(x)\ne \emptyset \right\} ,\\ {\text {ran}}A:=\left\{ x\in {\mathbb {R}}^n : x\in A(z) \text { for some } z\in {\mathbb {R}}^n \right\} ,\\ {\text {Fix}}A:=\left\{ x\in {\mathbb {R}}^n : x\in A(x)\right\} \quad \text {and} \quad {\text {zer}}A:=\left\{ x\in {\mathbb {R}}^n : 0\in A(x)\right\} . \end{aligned}$$

The inverse of A, denoted by $A^{-1}$, is the operator defined via its graph by ${\text {gra}}A^{-1}:=\{(u,x)\in {\mathbb {R}}^n \times {\mathbb {R}}^n: u\in A(x)\}$. We denote the identity mapping by ${\text {Id}}$. The resolvent of the operator $A:{\mathbb {R}}^n\rightrightarrows {\mathbb {R}}^n$ with parameter $\gamma >0$ is the operator $J_{\gamma A}$ defined by

$$\begin{aligned} J_{\gamma A}:=({\text {Id}}+\gamma A)^{-1}. \end{aligned}$$

The $\lambda$-relaxed resolvent of A with parameter $\gamma >0$ is the operator $J^{\lambda }_{\gamma A}$ defined by

$$\begin{aligned} J^{\lambda }_{\gamma A}:=(1-\lambda ){\text {Id}}+ \lambda J_{\gamma A}. \end{aligned}$$

Definition 2.1

Let $D\subseteq {\mathbb {R}}^n$ be a nonempty set. The mapping $T:D\rightarrow {\mathbb {R}}^n$ is said to be

• (i) Lipschitz continuous with Lipschitz constant $l>0$ if

  $$\begin{aligned} \Vert T(x)-T(y)\Vert \le l\Vert x-y\Vert , \quad \forall x,y\in D; \end{aligned}$$

• (ii) nonexpansive if it is Lipschitz continuous with constant $l=1$;

• (iii) conically $\theta$-averaged, where $\theta >0$, if there exists a nonexpansive mapping $R:D\rightarrow {\mathbb {R}}^n$ such that

  $$\begin{aligned} T=(1-\theta )I+\theta R. \end{aligned}$$

Conically $\theta$-averaged mappings were studied in [8], in which they were referred to as conically nonexpansive mappings. They can be viewed as a natural extension of the classical $\theta$-averaged mappings (see, e.g., [5, Definition 4.33]). Additional properties and detailed discussions can be found in [3, 25].

An extended real-valued function $f:{\mathbb {R}}^n\rightarrow {]-\infty ,+\infty ]}$ is said to be proper if its (effective) domain, the set ${\text {dom}}f:=\{x\in {\mathbb {R}}^n : f(x)<+\infty \}$, is nonempty. We say that f is lower semicontinuous (l.s.c.) if, at any ${\bar{x}}\in {\mathbb {R}}^n$,

$$\begin{aligned} f({{\bar{x}}})\le \liminf _{x\rightarrow {{\bar{x}}}} f(x). \end{aligned}$$

Let $\alpha \in {\mathbb {R}}$. We say that f is $\alpha$-convex if $f-\frac{\alpha }{2}\Vert \cdot \Vert ^2$ is convex, equivalently, if

$$\begin{aligned} f((1-\lambda )x+\lambda y)\le \lambda f(x)+(1-\lambda )f(y)-\frac{\alpha }{2}\lambda (1-\lambda )\Vert x-y\Vert ^2, \quad \forall x,y\in {\mathbb {R}}^n,\ \lambda \in [0,1]. \end{aligned}$$

In particular, f is convex if and only if f is 0-convex. For an $\alpha$-convex function f, we say that f is strongly convex if $\alpha >0$ and we say that f is weakly convex (or hypoconvex) if $\alpha <0$. It follows that if $f_1$ is $\alpha _1$-convex and $f_2$ is $\alpha _2$-convex, then $f_1+f_2$ is $(\alpha _1+\alpha _2)$-convex.

The function f is coercive if

$$\begin{aligned} \lim _{\Vert x\Vert \rightarrow \infty }f(x)=+\infty \end{aligned}$$

and supercoercive if

$$\begin{aligned} \lim _{\Vert x\Vert \rightarrow \infty }\frac{f(x)}{\Vert x\Vert }=+\infty . \end{aligned}$$

One can verify that (see, e.g., [5, Corollary 11.17])

$$\begin{aligned} \text {strong convexity }\implies \text { supercoercivity }\implies \text {coercivity}. \end{aligned}$$

Let $\gamma >0$. The proximal operator with parameter $\gamma$ associated with the function f is defined by

$$\begin{aligned} {\text {prox}}_{\gamma f}: {\mathbb {R}}^n\rightrightarrows {\mathbb {R}}^n:y\mapsto {\mathop {{{\,\mathrm{argmin}\,}}}\limits _{x\in {\mathbb {R}}^n}}\left\{ f(x)+\frac{1}{2\gamma }\Vert x-y\Vert ^2\right\} , \quad \forall y\in {\mathbb {R}}^n. \end{aligned}$$

Let $x\in {\text {dom}}f$. The (convex) subdifferential of f at x is the set

$$\begin{aligned} \partial f(x):=\{u\in {\mathbb {R}}^n : \langle y-x,u\rangle +f(x)\le f(y),\quad \forall y\in {\mathbb {R}}^n\}. \end{aligned}$$

The Fréchet subdifferential of f at x is the set

$$\begin{aligned} {\widehat{\partial }}f(x):=\left\{ u\in {\mathbb {R}}^n : \liminf _{\begin{array}{c} y\rightarrow x\\ y\ne x \end{array}} \frac{f(y)-f(x)-\langle u,y-x\rangle }{\Vert y-x\Vert }\ge 0\right\} . \end{aligned}$$

When f is differentiable at x, we denote its gradient at x by $\nabla f(x)$. We recall the following facts regarding subdifferentials and gradients.

Fact 2.1

Let $f,g:{\mathbb {R}}^n\rightarrow {]-\infty ,+\infty ]}$ be proper and let $M\in {\mathbb {R}}^{n\times m}$.

• (i) $\partial f(x)\subseteq {\widehat{\partial }}f(x)$ for all $x\in {\text {dom}}f$.

• (ii) If f is convex, then ${\widehat{\partial }}f(x)=\partial f(x)$ for all $x\in {\text {dom}}f$.

• (iii) If f is differentiable at $x\in {\text {dom}}f$, then ${\widehat{\partial }}f(x)=\{\nabla f(x)\}$.

• (iv) $0\in \partial f({\bar{x}})$ if and only if ${\bar{x}}\in {\text {dom}}f$ minimizes f over ${\mathbb {R}}^n$.

• (v) $0\in {\widehat{\partial }}f({\bar{x}})$ if f attains a local minimum at ${\bar{x}}\in {\text {dom}}f$.

• (vi) If g is differentiable at $x\in {\text {dom}}f\cap {\text {dom}}g$, then ${\widehat{\partial }}(f+g)(x)={\widehat{\partial }}f(x)+\nabla g(x)$.

• (vii) If f and g are lower semicontinuous, then

  $$\begin{aligned} {\widehat{\partial }}f(x)+{\widehat{\partial }}g(x)\subseteq {\widehat{\partial }}(f+g)(x) \ \ \text {for all}\ x\in {\text {dom}}f\cap {\text {dom}}g. \end{aligned}$$

• (viii) If f is lower semicontinuous, then

  $$\begin{aligned} M^T{\widehat{\partial }}f(Mx)\subseteq {\widehat{\partial }}(f\circ M)(x)\ \ \text {for all}\ x\in {\mathbb {R}}^m\ \text {such that}\ Mx\in {\text {dom}}f. \end{aligned}$$

Proof

(i): See, e.g., [36, Proposition 8.6]. (ii): See, e.g., [36, Proposition 8.12]. (iii): See, e.g., [29, Proposition 1.1]. (iv): See, e.g., [5, Theorem 16.3]. (v): See, e.g., [29, Proposition 1.10]. (vi): See, e.g., [29, Corollary 1.12.2]. (vii): See, e.g., [36, Corollary 10.9]. (viii): See, e.g, [36, Theorem 10.6].$\square$

In order to carry out our analysis, we adopt the Fréchet subdifferential. However, our approach is applicable if one adopts other notions of the subdifferentials, such as the Mordukhovich subdifferential or the Clarke-Rockafellar subdifferential since these notions coincide for $\alpha$-convex functions (see [8, Proposition 6.3]).

Finally, let $f,g:{\mathbb {R}}^n\rightarrow {]}-\infty ,+\infty ]$ be proper and convex. We recall that the recession function of f is defined by

$$\begin{aligned} {\text {rec}}f:{\mathbb {R}}^n\rightarrow {]}-\infty ,+\infty ]: y \mapsto \sup _{x\in {\text {dom}}f}\{f(x+y) - f(x)\}, \end{aligned}$$

the Fenchel conjugate of f is defined by

$$\begin{aligned} f^*:{\mathbb {R}}^n\rightarrow {]}-\infty ,+\infty ]: u \mapsto \sup _{x\in {\mathbb {R}}^n}\{\langle u,x\rangle - f(x)\}, \end{aligned}$$

and the infimal convolution of f and g is defined by

$$\begin{aligned} f\square g:{\mathbb {R}}^n\rightarrow {[}-\infty ,+\infty ]: x\mapsto \inf _{y\in {\mathbb {R}}^n}\{f(y)+g(x-y)\}. \end{aligned}$$

3 Generalized Monotonicity and the Adaptive Douglas–Rachford Algorithm

We recall the following notions of generalized monotonicity.

Definition 3.1

Let $A:{\mathbb {R}}^n\rightrightarrows {\mathbb {R}}^n$ and let $\alpha \in {\mathbb {R}}$. Then A is said to be

• (i) $\alpha$-monotone if

  $$\begin{aligned} \langle x-y,u-v\rangle \ge \alpha \Vert x-y\Vert ^2,\quad \forall (x,u),(y,v)\in {\text {gra}}A; \end{aligned}$$

• (ii) $\alpha$-comonotone if $A^{-1}$ is $\alpha$-monotone, i.e.,

  $$\begin{aligned} \langle x-y,u-v\rangle \ge \alpha \Vert u-v\Vert ^2,\quad \forall (x,u),(y,v)\in {\text {gra}}A. \end{aligned}$$

An $\alpha$-monotone (resp. $\alpha$-comonotone) operator A is said to be maximally $\alpha$-monotone (resp. maximally $\alpha$-comonotone) if there is no $\alpha$-monotone (resp. $\alpha$-comonotone) operator $B:{\mathbb {R}}^n\rightrightarrows {\mathbb {R}}^n$ such that ${\text {gra}}A$ is properly contained in ${\text {gra}}B$.

Remark 3.1

We note that in the case where $\alpha =0$ in Definition 3.1, both 0-monotonicity and 0-comonotonicity simply mean monotonicity (see, for example, [5, Definition 20.1]). In the case where $\alpha >0$, $\alpha$-monotonicity is also referred to as strong monotonicity (see, e.g., [5, Definition 22.1(iv)]) and $\alpha$-comonotonicity is also referred to as cocoercivity (see, e.g., [5, Definition 4.10(iv)]). In the case where $\alpha <0$, $\alpha$-monotonicity is also referred to as hypomonotonicity (or weak monotonicity) and $\alpha$-comonotonicity is also referred to as cohypomonotonicity (see, e.g, [13, Definition 2.2]).

Fact 3.1

(maximal monotonicity of the subdifferential) Let $\alpha \in {\mathbb {R}}$ and suppose that ${f:{\mathbb {R}}^n\rightarrow ]-\infty ,+\infty ]}$ is $\alpha$-convex. Then the Fréchet subdifferential of f, ${\widehat{\partial }} f:{\mathbb {R}}^n\rightrightarrows {\mathbb {R}}^n$, is maximally $\alpha$-monotone.

Proof

See, e.g., [16, Lemma 5.2].$\square$

We recall that under certain assumptions on the monotonicity parameters, the resolvents of comonotone operators are conically averaged.

Fact 3.2

(resolvents of comonotone operators) Let $\alpha \in {\mathbb {R}}$ and set $\gamma >0$ such that $\gamma >-\alpha$. If $A:{\mathbb {R}}^n\rightrightarrows {\mathbb {R}}^n$ is $\alpha$-comonotone, then

• (i) $J_{\gamma A}$ is single-valued and conically $\frac{\gamma }{2(\gamma +\alpha )}$-averaged;

• (ii) ${\text {dom}}J_{\gamma A}={\mathbb {R}}^n$ if and only if A is maximally $\alpha$-comonotone.

Proof

See [3, Propositions 3.7 and 3.8(i)] and [8, Proposition 3.7(v) &(vi)].$\square$

Fact 3.3

(maximal comonotonicity) Let $\alpha \in {\mathbb {R}}$ and $A:{\mathbb {R}}^n\rightrightarrows {\mathbb {R}}^n$. The following hold.

• (i) A is maximally $\alpha$-comonotone $\iff$ $A^{-1}$ is maximally $\alpha$-monotone.

• (ii) Suppose that $\alpha \ge 0$. Then

  $$\begin{aligned} A \text { is maximally } \alpha \text {-comonotone}\iff \begin{array}{c} A \text { is } \alpha \text {-comonotone}\\ \text {and maximally monotone.}\end{array} \end{aligned}$$

Proof

(i): Follows directly from Definition 3.1. (ii): Apply [16, Proposition 3.5(i)] to the operator $A^{-1}$ (alternatively, see [3, Proposition 3.2(ii)]).$\square$

Lemma 3.1

(Closedness of graph) Let $\alpha \in {\mathbb {R}}$ and let $A:{\mathbb {R}}^n\rightrightarrows {\mathbb {R}}^n$ be maximally $\alpha$-comonotone. Then ${\text {gra}}A$ is closed.

Proof

Let ${(x_k,u_k)}_{k=0}^{\infty }\subseteq {\text {gra}}A$ such that $(x_k,u_k)\rightarrow (x,u)\in {\mathbb {R}}^n\times {\mathbb {R}}^n$. By employing Fact 3.3(i), we see that $A^{-1}$ is maximally $\alpha$-monotone, which is equivalent to $B:=A^{-1}-\alpha {\text {Id}}$ being maximally monotone. Consequently, ${\text {gra}}B$ is closed (see, for example, [5, Proposition 20.38]). Since ${(u_k,x_k-\alpha u_k)}_{k=0}^{\infty }\subseteq {\text {gra}}B$ and $(u_k,x_k-\alpha u_k)\rightarrow (u,x-\alpha u)$, we conclude that $(u,x-\alpha u)\in {\text {gra}}B$, which, in turn, implies that $(x,u)\in {\text {gra}}A$.$\square$

We conclude this section by recalling the convergence of the adaptive Douglas–Rachford (aDR) algorithm for maximally comonotone operators. The aDR can be viewed as an extension of the classical Douglas–Rachford splitting algorithm [18, 31], originally utilized to find a zero of the sum of two maximally monotone operators by employing their resolvents. The aDR algorithm was recently presented and studied in [16] in order to find a zero of the sum of a strongly monotone operator and a weakly monotone operator. This analysis was later extended in [3] to include, in particular, the case of a strongly comonotone operator and a weakly comonotone operator. Convergence results for the shadow sequence of the aDR (i.e., the image of the aDR sequence under the resolvent) in infinite-dimensional spaces have been recently provided in [2]. We recall the following fact regarding the convergence of the aDR for comonotone operators.

Fact 3.4

(aDR for comonotone operators) Let $\alpha ,\beta \in {\mathbb {R}}$ be such that $\alpha +\beta \ge 0$. Let $A:{\mathbb {R}}^n\rightrightarrows {\mathbb {R}}^n$ be a maximally $\alpha$-comonotone operator and let $B:{\mathbb {R}}^n\rightrightarrows {\mathbb {R}}^n$ be a maximally $\beta$-comonotone operator such that ${\text {zer}}(A+B)\ne \emptyset$. Suppose that $(\gamma ,\delta )\in {\mathbb {R}}^2_{++}$ satisfy

$$\begin{aligned} 0<\gamma +2\alpha =\delta ,&\quad \text { if } \alpha +\beta =0, \end{aligned}$$

(3a)

$$\begin{aligned} \text {or } \quad (\gamma +\delta )^2<4(\gamma +\alpha )(\delta +\beta ),&\quad \text { if } \alpha +\beta >0; \end{aligned}$$

(3b)

and set $(\lambda ,\mu )\in {\mathbb {R}}^2_{++}$ by

$$\begin{aligned} (\lambda -1)(\mu -1)=1 \quad \text {and}\quad \delta =(\lambda -1)\gamma . \end{aligned}$$

(4)

Set further $\kappa \in {]0,{\overline{\kappa }}[}$ where

$$\begin{aligned} {\overline{\kappa }}:=\left\{ \begin{array}{ll} 1, &{} \text {if } \alpha +\beta =0;\\ \displaystyle \frac{4(\gamma +\alpha )(\delta +\beta )-(\gamma +\delta )^2}{2(\gamma +\delta )(\alpha +\beta )}, &{} \text {if } \alpha +\beta >0. \end{array}\right. \end{aligned}$$

(5)

Finally, set $x_0\in {\mathbb {R}}^n$ and let $(x_k)_{k=0}^{\infty }$ be generated by the recurrence

$$\begin{aligned} x_{k+1}=T_{{\text {aDR}}}(x_k):=(1-\kappa )x_k+\kappa J^{\lambda }_{\gamma A}J^{\mu }_{\delta B}(x_k),\quad k=0,1,2,\ldots . \end{aligned}$$

(6)

Then

• (i) $x_k\rightarrow x^\star \in {\text {Fix}}T_{{\text {aDR}}}\text { and } J_{\delta B}(x^\star )\in {\text {zer}}(A+B);$

• (ii) $J_{\delta B}(x_k)\rightarrow J_{\delta B}(x^\star )\in {\text {zer}}(A+B);$

• (iii) $J_{\delta B}(x_k)-J_{\gamma A}J^{\mu }_{\delta B}(x_k)\rightarrow 0$.

Proof

We note that (3) implies that $\alpha +\gamma >0$ and $\delta +\beta >0$. In view of Fact 3.2, $J_{\gamma A}$ and $J_{\delta B}$ are single-valued with full domain and, consequently, the iteration in (6) is well defined. By [3, Theorem 5.4], we arrive at

$$\begin{aligned} x_k\rightarrow x^\star \in {\text {Fix}}T_{{\text {aDR}}}\quad \text {and}\quad x_{k}-T_{{\text {aDR}}}(x_{k})\rightarrow 0 \end{aligned}$$

which, combined with [16, Lemma 4.1], implies (i) and (iii). Finally, by invoking Fact 3.2(i) we see that $J_{\delta B}$ is conically averaged. This implies that $J_{\delta B}$ is Lipschitz continuous and, consequently, (ii) follows from (i).$\square$

4 Adaptive ADMM

The adaptive alternating direction method of multipliers requires natural generalized convexity assumptions as well as traditional assumptions on (${\mathcal {P}}$). We divide these conditions and constraint qualifications into three categories: generalized convexity assumptions, existence of solutions for (${\mathcal {P}}$) and existence and well posedness of our iterative steps. Compared with the traditional framework of the classical ADMM, we show that our settings are more general and admit a wider class of functions within the first category while maintaining traditional assumptions and constraint qualifications in the second and third categories. To this end, we recollect the most common and widely imposed conditions on the classical ADMM as well as equivalences and relations between them. We divide our discussion into the following subsections: convexity qualifications, critical points and minimizes, introduction of the aADMM, constraint qualifications and related conditions for existence of our iterative steps.

4.1 Convexity Assumptions

One of the underlying assumptions for the classical ADMM is that the functions f and g in (${\mathcal {P}}$) are proper, lower semicontinuous and convex. We adapt to a wider class of functions via the following natural assumption.

Assumption 4.1

Let $M\in {\mathbb {R}}^{m\times n}$ be a nonzero matrix. We assume that the function $f:{\mathbb {R}}^n\rightarrow ]-\infty ,+\infty ]$ is proper, lower semicontinuous and $\alpha$-convex, and $g:{\mathbb {R}}^m\rightarrow ]-\infty ,+\infty ]$ is proper, lower semicontinuous and $\beta$-convex where $\alpha , \beta \in {\mathbb {R}}$ are parameters such that

$$\begin{aligned} \alpha \ge 0\quad \text {and}\quad \alpha +\beta \Vert M\Vert ^2\ge 0. \end{aligned}$$

In order to characterize the solutions of (${\mathcal {P}}$) under Assumption 4.1, we will employ the following lemma.

Lemma 4.1

Let $M\in {\mathbb {R}}^{m\times n}$. Suppose that $g:{\mathbb {R}}^m\rightarrow ]-\infty ,+\infty ]$ is a $\beta$-convex function where $\beta <0$. Then $g\circ M$ is $\beta \Vert M\Vert ^2$-convex.

Proof

Let $x, y\in {\mathbb {R}}^n$ and $\lambda \in [0,1]$. Then the $\beta$-convexity of g implies that

$$\begin{aligned} (g\circ M)\big ((1-\lambda )x+\lambda y\big )=~&g\big ((1-\lambda )Mx+\lambda My\big )\\ \le ~&(1-\lambda )g(Mx)+\lambda g(My)\\ {}&-\dfrac{\beta }{2}\lambda (1-\lambda )\Vert Mx-My\Vert ^2\\ \le ~&(1-\lambda )(g\circ M)(x)+\lambda (g\circ M)(y)\\ {}&-\Big (\dfrac{\beta }{2}\Vert M\Vert ^2\Big )\lambda (1-\lambda )\Vert x-y\Vert ^2, \end{aligned}$$

i.e., $g\circ M$ is $\beta \Vert M\Vert ^2$-convex.$\square$

Lemma 4.2

Let Assumption 4.1 hold. Then $(x^\star ,z^\star )$ is a solution of (${\mathcal {P}}$) if and only if

$$\begin{aligned} Mx^\star =z^\star \quad \text {and}\quad 0\in \partial (f+g\circ M)(x^\star ). \end{aligned}$$

Proof

We note that (${\mathcal {P}}$) is equivalent to the unconstrained optimization problem of minimizing $f+g\circ M$ over ${\mathbb {R}}^n$. We claim that $f+g\circ M$ is a convex function. Indeed, under Assumption 4.1, if $\beta \ge 0$, then f as well as g are convex and so is $f+g\circ M$. If $\beta <0$, then Lemma 4.1 implies that $g\circ M$ is $\beta \Vert M\Vert ^2$-convex. Consequently, we see that $f+g\circ M$ is $(\alpha +\beta \Vert M\Vert ^2)$-convex. In particular, $f+g\circ M$ is convex since $\alpha +\beta \Vert M\Vert ^2\ge 0$. Finally, by recalling Fact 2.1(iv), we conclude that the minimizers of (${\mathcal {P}}$) are characterized by the first-order optimality condition $0\in \partial (f+g\circ M)(x^\star )$.$\square$

Remark 4.1

(on strongly-weakly convex settings) Under Assumption 4.1, problem (${\mathcal {P}}$) can be referred to as a strongly-weakly convex problem, see, e.g., [16, 27]. Splitting methods for this problem require computability of subdifferentials and their resolvents. We observe that by setting

$$\begin{aligned} {\tilde{f}}:=f+\frac{\beta }{2}\Vert M(\cdot )\Vert ^2\ \quad \ \text {and}\ \quad \ {\tilde{g}}:=g-\frac{\beta }{2}\Vert \cdot \Vert ^2, \end{aligned}$$

(${\mathcal {P}}$) is equivalent to

Under Assumption 4.1, both ${\tilde{f}}$ and ${\tilde{g}}$ are convex. Indeed, a straightforward verification implies that ${\tilde{g}}$ is convex. Furthermore, if $\beta \ge 0$, then ${\tilde{f}}$ is convex because f and $\frac{\beta }{2}\Vert M(\cdot )\Vert ^2$ are convex. If $\beta <0$, then $\frac{\beta }{2}\Vert M(\cdot )\Vert ^2$ is $\beta \Vert M\Vert ^2$-convex by Lemma 4.1. We note that f is $\alpha$-convex and $\alpha +\beta \Vert M\Vert ^2\ge 0$, so ${\tilde{f}}$ is $(\alpha +\beta \Vert M\Vert ^2)$-convex, in particular, convex.

Consequently, one can apply the classical ADMM to ($\widehat{{\mathcal {P}}}$) in order to solve (${\mathcal {P}}$) with a similar computational difficulty level. A similar strategy was pointed out as an alternative to the adaptive DR algorithm in [16, Remark 4.15].

Remark 4.2

(A non-symmetric scenario) We would like to emphasize that this approach is not symmetric with respect to the weakly-strongly convexity assumptions, that is, we do not allow f to be weakly-convex. The main reason is that even in the case where g is strongly convex, we cannot guarantee the strong convexity of the composition $g\circ M$, as we did with the weak convexity in Lemma 4.1. Thus, we do not assess the convexity of the equivalent problem ($\widehat{{\mathcal {P}}}$) discussed in Remark 4.1.

We will experiment with the approach outlined in Remark 4.1 in Sect. 6. However, from the theoretical perspective, we pursue a different path: We do not modify (${\mathcal {P}}$), instead, we provide an adaptive version of the ADMM which is admissible under the strongly-weakly convex setting of (${\mathcal {P}}$). To this end, we provide duality relations with the recent adaptive DR algorithm [16] which, in turn, are instrumental in the proof of convergence of our adaptive scheme. One of the justifications of our approach is that it complements and extends the natural and well-known duality relation between the classical ADMM and the classical DR algorithm to the strongly-weakly convex setting. Experiments with our approach and some comparisons to the approach in Remark 4.1 are also included in Sect. 6. In particular, we highlight the flexibility in the choice of parameters in our aADMM.

4.2 Critical Points

We address the issue of critical points and saddle points of the Lagrangian $L_0$ in (1), as well as their relations to the solutions of (${\mathcal {P}}$), under Assumption 4.1.

Definition 4.1

(critical points) We say that the tuple $(x^\star ,z^\star ,y^\star )\in {\mathbb {R}}^n\times {\mathbb {R}}^m\times {\mathbb {R}}^m$ is a critical point of the (unaugmented) Lagrangian $L_{0}$ of (${\mathcal {P}}$) if

$$\begin{aligned} -M^Ty^\star \in \partial f(x^\star ),\quad y^\star \in {\widehat{\partial }}g(z^\star )\quad \text {and}\quad Mx^\star -z^\star =0. \end{aligned}$$

(7)

We also recall that $(x^\star ,z^\star ,y^\star )$ is a saddle point of $L_0$ if

$$\begin{aligned} L_0(x^\star ,z^\star ,y)\le L_0(x^\star ,z^\star ,y^\star )\le L_0(x,z,y^\star ), \quad \forall (x,z,y)\in {\mathbb {R}}^n\times {\mathbb {R}}^m\times {\mathbb {R}}^m. \end{aligned}$$

Lemma 4.3

Let Assumption 4.1 hold. If $(x^\star ,z^\star ,y^\star )$ is a critical point of $L_{0}$, then $(x^\star ,z^\star )$ is solution of (${\mathcal {P}}$).

Proof

In view of (7), and by recalling Fact 2.1(viii) and (vii), we see that

$$\begin{aligned} 0 = -M^Ty^\star +M^Ty^\star&\in \partial f(x^\star )+M^T{\widehat{\partial }}g(Mx^\star )\\&\subseteq \partial f(x^\star )+{\widehat{\partial }}(g\circ M)(x^\star ) \subseteq {\widehat{\partial }}(f+g\circ M)(x^\star ). \end{aligned}$$

Consequently, by combining Lemma 4.2 and Fact 2.1(ii), we derive that $(x^\star ,z^\star )$ solves (${\mathcal {P}}$).$\square$

We see that any critical point produces a solution of (${\mathcal {P}}$). The converse implication, however, requires a constraint qualification.

Lemma 4.4

Suppose that Assumption 4.1 and one of the following assertions hold:

• (i) $0\in {\text {ri}}({\text {dom}}g - M({\text {dom}}f))$;

• (ii) ${\text {ri}}({\text {dom}}g)\cap {\text {ri}}( M({\text {dom}}f))\ne \emptyset$;

• (iii) ${\text {int}}({\text {dom}}g)\cap M({\text {dom}}f)\ne \emptyset \quad$ or $\quad ({\text {dom}}g)\cap {\text {int}}(M({\text {dom}}f))\ne \emptyset$.

Then the existence of critical points of $L_0$ is equivalent to the existence of solutions of (${\mathcal {P}}$).

Proof

$(\Rightarrow )$: Follows from Lemma 4.3.

$(\Leftarrow )$: We note that either (ii) or (iii) implies (i) (see, e.g., [5, Proposition 6.19]). Set ${\tilde{f}}$ and ${\tilde{g}}$ to be the convex functions in Remark 4.1. We observe that ${\text {dom}}f={\text {dom}}{\tilde{f}}$, ${\text {dom}}g={\text {dom}}{\tilde{g}}$, and that

$$\begin{aligned} \partial {\tilde{f}} = \partial f +\beta M^TM \quad ,\quad \partial {\tilde{g}} = {\widehat{\partial }} g -\beta {\text {Id}}. \end{aligned}$$

Since the constraint qualification $0\in {\text {ri}}({\text {dom}}{{\tilde{g}}} - M({\text {dom}}{{\tilde{f}}}))$ is satisfied, by employing subdifferential calculus (see [5, Theorem 16.47]) we arrive at

$$\begin{aligned} \partial (f+g\circ M)&=\partial ({\tilde{f}}+{\tilde{g}}\circ M)\\&=\partial {\tilde{f}} + M^T\circ \partial {\tilde{g}}\circ M\\&=\partial f +\beta M^TM + M^T\circ {\widehat{\partial }} g\circ M -\beta M^TM\\&=\partial f + M^T\circ {\widehat{\partial }} g\circ M. \end{aligned}$$

Finally, by invoking Lemma 4.2, if $(x^\star ,z^\star )$ is a solution of (${\mathcal {P}}$), then

$$\begin{aligned} z^\star =Mx^\star \quad \text {and}\quad 0\in \partial (f+g\circ M)(x^\star )=\partial f(x^\star )+M^T\circ {\widehat{\partial }}g\circ M(x^\star ). \end{aligned}$$

Consequently, there exists $y^\star \in {\mathbb {R}}^m$ such that $(x^\star ,z^\star ,y^\star )$ is a critical point of $L_0$.$\square$

The notion of a critical point and the one of a saddle point coincide in the case where both functions f and g are convex. We now show that in the case where convexity is absent, saddle points are still critical points.

Lemma 4.5

(Critical points vs saddle points) Let $f:{\mathbb {R}}^n\rightarrow ]-\infty ,\infty ]$ and $g:{\mathbb {R}}^m\rightarrow ]-\infty ,\infty ]$ be proper. Then, the saddle points of $L_0$ are also critical points. If, in addition, f and g are convex, then any critical point of $L_0$ is a saddle point.

Proof

Let $x^\star \in {\text {dom}}(f),\ z^\star \in {\text {dom}}(g)$. Then

$$\begin{aligned} f(x^\star )+&g(z^\star )+\langle y, Mx^\star -z^\star \rangle&\le f(x^\star )+g(z^\star )+\langle y^\star ,Mx^\star -z^\star \rangle , \quad \forall y\in {\mathbb {R}}^m, \end{aligned}$$

(8a)

$$\begin{aligned} \iff \quad&\langle y-y^\star , Mx^\star -z^\star \rangle&\le 0, \quad \forall y\in {\mathbb {R}}^m, \end{aligned}$$

(8b)

$$\begin{aligned} \iff \quad&Mx^\star&=z^\star . \end{aligned}$$

(8c)

Moreover,

$$\begin{aligned} f(x^\star )+g(z^\star )+\langle y^\star ,Mx^\star -z^\star \rangle&\le f(x)+g(z)+\langle y^\star , Mx-z\rangle , \end{aligned}$$

(9)

for all $(x,z)\in {\mathbb {R}}^n\times {\mathbb {R}}^m$, is equivalent to

$$\begin{aligned} f(x^\star )+\langle y^\star ,Mx^\star \rangle&\le f(x)+\langle y^\star ,Mx\rangle , \quad \forall x\in {\mathbb {R}}^n,\\ \text {and} \qquad \quad g(z^\star )-\langle y^\star ,z^\star \rangle&\le g(z)-\langle y^\star ,z\rangle , \quad \forall z\in {\mathbb {R}}^m, \end{aligned}$$

i.e.,

$$\begin{aligned} -M^T y^\star \in \partial f(x^\star ) \quad \text {and}\quad y^\star \in \partial g(z^\star )\subseteq {\widehat{\partial }} g(z^\star ). \end{aligned}$$

Hence, if $(x^\star ,z^\star ,y^\star )$ is a saddle point, then $(x^\star ,z^\star ,y^\star )$ is a critical point of $L_0$.

Conversely, if, in addition, f and g are convex and if $(x^\star ,z^\star ,y^\star )$ is a critical point of $L_0$, then

$$\begin{aligned} Mx^\star =z^\star \ ,\ -M^T y^\star \in \partial f(x^\star ) \quad \text {and}\quad y^\star \in {\widehat{\partial }} g(z^\star )=\partial g(z^\star ), \end{aligned}$$

which implies (8a) and (9), i.e., $(x^\star ,z^\star ,y^\star )$ is a saddle point of $L_0$.$\square$

In view of the relations between the critical points of $L_0$ and the solutions of (${\mathcal {P}}$), we impose the existence of a critical point in our convergence analysis.

Assumption 4.2

The Lagrangian $L_0$ has a critical point.

Remark 4.3

Assumption 4.2 is standard in the analysis of the ADMM and its variants in the convex framework. In this case, Lemma 4.5 implies that it is equivalent to the existence of saddle points, which is assumed in several classical studies such as [10, 20, 21].

Other authors obtain the existence of critical/saddle points from the nonemptyness of the solution set of (${\mathcal {P}}$) when combined with one of the constraint qualifications in Lemma 4.4. For instance, the Slater constraint qualification in Lemma 4.4(ii) is used in [11, 14] while [9, 34] incorporate the assumption in Lemma 4.4(i).

We now relate the critical points of the Lagrangian to the zeros of $Q+S$, where Q and S are the operators defined by

$$\begin{aligned} Q:{\mathbb {R}}^m\rightrightarrows {\mathbb {R}}^m: y\mapsto&\left\{ -Mx : -M^Ty \in \partial f(x)\right\} =(-M)\circ (\partial f)^{-1}\circ (-M^T)(y), \end{aligned}$$

(10a)

$$\begin{aligned} S:{\mathbb {R}}^m\rightrightarrows {\mathbb {R}}^m: y\mapsto&\left\{ z : y \in {\widehat{\partial }}g(z)\right\} =({\widehat{\partial }}g)^{-1}(y). \end{aligned}$$

(10b)

We will address the convergence of our aADMM by applying the adaptive DR algorithm [16] to Q and S. This is a natural extension of the classical relation between the ADMM and the DR algorithm in the convex case (see, e.g., [20, 34]) to our generalized setting.

Proposition 4.1

The Lagrangian $L_0$ has a critical point if and only if ${\text {zer}}(Q+S)\ne \emptyset$, where Q and S are the operators defined in (10). More precisely, $y^\star \in {\text {zer}}(Q+S)$ if and only if there exist $x^\star \in {\mathbb {R}}^n$ and $z^\star \in {\mathbb {R}}^m$ such that $(x^\star ,z^\star ,y^\star )$ is a critical point of $L_0$.

Proof

We observe that $y^\star \in {\text {zer}}(Q+S)$ if and only if there exists $z^\star \in {\mathbb {R}}^m$ such that

$$\begin{aligned} z^\star \in S(y^\star ) \quad \text {and}\quad -z^\star \in Q(y^\star ). \end{aligned}$$

(11)

The definition of Q and S implies that (11) is equivalent to $y^\star \in {\widehat{\partial }}g(z^\star )$ and the existence of $x^\star \in {\mathbb {R}}^n$ such that $z^\star =Mx^\star$ and $-M^Ty^\star \in \partial f(x^\star )$, that is, $(x^\star ,z^\star ,y^\star )$ is a critical point of $L_0$.$\square$

4.3 The Algorithm

We now formulate our adaptive version of the Alternating Direction Method of Multipliers, aADMM for short. The steps of the aADMM are analogous to the steps of the classical ADMM in (2); however, the aADMM is admissible in the strongly-weakly convex setting and it accommodates different penalty parameters in the two minimization steps. Specifically, we set an initial point $(x^0,z^0,y^0)\in {\mathbb {R}}^n\times {\mathbb {R}}^m\times {\mathbb {R}}^m$ and two parameters $\gamma ,\delta >0$. Then the aADMM iterates according to the recurrences

$$\begin{aligned} x^{k+1}&={\mathop {{{\,\mathrm{argmin}\,}}}\limits _{x\in {\mathbb {R}}^n}}L_\gamma (x,z^k,y^k), \end{aligned}$$

(12a)

$$\begin{aligned} z^{k+1}&={\mathop {{{\,\mathrm{argmin}\,}}}\limits _{z\in {\mathbb {R}}^m}}L_\delta (x^{k+1},z,y^k), \end{aligned}$$

(12b)

$$\begin{aligned} y^{k+1}&=y^k+\delta (Mx^{k+1}-z^{k+1}), \end{aligned}$$

(12c)

equivalently,

$$\begin{aligned} x^{k+1}&={\mathop {{{\,\mathrm{argmin}\,}}}\limits _{x\in {\mathbb {R}}^n}}\left\{ f(x) + \frac{\gamma }{2}\Big \Vert Mx-z^k+\frac{y^k}{\gamma }\Big \Vert ^2\right\} , \end{aligned}$$

(13a)

$$\begin{aligned} z^{k+1}&={\mathop {{{\,\mathrm{argmin}\,}}}\limits _{z\in {\mathbb {R}}^m}}\left\{ g(z)+ \frac{\delta }{2}\Big \Vert Mx^{k+1}-z+\frac{y^k}{\delta }\Big \Vert ^2\right\} , \end{aligned}$$

(13b)

$$\begin{aligned} y^{k+1}&=y^k+\delta (Mx^{k+1}-z^{k+1}). \end{aligned}$$

(13c)

Clearly, by letting $\gamma =\delta$, we obtain the steps of the original ADMM. Similar to the ADMM, the aADMM is only valid if the $x^k$-step in (12a) and the $z^k$-step in (12b) (equivalently, (13a) and (13b), respectively) are well defined. We will examine this issue in relation to the operators Q and S in (10). Our next argument follows the footsteps of [22] (see also [20]). It forms a foundation for convergence analysis of the aADMM by providing a sufficient condition for the existence of the z-update via the maximal comonotonicity of S.

Lemma 4.6

(Existence of the z-update) Let $g:{\mathbb {R}}^m\rightarrow ]-\infty ,\infty ]$ be proper, $\beta$-convex and lower semicontinuous. Let $x^{k+1}\in {\mathbb {R}}^n$, $y^k\in {\mathbb {R}}^m$ and $\delta >\max \{0,-\beta \}$. Then the operator S defined by (10b) is maximally $\beta$-comonotone. Consequently, $J_{\delta S}$ is single-valued with full domain and $z^{k+1}$ defined in (12b) is uniquely determined by

$$\begin{aligned} z^{k+1}=\frac{1}{\delta }\big ({\text {Id}}-J_{\delta S}\big )(y^k+\delta Mx^{k+1}), \end{aligned}$$

and

$$\begin{aligned} y^{k+1}=y^k+\delta (Mx^{k+1}-z^{k+1})= J_{\delta S}(y^k+\delta Mx^{k+1}). \end{aligned}$$

Proof

Since g is $\beta$-convex, Fact 3.1 implies that ${\widehat{\partial }}g$ is maximally $\beta$-monotone. Consequently, it follows from Fact 3.3(i) that $S=({\widehat{\partial }}g)^{-1}$ is maximally $\beta$-comonotone.

Now, since $\delta >-\beta$, Fact 3.2 implies that $J_{\delta S}$ is single-valued and has full domain. Furthermore, since g is $\beta$-convex and $\delta >-\beta$, the function inside the argmin in (12b) is convex. By employing Fact 2.1 (iv) and then (vi), we see that

which completes the proof.$\square$

We now provide a general condition for the existence of the x-update. We dedicate Section 4.4 to a detailed discussion of cases where this condition is satisfied.

Lemma 4.7

Let $M\in {\mathbb {R}}^{m\times n}$ be nonzero and let $f:{\mathbb {R}}^n\rightarrow ]-\infty ,\infty ]$ be proper, lower semicontinuous and $\alpha$-convex, where $\alpha \in {\mathbb {R}}_+$. Then the operator Q defined in (10a) is $\frac{\alpha }{\Vert M\Vert ^2}$-comonotone.

Proof

Let $(y_1,-Mx_1),(y_2,-Mx_2)\in {\text {gra}}Q$. Then $(x_1,-M^Ty_1),(x_2,-M^Ty_2)\in {\text {gra}}\partial f$. Since f is $\alpha$-convex, Fact 3.1 implies that $\partial f$ is $\alpha$-monotone. Consequently,

$$\begin{aligned} \langle x_1-x_2, -M^T(y_1-y_2)\rangle \ge \alpha \Vert x_1-x_2\Vert ^2, \end{aligned}$$

which implies that

$$\begin{aligned} \langle -M(x_1-x_2), y_1-y_2\rangle \ge \frac{\alpha }{\Vert M\Vert ^2}\Vert M\Vert ^2\Vert x_1-x_2\Vert ^2\ge \frac{\alpha }{\Vert M\Vert ^2}\Vert M(x_1-x_2)\Vert ^2. \end{aligned}$$

Thus, Q is $\frac{\alpha }{\Vert M\Vert ^2}$-comonotone.$\square$

Lemma 4.8

(Conditions for the existence of the x-update) Let $f:{\mathbb {R}}^n\rightarrow ]-\infty ,\infty ]$ be proper, convex and lower semicontinuous. Let $M\in {\mathbb {R}}^{m\times n}$ be nonzero. Let $y^k,z^k\in {\mathbb {R}}^m$ and $\gamma >0$. Then the following assertions are equivalent.

• (i) $x^{k+1}$ satisfies (12a);

• (ii) $x^{k+1}\in (\partial f)^{-1}(-M^Tv^k)$, where $v^k=y^k+\gamma (Mx^{k+1}-z^k)$;

• (iii) $v^k= J_{\gamma Q}(y^k-\gamma z^k)$, where Q is defined by (10a).

Consequently, $x^{k+1}$ in (12a) exists for all $(y^k,z^k)$ if and only if $J_{\gamma Q}$ has full domain.

Proof

By invoking Fact 2.1 (iv) and (vi), we see that

$$\begin{aligned}&x^{k+1}\text { satisfies }(\mathrm{12a})~~\nonumber \\ \iff ~~&0\in \partial f(x^{k+1})+M^Ty^k+\gamma M^T(Mx^{k+1}-z^k)\nonumber \\ \iff ~~&-M^Tv^k\in \partial f(x^{k+1}) \text {~~where~~}v^k=y^k+\gamma (Mx^{k+1}-z^k)\nonumber \\ \iff ~~&x^{k+1}\in (\partial f)^{-1}(-M^Tv^k)\text {~~where~~} y^k-\gamma z^k-v^k=-\gamma Mx^{k+1}\nonumber \\ \iff ~~&y^k-\gamma z^k -v^k\in -\gamma M\circ (\partial f)^{-1}\circ (-M^T)(v^k)\nonumber \\ \iff ~~&y^k-\gamma z^k \in ({\text {Id}}+\gamma Q)(v^k)\nonumber \\ \iff ~~&v^k = J_{\gamma Q}(y^k-\gamma z^k). \end{aligned}$$

(14)

In (14), we employed the single-valuedness of $J_{\gamma Q}$ which follows from Lemma 4.7 when combined with Fact 3.2(i).$\square$

4.4 Constraint Qualifications for the x-update

While the z-update is already well defined under a generalized convexity assumption (by Lemma 4.6), the x-update depends on the resolvent of Q having full domain (by Lemma 4.8). We now discuss constraint qualifications for the maximal comonotonicity of Q, which, in turn, guarantees full domain of its resolvent. To this end, we assume that

Assumption 4.3

The following constraint qualification holds:

$$\begin{aligned} 0\in {\text {ri}}({\text {dom}}f^* - {\text {ran}}M^T). \end{aligned}$$

(15)

Assumption 4.3 is satisfied in several cases which we detail in the following lemma. Some of the historical context and references to such cases in the classical ADMM literature are provided in Remark 4.4.

Lemma 4.9

(Sufficient conditions for Assumption 4.3) Let $f:{\mathbb {R}}^n\rightarrow ]-\infty ,+\infty ]$ be proper, convex and lower semicontinuous. Let $M\in {\mathbb {R}}^{m\times n}$. Then each of the following conditions implies (15):

• (i) ${\text {ri}}({\text {dom}}f^*)\cap {\text {ran}}M^T \ne \varnothing$.

• (ii) ${\text {ri}}({\text {ran}}\partial f)\cap {\text {ran}}M^T \ne \varnothing$.

• (iii) $({\text {rec}}f)(x)>0$ for all $x\in \ker M\setminus \{x\in {\mathbb {R}}^n : -({\text {rec}}f)(-x)=({\text {rec}}f)(x)=0\}.$

• (iv) f is coercive (in particular, supercoercive).

• (v) f is strongly convex.

• (vi) $M^TM$ is invertible.

Proof

(i): By [35, Corollary 6.6.2],

$$\begin{aligned} {\text {ri}}({\text {dom}}f^* - {\text {ran}}M^T)={\text {ri}}({\text {dom}}f^*) - {\text {ran}}M^T. \end{aligned}$$

Consequently, (i) follows from [5, Corollary 6.15].

(ii): By invoking (i) , it suffices to show that

$$\begin{aligned} {\text {ri}}({\text {dom}}f^*)={\text {ri}}({\text {ran}}\partial f). \end{aligned}$$

(16)

Indeed, by [5, Proposition 16.4(i) and Corollary 16.18(i)],

$$\begin{aligned} {\text {ri}}({\text {dom}}f^*)\subseteq {\text {dom}}\partial f^*\subseteq {\text {dom}}f^*. \end{aligned}$$

Now, by employing [35, Theorem 6.3],

$$\begin{aligned} {\text {cl}}({\text {dom}}f^*)={\text {cl}}({\text {dom}}\partial f^*) \quad \text {and}\quad {\text {ri}}({\text {dom}}f^*)={\text {ri}}({\text {dom}}\partial f^*). \end{aligned}$$

Finally, since ${\text {dom}}\partial f^*={\text {ran}}\partial f$, we arrive at (16).

(iii): We consider the function $F=f+h$, where $h=\eta \Vert M(\cdot )-a\Vert ^2$ for some $a\in {\mathbb {R}}^m$ and $\eta >0$. By [5, Proposition 9.30(vi)],

$$\begin{aligned} {\text {rec}}F = {\text {rec}}f +{\text {rec}}h. \end{aligned}$$

Moreover, since $\Vert \cdot \Vert ^2$ is supercoercive, [5, Proposition 9.30(vii) and Example 9.32] imply that

$$\begin{aligned} ({\text {rec}}h)(x):=\left\{ \begin{array}{ll} 0, &{} \text {if } Mx=0,\\ +\infty , &{} \text {otherwise}.\end{array}\right. \end{aligned}$$

Hence, (iii) implies that $({\text {rec}}F)(x)>0$ for all vectors $x\in {\mathbb {R}}^n$ except those satisfying $-{\text {rec}}F(-x)={\text {rec}}F(x)=0$. By [35, Corollary 13.3.4(b)], this is equivalent to

$$\begin{aligned} 0\in {\text {ri}}({\text {dom}}F^*). \end{aligned}$$

(17)

On the other hand, since ${\text {dom}}h^* = {\text {ran}}M^T$, by employing [5, Proposition 12.6(ii)] we see that

$$\begin{aligned} {\text {dom}}f^* - {\text {ran}}M^T = {\text {dom}}f^* + {\text {ran}}M^T = {\text {dom}}f^* +{\text {dom}}h^* = {\text {dom}}(f^*\square h^*). \end{aligned}$$

Now, since h has full domain, $0\in {\text {int}}({\text {dom}}f-{\text {dom}}h)$. Consequently, by [36, Theorem 11.23(a)] we arrive at $f^*\square h^*=(f+h)^*$ which, in turn, implies that

$$\begin{aligned} {\text {dom}}f^* - {\text {ran}}M^T = {\text {dom}}(f^*\square h^*)={\text {dom}}(f+h)^*={\text {dom}}F^*. \end{aligned}$$

(18)

By combining (17) and (18) we obtain (15).

(iv): If f is coercive, then [5, Proposition 14.16] implies that $0\in {\text {int}}({\text {dom}}f^*)\subseteq {\text {ri}}({\text {dom}}f^*)$. Since, clearly, $0\in {\text {ran}}M^T$, we employ (i) and conclude (15).

(v): Follows from (iv) since every strongly convex function is coercive.

(vi): If $M^TM$ is invertible, then ${\text {ran}}M^T={\mathbb {R}}^n$. Since ${\text {dom}}f^*\ne \varnothing$, (15) follows trivially.$\square$

We now prove the existence of the x-update via maximal comonotonicity of Q which is guaranteed by Assumptions 4.1 and 4.3.

Lemma 4.10

(Existence of the x-update under constraint qualifications) Let $M\in {\mathbb {R}}^{m\times n}$ be nonzero and let $f:{\mathbb {R}}^n\rightarrow ]-\infty ,\infty ]$ be proper, lower semicontinuous, and $\alpha$-convex for some $\alpha \in {\mathbb {R}}_+$. Let Assumption 4.3 hold. Then the operator Q defined in (10a) is maximally $\frac{\alpha }{\Vert M\Vert ^2}$-comonotone. Consequently, the x-update in (12a) is well defined and

$$\begin{aligned} y^k+\gamma (Mx^{k+1}-z^k) = J_{\gamma Q}(y^k-\gamma z^k). \end{aligned}$$

Proof

Since f is convex, proper and lsc, so is $f^*$ (see, e.g., [5, Proposition 13.13]). Consequently, since Assumption 4.3 holds, the constraint qualifications in the chain rule [35, Theorem 23.9] (see also [5, Corollary 16.53]) are met for the convex function $f^*$ and the linear operator $-M^T$ and we obtain

$$\begin{aligned} \partial (f^*\circ (-M^T))= (-M)\circ (\partial f^*) \circ (-M^T) = (-M)\circ (\partial f)^{-1} \circ (-M^T) = Q.\nonumber \\ \end{aligned}$$

(19)

We see that Q is the subdifferential of the proper, convex and lower semicontinuous function $f^*\circ (-M^T)$ and, as such, Q is maximally monotone by Fact 3.1. It now follows that Q is maximally $\frac{\alpha }{\Vert M\Vert ^2}$-comonotone by Lemma 4.7 and Fact 3.3(ii).

Finally, Fact 3.2 implies that $J_{\gamma Q}$ is single-valued with full domain. The existence of the x-update now follows from Lemma 4.8.$\square$

Remark 4.4

Assumption 4.3 and several of the constraint qualification in Lemma 4.9 have been widely used for the analysis of the classical ADMM in the literature. In this relation, we list some classical and recent references:

• (i) In [22], the convergence of the ADMM for the variational inequality problem

  $$\begin{aligned}&\text {find }x,w\in {\mathbb {R}}^n\text { such that}\\&w\in A(x)\quad \text {and}\quad \langle w,y-x\rangle +g(My)-g(Mx)\ge 0,\quad \forall y\in {\mathbb {R}}^n; \end{aligned}$$

  was established. One of the assumptions is that either A is strongly monotone or $M^TM$ is an isomorphism (see [22, Theorem 5.1]). When applied to problem (${\mathcal {P}}$), these assumptions become

  $$\begin{aligned} f\text { is strongly convex}\quad \text { or}\quad M^TM\text { is invertible}, \end{aligned}$$

  which implies Assumption 4.3 by Lemma 4.9 (v) and (vi).

• (ii) [10] is one of the most widely cited studies of the ADMM. Therein, no conditions are imposed (apart from the existence of saddle points; see Remark 4.3) in order to derive convergence of the ADMM. However, it was pointed out in [11] that this may fail since in this case the steps of the ADMM may not be well defined, i.e., the argmins may not exist. In particular, for the existence of $x^{k+1}$, the authors of [11] require the condition in Lemma 4.9(iii) (see [11, Assumption 1]).

• (iii) In [38], the condition in Lemma 4.9(i) was imposed to guarantee the existence of $x^{k+1}$.

• (iv) In [19], the condition in Lemma 4.9(ii) was utilized in order to obtain the chain rule in (19). It was referred to as dual normality (see [19, Definition 3.22 and Proposition 3.30]). The argument therein also follows directly from [35, Theorem 23.9]. The chain rule leads to the maximal monotonicity of Q, which, in turn, guarantees the existence of $x^{k+1}$.

• (v) The invertibility of $M^TM$ in Lemma 4.9(vi) is, arguably, the most common assumption for the convergence of ADMM in the literature. Indeed, it is assumed in [1, 9, 14, 21, 34], to name a few.

Although $M^TM$ being invertible or f being strongly convex are two of the more restrictive conditions in Lemma 4.9, as we show next, they do provide an additional strength: uniqueness of the x-update which, in turn, implies convergence of the sequence ${(x^k)}_{k=0}^{\infty }$. Assumption 4.3 alone only guarantees the convergence of the sequence ${(Mx^k)}_{k=0}^{\infty }$ (see Theorem 5.1).

Lemma 4.11

(Criteria for uniqueness of the x-update) Let $M\in {\mathbb {R}}^{m\times n}$ be nonzero and let $f:{\mathbb {R}}^n\rightarrow ]-\infty ,\infty ]$ be proper, lower semicontinuous and $\alpha$-convex, where $\alpha \in {\mathbb {R}}_+$. Set

$$\begin{aligned} v^k:= J_{\gamma Q}(y^k-\gamma z^k)\ \text {where}\ Q\ \text {is the operator defined in }(\mathrm{10a}). \end{aligned}$$

The following hold.

• (i) If $\alpha >0$ (i.e., f is strongly convex), then $(\partial f)^{-1}$ is Lipschitz continuous and the x-update in (12a) is uniquely defined by

  $$\begin{aligned} x^{k+1}=(\partial f)^{-1}(-M^Tv^k). \end{aligned}$$

• (ii) If $M^TM$ is invertible, then the x-update in (12a) is uniquely defined by

  $$\begin{aligned} x^{k+1}=(M^TM)^{-1}M^T\left( \tfrac{1}{\gamma }(v^k-y^k)+z^k\right) . \end{aligned}$$

Proof

By employing Lemma 4.9(v) and Lemma 4.9(vi), respectively, we see that the conditions in (i) and (ii) imply Assumption 4.3. Consequently, Lemma 4.10 implies that the x-update in (12a) is well defined and

$$\begin{aligned} v^k:=y^k+\gamma (Mx^{k+1}-z^k) = J_{\gamma Q}(y^k-\gamma z^k). \end{aligned}$$

Now, if f is $\alpha$-strongly convex ($\alpha >0$), then by combining Fact 3.1 with Fact 3.3(i) we see that $(\partial f)^{-1}$ is maximally $\alpha$-comonotone. Consequently, $(\partial f)^{-1}$ is Lipschitz continuous, in particular, single-valued. It follows that the inclusion in Lemma 4.8(ii) is an equality, i.e.,

$$\begin{aligned} x^{k+1}=(\partial f)^{-1}(-M^Tv^k). \end{aligned}$$

If $M^TM$ is invertible, since $v^k=y^k+\gamma (Mx^{k+1}-z^k)$, we conclude that

$$\begin{aligned} x^{k+1}=(M^TM)^{-1}(M^TM)x^{k+1}=(M^TM)^{-1}M^T\left( \tfrac{1}{\gamma }(v^k-y^k)+z^k\right) , \end{aligned}$$

which completes the proof.$\square$

Remark 4.5

We note that Lemma 4.11 is directly implied by (13a). Indeed, if f is strongly convex or M has full column rank (i.e., $M^TM$ is invertible), then the function inside the argmin in (13a) is strongly convex, which, in turn, implies existence and uniqueness of minimizers.

5 Convergence of the aADMM

In order to obtain convergence of the aADMM, we adapt $\gamma$ and $\delta$ to the convexity parameters of the two functions f and g. We will employ the following lemma in order to guarantee existence of such parameters.

Lemma 5.1

(Existence of parameters) Let $\alpha ,\beta \in {\mathbb {R}}$ such that $\alpha +\beta >0$. Then for every $\gamma ,\delta \in {\mathbb {R}}_{++}$ the following assertions are equivalent.

• (i) $2\delta (\alpha +\beta )+(\gamma +\delta )^2<4(\gamma +\alpha )(\delta +\beta )$.

• (ii) $\delta +2\beta >0$ and

  $$\begin{aligned} \gamma \in ] \delta +2\beta -\sqrt{2(\alpha +\beta )(\delta +2\beta )},\delta +2\beta +\sqrt{2(\alpha +\beta )(\delta +2\beta )}[. \end{aligned}$$

Proof

A straightforward computation implies that

$$\begin{aligned}&2\delta (\alpha +\beta )+(\gamma +\delta )^2<4(\gamma +\alpha )(\delta +\beta )\\ \iff \quad&\gamma ^2-2(\delta +2\beta )\gamma + (\delta +2\beta )(\delta -2\alpha )<0\\ \iff \quad&\left\{ \begin{array}{l} \delta +2\beta >0,\\ \delta +2\beta -\sqrt{2(\alpha +\beta )(\delta +2\beta )}<\gamma <\delta +2\beta +\sqrt{2(\alpha +\beta )(\delta +2\beta )};\end{array}\right. \end{aligned}$$

which completes the proof.$\square$

Theorem 5.1

(convergence of the aADMM) Suppose that Assumptions 4.1, 4.2 and 4.3 hold. Let $\delta >\max \{0,-2\beta \}$ and set

$$\begin{aligned}&\gamma =\delta +2\beta ,&\text {if } \alpha +\beta \Vert M\Vert ^2=0, \end{aligned}$$

(20a)

$$\begin{aligned}&\gamma \in ]\max \{0,\delta +2\beta - \varDelta _{\delta }\}, \delta +2\beta + \varDelta _{\delta } [,&\text {if } \alpha +\beta \Vert M\Vert ^2>0; \end{aligned}$$

(20b)

where

$$\begin{aligned} \varDelta _{\delta }:=\frac{1}{\Vert M\Vert }\sqrt{2\left( {\alpha }+\beta {\Vert M\Vert ^2}\right) (\delta +2\beta )}. \end{aligned}$$

Set $(x^0,z^0,y^0)\in {\mathbb {R}}^n\times {\mathbb {R}}^m\times {\mathbb {R}}^m$ and let ${(x^k,z^k,y^k)}_{k=0}^{\infty }$ be generated by the aADMM (12). Then

$$\begin{aligned} Mx^k\rightarrow Mx^\star ,\quad z^k\rightarrow z^\star \quad \text {and}\quad y^k\rightarrow y^\star , \end{aligned}$$

where $(x^\star ,z^\star ,y^\star )$ is a critical point of $L_0(x,z,y)$. Consequently, $(x^\star ,z^\star )$ is a solution of (${\mathcal {P}}$).

Proof

Let Q and S be defined by (10). Our aim is to establish that the sequence generated by the aADMM (12) corresponds to the sequence generated by the aDR (6) when applied to Q and S. Note that ${\text {zer}}(Q+S)\ne \emptyset$ due to Assumption 4.2 and Proposition 4.1.

On the one hand, for any $\beta$, it holds that $\max \{0,-2\beta \}\ge \max \{0,-\beta \}$. So $\delta >\max \{0,-\beta \}$. Consequently, Lemma 4.6 implies that S is maximally $\beta$-comonotone and that the z-update in (12b) is uniquely defined by

$$\begin{aligned} y^{k+1}= J_{\delta S}(y^{k+1}+\delta z^{k+1}). \end{aligned}$$

On the other hand, Lemma 4.10 implies that Q is maximally $\frac{\alpha }{\Vert M\Vert ^2}$-comonotone, that the x-update in (12a) is well defined and

$$\begin{aligned} v^k:=y^k+\gamma (Mx^{k+1}-z^k)= J_{\gamma Q}(y^k-\gamma z^k). \end{aligned}$$

Set $w^k:=y^k+\delta z^k$ for each $k=0,1,2,\ldots$. Set further

$$\begin{aligned} \lambda :=1+\frac{\delta }{\gamma } \quad \text {and}\quad \mu :=1+\frac{\gamma }{\delta }. \end{aligned}$$

Then, clearly, $\lambda ,\mu$ satisfy (4). We employ $J_{\delta S}$ and $J_{\gamma Q}$ in order to compute $J^{\lambda }_{\gamma Q}\big (J^{\mu }_{\delta S}(w^k)\big )$ via the following steps:

$$\begin{aligned} J_{\delta S}(w^k)&=J_{\delta S}(y^k+\delta z^k)=y^k,\\ J^{\mu }_{\delta S}(w^k)&=(1-\mu )w^k+\mu J_{\delta S}(w^k)\\&=(1-\mu )(y^k+\delta z^k)+\mu y^k\\&=y^k+(1-\mu )\delta z^k \\&=y^k-\gamma z^k,\\ J_{\gamma Q}\big (J^{\mu }_{\delta S}(w^k)\big )&=J_{\gamma Q}(y^k-\gamma z^k)=v^k,\\ \text {and so,}\quad \ J^{\lambda }_{\gamma Q}\big (J^{\mu }_{\delta S}(w^k)\big )&=(1-\lambda )J^{\mu }_{\delta S}(w^k)+\lambda J_{\gamma Q}\big (J^{\mu }_{\delta S}(w^k)\big )\\&=(1-\lambda )(y^k-\gamma z^k)+\lambda v^k\\&=y^k+\delta z^k+\lambda (v^k-y^k)\\&=w^k+\lambda (v^k-y^k). \end{aligned}$$

We also observe that

$$\begin{aligned} w^{k+1}&=y^{k+1}+\delta z^{k+1}=y^k+\delta Mx^{k+1}=y^k+(\lambda -1)\gamma Mx^{k+1}\\&=y^k+(\lambda -1)(v^k-y^k+\gamma z^k)=y^k+(\lambda -1)(v^k-y^k)+\delta z^k\\&=w^k+(\lambda -1)(v^k-y^k). \end{aligned}$$

Consequently, by setting $\kappa :=\frac{\lambda -1}{\lambda }=\frac{\delta }{\gamma +\delta }\in {]0,1[}$ and by recalling (6) we arrive at

$$\begin{aligned} T_{{\text {aDR}}}(w^k):=(1-\kappa )w^k+\kappa J^{\lambda }_{\gamma Q}\big (J^{\mu }_{\delta S}(w^k)\big )=w^k+(\lambda -1)(v^k-y^k)=w^{k+1}.\nonumber \\ \end{aligned}$$

(21)

Summing up, the sequence ${(w^k)}_{k=0}^{\infty }$ is generated by the aDR algorithm applied to S and Q.

We now apply Fact 3.4 to the two operators Q and S. To this end, it suffices to check that the conditions in Fact 3.4 for the parameters, i.e., conditions (3) and (5) for $\frac{\alpha }{\Vert M\Vert ^2},\beta ,\gamma ,\delta$, and $\kappa$, are met. By Assumption 4.1,

$$\begin{aligned} \frac{\alpha }{\Vert M\Vert ^2}+\beta \ge 0. \end{aligned}$$

If $\frac{\alpha }{\Vert M\Vert ^2}+\beta =0$, then (20a) implies $\delta =\gamma -2\beta =\gamma +2\frac{\alpha }{\Vert M\Vert ^2}$, that is, (3a) is satisfied.

If $\frac{\alpha }{\Vert M\Vert ^2}+\beta >0$, then, by Lemma 5.1, we see that (20b) implies that

$$\begin{aligned}&2\delta \left( \frac{\alpha }{\Vert M\Vert ^2}+\beta \right) +(\gamma +\delta )^2&<4\left( \gamma +\frac{\alpha }{\Vert M\Vert ^2}\right) (\delta +\beta ) \end{aligned}$$

(22a)

$$\begin{aligned} \iff&\frac{\delta }{\gamma +\delta }&< \frac{4\left( \gamma +\frac{\alpha }{\Vert M\Vert ^2}\right) (\delta +\beta )-(\gamma +\delta )^2}{2(\gamma +\delta )\left( \frac{\alpha }{\Vert M\Vert ^2}+\beta \right) }=:{\overline{\kappa }}. \end{aligned}$$

(22b)

On the one hand, (22a) implies

$$\begin{aligned} (\gamma +\delta )^2<4\left( \gamma +\frac{\alpha }{\Vert M\Vert ^2}\right) (\delta +\beta ), \end{aligned}$$

which leads to (3b). On the other hand, (22b) implies that $0<\kappa <{\overline{\kappa }}$, i.e., (5) is satisfied.

Consequently, we meet all of the conditions in order to apply Fact 3.4: Fact 3.4(i) implies that $w^k\rightarrow w^\star \in {\text {Fix}}T_{{\text {aDR}}}$ while Fact 3.4(ii) implies that

$$\begin{aligned} y^k=J_{\delta S}(w^k) \rightarrow J_{\delta S}(w^\star )=:y^\star \in {\text {zer}}(Q+S). \end{aligned}$$

By the convergence of $w^k$ and $y^k$, we see that

$$\begin{aligned} z^k=\frac{1}{\delta }(w^k-y^k)\rightarrow \frac{1}{\delta }(w^\star -y^\star )=:z^\star . \end{aligned}$$

Finally, Fact 3.4(iii) implies that $y^k-v^k\rightarrow 0$, thus, $v^k\rightarrow y^\star$ and

$$\begin{aligned} Mx^k\rightarrow z^\star . \end{aligned}$$

We prove that there exists $x^\star \in {\mathbb {R}}^n$ such that $Mx^\star =z^\star$ and that $(x^\star ,z^\star ,y^\star )$ is a critical point. Indeed, we note that

$$\begin{aligned} {(y^k,z^k)}_{k=0}^{\infty }\subseteq {\text {gra}}S \quad \text {and}\quad {(v^k,-Mx^{k+1})}_{k=0}^{\infty }\subseteq {\text {gra}}Q. \end{aligned}$$

(23)

By taking limits in (23) and by recalling Lemma 3.1, we conclude that $(y^\star ,z^\star )\in {\text {gra}}S$ and $(y^\star ,-z^\star )\in {\text {gra}}Q$, equivalently,

$$\begin{aligned} y^\star \in {\widehat{\partial }}g(z^\star ) \quad \text {and}\quad -M^Ty^\star \in \partial f(x^\star ), \end{aligned}$$

for some $x^\star$ such that $z^\star =Mx^\star$. Finally, since we now have a critical point $(x^\star ,z^\star ,y^\star )$, we invoke Lemma 4.3 which concludes the proof.$\square$

Remark 5.1

(on the strongly-weakly convex assumption) In the strongly-weakly convex settings, certain assumptions are usually imposed on the parameters $(\alpha ,\beta )$. In our adaptive approach, Assumption 4.1 requires

$$\begin{aligned} \alpha +\beta \Vert M\Vert ^2\ge 0. \end{aligned}$$

This is an improvement of [44, Assumption 3.1(i)] for the ADMM, which can be reformulated in the form

$$\begin{aligned} \alpha +\beta \Vert M\Vert ^2>0. \end{aligned}$$

(24)

In a different algorithmic approach, the convergence of the Primal-Dual Hybrid Gradient method for the strongly-weakly convex setting was established in [33] by assuming (24) (see [33, Theorem 2.3]). Summing up, we see that our analysis is applicable in the setting of the classical ADMM for convex functions (i.e., $\alpha =\beta =0$) while [33, 44] are not. This observation aligns with the analysis of the adaptive DR algorithm in [3, 16] (see [16, Remark 5.5]).

Remark 5.2

(parameters in the classical ADMM) We consider the classical ADMM in the case of strong convexity $\alpha +\beta \Vert M\Vert ^2>0$. We then set $\gamma =\delta \in {\mathbb {R}}_{++}$ for $\delta$ such that $\delta +2\beta >0$ and

$$\begin{aligned} \delta +2\beta -\sqrt{2\left( \frac{\alpha }{\Vert M\Vert ^2}+\beta \right) (\delta +2\beta )}<\delta <\delta +2\beta +\sqrt{2\left( \frac{\alpha }{\Vert M\Vert ^2}+\beta \right) (\delta +2\beta )}. \end{aligned}$$

which is equivalent to

$$\begin{aligned} \delta > \max \left\{ -2\beta ,\frac{-2\alpha \beta }{\alpha +\beta \Vert M\Vert ^2}\right\} =\frac{-2\alpha \beta }{\alpha +\beta \Vert M\Vert ^2}, \quad \text {if } \beta \le 0. \end{aligned}$$

This range of parameters improves the results in [44] which require (see [44, Assumption 3.1(ii)])

$$\begin{aligned} \delta > -2\beta +\frac{8\beta ^2\Vert MM^T\Vert }{\alpha +\beta \Vert M\Vert ^2} =\frac{-2\alpha \beta }{\alpha +\beta \Vert M\Vert ^2}+\frac{6\beta ^2\Vert M\Vert ^2}{\alpha +\beta \Vert M\Vert ^2}. \end{aligned}$$

Remark 5.3

(Self-duality of the aDR) In the proof of Theorem 5.1, we have shown that the aADMM algorithm is, in fact, a dual aDR iteration. We now discuss the case where $M={\text {Id}}$ in (${\mathcal {P}}$). In this case, it is known that the classical DR is self-dual in the sense of [19, Proposition 3.43], see also, [4, Corollary 4.3]. It is not difficult to show that the adaptive DR is also self-dual. Indeed, in the case where $M={\text {Id}}$, iteration (21) is the aDR applied to the operators

$$\begin{aligned} S=({\widehat{\partial }}g)^{-1} \quad \text {and}\quad Q=(-{\text {Id}})\circ (\partial f)^{-1}\circ (-{\text {Id}}). \end{aligned}$$

Therefore, one easily checks that

$$\begin{aligned} J_{\delta S}&={\text {Id}}-\delta \left( {\text {prox}}_{\tfrac{1}{\delta }g}\right) \circ \left( \frac{1}{\delta }{\text {Id}}\right) , \end{aligned}$$

(25a)

$$\begin{aligned} J_{\gamma Q}&={\text {Id}}+\gamma \left( {\text {prox}}_{\tfrac{1}{\gamma }f}\right) \circ \left( -\frac{1}{\gamma }{\text {Id}}\right) . \end{aligned}$$

(25b)

By substituting (5.3) into (21) and taking into account (4) and the change of variable $t^{k}:=\frac{1}{\delta }w^k$, we obtain the scheme

$$\begin{aligned} t^{k+1}=(1-\kappa )t^k + \kappa R_2(R_1 (t^{k})), \end{aligned}$$

where

$$\begin{aligned} R_1:&=(1-\lambda ){\text {Id}}+ \lambda {\text {prox}}_{\tfrac{1}{\delta }g},\\ R_2:&=(1-\mu ){\text {Id}}+ \mu {\text {prox}}_{\tfrac{1}{\gamma }f}. \end{aligned}$$

We see that the aADMM with $M={\text {Id}}$ is the aDR in [16, Theorem 5.4] applied to g and f with parameters $(\delta ^{-1},\gamma ^{-1},\lambda ,\mu )\in {\mathbb {R}}^4_{++}$ and $\kappa =\frac{\lambda -1}{\lambda }\in {]0,1[}$.

In Theorem 5.1, we see that the sequence ${(Mx^k)}_{k=0}^{\infty }$ converges; however, there is no indication as to whether ${(x^k)}_{k=0}^{\infty }$ converges or not. Similarly to the classical case (see, for instance, [1, Proposition 2.2] and [39, Proposition 2]), this can be remedied if we assume that $M^TM$ is invertible or f is strongly convex ($\alpha >0$).

Theorem 5.2

(convergence of the aADMM under stronger assumptions) Suppose that Assumptions 4.1, 4.2 and one of the following conditions hold:

• (i) f is strongly convex (i.e., $\alpha >0$),

• (ii) $M^TM$ is invertible.

Let $\delta >\max \{0,-2\beta \}$ and let $\gamma >0$ satisfy (20). Set $(x^0,z^0,y^0)\in {\mathbb {R}}^n\times {\mathbb {R}}^m\times {\mathbb {R}}^m$ and let ${(x^k,z^k,y^k)}_{k=0}^{\infty }$ be generated by the aADMM (12). Then

$$\begin{aligned} x^k\rightarrow x^\star ,\quad z^k\rightarrow z^\star \quad \text {and}\quad y^k\rightarrow y^\star , \end{aligned}$$

where $(x^\star ,z^\star ,y^\star )$ is a critical point of $L_0(x,z,y)$. Consequently, $(x^\star ,z^\star )$ is a solution of (${\mathcal {P}}$).

Proof

By employing Lemmas 4.9(v) and 4.9(vi), respectively, we see that the conditions in (i) and (ii) imply Assumption 4.3. Consequently, we employ Theorem 5.1 in order to obtain a critical point $(x^\star ,z^\star ,y^\star )$ of $L_0(x,z,y)$ where

$$\begin{aligned} Mx^k\rightarrow Mx^\star ,\quad z^k\rightarrow z^\star \quad \text {and}\quad y^k\rightarrow y^\star . \end{aligned}$$

Set $v^k:=y^k+\gamma (Mx^{k+1}-z^k)$, $k=0,1,\ldots$. Then $v^k\rightarrow y^\star$. If f is strongly convex, then, by employing Lemma 4.11(i), we conclude that $(\partial f)^{-1}$ is Lipschitz continuous and

$$\begin{aligned} x^{k+1}=(\partial f)^{-1}(-M^Tv^k) \rightarrow (\partial f)^{-1}(-M^Ty^\star )=x^\star . \end{aligned}$$

Suppose now that $M^TM$ is invertible. Then, by employing Lemma 4.11(ii), we conclude that

$$\begin{aligned} x^{k+1}=(M^TM)^{-1}M^T\left( \tfrac{1}{\gamma }(v^k-y^k)+z^k\right) \rightarrow (M^TM)^{-1}M^Tz^\star =x^\star , \end{aligned}$$

which completes the proof.$\square$

5.1 Summary: Existence and Convergence

For the sake of convenience and accessibility, we recollect and unify all of the conditions from our discussion regarding the existence of a solution of (${\mathcal {P}}$) and the convergence of the aADMM and the ADMM.

Corollary 5.1

(existence and convergence of aADMM) Let $M\in {\mathbb {R}}^{m\times n}$ be a nonzero matrix, let $f:{\mathbb {R}}^n\rightarrow ]-\infty ,+\infty ]$ be proper, lower semicontinuous and $\alpha$-convex, and let $g:{\mathbb {R}}^m\rightarrow ]-\infty ,+\infty ]$ be proper, lower semicontinuous and $\beta$-convex where $\alpha , \beta \in {\mathbb {R}}$ are parameters such that

$$\begin{aligned} \alpha \ge 0\quad \text {and}\quad \alpha +\beta \Vert M\Vert ^2\ge 0. \end{aligned}$$

Suppose that one of the following conditions holds:

• (A.1) the Lagrangian $L_0$ has a critical point,

• (A.2) the Lagrangian $L_0$ has a saddle point,

• (A.3) problem (${\mathcal {P}}$) has an optimal solution and $0\in {\text {ri}}({\text {dom}}g - M({\text {dom}}f))$;

and that one of the following conditions holds:

• (B.1) $0\in {\text {ri}}({\text {dom}}f^* - {\text {ran}}M^T)$,

• (B.2) ${\text {ri}}({\text {ran}}\partial f)\cap {\text {ran}}M^T \ne \varnothing$,

• (B.3) $({\text {rec}}f)(x)>0$ for all $x\in \ker M\setminus \{x\in {\mathbb {R}}^n : -({\text {rec}}f)(-x)=({\text {rec}}f)(x)=0\}$,

• (B.4) f is coercive (in particular, supercoercive),

• (B.5) $\alpha > 0$ (i.e., f is strongly convex),

• (B.6) $M^TM$ is invertible.

Let $\delta >\max \{0,-2\beta \}$ and set

$$\begin{aligned}&\gamma =\delta +2\beta ,&\text {if } \alpha +\beta \Vert M\Vert ^2=0,\\&\gamma \in ]\max \{0,\delta +2\beta - \varDelta _{\delta }\}, \delta +2\beta + \varDelta _{\delta } [,&\text {if } \alpha +\beta \Vert M\Vert ^2>0; \end{aligned}$$

where

$$\begin{aligned} \varDelta _{\delta }:=\frac{1}{\Vert M\Vert }\sqrt{2\left( {\alpha }+\beta {\Vert M\Vert ^2}\right) (\delta +2\beta )}. \end{aligned}$$

Set $(x^0,z^0,y^0)\in {\mathbb {R}}^n\times {\mathbb {R}}^m\times {\mathbb {R}}^m$ and let ${(x^k,z^k,y^k)}_{k=0}^{\infty }$ be generated by the aADMM (12). Then

$$\begin{aligned} Mx^k\rightarrow Mx^\star ,\quad z^k\rightarrow z^\star \quad \text {and}\quad y^k\rightarrow y^\star , \end{aligned}$$

where $(x^\star ,z^\star ,y^\star )$ is a critical point of $L_0(x,z,y)$. Consequently, $(x^\star ,z^\star )$ is a solution of (${\mathcal {P}}$). If, in particular, (B.5) or (B.6) holds, then $x^k\rightarrow x^\star$.

Proof

Clearly, Assumption 4.1 holds. By Lemma 4.4 and Lemma 4.5, each one of the conditions (A.1)–(A.3) implies Assumption 4.2. Finally, by Lemma 4.9, each one of the conditions (B.1)–(B.6) implies Assumption 4.3. We conclude the proof by invoking Theorem 5.1 and Theorem 5.2.$\square$

As we point out in Remark 5.1, our assumptions on (${\mathcal {P}}$) extend the framework of the classical ADMM for two convex functions.

Corollary 5.2

(existence and convergence of ADMM) Let $M\in {\mathbb {R}}^{m\times n}$ be a nonzero matrix and let $f:{\mathbb {R}}^n\rightarrow ]-\infty ,+\infty ]$ and $g:{\mathbb {R}}^m\rightarrow ]-\infty ,+\infty ]$ be proper, lower semicontinuous and convex. Suppose that one of the following conditions holds:

• (A.1) the Lagrangian $L_0$ has a saddle point (equivalently, a critical point),

• (A.2) problem (${\mathcal {P}}$) has an optimal solution and $0\in {\text {ri}}({\text {dom}}g - M({\text {dom}}f))$;

and that one of the following conditions holds:

• (B.1) $0\in {\text {ri}}({\text {dom}}f^* - {\text {ran}}M^T)$,

• (B.2) ${\text {ri}}({\text {ran}}\partial f)\cap {\text {ran}}M^T \ne \varnothing$,

• (B.3) $({\text {rec}}f)(x)>0$ for all $x\in \ker M\setminus \{x\in {\mathbb {R}}^n : -({\text {rec}}f)(-x)=({\text {rec}}f)(x)=0\}$,

• (B.4) f is coercive (in particular, supercoercive),

• (B.5) f is strongly convex,

• (B.6) $M^TM$ is invertible.

Let $\gamma >0$. Set $(x^0,z^0,y^0)\in {\mathbb {R}}^n\times {\mathbb {R}}^m\times {\mathbb {R}}^m$ and let ${(x^k,z^k,y^k)}_{k=0}^{\infty }$ be generated by the ADMM (2). Then

$$\begin{aligned} Mx^k\rightarrow Mx^\star ,\quad z^k\rightarrow z^\star \quad \text {and}\quad y^k\rightarrow y^\star , \end{aligned}$$

where $(x^\star ,z^\star ,y^\star )$ is a critical point of $L_0(x,z,y)$. Consequently, $(x^\star ,z^\star )$ is a solution of (${\mathcal {P}}$). If, in particular, (B.5) or (B.6) holds, then $x^k\rightarrow x^\star$.

Proof

The proof follows from Corollary 5.1 when we set $\alpha =\beta =0$.$\square$

5.2 Optimality Conditions and Stopping Criteria

By following [10, § 3.3], we discuss the primal-dual residual stopping criteria for the aADMM which we will employ in Sect. 6 for our numerical experiments.

By Definition 4.1, $(x^\star ,z^\star ,y^\star )$ is a critical point if

$$\begin{aligned}&0\in \partial f(x^\star )+M^Ty^\star , \end{aligned}$$

(26a)

$$\begin{aligned}&0\in {\widehat{\partial }}g(z^\star )-y^\star , \end{aligned}$$

(26b)

$$\begin{aligned}&Mx^\star -z^\star =0. \end{aligned}$$

(26c)

Clearly, the sequence $r^{k}:=Mx^{k}-z^{k}$ can be viewed as residual for (26c). By optimality at each step in (12), we obtain

$$\begin{aligned} 0&\in \partial f(x^{k+1})+M^Ty^k+\gamma M^T(Mx^{k+1}-z^k),\\ 0&\in {\widehat{\partial }}g(z^{k+1})-y^k-\delta (Mx^{k+1}-z^{k+1}). \end{aligned}$$

We note that $y^{k+1}=y^k+\delta (Mx^{k+1}-z^{k+1})$. Consequently,

$$\begin{aligned} 0&\in \partial f(x^{k+1})+M^Ty^{k+1}-\delta M^T(Mx^{k+1}-z^{k+1})+\gamma M^T(Mx^{k+1}-z^k),\\ 0&\in {\widehat{\partial }}g(z^{k+1})-y^{k+1}. \end{aligned}$$

We see that (26b) holds at each step whereas for (26a) we will monitor the dual residual

$$\begin{aligned} \begin{aligned} s^{k+1}:=&-\delta M^T(Mx^{k+1}-z^{k+1})+\gamma M^T(Mx^{k+1}-z^k)\\ =&M^T(\gamma z^{k}-\delta z^{k+1}-(\gamma -\delta )Mx^{k+1}). \end{aligned} \end{aligned}$$

We will therefore employ the primal-dual residual stopping criteria

$$\begin{aligned} \Vert r^k\Vert :=\Vert Mx^{k}-z^{k}\Vert&\le \epsilon _{\text {primal}}, \end{aligned}$$

(27a)

$$\begin{aligned} \Vert s^k\Vert :=\Vert M^T(\gamma z^{k-1}-\delta z^k-(\gamma -\delta )Mx^k)\Vert&\le \epsilon _{\text {dual}}, \end{aligned}$$

(27b)

for some fixed $\epsilon _{\text {primal}}>0$ and $\epsilon _{\text {dual}}>0$. We note that the case where $\delta =\gamma$ in (27) coincides with the primal-dual stopping criteria employed for the classical ADMM (see [10, § 3.3]). Finally, $\epsilon _{\text {primal}}$ and $\epsilon _{\text {dual}}$ may be chosen using absolute and relative tolerances, for example,

$$\begin{aligned} \epsilon _{\text {primal}}&= \sqrt{m}~\epsilon _{\text {abs}}+\epsilon _{\text {rel}}\max \{\Vert Mx^k\Vert ,\Vert z^k\Vert \},\\ \epsilon _{\text {dual}}&= \sqrt{n}~\epsilon _{\text {abs}}+\epsilon _{\text {rel}}\Vert M^Tz^k\Vert , \end{aligned}$$

where m and n are the dimensions of the matrix M.

Remark 5.4

(Stopping criteria from the aDR perspective) As a counterpart, we examine the stopping criteria from the perspective of the aDR algorithm. By employing the notations in the proof of Theorem 5.1, we consider

$$\begin{aligned} w^k:=y^k+\delta z^k \quad \implies \quad y^k=J_{\delta S}(w^k). \end{aligned}$$

Since $w^k\rightarrow w^\star \in {\text {Fix}}T_{\text {aDR}}$, it is reasonable to employ the Cauchy-type stopping criteria

$$\begin{aligned} \Vert w^{k+1}-w^k\Vert \le \epsilon _{\text {aDR}}. \end{aligned}$$

(28)

We observe that

$$\begin{aligned} r^k&=\delta ^{-1}(y^k-y^{k-1}),\\ s^k&=M^T((\delta -\gamma )Mx^k -\delta z^k+\gamma z^k) + M^T\gamma (z^{k-1}-z^k)\\&=M^T(\delta -\gamma )r^k+M^T\gamma (z^{k-1}-z^{k}). \end{aligned}$$

Consequently, (27) is equivalent to $\Vert y^{k+1}-y^k\Vert$ and $\Vert z^{k+1}-z^k\Vert$ being small. By the triangle inequality,

$$\begin{aligned} \Vert w^{k+1}-w^k\Vert \le \Vert y^{k+1}-y^k\Vert +\delta \Vert z^{k+1}-z^k\Vert . \end{aligned}$$

(29)

On the other hand, since $z^k\in S(y^k)$ and since S is maximally $\beta$-comonotone, we obtain

$$\begin{aligned} \Vert w^{k+1}-w^k\Vert ^2&=\Vert (y^{k+1}-y^k) + \delta (z^{k+1}-z^k)\Vert ^2\nonumber \\&=\Vert y^{k+1}-y^k\Vert ^2+\delta ^2\Vert z^{k+1}-z^k\Vert ^2 +2\delta \langle y^{k+1}-y^k, z^{k+1}-z^k\rangle \nonumber \\&\ge \Vert y^{k+1}-y^k\Vert ^2+\delta (\delta +2\beta )\Vert z^{k+1}-z^k\Vert ^2. \end{aligned}$$

(30)

In view of (29) and (30), we see that the Cauchy stopping criteria (28) with appropriately chosen $\epsilon _{\text {aDR}}$ is equivalent to (27), which justifies the use of primal-dual residual stopping criteria.

6 Numerical Experiments

We now examine the applicability and efficiency of our aADMM with numerical experiments. To this end, we focus on a total variation signal denoising problem for which the classical ADMM has been widely used (see, e.g., [12, 14, 15, 40] and the references therein). All of our codes are in Python 3.7. The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

Suppose that a discretized observed signal ${{\widehat{\phi }}}\in {\mathbb {R}}^n$ is the result of

$$\begin{aligned} {{\widehat{\phi }}}= \phi + \xi , \end{aligned}$$

where $\phi \in {\mathbb {R}}^n$ is the original signal and $\xi \in {\mathbb {R}}^n$ is a Gaussian noise with 0 mean and variance $\sigma ^2$. The objective of the denoising is to obtain an accurate approximation of $\phi$ from ${{\widehat{\phi }}}$. A common approach consists of solving the total variation regularization problem [37] (see, e.g., [10, §6.4.1])

$$\begin{aligned} \min _{x\in {\mathbb {R}}^n} \frac{1}{2}\Vert x-{{\widehat{\phi }}}\Vert ^2 + \omega P(Dx), \end{aligned}$$

(31)

where $\omega >0$ is the regularization parameter, $P:{\mathbb {R}}^{n-1}\rightarrow {\mathbb {R}}_+$ is a penalty function in order to induce sparsity and $D\in {\mathbb {R}}^{n\times (n-1)}$ is the total variation matrix defined component-wise by

$$\begin{aligned} D_{ij}:=\left\{ \begin{array}{ll} 1, &{}\text {if } j=i;\\ -1, &{}\text {if } j=i+1;\\ 0, &{}\text {otherwise.} \end{array}\right. \end{aligned}$$

We observe that problem (31) is of the form (${\mathcal {P}}$) when we let

$$\begin{aligned} f:=\frac{1}{2}\Vert \cdot -{{\widehat{\phi }}} \Vert ^2,\ g=\omega P(\cdot ), \text { and }M:=D. \end{aligned}$$

Moreover, the particular structure of this problem enables an easy computation of the ADMM iteration, as we show next.

x-update for quadratic functions Since f is a quadratic function, the x-update of the ADMM and the aADMM can be obtained via the solution of a system of linear equations. More precisely, steps (2a) and (12a) are computed by solving the linear system

$$\begin{aligned} ({\text {Id}}+\gamma M^TM)x^{k+1}=M^T(\gamma z^k-y^k)+{{\widehat{\phi }}}. \end{aligned}$$

z-update as a proximal step The minimization step with respect to z can be computed via the proximity operator of g. Indeed, (12b) reduces to

$$\begin{aligned} z^{k+1}={\text {prox}}_{\frac{1}{\delta }g}(Mx^{k+1}+\delta ^{-1}y^k)={\text {prox}}_{\frac{\omega }{\delta }P}(Mx^{k+1}+\delta ^{-1}y^k), \end{aligned}$$

(32)

whereas for (2b) one only replaces $\delta$ by $\gamma$ in (32).

We assume that the penalty function is separable in the sense that there exists $p:{\mathbb {R}}\rightarrow {\mathbb {R}}_+$ such that

$$\begin{aligned} P(z)=\sum _{i=1}^{n-1} p(z_i), \quad \text {for all } z=(z_1,\ldots ,z_{n-1})\in {\mathbb {R}}^{n-1}. \end{aligned}$$

The proximal mapping of P, usually referred to as thresholding or shrinkage, can be computed component-wise. The type of penalty function chosen in (31), together with the regularization parameter $\omega$, has a significant impact on the quality of the denoised solution. In Table 1, we list three types of penalty functions and their corresponding thresholding mappings (see, e.g., [43]).

Table 1 Three penalty functions and the corresponding thresholding mappings

The hard penalty is associated with the $l_0$-norm, it is the one to impose sparsity on the solution. Since the hard penalty is nonconvex (in fact, it is not $\alpha$-convex for any choice of $\alpha \in {\mathbb {R}}$), there is no guarantee for the convergence of the ADMM when applied to this problem. As an alternative, the $l_0$-norm is replaced by the $l_1$-norm, leading to the proximal mapping known as soft thresholding. Although convex, this penalty may yield to biased solutions when the variation of the original signal is large. In order to obtain less biased solutions, some weakly convex penalties, such as the firm thresholding [24], associated to a minimax concave penalty, arises as a tradeoff between the hard and the soft thresholdings (see Fig. 1).

Fig. 1

Illustration of the hard, soft and firm penalty (with $\zeta =4$) functions and the corresponding thresholding mappings (with $\gamma =2$)

We observe that the firm penalty function $p^{(F)}_{\zeta }(x)$ is weakly convex with parameter $\frac{-1}{\zeta }$. Indeed, one verifies that the function $p^{(F)}_{\zeta }(x)+\frac{x^2}{2\zeta }$ is convex either by direct computation or via a more general argument such as [7, Theorem 5.4].

Since f is 1-strongly convex, Assumption 4.1 holds whenever $\zeta \ge 4\omega$ since

$$\begin{aligned} 1-\Vert D\Vert ^2\frac{\omega }{\zeta }\ge 0 \quad \iff \quad \zeta \ge \Vert D\Vert ^2\omega \end{aligned}$$

and the fact that $\Vert D\Vert \le 2$.

6.1 Experiment 1: Convex versus Weakly Convex Penalties

In our first experiment, we aim to show that using a weakly convex penalty function may produce more accurate solutions than the $l_1$-norm in certain circumstances. To this end, we employ generated¹block signals (piecewise constant signals) to which we add a gaussian noise with standard deviation $\sigma =0.5$. Given a generated noisy signal, for 50 values of the penalty parameter $\omega$ equally distributed in the interval [0.1, 5], we compute two solutions of problem (31), one with respect to the soft thresholding (convex) and another with respect to the firm one (weakly convex) with $\zeta =4\omega$. In order to measure the quality of the reconstruction of a denoised signal $x=(x_1,\ldots ,x_n)\in {\mathbb {R}}^n$ with respect to the original signal $\phi =(\phi _1,\ldots ,\phi _n)\in {\mathbb {R}}^n$, we employ the mean absolute error (MAE), defined by

$$\begin{aligned} {\text {MAE}}(x,\phi )=\frac{1}{n}\sum _{i=1}^n |x_i-\phi _i|. \end{aligned}$$

The results for a signal of size $n=256$ are shown in Fig. 2a. We see that the weakly convex penalty (firm) achieves more accurate solutions. Indeed, the MAE of the solution produced by the firm thresholding is always smaller than that of the soft thresholding, except for small values of $\omega$ for which the quality of both solutions is deficient. In order to visualize the performance of each penalty function, we plot in Fig. 2b the denoised solutions for $\omega =2$, as well as the original and the noisy signals. We see that the firm thresholding produces less biased solutions at the break points of the signal, in particular, at the break points corresponding to relatively short pieces, where the true variation of the original signal is large.

Fig. 2

Denoising of a block signal of size $n=256$ with soft and firm thresholdings. a Mean absolute error of the solutions for each penalty type with respect to the regularization parameter $\omega$. b Plot of the original, noised and the two denoised signals for $\omega =2$

We repeated the experiment for different signal size n and different variance of the noise $\sigma$. The results are similar: the firm thresholding produces solutions with less error for all large enough values of the penalty parameter $\omega$. Due to the similarity, we do not include these in this presentation.

For denoising with the soft thresholding, we used the classical ADMM, whereas for the firm denoising we employed the aADMM. In this experiment, we focused on the quality of the solutions produced by each penalty function in order to motivate the application of weakly convex functions, rather than the algorithm performance. In our second experiment, we do focus on the performance of the algorithm.

6.2 Experiment 2: ADMM Versus aADMM

We now examine the efficiency of the aADMM for signal denoising with weakly convex penalty. We focus on solving the total variation regularization problem (31) with firm thresholding. We consider generated block signals of different sizes n, noised with a Gaussian error of standard deviation $\sigma$. For every size, we set the parameters

$$\begin{aligned} \sigma :=0.5,\quad \omega :=2\quad \text {and}\quad \zeta :=4\omega =8. \end{aligned}$$

(33)

As noted in Remark 4.1, we can apply the classical ADMM to problem (31) with a weakly convex penalty $P^{(F)}_{\zeta }$ via a convex reformulation. Thus, we compare the performance between the ADMM and the aADMM. For each $n\in \{1000,2000,\ldots ,10000\}$, we generated 10 noisy signals randomly. Then, for each of these noisy signals, we run the ADMM with 10 random starting points, for each $\gamma \in \{0.2,0.4,\ldots ,7.0\}$. At each instance, the aADDM was also launched for the same value of $\gamma$, while the parameter $\delta$ in the z-update step was set to

$$\begin{aligned} \delta :=\gamma -2\beta =\gamma +\frac{2\omega }{\zeta }=\gamma +\frac{1}{2} \end{aligned}$$

(34)

so that the conditions for convergence in (20) hold. For both algorithms, we employ the primal-dual residuals stopping criteria from Sect. 5.2 where we set $\epsilon _{\text {abs}}=\epsilon _{\text {rel}}:=10^{-4}$.

The results of the experiments are shown in Fig. 3: We plot the median ratio between the number of iterations required by aADMM and ADMM with respect to $\gamma$, for each size. A ratio less than one indicates that the aADMM converged faster. While, on average, both algorithms behave similarly for large values of $\gamma$, the superiority of aADMM for small values of $\gamma$, where the ratio is always smaller than 1, is evident in this experiment.

Fig. 3

Median of 100 ratios between the median (among 50 instances) of iterations required to converge by aADMM and classical ADMM, with respect to the penalty parameter $\gamma$, for denoising signals of sizes $1000,2000,\ldots ,10000$ with firm thresholding

Fig. 4

Percentile of all 1000 ratios between the numbers of iterations of aADMM and classical ADMM, with respect to the penalty parameter $\gamma$ for denoising signals with firm thresholding

In Fig. 4, we plot the percentiles $0,5,\ldots ,95$ and 100 of the ratios between the numbers of iterations with respect to $\gamma$ (for all sizes). This plot exhibits a small variance of the ratio, which demonstrates that the medians in Fig. 3 are suitable representatives. Indeed, the curve for 95%-percentile still lies close to 1, which indicates that the aADMM is at least comparable with (or even better than) the ADMM within 95% of the times. In fact, the curve for the 70%-percentile lies entirely below 1. This implies that for all tested values of $\gamma$ and all instances, the aADMM was at least as fast as the ADMM 70% of the time.

Finally, in order to better analyze the results, we further examine the outputs for $n=1000$, $n=5000$ and $n=10000$ in Fig. 5. Instead of the ratios between both algorithms, we plot the median of the number iterations required by each of the algorithms separately. On the one hand, we confirm our previous conclusions: for every fixed value of $\gamma$, the aADMM is as rapid as the classical ADMM (and much faster for small $\gamma$). On the other hand, if one was able to predict the optimal choice for $\gamma$, then both algorithms perform similarly. However, the optimal $\gamma$ is unknown.

Fig. 5

Median (among 100 instances) of iterations required to converge by aADMM and ADMM, with respect to the penalty parameter $\gamma$, for denoising signals of sizes 1000, 5000 and 10000 with firm thresholding

6.3 Experiment 3: Comparison between ADMM, aADMM and PDHGM

We conclude our experiments by incorporating the primal-dual hybrid gradient method [33], denoted PDHGM in short, into our comparison. For this experiment, we used the parameter setting in (33) but with $\zeta :=9$ so that the restriction in (24) holds. This is required for the convergence of PDHGM in the strongly-weakly convex setting.

For a generated noised block signal of length $n=1000$, we run ADMM, aADMM and PDHGM. For ADMM and aADMM, the parameter $\gamma$ was optimally chosen according to the results obtained in Fig. 5, while $\delta$ in the aADMM was computed as in (34). The parameters of the PDHGM did not seem to have a big effect on the convergence rate in this experiment. Nevertheless, we roughly tuned them for best performance. The same experiment was repeated for a larger signal of length 5000. The results for both signals are shown in Fig. 6. We observe superiority of the ADMM/aADMM compared to the PDHGM in these particular instances, with a slight advantage for the aADMM over the classical ADMM, which is in agreement with our previous results.

Fig. 6

Comparison between ADMM, aADMM and PDHGM for denoising two signals of sizes 1000 and 5000. For each algorithm we plot $\max \{\Vert Mx^{k+1}-z^{k+1}\Vert ,\Vert x^{k+1}-x^{k}\Vert , \Vert z^{k+1}-z^{k}\Vert \}$ with respect CPU time in seconds

7 Conclusions

We provided an adaptive version of the alternating direction method of multipliers for solving linearly constrained optimization problems where the objective is the sum of a weakly convex function and a strongly convex function. Convergence of our scheme was derived as dual to the convergence of the adaptive Douglas–Rachford splitting algorithm. Consequently, the theory regarding the dual relations between the classical ADMM and the classical DR algorithm have been extended to and established in the strongly-weakly convex framework. In the process, we have also relaxed stronger assumptions imposed in other studies where the ADMM was applied in this framework (see Remarks 5.1 and 5.2).

The performance of our scheme was tested in numerical experiments of signal denoising. In our experiments, we observed that the aADMM outperforms the classical ADMM in terms of the required number of iterations. However, our numerical experiments are far from providing a complete computational study. A detailed and comprehensive numerical analysis will be the subject matter of future studies.