Abstract
The linearized Boltzmann collision operator has a central role in many important applications of the Boltzmann equation. Recently some important classical properties of the linearized collision operator for monatomic single species were extended to multicomponent monatomic gases and polyatomic single species. For multicomponent polyatomic gases, the case where the polyatomicity is modelled by a discrete internal energy variable was considered lately. Here we consider the corresponding case for a continuous internal energy variable. Compactness results, stating that the linearized operator can be decomposed into a sum of a positive multiplication operator, the collision frequency, and a compact operator, bringing e.g., self-adjointness, is extended from the classical result for monatomic single species, under reasonable assumptions on the collision kernel. With a probabilistic formulation of the collision operator as a starting point, the compactness property is shown by a decomposition, such that the terms are, or at least are uniform limits of, Hilbert–Schmidt integral operators and therefore are compact operators. Moreover, bounds on—including coercivity of—the collision frequency are obtained for hard sphere like, as well as hard potentials with cutoff like, models, from which Fredholmness of the linearized collision operator follows, as well as its domain.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The Boltzmann equation is a fundamental equation of kinetic theory of gases, e.g., for computations of the flow around a space shuttle in the upper atmosphere during reentry [1]. Studies of the main properties of the linearized collision operator are of great importance in gaining increased knowledge about related problems, see, e.g., [12] and references therein. The linearized collision operator, obtained by considering deviations of an equilibrium, or Maxwellian, distribution, can in a natural way be written as a sum of a positive multiplication operator—the collision frequency—and an integral operator \(-K\). Compact properties of the integral operator K (for angular cut-off kernels) are extensively studied for monatomic single species, see, e.g., [12, 14, 18, 21], and more recently for monatomic multi-component mixtures [4, 8]. Extensions to polyatomic single species, where the polyatomicity is modeled by either a discrete, or, a continuous internal energy variable [4, 5] and polyatomic multicomponent mixtures [2], where the polyatomicity is modeled by discrete internal energy variables, have also been conducted. For models, assuming a continuous internal energy variable, see also [7] for the case of molecules undergoing resonant collisions (for which internal energy and kinetic energy, respectively, are conserved under collisions), and [10, 11] for diatomic and polyatomic gases, respectively—with more restrictive—concerning the models considered in [16], allowing some others in return—assumptions on the collision kernels than in [5], but also a more direct approach. The integral operator can be written as the sum of a Hilbert–Schmidt integral operator and an approximately Hilbert–Schmidt integral operator—which is a uniform limit of Hilbert–Schmidt integral operators (cf. Lemma 4 in Sect. 4) [17], and so compactness of the integral operator K can be obtained. In this work, we extend the results of [4, 5] for monatomic multicomponent mixtures and polyatomic single species, where the polyatomicity is modeled by a continuous internal energy variable [9, 16], to the case of multicomponent mixtures of monatomic and/or polyatomic gases, where the polyatomicity is modeled by a continuous internal energy variable [1, 13]. To consider mixtures of monatomic and polyatomic molecules are of highest relevance in, e.g., the upper atmosphere [1].
Following the lines of [2, 4, 5], motivated by an approach by Kogan in [20, Sect. 2.8] for the monatomic single species case, a probabilistic formulation of the collision operator is considered as the starting point. With this approach, it is shown that the integral operator K can be written as a sum of Hilbert–Schmidt integral operators and operators, which are uniform limits of Hilbert–Schmidt integral operators— and so compactness of the integral operator K follows. The operator K is self-adjoint, as well as the collision frequency. Thus the linearized collision operator, as the sum of two self-adjoint operators whereof (at least) one is bounded, is also self-adjoint.
For models corresponding to hard sphere models, as well as hard potentials with cut off models, in the monatomic case, bounds on the collision frequency are obtained. Here we also want to point out reference [15], where the corresponding upper bound in [5] for the single species case was improved. Then the collision frequency is coercive and becomes a Fredholm operator. The set of Fredholm operators is closed under addition with compact operators. Therefore, also the linearized collision operator becomes a Fredholm operator by the compactness of the integral operator K. The Fredholm property is vital in the Chapman-Enskog process, and the Fredholmness of the linearized operator supply with the Fredholm property, taken for granted in [1], for those models. Note that for monatomic species, the linearized operator is not Fredholm for soft potential models, unlike for hard potential models. The domain of collision frequency—and, hence, of the linearized collision operator as well—follows directly by the obtained bounds
For hard sphere like models the linearized collision operator satisfies all the properties of the general linear operator in the abstract half-space problem considered in [3], and, hence, the existence results in [3] apply.
The rest of the paper is organized as follows. In Sect. 2, the model considered is presented. The probabilistic formulation of the collision operators considered and its relations to more classical formulations [1, 13] are accounted for in Sect. 2.1. Some results for the collision operators in Sect. 2.2 and the linearized collision operator in Sect. 2.3 are reviewed. Section 3 is devoted to the main results of this paper, while the main proofs are addressed in Sects. 4 and 5; a proof of compactness of the integral operators K is presented in Sect. 4, while a proof of the bounds on the collision frequency appears in Sect. 5.
2 Model
This section concerns the model considered. Probabilistic formulations of the collision operators are considered, whose relations to more classical formulations are accounted for. Known properties of the models and corresponding linearized collision operators are also reviewed.
Consider a multicomponent mixture of s species \(a_{1},\ldots ,a_{s}\), with \( s_{0}\) monatomic and \(s_{1}:=s-s_{0}\) polyatomic species, and masses \( m_{1},\ldots ,m_{s}\), respectively, and introduce the index sets
Here the polyatomicity is modeled by a continuous internal energy variable \( I\in \) \({\mathbb {R}}_{+}\) [6].
The distribution functions are of the form \(f=\left( f_{1},\ldots ,f_{s}\right) \), where for \(\alpha \in {\mathcal {I}}\) the component \(f_{\alpha }=f_{\alpha }\left( t,{\textbf{x}},{\textbf{Z}}\right) \), with
\(\left\{ t,I\right\} \subset {\mathbb {R}}_{+}\), \({\textbf{x}}=\left( x,y,z\right) \in {\mathbb {R}}^{3}\), and \(\varvec{\xi }=\left( \xi _{x},\xi _{y},\xi _{z}\right) \in {\mathbb {R}}^{3}\), is the distribution function for species \(a_{\alpha }\).
Moreover, consider the real Hilbert space
with inner product
The evolution of the distribution functions is (in the absence of external forces) described by the (vector) Boltzmann equation
where the (vector) collision operator \(Q=\left( Q_{1},\ldots ,Q_{s}\right) \) is a quadratic bilinear operator that accounts for the change of velocities and internal energies of particles due to binary collisions (assuming that the gas is rarefied, such that other collisions are negligible). Here the component \(Q_{\alpha }\), with \(\alpha \in {\mathcal {I}}\), is the collision operator for species \(a_{\alpha }\).
A collision between two particles of species \(a_{\alpha }\) and \(a_{\beta }\), where \(\left\{ \alpha ,\beta \right\} \subseteq {\mathcal {I}}\), respectively, can be represented by two pre-collisional elements, each element consisting of a microscopic velocity and possibly also an internal energy, \({\textbf{Z}}\) and \({\textbf{Z}}_{*}\), and two corresponding post-collisional elements, \( {\textbf{Z}}^{\prime }\) and \({\textbf{Z}}_{*}^{\prime }\). The notation for pre- and post-collisional pairs may be interchanged as well. Due to momentum and total energy conservation, the following relations have to be satisfied by the elements
and if \(\left( \alpha ,\beta \right) \in {\mathcal {I}}_{mono}^{2}\) (mono/mono-interactions)
if \(\left( \alpha ,\beta \right) \in {\mathcal {I}}_{mono}\times {\mathcal {I}} _{poly}\) (mono/poly-interactions)
if \(\left( \alpha ,\beta \right) \in {\mathcal {I}}_{poly}\times {\mathcal {I}} _{mono}\) (poly/mono-interactions)
while if \(\left( \alpha ,\beta \right) \in {\mathcal {I}}_{poly}^{2}\) (poly/poly-interactions)
2.1 Collision Operator
The (vector) collision operator \(Q=\left( Q_{1},\ldots ,Q_{s}\right) \) has components that can be written in the following form
Here and below the abbreviations
where \({\textbf{Z}}_{*}\), \({\textbf{Z}}^{\prime }\), and \({\textbf{Z}}_{*}^{\prime }\), are defined as the natural extension of definition (1), i.e. denoting \(\mathbf {Z_{*}=Z_{*\alpha }}=\left\{ \begin{array}{l} \varvec{\xi }_{*}\quad \text { for }\alpha \in {\mathcal {I}}_{mono} \\ \left( \varvec{\xi }_{*},I_{*}\right) \ \ \text { for }\alpha \in {\mathcal {I}}_{poly} \end{array} \right. \) etc., are used for \(\alpha \in {\mathcal {I}}\). Moreover, the degeneracies or renormalization weights \(\varphi _{\alpha }=\varphi _{\alpha }\left( I\right) \), \(\alpha \in {\mathcal {I}}\), with \(\varphi _{\alpha }=1\) for \(\alpha \in {\mathcal {I}}_{mono}\), are positive functions for \(I>0\). A typical choice of the degeneracies is [16]
where \(\delta ^{\left( 1\right) }=...=\delta ^{\left( s_{0}\right) }=2\), while \(\delta ^{\left( \alpha \right) }\), with \(\delta ^{\left( \alpha \right) }\ge 2\), denote the number of internal degrees of freedom of the species for \(\alpha \in {\mathcal {I}}_{poly}\). Our main results in Sect. 3 below will be stated and proven for this particular choice of degeneracies.
Note that in the literature it is usual to use a slightly different setting [1, 9, 13], where already renormalized distribution functions are considered, opting to consider a weighted measure—where the renormalization weights appear as weights—with respect to I. However, this is merely due to a different scaling of the distribution functions considered.
The transition probabilities \(W_{\alpha \beta }\) are of the form, cf. [4, 5],
Here \(\varvec{\delta }_{3}\) and \(\varvec{\delta }_{1}\) denote the Dirac’s delta function in \({\mathbb {R}}^{3}\) and \({\mathbb {R}}\), respectively—\( \widehat{\varvec{\delta }}_{1}\) and \(\widehat{\varvec{\delta }}_{3}\) taking the conservation of momentum and total energy into account. Note that for \(\alpha \in {\mathcal {I}}_{mono}\) the scattering cross sections \(\sigma _{\alpha \beta }\) are independent of I and \(I^{\prime }\), while correspondingly, for \(\beta \in {\mathcal {I}}_{mono}\) the scattering cross sections \(\sigma _{\alpha \beta }\) are independent of \(I_{*}\) and \( I_{*}^{\prime }\). Moreover, we have chosen—even if this means not being completely consistent—to not indicate the dependence of species in the notation, if—like for the energy gap \(\Delta I\)—the dependence is only up to if the species are monatomic or polyatomic.
It is assumed that the scattering cross sections \(\sigma _{\alpha \beta }\) for \(\left( \alpha ,\beta \right) \in {\mathcal {I}}^{2}\) satisfy the microreversibility conditions
Furthermore, to obtain invariance of change of particles in a collision, it is assumed that the scattering cross sections \(\sigma _{\alpha \beta }\) for \( \left( \alpha ,\beta \right) \in {\mathcal {I}}^{2}\) satisfy the symmetry relations
while
The invariance under change of particles in a collision, which follows directly by the definition of the transition probability (3) and the symmetry relations (5), (6) for the collision frequency, and the microreversibility of the collisions (4), implies that the transition probabilities (3) satisfy the relations
Applying known properties of Dirac’s delta function, the transition probabilities may be transformed to
Remark 1
Note that
where \(E_{\alpha \beta }=\dfrac{\mu _{\alpha \beta }}{2}\left| {\textbf{g}} \right| ^{2}+{\textbf{1}}_{\alpha \in {\mathcal {I}}_{poly}}I+{\textbf{1}} _{\beta \in {\mathcal {I}}_{poly}}I_{*}\ \)is the total energy in the center of mass frame, and, correspondingly, \(E_{\alpha \beta }^{\prime }=\dfrac{\mu _{\alpha \beta }}{2}\left| {\textbf{g}}^{\prime }\right| ^{2}+\textbf{1 }_{\alpha \in {\mathcal {I}}_{poly}}I^{\prime }+{\textbf{1}}_{\beta \in \mathcal {I }_{poly}}I_{*}^{\prime }\).
Observe that, by a series of change of variables:\(\{\varvec{\xi }^{\prime }, \varvec{\xi }_{*}^{\prime }\} \rightarrow \Bigg \{{\textbf{g}}^{\prime } = \varvec{\xi }^{\prime }-\varvec{\xi }_{*}^{\prime }, {\textbf{G}}_{\alpha \beta }^{\prime }=\dfrac{m_{\alpha }\varvec{\xi }^{\prime }+m_{\beta }\varvec{\xi }_{*}^{\prime }}{m_{\alpha }+m_{\beta }}\Bigg \}\), followed by a change to spherical coordinates \(\Bigg \{{\textbf{g}}^{\prime }\Bigg \} \rightarrow \Bigg \{\vert {\textbf{g}}^{\prime }\vert ,\varvec{\sigma }=\dfrac{{\textbf{g}}^{\prime }}{\vert {\textbf{g}}^{\prime }\vert }\Bigg \}\),
while, if \(a_{\beta }\) is polyatomic, \(\beta \in {\mathcal {I}}_{poly}\), by applying the additional change of variables \(\left\{ \left| {\textbf{g}} ^{\prime }\right| ,I_{*}^{\prime }\right\} \rightarrow \left\{ R= \dfrac{\mu _{\alpha \beta }}{2}\dfrac{\left| {\textbf{g}}^{\prime }\right| ^{2}}{E_{\alpha \beta }},E_{\alpha \beta }^{\prime }=\dfrac{\mu _{\alpha \beta }}{2}\left| {\textbf{g}}^{\prime }\right| ^{2}+I^{\prime }+I_{*}^{\prime }\right\} \),
and, finally, if additionally \(\alpha \in {\mathcal {I}}_{poly}\), the change \( \left\{ I^{\prime }\right\} \rightarrow \left\{ r=\dfrac{I^{\prime }}{\left( 1-R\right) E_{\alpha \beta }}\right\} \) leads to
Then for two monatomic species, i.e., \(\left( \alpha ,\beta \right) \in {\mathcal {I}}_{mono}^{2}\), (mono/mono-case)
or, with \(\varphi _{\alpha }\left( I\right) =I^{\delta ^{\left( \alpha \right) }/2-1}\), \(\alpha \in {\mathcal {I}}\), for a monatomic species and a polyatomic species, i.e., either \(\left( \alpha ,\beta \right) \in \mathcal {I }_{mono}\times {\mathcal {I}}_{poly}\) (mono/poly-case)
or, \(\left( \alpha ,\beta \right) \in \mathcal {I}_{poly}\times \mathcal {I}_{mono}\) (poly/mono-case)
and, finally, again with \(\varphi _{\alpha }\left( I\right) =I^{\delta ^{\left( \alpha \right) }/2-1}\), \(\alpha \in {\mathcal {I}}\), for two polyatomic species, i.e., with \(\left( \alpha ,\beta \right) \in {\mathcal {I}} _{poly}^{2}\) (poly/poly-case)
where

This results in more familiar forms of the Boltzmann collision operators for mixtures of monatomic and/or polyatomic molecules modeled with a continuous energy variable, cf., e.g., [1, 13]. Here and below the internal energy gaps are given by \(\Delta I=0\) in the mono/mono-case, \( \Delta I=I_{*}^{\prime }-I_{*}\) in the mono/poly-case, \(\Delta I=I^{\prime }-I\) in the poly/mono-case, while in the poly/poly-case \(\Delta I=I^{\prime }+I_{*}^{\prime }-I-I_{*}\).
2.2 Collision Invariants and Maxwellian Distributions
The following lemma follows directly by the relations (7).
Lemma 1
The measures
are invariant under the (ordered) interchange
of variables for \(\left( \alpha ,\beta \right) \in {\mathcal {I}}^{2}\), while
are invariant under the (ordered) interchange of variables
The weak form of the collision operator Q(f, f) reads
for any function \(g=\left( g_{1},\ldots ,g_{s}\right) \), with \(g_{\alpha }=g_{\alpha }({\textbf{Z}})\), such that the first integrals are defined for all \(\left( \alpha ,\beta \right) \in {\mathcal {I}}^{2}\), while the following equalities are obtained by applying Lemma 1.
Denote for any function \(g=\left( g_{1},\ldots ,g_{s}\right) \), with \(g_{\alpha }=g_{\alpha }({\textbf{Z}})\),
We have the following proposition.
Proposition 1
Let \(g=\left( g_{1},\ldots ,g_{s}\right) \), where \(g_{\alpha }=g_{\alpha }({\textbf{Z}})\), be such that
is defined for any \(\left( \alpha ,\beta \right) \in {\mathcal {I}}^{2}\). Then
Definition 1
A function \(g=\left( g_{1},\ldots ,g_{s}\right) \), where \(g_{\alpha }=g_{\alpha }({\textbf{Z}})\),is a collision invariant if
for all \(\left( \alpha ,\beta \right) \in {\mathcal {I}}^{2}\).
It is clear that \(e_{1},\) \(...,e_{s},\) \(m\xi _{x},\) \(m\xi _{y},\) \(m\xi _{z},\) and \(m\left| \varvec{\xi }\right| ^{2}+2{\mathbb {I}}\), denoting here \( m=\left( m_{1},\ldots ,m_{s}\right) \), \({\mathbb {I}}=(\underset{s_{0}}{\underbrace{ 0,\ldots ,0}},\underset{s_{1}=s-s_{0}}{\underbrace{I,\ldots ,I}})\), and by \(\left\{ e_{1},\ldots ,e_{s}\right\} \) the standard basis of \({\mathbb {R}}^{s}\), are collision invariants—corresponding to conservation of mass(es), momentum, and total energy.
In fact, we have the following proposition, cf. [1, 13].
Proposition 2
Let \(m=\left( m_{1},\ldots ,m_{s}\right) \), \({\mathbb {I}}=(\underset{ s_{0}}{\underbrace{0,\ldots ,0}},\underset{s_{1}}{\underbrace{I,\ldots ,I}})\), and \( \left\{ e_{1},\ldots ,e_{s}\right\} \) be the standard basis of \({\mathbb {R}}^{s}\). Then the vector space of collision invariants is generated by
Define
where \(\varphi =\varphi (I)=\textrm{diag}\left( \varphi _{1}(I),\ldots ,\varphi _{s}(I)\right) \). It follows by Proposition 1 that
Since \(\left( x-1\right) \textrm{log}\left( x\right) \ge 0\) for \(x>0\), with equality if and only if \(x=1\),
with equality if and only if for all \(\left( \alpha ,\beta \right) \in {\mathcal {I}}^{2}\)
or, equivalently, if and only if
For any equilibrium, or, Maxwellian, distribution \(M=(M_{1},\ldots ,M_{s})\), it follows by identity (11), since \(Q(M,M)\equiv 0\), that
Hence, \(\log \left( \varphi ^{-1}M\right) =\left( \log \dfrac{M_{1}}{\varphi _{1}\left( I\right) },\ldots ,\log \dfrac{M_{s}}{\varphi _{s}(I)}\right) \) is a collision invariant, and the components of the Maxwellian distributions \( M=(M_{1},\ldots ,M_{s})\) are of the form
where \(n_{\alpha }=\left( M,e_{_{\alpha }}\right) \), \( {\textbf{u}}=\dfrac{1}{\rho }\left( M,m\varvec{\xi }\right) \), and \(T= \dfrac{1}{3nk_{B}}\left( M,m\left| \varvec{\xi }-{\textbf{u}} \right| ^{2}\right) \), with mass vector \(m=(m_{1},\ldots ,m_{s})\), \( n=\sum \limits _{\alpha =1}^{s}n_{\alpha }\), \(\rho =\sum \limits _{\alpha =1}^{s}m_{\alpha }n_{\alpha }\), and normalization factors \(q_{\alpha }=\int _{0}^{\infty }\varphi _{\alpha }\left( I\right) e^{-I/\left( k_{B}T\right) }\,dI\) for \(\alpha \in {\mathcal {I}}_{poly}\), while \(k_{B}\) denote the Boltzmann constant.
For the typical case \(\varphi _{\alpha }\left( I\right) =I^{\delta ^{\left( \alpha \right) }/2-1}\), \(\alpha \in {\mathcal {I}}\),
where \(\Gamma =\Gamma (n)\) denote the Gamma function \(\Gamma (n)=\int _{0}^{\infty }x^{n-1}e^{-x}\,dx\).
Note that, by Eq. (11), any Maxwellian distribution \(M=(M_{1},\ldots ,M_{s})\) satisfies the relations
for any \(\left( \alpha ,\beta \right) \in {\mathcal {I}}^{2}\).
Remark 2
Introducing the \({\mathcal {H}}\)-functional
an \({\mathcal {H}}\)-theorem can be obtained, cf. [1, 13].
2.3 Linearized Collision Operator
Consider a deviation of a centered and normalized Maxwellian \( M=(M_{1},\ldots ,M_{s})\), where
with \({\overline{q}}_{\alpha }=\int _{0}^{\infty }\varphi _{\alpha }\left( I\right) e^{-I}\,dI\) for \(\alpha \in {\mathcal {I}}_{poly}\), of the form
For \(\alpha \in {\mathcal {I}}\), the typical case \(\varphi _{\alpha }\left( I\right) =I^{\delta ^{\left( \alpha \right) }/2-1}\) implies that \(\overline{q }_{\alpha }=\) \(\Gamma \left( \delta ^{\left( \alpha \right) }/2\right) \).
Insertion in the Boltzmann equation (2) results in the system
where the components of the linearized collision operator \({\mathcal {L}} =\left( {\mathcal {L}}_{1},\ldots ,{\mathcal {L}}_{s}\right) \) are given by
with
while the components of the quadratic term \(\Gamma =\left( \Gamma _{1},\ldots ,\Gamma _{s}\right) \) are given by
for \(\alpha \in {\mathcal {I}}\). The multiplication operator \(\Lambda \) defined by
is a closed, densely defined, self-adjoint operator on \(\mathcal {{\mathfrak {h}} }\). It is Fredholm, as well, if and only if \(\Lambda \) is coercive.
The following lemma follows immediately by Lemma 1.
Lemma 2
For any \(\left( \alpha ,\beta \right) \in {\mathcal {I}}^{2}\) the measure
is invariant under the (ordered) interchange (9) of variables, while
is invariant under the (ordered) interchange (10) of variables
The weak form of the linearized collision operator \({\mathcal {L}}\) reads
for any function \(g=\left( g_{1},\ldots ,g_{s}\right) \), with \(g_{\alpha }=g_{\alpha }({\textbf{Z}})\), such that the first integrals are defined for all \(\left\{ \alpha ,\beta \right\} \subseteq {\mathcal {I}}\), while the following equalities are obtained by applying Lemma 2. The following lemma follows.
Lemma 3
Let \(g=\left( g_{1},\ldots ,g_{s}\right) \), where \(g_{\alpha }=g_{\alpha }({\textbf{Z}})\), be such that
is defined for any \(\left( \alpha ,\beta \right) \in {\mathcal {I}}^{2}\). Then
Proposition 3
The linearized collision operator is symmetric and nonnegative,
and the kernel of \({\mathcal {L}}\), \(\ker {\mathcal {L}}\), is generated by
where \(m=\left( m_{1},\ldots ,m_{s}\right) \), \({\mathbb {I}}=(\underset{s_{0}}{ \underbrace{0,\ldots ,0}},\underset{s_{1}}{\underbrace{I,\ldots ,I}})\), and \( {\mathcal {M}}=\textrm{diag}\left( M_{1},\ldots ,M_{s}\right) \).
Proof
By Lemma 3, it is immediate that \(\left( {\mathcal {L}}h,g\right) =\left( h,{\mathcal {L}}g\right) \), and
Furthermore, \(h\in \ker {\mathcal {L}}\) if and only if \(\left( {\mathcal {L}} h,h\right) =0\), which will be fulfilled if and only if for all \(\left( \alpha ,\beta \right) \in {\mathcal {I}}^{2}\)
i.e., if and only if \({\mathcal {M}}^{-1/2}h\) is a collision invariant. The last part of the lemma follows by Proposition 2. \(\square \)
Remark 3
Note also that the quadratic term is orthogonal to the kernel of \({\mathcal {L}} \), i.e., we have that \(\Gamma \left( h,h\right) \in \left( \ker {\mathcal {L}}\right) ^{\perp _{\mathcal {{\mathfrak {h}}}}}\).
3 Main Results
This section is devoted to the main results, concerning compact properties in Theorem 1 and bounds of collision frequencies in Theorem 2. Below we restrict to the particular case \(\varphi _{\alpha }\left( I\right) =I^{\delta ^{\left( \alpha \right) }/2-1}\) for \(\alpha \in \mathcal { I}\).
Assume that for some positive number \(\gamma \), such that \(0<\gamma <1\), there is for all \(\left( \alpha ,\beta \right) \in {\mathcal {I}}^{2}\) a bound
for \(\mu _{\alpha \beta }\left| {\textbf{g}}\right| ^{2}>2\Delta I\), on the scattering cross sections, or, equivalently, the bound
for \(\mu _{\alpha \beta }\left| {\textbf{g}}\right| ^{2}>2\Delta I\), on the collision kernels. Here, for \(\left( \alpha ,\beta \right) \in {\mathcal {I}}^{2}\), \({\mathcal {E}}_{\alpha \beta }=1\) if \(\alpha \in {\mathcal {I}} _{mono}\) and \({\mathcal {E}}_{\alpha \beta }^{*}=1\) if \(\beta \in \mathcal {I }_{mono}\), while, otherwise,
Remark 4
In the single polyatomic case, i.e., with \(s=s_{1}=1\), assumption (15) (or, (16)), differs from the one in [4], by an extra factor \(E^{1/2}=E_{11}^{1/2}\) in the denominator, resulting in the factor \(E^{1/2}=E_{11}^{1/2}\) instead of E in assumption (16). This rules out the superhard potential like models considered in [4], while it opens up for some soft potential like models, not covered in [4], in return.
The following result may be obtained.
Theorem 1
Assume that for all \(\left\{ \alpha ,\beta \right\} \subseteq {\mathcal {I}}\) the scattering cross sections \(\sigma _{\alpha \beta }\) satisfy the bound (15) for some positive number \(\gamma \), \( 0<\gamma <1\).
Then the operator \(K=\left( K_{1},\ldots ,K_{s}\right) \), with the components \( K_{\alpha }\) given by (14) is a self-adjoint compact operator on \(\mathcal {{\mathfrak {h}}}=\left( L^{2}\left( d\varvec{\xi } \right) \right) ^{s_{0}}\times \left( L^{2}\left( d\varvec{\xi } dI\right) \right) ^{s_{1}}\).
The proof of Theorem 1 will be addressed in Sect. 4.
Corollary 1
The linearized collision operator \({\mathcal {L}}\), with scattering cross sections satisfying (15), is a closed, densely defined, self-adjoint operator on \(\mathcal {{\mathfrak {h}}}\).
Proof
By Theorem 1, the linear operator \({\mathcal {L}}=\Lambda -K\) is closed as the sum of a closed and a bounded operator, and densely defined, since the domains of the linear operators \({\mathcal {L}}\) and \(\Lambda \) are equal; \(D({\mathcal {L}})=D(\Lambda )\). Furthermore, it is a self-adjoint operator, since the set of self-adjoint operators is closed under addition of bounded self-adjoint operators, see Theorem 4.3 of Chapter V in [19]. \(\square \)
Now consider the scattering cross sections
for some positive constants \(C_{\alpha \beta }>0\) for all \(\left( \alpha ,\beta \right) \in {\mathcal {I}}^{2}\) and nonnegative number \(\eta \) less than 1, \(0\le \eta <1,\)—cf. hard sphere models for \(\eta =0\).
In fact, it would be enough with the bounds (for \(\mu _{\alpha \beta }\left| {\textbf{g}}\right| ^{2}>2\Delta I\))
for some nonnegative number \(\eta \) less than 1, \(0\le \eta <1\), and some positive constants \(C_{\pm }>0\), on the scattering cross sections—cf. hard potential with cut-off models.
The following bounds restricted to single species were obtained in [5, 15]. In [15] the improved—compared to the one in [5]—upper bound below was shown for single species.
Theorem 2
The linearized collision operator \({\mathcal {L}}\), with scattering cross sections (17) (or (18)), can be split into a positive multiplication operator \(\Lambda \), where \(\Lambda \left( f\right) =\nu f\), with \(\nu =\nu (\textbf{Z})\), minus a compact operator K on \(\mathcal { {\mathfrak {h}}}\), such that there exist positive numbers \(\nu _{-}\) and \(\nu _{+}\), where \(0<\nu _{-}<\nu _{+}\), for which, for any \(\alpha \in {\mathcal {I}}\)
The decomposition follows by decomposition (13), (14) and Theorem 1, while the bounds (19) on the collision frequency will be proven in Sect. 5.
Corollary 2
The linearized collision operator \({\mathcal {L}}\), with scattering cross section (17) (or (18)), is a Fredholm operator with domain
Proof
By Theorem 2 the multiplication operator \(\Lambda \) is coercive, and thus it is a Fredholm operator. Furthermore, the set of Fredholm operators is closed under addition of compact operators, see Theorem 5.26 of Chapter IV in [19] and its proof, so, by Theorem 2, \( {\mathcal {L}}\) is a Fredholm operator. \(\square \)
We stress that Corollary 2 finally yields the Fredholmness of the linearized operator assumed in [1] for kernels of the form (17) or (18).
For hard sphere like models we obtain the following result.
Corollary 3
For the linearized collision operator \({\mathcal {L}}\), with scattering cross section (17 (or (18)) where \(\eta =0\), there exists a positive number \(\lambda \), \( 0<\lambda <1\), such that
for all \(h\in D\left( {\mathcal {L}}\right) \cap \textrm{Im}{\mathcal {L}}\).
Proof
Let \(h\in D\left( {\mathcal {L}}\right) \cap \left( \textrm{ker}{\mathcal {L}} \right) ^{\perp }=D\left( {\mathcal {L}}\right) \cap \textrm{Im}{\mathcal {L}}\). As a Fredholm operator, \({\mathcal {L}}\) is closed with a closed range, and as a compact operator, K is bounded, and so there are positive constants \(\nu _{0}>0\) and \(c_{K}>0\), such that
Let \(\lambda =\dfrac{\nu _{0}}{\nu _{0}+c_{K}}\). Then the corollary follows, since
\(\square \)
Remark 5
By Proposition 3 and Corollary 1-3 the linearized operator \({\mathcal {L}}\) fulfills the properties assumed on the linear operators in [3], and, hence, the results for the abstract linearized half-space problem therein can be applied to hard sphere like models for mixtures of monatomic and polyatomic gases.
4 Compactness
This section concerns the proof of Theorem 1. Note that in the proof the kernels are rewritten in such a way that \({\textbf{Z}}_{*}\)—and not \({\textbf{Z}}^{\prime }\) or \({\textbf{Z}}_{*}^{\prime }\)—always will be arguments of the distribution functions. As for single species, either \({\textbf{Z}}_{*}\) is an argument in the loss term (like \({\textbf{Z}} \)) or in the gain term (unlike \({\textbf{Z}}\)) of the collision operator. However, in the latter case, unlike for single species, for mixtures one has to differ between two different cases; either \({\textbf{Z}}_{*}\) is associated to the same species as \({\textbf{Z}}\), or not. The kernels of the terms from the loss part of the collision operator will be shown to be Hilbert–Schmidt in a quite direct way. The kernels of some of the terms—for which \({\textbf{Z}}_{*}\) is associated to the same species as \(\textbf{Z}\)—from the gain parts of the collision operators will be shown to be uniform limits of Hilbert–Schmidt integral operators, i.e., approximately Hilbert–Schmidt in the sense of Lemma 4. Furthermore, it will be shown that the kernels of the remaining terms—for which \({\textbf{Z}}_{*} \) is associated to the opposite species to \({\textbf{Z}}\)—from the gain parts of the collision operators are Hilbert–Schmidt.
To show the compactness properties—when the terms are not necessarily Hilbert–Schmidt integral operators themselves—the following result will be applied. Denote, for any (nonzero) natural number N,
Here, either \({\textbf{Z}}=\varvec{\xi }\) and \(\mathbb {Y=R}^{3}\), or, \( {\textbf{Z}}=\left( \varvec{\xi },I\right) \) and \(\mathbb {Y=R}^{3}\times {\mathbb {R}}_{+}\), and correspondingly, either \({\textbf{Z}}_{*}=\varvec{ \xi }_{*}\) and \(\mathbb {Y_{*}=R}^{3}\), or, \({\textbf{Z}}_{*}=\left( \varvec{\xi }_{*},I_{*}\right) \) and \(\mathbb {Y_{*}=R}^{3}\times {\mathbb {R}}_{+}\). Then we have the following lemma, cf. Glassey [17, Lemma 3.5.1] and Drange [14].
Lemma 4
Assume that \(Tf\left( {\textbf{Z}}\right) =\int _{{\mathbb {Y}}_{*}}b({\textbf{Z}},{\textbf{Z}}_{*})f\left( {\textbf{Z}}_{*}\right) \,d {\textbf{Z}}_{*}\), with \(b({\textbf{Z}},{\textbf{Z}}_{*})\ge 0\). Then T is compact on \(L^{2}\left( d{\textbf{Z}}\right) \) if
-
(i)
\(\int _{{\mathbb {Y}}}b({\textbf{Z}},{\textbf{Z}}_{*})\,d{\textbf{Z}}\) is bounded in \({\textbf{Z}}_{*}\);
-
(ii)
\(b^{(N)}\in L^{2}\left( d{\textbf{Z}}\,d{\textbf{Z}}_{*}\right) \) for any (nonzero) natural number N;
-
(iii)
\(\underset{{\textbf{Z}}\in {\mathbb {Y}}}{\sup }\int _{{\mathbb {Y}}_{*}}b( {\textbf{Z}},{\textbf{Z}}_{*})-b^{(N)}({\textbf{Z}},{\textbf{Z}}_{*})\,d {\textbf{Z}}_{*}\rightarrow 0\) as \(N\rightarrow \infty \).
Then T is the uniform limit of Hilbert–Schmidt integral operators [17, Lemma 3.5.1] and we say that the kernel \(b({\textbf{Z}},{\textbf{Z}} _{*})\) is approximately Hilbert–Schmidt, while T is an approximately Hilbert–Schmidt integral operator. The reader is referred to Glassey [17, Lemma 3.5.1] for a proof of Lemma 4.
Now we turn to the proof of Theorem 1. Note that throughout the proof C will denote a generic positive constant. Moreover, remind that \( \varphi _{\alpha }\left( I\right) =I^{\delta ^{\left( \alpha \right) }/2-1}\) for \(\alpha \in {\mathcal {I}}\) below.
Proof
For \(\alpha \in {\mathcal {I}}\) rewrite expression (14) as
with
Due to relations (7), the relations
are satisfied. By renaming \(\left\{ {\textbf{Z}}_{*}\right\} \leftrightarrows \left\{ {\textbf{Z}}_{*}^{\prime }\right\} \),
Moreover, by renaming \(\left\{ {\textbf{Z}}_{*}\right\} \leftrightarrows \left\{ {\textbf{Z}}^{\prime }\right\} \),
It follows that
By applying the second relation of (20) and renaming \( \left\{ {\textbf{Z}}^{\prime }\right\} \leftrightarrows \left\{ {\textbf{Z}} _{*}^{\prime }\right\} \),
Moreover,
since, by applying the first relation of (20) and renaming \(\left\{ {\textbf{Z}}^{\prime }\right\} \leftrightarrows \left\{ {\textbf{Z}}_{*}^{\prime }\right\} \),
while, by renaming \(\left\{ {\textbf{Z}}^{\prime }\right\} \leftrightarrows \left\{ {\textbf{Z}}_{*}^{\prime }\right\} \), after applying the first two relations of (20)
Now the compactness of the three different types of collision kernel will be considered separately. Note that, if \(\alpha =\beta \), by applying the last relation of (20), \(k_{\alpha \beta 2}^{\left( \beta \right) }({\textbf{Z}},{\textbf{Z}}_{*})=k_{\alpha \beta }^{\left( \alpha \right) }({\textbf{Z}},{\textbf{Z}}_{*})\), and we will remain with only two cases—the first two below. Even if \(m_{\alpha }=m_{\beta }\), the kernels \( k_{\alpha \beta }^{\left( \alpha \right) }({\textbf{Z}},{\textbf{Z}}_{*})\) and \(k_{\alpha \beta 2}^{\left( \beta \right) }({\textbf{Z}},{\textbf{Z}}_{*})\) are structurally equal, and we (in principle) remain with (first) two cases (the second one twice).
I. Compactness of \(K_{\alpha \beta 1}=\int _{{\mathcal {Z}}_{\beta }}k_{\alpha \beta 1}^{\left( \beta \right) }({\textbf{Z}},{\textbf{Z}}_{*})\,h_{\beta *}\,d{\textbf{Z}}_{*}\) for any indices \(\left( \alpha ,\beta \right) \in {\mathcal {I}}^{2}\).
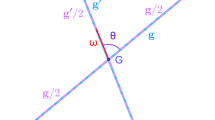
By a change of variables, cf. Figure 1,
noting identity (8) and using relation (12), expression (21) of \(k_{\alpha \beta 1}^{\left( \beta \right) }\) may be written as
Note that
Since \(E_{\alpha \beta }\ge C\Psi _{\alpha \beta }\), it follows, by assumption (15), that
Then, by assumption (15) and
where \(E_{\alpha \beta }=\mu _{\alpha \beta }\left| {\textbf{g}} \right| ^{2}/2+{\textbf{1}}_{\alpha \in {\mathcal {I}}_{poly}}I+{\textbf{1}} _{\beta \in {\mathcal {I}}_{poly}}I_{*}\), the bound
may be obtained. Hence, by applying the bound (24) and first changing variables of integration \(\left\{ \varvec{\xi }, \varvec{\xi }_{*}\right\} \rightarrow \left\{ {\textbf{g}},{\textbf{G}} _{\alpha \beta }\right\} \), with unitary Jacobian, and then to spherical coordinates,
Therefore,
are Hilbert–Schmidt integral operators and as such compact on \(L^{2}\left( d {\textbf{Z}}\right) \), see, e.g., Theorem 7.83 in [22], for \( \left( \alpha ,\beta \right) \in {\mathcal {I}}^{2}\).
II. Compactness of \(K_{\alpha \beta 3}=\int _{{\mathcal {Z}}_{\alpha }}k_{\alpha \beta }^{\left( \alpha \right) }({\textbf{Z}},{\textbf{Z}}_{*})\,h_{\alpha *}\,d{\textbf{Z}}_{*}\) for any indices \(\left( \alpha ,\beta \right) \in {\mathcal {I}}^{2}\).
Note that, cf. Figure 2,
with \({\widetilde{\sigma }}_{\alpha \beta }=\sigma _{\alpha \beta }\left( \left| \widetilde{{\textbf{g}}}\right| ,\dfrac{\widetilde{{\textbf{g}}} \cdot {\textbf{g}}_{*}}{\left| \widetilde{{\textbf{g}}}\right| \left| {\textbf{g}}_{*}\right| },I,I^{\prime },I_{*},I_{*}^{\prime }\right) \), \({\textbf{g}}=\varvec{\xi }-\varvec{\xi }_{*} \), \({\textbf{g}}^{\prime }=\varvec{\xi }^{\prime }-\varvec{\xi } _{*}^{\prime }\), \(\widetilde{{\textbf{g}}}=\varvec{\xi }-\varvec{ \xi }^{\prime }\), \({\textbf{g}}_{*}=\varvec{\xi }_{*}-\varvec{ \xi }_{*}^{\prime }\), \(\Delta I_{*}={\textbf{1}}_{\alpha \in \mathcal {I }_{poly}}\left( I_{*}-I\right) +{\textbf{1}}_{\beta \in {\mathcal {I}} _{poly}}\left( I_{*}^{\prime }-I^{\prime }\right) \), and \(\chi _{+} =\left( \varvec{\xi }_{*}^{\prime }-\varvec{\xi }\right) \cdot {\textbf{n}} \), where \({\textbf{n}}=\dfrac{{\textbf{g}}}{\left| {\textbf{g}}\right| }\).
By performing the change of variables \(\left\{ \varvec{\xi }^{\prime }, \varvec{\xi }_{*}^{\prime }\right\} \rightarrow \left\{ {\textbf{g}} ^{\prime }=\varvec{\xi }^{\prime }-\varvec{\xi }_{*}^{\prime },~ \widehat{{\textbf{g}}}=\varvec{\xi }_{*}^{\prime }-\varvec{\xi } \right\} \), with
the expression (21) of \(k_{\alpha \beta }^{\left( \alpha \right) }\) may be rewritten in the following way
Here, see Fig. 2,
implying that
where
Denote \(\widetilde{{\mathcal {E}}}_{\alpha \beta }=1\) if \(\alpha \in {\mathcal {I}} _{mono}\) and \(\widetilde{{\mathcal {E}}}_{\alpha \beta }^{*}=1\) if \(\beta \in {\mathcal {I}}_{mono}\), while, otherwise,
Let \(0\le \varpi \le 1\), with \(\varpi \equiv 0\) if \(\alpha \in {\mathcal {I}} _{mono}\). If \(\alpha \in {\mathcal {I}}_{poly}\), then
Denoting \(\left( {\mathbb {R}}^{3}\right) ^{\perp _{{\textbf{n}}}}=\left\{ {\textbf{w}}\in {\mathbb {R}}^{3};\text { }{\textbf{w}}\perp {\textbf{n}}\right\} \), we obtain the bound
By the bounds (25) and (26), and assumption (15), for any number \(\kappa \), \(0\le \kappa \le 1-\varpi \),
For \(0\le \kappa \le 1-\varpi \), by the bound (27) and the Cauchy-Schwarz inequality,
If \(\alpha \in {\mathcal {I}}_{poly}\), by the change of variables \(I_{*}\rightarrow \Phi =\left| {\textbf{g}}\right| -2\left| \varvec{ \xi }\right| \cos \varphi +2\chi _{\alpha }\), noting that
for any positive number \(a>0\), the bound
may be obtained. Note also that
Then, by the bounds (28) for \(\kappa =1-\varpi =\left\{ \begin{array}{l} 0\text { if }I\le 1 \\ 1\text { if }I>1 \end{array} \right. \), (29), and (30), one have that, \(k_{\alpha \beta }^{\left( \alpha \right) }({\textbf{Z}},{\textbf{Z}}_{*}) {\textbf{1}}_{{\mathfrak {h}}_{N}}\in L^{2}\left( d{\textbf{Z}}d{\textbf{Z}}_{*}\right) \) for any (nonzero) natural number N, since
Note that, by the bound (27) for \(\kappa =0\) and if \( I_{*}>1\), \(\varpi \equiv 0\),
The integral of \(k_{\alpha \beta }^{\left( \alpha \right) }({\textbf{Z}}, {\textbf{Z}}_{*})\) with respect to \({\textbf{Z}}\) over \({\mathcal {Z}}_{\alpha } \) is bounded in \({\textbf{Z}}_{*}\). Indeed, due to the symmetry (22) of the kernel \(k_{\alpha \beta }^{\left( \alpha \right) }\), follows, by the bounds (29) and (31), that
Aiming to prove that
for \(\left| \varvec{\xi }\right| \ne 0\), split the domain \( {\mathbb {R}}^{3}\times {\mathbb {R}}_{+}\) into two subdomains
By the bounds (29) and (31) (for \( \varpi =0\)), it can be shown that the restriction of bound (32) to the domain \({\mathcal {D}}_{+}\) is satisfied for \(\left| \varvec{\xi }\right| \ne 0\)
On the other hand, by the bound (31) (for \(\varpi =1/2\) if \(\alpha \in {\mathcal {I}}_{poly}\)), it can be shown that the restriction of bound (32) to the domain \({\mathcal {D}}_{-}\) is satisfied for \(\left| \varvec{\xi }\right| \ne 0\)
Here the second inequality follows for \(\left| \varvec{\xi } \right| \ne 0\), with \(\chi _{R}^{\alpha }=\Delta I_{*}/\left( m_{\alpha }R\right) \), by
which is obtained by a change to spherical coordinates followed by the change of variables \(\varphi \rightarrow \Phi =R-2\left| \varvec{\xi }\right| \cos \varphi +2\chi _{R}^{\alpha }\), with \(d\Phi =\left| \varvec{\xi }\right| \sin \varphi \,d\varphi \).
Note that \(f(x)=\dfrac{1+\log (1+x)}{x}\) is a decreasing function for \(x>0\). Therefore, by the bounds (29), (31), and (32),
Hence, by Lemma 4, the operators
are compact on \(L^{2}\left( d{\textbf{Z}}_{\alpha }\right) \) for \(\left( \alpha ,\beta \right) \in {\mathcal {I}}^{2}\).
III. Compactness of \(K_{\alpha \beta 2}=\int \limits _{{\mathcal {Z}} _{\beta }}k_{\alpha \beta 2}^{\left( \beta \right) }({\textbf{Z}},{\textbf{Z}} _{*})\,h_{\beta *}\,d{\textbf{Z}}_{*}\) for any indices \(\left( \alpha ,\beta \right) \in {\mathcal {I}}^{2}\).
Assume that \(m_{\alpha }\ne m_{\beta }\) and denote
Furthermore, denote \(\widehat{{\mathcal {E}}}_{\alpha \beta }=1\) if \(\alpha \in {\mathcal {I}}_{mono}\) and \(\widehat{{\mathcal {E}}}_{\alpha \beta }^{*}=1\) if \(\beta \in {\mathcal {I}}_{mono}\), while, otherwise,
Note that, cf. Figure 3,
Then, by a change of variables \(\left\{ \varvec{\xi }^{\prime }, \varvec{\xi }_{*}^{\prime }\right\} \rightarrow \left\{ \!\left| {\textbf{g}}^{\prime }\right| ,\varvec{\sigma }=\dfrac{{\textbf{g}} ^{\prime }}{\left| {\textbf{g}}^{\prime }\right| },{\textbf{g}}_{\alpha \beta }^{\prime }=\dfrac{m_{\alpha }\varvec{\xi }^{\prime }-m_{\beta } \varvec{\xi }_{*}^{\prime }}{m_{\alpha }-m_{\beta }}\!\right\} \), with \({\textbf{g}}^{\prime }=\varvec{\xi }^{\prime }-\varvec{\xi } _{*}^{\prime }\), where
and substitution of expression (33) in the expression (21) of \(k_{\alpha \beta 2}^{\left( \beta \right) }\), one obtain
However, also
and, furthermore,
By straightforward calculations, with \(\varvec{\sigma }={\textbf{g}} ^{\prime }/\left| {\textbf{g}}^{\prime }\right| \),
It follows, again by straightforward calculations, that
Applying the Cauchy-Schwarz inequality, we obtain that
since for \(\left( \alpha ,\beta \right) \in {\mathcal {I}}^{2}\)
Note that \(\max \left( \left| \widehat{{\textbf{g}}}\right| ,\left| \overline{{\textbf{g}}}\right| \right) \ge \left| \textbf{ g}\right| \), cf. Figure 3.
H1. If \(\min \left( \left| \widehat{{\textbf{g}}}\right| ,\left| \overline{{\textbf{g}}}\right| \right) \ge 1\), then \( \left| \widehat{{\textbf{g}}}\right| \left| \overline{{\textbf{g}}} \right| \ge \max \left( \left| \widehat{{\textbf{g}}}\right| ,\left| \overline{{\textbf{g}}}\right| \right) \ge \left| \textbf{ g}\right| \), and
Observe that \(\left| {\textbf{g}}^{\prime }\right| ^{2}\left( M_{\alpha }^{\prime }M_{\beta *}^{\prime }\right) ^{1/4}\le Ce^{-\left( I^{\prime }+I_{*}^{\prime }\right) /4}\), since \(x^{2}e^{-ax^{2}}\le 1/\left( ae\right) \) for any positive number \(a>0\). Hence, by expression (34), assumption (15), and inequalities (37)-(38), one may obtain the following bound
H2. If \(\min \left( \left| \widehat{{\textbf{g}}}\right| ,\left| \overline{{\textbf{g}}}\right| \right) <1\), then either of the two cases below apply:
-
(i)
\(\left| \widehat{{\textbf{g}}}\right| =\max \left( \left| \widehat{{\textbf{g}}}\right| ,\left| \overline{{\textbf{g}}}\right| \right) \ge \left| {\textbf{g}}\right| \) and \(\left| \overline{ {\textbf{g}}}\right| =\min \left( \left| \widehat{{\textbf{g}}} \right| ,\left| \overline{{\textbf{g}}}\right| \right) <1\), and, hence,
$$\begin{aligned} \frac{\left| \widehat{{\textbf{g}}}\right| \left| \overline{ {\textbf{g}}}\right| +\left( \left| \widehat{{\textbf{g}}}\right| \left| \overline{{\textbf{g}}}\right| \right) ^{\gamma /2}}{\left| \widehat{{\textbf{g}}}\right| ^{2}}\le \frac{1}{\left| \widehat{ {\textbf{g}}}\right| }\left( 1+\frac{1}{\left| {\textbf{g}}\right| ^{1-\gamma /2}}\right) \le \frac{C}{\left| \widehat{{\textbf{g}}} \right| }\left( 1+\frac{1}{\left| {\textbf{g}}\right| }\right) \text {,} \end{aligned}$$and then, by expression (35), assumption (15), and inequalities (37)–(38), the bound (39) is again satisfied.
-
(ii)
\(\left| \overline{{\textbf{g}}}\right| =\max \left( \left| \widehat{{\textbf{g}}}\right| ,\left| \overline{{\textbf{g}}}\right| \right) \ge \left| {\textbf{g}}\right| \) and \(\left| \widehat{ {\textbf{g}}}\right| =\min \left( \left| \widehat{{\textbf{g}}} \right| ,\left| \overline{{\textbf{g}}}\right| \right) <1\), implying, correspondingly, that
$$\begin{aligned} \frac{\left| \widehat{{\textbf{g}}}\right| \left| \overline{ {\textbf{g}}}\right| +\left( \left| \widehat{{\textbf{g}}}\right| \left| \overline{{\textbf{g}}}\right| \right) ^{\gamma /2}}{\left| \overline{{\textbf{g}}}\right| ^{2}}\le \frac{C}{\left| \overline{ {\textbf{g}}}\right| }\left( 1+\frac{1}{\left| {\textbf{g}}\right| } \right) , \end{aligned}$$and, hence, by expression (36), assumption (15), and inequalities (37)–(38), the bound (39) is again obtained.
Note that
where
Moreover, for \(\alpha \in {\mathcal {I}}_{poly}\)
and for \(\beta \in {\mathcal {I}}_{poly}\)
where \(0\le \pi _{\gamma }\le 1-\zeta _{\gamma }\) and \(0\le \zeta _{\gamma }<1/2\) for \(\gamma \in \left\{ \alpha ,\beta \right\} \). If the species \(a_{\gamma }\) is monatomic, \(\gamma \in {\mathcal {I}}_{mono}\), let \( 1-\zeta _{\gamma }=\pi _{\gamma }=0\).
Therefore, by the bounds (39), (41), and (42), and expression (40), changing variables of integration \(\left\{ \varvec{\xi },\varvec{ \xi }_{*}\right\} \rightarrow \left\{ {\textbf{g}},{\textbf{g}}_{\alpha \beta }\right\} \), with unitary Jacobian,
for \(\Omega \subseteq {\mathbb {R}}^{3}\), since, by a change to spherical coordinates,
Without loss of generality we can assume that \(m_{\alpha }>m_{\beta }\), and then \(A_{1}>0\). On the other hand, for \(\Omega \subseteq {\mathbb {R}}^{3}\), by inequality (37), and the bounds (39), (41), and (42), also
By the bound (43), with \(\zeta _{\gamma }=4\pi _{\gamma }=4/9\ \)if \(\gamma \in {\mathcal {I}}_{poly}\)—remind that \(1-\zeta _{\gamma }=\pi _{\gamma }=0\) if \(\gamma \in {\mathcal {I}}_{mono}\)—
This covers the case \(\left( \alpha ,\beta \right) \in {\mathcal {I}} _{mono}^{2} \) completely.
Now assume that \(\beta \in {\mathcal {I}}_{poly}\), and consider the case \( I_{*}\ge I\), assuming that \(I_{*}>1\)—else \(\left( I,I_{*}\right) \in \left[ 0,1\right] ^{2}\). Then, by the bound (43), with \(\zeta _{\alpha }=2\pi _{\alpha }=\left\{ \begin{array}{l} 2/5\text { if }I\le 1 \\ \ \ 0\text { if }I>1 \end{array} \right. \) if \(\alpha \in {\mathcal {I}}_{poly} - \pi _{\alpha }=0\) if \(\alpha \in {\mathcal {I}}_{mono}\)—and \(\zeta _{\beta }=10\pi _{\beta }=10/21\),
This covers the case \(\left( \alpha ,\beta \right) \in {\mathcal {I}} _{mono}\times {\mathcal {I}}_{poly}\) completely, and the case \(\left( \alpha ,\beta \right) \in {\mathcal {I}}_{poly}^{2}\) partly.
On the other hand, if \(\alpha \in {\mathcal {I}}_{poly}\), considering the case \( I\ge I_{*}\), assume that \(I>1\)—else \(\left( I,I_{*}\right) \in \left[ 0,1\right] ^{2}\). Then, by the bound (44), with \(\pi _{\alpha }=\zeta _{\alpha }=0\) and \(\zeta _{\beta }=2\pi _{\beta }=2/5\ \)if \(\beta \in {\mathcal {I}}_{poly}\),
If, additionally, assuming that the species \(a_{\beta }\) is polyatomic, \( \beta \in {\mathcal {I}}_{poly}\), then, again by the bound (44), with \(\zeta _{\alpha }=\zeta _{\beta }=0\) and \(1-2\pi _{\alpha }=\pi _{\beta }=3/5\),
This completes the case \(\left( \alpha ,\beta \right) \in {\mathcal {I}} _{poly}^{2}\).
Assume now instead that, additionally, the species \(a_{\beta }\) is monatomic, \(\beta \in {\mathcal {I}}_{mono}\). Then, If \(A_{1}I\le A_{2}\left| {\textbf{g}}\right| ^{2}\), by the bound (43), with \( \zeta _{\alpha }=\zeta _{\beta }=1-\pi _{\beta }=\pi _{\alpha }=0\),
On the other hand, if \(A_{1}I\ge A_{2}\left| {\textbf{g}}\right| ^{2}\), noting that
and, hence,
then, by the bounds (39), (37), and (41), with \(\zeta _{\alpha }=1-\pi _{\alpha }=0\), changing variables of integration \(\left\{ \varvec{\xi },\varvec{\xi }_{*}\right\} \rightarrow \left\{ {\textbf{g}},{\textbf{g}}_{\alpha \beta }\right\} \), with unitary Jacobian,
Then the case \(\left( \alpha ,\beta \right) \in {\mathcal {I}}_{poly}\times {\mathcal {I}}_{mono}\) is covered completely.
Concluding, \(\left( k_{\alpha \beta 2}^{\left( \beta \right) }({\textbf{Z}}, {\textbf{Z}}_{*})\right) ^{2}\in L^{2}\left( d{\textbf{Z}}\;d {\textbf{Z}}_{*}\right) \), implying that
are Hilbert–Schmidt integral operators, and as such continuous and compact on \(L^{2}\left( d{\textbf{Z}}\right) \), see [22, Theorem 7.83], for \(\left( \alpha ,\beta \right) \in {\mathcal {I}}^{2}\).
On the other hand, if \(m_{\alpha }=m_{\beta }\), then
with \(\widehat{{\textbf{g}}}=\varvec{\xi }-\varvec{\xi }_{*}^{\prime }\) and \(\overline{{\textbf{g}}}=\varvec{\xi }_{*}- \varvec{\xi }\). Here, with \({\textbf{g}}=\varvec{\xi }-\varvec{\xi }_{*}\) and \({\textbf{n}}=\mathbf {g/}\left| {\textbf{g}}\right| \),
Then similar arguments to the ones for \(k_{\alpha \beta }^{\left( \alpha \right) }({\textbf{Z}},{\textbf{Z}}_{*})\) (with \(m_{\alpha }=m_{\beta }\)) above, can be applied.
Concluding, the operator
is a compact self-adjoint operator on \(\mathcal {{\mathfrak {h}}}\). Self-adjointness is due to the symmetry relations (22), (23), cf. [23, p. 198]. \(\square \)
5 Bounds on the Collision Frequency
This section concerns the proof of Theorem 2. Note that throughout the proof, C will denote a generic positive constants. Moreover, remind that \(\varphi _{\alpha }\left( I\right) =I^{\delta ^{\left( \alpha \right) }/2-1}\) for \(\alpha \in {\mathcal {I}}\) below.
Proof
Noting identity (8), under assumption (17), the collision frequencies \(\nu _{\alpha }\) equal
for \(\alpha \in {\mathcal {I}}\). Clearly,
Then, if the species \(a_{\alpha }\) is monatomic, \(\alpha \in {\mathcal {I}} _{mono}\),
while if \(a_{\alpha }\) is polyatomic, \(\alpha \in {\mathcal {I}}_{poly}\),
Now it follows that
Hence, there is a positive constant \(\upsilon _{-}>0\), such that for all \( \alpha \in {\mathcal {I}}\)
On the other hand,
implying, since, clearly, \(E_{\alpha \beta }\le \left( 1+\mu _{\alpha \beta }\left| {\textbf{g}}\right| ^{2}/2+{\textbf{1}}_{\alpha \in {\mathcal {I}} _{poly}}I\right) \left( 1+{\textbf{1}}_{\beta \in {\mathcal {I}}_{poly}}I_{*}\right) \), that
Hence, there is a positive constant \(\nu _{+}>0\), such that for all \(\alpha \in {\mathcal {I}}\)
\(\square \)
Data Availability
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
References
Baranger, C., Bisi, M., Brull, S., Desvillettes, L.: On the Chapman–Enskog asymptotics for a mixture of monatomic and polyatomic rarefied gases. Kinet. Relat. Models 11, 821–858 (2018)
Bernhoff, N.: Compactness property of the linearized Boltzmann collision operator for a multicomponent polyatomic gas. arXiV Preprint (2022). arXiv:2212.02160
Bernhoff, N.: Linear half-space problems in kinetic theory: abstract formulation and regime transitions. Int. J. Math. 34(2350091), 1–41 (2023)
Bernhoff, N.: Linearized Boltzmann collision operator: I. Polyatomic molecules modeled by a discrete internal energy variable and multicomponent mixtures. Acta Appl. Math. 183(3), 1–45 (2023)
Bernhoff, N.: Linearized Boltzmann collision operator: II. Polyatomic molecules modeled by a continuous internal energy variable. Kinet. Relat. Models 16, 828–849 (2023)
Borgnakke, C., Larsen, P.S.: Statistical collision model for Monte-Carlo simulation of polyatomic mixtures. J. Comput. Phys. 18, 405–420 (1975)
Borsoni, T., Boudin, L., Salvarani, F.: Compactness property of the linearized Boltzmann operator for a polyatomic gas undergoing resonant collisions. J. Math Anal. Appl. 517(126579), 1–30 (2023)
Boudin, L., Grec, B., Pavić, M., Salvarani, F.: Diffusion asymptotics of a kinetic model for gaseous mixtures. Kinet. Relat. Models 6, 137–157 (2013)
Bourgat, J.-F., Desvillettes, L., Le Tallec, P., Perthame, B.: Microreversible collisions for polyatomic gases and Boltzmann’s theorem. Eur. J. Mech. B Fluids 13, 237–254 (1994)
Brull, S., Shahine, M., Thieullen, P.: Compactness property of the linearized Boltzmann operator for a diatomic single gas model. Netw. Heterog. Media 17, 847–861 (2022)
Brull, S., Shahine, M., Thieullen, P.: Fredholm property of the linearized Boltzmann operator for a polyatomic single gas model. Kinet. Relat. Models 17, 234–252 (2023)
Cercignani, C.: The Boltzmann Equation and Its Applications. Springer, New York (1988)
Desvillettes, L., Monaco, R., Salvarani, F.: A kinetic model allowing to obtain the energy law of polytropic gases in the presence of chemical reactions. Eur. J. Mech. B Fluids 24, 219–236 (2005)
Drange, H.B.: The linearized Boltzmann collision operator for cut-off potentials. SIAM J. Appl. Math. 29, 665–676 (1975)
Duan, R., Li, Z.: Global bounded solutions to the Boltzmann equation for a polyatomic gas. Int. J. Math. 34(7), 2350036 (2023)
Gamba, I., Pavic-Colic, M.: On the Cauchy problem for Boltzmann equation modelling polyatomic gas. J. Math. Phys. 64(013303), 1–51 (2023)
Glassey, R.T.: The Cauchy Problem in Kinetic Theory. SIAM, Philadelphia (1996)
Grad, H.: Asymptotic theory of the Boltzmann equation II. In: Laurmann, J.A. (ed.) Rarefied Gas Dynamics, vol. I, pp. 26–59. Academic Press, New York (1963)
Kato, T.: Perturbation Theory for Linear Operators. Springer, Berlin (1980)
Kogan, M.N.: Rarefied Gas Dynamics. Plenum Press, New York (1969)
Levermore, D., Sun, W.: Compactness of the gain parts of the linearized Boltzmann operator with weakly cutoff kernels. Kinet. Relat. Models 3, 335–351 (2010)
Renardy, M., Rogers, R.C.: An Introduction to Partial Differential Equations, 2nd edn. Springer, Berlin (1993)
Yoshida, K.: Functional Analysis. Springer, Berlin (1965)
Funding
Open access funding provided by Karlstad University. No funding was received for conducting this study.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The author has no relevant financial or non-financial interests to disclose.
Additional information
Communicated by Michael Kiessling.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bernhoff, N. Compactness Property of the Linearized Boltzmann Collision Operator for a Mixture of Monatomic and Polyatomic Species. J Stat Phys 191, 32 (2024). https://doi.org/10.1007/s10955-024-03245-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10955-024-03245-4