Abstract
From a unified vision of vector valued solutions in weighted Banach spaces, this paper establishes the existence and uniqueness for space homogeneous Boltzmann bi-linear systems with conservative collisional forms arising in complex gas dynamical structures. This broader vision is directly applied to dilute multi-component gas mixtures composed of both monatomic and polyatomic gases. Such models can be viewed as extensions of scalar Boltzmann binary elastic flows, as much as monatomic gas mixtures with disparate masses and single polyatomic gases, providing a unified approach for vector valued solutions in weighted Banach spaces. Novel aspects of this work include developing the extension of a general ODE theory in vector valued weighted Banach spaces, precise lower bounds for the collision frequency in terms of the weighted Banach norm, energy identities, angular or compact manifold averaging lemmas which provide coerciveness resulting into global in time stability, a new combinatorics estimate for p-binomial forms producing sharper estimates for the k-moments of bi-linear collisional forms. These techniques enable the Cauchy problem improvement that resolves the model with initial data corresponding to strictly positive and bounded initial vector valued mass and total energy, in addition to only a \(2^+\) moment determined by the hard potential rates discrepancy, a result comparable in generality to the classical Cauchy theory of the scalar homogeneous Boltzmann equation.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The goal of the present paper is to establish the rigorous result on existence and uniqueness for the coupled system of space homogeneous Boltzmann equations modelling a mixture composed of \(P\ge 1\) species of monatomic and polyatomic gases proposed in [5]. The idea of such kinetic model is to describe a state of each gas component with its own single-particle distribution function. Fixing one mixture component, say \({\mathcal {A}}_i\), for any \(i\in \left\{ 1, \dots , P\right\} \), the main mechanism driving the change of the corresponding distribution function is its interactions with all other mixture constituents through Boltzmann-like bi-linear collision forms, leading to a coupled system governing the dynamics of the gas mixture as a whole.
A core ingredient of the Boltzmann flow is the bi-linear collision form or operator, an integral operator which describes the mutual species–species interactions. In the current setting of a mixture of monatomic and polyatomic molecules there are four types of collision operators depending on whether the fixed species \({\mathcal {A}}_i\) is monatomic or polyatomic and whether the collision partner of such component belongs to a monatomic or polyatomic mixture component. We prove estimates on statistical moments of the vector valued collision operator that accounts for different possible interactions among species, which then allow to prove a priori estimates on the system solution. The collision operator’s kernels are assumed to be of hard potential form for the total collisional energy for at least one species–species interaction per each mixture component allowing Maxwell interactions as well. The scattering part of such kernels is assumed integrable, as much as the part related to the energy exchange variables for polyatomic mixture components. Such a family of collision kernels is shown to be relevant in physics and engineering applications that involve polyatomic gas interactions. Applying a general ODE theory in Banach spaces, the Cauchy problem is resolved for the initial data corresponding to strictly positive and bounded initial species’ mass and bounded mixture’s total energy, and a \(2^+\) moment determined by the hard potential rates discrepancy. The presented result unifies approaches for the classical single monatomic Boltzmann equation [2] and recently obtained results in the case of monatomic mixtures [36] and single polyatomic gases [37].
The kinetic theory of polyatomic gases and mixtures has recently become an active field of research and the rigorous theory has been developed in certain physical contexts that can be understood as a special case of the gas mixture model analysed in this paper. For the system of Boltzmann equations describing a mixture of solely monatomic gases, which can be seen as a sub-system of the present model when all P species are monatomic, in the linearized setting, well-posedness, stability, compactness, energy method and hypocoercivity-related issues were studied in [7, 12, 17, 18, 22, 23, 26]. In the spatial homogeneous case, questions about well-posedness and regularity for the system of non-linear Boltzmann equations, were addressed in [27, 36] with integrable angular part and in [4] for an angular part modelling long-range interactions (the so-called non-cutoff scattering).
Polyatomic gases bring another level of difficulty. An underlying physical effect is the internal energy exchange during the collision, apart from the usual translational energy of the relative motion of the colliding particles. The microscopic internal energy can be modelled as discrete or continuous variable, leading to the two branches in the kinetic theory of polyatomic gases: the semi-classical [39, 40, 44] and the continuous [20, 29, 30] approaches. A general framework unifying these two approaches was recently presented in [9, 14].
In this paper, we focus on the continuous kinetic approach that uses the Borgnakke-Larsen procedure for the collision parametrization [13], which makes the model accessible both from the rigorous analytical and computational points of view. From the particle perspective, this parametrization can be interpreted as a direct simulation Monte Carlo (DSMC) algorithm for sampling particles’ internal energy exchanges [31]. The corresponding Boltzmann equation for a single polyatomic gas (\(P=1\)) or a polyatomic gas mixture (\(P>1\)) can be also seen as a subsystem of our present model when all species are polyatomic. Recently, a compactness result has been obtained for the linearized polyatomic Boltzmann operator in [8, 24, 25] and in [15] for the model of resonant collisions [19]. The global well-posedness for bounded mild solutions near global equilibria on torus is established in [34]. For the space homogeneous setting and the full non-linear Boltzmann operator, well-possedness and \(L^1\) regularity were tackled in [37]. In particular, a form of the collision kernel which corresponds to hard potentials in both relative velocity and microscopic internal energy is proposed. It is shown to be highly physically relevant, as it provides transport coefficients that match experimental data [32, 33] for polytropic or calorically perfect polyatomic gases, and contains as a special case the collision kernel used in DSMC method with the variable hard sphere cross-section [31].
Motivated by the success in the analysis of space homogeneous problems for separately monatomic mixtures [4, 27, 36] and a single polyatomic gas [37], the aim of this paper is to establish the existence and uniqueness theory for a system of Boltzmann equations describing a mixture that involves both monatomic and polyatomic gases. We consider the model with different types of collision operators proposed in [5] and slightly modify it, in order to work with the \(L^1\) plain space in the energy variable. This setting corresponds to the non-weighted one as described in [32], and coincides with the model used in [6]. Moreover, it reduces to [20] for the single polyatomic gas model, analysed in [37]. The approach to prove existence and uniqueness is based on an abstract ODE theory [42], first proposed by Bressan [21] in the context of scalar kinetic equations. The method was recently revised in [1, 2], and was successfully used not only in [27, 36, 37], but also in dissipative kinetic problems [1] and the weak wave turbulence models for stratified flows [38].
The aforementioned approach is quite general in the context of kinetic operators with integrable kinetic kernels where gain and loss collision operators can be treated independently; the path to be followed is similar in all these problems consisting of some key steps. The implementation of such steps varies from case to case, however in the current case, due to the complexity of the underlying interactions happening in the general systems considered here, the arguments are more intricate leading to new ideas in the mathematical treatment which focus on the essential mechanisms of energy transfer between pairwise collisions. The first notable improvement is capturing the general structure of the energy pairwise collision interchange given in Lemma 5.1. Second, based on such general structure, we exploit the natural occurring averaging in the gain collision operators to show the dissipative character of each pairwise interaction. This character manifests in the fact that higher statistical moments of pairwise collisions are uniformly controlled over time. For the classical Boltzmann case this result is known as the Povzner Lemma and dates back to [10, 11, 28, 47]. We address this result here more precisely as Compact Manifold (or angular) Averaging Lemma, presented and proved in Lemma 5.2 for the general models considered here using a more sophisticated method of proof based on the decomposition of the pairwise interaction domain. This method is particularly useful for pairwise polyatomic interactions where the averaging effect occurs in the scattering angle and the internal energy exchange variables in a complex manner. The Compact Manifold Averaging Lemma is complemented with a coerciveness estimate for the loss collision operator, done in Lemma A.1. A dominant effect of the loss operator with respect to the gain operator in terms of higher moments is deduced from these considerations, given in Lemma 5.9. A final preparatory step consists in finding a priori higher moment estimates of the Boltzmann system solution. Namely, a moment ordinary differential inequality (ODI), satisfied by a suitable Banach space moment-norm of the solution, is derived in Lemma 6.1, which yields generation and propagation of statistical moments properties used later to implement an abstract ODI argument, here presented in Sect. 7.
The analysis is performed under a quite general assumption on the collision kernel or transition probability – it is assumed to be of the Maxwell-hard potential form for the collisional total energy (which reduces to the relative speed when only monatomic interactions are involved) with possible different rates \(\gamma _{ij}\ge 0\) satisfying \(\max _j \gamma _{ij} >0\). In addition, the angular part is assumed integrable and the collision kernel is assumed to be bounded from above and below by integrable partition functions of the Borgnakke-Larsen procedure. This assumption is general enough to cover already established theory for monatomic mixture and single polyatomic models and is compatible with the analysis of the linearized Boltzmann polyatomic operator performed in [6, 8, 25, 34].
The existence and uniqueness of the system solution is proven for initial data corresponding to strictly positive and bounded species mass (zero order species moment) and mixture total energy (second order mixture moment), which are all conserved quantities for the Boltzmann flow in the absence of chemical reactions (energy is interchanged between species though). Moreover, a mixture moment of the order \((2+\max _{ij}\{\gamma _{ij}\} - \min _{i}\max _{j}\{\gamma _{ij}\})^+\) is required to be bounded. The approach developed in this paper has an optimal value of \(2^+\) when \(\max _{ij}\{\gamma _{ij}\} = \min _{i}\max _{j}\{\gamma _{ij}\}\), which improves results of [37]. Another significant improvement is to incorporate arguments of [4] and to allow the range of \(\gamma _{ij}\) to be [0, 2] with at least one strictly positive \(\gamma _{ij}\) for each component i, which extends the previous results of [27, 36] in the monatomic mixture case that require all \(\gamma _{ij} > 0\). All the analysis is performed for general integrable angular scattering.
We stress that the physical framework of multi-component gas mixtures composed of both monatomic and polyatomic gases considered in this paper is highly relevant in applications since, for instance, air itself is a mixture of monatomic (such as Ar, O, N) and polyatomic (such as O\(_2\), N\(_2\), CO\(_2\)) components. Thus, it is necessary to transcend the classical Boltzmann equation that models an ideal gas composed of identical structureless particles. This work is a step in that direction.
The paper is organized as follows. In Sect. 2, the system of Boltzmann equations describing a mixture of monatomic and polyatomic gases is presented. The notation and functional spaces are introduced in Sect. 3, while assumptions on the collision kernel are listed in Sect. 4. Section 5 deals with estimates on the vector valued collision operator. Namely, we prove various energy identities and estimates for different types of species-species interactions in Sect. 5.1 that allow to prove the Averaging Lemma in Sect. 5.2, yielding estimates on statistical moments for the collision operator firstly written in a bi-linear form in Sect. 5.3 and then in the vector valued form in Sect. 5.4. This study allows to derive polynomial moments a priori estimates on the system solution in Sect. 6. Finally, existence and uniqueness theory is established in Sect. 7 and some technical results and general theorems used in the paper are listed in Appendix A.
2 System of Boltzmann Equations Modelling a Gas Mixture Composed of Monatomic and Polyatomic Gases
We consider a mixture of M monatomic and \((P-M)\) polyatomic gases. Each monatomic component \({\mathcal {A}}_i\), \(i=1,\dots ,M\), is described with the distribution function \(f_i(t,v)\ge 0\) depending on time \(t>0\) and molecular velocity \(v\in {\mathbb {R}}^d\). Polyatomic gases are modelled based on the continuous internal energy approach [20, 29, 30] which amounts to assume that a polyatomic component \({\mathcal {A}}_i\), \(i=M+1,\dots ,P\), of the mixture is described with the distribution function \(f_i(t,v,I)\ge 0\) depending on time \(t>0\), molecular velocity \(v \in {\mathbb {R}}^d\) and also molecular microscopic internal energy \(I \in [0,\infty )\). Assuming that distribution functions change due to mutual interactions, the dynamics of the mixture is characterized by the system of Boltzmann equations, here written in the space homogeneous setting,
where for the brevity we omit to write dependence on t. Note that (1) contains four collision operators that describe collisions of various type of gases and, as such, are different in nature. Namely, for the fixed monatomic species \({\mathcal {A}}_i\), \(i\in \{1,\dots ,M\}\), the pairwise interaction can be mono-mono when \(j\in \left\{ 1, \dots ,M\right\} \) or mono-poly for \(j\in \left\{ M+1, \dots , P\right\} \). Similarly, when the species \({\mathcal {A}}_i\) is polyatomic i.e. \(i\in \{M+1,\dots ,P\}\), we distinguish poly-mono interaction when \(j\in \left\{ 1, \dots ,M\right\} \) or poly-poly for \(j\in \left\{ M+1, \dots , P\right\} \). The form of corresponding four collision operators was introduced in [5] following the approach given in [29, 30], called the weighted setting in [32]. In this paper, motivated by the rigorous analysis for a single polyatomic gas [37], we will follow [20] and rewrite the collision operators of [5] in the non-weighted setting in the spirit of [32].
The system of Boltzmann-like equations (1) can be written in a vector form by introducing the vector valued distribution function \({\mathbb {F}}\) and the vector valued collision operator \({\mathbb {Q}}({\mathbb {F}})\)
Therefore, the system (1) in the vector valued form, and together with initial data reads
The next section introduces the collision operator \({\mathbb {Q}}({\mathbb {F}})\) for each of four possible binary interactions between molecules of monatomic and polyatomic species.
2.1 Collision Operators for Interactions Between Monatomic Gases
For \(i,j\in \left\{ 1, \dots , M \right\} \), the collision operator in a bilinear form for distribution functions \(f(t, v)\ge 0\) and \(g(t,v)\ge 0\) describing species \({\mathcal {A}}_i\) and \({\mathcal {A}}_j\), respectively, reads
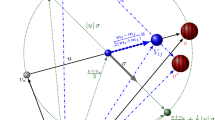
where in the gain part \(v'\) and \(v'_*\) are pre-collisional velocities expressed as functions of the post-collisional ones v, \(v_*\) and a parameter \(\sigma \) in the center-of-mass framework defined by vectors of the center of mass velocity V, relative velocity u and reduced mass \(\mu _{ij}\),
namely,
while the collision kernel \({\mathcal {B}}_{ij} \) satisfies the following microreversibility assumptions
Equations (6) are \(\sigma -\)parametrization of the conservation laws of momentum and kinetic energy of a colliding pair of molecules, namely,
or equivalently
The kinetic energy can be represented in the center-of-mass framework,
which is by (9) a conserved quantity.
The collision operator weak form is carefully explained in [16], i.e. for any suitable test functions \(\omega (v)\) and \(\chi (v)\),
2.2 Collision Operators for Interaction Between Polyatomic Gases
Let \(i,j\in \left\{ M+1, \dots , P \right\} \), i.e. we consider two colliding polyatomic molecules. Let one be of mass \(m_i\) and velocity-internal energy \((v', I')\) and the another one of mass \(m_j\) and velocity-internal energy \((v'_*, I'_*)\), that change to (v, I) and \((v_*, I_*)\) (with same masses), respectively, after the collision. We assume that collisions are elastic in the sense that momentum and the total (kinetic + microscopic internal) energy are conserved during the collision,
These laws can be rewritten in the center-of-mass framework (5), namely,
with the energy
In order to express pre–collisional velocities and internal energies in the original particle framework, the so-called Borgnakke-Larsen procedure [13, 20] is used. The idea is to parametrize equations (13) with the scattering direction \(\sigma \in {\mathbb {S}}^{d-1}\) and energy exchange variables \(R, r \in [0,1]\). More precisely, first split the kinetic and internal energy part of the total energy with \(R \in [0,1]\),
Then, the kinetic part is distributed among particles with \(\sigma \in {\mathbb {S}}^{d-1}\) and total internal energy is split on particles’ internal energies with \(r\in [0,1]\),
For the convenience, we introduce the primed parameters as well, \(\sigma ' \in {\mathbb {S}}^{d-1}\), \(r', R' \in [0,1]\),
The transformation \({\mathcal {T}}_{pp}: (v, v_*, I, I_*, r, R, \sigma ) \mapsto (v', v'_*, I', I'_*, r', R', \sigma ')\) is an involution and its Jacobian, which will deeply influence the structure of collision operator, is computed in [30],
The collision operator for distributions functions \(f:= f(t,v,I)\ge 0\) and \(g:= g(t,v,I)\ge 0\) describing species \({\mathcal {A}}_i\) and \({\mathcal {A}}_j\), respectively, used in this paper is a variant of the one proposed in [30],
where the pre-collisional quantities \(v'\), \(v'_*\), \(I'\) and \(I'_*\) are defined in (15), \(\alpha _i, \alpha _j >-1\) are constants related to the specific heats of the polyatomic gas [33], parameters’ function given by
and the collision kernel \( {\mathcal {B}}_{ij}\) satisfies the microreversibility assumptions
corresponding to the interchange of pre- and post-collisional molecules, and the interchange of colliding molecules. It is important to notice that the choice of functions (19) depends on the weight factor in the collision operator (18) because it ensures its invariance, since the factor
is invariant with respect to the changes described in (20). Together with the Jacobian (17), this implies the invariance of the measure
with respect to changes from (20). These considerations yield the well defined weak form,
for any suitable test functions \(\omega (v,I)\) and \(\chi (v,I)\).
2.3 Collision Operators for Interactions Between Monatomic and Polyatomic Gases
Let \({\mathcal {A}}_j\), \(j\in \left\{ 1, \dots , M \right\} \), be a monatomic component of the mixture described with the distribution function \(g(t,v) \ge 0\) and \({\mathcal {A}}_i\), \(i\in \left\{ M+1, \dots , P \right\} \), the polyatomic component characterized by the distribution function \(f(t,v,I) \ge 0\).
Since molecules differ in nature, the corresponding study of molecular collisions will depend on which molecule the internal energy is associated to – whether to the molecule of interest or the partner in collision. This raises the definition of two different collision operators,
-
(i)
collision operator \(Q_{ij}(f,g)(v,I)\) describing the influence of a monatomic component \({\mathcal {A}}_j\) on the polyatomic one \({\mathcal {A}}_i\) and acting on (v, I) pair (poly-mono interaction),
-
(ii)
collision operator \(Q_{ji}(g,f)(v)\) describing the influence of a polyatomic component \({\mathcal {A}}_i\) on the monatomic one \({\mathcal {A}}_j\) and acting on v only (mono-poly interaction).
2.3.1 Case (i): Study of Poly–Mono Interaction
We consider a pair of colliding molecules, one polyatomic molecule of mass \(m_i\) and velocity-internal energy \((v', I')\) which collides with the monatomic partner of mass \(m_j\) and velocity \(v'_*\). After the collision, they belong to the same species so masses do not change, but the velocity–internal energy pair of a polyatomic molecule become (v, I), while the velocity of the monatomic molecule changes to \(v_*\). This collision is assumed elastic, in the sense that momentum and total energy are preserved during the collision,
For this setting we introduce the center-of-mass framework (5) together with the energy
Then, laws (22) are equivalent to
These laws are parametrized with the angular parameter \(\sigma \in {\mathbb {S}}^{d-1}\) and a parameter \(R\in [0,1]\),
We complement these equations with the definition of primed parameters \(\sigma ' \in {\mathbb {S}}^{d-1}\), \( R' \in [0,1]\),
2.3.2 Case (ii): Study of Mono–Poly Interaction
Let consider the counterpart problem for the Case (i). Now we fix the monatomic molecule with mass \(m_j\) and velocity \(w'\) which changes to v due to a collision with the polyatomic molecule partner of mass \(m_i\) and velocity-internal energy pair \((w'_*, I'_*)\) that changes to \((v_*, I_*)\) after the collision. During the collision, the following conservation laws hold
Introducing the center-of-mass reference framework with (5) and the center of mass velocity W which differs from V by the mass interchange \(m_i \leftrightarrow m_j\),
(27) can be rewritten as
Similarly as in (25), these equations are parametrized with \(\sigma \in {\mathbb {S}}^{d-1}\) and \(R\in [0,1]\),
For convenience, we also express primed parameters \((\sigma ', R')\) in terms of non-primed quantities,
Lemma 2.1
Let \(i\in \left\{ M+1, \dots , P \right\} \) and \(j\in \left\{ 1, \dots , M \right\} \). Let \(\alpha _i > -1\) and define
Consider transformations
-
\({\varvec{Part (i)}}\) Transformations \({\mathcal {T}}_{pm}\) and \({\mathcal {T}}_{mp}\) are involutions and their Jacobians, respectively, \(J_{{\mathcal {T}}_{pm}} : = \left| \frac{\partial (v', v'_{*}, I', \sigma ',R')}{\partial (v,v_*,I_*,\sigma ,R) } \right| \) and \(J_{{\mathcal {T}}_{mp}} : = \left| \frac{\partial (w', w'_{*}, I'_{*}, \sigma ', R')}{\partial (v,v_*,I_*,\sigma ,R)} \right| \), are
$$\begin{aligned} J_{{\mathcal {T}}_{pm}} = J_{{\mathcal {T}}_{mp}} = \frac{\sqrt{R}}{\sqrt{R'}}, \end{aligned}$$(35)where \(R'\) is understood as (26) for \({\mathcal {T}}_{pm}\) and as (31) for \({\mathcal {T}}_{mp}\).
-
\({\varvec{Part (ii.a)}}\) The following measure is invariant under the collision transformation \({\mathcal {T}}_{pm}\),
$$\begin{aligned} I^{\alpha _i} \, d_i(R)\, \textrm{d}R \, \textrm{d}\sigma \, \textrm{d}v_* \, \textrm{d}v \, \textrm{d}I, \end{aligned}$$(36) -
\({\varvec{Part (ii.b)}}\) The following measure is invariant under the collision transformation \({\mathcal {T}}_{mp}\),
$$\begin{aligned} I_*^{\alpha _i} \, d_i(R)\, \textrm{d}R \, \textrm{d}\sigma \, \textrm{d}v_* \, \textrm{d}I_* \, \textrm{d}v. \end{aligned}$$(37)
2.3.3 Interchange of the Collision Reference
The aforementioned considerations concern relations connecting pre– and post–collisional quantities. It remains to study a transformation describing the interchange of a collision reference in the case of mixed poly-mono and mono–poly interactions. Take a monatomic molecule of mass \(m_j\), \( j\in \{1,\dots ,M\}\), and velocity \(v_*\) and a polyatomic molecule of mass \(m_i\), \( i\in \{M+1,\dots ,P\}\), and velocity-internal energy (v, I), so the poly–mono interaction. Collision reference interchange is a transformation constructed such that if \((v_*, v, I) \leftrightarrow (v, v_*, I_*=I)\) then the same change should hold before the collision i.e. \((v'_*, v', I') \leftrightarrow (w', w'_*, I'_*)\). Thus, we are led to consider the transformation
Then, for fixed \(i \in \{M+1,\dots ,P\}\) and \(j \in \{1,\dots ,M\}\), \( {\mathcal {T}}_{pm}( {\mathcal {I}}(v,v_*,I,\sigma ,R)) = (w'_*, w', I'_*, -\sigma ', R')\) and \( {\mathcal {T}}_{mp}( {\mathcal {I}}(v,v_*,I,\sigma ,R)) = (v'_*, v', I', -\sigma ', R')\).
2.3.4 Case (i): Collision Operator for Poly–Mono Interaction
The influence of a monatomic component \({\mathcal {A}}_j\) described by distribution function \(g(t, v) \ge 0\) on the polyatomic one \({\mathcal {A}}_i\) with distribution function \(f(t,v,I) \ge 0\) is captured with the collision operator
where the measure \(d_i(R)\) is given in (32) and the collision kernel satisfies the following micro-reversibility properties
with \(v'\), \(v'_*\), \(I'\) as defined in (25).
2.3.5 Case (ii): Collision Operator for Mono–Poly Interaction
The influence of a polyatomic component \({\mathcal {A}}_i\) characterized via distribution function \(f(t, v, I) \ge 0\) on the monatomic gas component \({\mathcal {A}}_j\) with distribution function \(g(t, v) \ge 0\) is described with the collision operator
where the measure \(d_i(R)\) is given in (32) and the collision kernel is assumed to satisfy the micro-reversibility properties
and \(w'\), \(w'_*\), \(I'_*\) are given in (30).
2.3.6 Weak Form of the Collision Operators for Poly–Mono & Mono–Poly Interactions
Lemma 2.1 ensures a well-defined weak form of the collision operators (39) and (41). The conservative form of the weak formulation is obtained when all operators in the interaction of two species are considered simultaneously. Indeed, for any suitable test functions \( \omega (v,I) \) and \(\chi (v)\), the following weak form is obtained [5],
where the involved quantities are detailed throughout the Sect. 2.3.
2.4 Weak Form of the Vector Valued Collision Operator
Take a suitable vector valued test function X
Collecting collision operator weak forms for each pair of species, stated above in (11), (43) and (21), the conservative weak form of the vector valued collision operator defined in (2) reads
Note that conservation laws of particles’ energies (8), (12) and (22) imply conservation properties of the vector valued collision operator. Namely, define Lebesgue brackets
Then, for the choice \(\chi _{i}(\cdot ) = \langle \cdot \rangle _i^2\),
If \(\chi _{i}(\cdot ) =1\), then the following conservation per each species holds
3 Notation and Functional Spaces
A natural framework to solve the spatially homogeneous Boltzmann equation is the space of integrable functions appropriately weighted. In the present setting, with Lebesgue brackets introduced in (47), the Banach space associated to the mixture constituent \({\mathcal {A}}_i\) is defined by
for any \(q\ge 0\). The same notion is introduced for the vector valued Banach spaces associated to the whole mixture,
A closely related concept is the one of polynomial moments.
Definition 3.1
The i-th polynomial moment of order \(q\ge 0\) for a suitable function f(t, v) for \(i =1,\dots , M\), and f(t, v, I) for \(i =M+1,\dots , P\), is defined by
Note that when \(f \ge 0\), the notion of polynomial moment coincides with \(L^1\) norms. Moreover, for any i, whether \(i \in \left\{ 1, \dots , M \right\} \) or \(i \in \left\{ M + 1, \dots , P \right\} \), the monotonicity property holds
Definition 3.2
The polynomial moment of order \(q\ge 0\) for a suitable vector valued function (2) is defined with
The i-th polynomial moment of order 0, \({\mathfrak {m}}_0^i[f]\), has a physical intuition of \({\mathcal {A}}_i\)-th species number density described with the distribution function \(f\ge 0\), whereas polynomial moment of the second order, \({\mathfrak {m}}_2[{\mathbb {F}}]\), is physically interpreted as the sum of number density and total specific energy of the mixture described with the vector valued distribution function \({\mathbb {F}}\ge 0\). Note that by conservative properties of the weak form (49) and (48), these quantities are conserved for the Boltzmann flow.
4 Assumptions on the Collision Kernels
In this section, we summarize the assumptions we impose on the collision kernels \({\mathcal {B}}_{ij}\), \(i,j\in \left\{ 1, \dots , P \right\} \), that depend on the nature of the interactions. Our aim is to cover as many models as possible, and thus assumptions are formulated in a rather general manner involving upper and lower bounds on \({\mathcal {B}}_{ij}\).
The main reason for this approach is to build a flexible strategy valid for a wide range of collision kernels suitable for interactions involving polyatomic gases. Our motivation comes from the analysis of the Boltzmann equation modelling a single polyatomic gas [37], which successfully found its application in engineering modelling, as in [33] for gas transport coefficients that match experimentally measured values, suggesting that the collision kernel model is appropriate. Of course, for interactions involving only monatomic molecules, our assumption reduces to the frequently used model of hard potentials.
For any pair of indices \(i, j \in \left\{ 1, \dots , P \right\} \), the rate \(\gamma _{ij}\) is supposed to have the following properties
We also denote
4.1 Mono–Mono Interactions
The collision kernels \({\mathcal {B}}_{ij}(v, v_*, \sigma )\), \(i, j \in \left\{ 1, \dots , M \right\} \) introduced in (7) describing interactions between monatomic molecules are assumed to take the following form
where the angular part is assumed non-negative, integrable and symmetric with respect to the interchange \(i\leftrightarrow j\),
and \(\tilde{{\mathcal {B}}}_{ij}(v, v_*)\) is the usual model of hard potentials (up to a multiplicative constant),
with \(\gamma _{ij}\) from (55).
4.2 Poly–Mono and Mono–Poly Interactions
For \(i \in \left\{ M+1, \dots , P \right\} \) and \( j \in \left\{ 1, \dots , M \right\} \), the collision kernels \( {\mathcal {B}}_{ij}(v, v_*, I, \sigma , R)\) defined by (40) are supposed to satisfy the following bounds
where the angular part \( b_{ij}({\hat{u}}\cdot \sigma )\) is assumed to be as in (58), and non-negative functions \( {\tilde{b}}_{ij}^{lb}(R)\), \( {\tilde{b}}_{ij}^{ub}(R)\) are assumed to have the following integrability properties,
where \(d_i(R) \) is from (32). The velocity-internal energy part is assumed to have the following form
with \(\gamma _{ij}\) from (55).
4.3 Poly–Poly Interactions
For indices \(i, j \in \left\{ M+1, \dots , P \right\} \), which describe interactions between polyatomic molecules solely, the collision kernels \({\mathcal {B}}_{ij}(v, v_*, I, I_*, \sigma , r, R)\) are assumed to satisfy the following bounds
where the angular part \(b_{ij}({\hat{u}}\cdot \sigma )\) is supposed as in (58), and non-negative functions \({\tilde{b}}_{ij}^{lb}(r, R)\), \({\tilde{b}}_{ij}^{ub}(r, R)\) are assumed to have the following integrability properties
where the function \(d_{ij}(r,R)\) was introduced in (19). The velocity-internal energy part \(\tilde{{\mathcal {B}}}_{ij}(v, v_*,I, I_*)\) takes the following form
with \(\gamma _{ij}\) from (55).
4.4 Remarks
Note that all three assumptions (59), (62) and (65) on the form of \(\tilde{{\mathcal {B}}}_{ij}\) can be written concisely as
where the energy \(E_{ij}\) is to be understood as (10), (23) or (14) depending on indices i, j. Moreover, such a form of \( \tilde{{\mathcal {B}}}_{ij}\) is micro-reversible itself, by (9), (24) and (13).
Integrability properties (58) and (61) led us to define constants
and by (64),
For convenience, we also introduce the constant for monatomic interaction which actually reduces to the \(L^1\) norm of the angular part, i.e.
Note that discrepancy in constants \(\kappa _{ij}^{lb}\) and \(\kappa _{ij}^{ub}\) is due to estimates on the parts of the collision kernels that is concerned with energy exchange variables. This difference disappears when, for instance, \({\tilde{b}}_{ij}^{lb} = {\tilde{b}}_{ij}^{ub} =1\) i.e. for the choice \({\mathcal {B}}_{ij}=b_{ij}({\hat{u}}\cdot \sigma ) \, \tilde{{\mathcal {B}}}_{ij}\), which is a possible choice due to micro-reversibility properties of \(\tilde{{\mathcal {B}}}_{ij}\) defined by (66) .
4.5 An Example of the Collision Kernel
Besides the model \({\mathcal {B}}_{ij}=b_{ij}({\hat{u}}\cdot \sigma ) \, \tilde{{\mathcal {B}}}_{ij}\), with \( \tilde{{\mathcal {B}}}_{ij}\) from (66), mentioned in the above Remark 4.4, which for a single species polyatomic gas corresponds to the Model 1 in [37], we bring another example corresponding to Models 2 and 3 in [37], showed to be successful in providing physical intuition of the single Boltzmann model for a polyatomic gas [32, 33]. For \(i \in \left\{ M+1, \dots , P \right\} \) and \( j \in \left\{ 1, \dots , M \right\} \), consider
while for \(i, j \in \left\{ M+1, \dots , P \right\} \) take
Then, assumptions (60), (63) are satisfied, for example, by choosing
for \(i \in \left\{ M+1, \dots , P \right\} \) and \( j \in \left\{ 1, \dots , M \right\} \), and
for \(i, j \in \left\{ M+1, \dots , P \right\} \).
5 Estimates on the Collision Operator
The first step in the well-posedness proof is to show dissipative character of the gain operator’s k-th moment reached by averaging post-collisional velocities or velocity-internal energy pairs. The original technique was introduced by Bobylev in [10], which uses decomposition of the post-collisional velocities in the center-of-mass framework and relies on symmetries built in the model of a single monatomic gas. This idea was lately used for different frameworks, as for inelastic collisions [11], granular gases [3], more general cross sections [35, 41, 45, 46]. Recently, the authors developed an averaging tool for monatomic gas mixtures [4, 27, 36] and single polyatomic gases [37], which relies on the representation of post-collisional velocities (and internal energies for polyatomic interactions) in a convex combination form of the energies in the center-of-mass framework.
Exploiting this idea, we will first represent post-collisional quantities in a suitable convex combination form in the upcoming Sect. 5.1, which will be the basis for the averaging over the space of parameters in Sect. 5.2, crucial to show dissipation of the gain operator.
5.1 Energy Identities and Estimates
We first introduce notation that will be used in this section. The parameter \(s_{ij} \in (0,1)\) convexly splits the sum of masses \(m_i + m_j\),
Its minimum will play an important role in computations,
For the two colliding molecules, the total energy (kinetic or kinetic+internal) during collision, which is a conserved quantity, will be written in brackets form of (47),
where the argument in the brackets can be either velocity or velocity-internal energy pair depending on whether i or j belong to \(\left\{ 1, \dots , M \right\} \) or \(\left\{ M+ 1, \dots , P \right\} \). This total energy in brackets form can be written in the center-of-mass reference framework (5),
where \(E_{ij}\) is (10) for \(i, j \in \left\{ 1, \dots , M \right\} \), (14) for \(i, j \in \left\{ M+ 1, \dots , P \right\} \) and (23) if \(i \in \left\{ M+ 1, \dots , P \right\} \) and \(j \in \left\{ 1, \dots , M \right\} \).
The goal of the upcoming lemma is to express the total energy (73) in convex components in order to represent each primed bracket \(\langle \cdot ' \rangle _i^2\) and \( \langle \cdot ' \rangle _j^2\) separately in terms of non-primed quantities.
Lemma 5.1
(Energy Identity Lemma) The following energy identities and estimates hold, depending on the nature of particle interactions,
-
Part (i): mono–mono interactions Let \(i, j \in \left\{ 1, \dots , M \right\} \) and the primed velocities be defined in (6). Then, there exist non-negative functions \(p_{ij}\), \(q_{ij}\) and \(\lambda _{ij}\) which depend only on velocities v, \(v_*\) and parameter \(s_{ij}\) from (70) and satisfy \(p_{ij} + q_{ij} = 1 \), such that the following representation hold,
$$\begin{aligned} \langle v' \rangle _i^2 = E^{\langle \rangle }_{ij} \, p_{ij} + \lambda _{ij} {\hat{V}} \cdot \sigma , \qquad \langle v'_* \rangle _j^2 = E^{\langle \rangle }_{ij} \, q_{ij} - \lambda _{ij} {\hat{V}} \cdot \sigma , \end{aligned}$$(74)and the following estimate
$$\begin{aligned} \langle v' \rangle _i^2, \ \langle v'_* \rangle _j^2 \le \left( 1 - {\bar{s}}_{ij}\left( 1 - |{\hat{V}} \cdot \sigma | \right) \right) E^{\langle \rangle }_{ij}, \end{aligned}$$(75)where \(E^{\langle \rangle }_{ij} = \langle v \rangle _i^2 + \langle v_* \rangle _j^2 \) and \({\bar{s}}_{ij}\) is given in (71).
-
Part (ii): poly–poly interactions Let \(i,j \in \left\{ M+1, \dots , P \right\} \) and the primed velocity - internal energy pairs be defined in (15). There exist non-negative functions \({\tilde{p}}_{ij}\), \({\tilde{q}}_{ij}\), \({\tilde{t}}_{ij}\) and \(\lambda _{ij}\) which depend on velocities v, \(v_*\), internal energies I, \(I_*\), energy exchange variable R and mass ratio \(s_{ij}\) from (70) such that the following convexity property holds \( {\tilde{p}}_{ij} + {\tilde{q}}_{ij} + {\tilde{t}}_{ij} =1\) and representation of the primed velocity - internal energy pairs,
$$\begin{aligned} \langle v', I' \rangle _i^2 = E^{\langle \rangle }_{ij} \left( {\tilde{p}}_{ij} + r \, {\tilde{t}}_{ij} \right) + \lambda _{ij} {\hat{V}} \cdot \sigma , \quad \langle v'_*, I'_* \rangle _j^2 = E^{\langle \rangle }_{ij} \left( {\tilde{q}}_{ij} + (1-r) {\tilde{t}}_{ij} \right) - \lambda _{ij} {\hat{V}} \cdot \sigma ,\nonumber \\ \end{aligned}$$(76)where \(E^{\langle \rangle }_{ij} = \langle v, I \rangle _i^2 + \langle v_*, I_* \rangle _j^2\). Moreover, the following estimate holds
$$\begin{aligned} \begin{aligned} \langle v', I' \rangle _i^2&\le E^{\langle \rangle }_{ij} \left( 1- {\tilde{q}}_{ij} (1-|{\hat{V}} \cdot \sigma |) - {\tilde{t}}_{ij} (1-r) \right) , \\ \langle v'_*, I'_* \rangle _j^2&\le E^{\langle \rangle }_{ij} \left( 1- {\tilde{p}}_{ij} (1-|{\hat{V}} \cdot \sigma |) - {\tilde{t}}_{ij} r \right) , \end{aligned} \end{aligned}$$(77)where the involved terms satisfy
$$\begin{aligned} ( {\tilde{p}}_{ij} + {\tilde{t}}_{ij} ), \ ( {\tilde{q}}_{ij} + {\tilde{t}}_{ij} ) \ge {\bar{s}}_{ij}, \end{aligned}$$(78)with \({\bar{s}}_{ij}\) from (71).
-
Part (iii) - poly–mono and mono–poly interactions Consider \(i\in \left\{ M+1, \dots , P \right\} \) and \( j \in \left\{ 1, \dots , M \right\} \). Let the primed velocity-internal energy pair \((v', I')\) and the primed velocity \(v'_*\) be defined as in (25). There exist non-negative functions \({\tilde{p}}_{ij}\), \({\tilde{q}}_{ij}\), \({\tilde{t}}_{ij}\) and \(\lambda _{ij}\) depending on v, \(v_*\), I, R and \(s_{ij}\) from (70) such that it holds the convexity property \( {\tilde{p}}_{ij} + {\tilde{q}}_{ij} + {\tilde{t}}_{ij} =1\) and the representation
$$\begin{aligned} \langle v', I' \rangle _i^2 = \left( {\tilde{p}}_{ij} + {\tilde{t}}_{ij} \right) E^{\langle \rangle }_{ij} + \lambda _{ij} {\hat{V}} \cdot \sigma , \qquad \langle v'_* \rangle _j^2 = {\tilde{q}}_{ij} \, E^{\langle \rangle }_{ij} - \lambda _{ij} {\hat{V}} \cdot \sigma , \end{aligned}$$(79)with \(E^{\langle \rangle }_{ij} = \langle v, I \rangle _i^2 + \langle v_* \rangle _j^2\). Moreover, the following estimate holds
$$\begin{aligned} \langle v', I' \rangle _i^2, \ \langle v'_* \rangle _j^2 \le \left( 1 - {\bar{s}}_{ij}R \left( 1 - |{\hat{V}} \cdot \sigma | \right) \right) E^{\langle \rangle }_{ij}, \end{aligned}$$(80)with \({\bar{s}}_{ij}\) from (71).
Proof
First define the function \(\Theta _{ij}\) which depends on velocities or velocity-internal energy pairs solely,
The part \( \left( 1 - \Theta _{ij} \right) E^{\langle \rangle }_{ij} \) is further split depending on the type of molecular interaction.
Mono–mono interactions This type of interactions was already studied in [36], Lemma 4.1. Defining
the representation (74) and estimate (75) hold.
Poly–poly interactions For \(i,j \in \left\{ M+1, \dots , P \right\} \), in order to split the term \(\left( 1 - \Theta _{ij} \ \right) E^{\langle \rangle }_{ij}\), we introduce the function \(\Sigma _{ij}\) that, except on velocities and internal energies like for \(\Theta _{ij} \), additionally depends on the parameter R,
We then define the following functions in terms of convex combination functions,
Taking the square of the primed velocities and internal energies from (15) and combining them into the bracket form (47), for the term \( \langle v', I' \rangle _i^2 \) it follows
and similarly for the counterpart \( \langle v'_*, I'_* \rangle _i^2\). Expressing
the representation (76) is obtained. Note that for a single polyatomic gas corresponding to the case \(s_{ij}=1/2\), the representation (76) coincides with the one introduced in [37].
To prove the second part, note that by Young’s inequality the following estimates on \(\lambda _{ij}\) hold
Then, from (76) the following estimates are straightforward,
yielding (77). Estimate (78) follows from
by (71).
Poly–mono and mono–poly interactions For \(i\in \left\{ M+1, \dots , P \right\} \) and \(j\in \left\{ 1, \dots , M \right\} \), functions \({\tilde{p}}_{ij}\), \({\tilde{q}}_{ij}\) and \({\tilde{t}}_{ij}\) are of the same form as (84) for poly–poly interactions, except that the total energy in the center-of-mass framework \(E_{ij}\) is understood as (23).
For the second part, we use the estimate on \(\lambda _{ij}\) as in (85). Then from the representation (79), the following estimates hold,
Note that
where the last inequality is due to
This implies (80), which concludes the proof. \(\square \)
5.2 Compact Manifold Averaging Lemma
The next goal is to show that estimates on the primed quantities \(\langle \cdot ' \rangle _i^2\), \( \langle \cdot ' \rangle _j^2\), proved in the previous lemma yield decay properties of their \(k-\)th power \(\langle \cdot ' \rangle _i^k\), \( \langle \cdot ' \rangle _j^k\), with respect to k when averaged over a suitable compact domain, such as angular transitions and partition functions, describing transition probability rates depending on the particles’ interaction nature.
To this end, we prove the following key lemma, highlighting a novel method of proof flexible enough to conveniently adapt to all type of interactions satisfying the general pairwise energy transfer identity structure of Lemma 5.1.
Lemma 5.2
(Compact Manifold Averaging Lemma) With the notation of Lemma 5.1 and the assumptions on collision kernels stated in Sect. 4, there exist non-negative constants \({\mathcal {C}}^{ij}_k\) decreasing in \(k\ge 0\) and with \(\lim _{k\rightarrow \infty }{\mathcal {C}}^{ij}_k=0\) or more precisely
such that the following estimates hold, depending on the nature of particle interactions.
-
Part (i): mono–mono interactions For \(i, j \in \left\{ 1, \dots , M \right\} \),
$$\begin{aligned} \int _{{\mathbb {S}}^{d-1}} \left( 1 - {\bar{s}}_{ij}\left( 1 - |{\hat{V}} \cdot \sigma | \right) \right) ^k b_{ij}({\hat{u}}\cdot \sigma ) \, \textrm{d}\sigma \le {\mathcal {C}}^{ij}_k. \end{aligned}$$(87) -
Part (ii): poly–poly interactions When \(i,j \in \left\{ M+1, \dots , P \right\} \),
$$\begin{aligned} \begin{aligned}&\int _{{\mathbb {S}}^{d-1}\times [0,1]^2}\left( 1- {\tilde{q}}_{ij} (1-|{\hat{V}} \cdot \sigma |) - {\tilde{t}}_{ij} (1-r) \right) ^k b_{ij}({\hat{u}}\cdot \sigma ) \, {\tilde{b}}_{ij}^{ub}(r,R)\, d_{ij}(r,R)\, \textrm{d}\sigma \, \textrm{d}r \, \textrm{d}R\\&\quad \le {\mathcal {C}}^{ij}_k\,, \\&\text {and}\\&\int _{{\mathbb {S}}^{d-1}\times [0,1]^2} \left( 1- {\tilde{p}}_{ij} (1-|{\hat{V}} \cdot \sigma |) - {\tilde{t}}_{ij} r \right) ^k b_{ij}({\hat{u}}\cdot \sigma ) \, {\tilde{b}}_{ij}^{ub}(r,R)\, d_{ij}(r,R)\, \textrm{d}\sigma \, \textrm{d}r \, \textrm{d}R \le {\mathcal {C}}^{ij}_k\,. \end{aligned} \end{aligned}$$(88) -
Part (iii): poly–mono and mono–poly interactions Consider \(i\in \left\{ M+1, \dots , P \right\} \) and \( j \in \left\{ 1, \dots , M \right\} \). Then,
$$\begin{aligned} \int _{{\mathbb {S}}^{d-1}\times [0,1]} \left( 1 - {\bar{s}}_{ij}R \left( 1 - |{\hat{V}} \cdot \sigma | \right) \right) ^k b_{ij}({\hat{u}}\cdot \sigma ) \, {\tilde{b}}_{ij}^{ub}(R)\, d_i(R)\, \textrm{d}\sigma \, \textrm{d}R \le {\mathcal {C}}^{ij}_k\,. \end{aligned}$$(89)
As a consequence of the estimates (87), (88), and (89), there exists \({\bar{k}}_*\), depending only on the angular part \(b_{ij}({\hat{u}}\cdot \sigma )\) and functions \(b_{ij}^{ub}\) of energy exchange variables, such that for all \(i,j\in \left\{ 1, \dots , P \right\} \),
with \(\kappa _{ij}^{lb}\) provided in (69), (68) and (67), respectively for each type of particles’ interactions.
Proof
We prove each type of interaction separately. The idea of the proof is to split the domain of integration into sub-domains, one sub-domain, \(A_\varepsilon ^0\), on which the term raised on power k is strictly less than 1, guarantying the power decay in k, and its complement whose measure will be \({{\scriptscriptstyle {\mathcal {O}}}} (\varepsilon )\). A suitable choice of \(\varepsilon \) in terms of k will allow to conclude the proof.
Mono–mono interactions Split the sphere \({\mathbb {S}}^{d-1}\) into two sub-regions:
In \(A_\varepsilon ^0 \) the following inequality holds
since both \({\bar{s}}_{ij}, \varepsilon > 0\). Therefore, the averaging over this domain will ensure the power decay in k, i.e. the left-hand side of (87) is estimated as
It remains to show that the last term is of order \({{\scriptscriptstyle {\mathcal {O}}}} (\varepsilon )\). To that end, consider the family of measurable functions \(\Phi _\varepsilon ({\hat{V}}, {\hat{u}}): {\mathbb {S}}^{d-1}\times {\mathbb {S}}^{d-1}\rightarrow [0,\infty )\), for \(\varepsilon >0\) defined as
Let us prove that \(\Phi _\varepsilon ({\hat{V}}, {\hat{u}})\) converges uniformly (in the variables \({\hat{V}}, {\hat{u}}\)) to zero as \(\varepsilon \rightarrow 0\). To this end, fix \(\delta >0\) and note that for any \(K>0\)
For \(\Phi ^1_\varepsilon ({\hat{V}}, {\hat{u}})\) we use polar coordinates setting \(\cos (\theta )={\hat{u}}\cdot \sigma \) with \({\hat{u}}\) arbitrary but fixed. Then, due to the monotone convergence theorem, there exists a sufficiently large \(K:=K(\delta ,b_{ij})\) such that
As for \(\Phi ^2_\varepsilon ({\hat{V}}, {\hat{u}})\),
Thus, choosing \(\varepsilon <\frac{\delta }{4|{\mathbb {S}}^{d-2}|K}=:\varepsilon _*(\delta ,b_{ij})\) it holds that \(\Phi ^2_\varepsilon ({\hat{V}}, {\hat{u}})\le \frac{\delta }{2}\). Consequently,
In the sequel we simply write that \(\sup _{{\hat{V}}, {\hat{u}}}\Phi _\varepsilon ({\hat{V}}, {\hat{u}})={{\scriptscriptstyle {\mathcal {O}}}} (\varepsilon )\). Returning to (91), we conclude that
With the choice \(\varepsilon =k^{-a}\), with \(a\in (0,1)\), it holds that
and therefore,
Poly–poly interactions For the first estimate in (88), split the region \({\mathbb {S}}^{d-1}\times [0,1]\) into three sub-regions:
In \(A_\varepsilon ^0\), thanks to (78),
Denoting
the left-hand side of (88) becomes
where for the latter integral we invoked the monotone convergence theorem. The estimate follows, as in the previous case, choosing \(\varepsilon =k^{-a}\), with \(a\in (0,1)\).
For the second estimate in (88) we proceed similarly by considering the regions
Then, for \(A_\varepsilon ^0\) the estimate (78) yields
and therefore
To conclude choose \(\varepsilon =k^{-a}\), with \(a\in (0,1)\).
Poly–mono and mono–poly interactions Split the region \({\mathbb {S}}^{d-1}\times [0,1]\) into three sub-regions:
Since in \(A_\varepsilon ^0\) the following bound holds,
the left-hand side of (89) can be estimated as
where we denoted
We conclude taking \(\varepsilon =k^{-\frac{a}{2}}\), with \(a\in (0,1)\). \(\square \)
Remark 5.3
A particular important case is when the kernels are all bounded
In such case there is an explicit rate for \( {\mathcal {C}}_k^{ij}\), namely, \({\mathcal {C}}_k^{ij} \le \frac{C}{\sqrt{k}}\). Indeed, we analyse the most restrictive case of poly–mono and mono–poly interactions. One splits \({\mathbb {S}}^{d-1}\times [0,1]\) into the subregions
In \(A_\varepsilon \)
so that
Whereas, in \(A_\varepsilon ^c\)
The result follows minimising in \(\varepsilon \), that is choosing \(\varepsilon \sim \frac{1}{\sqrt{k}}\).
Corollary 5.4
With the notation of Lemma 5.1 and 5.2 and the assumptions on collision kernels stated in Sect. 4, the following estimates hold,
-
Part (i): mono–mono interactions For \(i, j \in \left\{ 1, \dots , M \right\} \)
$$\begin{aligned} {\mathcal {G}}^+_{ij}(v, v_*) := \int _{{\mathbb {S}}^{d-1}} \left( \langle v' \rangle _i^{k} + \langle v'_*\rangle _j^{k} \right) b_{ij}({\hat{u}}\cdot \sigma ) \, \textrm{d}\sigma \le 2 \, {\mathcal {C}}^{ij}_k\left( \langle v \rangle _i^{2} + \langle v_* \rangle _j^{2} \right) ^{k/2}. \end{aligned}$$(95) -
Part (ii): poly–poly interactions For \(i,j \in \left\{ M+1, \dots , P \right\} \)
$$\begin{aligned} \begin{aligned}&{\mathcal {G}}^+_{ij}(v, v_*, I, I_*)\\&\quad := \int _{{\mathbb {S}}^{d-1}\times [0,1]^2} \left( \langle v', I' \rangle _i^{k} + \langle v'_*, I'_* \rangle _j^{k} \right) b_{ij}({\hat{u}}\cdot \sigma ) \, {\tilde{b}}_{ij}^{ub}(r,R)\, d_{ij}(r,R)\, \textrm{d}\sigma \, \textrm{d}r \, \textrm{d}R \\&\quad \le 2 \, {\mathcal {C}}^{ij}_k\left( \langle v, I \rangle _i^{2} + \langle v_*, I_* \rangle _j^{2} \right) ^{k/2}. \end{aligned} \end{aligned}$$(96) -
Part (iii): poly–mono and mono–poly interactions Consider \(i\in \left\{ M+1, \dots , P \right\} \) and \( j \in \left\{ 1, \dots , M \right\} \).
$$\begin{aligned} \begin{aligned} {\mathcal {G}}^+_{ij}(v, v_*, I)&:= \int _{{\mathbb {S}}^{d-1}\times [0,1]} \left( \langle v', I' \rangle _i^{k} + \langle v'_*\rangle _j^{k} \right) b_{ij}({\hat{u}}\cdot \sigma ) \, {\tilde{b}}_{ij}^{ub}(R)\, d_i(R)\, \textrm{d}\sigma \, \textrm{d}R \\&\le 2 \, {\mathcal {C}}^{ij}_k\left( \langle v, I \rangle _i^{2} + \langle v_*\rangle _j^{2} \right) ^{k/2}, \end{aligned} \end{aligned}$$(97)
where the constant \({\mathcal {C}}^{ij}_k\) is characterized in Lemma 5.2.
Proof
The estimates follow from Lemma 5.1 and 5.2. \(\square \)
5.3 Estimates on the k-Moments of the Collision Operator in a Bi-linear Form
In this section, we will consider moments of the collision operator written in a bi-linear form. Namely, depending on i and j, whether they refer to monatomic or polyatomic species, there are three bi-linear forms,
- (i):
-
\(i, j \in \left\{ 1, \dots , M \right\} \)
$$\begin{aligned} {\mathcal {Q}}_k^{ij}[f,g] := \int _{{\mathbb {R}}^d} Q_{ij}(f,g)(v) \, \langle v \rangle _i^{k} \, \textrm{d}v + \int _{{\mathbb {R}}^d} Q_{ji}(g,f)(v) \, \langle v \rangle _j^{k} \, \textrm{d}v, \end{aligned}$$(98) - (ii):
-
\(i\in \left\{ M+1, \dots , P \right\} \) and \( j \in \left\{ 1, \dots , M \right\} \)
$$\begin{aligned} {\mathcal {Q}}_k^{ij}[f,g] := \int _{{\mathbb {R}}^d \times [0,\infty )} Q_{ij}(f,g)(v, I) \, \langle v, I \rangle _i^{k} \, \textrm{d}v\, \textrm{d}I + \int _{{\mathbb {R}}^d} Q_{ji}(g,f)(v) \, \langle v \rangle _j^{k} \, \textrm{d}v,\nonumber \\ \end{aligned}$$(99) - (iii):
-
\(i,j \in \left\{ M+1, \dots , P \right\} \)
$$\begin{aligned} {\mathcal {Q}}_k^{ij}[f,g]:= & {} \int _{{\mathbb {R}}^d \times [0,\infty )} Q_{ij}(f,g)(v, I) \, \langle v, I \rangle _i^{k} \, \textrm{d}v\, \textrm{d}I \nonumber \\{} & {} + \int _{{\mathbb {R}}^d \times [0,\infty )} Q_{ji}(g,f)(v, I) \, \langle v, I \rangle _j^{k} \, \textrm{d}v\, \textrm{d}I. \end{aligned}$$(100)
The goal of this section is to estimate these bi-linear forms in terms of suitable statistical moments of the input functions f and g with the help of the Compact Manifold Average Lemma, as presented in Lemma 5.2 or Corollary 5.4, and the following pointwise lemma which provides, in the sequel, a new estimate valid in the whole range \(k>2\) for propagation of moments estimates.
Lemma 5.5
(p-Binomial inequality) Assume \(p>1\). For all \(x, y>0\), the following inequality holds
Proof
Consider the function \(\varphi (z)=z^{p} + 1 + 2^{p+1}z - (z+1)^{p}\) in \(z\in [0,1]\). Note that \(\varphi (0)=0\) and \(\varphi '(0)>0\), that is \(\varphi \) is nonnegative in some \([0,z_*]\). Certainly \(z_*\ge z_{c}\) with \(z_{c}\) the smallest critical point of \(\varphi \) in (0, 1). Now, \(\varphi '(z)=p\,z^{p-1} + 2^{p+1} - p\,(z+1)^{p-1}\), therefore \(\varphi '(z_c)=0\) implies
That is, \(z_{c}\ge \big (\frac{4}{p}\big )^{\frac{1}{p-1}}\,2-1\). It is not difficult to check that \(\big (\frac{4}{p}\big )^{\frac{1}{p-1}}\ge \frac{3}{4}\), for \(p>1\), which implies that \(z_{c}\ge \frac{1}{2}\). Consequently, \(\varphi \ge 0\) in the interval \([0,\frac{1}{2}]\). As for the interval \((\frac{1}{2},1]\) note that in such interval
This proves that \(\varphi \) is nonnegative in [0, 1], that is
Now, for \(x, y>0\) write
and, then, conclude applying the aforementioned inequality with \(z=\frac{x}{y}\) and \(z=\frac{y}{x}\) respectively. \(\square \)
Lemma 5.6
Let non-negative functions \(f, g \in L^1_{k+\bar{{\bar{\gamma }}}}\), with \(k \ge {\bar{k}}_*\), \({\bar{k}}_*\) is from (90), \(\bar{{\bar{\gamma }}}\) from (56). There exist non-negative constants \( A_\star ^{ij}, \varepsilon >0\) and \({B}^{ij}_{k}\), such that the following estimate holds on the bi-linear forms (98)–(100) with the collision kernel satisfying assumptions stated in Sect. 4,
where expressions are to be understood depending on indices i and j according to (52). Constants are explicitly computed in the proof with the final expression given in Remark 5.7.
Proof
We firstly present the proof for poly–poly interactions, so taking \(i,j \in \left\{ M+1, \dots , P \right\} \). By the weak form (21) and assumptions on the collision kernel,
The term \( {\mathcal {G}}^+_{ij}(v, v_*, I, I_*) \) introduced in (96) can be split by exploiting the estimate (101), given in Lemma 5.5, yielding
where the constant \({\tilde{c}}_k\) is
This estimate implies
Since, by the assumption of this lemma, \(k \ge {\bar{k}}_*\) with \({\bar{k}}_*\) from (90), the constant in front of the highest order term is strictly positive. Moreover, as \({\mathcal {C}}_k^{ij} \) is decreasing in k, we choose
Using the lower bound for the negative term and the upper bound for the positive term from (183) in the Appendix Lemma A.1,
Majorizing the indicator functions and switching to the moment notation (52), we rewrite the previous inequality as
The monotonicity of moments (53) allows to bound positive terms in (108) related to the moments of the order containing \(\gamma _{ij}\) by moments of the same order but involving \(\bar{{\bar{\gamma }}}_{i}\) or \(\bar{{\bar{\gamma }}}_{j}\) instead of \(\gamma _{ij}\), see (55). This will be an essential step for the upcoming moments interpolation which requires strict positivity of rates \(\bar{{\bar{\gamma }}}_{i}, \bar{{\bar{\gamma }}}_{j}>0\). Thus, (108) becomes
Next, we invoke arguments of [2] that involve moment interpolation formulas
where \(\ell \) will be either i or j. For simplicity of the notation, we drop for the moment the reference to the distribution function, i.e. we shorten \({\mathfrak {m}}^i:= {\mathfrak {m}}^i[f]\).
Thus, since \(\bar{{\bar{\gamma }}}_{\ell }>0\), (110) yields
Incorporating these estimates into (109) and using moment monotonicity (53) for \(0 < \bar{{\bar{\gamma }}}_{i}, \bar{{\bar{\gamma }}}_{j}\le 2\),
with constants
In order to factorize terms of the order \(k+\bar{{\bar{\gamma }}}_{i}\) and \(k+\bar{{\bar{\gamma }}}_{j}\), we use Young’s inequality,
and proceed separately for each term.
Term \(T_1\). For the first term of \(T_1\), Young’s inequality (113) implies
with the notation
and the choice
The very same computations imply for the counterpart,
Thus, term \(T_1\) is estimated as follows,
where the involved terms are specified in (114) with (115).
Term \(T_2\). In a similar fashion, for the first part of term \(T_2\), Young’s inequality (113) implies
with the choice
and notation
Thus, for \(T_2\) we conclude
Gathering (116) and (119), the bi-linear form \({\mathcal {Q}}_{ij}\) becomes
where all constants are merged into the one,
and we denoted
which concludes the proof for poly–poly interaction when \(i,j \in \left\{ M+1, \dots , P \right\} \).
For monatomic gases, i.e. \(i, j \in \left\{ 1, \dots , M \right\} \), the weak form (11) together with the appropriate assumptions on the collision kernel from Sect. 4 and Lemma 5.4 imply,
With this estimate at hand, the same arguments as for the poly–poly interaction lead to the desired estimate (102). Similarly, for poly–mono interaction when \(i \in \left\{ M+1, \dots , P \right\} \) and \( j \in \left\{ 1, \dots , M \right\} \), the weak form (43), assumptions on the collision kernel from Sect. 4 and Lemma 5.4 yield
and, again, proceeding in the same fashion as for poly–poly interaction leads to (102), which concludes the proof. \(\square \)
Remark 5.7
The constant \(B^{ij}_{k}[f,g]\) is explicit and depends on k, \(\varepsilon \), \(\bar{{\bar{\gamma }}}_{i}\), \(\bar{{\bar{\gamma }}}_{j}\) and on f and g through their zero and second order species moment. Its formula is given in (120) after gathering expressions for \({\tilde{K}}_1^{ij}[f,g]\) and \( {\tilde{K}}_2^{ij}[f,g]\),
where \({\tilde{A}}_\star ^{ij}\) is from (107), \({\mathcal {C}}^{ij}_k\) as in (86) and \({\tilde{c}}_k\) is specified in (106).
Lemma 5.8
Let non-negative functions \(f, g \in L^1_{k}\), with \(k > 2\). The following inequality holds for the bi-linear forms (98)–(100) with the collision kernel satisfying assumptions stated in Sect. 4,
with \( \kappa _{ij}^{ub} \) from (68) and \({\tilde{c}}_k\) from (106).
Proof
As in the previous Lemma 5.6, we present the proof for poly–poly interactions, i.e. for \(i,j \in \left\{ M+1, \dots , P \right\} \) keeping in mind that other types of interactions follow the same strategy.
Start with the bi-linear form (103),
Then the primed quantities are estimated in terms of non-primed by using the conservation of energy (12). Indeed, for \(k > 2\),
The last term is estimated via (105), which in combination with the loss term implies cancellation of the highest order moment,
Then, the assumption on the collision kernel (63) allows to integrate over \((\sigma , r, R)\) implying, with notation (68),
The last step consists in exploiting the upper bound (183) and conveniently using the indicator functions, as in the previous lemma, to get
where the last estimate is due to monotonicity of moments (53). \(\square \)
5.4 Estimates on the Moments of the Vector Valued Collision Operator
In this section, we consider the vector valued distribution function \({\mathbb {F}}\) and the collision operator \({\mathbb {Q}}({\mathbb {F}})\) as introduced in (2) and provide estimates on the collision operator moments in terms of the moments of the distribution function \({\mathbb {F}}\). In other words, we switch from the bi-linear forms presented in Sect. 5.3 to a vector valued form that combines all possible interactions among species \({\mathcal {A}}_i\) and \({\mathcal {A}}_j\), for \(i,j=1,\dots ,P\). For this Section, recall Definition 3.2 of polynomial moments for vector valued function \({\mathbb {F}}\).
Lemma 5.9
Take the vector valued collision operator \({\mathbb {Q}}({\mathbb {F}})\) defined in (2) with the collision kernel satisfying assumptions stated in Sect. 4. The following estimates on \({\mathfrak {m}}_k[{\mathbb {Q}}({\mathbb {F}})]\) hold,
-
(1)
For \(k>2\), assuming that each component \(f_i\) of the vector valued distribution function \({\mathbb {F}}\) satisfy assumptions of Lemma 5.8
$$\begin{aligned} {\mathfrak {m}}_k[{\mathbb {Q}}({\mathbb {F}})] \le D_k \, {\mathfrak {m}}_{k}[{\mathbb {F}}], \end{aligned}$$(123)with \(D_k\) explicitly given in (126).
-
(2)
For \(k \ge {\bar{k}}_*\), assuming that each component \(f_i\) of the vector valued distribution function \({\mathbb {F}}\) satisfy assumptions of Lemma 5.6 and additionally \({\mathfrak {m}}^i_0[f_i]>0\) for each \(i=1,\dots ,P\), there exist positive constants \({A}_\star \) and \(B_k\) related to those in Lemma 5.6 such that
$$\begin{aligned} {\mathfrak {m}}_k[{\mathbb {Q}}({\mathbb {F}})] \le - {A}_\star \, {\mathfrak {m}}_2[{\mathbb {F}}]^{-\frac{{\bar{\gamma }}}{k-2}} \ {\mathfrak {m}}_{k}[{\mathbb {F}}]^{1+\frac{{\bar{\gamma }}}{k-2}} + B_k, \end{aligned}$$(124)with \({\bar{\gamma }}\) defined in (56). An explicit choice for \(A_\star \) is given in (128) and asymptotic expression of \(B_{k}\) in (130).
Proof
Starting from the definition of moments (52) for a vector valued function, the first goal is to write \({\mathfrak {m}}_k\)-th moment of the collision operator \({\mathbb {Q}}({\mathbb {F}})\) in terms of bi-linear forms (98), (99) and (100). To that end, we use the weak form (46) for the test function \(\psi _i(\cdot ) = \langle \cdot \rangle _i^k\),
For the first part of the statement valid for any \(k>2\), plugging the estimate (122) on each bi-linear form and rearranging the sum,
which leads to the statement (123) with the constant
The second part valid for \(k\ge {\bar{k}}_*\) starts with (125). Estimates (102) on bi-linear forms and rearrangement of the sum imply
where for the simplicity of notation, we denoted \( {\mathfrak {m}}^i_k := {\mathfrak {m}}^i_k[f_i]\) and \({B}^{ij}_k:= {B}^{ij}_k[f_i,f_j]\), since the reference to the distribution function is clear in this case.
The first goal is to absorb the term multiplying a small constant \(\varepsilon \) by a negative term. To that end, we use the lower bound for the negative term. Since \(A_\star ^{ij}>0\) and by assumption \({\mathfrak {m}}^j_0 >0\) for every j, we denote
On the other side,
with \(\bar{{\bar{\gamma }}}_{i}\) introduced in (55). Thus, (127) becomes
Therefore, the choice
ensures the negative sign of the coefficient of the highest order term. Estimating
with \({\bar{\gamma }}\) from (56), we get the bound on the vector valued collision operator in terms of the polynomial moments of the vector valued distribution function,
Finally, the species-moment interpolation (111) for \({\mathfrak {m}}^i_k\) implies the moment interpolation for the \(k-\)th moment of the vector valued \({\mathbb {F}}\) by Hölder’s inequality,
which gives the lower bound for \( {\mathfrak {m}}_{k + {\bar{\gamma }}}\),
and therefore for (127) implies
which is exactly the desired estimate (124).
In addition, constants \({\tilde{K}}_1^{ij}[f_i,f_j]\) and \({\tilde{K}}_2^{ij}[f_i,f_j]\) in Remark 5.7 can be made explicit by plugging the choice of \(\varepsilon \) from (129), namely,
A simple comparison of the constants shows that the one driving the asymptotic behaviour in \(B_{k}\), as k increases, is the latter. Thus,
\(\square \)
6 Polynomial Moments a Priori Estimates on the Solution to the Boltzmann System
In this section, we prove a priori estimates on polynomial moments for the solution of the system of Boltzmann equations (3).
Proposition 6.1
(Moment ODI) Let \({\mathbb {F}}=[f_i]_{1\le i \le P} \ge 0\) be a solution of the system of Boltzmann equations (3) having the collision kernel satisfying assumptions listed in Sect. 4. The k-th polynomial moment of the system solution \({\mathbb {F}}\) satisfies the following ODIs,
-
(1)
For \(k>2\) and \({\mathbb {F}}\in L^1_k\),
$$\begin{aligned} \frac{\textrm{d}{\mathfrak {m}}_k[{\mathbb {F}}]}{\textrm{d}t} \le D_k \, {\mathfrak {m}}_{k}[{\mathbb {F}}], \end{aligned}$$(131) -
(2)
For \(k \ge {\bar{k}}_*\), \({\bar{k}}_*\) from (90), and for \({\mathbb {F}}\in L^1_{k+\bar{{\bar{\gamma }}}}\), \(\bar{{\bar{\gamma }}}\) from (56), with additionally \({\mathfrak {m}}^i_0[f_i]>0\) for each \(i=1,\dots ,P\). Then for any \({\bar{\gamma }}>0\) defined in (56),
$$\begin{aligned} \frac{\textrm{d}{\mathfrak {m}}_k[{\mathbb {F}}]}{\textrm{d}t} \le - A_{\star }\, {\mathfrak {m}}_2[{\mathbb {F}}]^{-\frac{{\bar{\gamma }}}{k-2}} \ {\mathfrak {m}}_{k}[{\mathbb {F}}]^{1+\frac{{\bar{\gamma }}}{k-2}} + B_k, \end{aligned}$$(132)
where explicit form of constants \({A}_\star >0\) and \(B_k, {D_k}\ge 0\) is given in Lemma 5.9.
Proof
The proof follows by taking \({\mathfrak {m}}_k\)-th moment of the Boltzmann system (3),
and applying the estimate on the collision operator polynomial moment (124). \(\square \)
Theorem 6.2
(Generation and propagation of polynomial moments) Let \({\mathbb {F}}\) satisfy assumptions of the Proposition 6.1 , then the following estimates hold,
-
(1)
(Polynomial moments generation estimate.) Define
$$\begin{aligned} E_{k}= {\mathfrak {m}}_2[{\mathbb {F}}]^{\frac{{\bar{\gamma }}}{k-2 + {\bar{\gamma }}}} \left( \frac{B_{k}}{A_{\star }} \right) ^{\frac{k-2}{k-2+{\bar{\gamma }}}}. \end{aligned}$$(134)Then for any \(k \ge {\bar{k}}_*\),
$$\begin{aligned} {\mathfrak {m}}_{k}[{\mathbb {F}}](t) \le {E}_{k} + {\mathfrak {m}}_2[{\mathbb {F}}] \left( \frac{k-2}{{\bar{\gamma }}A_{\star }} \right) ^\frac{k-2}{{\bar{\gamma }}} t^{-\frac{k-2}{{\bar{\gamma }}}}, \qquad \forall t>0, \end{aligned}$$(135)whereas for \(2< k < {\bar{k}}_*\),
$$\begin{aligned} {\mathfrak {m}}_k[{\mathbb {F}}](t) \le {\mathfrak {m}}_2[{\mathbb {F}}]^\frac{{\bar{k}}_*- k+1}{{\bar{k}}_*-1} \left( {E}_{{\bar{k}}_*+1}\right) ^{\frac{k-2}{{\bar{k}}_*-1}} + {\mathfrak {m}}_2[{\mathbb {F}}]^{\frac{1}{{\bar{k}}_*-1}} \left( \frac{{\bar{k}}_*-1}{{\bar{\gamma }}A_{\star }} \right) ^\frac{k-2}{{\bar{\gamma }}} t^{-\frac{k-2}{{\bar{\gamma }}}}, \qquad \forall t>0.\nonumber \\ \end{aligned}$$(136) -
(2)
(Polynomial moments propagation estimate.) Moreover, assume \( {\mathfrak {m}}_{k}[{\mathbb {F}}](0) < \infty \). Then for any \(k \ge {\bar{k}}_*\), the following estimate holds
$$\begin{aligned} {\mathfrak {m}}_{k}[{\mathbb {F}}](t) \le \max \left\{ E_{k}, {\mathfrak {m}}_{k}[{\mathbb {F}}](0) \right\} , \qquad \forall t\ge 0. \end{aligned}$$(137)Define
$$\begin{aligned} {\tilde{E}}_k = {\mathfrak {m}}_2^\frac{{\bar{k}}_*- k+1}{{\bar{k}}_*-1} \left( {E}_{{\bar{k}}_*+1}\right) ^{\frac{k-2}{{\bar{k}}_*-1}} + {\mathfrak {m}}_2^{\frac{1}{{\bar{k}}_*-1}} \left( \frac{{\bar{k}}_*-1}{{\bar{\gamma }}A_{\star }} \right) ^\frac{k-2}{{\bar{\gamma }}} D_k^{\frac{k-2}{{\bar{\gamma }}}}, \end{aligned}$$(138)with \(D_k\) from (126). Then for \(2<k<{\bar{k}}_*\),
$$\begin{aligned} {\mathfrak {m}}_{k}[{\mathbb {F}}]{(t)} \le \max \left\{ {\tilde{E}}_k, e \, {\mathfrak {m}}_{k}[{\mathbb {F}}](0) \right\} , \qquad \forall t{\ge }0. \end{aligned}$$(139)
Proof
The proof relies on the ODE comparison principle, already used in [2, 37]. First note that \({E}_k\) is the equilibrium solution of the associated upper ODE problem
where we abbreviated \({\mathfrak {m}}_{k}:= {\mathfrak {m}}_{k}[{\mathbb {F}}]\). If \(y(0) = {\mathfrak {m}}_{k}(0) < \infty \), then the propagation estimate (137) follows, since
The generation estimate is proven by constructing the function as in [37],
and applying the comparison principle for ODEs stated in the Lemma A.3 proved in [2] that yields the estimate on the solution of the moment ODI (132),
for \(k>{\bar{k}}_*\). For \(2< k < {\bar{k}}_*\), firstly the interpolation argument is used,
Then, for \({\mathfrak {m}}_{{\bar{k}}_*+1}\) we apply the inequality above (142) and get, since \((k-2)/({\bar{k}}_*-1)<1\),
The propagation result for \(2<k<{\bar{k}}_*\) firstly uses the ODI (131) which for short time implies
Then, for \(t>\frac{1}{D_k}\), use generation of moments (136) that yields
Taking the maximum of the two constants completes the proof. \(\square \)
7 Existence and Uniqueness Theory
In this section, we prove the existence and uniqueness theory for the Cauchy problem (3). To that end, we first define the set of initial data.
For \(i=1,\dots , P\), fix constants \(C^i_0, C_2, C_{\star }>0\), with
where \(\bar{{\bar{\gamma }}}\) is from (56) and \({\bar{k}}_*\) is introduced in (90). Then define the set \(\Omega \subseteq L^1_2\)
The following theorem holds.
Theorem 7.1
Let the collision kernel satisfy assumptions stated in Sect. 4 with \(\gamma _{ij}\) satisfying (55)–(56). Assume that \({\mathbb {F}}_0 \in \Omega \). Then the Cauchy problem (3) has a unique solution in \({\mathcal {C}}([0,\infty ), \Omega ) \cap {\mathcal {C}}^1((0,\infty ), L^1_2)\).
Our final result uses Theorem 7.1 to find solutions in the bigger space
Theorem 7.2
Let the collision kernel satisfy assumptions stated in Sect. 4 with \(\gamma _{ij}\) satisfying (55)–(56). Assume that \({\mathbb {F}}_0 \in {{\tilde{\Omega }}}\). Then the Cauchy problem (3) has a unique solution in \({\mathcal {C}}([0,\infty ), {{\tilde{\Omega }}}) \cap {\mathcal {C}}^1((0,\infty ), L^1_2)\).
Proof of Theorem 7.1
The goal is apply Theorem A.4 from the general ODE theory. For the collision operator \({\mathbb {Q}}\) understood as a mapping \({\mathbb {Q}}: \Omega \rightarrow L_{2}^1\), we will prove the following conditions for \({\mathbb {F}}, {\mathbb {G}}\in \Omega \),
-
(1)
Hölder continuity condition
$$\begin{aligned} \left\| {\mathbb {Q}}({\mathbb {F}}) - {\mathbb {Q}}({\mathbb {G}}) \right\| _{L^1_{2}} \le C_H \left\| {\mathbb {F}}-{\mathbb {G}}\right\| _{L^1_{2}}^{1/2}, \end{aligned}$$(146)with the constant \(C_H = 6 \, C_{\star }^{3/2} \max _{1 \le i, j \le P}(\kappa _{ij}^{ub})\),
-
(2)
Sub-tangent condition
$$\begin{aligned} \lim \limits _{h\rightarrow 0+} \frac{\text {dist}\left( {\mathbb {F}}+ h {\mathbb {Q}}({\mathbb {F}}), \Omega \right) }{h} =0, \quad \text {with} \quad \text {dist}\left( {\mathbb {G}},\Omega \right) =\inf _{\omega \in \Omega } \left\| {\mathbb {G}}-\omega \right\| _{L_{2}^1}. \end{aligned}$$ -
(3)
One-sided Lipschitz condition
$$\begin{aligned} \left[ {\mathbb {F}}- {\mathbb {G}}, {\mathbb {Q}}({\mathbb {F}}) - {\mathbb {Q}}({\mathbb {G}}) \right] \le C_L \left\| {\mathbb {F}}-{\mathbb {G}}\right\| _{L^1_{2}}, \end{aligned}$$(147)with the constant \(C_L = { 2} \, C_{\star }\, \max _{1 \le i, j \le P}(\kappa _{ij}^{ub})\), where brackets are defined in (190).
\(\square \)
Hölder continuity condition Firstly, we introduce some notation, namely,
Then, we notice that the bi-linear structure of all collision operators allows to write
for any possible combination of \(i, j \in \left\{ 1, \dots , P \right\} \), and with the notation (148), (2). Therefore, the left-hand side of (146) becomes
For each combination of i and j we proceed separately.
Case (i): mono–mono interactions Let \(i, j\in \left\{ 1, \dots , M\right\} \) and take generic real-valued functions f and g. The norm of the collision operator (4) is estimated as follows
For the first term \(T_1\), coming from the gain part, for the weight we use the estimate (186) and for the collision kernel \( {\mathcal {B}}_{ij}:={\mathcal {B}}_{ij}(v, v_*, \sigma )\) we use the microreversibility property (7) together with the assumption on its form (57), (59) and again (186),
It remains to interchange pre-post variables and obtain
For the second term \(T_2\) in (151) coming from the loss term, we only make use of the collision kernel form (57), (59) together with the estimate (186), which together lead to
and
Therefore, gathering (152) and (153), and using monotonicity of norms in (153), (151) becomes
For one part of the sum in (150), this implies
in the light of (69).
Case (ii): poly–mono and mono–poly interactions From the sum in (150), we split the terms involving different types of indices,
For the first two terms, using definition of the collision operator (41) describing mono-poly interaction, for some \(f=f(t,v,I)\) and \(g=g(t,v)\), its \(L^1_{2,j}\) norm can be estimated as follows,
Interchanging the collision reference using the transformation (38) and exploring micro-reversibility of the collision kernel (42),
For the first term \(T_3\), we additionally interchange pre- and post-quantities with transformation \({\mathcal {T}}_{pm}\) and using Lemma 2.1, after the use of estimates (60), (62) on the collision kernel \({\mathcal {B}}_{ij}:={\mathcal {B}}_{ij}(v, v_*, I, \sigma , R)\) and on the weight (187) that yield
Therefore,
For the second term \(T_4\), we only use the estimate on \({\mathcal {B}}_{ij}\) from (60), (62) and (187),
implying
Therefore, (157) and (158) imply for (156), after the use of norm monotonicity (53),
On the other side, for the last two terms of (155), we use the collision operator (39) that describes poly-mono interaction, and estimate its \(L^1_{2,i}\) norm for some \(f=f(t,v,I)\) and \(g=g(t,v)\),
Incorporating the same arguments as for the counterpart term (156) since the same collision kernel is used with assumptions (60), (62) and the same upper bounds apply to the weight \(\langle v_* \rangle _j\) in that context, and to the weight \(\langle v, I \rangle _i\) in the present one, by virtue of (187), it yields
Finally, (159) and (160) allow to conclude for (155),
with \(\kappa _{ij}\) from (67).
Case (iii): poly–poly interactions For interactions involving only polyatomic molecules, \(i, j \in \left\{ M+1, \dots , P \right\} \), the \(L^1_{2,i}\) norm of the corresponding collision operator (18) for some real-valued functions f, g can be estimated as follows
Using the same strategy as in the previous paragraphs which involves the assumption on the collision kernel (63) and (65) together with the upper bounds (188), we obtain
after exploiting the monotonicity of norms (53). Thus, the part of the sum in (150) related to only polyatomic interaction becomes
Summarizing (154), (161) and (162), the left-hand side of the Hölder condition (150) becomes
with \(\bar{{\bar{\gamma }}}\) from (56). Interpolating the \((2+\bar{{\bar{\gamma }}})\)-th norm of \({\mathbb {H}}\),
Since \({\mathbb {F}}, {\mathbb {G}}\) are non-negative, it follows \(|h_i| \le f_i + g_i = l_i\), and therefore
by monotonicity of norms. Since \({\mathbb {F}}, {\mathbb {G}}\in \Omega \), it implies
This allows to finally conclude for (150)
which is exactly (146) with the constant as announced.
Sub-tangent condition As shown in [2], the sub-tangent condition follows from the lemma below.
Lemma 7.3
Fix \( {\mathbb {F}}\in \Omega \). Then for any \(\varepsilon > 0\) there exists \(h_*>0\) such that the set B centered at \({\mathbb {F}}+h \, {\mathbb {Q}}({\mathbb {F}})\) with radius \(h \, \varepsilon \) denoted by \( B(f+h Q(f,f), h \epsilon ), \) has a non-empty intersection with \(\Omega \)
Proof
For \( \rho >0\) to be determined later, we define sets depending on the index i,
For the fixed \({\mathbb {F}}\in \Omega \), we define its truncation function
In the spirit of [2], we construct the function of the form
such that for a certain choice of \(\rho \) and h, it is an element of the intersection (164).
Firstly, we prove that \({\mathbb {W}}_\rho \) is non-negative on a certain interval for h. To that end, for \(i \in \left\{ 1, \dots , M \right\} \), we define the collision frequency and develop its upper bound, by virtue of the assumption on the collision kernels stated in Sect. 4 and Lemma A.1,
with the constant
Since for \(v \in B_i(\rho )\) is \(\langle v\rangle _i^2 \le 1 + \rho ^2\), the estimate (167) combined with the truncated function (165) yields
For \(i \in \left\{ M+1, \dots , P \right\} \), the same computations lead to the upper bound for the collision frequency,
which combined with the truncated function (165) implies, by \(\langle v, I \rangle _i \le 1 + \rho ^2\) for \((v, I) \in B_i(\rho )\),
For \({\mathbb {W}}_\rho \), (169) and (170) yield positivity of \({\mathbb {W}}_\rho \) for certain h,
for the choice of h as follows, defining \(h_*\) from the lemma’s statement,
Conservative properties of the collision operator \({\mathbb {Q}}\) imply
In order to show the boundness of \({\mathfrak {m}}_{k_*}[{\mathbb {W}}_\rho ]\), the bound on \( {\mathfrak {m}}_k[{\mathbb {Q}}({\mathbb {F}})] \) is recalled (124),
Incorporating arguments of [2], the map \({\mathcal {L}}_k: [0, \infty ) \rightarrow {\mathbb {R}}\) has only one root given in (134) at which it changes from positive to negative and its maximal value is achieved at \(B_k\), i.e. \({\mathcal {L}}_k(x) \le B_k\), for any \(x \in [0, \infty )\). In particular, for \(k=k_*\), and assuming \({\mathfrak {m}}_{k_*}[{\mathbb {F}}]\le E_{k_*}\), for \({\mathbb {W}}_\rho \) we get
Otherwise, in the case \({\mathfrak {m}}_{k_*}[{\mathbb {F}}] > E_{k_*}\), we take sufficiently large \(\rho \) to ensure
leading to
Thus, we conclude \( {\mathfrak {m}}_{k_*}[{\mathbb {W}}_\rho ] \le C_{\star }\), which together with (171) and (173) implies \({\mathbb {W}}_\rho \in \Omega \) for sufficiently large \(\rho \) to have (174) and h as defined in (172).
On the other side, for this element \({\mathbb {W}}_\rho \in \Omega \), by the Hölder property (146),
for sufficiently large \(\rho \).
Therefore, we conclude that \({\mathbb {W}}_\rho \) as defined in (166) for \(\rho \) sufficiently large to ensure both (174) and (175) and the corresponding h from (172) is an intersection element of \(\Omega \) and \( B({\mathbb {F}}+h \, {\mathbb {Q}}({\mathbb {F}}), h \, \varepsilon )\), proving (164) and concluding this lemma and the sub-tangent condition. \(\square \)
One-sided Lipschitz condition Denote the vector valued \(\chi \) such that \(\chi _i(\cdot ) = \text {sign}( (f_i - g_i)(\cdot ) ) \langle \cdot \rangle _i^2\), where the argument is either v for \(i\in \left\{ 1, \dots ,M \right\} \) or (v, I) for \(i\in \left\{ M+1, \dots , P\right\} \). Definition of the brackets (190) yields
The bi-linear structure of the collision operator (149) with the notation (148) together with the weak form (46) imply
with notation
First take \(i, j \in \left\{ 1, \dots , M \right\} \). Conservation law of the energy (8) implies the following bound
The same computations are performed with brackets that include internal energy, for solely polyatomic interactions \(i, j \in \left\{ M+1, \dots , P \right\} \). For \( j \in \left\{ 1, \dots , M \right\} \) and \(i \in \left\{ M+1, \dots , P \right\} \),
These estimates imply for (176),
Using upper bounds on the collision kernels as stated in Sect. 4 and Lemma A.2, together with the upper bounds on \(\gamma _{ij}\) from (56),
since \({\mathbb {F}}, {\mathbb {G}}\in \Omega \) and \(\bar{{\bar{\gamma }}}\le 2\). This concludes the proof. \(\square \)
The idea of the proof of Theorem 7.2 is to use the fact that the Boltzmann operator is one-sided Lipschitz assuming only \((2 + \bar{{\bar{\gamma }}}- {\bar{\gamma }})^+\) moments, thus, an approximating sequence of solutions can be drawn from Theorem 7.1 and pass to the limit. This follows a similar, but perhaps more direct, idea from [43] and can be found in detail in [2, Lemma 23].
Proof of Theorem 7.2
Let \(0\le {\mathbb {F}}_0\in {{\tilde{\Omega }}}\). Then, by density, there exits an approximating sequence \(\{{\mathbb {F}}^{j}_0\} \subset \Omega \) to \({\mathbb {F}}_0\), say strongly in \(L^1({{\tilde{\Omega }}})\). Now, following the computations performed for the one-sided Lipschitz condition and the inequality (178), it holds that, for any \(j\,,\,l\in {\mathbb {N}}\),
where \({\mathbb {F}}^j\) is the solution to the Boltzmann problem associated to the initial condition \({\mathbb {F}}^j_0\), given in Theorem 7.1 and brackets are defined in (190). Use moment interpolation formula (110) together with the Hölder inequality to control the norm
choosing for any \(\varepsilon \in (0,{\bar{\gamma }})\)
and taking \(\varepsilon \) sufficiently small such that \(2 < 2+k_1 = (2 + \bar{{\bar{\gamma }}}- {\bar{\gamma }})^+\). Consequently, it follows by propagation of moments, estimates (137) or (139), that
In this inequality we used that \(\max \big \{ {\mathfrak {m}}_{2+k_1}[{\mathbb {F}}^{j}_0], {\mathfrak {m}}_{2+k_1}[{\mathbb {F}}^{l}_0]\big \}\le 2\,{\mathfrak {m}}_{2+k_1}[{\mathbb {F}}_0]\), taking j and \(l\in {\mathbb {N}}\) sufficiently large if necessary. Also, this choice of \(k_1\) and \(k_2\) implies that
which leads, thanks to generation of moments (estimates (135) or (136)), that
and consequently,
Then, performing integration in (180) it holds that
Since \(\{{\mathbb {F}}^{j}_0\}\) is Cauchy in \(L^{1}_{2}\), previous estimate implies that \(\{{\mathbb {F}}^{j}(t)\}\) is Cauchy in \(L^{\infty }([0,T),L^{1}_{2})\) for any \(T>0\) and, as such, there is a strong limit \({\mathbb {F}}\) for such sequence. The theorem follows after passing to the limit since the limit \({\mathbb {F}}\) solves the mixture system with associated initial datum \({\mathbb {F}}_0\). The fact that \({\mathbb {F}}\in {\mathcal {C}}([0,\infty ), {{\tilde{\Omega }}}) \cap {\mathcal {C}}^1((0,\infty ), L^1_2)\) follows a standard argument. \(\square \)
Data Availibility Statement
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
References
Alonso, R., Bagland, V., Cheng, Y., Lods, B.: One-dimensional dissipative Boltzmann equation: measure solutions, cooling rate, and self-similar profile. SIAM J. Math. Anal. 50(1), 1278–1321 (2018)
Alonso, R.J., Gamba, I.M.: The Boltzmann equation for hard potentials with integrable angular transition: coerciveness, exponential tails rates, and Lebesgue integrability. ArXiv. 2211.09188 (2023)
Alonso, R.J., Lods, B.: Free cooling and high-energy tails of granular gases with variable restitution coefficient. SIAM J. Math. Anal. 42(6), 2499–2538 (2010)
Alonso, R.J., Orf, H.: Statistical moments and integrability properties of monatomic gas mixtures with long range interactions. ArXiv: 2204.09160 (2022)
Baranger, C., Bisi, M., Brull, S., Desvillettes, L.: On the Chapman-Enskog asymptotics for a mixture of monoatomic and polyatomic rarefied gases. Kinet. Relat. Models 11(4), 821–858 (2018)
Bernhoff, N.: Compactness property of the linearized Boltzmann collision operator for a mixture of monatomic and polyatomic species. ArXiv: 2303.05845 (2023)
Bernhoff, N.: Linearized Boltzmann collision operator: I. Polyatomic molecules modeled by a discrete internal energy variable and multicomponent mixtures. Acta Appl. Math. 183, 3 (2023)
Bernhoff, N.: Linearized Boltzmann collision operator: II. Polyatomic molecules modeled by a continuous internal energy variable. Kinet. Relat. Models 16(6), 828–849 (2023)
Bisi, M., Borsoni, T., Groppi, M.: An internal state kinetic model for chemically reacting mixtures of monatomic and polyatomic gases. Kinetic Relat. Models (2023)
Bobylev, A.V.: Moment inequalities for the Boltzmann equation and applications to spatially homogeneous problems. J. Stat. Phys. 88(5–6), 1183–1214 (1997)
Bobylev, A.V., Gamba, I.M., Panferov, V.A.: Moment inequalities and high-energy tails for Boltzmann equations with inelastic interactions. J. Stat. Phys. 116(5–6), 1651–1682 (2004)
Bondesan, A., Boudin, L., Briant, M., Grec, B.: Stability of the spectral gap for the Boltzmann multi-species operator linearized around non-equilibrium Maxwell distributions. Commun. Pure Appl. Anal. 19(5), 2549–2573 (2020)
Borgnakke, C., Larsen, P.S.: Statistical collision model for Monte Carlo simulation of polyatomic gas mixture. J. Comput. Phys. 18(4), 405–420 (1975)
Borsoni, T., Bisi, M., Groppi, M.: A general framework for the kinetic modelling of polyatomic gases. Commun. Math. Phys. 393, 215–266 (2022)
Borsoni, T., Boudin, L., Salvarani, F.: Compactness property of the linearized Boltzmann operator for a polyatomic gas undergoing resonant collisions. J. Math. Anal. Appl. 517(1), 126579 (2023)
Boudin, L., Grec, B., Pavan, V.: The Maxwell-Stefan diffusion limit for a kinetic model of mixtures with general cross sections. Nonlinear Anal. 159, 40–61 (2017)
Boudin, L., Grec, B., Pavić, M., Salvarani, F.: Diffusion asymptotics of a kinetic model for gaseous mixtures. Kinet. Relat. Models 6(1), 137–157 (2013)
Boudin, L., Grec, B., Pavić-Čolić, M., Simić, S.: Energy method for the Boltzmann equation of monatomic gaseous mixtures. Commun. Math. Sci., 22(1), 137–166 (2024)
Boudin, L., Rossi, A., Salvarani, F.: A kinetic model of polyatomic gas with resonant collisions. Ric. Mat. (2022)
Bourgat, J.-F., Desvillettes, L., Le Tallec, P., Perthame, B.: Microreversible collisions for polyatomic gases and Boltzmann’s theorem. Eur. J. Mech. B Fluids 13(2), 237–254 (1994)
Bressan, A.: Notes on the Boltzmann Equation. S.I.S.S.A, Lecture Notes for a Summer Course (2005)
Briant, M.: Stability of global equilibrium for the multi-species Boltzmann equation in \(L^\infty \) settings. Discret. Contin. Dyn. Syst. 36(12), 6669–6688 (2016)
Briant, M., Daus, E.S.: The Boltzmann equation for a multi-species mixture close to global equilibrium. Arch. Ration. Mech. Anal. 222(3), 1367–1443 (2016)
Brull, S., Shahine, M., Thieullen, P.: Compactness property of the linearized Boltzmann operator for a diatomic single gas model. Netw. Heterog. Med. 17(6), 847–861 (2022)
Brull, S., Shahine, M., Thieullen, P.: Fredholm property of the linearized Boltzmann operator for a polyatomic single gas model. Kinet. Relat. Models (2023)
Daus, E.S., Jüngel, A., Mouhot, C., Zamponi, N.: Hypocoercivity for a linearized multispecies Boltzmann system. SIAM J. Math. Anal. 48(1), 538–568 (2016)
de la Canal, E., Gamba, I.M., Pavić-Čolić, M.: On existence, uniqueness and Banach space regularity for solutions of Boltzmann equations systems for monatomic gas mixtures. From particle systems to partial differential equations. Springer Proc. Math. Stat. 352, 99–121 (2021)
Desvillettes, L.: Some applications of the method of moments for the homogeneous Boltzmann and Kac equations. Arch. Ration. Mech. Anal. 123(4), 387–404 (1993)
Desvillettes, L.: Sur un modèle de type Borgnakke-Larsen conduisant à des lois d’energie non-linéaires en température pour les gaz parfaits polyatomiques. Ann. Fac. Sci. Toulouse Math. 6, 257–262 (1997)
Desvillettes, L., Monaco, R., Salvarani, F.: A kinetic model allowing to obtain the energy law of polytropic gases in the presence of chemical reactions. Eur. J. Mech. B Fluids 24(2), 219–236 (2005)
Djordjić, V., Oblapenko, G., Pavić-Čolić, M., Torrilhon, M.: Boltzmann collision operator for polyatomic gases in agreement with experimental data and DSMC method. Contin. Mech. Thermodyn. 35(1), 103–119 (2023)
Djordjić, V., Pavić-Čolić, M., Spasojević, N.: Polytropic gas modelling at kinetic and macroscopic levels. Kinet. Relat. Models 14(3), 483–522 (2021)
Djordjić, V., Pavić-Čolić, M., Torrilhon, M.: Consistent, explicit and accessible Boltzmann collision operator for polyatomic gases. Phys. Rev. E 104, 025309 (2021)
Duan, R., Li, Z.: Global bounded solutions to the Boltzmann equation for a polyatomic gas. Int. J. Math. 34(7), 2350036 (2023)
Gamba, I.M., Panferov, V., Villani, C.: Upper Maxwellian bounds for the spatially homogeneous Boltzmann equation. Arch. Ration. Mech. Anal. 194(1), 253–282 (2009)
Gamba, I.M., Pavić-Čolić, M.: On existence and uniqueness to homogeneous Boltzmann flows of monatomic gas mixtures. Arch. Ration. Mech. Anal. 235(1), 723–781 (2020)
Gamba, I.M., Pavić-Čolić, M.: On the Cauchy problem for Boltzmann equation modeling a polyatomic gas. J. Math. Phys. 64, 013303 (2023)
Gamba, I.M., Smith, L.M., Tran, M.-B.: On the wave turbulence theory for stratified flows in the ocean. Math. Models Methods Appl. Sci. 30(1), 105–137 (2020)
Giovangigli, V.: Multicomponent Flow Modeling. Modeling and Simulation in Science, Engineering and Technology. Birkhäuser Boston, Inc., Boston, MA (1999)
Groppi, M., Spiga, G.: Kinetic approach to chemical reactions and inelastic transitions in a rarefied gas. J. Math. Chem. 26, 197–219 (1999)
Lu, X., Mouhot, C.: On measure solutions of the Boltzmann equation, part I: moment production and stability estimates. J. Differ. Equ. 252(4), 3305–3363 (2012)
Martin, R.H.: Jr. Nonlinear operators and differential equations in Banach spaces. Pure and Applied Mathematics. Wiley-Interscience [John Wiley & Sons], New York (1976)
Mischler, S., Wennberg, B.: On the spatially homogeneous Boltzmann equation. Ann. Inst. H. Poincaré C Anal. Non Linéaire, 16(4):467–501 (1999)
Nagnibeda, E., Kustova, E.: Non-equilibrium Reacting Gas Flows. Heat and Mass Transfer. Springer, Berlin (2009)
Pavić-Čolić, M., Tasković, M.: Propagation of stretched exponential moments for the Kac equation and Boltzmann equation with Maxwell molecules. Kinet. Relat. Models 11(3), 597–613 (2018)
Tasković, M., Alonso, R.J., Gamba, I.M., Pavlović, N.: On Mittag-Leffler moments for the Boltzmann equation for hard potentials without cutoff. SIAM J. Math. Anal. 50(1), 834–869 (2018)
Wennberg, B.: Entropy dissipation and moment production for the Boltzmann equation. J. Stat. Phys. 86(5–6), 1053–1066 (1997)
Acknowledgements
R. J. Alonso was supported by the Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq), grant Bolsa de Produtividade em Pesquisa (303325/2019-4). M. Čolić gratefully acknowledges the support from the Science Fund of the Republic of Serbia, PROMIS, #6066089, MaKiPol and the Ministry of Education, Science and Technological Development of the Republic of Serbia #451-03-47/2023-01/200125, as well as from the Alexander von Humboldt Foundation. I. M. Gamba was supported by USA grants from the National Science Foundation DMS-2009736, and the Department of Energy grant DESC0016283 on Simulation Center for Runaway Electron Avoidance and Mitigation.
Funding
Open Access funding provided by the Qatar National Library.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of interest
The authors have no relevant financial or non-financial interests to disclose.
Additional information
Communicated by Clement Mouhot.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A.
Appendix A.
Lemma A.1
(Bounds on the collision kernels) For the collision kernels (59), (62), (65) the following estimates hold,
where the involved constant \(L_{ij}\) does not depend on the nature of interactions, but only on mass species and the rate \(\gamma _{ij}\),
with \({\bar{s}}_{ij}\) as defined in (71).
Proof
Let \(i, j \in \left\{ M+1, \dots , P \right\} \).
Upper bound Since the total energy in center-of-mass framework is only a part of the total energy in particles’ framework, due to
with \(E_{ij}\) from (65), it follows
Since \(\gamma _{ij}/2 \le 1\),
as stated in (183).
Lower bound Triangle inequality \(| v- v_* | \ge |v| - |v_*|\) and few rearrangements imply
Thus,
Taking the last inequality to the power \(\gamma _{ij}\),
implying
proving (183).
For other types of interactions, similar computations can be performed. \(\square \)
Lemma A.2
Let the energy in the center-of-mass framework \(E_{ij}\) be (10), (23) and (14) depending on different combinations of \(i, j \in \left\{ 1, \dots , P\right\} \) or nature of particles’ interaction. The following estimates hold,
Proof
Let \(j \in \left\{ 1,\ldots ,M\right\} \), \(i \in \left\{ M+1,\ldots ,P \right\} \). From (23) it follows
The conservation law of the energy (22) implies
which yields
Taking the square root, we get (187).
For other combinations of i and j similar computations can be performed to conclude the proof. \(\square \)
Lemma A.3
(ODI’s Comparison Lemma for Moments Generation, [2]) Let A, B and c be positive constants and consider a function y(t) which is absolute continuous in \(t \in (0, \infty )\) and satisfies
Then
for the choice
Proof
We start noticing that
and that
For the latter we invoked the binomial inequality \(( 1+ \frac{K}{t^\beta } )^{1+c} \ge 1+ (\frac{K}{t^\beta })^{1+c}\). With the choice of \(E,\,\beta \) and K as suggested in the statement of the lemma it follows then
Next, note that for any \(\epsilon >0\) the translation \(z_\epsilon (t):=z(t-\epsilon )\) satisfies (189) for \(t>\epsilon \) due to the time invariance of the inequality. Moreover, since y(t) is absolute continuous in \(t\in [\epsilon ,\infty )\), there exists \(\delta _*>0\) such that \(z_{\epsilon }(\epsilon +\delta )\ge y(\epsilon +\delta )\) for any \(\delta \in (0,\delta _*]\). Consequently, we conclude the following setting for any \(\epsilon >0\) and \(\delta \in (0,\delta _*]\)
Since both \(z_\epsilon (t)\) and y(t) are absolutely continuous in \(t\in [\epsilon +\delta ,\infty )\), we can use a standard comparison in ODE to conclude that \(z_\epsilon (t)\ge y(t)\) for \(t>\epsilon +\delta \), valid for any \(\epsilon >0\) and \(\delta \in (0,\delta _*]\). Thus, sending first \(\delta \) to zero and then \(\epsilon \) to zero it follows that \(z(t)\ge y(t)\) for any \(t>0\) which is the statement of the lemma. \(\square \)
Theorem A.4
(Existence and Uniqueness Theory for ODE in Banach spaces) Let \(E:=(E,\left\| \cdot \right\| )\) be a Banach space, \({\mathcal {S}}\) be a bounded, convex and closed subset of E, and \({\mathcal {Q}}:{\mathcal {S}}\rightarrow E\) be an operator satisfying the following properties:
-
(a)
Hölder continuity condition
$$\begin{aligned} \left\| {\mathcal {Q}}[u] - {\mathcal {Q}}[v] \right\| \le C \left\| u-v \right\| ^{\beta }, \ \beta \in (0,1), \ \forall u, v \in {\mathcal {S}}; \end{aligned}$$ -
(b)
Sub-tangent condition
$$\begin{aligned} \lim \limits _{h\rightarrow 0+} \frac{\text {dist}\left( u + h {\mathcal {Q}}[u], {\mathcal {S}} \right) }{h} =0, \ \forall u \in {\mathcal {S}}; \end{aligned}$$ -
(c)
One-sided Lipschitz condition
$$\begin{aligned} \left[ {\mathcal {Q}}[u] - {\mathcal {Q}}[v], u - v \right] \le C \left\| u-v \right\| , \ \forall u, v \in {\mathcal {S}}, \end{aligned}$$where \(\left[ \varphi ,\phi \right] =\lim _{h\rightarrow 0^-} h^{-1}\left( \left\| \phi + h \varphi \right\| - \left\| \phi \right\| \right) \).
Then the equation
has a unique solution in \(C([0,\infty ),{\mathcal {S}})\cap C^1((0,\infty ),E)\).
The proof of this Theorem on ODE flows on Banach spaces can be found in [2]. As pointed out in [2], for \(E:=L_{2}^1\), the Lipschitz brackets are
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Alonso, R.J., Čolić, M. & Gamba, I.M. The Cauchy Problem for Boltzmann Bi-linear Systems: The Mixing of Monatomic and Polyatomic Gases. J Stat Phys 191, 9 (2024). https://doi.org/10.1007/s10955-023-03221-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10955-023-03221-4
Keywords
- System of Boltzmann equations
- Compact manifold averaging
- Statistical moment estimates for bi-linear integral forms
- Multi-component gas mixtures