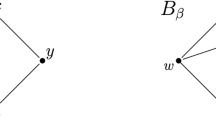Abstract
We use the lace expansion to prove an infra-red bound for site percolation on the hypercubic lattice in high dimension. This implies the triangle condition and allows us to derive several critical exponents that characterize mean-field behavior in high dimensions.
Similar content being viewed by others
1 Introduction
1.1 Site Percolation on the Hypercubic Lattice
We consider site percolation on the hypercubic lattice \(\mathbb Z^d\), where sites are independently occupied with probability \(p\in [0,1]\), and otherwise vacant. More formally, for \(p \in [0,1]\), we consider the probability space \((\Omega , \mathcal F, \mathbb P_p)\), where \(\Omega = \{0,1\}^{\mathbb Z^d}\), the \(\sigma \)-algebra \(\mathcal F\) is generated by the cylinder sets, and \(\mathbb P_p= \bigotimes _{x\in \mathbb Z^d} \text {Ber}(p)\) is a product-Bernoulli measure. We call \(\omega \in \Omega \) a configuration and say that a site \(x\in \mathbb Z^d\) is occupied in \(\omega \) if \(\omega (x)=1\). If \(\omega (x)=0\), we say that the site x is vacant. For convenience, we identify \(\omega \) with the set of occupied sites \(\{x\in \mathbb Z^d: \omega (x)=1\}\).
Given a configuration \(\omega \), we say that two points \(x \ne y\in \mathbb Z^d\) are connected and write \(x \longleftrightarrow y\) if there is an occupied path between x and y—that is, there are points \(x=v_0, \ldots , v_k=y\) in \(\mathbb Z^d\) with \(k\in \mathbb N_0 := \mathbb N\cup \{0\}\) such that \(| v_i-v_{i-1}| = 1\) (with \(|y| = \sum _{i=1}^{d} |y_i|\) the 1-norm) for all \(1 \le i \le k\), and \(v_i\in \omega \) for \(1 \le i \le k-1\) (i.e., all inner sites are occupied). Two neighbors are automatically connected (i.e., \(\{x \longleftrightarrow y\}=\Omega \) for all x, y with \(|x-y|=1\)). Many authors prefer a different definition of connectivity by requiring both endpoints to be occupied as well. These two notions are closely related and we explain our choice in Sect. 1.4. Moreover, we adopt the convention that \(\{x \longleftrightarrow x\}=\varnothing \), that is, x is not connected to itself.
We define the cluster of x to be \(\mathscr {C}(x):= \{x\} \cup \{y \in \omega : x \longleftrightarrow y\}\). Note that apart from x itself, points in \(\mathscr {C}(x)\) need to be occupied. We also define the expected cluster size (or susceptibility) \(\chi (p) = \mathbb E_p[|\mathscr {C}(\mathbf {0})|]\), where for a set \(A \subseteq \mathbb Z^d\), we let |A| denote the cardinality of A, and \(\mathbf {0}\) the origin in \(\mathbb Z^d\).
We define the two-point function \(\tau _p:\mathbb Z^d\rightarrow [0,1]\) by
The percolation probability is defined as \(\theta (p) := \mathbb P_p(\mathbf {0}\longleftrightarrow \infty ) = \mathbb P_p( | \mathscr {C}(\mathbf {0})| = \infty )\). We note that \(p \mapsto \theta (p)\) is increasing and define the critical point for \(\theta \) as
Note that we can define a critical point \(p_c(G)\) for any graph G. As we only concern ourselves with \(\mathbb Z^d\), we write \(p_c\) or \(p_c(d)\) the refer to the critical point of \(\mathbb Z^d\).
1.2 Main Result
The triangle condition is a versatile criterion for several critical exponents to exist and to take on their mean-field value. In order to introduce this condition, we define the open triangle diagram as
and the triangle diagram as \(\triangle _p = \sup _{x \in \mathbb Z^d} \triangle _p(x)\). In the above, the convolution ‘\(*\)’ is defined as \((f*g)(x) = \sum _{y\in \mathbb Z^d} f(y) g(x-y)\). We also set \(f^{*j} =f^{*(j-1)} *f\) and \(f^{*1} \equiv f\). The triangle condition is the condition that \(\triangle _{p_c} <\infty \). To state Theorem 1.1, we recall that the discrete Fourier transform of an absolutely summable function \(f:\mathbb Z^d\rightarrow \mathbb R\) is defined as \(\widehat{f}:(-\pi ,\pi ]^d\rightarrow \mathbb C\) with
where \(k\cdot x = \sum _{j=1}^{d} k_j x_j\) denotes the scalar product. Letting \(D(x) = \tfrac{1}{2d} \mathbbm {1}_{\{|x|=1\}}\) for \(x\in \mathbb Z^d\) be the step distribution of simple random walk, we can formulate our main theorem:
Theorem 1.1
(The triangle condition and the infra-red bound) There exist \(d_0 \ge 6\) and a constant \(C=C(d_0)\) such that, for all \(d > d_0\),
for all \(k \in (-\pi , \pi ]^d\) uniformly in \(p \in [0,p_c]\) (we interpret the right-hand side of (1.1) as \(\infty \) for \(k=0\)). Additionally, \(\triangle _p \le C/d\) uniformly in \([0, p_c]\), and the triangle condition holds.
1.3 Consequences of the Infra-Red Bound
The triangle condition is the classical criterion for mean-field behavior in percolation models. The triangle condition implies readily that \(\theta (p_c)=0\) (since otherwise \(\triangle _{p_c}\) could not be finite), a problem that is still open in smaller dimension (except \(d=2\)).
Moreover, the triangle condition implies that a number of critical exponents take on their mean-field values. Indeed, using results by Aizenman and Newman [1, Section 7.7], the triangle condition implies that the critical exponent \(\gamma \) exists and takes its mean-field value 1, that is
for \(p<p_c\) and constants \(0<c<C\). We write \(\chi (p) \sim (p_c-p)^{-1}\) as \(p\nearrow p_c\) for the behavior of \(\chi \) as in (1.2). There are several other critical exponents that are predicted to exist. For example, \(\theta (p) \sim (p-p_c)^\beta \) as \(p \searrow p_c\), and \(\mathbb P_{p_c}(|\mathscr {C}(\mathbf {0})| \ge n) \sim n^{-1/\delta }\) as \(n\rightarrow \infty \).
Barsky and Aizenman [2] show that under the triangle condition,
Their results are stated for a class of percolation models including site percolation. Hence, Theorem 1.1 implies (1.3). However, “for simplicity of presentation”, the presentation of the proofs is restricted to bond percolation models.
Moreover, as shown by Nguyen [22], Theorem 1.1 implies that \(\Delta =2\), where \(\Delta \) is the gap exponent.
1.4 Discussion of Literature and Results
Percolation theory is a fundamental part of contemporary probability theory and its foundations are generally attributed to a 1957 paper of Broadbent and Hammersley [6]. Meanwhile, a number of textbooks appeared, and we refer to Grimmett [10] for a comprehensive treatment of the subject, as well as Bollobás and Riordan [4], Werner [27] and Beffara and Duminil-Copin [3] for extra emphasis on the exciting recent progress in two-dimensional percolation.
The investigation of percolation in high dimensions was started by the seminal 1990 paper of Hara and Slade [12], who applied the lace expansion to prove the triangle condition for bond percolation in high dimension. A number of modifications and extensions of the lace expansion method for bond percolation have appeared in the meantime. The expansion itself is presented in Slade’s Saint Flour notes [24]. A detailed account of the full lace expansion proof for bond percolation (including convergence of the expansion and related results) is given in a recent textbook by the first author and van der Hofstad [17].
Despite the fantastic understanding of bond percolation in high dimensions, site percolation is not yet analyzed with this method, and the present paper aims to remedy this situation. Together with van der Hofstad and Last [15], we recently applied the lace expansion to the random connection model, which can be viewed as a continuum site percolation model. The aim of this paper is to give a rigorous exhibition of the lace expansion applied to one of the simplest site percolation lattice models. We have chosen to set up the proofs in a similar fashion to corresponding work for bond percolation, making it easier to oversee by readers who are familiar with that literature. Indeed, Sects. 3 and 4 follow rather closely the well-established method in [5, 17, 18], which are all based on Hara and Slade’s foundational work [12]. Interestingly, there is a difference in the expansion itself, which has numerous repercussions in the diagrammatic bounds and also in the different form of the infrared bounds. We now explain these differences in more detail.
A key insight for the analysis of high-dimensional site percolation is the frequent occurrence of pivotal points, which are crucial for the setup of the lace expansion. Suppose two sites x and y are connected, then an intermediate vertex u is pivotal for this connection if every occupied path from x to y passes through u. We then break up the original connection event in two parts: a connection between x and u, and a second connection between u and y. In high dimension, we expect the two connection events to behave rather independently, except for their joint dependence on the occupation status of u. This little thought demonstrates that it is highly convenient to define connectivity events as in Sect. 1.1, and thus treat the occupation of the vertex u independent of the two new connection events. A more conventional choice of connectivity, where two points can only be connected if they are both occupied, is obtained a posteriori via
Our definition of \(\tau _p\) avoids divisions by p, not only in the triangle, but throughout Sects. 2 and 3.
Paying close attention to the right number of factors of p is a guiding thread of the technical aspects of Sects. 3 and 4 that sets site percolation apart from bond percolation. Like it is done in bond percolation, the diagrammatic events by which we bound the lace-expansion coefficients depend on quite a few more points than the pivotal points. In contrast, every pair of points among these that may coincide hides a case distinction, and a coincidence case leads to a new diagram, typically with a smaller number of factors of p (see, e.g., (3.2)). We handle this, for example, by encoding such coincidences in \(\tau _p^\circ \) and \(\tau _p^\bullet \) (which are variations of \(\tau _p\) respecting an extra factor of p and/or interactions at \(\mathbf {0}\)), see Definition 3.3. In Sect. 4, the mismatching number of p’s and \(\tau _p\)’s in \(\triangle _p\) needs to be resolved.
The differing diagrams in Sect. 3 due to coincidences already appear in the lace-expansion coefficients of small order. This manifests itself in the answer to a classical question for high-dimensional percolation; namely, to devise an expansion of the critical threshold \(p_c(d)\) when \(d\rightarrow \infty \). It is known in the physics literature that
The first four terms are due to Gaunt, Ruskin and Sykes [9], the latter two were found recently by Mertens and Moore [21] by exploiting involved numerical methods.
The lace expansion devised in this paper enables us to give a rigorous proof of the first terms of (1.5). Indeed, we use the representation obtained in this paper to show that
This is the content of a separate paper [14]. Deriving \(p_c\) expansions from lace expansion coefficients has been earlier achieved for bond percolation by Hara and Slade [13] and van der Hofstad and Slade [26]. Comparing (1.6) to their expansion for bond percolation confirms that already the second coefficient is different.
Proposition 4.2 proves the convergence of the lace expansion for \(p<p_c\), yielding an identity for \(\tau _p\) of the form
where C is the direct-connectedness function and \(C(\cdot )=2d D(\cdot ) + \Pi _p(\cdot )\) (for a definition of \(\Pi _p\), see Definition 2.8 and Proposition 4.2). In fluid-state statistical mechanics, (1.7) is known as the Ornstein–Zernike equation (OZE), a classical equation that is typically associated to the total correlation function.
We can juxtapose (1.7) with the converging lace expansion for bond percolation. There, \(\tau _p^{\text {bond}}(x)\) is the probability that \(\mathbf {0}\) and x are connected by a path of occupied bonds, and we have
where \(C^{\text {bond}}(x) = \mathbbm {1}_{\{x = \mathbf {0}\}} + \Pi _p^{\text {bond}}(x)\). Thus, there is an extra convolution with 2dD. Only for the site percolation two-point function (as defined in this paper), the lace expansion coincides with the OZE.
We want to touch on how this relates to the infra-red bound (1.1). To this end, define the random walk Green’s function as \(G_\lambda (x) = \sum _{m \ge 0} \lambda ^m D^{*m}(x)\) for \(\lambda \in (0,1]\). Consequently,
One of the key ideas behind the lace expansion for bond percolation is to show that the two-point function is close to \(G_\lambda \) in an appropriate sense (this includes an appropriate parametrization of \(\lambda \)). Solving the OZE in Fourier space for \({\widehat{\tau }}_p\) already hints at the fact that in site percolation, \(p{\widehat{\tau }}_p\) should be close to \( {\widehat{G}}_\lambda \widehat{D}\) and \(p\tau _p\) should be close to \(D*G_\lambda \). As a technical remark, we note that \({\widehat{G}}_\lambda \) is uniformly lower-bounded, whereas \({\widehat{G}}_\lambda {\widehat{D}}\) is not, which poses some inconvenience later on.
The complete graph may be viewed as a mean-field model for percolation, in particular when we analyze clusters on high-dimensional tori, cf. [16]. Interestingly, the distinction between bond and site percolation exhibits itself rather drastically on the complete graph: for bond percolation, we obtain the usual Erdős-Rényi random graph with its well-known phase transition (see, e.g., [19]), whereas for site percolation, we obtain again a complete graph with a binomial number of points.
Theorem 1.1 proves the triangle condition in dimension \(d> d_0\) for sufficiently large \(d_0\). It is folklore in the physics literature that \(d_0=6\) suffices (6 is the “upper critical dimension”) but the perturbative nature of our argument does not allow us to derive that. Instead, we only get the result for some \(d_0\ge 6\). For bond percolation, already the original paper by Hara and Slade [12] treated a second, spread-out version of bond percolation, and they proved that for this model, \(d_0=6\) suffices (under suitable assumption on the spread-out nature). For ordinary bond percolation, it was announced that \(d_0=19\) suffices for the triangle condition in [11], and the number 19 circulated for many years in the community. Finally, Fitzner and van der Hofstad [7] devised involved numerical methods to rigorously verify that an adaptation of the method is applicable for \(d > d_0=10\). It is clear that an analogous result of Theorem 1.1 would hold for “spread-out site percolation” in suitable form (see e.g. [17, Section 5.2]).
1.5 Outline of the Paper
The paper is organized as follows. The aim of Sect. 2 is to establish a lace-expansion identity for \(\tau _p\), which is formulated in Proposition 2.9. To this end, we use Sect. 2.1 to state some known results that we are going to make use of in Sect. 2 as well as in later sections. We then introduce a lot of the language and quantities needed to state Proposition 2.9 in Sect. 2.2, followed by the actual derivation of the identity in Sect. 2.3.
Section 3 bounds the lace-expansion coefficients derived in Sect. 2.3 in terms of simpler diagrams, which are large sums over products of two-point (and related) functions. Section 4 finishes the argument via the so-called bootstrap argument. First, a bootstrap function f is introduced in Sect. 4.1. Among other things, it measures how close \({\widehat{\tau }}_p\) is to \({\widehat{G}}_\lambda \) (in a fractional sense). Section 4.2 shows convergence of the lace expansion for fixed \(p<p_c\). Moreover, assuming that f is bounded on \([0,p_c)\), it is shown that this convergence is uniform in p (see first and second part of Proposition 4.2). Lastly, Sect. 4.3 actually proves said boundedness of f.
2 The Expansion
2.1 The Standard Tools
We require two standard tools of percolation theory, namely Russo’s formula and the BK inequality, both for increasing events. Recall that A is called increasing if \(\omega \in A\) and \(\omega \subseteq \omega '\) implies \(\omega ' \in A\). Given \(\omega \) and an increasing event A, we introduce
If A is an increasing event determined by sites in \(\Lambda \subset \mathbb Z^d\) with \(|\Lambda |<\infty \), then Russo’s formula [23], proved independently by Margulis [20], tells us that
To state the BK inequality, let \(\Lambda \subset \mathbb Z^d\) be finite and, given \(\omega \in \Omega \), let
be the cylinder event of the restriction of \(\omega \) to \(\Lambda \). For two events A, B, we can define the disjoint occurrence as
The BK inequality, proved by van den Berg and Kesten [25] for increasing events, states that, given two increasing events A and B,
The following proposition about simple random walk will be of importance later:
Proposition 2.1
(Random walk triangle, [17], Proposition 5.5) Let \(m \in \mathbb N_0, n\ge 0\) and \(\lambda \in [0,1]\). Then there exists a constant \(c_{2m,n}^{\text {(RW)}}\) independent of d such that, for \(d>2n\),
In [17], \(d>4n\) is required; however, more careful analysis shows that \(d>2n\) suffices (see [5, (2.19)]). We will also need the following related result:
Proposition 2.2
(Related random walk bounds, [17], Exercise 5.4) Let \(m \in \{0,1\}\), \(\lambda \in [0,1]\), and \(r,n \ge 0\) such that \(d>2(n+r)\). Then, uniformly in \(k\in (-\pi ,\pi ]^d\),
where the constants \(c^{\text {(RW)}}_{\cdot ,\cdot }\) are from Proposition 2.1.
The following differential inequality is an application of Russo’s formula and the BK inequality. It applies them to events which are not determined by a finite set of sites. We refer to the literature [17, Lemma 4.4] for arguments justifying this and for a more detailed proof. Observation 2.3 will be of use in Sect. 4.
Observation 2.3
Let \(p < p_c\). Then
As a proof sketch, note that
The inequality for \(\chi (p)\) follows from the identity \(\chi (p) = 1+p {\widehat{\tau }}_p(0)\).
2.2 Definitions and Preparatory Statements
We need the following definitions:
Definition 2.4
(Elementary definitions) Let \(x,u\in \mathbb Z^d\) and \(A \subseteq \mathbb Z^d\).
-
1.
We set \(\omega ^x := \omega \cup \{x\}\) and \(\omega ^{u,x} := \omega \cup \{u,x\}\).
-
2.
We define \(J(x) := \mathbbm {1}_{\{|x|=1\}} = 2d D(x)\).
-
3.
Let \(\{u \longleftrightarrow x\text { in } A\}\) be the event that \(\{u \longleftrightarrow x\}\), and there is a path from u to x, all of whose inner vertices are elements of \(\omega \cap A\). Moreover, write \(\{u \longleftrightarrow x\text { off } A\} :=\{u \longleftrightarrow x\text { in } \mathbb Z^d\setminus A\}\).
-
4.
We define \(\{u \Longleftrightarrow x\} := \{u \longleftrightarrow x\} \circ \{u \longleftrightarrow x\} \) and say that u and x are doubly connected.
-
5.
We define the modified cluster of x with a designated vertex u as
$$\begin{aligned} {\widetilde{\mathscr {C}}}^{u}(x) := \{x\} \cup \{y \in \omega \setminus \{u\} : x \longleftrightarrow y \text { in } \mathbb Z^d\setminus \{u\} \} . \end{aligned}$$ -
6.
For a set \(A \subset \mathbb Z^d\), define \(\langle A \rangle := A \cup \{y \in \mathbb Z^d: \exists x \in A \text { s.t.} ~|x-y| = 1\}\) as the set A itself plus its external boundary.
Definition 2.4.1 allows us to speak of events like \(\{a \longleftrightarrow b\text { in } \omega ^x\}\) for \(a,b\in \mathbb Z^d\), which is the event that a is connected to b in the configuration where x is fixed to be occupied. We remark that \(\{x \longleftrightarrow y\text { in } \mathbb Z^d\} = \{x \longleftrightarrow y\} = \{x \longleftrightarrow y\text { in } \omega \}\) and that \(\{u \Longleftrightarrow x\} = \Omega \) for \(|u-x| = 1\). Similarly, \(\{u \Longleftrightarrow x\} = \varnothing \) for \(u=x\). The following, more specific definitions are important for the expansion:
Definition 2.5
(Extended connection probabilities and events) Let \(v,u,x \in \mathbb Z^d\) and \(A \subseteq \mathbb Z^d\).
-
1.
Define

In words, this is the event that u is connected to x, but either any path from u to x has an interior vertex in \(\langle A \rangle \), or x itself lies in \(\langle A \rangle \).
-
2.
Define
$$\begin{aligned} \tau _p^{A}(u,x) := \mathbbm {1}_{\{x \notin \langle A \rangle \}}\mathbb P_p(u \longleftrightarrow x\text { off } \langle A \rangle ). \end{aligned}$$ -
3.
We introduce \(\textsf {Piv}(u,x) := \textsf {Piv}(u \longleftrightarrow x)\) as the set of pivotal points for \(\{u \longleftrightarrow x\}\). That is, \(v \in \textsf {Piv}(u,x)\) if the event \(\{u \longleftrightarrow x\text { in } \omega ^v\}\) holds but \(\{u \longleftrightarrow x\text { in } \omega \setminus \{v\}\}\) does not.
-
4.
Define the events

First, we remark that  . Secondly, note that we have the relation
. Secondly, note that we have the relation

We next state a partitioning lemma (whose proof is left to the reader; see [15, Lemma 3.5]) relating the events E and \(E'\) to the connection event  :
:
Lemma 2.6
(Partitioning connection events) Let \(v,x\in \mathbb Z^d\) and \(A \subseteq \mathbb Z^d\). Then

and the appearing unions are disjoint.
The next lemma, titled the Cutting-point lemma, is at the heart of the expansion:
Lemma 2.7
(Cutting-point lemma) Let \(v,u,x\in \mathbb Z^d\) and \(A \subseteq \mathbb Z^d\). Then
Proof
The proof is a special case of the general setting of [15]. Since it is essential, we present it here. We abbreviate \({\widetilde{\mathscr {C}}} = {\widetilde{\mathscr {C}}}^u(v)\) and observe that
In the above, we can replace \({\widetilde{\mathscr {C}}}\) by \(\langle {\widetilde{\mathscr {C}}} \rangle \) in the middle event, as, by definition, we know that, apart from u, any site in \(\langle {\widetilde{\mathscr {C}}} \rangle \setminus {\widetilde{\mathscr {C}}}\) must be vacant. Now, since \(E'(v,u;A) \subseteq \{ v \longleftrightarrow u\}\), we get
Taking probabilities, conditioning on \({\widetilde{\mathscr {C}}}\), and observing that the status of u is independent of all other events, we see
making use of the fact that the first two events are measurable w.r.t. \({\widetilde{\mathscr {C}}}\). The proof is complete with the observation that under \(\mathbb E_p\), almost surely,
\(\square \)
2.3 Derivation of the Expansion
We introduce a sequence \((\omega _i)_{i\in \mathbb N_0}\) of independent site percolation configurations. For an event E taking place on \(\omega _i\), we highlight this by writing \(E_i\). We also stress the dependence of random variables on the particular configuration they depend on. For example, we write \(\mathscr {C}(u; \omega _i)\) to denote the cluster of u in configuration i.
Definition 2.8
( Lace-expansion coefficients) Let \(m\in \mathbb N, n\in \mathbb N_0\) and \(x\in \mathbb Z^d\). We define
where we recall that \(J(x) = \mathbbm {1}_{\{|x|=1\}}\) and moreover \(u_{-1}=\mathbf {0}, u_m=x\), and \(\mathscr {C}_{i} = {\widetilde{\mathscr {C}}}^{u_i}(u_{i-1};\omega _i)\). Let

Finally, set
It should be noted that the events \(E'(u_{i-1},u_i; {\mathscr {C}}_{i-1})_i\) appearing in Definition 2.8 take place on configuration i only if \(\mathscr {C}_{i-1}\) is taken to be a fixed set—otherwise, they are events determined by configurations \(i-1\) and i.
Proposition 2.9
(The lace expansion) Let \(p< p_c\), \(x\in \mathbb Z^d\), and \(n\in \mathbb N_0\). Then
Proof
We have

We can partition the last summand via the first pivotal point. Pointing out that  , we obtain
, we obtain

via the Cutting-point Lemma 2.7. Using (2.3) for \(A=\mathscr {C}_0\), we have

This proves the expansion identity for \(n=0\). Next, Lemmas 2.6 and 2.7 yield

Plugging this into (2.4), we use (2.3) for \(A={\widetilde{\mathscr {C}}}^{u_1}(u)\) to extract \(\Pi _p^{(1)}\) and get
Note that all appearing sums are bounded by \(\sum _{y} \tau _p(y)\). This sum is finite for \(p<p_c\), justifying the above changes in order of summation. The expansion for general n is an induction on n where the step is analogous to the step \(n=1\) (but heavier on notation). \(\square \)
3 Diagrammatic Bounds
3.1 Setup, Bounds for \(n=0\)
We use this section to state Lemma 3.1 and state bounds on \(\Pi _p^{(0)}\), which are rather simple to prove. The more involved bounds on \(\Pi _p^{(n)}\) for \(n\ge 1\) are dealt with in Sect. 3.2. Note that if \(f(-x) = f(x)\), then \(\widehat{f}(k) = \sum _{x \in \mathbb Z^d} \cos (k \cdot x) f(x)\). We furthermore have the following tool at our disposal:
Lemma 3.1
(Split of cosines, [8], Lemma 2.13) Let \(t \in \mathbb R\) and \(t_i \in \mathbb R\) for \(i=1, \ldots , n\) such that \(t = \sum _{i=1}^{n} t_i\). Then
We begin by treating the coefficient for \(n=0\), giving a glimpse into the nature of the bounds to follow in Sects. 3.2 and 3.3. To this end, we define the two displacement quantities
Proposition 3.2
(Bounds for \(n=0\)) For \(k\in (-\pi ,\pi ]^d\),
Proof
Note that \(|x| \le 1\) implies \(\Pi _p^{(0)}(x) =0\) by definition. For \(|x| \ge 2\), we have
Summation over x gives the first bound. The last bound is obtained by applying Lemma 3.1 to the bounds derived for \(\Pi _p^{(0)}(x)\):
Resolving the sums gives the claimed convolution. \(\square \)
3.2 Bounds in Terms of Diagrams
The main result of this section is Proposition 3.5, providing bounds on the lace-expansion coefficients in terms of so-called diagrams, which are sums over products of two-point (and related) functions. To state it, we introduce some functions related to \(\tau _p\) as well as several “modified triangles” closely related to \(\triangle _p\). We denote by \(\delta _{x,y} = \mathbbm {1}_{\{x=y\}}\) the Kronecker delta.
Definition 3.3
( Modified two-point functions) Let \(x\in \mathbb Z^d\) and define
Definition 3.4
( Modified triangles) We let \(\triangle _p^\circ (x) = p^2(\tau _p^\circ *\tau _p*\tau _p)(x), \triangle _p^{\bullet }(x) = p(\tau _p^\bullet *\tau _p*\tau _p)(x), \triangle _p^{\bullet \circ }(x) = p(\tau _p^\bullet *\tau _p^\circ *\tau _p)(x)\), and \(\triangle _p^{\bullet \bullet \circ }(x) = (\tau _p^\bullet *\tau _p^\bullet *\tau _p^\circ )(x)\). We also set
and \(T_p := (1+\triangle _p) \triangle _p^{\bullet \circ }+ \triangle _p\triangle _p^{\bullet \bullet \circ }\).
Definitions 3.3 and 3.4 allow us to properly keep track of factors of p, which turns out to be important throughout Sect. 3.
Proposition 3.5
(Triangle bounds on the lace-expansion coefficients) For \(n\ge 0\),
The proof of Proposition 3.5 relies on two intermediate steps, successively giving bounds on \(\sum \Pi _p^{(n)}\). These two steps are captured in Lemmas 3.7 and 3.10, respectively. We first state the former lemma.
Recall that \(\Pi _p^{(n)}\) is defined on independent percolation configurations \(\omega _0, \ldots , \omega _n\). A crucial step in proving Proposition 3.5 is to group events taking place on the percolation configuration i, and then to use the independence of the different configurations. To this end, note that event \(E'(u_{i-1}, u_i; \mathscr {C}_{i-1})_i\) takes place on configuration i only if \(\mathscr {C}_{i-1}\) is considered to be a fixed set. Otherwise, it is a product event made up of the connection events of configuration i as well as a connection event in configuration \(i-1\), preventing a direct use of the independence of the \(\omega _i\). Resolving this issue is one of the goals of Lemma 3.7; another is to give bounds in terms of the simpler events (amenable to application of the BK inequality) introduced below in Definition 3.6:
The F events represented graphically. For lines with double arrows, we may have coincidence of the endpoints, for lines without double arrows, we do not. The area with grey tiles indicates that its three boundary points are either all distinct or collapsed into a single point. These diagrams also serve as a pictorial representation of the function \(\phi _0, \phi , \phi _n\). There, lines with double arrows represent factors of \(\tau _p^\circ \) and lines without double arrows represent factors of \(\tau _p\)
Definition 3.6
(Bounding events) Let \(x,y\in \mathbb Z^d\). We define
Let now \(i \in \{1, \ldots , n\}\) and let \(a,b,t,w,z,u \in \mathbb Z^d\). We define
The coincidence requirements in \(F^{(2)}\) mean that among the points \(t_i, w_i, z_i, u_i\), the point \(w_i\) may coincide only with \(t_i\); and additionally, the triple \(\{t_i,z_i,u_i\}\) are either all distinct, or collapsed into a single point. The above events are depicted in Fig. 1.
For intervals [a, b], we use the notation \(\vec x_{[a,b]} = (x_a, x_{a+1}, \ldots , x_b)\). This is not to be confused with the notation \(\vec v_i\) from Definition 3.6. We use the notation \((\mathbb Z^d)^{(m,1)}\) to denote the set of vectors \(\{\vec y_{[1,m]} \in (\mathbb Z^d)^m: y_i \ne y_{i+1} \ \forall 1 \le i < m\}\).
Lemma 3.7
(Coefficient bounds in terms of F events) For \(n \ge 1\) and \((u_0, \ldots , u_{n-1}, x) \in (\mathbb Z^d)^{(n+1,1)}\),
where \(\vec v_i = (u_{i-1}, t_i,w_i,z_i,u_i, z_{i+1})\) and \(u_n = x\).
The proof is analogous to the one in [15, Lemma 4.12] and we do not perform it here. The second important lemma is Lemma 3.10, and its bounds are phrased in terms of the following functions:
Definition 3.8
(The \(\psi \) and \(\phi \) functions) Let \(n \ge 1\) and \(a_1,a_2,b,w,t,u,z \in \mathbb Z^d\). We define
Moreover, we define
and \(\psi := \psi ^{(1)} + \psi ^{(2)}\). Furthermore, for \(j \in \{1,2\}\), let
and \({\tilde{\phi }}_0(b,w,u,z) := \tilde{\psi }_0(b,w,u) \tau _p^\circ (z-w)\) as well as \(\phi := \phi ^{(1)} + \phi ^{(2)}\).
We remark that \(\psi _0 \le \tilde{\psi }_0\) as well as \(\phi _0 \le {\tilde{\phi }}_0\), and we are going to use this fact later on. In the definition of \(\phi ^{(j)}\), the factor \(\tau _p^\circ (z)\) cancels out. In that sense, \(\phi ^{(j)}\) is obtained from \(\psi ^{(j)}\) by “replacing” the factor \(\tau _p^\circ (z-a_1)\) by the factor \(\tau _p^\circ (b-w)\), and the two functions are closely related.
We first obtain a bound on \(\Pi _p^{(n)}\) in terms of the F events (this is Lemma 3.7). Bounding those with the BK inequality, we will naturally observe the \(\phi \) functions (Lemma 3.10). To decompose them further, we would like to apply induction; for this purpose, the \(\psi \) functions are much better-suited. By introducing both the \(\phi \) and \(\psi \) functions, we increase the readability throughout this section (and later ones).
Definition 3.9
(The \(\Psi \) function) Let \(w_n, u_n \in \mathbb Z^d\) and define
where \(\vec t_{[1,n]}, \vec z_{[1,n]}, \vec w_{[0,n-1]} \in (\mathbb Z^d)^n\) and \(\vec u_{[0,n-1]} \in (\mathbb Z^d)^{(n,1)}\).
We remark that \(\Psi ^{(n)}(x,x)=0\), resulting from the fact that the \(\phi \) functions in Definition 3.8 output 0 for \(w=u\). We are going to make use of this later.
Lemma 3.10
(Bound in terms of \(\psi \) functions) For \(n\ge 0\),
Proof
Note first that according to Definition 2.8, the function \(\Pi _p^{(n)}\) contains the event \(E'(u_{i-1}, u_i; \mathscr {C}_{i-1})\), which is itself contained in \(\{u_{i-1} \longleftrightarrow u_i\}\). This is why we may assume that the points \(u_0, \ldots , u_n\) in the definition of \(\Pi _p^{(n)}\) satisfy \(u_{i-1} \ne u_i\). Together with Lemma 3.7, this yields a bound on \(\Pi _p^{(n)}\) of the form
where we recall that \(\vec v_i = (u_{i-1}, t_i,w_i,z_i,u_i, z_{i+1})\). In the first line, \(\vec t, \vec w,\vec z\) are occupied points as in Lemma 3.7. In both lines, \(\vec u_{[0,n]} \in (\mathbb Z^d)^{(n+1,1)}\), and in the second line, \(\vec t, \vec w, \vec z \in (\mathbb Z^d)^n\). Crucially, in the second inequality of (3.2), the factorization occurs due to the independence of the different percolation configurations. Moreover, it is crucial here that the number of factors of p (appearing when we switch from a sum over points in \(\omega \) to a sum over points in \(\mathbb Z^d\)) depends on the number of coinciding points.
We can now decompose the F events by heavy use of the BK inequality, producing bounds in terms of the \(\phi \) functions introduced in Definition 3.8. We start by bounding
We continue to bound
Plugging these bounds into (3.2), we obtain the new bound
where \(\vec t_{[1,n]}, \vec w_{[0,n-1]}, \vec z_{[1,n]} \in (\mathbb Z^d)^n\), and \(\vec u_{[0,n]}\in (\mathbb Z^d)^{(n+1,1)}\). We rewrite the right-hand side of (3.3) by replacing the \(\phi _0, \phi _n\) and \(\phi \) functions by \(\psi _0, \psi _n\) and \(\psi \) functions. As the additional factors arising from this replacement exactly cancel out, this gives the first bound in Lemma 3.10. The observation
gives the second bound and finishes the proof. \(\square \)
We can now prove Proposition 3.5:
Proof of Proposition 3.5
We show that
which is sufficient due to (3.1). The proof of (3.5) is by induction on n. For the base case, we bound
Let now \(n \ge 1\). Then
The fact that \(\Psi ^{(n)}(x,x) = 0\) for any n and x allows us to assume \(w' \ne u'\) in the supremum in the second line of (3.6). After applying the induction hypothesis, it remains to bound the second factor for \(w' \ne u'\), which we rewrite as \(\sup _{a \ne \mathbf {0}} \sum _{t,w,z,u \ne a} \psi (\mathbf {0},a,t,w,z,u)\) by translation invariance. As it is a sum of two terms (originating from \(\psi ^{(1)}\) and \(\psi ^{(2)}\)), we start with the first one and obtain
Before treating the second term, we show how to obtain the bound from (3.7) pictorially, using diagrams very similar to the ones introduced in Fig. 2. In particular, factors of \(\tau _p\) are represented by lines, factors of \(\tau _p^\bullet \) and \(\tau _p^\circ \) by lines with an added ‘\(\bullet \)’ or ‘\(\circ \)’, respectively. Points summed over are represented by squares, other points (which we mostly take the supremum over, for example point a) are represented by colored disks. Hence, we interpret the factor \(\tau _p(z-t)\) as a line between t and z. Since both endpoints are summed over, we display them as squares (and without labels t or z). We interpret the factor \(\tau _p^\circ (z)\) as a (\(\circ \)-decorated) line between \(\mathbf {0}\) and z; the origin is represented by lack of decorating the incident line. Finally, we indicate the distinctness of a pair of points (in our case \(\mathbf {0}\ne a\)) by a disrupted two-headed arrow

. With this notation, (3.7) becomes

The second term in \(\psi \), originating from \(\psi ^{(2)}\), contains an indicator. Resolving it splits this term into two further terms. We first consider the term arising from \(|\{t,z,u\}| = 1\), which forces \(w \ne t=u=z\), and the term is of the form

Turning to the term due to \(|\{t,z,u\}| = 3\), with a substitution of the form \(y'=y-u\) for \(y\in \{t,w,z\}\) in the second line, we see that
This concludes the proof. However, we also want to show how to execute the bound in (3.8) using diagrams. To do so, we need to represent a substitution in pictorial form. Note that after the substitution, the sum over point u is w.r.t. two factors, namely \(\tau _p^\circ (z'+u) \tau _p^\bullet (a-w'-u)\). We interpret these two factors as a line between \(-u\) and \(z'\) and a line between \(-(u-a)\) and \(w'\). In this sense, the two lines do not meet in u, but they have endpoints that are a constant vector a apart. We represent this as

The bound in (3.8) thus becomes

where we point out that we did not use \(a \ne \mathbf {0}\) for the bound \(\triangle _p^{\bullet \bullet \circ }\), and so it was not indicated in the diagram. \(\square \)
The following corollary will be needed later to show that the limit \(\Pi _{p,n}\) for \(n \rightarrow \infty \) exists:
Corollary 3.11
For \(n \ge 1\),
Proof
Note that
Since we do not sum over x, we bound the factors depending on x by 1, and so
implies the claim together with Proposition 3.5. \(\square \)
3.3 Displacement Bounds
The aim of this section is to give bounds on \(p \sum _x [1-\cos (k\cdot x)] \Pi _p^{(n)}(x)\). Such bounds are important in the analysis in Sect. 4. We regard \([1-\cos (k\cdot x)]\) as a “displacement factor”. To state the main results, Propositions 3.13 and 3.14, we introduce some displacement quantities:
Definition 3.12
(Diagrammatic displacement quantities) Let \(x\in \mathbb Z^d\) and \(k \in (-\pi ,\pi ]^d\). Define
Note that Proposition 3.2 already provides displacement bounds for \(n=0\). The following two results give bounds for \(n\ge 1\):
Proposition 3.13
(Displacement bounds for \(n \ge 2\)) For \(n \ge 2\) and \(x\in \mathbb Z^d\),
Proposition 3.14
(Displacement bounds for \(n=1\)) For \(x\in \mathbb Z^d\),
In preparation for the proofs, we define a function \({\bar{\Psi }}^{(n)}\), similar to \(\Psi ^{(n)}\), and prove an almost identical bound to the one in Proposition 3.5. Let \({\bar{\Psi }}^{(0)}(t,z) = \phi _n(\mathbf {0},t,z,\mathbf {0}) / \tau _p^\bullet (t)\). For \(i \ge 1\), define
Note that in \(\phi ^{(2)}\), the points t and w swap roles, so that in both \(\phi ^{(1)}\) and \(\phi ^{(2)}\), u is adjacent to \(t'\) and t is the point adjacent to \(\mathbf {0}\); and in particular, the factor \(\tau _p^\bullet (t)\) cancels out. The following lemma, in combination with Lemma 3.10, is analogous to the bound (3.5), and so is its proof, which is omitted.
Lemma 3.15
For \(n \ge 0\),
Proof of Proposition 3.13
Setting \(\vec v_i = (w_{i-1}, u_{i-1}, t_i,w_i,z_i,u_i)\), we use the bound
which is, in essence, the first bound of Lemma 3.10. The next step is to distribute the displacement factor \(1-\cos (k\cdot x)\) over the \(n+1\) segments. To this end, we write \(x = \sum _{i=0}^{n} d_i\), where \(d_i =w_i-u_{i-1}\) for even i and \(d_i=u_i-w_{i-1}\) for odd i (with the convention \(u_{-1}=\mathbf {0}\) and \(w_n=u_n=x\)). Over the course of this proof, we drop the subscript i and are then confronted with a displacement \(d=d_i\) (which is not to be confused with the dimension).
Using the Cosine-split Lemma 3.1, we obtain
with \(d_i\) as introduced above. We now handle these terms for different i.
\({{\mathbf{Case}}~{\mathbf{(a)}}: i\in \{0,n\}.}\) Let us start with \(i=n\), so that \(d_n \in \{x-u_{n-1}, x-w_{n-1}\}\). The summand for \(i=n\) in (3.10) is equal to
where \(d'\in \{x-w, x-u\}\) and \(d\in \{x,x-u\}\). We expand the indicator in \(\psi _n\) into two cases. If \(t=z=x\), then we can bound the maximum in (3.11) by \(p\sum _x [1-\cos (k\cdot d)] \tau _p^\circ (x) \tau _p(x-u)\), which is bounded by \(W_p(k)\) for both values of d. If t, z, x are distinct points, then for \(d=x\), the maximum in (3.11) becomes

Note that in the pictorial representation, we represent the factor \([1-\cos (k \cdot (x-\mathbf {0}))]\) by a line from \(\mathbf {0}\) to x carrying a ‘\(\times \)’ symbol. We use the Cosine-split Lemma 3.1 again to bound
which results in

It is not hard to see that a displacement \(d=x-u\) yields the same bound. Similar computations show that the case \(i=0\) yields a contribution of at most
\({{\mathbf{Case}}~{\mathbf{(b)}}: 1 \le i < n.}\) We want to apply both the bound (3.5) and Lemma 3.15. To this end, we rewrite the i-th summand in (3.10) as
where we use the substitution \(b_j'=x-b_j\) in the second line and the bound \(\triangle _p^{\bullet }(\mathbf {0}) \le \triangle _p^{\bullet \bullet \circ }\) in the last line. It remains to bound the sum over \({\tilde{\phi }}\). We first handle the term due to \(\phi ^{(1)}\), and we call it \({\tilde{\phi }}^{(1)}\). Depending on the orientation of the diagram (i.e., the parity of i), the displacement \(d=d_i\) is either \(d=w-a=(w-t)+(t-a)\) or \(d=u=(u-z)+z\). We perform the bound for \(d=u\) and use the Cosine-split Lemma 3.1 once, so that we now have a displacement on an actual edge. In pictorial bounds, abbreviating \(\vec v=(\mathbf {0},a,t,w,z,u,b+x,x;k,u)\), this yields

The bound in (3.12) consists of three summands. The first is

the second is

and the third is

The displacement \(d=w-a\) satisfies the same bound. In total, the contribution in \({\tilde{\phi }}\) due to \(\phi ^{(1)}\) is at most
Let us now tend to \({\tilde{\phi }}^{(2)}\). To this end, we first write \({\tilde{\phi }}^{(2)} = \sum _{j=3}^{5} {\tilde{\phi }}^{(j)}\), where
Again, we set \(\vec v=(\mathbf {0},a,t,w,z,u,b+x,x;k,u)\). Then

The first term in (3.13) is

the second term is

and the third term is

We are left to handle the last diagram appearing in the last bound of (3.14), which contains one factor \(\tau _p^\circ \) and one factor \(\tau _p^\bullet \). We distinguish the case where neither collapses (this leads to the diagram \(H_p(k)\)) and the case where at least one of the factors collapses. Using \(\tau _p^\bullet \le \tau _p^\circ \) and the substitution \(y'=y-u\) for \(y\in \{w,z,t\}\), we obtain

In total, this yields an upper bound on (3.13) of the form
The same bound is good enough for the displacement \(d=w-a\). Turning to \(j=4\), we consider the displacement \(d=u\) and see that

which is also satisfied for \(d=w-a\). Finally, \(j=5\) forces \(d=u\), and we have

and we see that this bound is not good enough for \(n=2\). To get a better bound for \(n=2\), we bound

where we recall that \(\tilde{\psi }_0\) is an upper bound on \(\psi _0\) (see Definition 3.8). The above bound is due to the fact that, thanks to (3.4), the supremum over the sum over \(\psi _n\) is bounded by the supremum in (3.6). \(\square \)
Proof of Proposition 3.14
Let \(n=1\). Expanding the two cases in the indicator of \(\phi _n\) gives
where we used the bound \(\phi _0 \le \tilde{\phi }_0\) (see Definition 3.8) for the first summand. Since \(\phi _0\) is a sum of two terms, (3.15) is equal to
We use the Cosine-split Lemma 3.1 on the first term of (3.16) to decompose \(x=u + (z-u) + (x-z)\), which gives

The second term in (3.16) is \(p^2 (J*\tau _{p,k}*\tau _p)(\mathbf {0})\). Depicting the factor \(\gamma _p\) as a disrupted line

, the third term in (3.16) is

In the above, we have used that \(\gamma _p(x) \le \tau _p(x)\) as well as \(\gamma _p(x) \le p (J*\tau _p)(x) \le p\tau _p^{*2}(x)\). \(\square \)
4 Bootstrap Analysis
4.1 Introduction of the Bootstrap Functions
This section brings the previous results together to prove Proposition 4.2, from which Theorem 1.1 follows with little extra effort. The remaining strategy of proof is standard and described in detail in [17]. In short, it is the following: We introduce the bootstrap function f in (4.1). In Sect. 4.2, and in particular in Proposition 4.2, we prove several bounds in terms of f, including bounds uniform in \(p \in [0,p_c)\) under the additional assumption that f is uniformly bounded.
In Sect. 4.3, we show that \(f(0) \le 3\) and that f is continuous on \([0,p_c)\). Lastly, we show that on \([0,p_c)\), the bound \(f\le 4\) implies \(f\le 3\). This is called the improvement of the bounds, and it is shown by employing the implications from Sect. 4.2. As a consequence of this, the results from Sect. 4.2 indeed hold uniformly in \(p\in [0,p_c)\), and we may extend them to \(p_c\) by a limiting argument.
Let us recall the notation \(\tau _{p,k}(x) = [1-\cos (k\cdot x)] \tau _p(x), J_k(x) = [1-\cos (k\cdot x)] J(x)\). We extend this to \(D_k(x) = [1-\cos (k\cdot x)] D(x)\). We note that \(\chi (p)\) was defined as \(\chi (p) = \mathbb E[|\mathscr {C}(\mathbf {0})|]\) and that \(\chi (p) = 1 + p \sum _{x \in \mathbb Z^d} \tau _p(x)\). We define
We define the bootstrap function \(f= f_1 \vee f_2 \vee f_3\) with
where \({\widehat{U}}_{\lambda _p}\) is defined as
We note that \({\widehat{\tau }}_{p,k}\) relates to \(\Delta _k {\widehat{\tau }}_p\), the discretized second derivative of \({\widehat{\tau }}_p\), as follows:
The following result bounds the discretized second derivative of the random walk Green’s function:
Lemma 4.1
(Bounds on \(\Delta _k\), [24], Lemma 5.7) Let \(a(x) = a(-x)\) for all \(x\in \mathbb Z^d\), set \(\widehat{A}(k) = (1-\widehat{a}(k))^{-1}\), and let \(k,l\in (-\pi ,\pi ]^d\). Then
In particular,
A natural first guess for \(f_3\) might have been \(\sup p |\Delta _k{\widehat{\tau }}_p(l)| / | \Delta _k {\widehat{G}}_{\lambda _p}(l)|\). However, \(\Delta _k {\widehat{G}}_{\lambda _p}(l)\) may have roots, which makes this guess an inconvenient choice for \(f_3\). In contrast, \({\widehat{U}}_{\lambda _p}(k,l) >0\) for \(k \ne 0\). Hence, the bound in Lemma 4.1 supports the idea that \(f_3\) is a reasonable definition.
4.2 Consequences of the Diagrammatic Bounds
The main result of this section, and a crucial result in this paper, is Proposition 4.2. Proposition 4.2 proves (in high dimension) the convergence of the lace expansion derived in Proposition 2.9 by giving bounds on the lace-expansion coefficients. Under the additional assumption that \(f\le 4\) on \([0,p_c)\), these bounds are uniform in \(p\in [0,p_c)\).
Proposition 4.2
(Convergence of the lace expansion and Ornstein–Zernike equation)
-
1.
Let \(n\in \mathbb N_0\) and \(p \in [0,p_c)\). Then there is \(d_0 \ge 6\) and a constant \(c_f=c(f(p))\) (increasing in f and independent of d) such that, for all \(d > d_0\),
$$\begin{aligned} \sum _{x\in \mathbb Z^d} p | \Pi _{p,n}(x)| \le c_f/d,&\qquad \sum _{x\in \mathbb Z^d} [1-\cos (k\cdot x)\big ] p | \Pi _{p,n}(x)| \le [1-{\widehat{D}}(k)] c_f/d, \end{aligned}$$(4.2)$$\begin{aligned} \sup _{x\in \mathbb Z^d}&p \sum _{m=0}^{n} | \Pi _p^{(m)}(x)| \le c_f, \end{aligned}$$(4.3)and
$$\begin{aligned} \sum _{x\in \mathbb Z^d} |R_{p,n}(x)| \le c_f (c_f/d)^n {\widehat{\tau }}_p(0). \end{aligned}$$(4.4)Consequently, \(\Pi _p :=\lim _{n\rightarrow \infty } \Pi _{p,n}\) is well defined and \(\tau _p\) satisfies the Ornstein–Zernike equation (OZE), taking the form
$$\begin{aligned} \tau _p(x) = J(x) + \Pi _p(x) + p\big ((J+\Pi _p)*\tau _p\big )(x). \end{aligned}$$(4.5) -
2.
Let \(f \le 4\) on \([0,p_c)\). Then there is a constant c and \(d_0 \ge 6\) such that the bounds (4.2), (4.3), (4.4) hold for all \(d > d_0\) with \(c_f\) replaced by c for all \(p \in [0,p_c)\). Moreover, the OZE (4.5) holds.
A standard assumption in the lace expansion literature is a bound on f(p) (often \(f(p)\le 4\) as in part 2 of the proposition), and then it is shown that this implies \(f(p) \le 3\). This is part of the so-called bootstrap argument.
We first formulate part 1 of Proposition 4.2 (of which part 2 follows straightforwardly) demonstrating that the bootstrap argument is not necessary to obtain convergence of the lace expansion and thus establish the OZE for a fixed value \(p<p_c\) provided that the dimension is large enough. However, without uniformity in p, \(d_0\) might depend on p and diverge as \(p \nearrow p_c\). Hence, this approach alone does not allow to extend the results to \(p_c\).
It is at this point that the bootstrap argument (and thus Sect. 4.3) comes into play. In Sect. 4.3, we indeed prove that \(f \le 4\) and so the second part of Proposition 4.2 applies. This is instrumental in proving Theorem 1.1. We get the following corollary:
Corollary 4.3
(OZE at \(p_c\)) There is \(d_0\) such that for all \(d>d_0\), the limit \(\Pi _{p_c} = \lim _{p \nearrow p_c} \Pi _p\) exists and is given by \(\Pi _{p_c}= \sum _{n \ge 0} (-1)^n \Pi _{p_c}^{(n)}\), where \(\Pi _{p_c}^{(n)}\) is the extension of Definition 2.8 at \(p=p_c\). Consequently, the bounds in Proposition 4.2 and the OZE (4.5) extend to \(p_c\).
Proposition 4.2 follows without too much effort as a consequence of Lemmas 4.7, 4.8, 4.9, and 4.10. Part of the lace expansion’s general strategy of proof in the bootstrap analysis is to use the Inverse Fourier Theorem to write
and then to use an assumed bound on \(f_2\) to replace \({\widehat{\tau }}_p\) by \({\widehat{G}}_{\lambda _p}\). For site percolation, this poses a problem, since we are missing one factor of p. Overcoming this issue poses a novelty of Sect. 4. The following two observations turn out to be helpful for this:
Observation 4.4
(Convolutions of \(J\)) Let \(m\in \mathbb N\) and \(x\in \mathbb Z^d\) with \(m \ge |x|\). Then there is a constant \(c=c(m,x)\) with \(c \le m!\) such that
Proof
This is an elementary matter of counting the number of m-step walks from \(\mathbf {0}\) to x. If \(m-|x|\) is odd, then there is no way of getting from \(\mathbf {0}\) to x in m steps.
So assume that \(m-|x|\) is even. To get from \(\mathbf {0}\) to x, |x| steps must be chosen to reach x. Only taking these |x| steps (in any order) would amount to a shortest \(\mathbf {0}\)-x-path. Out of the remaining steps, half can be chosen freely (each producing a factor of 2d), and the other half must compensate them. In counting the different walks, we have to respect the at most m! unique ways of ordering the steps. \(\square \)
We remark that this also shows that the maximum is attained for \(x=\mathbf {0}\) when m is even and for x being a neighbor of \(\mathbf {0}\) when m is odd.
Observation 4.5
(Elementary bounds on \(\tau _p^{*n}\)) Let \(n, m\in \mathbb N\). Then there is \(c=c(m,n)\) such that, for all \(p\in [0,1]\) and \(x \in \mathbb Z^d\),
where we use the convention that \(\sum _{l=0}^{m-n}\) vanishes for \(n>m\).
Proof
The observation heavily relies on the bound
Note that the left-hand side equals 0 when \(x=\mathbf {0}\). We prove the statement by induction on \(m-n\); for the base case, let \(m\le n\). Then we apply (4.6) to m of the n convoluted \(\tau _p\) terms to obtain
Let now \(m-n>0\). Applying (4.6) once yields a sum of two terms, namely
We can apply the induction hypothesis on the second term with \({\tilde{m}} = m-1\) and \({\tilde{n}}=n\), producing terms of the sought-after form. Now, observe that application of (4.6) yields
for \(1 \le j <n\). For every j, the second term can be bounded by the induction hypothesis for \({\tilde{m}}=m-j-1\) and \({\tilde{n}} = n-j\) (so that \({\tilde{m}} - {\tilde{n}} < m-n\)) with suitable c(m, n). Hence, we can iteratively break down (4.7); after applying (4.8) for \(j=n-1\), we are left with the term \(J^{*n}(x)\), finishing the proof. \(\square \)
We now define
Note that \(W_p\) from Definition 3.12 relates to the above definition via \(W_p = pW_p^{(0,0)} + pW_p^{(0,1)}\). Moreover, \(\triangle _p(x) = p^2 V^{(0,3)}(x) \).
Lemma 4.6
(Bounds on \(V_p^{(m,n)}, W_p^{(m,n)}, {\widetilde{W}}_p^{(m,n)}\)) Let \(p \in [0,p_c)\) and \(m,n\in \mathbb N_0\) with \(d>\tfrac{20}{9} n\). Then there is a constant \(c_f=c(m,n,f(p))\) (increasing in f) such that the following hold true:
-
1.
For \(m+n \ge 2\),
$$\begin{aligned} p^{m+n-1} V_p^{(m,n)}(a) \le {\left\{ \begin{array}{ll} c_f &{}\text{ if } m+n =2 \text { and } a=\mathbf {0}, \\ c_f/d &{} \text{ else }. \end{array}\right. } \end{aligned}$$ -
2.
For \(m+n \ge 1\), and under the additional assumption \(d >2n+4\) for the bound on \(W_p^{(m,n)}\),
$$\begin{aligned} p^{m+n} \max \Big \{ \sup _{a \in \mathbb Z^d} {\widetilde{W}}_p^{(m,n)}(a;k), \sup _{a\in \mathbb Z^d} W_p^{(m,n)}(a;k) \Big \} \le [1-{\widehat{D}}(k)] \times {\left\{ \begin{array}{ll} c_f &{}\text{ if } m+n \le 2, \\ c_f/d &{} \text{ if } m+n \ge 3. \end{array}\right. } \end{aligned}$$
We apply Lemma 4.6 for \(n \le 3\), and so \(d\ge 7 > 60/9\) for the dimension suffices.
Proof
\(\underline{\hbox {Bound}~\hbox {on}~V_p.}\) We start with the case \(m\ge 4\) where we can rewrite the left-hand side via Fourier transform and apply Hölder’s inequality to obtain
We note that the number 10 in the exponent holds no special meaning other than that it is large enough to make the following arguments work. The first factor in (4.9) is handled by Observation 4.4, as
and \(m \ge 4\). Regarding the second factor in (4.9), note that \(10j/9 \le 10n/9 < d/2 \) and so Proposition 2.1 gives a uniform upper bound. We remark that the exponent 10 in (4.9) is convenient because it is even and allows us to apply Lemma 4.6 in dimension \(d\ge 7\).
If \(m<4\), then we first use Observation 4.5 with \({\tilde{m}}= 4-m\) to get that \(p^{m+n-1}V_p^{(m,n)}\) is bounded by a sum of terms of two types, which are constant multiples of
where \(0 \le l \le 4-m-1\) (and therefore \(s \ge 2\)) and \(1 \le j \le n\). If s is odd, we can write \(s= 2r+1\) for some \(r \ge 1\), and Observation 4.4 gives
Similarly, if s is even and \(a \ne \mathbf {0}\) or \(s \ge 4\), then \(p^{s-1} J^{*s}(a) \le c_f/d\). Finally, if \(s=2\) and \(a=\mathbf {0}\), then \(p (J*J)(\mathbf {0}) \le c_f\). This shows that the terms of the first type in (4.10) are of the correct order. The second type is of the form \(p^{4+j-1} V_p^{(4,j)}(a)\) and included in the previous considerations. Together this proves the claimed bound on \(V_p^{(m,n)}\).
\(\underline{\hbox {Bound}~\hbox {on}~{\widetilde{W}}_p.}\) Let first \(m+n \ge 3\). Then
applying the bound on \(V_p\).
Consider now \(m+n=2\). Using first that \(J\le \tau _p\) and then (4.6),
The second and third summand right-hand side of (4.11) can be dealt with as before, we only have to deal with the first summand. Indeed,
and we can choose \(c_f = f_1(p)^2\).
Finally, for \(m+n=1\), we have \(p {\widetilde{W}}_p^{(m,n)}(a;k) \le p {\widetilde{W}}_p^{(1,0)}(a;k) + p^2 {\widetilde{W}}_p^{(1,1)}(a;k)\). The second term was already bounded, the first is
\(\underline{\hbox {Bound}~\hbox {on}~W_p.}\) We note that a combination of (4.6) and the Cosine-split Lemma 3.1 yields
Applying this repeatedly, we can bound \(p^{m+n} W_p^{(m,n)}(a;k)\) by a sum of quantities of the form \( p^{s+t} {\widetilde{W}}_p^{(s,t)}\) (where \(s+t \ge 1\)) plus \(c(m,n) p^{m+n} W_p^{(m,n)}\), where we can now assume \(m \ge 4\) w.l.o.g. The terms of the form \({\widetilde{W}}_p^{(s,t)}\) were bounded above already. Similarly to how we obtained the bound (4.9), we bound the last term by applying Hölder’s inequality, and so
where the last bound is due to Proposition 2.2 and the value of \(c_f\) has changed in the last line. \(\square \)
The proofs of the following lemmas, bounding the quantities appearing in Sect. 3, are direct consequences of Lemma 4.6.
Lemma 4.7
(Bounds on various triangles) Let \(p \in [0,p_c)\) and \(d>6\). Then there is \(c_f=c(f(p))\) (increasing in f) such that
Proof
Note that
For the bound on \(p \tau _p\le p\), we use that \(p \le f_1(p)/d\). For all remaining quantities, we use Lemma 4.6, which is applicable since \(n \le 3\) and \(\tfrac{20}{9} n \le \tfrac{60}{9} < 7 \le d\). \(\square \)
Lemma 4.8
(Bound on \(W_p\)) Let \(p \in [0,p_c)\) and \(d>6\). Then there is a constant \(c_f=c(f(p))\) (increasing in f) such that
Proof
By (4.12),
The proof follows from Lemma 4.6 together with the observation that
\(\square \)
Lemma 4.9
(Bounds on \(\Pi _p^{(0)}\) and \(\Pi _p^{(1)}\)) Let \(p \in [0,p_c), i\in \{0,1\}\), and \(d>6\). Then there is a constant \(c_f=c(f(p))\) (increasing in f) such that
Proof
We recall the two bounds obtained in Proposition 3.2. The first one yields \(p|{\widehat{\Pi }}_p^{(0)}(k)| \le p^3 V_p^{(2,2)}(\mathbf {0})\), the second one yields
All of these bounds are handled directly by Lemma 4.6. Similarly, the only quantity in the bound of Proposition 3.14 that was not bounded already is \(p^2 W_p^{(1,1)}(\mathbf {0};k)\). By a combination of (4.6) and (4.12), we can bound
But \(0 \le {\widetilde{W}}_p^{(2,0)}(\mathbf {0};k) \le 2 J^{\star 3}(\mathbf {0}) = 0\) by Observation 4.4. The other three terms are bounded by Lemma 4.6. \(\square \)
Lemma 4.10
(Displacement bounds on \(H_p\)) Let \(p \in [0,p_c)\) and \(d>6\). Then there is a constant \(c_f=c(f(p))\) (increasing in f) such that
Proof
We recall that
We bound the factor \(\tau _p(z) \le J(z) + p(J*\tau _p)(z)\), splitting \(H_p\) into a sum of two. The first term is easy to bound. Indeed,
by the previous Lemmas 4.6-4.8. We can thus focus on bounding
To prove such a bound (and thus the lemma), we need to recycle some ideas from the proof of Lemma 4.6 in a more involved fashion. To this end, let
and note that \(\tau _p(x) \le \sigma (x)\) by (4.6). Consequently, (4.14) is bounded by \({\widetilde{H}}_p(a_1,a_2;k)\), where we define
By the Inverse Fourier Theorem, we can write
(For details on the above identity, see [15, Lemma 5.7] and the corresponding bounds on \(H_\lambda \) therein.) We bound
Opening the brackets in (4.15) gives rise to three summands. We show how to treat the third one. Applying Cauchy-Schwarz, we obtain
The square brackets indicate how we want to decompose the integrals. We first bound (4.16), and we start with the integral over \(l_3\). We intend to treat the five summands constituting \({\widehat{\sigma }}(l_3-l_2)\) simultaneously. Indeed, note that with our bound on \(f_2\),
With this,
by the same considerations that were performed in (4.13). We use the same approach to treat the integral over \(l_2\) in (4.16). Applying (4.18) to all three factors of \({\widehat{\sigma }}\) gives rise to tuples \((j_i,n_i)\) for \(i\in [3]\), and so
We finish by proving that the integral over \(l_1\) in (4.16) is bounded by a constant. Indeed,
This proves that (4.16) is bounded by \((c_f/d)^{1/2}\). Note that (4.17) is very similar to (4.16), and the same bounds can be applied to get a bound of \((c_f/d)^{1/2}\). Since the other two terms in (4.15) are handled analogously, we obtain the bound \({\widetilde{H}}_p(b_1,b_2;k) \le [1-{\widehat{D}}(k)] c_f/d\), which is what was claimed. \(\square \)
Proof of Proposition 4.2
Recalling the bounds on \(|\Pi _p^{(m)}(k)|\) obtained in Propositions 3.2 and 3.5, and the bounds on \(|\Pi _p^{(m)}(k) - \Pi _p^{(m)}(0)|\) obtained in Propositions 3.2, 3.14, and 3.13, we can combine them with the bounds just obtained in Lemmas 4.7, 4.8, 4.9, and 4.10. This gives
Summing the above terms over m, we recognize the geometric series in their bounds. The series converges for sufficiently large d. If \(f \le 4\) on \([0,p_c)\), we can replace \(c_f\) by \(c=c_4\) in the above, so that the bounds are uniform in \(p\in [0,p_c)\), which means that the value of d above which the series converges is independent of p. Hence,
The bound (4.3) follows from Corollary 3.11 by analogous arguments. Recalling the definition of the remainder term yields the straight-forward bound
applying (4.19). Hence, if \(c_f/d<1\) and \(p<p_c\), then \(\sum _x R_{p,n}(x) \rightarrow 0\) as \(n\rightarrow \infty \). Again, if \(f\le 4\), we can replace \(c_f\) by \(c=c_4\) in (4.20) and the smallness of (c/d) does not depend on the value of p.
The existence of the limit \(\Pi _p\) follows by dominated convergence with the bound (4.3). Together with (4.20), this implies that the lace expansion identity in Proposition 2.9 converges as \(n\rightarrow \infty \) and satisfies the OZE. \(\square \)
Corollary 4.3 as well as the main theorem now follow from Proposition 4.2 in conjunction with Proposition 4.12, which is proven in Sect. 4.3 below.
Proof of Corollary 4.3 and Theorem 1.1
Proposition 4.12 implies that indeed \(f(p)\le 3\) for all \(p\in [0,p_c)\), and therefore, the consequences in the second part of Proposition 4.2 are valid. Lemma 4.7 together with Fatou’s lemma and pointwise convergence of \(\tau _p(x)\) to \(\tau _{p_c}(x)\) then implies the triangle condition.
The remaining arguments are analogous to the proofs of [15, Corollary 6.1] and [15, Theorem 1.1]. The rough idea for the proof of Corollary 4.3 is to use \(\theta (p_c)=0\) (which follows from the triangle condition) to couple the model at \(p_c\) with the model at \(p<p_c\), and then show that, as \(p \nearrow p_c\), the (a.s.) finite cluster of the origin is eventually the same. For the full argument and the proof of the infra-red bound, we refer to [15]. \(\square \)
4.3 Completing the Bootstrap Argument
It remains to prove that \(f \le 4\) on \([0,p_c)\) so that we can apply the second part of Proposition 4.2. This is achieved by Proposition 4.12, where three claims are made: First, \(f(0)\le 4 \), secondly, f is continuous in the subcritical regime, and thirdly, f does not take values in (3, 4] on \([0,p_c)\). This implies the desired boundedness of f. The following observation will be needed to prove the third part of Proposition 4.12:
Observation 4.11
Suppose \(a(x) = a(-x)\) for all \(x\in \mathbb Z^d\). Then
for all \(k,l\in (-\pi ,\pi ]^d\) (where \(\widehat{|a|}\) denotes the Fourier transform of |a|). As a consequence, \(|{\widehat{D}}_k(l)| \le 1-{\widehat{D}}(k)\). Moreover, there is \(d_0 \ge 6\) a constant \(c_f=c(f(p))\) (increasing in f) such that, for all \(d > d_0\),
Proof
The statement for general a can be found, for example, in [17, (8.2.29)]. For convenience, we give the proof. Setting \(a_k(x)=[1-\cos (k\cdot x)] a(x)\), we have
The consequence about \({\widehat{D}}\) now follows from \(D(x) \ge 0\) for all x. Moreover, the statement for \(\Delta _k p{\widehat{\Pi }}_p(l)\) follows applying the observation to \(a=\Pi _p\) together with the bounds in (4.2). \(\square \)
Proposition 4.12
The following are true:
-
1.
The function f satisfies \(f(0) \le 3\).
-
2.
The function f is continuous on \([0,p_c)\).
-
3.
Let d be sufficiently large; then assuming \(f(p) \le 4\) implies \(f(p) \le 3\) for all \(p \in [0,p_c)\).
Consequently, there is some \(d_0\) such that \(f(p) \le 3\) uniformly for all \(p \in [0,p_c)\) and \(d > d_0\).
As a remark, in the third step of Proposition 4.12, we prove the stronger statement \(f_i(p) \le 1+ const / d\) for \(i \in \{1,2\}\). In the remainder of the paper, we prove this proposition and thereby finish the proof the main theorem. We prove each of the three assertions separately.
1. Bounds on f (0). This one is straightforward. As \(f_1(p) = 2dp\), we have \(f_1(0)=0\).
Further, recall that \(\lambda _p =1-1/\chi (p)\), and so \(\lambda _0=0\) and \(\widehat{G}_{\lambda _0}(k)=\widehat{G}_0(k) = 1\) for all \(k\in (-\pi ,\pi ]^d\). Since both \(p|{\widehat{\tau }}_p(k)|\) and \(p |{\widehat{\tau }}_{p,k}(l)|\) equal 0 at \(p=0\), recalling the definitions of \(f_2\) and \(f_3\) in (4.1), we conclude that \(f_2(0) = f_3(0) =0\). In summary, \(f(0)=0\).
2. Continuity of f . The continuity of \(f_1\) is obvious. For the continuity of \(f_2\) and \(f_3\), we proceed as in [17], that is, we prove continuity on \([0,p_c-\varepsilon ]\) for every \(0<\varepsilon <p_c\). This again is done by taking derivatives and bounding them uniformly in k and in \(p \in [0,p_c-\varepsilon ]\). To this end, we calculate
Since \(\lambda _p = 1-1/\chi (p)\),
Further, since \({\widehat{\tau }}_p(0)\) is non-decreasing,
We use Observation 2.3 to obtain
and the same bound as in (4.23) applies. The interchange of sum and derivative is justified as both sums are absolutely summable. Note that \(\, \mathrm {d}{\widehat{G}}_\lambda (k)/\, \mathrm {d}\lambda = {\widehat{D}}(k) {\widehat{G}}_\lambda (k)^2\), and this is bounded by \(\chi (p_c-\varepsilon )^2\) for \(\lambda =\lambda _p\) by (4.22). Finally, by Observation 2.3,
which is bounded by (4.23) again. In conclusion, all terms in (4.21) are bounded uniformly in k and p, which proves the continuity of \(f_2\). We can treat \(f_3\) in the exact same manner, as it is composed of terms of the same type as the ones we just bounded.
3. The forbidden region (3, 4]. Note that we assume \(f(p) \le 4\) in the following, and so the second part of Proposition 4.2 applies with \(c=c_4\).
\(\underline{\hbox {Improvement}~\hbox {of}~f_1.}\) Recalling the definition of \(\lambda _p \in [0,1]\), this implies
\(\underline{\hbox {Improvement}~\hbox {of}~f_2.}\) We introduce \(a = p(J+ \Pi _p)\), and moreover
By adapting the analogous argument from [15, proof of Theorem 1.1], we can show that \(1-\widehat{a}(k)>0\). Therefore, under the assumption that \(f(p) \le 4\), we have \(p{\widehat{\tau }}_p(k) = \widehat{N}(k)/\widehat{F}(k)= \widehat{a}(k)/(1-\widehat{a}(k))\), and furthermore \(\lambda _p= \widehat{a}(0)\). In the following lines, M and \(M'\) denote constants (typically multiples of \(c_4\)) whose value may change from line to line. An important observation is that
We are now ready to treat \(f_2\). Since \(|\widehat{N}(k)| \le 1+M/d\) and by the triangle inequality,
Also,
The first term in the right-hand side of (4.25) is bounded by \([1-{\widehat{D}}(k)] M/d\). In the second term, recalling that \(\widehat{a}(0)=\lambda _p\), we add and subtract \(p{\widehat{\Pi }}_p(0)\) in the numerator, and so
for some constant \(M'\). In the second to last bound, we have used that \(p{\widehat{\Pi }}_p(0) - p{\widehat{\Pi }}_p(k) \le [1-{\widehat{D}}(k)] M/d\). For the last, we have used that \(1-{\widehat{D}}(k) \le 2(1-\lambda _p{\widehat{D}}(k)) = 2 {\widehat{G}}_{\lambda _p}(k)^{-1}\). Putting this back into (4.24), we obtain
This concludes the improvement on \(f_2\). Before dealing with \(f_3\), we make an important observation:
Observation 4.13
Given the improved bounds on \(f_1\) and \(f_2\),
Proof
Consider first those p such that \(2dp \le 3/7\). Then
for d sufficiently large. Next, consider those \(k\in (-\pi ,\pi ]^d\) such that \(|{\widehat{D}}(k)| \le 7/8\). Then
such that \(2dp> 3/7\) and k such that \(|{\widehat{D}}(k)| > 7/8\). We write \(1-\lambda _p {\widehat{D}}(k) = {\widehat{G}}_{\lambda _p}(k)^{-1}\) and \(1-\widehat{a}(k)= {\widehat{\tau }}_p(k)/\widehat{a}(k)\). Since \(2dp|{\widehat{D}}(k)| \ge 3/8\), we obtain
for d sufficiently large. \(\square \)
\(\underline{\hbox {Improvement}~\hbox {of}~f_3.}\) Elementary calculations give
We bound each of the three terms (I)-(III) separately. For the first term,
In the above, we have first used Observation 4.13, then Observation 4.11, and finally the fact that \({\widehat{G}}_{\lambda _p}(l+k) \ge 1/2\). Note that if we obtained similar bounds on (II) and (III), we could prove a bound of the form \(|\Delta _k {\widehat{\tau }}_p(l)| \le c {\widehat{U}}_{\lambda _p}(k,l)\) for the right constant c and the improvement of \(f_3\) would be complete.
To deal with (II), we need a bound on \(\widehat{a}(l+\sigma k)-\widehat{a}(l)\) for \(\sigma \in \{\pm 1\}\). As in [17, (8.4.19)-(8.4.21)],
and similarly
Putting this together yields
Combining (4.26) with Observation 4.13 yields
To bound (III), we want to use Lemma 4.1. We first provide bounds for the three types of quantities arising in the use of the lemma. First, note that \(|\widehat{a}(l)| \le 4+M/d\). Next, we observe
The third ingredient we need is Observation 4.13, which produces \(|1-\widehat{a}(l)|^{-1} \le 3 {\widehat{G}}_{\lambda _p}(l)\). Putting all this together and applying Lemma 4.1 gives
noting that \({\widehat{G}}_{\lambda _p}(l) [1-{\widehat{D}}(l)] \le 2\). In summary, \(\text {(I)}+\text {(II)}+\text {(III)} \le 3 {\widehat{U}}_{\lambda _p}(k,l),\) which finishes the improvement on \(f_3\). This finishes the proof of Proposition 4.12, and therewith also the proof of Theorem 1.1.
References
Aizenman, M., Newman, C.M.: Tree graph inequalities and critical behavior in percolation models. J. Stat. Phys. 36, 107–144 (1984)
Barsky, D.J., Aizenman, M.: Percolation critical exponents under the triangle condition. Ann. Probab. 19(4), 1520–1536 (1991)
Beffara, V., Duminil-Copin, H.: Planar percolation with a glimpse of Schramm–Loewner evolution. Probab. Surv. 10, 1–50 (2013)
Bollobás, B., Riordan, O.: Percolation. Cambridge University Press, Cambridge (2006)
Borgs, C., Chayes, J.T., van der Hofstad, R., Slade, G., Spencer, J.: Random subgraphs of finite graphs. II: the lace expansion and the triangle condition. Ann. Probab. 33(5), 1886–1944 (2005)
Broadbent, S.B., Hammersley, J.M.: Percolation processes. I: crystals and mazes. Proc. Camb. Philos. Soc. 53, 629–641 (1957)
Fitzner, R., van der Hofstad, R.: Mean-field behavior for nearest-neighbor percolation in \(d>10\), Electron. J. Probab. 22 (2017), 65, Id/No 43
Fitzner, R., van der Hofstad, R.: Generalized approach to the non-backtracking lace expansion. Probab. Theory Relat. Fields 169(3–4), 1041–1119 (2017)
Gaunt, D.S., Sykes, M.F., Ruskin, H.J.: Percolation processes in d-dimensions. J. Phys. A 9(11), 1899–1911 (1976)
Grimmett, G.: Percolation, 2nd ed., Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 321, Springer, Berlin (1999)
Hara, T., Slade, G.: Mean-field behaviour and the lace expansion, Probability and phase transition. In: Proceedings of the NATO Advanced Study Institute on probability theory of spatial disorder and phase transition, Cambridge, July 4-16, 1993, Dordrecht: Kluwer Academic Publishers, (1994), pp. 87–122
Hara, T., Slade, G.: Mean-field critical behaviour for percolation in high dimensions. Commun. Math. Phys. 128(2), 333–391 (1990)
Hara, T., Slade, G.: The self-avoiding-walk and percolation critical points in high dimensions. Comb. Probab. Comput. 4(3), 197–215 (1995)
Heydenreich, M., Matzke, K.: Expansion for the critical point of site percolation: the first three terms, arXiv e-prints (2019), arXiv:1912.04584
Heydenreich, M., van der Hofstad, R., Last, G., Matzke, K.: Lace expansion and mean-field behavior for the random connection model, arXiv e-prints (2019), arXiv:1908.11356
Heydenreich, M., van der Hofstad, R.: Random graph asymptotics on high-dimensional tori. Commun. Math. Phys. 270(2), 335–358 (2007)
Heydenreich, M., van der Hofstad, R.: Progress in High-Dimensional Percolation and Random Graphs. Springer, Cham (2017)
Heydenreich, M., van der Hofstad, R., Sakai, A.: Mean-field behavior for long- and finite range Ising model, percolation and self-avoiding walk. J. Stat. Phys. 132(6), 1001–1049 (2008)
Janson, S., Łuczak, T., Ruciński, A.: Random Graphs, New York. Wiley, New York (2000)
Margulis, G.A.: Probabilistic properties of graphs with large connectivity. Probl. Peredachi Inf. 10(2), 101–109 (1974). (Russian)
Mertens, S., Moore, C.: Series expansion of the percolation threshold on hypercubic lattices, J. Phys. A 51 (2018), no. 47, 38, Id/No 475001
Nguyen, B.G.: Gap exponents for percolation processes with triangle condition. J. Stat. Phys. 49(1–2), 235–243 (1987)
Russo, L.: On the critical percolation probabilities. Z. Wahrscheinlichkeitstheor. Verw. Geb. 56, 229–237 (1981)
Slade, G.: The Lace Expansion and Its Application. École d’Été de Probabilités de Saint-Flour XXXIV–2004, vol. 1879, Berlin: Springer (2006)
van den Berg, J., Kesten, H.: Inequalities with applications to percolation and reliability. J. Appl. Probab. 22, 556–569 (1985)
van der Hofstad, R., Slade, G.: Expansion in \(n^{-1}\) for percolation critical values on the \(n\)-cube and \(\mathbb{Z}^n\): the first three terms. Comb. Probab. Comput. 15(5), 695–713 (2006)
Werner, W.: Percolation et modèle d’Ising, vol. 16. Société Mathématique de France, Paris (2009)
Acknowledgements
Open Access funding provided by Projekt DEAL. We thank Günter Last, Remco van der Hofstad, and Andrea Schmidbauer for numerous discussions about the lace expansion, which are reflected in the presented paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Hal Tasaki.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Heydenreich, M., Matzke, K. Critical Site Percolation in High Dimension. J Stat Phys 181, 816–853 (2020). https://doi.org/10.1007/s10955-020-02607-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10955-020-02607-y