1 Introduction

The interest in the physical properties of the 3d elements is an old endeavor [1 and the references therein]. For example, studies on the magnetic, electronic, and elastic properties have been reported [2,3,4,5,6,7,8,9,10]. Works on the phase transition in Fe under pressure [2] and the dependence of the magnetization on temperature for iron nanoparticles [3] have been done.

Classical models, e.g., a model based on the premises of classical statistical mechanics, have been used to investigate the anisotropic magnetic properties of the 3d elements and their compounds [4, 10] and the size-dependent magnetic properties of elements, e.g., Fe and Gd [5, 6]. Recently, the anisotropic magnetocaloric effect (AMCE) in Fe has been reported [6]. Both of the mean-field model and a Hubbard-like model Hamiltonian, where electron–electron interaction is taken into account within the mean-field theory, were reported [7, 8]. The effect of high magnetic field on the magnetocaloric effect was reported by Tishin [9].

In the present paper, we present a detailed calculation, for Fe, Ni, and Co, of the magnetic, magnetothermal, e.g., heat capacity and entropy, and the magnetocaloric properties: the isothermal change in entropy and the adiabatic change in temperature. The relative cooling powers are also calculated and compared with bench-mark Gd and other Gd-based compounds. The nature of the magnetic phase transition in these elements is also investigated, in the light of the temperature and field dependences of the aforementioned properties, together with the Arrott plots and universal curves. At the end, we report on the temperature dependence of the magnetization and the isothermal change in entropy, for amorphous Fe, and compare these properties with its counterparts in crystalline Fe.

2 Model and Analysis

In the mean-field theory (MFT) [11,12,13,14,15,16,17], the interaction between the magnetic moments is taken into consideration and is represented as a uniform internal (mean) field. The origin of the internal field, as described by Heisenberg, is the scalar product of spin operators. The internal field could be evaluated, from the magnetization, through a self-consistent calculation, unlike systems of non-interacting moments, e.g., paramagnetic systems where no internal field exists. The effective field is the sum of the external applied field and the internal field. There are some limitations, however, of the mean-field model at very low temperatures due to spin waves excitation and around the Curie temperature due to critical fluctuations. Albeit this limitation, the mean-field theory proved to be suitable in handling different crystalline and amorphous systems with up to three sublattices.

The effective magnetic field Heff of any of the elements: Fe, Ni, and Co can be expressed as follows:

$$H_{eff}\left(T\right)=H+d\left[n_{tt}M\left(T\right)\right]$$
(1)

where H is the external applied magnetic field and \(M\left(T\right)\) is the magnetic moment at temperature T. The factor \(d={N}_{A }\rho {\mu }_{B}/A\) converts the atomic moment from \({\mu }_{B}\) to Gauss, where A is the atomic mass in g per mole, \(\rho\) is the density in \(\mathrm{g}/{\mathrm{cm}}^{3}\), \({N}_{A}\) is Avogadro’s number and the molecular field coefficient \({n}_{tt}\) is dimensionless, and the symbol t stands for either Fe, Co, or Ni.

The magnetic moment M (T, H) of any of the three elements is given by the equation:

$$M(T,H)=M_JB_J\left(x\right)$$
(2)

where \({B}_{J}\left(x\right)\) is the Brillouin function:

$${B}_{J}\left(x\right)=\frac{2J+1}{2J}\mathrm{coth}\left(\frac{2J+1}{2J}x\right)-\frac{1}{2J}\mathrm{coth}\left(\frac{x}{2J}\right)$$
(3)
$$x=\frac{{M}_{J}H}{{K}_{B}T}$$
(4)
\(J\) :

is the total angular momentum quantum number.

\(M_J\;=\;g\mu_BJ\) :

 the magnetic moment per atom.

From the following Maxwell relation, the magnetic entropy change is calculated [11]:

$${\left(\frac{\partial S\left(T\right)}{\partial H}\right)}_{T}={\left(\frac{\partial M\left(T\right)}{\partial T}\right)}_{H}$$
$$\Delta S_m\left(T\right)=\int_{H_0}^{H_f}{\textstyle\frac{\partial M\left(T\right)}{\partial T}}dH$$
(5)

The above integral could be cast into a summation by using the well-known trapezoidal rule [18, 19]:

$$\Delta S_m\left(T\right)={\textstyle\sum_i^{i\;+\;1}}\;\frac{M_{i\;+\;1}\left(H_{i\;+\;1},\;T_{i\;+\;1}\right)\;-\;M_i\left(H_i,\;T_i\right)}{T_{i\;+\;1}-T_i}\Delta H_i$$
(6)

The total heat capacity \({C}_{tot}\) includes three contributions: the magnetic heat capacity \({C}_{m}\), the lattice heat capacity \({C}_{l}\), and the electronic heat capacity \({C}_{e}\) [20].

$${C}_{tot}={C}_{m}+{C}_{l}+{C}_{e}$$
(7)

First, from the temperature derivative of the magnetic energy, we can calculate the magnetic contribution to heat capacity:

$${U}_{m}=-\frac{1}{2}{n}_{tt}{M}^{2}\left(T\right)$$
(8)
$$C_m\left(T\right)=\frac{\partial U_m}{\partial T}$$
(9)

From the integration of the magnetic heat capacity, the magnetic entropy may be calculated as follows:

$$S_m\left(T\right)=\int_0^T{\textstyle\frac{C_m\left(T\right)}T}dT$$
(10)

The theoretical maximum of the magnetic entropy is given by [11]

$${S}_{m}\left(max\right)=R\;Ln\left(2J+1\right)$$
(11)

where \(R\) is the gas constant.

Second, the lattice contribution to heat capacity is calculated from the Debye model [21, 22]:

$$C_l=9N_a\;k{(\frac T{\theta_D})}^3\int\limits_0^\frac{\theta_D}T\frac{e^y{\;y}^4}{{(e^y-1)}^2}dy$$
(12)

where \(y=\nicefrac{{\theta }_{D}}{T}\) and \({\theta }_{D}\) is Debye temperature.

Third, the electronic heat capacity is proportional to temperature and is given by [23]:

$${C}_{e}={\gamma }_{e}T=\left({\pi }^{2}/3\right){k}^{2}{N}_{a}\;N\left({E}_{f}\right)T$$
(13)

where \({\gamma }_{e}\) is the electronic heat capacity coefficient and \(N\left({E}_{f}\right)\) is the density-of-states at Fermi energy.

From Gibb’s free energy, the Landau–Ginsburg theory is expressed as follows [24, 25]:

$$F=\frac{1}{2}\;A\left(T\right){M}^{2}+\frac{1}{4}B\left(T\right){M}^{4}+\frac{1}{6}C\left(T\right){M}^{6}-M.H$$
(14)

The magnetic entropy change is:

$$\Delta {S}_{m}\left(T\right)=-{\left(\frac{dF}{dT}\right)}_{H}=-\frac{1}{2}\frac{dA\left(T\right)}{dT}{M}^{2}-\frac{1}{4}\frac{dB\left(T\right)}{dT}{M}^{4}+\dots$$
(15)

From the equilibrium condition at \({T}_{c}\), \(\frac{\partial F}{\partial M}=0\) the magnetic equation of state is:

$$H=A\left(T\right)M+B\left(T\right){M}^{3}+\dots$$
(16)
$$\frac{H}{M}=A\left(T\right)+B\left(T\right){M}^{2}+\dots$$
(17)

where \(A\left(T\right)\) and \(B\left(T\right)\) are Landau’s coefficients.

The adiabatic temperature change [20, 26] can be calculated from the following:

$${\Delta T}_{ad=}\overset{H_f}{\underset{H_0}{-\int}}\frac T{C_{tot}(T,H)}\frac{\partial M(T,H)}{\partial T}dH$$
(18)

By using the Arrott–Belov–Kouvel (ABK) [27,28,29], the Arrott plots, i.e., the \({M}^{2}\) vs \(H/M\) plot, in the ferromagnetic region at different temperatures close to \({T}_{c}\), can be used to estimate the spontaneous magnetization and the Curie temperature. The Arrott plots are also used to determine the order of the phase transition involved, i.e., a second-order (SOPT) or a first-order phase transition (FOPT), from the sign of the plots slopes. Namely, positive slopes indicate SOPT, whereas negative slopes or s-shaped slopes indicate FOPT [30, 31].

The relation between \(\Delta {S}_{m}/\Delta {S}_{m}^{peak}\) and \(\theta\) is well known as the universal curve [32], one may choose the reference temperature \({T}_{r}\) such that:

$$\Delta {S}_{m}\left({T}_{r}\right)=0.7\Delta {S}_{m}^{peak}$$
(19)

where \(\theta\) is defined by:

$$\theta =(T-{T}_{c})/\left({T}_{r}-{T}_{c}\right)$$
(20)

The relative cooling power RCP(S) [17, 33] is defined as follows:

$$RCP\left(S\right)=\Delta S_{max}\left(T\right)\times\delta T_{FWHM}$$
(21)

where \(\delta {T}_{FWHM}\) is the full width at half maximum of the magnetic entropy change curve and \(\Delta {S}_{max}\left(T\right)\) is the maximum magnetic entropy change.

Another figure-of-merit for the magnetocaloric materials is the RCP (T) defined as [33, 34]:

$$RCP\left(T\right)=\Delta T_{max}\times\delta T_{FWHM}$$
(22)

where δTFWHM is the full width at half maximum of the ΔTad vs. T plot.

3 Results and Discussion

3.1 Magnetization

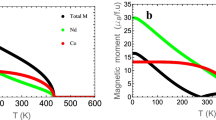
Figure 1a−c display the calculated magnetic moment as function of temperature for Fe, Ni, and Co respectively in fields of 0 and 5 T. The magnetic moment at very low temperatures and the Curie temperatures of these three elements agree very well with experimental data, e.g., the magnetic moments are 2.2, 0.6, and 1.7 μB and Tc values are 1040, 630, and 1400 K respectively. Although the data in Fig. 1 are well known, we have found it necessary to show in order to demonstrate the fair success of the MFT theory. It is well known that both ∆Sm and ∆Tad do depend on the temperature derivative of the magnetization at constant field and therefore on the MFT-calculated magnetization.

Fig. 1
figure 1

a Magnetic moment dependence on temperature, in 0 and 5 T, for Fe. b Magnetic moment dependence on temperature, in 0 and 5 T, for Ni. c Magnetic moment dependence on temperature in 0 and 5 T, for Co

Full size image

3.2 Magnetic Heat Capacity and Entropy

The magnetic contribution to heat capacity has been calculated from the magnetic energy (Eqs. 8 and 9). The magnetic specific heat of Ni is shown in Fig. 2 in a temperature range up to 700 K. The field dependence, at Tc, is clearly that of materials with SOPT [35]. The magnetic specific heat of Fe and Co show similar behavior.

Fig. 2
figure 2

Magnetic specific heat of Ni vs. temperature, in different fields

Full size image

The temperature dependence of the magnetic entropy of the three elements, in zero field, is shown in Fig. 3. The maximum values of the magnetic entropy, at and above Tc, as calculated from the mean-field theory are shown together with those calculated from the Eq. 11 e.g. [36]. The agreement is excellent as shown in Table 1.

Fig. 3
figure 3

Magnetic entropy of Fe, Ni, and Co, in zero field

Full size image
Table 1 Maximum Sm, in zero field, using Maxwell relation and the shown equation
Full size table

3.3 The Isothermal Change in Entropy

The temperature dependence of the isothermal change in entropy for field changes 2, 4, 6, and 8 T, calculated from Maxwell relation via the trapezoidal method (Eqs. 5 and 6), is shown in Fig. 4a−c.

Fig. 4
figure 4

a Isothermal change in entropy for Fe in different fields. b Isothermal change in entropy for Ni in different fields. c Isothermal change in entropy for cobalt in different fields

Full size image

Table 2 lists both ∆S and RCP values in a 6 T field change. Moreover, the features of the temperature and field dependences of ∆S are those of SOPT materials [35].

Table 2 Maximum isothermal entropy change and RCP(S), in 6 T, for the three elements
Full size table

We listed in Table 2 the isothermal change in entropy [18] and the corresponding (Eq. 21) RCP values in J/mol, for the three elements, in a 6 T field.

de Oliveira [37] used an itinerant electron model to study MCE in Fe, Co, Ni, and YFe3. For the three elements, he reported ΔSmax of nearly: 8, 4, and 4 J/kg K in a 2.16 T field. These are 0.447, 0.235, and 0.236 J/mol K respectively. These values are about 2–3 times larger than our mean-field values.

3.4 The Adiabatic Change in Temperature

The adiabatic change in temperature for the three elements is shown in Fig. 5a−c in different magnetic fields.

Fig. 5
figure 5

a Adiabatic change in temperature vs. temperature for Fe in different fields. b Adiabatic change in temperature vs. temperature for Ni in different fields. c Adiabatic change in temperature vs. temperature for cobalt in different fields

Full size image

The values of ΔTmax (K) for the three elements, as reported by De Oliveira [37], are in the range 2.5–5 K for fields in the range 2.16–3 T. Our values are in the range 1–7 K for fields in the range 2–4 T.

The RCP/ΔH values shown in Table 3 are to be compared with those of known materials, in the same units of course, e.g., 161.2 for Gd in 6 T, 96.0 for Gd5 Si 2.06 Ge1.94 in 5 T, 109.2 for Gd5Si4 in 5 T, and 145.1 for Gd4Bi3 in 10 T [33, 38].

Table 3 Adiabatic change in temperature, RCP (T) in 6 T field and RCP (T) per tesla
Full size table

3.5 High Field Effects

Figure 6a shows ∆Sm for Fe in fields up to 300 T. Two features of this figure are firstly, the peak temperature Tpeak coincides with Tc even for these high fields using the present mean-field calculation. This has been reported by [39], using numerical calculation, but for much lower fields (≤ 1.5 T). However, Franco et al. showed, by using the Heisenberg model, that Tpeak > Tc. Secondly, the curves become more flat, i.e. the FWHM of any given curve, in case of using high fields, becomes larger.

Fig. 6
figure 6

a Isothermal entropy change vs. temperature, for Fe, in fields of: 20, 100, and 300 T. b Adiabatic change in temperature vs. temperature, for Fe, in fields of: 20, 40, 60, and 100 T

Full size image

The adiabatic change in temperature, in high fields, has been studied by Tishin [9]. Figure 6b shows our results for Fe in fields of 20, 40, 60, and 100 T. It is clear from that the maximum of ΔTad shifts as the field increases. The same trend is found for Co.

3.6 Arrott Plots and the Universal Curves

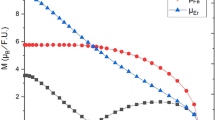
The Arrott plots are used to study the nature of the phase transition [28, 29] and the itinerant nature [9] of the electrons in Fe, Co, and Ni. Weak itinerant nature was found for Fe. The straight lines of the same slopes and the values of M2 in zero field (Fig. 7) are indicative of weak itinerant nature according to Eq. 23 [40]. We have found that the percentage error between M2 values in zero field is in the 3.4–19% as calculated from the mean-field theory and from the following equation:

Fig. 7
figure 7

Arrott plots for Fe in field up to 1 T

Full size image
$${M(H,T)}^{2}={M(0.0)}^{2}\left[\left(1-\frac{{T}^{2}}{{T}_{c}^{2}}\right)+\frac{2{x}_{0}H}{M\left(H,T\right)}\right]$$
(23)

Figure 8a, b display the universal curves for Fe and Ni respectively. The features are clearly those of SOPT. In materials with FOPT, the low temperature (ϴ < 0) curves do not collapse but clearly diverge as the field changes [41].

Fig. 8
figure 8

a The universal curve for Fe. b The universal curve for Ni

Full size image

3.7 Amorphous Fe

The amorphous alloys are known to have advantages in the field of magnetic refrigeration due to several factors [42]. Because of these advantages, we have calculated the temperature dependence of the magnetic moment in amorphous Fe using the mean-field model as well. Figure 9 displays our calculation. The exchange coefficient between Fe atoms in the amorphous case is much less (~ 30%) than its crystalline counterpart as reported by Grinstaff [43]. Both of the magnetic moment, at very low temperatures, and the Curie temperature are significantly reduced relative to crystalline Fe. In particular, Tc is about 580 K and the magnetic moment is about 1.6 μB.

Fig. 9
figure 9

The magnetization dependence on temperature, in zero field, for amorphous Fe

Full size image

We have calculated the isothermal entropy change for a-Fe. The results are shown in Fig. 10. The curves also have their maximum at Tc, but their maxima ΔS are close to those of crystalline Fe, in the same field.

Fig. 10
figure 10

The isothermal change in entropy for amorphous Fe

Full size image

The absence of data on the total heat capacity of a-Fe, up to our knowledge, does not enable us to calculate the adiabatic change in temperature and compare it with that of crystalline Fe.

4 Conclusions

We have calculated the thermomagnetic and the magnetocaloric properties for Fe, Co and Ni using the mean-field theory. The isothermal entropy change \({\Delta S}_{m}\) has been calculated using Maxwell’s relation. The highest ordinary \({\Delta S}_{m}\) for Fe, Co, and Ni, respectively, is 0.3, 0.23, and 0.17 \(\mathrm{J}/\mathrm{mol K}\) for a magnetic field change of 6 T. The adiabatic temperature change \({\Delta T}_{\mathrm{ad}}\) for Fe, Co, and Ni respectively, is 9, 8.6, and 2.8 K for a magnetic field change of 6 T. The relative cooling power RCP (T) is fairly comparable to those of Gd and some Gd-based MCE materials. Amorphous Fe has much less Curie temperature and a smaller spontaneous magnetic moment than its crystalline counterpart; however, its isothermal entropy change is comparable to crystalline Fe. The temperature and field dependences of the magnetization, magnetic entropy, magnetic specific heat, Arrott plots, and universal curves showed that the phase transition in these three elements is of the second order. The mean-field theory proved to be appropriate for calculating the abovementioned properties.