Magnetothermal Properties and Magnetocaloric Effect in R₃Co₁₁B₄

Abstract

We present a study on the magnetic properties and magnetocaloric effect (MCE) in R₃Co₁₁B₄, where R = Pr, Nd, Tb, Dy, and Ho. The two-sublattice model is used for calculating magnetization, magnetic heat capacity, isothermal entropy change ∆S_m, and adiabatic temperature change ∆T_ad, for different magnetic field changes ∆H = 1.5, 3, and 5 T and at temperatures up to 600 K. Direct and inverse MCE are shown to take place in the ferrimagnetic compounds with R = Tb, Dy, and Ho. The maximum isothermal magnetic entropy change and maximum adiabatic temperature change have been calculated for ferromagnetic Nd₃Co₁₁B₄ compound to be 1.85 J/K mol and 6.5 K at T_c = 432 K, for a field change ∆H = 5 T. The relative cooling power (RCP) is in the 44–161 J/mol range for the same field change. Also, the type of phase transition is investigated in the light of Arrott plots, universal curves, and the features of the temperature and field dependences of the magnetization, heat capacity, entropy, and the magnetocaloric properties. Those features confirm that the transition at the Curie temperature of these compounds is of the second order.

1 Introduction

The magnetocaloric effect has been discussed before for rare earth inter-metallic compounds [1,2,3]. A large variety of functional materials useful for technological applications such as magnetic refrigeration has been reported. Magnetic refrigeration is hoped to be a good, more efficient, and environmentally safer alternative to traditional refrigeration [4,5,6]. Many studies have been done to investigate the room-temperature magnetocaloric effect (MCE) materials such as La_1-xLi_xMnO₃ [7], Gd₅Si₂Ge₂ [8], NiMnIn [9], and NiMnSb [10]. Also, the MEC was studied on other materials such as RCo₂ [11], RCuAl [12], RMn₂Si₂, and HoCoSi [13]. The direct and inverse MCE have been observed in Heusler alloys [14] and ferrimagnetic materials such as RFe₂ [15, 16] and DySb [17]. The magnetic properties of R₃Co₁₁B₄ have been reported by Tetean et al. [18] and Xiang-Mu et al. [19]. In this work, we present a theoretical calculation of the magnetothermal properties and the magnetocaloric effect in R₃Co₁₁B₄ compounds. In particular, we report on the isothermal change in entropy, the adiabatic change in temperature, and the relative cooling power in fields up to 5 T and at temperatures up to and above the Curie temperature of the compounds under study.

2 Model and Analysis

The exchange field of two sublattices systems can be expressed as follows [20, 21]:

$${\mathrm{H}}_{\mathrm{R}}\left(\mathrm{T}\right)=\mathrm{H}+\mathrm{d}\left[{ 3\mathrm{n}}_{\mathrm{RR}}{\mathrm{M}}_{\mathrm{R}}\left(\mathrm{T}\right)+ {11\mathrm{n}}_{\mathrm{RCo}}{\mathrm{M}}_{\mathrm{Co}}\left(\mathrm{T}\right)\right]$$

(1)

$${\mathrm{H}}_{\mathrm{Co}}\left(\mathrm{T}\right)=\mathrm{H}+\mathrm{d}\left[{3\mathrm{ n}}_{\mathrm{RCo}}{\mathrm{M}}_{\mathrm{R}}\left(\mathrm{T}\right)+{11\mathrm{n}}_{\mathrm{CoCo}}{\mathrm{M}}_{\mathrm{Co}}\left(\mathrm{T}\right)\right]$$

(2)

where H is the external applied magnetic field, and M_R(T) and M_Co(T) are the magnetic moments for rare earth and cobalt, respectively, at temperature T. The factor d = N_A ρ μ_B/A converts the moment per formula unit of R₃Co₁₁B₄ from μ_B to A/m, where ρ is the density of the compound in kg/m³, N_A is Avogadro’s number, and A is a formula unit weight of compound in kg per mole. The molecular field coefficients n_RR, n_CoCo, and n_RCo are dimensionless.

$${\mathrm{M}}_{\mathrm{R }}\left(\mathrm{T}\right)={\mathrm{M}}_{\mathrm{R}}\left(0\right){\mathrm{B}}_{{\mathrm{J}}_{\mathrm{R}}}\left(\frac{{\mathrm{M}}_{\mathrm{R}}\left(0\right){\mathrm{H}}_{\mathrm{R}}\left(\mathrm{T}\right)}{{\mathrm{k}}_{\mathrm{B}}\mathrm{T}}\right)$$

(3)

$${\mathrm{M}}_{\mathrm{Co }}\left(\mathrm{T}\right)={\mathrm{M}}_{\mathrm{Co}}\left(0\right){\mathrm{B}}_{{\mathrm{J}}_{\mathrm{Co}}}\left(\frac{{\mathrm{M}}_{\mathrm{Co}}\left(0\right){\mathrm{H}}_{\mathrm{Co}}\left(\mathrm{T}\right)}{{\mathrm{k}}_{\mathrm{B}}\mathrm{T}}\right)$$

(4)

M_Co(0) and M_R(0) are the magnetic moments of cobalt and rare earth at T = 0 K, respectively, and M_R(0) = g_R J_R, where g and J have their usual meaning. M_co(0) is, however, obtained from the experimental low temperature data.

B_J(y) is the Brillouin function:

$${\mathrm B}_{\mathrm J}\left(\mathrm y\right)=\frac{2\mathrm J+1}{2\mathrm J}\;\coth\;\left(\frac{2\mathrm J+1}{2\mathrm J}\mathrm y\right)-\frac1{2\mathrm J}\;\coth\;\left(\frac1{2\mathrm J}\mathrm y\right)$$

(5)

and $\mathrm{y}=\frac{\mathrm{\mu H}}{\mathrm{kT}}$

The total magnetization can be calculated from:

$${\mathrm{M}}_{\mathrm{Total}}\left(\mathrm{T}\right)={ 3\mathrm{M}}_{\mathrm{R}}\left(\mathrm{T}\right)\pm 11{\mathrm{M}}_{\mathrm{Co}}\left(\mathrm{T}\right)$$

(6)

The magnetic entropy change is calculated from the thermodynamic Maxwell relation:

$${\left(\frac{\partial \mathrm{S}(\mathrm{T})}{\partial \mathrm{H}}\right)}_{\mathrm{T}}={\left(\frac{ \partial \mathrm{M}(\mathrm{T})}{\partial \mathrm{T}}\right)}_{\mathrm{H}}$$

$$\Delta {\mathrm{S}}_{\mathrm{m}}(\mathrm{T})={\int }_{{\mathrm{H}}_{0}}^{{\mathrm{H}}_{\mathrm{f}}}\frac{\partial \mathrm{M}\left(\mathrm{T}\right)}{\partial \mathrm{T}}\mathrm{ dH}$$

(7)

The magnetic entropy change is calculated also by using trapezoidal rule, as reported, for example, by Tishin et al. [22].

$${\Delta S}_{m}(\mathrm{T})={\sum }_{\mathrm{i}}^{\mathrm{i}+1}\frac{\left({\mathrm{M}}_{\mathrm{i}+1}({\mathrm{H}}_{\mathrm{i}+1},{\mathrm{T}}_{\mathrm{i}+1})-{\mathrm{M}}_{\mathrm{i}}({\mathrm{H}}_{\mathrm{i}},{\mathrm{T}}_{\mathrm{i}}\right)}{{\mathrm{T}}_{\mathrm{i}+1}-{\mathrm{T}}_{\mathrm{i}}}\Delta {\mathrm{H}}_{\mathrm{i}}$$

(8)

where M(H) is the isothermal magnetization.

A universal curve [23] is the relation between △S_m/△${\mathrm{S}}_{\mathrm{m}}^{\mathrm{peak}}$ and ϴ, where ϴ is defined as follows:

$$\uptheta=\left(\mathrm T-{\mathrm T}_{\mathrm C}\right)/\left({\mathrm T}_{\mathrm r}-{\mathrm T}_{\mathrm C}\right)$$

(9)

One may choose the reference temperature T_r such that [23]:

$${\Delta\mathrm S}_{\mathrm m}\left({\mathrm T}_{\mathrm r}\right)=0.7{\Delta\mathrm S}_{\mathrm m}^{\mathrm{peak}}$$

(10)

The total heat capacity C_tot includes three contributions: the magnetic heat capacity C_m, the electronic heat capacity C_e, and the lattice heat capacity C_l [24, 25]:

$${\mathrm{C}}_{\mathrm{tot}}={\mathrm{C}}_{1}+{\mathrm{C}}_{\mathrm{e}}+{\mathrm{C}}_{\mathrm{m}}$$

(11)

First, we calculate the magnetic energy for the system in order to calculate the magnetic contribution to heat capacity:

$$\mathrm{U}=-\frac{1}{2}\left({\mathrm{n}}_{\mathrm{RR}}{\mathrm{M}}_{\mathrm{R}}^{2}\left(\mathrm{T}\right)+{\mathrm{n}}_{\mathrm{CoCo}}{\mathrm{M}}_{\mathrm{Co}}^{2}\left(\mathrm{T}\right)+2{\mathrm{n}}_{\mathrm{RCo}}{\mathrm{M}}_{\mathrm{R}}\left(\mathrm{T}\right){\mathrm{M}}_{\mathrm{Co}}\left(\mathrm{T}\right)\right)$$

(12)

The magnetic contribution to heat capacity is calculated from the temperature-derivative of magnetic energy:

$${\mathrm{C}}_{m}\left(\mathrm{T}\right)= \frac{\partial \mathrm{U}}{\partial \mathrm{T}}$$

(13)

Second, the electronic contribution to heat capacity is proportional to temperature and may become a dominant term at very low temperatures; the electronic heat capacity is given by [26]:

$${\mathrm C}_{\mathrm e}=\gamma_{\mathrm e}\mathrm T=\left(\pi^2/3\right)\;\mathrm k^2\;{\mathrm N}_{\mathrm a}\;N\;\left({\mathrm E}_{\mathrm f}\right)\mathrm T$$

(14)

where γ_e is the electronic heat-capacity coefficient and N (E_f) is the density-of-states at Fermi energy.

Third, the lattice contribution to heat capacity is expressed in the Debye model, as follows:

$${\mathrm C}_1=9\;\mathrm N\mathrm a\;\mathrm k\;{(\frac{\mathrm T}{\theta_D})}^3\int_0^{\theta_{{\mathrm D}_{/_{\mathrm T}}}}\;\frac{e^x\;\mathrm x^4}{(\mathrm e^x-1)^2}\;\mathrm{dx}$$

(15)

where x = ϴ_D/T and ϴ_D is Debye temperature.

The adiabatic temperature change [24] can be calculated from the following:

$$\Delta{\mathrm T}_{\mathrm{ad}}=\int_{{\mathrm H}_0}^{{\mathrm H}_{\mathrm f}}\;\frac{\mathrm T}{{\mathrm C}_{\mathrm{tot}}}\;\frac{\partial\mathrm M\left(\mathrm T\right)}{\partial\mathrm T}\;\mathrm{dH}$$

(16)

According to Arrot-Belov-Kouvel (ABK) [27, 28], the Arrott plots M² vs. H/M and M² vs. ∆S_m in the ferromagnetic region at different temperatures, close to T_c, can be used to estimate the spontaneous magnetization and the Curie temperature.

From Landau-Ginsburg theory [29], Gibb’s free energy is expressed as follows:

$$\mathrm{F}=\frac{1}{2}\mathrm{A}\left(\mathrm{T}\right){\mathrm{M}}^{2}+\frac{1}{4}\mathrm{B}\left(\mathrm{T}\right){\mathrm{M}}^{4}+\frac{1}{6}\mathrm{C}\left(\mathrm{T}\right){\mathrm{M}}^{6}-\mathrm{M}.\mathrm{H}$$

(17)

The magnetic entropy change obtained from Gibb’s free energy:

$$\Delta {\mathrm{S}}_{\mathrm{m}}\left(\mathrm{T}\right)=-({\frac{\mathrm{dF}}{\mathrm{dT}})}_{\mathrm{H}}=-\frac{1}{2}\frac{\mathrm{dA}\left(\mathrm{T}\right)}{\mathrm{dT}}{\mathrm{M}}^{2}-\frac{1}{4}\frac{\mathrm{dB}\left(\mathrm{T}\right)}{\mathrm{dT}}{\mathrm{M}}^{4}+\dots$$

(18)

From the equilibrium condition at T_c, $\frac{\partial \mathrm{F}}{\partial \mathrm{M}}=0$ the magnetic equation of state is:

$$\mathrm{H}=\mathrm{A}\left(\mathrm{T}\right)\mathrm{M}+\mathrm{B}(\mathrm{T}){\mathrm{M}}^{3}+. .$$

(19)

$$\frac{\mathrm{H}}{\mathrm{M}}=\mathrm{A}\left(\mathrm{T}\right)+\mathrm{B}\left(\mathrm{T}\right){\mathrm{M}}^{2}+. .$$

(20)

where A(T) and B(T) are Landau’s coefficients.

The relative cooling power (RCP) [30] is defined as follows:

$$\mathrm{RCP}={\Delta \mathrm{S}}_{\mathrm{max}}\left(T\right)*{\mathrm{\delta T}}_{\mathrm{FWHM}}$$

(21)

where ∆S_max (T) is the maximum magnetic entropy change and δT_FWHM is the full width at half maximum of the magnetic entropy change curve.

3 Results and Discussion

3.1 Magnetization

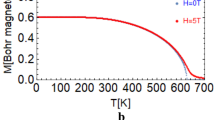
In this study, we calculated the temperature dependences of the magnetization of the rare-earth, Co, and R₃Co₁₁B₄ system, where R = Pr, Nd, Tb, Dy, and Ho. Ferromagnetic coupling is present in compounds with R = Nd and Pr, whereas compounds with R = Tb, Dy, and Ho show ferrimagnetic coupling with compensation points. Figure 1(a) exhibits the magnetization of the two sublattices of Nd and Co, and the total magnetization of the compound. Figure 1(b) shows the same but for the ferrimagnetic compound with R = Dy where a compensation point is present. We may remark that the magnetic moments, at 0 K, for the Nd and Dy atoms are as follows: M_Nd (0) = g_Nd × J_Nd = (8/11) × (7/2) = 2.54 μ_B/atom and M_Dy (0) = g_Dy × J_Dy = (4/3) × (15/2) = 10 μ_B/atom. It is known that the nature of the magnetic moment in R-atoms is localized whereas that of the 3d-transition elements (Co in the present study) is relatively itinerant. Therefore, the magnetic moment of the cobalt sublattice is determined from the experimental data of the total magnetization and from the localized moments of the R-elements, as shown above. In the Nd compound, the cobalt moment per atom is M_Co(0) = 4.4/11 = 0.4 μ_B, but it is different in the Dy compound, i.e., M_Co(0) = 13.36/11 = 1.214 μ_B [19]. We may recall that, in the elemental cobalt, the magnetic moment of a Co atom, at 0 K, is 1.7 μ_B; however, it might be drastically different in some R-Co compounds; e.g., in RCo₂ compounds, the Co moment vanishes [31]. For the elemental Dy, however, M_Dy (0) = 10 μ_B, this same value of M_Dy (0), in the Dy₃Co₁₁B₄ compound, led to the observed experimental total magnetization of the compound.

Fig. 1

Total and sublattice magnetizations vs. temperature in zero magnetic field for (a) Nd₃Co₁₁B₄ and (b) Dy₃Co₁₁B

Results of total magnetization and Curie temperatures, for the R₃Co₁₁B₄ system, are shown in Table 1. In this table, the percentage difference between our calculated magnetic moment, at very low temperatures, and the experimentally determined moments [18] is displayed. This difference is only ≤ 0.6%. The corresponding difference in the Curie temperature data is ≤ 7%. We may also refer to the value of the magnetic moment of the Nd₃Co₁₁B₄ compound, as evaluated by the band calculation [32], i.e., 15.87 µ_B/f.u which is about 30% off the experimental value 12.2 µ_B/f.u reported in the same reference. It is worth mentioning that, in our mean-field calculation of M (T, H), we picked up initial magnetic moment values, at temperatures (with a step of 1 K) up to Curie temperature and in a specific field, and checked, in an iteration process, whether they are possible simultaneous solutions to the well-known Brillouin functions. This iteration process was performed with an accuracy of 10⁻⁷.

Table 1 The calculated and experimental [18] net magnetic moment, in zero field and 0 K, and the Curie temperatures for R₃Co₁₁B₄ system

3.2 Total Heat Capacity

Basically, the calculation of the adiabatic change in temperature depends on both of the temperature change of the magnetization and total heat capacity (Eq. 16). There are three contributions to the total heat capacity for R₃Co₁₁B₄, as we mentioned before in Eq. (11). First, the magnetic heat capacity has been calculated from Eq. (13), and is shown, for different magnetic fields: 0, 1.5, 3, and 5 T, for Nd₃Co₁₁B₄ and Ho₃Co₁₁B₄ in Fig. 2a and b, respectively. Second, electronic heat capacity is calculated from the coefficient γ_e, which is obtained from the materials project [33], A Szajek [34], and A Kowalczyk et al. [32] as shown in Table 2. The Debye temperatures of Nd₃Co₁₁B₄ and Gd₃Co₁₁B₄ are 475 and 450 K, respectively, as reported by Li et al. [35]. Debye temperatures for the rest of the systems we report on here are not available and we assumed that their Debye temperature is around 450 K.

Fig. 2

Temperature dependence of magnetic specific heat for (a) Nd₃Co₁₁B₄ and (b) Ho₃Co₁₁B₄, in external fields of 0, 1.5, 3, and 5 T

Table 2 The isothermal magnetic entropy change, for different magnetic field changes, in R₃Co₁₁B₄ system using the trapezoidal and Maxwell methods

3.3 The Isothermal Entropy Change

The isothermal change in entropy has been calculated by two methods: by Maxwell’s relation (Eq. 7) and by the trapezoidal method (Eq. 8). Figure 3(a) shows the isothermal magnetic entropy change for R = Nd. Only direct MCE is present in this (and in the R = Pr) ferromagnetic system. For the ferrimagnetic compound with R = Dy, the isothermal magnetic entropy, for different magnetic field changes, is shown in Fig. 3(b) and it exhibits both direct and inverse MCE; i.e., two peaks are present: the first one at the Curie temperature, and the second one at a temperature below the compensation temperature. Comparing data of △S_m, using Maxwell relation and the trapezoidal method, showed a reasonable agreement between the two methods, in particular for small field changes (Table 2). In the trapezoidal method, which casts the Maxwell integral into a summation, we chose small field changes in order for the summation to be as accurate as possible. For the sake of comparison with bench-mark materials and other R₃Co₁₁B₄ compounds, e.g., (Gd_xY_1-x)₃Co₁₁B₄, we compare our results of ΔS_m, which is in the range 0.7 to 2.5 J/ mol K at field 5 T, with that of Gd metal, i.e., 1.48 J/mol K at H = 5 T as reported by Wang et al. [36] and with the work of Burzo et al. on (Gd_xY_1-x)₃Co₁₁B₄ [37], who reported a ΔS_m about 2.4 J/mol K at ΔH = 3 T.

Fig. 3

Isothermal entropy change vs. T, for (a) Nd₃Co₁₁B₄ and (b) Dy₃Co₁₁B₄, for field changes of 1.5, 3, and 5 T

Table 3 The adiabatic temperature change, for different field changes

3.4 Adiabatic Temperature Change

In this part, we report on the adiabatic temperature change. Because of a weak dependence of the total heat capacity on the applied magnetic field, around T_c for the studied compounds, for example, for R = Dy (Fig. 4), the term T/${\mathrm{C}}_{\mathrm{tot}}$ is taken out of the integral in Eq. 16. Figure 5(a and b) shows the adiabatic temperature change for R = Nd and Dy, respectively. The results, for four studied compounds, are shown in Table 3. The maximum value for ΔT is 6.5 K, for an applied magnetic field 5 T, in case of Nd₃Co₁₁B₄; i.e., the temperature is decreasing by a rate of 1.3 K/T.

Table 4 Relative cooling power (RCP) in J/mol for different field changes

3.5 The Relative Cooling Power

The relative cooling power is a figure-of-merit in the field of magnetic refrigeration and is calculated, for different field changes by Eq. (21). The RCP increases with increasing the applied magnetic field, and the results are summarized in Table 4. The RCP is in the range 17.48 to 160.95 J/ mol at field 5 T, as compared to about 108.33 J/ mol at 5 T for Gd as reported by Wang et al. [36].

Fig. 4

The dependence of T/C_tot on temperature in H = 1.5, 3, and 5 T for Dy₃Co₁₁B₄

Fig. 5

Adiabatic temperature change vs. T for (a) Nd₃Co₁₁B₄ and (b) Dy₃Co₁₁B₄ for field changes of 1.5, 3, and 5 T

3.6 Arrott Plots

Figures 6(a, b) and 7(a, b) show (H/M) vs. M² and ∆S_m vs. M² plots for R = Nd and Dy, respectively, in different magnetic fields, and at temperatures close to T_c. The positive slopes of these plots indicate a second-order phase transition. The curve starting from the origin represents the data at T_c and this is in agreement with temperature dependence of magnetization, according to the Banerjee criterion [28].

Fig. 6

(a) H/M vs. M² and (b) ΔS_m vs. M.² for Nd₃Co₁₁B₄ compound in applied fields of 0.1, 1, 2, 3, 4, and 5 T, Tc = 432 K

Fig. 7

(a) H/M vs. M² and (b) ΔS_m vs. M.² for Dy₃Co₁₁B₄ compound in applied fields of 0.1, 1, 2, 3, 4, and 5 T, Tc = 404 K

3.7 Universal Curve

Figure 8 shows the universal curve of Dy₃Co₁₁B₄ in applied magnetic fields of 1.5, 3, and 5 T. The normalized magnetic entropy change curves fairly collapse onto a unique curve, which confirms that the phase transition in the R₃Co₁₁B₄ system is of the second order.

Fig. 8

Universal curves of the Dy₃Co₁₁B₄ for field changes of 1.5, 3, and 5 T

3.8 The Field-Dependence of the Magnetic Entropy Change

Figure 9 shows the field dependence of the magnetic entropy change for R₃Co₁₁B₄ system. According to the MFT, the relation ΔS_m vs. (H/T_C)^2/3 is another criterion for existence of a second-order magnetic phase transition [38, 39].

Fig. 9

ΔS_m vs. (H/T_C).^2/3, for R₃Co₁₁B₄ compounds in applied fields from 0.1 to 5 T

4 Conclusion

We calculated the magnetothermal and MC properties, △S_m and △T_ad for R₃Co₁₁B₄ system using the mean-field theory. Magnetization calculations showed that compounds with R = Tb, Dy, and Ho are ferrimagnetic compounds, whereas those with R = Pr and Nd are ferromagnetic. △S_m is calculated by two methods: Maxwell’s relation and the trapezoidal method. The two methods give fairly similar results. The highest ordinary MCE △S_m, △T_ad, and RCP are 2.5 J/mol K, 6.6 K, and 161 J/mol for R = Nd for a magnetic field change of 5 T. The temperature and field dependencies of the magnetic properties, △S_m, △T_ad, Arrott plots, and the universal curves showed that the phase transition in these compounds is of the second order. The mean-field analysis is suitable for studying the magnetothermal properties and magnetocaloric effect of the R₃Co₁₁B₄ system.