1 Introduction

Fullerenes, a family of closed-cage carbon molecules, have attracted considerable interest since their discovery in 1985 [1, 2]. Several excellent books and reviews details the advances achieved in the field of chemistry and physics of fullerenes (see e.g. [3,4,5,6,7] and the references therein). In past decades a new research area has emerged in mathematical chemistry providing a topological and graph theoretical descriptions of fullerenes [8,9,10,11,12]. Fullerenes are topologically distinct from other allotropes of carbon, such as diamond or graphite. They are unable to transform into different class of allotropes unless breaking and reformation of the molecular bonds. States with this absence of continuity in topology are often termed topologically protected, or topologically stable. In the last decade a new topologically protected magnetic object, a spin swirling vortex-like magnetic Skyrmion received widespread attention due to its potential application in spintronic devices [13, 14]. In a Skyrmion the magnetic moments swirl so that the spins at its periphery point in the opposite direction to the spins at the center. Skyrmions can be characterized by their topological charge which is a measure of the winding of the normalized atomic magnetic moments. The mathematical concept of Skyrmions was first introduced in high energy physics [15]. There are some studies [16, 17] which established a relation between the Skyrmion solutions in nuclear physics and fullerene cages.

In the present paper we introduce a topological charge in a manner similar to the winding number of magnetic Skyrmions, but instead of magnetic moments at different lattice sites unit vectors parallel to appropriately chosen hybrid orbitals of the carbon atoms are considered. A fullerene molecule is a trivalent polyhedron with exactly three edges joining every vertex occupied by a carbon atom. The three edges starting from a vertex define the directions of the p orbitals in the sp hybrids parallel to the bonds. Applying the orthogonality requirements the fourth sp orbital pointing out of the cage can easily be constructed. These orbitals will be referred as \(\pi \) orbitals in the following, however, rigorously defined \(\pi \) orbitals exist only in planar molecules. The topological charge of a fullerene will be calculated based on these out of cage \(\pi \) orbitals.

In this paper we construct all even fullerene isomers from \(C_{20}\) up to \(C_{70}\). After optimizing the geometry of the molecules the relation between the topological charge and the atomization energy is analysed.

2 Method

Based on the algorithms described in Ref. [18] we have constructed all of the 30579 fullerene isomers \( C_{n} \) for each even \( n \) with \( 20 \le n \le 70 \). After minimizing the total energies we calculated the \(\pi \)-orbitals at each atom. With the help of these \(\pi \)-orbitals we defined and calculated the topological charges of the generated isomers.

2.1 Construction of fullerene isomers

For each even \( n \) with \( 20 \le n \le 70 \) we applied the spiral conjecture [18] for producing the spiral code of all of the isomers. According to the spiral conjecture the surface of a fullerene polyhedron may be unwound in a continuous spiral strip of edge-sharing pentagons and hexagons such that each new face in the spiral after the second shares an edge with both (a) its immediate predecessor in the spiral and (b) the first face in the preceding spiral that still has an open edge. Since all of the fullerenes contain twelve pentagons the spiral code contains a list of twelve numbers indicating their position in the spiral. See Ref. [18] for the details of the construction of the adjacency matrix. As an example of the spiral code for the buckminsterfullerene is \( (1,7,9,11,13,15,18,20,22,24,26,32) \). With the help of the spiral code we calculated the adjacency matrix \( \mathbf{A} \) of the system. Here \( A_{ij} = 1 \) if atoms \(i \) and \( j \) are neighbours and \( A_{ij} = 0 \) in other cases.

We used the topological coordinate method [18] to calculate the initial coordinates of the fullerene described by the given spiral code. An eigenvector \( \mathbf{C}^{k} \) of the adjacency matrix \( \mathbf{A} \) is a bi-lobal eigenvector, if the atoms of the fullerene can be put in two sets \( S_{1} \) and \( S_{2} \) where in both sets the atoms are connected and the set \( S_{1} \) contains all of atoms \( i \) if for the \( C^{k}_{i} \) coefficient \( C^{k}_{i} > 0 \) and the set \( S_{2} \) contains all of the atoms \( i \) with the property \( C^{k}_{i} < 0 \) [18, 19]. Finding the three bi-lobal eigenvectors and their corresponding eigenvalues \( \mathbf{C}^{k_x} \), \(a_{k_x} \); \( \mathbf{C}^{k_y} \), \(a_{k_y} \);\( \mathbf{C}^{k_z} \) , \(a_{k_z} \), of matrix \( \mathbf{A} \), the topological coordinates \( (X_{i}, Y_{i}, Z_{i}) \) of atom \( i \) are

$$\begin{aligned} \begin{aligned} X_{i}&= C^{k_x}_{i}s_x \\ Y_{i}&= C^{k_y}_{i}s_y \\ Z_{i}&= C^{k_z}_{i}s_z \end{aligned} \end{aligned}$$
(1)

and the scaling factors are the followings:

$$\begin{aligned} \begin{aligned} s_x&= \frac{1}{\sqrt{ a_{1} -a_{k_x}}} \\ s_y&= \frac{1}{\sqrt{ a_{1} -a_{k_y}}} \\ s_z&= \frac{1}{\sqrt{ a_{1} -a_{k_z}}} \, \end{aligned} \end{aligned}$$
(2)

where \(a_1\) is the highest eigenvalue of the adjacency matrix.

Using as input the topological coordinates, we minimized the total energy with the help of the Brenner potential [20]. Here we applied the conjugate gradient method and supposed only interactions between the neighbouring atoms. The initial configuration provided by the topological method is close enough to the configuration belonging to the local minimum that the optimization procedure can not destroy the cage like structure [21]. In the next step we continued the minimization with a Density Functional Theory adjusted Tight Binding method (DFT-TB) [22].

2.2 Calculation of the hybrid orbitals

Supposing the atomic orbitals \( |s \rangle \), \( |p_{x} \rangle \), \( |p_{y} \rangle \), \( |p_{z} \rangle \) on each carbon atom, we defined the following hybrid orbitals [23, 24]:

$$\begin{aligned} \begin{aligned} |h_{1} \rangle&= N_{1}( |s \rangle + \lambda _{1} |p_{1} \rangle ) \\ |h_{2} \rangle&= N_{2}( |s \rangle + \lambda _{2} |p_{2} \rangle ) \\ |h_{3} \rangle&= N_{3}( |s \rangle + \lambda _{3} |p_{3} \rangle ) \\ |h_{\pi } \rangle&= N_{\pi }( |s \rangle + \lambda _{\pi } |p_{\pi } \rangle ) \end{aligned} \end{aligned}$$
(3)

where \( |p_{1} \rangle \), \( |p_{2} \rangle \) and \( |p_{3} \rangle \) are \( |p \rangle \) functions directed along the three inter-nuclear axes to the adjacent atoms. That is \( |p_{i} \rangle = u^{i}_{x} |p_{x} \rangle + u^{i}_{y} |p_{y} \rangle + u^{i}_{z} |p_{z} \rangle \) and the unit vector \( \mathbf{u^{i} } = (u^{i}_{x}, u^{i}_{y}, u^{i}_{z} ) \) points to the adjacent atom \( i \). To make the description simpler we call the orbitals \( |h_{1} \rangle \), \( |h_{2} \rangle \) and \( |h_{3} \rangle \) \( \sigma \)-orbitals and the \( |h_{\pi } \rangle \) orbital \( \pi \)-orbital. The angles between the \( \sigma \)-orbitals are \( (\theta _{12} , \theta _{23}, \theta _{31} ) \) and the angles between a \( \sigma \)-orbital and a \( \pi \)-orbital are \( (\theta _{1\pi } , \theta _{2\pi }, \theta _{3\pi } ) \).

From the orthogonality conditions of the functions \( |h_{1} \rangle \), \( |h_{2} \rangle \) and \( |h_{3} \rangle \) follows

$$\begin{aligned} \begin{aligned} \lambda ^{2}_{1}&= -\frac{\cos \theta _{23}}{ \cos \theta _{12} \cos \theta _{31} } \\ \lambda ^{2}_{2}&= -\frac{\cos \theta _{31}}{ \cos \theta _{23} \cos \theta _{12} } \\ \lambda ^{2}_{3}&= -\frac{\cos \theta _{12}}{ \cos \theta _{31} \cos \theta _{23} } \end{aligned} \end{aligned}$$
(4)

The orthogonality conditions of the functions \( |h_{i} \rangle \), and \( |h_{\pi } \rangle \) gives

$$\begin{aligned} \begin{aligned}&1+\lambda _{1}\lambda _{\pi }(u^{1}_{x}u^{\pi }_{x} + u^{1}_{y}u^{\pi }_{y} + u^{1}_{z}u^{\pi }_{z}) = 0 \\&1+\lambda _{2}\lambda _{\pi }(u^{2}_{x}u^{\pi }_{x} + u^{2}_{y}u^{\pi }_{y} + u^{2}_{z}u^{\pi }_{z}) = 0 \\&1+\lambda _{3}\lambda _{\pi }(u^{3}_{x}u^{\pi }_{x} + u^{3}_{y}u^{\pi }_{y} + u^{3}_{z}u^{\pi }_{z}) = 0 \end{aligned} \end{aligned}$$
(5)

Taking differences of the above equations yields

$$\begin{aligned} \begin{aligned}&(u^{3}_{x}\lambda _{3} - u^{2}_{x}\lambda _{2})u^{\pi }_{x} + (u^{3}_{y}\lambda _{3} - u^{2}_{y}\lambda _{2})u^{\pi }_{y} + (u^{3}_{z}\lambda _{3} - u^{2}_{z}\lambda _{2})u^{\pi }_{z} = 0 \\&(u^{1}_{x}\lambda _{1} - u^{3}_{x}\lambda _{3})u^{\pi }_{x} + (u^{1}_{y}\lambda _{1} - u^{3}_{y}\lambda _{3})u^{\pi }_{y} + (u^{1}_{z}\lambda _{1} - u^{3}_{z}\lambda _{3})u^{\pi }_{z} = 0 \\&(u^{2}_{x}\lambda _{2} - u^{1}_{x}\lambda _{1})u^{\pi }_{x} + (u^{2}_{y}\lambda _{2} - u^{1}_{y}\lambda _{1})u^{\pi }_{y} + (u^{2}_{z}\lambda _{2} - u^{1}_{z}\lambda _{1})u^{\pi }_{z} = 0 \end{aligned} \end{aligned}$$
(6)

Substituting the \(\lambda \) values of Eqs. (4) into (6) and after simplification we obtain

$$\begin{aligned}&(u^{3}_{x}\cos \theta _{12} - u^{2}_{x}\cos \theta _{31})u^{\pi }_{x} + (u^{3}_{y}\cos \theta _{12} - u^{2}_{y}\cos \theta _{31})u^{\pi }_{y} \end{aligned}$$
(7)
$$\begin{aligned}&\quad + (u^{3}_{z}\cos \theta _{12} - u^{2}_{z}\cos \theta _{31})u^{\pi }_{z} = 0 \end{aligned}$$
(8)
$$\begin{aligned}&(u^{1}_{x}\cos \theta _{23} - u^{3}_{x}\cos \theta _{12})u^{\pi }_{x} + (u^{1}_{y}\cos \theta _{23} - u^{3}_{y}\cos \theta _{12})u^{\pi }_{y} \end{aligned}$$
(9)
$$\begin{aligned}&\quad + (u^{1}_{z}\cos \theta _{23} - u^{3}_{z}\cos \theta _{12})u^{\pi }_{z} = 0 \end{aligned}$$
(10)
$$\begin{aligned}&(u^{2}_{x}\cos \theta _{31} - u^{1}_{x}\cos \theta _{23})u^{\pi }_{x} + (u^{2}_{y}\cos \theta _{31} - u^{1}_{y}\cos \theta _{23})u^{\pi }_{y} \end{aligned}$$
(11)
$$\begin{aligned}&\quad + (u^{2}_{z}\cos \theta _{31} - u^{1}_{z}\cos \theta _{23})u^{\pi }_{z} = 0 \end{aligned}$$
(12)

The solution of the above equations give the \( \pi \)- orbital unit vectors \( \mathbf{u}^{{\pi }} = (u^{\pi }_{x}, u^{\pi }_{y}, u^{\pi }_{z} ) \) for each atom of the fullerene.

2.3 Definition of the topological charges

In the continuum case, the topological charge \( Q \) of a three-component spin field \( \mathbf{s}(x,y) \), \( \mathbf{s}(x,y)^{2} =1 \), is defined [25] by

$$\begin{aligned} \begin{aligned} Q = \frac{1}{4\pi } \iint _A \mathbf{{s}}(\partial _x \mathbf{s} \times \partial _y \mathbf{s}) \,dx \,dy \end{aligned} \end{aligned}$$
(13)

which is the number of times the \( \mathbf{s}(x,y) \) winds around the sphere \( S^{2} \). The meaning of this definition can be understood from the followings.

A solid angle \( \Omega \) in steradians equals the area of a segment on a sphere with unit radius.

$$\begin{aligned} \begin{aligned} \Omega = \iint _A \frac{\mathbf{{n}}d\mathbf{A}}{\rho ^{2}} \end{aligned} \end{aligned}$$
(14)

Here \( \rho =1 \) is the radius of the sphere and \( \mathbf{n} \) is the normal vector of the surface. Let us take the spin field \( \mathbf{s}(x,y) \) at the following three positions \( \mathbf{s}(x,y) \), \( \mathbf{s}(x+dx,y) \) and \( \mathbf{s}(x,y+dy) \). As these are unit vectors, from the previous Equation follows, that drawing them from the same origin, their endpoints determines the following solid angle \( d\Omega \)

$$\begin{aligned} \begin{aligned} d\Omega&= \mathbf{{n}}d\mathbf{A} = \mathbf{{n}}(\mathbf{s}(x+dx,y) -\mathbf{s}(x,y) )\times (\mathbf{s}(x,y+dy) -\mathbf{s}(x,y)) = \\&= \mathbf{{n}}(\partial _x \mathbf{s}dx)\times (\partial _y \mathbf{s}dy) = \mathbf{{s}}(\partial _x \mathbf{s})\times (\partial _y \mathbf{s})dxdy \end{aligned} \end{aligned}$$
(15)

In the case of infinitesimally small surface element the normal vector \(\mathbf {n}\) can be replaced by one of spin field vectors in the last step. Substituting Eqs. (15) into (14) gives (13).

The definition of the topological charge of a discrete lattice of spins \( \mathbf{s}_i \), \( \mathbf{s}_i^{2} =1 \), where \( i \) runs over all the lattice sites is [25, 26]

$$\begin{aligned} \begin{aligned} Q = \frac{1}{4\pi } \sum _{l} \Omega _l \end{aligned} \end{aligned}$$
(16)

with [26,27,28]

$$\begin{aligned} \begin{aligned} \cos \left( \frac{\Omega _l}{2}\right) = \frac{1+\mathbf{s}_i\mathbf{s}_j +\mathbf{s}_i\mathbf{s}_k +\mathbf{s}_j\mathbf{s}_k }{\sqrt{2(1+\mathbf{s}_i\mathbf{s}_j)(1+\mathbf{s}_j\mathbf{s}_k)(1+\mathbf{s}_k\mathbf{s}_i)}} \end{aligned} \end{aligned}$$
(17)

where \( l \) runs over all elementary triangles of the hexagonal lattice, \( \Omega _l \) is the solid angle, i.e. the area of the spherical triangle with vertices \( \mathbf{s}_i \), \( \mathbf{s}_j \) and \( \mathbf{s}_k \).The sites \( i \), \( j \) and \( k \) of each elementary triangle are numbered in such a way that the rotation vector defined by the order \( i \) \( j \) \( k \) shows to the direction of the positive \( z \) axis. The sign of \( \Omega _l \) is determined as \( sign \left( \Omega _l\right) = sign\left( {\mathbf{s}_i}({\mathbf{s}_j}\times {{\mathbf{s}_k}})\right) \).

2.4 Calculation of the topological charges of fullerenes

When we calculated the hybrid orbitals \( |h_{1} \rangle \), \( |h_{2} \rangle \), \( |h_{3} \rangle \) and \( |h_{\pi } \rangle \), we obtained the unit vectors \( \mathbf{u}^{{\pi }} = (u^{\pi }_{x}, u^{\pi }_{y}, u^{\pi }_{z} ) \) for each atom of the structure. We shall use these unit vectors for calculating the topological charges of the fullerene. As the fullerenes contain only pentagons and hexagons, we divide each polygon into triangles drawing diagonals from a vertex for each polygon. The topological charge of fullerenes is given by the Eq. (16), but Eq. (17) is replaced by

$$\begin{aligned} \begin{aligned} \cos \left( \frac{\Omega _l}{2}\right) = \frac{1+\mathbf{u}^{\pi }_i\mathbf{u}^{\pi }_j +\mathbf{u}^{\pi }_i\mathbf{u}^{\pi }_k +\mathbf{u}^{\pi }_j\mathbf{u}^{\pi }_k }{\sqrt{2(1+\mathbf{u}^{\pi }_i\mathbf{u}^{\pi }_j)(1+\mathbf{u}^{\pi }_j\mathbf{u}^{\pi }_k)(1+\mathbf{u}^{\pi }_k\mathbf{u}^{\pi }_i)}} \end{aligned} \end{aligned}$$
(18)

where \( l \) runs over all elementary triangles of the pentagons and hexagons, \( \Omega _l \) is the solid angle, i.e. the area of the spherical triangle with vertices \( \mathbf{u}^{\pi }_i \), \( \mathbf{u}^{\pi }_j \) and \( \mathbf{u}^{\pi }_k \). The sites \( i \), \( j \) and \( k \) of each elementary triangle are numbered in such a way that the rotation vector defined by the order \( i \) \( j \) \( k \) shows out of the fullerene surface. The sign of \( \Omega _l \) is determined as \( sign \left( \Omega _l\right) = sign\left( {\mathbf{u}^{\pi }_i}({\mathbf{u}^{{\pi }}_j}\times {{\mathbf{u}^{{\pi }}_k}})\right) \).

We define also the quantity bump number of fullerenes as

$$\begin{aligned} \begin{aligned} Q_{b} = \frac{1}{4\pi } \sum _{l} {|\Omega _l |} \end{aligned} \end{aligned}$$
(19)

Namely when \( \Omega _l \) is negative the surface has a negative curvature which can be interpreted as the surface bumps up or down. The bump number has the relation \( 1 \le Q_{b} \). The value \( 1 = Q_{b} \) belongs to the case of zero bumps.

3 Results

We have calculated the relaxed geometry, the atomisation energy \( E_{at} \), the topological charges and the bump numbers for all of the 30579 fullerene isomers \( C_{n} \) for each even \( n \) with \( 20 \le n \le 70 \). The atomisation energies were defined as

$$\begin{aligned} \begin{aligned} E_{at} = \frac{E_{tot}}{ n} -E_a \end{aligned} \end{aligned}$$
(20)

where \( E_{tot} \) is the tight binding total energy of the fullerene with \( n \) carbon atoms and \( E_{a} \) is the tight binding total energy of one isolated carbon atom [22].

Applying Eqs. (16) and (18) we obtained that the topological charge \( \Omega _l \) equals to one for each fullerenes, independent of \( n \) and isomer. From this follows that the average topological charge \( \Omega _{triangle} \) of a triangle equals to \( \Omega _{triangle} = \frac{1}{2(n-2)} \). This follows from Euler’s theorem \( V-E+F =2 \) and that each pentagon and hexagon was divided in order into 3 and 4 triangles.

Fig. 1
figure 1

The atomization energy \(E_{at}\) as the function of the bump number \(Q_b\) for the a \(C_{60}\), b \(C_{66}\), c \(C_{20} - C_{68}\) and d \(C_{70}\) fullerenes

Full size image

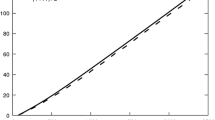
Figure 1a, b, c, and d show in order the atomisation energies in the function of the bump numbers \( Q_{b} \) for fullerenes \( C_{60}, C_{66}, C_{20}-C_{58}\) and \( C_{70} \). Usually the bump number of the most stable fullerenes equals to one. We have found the tendency, that as the stability of the fullerenes decreases the maximum value of the bump number increases as well. There are also fullerenes of value \( Q_{b} = 1 \) even for low stability fullerenes too.

In conclusion we can say that for fullerenes the topological number equals to one and the bump number increases as the stability of the fullerenes decreases, but there are bump numbers with the value one at structures of lower stability as well.