1 Introduction

Nanoparticles are increasingly considered for application in various ways in new, advanced technologies, probably the most significant of them is their use as catalysts or catalyst supports, not only in industrial settings but also as parts of user application devices or materials, e.g. self-cleaning mirrors or coatings or small-scale water purification systems [1,2,3]. A high number of nanoparticle synthesis methods have already been developed [1,2,3,4,5,6,7,8,9,10,11,12], and by now it is clear that the size of a nanoparticle fundamentally influences both its catalytic activity and toxicity. Therefore, controlling the size (and to a lesser extent, the shape) of nanoparticles is of primary importance for the potential applications.

The size distribution of nanoparticles is a central question in nanoparticle synthesis. It is clear that this distribution is governed by the formation kinetics of the nanoparticles, and nanoparticles are typically thermodynamically unstable compared to the bulk solid phase. So the control of particle size and distribution must rely on kinetic considerations.

Kinetic models of nanoparticle formation are usually complicated. The reason for this fact is that fundamental kinetic considerations require that each nanoparticle with a different size should be handled as a separate chemical species. Consequently, in any system of kinetic ordinary differential equations, the number of dependent variables is very high. Notable progress has been reached in handling such systems using the principle of lumping, which means that a number of different chemical species are handled as a single species and the form of the rate law is adjusted to allow for this fact [13,14,15,16,17,18,19,20,21,22,23,24]. Recently, the technique mechanism-enabled population balance modeling has been introduced [21, 24], which is able to give meaningful predictions for particle size distributions.

In our previous article [25], we showed that the analytical solution of a non-lumped kinetic model is still possible despite the fact that it has an infinite number of concentration variables. The model itself was based on pervious experimental results and theoretical considerations [4, 5, 26,27,28,29,30,31]. In the present work, we show that similar analytical solutions can be found in a limited number of other kinetic models as well. This paper will first state a general nucleation-growth type kinetic model, than identify the cases in which finding a symbolic solution is feasible. In two cases in addition to the one already known [25], the full solution is presented. In a number of other cases, some partial solutions are available. The main text of this paper will state all solutions without derivations or proofs. For those who are interested in the mathematical details, these are deposited in the Supplementary Information.

2 Results and discussion

A general nucleation-growth type kinetic model In this paper, a general class of models for nanoparticle formation will be considered, which is based on previous attempts to build such models and a comparison of experimental results [4, 5, 26,27,28,29,30,31]. The model contains three different kinds of steps, two of which represent nucleation, whereas the third one includes particle growth.

In the following models, M will denote a single monomeric unit of the nanoparticle, P will be a nucleation inductor, whereas Ci will represent a nanoparticle that contains exactly i monomeric units (i is a positive integer). The first step is called spontaneous nucleation. The chemical reaction and the rate equation are given as follows:

$$n{\mathrm{M}}\xrightarrow{{k_{{\mathrm{n}}} }}{\mathrm{C}}_{n} \quad \quad r_{{\mathrm{M}}} = k_{{\mathrm{M}}} \left[ {\mathrm{M}} \right]^{n}$$
(1)

The positive integer n here represents the lowest number of monomeric units that form a meaningful nucleus. It should be noted that not even n = 1 is excluded from the present analysis. Chemically, this would represent a case where only one monomeric unit is necessary for nucleation and possibly some other, unspecified reactants that do not influence the rate of the reaction.

The second step is also a nucleation step, but it is imagined to be caused by an external inductor P:

$${\mathrm{P}} + n{\mathrm{M}}\xrightarrow{{k_{{\mathrm{p}}} }}{\mathrm{C}}_{n} \quad \quad r_{{\mathrm{P}}} = k_{{\mathrm{P}}} \left[ {\mathrm{P}} \right]$$
(2)

Note that using such inductors is very common in polymerization studies [31], and nanoparticle formation experiments also often include a reagent whose only role is to help the formation of first nanoparticle nuclei [1,2,3,4,5,6,7,8,9,10,11,12].

The third step is nanoparticle growth, and is represented by the following chemical process and rate equation:

$${\mathrm{C}}_{i} + {\mathrm{M}}\xrightarrow{{k_{{{\mathrm{g}},i}} }}{\mathrm{C}}_{{i + 1}} \quad i \ge n\quad \quad r_{{{\mathrm{g,i}}}} = K\left( i \right)k_{{\mathrm{g}}} \left[ {\mathrm{M}} \right]\left[ {{\mathrm{C}}_{i} } \right]$$
(3)

This simple notation actually represents an infinitely large number of possible steps. It is assumed that nanoparticle growth can only occur through the stepwise addition of monomeric units, which means that the possible reaction of different nanoparticles with each other (called aggregation) is excluded from nucleation-growth type models. The function K(i) in Eq. 3 is called a kernel function, it describes how the growth rate constant of a nanoparticle depends on its size [26,27,28,29,30]. Four possible and practically useful kernel functions are shown in Table 1.

Table 1 Typical kernel functions in the nucleation-growth type nanoparticle formation models
Full size table

The mass kernel implies that the reactivity of a nanoparticle is directly proportional to its mass, which is proportional to the number of monomeric units in it. The surface kernel assumes that the reactivity is proportional to the surface of the nanoparticle. The Brownian kernel [26] shows a proportionality with the diameter (or radius) of the nanoparticle, whereas the diffusion kernel posits that the reactivity is independent of the particle size. The name of this last kernel function derives from the fact that the expected value of a diffusion controlled rate constant is independent of the size of a particle in general: the lower mobility of a larger particle is exactly compensated by the fact that it has a larger reactive cross section [32]. In the following considerations, we will show possible analytical results for the mass and diffusion kernels. We also attempted to use the surface and Brownian kernels, but thus far have found no meaningful possibilities to extract analytical solutions.

The system of simultaneous ordinary differential equations that describes the general model investigated here is as follows:

$$\begin{aligned} \frac{{{{\mathrm{d}[{M}]}}}}{{{\mathrm{d}}t}} & = - nk_{{\mathrm{M}}} {{[{M}]}}^{n} - nk_{{\mathrm{P}}} {{[{P}]}} - \sum\limits_{{j = n}}^{\infty } {K\left( j \right)k_{{\mathrm{g}}} {{[{M}][\mathrm{C}}}_{j} ]} \\ \frac{{{{{d}[\mathrm{C}}}_{n} ]}}{{{\mathrm{d}}t}} & = k_{{\mathrm{M}}} {{[{M}]}}^{n} + k_{{\mathrm{P}}} [P] - K\left( n \right)k_{{\mathrm{g}}} {{[{M}][\mathrm{C}}}_{n} ] \\ \frac{{{{{d}[\mathrm{C}}}_{i} ]}}{{{\mathrm{d}}t}} & = K\left( {i - 1} \right)k_{{\mathrm{g}}} {{[{M}][\mathrm{C}}}_{{i - 1}} ] - K\left( i \right)k_{{\mathrm{g}}} {{[{M}][\mathrm{C}}}_{i} ]\quad i > n \\ \frac{{{{{d}[{P}]}}}}{{{\mathrm{d}}t}} & = - k_{{\mathrm{P}}} {{[{P}]}} \\ \end{aligned}$$
(4)

The typical initial conditions of nanoparticle formation are such when at time t = 0, the initial concentration of the monomeric unit is [M]0, the initial concentration of the inductor is [P]0, whereas all of the nanoparticles are absent, i.e. [Ci]0 = 0.

As in our initial study [25], it is useful to introduce dimensionless (or scaled) physical properties to simplify the differential equation somewhat. This process does not limit the general nature of the results obtained in any way. Dimensionless concentrations m, p, and ci, dimensionless time τ, and dimensionless rate constants α and

$$\begin{aligned} c_{i} & = \frac{{{\text{[C}}_{i} {]}}}{{{[}\text{M} {]}_{{\text{0}}} }} \\ m & = \frac{{{\text{[M]}}}}{{{[}\text{M} {]}_{{\text{0}}} }} \\ p & = \frac{{{\text{[P]}}}}{{{[}\text{M} {]}_{{\text{0}}} }} \\ \tau & = k_{{\text{g}}} {[}\text{M} {]}_{{\text{0}}} t \\ \alpha & = \frac{{k_{{\text{M}}} {[}\text{M} {]}_{{\text{0}}} ^{{n - 2}} }}{{k_{{\text{g}}} }} \\ \beta & = \frac{{k_{{\text{P}}} }}{{{[}\text{M} {]}_{{\text{0}}} k_{{\text{g}}} }} \\ \end{aligned}$$
(5)

β are introduced as follows:It should be noted that all of these properties are non-negative real numbers because of their physical meaning. Using these new, dimensionless quantities, Eq. 4 can be re-stated as follows:

$$\begin{aligned} \frac{{{\mathrm{d}}m}}{{{\mathrm{d}}\tau }} & = - n\alpha m^{n} - n\beta p - m\sum\limits_{{j = n}}^{\infty } {K\left( j \right)c_{j} } \\ \frac{{{\mathrm{d}}c_{n} }}{{{\mathrm{d}}\tau }} & = \alpha m^{n} + \beta p - K\left( n \right)mc_{n} \\ \frac{{{\mathrm{d}}c_{i} }}{{{\mathrm{d}}\tau }} & = K\left( {i - 1} \right)mc_{{i - 1}} - K\left( i \right)mc_{i} \quad i > n \\ \frac{{{\mathrm{d}}p}}{{{\mathrm{d}}\tau }} & = - \beta p \\ \end{aligned}$$
(6)

Some possible analytical solutions of Eq. 6 will be shown in this article. As the induction is either exclusively spontaneous or induced in practical cases, only the case αβ = 0 will be considered for the mass and diffusion kernel functions. Also, the physically meaningful models are typically characterized by α « 1and p0 = [P]0/[M]0 « 1.

General remarks Obviously, the solutions of Eq. 6 depend on the particular kernel function and the values on n. However, there are a few considerations that can be applied independently of these variables.

First, it can be seen that the last part in Eq. 6 (for the derivative of p) is a stand-alone ordinary differential equation. So whenever β > 0, the time dependence of p can be given very simply:

$$p = p_{0} \mathrm{e} ^{{ - \beta \tau }}$$
(7)

Here p0 is the initial value of p at t = 0 (i.e. p0 = [P]0/[M]0).

Furthermore, the qth moment of the variables ci is often a useful mathematical tool during the solution. It is defined as:

$$\mu _{q} = \sum\limits_{{i = n}}^{\infty } {i^{q} c_{i} }$$
(8)

It should be noted that q can be any real number, it is neither an integer nor necessarily positive. The first moment (q = 1) has a clear physical meaning: it gives the total number of monomeric units present in the nanoparticles. For the first moment, the following differential equation can be derived:

$$\frac{{{\mathrm{d}}\mu _{1} }}{{{\mathrm{d}}\tau }} = n\alpha m^{n} + n\beta p + \sum\limits_{{i = n}}^{\infty } {K\left( i \right)mc_{i} }$$
(9)

This derivative is exactly the opposite of the derivative for m in Eq. 6, so the following equation is valid:

$$\frac{{{\mathrm{d}}\mu _{1} }}{{{\mathrm{d}}\tau }} + \frac{{{\mathrm{d}}m}}{{{\mathrm{d}}\tau }} = 0$$
(10)

As all ci values are zero at t = 0, so the initial value of μ1 is also 0. In addition, the initial value of m is 1 because of the scaling. Therefore, integrating Eq. 10 gives the following formula:

$$\mu _{1} + m = 1$$
(11)

This equation is the same as the mass conservation law for the system (i.e. none of the processes changes the total number of monomeric units in the system). It is also noted that the time derivative of μ1 is always positive, which means that it is a monotonically increasing function and by the same argument, m is a monotonically decreasing function of dimensionless time.

The zeroth moment (μ0) also has a physical meaning: it is the sum of the concentrations of the nanoparticles. It is connected to the other functions by the following differential equation:

$$\frac{{{\mathrm{d}}\mu _{0} }}{{{\mathrm{d}}\tau }} = \alpha m^{n} + \beta p$$
(12)

Again, it must be remarked that μ0 is a monotonically increasing function. It is also interesting to note that for induced nucleation (α = 0), μ0 only depends on the nucleation process irrespectively of the kernel function used, and its time dependence can be given as follows:

$$\mu _{0} = p_{0} \left( {1 - \mathrm{e} ^{{ - \beta \tau }} } \right)$$
(13)

With this equation, the general considerations seem to be exhausted. Further results will be given for specific kernel functions.

Diffusion kernel, spontaneous nucleation This is the specific case for which K(i) = 1 and β = 0. The infinite sum appearing in the first part of Eq. 6 (giving the time derivative of m) becomes identical to μ0 in this case:

$$\frac{{{\mathrm{d}}m}}{{{\mathrm{d}}\tau }} = - n\alpha m^{n} - m\mu _{0}$$
(14)

Considering Eq. 12 with β = 0 together with the previous equation, and also recalling the fact that μ0 is monotonically increasing, m can be sought as a function of μ0 instead of τ:

$$\frac{{{\mathrm{d}}m}}{{{\mathrm{d}}\mu _{0} }} = - n - \frac{{\mu _{0} }}{\alpha }m^{{1 - n}}$$
(15)

It seems difficult to find a general solution of this ordinary differential equation for any value of n. However, only positive integers are physically meaningful here. The case n = 1 is a particularly simple one as the right hand side does not depend on m in this case, and the equation can be solved by a simple integration:

$$m = - \frac{1}{{2\alpha }}\mu _{0} ^{2} - \mu _{0} + 1$$
(16)

Note that the initial condition is μ0 = 0 when m = 1, it was already built into the solution given in Eq. 16. It is clear that the final value (at τ = ∞) of m is zero as all monomeric units are consumed. Therefore, the final value μ0 can be found by substituting m = 0 into Eq. 16. The result is:

$$\mathop {\lim }\limits_{{\tau \to \infty }} \mu _{0} = \sqrt {\alpha ^{2} + 2\alpha } - \alpha$$
(17)

Substituting Eq. 16 back into Eq. 12 at β = 0 gives the following ordinary differential equation for μ0:

$$\frac{{{\mathrm{d}}\mu _{0} }}{{{\mathrm{d}}\tau }} = - \frac{{\mu _{0} ^{2} }}{2} - \alpha \mu _{0} + \alpha$$
(18)

This is a separable differential equation, its solution can be found after lengthy, but routine calculations (th stands for the hyperbolic tangent function, arth for the inverse hyperbolic tangent function in the formula):

$$\mu _{0} = - \alpha + \sqrt {\alpha \left( {2 + \alpha } \right)} \;\mathrm{th} \left( {\frac{{\tau \sqrt {\alpha \left( {2 + \alpha } \right)} }}{2} + {\mathrm{arth}}\left( {\sqrt {\frac{\alpha }{{2 + \alpha }}} } \right)} \right)$$
(19)

Through Eq. 19, the time dependences of all ci functions become available in an analytical form. Using the same strategy of considering the dependence on μ0 rather than directly on τ, the relevant part of Eq. 6 can be transformed into a system of linear, first order ordinary differential equations:

$$\begin{aligned} \frac{{{\mathrm{d}}c_{1} }}{{{\mathrm{d}}\mu _{0} }} & = 1 - \frac{{c_{1} }}{\alpha } \\ \frac{{{\mathrm{d}}c_{i} }}{{{\mathrm{d}}\mu _{0} }} & = \frac{{c_{{i - 1}} }}{\alpha } - \frac{{c_{i} }}{\alpha }\quad i > 1 \\ \end{aligned}$$
(20)

This class of ordinary differential equations is encountered in chemical kinetics [33]. The general solution is:

$$c_{i} = \alpha - \alpha \mathrm{e} ^{{ - \mu _{0} /\alpha }} \sum\limits_{{j = 0}}^{{i - 1}} {\frac{1}{{j!}}\left( {\frac{{\mu _{0} }}{\alpha }} \right)^{j} }$$
(21)

So the full analytical solution was found for the case of diffusion kernel, spontaneous nucleation, n = 1.

Now moving on for n = 2, Eq. 15 takes the following particular form:

$$\frac{{{\mathrm{d}}m}}{{{\mathrm{d}}\mu _{0} }} = - 1 - \frac{{\mu _{0} }}{{\alpha m}}$$
(22)

The solution of this ordinary differential equation can only be given in an implicit form:

$$2\sqrt {\frac{\alpha }{{1 - \alpha }}} \arctan \left( {\sqrt {\frac{\alpha }{{1 - \alpha }}} \frac{{\mu _{0} + m}}{{\mu _{0} }}} \right) = \pi \sqrt {\frac{\alpha }{{1 - \alpha }}} + \ln \left( {\frac{{\mu _{0}^{2} }}{\alpha } + 2m\mu _{0} + m^{2} } \right)$$
(23)

The notation arctan refers to the arcus tangent function here. This implicit form cannot be used directly at m = 1, but there the initial conditions give μ0 = 0 directly. Also, the solution is restricted to the case α ≠ 4. This is not much of a limitation as α  ≪  1 under typical conditions that are physically relevant. Furthermore, the final value of μ0 can be given for the case as well:

$$\mathop {\lim }\limits_{{\tau \to \infty }} \mu _{0} = \sqrt \alpha \mathrm{e} ^{{\sqrt {\frac{\alpha }{{1 - \alpha }}} \left( {\arctan \left( {\sqrt {\frac{\alpha }{{1 - \alpha }}} } \right) - \frac{\pi }{2}} \right)}}$$
(24)

For other positive integer values of n, no analytical formulas could be obtained.

Diffusion kernel, induced nucleation This is the specific case for which K(i) = 1 and α = 0. Equations 7 and 13 are valid here, so the final value of the zeroth moment can be given readily:

$$\mathop {\lim }\limits_{{\tau \to \infty }} \mu _{0} = p_{0}$$
(25)

Under these conditions, the differential equation for m takes the following form:

$$\frac{{{\mathrm{d}}m}}{{{\mathrm{d}}\tau }} = - n\beta p_{0} \mathrm{e} ^{{ - \beta \tau }} - mp_{0} \left( {1 - \mathrm{e} ^{{ - \beta \tau }} } \right)$$
(26)

The solution is:

$$m = \mathrm{e} ^{{p_{0} /\beta - p_{0} \mathrm{e} ^{{ - \beta \tau }} /\beta - p_{0} \tau }} - n\beta p_{0} \mathrm{e} ^{{ - p_{0} \mathrm{e} ^{{ - \beta \tau }} /\beta - p_{0} \tau }} \int\limits_{0}^{\tau } {\mathrm{e} ^{{p_{0} \mathrm{e} ^{{ - \beta \xi }} /\beta + p_{0} \xi - \beta \xi }} {\mathrm{d}}\xi }$$
(27)

No analytical expressions were found for the ci variables in this case.

Mass kernel, spontaneous nucleation This is the specific case for which K(i) = i and β = 0. The infinite sum appearing in the first part of Eq. 6 (giving the time derivative of m) becomes identical to μ1, which – as shown in Eq. 11—is identical to 1 − m. Consequently, the first part of Eq. 6 becomes a stand-alone ordinary differential equation giving the dependence of m on τ:

$$\frac{{{\mathrm{d}}m}}{{{\mathrm{d}}\tau }} = - n\alpha m^{n} - m\left( {1 - m} \right)$$
(28)

This is a separable ordinary differential equation. Yet a general solution of this equation does not seem to be accessible. However, similarly to the case of diffusion kernel, formulas can be found for the smallest values of n.

For n = 1, the solution of Eq. 28 is:

$$m = \frac{{\alpha + 1}}{{\alpha \mathrm{e} ^{{\left( {\alpha + 1} \right)\tau }} + 1}}$$
(29)

The same solution for n = 2 is:

$$m = \frac{1}{{1 - 2\alpha + 2\alpha \mathrm{e} ^{\tau } }}$$
(30)

For n = 3, the solution remains implicit:

$$\tau = \frac{1}{{\sqrt {1 - 12\alpha } }}\left[ {\mathrm{arth} \left( {\frac{{6\alpha m - 1}}{{\sqrt {1 - 12\alpha } }}} \right) - \mathrm{arth} \left( {\frac{{6\alpha - 1}}{{\sqrt {1 - 12\alpha } }}} \right)} \right] + \frac{1}{2}\ln \left( {1 - \frac{1}{{3\alpha m}} + \frac{1}{{3\alpha m^{2} }}} \right)$$
(31)

For higher values of n, no meaningful formulas could be obtained.

It was found that for the mass kernel function, it is convenient to consider concentrations ci as a function of m rather than τ. In this way, the ordinary differential equation defining cn is as follows:

$$\frac{{{\mathrm{d}}c_{n} }}{{{\mathrm{d}}m}} = \frac{{nc_{n} - \alpha m^{{n - 1}} }}{{n\alpha m^{{n - 1}} + \left( {1 - m} \right)}}$$
(32)

Again, no general solution was found for this form, but particular formulas have been obtained for specific values of n. For n = 1, the solution is:

$$c_{1} = \frac{{\alpha - \alpha m}}{{1 + \alpha - m}}$$
(33)

For n = 2, the solution of Eq. 32 is:

$$c_{2} = - \frac{\alpha }{{4\alpha - 6}}\left( {1 + 2m} \right) + \frac{{3\alpha }}{{4\alpha - 6}}\left( {\frac{1}{{2\alpha }} - \frac{m}{{2\alpha }} + m} \right)^{{2/\left( {2\alpha - 1} \right)}}$$
(34)

For n = 3, the software Mathematica returned a symbolic solution of Eq. 32 using hypergeometric functions in the complex number plane (see Supplementary Information), it was so complicated that any attempts to use it in practice seemed futile.

For variables ci (i > n) considered as a function of τ, the relevant part of Eq. 6 reduces to the following form:

$$\frac{{{\mathrm{d}}c_{i} }}{{{\mathrm{d}}m}} = \frac{{ic_{i} - \left( {i - 1} \right)c_{{i - 1}} }}{{n\alpha m^{{n - 1}} + 1 - m}}\quad i > n$$
(35)

This equation makes it possible to calculate the variables ci successively once the first one (i.e. cn) is known. For n = 1, the general solution is found as:

$$c_{i} = \frac{\alpha }{i}\left( {\frac{{1 - m}}{{\alpha + 1 - m}}} \right)^{i}$$
(36)

The case n = 2 here bears some special practical relevance [4, 5, 17]. In our previous publication that was solely dedicated to this particular system [25], lengthy derivations were developed to show that the analytical solution is:

$$c_{i} = \frac{{\alpha \left( {i - 1} \right)!\left( { - 1} \right)^{{i - 1}} \left( {m - 1} \right)}}{{\prod\nolimits_{{j = 2}}^{i} {\left( {2\alpha - j - 1} \right)} }} + \sum\limits_{{j = 2}}^{i} {\frac{{\alpha \left( {j^{2} - 1} \right)}}{{j\left( {2\alpha - j - 1} \right)}}\left( {\begin{array}{*{20}c} {i - 1} \\ {j - 1} \\ \end{array} } \right)\left( { - 1} \right)^{j} \left[ {\left( {\frac{{1 - m}}{{2\alpha }} + m} \right)^{{j/\left( {2\alpha - 1} \right)}} - 1} \right]}$$
(37)

For higher values of n, the successive solution procedure could not even be started as no explicit formulas were gained for cn at n ≥ 3.

Unlike in the case of the diffusion kernel, μ0 does not play a special role for the mass kernel in obtaining the analytical solution. Yet the value of the zeroth moment has some importance on its own when the average particle size is calculated, which is the most common property available from experimental works. This property can be calculated by integrating Eq. 12 at β = 0:

$$\frac{{{\mathrm{d}}\mu _{0} }}{{{\mathrm{d}}\tau }} = \alpha m^{n}$$
(38)

Alternatively, μ0 can also be sought as the function of m by combining Eqs. 28 and 38:

$$\frac{{{\mathrm{d}}\mu _{0} }}{{{\mathrm{d}}m}} = - \frac{\alpha }{{n\alpha + \left( {1 - m} \right)m^{{1 - n}} }}$$
(39)

For n = 1, the zeroth moment can be given based on both equations:

$$\mu _{0} = \alpha \left( {\alpha + 1} \right)\tau + \alpha \ln \left( {\frac{{1 + \alpha }}{{1 + \alpha \mathrm{e} ^{{\left( {\alpha + 1} \right)\tau }} }}} \right) = \alpha \ln \left( {1 + \frac{1}{\alpha } - \frac{m}{\alpha }} \right)$$
(40)

The same can be done for n = 2:

$$\mu _{0} = \frac{\alpha }{{\left( {1 - 2\alpha } \right)\left( {1 - 2\alpha + 2\alpha \mathrm{e} ^{\tau } } \right)}} + \frac{{\alpha \tau - \alpha + 2\alpha ^{2} }}{{\left( {1 - 2\alpha } \right)^{2} }} - \frac{{\alpha \ln \left( {1 - 2\alpha + 2\alpha \mathrm{e} ^{\tau } } \right)}}{{\left( {1 - 2\alpha } \right)^{2} }} = \frac{{\alpha m - \alpha }}{{1 - 2\alpha }} + \frac{{\alpha \ln \left( {\frac{1}{{2\alpha }} - \frac{m}{{2\alpha }} + m} \right)}}{{\left( {1 - 2\alpha } \right)^{2} }}$$
(41)

For n = 3, an explicit analytical formula can be given for the dependence on m:

$$\mu _{0} = \frac{{1 - m}}{3} + \frac{{\left( {1 - 6\alpha } \right)}}{{9\alpha \sqrt {1 - 12\alpha } }}\mathrm{arth} \left( {\frac{{\left( {1 - m} \right)\sqrt {1 - 12\alpha } }}{{1 + 6\alpha m - m}}} \right) - \frac{1}{{18\alpha }}\ln \left( {\frac{1}{{3\alpha }} - \frac{m}{{3\alpha }} + m^{2} } \right)$$
(42)

Similar explicit formula could not be obtained for n ≥ 4.

Mass kernel, induced nucleation This is the specific case for which K(i) = i and α = 0. Equations 7, 13 and 25 are valid for this case as well. Under these conditions, the differential equation for m takes the following form:

$$\frac{{{\mathrm{d}}m}}{{{\mathrm{d}}\tau }} = - n\beta p_{0} \mathrm{e} ^{{ - \beta \tau }} - m\left( {1 - m} \right)$$
(43)

The software Mathematica identified a solution of this differential equation with the confluent hypergeometric and gamma functions (see Supplementary Information), but this was too complicated for any practical use.

Particle size average and distribution in the final state In experimental studies of nanoparticle formation, the average particle size is the most common property that is used to characterize the process. As shown previously [25], the average number of monomeric units (N) in the nanoparticles formed can be simply calculated as the ration of the first and the zeroth moments:

$$N = \frac{{\mu _{1} }}{{\mu _{0} }} = \frac{{1 - m}}{{\mu _{0} }}$$
(44)

As defined in Eq. 44, N is a function of time (or m). In typical experimental works, on the other hand, it is only determined after the completion of the process [1,2,3,4,5,6,7,8,9,10,11,12], so the most relevant property from theoretical studies is its limiting value at infinite time:

$$N_{\infty } = \frac{1}{{\lim _{{m \to 0}} \mu _{0} }}$$
(45)

For induced nucleation, N∞ = 1/p0 always holds. Table 2 summarizes the analytical formulas obtained for N∞ in various models.

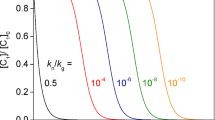
Table 2 Formulas suitable for calculating the average number of monomeric units in nanoparticles at the end of the process for spontaneous nucleation
Full size table

The five different functions (N∞ vs. α) are displayed graphically in Fig. 1. It is seen that large average particle sizes are expected when the rate constant of the spontaneous nucleation is orders of magnitude smaller than the rate constants of particle growth. In addition, the curves are close to independent of the value of n.

Fig. 1
figure 1

The average number of monomeric units in a particle (N∞) as a function the dimensionless rate constant of the spontaneous nucleation (α) in various models. D1: diffusion kernel with n = 1; D2: diffusion kernel with n = 2; M1: mass kernel with n = 1; M2: mass kernel with n = 2; M3: mass kernel with n = 3

Full size image

Experimental determinations of nanoparticle size distributions are also common in the literature [1,2,3,4,5,6,7,8,9,10,11,12]. Similarly to the average sizes, this is also almost exclusively done in the final state. For the three systems where the full solution of the model was obtained, these distributions can be given by finding the values of ci in the final state.

For the diffusion kernel at n = 1:

$$\mathop {\lim }\limits_{{\tau \to \infty }} c_{i} = \alpha - \alpha \mathrm{e} ^{{1 - \sqrt {1 + 2/\alpha } }} \sum\limits_{{j = 0}}^{{i - 1}} {\frac{1}{{j!}}\left( {\sqrt {1 + 2/\alpha } - 1} \right)^{j} }$$
(46)

Similarly, for the mass kernel at n = 1:

$$\mathop {\lim }\limits_{{\tau \to \infty }} c_{i} = \frac{\alpha }{i}\left( {\frac{1}{{\alpha + 1}}} \right)^{i}$$
(47)

For the mass kernel at n = 2:

$$\mathop {\lim }\limits_{{\tau \to \infty }} c_{i} = \frac{{\alpha \left( {i - 1} \right)!\left( { - 1} \right)^{i} }}{{\prod\nolimits_{{j = 2}}^{i} {\left( {2\alpha - j - 1} \right)} }} + \sum\limits_{{j = 2}}^{i} {\frac{{\alpha \left( {j^{2} - 1} \right)}}{{j\left( {2\alpha - j - 1} \right)}}\left( {\begin{array}{*{20}c} {i - 1} \\ {j - 1} \\ \end{array} } \right)\left( { - 1} \right)^{j} \left[ {\left( {\frac{1}{{2\alpha }}} \right)^{{j/\left( {2\alpha - 1} \right)}} - 1} \right]}$$
(48)

For the mass kernel at n = 2, whose solution was already found in our previous work, it was pointed out there is no extremum on the distribution as ci values decrease monotonically as i increases, although the actual numerical calculations are difficult because of the large binomial coefficients with alternating signs [25, 34, 35]. It was shown here that the final distributions are also monotonically decreasing for both the diffusion kernel and the mass kernel at n = 1 (see Supplementary Information).

Time dependence of the concentration of the monomeric unit In some cases, the concentration of the monomeric unit could be followed as a function of time in experimental studies [5]. Therefore, the dependence of the dimensionless concentration of the monomeric unit on dimensionless time is shown in Fig. 2 for the two cases where the solution is reported the first time in the present paper (diffusion and mass kernels with n = 1). Figure 2 shows that the time dependences show the peculiar induction behavior [36, 37] that was observed in a number of experimental studies [13,14,15, 18, 38].

Fig. 2
figure 2

The dimensionless concentration of the monomeric unit (m) as a function of dimensionless time (τ) in two models at α = 10−4. D1: diffusion kernel with n = 1; M1: mass kernel with n = 1

Full size image

3 Conclusion

In addition to the one solution already known, this work has shown that full symbolic solutions are available for the kinetic ordinary differential equations of two other nucleation-growth type nanoparticle formation models. The presented analysis also implies that reaching similar achievements would be very difficult for other models. Therefore, for experimentally important cases, using approximations is probably inevitable. However, the approximations should not necessarily involve lumping variables. For any approximations in kinetic models of nanoparticle growth, the three known exact analytical solutions should serve as benchmark tests for proving the validity of the approach.