1 Introduction

W. F. (Joe) Vinen devoted most of his scientific life to the study of helium at low temperatures, both \(^3\)He and \(^4\)He—in the fluid, superfluid and solid phases. Much of this rich seam of work, both experimental and theoretical, concerned quantized vortices. However, he also made important contributions to the study of magnetic flux lines, which are the analogous quantized topological objects in superconductors. He emphasized what could be learned by looking at the fundamental similarities between superfluids and superconductors, particularly the existence of the condensate wavefunction in both Bose and Fermi systems. The Birmingham work discussed in this paper may or may not have Vinen as a co-author, but was all inspired by his deep understanding of the superfluid state of matter, and much of this is still of interest today.

2 The Condensate Wavefunction

An important part of the legacy left by any scientific leader is the education and training they impart to their co-workers and students. One of the important concepts that Vinen passed on in Birmingham, and to the wider public by his chapter in the ‘Bible of Superconductivity’ [1], was that of the Condensate Wavefunction. This is the (complex) order parameter that becomes nonzero on cooling below the temperature of the second-order transition to the superfluid/superconducting state. Vinen emphasized that it embodies ‘macroscopic quantum coherence’ [2]. The single-valuedness of the condensate wavefunction entails the existence of quantized vortices and flux lines. It is tempting to imagine that for \(^4\)He, the order parameter is just the wavefunction of the superfluid helium atoms. For an ideal Bose gas, this would be a single-particle wavefunction because—at temperature \(T = 0\) and zero superfluid velocity \({\textbf{v}}_s\)—all of the atoms would be Bose-condensed into the same \(\hbar {\textbf{k}} = 0\) zero momentum state. However, liquid helium is by no means an ideal Bose gas (and in any case, such an ideal system would cease to be a superfluid at any nonzero \({\textbf{v}}_s\)). Instead, the \(^4\)He atoms are strongly interacting in the liquid, which means that their wavefunctions include a large fraction of virtual k \(\ne 0\) states. Nevertheless, so long as there is a finite fraction (i.e., a macroscopic number) of helium atoms in the same state, (i) the system is superfluid; (ii) the superfluid density at \(T = 0\) is that of the whole fluid and (iii) the bare helium mass m appears in the momentum equation \(\hbar {\textbf{k}} = m {\textbf{v}}_s\). Hence, the practical effect is as though the simple wavefunction picture applies. In superconductors, a similar—apparently single-particle—wavefunction describes the macroscopic quantum coherence of the state. However, this has to be regarded as the wavefunction for the center of mass of the Cooper pairs [1, 2]. This has the consequence that the quantum of magnetic flux in a superconductor is \(\Phi _0 = h / 2e\) and not h/e [3, 4].

We can extend the condensate approach to finite temperatures, where an empirical 'two fluid model' of both superfluids and superconductors has been employed. This supposes that the total density \(\rho\) can be written as a sum of normal and superfluid densities \(\rho _n\) and \(\rho _s\). However, \(\rho _n\) is not an actual separate fluid, but the effect of thermal excitations of the condensate. The calculation goes as follows. If the superfluid is moving at \({\textbf{v}}_s\) in the laboratory frame, the energy \(\epsilon\) (in that frame) of an excitation of wavevector k is modified:

$$\begin{aligned} \epsilon ({\textbf{k}}, {\textbf{v}}_s) = \epsilon ({\textbf{k}})+ \hbar \, {\textbf{k}}. {\textbf{v}}_s \end{aligned}$$
(1)

The equilibrium occupation f of these excitations is no longer centered at \({\textbf{k}} = 0\). (f is the Fermi or Bose distribution function, depending whether we are dealing with a superconductor or \(^4\)He.) To first order in \({\textbf{v}}_s\), the change is:

$$\begin{aligned} \delta f({\textbf{k}}) = \frac{\partial f}{\partial \epsilon }\, \hbar \,{\textbf{k}}. {\textbf{v}}_s. \end{aligned}$$
(2)

This displaced distribution carries a momentum P per unit volume given by:

$$\begin{aligned} {\textbf{P}} = \frac{g}{8\pi ^3}\int \delta f\,\hbar ~{\textbf{k}}\,d^3{\textbf{k}}=\frac{g \hbar ^2}{8\pi ^3}\int \frac{\partial f}{\partial \epsilon }({\textbf{k}}. {\textbf{v}}_s){\textbf{k}}\,d^3{\textbf{k}}, \end{aligned}$$
(3)

where \(g =2\) for the two states of spin of fermion quasi-particles and \(g=1\) for the excitations in helium. Integrating over the directions of k in the isotropic case, this can further be written:

$$\begin{aligned} {\textbf{P}} = \frac{g\hbar ^2}{6\pi ^2}\int k^2\left( \frac{\partial f}{\partial \epsilon }/\frac{\partial \epsilon }{\partial k}\right) d\epsilon \cdot {\textbf{v}}_s = - \rho _n {\textbf{v}}_s. \end{aligned}$$
(4)

The negative sign of \({\partial f}/ {\partial \epsilon }\) indicates that the quantity multiplying \({\textbf{v}}_s\) is negative and cancels a part of the momentum \(\rho {\textbf{v}}_s\) carried by the condensate. This is the 'part of the fluid' which is at rest in the laboratory frame in equilibrium, so we write its contribution as -\(\rho _n {\textbf{v}}_s\). The remainder of the momentum is superflow. Thus, \(\rho _s\) is defined as the difference of two quantities: \(\rho _s = \rho -\rho _n\) [1]. The excitations giving rise to the normal fluid in helium are phonons plus ‘rotons’ at higher energy, whereas in superconductors, they are unpaired electronic quasiparticles. In both cases, the critical temperature \(T_c\) for the disappearance of superfluidity/superconductivity is that temperature where \(\rho _n\) has risen to be equal to \(\rho\).

3 Flux Flow in Superconductors

3.1 Analogy Between Rotating Helium and Type-II Superconductors

If a cylindrical container of superfluid \(^4\)He is rotated about the cylinder axis, then for all rotation rates larger than a small value \(\Omega _{c1}\), which depends on the cylinder radius, the equilibrium situation is that of an array of quantized vortex lines within the fluid. Each line carries a quantum of circulation equal to h/m, with the density of vortex lines increasing with \(\Omega\). In principle, at sufficiently large \(\Omega _{c2}\), the vortex cores would overlap, and the superfluid would revert to the normal state. [In fact, due to the \(\sim 1\)Å size of the cores near \(T=0\), the upper critical frequency \(\Omega _{c2} \sim 10^{12}\) rads\(^{-1}\), it is unlikely that this condition can be reached in practice in \(^4\)He.]

As pointed out by Vinen [1], this general behavior has an analogy in the response to a magnetic field of a Type-II superconductor (\(\kappa = \lambda / \xi > 1/\surd 2\), where \(\lambda\) and \(\xi\) are the magnetic penetration depth and coherence length, respectively). In this case, flux lines enter at a field \(H_{c1}\), mainly determined by the value of the length \(\lambda\), and the superconductivity is finally destroyed when the vortex cores of size \(\sim \xi\) overlap at \(H_{c2}\) [1, 2]. In this case, the size of \(\xi\) often gives values of \(B_{c2} = \mu _0 H_{c2}\) in the Tesla range, achievable in a laboratory. It is widely appreciated that the only superconductors capable of operating at high fields have large values of \(\kappa\) and large upper critical fields \(H_{c2}\). In comparison, \(^4\)He behaves like an extreme Type-II superfluid.

3.2 Effect of a Transport Current

When a transport current passes perpendicular to a flux line in a superconductor, there is a force on the flux line. This is expected to arise from the Magnus force which applies to vortex lines in superfluids and equally to classical vortices in normal fluids. This arises essentially from the Bernouilli effect: The sum of the transport supercurrent velocity and the velocity due to the vortex circulation are different on opposite sides of a vortex. If this force causes the flux line to move, there will be dissipation, and perfect superconductivity is lost. Hence, for practical applications such as wires for superconducting magnets, the flux lines have to be pinned in position by suitably designed inhomogeneities. However, from the pure scientific point of view, there is great interest in the exact nature and magnitude of the force, and the resulting motion of the flux lines in the absence of pinning. To investigate this experimentally is challenging, as large currents have to be passed to overcome any residual pinning forces. The approach used by Vinen and co-workers [5] was to use a contactless method of measurement: A small change \(\sim 1\) mT in applied field induces large eddy currents in the sample. The decay time of the field due to these currents can be observed with a pickup coil and is a measure of the resistivity of the sample [6].

The theory of the resulting flux motion is extrememely complicated, as the magnitude and phase of the order parameter is changing with time, and it is by no means clear where currents flow and how forces on flux lines are transmitted to the lattice. The initial work required approximate models, limited to temperatures well below \(T_c\), which nevertheless have provided a reasonable account of experimental data (e.g., [5, 7]). One widely cited model is that of Bardeen and Stephen [8], but a more physically based model, which correctly predicts the field-dependence of the Hall effect [7], is that of Nozières and Vinen [9], later extended by Vinen and Warren [10]. There are two simple results to quote. Firstly, the field-dependence of the resistivity \(\rho (B)\) when the flux lines are free to move:

$$\begin{aligned} \rho (B)\simeq \frac{B}{B_{c2}} \times \rho _n, \end{aligned}$$
(5)

where here \(\rho _n\) represents the resistivity in the normal state, and B is the average induction in the sample. Secondly, if the flux lines move with a velocity v\(_L\), then the electric field E connected with the flux line motion in the mixed state is given by:

$$\begin{aligned} {\textbf{E}} = -{\textbf{v}}_L \times {\textbf{B}}. \end{aligned}$$
(6)

This equation looks as though it is related to electromagnetic induction when a conductor is moved at velocity -\({\textbf{v}}_L\) through a field. However, neither conductor nor field is moving in this case. It is better to think of this as an example of the time-dependent Josephson effect, where a voltage difference arises when there is a time-dependent phase difference between two parts of a superconductor [11]. The phase change of the order parameter is of course directly related to the passage of the flux lines across it, with each flux line carrying a phase of 2\(\pi\). Incidentally, the velocity v\(_L\) has been measured directly by a neutron scattering technique [12]. Vinen’s work has also been cited in a discussion of the motion of magnetic flux lines in the superconducting parts of neutron stars [13].

Fig. 1
figure 1

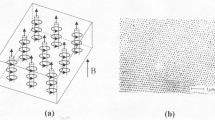
a Flux flow geometry described by Eq. 6. b Geometry envisaged for an ‘Ettingshausen Fridge.’ In both cases, the magnetic induction is throughout the samples and is perpendicular to the page

Full size image

The geometry expressed by Eq. 6 is schematically represented in Fig. 1a. In a normal metal with this geometry, there is in addition a small transverse (Hall effect) voltage. In the superconducting mixed state, there is also a Hall effect, which is predicted [9, 10] to have the same value as in the normal state just above \(B_{c2}\). This transverse voltage arises because \({\textbf{v}}_L\) is not exactly perpendicular to the direction of the current flow but is at the Hall angle to the perpendicular. Early experiments often gave discordant results for this small voltage, because slight grooves in the surface of the sample may cause ‘guided motion’ of the vortices [9], which can give a Hall voltage quite different in sign or magnitude from that expected. A later experiment using very large currents to minimize the effect of pinning confirmed Vinen’s predictions [7]. These complications should be borne in mind, as measurements of the Hall effect in the mixed state of High \(T_c\) superconductors continue to this day (e.g., [14]) and often show anomalous behavior, such as sign reversal. However, in these materials, there are additional phenomena, such as charge density waves, unusual energy-dependence of scattering times, fluctuations and the existence of a vortex liquid, which had no place in pre-High \(T_c\) materials and may account for the anomalies.

3.3 Thermal Hall Effect and the ‘Ettingshausen Fridge’

Many years ago, Ettingshausen encountered an effect, formerly known by his name, but now by the less obscure term: ‘Thermal Hall Effect.’ This is the appearance of a transverse temperature difference, when a current is passed a through a material in a perpendicular magnetic field [15]. As we see in Fig. 1a, flux lines are created at the left of the sample and destroyed on the right, and the vortex cores have entropy, so their creation causes a temperature drop and their destruction a temperature rise. In a superconductor not too close to \(B_{c2}\) or \(T_c\), this effect is expected to be strong, as most of the excitations and entropy in the material will be localized in the vortex cores, and carried across the sample with the flux lines.

This led Vinen to suggest to the Birmingham group the possibility of a low-temperature ‘Ettingshausen Fridge,’ using the geometry of Fig. 1b, which would transfer heat from low to high temperatures by the motion of vortices. The core of a flux line has approximately the same heat capacity as a normal region of radius \(\sim \xi\), so its entropy varies approximately linearly with T, similar to that of \(^3\)He in a dilution fridge. However, the Ettingshausen fridge would need no expensive \(^3\)He, no gas handling system and no fine capillaries that could become blocked; instead: only a moderate magnetic field and a high-current, low-voltage supply, such as that used for superconducting magnets. Despite the fact that there is dissipation due to the flux line motion, the equations indicated that in principle, this refrigerator should work under suitable conditions, partly due to the fact that the flux line cores would soak up entropy as they moved up the temperature gradient, and partly due to the fact that the presence of flux lines can reduce the thermal conductivity (as we shall see in the next section). However, in a practical situation, there is flux pinning, and this turned out to be the Achilles heel of the idea. In particular, any barrier to flux entry at the cold end would introduce extra heating exactly where it was not wanted, so this theoretical work was abandoned and not published. This effect is not merely a historical footnote: Thermal Hall effect measurements are a current experimental technique to help to understand High \(T_c\) and other unconventional superconductors (e.g., [16]). However, it turns out that strong signals are also present in the normal and insulating parts of the cuprate phase diagram, where phonon thermal conductivity may be dominant. This raises the question as to how uncharged excitations in these materials can show vortex-like chirality in a magnetic field.

4 Transport in the Mixed State

4.1 Background

When Vinen was invited in his early thirties to take a professorship and form a research group at the University of Birmingham, he instituted a program of research on transport in the mixed state of Type-II superconductors. This vortex state had become ‘respectable,’ once it was realized that Type-II materials were well-defined analogs of rotating superfluid helium, and that they were qualitatively described by the Ginzburg–Landau equations ([17] is an account of this theory—originally published in Russian [18]). This program of research was backed up by a parallel effort to produce highly purified single crystals of niobium (the most suitable of the three Type-II elemental superconductors; the others are vanadium—not easily purified and technetium—radioactive). The aim of the purification was to produce superconductors in the 'clean limit,' i.e., with the electron mean free path \(\ell>> \xi\), the coherence length. In addition to the flux flow measurements described above, two other transport measurements adopted were ultrasonic attenuation, which is sensitive to the viscosity of the superconducting state, and thermal conductivity, which can be due to either electrons (bound in the flux line cores or delocalized) or phonons, and can be affected by the interactions between them.

4.2 Ultrasonic Attenuation

The variation of ultrasonic attenuation with temperature in the zero-field superconducting state was one of the key experimental results that were quoted in support of the BCS theory of superconductivity [19]. Denoting the attenuation coefficients in superconducting and normal states as \(\alpha _s\) and \(\alpha _n\), BCS derived the formula:

$$\begin{aligned} \frac{\alpha _s}{\alpha _n} = 2f(\Delta (T)), \end{aligned}$$
(7)

where \(\Delta (T)\) is the temperature-dependent energy gap in the electronic quasi-particle excitation spectrum, and \(f(\epsilon )\) is the Fermi function for an excitation of energy \(\epsilon\) at a temperature T. Note that the D.C. resistivity falls to zero immediately on cooling below \(T_c\), because the unpaired electronic quasi-particles are 'shorted out' by even a small fraction of superconducting condensate. On the other hand, ultrasonic attenuation falls slowly to zero at \(T=0\) on cooling below \(T_c\), because it is at finite frequency, and is sensitive to the viscosity due to unpaired electronic quasi-particles [20]. Under the conditions of the experiments carried out in Birmingham, the absolute value of attenuation would be proportional to the mean free path of these electronic quasi-particles. The aim of the measurements was to understand the field-dependence of the attenuation ratio \(\alpha _s / \alpha _n\), as superconductivity was steadily weakened to zero at \(B_{c2}\). This was achieved by the application of a field and therefore introduction of a density of flux lines proportional to the average magnetic induction B in the mixed state. An overall account of both attenuation and thermal conductivity results and their interpretation was given by Vinen [21], and we discuss the important results here.

A most interesting result was obtained at a temperature sufficiently above base that the thermally excited quasi-particles gave a measurable attenuation in the superconducting state in zero field. When a field was applied and flux lines began entering the sample, this attenuation decreased. The field could hardly have decreased the density of quasi-particles, so this suggested that their mean free path had been reduced, by scattering off the flux lines. This evokes the seminal work of Vinen on ‘mutual friction’ between vortex lines and excitations in rotating superfluid helium [22]. However, the scattering processes are different: In helium, it is the superfluid velocity field around the vortex that causes the scattering. In superconductors, the scattering process is much more subtle. As pointed out by Vinen [21], flux line cores are much larger than the wavelength of the electronic excitations at the Fermi surface, so they can only alter the electronic momentum by a small amount, giving scattering through small angles only. However, in a superconductor, scattering from an electron-like quasi-particle to a hole-like one and vice versa can occur. (This is generally known today as ‘Andreev Scattering’ [23].) In the case of ultrasonic attenuation, this process reduces the transport mean free path [21, 24, 25], whereas in the case of electrical conductivity, such a scattering process is ineffective.

It is apparent from the experiments [21, 26] that this scattering process continues toward \(B_{c2}\). This is perhaps surprising, since one might expect that a regular lattice of flux lines would no more cause incoherent scattering than a regular crystal lattice. The observed scattering may in fact be because the crystal and flux line lattices would be incommensurate [26].

We return to the temperature-dependence of the attenuation in the Meissner state at zero field, which was a major initial experimental support for the BCS theory. In the ultra-pure niobium samples prepared in Birmingham, absorption and emission of thermal phonons contribute noticeably to the temperature-dependence of both resistivity and ultrasonic attenuation in the normal state [27]. In the superconducting state, such inelastic processes can also connect electron- and hole-like states [28], and hence reduce the transport mean free path for ultrasonic attenuation [27, 29]. This results in big experimental deviations [27] from the BCS prediction for the attenuation ratio in Eq. 7. It was fortunate that the initial measurements were in samples where elastic scattering tended to dominate. In this case and for an isotropic energy gap, the mean free paths in normal and superconducting states are identical and energy-independent [20], so that Eq. 7 is obeyed. (Interestingly, for quasi-particles in the superconducting state, both the impurity scattering time and group velocity are energy-dependent but these changes exactly cancel to give a constant \(\ell\) [28].)

4.3 Thermal Conductivity

By way of introduction, we describe the temperature-dependence of the thermal conductivity \(\kappa _n\) and \(\kappa _s\) in the normal and Meissner states of a moderately pure superconductor (e.g., [30]). If the transport lifetime is controlled by impurities, it will be temperature-independent, and in the normal state \(\kappa _n \propto T\), due to the temperature-dependence of the electronic heat capacity, as \(\kappa _n\) is dominated by the electronic contribution. In purer samples, inelastic interactions of electrons with phonons, despite being small angle, are effective in reducing the transport lifetime at higher temperatures, as the phonons relax the electron energy distribution back to equilibrium. In extremely pure samples, this can even lead to \(\kappa _n\) rising with decreasing T, until impurity scattering takes over at the lowest temperatures and \(\kappa _n\) falls again.

As one cools below \(T_c\) in the Meissner state, \(\kappa _s\) falls as the electrons join the condensate and the electronic contribution goes to zero at \(T=0\) because the condensate has no entropy. However, the disappearance of the electronic quasi-particles and the increase in the energy gap mean that thermal phonons are no longer absorbed by electrons, and the phonon mean free path increases rapidly. This can lead to a peak in \(\kappa _s\) when the phonon mean free path reaches its maximum value—controlled by defects or the sample edges. At lower temperature, the sample behaves like an insulator with \(\kappa _s \propto T^n\) with \(n \sim 3\)—entirely due to phonons. In purer samples, the electronic contribution may be more dominant, and the intermediate peak in \(\kappa _s\) may not be present. In addition, the fall at \(T_c\) is much steeper, due to the extra inelastic electron–hole scattering in the superconducting state, as described earlier. The application to thermal conductivity is described in the following theoretical papers: [28, 29, 31].

Fig. 2
figure 2

Thermal conductivity vs. magnetic induction B along [100] in an Nb crystal with residual resistance ratio 1300. a Absolute values of \(\kappa _m(B)\) at \(T<< T_c\) with \(B~\Vert\) heat current (after [32]). b Normalized values of \(\kappa _m(B)\) at \(T \sim 0.45T_c\); full symbols: \(B~\Vert\) heat current; open symbols: \(B~\perp\) heat current (after [21])

Full size image

In Fig. 2, we show some typical results for the thermal conductivity in the mixed state \(\kappa _m\) as a function of magnetic induction in a niobium crystal. At zero field and \(T<<T_c\) as shown in Fig. 2a, \(\kappa _m\) is dominated by phonon thermal conduction. The initial fall with B up to about 30 mT is due to absorption of the phonons by the 'normal' electrons in the flux line cores of radius \(\sim \xi\). It was estimated by Vinen [21] that the phonon attenuation coefficient in the cores is comparable with that in the normal state at the same temperature. This behavior is in sharp contrast with that seen in ultrasonic attenuation, where there was no increase in attenuation proportional to the area occupied by the flux lines. It should be noted, however, that the frequencies and wavelengths involved in the two cases are completely different. The theoretical situation is that the bound states in the cores are actually mixed electron–hole states [33, 34] which have different properties from normal electrons, although a similar density of states. They are expected to have a weak absorption of sound [21]. This agrees with the ultrasonic attenuation measurements but is at variance with the much higher frequency behavior probed by thermal conductivity.

Another predicted property of the quasi-particle states bound in the cores is that they have a very low group velocity along the cores. This is confirmed by the data in Fig. 2a, where the flux lines are parallel to the heat current. At 0.2 T, which is about half \(B_{c2}\) at this temperature, the conductivity (although increasing with B) is less than 3% of the normal state value, so the cores conduct heat much less well than they would if they were rods of normal material.

Further information is obtained from Fig. 2b, where the conductivity at this much higher temperature is dominated by electronic quasi-particles. Once again, \(\kappa _m\) falls with B, but the mechanism is quite different: It is once again Andreev scattering [21, 24, 25] reducing the transport mean free path. The fairly similar behavior of the parallel and perpendicular field results indicates that the scattering cross section is not a strong function of angle. Finally, we note the behavior near \(B_{c2}\): a very sharp rise to the normal value. The purity-dependence of this effect [21] indicates that Andreev scattering continues to be effective all the way to the upper critical field, just as in the case of ultrasonic attenuation. We finish this discussion by bringing it up to date: It is quite difficult to determine values of \(B_{c2}\) in cuprate superconductors, but a recent technique for doing so has been the observation of a drop in thermal conductivity on entering the mixed state [35]. Presumably, this drop is at least partly due to the Andreev electron–hole scattering, which is expected to occur in these d-wave materials also [36].

5 High \(T_c\) Research

Research on superconductivity became less fashionable after the publication of the ‘nail in the coffin of superconductivity’ [37]—a comprehensive review which gave the impression that all important questions had been considered and dealt with. However, when High \(T_c\) superconductors burst upon the scene in 1986, the group at Birmingham, who had learned so much from Vinen, were able to act quickly. Appropriately enough, they were the first group to obtain direct evidence via a measurement of the flux quantum that electrons form pairs in these materials [38]. In this work, Vinen played an important background role. While simultaneously overseeing ongoing research into ions below the surface of superfluid helium, he was instrumental in establishing across the University a ‘Portfolio Partnership,’ which was funded to support pure and applied superconductivity research under the leadership of Colin Gough. Vinen was also a member of the advisory group for the Interdisciplinary Research Centre on superconductivity, which was set up in Cambridge at about the same time. He also found time to interact with Birmingham research on the ‘paramagnetic Meissner effect.’ This is the appearance of a positive instead of a negative moment on cooling some superconducting samples through \(T_c\) in a small field. In the early years of High \(T_c\) research, it was not always clear which of the observed properties were intrinsic, and this phenomenon required investigation. Vinen contributed to a careful experimental and theoretical study [39], in which it was concluded that this phenomenon was almost certainly not intrinsic, and indeed, it has been observed in conventional superconductors also.

Although not part of High \(T_c\) research, we conclude this section with a reference to Vinen’s last paper on superconductors, which was a theoretical paper about flux line motion, making clear the role of the Magnus force and topological ideas [40], thus returning to subjects first covered at the beginning of his career.

6 Discussion

An overwhelming impression that one gains in reviewing Joe Vinen’s scientific work is his huge care in both experiment and interpretation and not rushing to publish. This caution contrasts with the pressures experienced by researchers today to find the most exciting explanation of their results and rapidly write a short paper, which will appeal to the editor of a high-profile journal, and hopefully advance their career. It is also noticeable that many of his experiments depended on specialized home-built apparatus, often relying on the expertise of skilled technicians to realize it. This is in contrast with expensive commercial measuring systems, where the experimenter is isolated from the actual measurement process. While he was a highly skilled experimenter, Joe Vinen had an extremely deep theoretical understanding, especially in the fields of hydrodynamics, thermodynamics, superconductivity and superfluidity. He employed this to exemplary effect in critical analysis of experimental results, and this example is an important part of his enduring legacy.