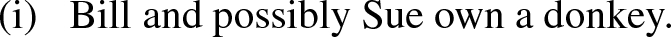Abstract
This paper provides a detailed comparison between discourse representation theory (DRT) and dependent type semantics (DTS), two frameworks for discourse semantics. Although it is often stated that DRT and those frameworks based on dependent types are mutually exchangeable, we argue that they differ with respect to variable handling, more specifically, how substitution and other operations on variables are defined. This manifests itself in two recalcitrant problems posed for DRT; namely, the overwrite problem and the duplication problem. We will see that these problems still pose a challenge for various extended compositional systems based on DRT, while they do not arise in a framework of DTS where substitution and other operations are defined in the standard type-theoretic manner without stipulating any additional constraints. We also compare the notions of contexts underlying these two kinds of frameworks, namely, contexts represented as assignment functions and contexts represented as proof terms, and see what different predictions they make for some linguistic examples.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Formal semantic frameworks designed to deal with dynamic phenomena within a representationalist theory of interpretation include Discourse Representation Theory (DRT) (Kamp 1981; Kamp and Reyle 1993; Kamp et al. 2011) and those based on Dependent Type Theory (Martin-Löf 1984). DRT introduces a level of semantic representations called Discourse Representation Structures (DRSs). The interpretation of a sentence involves a two-staged process: the construction of DRSs given the input discourse and a model-theoretic interpretation of those DRSs. There have been various proposals that extend and refine the original version of DRT, including Compositional DRT (Muskens 1996), an extension by Relational DRS (van Eijck and Kamp 1997; van Eijck 2001) and \(\lambda \)-DRT (Bos et al. 1994; Kohlhase et al. 1995).
Applications of Dependent Type Theory to natural language semantics originated from the work by Sundholm (1986) and Ranta (1994), followed by recent work on Modern Type Theory (MTT) (Luo 2012; Chatzikyriakidis and Zhaohui 2017), Type Theory with Records (TTR) (Cooper 2012), and Dependent Type Semantics (DTS) (Bekki 2014; Bekki and Mineshima 2017). Under the so-called Curry–Howard correspondence (the propositions-as-types principle), the notion of dependent types, a natural extension of simple types, is introduced to serve as the semantic representations of sentences. In contrast to model-theoretic frameworks like DRT, those frameworks based on Dependent Type Theory can be called proof-theoretic, emphasizing the role of inferences in interpreting sentences and discourses.
It has been often stated that these two kinds of semantic frameworks, DRT and those based on Dependent Type Theory, are equivalent and mutually exchangeable (Ahn and Kolb 1990; Fernando 2001); despite the difference in emphasis between the two frameworks, model-theoretic and proof-theoretic ones, a level of representations, i.e., DRS and dependent types, play an essential role in interpretation and there is a certain correspondence between them: see Ahn and Kolb (1990), Fernando (2001) for more details.
Against this view, we will argue that these two kinds of frameworks differ in the process of deriving semantic representations and the behavior of the theory itself.
DRT and its compositional extensions have a risk that two crucial notions in computational semantics that depend on substitution, namely, \(\beta \)-conversion and inference rules for quantification, will be only partially defined and incomplete. This would pose problems for compositional semantics and proof systems based on DRS. Also, as we will see later in detail, they do not provide a strict definition of \(\alpha \)-conversion, so that substitution of terms in DRSs remains partial and incomplete. This manifests in two recalcitrant problems posed for DRT: the overwrite problem (the so-called destructive update problem) and the duplication problem.
We will provide a comparison between a family of DRT-based frameworks and DTS (Bekki 2014; Bekki and Mineshima 2017), and reveal differences in their semantic analyses and derivation processes that result in theories that behave differently. We will also see that these two frameworks use different notions of contexts, namely, contexts represented as assignment functions and contexts represented as proof terms, which underlie their treatments of anaphora and context updates in general. As mentioned above, there are various semantic frameworks using dependent types, but it is difficult to find work on a detailed mechanism of a compositional mapping from syntactic structures to semantic representations based on dependent types.Footnote 1 By contrast, DTS provides a detailed compositional semantics. This is the reason why we will adopt DTS as a representative framework based on dependent types throughout this paper.
Although we will focus on a comparison between DRT and dependent types, there is an alternative to DRT that uses simply-typed \(\lambda \)-calculus for handling discourse dynamics (cf. de Groote et al. 2006). There are also various proposals on variable handling in a dynamic setting, specifically, those that can be subsumed as descendants of Dynamic Predicate Logic (DPL) (Groenendijk and Stokhof 1991). See Vermeulen (1993), Dekker (1994), and, Nouwen (2007), among many others. In contrast to DTS and DRT (Kamp and Reyle 1996; Kamp et al. 2011), systems based on DPL usually lack a proof-theoretic component.Footnote 2 Throughout this paper we will confine our discussion to a comparison between DRT and DTS.
The structure of this paper is as follows. In Sect. 2 we introduce DRT and its various extensions that were proposed in the last 20 years. In Sect. 3 we expose two problems caused by the divergence between DRT’s operations and those of ordinary logics, namely the overwrite problem and the duplication problem. In Sect. 4 we introduce the framework of DTS, and see how it can solve the overwrite problem and the duplication problem, which is an advantage of DTS over DRT. We also compare the notions of contexts underlying these two kinds of frameworks. We close the paper with conclusions in Sect. 5.
2 Discourse Representation Theory
Since the mid-1990s, DRT has been the name for a family of frameworks that extend the original, non-compositional theory proposed by Kamp (1981) and Kamp and Reyle (1993) in a compositional way. In this paper, we call the latter Classical DRT to distinguish it from the former.
2.1 Classical DRT
Classical DRT is known to be a non-compositional theory in two senses: It is intersententially non-compositional because it is not the case that each sentence is assigned a discourse representation structure (DRS), which can be determined only relative to its preceding discourse. It is also intrasententially non-compositional because it is not the case that each phrase is assigned a DRS, whose contribution to the whole DRS is determined only relative to the surrounding syntactic structure and its preceding discourse.
Unlike Classical DRT, extended frameworks such as Compositional DRT (Muskens 1996) (henceforth CDRT), Relational DRS (van Eijck and Kamp 1997), and \(\lambda \)-DRT (Bos et al. 1994) adopt a method of constructing the DRS of an entire discourse from sentential DRSs by composing them by merge operations (s.t. they are intersententially compositional) and of a sentence from lexical DRSs by composing them in a bottom-up manner (s.t. they are intrasententially compositional). They share the basic idea, that is, combining Classical DRT with the \(\lambda \)-operator and the operation of functional application, but are different in their way of implementing it. We will briefly review the definition of each representation system (CDRT, Relational DRS, and \(\lambda \)-DRT), focusing on how the compositional derivation of a DRS works in each system.
2.2 Compositional DRT
DRSs in CDRT are used as an abbreviation for the following relation.
Definition 1
(DRS in Compositional DRT) Let i, j be state variables.

The merge operation of DRSs in CDRT is defined as in Definition 2.
Definition 2
Let \(K_1, K_2\) be DRSs. The merge of \(K_1\) and \(K_2\), written \(K_1 ; K_2\), is defined as follows:

From this definition, the following lemma is derived.
Lemma 1
Let \(K_1 = (U_1, Cond _1), K_2 = (U_2, Cond _2)\) be DRSs. If none of the discourse referents \(u \in U_2\) occurs in any of the conditions in \( Cond _1\), then we have \(K_1 ; K_2\) = \(\,[U_1 \cup U_2 \mid Cond _1 \cup Cond _2]\).
An example DRS construction for the first sentence in (1a) is shown in (1b), and the DRSs for the two sentences in (1a) are merged as in (1c).

Superscript and subscript numbers in the sentence (1a) respectively specify the indices of discourse referents that they introduce and the discourse referents of their antecedents. The syntactic structure in (1b) and the DRSs in (1c) respectively show the intrasentential and intersentential compositions of DRSs in CDRT. One of the major differences of CDRT from Classical DRT is that discourse referents in CDRT are syntactically treated as constant symbols. This means that operations on variables such as substitution and renaming are not defined for discourse referents in CDRT.
2.3 Relational DRS
The definition of Relational DRSs is slightly different from the definition of DRSs in Classical DRT, as shown in Definition 3.
Definition 3
(DRS in Relational DRS)

The major difference of Relational DRS from Classical DRT is that discourse referents and predicates themselves qualify as DRSs according to Definition 3.1 and Definition 3.2 On the basis of the notion of DRSs, Relational DRSs (RDRSs) are defined as follows.
Definition 4
(RDRS)

Definition 4 shows that complex RDRSs are obtained by joining DRSs with join operator \(\bullet \). The reduction operation (in the sense of \(\beta \)-reduction) for complex RDRSs is defined by the set of reduction rules, as shown in Definition 5.
Definition 5
(Reduction rules for RDRSs)

Here the operator; is defined in the same way as in Definition 2. The notation [y / x]R is the result of substituting y for x in R. By reduction, the RDRS for the first sentence in the mini-discourse (2a) is derived as in (2b).

Then the two DRSs for the discourse are converted to a DRS as follows.

In this way, the extension by RDRS also achieves intrasentential and intersentential compositionality.
2.4 \(\lambda \)-DRT
Among several versions of \(\lambda \)-DRT, we discuss the one formulated by Kohlhase et al. (1995), which introduces the \(\delta \)-operator, the binder of discourse referents. The definition of the merging operations of DRSs is given in Definition 6, where \(\otimes \) and ; are intrasentential and intersentential merge operators, respectively.
Definition 6
(Merge in\(\lambda \)-DRT)

Using this definition, an example of DRS construction for the first sentence in (4a) is given in (4b), where @ is a binary operator for functional application. The two DRSs for the discourse are merged and computed as shown in (4c).

Note that each discourse referent in (4c) has a unique name. In \(\lambda \)-DRT, only those with unique names are treated as well-formed formulae (wff), as defined in Definition 7.
Definition 7
(wff in\(\lambda \)-DRT) Let A be DRS. A is a wff iff for all of A’s sub-expressions of the form \(A_1 \otimes A_2\), \(A_1 ; A_2\), \(A_1(A_2)\), \(A_1\) and \(A_2\) do not share the same discourse referents.
By Definition 7, each discourse referent has a unique name, which makes safe the union operation in Definition 6.
3 Two Problems About Variable Handling in DRT
In this section, we will see that operations on DRSs such as substitution, \(\alpha \)-conversion, and \(\beta \)-reduction behave differently than in standard type theories. This will bring about two problems: the overwrite problem and duplication problem. Since these problems have been recognized and discussed in the literature, we will mainly focus on the issues of variable handling and provide a survey of problematic cases of a family of DRT frameworks from that perspective.
In Sect. 3.1, we discuss the overwrite problem and see how it arises in each theory we reviewed in Sect. 2 In Sect. 3.2, we discuss the duplication problem and consider why it arises through examining the relationship between substitution and binding scope. In Sect. 3.3, we analyze the logical structures of DRT that cause these two problems.
3.1 The Overwrite Problem
The overwrite problem of DRT, first pointed out by Zeevat (1989), is that there is a case where a link between a discourse referent and an anaphoric expression unintentionally gets destroyed as a result of the merge operation. In Zeevat (1989), the merge operation is defined as Definition 8.
Definition 8
Let \(K_1 = (U_1, Cond _1)\) and \(K_2 = (U_2, Cond _2)\) be a DRS.
A problematic case where the overwrite problem occurs is exemplified by (5).

In (5a), a man and a woman denote different persons, but they are interpreted as the same person in DRS (5b) as a result of merging. Zeevat (1989) pointed out that discourse referents that are introduced should be restricted to avoid such problematic cases.
In the extended DRT frameworks in the previous section, this problem does not appear to happen since discourse referents that are introduced are assumed to be distinct with each other. However, this assumption does not save cases like (6), where a discourse referent for an indefinite NP gets copied.

If ‘Bill and Sue’ is interpreted as \(\lambda P.P (Bill); P (Sue)\), the sentence (6) is semantically equivalent to the conjunction that Bill owns a donkey and Sue owns a donkey. Thus there may be two different donkeys.
Let us consider two discourses where the sentence (6) is followed by the sentences (7a) and (7b).Footnote 3

In the following discussion, we will see how each extended DRT fails to give an appropriate DRS to these mini-discourses.Footnote 4
3.1.1 The Case of CDRT
The DRS for the mini-discourse (8) in terms of CDRT is given as (9).

According to Definition 2, the leftmost and the center DRSs of (9) are merged first. The merging of these two DRSs results in (10).

In (10), the discourse referent \(u_3\) refers to Sue’s donkey; thus there is no way to pick up Bill’s donkey from the subsequent discourse. Syntactically, discourse referents in CDRT are constant symbols, so that there is no way to change the names of discourse referents. As a result, it was impossible to rename the discourse referent \(u_3\) or distinguish the two occurrences of \(u_3\).Footnote 5
3.1.2 The Case of Relational DRS
The DRS for the mini-discourse (8) in terms of Relational DRS is given as (9).

According to Definition 5, we first merge the leftmost and the center DRSs of (12), then the merged DRS and the rightmost DRS are merged. When merging, the discourse referent that conflicts with others is substituted for a new discourse referent. The result of the combination is as shown in (13b).

In (13b), \(u_4\) and \(u_5\) denote Bill’s donkey and an apple respectively, so
 means that Bill’s donkey eats an apple. However, this does not capture the truth-condition of (11) where Sue’s donkey eats an apple.Footnote 6
means that Bill’s donkey eats an apple. However, this does not capture the truth-condition of (11) where Sue’s donkey eats an apple.Footnote 6
Since the substitution of RDRS considers only the RDRSs that immediately precedes or succeed it, the scope of substitution in (13a) only contains the central DRS. However, given the meaning of the sentence (11), \(u_3\) in the rightmost DRS must be substituted as well, so substitution defined in this way does not work well.Footnote 7
Note that widening the scope of substitution is not a good strategy: if \(u_3\) in the rightmost DRS is the same as \(u_3\) introduced by the leftmost DRS, it leads to another incorrect derivation. More generally, this result can be regarded as an instance of the following phenomenon (14):

In most logics and type theories, two logical expressions whose only difference is a variable name, are \(\alpha \)-equivalent, so the contents of the expression itself do not change even if we replace the subexpression like (14). Under this extension by RDRS, however, the scope of binding by discourse referent is taken to be wider than in standard logic, so the contents of the expression will be different if we do such a replacement. Therefore, we found that this extension leads to a theory in which renaming and substitution themselves are defined but \(\alpha \)-conversion cannot be performed.
3.1.3 The Case of \(\lambda \)-DRT
The DRS for the mini-discourse (15) in terms of \(\lambda \)-DRT is given as (16).

Since the discourse referents \(x_k\) and \(e_a\) in the leftmost and the center DRS in (16) conflict, the DRS in (16) is not well-formed according to Definition 7. Note that examples like (16) are not artificially created but derived from natural language examples. This means that the theory undergenerates for cases like (15), which is a problem for \(\lambda \)-DRT.
The version of \(\lambda \)-DRT presented in Kohlhase et al. (1995) attempts to restrict the range of its application by introducing the notion of sensible expression and substitutability. It is claimed that such a theory with additional constraints does not cause a problem in practice; however, the above discussion shows that there exists a problematic example in natural language.
3.2 Duplication Problem
The duplication problem pointed out in Kohlhase et al. (1995) is that the binding status of variables in a DRS can change after \(\beta \)-reduction during the process of building the representation of a sentence. Consider the following example:

Here we attach subscripts A, B, \(B_1\), and \(B_2\) to the variable Y in order to distinguish each occurrence of the same variable Y in the DRSs.
Generally speaking, the functional application and the interpretation function are expected to be confluent, as indicated by the diagram in (18), where M is the function and N is its argument. That is, the order of executing the functional application and applying the interpretation function is not relevant to the final output.

In a situation where the problem arises, as in (17), however, the binding status of the variable Y differs between (i) the case of evaluating the interpretation function first, i.e.,  and (ii) the case of evaluating the functional application first, i.e.,
and (ii) the case of evaluating the functional application first, i.e.,
 . To be more specific, when one evaluates the interpretation function first, that is, one interprets the DRS in (17a), the values of \(Y_A\) and \(Y_B\) may be different because \(Y_B\) is free. By contrast, when one evaluates functional application first, that is, one interprets the DRS in (17b), it may be the case that the values of \(Y_A\) and \(Y_{B_1}\) are the same and the value of \(Y_{B_2}\) is different from other occurrences of Y, since \(Y_{B_2}\) is free in this DRS. This means that functional application and the interpretation function are not confluent. The DRSs in (17) are ill-formed since the binding status of the different occurrences of the same discourse referent Y differs. Moreover, as pointed out in Kohlhase et al. (1995), it is difficult to give a syntactic restriction imposed on expressions that cause these problematic cases through \(\beta \)-reduction.
. To be more specific, when one evaluates the interpretation function first, that is, one interprets the DRS in (17a), the values of \(Y_A\) and \(Y_B\) may be different because \(Y_B\) is free. By contrast, when one evaluates functional application first, that is, one interprets the DRS in (17b), it may be the case that the values of \(Y_A\) and \(Y_{B_1}\) are the same and the value of \(Y_{B_2}\) is different from other occurrences of Y, since \(Y_{B_2}\) is free in this DRS. This means that functional application and the interpretation function are not confluent. The DRSs in (17) are ill-formed since the binding status of the different occurrences of the same discourse referent Y differs. Moreover, as pointed out in Kohlhase et al. (1995), it is difficult to give a syntactic restriction imposed on expressions that cause these problematic cases through \(\beta \)-reduction.
Let us examine whether the duplication problem is avoided in other extended DRTs. CDRT yields the same result as \(\lambda \)-DRT does since their behavior is the same with respect to \(\beta \)-reduction. In RDRS, intrasentential merging takes place at the level of RDRS, which is exemplified in (19) where \(R \rightarrow R'\) is defined as \(\lnot (R \bullet \lnot R')\).

As shown in (19), the result ends up in the same DRS as \(\lambda \)-DRT and CDRT, despite the differences in the derivation processes. Therefore, all the extended DRTs discussed in this paper fall into the duplication problem.
The reason for allowing such derivation is that there is no constraint on \(\beta \)-reduction: It is a standard assumption in the \(\lambda \)-calculus that one has to check free variables during \(\beta \)-reduction. However, such a constraint would bring about another problem in constructing DRS, because of the non-standard notion of binding in the extended DRT such as \(\lambda \)-DRT called dynamically bound variables. A variable x is dynamically bound iff x is a free variable within an argument given to a function in which the variable corresponding to its argument appears within the scope of x introduced by the universe of some DRS. This is exemplified by (20), whose DRS is derived as shown in (21).

Here x in walk(x) is dynamically bound. Such bindings are common in extended DRTs.
In most \(\lambda \)-calculi, when variables in the argument conflict the variables in a functional expression, they force renaming of the variables in the function to fresh ones. In the case of extended DRTs, however, such renaming is impossible, since (20) would become (22) when introducing such a renaming constraint.

In (23), the argument of man, i.e. y, and the argument of walk, i.e. x, are different, thus this derivation is incorrect. In other words, the notion of variable renaming during \(\beta \)-reduction, which is widely assumed in the \(\lambda \)-calculus, and the notion of dynamically bound variables are not compatible with each other. There does not seem to be a straightforward remedy to the duplication problem given the theoretical setting of the extended DRTs which we discussed in this paper.
3.3 Logical Structure of DRT
Both of the problems that we pointed out in this section are caused by the logical structure of DRT. In standard logic, the scope of substitution agrees with that of binding, so that all variables under the scope are substituted. In DRT, by contrast, the scope of substitution is wider than binding scope; thus \(\alpha \)-conversion and substitution in standard logic style would destroy the binding relations. Due to this feature, it is necessary to restrict the domain of definition of substitution in DRT: in the case of CDRT, discourse referents are treated as constant symbols, so substitution is not defined for them; Relational DRS defines substitution in consideration of free variables in the immediately following RDRS; \(\lambda \)-DRT checks substitutability in the definition of substitution.
Due to these restrictions on substitution, \(\beta \)-reduction is not fully defined in extended DRTs. The duplication problem shown in 3.2 is an instance of this general problem. Given that \(\beta \)-reduction plays an important role in composing DRSs, it is problematic that the safety of \(\beta \)-reduction is not guaranteed. Also, as a result of restricting substitution in order to keep binding relations, the binding relations of anaphora cannot be derived correctly. The overwrite problem shown in 3.1 is an instance of this problem.
Why does this happen even though extended DRTs are based on the \(\lambda \)-calculus? The reason lies in the difference between discourse referents in DRT and variables in the \(\lambda \)-calculus. The discourse referents in DRT play the role of binding variables as variables in first-order logic do. For example, the discourse referent x in (24a) plays almost the same role as x of \(\exists x\) does in (24b).

When extended DRTs introduced intrasentential compositionality into Classical DRT, the \(\lambda \)-calculus was integrated into DRT, but then, while variables bound by \(\lambda \)-operators behave as variables in first-order logic, discourse referents in extended DRTs behave differently, although they are bound by the same \(\lambda \)-operator, thus some property of the \(\lambda \)-calculus is lost.
The discrepancy between the status of variables and discourse referents causes the failure of \(\beta \)-reduction despite using the \(\lambda \)-calculus. To solve this problem, it is necessary for the discourse referents to share the same property as the binding variables in logic, but this is impossible as it will deprive them of their dynamic nature.
4 Dependent Type Semantics
DTS (Bekki 2014; Bekki and Mineshima 2017) is a proof-theoretic semantics based on Dependent Type Theory (Martin-Löf 1984). As we argued in the previous section, there are difficulties with DRT in that operations in standard logic such as substitution are not defined adequately. In DTS, by contrast, \(\alpha \)-conversion and \(\beta \)-conversion are defined in the standard type-theoretic manner without stipulating any additional constraints, so that the overwrite problem and the duplication problem do not arise in this framework. We will see that anaphora can be treated appropriately in the compositional framework of DTS. Moreover, we will compare the notions of contexts in DTS and DRT that underly their treatment of anaphora and context update.
4.1 Dependent Type Theory
Dependent type theory is an extension of the simply typed \(\lambda \)-calculus. It can be characterized by being able to treat types depending on terms. For instance, A(x) represents a type dependent on the term x.
DTS mainly uses two dependent types from dependent type theory, \(\varPi \)-type and \(\varSigma \)-type. The \(\varPi \)-type generalizes the function type from simply typed \(\lambda \)-calculus. We write  for the \(\varPi \)-type. A term f of
for the \(\varPi \)-type. A term f of  is a function such that for any term a of type A, f(a) is of type B(a). When the variable x does not occur free in B,
is a function such that for any term a of type A, f(a) is of type B(a). When the variable x does not occur free in B,  is reduced to functional type \(A \rightarrow B\). The \(\varSigma \)-type generalizes the product type in simply typed \(\lambda \)-calculus. We write
is reduced to functional type \(A \rightarrow B\). The \(\varSigma \)-type generalizes the product type in simply typed \(\lambda \)-calculus. We write  or
or
 for the \(\varSigma \)-type. A term of type
for the \(\varSigma \)-type. A term of type  is a pair (t, u) such that t is of type A and u is of type B(t). The projection functions \(\pi _1\) and \(\pi _2\) are defined so that \(\pi _1(t,u) = t\) and \(\pi _2(t,u) = u\). When the variable x does not occur free in B,
is a pair (t, u) such that t is of type A and u is of type B(t). The projection functions \(\pi _1\) and \(\pi _2\) are defined so that \(\pi _1(t,u) = t\) and \(\pi _2(t,u) = u\). When the variable x does not occur free in B,  is reduced to product type
is reduced to product type  .
.
Given the correspondence between types and propositions, i.e., the so-called Curry–Howard correspondence, types can be identified with propositions. In particular, \(\varPi \)-type and \(\varSigma \)-type correspond to universal quantification and existential quantification in logic. Using this correspondence, the semantic representation of a sentence in natural language can be specified in terms of a type. A term having a type that corresponds to a proposition is called a proof term. Given the identification of types with propositions, the notation t : A can be read as “t is a term of a type A” and “t is a proof term for the proposition A. Proof terms play a pivotal role in representing intrasentential and intersentential contexts in DTS.
\(\varPi \)-type and \(\varSigma \)-type have their own inference rules: formation rules, introduction rules and elimination rules. These rules are as follows.
Definition 9
(Formation, Introduction, and Elimination rule for the\(\varPi \)-type)

Definition 10
(Formation, Introduction, and Elimination rule for the\(\varSigma \)-type)

See e.g., Martin-Löf (1984) for more details on inference rules in Dependent Type Theory.
4.2 Anaphora Resolution in DTS
Since dependent type theory has types that depend on terms, it can represent the meaning of a proposition that depends on the meaning of its previous context. The dynamic conjunction of two semantic representations is defined in terms of \(\varSigma \)-types as in Definition 11.Footnote 8
Definition 11
Let M, N be semantic representations in DTS. The dynamic conjunction of M and N, written as M; N, is defined as follows:

where \(u \notin fv(M)\cup bv(M)\), that is, u does not occur free or bound in M
This definition provides a way to analyze intrasentential and intersentential anaphora in a unified compositional way.
As an illustration, consider the mini-discourse in (25a). A compositional derivation of the semantic representation for the first sentence is given in (25b), where for concreteness we assume CCG (Mark 2000) as a syntactic framework and use the lexical entries shown in Table 1.

Some remarks are in order about the derivation tree in (25). For the determiner a, we use a category variable T (see the lexical entry in Table 1), which can be instantiated by a syntactic category. In the case of the determiner in the subject position, T is instantiated by S, thus \(T/(T\backslash NP)/N\) resulting in \(S/(S\backslash NP)/N\), while the one in the object position, it is instantiated by \(S\backslash NP\), hence \(T/(T\backslash NP)/N\) resulting in \(S \backslash NP \backslash (S \backslash NP/NP)/N\).Footnote 9 Two semantic representations encoded as \(\lambda \)-terms are composed by the following combinatory rules: forward functional application rule \((<)\), which derives X : f(a) from X / Y : f and Y : a, and backward functional application rule \((>)\), which derives X : f(a) from X : a and \(Y\backslash X : f\), where X and Y are arbitrary syntactic categories. The semantic representation for the sentence is shown below. In a similar way, we can derive the semantic representation for the second sentence in the mini-discourse in (25a) as in (26).

Then, using dynamic conjunction implemented as the \(\varSigma \)-types, the semantic representations of the first and second sentences are combined as shown in (27), which gives the semantic representation for the whole discourse (25a).

Pronouns and other context-dependent expressions are represented by using the underspecified term\(@_i\). An underspecified term has an annotated type of the form \(@_i: A\), where the type A specifies the type of the term filling in \(@_i\). For instance, the pronoun he is represented as  and the pronoun it as
and the pronoun it as  , where the \(\varSigma \)-types are annotated to the underspecified term @. Note that the index in \(@_1\) and \(@_2\) in the semantic representations (27) is used to distinguish one underspecified term from another; in the semantic representation of a sentence that is compositionally derived, each occurrence of @ is assigned a mutually distinct index. Thus its role is different from that played in DRT.
, where the \(\varSigma \)-types are annotated to the underspecified term @. Note that the index in \(@_1\) and \(@_2\) in the semantic representations (27) is used to distinguish one underspecified term from another; in the semantic representation of a sentence that is compositionally derived, each occurrence of @ is assigned a mutually distinct index. Thus its role is different from that played in DRT.
In DTS, the process of resolving anaphora is formalized as a process of type checking. In the case of (27), anaphora can be resolved by substituting the underspecified terms \(@_1\) and \(@_2\) with a term having the annotated type. More specifically, given a semantic representation A that contains underspecified terms \(@_1, \ldots , @_n\) the process of anaphora resolution consists of three steps:
-
1.
First, the type checking is launched to prove
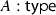 .
. -
2.
Then, for each underspecified term \(@_i : B_i\), where \(B_i\) is an annotated type, a process of proof search is triggered to construct a proof term having the type \(B_i\) in a given context.
-
3.
Finally, the underspecified term \(@_i : B_i\) in A is replaced by the constructed term \(t_i\) of type \(B_i\). By eliminating all the underspecified terms, one can obtain a fully specified semantic representation for the input sentence.
In the case of the semantic representation in (27), the type checking that ensures that this semantic representation has the type
 runs in the following way:
runs in the following way:

Here, \(\sigma \) is a signature that contains typing information for each predicate and other axioms representing background knowledge.
A process of proof search is triggered by the @-rule, in order to fill in the sub-derivations \({\mathcal {D}}_1\) and \({\mathcal {D}}_2\). The @-rule has the following form:

Here, \(A \ true\) means that there exists a proof term for A. Thus, the goal of the proof search is to find a proof term for the annotated type A. In the following derivations, we write t : A with a concrete proof term t, in place of \(A \ true\).
Let us suppose that the background knowledge contains axioms for the relevant predicates:

and

Assuming these judgements are in the signature \(\sigma \), the sub-derivation \(\mathcal {D}_1\) can be given as follows.

In this derivation, the formation rule for \(\varSigma \)-types (\(\varSigma F\)) in (28) plays a crucial role: the required proof term is constructed using a term for the \(\varSigma \)-types that is discharged at the final step in the derivation shown in (28).
In a similar way, the sub-derivation \({\mathcal {D}}_2\) in (28) can be given in the following way.

The sub-derivation \({\mathcal {D}}_1\) shows that a term having the annotated type  for \(@_1\) can be constructed as \((\pi _1 \pi _1 v, f(\pi _1 \pi _1 v)(\pi _2 \pi _1 v))\). The sub-derivation \({\mathcal {D}}_2\) shows that a term having the annotated type
for \(@_1\) can be constructed as \((\pi _1 \pi _1 v, f(\pi _1 \pi _1 v)(\pi _2 \pi _1 v))\). The sub-derivation \({\mathcal {D}}_2\) shows that a term having the annotated type  for \(@_2\) can be constructed as \((\pi _1 \pi _1 \pi _2 v, g(\pi _1 \pi _1 \pi _2 v)(\pi _2 \pi _2 \pi _1 v))\). Finally, by replacing these terms with \(@_1\) and \(@_2\) in the initial semantic representation in (27) and by computing the projection function \(\pi _1\) with the rule \(\pi _1 (m, n) = m\), we can obtain the following fully specified semantic representation.
for \(@_2\) can be constructed as \((\pi _1 \pi _1 \pi _2 v, g(\pi _1 \pi _1 \pi _2 v)(\pi _2 \pi _2 \pi _1 v))\). Finally, by replacing these terms with \(@_1\) and \(@_2\) in the initial semantic representation in (27) and by computing the projection function \(\pi _1\) with the rule \(\pi _1 (m, n) = m\), we can obtain the following fully specified semantic representation.

This representation captures the intended meaning of the discourse in (25a).
4.3 The Overwrite Problem
Let us consider the problematic case of a construction that causes the overwrite problem discussed in Sect. 3 The semantic representations of the two sentences in (30) are combined as shown in (31).

The type annotated with @ in (31) requires as its term a triplet (x, t, u) of a term x having type  , a proof term t of type
, a proof term t of type  , i.e., a proof term for the proposition that x is a donkey, and a proof term u of type
, i.e., a proof term for the proposition that x is a donkey, and a proof term u of type  , i.e., a proof term for the proposition that Bill owns x.Footnote 10 It is easily verified that, by type checking and proof construction, we may find the term \((\pi _1 \pi _1 \pi _1 q, (\pi _2 \pi _1 \pi _1 q, \pi _2 \pi _1q))\) having this type. By substituting the term @ with this term, we can obtain the following semantic representation.
, i.e., a proof term for the proposition that Bill owns x.Footnote 10 It is easily verified that, by type checking and proof construction, we may find the term \((\pi _1 \pi _1 \pi _1 q, (\pi _2 \pi _1 \pi _1 q, \pi _2 \pi _1q))\) having this type. By substituting the term @ with this term, we can obtain the following semantic representation.

In this way, a reading in which Bill’s donkey substitutes the term @ is derived.
When the term @ refers to Sue’s donkey, the term to be substituted must be a triplet \((x, t, u')\) where x and t are the same as before and \(u'\) is a proof term of type  , that is, a proof term for the proposition that Sue owns x. In a similar way to the first reading, we can construct a term \((\pi _1 \pi _1 \pi _2 q, (\pi _2 \pi _1 \pi _2 q, \pi _2 \pi _2q))\) satisfying this condition. It should be noted that the term corresponding to Sue’s donkey and the term corresponding to Bill’s donkey are distinguished by their derivation path, that is, the way a proof term is constructed, not by the name of the term. This way of distinguishing anaphoric dependencies makes it possible to derive two ways of picking up an object introduced by the first sentence in (30).
, that is, a proof term for the proposition that Sue owns x. In a similar way to the first reading, we can construct a term \((\pi _1 \pi _1 \pi _2 q, (\pi _2 \pi _1 \pi _2 q, \pi _2 \pi _2q))\) satisfying this condition. It should be noted that the term corresponding to Sue’s donkey and the term corresponding to Bill’s donkey are distinguished by their derivation path, that is, the way a proof term is constructed, not by the name of the term. This way of distinguishing anaphoric dependencies makes it possible to derive two ways of picking up an object introduced by the first sentence in (30).
4.4 The Duplication Problem
The semantic representation of (17), a representation causing the duplication problem for DRT, is schematized in DTS as in (33). For the sake of exposition, we distinguish the different occurrences of y by using the two subscripts 1 and 2.

In (33), \(y_1\) is a bound variable while \(y_2\) is a free variable. Following the substitution rule of dependent type theory, DTS renames \(y_1\) to avoid a clash of names for variables and obtains the semantic representation, where a fresh variable w is introduced.
In (33), the duplication problem is avoided and the two occurrences of y have the same binding status. DTS binds variables in the same way as dependent type theory does, which contrast with the status of dynamically bound variables in DRTs. Renaming does not conflict with the linguistic analysis and it can define the binding relations in a safe and clear way.
4.5 Contexts in DRT and DTS
Finally, let us discuss the differences between DRT and DTS with respect to the representation of contexts. Here the notion of context is broadly construed as a body of information that is introduced by the utterance of a sentence and is used subsequently to interpret the discourse. We can distinguish two different ways to representing contexts, namely, contexts as assignment functions and contexts as proof terms. In DRT, a context is represented by an assignment function. Generally an assignment function has a flat structure in the sense that an assignment function is a mere correspondence between discourse referents and entities.

Therefore, the name of a discourse referent is a key to fetch the entity that it refers to. However, as we have seen earlier, the distributive reading of (6) may give rise to a case in which this leads to a wrong prediction, such as the overwrite problem.
On the other hand, DTS uses a proof term to represent a context for establishing an anaphoric link. A proof term for a \(\varSigma \)-type has a tree structure; for instance, in the case of the semantic representation in (32), the context provided by the first sentence Bill and Sue own a donkey introduce the proof term q of the following type.

Here q is of a \(\varSigma \)-type, so it consists of a pair of proof terms. More specifically, let  ,
,  ,
,  ,
,  , and
, and  . Then we have \(q = ((d_1, t_1), u_1), ((d_2, t_2), u_2)\), which can be illustrated as follows.
. Then we have \(q = ((d_1, t_1), u_1), ((d_2, t_2), u_2)\), which can be illustrated as follows.

As we can see, a proof term can be regarded as specifying the position of the antecedent in a given context that is a tree of proof terms. Thus, we use the position within a proof term as the key to fetch the witness. Since all variables and predicates are located in different positions in the tree, it does not cause any conflict of variables as DRT does.
5 Conclusion
We have shown that some features in the logical structure of DRT cause problems in the case of extended, compositionalized DRTs, and that they cannot avoid the problems as long as they adopt the approach mentioned in the previous sections. We also have shown that these problems do not occur in DTS. Since DTS is based on dependent type theory, which is a natural extension of the simply-typed \(\lambda \)-calculus, it keeps the property of the binder-variable relation in the \(\lambda \)-calculus intact. DTS also derives a semantic representation which uses typed variables rather than discourse referents. Therefore, DTS keeps the safety of \(\beta \)-reduction and \(\alpha \)-conversion, which makes its logical structure robust.
To summarize, we have discussed that DRT and DTS have a different property with respect to their variable handling and compositionality. Although it is stated that they are the same in the sense that the semantic representations of one analysis can be translated into those of the other, we should also be aware of their differences: there exist semantic representations of DTS whose corresponding DRSs are not compositionally derivable in DRT.
Notes
A notable exception is Dynamic Categorial Grammar (DCG) presented in Martin (2013) and Martin and Pollard (2014), where dependent type theory is adopted in combination with the distinction between phenogrammar and tectogrammar in a similar way to \(\lambda \)-Grammar (Muskens 2003) and ACG (de Groote 2001). We will leave a comparison between DTS and DCG for another occasion. See also Gotham (2018) for a comparison between the version of DTS-based compositional semantics presented in Bekki (2014) and its reconstruction in simple type theory.
Groenendijk and Stokhof (1991) only gave a semantic definition of entailment (Definition 20, p. 67), but not a proof-theoretic one, so they do not have a proof system that derives entailment relations by mean of inference rules.
There are two uses of the definite determiner; anaphoric and non-anaphoric ones. If the determiner in the NP ‘the donkey’ in (7a) and (7b) were to be used non-anaphorically, the overwrite problem disappears. However, it seems that the non-anaphoric use of definites is typically restricted to those NPs that stand for a particular role or a function, for example: “the president”, “the tallest pilot”. These non-anaphoric definites can be interpreted as being uniquely satisfied independently of specific contexts. So, we interpreted definites in (7a, 7b) as anaphoric one since it seems a bit ad hoc to treat this example as an instance of non-anaphoric definites.
It might be objected that the sentence (6) should be analyzed as a plural construction, where the NP Bill and Sue denotes a plurality and an implicit distributivity operator derives the intended reading. However, a case like (i), where a sentential adverbial such as possibly and probably applies to a conjunct NP (cf. Zamparelli 2011), would be problematic to such a view.
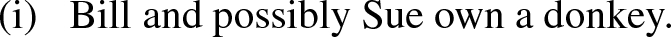
This problem was first pointed out for Partial CDRT, (Haug 2013). In contrast to CDRT, Partial CDRT puts off anaphora resolution until completing constructing DRS. More specifically, in Partial CDRT, discourse referents are initially treated as descriptions like “the next unfixed discourse referent”; pronouns are given lexical entries that involve a meta-predicate \( ant (x)\), a predicate which marks x an anaphoric discourse referent. These devices allow to postpone anaphoric resolution and to avoid the overwrite problem. However, Partial CDRT faces the duplication problem that we will discuss in Sect. 3.2 DTS is similar to Partial CDRT in that the process of anaphora resolution is postponed until a full semantic representation is constructed but differs in that it is formulated as a process of proof search triggered by type checking within its inference system (see Sect. 4.2 for more details). We have to leave a more detailed comparison for another occasion.
The RDRS approach adopts pre-indexing, where anaphora is resolved before constructing full semantic representations. This is one of the causes of the overwrite problem. A reviewer suggested that the problem could be avoided if one extends the RDRS approach with post-interpretational indexing along the lines proposed in classical DRT or Partial CDRT (Haug 2013). This would make a radical departure from the original proposal, though we find no difficulty in principle. We will leave open whether such an extension is a viable option.
van Eijck (2001) proposed a framework to solve this problem by introducing de Bruijn-style notation to DRT. However, the theory does not provide lexical items, and it is not clear how to extend this theory to intrasententially compositional settings. We plan to investigate the possibility of lexicalizing van Eijk’s theory and compare it with ours in future work, but this is beyond the scope of the present paper.
This definition of dynamic conjunction is simpler than that given in Bekki and Mineshima (2017) in that the notion of local contexts is eliminated.
Here slash operators / and \(\backslash \) are understood as right-associative. See Steedman Mark (2000) for more detail and Bekki and Kawazoe (2016) for implementation issues in CCG parser. Note that DTS is compatible with syntactic frameworks other than CCG, for example, Hybrid Type-Logical Grammar in Kubota and Levine (2015).
To be precise, it is a pair of the term and a pair of proof terms for a unary predicate and a binary predicate, but it can be rearranged by elimination rule and introduction rule of \(\varSigma \)-types. So it can be treated as a triplet.
References
Ahn, R., & Kolb, H.-P. (1990). Discourse representation meets constructive mathematics. In L. Kalman, & L. Polos (Eds.), Papers from the second symposium on logic and language (pp. 1–18). Akademiai Kiado.
Bekki, D. (2014). Representing anaphora with dependent types. In N. Asher & S. V. Soloviev (Eds.), Logical aspects of computational linguistics (LACL2014), LNCS 8535 (pp. 14–29). Berlin: Springer.
Bekki, D., & Kawazoe, A. (2016). Implementing variable vectors in a CCG parser. In Logical aspects of computational linguistics. Celebrating 20 years of LACL (1996–2016) (pp. 52–67). Springer.
Bekki, D., & Mineshima, K. (2017). Context-passing and underspecification in dependent type semantics. In modern perspectives in type theoretical semantics (p. 11). Springer.
Bos, J., Mastenbroek, E., Mcglashan, S., Millies, S., & Pinkal, M. (1994). A compositional DRS-based formalism for NLP applications. In In international workshop on computational semantics (pp. 21–31).
Chatzikyriakidis, S., & Luo, Z. (2017). On the interpretation of common nouns: Types versus predicates. In S. Chatzikyriakidis & Z. Luo (Eds.), Modern perspectives in type-theoretical semantics (pp. 43–70). Berlin: Springer.
Cooper, R. (2012). Type theory and semantics in flux. Handbook of the Philosophy of Science, 14, 271–323.
de Groote, P. (2001). Towards abstract categorial grammars. In Proceedings of the 39th annual meeting on association for computational linguistics (ACL2001) (pp. 252–259).
de Groote, P. (2006). Towards a Montagovian account of dynamics. Proceedings of semantics and linguistic theory XVI (pp. 1–16).
Dekker, P. (1994). Predicate logic with anaphora. Semantics and Linguistic Theory, 4, 79–95.
Fernando, T. (2001). A type reduction from proof-conditional to dynamic semantics. Journal of Philosophical Logic, 30(2), 121–153.
Gotham, M. (2018) A model-theoretic reconstruction of type-theoretic semantics for anaphora. In Formal grammar: 22nd international conference, FG 2017, Toulouse, France, July 22–23, 2017, Revised Selected Papers (pp. 37–53). Springer.
Groenendijk, J., & Stokhof, M. (1991). Dynamic predicate logic. Linguistics and Philosophy, 14(1), 39–100.
Haug, D. T. T., & Compositionality without syntactic coindexation. (2013). Partial dynamic semantics for anaphora. Journal of Semantics, 31, 274–294.
Kamp, H. (1981). A theory of truth and semantic representation. In Formal methods in the study of language. Mathematical Centre Tract 135.
Kamp, H., & Reyle, U. (1993). From discourse to logic: Introduction to model-theoretic semantics of natural language, formal logic and discourse representation theory. Berlin: Springer.
Kamp, H., & Reyle, U. (1996). A calculus for first order discourse representation structures. Journal of Logic, Language and Information, 5(3), 297–348.
Kamp, H., Van Genabith, J., & Reyle, U. (2011). Discourse representation theory (pp. 125–394). Berlin: Springer.
Kohlhase, M., Kuschert, S., Pinkal, M. (1995). Type-theoretic semantics for lambda-DRT. In Proceedings of the tenth Amsterdam colloquium (pp. 479–98).
Kubota, Y., & Levine, R. (2015) Scope parallelism in coordination in dependent type semantics. In JSAI international symposium on artificial intelligence (pp. 79–92). Springer.
Luo, Z. (2012). Formal semantics in modern type theories with coercive subtyping. Linguistics and Philosophy, 35(6), 491–513.
Martin, S. (2013) The dynamics of sense and implicature. Ph.D. thesis, Ohio State University.
Martin, S., & Pollard, C. (2014) A dynamic categorial grammar. In Proceedings of formal grammar 2014 (pp. 138–154). Springer.
Martin-Löf, P. (1984). Intuitionistic type theory. Berkeley: Bibliopolis.
Muskens, R. (1996). Combining Montague semantics and discourse representation. Linguistics and Philosophy, 19, 143–186.
Muskens, R. (2003). Language, lambdas, and logic. In G.-J. Kruijff & R. Oehrle (Eds.), Resource-sensitivity, binding and anaphora (pp. 23–54). Berlin: Springer.
Nouwen, R. (2007). On dependent pronouns and dynamic semantics. Journal of Philosophical Logic, 36(2), 123–154.
Ranta, A. (1994). Type-theoretical grammar. Oxford: Oxford University Press.
Steedman, M. J. (2000). The syntactic process. Cambridge: MIT Press.
Sundholm, G. (1986). Proof theory and meaning. Handbook of philosophical logic: Volume III: Alternatives in classical logic (pp. 471–506). Springer.
van Eijck, J. (2001). Incremental dynamics. Journal of Logic, Language and Information, 10(3), 319–351.
van Eijck, J., & Kamp, H. (1997). Representing discourse in context. In J. van Benthem & A. ter Meulen (Eds.), Handbook of logic and language. Cambridge: MIT Press.
Vermeulen, C. F. M. (1993). Sequence semantics for dynamic predicate logic. Journal of Logic, Language and Information, 2(3), 217–254.
Zamparelli, R. (2011). Coordination. In C. Maienborn, K. von Heusinger, & P. Portner (Eds.), Semantics: An international handbook of natural language meaning (pp. 1713–1741). Berlin: De Gruyter Mouton.
Zeevat, H. (1989). A compositional approach to discourse representation theory. Linguistics and Philosophy, 12, 95–131.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Yana, Y., Mineshima, K. & Bekki, D. Variable Handling and Compositionality: Comparing DRT and DTS. J of Log Lang and Inf 28, 261–285 (2019). https://doi.org/10.1007/s10849-019-09294-3
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10849-019-09294-3





 .
.