CMB, Hawking, Planck, and Hubble Scale Relations Consistent with Recent Quantization of General Relativity Theory

Abstract

We are demonstrating new relationships among the Hawking temperature, the Cosmic Microwave Background (CMB) temperature, and the Planck scale. When understood deeply, these are in line with recent advancements in cosmological quantization and its connection to the Planck scale. This is also completely consistent with a recently published method for quantizing Einstein’s general theory of relativity.

1 Background on the Hawking Temperature and the New CMB Temperature Formula

Hawking introduced the concept of Hawking temperature in 1974, as detailed in [1, 2]. It is defined as follows:

$$\begin{aligned} T_{Hw}=\frac{\hbar g}{k_b 2\pi c}. \end{aligned}$$

(1)

Where $k_b$ is the Boltzmann constant, and $\hbar$ is the reduced Planck constant, also known as the Dirac constant ($\hbar =\frac{h}{2\pi }$). Further, g represents the gravitational acceleration at the horizon of a Schwarzschild [3] black hole, and is defined as:

$$\begin{aligned} g=\frac{GM}{r_s^2}=\frac{GM}{\frac{(2GM)^2}{c^4}}=\frac{c^4}{4GM}. \end{aligned}$$

(2)

By substituting this expression back into the original Hawking formula, we arrive at another well-known way to express the Hawking temperature:

$$\begin{aligned} T_{Hw}=\frac{\hbar c^3}{k_b 8\pi GM}. \end{aligned}$$

(3)

For the Hubble sphere, the critical Friedmann [4] mass is defined as:

$$\begin{aligned} M_c=\frac{c^2R_H}{2G}. \end{aligned}$$

(4)

Here, $R_H=\frac{c}{H_0}$ represents the Hubble radius. Solving this equation for the Hubble radius, we obtain $R_H=\frac{2GM_c}{c^2}$.

It’s noteworthy that the Hubble radius is mathematically identical to the Schwarzschild radius $r_s=\frac{2GM}{c^2}$ when considering a critical universe. This similarity has led several researchers to speculate that we could be inside a gigantic black hole, as discussed by Patheria [5] and Stuckey [6]. This question continues to be a topic of discussion in recent papers [7,8,9]. In this discussion, we will not argue for or against the universe being a black hole but will follow the mathematics of a Hubble sphere with mass (equivalent energy) equal to the critical Friedmann mass. It’s important to note that the equivalence between the Schwarzschild radius and the Hubble radius holds true only in a critical universe and not after the expansion of space. However, for the sake of our current discussion, we can replace M with $M_c$ in the Hawking radiation formula and hypothetically treat the Hubble sphere as a black hole, resulting in the following Hawking temperature:

$$\begin{aligned} T_{Hw}=\frac{\hbar c^3}{k_b 8\pi GM_c}\approx 1.32\times 10^{-30}K. \end{aligned}$$

(5)

Next, we will perform a straightforward rewrite of the Hawking temperature. Despite its simplicity, this step will later assist us in understanding some important relationships between the cosmic scale, the Hawking temperature, and the CMB temperature:

$$\begin{aligned} T_{Hw}= & {} \frac{\hbar c^3}{k_b 8\pi G\frac{M_c}{m_p}m_p} \nonumber \\ T_{Hw}= & {} \frac{\hbar c^3}{k_b 8\pi Gm_p}\frac{m_p}{M_c} \nonumber \\ T_{Hw}= & {} \frac{\frac{\hbar c}{G}c^2}{k_b 8\pi m_p}\frac{m_p}{M_c} \end{aligned}$$

(6)

where $m_p$ is the Planck [10, 11] mass, it is important to note that $\frac{\hbar c}{G}=m_p^2$, so we obtain:

$$\begin{aligned} T_{Hw}= & {} \frac{m_pc^2}{k_b 8\pi }\frac{m_p}{M_c} \end{aligned}$$

(7)

and the Planck temperature [10, 12] is given by $T_p=\sqrt{\frac{\hbar c^5}{Gk_b^2}}=\frac{m_pc^2}{k_b}$, allowing us to rewrite the equation above as:

$$\begin{aligned} T_{Hw}= & {} \frac{T_p}{ 8\pi }\frac{m_p}{M_c} \end{aligned}$$

(8)

or as

$$\begin{aligned} T_{Hw}= & {} \frac{T_p}{ 8\pi }\frac{m_p}{\frac{c^2R_H}{2G}} \nonumber \\ T_{Hw}= & {} \frac{T_p}{ 8\pi }\frac{\frac{2Gm_p}{c^2}}{R_H} \nonumber \\ T_{Hw}= & {} \frac{T_p}{ 8\pi }\frac{2l_p}{R_H}. \end{aligned}$$

(9)

Tatum et al. [13, 14] heuristically suggested that the temperature inside the Hubble sphere is determined by a slightly modified Hawking temperature formula:

$$\begin{aligned} T_{H}=T_{CMB}=\frac{\hbar c^3}{k_b 8\pi G\sqrt{M_cm_p}}=\frac{\hbar c}{k_b 4\pi \sqrt{R_H2l_p}}\approx 2.725k. \end{aligned}$$

(10)

Haug and Wojnow [15] recently demonstrated that this CMB temperature formula can be derived from the Stefan-Boltzmann [16, 17] law, as we have also briefly shown in the appendix. Furthermore, they provided the following formula:

$$\begin{aligned} T_{CMB}=T_{H}=\frac{T_p}{8\pi }\sqrt{\frac{2l_p}{R_H}}\approx 2.725k. \end{aligned}$$

(11)

Equations 10 and 11 are identical from a deeper perspective. In a recent paper, Tatum, Haug, and Wojnow [18] have demonstrated that this new understanding of a deeper theoretical relationship between the CMB temperature and the Planck scale can be used in practice to significantly reduce the uncertainty in predictions of $H_0$, while fully taking into account uncertainty in input variables. We mention this not only because it has theoretical implications but also because it leads to practical improvements, opening the door to a new area of high-precision cosmology, where $R_H$, $t_H$, and $M_c$ can be predicted more accurately than ever before. One reason for this is that the precision in CMB temperature measurements and predictions has increased dramatically in recent years, see [19,20,21,22]. Additionally, an exact mathematical relation between CMB temperature and the Hubble constant also plays an important role here.

However, one should also be aware that there are unsolved challenges, such as the Hubble tension [23, 24]. We will not attempt to resolve the Hubble tension in this paper, but we mention it to humbly acknowledge that there could naturally be changes to the foundations of cosmology that might potentially affect the formulas presented here.

In this paper, we will build upon this foundation and introduce some intriguing relationships between the Hawking temperature, the CMB temperature, the Planck scale, and the large-scale structures of the cosmos.

2 Relationships between Hawking Temperature, CMB, Planck Scale, and the Hubble Scale

Here, we will simply start by squaring $T_{CMB}$ and dividing it by the square of $T_{Hw}$. This results in:

$$\begin{aligned} \frac{T_{CMB}^2}{T_{Hw}^2} = \frac{\left( \frac{T_p}{8\pi }\sqrt{\frac{2l_p}{R_H}}\right) ^2}{\left( \frac{T_p}{8\pi }\frac{2l_p}{R_H}\right) ^2} = \frac{\frac{2l_p}{R_H}}{\frac{4l_p^2}{R_H^2}} = \frac{R_H}{2l_p}. \end{aligned}$$

(12)

This implies that we must have:

$$\begin{aligned} R_H = 2l_p\frac{T_{CMB}^2}{T_{Hw}^2}. \end{aligned}$$

(13)

Similarly, for the Hubble time, we obtain:

$$\begin{aligned} t_H = 2t_p\frac{T_{CMB}^2}{T_{Hw}^2} \end{aligned}$$

(14)

where $t_p = \frac{l_p}{c}$ represents the Planck time. Furthermore, for the critical mass, we have:

$$\begin{aligned} M_c = m_p \frac{T_{CMB}^2}{T_{Hw}^2} \end{aligned}$$

(15)

and for the critical energy, we obtain:

$$\begin{aligned} M_cc^2 = E_p \frac{T_{CMB}^2}{T_{Hw}^2}. \end{aligned}$$

(16)

And for the Hubble constant, we obtain:

$$\begin{aligned} H_0 = \frac{1}{2}f_p\frac{T_{Hw}^2}{T_{CMB}^2} \end{aligned}$$

(17)

where $f_p = \frac{c}{l_p}$ represents the Planck frequency. Furthermore, the entropy of the Hubble sphere with a critical mass is then:

$$\begin{aligned} S_H=k_b4\pi \frac{T_{CMB}^4}{T_{Hw}^4}. \end{aligned}$$

(18)

That is, we have established a meaningful relation between the Hawking temperature, the CMB temperature, the Planck scale, and the large scales of the cosmos ($R_H$, $t_H$, $M_c$). In all of these, we have the parameter $\frac{T_{CMB}^2}{T_{Hw}^2}$, so a natural question arises as to whether this factor provides new insights into cosmology. We claim that it does, but these insights may not be readily apparent on the surface. We need to delve deeper into quantum gravity and quantum cosmology to uncover their significance.

We can also find the CMB temperature from the Hubble entropy; it is given by:

$$\begin{aligned} T_{CMB}=\frac{T_p}{8\pi \left( \frac{S_H}{4\pi k_b}\right) ^{\frac{1}{4}}} \end{aligned}$$

(19)

3 The Compton Wavelength

Before we delve into quantum cosmology, we need to briefly discuss the relationship between the Compton wavelength and mass. Compton [25] provided the following formula for what is now known as the Compton wavelength:

$$\begin{aligned} \bar{\lambda }=\frac{\hbar }{mc}. \end{aligned}$$

(20)

If we solve the Compton [25] wavelength formula with respect to mass, we obtain:

$$\begin{aligned} m=\frac{\hbar }{\bar{\lambda }}\frac{1}{c}. \end{aligned}$$

(21)

That formula, as we have asserted in multiple papers, can be used to describe the kilogram mass in any context, including the critical mass of the universe. Some may possibly protest here and argue that the Compton wavelength is only related to electrons, as it was initially determined indirectly through Compton scattering of electrons. First and foremost, there are also several papers discussing the potential Compton wavelength of the proton, as evidenced by [26] and [27]. It has been demonstrated in multiple papers [28, 29] that even composite masses can be described by (21). We believe that only elementary particles possess a physical Compton wavelength, while composite masses have an aggregated Compton wavelength in the following form:

$$\begin{aligned} m= & {} \sum _i^n m_i + \sum _j^N \frac{\pm E_j}{c^2} \nonumber \\ \frac{h}{\lambda }\frac{1}{c}= & {} \sum _{i=1}^n \frac{h}{\lambda _{i}}\frac{1}{c} + \sum _{j=1}^N \frac{\pm h\frac{c}{\lambda _{j}}}{c^2} \nonumber \\ \lambda= & {} \frac{1}{\sum _{i=1}^n \frac{1}{\lambda _i}+\sum _{j=1}^N \pm \frac{1}{\lambda _j} } . \end{aligned}$$

(22)

Here, i indicates the different elementary particles making up the mass m, and j indicates the different energies contributing to m, such as binding energy. We have a plus-minus sign (±) in front of what is related to energy, as there could be some energy types one need to extract to get the right mass and others one need to add. However, even pure energy can be seen as mass equivalent since we have $m = \frac{E}{c^2}$, so even pure energy can be treated in this way. For masses larger than the Planck mass, this means we will obtain an aggregated Compton wavelength smaller than the Planck length. Even if we consider the Planck length to be the smallest meaningful length of a physical Compton wavelength, this poses no issues because a Compton wavelength of a composite mass shorter than a Planck length is simply a mathematical aggregate useful for calculations, where none of the physical Compton wavelengths for elementary particles will be below the Planck length.

4 Finding the Planck Length as well as the Compton Wavelength of the Critical Mass from CMB and the Hubble Constant

We will commence the following derivation, starting from (11):

$$\begin{aligned} T_{CMB}= & {} \frac{T_p}{8\pi }\sqrt{\frac{2l_p}{R_H}} \nonumber \\ T_{CMB}= & {} \frac{\hbar c }{l_p k_b8\pi }\sqrt{\frac{2l_p}{\frac{2l_p^2}{\bar{\lambda }_c}}} \nonumber \\ T_{CMB}= & {} \frac{\hbar c }{l_p k_b8\pi }\sqrt{\frac{\bar{\lambda }_c}{l_p}} \nonumber \\ \frac{T_{CMB}^2 k_b^2 64\pi ^2}{\hbar ^2 c^2}= & {} \frac{\bar{\lambda }_c}{l_p^3} \nonumber \\ \frac{l_p^3}{ \bar{\lambda }_c}= & {} \frac{1}{T_{CMB}^2}\frac{ \hbar ^2 c^2}{ k_b^2 64\pi ^2}. \end{aligned}$$

(23)

Furthermore, Haug has demonstrated in his papers [30, 31] that the Hubble constant can be expressed as:

$$\begin{aligned} H_0=\frac{\bar{\lambda }_c c}{2l_p^2}. \end{aligned}$$

(24)

This implies that the Planck length can be calculated as follows:

$$\begin{aligned} l_p=\frac{H_0}{T_{CMB}^2} \frac{ \hbar ^2 c}{ k_b^2 32\pi ^2}. \end{aligned}$$

(25)

Both $H_0$ and $T_{CMB}$ can be determined without any knowledge of G. We can find $H_0$ from cosmological redshift [32]:

$$\begin{aligned} H_0\approx \frac{zc}{d} \end{aligned}$$

(26)

where d is the distance to the object emitting light, and z is the observed cosmological redshift. This naturally means we also have:

$$\begin{aligned} l_p=\frac{z}{d T_{CMB}^2 } \frac{ \hbar ^2 c^2}{ k_b^2 32\pi ^2}. \end{aligned}$$

(27)

So, this clearly offers another method to determine the Planck length independently of G from observations in the cosmos. This method is considerably simpler to implement in practice than the one described by Haug [31] in 2022. Its aim is not to achieve a more precise measurement of the Planck length compared to existing methods, but it is of great importance as it clearly demonstrates that the Planck length must also be apparent in cosmological observations; otherwise, we could not extract it from there.

It is worth noting that as early as 1984, Cahill [33, 34] suggested simply solving the Planck mass formula, $m_p=\sqrt{\frac{\hbar c}{G}}$, with respect to G and then expressing G from the Planck mass as $G=\frac{\hbar c}{m_p^2}$. However, in 1987, Cohen [35], who did a similar derivation, also pointed out that this would lead to an unsolvable circular argument, as there was no known method at the time to find the Planck units independently of calculating them from G, $\hbar$, or c. As recently as 2016, in an interesting paper by McCulloch [36], he highlighted the circular problem. In 2017, Haug [37] was the first to publish a method for finding the Planck length independently of G, and multiple publications on this topic have appeared since then, see for example [28].

Additionally, the reduced Compton wavelength of the critical mass of the universe can be determined from the CMB temperature and the Hubble constant.

$$\begin{aligned} \bar{\lambda }_c=\frac{H_0^3}{T_{CMB}^4} \frac{\hbar ^4 c}{ k_b^4 512\pi ^4}\approx 3.79\times 10^{-96} m. \end{aligned}$$

(28)

This value is much smaller than the Planck length. However, it’s important to note that this is not a physical Compton wavelength but an aggregate of Compton wavelengths from fundamental particles and energies that make up the rest mass of the critical Friedmann mass $M_c$. We do not need to distinguish between energy and mass, as energy is treated as rest mass equivalent according to $m=\frac{E}{c^2}$.

Alternatively, we can also determine the reduced Compton wavelength from a single cosmological redshift observation plus the CMB temperature. This gives:

$$\begin{aligned} \bar{\lambda }_c=\frac{z^3}{d^3T_{CMB}^4} \frac{\hbar ^4 c^4}{ k_b^4 512\pi ^4}. \end{aligned}$$

(29)

The fact that we can extract the Planck length and the reduced Compton wavelength directly from two cosmological observations is, in our view, more than just a coincidence. It implies that cosmology is fundamentally linked to the Planck scale and Compton scale of matter and energy, a connection that will become much clearer in the next section.

We can also determine the reduced Compton frequency in the universe per Planck time. It is given by:

$$\begin{aligned} f_c=\frac{l_p}{\bar{\lambda }}=\frac{\frac{H_0}{T_{CMB}^2} \frac{ \hbar ^2 c}{ k_b^2 32\pi ^2}}{\frac{H_0^3}{T_{CMB}^4} \frac{\hbar ^4 c}{ k_b^4 512\pi ^4}} \nonumber \\ f_c=\frac{l_p}{\bar{\lambda }}=\frac{T_{CMB}^2 k_b^2 16\pi ^2}{H_0^2 \hbar ^2} \end{aligned}$$

(30)

or

$$\begin{aligned} f_c=\frac{l_p}{\bar{\lambda }}=\frac{\frac{z}{d T_{CMB}^2 } \frac{ \hbar ^2 c^2}{ k_b^2 32\pi ^2}}{\frac{z^3}{d^3T_{CMB}^4} \frac{\hbar ^4 c^4}{ k_b^4 512\pi ^4}} \nonumber \\ f_c=\frac{l_p}{\bar{\lambda }}=\frac{d^3 T_{CMB}^2 k_b^2 16\pi ^2}{z^2 \hbar ^2c^2} \end{aligned}$$

(31)

5 The Deeper Meaning of the Relation Between Hawking, CMB and The Planck Scale and Quantum Gravity

For the critical mass of the universe, we will use the notation $\bar{\lambda }_c$ to indicate that it is the reduced Compton wavelength of the critical mass. Next, we insert $M_c$ into the formula below:

$$\begin{aligned} \frac{T_{CMB}^2}{T_{Hw}^2}= & {} \frac{R_H}{2l_p} \nonumber \\ \frac{T_{CMB}^2}{T_{Hw}^2}= & {} \frac{\frac{c^2R_H}{2G}}{\frac{c^2l_p}{G}} \nonumber \\ \frac{T_{CMB}^2}{T_{Hw}^2}= & {} \frac{M_c}{m_p} \nonumber \\ \frac{T_{CMB}^2}{T_{Hw}^2}= & {} \frac{l_p}{\bar{\lambda }_c}. \end{aligned}$$

(32)

And naturally, we then also have that $\frac{T_{CMB}}{T_{Hw}} = \sqrt{\frac{l_p}{\bar{\lambda }_c}}$. It’s important to note that we can find the reduced Compton wavelength of the critical Friedmann mass-energy without any knowledge of $\hbar$ or knowledge of the kilogram mass $M_c$, as demonstrated in the previous section. Additionally, the Planck length can be determined independently of any knowledge of G or c, as demonstrated in this paper as well as in [28].

The last line of (32) is, in our view, a very important result as it demonstrates the deepest level of understanding. What does $\frac{l_p}{\bar{\lambda }_c}$ represent? It is the reduced Compton frequency in the universe, mass (energy) per Planck time. We [38] have recently demonstrated that the reduced Compton wavelength is even mathematically identical to the rest-mass energy photon wavelength, so even energy can be treated in this way, as energy can be considered as rest-mass equivalent, as is often done. This should also be seen in line with the fact that we have been able to quantize general relativity theory without altering any outputs from general relativity theory; see [39, 40], where Einstein’s [41, 42] field equation is re-written as:

$$\begin{aligned} R_{\mu \nu } -\frac{1}{2}R g_{\mu \nu } =\frac{8\pi l_p^2}{\hbar c}T_{\mu \nu }. \end{aligned}$$

(33)

This yields a Schwarzschild solution of:

$$\begin{aligned} ds^2= & {} -\left( 1-\frac{2l_p}{r}\frac{l_p}{\bar{\lambda }_M}\right) c^2dt^2+ \left( 1-\frac{2l_p}{r}\frac{l_p}{\bar{\lambda }_M}\right) ^{-1}dr^2-r^2d{\Omega }^2 \end{aligned}$$

(34)

Where $\bar{\lambda }_M$ is the reduced Compton wavelength of the mass M, and $d\Omega ^2=(d\theta ^2+\sin ^2\theta d\phi ^2)$. This provides exactly the same predictions as the standard Schwarzschild solution but offers deeper insight in our view.

This factor $\frac{l_p}{\bar{\lambda }}$ then appears in every gravitational prediction derived from the theory of general relativity that can be empirically tested, as demonstrated in Table 2. This implies that we may have a comprehensive quantum gravity theory, along with its associated quantum cosmology. While this is a bold claim and should not be automatically accepted, we believe it merits sufficient attention from the physics community. Over time, multiple researchers can collectively assess whether this represents a breakthrough in our understanding of gravity and cosmology or not.

Table 1 summarizes the relationships between the Hubble scale, the Planck scale, and the factor $\frac{T_{CMB}^2}{T_{Hw}^2}$. In the rightmost column, we summarize that these formulas, when viewed from the deepest level, indicate that the Hubble scale is simply the reduced Compton frequency per Planck time $\frac{l_p}{\bar{\lambda }_c}$ multiplied by the various Planck units corresponding to the dimension we are examining within the Hubble sphere. The formulas in the far-right column have independently been derived by an alternative approach related to the same quantum cosmology described in [43]. That we can arrive at the same formulas by starting out from different aspects in terms of observations, etc., strengthens our view that this is a fully consistent theory.

Table 1 This table illustrates the relationships between the Hawking temperature and the CMB temperature, as well as the large-scale properties of the Hubble sphere

Table 2 The table displays a series of gravity predictions provided by general relativity theory, obtained both through the conventional expression of the field equation and the novel quantized formulation of the field equation

Table 2 displays standard gravity predictions derived from the quantized Planck form of the general relativity theory. These predictions are consistent with those of general relativity theory. We present this to demonstrate that the reduced Compton frequency per Planck time, $\frac{l_p}{\bar{\lambda }_M}$, appears in all these formulas as well. In our view, this is the cornerstone of gravity quantization.

6 More Alternative Ways to Express the Large Scale Properties of the Universe

In this section, we also demonstrate alternative ways to rewrite the equations from the previous section, relying solely on the CMB temperature, the Hawking temperature, and the Planck scale. Please refer to [13, 15, 18] as many of the formulas represented below can also be simply derived from these sources. As for the Hubble constant, we have:

$$\begin{aligned} H_0=\frac{T_{CMB}^2 }{T_p^2}\frac{32\pi ^2}{t_p} \end{aligned}$$

(35)

Where $t_p=\frac{l_p}{c}$ is the Planck time. Alternatively, we can express it from the Hawking temperature:

$$\begin{aligned} H_0=\frac{T_{Hw}^2}{ T_p^2}\frac{c 32\pi ^2}{\bar{\lambda }_c}. \end{aligned}$$

(36)

For the Hubble time, we have:

$$\begin{aligned} t_H=\frac{T_p^2}{T_{CMB}^2}\frac{t_p}{32\pi ^2}. \end{aligned}$$

(37)

or from Hawking temperature

$$\begin{aligned} t_H=\frac{T_p^2}{T_{CMB}^2}\frac{\bar{\lambda }_c}{c32\pi ^2}. \end{aligned}$$

(38)

For the Hubble radius, we have:

$$\begin{aligned} R_H=\frac{T_p^2}{T_{CMB}^2}\frac{l_p}{32\pi ^2}. \end{aligned}$$

(39)

or from the Hawking temperature:

$$\begin{aligned} R_H=\frac{T_p^2}{T_{CMB}^2}\frac{\bar{\lambda }_c}{32\pi ^2}. \end{aligned}$$

(40)

For the critical mass, we obtain:

$$\begin{aligned} M_c=\frac{\hbar }{c l_p}\frac{T_p^2}{T_{CMB}^2}\frac{1}{64\pi ^2}. \end{aligned}$$

(41)

or from the Hawking temperature:

$$\begin{aligned} M_c=\frac{\hbar \bar{\lambda }_c}{cl_p^2}\frac{T_p^2}{T_{Hw}^2}\frac{1}{64\pi ^2}. \end{aligned}$$

(42)

For the Hubble entropy, we obtain:

$$\begin{aligned} S_H=k_b\frac{T_p^4}{T_{CMB}^4}\frac{1}{1024\pi ^3}. \end{aligned}$$

(43)

Table 3 summarizes the equations in this section. However, we believe it is important to be aware that at the deepest level, all these formulas represent what is described in the rightmost column of Table 1.

Table 3 This table illustrates the relationship between Hawking temperature and CMB temperature, as well as the large-scale properties of the Hubble sphere

Hawking [1] derived his temperature consistent with the Schwarzschild [3] metric, which is also consistent with the critical Friedmann solution when $\Lambda =0$. The full $\Lambda$-CDM model naturally incorporates a cosmological constant. However, our model is not in conflict with it; rather, it appears that the cosmological constant plays a lesser role in determining the CMB temperature. One possible reason for this is that the CMB is often considered a relic of the earlier stage of the universe. Our approach seems to align more closely with the so-called $R_h=ct$ type cosmological models, which are actively discussed as an alternative to the $\Lambda$-CDM model to this day [44,45,46,47,48,49,50].

The approach described here should also be investigated for other metric solutions to Einstein’s field equations, not just the Schwarzschild metric. For example, the Kerr [51] and Kerr-Newman [52, 53] metrics, as well as the new Haug-Spavieri [54] metric.

7 CMB Decoupling

The CMB decoupling plays an important role in modern cosmology. Even though the CMB (10) and (11) clearly predict a CMB value that closely matches the observed CMB value now, predicting the CMB value going back in the cosmic epoch by linking it to z is more model-dependent. In the standard $\Lambda$-CDM model, as well as from observations, one has the relation $T_{cmb,t}=T_{cmb,0}(1+z)$ or the more general formula $T_{cmb,t}=T_{cmb,0}(1+z)^{1-\beta }$ (see [55, 56]). Observations have shown that $\beta$ must be very close to zero, as seen in, for example, [57]. We can again link this to the CMB (10) and (11) to the cosmological red-shift. This can most elegantly be done inside so called $R_H=ct$ cosmological models. $R_H=ct$ have been around for multiple decades and are actively discussed to this day, see [45,46,47,48,49]. John [44], one of the early inventors of $R_H=ct$ cosmological models, even claims that:

Some of those eternal coasting models are published even before the discovery of the accelerated expansion of the Universe and were shown to have none of the commonly discussed cosmological problems and also that $H_0t_0 = 1$. The $R_H = ct$ model is only the special (flat) case of the eternal coasting model.

Milne [58], in a recent paper, points out that more than 27 different observations have been compared between the $\Lambda$-CDM model and the $R_H=ct$ model, and the $R_H=ct$ model fits observations just as well, and in some cases, even better than the $\Lambda$-CDM model. In particular, Milne points out that observations from the early universe strongly favor the $R_H=ct$ type models. However, there is clearly no consensus on this, and there are also strong critics of $R_H=ct$ cosmological models, see for example [59]. However, most of the critics have been claimed not to be valid [60]. There is also not only one single $R_H=ct$ cosmological model, but underclasses of $R_H=ct$ models, such as growing black hole cosmology, see for example [50].

In this paper, we will not attempt to determine whether the $R_H=ct$ models are preferable to the $\Lambda$-CDM model. Rather, we acknowledge that considerable research by multiple scholars over several years is necessary to approach a consensus on this question. However, we can note that the formulas referenced as (10) and (11) are compatible with $R_H=ct$ cosmology. This compatibility is based on the assumption that the universe’s radius expands according to $R_H=ct$, without any additional space expansion as proposed in the $\Lambda$-CDM model. Furthermore, to align the Cosmic Microwave Background (CMB) (10) and (11) with the well-established equation $T_{cmb,t} = T_{cmb,0}(1 + z)$, it is necessary to adopt the perspective that cosmological redshift conforms to the approach recently suggested by Haug and Tatum [61]:

$$\begin{aligned} z=\frac{\lambda _{observed}-\lambda _{emitted}}{\lambda _{emitted}}=\sqrt{\frac{R_H}{R_t}}-1=\frac{\left( \frac{\hbar c}{k_b4\pi \sqrt{R_{h,t}2l_p}}\right) }{\left( \frac{\hbar c}{k_b4\pi \sqrt{R_H2l_p}}\right) }-1=\frac{T_{cmb,t}}{T_{cmb.0}}-1 \end{aligned}$$

(44)

In that case $R_{H,t}=ct$ and $R_H=\frac{c}{H_0}$ is the Hubble radius now, and the formula above, when solved for $T_{cmb,t}$, corresponds to the standard assumption of $T_{cmb,t}=T_{cmb,0}(1+z)$. The Photon decoupling is closely related to recombination, and the CMB temperature of about 3000K, that according to the $\Lambda$-CDM model occurred approximately 378,000 years after the Big Bang. This corresponds to a cosmological red-shift of about $z = 1100$ and a CMB temperature given by the formula $T_{cmb,t}=T_{cmb.0}(1+z)\approx 2.725K(1+1100)\approx 3000 K$. In reality, one has only measured the CMB temperature in relation to z for the cosmic epoch up to a $z=6.34$ (see [57]), and even here, the uncertainty in measurements is very large. Riechers et al. report a one standard deviation in the CMB temperature for that cosmic epoch of 16.4K to 30.2K. So, at the moment, the decoupling at $z=1100$ with a corresponding CMB temperature, even if there is lots of solid research behind it, is still mostly theory.

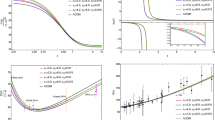
In our model, if we make it consistent with at least some subclasses of $R_H=ct$, cosmological models of the universe rather than the $\Lambda$-CDM, we find that the decoupling, if it happened at 3000K, occurred only about 12,052 years after the beginning of the universe. This is similar in time to what earlier suggested by Tatum and Seshavatharam [14], but then based on the assumption of a $\beta =\frac{1}{2}$ in $T_{cmb,t}=T_{cmb,0}(1+z)^{1-\beta }$ . This is much closer to the beginning of the universe than predicted by the $\Lambda$-CDM model. Figure 1 shows a graph of predicted CMB temperature at different epochs. Tatum and Seshavatharam [50] conducted a similar, interesting analysis, but they based it on $T_{cmb,t}=T_{cmb,0}(1+z)^{\frac{1}{2}}$ rather than $T_{cmb,t}=T_{cmb,0}(1+z)$. However, please also refer to their more recent paper [62], which is consistent with $\beta =0$.

Fig. 1

The figure illustrates the predicted Cosmic Microwave Background (CMB) temperature and cosmological redshift in relation to the number of years since the universe’s inception. If we align the CMB prediction formula with the tested principle $T_{cmb,t} = T_{cmb,0}(1 + z)$ and the cosmological model concept of $R_H = ct$, then the decoupling, which presumably occurred at approximately 3000K, must have happened about 12,052 years after the beginning of the universe. However, it’s worth noting that other possibilities not discussed in this article also exist

It remains uncertain whether we can empirically test whether the decoupling occurred significantly earlier than the $\Lambda$-CDM model suggests. However, investigating this possibility is important. As Milne has noted, the $\Lambda$-CDM model appears to face several challenges in accurately describing the early universe.

In Table 4, we show some time points from the very beginning of the universe to now, based on $R_H=ct$ cosmology, similar to the Tatum et. al model [13]. According to this perspective, the universe started with a temperature essentially close to the Planck temperature. If the decoupling event occurred at 3000K, it would have taken place 12,052 years after the beginning of the universe. The far-right column shows the reduced Compton frequency per Planck time in this observable universe, representing the quantization of gravity and aligning with the new approach to Planck quantizing general relativity described in Section 6.

Table 4 This table illustrates time since the beginning of the observable universe and corresponding properties of the universe since the beginning to the present when assuming the Hubble radius grows by $R_H=ct$

Planck scale cosmology seems to offer an alternative to the Big Bang hypothesis. The Big Bang hypothesis does not provide a good explanation of how all the mass and energy in the universe could fit into a singularity with no spatial volume, and what triggered the Big Bang. Planck scale cosmology can be interpreted as nothing can be compressed to more than the Planck mass density or inside a spatial volume smaller than the Planck volume. The observable universe could have started as a Planck mass black hole that has been growing in radius based on the $R_H=ct$ cosmological concept, similar to suggested in Tatum et. al [13]. There could even be many such black hole universes in the universe, each growing at $R_H=ct$. The new Haug-Spavieri [54] metric even seems to mathematically impose a maximum constraint on the mass density anywhere inside the Hubble sphere equal to the Planck mass density. This indicate the universe either had to start as a Planck mass black hole or that it alternatively the Hubble sphere could be a steady state black hole, two hypothesises that should be investigated further. Planck scale cosmology as presented in this paper also give a quantization of gravity, as it is clearly linked to the reduced Compton frequency per Planck time, see Section 6. The $\Lambda$-CDM model have not been able to link their theory to the Planck scale or to quantizastion of gravity.

8 Conclusion

We have demonstrated very simple relationships between the Hubble sphere, the CMB, Hawking temperature, and the Planck scale. At the deepest level, we find that $\frac{T_{CMB}^2}{T_{Hw}^2}=\frac{l_p}{\bar{\lambda }_c}$, which can be interpreted as the reduced Compton frequency of the critical mass and energy in the universe over the Planck time. All the large-scale properties of the Hubble sphere are essentially this frequency multiplied by the Planck unit with the same dimensions as those we want to study within the Hubble sphere. This is in full consistency with a recent reformulation of the theory of general relativity, where the reduced Compton frequency per Planck time in the gravity mass of interest also plays a central role. It appears that we have a quantum gravity theory that is fully coherent with quantum cosmology, linking the largest and smallest scales of the universe at the Planck scale. Furthermore, the Planck length can be extracted directly from cosmological observations without any knowledge of G.

Appendix

The formula to predict the CMB temperature (10) was first heuristically suggested by Tatum et al. in 2015. However, the lack of interest in it by the wider astrophysics community is likely due to the fact that it has never been demonstrated to be derivable from fundamental laws of physics. However in a recent paper, Haug and Wojnow [15], for the first time, demonstrated that the formula is directly derivable from the Stefan-Boltzmann law. In this appendix, we will briefly repeat that derivation but refer the readers to that paper for more details. According to Stefan-Boltzmann’s law, the luminosity of the Hubble sphere must be:

$$\begin{aligned} L_H=4\pi R_H^2\sigma T_{H}^4 \end{aligned}$$

(45)

Here $T_H$ is the temperature of the Hubble sphere. In addition, we take advantage of the recent developments in quantum gravity, where the hypothetical Planck mass particle seems to play an important role in all of gravity. The energy that is passing through such a particle from the Hubble sphere luminosity must be.

$$\begin{aligned} E=\frac{L_H}{4\pi l_p^2}. \end{aligned}$$

(46)

That is, we assume this particle has a Planck length radius. Furthermore, the radiant flux that is absorbed by the Planck sphere’s cross-section $\pi r^2 = \pi l_p^2$ is then expressed as:

$$\begin{aligned} \Phi _{abs}=\pi l_p^2 E=\pi l_p^2\frac{L_H}{4\pi l_p^2}=\pi l_p^2\frac{4\pi R_H^2\sigma T_{H}^4}{4\pi l_p^2}=\frac{\pi }{4} R_H^2\sigma T_{H}^4. \end{aligned}$$

(47)

Next, we will rely on a likely connection to the Hawking temperature. The Hawking temperature of a Planck mass particle is determined by Hawking radiation from such a micro black hole particle and is given by:

$$\begin{aligned} T_{Hw,p}=\frac{\hbar g}{2\pi c k_b}. \end{aligned}$$

(48)

Further the gravitational acceleration at the Planck mass micro black hole at the Schwarzschild radius of the Planck mass is $g=\frac{Gm_p}{r_s^2}=\frac{Gm_p}{(2l_p)^2}$. This leads to

$$\begin{aligned} T_{Hw,p}=\frac{\hbar g}{2\pi c k_b}=\frac{\hbar \frac{Gm_p}{r_s^2}}{2\pi c k_b}=\frac{\hbar c}{8\pi l_p k_b}=\frac{T_p}{8\pi }. \end{aligned}$$

(49)

where $T_p$ is the Planck temperature $T_p=\frac{1}{k_b}\sqrt{\frac{\hbar c^5}{G}}=\frac{m_pc^2}{k_b}$.

Further since the the Stefan-Boltzmann law involves a fourth power, then the flux emitted by Planck mass particles should be approximately equal to the flux absorbed. This is especially true when close to the steady state, where we have:

$$\begin{aligned} 4\pi l_p^2\sigma T_{Hw,p}^4=\pi l_p^2 E=\pi l_p^2\frac{4\pi R_H^2\sigma T_{H}^4}{4\pi l_p^2}=\pi R_H^2\sigma T_{H}^4. \end{aligned}$$

(50)

From this we get:

$$\begin{aligned} T_H = \frac{T_p}{8\pi }\sqrt{\frac{ 2l_p }{R_H }} \approx 2.72k. \end{aligned}$$

(51)

The Stefan-Boltzmann derivation is valid for the observable Hubble universe at any date, at least under the $R_H=ct$ concept. Furthermore, the values of $H_0$ and $T_{cmb}$ correspond only to today’s date.Haug and Wojnow also demonstrate mathematically how this is identical to the CMB temperature formula first heuristically presented by Tatum et al. In addition, Haug and Tatum [63] have recently derived the same formula from a geometric mean approach, assuming that the shortest possible wavelength is the Planck length and the longest possible wavelength is linked to either the diameter or the circumference of the Hubble sphere and that the CMB temperature is lined to the geometric mean wavelength of these two. It is not uncommon in physics to solve problems based on geometric means [64,65,66,67].