Abstract
The paper summarizes the conditions that are necessary to secure accurate measurements of the thermal conductivity of fluids using the transient hot-wire technique. The paper draws upon the development of the method over five decades to produce a prescription for its use. The purpose is to provide guidance on the implementation of the method to those who wish to make use of it for the first time. It is shown that instruments of the transient hot-wire type can produce measurements of the thermal conductivity with the smallest uncertainty yet achieved (± 0.2%). This can be achieved either when a finite element method (FEM) is employed to solve the relevant heat transfer equations for the instrument or when an approximate analytic solution is used to describe it over a limited range of experimental times from 0.1 s to 1 s. As well as establishing the constraints for the proper operation of the instrument we consider the means that should be employed to demonstrate that the experiment operates in accordance with the theoretical model of it. If the constraints are all satisfied then an uncertainty in thermal conductivity measurements of as little as ± 0.2–0.5% can be obtained for gases and liquids over a wide range of thermodynamic state from 0.1 MPa to 700 MPa and temperatures from 70 K to 500 K with the exception of near critical conditions. It is observed that many applications of the transient hot-wire technique do not conform to the constraints set out here and therefore may be burdened with very much greater uncertainties, sometimes large enough to render the results meaningless.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The transient hot-wire technique is a well-established, absolute technique, with a fully developed theoretical background [1], employed for the measurement of the thermal conductivity of fluids and solids with very low uncertainty. The evolution of the transient hot-wire technique has been described in detail elsewhere [2, 3]. If applied correctly, with the exception of the critical region and the very low-pressure gas region [1], it can achieve absolute uncertainties well below 1% for gases, liquids, and solids, and below 2% for molten metals and the effective thermal conductivity of two phases systems such as nanofluids [3].
In recent years however, the ‘simplification’ of the technique for commercial exploitation and its application to inhomogeneous multi-phase systems has led to measurements which are often significantly less accurate than is claimed and certainly less accurate than the best that could be achieved [4,5,6]. Given the technical benefits that could accrue from enhanced heat transport in fluids as has been claimed for so-called nanofluids [4, 7], it seems important to the present authors to establish for this new set of applications and a new generation of experimentalists the proper parameters and approach that should characterize all applications of the transient hot-wire technique for the measurement of the thermal conductivity in macroscopic systems. For that reason, in the following sections, a brief summary of the transient, hot-wire technique and its application will be given in a manner which emphasizes the constraints on its validity.
The full theory of the practical experimental technique is governed by the second order partial differential equation of transient heat conduction in a 3D space in a homogeneous system. The available approximate analytic solution for the description of the experimental technique [8], is valid provided that a restrictive set of conditions is obeyed, that can be satisfied by exceedingly careful instrumental design and operation [1, 8, 9]. Many of the recent applications of the transient hot-wire technique [4,5,6] have ignored these fundamental points and simplistic implementations inevitably lead to gross differences between the practical device and its theory. No amount of calibration or empirical adjustment can ever make up for this basic deficiency.
2 The Ideal Model and its Analytic Solution
The transient hot-wire technique is based on the observation of the temporal temperature rise of a thin vertical, resistive wire immersed in the single-phase material whose thermal conductivity is to be determined. The wire is initially in thermal equilibrium with its surroundings and a step voltage is applied to it. In this way, electrical current flows through the wire and heats it up. Therefore, the wire acts as a heat source of almost constant heat flux per unit length, producing a time-dependent temperature field inside the wire and the test material. Τhe evolution of the wire’s temperature depends in part on the thermal conductivity of the material around it.
The concept of the technique and the origin of the various constraints upon the design are most easily explained using an ideal model of the experiment. In first step in the formulation of an ideal model, an infinitely long, vertical thin source of heat is immersed in a stationary, infinite, isotropic material of temperature-independent thermal diffusivity α, and thermal conductivity λ, and which is initially (at t = 0) in thermodynamic equilibrium with the wire at temperature To. Furthermore, the heat transfer from the heat source, when a stepwise heat flow per unit length, q, is applied, is considered to be only conductive (radiation is considered negligible). Thus, the temperature field around the wire can be described by the partial differential heat conduction equation:
or
where \(c{}_{{\text{p}}}\) and ρ, are the specific heat and the density of the material around the wire, and r is the radial distance from center of the wire.
The thermal conductivity in Eq. 1 is only strictly defined for a homogeneous single phase, fluid. For inhomogeneous fluids (such as so-called nanofluids) the extension of the definition is heuristic and that apparent quantity may depend upon the distribution of the phases, the time and length scale of measurement as well as how the measurement is performed. The first constraint on the measurement technique, common to many methods follows.
- CONSTRAINT #1 :
-
Experiment must ensure that within its duration only conduction contributes to the measured heat transfer in a homogeneous fluid.
The following initial and boundary conditions are employed:
This problem is standard and the analytical solution of the above fundamental Eq. 2 for the temperature rise ΔΤ(r, t) has been given by Carslaw and Jaeger [10], as
where α is the constant thermal diffusivity of the surrounding material.
It has been shown [8] that the temperature rise at the point ro is the same as that at the surface of a thin wire of radius ro, provided that the wire has no heat capacity and an infinite thermal conductivity. At the position r = ro, for small values of \((r_{{\text{o}}}^{2} /4at)\) an expansion of the exponential integral is possible and we have
where C = eγ and γ is the Euler constant equal to 0.5772157.
The ideal model of the experiment is then finally formulated by requiring that the second and following terms on the right side of Eq. 7 can be considered negligible, and the ideal model working equation can be written as
Here the subscript id indicates the working equation only refers to the ideal model of the experiment. It reveals the possibility of obtaining λ the thermal conductivity of the test material from the slope of the line \(\Delta T_{{{\text{id}}}}\) versus lnt. It would also appear from this equation that the thermal diffusivity might be obtained from its intercept. However, the development of the model to account for all of the departures of a real experiment from the ideal model has been focused on the fact that the absolute value of the temperature rise is secondary to its dependence on time so that little attention has been paid to the corrections that would affect the absolute value of the temperature rise [1, 8]. For that it is not advised to use the method to derive the thermal diffusivity from measurements directly.
In practice the transient hot-wire technique makes use of a thin metallic wire of finite length to provide the heat source when a current flows through it and its resistance change with time is used to monitor the temperature rise within it. In order that Eq. 8 can be used for the evaluation of the thermal conductivity a large number of constraints must be satisfied. It will be the purpose of the next section to detail them. First though we set out a vital part of the thinking that underlies these constraints. Evidently, the practical instrument for the measurement of the thermal conductivity of a material inevitably introduces a number of departures from the ideal model. Therefore, if Eq. 8 is to be used to interpret experimental measurements a significant number of corrections have to be made to the acquired experimental data to adjust it to the ideal model described by Eq. 8. The design intention is that the experimental cell and operation are such that each individual departure from the ideal model is sufficiently small that each can be treated as a separate, additive correction to the measured temperature rise. In practice, the requisite smallness is obtained by a theoretical analysis of each departure and subsequent design of the instrument to ensure that no correction is ever more than 0.5% of the measured temperature rise. The reason for this is so that when we estimate a correction say to within 5% the residual effect upon the measured temperature rise is negligible. Here, the word negligible is intended to mean smaller than the combined random error in the measurement of the temperature rise and time. It has been verified in practice that such a constraint ensures that residual deviations between the theoretical and that observed ones should be no more than 0.01% and this in turn leads to thermal conductivity measurements with an expanded uncertainty of better than ± 0.5% [1, 11, 12]
With this background the temperature rise of the ideal model in terms of the one observed experimentally is [8]
where ΔTid (ro, t) is the ideal temperature rise ro at time t, introduced in Eq. 8, ΔTexp (t) is the temperature rise of the wire measured experimentally and Σi δΤi is a sum of the various corrections. The origin of each deviation from the ideal model has been explained and an explicit theoretical evaluation of the each correction to be applied has been made elsewhere [1]. We consider here only those that can be significant. These deviations can be separated into four categories by virtue of the means necessary to deal with them [1]. We note that in terms of ISO GUM (Part 6) all of the deviations between the ideal model and reality are “well understood”.
2.1 Deviations Whose Effects Can be Eliminated Entirely by Design and Operation
2.1.1 Convection
It is, of course, impossible to avoid convective motion of a heated fluid in the earth’s gravitational field. However, its effect on the measurements by the transient hot-wire technique can be eliminated by the adoption of a vertical wire and sufficiently short measurement duration. It is both possible and necessary to confirm this has been achieved [1]. If convection is present, then the linear temperature rise predicted by Eqs. 8 and 9, will not be followed. It follows that checking the linearity of the line of ΔTid vs lnt is an absolutely essential condition for each and every experiment. The manner in which such linearity should be confirmed, is detailed later. In the case of fluids, it has been shown experimentally [13, 14], that proper operation ensures no deviations from the linearity of Eq. 8 because of convection, in the time range 0.1 to 1 s, although longer times show clearly such an effect in some cases [1].
- CONSTRAINT #2 :
-
to avoid convective effects times larger than 1 s should not be employed (the corrected temperature rise, ΔTid vs lnt should be exactly linear between 0.1s and 1 s).
2.1.2 Knudsen Effect
The correction for the Knudsen effect has been described explicitly by Healy et al. [8], and it affects only gases of very low density. In practice, measurements can always be conducted at higher pressures or densities so that the effect is demonstrably negligible. If required, values of the thermal conductivity of a gas at low density can readily be obtained by extrapolation of values obtained at higher densities [11].
2.2 Deviations Where the Corrections are Sufficiently Small that Their Application has an Effect that is Less than 0.01% by Design or Operation.
2.2.1 Finite Wire Diameter
The ideal model that led to Eq. 7 and then Eq. 8, assumes that the line heat source is of infinitesimal diameter whereas, in practice, the wire has a finite diameter. Hence, the use of a wire with radius ro changes the inner boundary condition of Eq. 4 to:
However, the solution is again Eq. 7, for small values of \((r_{{\text{o}}}^{2} /4at)\) and the ideal model of Eq. 8, is again recovered.
2.2.2 Truncation Error
In deriving the working equation for the ideal model of Eq. 8 from Eq. 7 we neglected the terms beyond the first in the expansion of Eq. 7. Thus, to be able to use Eq. 8 to analyze the experimental observations we must apply a correction to the experimental data to account for this ‘truncation error’. The magnitude of the correction represented by the second and higher order terms can easily be examined and is evidently greater for the smaller thermal diffusivities characteristic of liquids at short times and larger wire radii. For example, for an experiment in toluene at 298 K (a ≈ 9×10−8 m2/s) then, at a time of 0.1 s for a wire of 20 μm diameter, the truncated terms constitute only 0.01 % of the temperature rise, whereas for a wire of 100 μm diameter, at the same time the truncated terms amount to about 3 % of the temperature rise. In the first case, if it is possible to estimate, the truncation error is below 0.01% and the allowable threshold and so is acceptable, whereas in the second case it is not. Thus, the correction for the neglect of higher order term should always be made, but is typically only small enough to be acceptable when the diameter of the hot-wire is below 25 μm. Not to make such a correction, in the case of a wire diameter of 100 μm, will cause an error of at least 3 % in the thermal conductivity reported. For this reason alone, wires of more than 25 μm diameter should never be employed.
Both effects 2.2.1 and 2.2.2 lead to the conclusion that the smallest wires possible should be employed consistent with availability and mechanical endurance under practical circumstances.
- CONSTRAINT #3 :
-
For measurements in liquids, wires of more than 25 μm diameter, should not be employed.
2.2.3 Radiation
In the case of transparent fluids, the heat fluxes due to conduction and radiation are independent and additive. Thus, given the small temperature rises involved the corresponding correction is usually negligible [8] or easily evaluated. Conversely, in the case of non-transparent fluids, that absorb at least some of the radiant energy emitted from the wire, Menashe and Wakeham [15] proved that, in practice, if radiation is present, this becomes evident when plotting the corrected experimental ΔTid values against lnt, because the line is no longer straight and there appear characteristic curvatures. In most cases examined to date [15] no sign of the effect of radiation has been observed. This is physically because the conductive element of heat transfer is determined by the gradient of the temperature (perhaps as much as 105 K/m for a wire of less than 25 μm diameter), whereas the radiative component is driven by the temperature difference to first order (a few Kelvin). Therefore, by the choice of small diameters wires; it is possible to ensure and verify the effect is negligible. Constraint 3 therefore covers this effect.
2.2.4 Viscous Heating
The inevitable movement of the fluid cause by its heating in a gravitational field must always lead to the generation of heat through viscous dissipation. It has been shown that this is always rendered negligible by the use of sufficiently small temperature rises [8].
2.2.5 Compression Work
Inevitably, when a fluid is heated in a closed vessel work is done compressing the fluid. The effect has been analytically estimated. It is largest for dilute gases but is then readily eliminated by the choice of a sufficiently large vessel containing the fluid [16]. Its elimination can be verified experimentally by varying the size of the vessel containing the fluid.
- CONSTRAINT #4 :
-
Choose a large enough vessel to contain the fluid.
2.3 Remaining Deviations Where Design and Operation Can Render the Correction Small (<0.5 % of ΔT id (r o, t)) but Where an Analysis Yields a Correction Whose Magnitude Can be Known Better than ±1 % So that the Residual Effect is 0.005%
2.3.1 Finite And Non-zero Properties of the Wire
This correction takes into account the non-zero radius of the wire ro, its finite thermal conductivity λW, and its heat capacity cp [8, 10, 14]
In the above equation, subscript w refers to the wire properties. Usually, the first term in the summation of Eq. 11 constitutes the major correction owing to finite properties of the wire. In practice, this correction has a larger effect at short times and for low density gases. As we have observed earlier, to preserve the integrity of the method it should never be allowed to be larger than 0.5 % of ∆ Tid. Substituting some numbers into the first term of Eq. 11, one can easily show that in a liquid a) for a wire of 10 μm radius, at 0.1 s, δTw = 0.01 K, while b) for a wire of, 50 μm radius at 0.1 s, δTw = 0.20 K. In the case of measurements in argon gas, for a wire of 10 μm radius, at 0.1 s, δTw = 0.22 K while, for a wire of 50 μm radius δTw = 5.35 K. For typical temperature rises (2 -3 K), all except the first of these values exceed the threshold of 0.5% of the temperature rise. It follows that the time range of observations of the temperature rise should be limited to a time above that for which the correction for the finite properties of the wire falls to < 0.5 % of the wire temperature rise. In practice, this can be readily satisfied for liquids with a wire diameter no greater than 25 μm. For gases, wires with diameters less than 10 μm must be used.
- CONSTRAINT #5 :
-
In order to allow correction for the finite properties of the wire, in liquids, wire with a diameter larger than 25 μm should not be employed, while for gases less than 10-μm-diameter wires ought to be used.
2.3.2 Outer Boundary Correction
The fluid sample must obviously be contained and there is often a desire to reduce the total volume of the sample for reasons of safety or expense and so to make the container as small as possible. The finite volume of the material, causes a deviation from the ideal model, in that there is an outer boundary at a distance r = b, where b is the radius of the vessel. This leads to the modification of the outer boundary condition as described by Eq. 5,
An original, complex analytic expression of the corresponding correction was given by Carslaw and Jaeger [10] as early as 1959, but Healy et al. [8] proposed a simplified form of the original equation in 1976:
where gν are the roots of J0(gν) = 0, and J0 and Y0 are Bessel functions.
Except for gases with the highest thermal diffusivity at low density, the effect can be rendered negligible by placing the cell wall more than 0.5 cm away from the wire [8].
- CONSTRAINT #6 :
-
Cell wall must be more than 0.5 cm away from the wire (liquids or gases), and best practice suggest the correction should always be applied because it is simply done and it can never be wrong to do so.
2.3.3 Sample Physical Properties that Vary with Temperature
The variation of the thermal conductivity and the heat capacity of the sample with temperature, produce a correction that should be applied to the ideal solution. The analysis carried out by Healy et al. [8], considered a linear perturbation of these properties; they showed that the temperature, Tr, to which the thermal conductivity deduced from the linear slope of the line ΔTid vs lnt refers is
where To is the initial equilibrium temperature of the material, and ΔT(t1) and ΔT(t2) are the temperature rise measured experimentally at the initial observed time t1 and the final time t2, respectively. This correction to the reference temperature for the thermal conductivity is not negligible and must always be performed.
- CONSTRAINT #7 :
-
Thermal conductivity must always be referred to the corrected reference temperature.
2.3.4 Wire Insulation
In the case where the sample to be measured is polar or electrically conducting, it is necessary to apply an insulating coating to the bare metallic wire, to avoid a series of unwanted phenomena. The latter include current leaking through the test material, polarization on the wire’s surface, and distortions to the voltage signals. Wakeham and Zalaf [17], based on the previous work of Nagasaka and Nagashima [18], and Alloush et al. [19] over a limited range of conditions, managed to overcome some of the aforementioned constraints to a significant extent, by establishing the use of a tantalum wire with an insulating layer made of its own pentoxide, via an in situ anodization process. Hence, provided that the wire and its coating are made of a suitable material and that the coating is sufficiently thin (in the case of the tantalum oxide a layer thickness < 200 nm) an analytic correction exists [18].
- CONSTRAINT #8 :
-
In the case of polar or electrical conducting liquids, use insulated wire with a coating that renders the correction for its presence less than 0.5%.
2.4 Remaining Effects—Treated Experimentally
2.4.1 End Effects
The wire employed in practice cannot be infinitely long, as assumed in the ideal model and thus there are always effects at the ends of a supported, finite wire owing to conduction in an axial direction not amenable to exact analysis. A rigorous analysis of this problem is not available, so these ‘end effects’ must, be eliminated experimentally. Two main approaches to achieve this elimination have been adopted.
The first solution uses a single wire with potential leads of a smaller diameter attached about a central section of its length. The potential leads are used to measure the potential difference over the section of the wire between them and thereby deduce the resistance change following from the temperature change of the wire. If the wires comprising the potential leads are of sufficiently small diameter compared with the heating wire, then there could be an insignificant heat loss through them and the whole of the wire between the potential leads behaves as a finite section of an infinite wire. An evaluation of the effect of these potential taps should always be conducted to show that this is the case. In practice, this has not been performed and for hot wires with a diameter of 10 μm, the connection of wires of much less than 1 μm diameter is essentially impossible so that this method cannot be recommended.
The other approach employs two wires, nominally identical except for their length. If both wires are subject to the same heating current then the end effects in each case will be the same provided that each is sufficiently long that a central section attains the temperature appropriate to an infinite wire [8, 20]. Thus, if arrangements are made to measure the difference of resistance of the two wires as a function of time, it will correspond to the resistance change of a finite section of an infinite wire, from which the temperature rise can be determined. This approach is adopted in all the work that has led to thermal conductivity data with the lowest uncertainty.
As far as the appropriate length of the wires is concerned, Antoniadis et al. [21] have presented a Finite Element Method simulation of the heat distribution around the end of a 25 μm-thick tantalum wire, welded onto a 1 mm-thick support, also made of tantalum, after heating it for 1 s in water. The isotherms reflecting the temperature changes inside and around the wire are shown in Fig. 1. Figure 1 shows only the first 5 mm of the wire. The FEM analysis showed that the end effects cover a distance of about 1 cm from the support. Therefore, keeping in mind that the two wires are welded at both ends and that the goal is to subtract the end effects and leave a finite section of wire long enough to be a finite part of an infinite wire (3 cm at least). Of course, the minimum difference of length between the two wires is determined by the sensitivity of the means of detecting its resistance change with time. It is worth noting that the use of a single 5 cm length wire without any end-effect correction, results in a 15% difference in the resistance of the wire from that of a wire with no end effects.
- CONSTRAINT #9 :
-
To avoid end effects, use 2 wires, a short one of length > 2 cm and a long wires of length > 5 cm.
2.5 Summary of Constraints
Table 1 shows a summary of the constraints discussed for proper operation of the Transient Hot-Wire technique with liquids and gases. These constraints ensure that the corrections to be applied to the temperature rise are always sufficiently small that they can be estimated with an accuracy comparable with the noise level in the measurements. This implies of course that the corrections must always be applied.
2.5.1 Checking the Linearity of ΔΤ vs lnt
At several points during the foregoing exposition, we have emphasized the need to derive the thermal conductivity of the fluid from the slope of the line between the ΔTid and lnt over a range of time determined by the operation of a variety of constraints. At the same time, we have been at pains to point out that the linearity of this plot is a means of demonstrating that the experiment operates in all respects in accord with the theory of it.
For those reasons it is important to verify that the experimental plot is indeed linear for each and every measurement. It is common practice in the processes of regression fits using least squares processes to examine simply the regression coefficient R to determine whether one has a good fit to a linear function or not. It is a matter of experience that this is inadequate and inappropriate for the analysis of the THW experiments. This is because very small systematic curvature in the experimental data return a regression coefficient very close to unity.
For that reason, best practice for use with such experiments is to construct a linear fit over say the first five data points at the shortest times in the interval studied and to record the slope and its standard deviation for such a fit. The fitting is then repeated after adding the next later time and the reported fitted coefficients recorded again. This is repeated until all the data points have been included. If the observations are truly linear and as more points are included the standard deviation estimated in the slope will fall and, within its estimated standard deviation, the slope of the line will remain constant. This is a very stringent test of the data but unless it is carried out small curvatures can be overlooked and the true value of the thermal conductivity depends on the particular time window chosen to evaluate the slope. It is regrettable that seldom is the detailed linearity of the plots reported and even less frequently is this method adopted.
3 The FEM Approach
A more recent, alternative approach to the approximate analytic solution described above, is to solve the full Fourier heat transfer equations in the wire and the test material, using numerical methods based upon the finite element method. In our case COMSOL Multiphysics Version 3.2, was employed but other readily available systems could be employed. It should be emphasized that this approach was simply not available when the modern version of the transient hot-wire technique was developed in the 1970’s.
In this approach Antoniadis et al. [21] employed a 2D heat conduction equation for wire, one for the fluid and a separate one for the insulation layer (in case of electrically conducting liquids). The numerical model consists of two subdomains: one which is a part of the circular cross–section of the hot wire and the other which is considered to be a fluid sample in which the wire is immersed. The wire is placed on the axis of the cylindrical sample so that one quadrant of the geometry need be considered which allows greater resolution in the solution for a given computational effort. In the finite element analysis, it is important that the model is able to represent accurately the local variation of all relevant quantities. The basic parameters that enable such accuracy are the spatial density of the mesh, and the size of the time steps used in the selected numerical solver. The optimized mesh employed includes 1,060 elements, with a higher density in regions where a higher temperature gradient is expected, (within and close to the metallic wire).
4 Validation of the Transient Hot-Wire Technique
As discussed above one of the necessary tests of any transient hot-wire measurement is that the observed temperature rise should conform with the theoretical description of it within the mutual error of theory and experiment. Figure 2 shows a typical temperature rise measured in water at 297.5 K and atmospheric pressure [21].
We devote some space here to a demonstration of the validity of measurements because it is exactly this that is omitted from most studies.
4.1 The Analytic Solution
We begin by examining the behavior of this experiment with respect to the approximate analytical solution for the temperature rise. For this experiment, a setup of two 25-μm-diameter Ta wires, differing only in length, 2 and 5 cm, anodized in situ, were employed. As was pointed out earlier we can consider only a range of time for such a comparison defined by the magnitude of the various corrections to be applied to the experimental temperature rise as a function of the time. In practice we have limited the magnitude of any correction to be no more than 0.5% of the temperature rise which means that times between 0.0025 s and 0.1 s have been disregarded (42 points) because for those very small times the heat capacity correction was larger than 0.5% of the temperature rise [14]. The outer boundary correction was always insignificant and the correction for the wire coating amounted to no more than 0.07% irrespective of time.
Figure 3 shows the fractional deviations from a linear fit of it as a function of the logarithm of time. The agreement is within ± 0.05% (at the 95% confidence level), and the value of the thermal conductivity of water obtained is 605.6 mW·m−1·K.−1 at 297.5 K. The uncertainty of this value obtained by this technique, if a G.U.M. analysis is carried out [22], is 0.5% (at the 95% confidence level) and a full analysis is given by Charitidou et al. [9]
It should be noted that the reference value for the thermal conductivity of water at 297.5 K proposed by the International Association for the Properties of Water and Steam (IAPWS) and the International Association for Transport Properties (IATP), is 605.5 ± 0.2% mW·m−1·K−1 [23] that is within 0.02% of the present measurement.
4.2 The FEM validation
Figure 4 shows the raw, uncorrected, experimental temperature rise in the same measurement as discussed above, without any corrections applied, and the temperature rise obtained by the FEM solution, over the entire range of measurements (0.0025 s to 0.1 s). In order to obtain the numerical solution we have employed as input values, the density of the metallic wire, its heat capacity, its thermal conductivity as well as the same quantities for the insulating coating. Finally, we need values for the radius of the wire and its coating and a density and heat capacity for the fluid. All of these quantities for the measurement in water are collected in Table 2. The thermal conductivity of the fluid is then determined as that value when the numerical solution shows the least-square deviation between the numerical solution and the experimental data. The residual percentage deviations between the optimum fit and the data are shown in Fig. 5 over the entire time range (0.0025 to 1 s). The following should be noted:
-
A)
The agreement between the experimental temperature rise points and those calculated by the FEM solution, is excellent over the entire time range from 0.0025 s to 1 s. We note that deviations are slightly larger at very short times, because in that range the slope of the temperature rise vs time curve, is considerably steeper.
-
B)
The value of the thermal conductivity obtained by FEM, is 604.0 mW·m−1·K−1 at 297.5 K. This value is obtained with an absolute uncertainty of 0.5%. The absolute uncertainty arises from uncertainties in the measurement of the wire diameter, the measurement of the heat flux and the FEM numerical error.
-
C)
The aforementioned value is within 0.2% of the values obtained from the application of the linearized analytical theory solution (605.6 mW·m−1·K−1) and the IAPWS-IATP reference value (605.5 mW·m−1·K−1) [23].
Finally, it is worth observing that if some of the properties of the observing system are not available directly, they maybe simultaneously derived by fitting the FEM solution to the experimental temperature rise, owing to the large number of data points available.
5 Discussion
The previous analysis clearly demonstrates the following:
-
A)
The full heat transfer set of equations governing the transient hot-wire experiment can be solved accurately by FEM, so that the temperature rises can be obtained within about 0.1% at worst, so that the thermal conductivity can be evaluated with an absolute uncertainty of about 0.5%.
-
B)
The approximate analytic solution can be employed without introducing additional errors, over the time range 0.1 s to 1 s, with an equivalent absolute uncertainty of about 0.5%. However, for this to be valid, the following conditions must be met.
-
a)
In both cases, it is absolutely essential that some means is adopted to eliminate the effects at the ends of the finite hot wires, or a three-dimensional heat transfer problem has to be solved.
-
b)
In order to be able to apply the analytical solution and thus determine the thermal conductivity from the slope of a line relating the ideal temperature rise to the logarithm of time each wire and any coating must be very thin, less than 25 μm diameter, so that the corrections to the line source model can be evaluated and applied without introducing significant error.
-
c)
Low values of the temperature rise, less than 4 K, must be employed to perturb the system as little as possible without losing resolution.
-
d)
Insulated wires should be employed for measurements in polar, or electrically-conducting liquids to avoid distortion of the electrical signals in the measurement system.
-
a)
These necessary conditions must be complemented by a demonstration that the expected congruence between experiment and theory is delivered.
Designs of cells conforming to the design constraints can be found in a number of references [1, 2]. Such cells have been applied to gases up to 750 K and pressures up to 70 MPa, and mostly organic liquids up to 400 K and 500 MPa. It has proved more difficult to sustain an uncertainty of a few parts in a thousand over a wide temperature range in gases. It is possible this is a result of the difficulty of maintaining a very thin platinum wire stationary and vertical when subjecting to transient heating [24, 25].
Here we note that some commercial implementations as well as some research instruments of what is called the transient hot-wire technique depart considerably from that we have set out here and conform to very few of the essential constraints we have outlined. Some indeed make use of a rather complicated composite probe of many materials in a tube of mm diameter and yet apply Eq. 8 for analysis. Others employ wires of 100 μm diameter, or more, or single wires with no end effects correction.
Although there may be reasons why these sensors could be applicable, they do not derive from the theory set out here or any published material. Equally, the Standard methodology set out by ASTM D7896 departs significantly in both theory and practice from what is described here. The consequences of these departures from the rigor advocated here cannot be determined.
6 Conclusions
In this paper, it has been confirmed that instruments operating according to the transient hot-wire technique can indeed produce excellent measurements when FEM is employed for the evaluation of the thermal conductivity of the fluid using the exact geometry of the hot-wire. It has furthermore been shown that an approximate analytic solution can be employed with equal success, over the time range 0.1 s to 1 s, with an equivalent absolute uncertainty of about 0.5%, provided a) two wires are employed, so end effects are canceled b) each wire is very thin (less than 25 μm diameter) so that the line source model and the corrections mentioned before are valid, but also its resistance change is accurately recorded. c) low values of the temperature rise, less than 4 K, must be employed in order to perturb the system as little as possible without losing resolution, and d) insulated wires are employed for measurements in electrically-conducting or polar liquids to avoid spurious electrical effects.
References
Experimental Thermodynamics. Vol. III, Measurement of the Transport Properties of Fluids, Eds. Wakeham, W.A., Nagashima, A., Sengers, J.V. (Blackwell Scientific Publications, London, 1991)
M.J. Assael, K.D. Antoniadis, W.A. Wakeham, Int. J. Thermophys. 31, 1051 (2010)
J.T. Wu, M.J. Assael, K.D. Antoniadis, Chapter 5.1. History of the transient hot Wire, in Experimental thermodynamics volume IX: advances in transport properties of fluids. ed. by V. Shalu (RSC Press, London, 2014)
G. Tertsinidou, M.J. Assael, W.A. Wakeham, Int. J. Thermophys. 36, 1367 (2015)
D. Velliadou, K.D. Antoniadis, A. Assimopoulou, M.J. Assael, W.A. Wakeham, Int. J. Thermophys. 43, 123 (2022)
M.J. Assael, A. Leipertz, E. MacPherson, Y. Nagasaka, C.A. Nieto de Castro, R.A. Perkins, K. Strom, E. Vogel, W.A. Wakeham, Int. J. Thermophys. 21, 1 (2000)
G.J. Tertsinidou, C. Tsolakidou, M. Pantzali, M.J. Assael, L. Colla, L. Fedele, S. Bobbo, W.A. Wakeham, J. Chem. Eng. Data 62, 491 (2017)
K. Healy, J.J. de Groot, J. Kestin, Physica 82C, 392 (1976)
E. Charitidou, M. Dix, M.J. Assael, C.A. Nieto de Castro, W.A. Wakeham, Int. J. Thermophys. 8, 511 (1987)
H.S. Carslaw, J.C. Jaeger, Conduction of heat in solids (Oxford University Press, Oxford, 1959)
M.J. Assael, W.A. Wakeham, J. Kestin, Int. J. Thermophys. 1, 7 (1980)
M.J. Assael, M. Dix, A. Lucas, W.A. Wakeham, J. Chem. Soc. Faraday Trans. 1(77), 439 (1981)
J. Pantolini, E. Guyon, M.G. Verlade, R. Balleux, S.G. Finiel, Rev. Phys. Appl. 12, 1849 (1977)
J.J. de Groot, J. Kestin, H. Sookiazian, Physica 75, 454 (1974)
J. Menashe, W.A. Wakeham, Int. J. Heat Mass Transf. 25, 661 (1982)
M.J. Assael, E. Karagiannidis, W.A. Wakeham, Int. J. Thermophys. 13, 735 (1992)
W.A. Wakeham, M. Zalaf, Fluid Phase Equilib. 36, 183 (1987)
Y. Nagasaka, A. Nagashima, J. Phys. E. 14, 1435 (1981)
A. Alloush, W.B. Gosney, W.A. Wakeham, Int. J. Thermophys. 3, 225 (1982)
J. Kestin, W.A. Wakeham, Physica 92A, 102 (1978)
K.D. Antoniadis, G.J. Tertsinidou, M.J. Assael, W.A. Wakeham, Int. J. Thermophys. 37, 78 (2016)
Evaluation of Measurement Data - Guide to the Expression of Uncertainty in Measurement (GUM) (Joint Committee for Guides in Metrology, 2008).
M.L. Huber, R.A. Perkins, D.G. Friend, J.V. Sengers, M.J. Assael, I.N. Metaxa, K. Miyagawa, R. Hellmann, E. Vogel, J. Phys. Chem. Ref. Data 41, 033102 (2012)
S. Jawad, W.A. Wakeham, Proc. 24th International Thermal Conductivity Conference, 505 (Pittsburgh, PA, USA, October 1997)
S.H. Jawad, M.J. Dix, W.A. Wakeham, Int. J. Thermophys. 45, 1 (1999)
Funding
Open access funding provided by HEAL-Link Greece. No funding was received for this work.
Author information
Authors and Affiliations
Contributions
All authors contributed equally.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests of a financial or personal nature.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Assael, M.J., Antoniadis, K.D., Velliadou, D. et al. Correct Use of the Transient Hot-Wire Technique for Thermal Conductivity Measurements on Fluids. Int J Thermophys 44, 85 (2023). https://doi.org/10.1007/s10765-023-03195-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10765-023-03195-1



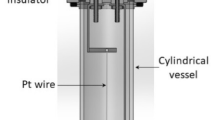




 ) FEM solution (Color figure online)
) FEM solution (Color figure online)