1 Introduction

The experimental method discussed in this review was proposed 1991 [1] and was designed for determining thermal transport of solids. The suggested arrangement is that of a plane, electrically insulated, and conducting pattern sandwiched between the surfaces of two pieces of the substrate material. This intimate encapsulation of the probe in the substrate makes it possible to very precisely keep track of the amount of power that is leaving the probe and heating the substrate. The arrangement is such that the pattern can be used both for Joule heating of the surfaces and at the same time be recording the temperature increases caused by the heating. The possibility to predict the exact dissemination of the power in the substrate makes it possible to calculate thermal conductivity from the transient recordings.

This experimental arrangement was originally named “transient plane source” (TPS) method for determining thermal conductivity and thermal diffusivity [1]. It is possible to use different patterns for the probe but so far, the most common pattern is that of a double spiral (DS), which is frequently referred to as the Hot Disc probe [2]. The properties determined with the Hot Disc method include thermal conductivity, thermal diffusivity, thermal effusivity, and volumetric specific heat. While the probes are of the same design and the electrical circuitry for heating and for recording the temperature stay the same, the arrangements of the sample pieces differ considerably. It is possible to experimentally arrange an insulating material on one side of the probe and the substrate on the other and then assume that all the power from the probe goes into the substrate, cf. [3, 4]. This arrangement can be used for less precise work and for comparative measurements often used for quality control purposes.

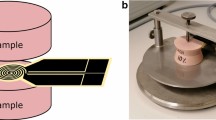
The essential component of this measuring arrangement is the probe working both as heat source and a temperature-sensing device. In the above-mentioned paper [1], possible designs of TPSs were discussed. Out of these, the Hot Disc has turned to be the most well functioning. This probe consists of double spiral pattern etched out of a thin (around 10 μm) metal foil and covered on both sides of thin electrically insulating films (thickness from 10 μm to 50 μm). The essentially circular probes can typically have diameters from 1 mm to 300 mm.

The experimental arrangement is simply that this rather thin probe is clamped between two pieces of the substrate material. Each piece having a flat surface and since the experiment is terminated before the heat wave reaches the outside boundaries of the substrate pieces no specific shape of the outsides is required as long as the condition of a reasonable probing depth is fulfilled. The heating of the probe is arranged via an electric Wheatstone bridge. If the temperature coefficient of the electrical resistivity of the metal—out of which the spiral has been etched—is known, it is possible to follow the mean temperature increase via the off-balance voltage of the bridge, as it is powered by a constant driving voltage.

The length of a transient recording with the probe located between the two sample pieces is limited because of the following considerations: (a) the theory developed for analyzing the experimental results assumes that the heat source is located inside an infinite solid and (b) if both the thermal conductivity and the thermal diffusivity are to be determined from a single transient recording it is imperative that the temperature field at the end of the transient recording has a certain extension related to the radius of the probe. Both of these conditions can be assessed and controlled via an estimation of the probing depth [2].

Since the insulating layers on the sides of the spiral are thin and the output of power from the spiral is constant, the temperature difference, which develops between the metal DS and the solid surfaces, becomes constant within a time, which is very short compared with normal times of transient recordings. If it is possible to consider the initial temperature difference across the insulating layers a constant, we are actually recording the temperature increases of the first “solid” surface of the substrate beyond the electrically insulating layer on the probe surfaces. This means that it is possible to record the true bulk properties of the substrate material. This facility does not exist when using steady-state methods for determining the thermal conductivity of a solid material and in this case, more elaborate methods involving samples of different sizes must be arranged to eliminate the influence from thermal contact resistances [5, 6].

For routine measurements, the method is suitable for materials having values of thermal conductivity, \(\lambda,\) in the approximate range of 0.050 W m–1 K–1 to 500 W m–1 K–1, values of thermal diffusivity, \(\alpha,\) in the approximate range of 0.1 (mm)2 s–1 to 100 (mm)2 s–1, and for temperatures, T, in the range of 25 K to 1500 K [7,8,9,10]. The specific heat capacity per unit volume, C, for an isotropic material can be obtained by dividing the thermal conductivity by the thermal diffusivity, i.e., \(C=\lambda/\alpha\) and is in the approximate range of 0.005 MJ m–3 K–1 to 5 MJ m−3 K–1.

It is here interesting to note that the same kind of experimental arrangement as described in this paper has been used to introduce transient measurements of Near-Field Thermal Radiation [11] with remarkable results.

1.1 Probing Depth

The probing depth, \(\Delta p,\) is a measure of how far into the specimen, in the direction of heat flow, a heat wave has traveled during the time window used for evaluating the thermal transport, cf. Chap. 10 in [12]. The probing depth is given by

$$\begin{aligned} \Delta p = \kappa \sqrt{\alpha \cdot t_{max}} \end{aligned},$$
(1)

where \(\kappa\) is a constant dependent on the sensitivity of the temperature recordings. A typical value for this constant in this kind of transient measurements is \(\kappa = 2,\) which is used throughout this document. In this expression, \(\alpha\) is the thermal diffusivity and \(t_{max}\) is the maximum time of the time window used for evaluating the transport properties.

It is important to estimate the probing depth both when planning and analyzing a measurement with the Hot Disc method and the reasons are two-fold: a) it indicates the minimum size of the substrate for the probe to be considered placed in an infinite medium and b) it defines the optimum extension of the temperature field in relation to the probe size for determining both the thermal conductivity and the thermal diffusivity from one single transient recording. The most practical arrangement is when these two conditions are made to coincide. For transient measurements in which the heat flow is strictly cylindrical or strictly plane, it is normally not possible to obtain more than one or a combination of two thermal transport coefficients. However, when using a strip source or a number of concentric strip sources, it is under certain conditions possible to obtain both the thermal conductivity and the thermal diffusivity from one single transient recording [13, 14]. For the purpose of finding these conditions, the theory of sensitivity coefficients can be used [15]. These are defined by the equation:

$$\begin{aligned} \beta _{q} = q \frac{\partial [\Delta T (t)]}{\partial q} \end{aligned},$$
(2)

where q can be the thermal conductivity, the thermal diffusivity, or the volumetric specific heat capacity. In this equation, \(\Delta T(t)\) is the mean temperature increase of the Hot Disc probe. The theory of sensitivity coefficients can be applied to define the time window that should be used to determine both the thermal conductivity and thermal diffusivity from one single experiment. From this theory, it has been established that

$$\begin{aligned} 1.1 \cdot r< \Delta p < 2.0 \cdot r \end{aligned},$$
(3)

where r is the mean radius of the outermost spiral of the probe [15]. From this expression, it is also obvious that the available material of the substrate pieces all around the probe should at least be somewhat in excess of the radius and there is no extra information available on the thermal transport if the sample size can accommodate a probing depth beyond two times the radius. The limits defined by Eq. 3 is given in Ref. [2], while a recent ambitious theoretical exercise [16] arrives at a slightly different range.

2 Experimental Arrangements

2.1 The Probe

The following practical design criteria were used when initially developing the probe. Priority 1: It should have a limited extension and not requiring any elongated substrates. Priority 2: The electrical resistance of the DS pattern, which is heating the sample surface and at the same time works as a temperature sensor, should be maximized. This last requirement is paramount for a high sensitivity and the avoidance of high currents in the experimental equipment.

Examples of probes are shown in Fig. 1. Probes can readily be manufactured with diameters from 1 mm to 100 mm using modern lithographic and etching methods. The size and the transport properties of the substrate determine the radius of the probe. A typical bifilar spiral is etched out of a 10-μm-thick metal foil and covered on both sides by a thin (from 10 μm to 100 μm) electrically insulating film. Nickel and Molybdenum are typical heater/temperature-sensing foils due to their relatively high temperature coefficient of electric resistivity and stability over wide temperature ranges [17]. To be able to use the probe as a sensor of the temperature increases in the experiments, it is necessary to establish the heating and sensing metals electrical resistivity as a function of temperature. As electrically insulating films, polyimide, mica, aluminum nitride, or aluminum oxide have been used, depending on the temperature range of exposure. (It was decided at an early stage of development to design probes simulating line sources rather than trying to simulate a plane source because of the possibility to achieve a higher sensitivity of the probe. The sensitivity is directly dependent on the total resistance of the probe pattern. At the same time, it is important not to have to resort to an evaporated pattern with TCR values which have to be established preferably prior to each separate measurement [18].)

The arms of the bifilar spiral have normally a width of around 0.20 mm for probes with an overall diameter of 15 mm or less and a width of about 0.35 mm for larger-diameter probes. The distance between the edges of the arms is typically the same as the width of the arms.

Fig. 1
figure 1

Hot disc probes with bifilar spiral as heating/sensing element

Full size image

As seen in Fig. 1, the geometrical pattern of the probe is that of a DS and there are two reasons for this design: (a) the electrical leads with connections to the spiral can be arranged at the edge of the probing area, which is minimizing their thermal disturbance—the reason being that the temperature increase in the probe arms at the edge of the spiral is appreciably lower than that at the probe center—experimental confirmation of this phenomenon was achieved through the utilization of infrared (IR) imaging on a hot disc probe [19], Fig. 2A.Footnote 1 Additionally, numerical simulations conducted in [20]Footnote 2 demonstrated that the temperature distribution of the probe reaches its highest point at the center, Fig. 2B and (b) when a DC current is passing through an electrical lead, a magnetic field is developing around the lead and this field has a well-defined direction. By arranging with a double spiral, these fields will minimize or totally cancel out since neighboring spiral leads carry their currents in opposite directions. In this way, any possible development of an electrical AC impedance would be counteracted. This is particularly important to minimize the rise time of the current pulse through the probe at the beginning of a transient recording.

Fig. 2
figure 2

(A) IR images and temperature line profiles of a Robax glass/plastic [19]. (B) Temperature map of the sensor along its central line [20]

Full size image

2.2 The Electrical Bridge

To initiate and record the transient increase in the electrical resistance of the probe an electrical bridge has been introduced [1, 21]. With the initially balanced bridge, the possibility opens to follow the resistance increases of the probe by recording the imbalance of the bridge with a sensitive voltmeter (Fig. 3) [22]. The probe is placed in series with a resistor having a resistance, which is strictly constant during the recording. The probe and the series resistor are combined with a precision potentiometer, the resistance of which is typically one hundred times larger than the sum of the resistances of the probe and the series resistor. This bridge circuit is then connected to a power supply which can deliver a constant voltage of around 20 V and a current in the range of 1 A. The voltmeter with which the off-balance voltages are recorded normally have a resolution of 6.5 digits when sampling at an integration time of 1 power line cycle. The series resistor, \(R_{s},\) shall ideally have a resistance, which is as close as possible to the initial resistance of the probe with its leads, \((R_{o}+R_{L}).\) If this condition is fulfilled, the output of power of the probe is very nearly constant throughout the transient recording [2].

The most common arrangement in transient measurements have traditionally been to work with a constant current through the heating/sensing element, which obviously gives a certain increase in the output of power. The case depicted in Fig. 2 shows an arrangement, in which the bridge operates under a constant voltage with the output of power, which is practically constant. The reason why the output of power is kept constant is related to the fact that as the resistance of the probe increases with the temperature rise of the probe, the current is simultaneously reduced because the driving voltage of the bridge is kept constant.

The temperature increases can readily be calculated from the electrical recordings accordingly [1]:

$$\begin{aligned} \Delta T (t) = (R_{s} + R_{L} + R_{o})\Delta U(t)[J_{o}R_{s} - \Delta U(t)]^{-1} (a R_{o})^{-1} \end{aligned}.$$
(4)

Here, \(\Delta U(t)\) is the recorded off-balance voltage, \(R_{L}\) is the total resistance of the leads, \(R_{s}\) is the series resistance, \(R_{o}\) is the initial resistance of the probe, and a is the Temperature Coefficient of Resistivity (TCR) of the probe. \(J_{o}\) is the current through the probe at the start of the transient. Since such a recording of the initial current can disturb the initial part of the transient, the value of this current can readily be obtained by measuring the driving voltage across the bridge at the very end of the transient before the power supply has been turned off. This measured voltage should then be divided by the sum \((R_{s} + R_{L} + R_{o}),\) which then gives the initial current through the probe. It is assumed that these three resistances are determined before initiating the transient recording.

There are two reasons why it is important to have a constant output of power: (a) when theoretically describing the thermal transport in and around the probe, it is the standard procedure to assume that the output of power is constant and (b) the assumption that the temperature difference between the sensing material and the first representative solid surface of the substrate pieces becomes constant within a short period of time, also rests on the requirement that the output of power is constant. (See below)

Fig. 3
figure 3

Circuit diagram of electrical bridge for powering and recording the resistance increase of the probe. Key: 1 Potentiometer; 2 Probe; and 3 Probe leads

Full size image

The general arrangement of a typical measuring situation with probe, probe environment, electrical circuitry, and computer is depicted in Fig. 4.

Fig. 4
figure 4

Basic layout of the apparatus

Full size image

2.3 Temperature Range of Application

The temperature environment of the substrate and probe provided by the chamber (which can be a furnace for temperatures above room temperature or a cryostat for temperatures below room temperature) shall ideally be controlled to within ± 0.1 K or better before and during a measurement over the chosen temperature range. The ultimate temperature range which is possible to cover is according to available literature from 25 K [7] to around 1500 K [8]. For most of the measurements with the Hot Disc method, the sensing metal has been Nickel, while at the highest temperatures, Molybdenum was preferred. It should be noted that the chamber need only be evacuated when working with slab specimens. The necessary vacuum can be achieved with a rotary pump reaching a pressure down to 1 hPa.

3 Analysis of Experimental Recordings

In the following different ways will be discussed on how to obtain the thermal transport of materials when studied by the Hot Disc method. The discussions will be limited to analytical solutions of the thermal conductivity equation which have been used successfully so far. The use of computer simulations is handy when testing certain new aspects related to thermal conduction and its influence on experimental situations.

Fig. 5
figure 5

Experimental setup depicting a hot disc probe positioned between two identical PMMA samples in a sandwich configuration

Full size image

3.1 Solutions for Different Substrates

3.1.1 Homogeneous and Isotropic Bulk Specimen

For small increases in the temperature of the probe, it is assumed that the resistance varies accordingly:

$$\begin{aligned} R(t)=R_{o} [1+a\cdot \Delta T(t)] \end{aligned},$$
(5)

where \(\Delta T(t)= \{T(t)-T(0)\}\) is the mean temperature increase of the probe; \(R_{0}\) is the initial resistance of the probe double spiral at initial temperature T(0); and a is the temperature coefficient of resistance (TCR) of the probe material (Fig. 5).

The temperature increase consists of two parts. One part, \(\Delta T_{i} (t),\) represents the temperature difference between the sensing spiral and the first solid surface of the substrate and the other part, \(\Delta T_s (t)\) is the temperature increase of the specimen surface. The total temperature increase can then be expressed as

$$\begin{aligned} \Delta T(t) = \Delta T_{i} (t) + \Delta T_s (t) \end{aligned}.$$
(6)

Assuming now that the heating of the first solid surface of the substrate pieces can be approximated by a number of concentric and equally spaced circular line sources, the solution of the thermal conductivity equation is given by [1, 23, 24]

$$\begin{aligned} \Delta T_s (\tau ) = P_o(\pi ^{3/2}r \lambda )^{-1} D(\tau ) \end{aligned},$$
(7)

where \(P_{0}\) is the power output of the probe, r is the radius of the outermost ring source, \(\lambda\) is the thermal conductivity of the specimen material, and \(\tau\) is defined as

$$\begin{aligned} \tau = (t/\theta )^{1/2} \end{aligned},$$
(8)

where \(\theta =r^2/\alpha,\) and \(D(\tau )\) are a dimensionless specific time function—often referred to as shape function—and defined as

$$\begin{aligned} D(\tau ) = [m(m+1)]^{-2} \int _{0}^{\tau }\sigma ^{-2}\left[ \sum _{l=1}^{m} l\sum _{k=1}^{m} k\cdot exp\left( \frac{-(l^2 + k^2)}{4m^2\sigma ^2}\right) I_{o}\left( \frac{lk}{2m^2\sigma^2}\right) \right] d\sigma \end{aligned}.$$
(9)

Here, m is the number of concentric ring sources and \(I_0\) is a modified Bessel function. This integral incorporates a singularity at \(\tau =0,\) which can be accounted for by a series expansion of this integral around the point of singularity (e.g., \(D(\tau )=\tau\) is a good approximation around \(\tau =0\)). This approximation is particularly warranted because the double spiral pattern is etched out from a thin-metal foil and is actually a number of concentric “strip” sources. Furthermore, solutions to the situation with strip sources instead of line sources has been presented in the following two papers, [25, 26]. The two solutions—“line” and “strip”—approach each other very quickly because of the comparatively long experimental times used when working with a number of concentric heat sources and a radius which is normally two orders of magnitude larger than the strip width.

The divergence problem related to the ideal Hot Disc solution has been discussed and treated by different authors [25, 26]. It appears difficult to develop an alternative ideal model without creating certain ambiguities when applying the solution to the center part of the probe pattern or when reverting to developing models using simulated corrections with special consideration of the width of the circular strips. It should be noted that there is an ideal analytical solution for a straight strip, which does not have any divergence problems and should be a good analytical model of how the heat is diffusing in the insulating layers surrounding the metal double spiral at times before the heat flow is entering the substrate material under investigation. A practical arrangement is to concatenate the Hot Strip and the Hot Disc ideal solutions to compensate for the divergence of the original Hot Disc solution, which seems to be important particularly when studying materials with low thermal conductivity and reduced thermal heat capacitance. The temperature increase at the very early stages can be calculated as if occurring in a straight strip with the heat having progressed a distance equal to the combined thickness of the insulating and the adhesive layers or half the distance between two adjacent circular strips whichever is shortest. The time of this progression of the heat wave can be estimated by the probing depth and the effective diffusivity of the insulating sheet of the probe and the adhesive used to keep the Hot Disc probe together. These times for a typical probe in which the circular strips have the same width as the openings between the strips are for a Kapton-insulated probe typically in the range of milliseconds. In all experiments, there appear unavoidable hardware and possible software delays at the very beginning of the transient, which warrants the introduction of a time correction, \(t_c\) [1]. This is accomplished by replacing \(\tau\) by \(\tau _c,\) where

$$\begin{aligned} \tau_c = [(t-t_c) / \theta )]^{1/2} \end{aligned}.$$
(10)

Typical time corrections are a fraction of a second and is normally limited to less than 0.5 % of the total measurement time.

\(\Delta T_{i} (t)\) becomes constant after a short period of time if the insulating layer is thin (typically less than 0.05 mm) and the output of power is constant. The time it takes to approach this constant value is determined by the relaxation time, \(\delta ^{2}/\alpha _i,\) where \(\delta\) is the thickness of the layer between the sensing spiral and the surface of the substrate and \(\alpha _i\) is the thermal diffusivity of this intercalated layer. For a typical insulated probe, this relaxation time is less than 10 ms and the time required to reach a constant temperature difference is then typically less than 100 ms.

The elimination of the thermal contact resistance—by noting that the initial temperature difference across the insulating layers around the double spiral quickly attain a constant value—has opened up the possibility to measure the true bulk properties of the material. From Eq. 7, it is obvious that, if the thermal diffusivity and the time correction are known, a linear relationship between the temperature increase, \(\Delta T_s (\tau ),\) and \(D(\tau ),\) can be established. Since this is not the case, the calculation of thermal conductivity and diffusivity starts with an iteration using the diffusivity, \(\alpha,\) and the time correction, \(t_c,\) as variables. Through such an iteration, a linear relationship is established between \(\Delta T_s (\tau )\) and \(D(\tau ).\) Using a least-squares fitting procedure, the diffusivity and time correction are obtained from the final step of the iteration procedure. The thermal conductivity, \(\lambda,\) is then determined from the slope of this line [1].

When the first iteration is completed, one may get the information that the initial time window should have been selected in a different way. This may be seen by the points which are deviating from the straight line. By removing such data points (at the beginning or the end of the transient), a correct time window is obtained for the analysis. To get a clear display of how the points are deviating from the straight line it is convenient to establish a graph of residuals. The material outside of the specimen boundaries might affect the temperature increase at the end of the transient (or time window used for evaluating the results) and become apparent in the graph of residuals. The recommended expression for the probing depth states that it should be larger than the radius but less than the diameter of the bifilar spiral of the probe. This is the condition for determining both the thermal conductivity and the thermal diffusivity from one single transient recording.

Fig. 6
figure 6

(A) Recorded experimental data showing the temporal evolution of temperature. (B) Temperature increase of the sensor plotted against the corresponding shape function obtained through an iterative procedure. (C) Residual plot depicting the temperature deviation from the iterated line observed in subfigure (B)

Full size image

3.1.2 Slab Specimens

In certain situations and when studying materials with high thermal conductivity and particularly when such materials only are available in small quantities, an investigation on the use of substrates in the form of slabs was initiated [27]. When solving the thermal conductivity equation for such a slab situation, the assumption was made that there is no loss of heat from the upper and lower most faces of the two specimen halves. The temperature increase can then be expressed as

$$\begin{aligned} \Delta T_s (\tau ) = P_o(\pi ^{3/2}r\lambda )^{-1} E(\tau ) \end{aligned},$$
(11)

where

$$\begin{aligned} \begin{aligned} E(\tau ) = [m(m+1)]^{-2} \int _{0}^{\tau }\sigma ^{-2} \left[ \sum _{l=1}^{m} l\sum _{k=1}^{m} k\cdot exp\left\{ \frac{-(l^2 + k^2)}{4m^2\sigma ^2}\right\} I_{o}\left\{ \frac{lk}{2m^2\sigma ^2}\right\} \right] d\sigma \\ \left[ 1 + 2\sum _{i=1}^{\infty }exp\left\{ -\frac{i^2}{\sigma ^2} \left( \frac{h}{r}\right) ^2\right\} \right] d\sigma \end{aligned} \end{aligned}$$
(12)

and h is the thickness of each of the two slabs. For establishing this solution, the “method of images” has been used. Regarding the practical application of this experimental method, it can be noted that the condition of “no loss” from the outer surfaces is fulfilled if the experiment is performed in vacuum or in still air. The choice here depends on the required accuracy. It can here be noted that this way of using the Hot Disc method has made it possible to study materials with very high thermal conductivities.

3.1.3 Anisotropic Specimen

By the use of this method, it is possible to determine both the thermal conductivity and the thermal diffusivity of a homogeneous and isotropic material. It is also possible to measure the properties of anisotropic materials, provided the substrate has a uniaxial structure and the probe is properly oriented. Assuming that the properties along the a- and b-axes are the same, but different from those along the c-axis, and also that the plane of the probe is mapped out by the a- and b-axes, then we have the following expression for the temperature increase [28]:

$$\begin{aligned} \Delta T_s (\tau _a) = P_o[\pi ^{3/2}r(\lambda _a\lambda _c)^{1/2}]^{-1} D(\tau _a) \end{aligned},$$
(13)

where \(\lambda _a\) is the thermal conductivity along the a-axis and\(\lambda _c\) is the thermal conductivity along the c-axis;

$$\begin{aligned} \tau _a = [t/\theta _a)]^{1/2} \quad \text {with} \quad \theta _a = r^2/\alpha _a \end{aligned}.$$
(14)

An iteration—similar to the one indicated above—gives the thermal diffusivity, \(\alpha _a,\) along the a-axis. Now, if the specific heat capacity per unit volume, C, (which is the product of the specific heat and the density) is known, then

$$\begin{aligned} \lambda _a = C \cdot \alpha _a \end{aligned}.$$
(15)

From the slope of the straight line fit, we get \(\lambda _c,\) and \(\lambda _a\) is known from Eq. 15. Finally, the thermal diffusivity along the c-axis can be calculated from \(\lambda _c=C \cdot \alpha _c\). We can in this way obtain the thermal conductivity and the thermal diffusivity in the two principal directions in a uniaxial material from one single transient recording, provided the volumetric specific heat of the specimen is known.

3.1.4 Thin-Film Specimen

There is a possibility to use the initial temperature difference {\(\Delta T_i (t)\)}, cf. Eq. (6), to measure the thermal conductivity of electrically insulating thin sheets [29]. When working with thin-film specimen, they are placed between two high-conducting substrates with a probe in the middle. If then a regular measurement is conducted on the high-conducting substrate and the initial temperature increase is retrieved, it is possible to calculate the thermal conductivity from the equation:

$$\begin{aligned} P_o= 2A\lambda _i\left( \frac{\Delta T_i}{\delta }\right) \end{aligned},$$
(16)

where \(P_0\) is the output power and A is the area of the probe, while \(\delta\) is the distance between the sensing metal probe pattern and the surface of the high-conducting substrate. In order to eliminate the influence from the probe insulation, it is necessary to make two experiments: one with and one without the insulating thin-film specimen. Following two such measurements, we can use the following equation to calculate the thermal conductivity of the thin-film specimen:

$$\begin{aligned} \frac{\delta _{probe} + \delta _{specimen}}{\lambda _{total}} = \frac{\delta _{probe}}{\lambda _{probe}} + \frac{\delta _{specimen}}{\lambda _{specimen}} \end{aligned},$$
(17)

\(\delta _{probe}\) is the thickness of the insulation on one side of the metal pattern, together with the adhesive of this side used for keeping the probe pattern and insulation together. \(\delta _{specimen}\) is the thickness of one of the thin specimens. The background material should as a rule of thumb have thermal conductivity which is about ten times higher than that of the thin-film specimen. It should here be noted that the thermal conductivity of the thin specimens is the apparent thermal conductivity in the direction normal to the film’s plane direction. In order to approach the bulk thermal conductivity of the material, out of which the thin film has been prepared, it would be necessary to make measurements on thin films of different thicknesses.

3.1.5 Low Thermally Conducting Specimens

This method can be used for measurements on materials with widely different thermal conductivities. Using a probe depicted in figures (1) and (2), measurements have been performed with good accuracy over the following approximate ranges: thermal conductivity from 0.050 W m−1 K–1 to 500 W m−1 K–1, thermal diffusivity from 0.100 mm2 s–1 to 100 mm2 s–1, and volumetric specific heat from 0.005 MJ m−3 K–1 to 5.0 MJ m−3 K–1 [2].

When studying materials with very low thermal conductivity, we must discriminate between two situations: (a) materials like fine-grained powders with low thermal conductivity and at the same time with comparatively high volumetric heat capacity—measurements on such materials can be carried out without any special consideration—and (b) materials with both low thermal conductivity and volumetric heat capacity—and consequently rather high thermal diffusivity. In the latter case, special care must be taken that it might be necessary to compensate for the heat capacity of the probe as well as for the heat loss through the electrical leads.

A rather good approximation of the power needed for raising the temperature of the probe can be given as follows:

$$\begin{aligned} \Delta P_{probe}(\tau ) = P_{o} \cdot d \cdot C_{probe} \cdot \alpha \cdot (2\sqrt{\pi }\cdot r \cdot \lambda )^{-1} \cdot \left[ \frac{1}{\tau } \cdot \frac{dD(\tau )}{d\tau }\right] \end{aligned}.$$
(18)

Here, \(\Delta P_{probe} (\tau )\) is the power consumed by the probe itself during transient, d is the total thickness of the probe, \(\alpha\) is the thermal diffusivity of the substrate, and \(C_{probe}\) is the total heat capacity of the probe. The heat capacity of the probe is weighted average based on the thickness of the sensing metal, the two insulating layers, and the adhesive used to keep the probe together. With the assumption that the leads are wide enough to avoid any self-heating and if the etched-out electrical leads are of a pattern as depicted in Fig. 7, the loss of power from the leads can be estimated by

$$\begin{aligned} \Delta P_{leads}(\tau ) = \frac{2\cdot \gamma \cdot P_{o} \cdot d_{m} \cdot \lambda _{m}}{\pi \cdot r} \cdot \left[ \frac{\delta }{r \cdot \lambda _{i}} + \frac{D(\tau )}{\sqrt{\pi } \cdot \lambda _{m}}\right] \cdot \left[ \left( \frac{l}{H-h}\right) \cdot ln\left( \frac{H}{h}\right) + \frac{L}{H}\right] ^{-1} \end{aligned}.$$
(19)

Here, \(d_{m}\) is the thickness of the metal pattern of the probe. The influence from the insulating layers is neglected because of the big difference between the thermal conductivity of the metal and that of the insulating layers. \(\lambda _m\) is the thermal conductivity of the heating and sensing metal of the probe. H, h, L, and l are given in Fig. 7, and \(\gamma\) is a correction factor with a value between 0.1 and 1.0.

Fig. 7
figure 7

A sketch of hot disc probe

Full size image

The formula for evaluating measurements on very low conducting materials is then the basic Eq. 7 modified by formulae (18) and (19) accordingly.

$$\begin{aligned} \Delta T_{s} (\tau ) = P_o \cdot [\pi ^{3/2} \cdot r \cdot \lambda ]^{-1} \cdot D(\tau ) \cdot \left[ 1- \frac{\Delta P_{probe}}{P_{o}} - \frac{\Delta P_{leads}}{P_{o}}\right] \end{aligned}.$$
(20)

Since the correction terms are small in this equation, it is possible to use a “fixed point iteration” procedure as explained in [2]. This procedure is necessary because the correction terms include both the thermal conductivity and the thermal diffusivity of the investigated material. A first step in the iteration would then be to assume that the correction terms are zero. The next step would then be to calculate the correction terms using the approximate values of the conductivity and the diffusivity. The iteration would then be terminated when the difference between the transport properties of two consecutive iterations would be less than say 0.5 %.

It is possible to reduce the influence from the electrical leads on the measurements of the transport properties, which is obvious from Figs. 1 and 7 and the correction term of Eq. 20 should primarily be used to estimate the size of this influence with a view to select the best design of the leads. When using Eq. 19, it should be noted that the power loss from the probe is estimated using the mean temperature increase of the probe, while the actual power loss is driven by the temperature increase of the outer-most circular strip source of the metal double spiral. This fact is inherent in the introduction of the correction factor \(\gamma\).

3.2 Unidirectional Heat Flow

A consequence of using the Hot Disc system with different substrate arrangements around the probe is that the heat flow is occurring in essentially two (slab configuration) or three dimensions (bulk/isotropic and anisotropic configurations). In all these cases, the thermal diffusivity is measured and obtained in the in-plane direction with reference to the plane of the probe [2].

A way to obtain both the thermal conductivity and the thermal diffusivity in the same, through-plane, direction is to arrange an experiment with unidirectional heat flow. There are in principle two ways to arrange for the heat to flow in one direction. For substrates with comparatively high thermal conductivity, it is possible to perform the experiment in vacuum or restrict the flow of heat in all but one direction. The other possibility is to use a comparatively large probe and limit the time of the experiment so that the probing depth of the recording is small compared with the extension of the plane probe. In both these cases, the possible patterns of the probe are not restricted to double spirals as long as the output of power per unit area can be considered constant.

As indicated above, the temperature increase can be seen as consisting of two parts. One part represents the temperature difference across the intercalated insulating layer and the other part represents the temperature increase of the specimen surface. Based on the solution of the thermal conductivity equation of the temperature increase of an infinitely large plane heat source in an infinite medium, the temperature increase of the substrate surfaces facing the probe is given by

$$\begin{aligned} \Delta T_{s}(t)=(P_{o}/A)\cdot [(t-t_{c})/(\pi \cdot \lambda \cdot C)]^{1/2} \end{aligned}.$$
(21)

Here, A is the area of the probe and from the slope of a plot of temperature increase versus the square root of time minus a small time correction we can obtain the product of the thermal conductivity and the volumetric heat capacity. This means that to determine the thermal transport with this method, it is necessary to know the specific heat and the density. This means that this particular way of measuring does not give as much information as the methods discussed above. However, there are situations when this method comes in handy, and they appear when the substrate is anisotropic and the thermal diffusivity in the in-plane direction is so high that the size of the substrate in that direction would be inconveniently large.

4 Experimental Arrangements Versus Ideal Model

A convenient way of analyzing an experimental recording with a probe having a metal double spiral for heating and recording temperature increases of the surfaces of the two substrate pieces is to use a suitable analytical solution to the thermal conductivity equation. How well suited a particular analytical solution is can readily be verified using computer simulations [20]. However, it is at present less convenient to use computer simulations to routinely analyze experimental data. (In the age of AI, it might be relevant to look forward to a time when we might not need to discuss details of ideal solutions to measuring equipment but rather the adjustments between the experimental arrangements and its proper physical and mathematical representation when using inverse mathematical simulations.)

4.1 Design of Double Spiral

For analyzing the data in a Hot Disc experiment, a solution stipulating that the surface of the substrate pieces is heated and probed by a limited number of circular and concentric line or strip sources is predicated. This model is applied to a situation with a double spiral consisting of metal strips electrically insulated from the heated and probed surfaces of a substrate. In addition, the temperature of the outer-most strip of the spiral can be influenced by its connection to electrical leads necessary to supply energy to and record resistance variations of the spiral.

There is a possibility to arrange a rather close relation between the pattern of a double spiral and that of the theoretical assumption of circular and concentric strip sources. Imagine that a pattern of concentric, circular and equally spaced line or strip sources is designed. Then, imagine a straight line though the center of the inner-most circular source. If then the half-plane on one side of the line is displaced a distance equal the distance between two near-by circular sources and the displacement is such that the cut-off circular sources are kept strictly perpendicular to the straight line, we are getting a rather perfect double spiral, which consists of two semi-circular patterns which closely make up a double spiral. The fact that it is possible to get an extended straight line when plotting the temperature increases versus the shape function when studying homogeneous materials is a good indication that the design of the double spiral approximates closely the assumption of concentric and equally spaced line or strip sources.

4.2 Thermal Contact Resistance Between the Probe Metal and the Surface of the Substrate

It is mechanically necessary and convenient to keep the thin-metal double spiral together by its sandwiching between two thin layers of an electrically insulating material. The reason for using insulating layers on both sides of the spiral is primarily related to the general necessity of using two sample pieces in Hot Disc measurements and the need to know precisely how the power is disseminated around the probe. A further requirement is that the insulating layers and the adhesive used for attaching the thin film to metal spiral should very precisely have the same thickness just to guarantee that the power supplied to the probe is equally divided between the two sample pieces.

It should be noted that it is possible with the kind of probes discussed in this paper to arrange single-sided experiments by attaching the probe to one side of a substrate piece and then try to thermally insulate the “free” side, cf. [3, 4]. This arrangement—referred to as a single-sided setup—can be used for rough estimations of the thermal conductivity of materials and specifically for comparative or quality assessments when the absolute values are of less importance.

The presence of an electrically insulating layer between the metal double spiral and the first solid surface of the substrate pieces is recorded at the early instances of the transient. It has been noted as an experimental fact and also verified by computer simulations that the temperature difference between the heating and probing metal and the substrate becomes constant rather quickly under special physical conditions. The relaxation time for the temperature difference to reach a constant value is given by the expression:

$$\begin{aligned} \Delta t = d^2/\kappa _i \end{aligned}.$$
(22)

Here, d is the distance between the metal and the substrate surface and \(\kappa _{i}\) is the weighted average of the thermal diffusivities of the same distance. This relation indicates that it is very important to keep the thickness of the insulating layers as small as possible. To get an estimation of the size of this relaxation time, it can be mentioned that insulating sheets with thicknesses ranging from 10 μm to 100 μm with a thermal diffusivity in the range of 0.10 mm2 s–1 are easily arranged. If we then assume that 5 relaxation times are needed to get a constant temperature difference, it is obvious that a constant value is reached after between 5 ms and 0.5 s.

The assumption that this temperature difference quickly becomes constant and after that stays constant rests on the stability or constancy of the output of power from the probe. Any variation in the power output during the transient recording would directly influence the recorded temperature increases and the recorded transport properties. This can be seen from Eq. 16 in the section on measurements on thin insulating films above. A direct consequence is that electrical arrangements for heating a probe based on the concept of constant current through the probe is not recommended because the output of power is in such cases increasing during the transient.

The shape function appearing in Eqs. 7, 11, 13, and 20 have all been derived from the thermal conductivity equation, which is solely dealing with diffusive conduction of heat in solids. This means that whenever there would be any other form or mode of gain or loss of heat from the probe, this would seriously distort the straight-line plots, which are being used in the process of analyzing the experimental data. Such forms or modes would be (1) loss of heat through the electrical leads, (2) influence from outside boundaries, (3) disturbance from the insulating layers between the heating and sensing spiral and the first surface of the sample pieces, (4) thermal radiation in transparent substrates, etc. Even if it is not possible to theoretically determine the details of these unwanted influences, it is obvious that the influence from the thermal contact resistance between the spiral and the substrate surface has a maximum at the beginning of the transient. Similarly, the influence from the electrical leads, from the outside boundaries, and from radiation would be highest at the end of the transient. These deviations from the straight-line plot of temperature increase versus shape function makes it necessary to delete experimental data points at the beginning and the end of the transient recordings. The most efficient way of assessing which points to delete is to make a simple plot of residuals. Using standard electrical instruments for powering the Wheatstone bridge and for reading the off-balance voltage, it is possible under stable thermal conditions to achieve a mean deviation of the recorded temperatures from the straight line of less than 20 μK over extended periods of time.

4.3 Assessment of Accuracy

The Hot Disc method makes it possible to obtain both the thermal conductivity and thermal diffusivity directly from measured quantities obtainable by or in connection with the transient recording. This means that it is not necessary to calibrate the probe or use it for interpolation between values obtained by other experimental procedures.

The necessary measured quantities are dependent on the substrate configuration and can be summarized as (1) electrical properties, (2) time recordings, (3) length dimensions, and (4) temperature recordings. Out of these the electrical, time, and length quantities are comparatively easy to obtain. Temperature measurements are traditionally somewhat more difficult. At the same time, such recordings are very important because the TCR forms the connection to all temperature increases recorded by the probe. In this sense, the accuracy of the determination of TCR reflects directly on how precisely the thermal conductivity can be determined.

The TCR is a temperature-dependent quantity normally determined by measuring the resistance of the electrical conductor as a function of temperature very often using a low current to avoid heating of the wire, which in principle deviates from the way the conductor is used as a Hot Disc probe. One additional precaution to be observed is the fact that the TCR changes very dramatically when working below or above the Curie point, which represents a big change of the magnetic properties in some metals including that of the Nickel metal at 627 K.

In the international standard ISO 22007-2 [2], the accuracy of the Hot Disc method is indicated around room temperature as follows. At or around the room temperature, the accuracy for thermal conductivity is estimated at 2 % to 5 % and for thermal diffusivity at 5 % to 10 %. For slab measurements and measurements at higher temperatures, it is estimated at 5 % to 7 % for thermal conductivity and at 7 % to 11 % for thermal diffusivity. The uncertainties indicated here relate to probes with polyimide insulations (insulation thickness between 7 μm and 40 μm), different probe radii (between 2 mm and 30 mm), and recordings of durations from 1 s to 1 000 s. These estimations are on a covering factor of 2 assuming a large number of recordings.

However, if measurements are repeated at the same temperature with the same probe and test equipment, the deviations between the measurements are very small [30]. The reason is that we are using the same TCR, the same probe radius, the same power output, and perhaps also the same time window for the measurement when evaluating the data. In such experiments, the repeatability of both the thermal conductivity and the thermal diffusivity is between 1 % and 2 %.

To assess the uncertainty of the hot disc method, Eqs. 7, 9, 11–13, 16, and 20 are taken as starting points. The accuracy of the thermal conductivity depends directly on the accuracy of the determination of the output of power, the radius of the hot disc probe, the thickness of the slab, and the thin-film specimens, and in addition, the slope of the straight line of temperature increase plotted against \(D(\tau )\) or \(E(\tau )\) functions is determined by the iterative fitting process, cf. Fig. 6C.

In spite of the fact that the Hot Disc method has been used when studying a large number of different materials under very variable conditions, there are some reports that the system has not met the expectations [26, 31]. It can here be noted that in many of these situations, the assumption has been made that it is possible to cover practically all situations with one and the same probe. It has turned out that it is important to use the facility available with this system and use probes of different diameters and in that way cover widely different volumes. It is obvious that the size of the probe is important when studying inhomogeneous materials. Similarly, it has proven important to use probes with comparatively large radius when studying materials with very low volumetric heat capacity.

5 Conclusions and a Look to the Future

The use of the Hot Disc method has opened up possibilities to study the thermal transport of solid materials over large temperature ranges. It is presently being used in both academic institutions and in industrial laboratories. One reason for the interest in the values of thermal conductivity of materials is its unique sensitivity on the actual structure and purity of materials. In this context, it should be noted that it is possible with this transient method to obtain the bulk properties of the material since it is possible to eliminate the influence from any thermal contact resistance which traditionally has been a serious problem when using steady-state methods.

It should also be noted that in parallel with the development of transient methods for studying thermal transport of materials, we have seen similar developments when studying Near-Field Thermal Radiation [11] and the specific heat of large samples over large temperature ranges [7].

Important for the future is that it has been determined by the scientific community that we should consider only one thermal transport property and that is the thermal conductivity [32]. Concurrently, we have that the thermal diffusivity is a direction-dependent property because the volumetric heat capacity is a true scalar Eq. (15) and the direction follows that of the thermal conductivity.

It is possible to measure the product of the thermal conductivity and the volumetric heat capacity—the square root of which is being referred to as thermal effusivity—in an experiment using a one-dimensional heat flow. One important aspect of such measurements is that we are obtaining the thermal conductivity and the thermal diffusivity in the same direction.

In all other situations discussed above, the direction of the measured thermal diffusivity is in the in-plane direction with reference to the probe. In addition to all measurements with the Hot Disc method related to isotropic materials, it is believed that much future measurements will be devoted to studies of anisotropic material.

Another area of considerable importance might be studies of systems for which it is only possible to define an apparent or effective thermal conductivity. Such systems might not be of much scientific interest but are of utmost importance in engineering situations. A specific advantage of the Hot Disc method relates to the simple fact that it is easy to investigate such systems using probes of different sizes (radii) and in that way be probing different volumes of the substrate material. Indications are that the radius of the probe should be at least an order of magnitude larger than the linear dimensions of, for instance, the grains in powdery environment in order to experimentally record a stable effective thermal conductivity.

Following the same venue of developments measurements of volumetric heat capacity on large samples—as compared with what is possible using differential scanning calorimetry (DSC)—have been performed over a large temperature range at the Cavendish Laboratory [7]. By changing the typical mm-sized samples in DSC measurements with typical Hot Disc cm-sized probes, the effective sample size is increased by orders of magnitude.

It is also interesting to note that much effort has—by scientists working on thermal transport—been put into studies of micro- and nano sized substrates [33], while in the times of establishment of huge battery producing facilities, the engineering community is looking for information on the thermal transport in systems of a quite different size and nature. The reason is that it is not easy and sometimes even impossible to directly predict the transport properties of a complex systems using data from micro- or nano-transport studies.