Seismic Characterization of Naturally Fractured Reservoirs with Monoclinic Symmetry Induced by Horizontal and Tilted Fractures from Amplitude Variation with Offset and Azimuth

Abstract

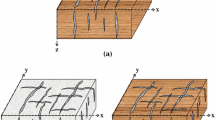
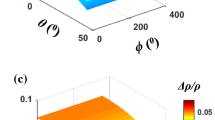
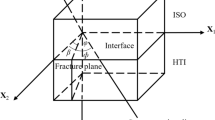
Geological and geophysical data acquired from naturally fractured hydrocarbon reservoirs usually exhibit the presence of multiple sets of fractures. Two different nonorthorhombic sets of fractures embedded in isotropic background rocks can reveal the anisotropic characteristics of monoclinic symmetry with a horizontal symmetry plane. Here, we focus on the modeling and inversion of the effective elastic properties in fractured reservoirs with monoclinic symmetry induced by a set of horizontal fractures and a set of tilted fractures with rotationally invariant properties embedded in purely isotropic host rock. To facilitate the seismic characterization of fractured reservoirs with monoclinic symmetry, we introduce two sets of fracture weakness parameters to replace the Thomsen-type anisotropic parameters and describe these two nonorthogonal sets of rotationally invariant fractures. With the incident and reflected P wave in such a monoclinic anisotropic medium, we perform the seismic characterization of two nonorthogonal sets of rotationally invariant fractures based on the reflected amplitudes variation with offset and azimuth (AVOAz). Using the linear-slip theory, we first derive the effective elastic stiffness tensor as a function of background isotropic elastic moduli, normal and shear weakness parameters of horizontal and tilted fractures, and the dip angle. We then derive the first-order perturbations in elastic stiffness tensor and formulate the linearized PP-wave reflection coefficient based on the seismic scattering theory. Next, we propose a robust AVOAz inversion approach to characterize these two nonorthogonal fractures with rotationally invariant fractures. Finally, synthetic and real data examples are used to demonstrate that the background elastic moduli and fracture properties can be reasonably estimated using the azimuthal seismic reflected amplitudes. The new formulation and inversion approach may provide us a useful tool to characterize the naturally fractured reservoirs with monoclinic symmetry induced by horizontal and tilted fractures in a more reasonable manner than previous method.

Appendices

Appendix 1: Perturbations in Stiffness Matrix of a Monoclinic Anisotropic Medium

The perturbations in the stiffness matrix of such a monoclinic anisotropic medium can be derived as

$$\Delta C_{{{\text{Mono}}{.}}} \approx \left[ {\begin{array}{*{20}c} {\Delta C_{11} } & {\Delta C_{12} } & {\Delta C_{13} } & 0 & {\Delta C_{15} } & 0 \\ {\Delta C_{12} } & {\Delta C_{22} } & {\Delta C_{23} } & 0 & {\Delta C_{25} } & 0 \\ {\Delta C_{13} } & {\Delta C_{23} } & {\Delta C_{33} } & 0 & {\Delta C_{35} } & 0 \\ 0 & 0 & 0 & {\Delta C_{44} } & 0 & {\Delta C_{46} } \\ {\Delta C_{15} } & {\Delta C_{25} } & {\Delta C_{35} } & 0 & {\Delta C_{55} } & 0 \\ 0 & 0 & 0 & {\Delta C_{46} } & 0 & {\Delta C_{66} } \\ \end{array} } \right],$$

(12)

with

$$\begin{aligned} \Delta C_{11} & \approx \Delta M_{{\text{b}}} { - }M_{{\text{b}}} \chi_{{\text{b}}}^{2} \Delta \delta_{{\text{N}}}^{{{\text{Hori}}.}} - \left( {\cos^{2} \theta^{0} \chi_{{\text{b}}} - \sin^{2} \theta^{0} } \right)^{2} M_{{\text{b}}} \Delta \delta_{{\text{N}}}^{{{\text{Tilted}}}} - \sin^{2} 2\theta^{0} \mu_{{\text{b}}} \Delta \delta_{{\text{T}}}^{{{\text{Tilted}}}} , \\ \Delta C_{12} & \approx \Delta \lambda_{b} - \lambda_{b} \chi_{b} \Delta \delta_{N}^{{{\text{Hori}}.}} - \left( {\chi_{b} \cos^{2} \theta^{0} + \sin^{2} \theta^{0} } \right)\lambda_{b} \Delta \delta_{N}^{{{\text{Tilted}}}} , \\ \Delta C_{13} & \approx \Delta \lambda_{{\text{b}}} - \lambda_{{\text{b}}} \Delta \delta_{{\text{N}}}^{{{\text{Hori}}{.}}} - \left[ {\frac{1}{4}\sin^{2} 2\theta^{0} \left( {1 - \chi_{{\text{b}}} } \right)^{2} + \chi_{{\text{b}}} } \right]M_{{\text{b}}} \Delta \delta_{{\text{N}}}^{{{\text{Tilted}}}} + \sin^{2} 2\theta^{0} \mu_{{\text{b}}} \Delta \delta_{{\text{T}}}^{{{\text{Tilted}}}} , \\ \Delta C_{15} & \approx \sin 2\theta^{0} \left( {\chi_{{\text{b}}} \cos^{2} \theta^{0} + \sin^{2} \theta^{0} } \right)\mu_{{\text{b}}} \Delta \delta_{{\text{N}}}^{{{\text{Tilted}}}} + \sin 2\theta^{0} \cos 2\theta^{0} \mu_{{\text{b}}} \Delta \delta_{{\text{T}}}^{{{\text{Tilted}}}} , \\ \Delta C_{22} & \approx \Delta M_{{\text{b}}} - M_{{\text{b}}} \chi_{{\text{b}}}^{2} \Delta \delta_{{\text{N}}}^{{{\text{Hori}}{.}}} - \chi_{{\text{b}}}^{2} M_{{\text{b}}} \Delta \delta_{{\text{N}}}^{{{\text{Tilted}}}} , \\ \Delta C_{23} & \approx \Delta \lambda_{{\text{b}}} - \lambda_{{\text{b}}} \Delta \delta_{{\text{N}}}^{{{\text{Hori}}{.}}} - \left( {\sin^{2} \theta^{0} \chi_{{\text{b}}} + \cos^{2} \theta^{0} } \right)\lambda_{{\text{b}}} \Delta \delta_{{\text{N}}}^{{{\text{Tilted}}}} , \\ \Delta C_{25} & \approx \sin 2\theta^{0} \chi_{{\text{b}}} \mu_{{\text{b}}} \Delta \delta_{{\text{N}}}^{{{\text{Tilted}}}} , \\ \Delta C_{33} & \approx \Delta M_{{\text{b}}} - M_{{\text{b}}} \Delta \delta_{{\text{N}}}^{{{\text{Hori}}{.}}} - \left( {\sin^{2} \theta^{0} \chi_{{\text{b}}} + \cos^{2} \theta^{0} } \right)^{2} M_{{\text{b}}} \Delta \delta_{{\text{N}}}^{{{\text{Tilted}}}} - \sin^{2} 2\theta^{0} \mu_{{\text{b}}} \Delta \delta_{{\text{T}}}^{{{\text{Tilted}}}} , \\ \Delta C_{35} & \approx \left( {\chi_{{\text{b}}} \sin^{2} \theta^{0} + \cos^{2} \theta^{0} } \right)\sin 2\theta^{0} \mu_{{\text{b}}} \Delta \delta_{{\text{N}}}^{{{\text{Tilted}}}} - \sin 2\theta^{0} \cos 2\theta^{0} \mu_{{\text{b}}} \Delta \delta_{{\text{T}}}^{{{\text{Tilted}}}} , \\ \Delta C_{44} & \approx \Delta \mu_{{\text{b}}} - \mu_{{\text{b}}} \Delta \delta_{{\text{T}}}^{{{\text{Hori}}{.}}} - \cos^{2} \theta^{0} \mu_{{\text{b}}} \Delta \delta_{{\text{T}}}^{{{\text{Tilted}}}} , \\ \Delta C_{46} & \approx \frac{1}{2}\sin 2\theta^{0} \mu_{{\text{b}}} \Delta \delta_{{\text{T}}}^{{{\text{Tilted}}}} , \\ \Delta C_{55} & \approx \Delta \mu_{{\text{b}}} - \mu_{{\text{b}}} \Delta \delta_{{\text{T}}}^{{{\text{Hori}}{.}}} - \frac{1}{4}\left( {1 - \chi_{{\text{b}}} } \right)^{2} \sin^{2} 2\theta^{0} M_{{\text{b}}} \Delta \delta_{{\text{N}}}^{{{\text{Tilted}}}} - \cos^{2} 2\theta^{0} \mu_{{\text{b}}} \Delta \delta_{{\text{T}}}^{{{\text{Tilted}}}} , \\ \Delta C_{66} & \approx \Delta \mu_{{\text{b}}} - \sin^{2} \theta^{0} \mu_{{\text{b}}} \Delta \delta_{{\text{T}}}^{{{\text{Tilted}}}} , \\ \end{aligned}$$

where $\Delta M_{{\text{b}}} = M_{{{\text{b}}2}} - M_{{{\text{b1}}}}$ and $\Delta \mu_{{\text{b}}} = \mu_{{{\text{b2}}}} - \mu_{{{\text{b1}}}}$ represent the changes in P- and S-wave moduli across the reflection interface, respectively, and $\Delta \lambda_{{\text{b}}} = \lambda_{{{\text{b2}}}} - \lambda_{{{\text{b1}}}}$ also represent the changes in the first Lamé parameter across the reflection interface; $\Delta \delta_{{\text{N}}}^{{{\text{Hori}}.}} = \delta_{{{\text{N2}}}}^{{{\text{Hori}}{.}}} - \delta_{{{\text{N1}}}}^{{{\text{Hori}}{.}}}$ and $\Delta \delta_{{\text{T}}}^{{{\text{Hori}}{.}}} = \delta_{{{\text{T2}}}}^{{{\text{Hori}}{.}}} - \delta_{{{\text{T1}}}}^{{{\text{Hori}}{.}}}$ represent the changes in normal and shear weaknesses of horizontal fractures across the reflection interface, respectively; $\Delta \delta_{{\text{N}}}^{{{\text{Tilted}}}} = \delta_{{{\text{N2}}}}^{{{\text{Tilted}}}} - \delta_{{{\text{N1}}}}^{{{\text{Tilted}}}}$ and $\Delta \delta_{{\text{T}}}^{{{\text{Tilted}}}} = \delta_{{{\text{T2}}}}^{{{\text{Tilted}}}} - \delta_{{{\text{T1}}}}^{{{\text{Tilted}}}}$ represent the changes in normal and shear weaknesses of tilted fractures across the reflection interface, respectively.

Appendix 2: Derivation of Linearized PP-Wave Reflection Coefficient of a Monoclinic Anisotropic Medium

Considering the opposite relations between η₁₅ and η₅₁, η₂₅ and η₅₂, η₃₅ and η₅₃, η₄₆ and η₆₄, the PP-wave reflection coefficient of a monoclinic anisotropic medium can be derived as

$$\begin{aligned} R_{{{\text{PP}}}} \left( {\theta ,\varphi } \right) & = \frac{1}{{4\rho_{{\text{b}}} \cos^{2} \theta }}\left( \begin{gathered} \Delta \rho \cos 2\theta + \Delta C_{11} \eta_{11} + 2\Delta C_{12} \eta_{12} + 2\Delta C_{13} \eta_{13} \hfill \\ \quad \quad + \Delta C_{22} \eta_{22} + 2\Delta C_{23} \eta_{23} + \Delta C_{33} \eta_{33} \hfill \\ \quad \quad + \Delta C_{44} \eta_{44} + \Delta C_{55} \eta_{55} + \Delta C_{66} \eta_{66} \hfill \\ \end{gathered} \right) \\ & = \frac{\Delta \rho \cos 2\theta }{{4\rho_{{\text{b}}} \cos^{2} \theta }} + \frac{1}{{4M_{{\text{b}}} \cos^{2} \theta }}\left[ \begin{gathered} \Delta C_{11} \sin^{4} \theta \cos^{4} \varphi + 2\Delta C_{12} \sin^{4} \theta \sin^{2} \varphi \cos^{2} \varphi \hfill \\ \quad \quad + 2\Delta C_{13} \sin^{2} \theta \cos^{2} \theta \cos^{2} \varphi + \Delta C_{22} \sin^{4} \theta \sin^{4} \varphi \hfill \\ \quad \quad + 2\Delta C_{23} \sin^{2} \theta \cos^{2} \theta \sin^{2} \varphi + \Delta C_{33} \cos^{4} \theta \hfill \\ \quad \quad - 4\Delta C_{44} \sin^{2} \theta \cos^{2} \theta \sin^{2} \varphi \hfill \\ \quad \quad - 4\Delta C_{55} \sin^{2} \theta \cos^{2} \theta \cos^{2} \varphi \hfill \\ \quad \quad + 4\Delta C_{66} \sin^{4} \theta \sin^{2} \varphi \cos^{2} \varphi \hfill \\ \end{gathered} \right]. \\ \end{aligned}$$

(13)

Substituting Eq. (12) into (13), we can get

$$\begin{aligned} R_{{{\text{PP}}}} \left( {\theta ,\varphi } \right) & = \frac{{\sec^{2} \theta }}{4}\frac{{\Delta M_{{\text{b}}} }}{{M_{{\text{b}}} }} - \sin^{2} \theta \left( {1 - \chi_{{\text{b}}} } \right)\frac{{\Delta \mu_{{\text{b}}} }}{{\mu_{{\text{b}}} }} + \frac{\cos 2\theta }{{4\cos^{2} \theta }}\frac{{\Delta \rho_{{\text{b}}} }}{{\rho_{{\text{b}}} }} \\ & \quad - \frac{{\sec^{2} \theta }}{4}\left( {\cos^{2} \theta + \chi_{{\text{b}}} \sin^{2} \theta } \right)^{2} \Delta \delta_{{\text{N}}}^{{{\text{Hori}}{.}}} + \frac{{\sin^{2} \theta }}{2}\left( {1 - \chi_{{\text{b}}} } \right)\Delta \delta_{{\text{T}}}^{{{\text{Hori}}{.}}} \\ & \quad - \left\{ \begin{gathered} \frac{1}{4}\left[ \begin{gathered} \chi_{{\text{b}}}^{2} \sec^{2} \theta - \left( {1 - \chi_{{\text{b}}} } \right)^{2} \sin^{2} \theta \tan^{2} \theta \cos^{4} \varphi \hfill \\ \quad \quad + 2\left( {1 - \chi_{{\text{b}}} } \right)^{2} \sin^{2} \theta \cos^{2} \varphi + 2\chi_{{\text{b}}} \left( {1 - \chi_{{\text{b}}} } \right) \hfill \\ \end{gathered} \right] \hfill \\ \quad \quad - \frac{{\sin^{2} \theta^{0} }}{2}\left[ \begin{gathered} \chi_{b} \left( {1 - \chi_{{\text{b}}} } \right) + \left( {1 - \chi_{{\text{b}}} } \right)^{2} \sin^{2} \theta \tan^{2} \theta \sin^{2} \varphi \cos^{2} \varphi \hfill \\ \quad \quad + \left( {1 - \chi_{{\text{b}}} } \right)\tan^{2} \theta \cos^{2} \varphi \hfill \\ \end{gathered} \right] \hfill \\ \quad \quad + \frac{{\cos^{4} \theta^{0} }}{4}\left[ {\left( {1 - \chi_{{\text{b}}} } \right)^{2} \left( {\sin \theta \tan \theta \cos^{2} \varphi + \cos \theta } \right)^{2} } \right] \hfill \\ \end{gathered} \right\}\Delta \delta_{{\text{N}}}^{{{\text{Tilted}}}} \\ & \quad + \left\{ \begin{gathered} \frac{1}{2}\left( {1 - \chi_{{\text{b}}} } \right)\left[ {\sin^{2} \theta \sin^{4} \varphi - \tan^{2} \theta \cos^{4} \varphi - \cos^{2} \theta } \right] \hfill \\ \quad \quad + \frac{{\sin^{2} \theta^{0} }}{2}\left( {1 - \chi_{{\text{b}}} } \right)\left[ \begin{gathered} \sin^{2} \theta \tan^{2} \theta \cos^{2} \varphi \cos 2\varphi \hfill \\ + \sin^{2} \theta \cos^{2} \varphi + \sin^{2} \theta \cos 2\varphi + \cos^{2} \theta \hfill \\ \end{gathered} \right] \hfill \\ \quad \quad + \frac{{\cos^{4} \theta^{0} }}{2}\left( {1 - \chi_{{\text{b}}} } \right)\left( {\tan \theta \cos^{2} \varphi + \sec \theta \cos \varphi } \right)^{2} \hfill \\ \end{gathered} \right\}\Delta \delta_{{\text{T}}}^{{{\text{Tilted}}}} . \\ \end{aligned}$$

(14)

Appendix 3: PP-Wave Reflection Coefficient in VTI, TTI and Orthorhombic Media

When there are no tilted fractures in such a monoclinic model, the PP-wave reflection coefficient can generate the reflection coefficient of a VTI medium as

$$\begin{aligned} R_{{{\text{PP}}}}^{{{\text{VTI}}}} \left( \theta \right) & = \frac{{\sec^{2} \theta }}{4}\frac{{\Delta M_{{\text{b}}} }}{{M_{{\text{b}}} }} - \sin^{2} \theta \left( {1 - \chi_{{\text{b}}} } \right)\frac{{\Delta \mu_{{\text{b}}} }}{{\mu_{{\text{b}}} }} + \frac{\cos 2\theta }{{4\cos^{2} \theta }}\frac{{\Delta \rho_{{\text{b}}} }}{{\rho_{{\text{b}}} }} \\ & \quad - \frac{{\sec^{2} \theta }}{4}\left( {\cos^{2} \theta + \chi_{{\text{b}}} \sin^{2} \theta } \right)^{2} \Delta \delta_{{\text{N}}}^{{{\text{Hori}}{.}}} + \frac{{\sin^{2} \theta }}{2}\left( {1 - \chi_{{\text{b}}} } \right)\Delta \delta_{{\text{T}}}^{{{\text{Hori}}{.}}} . \\ \end{aligned}$$

(15)

When there are no horizontal fractures in such a monoclinic model, the PP-wave reflection coefficient can generate the reflection coefficient of a TTI medium as

$$\begin{aligned} R_{{{\text{PP}}}}^{{{\text{TTI}}}} \left( {\theta ,\varphi ;\theta^{0} } \right) & = \frac{{\sec^{2} \theta }}{4}\frac{{\Delta M_{{\text{b}}} }}{{M_{{\text{b}}} }} - \sin^{2} \theta \left( {1 - \chi_{{\text{b}}} } \right)\frac{{\Delta \mu_{{\text{b}}} }}{{\mu_{{\text{b}}} }} + \frac{\cos 2\theta }{{4\cos^{2} \theta }}\frac{{\Delta \rho_{b} }}{{\rho_{b} }} \\ & \quad - \left\{ \begin{gathered} \frac{1}{4}\left[ \begin{gathered} \chi_{{\text{b}}}^{2} \sec^{2} \theta - \left( {1 - \chi_{{\text{b}}} } \right)^{2} \sin^{2} \theta \tan^{2} \theta \cos^{4} \varphi \hfill \\ \quad \quad + 2\left( {1 - \chi_{{\text{b}}} } \right)^{2} \sin^{2} \theta \cos^{2} \varphi - 2\chi_{{\text{b}}} \left( {1 - \chi_{{\text{b}}} } \right) \hfill \\ \end{gathered} \right] \hfill \\ \quad \quad - \frac{{\sin^{2} \theta^{0} }}{2}\left[ \begin{gathered} \chi_{{\text{b}}} \left( {1 - \chi_{{\text{b}}} } \right) + \left( {1 - \chi_{{\text{b}}} } \right)^{2} \sin^{2} \theta \tan^{2} \theta \sin^{2} \varphi \cos^{2} \varphi \hfill \\ + \left( {1 - \chi_{{\text{b}}} } \right)\tan^{2} \theta \cos^{2} \varphi \hfill \\ \end{gathered} \right] \hfill \\ \quad \quad + \frac{{\cos^{4} \theta^{0} }}{4}\left[ {\left( {1 - \chi_{{\text{b}}} } \right)^{2} \left( {\sin \theta \tan \theta \cos^{2} \varphi + \cos \theta } \right)^{2} } \right] \hfill \\ \end{gathered} \right\}\Delta \delta_{{\text{N}}}^{{{\text{Tilted}}}} \\ & \quad + \left\{ \begin{gathered} \frac{1}{2}\left( {1 - \chi_{{\text{b}}} } \right)\left[ {\sin^{2} \theta \sin^{4} \varphi - \tan^{2} \theta \cos^{4} \varphi - \cos^{2} \theta } \right] \hfill \\ \quad \quad + \frac{{\sin^{2} \theta^{0} }}{2}\left( {1 - \chi_{{\text{b}}} } \right)\left[ \begin{gathered} \sin^{2} \theta \tan^{2} \theta \cos^{2} \varphi \cos 2\varphi \hfill \\ \quad \quad + \sin^{2} \theta \cos^{2} \varphi + \sin^{2} \theta \cos 2\varphi + \cos^{2} \theta \hfill \\ \end{gathered} \right] \hfill \\ \quad \quad + \frac{{\cos^{4} \theta^{0} }}{2}\left( {1 - \chi_{{\text{b}}} } \right)\left( {\tan \theta \cos^{2} \varphi + \sec \theta \cos \varphi } \right)^{2} \hfill \\ \end{gathered} \right\}\Delta \delta_{{\text{T}}}^{{{\text{Tilted}}}} . \\ \end{aligned}$$

(16)

Equation (16) is consistent with the derived reflection coefficient by Chen et al. (2020) and Pan et al. (2021).

When the dip angle of tilted fractures is 90° in such a monoclinic model, the PP-wave reflection coefficient can generate the reflection coefficient of an orthorhombic medium as

$$\begin{aligned} R_{{{\text{PP}}}}^{{{\text{Orth}}{.}}} \left( {\theta ,\varphi ;\theta^{0} = 90^{ \circ } } \right) & = \frac{{\sec^{2} \theta }}{4}\frac{{\Delta M_{{\text{b}}} }}{{M_{{\text{b}}} }} - \sin^{2} \theta \left( {1 - \chi_{{\text{b}}} } \right)\frac{{\Delta \mu_{{\text{b}}} }}{{\mu_{{\text{b}}} }} + \frac{\cos 2\theta }{{4\cos^{2} \theta }}\frac{{\Delta \rho_{{\text{b}}} }}{{\rho_{{\text{b}}} }} \\ & \quad - \frac{{\sec^{2} \theta }}{4}\left( {\cos^{2} \theta + \chi_{{\text{b}}} \sin^{2} \theta } \right)^{2} \Delta \delta_{{\text{N}}}^{{{\text{Hori}}{.}}} + \frac{{\sin^{2} \theta }}{2}\left( {1 - \chi_{b} } \right)\Delta \delta_{{\text{T}}}^{{{\text{Hori}}{.}}} \\ & \quad - \left\{ \begin{gathered} \frac{1}{4}\left[ \begin{gathered} \chi_{{\text{b}}}^{2} \sec^{2} \theta - \left( {1 - \chi_{{\text{b}}} } \right)^{2} \sin^{2} \theta \tan^{2} \theta \cos^{4} \varphi \hfill \\ \quad \quad + 2\left( {1 - \chi_{{\text{b}}} } \right)^{2} \sin^{2} \theta \cos^{2} \varphi - 2\chi_{{\text{b}}} \left( {1 - \chi_{{\text{b}}} } \right) \hfill \\ \end{gathered} \right] \hfill \\ \quad \quad - \frac{1}{2}\left[ \begin{gathered} \chi_{{\text{b}}} \left( {1 - \chi_{{\text{b}}} } \right) + \left( {1 - \chi_{{\text{b}}} } \right)^{2} \sin^{2} \theta \tan^{2} \theta \sin^{2} \varphi \cos^{2} \varphi \hfill \\ \quad \quad + \left( {1 - \chi_{{\text{b}}} } \right)\tan^{2} \theta \cos^{2} \varphi \hfill \\ \end{gathered} \right] \hfill \\ \end{gathered} \right\}\Delta \delta_{{\text{N}}}^{{\theta^{0} = 90^{ \circ } }} \\ & \quad + \left\{ \begin{gathered} \frac{1}{2}\left( {1 - \chi_{{\text{b}}} } \right)\left[ {\sin^{2} \theta \sin^{4} \varphi - \tan^{2} \theta \cos^{4} \varphi - \cos^{2} \theta } \right] \hfill \\ \quad \quad + \frac{1}{2}\left( {1 - \chi_{{\text{b}}} } \right)\left[ \begin{gathered} \sin^{2} \theta \tan^{2} \theta \cos^{2} \varphi \cos 2\varphi \hfill \\ \quad \quad + \sin^{2} \theta \cos^{2} \varphi + \sin^{2} \theta \cos 2\varphi + \cos^{2} \theta \hfill \\ \end{gathered} \right] \hfill \\ \end{gathered} \right\}\Delta \delta_{{\text{T}}}^{{\theta^{0} = 90^{ \circ } }} . \\ \end{aligned}$$

(17)

Equation (17) is consistent with the derived reflection coefficient by Zhang et al. (2020).