Evaluation and performance comparison of different models for global solar radiation forecasting: a case study on five cities

Abstract

Recently, solar energy has emerged as the most promising renewable energy source to meet the world’s energy demands. However, to harness the potential of solar energy, accurate data on solar radiation are crucial. It is considered the first step in assessing solar resources for various applications and achieving energy sustainability goals. Due to the unavailability of solar radiation measurements in many parts of the world, several models have been developed to predict global solar radiation (GSR) at these locations. Thus, this study aims to evaluate the proficiency of several GSR models at five new locations and determine the most suitable one for GSR prediction. The study has further developed solar radiation models for these new locations, as well as general ones for the entire region, which does not have any GSR models despite the existence of many planned solar energy facilities in this area. Additionally, the study investigates the effect of changing the length of the validation dataset on models’ performance and accuracy, as well as assesses the introduced models’ generalization capability. To achieve these objectives, the observed data of GSR for approximately 37 years at studied locations are used to develop and validate the proposed models. The study’s findings reveal that Model 1 provides the best performance at all locations, with accuracy, coefficient of determination ($R^{2}$), ranging from 95 to 98%, except for the coastal location, where it is from 91 to 95%. The remaining performance indicators of the best models, such as RMSE, MABE, MAPE, and $r$, are good, and their values range from 0.7863 to 1.9097 (MJ m⁻² day⁻¹), from 0.6430 to 1.7060 (MJ m⁻² day⁻¹), from 3.4319 to 10.0890 (%), and from 0.9914 to 0.9981, respectively. The length of the validation dataset has a slight effect on the models’ performance, ranging from about 1% to 2%. Therefore, Model 1 is the recommended solar radiation model, which can provide precise and rapid estimates of global solar radiation. This approach could be used in the design and performance evaluation of many solar applications. The primary benefit of this approach in the current investigation is that temperature data are continuously and effortlessly recorded for various purposes.

1 Introduction

1.1 Overview and related work

In recent years, renewable energy sources have become increasingly important. The production of clean energy is essential for preventing climate change and mitigating its most severe consequences. The use of these clean energy sources can also promote sustainability goals, as well as support other sustainable concerns such as human resource development (Eesley, 2016; Piwowar-Sulej et al., 2023; Rao et al., 2023; Zhao et al., 2022). As the world grows more reliant on oil (Dagher & El Hariri, 2013), concerns about climate change and the concentration of mitigation actions on the energy sector have led to the implementation of energy conservation programs in many nations (Dagher & Yacoubian, 2012). Environmental pollution is one of the most significant barriers and hazards to sustainable development. Due to the conflicting effects of economic activity, overuse of natural resources, and environmental sustainability, environmental pollution has gained international attention (Alvarado et al., 2022; Chen & Dagestani, 2023a; Chen et al., 2023; Cihan et al., 2021; Dagestani et al., 2022, 2023; Shen et al., 2023; Su et al., 2023; Zhang et al., 2023). The use of sustainable energy sources, such as solar energy, can contribute to sustainable development and the reduction of the carbon footprint (Chen & Dagestani, 2023b; Kumar et al., 2023). Furthermore, the utilization of renewable energy sources may help improve the economy, which has suffered significantly in recent years due to various factors, including the spread of certain diseases (Dagestani, 2022; Guru et al., 2023; You et al., 2022), among other ways (Agarwal et al., 2023; Cheng et al., 2023; Dagar & Malik, 2023; Dagestani & Qing, 2022; Dagher, 2012; Tao et al., 2023; Zhou et al., 2023).

Currently, solar energy is regarded as one of the most potential renewable energy sources for meeting a significant portion of the world’s energy needs (Ali et al., 2022; Chanchangi et al., 2022; Dagher & Ruble, 2010, 2011; Eroğlu, 2022; Feng et al., 2019; Tlili, 2015). Thus, accurate solar radiation information is considered the initial step in determining the availability of solar energy (Doorga et al., 2019; Guermoui et al., 2020; Hassan et al., 2016a, 2016b; Karaman et al., 2021; Makade et al., 2021; Mawire et al., 2021; Saleh et al., 2021; Yıldırım et al., 2018; Zaaoumi et al., 2021). Also, it is the fundamental input for many solar energy applications (Chand et al., 2021; Chaudhary & Yadav, 2021; He et al., 2020; Quej et al., 2016). Because solar radiation data are not available in many regions, many solar radiation models have been presented to forecast the global solar radiation (Nwokolo & Ogbulezie, 2018; Tao et al., 2021; Yorukoglu & Celik, 2006; Youssef et al., 2016). Much research has been conducted to investigate the usefulness of various solar radiation models in measuring solar radiation availability at various places worldwide. The most regularly validated and widely used solar radiation models are those based on meteorological factors (Besharat et al., 2013; Bounoua et al., 2021; Samuel Chukwujindu, 2017). These models rely on empirical correlations and meteorological data, such as sunlight duration, temperature, cloud cover, and relative humidity, which are the most often employed meteorological variables to predict Global Solar Radiation (GSR). The fundamental sunshine-based model was provided by Aͦngström (1924). Prescott (1940) adapted Aͦngström (1924) model that has become the most extensively used one to estimate solar radiation at various sites throughout the world (Almorox et al., 2005; Besharat et al., 2013). Al-Mostafa et al. (2014) studied the efficacy of fifty-two solar radiation models based on sunshine data to predict the monthly mean GSR on a horizontal plane in Jouf region, KSA. The finding demonstrated that certain models are completely unsuited for usage in this region (Jouf), while others perform differently. Similarly, the best solar model for evaluating the monthly GSR on a horizontal ground at six sites in Algeria was presented by Mecibah et al. (2014). Despotovic et al. (2015) reviewed and analyzed different GSR models depending on sunshine data. They sought to analyze several models on a worldwide scale, which may be useful in selecting the most appropriate sunshine-based model. Barbaro et al. (1978) model was modified by Robaa (2009) to calculate GSR in Egypt. Hassan et al. (2018) investigated the effectiveness of several sunshine-based GSR models in the case study of New Borg El-Arab city, Egypt. The collected findings demonstrated that the general form of Robaa model (Robaa, 2009) performs well in calculating GSR. Ajayi et al. (2014) introduced a solar radiation model to predict daily values of GSR in Nigeria, which provided high agreement between estimated values and observed data. El-Metwally (2005) conducted a research on sunshine and GSR forecasting in several Egyptian sites, and he sought to create a simple nonlinear method to evaluate relative sunshine period and GSR.

Similarly, Hargreaves and Samani (1982) devised a simple model for predicting solar radiation that relied just on the lowest and maximum temperatures. Annandale et al. (2002) adapted Hargreaves and Samani (1982) model to calculate the effects of decreasing altitude and air thickness on GSR. As well, Allen (1997) provided a self-calibrated model based on Hargreaves and Samani model (1982) to predict monthly mean GSR. El-Metwally also suggested three simple new models for calculating GSR horizontally in Egypt depending on the lowest and maximum temperature and cloud cover (El-Metwally, 2004). Quej et al. (2016) investigated the accuracy and application of thirteen empirical-based models for calculating GSR in the Yucatan Peninsula, Mexico. The findings illustrate that the new model that was developed based on temperature and other meteorological variables provides the best forecast of GSR at all sites. Mghouchi et al. (2016) studied the proficiency of three models under all sky conditions in Tetuan, Morocco, to assess various parts of solar radiation flux on a horizontal plane. Youssef et al. (2016) evaluated the efficacy of more than thirty models, which do not depend on sunshine data, for calculating the GSR on horizontal ground. Their findings indicated that the models which are depend on solar declination angle and extra-terrestrial radiation, Türk Togrul and Onat (1999) and Ertekin & Yaldiz (1999) models, gave the most accurate prediction. Almorox et al. (2011) investigated the challenge of calibrating seven current solar radiation models and establishing a new model to predict GSR using temperature obtained from seven stations in Madrid, Spain. The collected findings demonstrated that empirical models that rely on temperature provide good predictions at any location if their coefficients are properly adapted. Furthermore, for all sites, the newly proposed model delivers the highest accurate forecast. Besharat et al. (2013) assessed the proficiency and application of existing empirical models for evaluating the monthly average daily GSR on a horizontal plane in Yazd, Iran. The findings illustrate that all developed correlations yield good predictions, with El-Metwally model (2005) providing the highest accurate prediction.

Generally, regression-based approaches to solar radiation estimation often have the benefit of having readily available equipment for measuring the climatic variables that are utilized as model input variables. As a result, most sites’ data are often available. These regression models have demonstrated the ability to construct a strong and positive relationship between observed meteorological variables and solar radiation over a wide range of locations. They are also quite straightforward to perform and fairly precise. The equipment needed to measure sunshine and cloud data is frequently more expensive and not usually available at meteorological stations, in contrast to the equipment needed to monitor temperature. This presumption suggests that knowledge about clouds or sunshine is typically unattainable (Babatunde et al., 2023).

1.2 Contribution statement

In general, sunshine-based models outperform other meteorological parameter-based models (Al-Mostafa et al., 2014). Sunshine data, on the other hand, is not as publicly available as other weather variables such as air temperature that are gathered at conventional weather stations (Li et al., 2014). As a result, sunshine-based solar models are challenging to apply in locations where sunshine information is absent (El-Metwally, 2005; Kumar et al., 2015). Owing to the absence of sunshine data at the majority of stations throughout the world, Hassan et al. (2016a, 2016b) proposed many new temperature-based models to forecast GSR as a substitute to the frequently employed sunshine-based models. To estimate the monthly average daily GSR horizontally, these new models are built, evaluated, and compared with three additional temperature-based models obtained from the literature. The findings display that the local model of the best model from these newly suggested temperature-based models (Hassan et al., 2016a, 2016b Model 6) provides accurate GSR forecasts at different sites. As well, they concluded that an accurate and quick prediction of global solar radiation can be provided using this newly suggested model.

In this sense, the goal of this work is to study the proficiency of several empirical models at five new locations to evaluate the strengths and weaknesses of these models and determine which one is the most suitable for GSR prediction. Furthermore, solar radiation models are developed for these new locations as well as general ones for the whole region, the Suez Canal Zone, which does not have any GSR models even though there are several proposed solar energy projects in this area. The Egyptian Ministry of Electricity, NREA, suggests a number of sites with solar energy potential for photovoltaic installations around Egypt. One such site is “ZAAFRANA Solar Park,” which is situated in the investigated region (the Suez Canal’s Zone). An essential first step in evaluating the feasibility and effectiveness of such solar energy application operations is evaluating estimates of solar radiation. Thus, Global Solar Radiation, GSR, observed data over 37 years at the studied locations are utilized, as a case study, to construct and evaluate the developed models in this article. The following points can be regarded as some of the novelties and contributions of this study:

• Development of exact GSR models for the researched areas as well as the entire region, which currently lacks GSR models despite the existence of many planned solar energy facilities.

• Investigate performance for three models at five new locations, especially at coastal ones, for accurate GSR forecasting on a horizontal surface.

• Study the effect of changing the length of the validation data set on models’ performance and accuracy.

• Assessing performance for one of the best Temp-Based Models, Model 1 (Hassan et al., 2016a, 2016b), which has been presented recently, to estimate GSR at these new sites and after a period of years.

• Evaluation and performance comparison for these selected GSR models in evaluating Monthly Average Daily GSR on a horizontal plane (MADGSR).

• Present local formulas for estimating MADGSR at these cities, as well as general ones for the whole region (Suez Canal’s Zone) due to its importance and the existence of different solar energy projects such as Zaafrana Solar Park.

• Perform a comparative study of the GSR models that have been identified as the most effective based on the results obtained from two recently proposed research studies, to evaluate the strengths and weaknesses of these models and determine which one is the most suitable for GSR prediction.

This comprehensive research provides important information for designers, engineers, and others interested in solar energy usage at the study sites. As mentioned above, these studied region has been planned to have several proposed solar energy projects such as “ZAAFRANA Solar Park.” In addition, providing this essential information for different solar energy projects in this region will help in promoting sustainable development and economy, as well as the reduction of the carbon footprint.

1.3 Paper organization

To provide more explanation, Fig. 1 depicts the overall flowchart of the work and all of its phases, including data processing, model construction, performance evaluation, performance comparison, and, at the end, the major findings of the work. The remainder of the paper is arranged as follows: the global solar radiation models are described in Sect. 2.1. Then, Sect. 2.2 presents more information about the used indicators for evaluating models’ performance and accuracy. Data collection and extra-terrestrial solar radiation calculation method are explained in Sect. 2.3. Section 3 introduces both experimental results and discussions for the studied models, including performance comparison for these developed models using different validation data sets. Finally, the conclusion and future work are presented in Sect. 4.

Fig. 1

General flowchart of the present study with a clarification for its various stages

2 Materials and methods

2.1 Solar radiation modeling

In general, the developed solar radiation models rely on linear and nonlinear relations. They present a correlation between incident solar radiation and other climatic parameters like cloud cover, relative humidity, temperature (minimum, ambient, or maximum), and sunshine period (Khalil & Shaffie, 2013a). Generally, the GSR models which depend on temperature can be considered one of the best models because temperature data are readily available compared with the other meteorological parameters, and it is already recorded very easily and continuously for other purposes (Li et al., 2014).

Hassan et al. (2016a, 2016b) proposed novel temperature-based models as another option to the frequently utilized ones, sunshine-based methods. The results showed that the local formula for the most accurate model, from these novel temperature-based models, provided excellent prediction for GSR at various sites. Also, this best model outperforms the two best models which depend on the sunshine parameter in the literature. In another paper (Youssef et al., 2016), they studied how thirty-one non-sunshine-based solar models perform in GSR prediction on a horizontal plane. These models are classified into six categories (only based on temperature, only based on cloud cover, only based on relative humidity, only based on alien solar energy and solar declination angle, only based on temperature, and only based on relative humidity and air temperature). The most accurate models which showed excellent performance within temperature-based group and temperature-relative humidity-based group will be selected and compared with the former one, the novel temperature-based model which has been presented recently for estimating global solar radiation (Hassan et al., 2016a, 2016b). These models are defined as follows:

Model 1 (Hassan et al., 2016a, 2016b):

$${\raise0.7ex\hbox{$G$} \!\mathord{\left/ {\vphantom {G {G_{0} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${G_{0} }$}}\; = \;a T^{b} G_{0} \; + \;c$$

(1)

Model 2 (Youssef et al., 2016):

$$G\; = \;a\; + \;b G_{0} \; + \;c T$$

(2)

Model 3 (Youssef et al., 2016):

$$G\; = \;\left( {a T_{{{\text{Max}}}} \; + \;b T_{{{\text{Min}}}} \; + \;c RH} \right)\; \times \;G_{0} \; + \;d$$

(3)

where a, b, c, and d represent the coefficients, and $T$, $T_{{{\text{Max}}}}$, $T_{{{\text{Min}}}}$, $RH$, $G$, and $G_{0}$ are the monthly mean values of daily air temperature (°C), maximum and minimum temperature (°C), relative humidity (%), GSR on a horizontal ground (MJ/m² day⁻¹), and extra-terrestrial solar radiation on a horizontal plane (MJ/m² day⁻¹), respectively.

For the sake of simplicity, temperature data are used in this study since, to a great extent, it is easier to get in most climate stations than other weather characteristics. Concerning its dependence on solar radiation, it is evident that the behavior of the surface of the earth in response to solar radiation obtained from the sun can shed light on the tight link between solar radiation and the surrounding temperature (Dincer et al., 1996). Shortwave electromagnetic radiation from the sun is absorbed by the earth’s surface, warming the atmosphere as a result. Some of the absorbed energy is released as longwave radiation by the heated earth, warming the nearby ambient air. Rather than being heated directly by sunlight, the ambient air is heated indirectly through contact with the planet’s surface. There is a phase delay in this process between the cycles of temperature and solar radiation (Atkins, n.d.). In general, radiation balance and air mass advection can have an impact on variations in air temperature. The local air temperature and radiation balance are affected by the kind of surface cover, the percentage of clouds, the time of day, and the season. The annual temperature cycle, which demonstrates a strong correlation between solar radiation and surrounding temperature, would be a good way to track the regular variations in solar radiation that occur during the course of a year (Dincer et al., 1996). Thus, the primary focus of this study is to develop unique correlations between temperature and solar radiation, which is considered a major claim in the present study.

In fact, the main concept for developing the new economic zones is to create new societies providing new jobs to attract young people to this newly developing area. Moreover, developing these new generations of cities based on renewable energy resources such as solar energy creates more extra jobs in the field of renewable energy, which enhances the job market related to renewable and green energy. Furthermore, evaluating the solar energy resources in this new region using the developed numerical model increases the utilization of solar energy as a renewable source of energy reducing the carbon footprint for any economic activities in the region supporting the concept of environmentally friendly societies. This motivates the cultural shift of society toward the new concept of sustainable green cities for future development trends for new cities and societies. Thus, the current study attempts to develop an accurate model, which can be considered as a simple tool to evaluate solar energy resources based on temperature data available in a certain location. The predictions from this simple tool can be used as input to the feasibility studies related to any future development plans for solar energy projects at these locations. This enables the decision-makers to evaluate the economic feasibility and payback period for any future project related to solar energy.

2.2 Evaluating Models’ Performance

The developed models’ performance in this study is examined and evaluated using the most frequently applied indicators such as the coefficient of determination ($R^{2}$), mean percentage error (MPE), mean absolute percentage error (MAPE), mean bias error (MBE), root-mean-square error (RMSE), correlation coefficient ($r$), and mean absolute bias error (MABE) (Besharat et al., 2013; Cihan et al., 2021; Hassan et al., 2016a, 2016b; Youssef et al., 2016). The accepted values of these errors, MPE, MAPE, RMSE, MBE, and MABE, are between ± 10%, and the values of $R^{2}$ and $r$ are between 0 and 1 (0 ≤ $R^{2}$, $r$ ≤ 1), where their ideal values which close to the unity (Ajayi et al., 2014; Hai et al., 2020; Khorasanizadeh & Mohammadi, 2013a). The equations for these indicators are defined as:

$${\text{MBE}}\; = \;\frac{1}{n} \mathop \sum \limits_{{{\text{i}}\; = \;1}}^{n} \left( {G_{{{\text{i}}.\;c}} \; - \; G_{{{\text{i}}.{\text{m}}}} } \right)$$

(4)

$${\text{MPE}}\; = \;\frac{1}{n} \mathop \sum \limits_{{{\text{i}} = 1}}^{n} \left( {\frac{{G_{{{\text{i}}.{\text{c}}}} - G_{{{\text{i}}.{\text{m}}}} }}{{G_{{{\text{i}}.{\text{m}}}} }}} \right)\; \times \;100$$

(5)

$${\text{RMSE}}\; = \;\left[ {\frac{1}{n} \mathop \sum \limits_{{{\text{i}} = 1}}^{{\text{n}}} \left( {G_{{{\text{i}}.{\text{c}}}} - G_{{{\text{i}}.{\text{m}}}} } \right)^{2} } \right]^{1/2}$$

(6)

$${\text{MABE}}\; = \;\frac{1}{n} \mathop \sum \limits_{{{\text{i}}\; = \,1}}^{n} \left| {\left( {G_{{{\text{i}}.\;{\text{c}}}} \; - \; G_{{{\text{i}}.\;{\text{m}}}} } \right)} \right|$$

(7)

$${\text{MAPE}}\; = \;\frac{1}{n} \mathop \sum \limits_{{{\text{i}}\; = 1}}^{n} \left| {\left( {\frac{{G_{{{\text{i}}.\;{\text{c}}}} \; - \; G_{{{\text{i}}.{\text{m}}}} }}{{G_{{{\text{i}}.\;{\text{m}}}} }}} \right)\; \times \;100} \right|$$

(8)

$$r\; = \;\frac{{\mathop \sum \nolimits_{{{\text{i}} = 1}}^{n} \left( {G_{{{\text{i}}.\;{\text{m}} }} \; - \; \overline{{G_{{\text{m}}} }} } \right)\left( {G_{{{\text{i}}.{\text{c}} }} \; - \; \overline{{G_{{\text{c}}} }} } \right)}}{{\left[ {\mathop \sum \nolimits_{{{\text{i}}\, = \;1}}^{n} \left( {G_{{{\text{i}}.{\text{m}} }} \; - \; \overline{{G_{{\text{m}}} }} } \right)^{2} \mathop \sum \nolimits_{{{\text{i}} = 1}}^{n} \left( {G_{{{\text{i}}.\;{\text{c}} }} - \overline{{G_{{\text{c}}} }} } \right)^{2} } \right]^{1/2} }}$$

(9)

$$R^{2} \; = \;1 - \frac{{\mathop \sum \nolimits_{{{\text{i}} = 1}}^{n} \left( {G_{{{\text{i}}.\;{\text{m}}}} - G_{{{\text{i}}.\;{\text{c}}}} } \right)^{2} }}{{\mathop \sum \nolimits_{{{\text{i}} = 1}}^{n} \left( {G_{{{\text{i}}.\;{\text{m}} }} - \overline{{G_{{\text{m}}} }} } \right)^{2} }}$$

(10)

$$e\; = \;\left( {\frac{{G_{{{\text{i}},\;{\text{c}}}} - G_{{{\text{i}},\;{\text{m}}}} }}{{G_{{{\text{i}},\;{\text{m}}}} }}} \right)\; \times \;100$$

(11)

where $n$ is the observation number,$G_{{{\text{i}}.{\text{c}}}}$ and $G_{{{\text{i}}.{\text{m}}}}$ are the ${\text{i}}$th predicted and calculated values, and $\overline{{G_{{\text{m}}} }}$ and $\overline{{G_{{\text{c}}} }}$ are the average values of the observed and predicted values.

Coefficient of determination values, $R^{2}$, donate knowledge about the goodness of fit between the predicted and the measured values. Coefficient of determination and correlation coefficient values range from 0 to 1, with the greatest number being the intended value. Mean bias error (MBE) statistics provide info about the long-term model’s proficiency. While the MBE’s negative values point to underestimation, the positive values refer to overestimation, and the small values consider the desired ones. RMSE’s value is always positive and gives feedback about the short-term model’s efficacy. Smaller RMSE values imply a high model’s accuracy, whereas zero values represent the optimum value. The agreement between the value of the measured and the calculated $G$ for each month can be expressed by relative percentage error ($e$), and its preferable values lie between −10 and + 10 (%).

2.3 Data collection

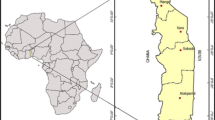
The study utilized weather data collected over a period of 37 years, from January 1, 1984 to December 31, 2020, to develop and test models that predict monthly average daily GSR on a horizontal plane. The data include temperature (minimum, ambient, and maximum), relative humidity, and GSR, and was obtained from NASA’s Surface Meteorology and Solar Energy power data access, a source that has been used in several other studies (M. A. Ali et al., 2016; Fadare, 2009; Hassan et al., 2018; Hassan et al., 2016a, 2016b; Hassan et al., 2016a, 2016b; NASA Surface Meteorology and Solar Energy, n.d.; Youssef et al., 2016). As mentioned above, the study aims to verify the applicability of the established models for predicting the monthly average daily GSR for selected cities and the Suez Canal zone as a whole. Thus, the developed models’ performance is evaluated and compared to observed data of GSR at the five selected sites. Furthermore, the suggested models’ generalizability is investigated for the Suez Canal’s zone and examined at the five studied locations too, namely Port Said, El Kantara, Ismailia, Fayid, and Suez. These selected cities are distributed over the Suez Canal’s zone as demonstrated in Fig. 2, as well as their geographical information is illustrated in Table 1.

Fig. 2

Distribution of the selected locations in the Suez Canal’s zone, Egypt (I-cias, n.d.)

Table 1 Geographical information for the five studied cities

Concerning the NASA weather dataset, in general, it facilitates the study of climate and climatic phenomena by acting as an extensive and ongoing record of climatic data obtained from satellite observations. The NASA database is noteworthy due to its worldwide breadth and chronological consistency. It is a trustworthy source of data since it has been shown to be accurate enough in comparison with traditional observations made on the ground. As such, the NASA record may be used with effectiveness in situations when there are insufficient or no ground records. Despite the widespread belief that observations taken on land are more accurate than those taken from space, the necessary meteorological variables for this investigation were derived using NASA data. There were two key considerations in this choice. First of all, the NASA collection contains all of the pertinent weather parameters for the regions that are being studied. Second, there are issues with the precision of on-site observations, which are frequently brought on by procedural mistakes, deficiencies in the collected datasets, or calibration problems that might result in inaccurate data collection (Abdo & El-Shimy, 2013; Fadare, 2009). On the other side, numerous measures made on the ground have been used to assess the accuracy of NASA data, which comes from satellite observations. NASA calculates that the Mean Bias Error (MBE) ranges from −2% to + 0.7%, despite the fact that the validity of these ground-based observations themselves is not usually carefully evaluated (NASA, n.d.)

Besides, a custom program developed in C# programming language is used to calculate the values of declination angle and extra-terrestrial solar radiation, as well as the monthly average daily values for all the mentioned parameters. Extra-terrestrial solar radiation, $G_{0}$, is the solar radiation that originates outside the earth’s atmosphere, and it is defined as (Ayodele & Ogunjuyigbe, 2015; Jiang, 2009):

$$G_{{\text{o}}} \; = \;\frac{{24 \; \times \;3600 G_{{{\text{sc}}}} }}{\pi } k\left[ {\left( {\frac{\pi \omega }{{180}}} \right)\sin \left( L \right)\sin \left( \delta \right)\; + \;\cos \left( L \right)\cos \left( \delta \right){\text{sin}}\left( \omega \right)} \right]$$

(12)

$G_{{{\text{sc}}}}$ donates the solar constant ($G_{{{\text{sc}}}} =$ 1367 W/m²) (Camacho et al., 2012; Khalil & Shaffie, 2013b), k refers to the earth’s orbit eccentricity correlation factor, $\omega$ points to the hour angle at sunset (degree), $L$ indicates to the latitude angle (degree), and δ is the declination angle (degree). k, δ, and $\omega$ are defined as (Karakoti et al., 2012):

$$k = \left[ {1 + 0.033\cos \left( {\frac{360 N}{{365}}} \right)} \right]$$

(13)

$$\delta = 23.45 \sin \left[ {\frac{360}{{365}}\left( {284 + N} \right)} \right]$$

(14)

$$\omega = \cos^{ - 1} \left[ { - \tan \left( L \right){\text{tan}}\left( \delta \right)} \right]$$

(15)

$N$ refers to the year-day number beginning from January 1.

3 Results and Discussion

The observed data of GSR, temperature (minimum, ambient, and maximum), and relative humidity are separated into three subgroups and averaged to provide the monthly average daily values. The first subset (January 1, 1984–December 31, 2017) is utilized for building models using regression analysis (Ajayi et al., 2014; Besharat et al., 2013; Khorasanizadeh & Mohammadi, 2013b). The coefficients’ values matching the observed data in selected locations are acquired and summarized in Table 2. Similarly, the general empirical coefficients for the whole region of the Suez Canal’s zone for three models are calculated and represented in Table 2.

Table 2 Empirical coefficients for the selected five cities and for the Suez Canal’s Zone, Egypt

On the other hand, the validation process is performed using two different validation data sets. The first one, from January 2018 to December 2020, is the average data of three years. The second validation data set, from January 2018 to December 2018, is the average data for one year, 2018. These two validation data sets will be utilized to assess and validate the established models in this study. Also, they will be used to investigate the effect of changing the length/period of the validation data set on models’ performance and accuracy, using these long and short period of validation data set (average data of three years and average data of one year). The prediction of the three proposed models, Eqs. (1–3), are compared with the measured values of the monthly average daily global solar radiation, and the most common statistical indicators, named RMSE, MBE, MPE, MAPE, MABE, $e$, $r$, and R², are computed using equations Eqs. (4–11).

The following sections introduce the obtained results from the validation process using each validation data set (Validation Data Set 1: three-year data average, Validation Data Set 2: one-year data average) and their discussion. For each validation data set, firstly, the obtained results of the local formulas are discussed followed by the general formulas’ results discussion, and hence a comparison between both formulas (Local and General) is presented. Besides, a performance comparison between these developed models (Model 1, Model 2, and Model 3) at each city is explained. Finally, the revealed results from these two validation data sets (Data Set 1 and Data Set 2) are compared and discussed, too.

3.1 Validation using Data Set 1 (2018–2020)

This validating data set employed the average data of three years, from January 1, 2018 to December 31, 2020. The measured data for all used parameters as well as the extra-terrestrial solar radiation data at each city are averaged to get the monthly mean values. The models’ prediction is compared to the observed data at each city, where all statistical indicators (MBE, RMSE, MPE, MAPE, $e$, MABE, $R^{2}$ and $r$) are computed using Eqs. (4)–(11) for the developed models and summarized in Table 3. Based on the received results, the best model at each city is recognized after comparing the obtained statistical indicators together, and it will have the largest R² value (Ajayi et al., 2014; Hassan et al., 2016a, 2016b; Hassan et al., 2016a, 2016b; Khorasanizadeh & Mohammadi, 2013a; Li et al., 2010). The greatest models are highlighted in bold as illustrated in Table 3.

Table 3 Statistical errors for the local formulas of the proposed models using validation Data Set 1 (2018–2020)

Based on the comparison with the observed data of GSR, the developed models at the selected sites showed good performance, with the coefficient of determination (R²) ranging from 94 to 97% at all locations except for Port Said city, it is larger than 91%. This fall in R² value can be justified by different climatic variables, particularly at coastal sites, like Port Said city, which is located very close to the Mediterranean Sea as displayed in Fig. 1 (El-Metwally, 2004; Khorasanizadeh & Mohammadi, 2013a). While the models’ prediction is considerably declined at Port Said city, their prediction is very good at the four remaining cities. Despite this low performance at Port Said city, the values for all statistical errors (MBE, MPE, RMSE, MABE, and MAPE) are within the accepted limit of ± 10%, and R² values are greater than 91%, which refers to good fitting between predicted and measured values.

Overall, it can be noted that all models have excellent RMSE and MBE values which range from 0.9 to 1.8 (MJ m⁻² day⁻¹) and from 0.7 to 1.7 (MJ m⁻² day⁻¹), successively. Also, Model 1, Eq. (1), provides the best performance among all developed models. Despite Model 1 and Model 2 being based on the same input parameters, ambient temperature and extra-terrestrial solar radiation, Model 1 has the most accurate estimation. Its R² values at the five selected cities, Port Said, El Kantara, Ismailia, Fayid, and Suez, are 0.9196%, 0.9664%, 0.9664%, 0.9664%, 0.9664%, and 0.9727%, respectively. Model 2 ranked second, and its performance is significantly close to Model 1. Furthermore, although Model 3 depends on relative humidity as one of its input parameters, it does not improve its performance compared with the other models, even at coastal sites such as Port Said City. For more clarification, the best model’s estimations are compared with the observed data at the five selected cities as demonstrated in Fig. 3. Similarly, Fig. 4 shows the statistical indicators graph for the local models at the five selected locations using validation Data Set 1 (data of three years average, 2018–2020).

Fig. 3

Overall performance for the best models of local formulas using validation Data Set 1 (2018–2020)

Fig. 4

Statistical errors graph for all models of the local formulas using validation Data Set 1 (2018–2020)

General formulas, on the other side, all measured data of used parameters ($T$, $T_{{{\text{Max}}}}$, $T_{{{\text{Min}}}}$, $RH$, $G$, and $G_{0}$) at the five selected cities of the Suez Canal’s zone (as displayed in Fig. 1) are averaged and utilized to assess the generalizability capacity of the developed models throughout the whole Suez Canal zone in Egypt. The general coefficients are calculated from the averaged data using regression analysis (Ajayi et al., 2014; Besharat et al., 2013; Khorasanizadeh & Mohammadi, 2013b) and given in Table 2. The estimation of the developed models’ general formulae is compared to the observed data of the five cities. Table 4 summarizes the obtained statistical errors for the general formulas’ prediction at each city.

Table 4 Statistical errors for the general formulas of the proposed models using validation Data Set 1 (2018–2020)

According to the results, what stands out from Table 4 is that, whereas the performance for both Model 1 and Model 2 at Port Said city is improved considerably by about 4% (R² values increased from about 91% to more than 95%), the performance of Model 3 is dramatically deteriorated (R² values dropped from about 91% to about 78%) and its MPE values also exceeded the acceptable range ± 10%, equals 12.4784 (MJ m⁻² day⁻¹). This decline may be returned to this model, Model 3, which depends on relative humidity as one of its input parameters, and when the five cities’ data were averaged, it led to a significant change in RH values especially at this coastal site.

Additionally, Model 1 still ranked first in three cities, Port Said, Fayid, and Suez, and second in the remaining two cities, El Kantara and Ismailia, with performance very close to the first one, Model 3, with about 0.003% difference in R² values, 0.9801% and 0.9835%, respectively. Also, the models’ performance at Suez City is slightly decreased by about 2% compared with the performance of the local formulas, and their R² values larger than 94%. This marginal decline in models’ performance at Suez City usually occurs in general models which are adjusted to cover larger areas or zones in contrast to local models that are calibrated on the local data (Hassan et al., 2016a, 2016b; Hassan et al., 2016a, 2016b; Li et al., 2014).

In general, it is also clear from Table 4 that the models’ performance improved significantly at all locations except for Suez City, performance of the three models slightly decreased, as well as for Model 3 at Port Said City where performance dramatically collapsed. Additionally, Model 1 provides the best performance in comparison with the other models almost at all sites, especially at coastal ones. Moreover, its performance is approximately stable and reliable and does not experience a significant unfavorable change. In contrast, its prediction accuracy is improved in all cities except for Suez, where it has marginally declined. The R² values for Model 1 are between 0.95% and 0.98%, which refers to a good fitting between the model’s estimation and measured values. Figure 5 displays the statistical error graph for the general models at the five selected sites using the validation Data Set 1 (2018–2020). In addition, the forecast of the best general models compared against the observed data at the five selected cities is illustrated in Fig. 6.

Fig. 5

Statistical errors graph for all models of the general formulas using validation Data Set 1 (2018–2020)

Fig. 6

Prediction of the best local models and the best general models using validation Data Set 1 (2018–2020)

Regarding comparison, the performance for both the local and the general formulas is compared based on the result of the validation process using Data Set 1 (2018–2020). The best models from both formulas are selected and compared together as presented in Table 5. The most accurate model at each location is identified and indicated in bold as seen in the table. It is worth noting that while the general formula of Model 3 provided the best performance at two cities, El Kantara and Ismailia, with R² values > 98%, the formulas of Model 1, either the local one or the general one, showed the best performance at the remaining three cities, Port Said, Fayid, and Suez, and its R² values are greater than 95%, 97%, and 97%, respectively. Also, its local formulae at the remaining two sites, El Kantara and Ismailia, have excellent prediction with R² > 96%, and its general formula at Port Said city improved the performance (R² > 95%) with about 4% compared to its local formula.

Table 5 Performance comparison for the best models (local and general) using validation Data Set 1 (2018–2020)

For more clarification, the results of the performance comparison for the best local model and the best general model at the five locations are displayed in Fig. 6, and graphs of their statistical indicators are represented in Fig. 7. Furthermore, the relative percentage error ($e$) is calculated for these best models (local and general) through the twelve months and summarized in Table 6. Generally, what is clear from the table is that while local and general models performed lower at the coastal city, like Port Said, their values of relative error slightly exceeded the preferred range ± 10% for some months, they showed perfect performance at the remaining four cities almost for all months except for some Winter’s months, for example, the local formulas of Model 1 in November. The reason for this can be explained by different weather conditions particularly in Winter months such as clouds and rains (El-Metwally, 2004; Hassan et al., 2016a, 2016b; Hassan et al., 2016a, 2016b; Khorasanizadeh & Mohammadi, 2013a). Also, it is noted that the relative error values were reduced at Port Said (coastal city) in contrast with its values at Suez city. This may be interpolated by the averaging process for the measured data of the five selected cities leading to improved values of different parameters ($T$, $T_{{{\text{Max}}}}$, $T_{{{\text{Min}}}}$, $RH$, $G$, and $G_{0}$) at Port Said city, and vice versa at Suez city. On the contrary, the relative error values for the general formulas of Model 3 at El Kantara and Ismailia are in the range. For more clarification, the relative errors graph for the best local and general models is shown in Fig. 8.

Fig. 7

Errors comparison for the best local and general models using validation Data Set 1 (2018–2020)

Table 6 Relative errors for the best local and general models using validation Data Set 1 (2018–2020)

Fig. 8

Relative errors for the best models (local and general) using validation Data Set 1 (2018–2020)

3.2 Validation using Data Set 2 (2018)

Looking at the second data set, Validation Data Set 2 (2018), the same manner that has been carried out with Validation Data Set 1 is conducted with Data Set 2. Firstly, the measured data of all parameters for only one year, from January 1, 2018 to December 31, 2018, at each city are averaged to get the monthly average values. Then, models’ predictions are compared against observed data, and all indicators are computed for both local and general formulas at each site as seen in Table 7. Also, the most accurate models are identified and pointed in bold as displayed in the table.

Table 7 Statistical errors for both formulas (local and general) of the proposed models using validation Data Set 2 (2018)

Focusing on the local formulas, the revealed results show that at the coastal city (Port Said), the three developed models showed low performance, and their MPE values slightly exceeded the range ± 10%, 10.5113, 10.3519, and 10.0890, respectively. Also, relative humidity, RH, which is an additional input parameter in Model 3 improves the model’s performance by about 1% compared with the other models. This drop in models’ performance returns to bad weather conditions at the coastal sites as mentioned before (El-Metwally, 2004; Khorasanizadeh & Mohammadi, 2013a). On the contrary, in the remaining four cities, while Model 3 provided moderate performance with R² values between 92 and 94%, Model 1 and Model 2 showed perfect performance with R² > 96% and their performance is almost identical. Generally, despite lower prediction at Port Said City, the models’ prediction at the remaining cities was good especially Model 1 and Model 2, and their statistical indicators are in the acceptable ranges.

Regarding general formulas, it is very pertinent to note that at Port Said city, the performance of Model 3 is significantly deteriorated with R² equals 0.77% and MPE is larger than 12%, out of the range (± 10%). This decrease can be explained by Model 3 mainly based on RH as one of its input parameters, which changed a lot when it was averaged for the five selected locations compared with its local values, as well as taking into consideration the difference within weather conditions at the coastal city (Port Said) and the other four cities. Model 1 gave the best prediction followed by Model 2 with R² > 94%. Alternatively, at the remaining locations, the three models displayed excellent estimation at El Kantara, Ismailia, and Fayid, where their performance is approximately alike, with R² values > 97%. Moreover, Model 1 was the best one in Fayid and Suez cities. Overall, it can be observed that whereas some of the general formulas at some locations weakened or slightly decreased the performance, others, almost the majority of them, improved it. For example, the general formulas of Model 1 and Model 2 at Port Said city amended the performance significantly. Additionally, all models performed well except the general formula of Model 3 at Port Said city, and Model 1 has the most accurate prediction at three cities (Port Said, Faid, and Suez) and at the remaining two cities, its performance is approximately the same as the best model, Model 3. Of more interest, the statistical indicators for both local and general models at the five sites are graphed and demonstrated in Figs. 12 and 13 (in the Appendix).

Local and general formulas one-year comparison (2018), on the other hand, shows that firstly, Model 1 has the most stable and reliable performance among all models with good R² values. Also, if it is not ranked the first one, its performance will approximately coincide with the performance of the best. Performance of the general formulas generally improves models’ performance with some exceptions, for instance, the general one of Model 3 at Port Said as well as the slight decrease in models’ performance at Suez compared with its local one. Also, the general formulae of Model 3 is not recommended for use at the coastal sites. The overall performance comparison for both the best models, both local and general, at all cities and their statistical indicators are shown in Fig. 9, Fig. 10, respectively. Furthermore, the relative error values, ($e$), are calculated for these best models (local and general) through the year months and summarized in Table 8. It is worth mentioning that while relative error values for some months at the coastal city (Port Said) for both local and general formulas overstep the preferred range, the majority of its values at the other cities are in the range except for some winter’s months own to unwell weather conditions as mentioned previously, where its values rarely and slightly exceed the scope. Also, the relative error values of general formulas are slightly better than local ones. For more illumination, the relative errors for the best local and general models are shown in Fig. 14 (in the Appendix).

Fig. 9

Prediction of the best local models and the best general models using validation Data Set 2 (2018)

Fig. 10

Errors comparison for the best local and general models using validation Data Set 2 (2018)

Table 8 Relative errors for the best local and general models using validation Data Set 2 (2018)

3.3 Validation data sets comparison

Of more interest, the two validation data sets are compared together, Validation Data Set 1 (Three years data average: 2018–2020) and Validation Data Set 2 (One-year data: 2018). The obtained results from this comparison can provide several valuable information; for example, knowing the effect of changing the length of the validation data set on models’ performance and accuracy, as well as determining the most accurate, stable, and reliable model at various sites that have different weather conditions. Therefore, the received results of statistical indicators from the two validation data sets, as previously shown in Table 3, 4, and 7, are compared together, as well as the revealed results of relative error in Table 6 and 8.

Looking at the local formulas of Validation Data Set 1 and 2, it can be marked that at the coastal city (Port Said city), while the performance of Model 1 and 2 marginally declined by about 1% (from 91 to 90% for Validation Data Set 1 and Validation Data Set 1, respectively), the performance of Model 3 is almost stable. Additionally, the MPE values for Validation Data Set 2 (2018) are just over 10%. For Kantara, Ismailia, and Fayid, although the performance of Model 3 decreased by about 2%, the performance of Model 1 and 2 is approximately the same, with R² > 96%. As for Suez City, all models’ performance falls somewhat with about 1%, which is normal at the coastal places.

On the other side, the general formulas of the two validation data sets, for Port Said city, Model 1 and 2 showed the best performance, which marginally slipped by about 1% from 95 to 94%. Conversely, the general formulas of Model 3, for both validation data sets, are dramatically collapsed with R² values around 77%. At Kantara and Ismailia, whereas the performance of Model 2 was almost unchanged with R² equals 97%, the performance of Model 1 and 3 had very little change with about 1%, from 98 to 97%. At Fayid City, the performance of Models 1 and 2 did not change (R² is 97%) while the performance of Model 3 increased from 96 to 97%. For Suez City, Model 1 and Model 2 almost have the same performance, where R² is 95% and 94% for the two validation data sets. Also, the performance of Model 3 slightly falls from 94 to 93%, about 1%.

Generally, according to the obtained results of the two validation data sets comparison (Data Set 1: 2018–2020, and Data Set 2: 2018) for both the local and general models, it is worthwhile to note that firstly, the length of the validation data set does not have a big effect on models’ performance. Actually, the change in models’ accuracy is very slight, from about 1% to 2%. Furthermore, Model 1 can be considered the most stable, accurate, and reliable model at different sites, where its performance is located between 95 and 98% except for Port Said City, which is from 91 to 95%. Similarly, the relative error value is compared for the two validation data sets, and it is noticed that while it is increased for some months, especially winter ones, at some locations like Port Said city, it is also decreased at other places such as Suez city.

Of more interest, the best locals’ and generals’ formulas for the Validation Data Set 1 (2018–2020) and the Validation Data Set 2 (2018) are compared together. Table 9 shows the statistical indicators comparison, while Table 10 introduces the relative errors comparison. The results show that all statistical errors are within the range of ± 10%, and the performance of the best models is very close to each other. The formulae of Model 1 is approximately the most accurate one among all models, as noted in Table 9, as well as it is the most repeated one as the best formulae, with perfect R² values. Model 1 also is the most stable model and has the most accurate estimation at the majority of locations, even at coastal sites with a slight decline in its performance. Moreover, the length of the validation data set has a slight effect on the models’ performance and accuracy. For more illustration, the statistical errors for all best models, locals and generals, using both validation data sets, Data Set 1 (2018–2020) and Data Set 2 (2018), are clarified in Fig. 11a and b. Based on the revealed results from the comparison of the two validation data sets together, as well as the locals’ and the generals’ formulas, Model 1 (Hassan Model (Hassan et al., 2016a, 2016b), Eq. 1) can be considered the most recommended one to estimate GSR on a horizontal plane at the study’s locations (five selected cities and the Suez Canal’s Zone).

Table 9 Statistical error comparison for all best models (locals and the generals) using the Validation Data Set 1 (2018–2020) and Validation Data Set 2 (2018)

Table 10 Relative error comparison for all best models (locals and the generals) using the validation Data Set 1 (2018–2020) and validation Data Set 2 (2018)

Fig. 11

a Statistical errors’ comparison for all best models, locals and generals, using both validation data sets, Data Set 1 (2018–2020) and Data Set 2 (2018). b Statistical errors’ comparison for all best models, locals and generals, using both validation data sets, Data Set 1 (2018–2020) and Data Set 2 (2018)

Based on the predicted solar energy resources for the five cities located in the Suez Canal Economic Zone (SCZONE), the results show good average values of solar radiation around the year. These results are consistent with the fact that SCZONE is located within the global solar belt (between the latitudes of ± 35˚) with high solar potential which has still not been effectively exploited. The proposed mathematical model that considered a simple accurate quantitative tool to prove the feasibility of solar energy utilization in this newly developed economic region. The results of this accurate tool support the suggested polices for green and sustainable development in this new economic region. These policies attract a lot of green investments which aim to produce different products with low carbon foot print to satisfy the future and modern international requirements of clean production and environmental-friendly products consistent with global Sustainable Development Goals (SDGs).

In general, the issue of providing preliminary data for global solar radiation in an accurate manner has become easier, as the results indicate that the best models in this study performed well in the GSR forecast. These best models can anticipate GSR in the analyzed areas with high accuracy at any moment, and they can do so more quickly and with more applicability. Their R² ranges from 95 to 98% at all sites except for coastal one, which is from 91 to 95%. As a result, they are the ones that are advised to forecast GSR at the investigated areas in particular or throughout the Suez Canal Zone. Additionally, it is suitable for horizontal GSR forecasting at any location, and its empirical coefficients have to be calibrated using local data when it is used in other sites because it is site-dependent. Moreover, by using this developed model, Model 1, forecasting solar radiation may be readily achieved with adequate dependability at a variety of locations when no device for detecting solar radiation is available. Furthermore, the temperature parameter is being captured simply and constantly for other purposes, which is seen to be the key advantage of this strategy in the current study. For more clarification, the graphical presentations of the study’s findings are presented in Fig. 15 (in the Appendix). In other words, the developed mathematical models in this study are considered an accurate and simple tool based on the available temperature data to evaluate the available solar energy resources for different locations. This can help the policymakers to identify different opportunities for solar energy utilization as a part of the green sustainable plan reducing the carbon footprint toward the low or zero-carbon policies for a certain region such as the Suez Canal Economic Zone.

4 Conclusion and future work

Solar energy is believed to be the most promising renewable energy source globally, and as such, accurate data on solar radiation is essential in evaluating solar resources for various applications. These data are considered the first step in achieving energy sustainability goals and satisfying the world’s energy demand. However, the unavailability of solar radiation measurements in many regions of the world has necessitated the development of several global solar radiation (GSR) models to predict solar radiation in these locations. In this regard, the present work evaluated the proficiency of several GSR models at five new locations and determined the most suitable one for GSR prediction. The study has further developed solar radiation models for these new locations, as well as general ones for the entire region, which does not have any GSR models regardless of the existence of many proposed solar energy projects in this zone. These sites are Port Said, El Kantara, Ismailia, Fayid, and Suez. Additionally, the study investigates the effect of changing the length of the validation dataset on models’ performance and accuracy, as well as assesses the introduced models’ generalization capability. The study revealed that Model 1 (Hassan et al. Model), Eq. 1, outperformed other models in terms of stability, accuracy, and reliability at different locations. Its performance, measured by R² value, was found to be between 95 and 98%, except for the coastal city (Port Said), where it ranged between 91 and 95%. The study also found that the length of the validation data set had a negligible effect on the models’ performance, which ranged from about 1% to 2%. Furthermore, Model 1 showed consistent performance even after a prolonged period, and its accuracy was still highly accurate when compared to its 2016 results. Therefore, Model 1 is an excellent GSR estimation model on a flat plane with high precision, and it can be combined with other long- or short-term weather forecast methods to achieve high applicability. In particular, accurate temperature predictions from these weather forecast methods can be used as inputs to Model 1 for precise GSR forecast. Consequently, Model 1 is the recommended solar radiation model for the studied locations and other sites globally, with an accepted error limit and high precision.

However, because of its slightly low performance at the coastal location, it is planned to investigate and study integrating effective weather parameters such as relative humidity into Model 1 (Eq. 1) and check its effects on the model’s prediction and accuracy. Additionally, the study aims to compare the performance of the best empirical model obtained from this study with other techniques such as machine learning methods, including artificial neural networks, at the same studied locations, especially the coastal ones.

Appendix

See Figs. 12, 13, 14 and 15.

Fig. 12

Statistical errors graph for all models of the local formulas using validation Data Set 2 (2018)

Fig. 13

Statistical errors graph for all models of the general formulas using validation Data Set 2 (2018)

Fig. 14

Relative errors for the best local and general models using validation Data Set 2 (2018)

Fig. 15

Graphical presentations of the study’s findings