Analytical and Numerical Solution for the Time Fractional Black-Scholes Model Under Jump-Diffusion

Abstract

In this work, we study the numerical solution for time fractional Black-Scholes model under jump-diffusion involving a Caputo differential operator. For simplicity of the analysis, the model problem is converted into a time fractional partial integro-differential equation with a Fredholm integral operator. The L1 discretization is introduced on a graded mesh to approximate the temporal derivative. A second order central difference scheme is used to replace the spatial derivatives and the composite trapezoidal approximation is employed to discretize the integral part. The stability results for the proposed numerical scheme are derived with a sharp error estimation. A rigorous analysis proves that the optimal rate of convergence is obtained for a suitable choice of the grading parameter. Further, we introduce the Adomian decomposition method to find out an analytical approximate solution of the given model and the results are compared with the numerical solutions. The main advantage of the fully discretized numerical method is that it not only resolves the initial singularity occurred due to the presence of the fractional operator, but it also gives a higher rate of convergence compared to the uniform mesh. On the other hand, the Adomian decomposition method gives the analytical solution as well as a numerical approximation of the solution which does not involve any mesh discretization. Furthermore, the method does not require a large amount of computer memory and is free of rounding errors. Some experiments are performed for both methods and it is shown that the results agree well with the theoretical findings. In addition, the proposed schemes are investigated on numerous European option pricing jump-diffusion models such as Merton’s jump-diffusion and Kou’s jump-diffusion for both European call and put options.

1 Introduction

Let $(S,\tau )\in {\mathbb {R}}^+\times (0,T]$ and ${\mathscr {W}}(S,\tau )$ denote the option price that depends on the underlying asset price S with the current time $\tau$. Then, the time fractional Black-Scholes (TFBS) model for option price under jump-diffusion can be described as:

$$\begin{aligned} \left\{ \begin{array}{ll} \partial _{\tau }^{\alpha }{\mathscr {W}}(S,\tau ) +\dfrac{1}{2}\sigma ^2S^2\dfrac{\partial ^2{\mathscr {W}}(S,\tau )}{\partial S^2} +(r-\lambda k)S\dfrac{\partial {\mathscr {W}}(S,\tau )}{\partial S}\\ -(r+\lambda ){\mathscr {W}}(S,\tau )+\lambda \displaystyle {\int _0^\infty } {\mathscr {W}}(S\xi ,\tau ){\mathscr {G}}(\xi )\;d\xi =0,\\ \text {subject to the boundary conditions:}\\ {\mathscr {W}}(0,\tau )=\eta (\tau ),\;{\mathscr {W}}(S,\tau )=\zeta (\tau ) \text { as }S\rightarrow \infty \\ \text {and the terminal condition}\\ {\mathscr {W}}(S,T)={\mathscr {Q}}(S),\; S\in (0,\infty ). \end{array}\right. \end{aligned}$$

(1)

Here, $0<\alpha <1$, r is the risk-free interest rate and $\sigma$ denotes the volatility of the returns from the underlying asset, $\lambda >0$ is the intensity of the independent Poisson process and T is the expiry time. k is the expected relative jump size which is assumed to adopt one of the two forms:

$$\begin{aligned} k:={\textbf{E}}(\xi -1)={\left\{ \begin{array}{ll} \exp \Big (\mu _J+\dfrac{\sigma _J^2}{2}\Big )-1 ~~ \text {under Mertons jump-diffusion model},\\ \dfrac{p\xi _1}{\xi _1-1}+\dfrac{q\xi _2}{\xi _1+1}-1 \text {under Kous jump-diffusion model}, \end{array}\right. } \end{aligned}$$

where $\mu _J$ and $\sigma _J$ are respectively the mean and the variance of the jump in return. ${\textbf{E}}(.)$ denotes the expectation operator and $\xi -1$ is the impulse function making a jump from S to $S\xi$, with $\xi _1>0,\xi _2>0,p>0$ and $q=1-p$. Further, ${\mathscr {G}}(\xi )$ represents the probability density function of the jump with amplitude $\xi$ satisfying that $\forall \xi ,\; {\mathscr {G}}(\xi )\ge 0$ with $\displaystyle {\int _0^\infty }{\mathscr {G}}(\xi )d\xi =1$ and is defined by

$$\begin{aligned} {\mathscr {G}}(\xi )={\left\{ \begin{array}{ll} \dfrac{1}{\sqrt{2\pi }\sigma _J\xi }e^{-\dfrac{(\ln \xi -\mu _J)^2}{2\sigma _J^2}}~ \text {(Merton's jump-diffusion)},\\ \dfrac{1}{\xi }\Big [p\xi _1e^{-\xi _1\ln (\xi )}{\textbf{H}} (\ln (\xi ))+q\xi _2e^{\xi _2\ln (\xi )}{\textbf{H}}(-\ln (\xi ))\Big ]\text {(Kou's jump-diffusion)}, \end{array}\right. } \end{aligned}$$

where ${\textbf{H}}(.)$ is the Heaviside function. ${\mathscr {Q}}(S)$ is considered as a pay-off function which can be described for European options as:

$$\begin{aligned} {\mathscr {Q}}(S)={\left\{ \begin{array}{ll} \max (S-K,0) ~~~\text { for a European call option},\\ \max (K-S,0) ~~~\text { for a European put option}, \end{array}\right. } \end{aligned}$$

where K denotes the strike price of the option. In particular, when $\alpha =1$, the model (1) describes the classical Black-Scholes jump-diffusion model (Kadalbajoo et al., 2015a; Moon et al., 2014). In this paper our aim is to study the impact of the fractional operator on the options price based on numerical simulations.

The hypothesis behind the option pricing is a probabilistic approach to assigning a value to an options contract. The main aim of this theory is to calculate the probability that an option will be exercised or be in the money at expiration. An option provides the holder with the right to buy or sell a specified quantity of an underlying asset at a fixed price (called a strike price or an exercise price) at or before the expiration date of the option. There are two types of options: call options and put options. Call options allow the option holder to buy an asset at a prespecified price, whereas put options allow the holder to sell an asset at a prespecified price. Some commonly used models to price an option include the Black-Scholes (B-S) model, binomial tree, Monte-Carlo simulation, etc. Among them, the B-S model is one of the most highly regarded pricing models that includes the variables representing the strike price of the option, the stock price, time to expiration, the risk-free interest rate of return and volatility. There are many equivalent studies in the available literature addressing analytical and numerical investigations of the B-S model (see (Mehdizadeh et al., 2022; Rao, 2018; Valkov, 2014) among others). In this study, our main focus is on a fractional B-S model as in the current models, the fractional differential calculus is continuously updating its profile by considering many numerical methods such as the finite difference method (FDM) (Gracia et al., 2018; Santra &Mohapatra, 2021a), the finite element method (Ford et al., 2011), the Adomian decomposition method (ADM) (Panda et al., 2021), the homotopy perturbation method (HPM) (Das et al., 2020), the modified Laplace decomposition method (Hamoud & Ghadle, 2018), and a radial basis function-generated finite difference method (Nikan et al., 2022), etc. Wyss in Wyss (2000) introduced the TFBS model by replacing the first derivative in time by a fractional derivative in which he gave the complete solution of the model. Its accuracy and efficiency in predicting option prices have enabled options traders to increase their trading volume by a significant margin. The TFBS model has recently been solved numerically by several methods. A detailed study can be found in Golbabai et al. (2019); Golbabai &Nikan (2020); Nikan et al. (2021). Further, the Chebyshev collocation method was adopted in Mesgarani et al. (2020) to provide a numerical solution to the TFBS equation. Özdemir and Yavuz in Ozdemir &Yavuz (2017) used the multivariate Padé approximation for the numerical solution of a TFBS model. An implicit finite difference scheme was constructed in Song &Wang (2013) for numerical discretization of a TFBS model. A high accuracy numerical method was designed in Roul (2019) to solve a TFBS European option pricing model in which the author discussed the convergence analysis of the proposed method. Recently, a robust FDM was set up in Nuugulu et al. (2021) for a numerical study of the TFBS equation. Further, many semi analytical approaches were studied for analytical as well as numerical investigations of the TFBS equation. For instance, Fall et al. in Fall et al. (2019) applied the HPM to obtain the analytical solution of a fractional B-S model involving the Caputo fractional derivative. The Laplace HPM was used in Kumar et al. (2012) to get an analytical approximate solution of a European option pricing model. Also in Ampun &Sawangtong (2021), an approximate analytical solution was studied for a TFBS equation governed by European option pricing model. For more investigation about numerical solutions of TFBS model, the reader can refer to Akrami and Erjaee (2015); Korbel and Luchko (2016); Kumar et al. (2014); Thanompolkrang et al. (2021); Tomovski et al. (2020) and references therein.

It is noticed that jumps appear continuously in the discrete movement of the stock price due to inconsistent behavior of the B-S model to capture the real stock price with constant volatility and these jumps cannot be solved by the usual B-S model. To overcome this phenomena, Merton in Merton (1976) and Kou in Kou (2002) introduced the jump-diffusion models as an extension of the jump process. The jump-diffusion models consist of two parts, a jump part and a diffusion part. The diffusion part is determined by a common Brownian motion and the second part is determined by an impulse-function and a distribution function. The impulse-function causes price changes in the underlying asset, and is determined by a distribution function, whereas the jump part enables to model sudden and unexpected price jumps of the underlying asset. Very few articles are available in the literature to deal with the B-S equation under jump-diffusion model. The Crank-Nicolson Leap-Frog finite difference scheme was used in Kadalbajoo et al. (2015b) and a spline collocation method was introduced in Kadalbajoo et al. (2015a) for numerical investigation of B-S jump-diffusion equation. A finite element method was proposed in Liu et al. (2019) to solve B-S equation under jump-diffusion model. For more investigation, one may refer to the book (Cont &Tankov, 2004), and the articles (Kim et al., 2019; Moon et al., 2014). To the best of our knowledge, there is no literature available where the B-S jump-diffusion models are examined including fractional order derivatives.

In this work, we generalize the usual B-S jump-diffusion model by replacing the first order derivative in time by a fractional one of order $\alpha \in (0,1)$. We present an efficient FDM to discretize the TFBS equation under jump-diffusion model involving a Caputo fractional derivative. For simplicity of the analysis, the model problem is converted into a time fractional partial integro-differential equation (PIDE) with a Fredholm integral operator. To construct the scheme, the L1 discretization is introduced on a graded mesh to approximate the temporal derivative, the second order central difference scheme is used for the spatial derivatives and the composite trapezoidal approximation is used to discretize the Fredholm operator. The convergence analysis is carried out and it is shown that the optimal rate of convergence is attained for a suitable choice of the grading parameter. In addition, we consider the ADM to find out an analytical approximate solution of the given model. The numerical experiments are done for FDM as well as for ADM and it is proved that the results are in good agreement with the theoretical findings. Further, the proposed schemes are investigated on numerous European option pricing under jump-diffusion models such as Merton’s jump-diffusion, Kou’s jump-diffusion for both European call options as well as European put options.

Now, we introduce some basic definitions and preliminaries about fractional integrals and fractional derivatives, and some well known properties, that will be used later in our analysis (more details about fractional calculus can be found in Diethelm (2010); Podlubny (1999)).

Definition 1

Let $\phi (x,t)$ be any continuous function defined on ${\mathfrak {D}}$, ${\mathfrak {D}}$ is some closed set in ${\mathbb {R}}^2$. The Riemann-Liouville fractional integral of $\phi (x,t)$ is denoted by ${\mathscr {J}}^\beta \phi$ and is defined by:

$$\begin{aligned} {\mathscr {J}}^\beta \phi (x,t)=\dfrac{1}{\Gamma (\beta )}\displaystyle {\int _{0}^t}(t-\rho ) ^{\beta -1}\phi (x,\rho )d\rho ,~~t>0,~\beta \in {\mathbb {R}}^+. \end{aligned}$$

Definition 2

The Caputo fractional derivative of the function $\phi (x,t)$ at the point $(x,t)\in S$ is defined as:

$$\begin{aligned} \partial _t^\beta \phi (x,t)={\left\{ \begin{array}{ll} \Bigg [{\mathscr {J}}^{m-\beta }\Big (\dfrac{\partial ^m \phi }{\partial t^m}\Big )\Bigg ](x,t)\;\;\text {for } m-1<\beta < m, m\in {\mathbb {N}}\\ \dfrac{\partial ^m \phi }{\partial t^m}(x,t)\;\;\text { for }\;\beta =m, m\in {\mathbb {N}}. \end{array}\right. } \end{aligned}$$

Here, $\beta$ is the order of the derivative and considered to be a positive real number. If $\phi$ is constant, then $\partial _t^\beta \phi =0$. For any $\nu \in {\mathbb {R}}$, $m\in {\mathbb {N}}$, we have the following properties:

• 1. $\partial _{t}^{\beta } t^{\nu } = \begin{array}{*{20}c} {\left\{ \begin{gathered} 0 \hfill \\ \frac{{\Gamma (\nu + 1)}}{{\Gamma (\nu - \beta + 1)}}t^{{\nu - \beta }} \hfill \\ \end{gathered} \right.} & \begin{gathered} {\text{if }}m - 1 < \beta < m,\nu \le m - 1, \hfill \\ {\text{if }}m - 1 < \beta < m,\nu > m - 1. \hfill \\ \end{gathered} \\ \end{array}$

• 2. ${\mathcal{J}}^{\beta } t^{\nu } = \begin{array}{*{20}c} {\frac{{\Gamma (\nu + 1)}}{{\Gamma (\nu + \beta + 1)}}t^{{\nu + \beta }} } & {{\text{if }}m - 1 < \beta < m,\nu \ge 0.} \\ \end{array}$.

• 3. $\partial _t^\beta {\mathscr {J}}^\beta \phi (x,t)=\phi (x,t)$, but ${\mathscr {J}}^\beta \partial _t^\beta \phi (x,t)=\phi (x,t) -\displaystyle {\sum _{k=0}^{m-1}}\dfrac{\partial ^k}{\partial t^k}\phi (x,0)\dfrac{t^k}{k!}$, $\;m-1<\beta <m$.

• 4. $\partial _t^\beta \{c_1 \phi _1(x,t)\pm c_2 \phi _2(x,t)\}=c_1\partial _t^\beta \phi _1(x,t)\pm c_2\partial _t^\beta \phi _2(x,t)$, and ${\mathscr {J}}^\beta \{c_1 \phi _1(x,t)\pm c_2 \phi _2(x,t)\}=c_1{\mathscr {J}}^\beta \phi _1(x,t)\pm c_2{\mathscr {J}}^\beta \phi _2(x,t)$,

where $c_1,c_2$ are some constants. If $\{{\mathcal {V}}_m^n\}_{m=0,n=0}^{M,N}$ is the mesh function corresponding to a continuous function ${\mathcal {V}}:{\mathfrak {B}}\subset {\mathbb {R}}^2\rightarrow {\mathbb {R}}$, then one can define

$$\begin{aligned} \Vert {\mathcal {V}}\Vert :=\max _{(x,t)\in \bar{{\mathfrak {B}}}} |{\mathcal {V}}(x,t)|\;\;\text {and }\;\Vert {\mathcal {V}}^n\Vert :=\max _{0\le m\le M}|{\mathcal {V}}_m^n|. \end{aligned}$$

2 The Continuous Problem

Set $S=Ke^x,\tau =T-t$ and $\xi =e^{y-x}$. Using this transformation, (1) is converted into

$$\begin{aligned} \left\{ \begin{array}{ll} -\partial _{t}^{\alpha }{\mathscr {W}}(Ke^x,T-t) +\dfrac{\sigma ^2}{2}\dfrac{\partial ^2{\mathscr {W}}(Ke^x,T-t)}{\partial x^2} +(r-\dfrac{\sigma ^2}{2}-\lambda k)\dfrac{\partial {\mathscr {W}}(Ke^x,T-t)}{\partial x}\\ -(r+\lambda ){\mathscr {W}}(Ke^x,T-t) +\lambda \displaystyle {\int _{-\infty }^\infty } {\mathscr {W}}(Ke^y,T-t){\mathscr {G}}(e^{y-x})e^{y-x}\;dy=0,\\ (x,t)\in {\mathbb {R}}\times (0,T], \text { satisfying}\\ {\mathscr {W}}(Ke^{-\infty },T-t)=\eta (T-t),\;{\mathscr {W}}(Ke^\infty ,T-t)=\zeta (T-t);\\ {\mathscr {W}}(Ke^x,T)={\mathscr {Q}}(Ke^x). \end{array}\right. \end{aligned}$$

(2)

It is crucial to work within a constrained interval in order to get a good numerical approximation of the solution of the above-mentioned model. Therefore, we truncate the interval in the spatial variable, and instead of the domain ${\mathbb {R}}\times (0,T]$, we consider the bounded domain $\Omega :=[-L,L]\times (0,T]$. Putting ${\mathcal {U}}(x,t)={\mathscr {W}}(Ke^x,T-t)$, (2) yields

$$\begin{aligned} \left\{ \begin{array}{ll} \partial _{t}^{\alpha }{\mathcal {U}}(x,t)= A\dfrac{\partial ^2{\mathcal {U}}(x,t)}{\partial x^2} +B\dfrac{\partial {\mathcal {U}}(x,t)}{\partial x} -D{\mathcal {U}}(x,t)+\lambda \displaystyle {\int _{-L}^L} {\mathcal {U}}(y,t)g(y-x)\;dy+f(x,t),\\ (x,t)\in [-L,L]\times (0,T], \text { with}\\ {\mathcal {U}}(-L,t)={\tilde{\eta }}(t),\;{\mathcal {U}}(L,t)={\tilde{\zeta }}(t)\;\forall t\in (0,T];\\ {\mathcal {U}}(x,0)=\tilde{{\mathscr {Q}}}(x)\;\forall x\in [-L,L], \end{array}\right. \end{aligned}$$

(3)

where $A=\sigma ^2/2,B=r-A-\lambda k$ and $D=r+\lambda$. The functions ${\tilde{\eta }},{\tilde{\zeta }}$ and $\tilde{{\mathscr {Q}}}$ correspond to the functions $\eta ,\zeta$ and ${\mathscr {Q}}$, respectively in the transformed domain and are defined by: ${\tilde{\eta }}(t)=\eta (T-t),~ {\tilde{\zeta }}(t)=\zeta (T-t),~\tilde{{\mathscr {Q}}}(x) ={\mathscr {Q}}(Ke^x)$. The source term f(x, t) is introduced only for partial fulfillment of the validation in the numerical experiment section. Further, $g(y)={\mathscr {G}}(e^y)e^y$ and under the above transformation g(y) can be expressed explicitly as:

$$\begin{aligned} g(y):={\left\{ \begin{array}{ll} \dfrac{1}{\sqrt{2\pi }\sigma _J}e^{-\dfrac{(y-\mu _J)^2}{2\sigma _J^2}}~~~~~~~~~~~~~~~~~~ \text { (Merton's jump-diffusion model)},\\ \Big [p\xi _1e^{-\xi _1y}{\textbf{H}}(y)+q\xi _2e^{\xi _2y}{\textbf{H}}(-y)\Big ]~~\text { (Kou's jump-diffusion model)}. \end{array}\right. } \end{aligned}$$

Under certain assumptions on $\sigma ,r,k,\lambda$ and on the probability density function g, together with the following bounds on the derivatives of ${\mathcal {U}}$

$$\begin{aligned} \left\{ \begin{array}{ll} \Bigg |\dfrac{\partial ^i{\mathcal {U}}}{\partial x^i}(x,t) \Bigg |\le C,~~~\forall ~i=0,1,2,3,4;\\ \Bigg |\dfrac{\partial ^j{\mathcal {U}}}{\partial t^j}(x,t)\Bigg |\le C(1+t^{\alpha -j}),~~~\forall ~j=0,1,2, \end{array}\right. \end{aligned}$$

(4)

the existence and uniqueness of the solution ${\mathcal {U}}(x,t)\in {\mathcal {C}}_x^\infty ({\bar{\Omega }},{\mathbb {R}})$ of (3) for $(x,t)\in \Omega$ can be guaranteed. $C>0$ denotes a generic constant which can take different values at different places. For more information, the reader may refer to the book (Cont &Tankov, 2004) and the articles (Gracia et al., 2018; Kadalbajoo et al., 2015a; Santra &Mohapatra, 2021b). Here, ${\mathcal {C}}_x^\infty ({\bar{\Omega }},{\mathbb {R}})$ is a subspace of ${\mathcal {C}}({\bar{\Omega }},{\mathbb {R}})$ in which the functions are infinitely differentiable in the x variable with the norm defined by:

$$\begin{aligned}\Vert {\mathscr {V}}\Vert _{{\mathcal {C}}_x^\infty ({\bar{\Omega }},{\mathbb {R}})}=\sup _{k\ge 0}\sup _{(x,t)\in {\bar{\Omega }}}\Big |\dfrac{\partial ^k{\mathscr {V}}(x,t)}{\partial x^k}\Big |,\end{aligned}$$

where ${\mathcal {C}}({\bar{\Omega }},{\mathbb {R}})$ denotes the set of all real-valued continuous functions defined on ${\bar{\Omega }}$. The convergence analysis for the ADM will be done based on the norm defined above.

2.1 Analytical Approximate Solution

In this section, we successfully apply the ADM for obtaining the analytical as well as the numerical approximation of (3). According to ADM, the solution of (3) can be expressed in terms of an infinite series as:

$$\begin{aligned} {\mathcal {U}}(x,t)=\sum _{j=0}^{\infty }{\mathcal {U}}_j(x,t). \end{aligned}$$

(5)

If the model problem involves any nonlinear term, then it can be approximated by Adomian polynomials (see (Panda et al., 2021)). Since (3) does not involve any nonlinear term, we don’t need the Adomian polynomials. Applying ${\mathscr {J}}^\alpha$ to both sides of (3), we get

$$\begin{aligned} {\mathcal {U}}(x,t)=\,\,&{\mathcal {U}}(x,0)+{\mathscr {J}}^\alpha \Big [f(x,t)\Big ] +A{\mathscr {J}}^\alpha \Bigg [\dfrac{\partial ^2{\mathcal {U}}}{\partial x^2}\Bigg ] +B{\mathscr {J}}^\alpha \Bigg [\dfrac{\partial {\mathcal {U}}}{\partial x}\Bigg ]-D{\mathscr {J}}^\alpha \Big [{\mathcal {U}}(x,t)\Big ]\nonumber \\&+\lambda {\mathscr {J}}^\alpha \Bigg [\displaystyle {\int _{-L}^L} {\mathcal {U}}(y,t)g(y-x)~dy\Bigg ]. \end{aligned}$$

(6)

Substituting (5) into (6) and comparing both sides, we reach at the following recursive algorithm:

$$ \left\{ \begin{aligned} {\mathcal{U}}_{0} (x,t) = & \,\,\widetilde{{\mathcal{Q}}}(x) + {\mathcal{J}}^{\alpha } \left[ {f(x,t)} \right], \\ {\mathcal{U}}_{{j + 1}} (x,t) = & \,\,A{\mathcal{J}}^{\alpha } \left[ {\frac{{\partial ^{2} }}{{\partial x^{2} }}{\mathcal{U}}_{j} (x,t)} \right] + B{\mathcal{J}}^{\alpha } \left[ {\frac{\partial }{{\partial x}}{\mathcal{U}}_{j} (x,t)} \right] - D{\mathcal{J}}^{\alpha } \left[ {{\mathcal{U}}_{j} (x,t)} \right] \\ + & \,\,\lambda {\mathcal{J}}^{\alpha } \left[ {\mathop \int \limits_{{ - L}}^{L} {\mathcal{U}}_{j} (y,t)g(y - x)~dy} \right],~{\text{ for }}j = 0,1,2, \cdots . \\ \end{aligned} \right. $$

(7)

The exact solution is given by: ${\mathcal {U}}(x,t)= \displaystyle { \lim _{{\mathscr {N}}\rightarrow \infty }\sum _{j=0}^{{\mathscr {N}}}}{\mathcal {U}}_j(x,t)$. One can get an analytical approximate solution by truncating the series up to a finite number of terms (say ${\mathscr {N}}$ terms). In this case, the approximate solution is ${\mathscr {U}}_{{\mathscr {N}}}=\displaystyle {\sum _{j=0}^{{\mathscr {N}}-1}}{\mathcal {U}}_j(x,t)$.

Theorem 1

Let $f(x,t)\in {\mathcal {C}}_x^\infty ({\bar{\Omega }},{\mathbb {R}})$ and $\tilde{{\mathscr {Q}}}(x),g(x)\in {{\mathcal {C}}_x^\infty ([-L,L],{\mathbb {R}})}$. Then the series solution for (3) represented by (5) converges uniformly on ${\bar{\Omega }}$.

Proof

The idea that we have used to prove this theorem has been used in Das et al. (2020). The additional assumption that we need is that $\vartheta :=\dfrac{(|A|+|B|+|D|+2\lambda L{\mathbb {G}})T^\alpha }{\Gamma (\alpha +1)}<1$, where $\Vert g\Vert _{{\mathcal {C}}_x^\infty ({\bar{\Omega }},{\mathbb {R}})}\le {\mathbb {G}}$. Since $f(x,t)\in {\mathcal {C}}_x^\infty ({\bar{\Omega }},{\mathbb {R}})$ and $\tilde{{\mathscr {Q}}}(x)\in {\mathcal {C}}_x^\infty ([-L,L],{\mathbb {R}})$, so ${\mathcal {U}}_0\in {\mathcal {C}}_x^\infty ({\bar{\Omega }},{\mathbb {R}})$. Then, there exists an ${\mathscr {M}}>0$ such that $|{\mathcal {U}}_0|\le \displaystyle {\sup _{k\ge 0} \sup _{(x,t)\in {\bar{\Omega }}}}\Big |\dfrac{\partial ^k{\mathcal {U}}_0(x,t)}{\partial x^k}\Big |=\Vert {\mathcal {U}}_0\Vert _{C_x^\infty ({\bar{\Omega }},{\mathbb {R}})}\le {\mathscr {M}}$. Then, the expression described in (7) confirms that ${\mathcal {U}}_j\in {\mathcal {C}}_x^\infty ({\bar{\Omega }},{\mathbb {R}})$, for $j=1,2,\ldots$. Now, we apply the principle of mathematical induction to prove that $|{\mathcal {U}}_j|\le {\mathscr {M}}\vartheta ^j~\forall ~j=1,2,3, \ldots$. For $j=1$, we have

$$\begin{aligned} |{\mathcal {U}}_1|&\le \displaystyle {\sup _{k\ge 0}\sup _{(x,t)\in {\bar{\Omega }}}}\Big |\dfrac{\partial ^k{\mathcal {U}}_1(x,t)}{\partial x^k}\Big |=\Vert {\mathcal {U}}_1\Vert _{C_x^\infty ({\bar{\Omega }},{\mathbb {R}})}\le |A|{\mathscr {J}}^\alpha \Bigg [\Big \Vert \dfrac{\partial ^2 {\mathcal {U}}_0}{\partial x^2}\Big \Vert _{C_x^\infty ({\bar{\Omega }},{\mathbb {R}})}\Bigg ] +|B|{\mathscr {J}}^\alpha \Bigg [\Big \Vert \dfrac{\partial {\mathcal {U}}_0}{\partial x}\Big \Vert _{C_x^\infty ({\bar{\Omega }},{\mathbb {R}})}\Bigg ]\\&~~~~~~~+|D|{\mathscr {J}}^\alpha \Big [\Vert {\mathcal {U}}_0\Vert _{C_x^\infty ({\bar{\Omega }},{\mathbb {R}})}\Big ] +\lambda {\mathscr {J}}^\alpha \Bigg [\displaystyle {\int _{-L}^L}\Vert {\mathcal {U}}_0\Vert _{C_x^\infty ({\bar{\Omega }},{\mathbb {R}})}\Vert g\Vert _{C_x^\infty ({\bar{\Omega }},{\mathbb {R}})}~dy\Bigg ]\\&=|A|{\mathscr {J}}^\alpha \Bigg [\displaystyle {\sup _{k\ge 0} \sup _{(x,t)\in {\bar{\Omega }}}}\Big |\dfrac{\partial ^{k+2}{\mathcal {U} }_0(x,t)}{\partial x^{k+2}}\Big |\Bigg ] +|B|{\mathscr {J}} ^\alpha \Bigg [\displaystyle {\sup _{k\ge 0}\sup _{(x,t)\in {\bar{\Omega }}}} \Big |\dfrac{\partial ^{k+1}{\mathcal {U}}_0(x,t)}{\partial x^{k+1}}\Big |\Bigg ] +|D|{\mathscr {J}}^\alpha \Big [\Vert {\mathcal {U}}_0\Vert _{C_x^\infty ({\bar{\Omega }} ,{\mathbb {R}})}\Big ]\\&~~~~~~~ +\lambda {\mathscr {J}}^\alpha \Bigg [\displaystyle {\int _{-L}^L}\Vert {\mathcal {U}}_0\Vert _{C_x^\infty ({\bar{\Omega }},{\mathbb {R}})}\Vert g\Vert _{C_x^\infty ({\bar{\Omega }},{\mathbb {R}})}~dy\Bigg ]\\&\le \dfrac{|A|}{\Gamma (\alpha )}\int _0^t (t-s)^{\alpha -1}\Vert {\mathcal {U}}_0\Vert _{C_x^\infty ({\bar{\Omega }},{\mathbb {R}})}ds +\dfrac{|B|}{\Gamma (\alpha )}\int _0^t (t-s)^{\alpha -1}\Vert {\mathcal {U}}_0\Vert _{C_x^\infty ({\bar{\Omega }},{\mathbb {R}})}ds \\&~~~~~~~+\dfrac{|D|}{\Gamma (\alpha )}\int _0^t (t-s)^{\alpha -1}\Vert {\mathcal {U}}_0\Vert _{C_x^\infty ({\bar{\Omega }},{\mathbb {R}})}ds +\dfrac{\lambda {\mathbb {G}}}{\Gamma (\alpha )}\int _0^t (t-s)^{\alpha -1}\int _{-L}^L\Vert {\mathcal {U}}_0\Vert _{C_x^\infty ({\bar{\Omega }},{\mathbb {R}})}dy~ds\\&\le \Bigg [\dfrac{(|A|+|B|+|D|+2\lambda L{\mathbb {G}})T^\alpha }{\Gamma (\alpha +1)}\Bigg ]\Vert {\mathcal {U}}_0\Vert _{C_x^\infty ({\bar{\Omega }},{\mathbb {R}})}\le {\mathscr {M}}\vartheta . \end{aligned}$$

Suppose that the inequality holds true for $j=p-1,~p\in {\mathbb {N}}$ i.e., $|{\mathcal {U}}_{p-1}|\le \displaystyle {\sup _{k\ge 0} \sup _{(x,t)\in {\bar{\Omega }}}}\Big |\dfrac{\partial ^k{\mathcal {U}}_{p-1}(x,t)}{\partial x^k}\Big |=\Vert {\mathcal {U}}_{p-1}\Vert _{C_x^\infty ({\bar{\Omega }},{\mathbb {R}})}\le {\mathscr {M}}\vartheta ^{p-1}$. Then for $j=p$, we get

$$\begin{aligned} |{\mathcal {U}}_p|&\le \displaystyle {\sup _{k\ge 0}\sup _{(x,t) \in {\bar{\Omega }}}}\Big |\dfrac{\partial ^k{\mathcal {U}}_p(x,t)}{\partial x^k}\Big |=\Vert {\mathcal {U}}_p\Vert _{C_x^\infty ({\bar{\Omega }},{\mathbb {R}})}\le |A|{\mathscr {J}}^\alpha \Bigg [\Big \Vert \dfrac{\partial ^2 {\mathcal {U}}_{p-1}}{\partial x^2}\Big \Vert _{C_x^\infty ({\bar{\Omega }},{\mathbb {R}})}\Bigg ] +|B|{\mathscr {J}}^\alpha \Bigg [\Big \Vert \dfrac{\partial {\mathcal {U}}_{p-1}}{\partial x}\Big \Vert _{C_x^\infty ({\bar{\Omega }},{\mathbb {R}})}\Bigg ]\\&~~~~~~~~~~~~+|D|{\mathscr {J}}^\alpha \Big [\Vert {\mathcal {U}}_{p-1}\Vert _{C_x^ \infty ({\bar{\Omega }},{\mathbb {R}})}\Big ] +\lambda {\mathscr {J}}^\alpha \Bigg [\displaystyle {\int _{-L}^L}\Vert {\mathcal {U}}_{p-1} \Vert _{C_x^\infty ({\bar{\Omega }},{\mathbb {R}})}\Vert g\Vert _{C_x^\infty ({\bar{\Omega }}, {\mathbb {R}})}~dy\Bigg ]\\&=|A|{\mathscr {J}}^\alpha \Bigg [\displaystyle {\sup _{k\ge 0}\sup _{(x,t) \in {\bar{\Omega }}}}\Big |\dfrac{\partial ^{k+2}{\mathcal {U}}_{p-1}(x,t)}{\partial x^{k+2}}\Big |\Bigg ] +|B|{\mathscr {J}}^\alpha \Bigg [\displaystyle {\sup _{k\ge 0}\sup _{(x,t)\in {\bar{\Omega }}}}\Big |\dfrac{\partial ^{k+1}{\mathcal {U}}_{p-1}(x,t)}{\partial x^{k+1}}\Big |\Bigg ]\\&~~~~~~~~~~~~+|D|{\mathscr {J}}^\alpha \Big [\Vert {\mathcal {U}}_ {p-1}\Vert _{C_x^\infty ({\bar{\Omega }},{\mathbb {R}})}\Big ] +\lambda {\mathscr {J}}^\alpha \Bigg [\displaystyle {\int _{-L}^L}\Vert {\mathcal {U}}_{p-1} \Vert _{C_x^\infty ({\bar{\Omega }},{\mathbb {R}})}\Vert g\Vert _{C_x^\infty ({\bar{\Omega }},{\mathbb {R}})}~dy\Bigg ]\\&\le \dfrac{|A|}{\Gamma (\alpha )}\int _0^t (t-s)^{\alpha -1}\Vert {\mathcal {U}}_{p-1}\Vert _{C_x^\infty ({\bar{\Omega }},{\mathbb {R}})}ds +\dfrac{|B|}{\Gamma (\alpha )}\int _0^t (t-s)^{\alpha -1}\Vert {\mathcal {U}}_{p-1}\Vert _{C_x^\infty ({\bar{\Omega }},{\mathbb {R}})}ds \\&~~~~~~~~~~~~+\dfrac{|D|}{\Gamma (\alpha )}\int _0^t (t-s)^{\alpha -1}\Vert {\mathcal {U}}_{p-1}\Vert _{C_x^\infty ({\bar{\Omega }},{\mathbb {R}})}ds +\dfrac{\lambda {\mathbb {G}}}{\Gamma (\alpha )}\int _0^t (t-s)^{\alpha -1} \int _{-L}^L\Vert {\mathcal {U}}_{p-1}\Vert _{C_x^\infty ({\bar{\Omega }},{\mathbb {R}})}dy~ds\\&\le \Bigg [\dfrac{(|A|+|B|+|D|+2\lambda L{\mathbb {G}})T^\alpha }{\Gamma (\alpha +1)}\Bigg ]\Vert {\mathcal {U}}_{p-1} \Vert _{C_x^\infty ({\bar{\Omega }},{\mathbb {R}})}\le \vartheta {\mathscr {M}}\vartheta ^{p-1}= {\mathscr {M}}\vartheta ^p. \end{aligned}$$

Therefore, we have $\Bigg |\displaystyle {\sum _{j=0}^\infty }{\mathcal {U}}_j(x,t)\Bigg |\le \displaystyle {\sum _{j=0}^\infty }|{\mathcal {U}}_j|\le \displaystyle {\sum _{j=0}^\infty }{\mathscr {M}}\vartheta ^j$. Notice that since $\vartheta \in (0,1)$, the series $\displaystyle {\sum _{j=0}^\infty }{\mathscr {M}}\vartheta ^j$ is a convergent geometric series. Hence, by the Weierstrass M-test, one can conclude that the series $\displaystyle {\sum _{j=0}^\infty }{\mathcal {U}}_j(x,t)$ converges uniformly on ${\bar{\Omega }}$. $\square$

3 Finite Difference Approximation

For numerical discretization, a uniform mesh is used in the spatial direction whereas, a graded mesh is introduced to discretize the temporal direction.

3.1 Time Discretization

Let, N be a fixed positive integer and set $t_n=T\Big (\dfrac{n}{N}\Big )^\varrho$ for $n=0,1,\cdots ,N$. $\varrho \ge 1$ is the grading parameter. If $\varrho =1$ then the mesh will be uniform. Take $\Delta t_n=t_n-t_{n-1},\;n=1,2,\cdots ,N$. At each $t=t_n$, the Caputo fractional derivative $\partial _t^\alpha {\mathcal {U}}$ is defined by

$$\begin{aligned} \partial _t^\alpha {\mathcal {U}}(x,t_n)=\dfrac{1}{\Gamma (1-\alpha )} \displaystyle {\sum _{l=0}^{n-1}\int _{s=t_l}^{t_{l+1}}}(t_n-s)^{-\alpha }\dfrac{\partial {\mathcal {U}}}{\partial s}(x,s)\;ds. \end{aligned}$$

The L1 discretization is used to approximate $\partial _t^\alpha {\mathcal {U}}(x,t_n)$ as follows:

$$\begin{aligned} \partial _t^\alpha {\mathcal {U}}(x,t_n)\approx \partial _N^\alpha {\mathcal {U}}^n:&= \dfrac{1}{\Gamma (1-\alpha )}\sum _{l=0}^{n-1}\dfrac{{\mathcal {U}}^{l+1}-{\mathcal {U}}^l}{\Delta t_{l+1}} \int _{s=t_l}^{t_{l+1}}(t_n-s)^{-\alpha }\;ds\\&=\dfrac{1}{\Gamma (2-\alpha )}\sum _{l=0}^{n-1}\dfrac{{\mathcal {U}}^{l+1}-{\mathcal {U}}^l}{\Delta t_{l+1}} \Big [(t_n-t_l)^{1-\alpha }-(t_n-t_{l+1})^{1-\alpha }\Big ]\\&=\dfrac{d_{n,1}^{(\alpha )}}{\Gamma (2-\alpha )}{\mathcal {U}}^n -\dfrac{d_{n,n}^{(\alpha )}}{\Gamma (2-\alpha )}{\mathcal {U}}^0+\dfrac{1}{\Gamma (2-\alpha )}\sum _{l=1}^{n-1}\Big [d_{n,l+1}^{(\alpha )}-d_{n,l} ^{(\alpha )}\Big ]{\mathcal {U}}^{n-l}, \end{aligned}$$

where for each $n=1,2,\cdots ,N$, $d_{n,l}^{(\alpha )}$ is defined by

$$\begin{aligned} d_{n,l}^{(\alpha )}:=\dfrac{(t_n-t_{n-l})^{1-\alpha }-(t_n-t_{n-l+1})^{1-\alpha }}{\Delta t_{n-l+1}},\;l=1,2,\cdots ,n. \end{aligned}$$

Particularly, $d_{n,1}^{(\alpha )}=\Delta t_n^{-\alpha }$. The mean value theorem gives $(1-\alpha )(t_n-t_{n-l})^{-\alpha }\le d_{n,l}^{(\alpha )}\le (1-\alpha )(t_n-t_{n-l+1})^{-\alpha }$ and hence, we have

$$\begin{aligned} d_{n,l+1}^{(\alpha )}\le d_{n,l}^{(\alpha )}. \end{aligned}$$

(8)

For further study about L1 discretization, the reader may refer to Gracia et al. (2018); Huang et al. (2020); Santra and Mohapatra (2020).

3.2 Space Discretization

Take $M\in {\mathbb {N}}$ be fixed and set $x_m=-L+m\Delta x$ for $m=0,1,\cdots ,M$, where $x_0=-L, x_M=L$ and the mesh parameter $\Delta x=2\,L/M$. At each $x=x_m$, the spatial derivatives $\dfrac{\partial {\mathcal {U}}}{\partial x}$ and $\dfrac{\partial ^2{\mathcal {U}}}{\partial x^2}$ are discretized as:

$$\begin{aligned} \begin{array}{ll} \dfrac{\partial {\mathcal {U}}}{\partial x}(x_m,t)\approx {\mathscr {D}}_x^0{\mathcal {U}}_m:=\dfrac{{\mathcal {U}}_{m+1}-{\mathcal {U}}_{m-1}}{2\Delta x},\\ \dfrac{\partial ^2 {\mathcal {U}}}{\partial x^2}(x_m,t)\approx \delta _x^2{\mathcal {U}}_m:=\dfrac{{\mathcal {U}}_{m+1}-2{\mathcal {U}}_{m} +{\mathcal {U}}_{m-1}}{(\Delta x)^2}. \end{array} \end{aligned}$$

Finally, the nonuniform mesh $\{(x_m,t_n):\;m=0,1,\cdots ,M;\;n=0,1,\cdots ,N\}$ is constructed and at each mesh points $(x_m,t_n)$, we have the following approximations:

$$\begin{aligned} \left\{ \begin{array}{ll} \partial _t^\alpha {\mathcal {U}}(x_m,t_n)\approx \partial _N^\alpha {\mathcal {U}}_m^n:=\dfrac{d_{n,1}^{(\alpha )}}{\Gamma (2-\alpha )} {\mathcal {U}}_m^n-\dfrac{d_{n,n}^{(\alpha )}}{\Gamma (2-\alpha )} {\mathcal {U}}_m^0+\dfrac{1}{\Gamma (2-\alpha )}\displaystyle {\sum _{l=1}^{n-1}} \Big [d_{n,l+1}^{(\alpha )}-d_{n,l}^{(\alpha )}\Big ]{\mathcal {U}}_m^{n-l},\\ \dfrac{\partial {\mathcal {U}}}{\partial x}(x_m,t_n)\approx {\mathscr {D}}_x^0{\mathcal {U}}_m^n:=\dfrac{{\mathcal {U}}_{m+1}^n-{\mathcal {U}}_{m-1}^n}{2\Delta x},\\ \dfrac{\partial ^2 {\mathcal {U}}}{\partial x^2}(x_m,t_n)\approx \delta _x^2{\mathcal {U}}_m^n:=\dfrac{{\mathcal {U}}_{m+1}^n-2{\mathcal {U}}_{m}^n +{\mathcal {U}}_{m-1}^n}{(\Delta x)^2}. \end{array}\right. \end{aligned}$$

(9)

Therefore, (3) becomes

$$\begin{aligned} \left\{ \begin{array}{ll} \partial _{N}^{\alpha }{\mathcal {U}}(x_m,t_n)- A\delta _x^2{\mathcal {U}}(x_m,t_n) -B{\mathscr {D}}_x^0{\mathcal {U}}(x_m,t_n) +D{\mathcal {U}}(x_m,t_n)\\ -\lambda \displaystyle {\int _{x_0}^{x_M}} {\mathcal {U}} (y,t_n)g(y-x_m)\;dy=f(x_m,t_n)+{\mathscr {R}}_{m,n}^{(1)} +{\mathscr {R}}_{m,n}^{(2)}+{\mathscr {R}}_{m,n}^{(3)}\\ \text {for }1\le m\le M-1;\;1\le n\le N, \text { with}\\ {\mathcal {U}}(x_0,t_n)={\tilde{\eta }}(t_n),\;{\mathcal {U}}(x_M,t_n) ={\tilde{\zeta }}(t_n)\;\forall \; 1\le n\le N;\\ {\mathcal {U}}(x_m,t_0)=\tilde{{\mathscr {Q}}}(x_m)\;\forall \; 0\le m\le M, \end{array}\right. \end{aligned}$$

(10)

where ${\mathscr {R}}_{m,n}^{(1)}=(\partial _N^\alpha -\partial _t^\alpha ) {\mathcal {U}}(x_m,t_n)$, ${\mathscr {R}}_{m,n}^{(2)}=A\Big (\dfrac{\partial ^2}{\partial x^2}-\delta _x^2\Big ){\mathcal {U}}(x_m,t_n)$ and ${\mathscr {R}}_{m,n}^{(3)}=B\Big (\dfrac{\partial }{\partial x}-{\mathscr {D}}_x^0\Big ){\mathcal {U}}(x_m,t_n)$. It remains to approximate the Fredholm integral part. The composite trapezoidal rule is used to discretize it. Here, the $n^{\text {th}}$ level solution is approximated by the $(n-1)^{\text {th}}$ level solution, which will produce an error of order $O(N^{-\varrho \alpha })$ based on the choice of a suitable grading parameter $\varrho$, such that $\displaystyle {\max _{n}}~\Delta t_n=O(t_1)$. The error bound is obtained as follows:

$$\begin{aligned} |{\mathcal {U}}(x_n,t_n)-{\mathcal {U}}(x_n,t_{n-1})|&\le \int _{s=t_{n-1}}^{t_n}\Big |\dfrac{\partial {\mathcal {U}}}{\partial s}\Big |~ds\le C\int _{s=t_{n-1}}^{t_n}s^{\alpha -1}~ds\\&\le C\Delta t_n(t_{n-1})^{\alpha -1}\le C\Delta t_n(t_1)^{\alpha -1} = C\Big (\dfrac{\Delta t_n}{t_1}\Big )t_1^{\alpha }\\&\le C \Big [T\Big (\dfrac{1}{N}\Big )^\varrho \Big ]^\alpha =C T^\alpha N^{-\varrho \alpha }\le CN^{-\varrho \alpha }. \end{aligned}$$

Here, in the first inequality, we have used the bounds given in (4). The approximation to the integral operator is then given by:

$$\begin{aligned} \lambda \displaystyle {\int _{x_0}^{x_M}} {\mathcal {U}}&(y,t_n)g(y-x_m)\;dy= \lambda \displaystyle {\int _{x_0}^{x_M}} {\mathcal {U}}(y,t_{n-1}) g(y-x_m)\;dy+{O(N^{-\varrho \alpha })}\\ =&\lambda \displaystyle {\sum _{l=0}^{M-1}\int _{x_l}^{x_{l+1}}} {\mathcal {U}}(y,t_{n-1})g(y-x_m)\;dy+{O(N^{-\varrho \alpha })}\\ =&\dfrac{\lambda \Delta x}{2}\displaystyle {\sum _{l=0}^{M-1}}\Big [{\mathcal {U}}(x_l,t_{n-1}) g(x_l-x_m)+{\mathcal {U}}(x_{l+1},t_{n-1})g(x_{l+1}-x_m)\Big ] +{\mathscr {R}}_{m,n}^{(4)}. \end{aligned}$$

The Taylor series expansion gives the bounds for the remainder term ${\mathscr {R}}_{m,n}^{(4)}$ as:

$$\begin{aligned} \Big \Vert {\mathscr {R}}_{m,n}^{(4)}\Big \Vert \le C ({N^{-\varrho \alpha }}+(\Delta x)^2)~~~~\forall ~0\le m\le M;\;0<n\le N. \end{aligned}$$

(11)

Then, (10) reduces to

$$\begin{aligned} \left\{ \begin{array}{ll} \partial _{N}^{\alpha }{\mathcal {U}}(x_m,t_n)- A\delta _x^2{\mathcal {U}}(x_m,t_n) -B{\mathscr {D}}_x^0{\mathcal {U}}(x_m,t_n)+D{\mathcal {U}}(x_m,t_n) =F(x_m,t_n)+{\mathscr {R}}_{m,n}\\ \text {for }1\le m\le M-1;\;1\le n\le N, \text { with}\\ {\mathcal {U}}(x_0,t_n)={\tilde{\eta }}(t_n),\;{\mathcal {U}}(x_M,t_n) ={\tilde{\zeta }}(t_n)\;\forall \; 1\le n\le N;\\ {\mathcal {U}}(x_m,t_0)=\tilde{{\mathscr {Q}}}(x_m)\;\forall \; 0\le m\le M, \end{array}\right. \end{aligned}$$

(12)

where $F(x_m,t_n)=f(x_m,t_n)+\dfrac{\lambda \Delta x}{2}\displaystyle {\sum _{l=0}^{M-1}}\Big [{\mathcal {U}}(x_l,t_{n-1}) g(x_l-x_m)+{\mathcal {U}}(x_{l+1},t_{n-1})g(x_{l+1}-x_m)\Big ]$ and the remainder term ${\mathscr {R}}_{m,n}$ is given by

$$\begin{aligned} {\mathscr {R}}_{m,n}={\mathscr {R}}_{m,n}^{(1)}+{\mathscr {R}}_{m,n}^{(2)} +{\mathscr {R}}_{m,n}^{(3)}+{\mathscr {R}}_{m,n}^{(4)},~~~0\le m\le M;\;0< n\le N. \end{aligned}$$

(13)

Neglecting ${\mathscr {R}}_{m,n}$, (12) reduces to the following discrete problem:

$$\begin{aligned} \left\{ \begin{array}{ll} \partial _{N}^{\alpha }{\mathcal {U}}_m^n- A\delta _x^2{\mathcal {U}}_m^n -B{\mathscr {D}}_x^0{\mathcal {U}}_m^n +D{\mathcal {U}}_m^n=F(x_m,t_n),~ \text {for }1\le m\le M-1;\;1\le n\le N,\\ {\mathcal {U}}_0^n={\tilde{\eta }}(t_n),\;{\mathcal {U}}_M^n ={\tilde{\zeta }}(t_n)\;\forall \; 1\le n\le N;\\ {\mathcal {U}}_m^0=\tilde{{\mathscr {Q}}}(x_m)\;\forall \; 0\le m\le M. \end{array}\right. \end{aligned}$$

(14)

Using (9), the following implicit scheme is obtained.

$$\begin{aligned} \left\{ \begin{array}{ll} \Big [-\dfrac{A}{(\Delta x)^2}+\dfrac{B}{2\Delta x}\Big ]{\mathcal {U}}_{m-1}^n+\Big [\dfrac{d_{n,1}^{(\alpha )}}{\Gamma (2-\alpha )}+\dfrac{2A}{(\Delta x)^2}+D\Big ]{\mathcal {U}}_m^n+\Big [-\dfrac{A}{(\Delta x)^2}-\dfrac{B}{2\Delta x}\Big ]{\mathcal {U}}_{m+1}^n ={\mathscr {F}}_m^{n-1}\\ \text {for } 1\le m\le M-1;\;1\le n\le N,\\ {\mathcal {U}}_0^n={\tilde{\eta }}(t_n),\;{\mathcal {U}}_M^n ={\tilde{\zeta }}(t_n)\;\forall \; 1\le n\le N;\\ {\mathcal {U}}_m^0=\tilde{{\mathscr {Q}}}(x_m)\;\forall \; 0\le m\le M. \end{array}\right. \end{aligned}$$

(15)

For each $m=1,2,\cdots ,M-1$, ${\mathscr {F}}_m^0=\dfrac{d_{n,n}^{(\alpha )}}{\Gamma (2-\alpha )}\,{\mathcal {U}}_m^0+F(x_m,t_1)$, and for each $n=2,3,\ldots ,N$, we have

$$\begin{aligned} {\mathscr {F}}_m^{n-1}=\dfrac{d_{n,n}^{(\alpha )}}{\Gamma (2-\alpha )} \,{\mathcal {U}}_m^0-\dfrac{1}{\Gamma (2-\alpha )}\displaystyle {\sum _{l=1}^{n-1}}\Big [d_{n,l+1}^{(\alpha )}-d_{n,l}^{(\alpha )}\Big ]{\mathcal {U}}_m^{n-l}+F(x_m,t_n), \end{aligned}$$

$m=1,2,\ldots ,M-1$. The coefficient matrix associated with the discrete operator is tridiagonal. Notice that $A\ge 0,\;D\ge 0$. For stability, the matrix needs to be imposed in correct sign pattern and it is done by making the nonrestrictive assumption that M satisfies $\dfrac{L|B|}{|A|}\le M$.

4 Error Analysis of the Finite Difference Method

The complete error bounds for the numerical solution of (1) obtained by using the proposed FDM given by the discrete scheme (14) is discussed in this section. One can see that the stability multipliers are taken into account to show the convergence results.

4.1 Stability of the Scheme

The discrete scheme (15) can be rewritten as:

$$\begin{aligned} \left\{ \begin{array}{ll} \Big [\dfrac{d_{n,1}^{(\alpha )}}{\Gamma (2-\alpha )}+\dfrac{2A}{(\Delta x)^2}+D\Big ]{\mathcal {U}}_m^n =\Big [\dfrac{A}{(\Delta x)^2}-\dfrac{B}{2\Delta x}\Big ]{\mathcal {U}}_{m-1}^n+\Big [\dfrac{A}{(\Delta x)^2}+\dfrac{B}{2\Delta x}\Big ]{\mathcal {U}}_{m+1}^n +\dfrac{d_{n,n}^{(\alpha )}}{\Gamma (2-\alpha )}{\mathcal {U}}_m^0\\ +\dfrac{1}{\Gamma (2-\alpha )}\displaystyle {\sum _{l=1}^{n-1}} \Big [d_{n,l}^{(\alpha )}-d_{n,l+1}^{(\alpha )}\Big ]{\mathcal {U}}_m^{n-l}+F(x_m,t_n)\\ \text {for } 1\le m\le M-1;\;1\le n\le N,\\ {\mathcal {U}}_0^n={\tilde{\eta }}(t_n),\;{\mathcal {U}}_M^n ={\tilde{\zeta }}(t_n)\;\forall \; 1\le n\le N;\\ {\mathcal {U}}_m^0=\tilde{{\mathscr {Q}}}(x_m)\;\forall \; 0\le m\le M. \end{array}\right. \end{aligned}$$

Lemma 2

The solution of the discrete problem (14) satisfies the following inequality:

$$\begin{aligned} \Vert {\mathcal {U}}^n\Vert \le \Delta t_n^\alpha \Big [\Gamma (2-\alpha )\Vert F^n\Vert +d_{n,n}^{(\alpha )}\Vert {\mathcal {U}}^0\Vert +\displaystyle {\sum _{l=1}^{n-1}}\Big [d_{n,l}^{(\alpha )}-d_{n,l+1} ^{(\alpha )}\Big ]\Vert {\mathcal {U}}^{n-l}\Vert \Big ],\; \forall \;1\le n\le N, \end{aligned}$$

Proof

The idea that we have used here is discussed in Stynes et al. (2017). For any fixed $n\in \{1,2,\ldots ,N\}$, choose $m^*$ in such a way that $|{\mathcal {U}}_{m^*}^n|=\Vert {\mathcal {U}}^n\Vert$. Therefore at the mesh point $(x_{m^*},t_n)$, we have

$$\begin{aligned} \Big [\dfrac{d_{n,1}^{(\alpha )}}{\Gamma (2-\alpha )}+\dfrac{2A}{(\Delta x)^2}+D\Big ]{\mathcal {U}}_{m^*}^n =&\Big [\dfrac{A}{(\Delta x)^2}-\dfrac{B}{2\Delta x}\Big ]{\mathcal {U}}_{m^*-1}^n +\Big [\dfrac{A}{(\Delta x)^2}+\dfrac{B}{2\Delta x}\Big ]{\mathcal {U}}_{m^*+1}^n\\&+\dfrac{d_{n,n}^{(\alpha )}}{\Gamma (2-\alpha )}{\mathcal {U}}_{m^*}^0 +\dfrac{1}{\Gamma (2-\alpha )}\displaystyle {\sum _{l=1}^{n-1}} \Big [d_{n,l}^{(\alpha )}-d_{n,l+1}^{(\alpha )}\Big ]{\mathcal {U}}_{m^*}^{n-l}+F_{m^*}^n. \end{aligned}$$

Notice that $D\ge 0$ and the choice of $m^*$ yields

$$\begin{aligned} \Big [\dfrac{d_{n,1}^{(\alpha )}}{\Gamma (2-\alpha )}+\dfrac{2A}{(\Delta x)^2}\Big ]\Vert {\mathcal {U}}^n\Vert \le&\Big [\dfrac{A}{(\Delta x)^2}-\dfrac{B}{2\Delta x}\Big ]\Vert {\mathcal {U}}^n\Vert +\Big [\dfrac{A}{(\Delta x)^2}+\dfrac{B}{2\Delta x}\Vert {\mathcal {U}}^n\Vert \\&+\Bigg |\dfrac{d_{n,n}^{(\alpha )}}{\Gamma (2-\alpha )}{\mathcal {U}}_{m^*}^0 +\dfrac{1}{\Gamma (2-\alpha )}\displaystyle {\sum _{l=1}^{n-1}}\Big [d_{n,l} ^{(\alpha )}-d_{n,l+1}^{(\alpha )}\Big ]{\mathcal {U}}_{m^*}^{n-l}+F_{m^*}^n\Bigg |\\ =\dfrac{2A}{(\Delta x)^2}\Vert {\mathcal {U}}^n\Vert&+\Bigg |\dfrac{d_{n,n}^{(\alpha )}}{\Gamma (2-\alpha )}{\mathcal {U}}_{m^*}^0 +\dfrac{1}{\Gamma (2-\alpha )}\displaystyle {\sum _{l=1}^{n-1}} \Big [d_{n,l}^{(\alpha )}-d_{n,l+1}^{(\alpha )}\Big ]{\mathcal {U}}_{m^*}^{n-l}+F_{m^*}^n\Bigg |, \end{aligned}$$

which is equivalent to

$$\begin{aligned} d_{n,1}^{(\alpha )}\Vert {\mathcal {U}}^n\Vert \le \Bigg |\Gamma (2-\alpha )F_{m^*}^n+d_{n,n}^{(\alpha )} {\mathcal {U}}_{m^*}^0 +\displaystyle {\sum _{l=1}^{n-1}}\Big [d_{n,l}^{(\alpha )} -d_{n,l+1}^{(\alpha )}\Big ]{\mathcal {U}}_{m^*}^{n-l}\Bigg |. \end{aligned}$$

Now, using (8) and dividing both sides by $d_{n,1}^{(\alpha )}$, we obtain

$$\begin{aligned} \Vert {\mathcal {U}}^n\Vert \le \Delta t_n^\alpha \Big [\Gamma (2-\alpha )\Vert F^n\Vert +d_{n,n}^{(\alpha )} \Vert {\mathcal {U}}^0\Vert +\displaystyle {\sum _{l=1}^{n-1}} \Big [d_{n,l}^{(\alpha )}-d_{n,l+1}^{(\alpha )}\Big ]\Vert {\mathcal {U}}^{n-l}\Vert \Big ], \end{aligned}$$

which is the required result. $\square$

Define the stability multipliers $\Lambda _{n,j}$, for $n=1,2,\ldots ,N$; $j=1,2,\ldots ,n-1$ by

$$\begin{aligned} \Lambda _{n,n}=1,\;\Lambda _{n,j} =\sum _{l=1}^{n-j}\Delta t_{n-l}^\alpha \Big [d_{n,l}^{(\alpha )} -d_{n,l+1}^{(\alpha )}\Big ]\Lambda _{n-l,j}. \end{aligned}$$

From (8), it can be observed that $\Lambda _{n,j}\ge 0\;\forall \; n,j$. The following lemma reveals a more general stability result in terms of stability multipliers.

Lemma 4.2

For each $n=1,2,\ldots ,N$, one has

$$\begin{aligned} \Vert {\mathcal {U}}^n\Vert \le \Vert {\mathcal {U}}^0\Vert + \Delta t_n^\alpha \Gamma (2-\alpha )\displaystyle {\sum _{j=1}^n}\Lambda _{n,j}\Vert F^j\Vert . \end{aligned}$$

Proof

The proof of this lemma is available in Stynes et al. (2017). $\square$

4.2 Convergence of the Scheme

To show the convergence of the scheme, first we calculate the truncation error bounds for $\partial _N^\alpha ,\delta _x^2,{\mathscr {D}}_x^0$ for each $(x_m,t_n)$. Then using the stability results, the complete error bounds for the numerical solution obtained by the proposed FDM are established.

Lemma 4.3

Let the solution of (1) satisfies (4). Then the remainder term ${\mathscr {R}}_{m,n}^{(1)}$ satisfies the following inequality:

$$\begin{aligned} \Big \Vert {\mathscr {R}}_{m,n}^{(1)}\Big \Vert \le Cn^{-\min \{\varrho \alpha ,~ 2-\alpha \}}\;\forall ~0\le m\le M;\;0< n\le N. \end{aligned}$$

Proof

It can be obtained in a similar way as was done in Huang et al. (2020). $\square$

Lemma 4.4

For the discrete operators $\delta _x^2$ and ${\mathscr {D}}_x^0$ for all, one has

$$\begin{aligned} \Big \Vert {\mathscr {R}}_{m,n}^{(2)}\Big \Vert \le C(\Delta x)^2; ~~\Big \Vert {\mathscr {R}}_{m,n}^{(3)}\Big \Vert \le C(\Delta x)^2\;\;\forall (x_m,t_n)\in [-L,L]\times (0,T]. \end{aligned}$$

Proof

Using Taylor series expansion, one can easily prove the above inequalities. $\square$

Denote $\Vert {\mathscr {E}}_m^n\Vert =\Vert {\mathcal {U}}(x_m,t_n)-{\mathcal {U}}_m^n\Vert$ as the maximum errors at each $(x_m,t_n)$. The error equation can be obtained by subtracting (14) from (12) as follows:

$$\begin{aligned} \left\{ \begin{array}{ll} \partial _{N}^{\alpha }{\mathscr {E}}_m^n-A\delta _x^2{\mathscr {E}}_m^n -B{\mathscr {D}}_x^0{\mathscr {E}}_m^n +D{\mathscr {E}}_m^n={\mathscr {R}}_{m,n},~ 1\le m\le M-1,\;1\le n\le N,\\ {\mathscr {E}}_0^n={\mathscr {E}}_M^n=0\;\forall \; 0< n\le N;\\ {\mathscr {E}}_m^0=0\;\forall \; 0\le m\le M. \end{array}\right. \end{aligned}$$

(16)

Theorem 4.5

If $\{{\mathcal {U}}(x_m,t_n)\}_{m,n=0}^{M,N}$ and $\{{\mathcal {U}}_m^n\}_{m,n=0}^{M,N}$ denote the exact solution and the computed solution of (3) by using the scheme (14), then for each $(x_m,t_n)\in [-L,L]\times (0,T]$, one has the following error bounds:

$$\begin{aligned} \Big \Vert {\mathscr {E}}_m^n\Big \Vert \le CT^{\alpha }\Big [N^{-\min \{\varrho \alpha ,~2-\alpha \}}+(\Delta x)^2\Big ]. \end{aligned}$$

Proof

According to Lemma 4.2, the solution of the discrete problem (16) satisfies

$$\begin{aligned} \Big \Vert {\mathscr {E}}_m^n\Big \Vert \le \Big \Vert {\mathscr {E}}_m^0\Big \Vert + \Delta t_n^\alpha \Gamma (2-\alpha )\displaystyle {\sum _{j=1}^n} \Lambda _{n,j}\Big \Vert {\mathscr {R}}_{m,j}\Big \Vert . \end{aligned}$$

Notice that ${\mathscr {R}}_{m,j}={\mathscr {R}}_{m,j}^{(1)}+{\mathscr {R}}_{m,j}^{(2)} +{\mathscr {R}}_{m,j}^{(3)}+{\mathscr {R}}_{m,j}^{(4)}$. Using triangle inequality and then, applying Lemmas 4.3, 4.4, and error bounds displayed in (11), we have

$$\begin{aligned} \Big \Vert {\mathscr {E}}_m^n\Big \Vert \le&\Gamma (2-\alpha )\Bigg [\Delta t_n^\alpha \displaystyle {\sum _{j=1}^n}\Lambda _{n,j}\Big \Vert {\mathscr {R}}_{m,j}^{(1)}\Big \Vert + \Delta t_n^\alpha \displaystyle {\sum _{j=1}^n}\Lambda _{n,j}\Big \Vert {\mathscr {R}}_{m,j}^{(2)}\Big \Vert + \Delta t_n^\alpha \displaystyle {\sum _{j=1}^n}\Lambda _{n,j}\Big \Vert {\mathscr {R}}_{m,j}^{(3)}\Big \Vert \\&+ \Delta t_n^\alpha \displaystyle {\sum _{j=1}^n}\Lambda _{n,j}\Big \Vert {\mathscr {R}}_{m,j}^{(4)}\Big \Vert \Bigg ]\\ \le&C\Gamma (2-\alpha )\Bigg [\Delta t_n^\alpha \displaystyle {\sum _{j=1}^n}\Lambda _{n,j}j^{-\min \{\varrho \alpha ,~2-\alpha \}}+ \Delta t_n^\alpha \displaystyle {\sum _{j=1}^n}\Lambda _{n,j}(\Delta x)^2+ \Delta t_n^\alpha \displaystyle {\sum _{j=1}^n}\Lambda _{n,j}(\Delta x)^2\\&+{ \Delta t_n^\alpha \displaystyle {\sum _{j=1}^n}\Lambda _{n,j}N^{-\varrho \alpha }}+ \Delta t_n^\alpha \displaystyle {\sum _{j=1}^n}\Lambda _{n,j}(\Delta x)^2\Bigg ]. \end{aligned}$$

If a parameter $\gamma$ be such that $\gamma \le \varrho \alpha$, then one has $\Delta t_n^\alpha \displaystyle {\sum _{j=1}^n}j^{-\gamma }\Lambda _{n,j}\le \dfrac{T^{\alpha }N^{-\gamma }}{1-\alpha },~n=1,2,\ldots ,N$. For more details, one may refer ((Stynes et al., 2017)). Now, using this result to the above inequality with $\gamma =\min \{\varrho \alpha ,~2-\alpha \}$ for the first term and $\gamma =0$ for the remaining terms, we obtain

$$\begin{aligned} \Big \Vert {\mathscr {E}}_m^n\Big \Vert&\le C\Gamma (2-\alpha )\Bigg [\dfrac{T^\alpha N^{-\min \{\varrho \alpha ,~2-\alpha \}}}{1-\alpha }+ \dfrac{T^\alpha (\Delta x)^2}{1-\alpha }+ \dfrac{T^\alpha (\Delta x)^2}{1-\alpha } +{\dfrac{T^\alpha N^{-\varrho \alpha }}{1-\alpha }}+ \dfrac{T^\alpha (\Delta x)^2}{1-\alpha }\Bigg ]\\&\le CT^{\alpha }\Big [N^{-\min \{\varrho \alpha ,~2-\alpha \}}+(\Delta x)^2\Big ], \end{aligned}$$

which is the desired bound. $\square$

Remark 4.6

If $\varrho \ge (2-\alpha )/\alpha$, the above error bounds can be rewritten as:

$$\begin{aligned} \Big \Vert {\mathscr {E}}_m^n\Big \Vert \le CT^{\alpha }\Big [N^{-(2-\alpha )}+(\Delta x)^2\Big ]. \end{aligned}$$

5 Results and Discussion

Several tests are performed on TFBS equations under Merton’s jump diffusion model as well as Kou’s jump diffusion model. The graphical representation of the numerical solutions obtained by both the techniques FDM and ADM are shown. Further, the solution obtained by FDM is compared with the solution obtained by ADM. The numerical data was obtained using the mathematical software MATLAB R2015a, which was also used to get the graphical representations.

5.1 Experiments on Merton’s Model

Example 5.1

Consider the following TFBS equation under Merton’s jump-diffusion model governing a European call option:

$$\begin{aligned} \left\{ \begin{array}{ll} \partial _{\tau }^{\alpha }{\mathscr {W}}(S,\tau ) +\dfrac{1}{2}\sigma ^2S^2\dfrac{\partial ^2{\mathscr {W}}(S,\tau )}{\partial S^2} +(r-\lambda k)S\dfrac{\partial {\mathscr {W}}(S,\tau )}{\partial S}\\ -(r+\lambda ){\mathscr {W}}(S,\tau )+\lambda \displaystyle {\int _{0.1}^{200}} {\mathscr {W}}(S\xi ,\tau ){\mathscr {G}}(\xi )\;d\xi =0,\\ (S,\tau )\in [0.1,200]\times (0,T], \text { with}\\ {\mathscr {W}}(0.1,\tau )=0,\;{\mathscr {W}}(200,\tau ) =200-Ke^{-r(T-\tau )}~\forall ~ \tau \in (0,T],\\ {\mathscr {W}}(S,T)=\max \{S-K,0\}~\forall ~ S\in [0.1,200]. \end{array}\right. \end{aligned}$$

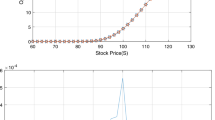
Here, $\alpha \in (0,1)$ and the parameters are given by: $\sigma =0.15,r=0.05,\lambda =0.10,\sigma _J=0.45$ and $\mu _J=-0.90$. $T=0.25$ (year) and the strike price $K=100$. Further, k is defined as: $k=\exp \Big (\mu _J+\dfrac{\sigma _J^2}{2}\Big )-1$. The surface plot displayed in Fig. 1a represents the numerical solution obtained by the proposed FDM with $\alpha =0.4,\varrho =(2-\alpha )/2\alpha$ and $M=N=30$. The solution obtained by ADM with ${\mathscr {N}}=3$ is plotted in Fig. 1b. The curves represented in Fig. 2 show the European call option prices with different values of $\alpha$ at $t=0.25$ for Example 5.1. The presence of the fractional differential operator in the model has a keen impact on the profile of the option price. It can be noticed that the option value decreases as $\alpha$ increases when the stock price is greater than the strike price.

Example 5.2

Let $\alpha \in (0,1)$. Consider another TFBS equation which describes a European put option under Merton’s jump-diffusion model.

$$\begin{aligned} \left\{ \begin{array}{ll} \partial _{\tau }^{\alpha }{\mathscr {W}}(S,\tau ) +\dfrac{1}{2}\sigma ^2S^2\dfrac{\partial ^2{\mathscr {W}}(S,\tau )}{\partial S^2} +(r-\lambda k)S\dfrac{\partial {\mathscr {W}}(S,\tau )}{\partial S}\\ -(r+\lambda ){\mathscr {W}}(S,\tau )+\lambda \displaystyle {\int _{0.1}^{200}} {\mathscr {W}}(S\xi ,\tau ){\mathscr {G}}(\xi )\;d\xi =0,\\ (S,\tau )\in [0.1,200]\times (0,T], \text { with}\\ {\mathscr {W}}(0.1,\tau )=Ke^{-r(T-\tau )},\;{\mathscr {W}}(200,\tau )=0~\forall ~ \tau \in (0,T],\\ {\mathscr {W}}(S,T)=\max \{K-S,0\}~\forall ~ S\in [0.1,200], \end{array}\right. \end{aligned}$$

where $\sigma =0.30,r=0.05,\lambda =1,\sigma _J=0.5$ and $\mu _J=-0.90$. $T=0.50$ (year) and the strike price $K=100$. Further, $k=\exp \Big (\mu _J+\dfrac{\sigma _J^2}{2}\Big )-1$. The numerical solution of the European put option price is shown in Fig. 3a with $\alpha =0.3,\varrho =(2-\alpha )2\alpha$ and $M=N=30$ by FDM whereas, Fig. 3b displays the approximate solution by ADM with ${\mathscr {N}}=3$. The cross section view is shown in Fig. 4 and it represents the put option value at $t=0.5$. One can observe that the price value increases as $\alpha$ increases when the stock price is less that the strike price.

5.2 Experiments on Kou’s Model

Example 5.3

Consider the following TFBS equation under Kou’s jump-diffusion model governing a European call option:

$$\begin{aligned} \left\{ \begin{array}{ll} \partial _{\tau }^{\alpha }{\mathscr {W}}(S,\tau ) +\dfrac{1}{2}\sigma ^2S^2\dfrac{\partial ^2{\mathscr {W}}(S,\tau )}{\partial S^2} +(r-\lambda k)S\dfrac{\partial {\mathscr {W}}(S,\tau )}{\partial S}\\ -(r+\lambda ){\mathscr {W}}(S,\tau )+\lambda \displaystyle {\int _{3}^{50}} {\mathscr {W}}(S\xi ,\tau ){\mathscr {G}}(\xi )\;d\xi =0,\\ (S,\tau )\in [3,50]\times (0,T], \text { with}\\ {\mathscr {W}}(3,\tau )=0,\;{\mathscr {W}}(50,\tau )=50-Ke^{-r(T-\tau )}~\forall ~ \tau \in (0,T],\\ {\mathscr {W}}(S,T)=\max \{S-K,0\}~\forall ~ S\in [3,50]. \end{array}\right. \end{aligned}$$

Here, $\alpha \in (0,1)$ and the parameters are given by: $\sigma =0.15,r=0.05,\lambda =0.10,\xi _1=3.0465,\xi _2=3.0775$ and $p=0.3445$. $T=0.25$ (year) and the strike price $K=30$. For Kou’s model, k is defined as: $k=\dfrac{p\xi _1}{\xi _1-1}+\dfrac{(1-p)\xi _2}{\xi _1+1}-1$. Here, we apply FDM as well as ADM for the numerical solution of Example 5.3 and it’s graphical representation is shown in Fig. 5 with $\alpha =0.5$. The comparison of European call option price in displayed in Fig. 6 for $\alpha =0.25,0.45,0.65,0.85$. The value of $\alpha$ influences the value of the option price.

Example 5.4

Let $\alpha \in (0,1)$. Consider another TFBS equation which describes a European put option under Kou’s jump-diffusion model.

$$\begin{aligned} \left\{ \begin{array}{ll} \partial _{\tau }^{\alpha }{\mathscr {W}}(S,\tau ) +\dfrac{1}{2}\sigma ^2S^2\dfrac{\partial ^2{\mathscr {W}}(S,\tau )}{\partial S^2} +(r-\lambda k)S\dfrac{\partial {\mathscr {W}}(S,\tau )}{\partial S}\\ -(r+\lambda ){\mathscr {W}}(S,\tau )+\lambda \displaystyle {\int _{3}^{50}} {\mathscr {W}}(S\xi ,\tau ){\mathscr {G}}(\xi )\;d\xi =0,\\ (S,\tau )\in [3,50]\times (0,T], \text { with}\\ {\mathscr {W}}(3,\tau )=(K-3)e^{-r(T-\tau )},\;{\mathscr {W}}(50,\tau ) =0~\forall ~ \tau \in (0,T],\\ {\mathscr {W}}(S,T)=\max \{K-S,0\}~\forall ~ S\in [3,50]. \end{array}\right. \end{aligned}$$

Here, the parameters are given by: $\sigma =0.25,r=0.05,\lambda =0.10,\xi _1=3.0465,\xi _2=3.0775$ and $p=0.3445$. $T=1$ (year) and the strike price $K=30$. Further, $k=\dfrac{p\xi _1}{\xi _1-1}+\dfrac{(1-p)\xi _2}{\xi _1+1}-1$. The numerical solutions corresponding to the European put option price are displayed in Fig. 7a (FDM with $M=N=30$) and Fig. 7b (ADM with ${\mathscr {N}}=3$) with $\alpha =0.2$ for Example 5.4. Figure 8 represents the European put option value under Kou’s jump-diffusion model for different $\alpha =0.35,0.55,0.75,0.95$ on the stock price domain $S\in [3,50]$. The value of $\alpha$ apparently influences on the option price.

The following example we consider here is a generalized version of the TFBS equation under Merton’s jump-diffusion model with known exact solution to validate the theoretical analysis.

Example 5.5

Let $\alpha \in (0,1)$. Consider the following TFBS equation under Merton’s jump-diffusion model as:

$$\begin{aligned} \left\{ \begin{array}{ll} \partial _{t}^{\alpha }{\mathcal {U}}(x,t)= A\dfrac{\partial ^2{\mathcal {U}}(x,t)}{\partial x^2} +B\dfrac{\partial {\mathcal {U}}(x,t)}{\partial x} -D{\mathcal {U}}(x,t)+\lambda \displaystyle {\int _{-1}^1} {\mathcal {U}}(y,t)g(y-x)\;dy+f(x,t),\\ (x,t)\in [-1,1]\times (0,1], \text { with}\\ {\mathcal {U}}(-1,t)={\mathcal {U}}(1,t)=t^\alpha e^{1/2\sigma _J^2}\;\forall t\in (0,1];\\ {\mathcal {U}}(x,0)=0\;\forall x\in [-1,1], \end{array}\right. \end{aligned}$$

where the parameters are given by: $\sigma =0.1,r=0.05,\lambda =0.01,\sigma _J=0.5$ and $\mu _J=0$. Then, $A=\sigma ^2/2,B=r-A-\lambda k$ and $D=r+\lambda$. k is defined as: $k=\exp \Big (\mu _J+\dfrac{\sigma _J^2}{2}\Big )-1$. Here, f(x, t) is chosen in such a way that the exact solution of Example 5.5 be ${\mathcal {U}}(x,t)=t^\alpha e^{x^2/2\sigma _J^2}$. If $\{{\mathcal {U}}(x_m,t_n)\}_{m=0,n=0}^{M,N}$ and $\{{\mathcal {U}}_m^n\}_{m=0,n=0}^{M,N}$ be the exact and the corresponding numerical solution obtained by using FDM, then the maximum error and the rate of convergence are estimated by the following formula:

$$\begin{aligned} {\mathscr {E}}^{M,N}=\max _{(x_m,t_n)\in {\bar{\Omega }}} \Big |{\mathcal {U}}(x_m,t_n)-{\mathcal {U}}_m^n\Big |,~{\mathscr {P}}^{M,N}=\log _2\Big (\dfrac{{\mathscr {E}} ^{M,N}}{{\mathscr {E}}^{2M,2N}}\Big ). \end{aligned}$$

If ${\mathscr {U}}_{{\mathscr {N}}}=\displaystyle {\sum _{j=0}^{{\mathscr {N}}-1}}{\mathcal {U}}_j(x,t)$ denotes the ${\mathscr {N}}$ term approximate solution by ADM, then the absolute error is computed as: ${\mathscr {E}}_{{\mathscr {N}}}=\Big |{\mathcal {U}}(x,t) -{\mathscr {U}}_{{\mathscr {N}}}(x,t)\Big |, ~(x,t)\in {\bar{\Omega }}$.

The surface displayed in Fig. 9a shows the analytical solution with $\alpha =0.3,\varrho =(2-\alpha )/2\alpha$ and $M=N=32$ for Example 5.5. With same parameters, the solution obtained by FDM is shown in Fig. 9b. Similarly, for $\alpha =0.6$, the analytical and the corresponding approximate solution obtained by ADM are shown in Fig. 10a and b respectively with ${\mathscr {N}}=2$. The maximum error is shown in graphical representation (see Fig. 11) with $\varrho =2(2-\alpha )/\alpha , (2-\alpha )/\alpha$ for different values of $\alpha$. One can see that for a fixed $\alpha$, the error represented by the curve decreases for increasing values of M, N. This proves the convergence of the finite difference scheme. The log-log plots of the errors and the error bounds are shown in Fig. 12 for different values of $\alpha$. Table 1 indicates ${\mathscr {E}}^{M,N}$ and ${\mathscr {P}}^{M,N}$ with fixed $\alpha =0.4$ and varying M, N for different grading parameters. It can be observed that if we consider the uniform mesh ($\varrho =1$), we are getting $\alpha =0.4$ rate of convergence whereas for $\varrho =(2-\alpha )/2\alpha$, the scheme gives $(2-\alpha )/2=0.8$ rate of convergence. Similarly, for $\varrho =(2-\alpha )/\alpha ,2(2-\alpha )/\alpha$, it produces $2-\alpha =1.6$ rate of convergence. Therefore, we are getting higher rate of convergence on graded mesh compared to the uniform mesh and the optimal rate of convergence is obtained by making $\varrho \ge (2-\alpha )/\alpha$ which is same as we obtained theoretically (see Theorem 4.5 and Remark 4.6). Similar arguments can be explained for Table 2 with $\alpha =0.6$ and Table 3 with $\alpha =0.8$ respectively. Finally, we compare the absolute errors obtained by ADM with FDM in Table 4 for $\alpha =0.3,0.5,0.7$.

6 Concluding Remarks

In this work, a fully discrete finite difference scheme is constructed on a nonuniform mesh to solve a time fractional Black-Scholes equation under jump-diffusion model. The L1 discretization is used on a time graded mesh to discretize the temporal derivative whereas the spatial derivatives are approximated by second order central difference schemes in which the spatial direction is discretized uniformly. The error analysis is carried out and it is proved that the nonuniform mesh is more effective than uniform mesh to solve such model. A rigorous analysis proves that the optimal rate of convergence is obtained for a suitable choice of the grading parameter. Further, a analytical approximate solution is presented with the help of Adomian decomposition method. Several experiments are done on the Merton’s jump-diffusion model as well as the Kou’s jump-diffusion model. The solution obtained by both FDM and ADM are presented graphically and it can be observed that the numerical solution is well agreement with the exact solution. Also, it is noticed that the presence of the fractional derivative in the model has a keen impact on the value of the option price. Computed error and the rate of convergence are shown in shape of tables which demonstrate the accuracy of the theoretical findings.

Fig. 1

Surfaces represent numerical solutions for Example 5.1 with $\alpha =0.4, M=N=30$

Fig. 2

European call option price for Example 5.1

Fig. 3

Surfaces represent numerical solutions for Example 5.2 with $\alpha =0.3, M=N=30$

Fig. 4

European put option price for Example 5.2

Fig. 5

Surfaces represent numerical solutions for Example 5.3 with $\alpha =0.5, M=N=30$

Fig. 6

European call option price for Example 5.3

Fig. 7

Surfaces represent numerical solutions for Example 5.4 with $\alpha =0.2, M=N=30$

Fig. 8

European put option price for Example 5.4

Fig. 9

Analytical and numerical solutions for Example 5.5 with $\alpha =0.3, M=N=32$

Fig. 10

Analytical and numerical solutions for Example 5.5 with $\alpha =0.6, M=N=32$

Fig. 11

Maximum errors for Example 5.5

Fig. 12

Log-log plots for Example 5.5 with $\varrho =2(2-\alpha )/\alpha$

Table 1 ${\mathscr {E}}^{M,N}$ and ${\mathscr {P}}^{M,N}$ for Example 5.5 with $\alpha =0.4$

Table 2 ${\mathscr {E}}^{M,N}$ and ${\mathscr {P}}^{M,N}$ for Example 5.5 with $\alpha =0.6$

Table 3 ${\mathscr {E}}^{M,N}$ and ${\mathscr {P}}^{M,N}$ for Example 5.5 with $\alpha =0.8$

Table 4 Absolute errors obtained by ADM and FDM for Example 5.5