Introduction

The Black–Scholes model (BSM) is a mathematical equation for pricing and options treaty. In special, the model computes the transformation over time of financial mechanisms (such as stocks or futures). It presumes that they will have a lognormal distribution of prices. Using this presumption and factoring in other great variables, the model concludes the value of a call option. In 1973, pricing options have experienced a lot of consideration that the first time Black and Scholes [1] and Merton [2] proposed BSM for them. Although this model is very favorite, it has some deficiencies like lacking the “volatility smile”[3] in the actual marketplaces. A strong tool for generalization of this model is the use of fractional derivatives and integrals due to its non-local nature [4]. The concept and applications of fractional calculus have greatly expanded over the nineteenth and twentieth centuries, and numerous authors have provided descriptions for fractional derivatives. One of the most popular fractional derivatives is the left and right Caputo derivative of any arbitrary order, real or complex, which is defined as

$$\begin{aligned} \begin{aligned}&{}_{a}{\mathcal {D}}_{t}^{\alpha }u(x, t)=\\&\frac{1}{\Gamma (n-\alpha )}\int _{a}^{t}{(t-\tau )^{n-\alpha -1}}\frac{{\partial }^{n} u(x, \tau ) }{\partial {\tau }^{n}}d\tau , ~~n-1<\alpha<n, \\&{}_{t}{\mathcal {D}}_{b}^{\alpha }u(x, t)=\\&\frac{(-1)^{n}}{\Gamma (n-\alpha )}\int _{t}^{b}{(\tau -t)^{n-\alpha -1}}\frac{{\partial }^{n} u(x, \tau ) }{\partial {\tau }^{n}}d\tau , ~~n-1<\alpha <n, \end{aligned} \end{aligned}$$

respectively. In addition, taking \(\alpha \rightarrow n\), leads to \(\lim \limits _{\alpha \rightarrow n}{}_{a}{\mathcal {D}}_{t}^{\alpha }u(x, t)=\frac{{\partial }^{n} u(x, t) }{\partial {t}^{n}}\) and \(\lim \limits _{\alpha \rightarrow n}{}_{t}{\mathcal {D}}_{b}^{\alpha }u(x, t)=\frac{{\partial }^{n} u(x, t) }{\partial {t}^{n}}\). There are many ways to solve fractional differential equations such as finite difference methods [5, 6], finite element methods [7], finite volume methods [8], spectral methods [9, 10], and meshless methods [11]. In recently, many authors applied the various methods for solving these equations [12,13,14].

The detection of the fractional form of the stochastic process led to the discovery of fractional calculus into financial theory. In 2000, a time-fractional BSM was presented by Wyss [15] for the first time. In this article, we consider the presented equation by Wyss, which is as follows

$$\begin{aligned} \begin{aligned}&{}_{0}\mathcal {D}_{t} ^{\alpha } u(x,t)=\rho \frac{\partial ^{2}u(x,t)}{\partial x^{2}} +\mu \frac{\partial u(x,t)}{\partial x}-ru(x,t)+f(x,t),\\&0< x< 1,~~~ 0< t \le T,~~~ 0 < \alpha \le 1, \end{aligned} \end{aligned}$$
(1)

with the following initial and boundary conditions

$$\begin{aligned} \begin{aligned}&u(x, 0)=\psi (x),\quad 0<x<1,\\&u(0, t)=\varphi _{0}(t),\quad u(1, t)=\varphi _{1}(t), \quad 0<t\le T, \end{aligned} \end{aligned}$$
(2)

where \(\rho =\frac{1}{2}\sigma ^{2}>0\), \(\mu = r-\rho\) and \(r>0\) are the known constant and f(x, t) is the source term. When \(\rho >0\), \(\mu =0\), \(r\ne 0\) and \(\rho >0\), \(\mu <0\), \(r=0\), the model (1) is a reaction–diffusion and time-fractional advection–diffusion model, respectively.

There is even more method for determining the analytical process as [16,17,18,19]. Because it is difficult to receive an accurate solution, different approaches to estimate them are presented in [20,21,22,23,24,25]. In recent years, a finite-difference schema in second-order accurate and an implicit finite difference model with first-order is used for solving TFBSE-EO in [26] and [27], respectively. In addition, an explicit–implicit numerical method is proposed by Bhowmik In 2014 to solve the partial integrodifferential equation [28] which is the base of the option pricing hypothesis. In [29], Chen evaluated to price American options with using a predictor-corrector. In 2016, Zhang proposed a discrete implicit numerical scheme for pricing American options [30].

The outline of this paper is organized as below: In Sect. 2, by using linear interpolation for the time variable we get the semi-discrete design of the TFBSE-EO. So, we will consider the stability and convergence analysis. In Sect. 3, we apply a Chebyshev collocation method of the second kind for approximating the spatial fractional derivative for obtaining the full scheme. Finally, the fourth section contains two numerical examples to show the efficiency of the method.

The investigated analysis of the temporal-discrete scheme

In this section, we first present some notations and define the functional space with the \(L_{2}\)-norm, \(\Vert u(x)\Vert _{2}=\langle u(x), u(x)\rangle ^{\frac{1}{2}}\), as following that has used in our paper.

$$\begin{aligned} \mathcal {H}^{n}_{\Omega }(\varphi )=\{\varphi \in L^{2}(\Omega ),~~ \frac{\partial ^{\alpha }\varphi }{\partial x^{\alpha }} \in L^{2}(\Omega ),~ \forall ~|\alpha |\le n \}, \end{aligned}$$

where \(L^{2}(\Omega )\) is the space of measurable function with the square of Lebesgue integrable in \(\Omega\).

Lemma 1

(See [31]) The Caputo derivative for \(0<\alpha \le 1\) is discretized by the linear model as

$$\begin{aligned} {}_{0}{\mathcal {D}}_{t}^{\alpha }u(x,t)=\frac{ \delta \tau ^{-\alpha }}{\Gamma (2-\alpha )}\sum _{j=0}^{M}{\lambda }_{M,j}u(x,\tau _{j})+\mathcal {O}({ \delta \tau } ^{2-\alpha }), \end{aligned}$$
(3)

where \(\tau _{j}=j\delta \tau ,~ j=0, 1, \ldots , M\) is time nodes with the step size \(\delta \tau =\frac{T}{M}\) and

$$\begin{aligned} {\lambda }_{M,j}= {\left\{ \begin{array}{ll} 1, &{} j=M, \\ (M-j-1)^{1-\alpha }-2(M-j)^{1-\alpha }+(M-j+1)^{1-\alpha }, &{} 1\le j< M,\\ (M-1)^{1-\alpha }-(M)^{1-\alpha }, &{} j=0. \\ \end{array}\right. } \end{aligned}$$
(4)

Let us that we denote \(u^{j}=u(x,t_{j}), {\overline{\rho }}=\Gamma (2-\alpha )\rho , {\overline{\mu }}=\Gamma (2-\alpha )\mu , {\mathfrak {r}}=r\Gamma (2-\alpha ), F^{M}=\Gamma (2-\alpha )f(x,t_{M})\) and \({{\overline{\lambda }}}_{M,j}=-{\lambda }_{M,j}\), then a semi-discrete scheme of Eq. (1) will be achieved by applying the Lemma 2 as

$$\begin{aligned} (\lambda _{M,M}+{\mathfrak {r}}\delta \tau ^{\alpha })u^{M}-{\overline{\rho }}\delta \tau ^{\alpha }\frac{\partial ^{2}u^{M}}{\partial x^{2}} -{\overline{\mu }}\delta \tau ^{\alpha }\frac{\partial u^{M}}{\partial x} =\sum _{j=0}^{M-1}{{\overline{\lambda }}}_{M,j}u^{j}+\delta \tau ^{\alpha }F^{M}+\delta \tau ^{\alpha }\mathcal {R}^{M}, \end{aligned}$$
(5)

where C is a positive constant such that \(\mathcal {R}^{M}\le C\mathcal {O}({ \delta \tau } ^{2-\alpha })\). After eliminating \(\mathcal {R}^{M}\) in the mentioned relation, the following semi-discrete scheme can be received

$$\begin{aligned} {\left\{ \begin{array}{ll} ({\lambda }_{M,M}+{\mathfrak {r}}\delta \tau ^{\alpha })U^{M}-{\overline{\rho }}\delta \tau ^{\alpha }\frac{\partial ^{2}U^{M}}{\partial x^{2}} -{\overline{\mu }}\delta \tau ^{\alpha }\frac{\partial U^{M}}{\partial x} =\sum \limits _{j=0}^{M-1}{{\overline{\lambda }}}_{M,j}U^{j}+\delta \tau ^{\alpha }F^{M},\\ U^{0}(x)=\psi (x),~~~ 0<x<1,\\ U^{j}(0)=\varphi _{0}(t_{j}),\quad U^{j}(1)=\varphi _{1}(t_{j}),~~~ j=0,1,\ldots ,M, \end{array}\right. } \end{aligned}$$
(6)

where \(U^{j},~~j=0,1,\ldots ,M\) is the approximate solution of Eq. (5).

It is necessary to prove the following lemma to find the convergence order and denote the unconditional stability of the semi-discrete scheme.

Lemma 2

Let \(U^{k}\in \mathcal {H}^{2}_{\Omega }, k=1, 2, \ldots , M\) and \(U^{0}\), be the solution and the initial condition of the semi-discrete (6), respectively, then we have

$$\begin{aligned} \Vert U^{k}\Vert \le C ( \Vert U^{0}\Vert +\max \limits _{0\le l\le M}\Vert F^{l}\Vert ), \end{aligned}$$

where C is a positive value.

Proof

Multiplying relation (6) by \(\upsilon \in \mathcal {H}^{2}_{\Omega }\) and then integrating, we conclude

$$\begin{aligned} ({\lambda }_{M,M}+{\mathfrak {r}}\delta \tau ^{\alpha })\langle U^{M}, \upsilon \rangle -{\overline{\rho }}\delta \tau ^{\alpha }\langle \frac{\partial ^{2}U^{M}}{\partial x^{2}}, \upsilon \rangle -{\overline{\mu }}\delta \tau ^{\alpha }\langle \frac{\partial U^{M}}{\partial x}, \upsilon \rangle =\sum \limits _{j=0}^{M-1}{{\overline{\lambda }}}_{M,j}\langle U^{j}, \upsilon \rangle +\delta \tau ^{\alpha } \langle F^{M}, \upsilon \rangle . \end{aligned}$$
(7)

The second and third terms on the left side of the above relation can be written as \(\langle \frac{\partial ^{2}U^{1}}{\partial x^{2}},U^{1}\rangle =-\langle \frac{\partial U^{1}}{\partial x}\frac{\partial U^{1}}{\partial x}\rangle\), \(\langle \frac{\partial U^{1}}{\partial x},U^{1}\rangle =0\), respectively and \({\lambda }_{M,M} =1\). Then, we get

$$\begin{aligned} {\mathfrak {r}}\delta \tau ^{\alpha }\langle U^{M}, \upsilon \rangle \le ({\lambda }_{M,M}+{\mathfrak {r}}\delta \tau ^{\alpha })\langle U^{M}, \upsilon \rangle \le \sum \limits _{j=0}^{M-1}{{\overline{\lambda }}}_{M,j}\langle U^{j}, \upsilon \rangle +\delta \tau ^{\alpha } \langle F^{M}, \upsilon \rangle . \end{aligned}$$
(8)

Now, we apply the mathematical induction on M. For \(M=1\) and denote \(\upsilon =U^{1}\) in Eq. (8), we get

$$\begin{aligned} {\mathfrak {r}}\delta \tau ^{\alpha }\langle U^{1},U^{1}\rangle \le {{\overline{\lambda }}}_{1,0}\langle U^{0},U^{1}\rangle +\delta \tau ^{\alpha }\langle F^{1},U^{1}\rangle . \end{aligned}$$

Handling the Cauchy–Schwarz inequality and \({{\overline{\lambda }}}_{1,0} \le 1\) so that we can write the following relation

$$\begin{aligned} \Vert U^{1}\Vert \le \frac{1}{{\mathfrak {r}}\delta \tau ^{\alpha }}\Vert U^{0}\Vert +\frac{1}{{\mathfrak {r}}}\Vert F^{1}\Vert \le C( \Vert U^{0}\Vert +\max \limits _{0\le l\le M}\Vert F^{l}\Vert ). \end{aligned}$$

Suppose for \(j=1, 2, \ldots , M-1\) the below equation is correct

$$\begin{aligned} \Vert U^{j}\Vert \le C( \Vert U^{0}\Vert +\max \limits _{0\le l\le M}\Vert F^{l}\Vert ). \end{aligned}$$
(9)

By using the relation (9), one can express the above relation as

$$\begin{aligned} {\mathfrak {r}}\delta \tau ^{\alpha }\Vert U^{M}\Vert \le C (\sum \limits _{j=0}^{M-1}{{\overline{\lambda }}}_{M,j} \Vert U^{0}\Vert +\max \limits _{0\le l\le M}\Vert F^{l}\Vert )+\delta \tau ^{\alpha }\Vert F^{M}\Vert . \end{aligned}$$

We know from [13] that \(1<\sum \limits _{j=0}^{M-1}{{\overline{\lambda }}}_{M,j}<2\). Thus, we can conclude

$$\begin{aligned} \Vert U^{M}\Vert \le C ( \Vert U^{0}\Vert +\max \limits _{0\le l\le M}\Vert F^{l}\Vert ). \end{aligned}$$

Therefore, the proof of Lemma 2 is completed. \(\square\)

Theorem 1

The achieved semi-discrete scheme (6) by the linear interpolation of the Lemma 2 is unconditionally stable.

Proof

Suppose the approximation solution and the initial condition of Eq. (6) be \(U^{M}\in \mathcal {H}^{2}_{\Omega }\) and \(U^{0}\), respectively. Then, the error \(\varepsilon ^{j}=u^{j}-U^{j}, ~j=0, 1, \ldots , M\) satisfies as following

$$\begin{aligned}&(1+{\mathfrak {r}}\delta \tau ^{\alpha })\langle \varepsilon ^{M},\varepsilon ^{M}\rangle -{\overline{\rho }}\delta \tau ^{\alpha }\langle \frac{\partial ^{2}\varepsilon ^{M}}{\partial x^{2}},\varepsilon ^{M}\rangle \\&\quad -{\overline{\mu }}\delta \tau ^{\alpha } \langle \frac{\partial \varepsilon ^{M}}{\partial x},\varepsilon ^{M}\rangle =\sum \limits _{j=0}^{M-1}{{\overline{\lambda }}}_{M,j}\langle \varepsilon ^{j},\varepsilon ^{M}\rangle . \end{aligned}$$

Using the Lemma 2 and the above relationship, we get

$$\begin{aligned} \Vert \varepsilon ^{M}\Vert \le C \Vert \varepsilon ^{0}\Vert . \end{aligned}$$

This completes the condition of unconditional stability. \(\square\)

Theorem 2

Suppose \(U^{k}\) and \(u^{k}\) for \(k=1, 2, \ldots , M\) be the approximate solution and the exact of relation (6) and (1), respectively with initial condition \(U^{0}=\psi (x)\). Then, we have the following error evaluation

$$\begin{aligned} \Vert u^{k} -U^{k} \Vert \le C \Vert \mathcal {O}({ \delta \tau ^{2-\alpha }})\Vert , \end{aligned}$$

where C is a positive constant.

Proof

Let \(\varepsilon ^{k}=\vert u^{k} -U^{k}\vert ,~k=1, 2, \ldots , M\) be the error term. We can indeed inscribe the following error equation

$$\begin{aligned}&(1+{\mathfrak {r}}\tau ^{\alpha })\langle \varepsilon ^{k},\varepsilon ^{k}\rangle -{\overline{\rho }}\delta \tau ^{\alpha }\langle \frac{\partial ^{2}\varepsilon ^{k}}{\partial x^{2}},\varepsilon ^{k}\rangle -{\overline{\mu }}\delta \tau ^{\alpha } \langle \frac{\partial \varepsilon ^{k}}{\partial x},\varepsilon ^{k}\rangle \nonumber \\&\quad =\sum \limits _{j=0}^{k-1}{{\overline{\lambda }}}_{k,j}\langle \varepsilon ^{j},\varepsilon ^{k}\rangle +\delta \tau ^{\alpha }\langle \mathcal {R}^{k},\varepsilon ^{k}\rangle , \end{aligned}$$
(10)

where \(\mathcal {R}^{M}\le C\mathcal {O}({ \delta \tau } ^{2-\alpha })\). By considering Lemma 2 and \(\Vert \varepsilon ^{0}\Vert =0\), we get

$$\begin{aligned} {\mathfrak {r}}\delta \tau ^{\alpha }\Vert \varepsilon ^{k}\Vert \le \delta \tau ^{\alpha }\Vert \mathcal {R}^{k}\Vert \Longrightarrow \Vert \varepsilon ^{k}\Vert \le \frac{1}{{\mathfrak {r}}}\Vert \mathcal {R}^{k}\Vert . \end{aligned}$$

Therefore, the theorem is proved. \(\square\)

Approximation in space: the Chebyshev collocation of the second kind

In the current section, we get the full scheme of Eq. (6) by using the shifted Chebyshev polynomials of the second kind \({\mathfrak {u}}_{i}(x), ~i=0,1,\ldots ,N\). The SCPSK is defined by the analytical structure of the Jacobi polynomials i.e. \({\mathfrak {u}}_{i}(x)=(i+1)\left( {\begin{array}{c}i+\frac{1}{2}\\ i\end{array}}\right) ^{-1}P_{i}^{\frac{1}{2},\frac{1}{2}}(2x-1),~i=0,1,\ldots ,N\) in the interval [0, 1] where \(P_{i}^{\frac{1}{2},\frac{1}{2}}(x)\) is the Jacobi polynomial.

The closed-form fractional derivative for the \(\eta -\)order is written as

$$\begin{aligned} \frac{\partial ^{\eta }({\mathfrak {u}}_{i}(x))}{\partial x^{\eta }} =\sum _{k=0}^{i-\lceil \eta \rceil }{\mathbf {N}}_{i, k}^{\eta } \times x^{i-k -\eta },\quad x\in [0, 1],\quad i=0, 1,\ldots , N, \end{aligned}$$
(11)

where \(\lceil \eta \rceil\) is the ceiling of value \(\eta\) and \({\mathbf {N}}_{i, k}^{\eta }\) is determined by

$$\begin{aligned} {\mathbf {N}}_{i, k}^{\eta }=\frac{(-1)^{k}4^{i-k}\Gamma (2i-k+2)\Gamma (i-k+1)}{\Gamma (k+1)\Gamma (2i-2k+2) \Gamma (i-k+1-\eta )}. \end{aligned}$$

It should be stated that \(\frac{\partial ^{\eta }({\mathfrak {u}}_{i}(x))}{\partial x^{\eta }}=0, ~i=0, 1, \ldots , \lceil \eta \rceil -1,~\eta >0\). Therefore, an expansion of \(u(x,t_{j})\) around the space variable is determined only by using the first \(N+1\)-terms of SCPSK in interval [0, 1] as below

$$\begin{aligned} u_{N}(x,t_{j})=\sum _{i=0}^{N}c_{i}^{j}{\mathfrak {u}}_{i}(x),~~j=0, 1, \ldots , M, \end{aligned}$$
(12)

where \(\lbrace c_{i}^{j}\rbrace _{i=0}^{N}\) is the unknown coefficients and define as follows [32]

$$\begin{aligned} c_{i}^{j}=\frac{8}{\pi }\int _{0}^{1}(x-x^{2})^{\frac{1}{2}}u_{N}(x, t_{j}){\mathfrak {u}}_{i}(x)dx. \end{aligned}$$
(13)

By applying the linearity properties of the fractional derivative and substituting Eq. (12) in (11), we get the following relation

$$\begin{aligned} \frac{\partial ^{\eta }(u_{N}(x,t_{j}))}{\partial x^{\eta }}=\sum _{i=\lceil \eta \rceil }^{N}\sum _{k=0}^{i-\eta }c_{i}^{j} {\mathbf {N}}_{i, k}^{\eta } \times x^{i-k -\eta }. \end{aligned}$$
(14)

Substituting Eqs. (12) and (14) in (6) and employing the collocation points \(\lbrace x_{s}\rbrace _{s=1}^{N-1}\) that are the roots of SCPSK \({\mathfrak {u}}_{N-1}(x)\), we achieve

$$\begin{aligned} \begin{aligned}&(\lambda _{j,j}+{\mathfrak {r}}\delta \tau ^{\alpha })\sum _{i=0}^{N}c ^{j}_{i}{\mathfrak {u}}_{i}(x_{s})-\quad {\overline{\rho }}\delta \tau ^{\alpha } \sum _{i=2}^{N}\sum _{k=0}^{i-2}c _{i}^{j}N_{i, k}^{2} x_{s}^{1-k-2 } -\\&{\overline{\mu }}\delta \tau ^{\alpha } \sum _{i=1}^{N}\sum _{k=0}^{i-1}c _{i}^{j} N_{i, k}^{1} x_{s}^{i-k-1}=\sum _{m=0}^{j-1}\sum _{i=0}^{N}{{\overline{\lambda }}}_{j,m}c _{i}^{m}{\mathfrak {u}}_{i}(x_{s})+\delta \tau ^{\alpha }F(x_{s},t_{j}),\\&~~j=1, 2, \ldots , M,~~~~s=0, 1, \ldots , N, \end{aligned} \end{aligned}$$
(15)

where \(c _{i}^{j}\) are the unknown coefficients. The initial solution \(\upsilon _{i}^{0}\) is determined by combining relation \(u(x, 0)=\psi (x)\) in Eq. (2). To determine the boundary conditions, we can substitute Eq. (12) in (2) as below

$$\begin{aligned} \sum _{i=0}^{N}(-1)^{i+2}(i+1)c _{i}^{j}=\varphi _{0}(t_{j}),~~ \sum _{i=0}^{N}(i+1)c_{i}^{j}=\varphi _{1}(t_{j}),~~j=1, 2, \ldots , M. \end{aligned}$$
(16)

The obtained relation at Eq. (15) with the boundary conditions (16) denotes the linear algebraic system in which one can be determined the unknown coefficients \(c_{i}^{i}, i=0, 1, 2, \ldots , N\) in each step of time j.

Numerical investigation

The introduced procedure of the Chebyshev collocation of the second kind in this section has a simple implementation for approaching TFBSE-EO. The numerical results in this section confirmed our claim. We then compare the achieved option prices from our scheme with those of [33] and [25] that our method gives better results. In addition, the accuracy and efficiency of the developed method demonstrated that they are obtained by the relation \(\mathcal {C}_{\mathcal {O}}=\log _{2}(\frac{E_{i+1}}{E_{i}})\) (the computational order is shown by \(\mathcal {C}_{\mathcal {O}}\)) so that \(E_{i+1}\) and \(E_{i}\) are errors matching to mesh size 2M and M, respectively.

Example 1

Consider the TFBSE-EO with the exact solution \(u(x, t)=(t+1)^{2}x^{2}(1-x)\)

$$\begin{aligned} {\left\{ \begin{array}{ll} {}_{0}\mathcal {D}_{t} ^{\alpha } u(x,t)=\rho \frac{\partial ^{2}u(x,t)}{\partial x^{2}} +\mu \frac{\partial u(x,t)}{\partial x}-ru(x,t)+f(x,t),\\ u(x,0)=x^{2}(1-x),~~~ 0<x<1,\\ u(0,t)=u(1,t)=0, \end{array}\right. } \end{aligned}$$

so that \(\sigma =0.25, \rho =\frac{1}{2}{\sigma }^{2}, \mu =r-\rho , r=0.05, \alpha =0.7\) and the source term \(f(x,t)=(\frac{2t^{2-\alpha }}{\Gamma (3-\alpha )}+\frac{2t^{1-\alpha }}{\Gamma (2-\alpha )})x^{2}(1-x)-(t+1)^{2}[\rho (2-6x)+\mu (2x-3x^{2})-rx^{2}(1-x)]\). The boundary conditions are homogeneous. The initial condition obtains with the exact solution.

Table 1 The \(L_{\infty }\) and \(L_{2}\) errors and computational order with \(N =7\) for Example 1 at \(T=1\)
Full size table
Table 2 Comparison of error and order convergence with the methods of [33] and [25] for Example 1 at \(T=1\)
Full size table
Fig. 1
figure 1

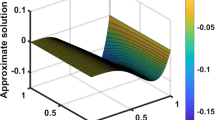
The scheme of the approximate solution (left panel) and absolute error (right panel) of Example 1 at \(T=1\) for \(N=5\) and \(M=400\)

Full size image

The results are demonstrated in Table 1 that hold up the theoretical results proved in Theorem 2, that is, a convergence order in time is \(\mathcal {O}(2-\alpha )\) at \(T=1\) with \(N=7\). In Table 2, we test the presented method for the computation of the European put option with the methods of [33] and [25]. We conclude that our results are better than others with a highly low space size. In Fig. 1, we plot the approximate solution (left panel) and absolute error (right panel) at \(T=1\) for \(N=5\) and \(M=400\).

Example 2

In this example, we consider the following TFBSE-EO with nonhomogeneous boundary conditions

$$\begin{aligned} {\left\{ \begin{array}{ll} {}_{0}\mathcal {D}_{t} ^{\alpha } u(x,t)=\rho \frac{\partial ^{2}u(x,t)}{\partial x^{2}} +\mu \frac{\partial u(x,t)}{\partial x}-ru(x,t)+f(x,t),\\ u(x,0)=x^{3}+x^{2}+1,~~~ 0<x<1,\\ u(0,t)=(t+1)^{2},~~~ u(1,t)=3(t+1)^{2}, \end{array}\right. } \end{aligned}$$

where the dependent parameters can be considered as \(\rho =1, \mu =r-\rho , r=0.5\) and \(\alpha =0.7\). The source term f(x, t) is achieved from the exact solution \(u(x, t)=(t+1)^{2}(x^{3}+x^{2}+1)\).

Table 3 \(L_{\infty }\) and \(L_{2}\) error and the temporal order for Example 2 with \(N=5\) at \(T=1\)
Full size table
Table 4 Comparison of error and order convergence with the methods of [33] and [25] for Example 2 at \(T=1\)
Full size table

The results of this problem are presented in Tables 3, 4. In Table 3, we obtain a convergence order that hold up the theoretical results proved in Theorem 2. In Table 4, we list comparisons between the present method with compact finite difference method [33] and radial basis functions based on finite difference scheme [25] that computational results confirm that our method gives better results.

Conclusion

The TFBSE-EO can be considered as a generalization of the classical Black–Scholes model. Due to the “globality” characteristic of the model’s fractional-order derivative, the numerical solutions of this model are more complicated than the integer-order model. Accordingly, in this article, a numerical model to solve TFBSE-EO is proposed. First, the time discretization via the linear interpolation with the \((2-\alpha )\)-order is described. Then, we explain how to obtain the approximated solution by using the Chebyshev collocation method based on the second kind. In addition, the unconditional stability of the time-discrete model is proved by using the energy method, and also it is shown that the convergence order of the time-discrete is \(\mathcal {O}(\tau ^{2-\alpha })\). To demonstrate the convergence order and precision of the numerical process, we have chosen two numerical examples with exact solutions so that the numerical result has denoted the accuracy of the current model.