Multi-objective generalized normal distribution optimization: a novel algorithm for multi-objective problems

Abstract

This study introduces the Multi-objective Generalized Normal Distribution Optimization (MOGNDO) algorithm, an advancement of the Generalized Normal Distribution Optimization (GNDO) algorithm, now adapted for multi-objective optimization tasks. The GNDO algorithm, previously known for its effectiveness in single-objective optimization, has been enhanced with two key features for multi-objective optimization. The first is the addition of an archival mechanism to store non-dominated Pareto optimal solutions, ensuring a detailed record of the best outcomes. The second enhancement is a new leader selection mechanism, designed to strategically identify and select the best solutions from the archive to guide the optimization process. This enhancement positions MOGNDO as a cutting-edge solution in multi-objective optimization, setting a new benchmark for evaluating its performance against leading algorithms in the field. The algorithm's effectiveness is rigorously tested across 35 varied case studies, encompassing both mathematical and engineering challenges, and benchmarked against prominent algorithms like MOPSO, MOGWO, MOHHO, MSSA, MOALO, MOMVO, and MOAOS. Utilizing metrics such as Generational Distance (GD), Inverted Generational Distance (IGD), and Maximum Spread (MS), the study underscores MOGNDO's ability to produce Pareto fronts of high quality, marked by exceptional precision and diversity. The results affirm MOGNDO's superior performance and versatility, not only in theoretical tests but also in addressing complex real-world engineering problems, showcasing its high convergence and coverage capabilities. The source codes of the MOGNDO algorithm are publicly available at https://nimakhodadadi.com/algorithms-%2B-codes.

1 Introduction

Computers have recently become a primary tool in various areas for tackling challenging problems. Computer-helped design is an area that stresses using computers in determining problems as well as making systems. A system's design process would have necessitated direct human involvement in the past. For example, if a developer intended to locate an optimum form for a high-rise building, s/he would need to initially develop a model and then utilize a wind tunnel to examine it.

Clearly, this design method was expensive and required significant time, with both these elements escalating sharply each year in line with human advancement.

The creation of computers accelerated the design procedure substantially several years back. This indicates that we can utilize computers to make a system without also the demand for a solitary model. Consequently, the design procedure's price and time are considerably less than before. Despite the reality that the device is a fantastic help, making a system still needs straight human participation. This causes a collection of experimentation where the developer attempts to develop an effective strategy. It is indisputable that a developer is prone to errors, which makes the design procedure undependable. The primary duty of a designer entails establishing the framework and utilizing computer software to discover optimal designs.

Optimization methods are widely regarded as practical approaches for determining the best computer designs. Most of the approximate techniques are global search methods, which are called metaheuristics. These methods are developed to alleviate the weaknesses of classical approaches. Metaheuristic algorithms can discover nearly global or global solutions through informed decision-making. Over the past several decades, a wide array of metaheuristic algorithms inspired by natural phenomena, collective behavior, and scientific principles have been proposed, such as Differential Evolution (DE) [1], Ant Colony Optimization (ACO) [2], Particle Swarm Optimization (PSO) [3], Hippopotamus Optimization (HO) [4] algorithm, Mountain Gazelle Optimizer (MGO) [5], Al-Biruni Earth Radius (BER) [6], Puma Optimization (PO) [7] and Stochastic Paint Optimizer (SPO) [8]. Algorithms such as Advanced Charged System Search (ACSS) [9], Chaos Game Optimization (CGO) [10], and Dynamic Arithmetic Optimization Algorithm (DAOA) [11] are called physics- or mathematics-based algorithms, which obey the rules in physics or mathematics. Many researchers utilized these algorithms to solve structural optimization problems such as trusses [12,13,14,15], frames [16,17,18], real structural engineering applications [19,20,21,22,23,24] and applications of medicine [25,26,27]. The research indicates that when applied to complex optimization issues, metaheuristic algorithms have the capability to provide highly accurate solutions within a practical timeframe. Ease of implementation, simple framework, good accuracy, and reasonable execution time are advantages of metaheuristic algorithms compared with the analytical techniques.

Addressing real-world problems presents several challenges that necessitate the use of specific tools. Multi-objectivity is one of the essential characteristics of real-world challenges that makes them difficult to solve. When multiple objectives need to be improved, a challenge is referred to as a multi-objective problem. Obviously, numerous objective optimizers need to be utilized to resolve such issues.

David Schaffer suggested an advanced concept in 1985 [28]. He explained how to use stochastic optimization techniques to solve multi-objective problems. Ever since, remarkably, a considerable variety of investigations have been committed to establishing multi-objective evolutionary/heuristic formulas. The application of stochastic optimization techniques to real-world scenarios has been made more accessible through the utilization of gradient-free methods and strategies that prevent getting trapped in local optima. Multi-objective optimization approaches are being used in various fields these days. Strength–Pareto Evolutionary Algorithm (SPEA) [29], Multi-objective Particle Swarm Optimization (MOPSO) [30], Multi-objective Artificial Vultures Optimization Algorithm (MOAVOA) [31], Multi-objective Evolutionary Algorithm based on Decomposition (MOEA/D) [32], Multi-objective Flower Algorithm (MOFA), Multi-objective Thermal Exchange Optimization (MOTEO) [33], Multi-objective Seagull Optimization Algorithm (MOSOA) [34], Multi-objective Stochastic Paint Optimizer (MOSPO) [35], Pareto–frontier Differential Evolution (PDE) [36], Multi-objective Moth-Flame Optimization (MMFA) [37], Multi-objective Salp Swarm Algorithm (MSSA) [38] and Multi-objective Artificial Hummingbird Algorithm (MOAHA) [39] are multi-objective optimization methods. Many of the single-objective methods that have been developed may also be used to address multi-objective optimization problems. Several of the most current ones are the Multi-objective Ant Lion Optimizer (MOALO) [40], Multi-objective Arithmetic Optimization Algorithm (MAOA) [41], Multi-objective Grey Wolf Optimizer [42], Multi-objective Material Generation Algorithm (MOMGA) [43], Multi-objective Multi-Verse Optimization (MOMVO) [44] and Multi-objective Harris Hawks Optimization (MOHHO) [45].

The generalized normal distribution optimization (GNDO), proposed recently by Zhang et al. [46], is recognized for its proficiency in globally searching optimal solutions to single-objective optimization problems. An initial glance at pertinent research demonstrates that GNDO has successfully resolved complex optimization challenges across numerous fields. The introduction of a novel multi-objective algorithm can be driven by various factors, including:

• I. This multi-objective algorithm provides superior performance compared to existing algorithms. This can be due to the incorporation of new techniques, optimization strategies, and design methodologies. The improved performance can make the algorithm more suitable for real-world applications.

• II. Presenting a new algorithm that has not been explored before can bring new insights into multi-objective optimization. By introducing a novel approach, one can contribute to the advancement of the field and potentially lead to breakthroughs in solving challenging problems.

• III. Multi-objective optimization problems can be diverse, and some may require specialized algorithms that are tailored to their specific requirements.

• IV. By presenting a new algorithm for the first time, one can compare it with state-of-the-art algorithms and demonstrate its superiority. This can help establish the new algorithm's effectiveness and provide a benchmark for future comparisons.

The main motivation for presenting MOGNDO is to create a multi-objective (MO) variant of GNDO, equipping it to tackle multi-objective optimization (MOO) algorithm issues. The authors have leveraged the CEC'20 test suite to gauge MOGNDO's performance. The concept proposed in the No Free Lunch (NFL) theory [47] influenced the development of a multi-objective variant of the existing single-objective GNDO method. To sum up, this paper offers the following contributions:

• The MOGNDO algorithm was formulated as a multi-objective adaptation of the GNDO algorithm, leveraging its benefits. The effectiveness of MOGNDO was measured against seven cutting-edge multi-objective optimization (MOO) algorithms using 35 mathematical benchmarks, encompassing CEC09, ZDT, DTLZ, and CEC2020.

• Five indicators were used to demonstrate MOGNDO's strength and robustness.

• In order to differentiate the proposed MOGNDO algorithm from other selected algorithms, a statistical test was conducted.

• The application of MOGNDO to optimize engineering problems further illustrated its credibility in solving real-world problems.

• Visual representations of the Pareto sets and Pareto fronts obtained by MOGNDO were also provided.

• The proposed MOGNDO algorithm was found to be superior in both qualitative and quantitative analyses.

• The MOGNDO algorithm was evaluated against other cutting-edge algorithms across multiple optimization problems, using diverse performance indicators.

According to the NFL [47] theorem, no optimization algorithm can solve all optimization issues, allowing scientists to propose new or improve existing algorithms to solve optimization challenges. This assertion holds valid for both single and multi-objective optimization methodologies. This theorem establishes that excellent results achieved by an optimizer on one set of problems do not assure equivalent outcomes on a different set of problems. This principle underlies numerous studies in the field, enabling researchers to modify existing methods for novel problem classes or develop new optimization algorithms. It also serves as both the basis and the inspiration for this study. This research introduces a multi-objective version of the recently suggested GNDO [46], capable of addressing optimization issues for diverse applications. As per the NFL theorem, current algorithms documented can address a wide range of problems, but they are only universal solutions to some optimization challenges. This research promotes the use of multi-objective GNDO to tackle emerging complexities. The processes utilized resemble those employed by MOGWO [42], yet the exploration and exploitation stages of MOGNDO are inherited from the GNDO algorithm.

The paper's remainder is prepared as follows: Sect. 2 explains the terminologies of MOO problems and their standard interpretations. Section 3 provides the standard version of GNDO as well as suggests the MOGNDO algorithm. Section 4 describes the outcomes, discussions, and evaluation of the test and the engineering problems utilized. As the last point, Sect. 5 gives the final thoughts on the work and also the future.

The methodologies employed bear similarity to those used by MOGWO [42], but the discovery and utilization phases of MOGNDO are taken from the GNDO algorithm. Here are some of the advantages that come with adopting this approach:

• The GNDO algorithm has been modified to include an archive to ensure that non-dominated solutions are recovered.

• It has been decided to include a grid mechanism in the GNDO to improve the non-dominated solutions currently in the archive.

• It has really been advised that a leader selection method be implemented based on the current best position of the population.

2 A study of the literature

Addressing single-objective optimization problems typically presents a more straightforward endeavor as compared to multi-objective optimization problems, owing primarily to the existence of a singular, unique solution governed by one objective function. This singularity in objective paves the way for a more facile process of comparing solutions and ascertaining the absolute optimal solution in single-objective contexts. Conversely, multi-objective optimization problems are characterized by a plurality of solutions, adding layers of complexity to the solution evaluation process [48, 49]. The following is an illustration of a MOO that can be formulated as a problem of minimization [50]:

$$Maximization:\quad {\text{F}}(\vec{x}) = \left\{ {f_1 \left( {\vec{x}} \right),{ }f_2 \left( {\vec{x}} \right),{ } \ldots ,f_z \left( {\vec{x}} \right)} \right\}$$

(1)

$$Subject\;to:{ }\quad g_i \left( {\vec{x}} \right) \ge 0\quad i = 1,2, \ldots ,{\text{Q}}$$

(2)

$$\quad \quad \quad \quad \quad h_i \left( {\vec{x}} \right) = 0\quad i = 1,2, \ldots ,P$$

(3)

$$\quad \quad \quad \quad \quad L_i \le x_i \le U_i \quad i = 1,2, \ldots ,{ }D$$

(4)

Here, the number of inequality constraints, equality constraints, variables, and objective functions are denoted by $Q, P, D$, and $Z$, respectively. The lower and upper limits of the $i$th variable are represented by $L_i$ and $U_i$.

First Definition:

Pareto dominance.$\vec{x}$ and $\vec{y}{ }$ are two solutions with cost functions as:

$$\vec{x} = (x_1 ,{ }x_2 , \ldots ,{ }x_k )\;{\text{and}}\;\vec{y} = (y_1 ,{ }y_2 , \ldots ,{ }y_k ).$$

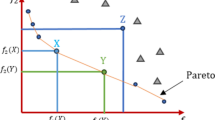
Referring to Fig. 1 and considering a minimization problem, it is stated that solution $\vec{x}$ dominates solution $\vec{y}$ ($noted{ }as{ }\vec{x} \prec \vec{y}$) only if none of $\overrightarrow {y }$'s cost components are less than the equivalent cost components of $\vec{x}$, and at least one component of $\vec{x}$ must be smaller than that of $\vec{y}$. This can be formally represented as follows:

$${ }\forall i \in \left\{ {1,2, \ldots ,{ }k} \right\}:\quad { }f_i \left( {\vec{x}} \right) \le f_i ({ }\vec{y}){ } \wedge \exists i \in \left\{ {1,2, \ldots ,k} \right\}:\quad { }f_i \left( {\vec{x}} \right) \le f_i ({ }\vec{y}){ }$$

(5)

Fig. 1

Pareto dominance

The concept of Pareto optimality is based on the definition of Pareto dominance [51]:

Second Definition:

Pareto optimality. A solution $\vec{x}{ } \in X$ is called Pareto-optimal if and only if:

$${\rm{\nexists }}\vec{y} \in X{ }|{ }\vec{y} \prec \vec{x}$$

(6)

The following description is provided for the Pareto optimal set, which comprises all non-dominated solutions to a specified problem [52]:

Third Definition:

Pareto optimal set. The computation of the Pareto optimal set $(P_s ){ }$ for a specific MOO is outlined as per Eq. (7). No feasible solution within this set can be dominated by any other feasible solution in the same set. The ensemble of Pareto optimal solutions is illustrated in Fig. 2.

$$P_s : = \{ { }\vec{x},\vec{y} \in X{ }|{\rm{\nexists }}{ }\vec{y} \prec \vec{x}{ }\}$$

(7)

Fig. 2

Pareto optimal solutions

Here is the formulation for the Pareto optimal front:

Fourth Definition:

Pareto optimal front. As depicted in Fig. 2, a Pareto front ($P_f$) represents the Pareto optimal set in the objective space. Based on the preceding definitions, the equation can be articulated as Eq. (8).

$$P_f { } = { }\{ F(\vec{x}),{ }\vec{x}{ } \in { }P_s \}$$

(8)

The comprehensive process of multi-objective optimization is illustrated in Fig. 3. This represents an intermediate or current front of non-dominated solutions found by the optimization process. It is an approximation of the True Pareto Front.

Fig. 3

Multi-objective optimization process

One of the most often used multi-objective GAs is NSGA II [53]. In this version, Pareto sets are labeled starting with the first non-dominated Front by a non-dominated sorting mechanism. A crowded-comparison operator assigns a crowding distance metric to each solution, subsequently steering the selection process based on this metric. In alignment with the concept of elitism, the algorithm opts for solutions with lower domination ranks for survival, and prefers solutions positioned in less congested locations, thereby maintaining solution diversity. In order to achieve a population that is the same size as the initial population, the technique for selecting non-dominated individuals must be performed several times. Finally, these steps are taken before an end condition is achieved.

Particle swarm optimization (PSO) [3] is another known technique that draws inspiration from the collective behavior of various species such as birds and fish. In every iteration, the particles (solutions) are inclined to align with the best personal and global solutions experienced by all particles until the iteration concludes. Coello and Lechuga [54] establishes a repository with a specific capacity to gather non-dominated solutions, which can be deployed in further process steps. In order to pinpoint areas of the objective function's search space that have been less explored, the search space is divided into equal-sized hypercubes. This feature allows the algorithm to preserve solution diversity and distribute them across the entire Pareto space, offering designers a broad range of options instead of concentrating on specific zones. MOPSO incorporates a mutation method known as disturbance to enhance solution randomness and variability [55, 56].

3 Multi-objective generalized normal distribution optimization

In the subsequent section, the GNDO algorithm is initially introduced. Following this, a multi-objective GNDO, aimed at resolving multi-objective optimization issues, is formulated and put forth in the scholarly work. Lastly, the computational complexity of MOGNDO is suggested.

3.1 Generalized normal distribution optimization (GNDO)

The GNDO algorithm was introduced by Zhang et al. [46]. Both exploration and exploitation are balanced via several strategies in the proposed method. Typically, the procedure of searching in methods that use a group of solutions involves three key phases. Initially, every starting solution is spread out. Next, these solutions begin moving towards the best solution, guided by specific searching and refining strategies. Eventually, they all converge near the best-found solution. This process can be explained using multiple normal distributions, where the location of each solution is considered as a variable that follows a normal distribution. At the beginning, the average location and the best location are far apart, and the variation in all solutions' locations is quite large. As the search progresses, the gap between the average location and the best location narrows, and the variation in locations decreases. In the final phase, both the distance from the average to the best location and the variation in solutions' locations are minimized.

GNDO features a straightforward framework, with its information sharing mechanisms comprising local exploitation and global exploration. Exploitation leverages a generalized normal distribution model, steered by the present average and optimal positions. Meanwhile, exploration involves the selection of three individuals at random. As outlined below, the procedure started with the creation of a random population:

$$x_{i,j}^t = l_j + \left( {u_j - l_j } \right) \times \lambda_5$$

(9)

where: $i = 1,2,3, \ldots ,N,\;{ }j = 1,2,3, \ldots ,D.$

where the number of design variables is defined by $D$, the number of population size is defined by $N$ the lower and upper boundary of the jth design variable is described by $l_j$ and $u_j$, respectively.${ }\lambda_5 { }$ is a random number in the interval of [0, 1].

3.1.1 Exploration

All created populations are evaluated via objective function. The following steps will be continued until satisfying the end criterion. Exploration and exploitation are switched with a generated random number for every solution in the population. Global exploration involves scanning the entire speech space to identify areas with potential. In GNDO, this exploration is conducted using three individuals chosen at random. The proposed method used an equation for exploration as follows:

$$v_i^t = x_i^t + \underbrace {\beta \times \left( {\left| {\lambda_3 } \right| \times v_1 } \right)}_{{\text{Local }}\;{\text{learning}}\;{\text{term}}} + \underbrace {\left( {1 - \beta } \right) \times \left( {\left| {\lambda_4 } \right| \times v_2 } \right)}_{{\text{Global}}\;{\text{learning}}\;{\text{term}}}$$

(10)

where two random distributions were created $\lambda_3$ and $\lambda_4$ from the normal distribution. The parameter $\beta { }$ is a random number between 0 and 1. The following are the two trail vectors $v_1$ and $v_2$:

$$v_1 = \left\{ {\begin{array}{*{20}l} {x_i^t - x_{{\text{p1}}}^t ,} \hfill & {if\; f({\text{x}}_i^t ) < f(x_{{\text{p1}}}^t )} \hfill \\ {x_{p1}^t - x_i^t ,} \hfill & {otherwise} \hfill \\ \end{array} } \right.$$

(11)

$$v_2 = \left\{ {\begin{array}{*{20}l} {x_{{\text{p2}}}^t - x_{{\text{p3}}}^t ,} \hfill & {if\; f({\text{x}}_{{\text{p2}}}^t ) < f(x_{{\text{p3}}}^t )} \hfill \\ {x_{{\text{p3}}}^t - x_{{\text{p2}}}^t ,} \hfill & {otherwise} \hfill \\ \end{array} } \right.$$

(12)

where three random integers number ($p1$, $p{2, }$ and $p3$) must satisfy $p1 \ne p2 \ne p3 \ne i$ are chosen from 1 to ${ }N$. Based on Eqs. (11) and (12), the second term on the right side of Eq. (10) is referred to as the local learning term. This denotes that solution $p1$ exchanges information with solution $i$. The third term on the right of Eq. (10) is termed global information sharing, signifying that individual $i$ receives information from individuals $p2$ and $p3$. The adjustment parameter $\beta$ is utilized to strike a balance between these two strategies for sharing information. Additionally, $\lambda_3$ and $\lambda_4$ are random variables following a standard normal distribution, enhancing GNDO's capability to explore a broader search space during global search activities. The inclusion of the absolute value symbol in Eq. (10) ensures alignment with the screening mechanism outlined in Eqs. (11) and (12).

3.1.2 Exploitation

Local exploitation involves the pursuit of improved solutions within the vicinity of the existing positions of all individuals in the search space. This approach is grounded in the correlation between the population's distribution of individuals and the normal distribution, enabling the construction of a generalized normal distribution model for optimization.

The proposed method used an equation for exploitation as follows:

$$v_i^t = \mu_i + \delta_i \times \eta ,\quad i = 1,2,3, \ldots ,N$$

(13)

$$M = \mathop \sum \limits_{i = 1}^N x_i^t$$

(14)

$$\mu = \frac{1}{3}\left( {x_i^t + x_{{\text{Best}}}^t + M} \right)$$

(15)

$$\delta = \sqrt {{\frac{1}{3}\left[ {\left( {x_i^t - \mu } \right)^2 + \left( {x_{{\text{Best}}}^t - \mu } \right)^2 + \left( {M - \mu } \right)^2 } \right]}}$$

(16)

$$\eta = \left\{ {\begin{array}{*{20}l} {\sqrt { - \log (\lambda_1 )} \times \cos (2\pi \lambda_2 ),} \hfill & {if\; a < = b} \hfill \\ {\sqrt { - \log (\lambda_1 )} \times \cos (2\pi \lambda_2 + \pi ),} \hfill & {otherwise} \hfill \\ \end{array} } \right.$$

(17)

where $v_i^t$ represents the trial vector for the ith individual at time $t$, $\mu_i$ denotes the generalized mean position of the ith individual, $\delta_i$ signifies the generalized standard variance, and $\eta$ is the penalty factor. In addition, three random numbers ($a$,${ }b$,${ }\lambda_1$ and ${ }\lambda_2$) are generated between 0 and 1, $x_{{\text{Best}}}^t$ is the best position and the mean position of the current population is defined as $x_{{\text{Best}}}^t$ and $M$, respectively.

It's important to recognize that the ith individual might not always identify a superior solution through either local exploitation or global exploration strategies. To ensure that improved solutions are carried forward into the subsequent generation's population, a selection mechanism has been devised, which can be described as follows:

$$x_i^{t + 1} = \left\{ {\begin{array}{*{20}l} {v_i^t ,} \hfill & {if f({\text{v}}_i^t ) < f(x_i^t )} \hfill \\ {x_i^t ,} \hfill & {otherwise} \hfill \\ \end{array} } \right.$$

(18)

The subsequent section will introduce the multi-objective variant of GNDO.

3.2 Multi-objective generalized normal distribution optimization (MOGNDO)

To carry out multi-objective optimization, two new components have been incorporated into the GNDO. These components resemble those used in MOPSO [30]. The initial element is an archive, which serves the purpose of preserving non-dominated Pareto optimal solutions that have been attained thus far. The subsequent element comprises a leader selection strategy that facilitates the identification of the most appropriate existing position solutions from the archive to serve as leaders for the search operation.

3.2.1 Archive mechanism (AM)

The designed external archive aims to preserve the solutions that are not dominated, as obtained up until now. It consists of two key elements: an archive controller and a grid. The archive controller determines whether or not a solution is to be included in the archive. Solutions that are dominated by those already in the archive are immediately excluded. Conversely, solutions not dominated are added to the archive. Should a current archive member be dominated by a new solution, the new solution replaces the older one. It is important to note that the archive has a limit on the number of its members.

When the archive reaches its capacity, an adaptive grid mechanism is activated. The grid's role is to maintain the diversity of solutions within the archive as much as possible. The objective space is segmented into multiple areas. If a new solution falls outside the existing grid boundaries, the grid is adjusted to encompass this new solution. If the solution is already within the grid, it is allocated to the area with the fewest solutions. There are four distinct scenarios that could occur:

• I. If a new member is outclassed by any existing archive solution, it is denied entry.

• II. A new solution that outclasses one or more archived solutions leads to the removal of those solutions, allowing the new solution to be included.

• III. New solutions that neither dominate nor are dominated by existing solutions are added to the archive.

• IV. When the archive is full, the grid mechanism reorganizes the objective space, removing a solution from the most crowded segment and adding the new solution to the least crowded segment to enhance diversity.

The likelihood of removing a solution rises in relation to the quantity of solutions within a given hypercube (segment). To free up space for new entries when the archive is at capacity, solutions are first targeted for removal from the most densely populated segments, with a solution being randomly selected for elimination. A unique situation arises when a solution is added outside the existing hypercubes; in such instances, all segments are expanded to encompass the new solution, potentially altering the segmentation of other solutions as well.

3.2.2 Leader selection mechanism (LSM)

The second element involves the mechanism for selecting a leader. the best solutions obtained so far are used as the current best position. This leading position then steers other search agents towards the most promising areas within the search space, with the objective of uncovering a solution that approximates the global optimum as closely as possible. However, in a search space with multiple objectives, comparing solutions directly becomes complex due to the principles of Pareto optimality outlined in the previous section. To navigate this complexity, a leader selection strategy is implemented. This strategy utilizes an archive that records the best non-dominated solutions identified up to the present. It selects leader from the less dense areas of the search space, offering one of these non-dominated solutions as the new optimal position. This selection process employs a roulette-wheel method, where the likelihood of each hypercube proposing a new leader is detailed in Eq. (19), highlighting that sparsely populated hypercubes are more likely to influence the selection of a new leader.

$$P_i = \frac{C}{K_i }$$

(19)

In the equation, $C$ is a constant number greater than one, and $K$ represents the number of acquired Pareto optimal solutions in the ith section.

The chance of a hypercube being chosen for leader selection is boosted as the count of solutions within it diminishes, acknowledging that certain exceptional scenarios may necessitate specific leader selections. As a result, the search consistently gravitates towards areas of the search space that have not been thoroughly explored or exposed, since the leader selection framework prioritizes hypercubes with minimal crowding and suggests leaders from various segments.

To improve the performance of MOGNDO for multi-objective problems, Eq. (14) needs to be adjusted as follows:

$$M = \frac{{\sum_{i = 1}^N x_i^{leader} }}{N}$$

(20)

In Eq. (20), $M$ stands for the average position of the leader population. With regards to computational complexity, where $n$ stands for the total population count and $m$ indicates the overall number of objectives, the computational complexity of MOGNDO is expressed as $O(mn^2 )$. This computational complexity is more efficient than methods such as NSGAII [53], which have a complexity of $O(mn^3 ).$ The pseudo-code of MOGNDO is ultimately provided as follows:

To grasp the theoretical efficiency of the proposed MOGNDO algorithm for multi-objective problems, a few points can be highlighted as follows:

• The external archive efficiently stores the top non-dominated solutions discovered up to now.

• The GNDO mechanism ensures both exploration and exploitation within the search for MOGNDO.

• The grid mechanism, alongside the leader selection component, preserves the archive's diversity throughout the optimization process.

• The roulette-wheel method used in selecting leader assigns a lower probability for choosing leader from the most populated hypercubes.

• The MOGNDO algorithm retains all the features of GNDO, indicating that the search agents explore and exploit the search space in an identical way.

The convergence of the MOGNDO algorithm undoubtedly derives from the GNDO algorithm since it employs the same mathematical framework to seek out optimal solutions. Search particles adjust their positions rapidly at the beginning of the optimization process and more slowly towards the end. This pattern ensures the algorithm's convergence within the search space. Selecting a single solution from the archive allows the MOGNDO algorithm to enhance its effectiveness. However, identifying a set of Pareto optimal solutions that also exhibits significant diversity poses a considerable challenge. To address this issue, we have drawn inspiration from the MOPSO algorithm, adopting its leader selection mechanism. We employed a roulette wheel approach and Eq. (19) to select a non-dominated solution from the archive and archive management strategies. It is evident that the archive must have a capacity limit, and the selection of solutions from the archive must aim to enhance overall distribution. In addition, if one solution from the archive is selected, the quality can be improved by the GNDO algorithm. However, it remains challenging to discover the set of Pareto optimal solutions with a wide range. This challenge has been surmounted through the integration of leader feature selection and archive maintenance.

In the MOGNDO algorithm, the initial step involves estimating the true Pareto optimal front for a given multi-objective optimization problem, starting with a randomly chosen collection of solutions. Each solution is evaluated based on multiple objectives. In single-objective optimization, comparing solutions is straightforward because there is only one objective function. For problems where the goal is to maximize, solution $X$ is considered superior to solution $Y {\text{if}} X > Y$. However, in the context of multi-objective optimization, solutions cannot be directly compared using simple relational operators due to the presence of multiple criteria for comparison. Here, one solution is deemed better than (or dominates) another if it has equal or superior performance across all objectives and excels in at least one objective function. The algorithm identifies and stores all non-dominated solutions in an archive. After the first iteration, it continually adjusts the solutions' positions using Eq. (9). This equation allows for the exchange of variables with either an archived solution or a non-dominated solution in the current set. The first method focuses on utilizing the best Pareto optimal solutions obtained so far, while the second method aids in exploring the search space more thoroughly. This process of refining the solutions continues until a predetermined stopping criterion is fulfilled. The algorithm also improves the distribution of solutions across all objectives by selecting solutions from less crowded areas of the archive.

All features of the MOGNDO are inherited by the GNDO algorithm, which suggests that search agents explore and exploit the search space in a similar fashion. The key difference is that MOGNDO employs an external archive to store the non-dominated services and conducts a search surrounding a set of archive members. Moreover, the proposed MOGNDO comes with a few constraints, which are as follows:

• The algorithm can only be used to optimize multi-objective problems with no more than three or four objectives. As the number of objectives increases, the effectiveness of MOGNDO decreases, which is a common issue with algorithms based on the Pareto principle. This is because the archive fills up quickly with non-dominated solutions, making it challenging to find optimal solutions for problems with more than four objectives.

• The algorithm is designed to solve optimization problems involving continuous variables, limiting its applicability to other types of problems, such as discrete or mixed-integer optimization problems.

4 Results and discussion

The effectiveness of the proposed approach is assessed in this section using performance metrics and 35 distinct case studies. These encompass unconstrained and constrained bi-objective and tri-objective mathematical problems, as well as practical engineering design problems. These tests and mathematical functions are used to ascertain the capability of multi-objective optimizers in addressing non-convex and non-linear challenges. The algorithm has been implemented in MATLAB 2022a, the details of which are described below. The computer specifications used to carry out this project are as follows: a Macintosh computer with OS X, powered by an Intel Core i9 platform, equipped with 16GB 2400MHz DDR4 RAM and a 2.3 GHz CPU (macOS Ventura).

4.1 Performance metrics

In order to evaluate the results of the algorithms, we employed five metrics in the following manner [58, 59]:

Generational distance (GD): The aggregate distance between potential solutions generated through various methods provides a smart metric for evaluating the convergence traits of multi-objective meta-heuristic algorithms.

$$GD = \left( {\frac{1}{{n_{pf} }}\mathop \sum \limits_{i = 1}^{n_{pf} } dis_i^2 } \right)^\frac{1}{2}$$

(21)

Spacing (S): A metric to demonstrate the degree of divergence among solution candidates when contrasted against various result sets obtained by multiple algorithms.

$$S = \left( {\frac{1}{{n_{pf} }}\mathop \sum \limits_{i = 1}^{n_{pf} } (d_i - \overline{d})^2 } \right)^\frac{1}{2} \quad where\;\overline{d} = { }\frac{1}{{n_{pf} }}\mathop \sum \limits_{i = 1}^{n_{pf} } d_i$$

(22)

Maximum spread (MS): This illustrates the dispersion of potential solutions amongst other achieved sets, taking into account the diverse optimal choices.

$$MS = \left[ {\frac{1}{m}\mathop \sum \limits_{i = 1}^m { }\left[ {\frac{{\min \left( {f_i^{max} ,F_i^{max} } \right) - {\text{max}}(f_i^{min} ,F_i^{min} )}}{{F_i^{max} - F_i^{min} }}} \right]^2 } \right]^\frac{1}{2}$$

(23)

Inverted generational distance (IGD): This measure enables precise performance assessment of Pareto front approximations using multi-objective optimization methods [60].

$$IGD = \frac{{\sqrt {{\sum_{i = 1}^n d_i^2 }} }}{n}$$

(24)

Wilcoxon rank-sum Test (WRT): The Wilcoxon rank-sum test, a non-parametric statistical technique, is employed to determine whether two or more datasets originate from an identical distribution. This test employs a significance level of 5%. This examination is utilized to conduct a comprehensive evaluation of the efficacy of the algorithm. As per the null hypothesis, if the mean metrics attained by the two algorithms under comparison are the same, there is no discernible difference in their performance. Conversely, the alternative hypothesis proposes that a difference exists in the mean metrics generated by the algorithms under comparison. The paper presents a comparative analysis of the algorithms, highlighting their differences with mathematical symbols such as subtraction, addition, and equality operators. These indicators denote whether the algorithm exhibits inferior performance, significantly superior performance, or no distinguishable difference, correspondingly.

The evaluation of the algorithms' performance in approximating Pareto optimal solutions is determined by the S and MS metrics, while the measurement of their convergence is based on the IGD and GD performance metrics. After conducting mean-based assessments to evaluate the performance of the algorithm and comparing it using the Wilcoxon rank-sum test, it was determined that the algorithm exhibited a high level of competitiveness and effectiveness.

4.1.1 Numerical setup

This section presents a comparison among MOPSO, MOGWO, MOHHO, MSSA, MOALO, MOMVO, MOAOS, and MOGNDO. The best figure from a set of Pareto optimal figures is emphasized. To ensure a fair comparison, all experiments are performed on the same device. Table 1 displays all initial parameters for the aforementioned algorithms. The parameters for the algorithm are set to their default values, minimizing the chance of superior parametrization bias, as advocated by Arcuri and Fraser [61]. Furthermore, the control parameters for the algorithms under comparison were derived from their respective references. The optimal parameter for each algorithm, as outlined in their references, is utilized in this context. It is important to note that all experiments incorporated 100 populations and a maximum of 1000 iterations. The efficiency of the proposed algorithm is evaluated in this section on 35 cases, including 7 unconstrained and constrained functions, ten traditional multi-objective CEC-09, eight engineering design problems, and 10 CEC-2020 problems.

Table 1 Parameters setting of all algorithms

The death penalty was used in multi-objective problems. However, the death penalty's role is to be used to discard solutions that are not feasible, and the knowledge of those solutions that are useful in solving the problem of controlled inviolable regions is not utilized [54]. Due to its simplicity and low computational cost, the MOGNDO algorithm has been equipped with a death penalty feature to deal with multiple constraints. The benchmark problems are offered in Tables 2, 3 and 4. Engineering design problems are considered one of the most challenging examination problems in literary works that give various multi-objective search spaces with different Pareto optimal fronts: convex, non-convex, discontinuous, and also multimodal. It might be observed that examination functions with varied features are picked to evaluate the efficiency of MOGNDO from various points of view. Although examination functions can help analyze an algorithm, solving real problems is constantly much more difficult. Tables 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 and 16 provide the results of 30 independent runs on the 100,000 function evaluations for all algorithms in this study.

Table 2 Mathematic ZDT and DTLZ problems

Table 3 CEC-09 problems with two objectives

Table 4 CEC-09 problems with three objectives

Table 5 Mathematic problem statistics results for the GD metric

Table 6 Mathematic problem statistics results for the IGD metric

Table 7 Mathematic problem statistics results for the MS metric

Table 8 Mathematic problem statistics results for the S metric

Table 9 CEC problem statistics results for the IGD metric

Table 10 CEC problem statistics results for the GD metric

Table 11 CEC problem statistics results for the MS metric

Table 12 CEC problem statistics results for the S metric

Table 13 Engineering problem statistics results for the IGD metric

Table 14 Engineering problem statistics results for the GD metric

Table 15 Engineering problem statistics results for the MS metric

Table 16 Engineering problem statistics results for the S metric

4.2 Numerical discussion of the ZDT and DTLZ test function

The initial set of problems consist of mathematical problems. The mean and standard deviation results for all performance metrics for ZDT and DTLZ problems are displayed in Tables 5, 6, 7 and 8. The results for the GD performance metric are indicated in Table 5. As per this table, the Pareto optimal solutions garnered by MOGNDO exhibit greater convergence than MOPSO, MOGWO, and MOHHO on ZDT1, ZDT2, and ZDT3.

The results when using the IGD metric are provided in Table 6. It can be seen that MOGNDO is slightly better than MOPSO in this metric. These outcomes reveal the efficiency of the MOGNDO algorithm is much steadier than MOPSO. Considering that IGD is an excellent measurement to benchmark an algorithm's convergence, these outcomes show that the proposed algorithm has a much better quantitative efficiency, both considering convergence and distribution convergence on this benchmark function.

The value of the outcomes for the IGD metric is depicted in Fig. 4. The worst outcomes come from MOHHO handling these benchmark problems. The boxplots depicted in Fig. 4 reveal that this algorithm yields highly unfavorable results, while MOGNDO's outcomes are more competitive in comparison. In addition, the boxplot of the MOGNDO is narrower than MOPSO, MOGWO and also MOHHO in most problems, revealing the strength of the MOGNDO algorithm is converging towards the true Pareto optimal front.

Fig. 4

Boxplot of the statistical results (IGD) for ZDT and DTLZ problems

Table 7 shows the MS performance metric of all algorithms. The coverage of Pareto optimal solutions for algorithms is calculated by the maximum spread metric. It is evident that the results of MOGNDO are better than MOPSO, MOHHO and MOGWO for all test problems. Thanks to this, the proposed method has competitive coverage in comparison with the other mentioned methods. MOGNDO obtains the best results in ZDT1, ZDT2, ZDT6, DTLZ2 and DTLZ4 problems.

Based on the analysis of the true Pareto optimal front and the best-obtained Pareto optimal fronts for the ZDT and DTLZ problems, it is evident from Fig. 5 that MOGNDO's Pareto optimal front consistently outperforms those of MOPSO, MOGWO, and MOHHO in the majority of scenarios. This is further substantiated by the Pareto optimal fronts for ZDT1, ZDT2, and ZDT3 shown in Fig. 5, where all Pareto optimal solutions estimated by MOGNDO align with the true Pareto Front. This confirms that the suggested MOGNDO algorithm has the potential to offer remarkable outcomes on multi-objective problems. The statistical results for tri-objective benchmarks (DTLZ2 and DTLZ4) are more challenging benchmarks, showing that this method is competitive for solving more than two objective problems. Figure 6 presents the true and the achieved Pareto Front for tri-objective issues from two viewing angles.

Fig. 5

True and obtained Pareto front for ZDT benchmarks

Fig. 6

True and obtained Pareto front for DTLZ2 and DTLZ4

To compare the diversity of MOGNDO with MOPSO, MOGWO and MOHHO algorithms concerning the spacing metric, the statistical results are obtained from 30 individual runs for ZDT and DTLZ benchmarks. Table 8 shows the results for the spacing performance metric. MOGNOD, MOHHO and MOGWO obtained the best results in terms of this metric simultaneously. It is clear that the MOGNDO presented here will provide a reasonably reliable estimate of true Pareto optimal solutions. Evidence of the MOGNDO's superiority over alternative approaches is presented in Tables 5, 6, 7, and 8 via the Wilcoxon's rank sum test.

4.3 Discussion of the CEC-09 test function

This section focuses on the results obtained from the evaluations of the CEC-09 test functions. Tables 9 and 10 present the statistical outcomes for the IGD and GD metrics, respectively. Table 9 highlights explicitly that the recommended MOGNDO algorithm demonstrates superior performance in terms of IGD metrics for UF1, UF2, UF4, UF9, and UF10. The statistical analysis of the IGD metric for the CEC-09 test functions is visualized in boxplot Fig. 7. It is worth discussing here that MOGNDO is really efficient for solving more challenging than two-objective problems since UF9 and UF10 are tri-objective function benchmarks. The outcomes and analyses prove that the MOGNDO algorithm can offer really more competitive and appealing outcomes on the multi-objective examination functions concerning the obtained Pareto Front, as seen in Fig. 8. The Pareto optimal front for the UF5 test problem differs from the first four tests in that it has discontinuities, making it a challenge to find the Pareto optimal set. This is evident in Fig. 8, where the numerous discontinuous areas pose a problem for all algorithms. The Pareto front for the UF6 test problem has three distinct regions and is quite similar to UF1. As shown in Fig. 8, MOGNDO has results that are closest to the Pareto front.

Fig. 7

Boxplot of the statistical results (IGD) for CEC-09 problems

Fig. 8

True and obtained Pareto front for CEC-09 benchmarks (UF1-7)

True and obtained Preto fronts of UF8, UF9, and UF10 are seen in Fig. 9 from different perspectives. According to Fig. 9, MOGNDO has generated one of the best Pareto sets for the three objective test problems. The figure demonstrates that MOGNDO has a good coverage and convergence, whereas the other algorithms have low convergence rates. In addition, the Pareto optimal set shown in Fig. 9 confirms that MOGNDO has better coverage than the other algorithms. As depicted in Table 10, 60% (UF1, UF2, UF3, UF4, UF8, and UF10) of all CEC-09 test functions for all algorithms in MOGNDO obtained the best results, which show that the distance between true and obtained Pareto Front is low in these examples.

Fig. 9

True and obtained Pareto front for CEC-09 benchmarks (UF8-10)

By running 30 times on CEC-09 optimization problems independently, the MS metric for MOPSO, MOGWO, MOHHO, and the proposed method is listed in Table 11. It is evident that MOGNDO shows good results compared with the other mentioned methods. These outcomes indicate the MOGNDO gains the best results of 5 CEC-09 benchmarks out of 10. The average and standard deviation of the S performance metric are listed in Table 12. UF1, UF2, UF3, UF8, UF9, and UF10 have the best results in terms of average. Inspecting the results on UF8, UF9, and UF10, which have three objective functions, the MOGNDO algorithm obtained the first rank. It proves the proposed method will also be a good choice for more than two objective function problems. The results of the Wilcoxon rank sum test, presented in Tables 9, 10, 11 and 12, provide strong evidence that MOGNDO surpasses the other evaluated methods significantly.

4.4 Discussion of the engineering problem results.

The last collection of examination functions is one of the most difficult ones and also consists of eight real engineering design problems. Equations (25) to (75) reveal that these problems have varied features. As a result, the very fit benchmarking the efficiency of the recommended MOGNDO algorithm. The different behavior of the best Pareto optimal fronts and the obtained Pareto fronts are shown compared to the true ones in Fig. 10. MOGNDO has superior coverage and convergence among all the algorithms. Based on the four superior metrics, as well as its acceptable coverage and convergence factors, MOGNDO is better equipped to provide better solutions for the BNH, CONSTR, WELDED BEAM, and SRN design problems than the other algorithms.

Fig. 10

True and obtained Pareto front for the engineering design problem

The convergence of the MOGNDO algorithm in the mentioned design problems is nearly 100% similar to the true Pareto Front, as shown in this figure. Convergence is reasonable due to this, and coverage is exceptionally high and nearly uniform.

Constraint multi-objective test problem:

4.3.1 CONSTR

There are two constraints and two design variables in this problem, which has a convex Pareto front.

$$Minimize: \quad f_1 \left( x \right) = x_1$$

(25)

$$Minimize:\quad f_2 \left( x \right) = (1 + x_2 )/x_1$$

(26)

$$where:\quad g_1 \left( x \right) = 6 - (x_2 + 9x_1 )$$

(27)

$$\begin{aligned} & g_2 \left( x \right) = 1 + (x_2 - 9x_1 ) \\ & \quad 0.1 \le x_1 \le 1, 0 \le x_2 \le 5 \\ \end{aligned}$$

(28)

4.3.2 SRN

Srinivas and Deb [63] suggested a continuous Pareto optimal front for the next problem as follows:

$$Minimize: f_1 \left( x \right) = 2 + \left( {x_1 -- 2} \right)^2 + \left( {x_2 -- 1} \right)^2$$

(29)

$$Minimize :\quad f_2 (x){ } = 9x_1 -- (x_2 -- 1)^2$$

(30)

$$where:\quad g_1 (x){ } = x_1^2 + x_2^2 - 255$$

(31)

$$\begin{aligned} & g_2 \left( x \right) = x_1 - 3x_2 + 10 \\ & \quad - 20 \le x_1 \le 20, - 20 \le x_2 \le 20 \\ \end{aligned}$$

(32)

4.3.3 BNH

Binh and Korn [64] were the first to propose this problem as follows:

$$Minimize:\quad f_1 (x) = 4x_1^2 + 4x_2^2$$

(33)

$$Minimize:\quad f_2 (x) = (x_1 - 5)^2 + (x_2 - 5)^2$$

(34)

$$where:\quad g_1 (x) = (x_1 - 5)^2 + x_2^2 - 25$$

(35)

$$\begin{aligned} & g_2 (x) = 7.7 - (x_1 - 8)^2 - (x_2 + 3)^2 \\ & \quad 0 \le x_1 \le 5, 0 \le x_2 \le 3 \\ \end{aligned}$$

(36)

4.3.4 OSY

Osyczka and Kundu [65] proposed five distinct regions for the OSY test issue. There are also six constraints and six design variables to consider as bellow:

$$Minimize:\quad f_1 (x) = x_1^2 + x_2^2 + x_3^2 + x_4^2 + x_5^2 + x_6^2$$

(37)

$$Minimize:\quad f_2 \left( x \right) = [25(x_1 - 2)^2 + (x_2 - 1)^2 + (x_3 - 1)^2 (x_4 - 4)^2 + (x_5 - 1)^2 ]$$

(38)

$$Where:\quad g_1 \left( x \right) = 2 - x_1 - x_2$$

(39)

$$g_3 (x) = - 2 - x_1 + x_2$$

(40)

$$g_4 (x) = - 2 + x_1 - 3x_2$$

(41)

$$g_5 (x) = - 4 + x_4 + (x_3 - 3)^2$$

(42)

$$\begin{aligned} & g_6 (x) = 4 - x_6 - (x_5 - 3)^3 \\ & \quad 0 \le x_1 \le 10, 0 \le x_2 \le 10, 1 \le x_3 \le 5 \\ & \quad 0 \le x_4 \le 6, 1 \le x_5 \le 5, 0 \le x_6 \le 10 \\ \end{aligned}$$

(43)

Constraint multi-objective engineering problems:

4.3.5 Four-bar truss design problem

The 4-bar truss design problem [66], in which the structural volume ($f_1$) and displacement ($f_2$) of a 4-bar truss should be minimized, is a well-known problem in the structural optimization field. There are four design variables ($x_1$-$x_4$) connected to the cross-sectional area of members 1, 2, 3, and 4, as shown in the equations below:

$$Minimize:\quad f_1 \left( x \right) = 200 \times \left( {2 \times x\left( 1 \right) + sqrt\left( {2 \times x\left( 2 \right)} \right) + sqrt\left( {x\left( 3 \right)} \right) + x\left( 4 \right)} \right)$$

(44)

$$Minimize:\quad f_2 (x) = 0.01 \times \left( {\frac{2}{x(1)}} \right) + \left( {\frac{2 \times sqrt(2)}{{x(2)}}} \right) - ((2 \times sqrt(2))/x(3)) + (2/x(1)))$$

(45)

$$\begin{aligned} & Where:\quad 1 \le x_1 \le 3, \;1.4142 \le x_2 \le 3 \\ & \quad \quad \quad \quad 1.4142 \le x_3 \le 3,\; 1 \le x_4 \le 3 \\ \end{aligned}$$

4.3.6 Welded beam design problem

Ray and Liew [67] suggested four constraints for the welded beam design issue. In this issue, the fabrication cost ($f_1$) and beam deflection ($f_2$) of a welded beam should be minimized. The thickness of the weld ($x_1$), the length of the clamped bar ($x_2$), the height of the bar ($x_3$) and the thickness of the bar ($x_4$) are the four design variables.

$$Minimize: \quad f_1 \left( x \right) = 1.10471 \times x(1)^2 \times x\left( 2 \right) + 0.04811 \times x(3) \times x(4) \times (14 + x(2))$$

(46)

$$Minimize:\quad f_2 \left( x \right) = 65856000/(30 \times 10^6 \times x(4) \times x(3)^3 )$$

(47)

$$Where:\quad g_1 \left( x \right) = \tau - 13600$$

(48)

$$g_2 (x) = \sigma - 30000$$

(49)

$$g_3 \left( x \right) = x\left( 1 \right) - x(4)$$

(50)

$$\begin{aligned} & g_4 \left( x \right) = 6000 - P \\ & \quad 0.125 \le x_1 \le 5, \; 0.1 \le x_2 \le 10 \\ & \quad 0.1 \le x_3 \le 10, \; 0.125 \le x_4 \le 5 \\ \end{aligned}$$

(51)

$$q = 6000*\left( {14 + \frac{x(2)}{2}} \right);\;D = sqrt\left( {\frac{x(2)^2 }{4} + \frac{x(1) + x(3))^2 }{4}} \right)$$

(52)

$$J = 2*\left( {x(1)*x(2)*sqrt(2)*\left( {\frac{x(2)^2 }{{12}} + \frac{(x(1) + x(3))^2 }{4}} \right)} \right)$$

(53)

$$\alpha = \frac{6000}{{sqrt(2)*x(1)*x(2)}}$$

(54)

$$\beta = Q*\frac{D}{J}$$

(55)

4.3.7 Disk brake design problem [67]

Ray and Liew [67] proposed the disc brake design issue, which has multiple constraints. Stopping time ($f_1$) and brake mass ($f_2$) for a disc brake are the two objectives to be minimized. The inner radius of the disc ($x_1$), the outer radius of the disc ($x_2$), the engaging force ($x_3$), and the number of friction surfaces ($x_4$) as well as four constraints, are shown in the following equations.

$$Minimize: \quad f_1 \left( x \right) = 4.9 \times (10)^{( - 5)} \times (x(2)^{(2)} - x(1)^{\left( 2 \right)} ) \times (x(4) - 1)$$

(56)

$$Minimize: \quad f_2 \left( x \right) = (9.82 \times (10)^{^{(6)} } )) \times (x(2))^{\left( 2 \right)} - x\left( 1 \right)^{\left( 2 \right)} ))/\left( {(x(2))^{\left( 3 \right)} - x(1)^{\left( 3 \right)} ) \times x\left( 4 \right) \times x\left( 3 \right)} \right)$$

(57)

$$g_1 \left( x \right) = 20 + x\left( 1 \right) - x(2)$$

(58)

$$g_2 \left( x \right) = 2.5 + \left( {x\left( 4 \right) + 1} \right) - 30$$

(59)

$$g_3 \left( x \right) = (x\left( 3 \right))/(3.14 \times \left( {x\left( 2 \right)^2 - x\left( 1 \right)^2 } \right)^2 ) - 0.4$$

(60)

$$g_4 \left( x \right) = {{\left( {2.22 \times \left( {10} \right)^{\left( { - 3} \right)} \times x\left( 3 \right) \times \left( {x\left( 2 \right)^3 - x\left( 1 \right)^3 } \right)} \right)} / {\left( {\left( {x\left( 2 \right)^2 - x\left( 1 \right)^2 } \right)^2 } \right) - 1}}$$

(61)

$$g_5 \left( x \right) = {{900 - \left( {2.66 \times \left( {10} \right)^{\left( { - 2} \right)} \times x\left( 3 \right) \times x\left( 4 \right) \times \left( {x\left( 2 \right)^3 - x\left( 1 \right)^3 } \right)} \right)} / {\left( {\left( {x\left( 2 \right)^2 - x\left( 1 \right)^2 } \right)^2 } \right)}}$$

(62)

$$\begin{aligned} & Where:\quad 55 \le x_1 \le 80, \; 75 \le x_2 \le 110 \\ & \quad \quad \quad \quad 1000 \le x_3 \le 3000, \;2 \le x_4 \le 20 \\ \end{aligned}$$

4.3.8 Speed reducer design problem

The weight ($f_1$) and stress ($f_2$) of a speed reducer should be minimized in the speed reducer design issue, which is well-known in the field of mechanical engineering [66, 68]. There are seven design variables: gear face width ($x_1$), teeth module ($x_2$), number of teeth of pinion ($x_3$ integer variable), distance between bearings 1 ($x_4$), distance between bearings 2 ($x_5$), diameter of shaft 1 ($x_6$), and diameter of shaft 2 ($x_7$) as well as eleven constraints.

$$\begin{aligned} & Minimize:\quad f_1 \left( x \right) = 0.7854 \times x\left( 1 \right) \times x(2)^2 \times (3.3333 \times x\left( {(3)^2 + 14.9334 \times x\left( 3 \right)} \right) \ldots \\ & \quad \quad \quad \quad \quad \quad - 43.0934) - 1.508 \times x(1) \times (x(6)^2 + x(7)^2 \\ \end{aligned}$$

(63)

$$Minimize: \quad f_2 (x) = ((sqrt(((745*x(4))/x(2)*x(3)))^2 + 19.9e6)/(0.1*x(6)^3 ))$$

(64)

$$where: \quad g_1 \left( x \right) = 27/(x\left( 1 \right) \times x\left( {2)^2 \times x\left( 3 \right)} \right) - 1$$

(65)

$$g_2 \left( x \right) = 397.5/(x\left( 1 \right) \times x(2)^2 \times x\left( {3)^2 } \right) - 1$$

(66)

$$g_3 \left( x \right) = (1.93 \times (x(4)^3 )/(x(2) \times x(3) \times (x(6)^4 ) - 1$$

(67)

$$g_4 \left( x \right) = (1.93 \times (x(5)^3 )/(x(2) \times x(3) \times (x(7)^4 ) - 1$$

(68)

$$g_5 \left( x \right) = ((sqrt((745 \times x\left( 4 \right))/x(2) \times x\left( {3)))^2 + 16.9e6} \right))/(110 \times x\left( {6)^3 } \right)) - 1$$

(69)

$$g_6 \left( x \right) = ((sqrt((745 \times x\left( 4 \right))/x(2) \times x\left( {3)))^2 + 157.5e6} \right))/(85 \times x\left( {7)^3 } \right)) - 1$$

(70)

$$g_7 \left( x \right) = ((x(2) \times x(3))/40) -- 1$$

(71)

$$\tau = sqrt\left( {\alpha^2 + 2 \times \alpha \times \beta \times \frac{x(2)}{{2 \times D}} + \beta^2 } \right)$$

(72)

$$\sigma = \frac{504000}{{x(4) \times x(3)^2 }}$$

(73)

$$tmpf = 4.013 \times \frac{30 \times 10^6 }{{196}}$$

(74)

$$P = tmpf \times sqrt\left( {x(3)^2 \times \frac{x(4)^6 }{{36}}} \right) \times \left( {1 - x(3) \times \frac{{sqrt\left( {\frac{30}{{48}}} \right)}}{28}} \right)$$

(75)

The performance of MOGNDO, in comparison with MOPSO, MOGWO, and MOHHO, shows a high degree of competitiveness, particularly in the best Pareto front-of-rest problems. The outcomes of these algorithms are quantitatively compared using a similar set of efficiency metrics, and the corresponding results are displayed in Tables 13, 14, 15 and 16.

Most of the constrained test function results, as depicted in Tables 13 and 14, highlight the superior performance of MOGNDO over the other three algorithms. This dominance is further evident in the Generational Distance (GD) and Inverted Generational Distance (IGD) metrics, suggesting outstanding convergence. Table 14 GD performance measurement results distinctly indicate the superiority of the newly proposed algorithm over MOPSO, MOGWO, and MOHHO. Additionally, the boxplot of the IGD metric for engineering problems, displayed in Fig. 11, verifies that MOGNDO outperformed the others in 75% of the engineering problems based on the IGD metric.

Fig. 11

Boxplot of the statistical results (IGD) for engineering problems

According to Tables 15 and 16, the statistical results for the MS and S metrics show that the proposed MOGNDO algorithm competes well with other algorithms. These tables list the average and standard deviation results for the MS and S performance metrics. The MOGNDO algorithm excels in terms of the MS performance metric. Furthermore, in some problems, the coverage of the proposed method on engineering test functions surpasses that of other algorithms. As evidenced by the results in these tables, MOGNDO can surpass other methods in identifying Pareto optimal fronts with distinct regions.

The results of examinations show that the MOGNDO algorithm has high convergence and coverage. The high convergence of this algorithm is inherited by its standard version and leader selection mechanism. The results showed that this method's merit is high coverage and is guaranteed by archive maintenance and leader feature selection function. Tables 13, 14, 15, and 16 present the results of a Wilcoxon rank sum test, demonstrating without a shadow of a doubt that the MOGNDO is the most effective of the other tested methods.

4.4 Discussion of the CEC20 problem results

This section assesses MOGNDO, the proposed multi-objective approach, and its ability to address various issues at CEC-2020. A comparison is made between MOPSO, MOGWO, MOHHO, MSSA, MOALO, MOMVO, and MOAOS. Information about the MMO evaluation functions is provided in [62]. The MMO evaluation process encompasses linear, non-linear, convex, and concave problems.

Figure 12 compares the ideal Pareto fronts against those achieved for the CEC-2020 benchmark problems labeled M1 through M10. The graphical representation clearly shows the disparity between the theoretical optimal Pareto fronts and those derived through our algorithm is remarkably small. For each of the ten benchmark problems presented, the results obtained from our algorithm align closely with the true Pareto fronts, showcasing a consistency not observed in the results from alternative algorithms, which exhibit notable variations for each problem scenario.

Fig. 12

True and obtained Pareto front for CEC-2020 problems

Table 17 elaborates on the statistical evaluation of the performance based on the GD metric. Here, the MOGNDO method stands out by achieving the best average GD values for a majority of the problems, precisely seven out of ten. The MOAOS follows as the second-best method, leading in mean values for three problems, while other evaluated methods did not produce notable results in this comparison. Furthermore, when examining the standard deviation of the GD performance, our method demonstrates a superior capability in pinpointing eight out of ten optimal solutions, outperforming MOAOS and MOHHO. The latter methods only manage to secure a commendable position in one instance for MOAOS, based on SD, underlining the robustness of our current approach in identifying solutions that closely adhere to the ideal outcomes.

Table 17 Mathematic problem statistics results for the GD metric

Table 18 provides an overview of the IGD metric's statistical results, indicating the MOGNDO method's dominance in obtaining the best average IGD values across eight of the ten problems. When considering the standard deviation of these results, MOGNDO again excels by securing the best outcomes in six instances. MOAOS is recognized for its performance according to the standard deviation of IGD, securing the second rank, whereas other methods lag behind in average and standard deviation measures.

Table 18 Mathematic problem statistics results for the IGD metric

The assessment continues with Table 19, which details the statistics for the S metric, highlighting that our method identifies the optimal average values in eight instances and excels in standard deviation measures for six instances. This demonstrates the method's effectiveness in ensuring diverse yet accurate solution sets. Other methods like MOPSO and MOHHO are noted for finding a couple and one optimal standard deviation value, respectively, but they do not match the overall efficacy of our approach.

Table 19 Mathematic problem statistics results for the S metric

Finally, Table 20 summarizes the performance evaluation based on the MS metric, where MOGNDO again leads by achieving the highest number of optimal average and standard deviation values across the benchmarks. This superiority is affirmed by results from the Wilcoxon rank sum test across Tables 17, 18, 19 and 20, solidifying MOGNDO's position as significantly more efficient in navigating and solving the CEC-2020 benchmark problems compared to the competing methods.

Table 20 Mathematic problem statistics results for the MS metric

Following is a summary of the experiment's findings:

• As shown in Tables 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19 and 20, the experimental results show that the MOGNDO algorithm has excellent coverage and convergence capabilities. Both the archive and non-dominated sorting maintenance methods contribute to MOGNDO's high coverage, but high convergence is a privilege from the GNDO algorithm.

• In the same way that other archive-based MO algorithms do, the MOGNDO makes use of the archive memory in order to store the non-dominated solutions discovered through the optimization process.

• Compared to other MO-like algorithms, the MOGNDO's superior performance can be attributed to its use of the original GNDO update mechanism, allowing it to investigate a greater number of non-dominated solutions while maintaining a high convergence and coverage rate.

5 Conclusion and future works

This research developed an early multi-objective variant of MOGNDO, which incorporated an archive to store non-dominated solutions and a selection mechanism to identify the "best" solutions for the GNDO algorithm. The archive had a crucial role in preserving and updating the solutions, while the recommended leader selection feature allowed the MOGNDO algorithm to demonstrate excellent coverage and convergence simultaneously. The algorithm was evaluated using 25 diverse mathematical and engineering design problems, highlighting its effectiveness in achieving a balance between the exploration and exploitation stages. Metrics such as GD, IGD, S, and MS were employed to assess the dominance and performance of the proposed method.

Qualitative outcomes documenting the most effective Pareto optimal front identified in 30 runs were also documented to validate these results. The proposed algorithm was compared with highly esteemed algorithms such as MOPSO, MOGWO, and MOHHO to validate these results. This comparison demonstrated that our algorithm offered a highly competitive performance relative to the mentioned algorithms. The results and findings thus suggested that advantages are held by the proposed algorithm over existing multi-objective algorithms, positioning it as an appealing solution for multi-objective optimization problems.

Future research will involve the development of a binary variant of the MOGNDO algorithm to address a broader spectrum of complex, real-world problems. Another prospective contribution lies in the creation of a version of the proposed algorithm that considers multiple objectives simultaneously. Moreover, future work is encouraged to utilize MOGNDO for a range of other engineering design problems, such as truss structures, real-time applications, and the development of structural health assessment.