Low-energy Earth–Moon transfers via Theory of Functional Connections and homotopy

Abstract

Numerous missions leverage the weak stability boundary in the Earth–Moon–Sun system to achieve a safe and cost-effective access to the lunar environment. These transfers are envisaged to play a significant role in upcoming missions. This paper proposes a novel method to design low-energy transfers by combining the recent Theory of Functional Connections with a homotopic continuation approach. Planar patched transfer legs within the Earth–Moon and Sun–Earth systems are continued into higher-fidelity models. Eventually, the full Earth–Moon transfer is adjusted to conform to the dynamics of the planar Earth–Moon Sun-perturbed, bi-circular restricted four-body problem. The novelty lies in the avoidance of any propagation during the continuation process and final convergence. This formulation is beneficial when an extensive grid search is performed, automatically generating over 2000 low-energy transfers. Subsequently, these are optimized through a standard direct transcription and multiple shooting algorithm. This work illustrates that two-impulse low-energy transfers modeled in chaotic dynamic environments can be effectively formulated in Theory of Functional Connections, hence simplifying their overall design process. Moreover, its synergy with a homotopic continuation approach is demonstrated.

1 Introduction

Space exploration is experiencing a flourishing growth. A multitude of missions have been recently launched in the cislunar space [CAPSTONE (Cheetham 2021), ArgoMoon (Di Tana et al. 2019), EQUULEUS (Funase et al. 2020)] and many others are planned for the near future (LUMIO (Topputo et al. 2023), Chang’e-6¹). The renewed interest in our natural satellite is confirmed by the ambitious ARTEMIS program and its Gateway (Smith et al. 2020), which plan to set an important step toward the human exploration of the solar system. In this context, the development of new techniques for mission design and trajectory optimization in dynamically rich environments is essential to make space even more appealing overall.

The design of low-energy interplanetary cruises is challenging because of the intrinsically chaotic dynamics governing the motion of a spacecraft (Topputo et al. 2005). Multiple attractors and perturbations act together, making the phase space highly nonlinear and rather complex to characterize. This causes the dynamics to be extremely sensitive to small variations in the states, and therefore, the design of trajectories in such environments is especially difficult. On the other hand, this intrinsic complexity enriches the phase space, thereby permitting otherwise impossible trajectories (Koon et al. 2000b). In this regime, the patched conic approximation is not suitable, and therefore, alternative methodologies are adopted. Simplified dynamic models reveal natural structures such as periodic orbits (Doedel et al. 2007) and invariant manifolds (Topputo et al. 2005) that can be exploited to generate preliminary transfers with low propulsive costs, ultimately refined into more realistic scenarios (Dei Tos and Topputo 2017). Overall, trajectories designed in these models enable for safer and more fuel-efficient transfers than standard high-energy ones, usually at the expense of longer travel times (Oshima et al. 2019).

Recently, numerous studies addressed the problem of designing low-energy transfers. Fantino and Castelli (2016) approximated invariant manifolds far from the primaries, thus simplifying the design of moon-to-moon transfers in the Jovian system. Lagrangian coherent structures are utilized in Onozaki et al. (2017) to represent the analogs of invariant manifolds in perturbed dynamic models. In their paper, Raffa et al. (2023) showed that Lagrangian descriptors are suitable to reveal organized regions of motion in dynamically rich environments. Lu et al. (2015) optimized a full Earth–Mars low-energy transfer using a differential evolution algorithm to patch different phases. An automated pathfinding using machine learning is investigated in Das-Stuart et al. (2020) to combine natural dynamic structures for rapid trajectories generation.

To widen the spectrum of methodologies for fast prototyping of transfers, this work proposes a novel approach. In particular, the design of two-impulse, low-energy, long-duration trajectories is the focus of this research. Two objectives are pursued. Firstly, a technique for effective Earth–Moon exterior trajectories design in intricate and chaotic dynamic regimes is developed. Secondly, a method is demonstrated to automate the generation of feasible two-impulse transfer trajectories, which are then optimized using a nonlinear programming problem formulation (Betts 1998).

Dynamic structures arising from simplified models are exploited to construct a first seeding trajectory composed of a departure leg from the Earth and an arrival one to the Moon, similar to what practiced in Koon et al. (2001). The departure and arrival legs are successively represented following the formulation proposed by the Theory of Functional Connections (TFC) (Mortari 2017b). Subsequently, they are refined into more realistic dynamic models through the application of a homotopic continuation approach (Allgower and Georg 2003). Eventually, the convergence to a full Earth–Moon transfer is achieved. This procedure circumvents the need for repeatedly performing numerical integration of the dynamic equations within a shooting framework, thereby facilitating the design process of transfer trajectories. The efficiency in terms of propellant cost, hereafter referred to simply as ‘cost’, is guaranteed by capitalizing on the weak stability boundary granted by the dynamics itself (Circi and Teofilatto 2001). After proving that such complex transfers can be accurately represented in TFC, an extensive grid search is performed to automatically generate a wide range of exterior Earth–Moon trajectories. These are eventually optimized through direct transcription and multiple shooting (Betts 1998), building upon the formulation proposed in Topputo (2013).

The remainder of the paper is structured as follows. In Sect. 2, the dynamic models and the theoretical fundamentals of the tools employed in this work are presented. Section 3 describes the devised method and the trajectory design approach. The procedure is then practiced to generate two-impulse, exterior Earth–Moon transfers in Sect. 4. Eventually, Sect. 5 summarizes the contributions of this study.

2 Background

2.1 Dynamic models

2.1.1 Planar circular restricted three-body problem

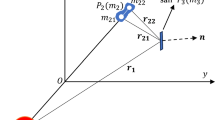
In the planar circular restricted three-body problem (CR3BP), two attractors P$_1$ and P$_2$ of masses $\mathrm m_1 > \mathrm m_2$, respectively, revolve in circular orbits about their common barycenter. The motion of a third body P$_3$ of negligible mass, representing the spacecraft, is ruled by the gravitational pull of the primaries. Furthermore, the trajectory is constrained to remain in the same plane.

Denoting with $\mu =\mathrm m_2/(\mathrm m_1+\mathrm m_2)$ the normalized gravitational parameter, the motion of P$_3$ can be represented in a convenient (x, y) rotating frame (rf) with the origin at the center of mass of the primaries and the x axis pointing toward the secondary. As per Szebehely (1967), the dynamic equations governing the motion of P$_3$ are formulated in normalized mass, distance, and time units as

$$\begin{aligned} \begin{aligned} \ddot{x}&= 2\dot{y}+\frac{\partial \Omega _3}{\partial x}, \\ \ddot{y}&= -2\dot{x}+\frac{\partial \Omega _3}{\partial y}, \end{aligned} \end{aligned}$$

(1)

where the effective potential $\Omega _3$ is defined as

$$\begin{aligned} \Omega _3(x, y) = \frac{1}{2}(x^2+y^2)+\frac{1-\mu }{r_1}+\frac{\mu }{r_2}+\frac{1}{2}\mu (1-\mu ). \end{aligned}$$

(2)

The distance of the spacecraft from the principal attractor P$_1$, located at $(-\mu , 0)$, is $r_1=[(x+\mu )^2+y^2]^{1/2}$, whereas the distance from the secondary P$_2$, located at $(1-\mu , 0)$, is $r_2=[(x+\mu -1)^2+y^2]^{1/2}$.

The dynamics gives rise to five equilibria, known as Lagrange points, three of which are collinear along the x axis (L$_1$, L$_2$, L$_3$), whereas the remaining two (L$_4$, L$_5$) are located at the vertices of two equilateral triangles with base extending from P$_1$ to P$_2$. The autonomous dynamics enables an integral of motion, the Jacobi constant, which is equal to (Szebehely 1967)

$$\begin{aligned} J(x, y, \dot{x}, \dot{y}) = 2\Omega _3(x, y)-(\dot{x}^2+\dot{y}^2). \end{aligned}$$

(3)

Depending on the Jacobi constant value, the spacecraft may or may not transit through specific areas in the configuration space, the boundaries of which delimit Hill’s region. In particular, Lagrange points set the energy levels at which transit gates open or close, either enabling or preventing the spacecraft from passing trough different realms (Szebehely 1967). Figure 1 graphically represents Hill’s region of the Earth–Moon system where, for instance, a spacecraft does not have enough energy to open the gate in L$_2$. Therefore, the passage from the interior to the exterior region and vice versa would be prevented. Table 1 reports the physical constants used in this work, both for the Sun–Earth (SE) and the Earth–Moon (EM) CR3BPs. The units of distance, time, and speed are used to map scaled quantities into physical units.

Fig. 1

Earth–Moon Hill’s region ($J={3.184\,164\,143}$): forbidden area in gray, [EMrf]

Table 1 Physical parameters of the Sun–Earth and Earth–Moon CR3BPs

2.1.2 Planar Sun–Earth Moon-perturbed bi-circular restricted four-body problem

The planar Sun–Earth Moon-perturbed bi-circular restricted four-body problem (SE-BCR4BP) introduces the perturbation of the Moon into the SE-CR3BP model. The Moon is assumed to revolve about the Earth in a circular orbit. This makes the model non-coherent, and therefore, the motion of the primaries does not respect Newton’s laws (Koon et al. 2011).

Referring to Fig. 2, the dynamic equations expressed in the (x, y) rotating system of reference are formulated as (Koon et al. 2000a)

$$\begin{aligned} \begin{aligned} \ddot{x}&= 2\dot{y}+\frac{\partial \Omega _4^{\mathrm{S\!E}}}{\partial x}, \\ \ddot{y}&= -2\dot{x}+\frac{\partial \Omega _4^{\mathrm{S\!E}}}{\partial y}, \end{aligned} \end{aligned}$$

(4)

where the new effective potential can be calculated starting from Eq. (2). Hence,

$$\begin{aligned} \Omega _4^{\textrm{S}\!\textrm{E}}(x, y, t) = \Omega _3^{\textrm{S}\!\textrm{E}}(x, y) + \frac{\textrm{m}_\textrm{M}}{r_3(t)}, \end{aligned}$$

(5)

with $\mathrm m_M$ being the mass of the Moon scaled with respect to the units of the SE-CR3BP. The distance of the spacecraft from the Moon is

$$\begin{aligned} r_3(t) = \left[ \big (x+\mu _{\textrm{S}\!\textrm{E}}-1-\rho _{\textrm{M}}\cos (\alpha _\textrm{M}(t))\big )^2 + \big (y-\rho _{\textrm{M}}\sin (\alpha _\textrm{M}(t))\big )^2\right] ^{1/2}, \end{aligned}$$

(6)

Fig. 2

SE-BCR4BP model (not to scale)

where $\rho _{\textrm{M}}$ is the scaled distance of the latter from the Earth. A time dependence appears, resulting in a non-autonomous dynamic system. The rotating frame is rotated with respect to the inertial reference (X, Y) by an angle t, which assumes the meaning of non-dimensional time parameter of the Sun–Earth system. The Moon phase angle $\alpha _{\textrm{M}}(t)$ is calculated as

$$\begin{aligned} \alpha _{\textrm{M}}(t) = \omega _{\textrm{M}} (t-t^{\mathrm{r\!e\!f}})+\alpha _\textrm{M}^{\mathrm{r\!e\!f}}, \end{aligned}$$

(7)

where $\omega _{\textrm{M}}$ is the Moon angular velocity relative to the Sun–Earth rotating frame. Besides, at time $t^{\mathrm{r\!e\!f}}$, the initial phase of the Moon equals $\alpha _{\textrm{M}}^{\mathrm{r\!e\!f}}$. Table 2 reports the model parameters, scaled to the reference values of the SE-CR3BP.

Table 2 Physical parameters of the SE-BCR4BP

2.1.3 Planar Earth–Moon Sun-perturbed bi-circular restricted four-body problem

In the hierarchy of astrodynamic models employed to describe the motion of a spacecraft, the planar Earth–Moon Sun-perturbed bi-circular restricted four-body problem (EM-BCR4BP) holds great importance. Indeed, this dynamic model permits a spacecraft to perform cost-efficient exterior transfers if the proper Earth–Moon–Sun configuration is matched (Circi and Teofilatto 2001). The Sun revolves in a circular orbit about the center of mass of the Earth–Moon system, resulting in a non-coherent description of the underlying dynamics (Simó et al. 1995).

Fig. 3

EM-BCR4BP model (not to scale)

Referring to Fig. 3, the dynamic equations of the EM-BCR4BP in the (x, y) rotating reference frame are formulated by incorporating the Sun in the EM-CR3BP, leading to (Topputo 2013)

$$\begin{aligned} \begin{aligned} \ddot{x}&= 2\dot{y}+\frac{\partial \Omega _4^{\textrm{E}\!\textrm{M}}}{\partial x}, \\ \ddot{y}&= -2\dot{x}+\frac{\partial \Omega _4^{\textrm{E}\!\textrm{M}}}{\partial y}, \end{aligned} \end{aligned}$$

(8)

where

$$\begin{aligned} \Omega _4^{\mathrm{E\!M}}(x, y, t) = \Omega _3^{\textrm{E}\!\textrm{M}}(x, y) + \frac{\textrm{m}_\textrm{S}}{r_3(t)}-\frac{\textrm{m}_\textrm{S}}{\rho _{\textrm{S}}^2}\big (x\cos (\alpha _\textrm{S}(t))+y\sin (\alpha _{\textrm{S}}(t))\big ). \end{aligned}$$

(9)

In the new effective potential, $\mathrm m_S$ represents the scaled mass of the Sun, with $\rho _{\textrm{S}}$ being its scaled distance from the Earth–Moon barycenter. The distance of the spacecraft from the Sun is

$$\begin{aligned} r_3(t) = \left[ \big (x-\rho _{\textrm{S}}\cos (\alpha _\textrm{S}(t))\big )^2+\big (y-\rho _{\textrm{S}}\sin (\alpha _\textrm{S}(t))\big )^2\right] ^{1/2}. \end{aligned}$$

(10)

The synodic frame is rotated with respect to a non-rotating one (X, Y) by t, in this case representing the non-dimensional time parameter of the Earth–Moon system. Furthermore, the time dependence t makes this dynamic model non-autonomous. The Sun phase angle $\alpha _{\textrm{S}}(t)$ in the Earth–Moon rotating frame can be expressed as

$$\begin{aligned} \alpha _{\textrm{S}}(t) = \omega _{\textrm{S}} (t-t^{\textrm{r}\!\textrm{e}\!\textrm{f}})+\alpha _\textrm{S}^{\textrm{r}\!\textrm{e}\!\textrm{f}}, \end{aligned}$$

(11)

where $\omega _{\textrm{S}}$ is the Sun angular velocity relative to the same frame and $\alpha _{\textrm{S}}^{\textrm{r}\!\textrm{e}\!\textrm{f}}$ is the phase angle of the Sun at the reference time $t^{\textrm{r}\!\textrm{e}\!\textrm{f}}$. Table 3 reports the parameters of this model, scaled to the values of the EM-CR3BP.

Table 3 Physical parameters of the EM-BCR4BP

2.2 Theory of Functional Connections

The TFC permits to formulate expressions representing all possible functions satisfying certain constraints (Mortari 2017b). Closely related to spectral methods for functional interpolation (Boyd 2001), the TFC is based on a linear combination of basis functions. However, in the TFC a set of k linear constraints is analytically embedded in the formulation, hence specializing the resulting functional (Mortari 2017b). This representation has been proven successful to solve mathematical problems such as approximation of solutions of differential equations (Mortari 2017a; Mortari et al. 2019; Leake et al. 2020). Recently, the TFC was adopted to solve astrodynamic problems as well (Johnston et al. 2021; de Almeida Junior et al. 2021).

The functional $x(t, g_x(t))$ satisfying a set of k given linear constraints can be expressed as (Johnston et al. 2021)

$$\begin{aligned} x(t,g_x(t)) = g_x(t) + \sum _{j=1}^{k} \phi _j(t)\,\rho _j(t,g_x(t)), \end{aligned}$$

(12)

where $g_x(t)$ is a free function, $\phi _j(t)$ are the switching functions, and $\rho _j(t,g_x(t))$ are the projection functionals enforcing the constraints. The free function is obtained as linear combination of m basis functions. In this work, these are chosen to be a set of Chebyshev polynomials of the first kind ($\varvec{h}(z(t))\in {\mathbb {R}}^{m}$) generated recursively (Mason and Handscomb 2002). A transformation is necessary to map the domain of the Chebyshev polynomials ($z\in [z_0,\,z_{\textrm{f}}]$, $z_0 = -1$ and $z_{\textrm{f}} = 1$) to the time domain (Mortari et al. 2019). It results that $g_x(t) = \varvec{h}(z(t))^\top \varvec{\xi }_x$, where $\varvec{\xi }_x\in {\mathbb {R}}^{m}$ is the vector of coefficients that must be estimated to perform the functional interpolation. The switching functions are expressed as $\phi _j(t)=s_i(t)\alpha _{ij}$ where k linearly independent supporting functions $s_i(t)$ are multiplied by $\alpha _{ij}$ coefficients. The purpose is to obtain k switching functions that are active, i.e., equal to 1, only when the respective constraints must be enforced. Simultaneously, the remaining inactive switching functions equal 0. The reader can refer to Mortari (2017b) for more details on the TFC.

In this study, a TFC formulation represents the solution of a two-point boundary value problem, thus describing the planar motion of a spacecraft during its travel. Two functionals are therefore needed to approximate the evolution of states, specifically x(t) and y(t), where the initial and final positions at times $t_0$ and $t_{\textrm{f}}$, respectively, are fixed. Two supporting functions computed as $s_i(t) = t^{i-1}$, for $i = 1,2$, are adopted to derive the switching functions $\phi _j(t)=\alpha _{1j}+t\,\alpha _{2j}$ so that

$$\begin{aligned} \begin{aligned} \phi _1(t_0) = 1, \quad&\phi _1(t_{\textrm{f}}) = 0;\\ \phi _2(t_0) = 0, \quad&\phi _2(t_{\textrm{f}}) = 1. \end{aligned} \end{aligned}$$

(13)

Reformulating Eq. (13), the system

$$\begin{aligned} \begin{bmatrix} 1 &{} t_0 \\ 1 &{} t_{\textrm{f}} \end{bmatrix} \begin{bmatrix} \alpha _{11} &{} \alpha _{12} \\ \alpha _{21} &{} \alpha _{22} \end{bmatrix} = \begin{bmatrix} 1 &{} 0 \\ 0 &{} 1 \end{bmatrix} \end{aligned}$$

(14)

is solved for $\alpha _{ij}$, and, consequently, the switching functions become

$$\begin{aligned} \phi _1(t) = \frac{t_{\textrm{f}}-t}{t_{\textrm{f}}-t_0} \quad \text {and}\quad \phi _2(t) = \frac{t-t_0}{t_{\textrm{f}}-t_0}. \end{aligned}$$

(15)

Equation (12) is then specialized for the two-point boundary value problem as

$$\begin{aligned} x(t,g_x(t)) = g_x(t) + \frac{t_{\textrm{f}}-t}{t_\textrm{f}-t_0}(x_0-g_x(t_0))+\frac{t-t_0}{t_{\textrm{f}}-t_0}(x_\textrm{f}-g_x(t_{\textrm{f}})), \end{aligned}$$

(16)

where the projection functionals are formulated such that the constraints are enforced when the respective switching functions are active. The same procedure is employed to formulate $y(t,g_y(t))$, which is function of its own unknown coefficients vector $\varvec{\xi }_y\in {\mathbb {R}}^{m}$.

As mentioned before, this study utilizes Chebyshev polynomials to perform the functional interpolation. The linear mapping

$$\begin{aligned} z=z_0+\frac{z_{\textrm{f}}-z_0}{t_{\textrm{f}}-t_0}(t-t_0) \quad \longleftrightarrow \quad t = t_0+\frac{t_{\textrm{f}}-t_0}{z_\textrm{f}-z_0}(z-z_0) \end{aligned}$$

(17)

is adopted to link the domain where the polynomials are defined to the time domain. Consequently, if one calculates the nth-order derivative of the free function with respect to time, for a general coordinate it results that (de Almeida Junior et al. 2021)

$$\begin{aligned} \frac{\text {d}^ng(t)}{\text {d}t^n} = \frac{\text {d}^n\varvec{h}}{\text {d}z^n}^\top \varvec{\xi }\left( \frac{\text {d}z}{\text {d}t}\right) ^n, \end{aligned}$$

(18)

where the last term is the mapping coefficient computed as

$$\begin{aligned} \frac{\text {d}z}{\text {d}t} = \frac{z_{\textrm{f}}-z_0}{t_{\textrm{f}}-t_0}. \end{aligned}$$

(19)

The two functionals $x(t,g_x(t))$ and $y(t,g_y(t))$ derived above are then substituted in the second-order differential equations (Eqs. (1), (4), or (8)) to formulate two nonlinear algebraic expressions $\textrm{F}_x(t,\varvec{\Xi })$ and $\textrm{F}_y(t,\varvec{\Xi })$ where the coefficients vectors grouped as $\varvec{\Xi } = [\varvec{\xi }_x;\, \varvec{\xi }_y]$ are the unknowns. To estimate the coefficients, the time domain must be discretized at some node points. This generates a system of equations that, in this study, is solved through a root-finding algorithm. The Chebyshev–Gauss–Lobatto nodes provide an optimal discretization scheme to be used with Chebyshev orthogonal polynomials (Wright 1964). Moreover, this discretization is denser at the boundaries of the domain, which is beneficial when representing the full Earth–Moon transfer and the dynamics is, consequently, more sensitive to small variations at its endpoints. Still, this choice has the drawback of reducing sensitivity far from the extremities of the transfer. If the trajectory involves an intermediate close flyby at either primary, the true motion of the spacecraft may no longer be accurately represented. Assuming that N points split the time domain, it follows that (Boyd 2001)

$$\begin{aligned} z_k = -\cos \!\left( \frac{k\pi }{\text {N}}\right) \quad \text {for} \quad k = 0,1,2,\dots ,\text {N}-1 \end{aligned}$$

(20)

are the discretization points of the domain where the Chebyshev polynomials are calculated. The problem is formulated as a root-finding; therefore, the number of nodes is equal to the number of Chebyshev polynomials employed for the functional interpolation. The resulting system of algebraic equations is expressed as

$$\begin{aligned} \mathbb {{L}}(\varvec{\Xi }) = \begin{Bmatrix} \textrm{F}_x(t_0,\varvec{\Xi }) \\ \vdots \\ \textrm{F}_x(t_{\textrm{f}},\varvec{\Xi }) \\ \textrm{F}_y(t_0,\varvec{\Xi }) \\ \vdots \\ \textrm{F}_y(t_{\textrm{f}},\varvec{\Xi }) \\ \end{Bmatrix} = \varvec{0}. \end{aligned}$$

(21)

The root-finding problem implemented adopts a QR decomposition to represent the Jacobian matrix of the system (refer to Appendix A.1 for the analytical computation of the partial derivatives) and an iterative Newton’s method to converge to the solution within a defined tolerance (Boyd 2001).

2.3 Homotopy continuation

The homotopic continuation approach is a progressive root-finding algorithm that, starting from a known seeding solution of a simplified problem, eventually converges to the unknown zero of a more complex, but yet similar, problem. Typically, a convex homotopy formulation is expressed as (Wang and Topputo 2022)

$$\begin{aligned} {\textbf {H}}(\varvec{\Xi },\lambda ):= (1 - \lambda ) {\textbf {G}}(\varvec{\Xi }) + \lambda {\textbf {{Q}}}(\varvec{\Xi }), \end{aligned}$$

(22)

where $\varvec{\Xi }$ is the vector of unknowns of the original problem. The continuation parameter $\lambda \in [0,\,1]$ leads to the solution of the non-trivial problem (${\textbf {H}}(\varvec{\Xi }_{\textrm{f}},1)=\varvec{0}$) starting from the known zero of the simpler one (${\textbf {H}}(\varvec{\Xi }_0,0)=\varvec{0}$). Since Eq. (21) is formulated as $\mathbb {{L}}(\varvec{\Xi }):\mathbb {{R}}^{2\text {N}}\rightarrow \mathbb {{R}}^{2\text {N}}$, one gets that ${\textbf {H}}(\varvec{\Xi },\lambda ):\mathbb {{R}}^{2\text {N}}\times \mathbb {{R}}\rightarrow \mathbb {{R}}^{2\text {N}}$. Even though the previous contracted notation is generally adopted throughout the paper, Eq. (23) explicitly specializes the formulation for the specific study case of this work.

$$\begin{aligned} \begin{aligned} {\textbf {H}}^{\text {S\!E}}(\varvec{\Xi }^{\text {S\!E}},\lambda )&= (1 - \lambda ) \mathbb {{L}}^{\text {S\!E-C\!R\!3\!B\!P}}(\varvec{\Xi }^{\text {S\!E}}) + \lambda \mathbb {{L}}^{\text {S\!E-B\!C\!R\!4\!B\!P}}(\varvec{\Xi }^{\text {S\!E}}), \\ {\textbf {H}}^{\text {E\!M}}(\varvec{\Xi }^{\text {E\!M}},\lambda )&= (1 - \lambda ) \mathbb {{L}}^{\text {E\!M-C\!R\!3\!B\!P}}(\varvec{\Xi }^{\text {E\!M}}) + \lambda \mathbb {{L}}^{\text {E\!M-B\!C\!R\!4\!B\!P}}(\varvec{\Xi }^{\text {E\!M}}). \end{aligned} \end{aligned}$$

(23)

Equation (23) states that the objective is to gradually refine a solution, initially adhering to a simplified dynamic model, toward satisfying a more complex regime.

The pseudo-arclength homotopy continuation algorithm attempts to follow the implicitly defined curve $\varvec{c}(s)\in {\textbf {H}}^{-1}(\varvec{0})$ from point $(\varvec{\Xi }_0,0)$ to $(\varvec{\Xi }_{\textrm{f}},1)$, that is, the curve parameterized with respect to the arclength s whose points are the zeros of ${\textbf {H}}(\varvec{\Xi },\lambda )$. Differentiating ${\textbf {H}}(\varvec{c}(s))$, it results that (Allgower and Georg 2003)

$$\begin{aligned} {\textbf {H}}'(\varvec{c}(s))\dot{\varvec{c}}(s)=\varvec{0}\quad \text {with} \quad \Vert \dot{\varvec{c}}(s)\Vert = 1 \end{aligned}$$

(24)

because of the properties of the arclength. Equation (24) clearly states that the tangent $\dot{\varvec{c}}(s)$ is orthogonal to all rows of the Jacobian matrix ${\textbf {H}}'(\varvec{c}(s))$; hence, it spans the one-dimensional kernel $\textrm{ker}\big ({\textbf {H}}'(\varvec{c}(s))\big )$.

As mentioned, the objective of the homotopy continuation algorithm is to trace the curve $\varvec{c}(s)$ until the convergence to the final solution. This can be formulated as the initial value problem

$$\begin{aligned} \left\{ \begin{aligned}&\dot{\varvec{u}} = \dot{\varvec{c}}(s) \\&\varvec{u}_0 = [\varvec{\Xi }_0,0] \end{aligned} \right. \end{aligned}$$

(25)

that is iteratively solved through a predictor–corrector algorithm. An Euler prediction step $\varvec{u}_{k+1}=\varvec{u}_{k}+h\dot{\varvec{u}}_{k}$ with variable step-size h approximates the solution at the next iteration. A Newton-like method based on a QR decomposition corrects the prediction until the condition ${\textbf {H}}(\varvec{u}_{k+1}) = \varvec{0}$ is matched within a certain tolerance (Allgower and Georg 2003). Eventually, the algorithm converges to the solution of ${\textbf {{Q}}}(\varvec{\Xi })$.

3 Method

In this paper, the generation of Earth–Moon transfers in chaotic dynamics is addressed incrementally. Firstly, fundamentals of dynamical systems theory are exploited to design a seeding trajectory composed of two legs. Subsequent steps are implemented to gradually refine the legs until the final convergence to a full transfer, this one formulated in a high-fidelity dynamic model. A grid search, followed by the solution of nonlinear programming problems, allows to generate a wide range of locally optimal Earth–Moon transfers. For reference, Fig. 4 provides a global overview of the workflow practiced in this study, which is described in detail in this section.

Fig. 4

Earth–Moon transfers design procedure

3.1 Earth–Moon transfer generation

This research proposes a method to generate and optimize low-energy Earth–Moon transfers. To formulate the problem, a spacecraft is assumed to depart impulsively from a circular Low Earth Orbit (LEO) at an altitude of 167 km. The target is a circular 100 km altitude Low Lunar Orbit (LLO). The insertion into the destination orbit is assumed to be impulsive too. At the end of the design process, the motion of the spacecraft must comply with the dynamics prescribed by the planar EM-BCR4BP.

The two orbits have been chosen to align with numerous previous works (refer to Topputo (2013) for a list of references in this regard). Several solutions are therefore available in the literature for a comparison with the results of this research.

3.1.1 The patched three-body method

Low-energy transfers are enabled by pathways arising from invariant manifolds associated with the Lagrange points of the CR3BP (Belbruno et al. 2010). A spacecraft can exploit these dynamic structures to efficiently transit regions in the configuration space, usually at the expenses of longer transfer times (Oshima et al. 2019).

In the context of a Earth–Moon transfer taking advantage of the solar perturbation to lower the cost, invariant manifolds of both the SE-CR3BP and the EM-CR3BP are exploited to generate an initial seeding trajectory. This is enabled by the favorable condition that the dynamic structures arising from these models interact each other (Koon et al. 2001). Consequently, the preliminary design of a transfer trajectory can be split into two legs matching in position at an intermediate patching point. Eventually, the full transfer is represented in the EM-BCR4BP. This is feasible because the EM-BCR4BP exhibits both an internal and an external regions of prevalence, that is, each simplified model provides an accurate approximation of the real dynamics in a specific sector of the configuration space (Castelli 2011).

Firstly, two transfer legs are designed: a departure from the LEO represented in the SE-CR3BP and an arrival to the LLO whose dynamics adheres to the EM-CR3BP. The two legs are patched at a common point to allow for the continuity in position of the transfer. A small $\Delta \!\textrm{V}$ compensates the slightly different velocity at the patching point (Koon et al. 2001).

Departure leg in SE-CR3BP

Lyapunov orbits about Lagrange points are the fundamental dynamic structures enabling convenient pathways in the planar Sun–Earth system. Dynamical systems theory suggests that invariant manifolds arise from periodic orbits about Lagrange points (Belbruno et al. 2010). In particular, left and right stable ${\mathcal {S}}$ and unstable ${\mathcal {U}}$ invariant manifolds, associated with a certain periodic orbit, can be generated by slightly perturbing the conditions of the orbit itself (Koon et al. 2011). An example of L$_2$ left stable (${\mathcal {S}}_{\mathrm{L_2}}^{\mathrm{S\!E}}$) and unstable (${\mathcal {U}}_\mathrm{L_2}^{\mathrm{S\!E}}$) invariant manifolds in the SE-CR3BP is represented in Fig. 5a. As depicted, the energy of the Lyapunov periodic orbit must be such that its invariant manifolds reach the vicinity of the Earth. This permits to exploit the tube dynamics to design a non-transit transfer leg departing impulsively from the LEO.

Arrival leg in EM-CR3BP

The arrival at the LLO exploits, at first, the right stable invariant manifold associated with a L$_2$ Lyapunov orbit in the EM-CR3BP (${\mathcal {S}}_{\mathrm{L_2}}^{\mathrm{E\!M}}$). Successively, its left unstable invariant manifold (${\mathcal {U}}_{\mathrm{L_2}}^\mathrm{E\!M}$) permits reaching the destination orbit. This second leg is therefore a transit orbit flown from the outer realm of the system to the inner one. The design of this leg satisfies both energetic and geometric requirements. The former prescribes that the energy of the spacecraft, as computed in the EM-CR3BP, must be just above that of the L$_2$ point to open the rightmost gate. The latter imposes that ${\mathcal {U}}_{\mathrm{L_2}}^{\mathrm{E\!M}}$ reaches the arrival orbit at the Moon in configuration space. An impulsive maneuver performs the final orbital insertion. Figure 5b shows the framework where the arrival leg is designed.

Fig. 5

Examples of tubes dynamics of the CR3BPs

Patching of the systems

This step searches a patching point ensuring the continuity of the transfer legs in the configuration space. In this work, the arrival leg is designed first, and the departure one is derived consequently. A Poincaré section in the SE-CR3BP serves to study the patching point, thus helping in gluing the two dynamic systems (Koon et al. 2001).

3.1.2 Representation in Theory of Functional Connections

Once the two transfer legs have been numerically generated in their respective CR3BPs, TFC functionals are formulated as per Eq. (16). An analytical approximation of the motion of the satellite is thus available and can be exploited during the continuation and successive stages. From this point on, the literature is extended.

Taking as an example the departure leg in the SE-CR3BP system, the trajectory resulting from the procedure in Sect. 3.1.1 serves to estimate the unknown coefficients of $x_{\mathrm{d\!e\!p}}(t,g_x(t))$ and $y_\mathrm{d\!e\!p}(t,g_y(t))$. Each TFC formulation is constrained at its boundaries to guarantee that the positions at the departure from the Earth and at the patching point are those previously obtained by the numerical propagation. Likewise, the time of flight (TOF) is conserved. Chebyshev polynomials with a maximum degree of 1000 are utilized for the interpolation, implying a trade-off between interpolation accuracy and computational burden. In a complex and highly chaotic dynamic environment, accurately approximating the motion of a spacecraft necessitates a large functional basis, yet computational efficiency must be guaranteed. The number of basis functions directly determines the number of discretization points (see Sect. 2.2). The basis functions and the supporting functions, from which the switching functions are generated, must be linearly independent (Mortari et al. 2019). Consequently, a maximum polynomial degree of 1000 entails using 999 Chebyshev polynomials (ranging from degree 2 to 1000) and a corresponding number of points N for discretizing the domain of interest. A least-squares minimization approach is followed to approximate the unknown coefficients $\varvec{\xi }_x^{\mathrm{d\!e\!p}}$ and $\varvec{\xi }_y^\mathrm{d\!e\!p}$, initially set to zero. On this purpose, the evolution in time of the position, velocity, and acceleration of the leg, obtained by the numerical propagation of the dynamic equations, is interpolated at the N discretization points using cubic splines. This is fed into a least-squares minimization algorithm, which performs the preliminary estimation of the unknown coefficients. The two 3N$\times$N Jacobian matrices, one for each spatial coordinate, are computed analytically and decomposed in QR. Then, the dynamics is imposed as per Eq. (21) and Newton’s method with adaptive step size refines the estimation of the unknown coefficients.

This entire procedure is practiced for both the departure and arrival legs. Figure 6 idealizes the interpolation passages, summarizing the steps from the initial TFC functional formulation to the final dynamical convergence to the real temporal evolution. In the figure, the x coordinate is considered without loss of generality.

Fig. 6

TFC interpolation of motion. (1) Initial TFC functional formulation; (2) TFC representation after least-squares minimization; (3) TFC dynamical convergence; (4) real evolution of the motion (initial numerical propagation)

3.1.3 Continuation of the legs

The TFC formulation proves suitable whenever a continuation procedure is pursued. In this paper, a pseudo-arclength homotopic approach is implemented. Specifically, the departure leg from the Earth and the arrival one to the Moon, originally generated in the SE-CR3BP and EM-CR3BP, respectively, are continued into their corresponding, more realistic SE-BCR4BP and EM-BCR4BP models. A gradual introduction of the additional perturbations favors a smoother transition to the refined legs, preserving the original geometrical properties as much as possible. This is achievable because the initial and final positions of each leg, along with the TOF, remain consistent with those obtained in the preceding stages. Additionally, studying the deformation of the original legs due to additional gravitational forces offers valuable insights into the behavior of the dynamic environments.

Referring to the departure leg from the Earth, the perturbation of the Moon is gradually introduced in the dynamics by multiplying the scaled mass of the Moon $\mathrm m_M$ in Eq. (5) by the continuation parameter $\lambda$. The homotopy continuation algorithm follows the implicitly defined solution curve $\varvec{c}(s)$ to stretch the solution from complying to the SE-CR3BP dynamics to conform to the full dynamics of the SE-BCR4BP. An equivalent approach is implemented to continue the arrival leg from the patching point to the LLO. In this case, the scaled mass of the Sun $\mathrm m_S$ in Eq. (9) is multiplied by $\lambda$, so ensuring a gradual transition from the EM-CR3BP to the EM-BCR4BP.

In both cases, the homotopy continuation algorithm requires the computation of the Jacobian matrices. The partial derivatives of the equations are computed with respect to the coefficients of the TFC formulation and the parameter $\lambda$. The analytical expression of these partial derivatives is implemented to enhance the computational efficiency, thereby expediting the continuation process. For reference, Appendix A reports their mathematical derivation.

3.1.4 Final convergence to the transfer trajectory

In this last stage, the full Earth–Moon transfer trajectory has to be represented in the EM-BCR4BP. In this regard, the departure leg from the LEO must undergo a transformation in order to adhere to the dynamics of the destination model. Furthermore, applying the procedure explained in the previous sections, the two legs only match in configuration space at the patching point; therefore, a small impulsive maneuver is required to perform the transition. A final TFC formulation gradually smooths out the intermediate impulse, thereby obtaining a pure two-impulse Earth–Moon transfer.

Kinematic transformation

A preliminary step is necessary to express the kinematics of the departure leg into the EM-BCR4BP framework. This procedure generates a curve not strictly satisfying the dynamic equations in Eq. (8). Notwithstanding, this curve provides a good approximation of the actual behavior of the trajectory at the departure from the Earth in the destination dynamic model. To perform the kinematic transformation from the SE-BCR4BP to the EM-BCR4BP, the states of the departure leg at each time instant, as formulated through the TFC representation, are first expressed in the Earth-centered non-rotating reference frame (Appendix 1 in Topputo (2013)). A scaling is applied to convert the leg in Earth–Moon dimensionless quantities. Finally, a roto-translation expresses the curve in the EM-BCR4BP synodic frame. The transformation must take into account the instantaneous angles that the two rotating frames have with respect to the inertial one, thereby accounting for the correct Earth–Moon–Sun configuration at each instant along the departure leg. On this purpose, the Sun position in the EM-BCR4BP at the time of Poincaré section crossing is derived from simple geometrical considerations.

Dynamics imposition

In the second step, the dynamics of the EM-BCR4BP is imposed to the curve representing the departure from the Earth. Two new TFC functionals, one for each position coordinate, are formulated. A least-squares minimization followed by a root-finding iterative process leads to the convergence of the departure leg consistently with the new dynamic framework.

Smoothing to the full Earth–Moon transfer trajectory

A final step removes the small impulsive maneuver, still present at the patching point, otherwise needed to perform the full Earth–Moon transfer trajectory. In this last stage, two TFC functionals are formulated. These two pursue the objective of representing the full transfer by smoothly converging to a trajectory adhering to the dynamics of the EM-BCR4BP, still preserving the geometrical characteristics of the two original legs and the overall TOF. The two endpoints are the departure from the LEO and the arrival to the LLO. Again, a least-squares minimizing over the departure and arrival legs approximates the unknown coefficients of the TFC functionals. A root-finding refines this prediction by imposing the satisfaction of the destination dynamics. This process naturally converges to a ballistic transfer trajectory, not implying anymore the need of an intermediate impulsive maneuver. The aforementioned TFC functionals are constructed employing a linear combination of Chebyshev polynomials with a maximum degree of 1600. This permits obtaining a transfer trajectory well interpolating the correct time evolution of the position coordinates of the spacecraft, even when dealing with highly sensitive solutions. For the purpose of performance analysis, the initial conditions (i.e., position and velocity of the spacecraft at the departure from the LEO) obtained after the convergence of the TFC functionals are numerically propagated. Next, the solution via TFC is compared against the numerically propagated trajectory, which is considered representative of the actual behavior, to assess the accuracy and reliability of the devised method.

3.2 Optimization of two-impulse Earth–Moon transfers

The generation of short-duration, high-energy, Earth–Moon transfers represented in TFC in both the EM-CR3BP and EM-BCR4BP was investigated in de Almeida Junior et al. (2021). On the contrary, the focus of this research is to widen the spectrum of application of TFC to represent long-duration, low-energy, exterior trajectories. This section presents the procedure to design a wide range of transfers. In the proposed approach, a grid search is implemented to generate admissible trajectories via TFC. Consequently, a nonlinear programming problem is formulated and optimized through direct transcription and multiple shooting (Topputo 2013; Oshima et al. 2019).

3.2.1 Grid search using the Theory of Functional Connections

A grid search in the EM-BCR4BP over the departure and arrival bi-dimensional positions is performed. Specifically, the two circular orbits at the endpoints of the transfer are discretized starting from ${0}^{\circ }$, in correspondence of the original departure and arrival points, to ${360}^{\circ }$, by an angular step of ${5}^{\circ }$. The TOF is maintained equal to the transfer duration of the refined trajectory generated in Sect. 3.1.4 to ensure comparability between transfers. The initial time, and therefore the Sun angle at the departure from the Earth, is retained fixed as well. This choice is beneficial to reduce the dimensionality of the initial grid search. Conversely, the initial time is introduced as a variable parameter in the nonlinear programming optimization problem to account for the non-autonomous nature of the dynamics.

For each combination of departure and arrival positions, two TFC functionals, one per coordinate, are formulated to represent the constrained time evolution of the position of the spacecraft during the full Earth–Moon transfer. Since all solutions are expected to belong to a common family of exterior trajectories, the numerical values obtained in the final smoothing in Sect. 3.1.4 are utilized to initialize the unknown coefficients multiplying the Chebyshev polynomials. Root-finding refines this approximation such that the newly obtained transfer trajectory satisfies the dynamics of the EM-BCR4BP. The convergence to a feasible solution is, however, not granted for all combinations of departure and arrival positions. Furthermore, as mentioned in Sect. 2.2, if the algorithm approaches a solution implying an intermediate close passage to one of the primaries, the resulting trajectory may no longer satisfy the correct dynamics. To ensure convergence to a feasible trajectory, the initial conditions obtained through the TFC formulation are propagated numerically. This serves a dual purpose. Firstly, if the numerically propagated transfer intersects the destination LLO at an epoch close to the TOF, it indicates that the TFC functionals correctly interpolated the solution. Secondly, given that the TFC formulation embeds no constraints apart from the initial and final positions, there is the possibility that the surfaces of the Earth and/or of the Moon get intersected while attempting the transfer. The numerical propagation, therefore, excludes all those solutions crossing the Earth surface, whereas an event detector halts the propagation upon reaching the destination LLO, regardless of the final position and transfer duration.

The grid search procedure aims at generating a multitude of admissible transfer trajectories used to initiate the subsequent optimization. In Topputo (2013) and Oshima et al. (2019), the authors propagated initial conditions belonging to the departure LEO until a defined maximum time was reached, irrespective whether the achieved final point belonged to the destination LLO or not. Subsequently, these seeds were fed to a nonlinear programming optimizer. Differently, the procedure implemented in this study is expected to streamline the process of generating trajectories more effectively, since the initial solutions to be optimized are already full Earth–Moon transfers.

3.2.2 Direct transcription and multiple shooting optimization

The formulation of the nonlinear programming problem (Betts 1998), implemented to optimize the TFC transfer trajectories, is here briefly reported. The trajectories are first sectioned subdividing the total transfer time into $\text {N}-1$ evenly spaced segments, each one bounded by two time instants respecting the relation

$$\begin{aligned} t_i=t_{0}+\frac{i-1}{\text {N}-1}(t_{\textrm{f}}-t_{0}) \quad \text {for} \quad i = 1,\dots ,\text {N}. \end{aligned}$$

(26)

Each discretization node $n_i$ introduces four variables to the optimization problem, namely the instantaneous states of the spacecraft. Moreover, the initial and final transfer times are also regarded as variables of the problem to account for the time dependency of the dynamic system. Therefore, a total of $4\text {N}+2$ unknowns $\varvec{x}$ must be determined during the optimization process, with N being the number of discretization points computed as $\text {N}=\textrm{floor}\big ((t_\textrm{f}-t_0)/0.6\big )$ (Oshima et al. 2019), which thereby accounts for the transfer duration.

The sum of the costs of the departure and arrival impulsive maneuvers is the objective function to be minimized

$$\begin{aligned} {\mathcal {J}} = \Delta \!\mathrm{V_{d\!e\!p}} + \Delta \!\mathrm{V_{a\!r\!r}}, \end{aligned}$$

(27)

where, expanding its components (Yagasaki 2004),

$$\begin{aligned} \begin{aligned} \Delta \!{{\text {V}}_{{\text {d}}\!{\text {e}}\!{\text {p}}}} =&\sqrt{(\dot{x}_{1}-y_1)^2+(\dot{y}_1+x_1+\mu _{{\text {E}}\!{\text {M}}})^2}-\sqrt{\frac{1- \mu _{{\text {E}}\!{\text {M}}}}{\text {r}_{{\text {d}}\!{\text {e}}\!{\text {p}}}}}, \\ \Delta \!{\text {V}}_{{\text {a}}\!{\text {r}}\!{\text {r}}} =&\sqrt{(\dot{x}_{\text {N}}- y_{\text {N}})^2+(\dot{y}_{\text {N}}+x_{\text {N}}+\mu _{\text {E}\!{\text {M}}}-1)^2}- \sqrt{\frac{\mu _{{\text {E}}\!{\text {M}}}}{{\text {r}}_{{\text {a}}\!{\text {r}}\!{\text {r}}}}}. \end{aligned} \end{aligned}$$

(28)

In the equations, $\mathrm{r_{d\!e\!p}}$ and $\mathrm{r_{a\!r\!r}}$ represent the scaled departure and arrival radii of circular orbits about the primaries, specifically 167 km of altitude for the LEO and 100 km of altitude for the LLO. This formulation assumes that the velocities at the endpoints are tangential to the respective local circular orbits, and this tangentiality condition is, along with the belonging to the reference circular orbits, enforced by (Yagasaki 2004)

$$\begin{aligned} \begin{aligned} \varvec{\Gamma }_{\mathrm{d\!e\!p}}:=&\begin{bmatrix} (x_1+\mu _{\mathrm{E\!M}})^2+y_1^2-{\textrm{r}_{\textrm{d}\!\textrm{e}\!\textrm{p}}}^2\\ (x_1+\mu _{\mathrm{E\!M}})(\dot{x}_1-y_1)+y_1(\dot{y}_1+x_1+\mu _\mathrm{E\!M}) \end{bmatrix} = \varvec{0},\\ \varvec{\Gamma }_{\mathrm{a\!r\!r}}:=&\begin{bmatrix} (x_{\textrm{N}}+\mu _{\mathrm{E\!M}}-1)^2+y_{\textrm{N}}^2-\mathrm{r_{a\!r\!r}}^2\\ (x_{\textrm{N}}+\mu _{\mathrm{E\!M}}-1)(\dot{x}_{\textrm{N}}-y_{\textrm{N}})+y_\textrm{N}(\dot{y}_{\textrm{N}}+x_{\textrm{N}}+\mu _{\mathrm{E\!M}}-1) \end{bmatrix} = \varvec{0}. \end{aligned} \end{aligned}$$

(29)

Indeed, as per Pernicka et al. (1994), burning in the direction of the local velocity maximizes the spacecraft energy variation, so optimizing the injection maneuvers.

Additional $\text {N}-1$ equality constraints are required to guarantee the continuity of the trajectory at the nodes. These are formulated as

$$\begin{aligned} \varvec{f}_i = \varvec{\varphi }(\varvec{x}_i,t_i;t_{i+1})-\varvec{x}_{i+1} \quad \text {for} \quad i = 1,\dots ,\text {N}-1, \end{aligned}$$

(30)

where $\varvec{\varphi }(\varvec{x}_i,t_i;t_{i+1})$ represents the flow of the ith section of the trajectory. In total, the problem is then subject to $4+4(\text {N}-1)$ equality constraints. Inequality constraints ensure that at each node the spacecraft does not impact with any of the primaries. This is mathematically expressed as (Topputo 2013)

$$\begin{aligned} \varvec{\eta }_i:= \begin{bmatrix} \textrm{R}_{\textrm{E}}^2-(x_i+\mu _{\mathrm{E\!M}})^2-y_i^2\\ \textrm{R}_{\textrm{M}}^2-(x_i+\mu _{\mathrm{E\!M}}-1)^2-y_i^2\\ \end{bmatrix} < \varvec{0} \quad \text {for} \quad i = 1,\dots ,\text {N}, \end{aligned}$$

(31)

where $\textrm{R}_{\textrm{E}}$ and $\textrm{R}_{\textrm{M}}$ represent the scaled geometrical radii of the Earth and the Moon, respectively. Finally, an inequality constraint guarantees that the final time comes subsequently to the initial one, namely $\tau = t_{0}-t_{\textrm{f}} < 0$. Overall, $2\text {N}+1$ inequality constraints are introduced in the problem.

In summary, the optimization problem aims to determine $4\text {N}+2$ unknowns while being subject to $4\text {N}$ equality constraints and $2\text {N}+1$ inequality constraints. Upon satisfying the latter, the presence of some degrees of freedom is beneficial to converge to a local optimal solution. The problem as here formulated is solved using the MATLAB function fmincon (active-set algorithm, ${10^{-10}}$ objective and constraints tolerances, Runge–Kutta algorithm of orders 7 and 8 (RK78) with absolute and relative tolerances of 2.5$\times 10^{-14}$ for trajectories integration). The gradient of the objective function and the Jacobian matrices of the constraints are analytically computed and provided to the optimizer (Topputo 2013; Oshima et al. 2019).

4 Results

The method outlined in Sect. 3.1 is now applied to design a baseline Earth–Moon transfer within the EM-BCR4BP dynamic model. Consequently, the procedure developed in Sect. 3.2 is executed to generate low-energy trajectories, later optimized through the nonlinear programming formulation.

4.1 Exterior transfer trajectory design

4.1.1 Transfer legs generation

The design process starts with the identification of a suitable energy level for the L$_2$ Lyapunov orbit in the EM-CR3BP. A Jacobi constant equal to 3.164 164 143 guarantees the opening of the L$_2$ gate and generates a left unstable manifold ${\mathcal {U}}_{\mathrm{L_2}}^{\mathrm{E\!M}}$ approaching the destination LLO. On the Sun–Earth side, a Lyapunov orbit of Jacobi constant equal to 3.000 778 817 produces a left stable manifold ${\mathcal {S}}_{\mathrm{L_2}}^{\mathrm{S\!E}}$ reaching the departure LEO. The propagation of these manifolds permits to start an iterative process leading to the generation of the two legs.

First of all, a horizontal Poincaré section is defined in between the Earth and the Moon in configuration space ($y=0$) in the EM-CR3BP system. Propagating ${\mathcal {U}}_{\mathrm{L_2}}^{\mathrm{E\!M}}$ until this section, the cutting of the two-dimensional manifold reduces to a one-dimensional closed curve easily representable in a plane. For the analysis, it is useful to plot this curve in the $(x, \dot{y})$ plane. Choosing a point inside this curve whose x coordinate equals the destination point on the LLO, a suitable transit orbit is obtained. The remaining state $\dot{x}$ can be readily calculated using Eq. (3).

Fig. 7

Earth–Moon–Sun configuration at patching point time (not to scale)

The conditions at the patching instant between the two dynamic systems must be defined. In this regard, a proper Earth–Moon–Sun configuration enabling the generation of a continuous transfer trajectory is sought. To simplify the analysis, the angle between the rotating frame of the SE-CR3BP and the inertial one is set to zero at the time the spacecraft is supposed to switch leg. The patching point is conveniently forced to belong, in configuration space, to a vertical line above the Earth in the Sun–Earth system, as depicted in Fig. 7. A Poincaré section $\Phi$ is thus defined with coordinates $x = 1-\mu _{\mathrm{S\!E}}$ and $y > 0$, that is, at an angle of $90^{\circ }$ in the Sun–Earth synodic frame. An iterative process is initiated to seek for a proper section on the right stable manifold ${\mathcal {S}}_{\mathrm{L_2}}^\mathrm{E\!M}$ of the Earth–Moon system such that once the resulting one-dimensional curve is kinematically expressed in the Sun–Earth system at $\Phi$, certain properties are assured. Figure 7 depicts the Earth–Moon–Sun instantaneous inertial configuration at the epoch the trajectory switches from the departure leg to the arrival one. The angle $\theta _{\mathrm{E\!M}}$ is formed by the Earth-to-Moon direction with respect to the X axis of the inertial frame at the time of the Poincaré section crossing. The objective is to find the angle $\varphi$ between the Poincaré section $\Phi$ and the Earth-to-Moon axis such that a spacecraft, placed in configuration space along $\Phi$, would ultimately reach the LLO if its states are propagated forward in the EM-CR3BP, whereas it would approach the LEO if backward propagated in the SE-CR3BP. Starting from an initial value of ${0}^{\circ }$, $\varphi$ is gradually incremented using a unitary step angle. At each iteration, the cut in the correspondence of $\Phi$ in the Sun–Earth system is generated and visualized in the $(y, \dot{y})$ plane. It is found that, setting $\varphi =60^{\circ }$, a suitable configuration of the three attractors is obtained. Figure 8 shows the resulting cut in the $(y, \dot{y})$ plane. The two curves identify the ${\mathcal {U}}_{\mathrm{L_2}}^{\mathrm{S\!E}}$ and the ${\mathcal {S}}_{\mathrm{L_2}}^{\mathrm{E\!M}}$ manifolds. The representation of ${\mathcal {S}}_{\mathrm{L_2}}^{\mathrm{E\!M}}$, originally generated in the Earth–Moon system, is the result of a transformation accounting for the instantaneous relative configuration of the three primaries. Point A indicates the state of the spacecraft after back-propagating the arrival conditions at the LLO previously defined and expressing the states at the correspondence of the patching point in the Sun–Earth system. As expected, this point lies internally to ${\mathcal {S}}_{\mathrm{L_2}}^{\mathrm{E\!M}}$, therefore confirming that the arrival leg is a transit orbit. To guarantee the continuity of the trajectory in the configuration space, the two legs must share the same y value on this plane. Recalling that the departure leg is a non-transit orbit in the Sun–Earth system, its states at $\Phi$ must lie outside ${\mathcal {U}}_{\mathrm{L_2}}^{\mathrm{S\!E}}$. Figure 8 helps in choosing point D such that, by back-propagation, the spacecraft twists and approaches the departure orbit about the Earth. Furthermore, as per Koon et al. (2001), the closer point D is to the unstable curve, the stronger the twisting effect will be. The propagation is terminated when the LEO is crossed. In Fig. 9, the result of this design can be appreciated in the Sun–Earth system. In this projection, the arrival leg and ${\mathcal {S}}_{\mathrm{L_2}}^\mathrm{E\!M}$ do not respect the dynamics of the SE-CR3BP since they are mere outcomes of the aforementioned transformation.

Fig. 8

Poincaré section $\Phi$ in Sun–Earth system

Fig. 9

Transfer legs, [SErf]. The spacecraft departs the Earth in a non-transit orbit, twists, and approaches the Moon from outside of its realm

4.1.2 Formulation in Theory of Functional Connections and homotopy continuation

The two legs, constituting the transfer seed, are formulated in TFC. For each leg, two TFC functionals are implemented and the unknown coefficients are estimated through least-squares minimization and root-finding.

Fig. 10

Homotopy continuation of transfer seeding legs, fixed TOF

The continuation of the departure leg is presented in Fig. 10a, whereas Fig. 10b shows the gradual refinement of the arrival leg at the Moon. The TOF of each leg is enforced to be equal to that of the respective seeding one. Hill’s regions depicted in the figures are generated over the seeding Jacobi constant values. In the plots, the transition is represented as a gradual change in color from red to black, for the departure leg, and from red to blue for the arrival one. The convergence to the refined legs is obtained by progressively increasing the lunar and solar perturbations, respectively. In the analysis, the step size h adopted in the Euler prediction step to solve Eq. (25) is set to 0.1. However, during the homotopic continuation process, it is allowed to vary freely if particularly challenging iterations are encountered.

An alternative formulation of TFC incorporates a variable TOF. Given an initial time $t_0$, the final time $t_{\textrm{f}}$ of the transfer leg can be estimated along with the unknown coefficients. To preserve the dimensionality of the problem, the maximum degree of the basis functions adopted for the TFC formulation of the y coordinate is reduced by one. The introduction of a variable transfer duration was expected to better indulge the dynamical deformation during the homotopic continuation process, offering potential advantages. Nevertheless, the least-squares minimization and root-finding procedures employed prior to continuation lead to solutions deviating from the initial seeding legs, as shown in Fig. 11. This deviation is particularly notable in the case of the arrival leg, as depicted in Fig. 11b, where the new solution crosses Hill’s region of the original seed, shown in green. Moreover, it turns out that the convergence in case of variable duration is very sensitive to the number of basis functions employed for the TFC formulation. If a different maximum degree for the interpolating polynomials had been utilized, the algorithm would have converged to another admissible, yet different, solution. This interesting behavior may be the focus of future research. Since no significant improvements have been identified with this new formulation and considering the dissimilarity to the original geometry of the seeding legs, the remaining analysis is based on the refined legs with fixed TOF.

Fig. 11

Homotopy continuation of transfer seeding legs, free TOF

Fig. 12

Solar effect to arrival leg, [EMrf]. TFC compensates for the perturbing acceleration that would, otherwise, deviate the desired trajectory

By virtue of the continuation process, it is interesting to observe the gradual deformation of the arrival leg caused by the progressive enhancement of the perturbation of the Sun. Figure 12 illustrates the acceleration vectors introduced by the additional attractor at various time instants of the seeding arrival leg, sampled at one-day intervals during the transfer time. Small blue dots denote the corresponding instants on the continued leg. To reach the destination LLO within a fixed TOF, the spacecraft has to fly on a trajectory that compensates for the new perturbative acceleration introduced into the dynamics. Consequently, the resulting refined leg exhibits a drifting rightwards. On the contrary, if not accounted for, the solar attraction disrupts the seeding leg, so preventing it from reaching the Moon realm. For reference, this trajectory is represented in black with small dots marking samples at one-day intervals.

4.1.3 Final smoothing

The two legs, refined into their respective higher-fidelity dynamic models, are the building blocks over which the final Earth–Moon transfer is constructed. The gradual transition toward more realistic dynamics facilitates the design of a trajectory preserving the qualitative behavior of the seeding legs.

As detailed in Sect. 3.1.4, a kinematic transformation of the departure leg is necessary to trace a curve in the Earth–Moon synodic frame. A TFC formulation over the departure leg imposes its compliance with the dynamics prescribed by the EM-BCR4BP model, thereby obtaining a coherent representation. Two last TFC functionals are constructed to approximate the full Earth–Moon transfer, thus smoothing out the intermediate impulsive maneuver. The least-squares minimization takes few milliseconds, whereas the consequent Newton’s algorithm converges in 3.80 seconds after 12 iterations² to a norm of the residuals, these computed as per Eq. (21), equal to $10^{-8}$. It should be emphasized that no other constraints are imposed to the functional formulation besides the positions at the endpoints. This means that the full trajectory may intersect the LLO before the final time. This happens, for example, if the destination position is on the other side of the Moon with respect to the approaching direction. To avoid this occurrence, a root-finding problem is employed to determine the epoch at which the spacecraft first crosses the LLO. This search is facilitated by the analytical formulation in TFC of the spacecraft position.

The full transfer trajectory is depicted in the Earth–Moon synodic frame in Fig. 13a, whereas Fig. 13b shows the results in the Earth-centered quasi-inertial (ECqi) frame. Hill’s region included in the synodic representation is generated considering the instantaneous Jacobi value at arrival time, equal to 3.151 261 080. Table 4 presents the initial conditions of the transfer in the Earth–Moon synodic frame, its duration, and cost. This information allows independent reproduction. To improve accuracy, the values are obtained numerically propagating a-posteriori the TFC initial conditions, considering an event detector at LLO crossing. A RK78 integrator with absolute and relative tolerances of $2.5\times 10^{-14}$ is utilized.

Fig. 13

Earth–Moon transfer trajectory

4.1.4 Error analysis

The accuracy of the TFC solution is assessed over the trajectory propagated numerically. Figure 14a depicts the logarithmic evolution of the TFC position coordinates percent errors computed as

$$\begin{aligned} \text {e}_\% = \left| \frac{\text {TFC}-\text {RK78}}{\text {RK78}}\right| \times 100. \end{aligned}$$

(32)

The red and black vertical lines in Fig. 14a correspond to the instants when the spacecraft crosses the x and y axes of the EM-BCR4BP system, respectively. As expected, the progression of the percent errors exhibits a consistent cyclic pattern, mirroring a trend reminiscent of the evolution of the spacecraft position in the Earth–Moon synodic frame. Although a gradual increase in percent errors is observed over time, they consistently remain bounded below 1.1% even when the trajectory eventually approaches the Moon. Figure 14b, instead, shows the evolution of the time-synchronized distance between the two trajectories. The green vertical line indicates the patching epoch of the initial two seeding legs. The maximum planar distance between the trajectories obtained via TFC and numerically propagating the initial conditions reaches a value of 8.60 km, in the near proximity of the destination position.

For the sake of completeness, time-frames where the EM-CR3BP better represents the dynamic behavior of the spacecraft (initial and final gray areas) and where, on the contrary, the SE-CR3BP is more appropriate (central yellow area), are distinguished in the figures. This discretization aligns with the concept of regions of prevalence, as explored in Castelli (2011), thereby enabling a practical classification of the three transfer phases in departure, coasting, and arrival. Nonetheless, due to the relatively short duration of the departure and the proper initial configuration of the primaries, the division into a departure plus coastal phase and a final arrival one closely approximates reality, allowing for the design procedure adopted in this research.

Table 4 Earth–Moon transfer trajectory

Fig. 14

Error analysis to assess the accuracy of the TFC solution with respect to the numerically propagated counterpart

4.2 Earth–Moon transfers optimization

The procedure detailed in Sect. 3.2 is now employed to generate a large number of Earth–Moon transfer trajectories in the EM-BCR4BP system. Initially, the grid search is conducted to generate low-energy exterior transfers, these represented in TFC. Approximately 2300 compliant trajectories are obtained, of which about 2000 are successfully optimized through direct transcription and multiple shooting. During processing, not all input TFC solutions converge to their optimized counterparts. This occurs either because a maximum number of iterations or function evaluations is reached (set to $10^4$ and $10^6$, respectively), or when, despite reaching convergence, the solution fails to meet the maximum tolerance error over the problem constraints, set to $10^{-10}$. Furthermore, the convergence speed strongly depends on the conditions of the input TFC solution, as it is discussed later in the section.

Fig. 15

Most efficient Earth–Moon transfer resulting from the TFC grid search (black) and its optimized counterpart (red). The solutions overlap almost perfectly

Figure 15 displays the most efficient transfer achieved through the initial grid search, which features a total cost of 3840.32 ms$^{-1}$ and a TOF of 162.05 days. The algorithm converges in approximately 38 seconds, after 111 iterations$^{2}$. Increasing the admissible norm of the residuals above $10^{-8}$ would accelerate convergence. However, this comes at the cost of reduced accuracy in the results, thereby opening the possibility of obtaining a trajectory that deviates from the true dynamics. The computational cost required for the least-squares minimization process to converge depends on the specific combination of boundary conditions considered. The chaotic nature of the environment makes certain regions of the phase space more dynamically challenging, necessitating higher computational time to successfully generate trajectories traversing those areas. Furthermore, the closer the boundaries align with those generating the reference trajectory obtained in Sect. 4.1.3, the faster the convergence is. Indeed, as discussed in Sect. 3.2.1, the unknown coefficients multiplying the basis functions are always initialized based on that initial solution. After solving the nonlinear programming problem, the optimized transfer trajectory total cost decreases to 3836.75 ms$^{-1}$, with a duration of 162.01 days. The modest improvement in transfer efficiency is attributed to the nearly tangential velocities to the departure and arrival circular orbits that the TFC trajectory already features. The multiple shooting algorithm converges in 0.65 seconds, after 8 iterations (20 function evaluations)$^{2}$. The convergence speed confirms that the input TFC solution is close to being a local minimum for the optimization problem. Therefore, the algorithm cannot significantly further improve the performances of the trajectory. The two transfers match almost perfectly, as their representations entirely overlap. In Fig. 15a, the small black dots indicate the points where the TFC trajectory is discretized prior to the optimization process. The forbidden region is computed over the arrival energy of the TFC transfer that is, however, almost identical to that of the optimized counterpart. Table 5 summarizes the initial conditions and performances of the Earth–Moon transfers here presented. The second column refers to the solution obtained with the TFC grid search, whose optimized counterpart is instead described in the third one.

Table 5 TFC grid search and optimized trajectory (best TFC)

Analyzing the results after the optimization of all TFC trajectories, the most efficient Earth–Moon transfer is reported in Fig. 16. In this case, Hill’s region is not shown because of the largely different Jacobi values between the two trajectories at arrival. The TFC solution, represented in black, presents a total transfer cost of 10814.74 ms$^{-1}$ and a duration of 162.05 days. The convergence time is about 44 seconds, and 126 iterations are required$^{2}$. The enormous cost for the maneuvers is due to the unfortunate conditions at the departure and arrival points, where the local velocities are almost perpendicular to the respective circular orbits. Nevertheless, as clearly shown in Fig. 16a, the optimized counterpart includes a Moon flyby at an altitude of 4032.91 km over its surface, 3.98 days after the departure from the Earth. This beneficial effect results in a transfer cost that is the cheapest obtained in this analysis, namely 3775.11 ms$^{-1}$ with a TOF of 163.68 days. The multiple shooting algorithm converges in 440.25 seconds, after 8664 iterations (218 767 function evaluations)$^{2}$. The large number of iterations confirms that the input TFC solution is far from being a local optimum of the problem. Its considerable cost and non-tangentiality to the departure and arrival orbits compel the algorithm to explore the search space more extensively. During this process, the closest basin of attraction leads to the described solution, which proves to be more cost-efficient than the one in the previous case. Table 6 reports the results of this analysis.

Fig. 16

Most efficient Earth–Moon transfer resulting from the optimization procedure and its TFC counterpart. The optimization converges to a solution performing a lunar flyby at an altitude of 4032.91 km over the Moon surface

Figure 17 plots the performances, expressed in terms of TOF and total cost, of all Earth–Moon transfers obtained after multiple shooting optimization. Despite the TFC solutions provided to the optimization algorithm feature a TOF of about 162.05 days, the converged counterparts are distributed within a range of ±20 days about the reference duration. Families of transfers emerge and are identified as clusters in the picture. Trajectories experiencing a lunar flyby are grouped within the black rectangle, the most efficient of which is marked with the asterisk. Remaining solutions do not exploit any intermediate close passage to the Moon, hence the higher costs.

Table 6 TFC grid search and optimized trajectory (best optimized)

Fig. 17

Performances of optimized trajectories. Clusters of solutions emerge, hence highlighting common transfers families

Table 7 Examples of Earth–Moon transfers available in the literature

For comparison, Table 7 includes examples of exterior Earth–Moon transfer trajectories available in the literature, ordered by TOF. For each work, the performances of the cheapest solution among those published are reported. The cost of the most efficient trajectory found after multiple shooting optimization aligns with the results of the references reported. Particularly, the inclusion of a lunar flyby generally proves beneficial in reducing the transfer cost. Regarding the TOF, the approach proposed in this study fixes it after generating the two seeding legs. Accordingly, all trajectories obtained with the TFC grid search feature almost identical TOFs. Consequently, the basins of attraction lead to optimized solutions exhibiting similar durations. To potentially reduce the transfer time, one could explore more convenient configurations of the three attractors at the intermediate patching point when generating the two seeding legs. Nevertheless, this fine tuning is beyond the scope of the research and could be the subject for future work. The conducted analysis suffices in identifying proper transfer conditions, irrespective of the resulting overall duration. A second option involves fixing the TOF during multiple shooting optimization. However, a transfer duration that significantly differs from the reference one could impede the convergence of the optimization algorithm. In fact, the input TFC trajectory may lie far from any admissible basin of attraction within the search space.

5 Conclusion

A novel methodology to design two-impulse, low-energy trajectories in multibody dynamic environments is presented in this work. The recently developed Theory of Functional Connections (TFC) proves suitable to generate exterior Earth–Moon transfers leveraging the solar perturbation, despite the chaoticity of the models.

An incremental approach is employed to guide the design toward the convergence of the sought solution. Firstly, two legs are generated to approximate an Earth–Moon transfer patching two planar circular restricted three-body problems. A homotopic continuation process based on the pseudo-arclength is implemented to gradually stretch the two legs. In a final step, the full Earth–Moon transfer trajectory is represented in TFC. After convergence, the resulting two-impulse trajectory adheres to the planar Earth–Moon Sun-perturbed, bi-circular restricted four-body problem dynamic model. A grid search via TFC over position points belonging to the departure and arrival circular orbits is performed to automatically generate more than 2000 trajectories, the best of which features a transfer cost of 3840.32 ms$^{-1}$ with a time of flight of 162.05 days. A nonlinear programming problem is formulated to optimize the transfers. After optimization, the cheapest one requires 3775.11 ms$^{-1}$ and takes 163.68 days.

The analytical representation in TFC proves to be particularly convenient anytime the solution must be refined into a more complex problem. Its synergy with a homotopic continuation procedure is indeed investigated. The results show that this approach smoothly and precisely refines trajectories into higher-fidelity dynamic models. To bound the number of interpolating polynomials necessary to represent chaotic solutions in TFC, it is conjectured that a combination of different basis functions might generate an optimal set of interpolating polynomials. Future research may focus on this aspect to reduce the computational heaviness of the algorithm.

TFC provides a favorable formulation to generate a multitude of admissible transfer trajectories directly connecting the departure and destination orbits. Since the representation in TFC is based on a time domain discretization that is denser at the endpoints of the transfer, poor performances are obtained if the spacecraft gets too close to one of the primaries besides the two extremities. However, this possibility is not of interest for the purpose of this research. Unlike similar works, a grid search based on the numerical propagation of the dynamic equations is no longer necessary to obtain compliant trajectories, thus enhancing efficiency. Overall, coupling TFC with continuation algorithms provides a valuable alternative to standard trajectory design methodologies in chaotic environments.

Appendix A: TFC and homotopy analytical derivatives

This appendix presents the analytical partial derivatives of the dynamic equations, reformulated as per Eq. (21).

1.1 A.1 Derivatives with respect to the unknown Chebyshev polynomials coefficients

The partial derivatives of the equations with respect to the unknown Chebyshev polynomials coefficients are derived, following the chain rule, as

$$\begin{aligned} \begin{aligned} \frac{\partial \textrm{F}_x}{\partial \varvec{\Xi }} =&\left[ \frac{\partial \textrm{F}_x}{\partial \ddot{x}} \frac{\partial \ddot{x}}{\partial \varvec{\xi }_x} + \frac{\partial \textrm{F}_x}{\partial x} \frac{\partial x}{\partial \varvec{\xi }_x},\, \frac{\partial \textrm{F}_x}{\partial \dot{y}} \frac{\partial \dot{y}}{\partial \varvec{\xi }_y} + \frac{\partial \textrm{F}_x}{\partial y} \frac{\partial y}{\partial \varvec{\xi }_y} \right] , \\ \frac{\partial \textrm{F}_y}{\partial \varvec{\Xi }} =&\left[ \frac{\partial \textrm{F}_y}{\partial \dot{x}} \frac{\partial \dot{x}}{\partial \varvec{\xi }_x} + \frac{\partial \textrm{F}_y}{\partial x} \frac{\partial x}{\partial \varvec{\xi }_x},\, \frac{\partial \textrm{F}_y}{\partial \ddot{y}} \frac{\partial \ddot{y}}{\partial \varvec{\xi }_y} + \frac{\partial \textrm{F}_y}{\partial y} \frac{\partial y}{\partial \varvec{\xi }_y} \right] , \\ \end{aligned} \end{aligned}$$

(A1)

where

$$\begin{aligned} \begin{aligned} \frac{\partial x}{\partial \varvec{\xi }_x}&= \frac{\partial y}{\partial \varvec{\xi }_y} = \varvec{h}^\top - \frac{t_{\textrm{f}}-t}{t_{\textrm{f}}-t_0} \varvec{h}\small |_0^\top - \frac{t-t_0}{t_{\textrm{f}}-t_0} \varvec{h}\small |_{\textrm{f}}^\top , \\ \frac{\partial \dot{x}}{\partial \varvec{\xi }_x}&= \frac{\partial \dot{y}}{\partial \varvec{\xi }_y} = \frac{\text {d}\varvec{h}}{\text {d}z}^\top \frac{z_{\textrm{f}}-z_0}{t_{\textrm{f}}-t_0} + \frac{1}{t_{\textrm{f}}-t_0} \varvec{h}\small |_0^\top - \frac{1}{t_{\textrm{f}}-t_0} \varvec{h}\small |_{\textrm{f}}^\top , \\ \frac{\partial \ddot{x}}{\partial \varvec{\xi }_x}&= \frac{\partial \ddot{y}}{\partial \varvec{\xi }_y} = \frac{\text {d}^2\varvec{h}}{\text {d}z^2}^\top \left( \frac{z_{\textrm{f}}-z_0}{t_{\textrm{f}}-t_0}\right) ^2. \\ \end{aligned} \end{aligned}$$

(A2)

This formulation is valid for all dynamic models represented by Eqs. (1), (4), and (8).

1.2 A.2 Derivatives with respect to the homotopy continuation parameter $\lambda$

In the SE-BCR4BP, the partial derivatives of the equations with respect to the homotopy continuation parameter are

$$\begin{aligned} \begin{aligned} \frac{{\partial } \textrm{F}_x}{{\partial }\lambda }&= \mathrm{m_M} \frac{x+\mu _{\mathrm{S\!E}}-1-\rho _{\textrm{M}}\cos (\alpha _{\textrm{M}}(t))}{r_3^3(t)}, \\ \frac{{\partial } \textrm{F}_y}{{\partial }\lambda }&= \mathrm{m_M} \frac{y-\rho _{\textrm{M}}\sin (\alpha _{\textrm{M}}(t))}{r_3^3(t)}, \\ \end{aligned} \end{aligned}$$

(A3)

whereas, in the EM-BCR4BP, they results to be

$$\begin{aligned} \begin{aligned} \frac{{\partial } \textrm{F}_x}{{\partial }\lambda }&= \mathrm{m_S} \left( \frac{x-\rho _{\textrm{S}}\cos (\alpha _{\textrm{S}}(t))}{r_3^3(t)}+\frac{\cos (\alpha _{\textrm{S}}(t))}{\rho _{\textrm{S}}^2}\right) , \\ \frac{{\partial } \textrm{F}_y}{{\partial }\lambda }&= \mathrm{m_S} \left( \frac{y-\rho _{\textrm{S}}\sin (\alpha _{\textrm{S}}(t))}{r_3^3(t)}+\frac{\sin (\alpha _{\textrm{S}}(t))}{\rho _{\textrm{S}}^2}\right) . \\ \end{aligned} \end{aligned}$$

(A4)