Uncertainties associated with integral-based solutions to geodetic boundary-value problems

Abstract

Physical geodesy applies potential theory to study the Earth’s gravitational field in space outside and up to a few km inside the Earth’s mass. Among various tools offered by this theory, boundary-value problems are particularly popular for the transformation or continuation of gravitational field parameters across space. Traditional problems, formulated and solved as early as in the nineteenth century, have been gradually supplemented with new problems, as new observational methods and data are available. In most cases, the emphasis is on formulating a functional relationship involving two functions in 3-D space; the values of one function are searched but unobservable; the values of the other function are observable but with errors. Such mathematical models (observation equations) are referred to as deterministic. Since observed data burdened with observational errors are used for their solutions, the relevant stochastic models must be formulated to provide uncertainties of the estimated parameters against which their quality can be evaluated. This article discusses the boundary-value problems of potential theory formulated for gravitational data currently or in the foreseeable future used by physical geodesy. Their solutions in the form of integral formulas and integral equations are reviewed, practical estimators applicable to numerical solutions of the deterministic models are formulated, and their related stochastic models are introduced. Deterministic and stochastic models represent a complete solution to problems in physical geodesy providing estimates of unknown parameters and their error variances (mean squared errors). On the other hand, analyses of error covariances can reveal problems related to the observed data and/or the design of the mathematical models. Numerical experiments demonstrate the applicability of stochastic models in practice.

1 Introduction

Physical geodesy is focused on studying the Earth’s physical properties (primarily its gravitational field and rotation) with regard to their geodetic applications, see, e.g., (Heiskanen and Moritz 1967). Similar to other sub-fields of geodesy (Vaníček and Krakiwsky 1987, Sect. 4.1), it combines theory, observational experiments, data analysis, and product applications. Although physical geodesy has used the classical Newtonian theory of gravitation for decades, see, e.g., (Vaníček and Krakiwsky 1987, Sect. 6.1), Einstein’s theory is increasingly applied nowadays as new observation sensors and methods are proposed and implemented, e.g. (Soffel and Frutos 2016).

The classical concept of physical geodesy is largely based on the potential theory which provides basic tools for describing the Earth’s gravitational field using the gravitational potential (geopotential) that satisfies Laplace’s differential equation in mass-free 3-D space. This condition limits the area of interest to the Earth’s exterior, where the harmonicity of the geopotential and its functionals (gravitational parameters in general) is guaranteed (neglecting atmosphere and all extraterrestrial masses). However, in geodesy there are also problems related to the Earth’s interior, such as the geoid modelling, where appropriate measures and methods must be implemented (gravitational effects of topographic and atmospheric masses outside the geoid are computed by forward modelling techniques and removed from observed data) to extend the applicability of the potential theory.

The potential theory has developed well since its introduction in the nineteenth century. In particular, the apparatus of boundary-value problems (BVP) has been often used in physical geodesy for transformation of the gravitational parameters or their continuation through mass-free space. Both steps can eventually be combined and solved simultaneously, e.g., (Novák 2003). Solutions based on surface integral equations with Green’s functions as integral kernels are often applied in geodesy, e.g., (Heck 2003). Due to abundant surface gravity data, the most frequently used BVPs in local studies are still those of Dirichlet and Stokes. While the former problem (Heiskanen and Moritz 1967, Sect. 1–16) is used for continuing gravitational parameters through mass-free space, the latter problem (Stokes 1849) is used to transform gravity (vertical gradient of the geopotential including the centrifugal effect) observed at the Earth’s surface into the geopotential.

However, these problems were sufficient at times when surface gravity was only observable. Since the 1980s, airborne gravimetry has been developed to provide first-order gradients of the geopotential (full gravitational vector) along flight lines. In the new millennium, satellite sensors have been designed that provided new types of data including second-order geopotential gradients along satellite orbits. Moreover, recent advances in experimental physics have suggested that geopotential gradients of the third order may one day be observable (Rosi et al. 2015). Respective BVPs for the first- and second-order geopotential gradients were formulated and solved using surface integrals with Green’s functions by Grafarend (2001) and van Gelderen and Rummel (2001). BVPs for the third-order geopotential gradient tensor were developed more recently by Šprlák and Novák (2016).

Applying geopotential gradients as boundary values result in over-determined BVPs, see (Sacerdote and Sansò 1985) or (Sansò 1988). They are usually solved for gradient combinations that can be expressed in terms of solid harmonics. Then, respective surface integrals can be derived that contain easily determinable kernel functions (van Gelderen and Rummel 2001). Such reduced BVPs can be solved using a standard least-squares adjustment that is also applied in this study. Surface integrals were derived for spherical and ellipsoidal boundaries, but only the spherical approximation is used in this study as local applications are considered.

The integral-based solutions to BVPs represent deterministic models that transform the geopotential gradients and/or continue them in space. In order to provide a complete solution for erroneous data, appropriate stochastic models must be also derived and implemented. Such models have been formulated and applied for the Stokes integral formula and the Dirichlet integral equation, which are involved in estimation of the local geoid model from measured scalar-valued gravity, e.g., (Moritz 1963; Rapp and Rummel 1975; Strang van Hees 1986; Farahani et al. 2017; Featherstone et al. 2018; Foroughi et al. 2019; McCubbine et al. 2019; Slobbe et al. 2019), and (Ophaug and Gerlach 2020).

But the gradient noise has been also considered in solving some other BVPs. For example, Xu (1992) recovered surface values of the first-order vertical gradients from satellite second-order gradients using integral equations stabilized by Tikhonov’s regularization. Xu et al. (2006) applied the variance component estimation within the context of ill-posed linear problems for processing satellite gradients. Eshagh and Sjöberg (2011) developed an integral-based method for transforming satellite second-order gradients to surface values of the first-order vertical gradients. This method was subsequently completed for mathematical models that propagated satellite second-order gradient errors (Eshagh and Ghorbannia 2014), and estimated truncation errors (Eshagh 2011a).

In this study, propagation of observation errors, closed-loop testing, and external error estimation associated with solutions of geodetic BVPs for geopotential gradients of up to the third order are formulated, tested, and discussed. Section 2 describes fundamentals important for formulation of mathematical models and introduces used notation. In Sect. 3, integral formulas and integral equations based on Green’s surface integrals formulated for the geopotential gradients up to the third order are reviewed and systematized. They represent deterministic models that solve specific BVPs associated with transformation or spatial continuation of the harmonic geopotential and its gradients.

Respective stochastic models that are formulated in Sect. 4 can be applied to estimate uncertainties associated with solutions based on erroneous gradient data. Possible scenarios are discussed, and examples of their implementation are given in Sect. 5. Assuming parameters of the observation noise are known, either partial (based on error variances) or full (based on error variances and covariances) noise propagation is evaluated. If independent reference values of the sought parameters are available, the external accuracy of the solution is also estimated. Finally, closed-loop tests are performed using a global model of the static Earth’s gravitational field to verify the correctness of selected mathematical models and appropriateness of applied numerical methods (implementation errors). Additionally, the design analysis can be used to define stochastic properties of the gradient data and their distribution in space for specific accuracy requirements. Section 6 summarizes main findings and concludes the study.

2 Fundamentals and notation

Basic mathematical and physical concepts, terminology, and notation used throughout the article are briefly summarized in this section.

2.1 Geometry and reference systems

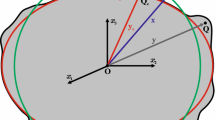
A Cartesian coordinate system is used to define the location of a point of interest in 3-D Euclidean space. A triad of Cartesian coordinates $\{x,y,z\}$ represents the components of the position vector $\textbf{x}$. Two different variants will be used: a local right-handed system with the moving origin, the x-axis pointing north, and the z-axis pointing radially outward, see, e.g., (Gruber et al. 2010). This local coordinate system is typically realized through an observation sensor that collects gradient data; in geodesy, it is known as a local north-oriented frame (LNOF). As the static global gravitational field of the Earth is considered, a global right-handed geocentric Cartesian system is also used: the origin is at the centre of the Earth’s mass, the Z-axis coincides with the mean axis of the Earth’s rotation, and the X-axis is defined as the intersection of the mean Greenwich meridian plane with the Earth’s equator. The two Cartesian systems will never be applied simultaneously as the spherical geocentric coordinates $\{r,\varphi ,\lambda \}$, i.e., the geocentric distance, spherical latitude, and longitude, are also used in the study, see Fig. 1. Equations transforming between spherical and Cartesian geocentric coordinates are well known.

Fig. 1

Coordinate systems, coordinates, and other geometric parameters

Integral formulas and integral equations transforming and continuing geopotential gradients are used as the chosen mathematical apparatus. They are developed in the spherical approximation, i.e., the integration domain is a geocentric sphere. The triad of spherical coordinates $\{r,\varphi ,\lambda \}$, abbreviated as $\{r,\Omega \},$ defines the geocentric position of the computation point P at or outside the mean geocentric sphere of radius $R = 6.371 \times 10^6$ m that approximates the Earth. The coordinates $\{R,\varphi ',\lambda '\}$, abbreviated as $\{R,\Omega '\}$, define the geocentric position of the integration point Q at the mean sphere. The condition $r \ge R$ will apply to all mathematical models. Cosine of the spherical distance $\psi$ between the two points reads, see Fig. 1,

$$\begin{aligned} u(\Omega ,\Omega '){} & {} = \cos \psi = \cos \varphi \ \cos \varphi ' \nonumber \\{} & {} \quad + \sin \varphi \ \sin \varphi ' \cos \ (\lambda - \lambda '),\, |u| \le 1\, \end{aligned}$$

(1)

and the so-called attenuation factor (for points up to $5 \times 10^5$ m above the mean sphere that corresponds to altitudes of low-orbiting satellites collecting gradient data)

$$\begin{aligned} t(r) = \frac{R}{r},\,\ \quad 0.9 < t \le 1. \end{aligned}$$

(2)

Moreover, the r-normalized Euclidean distance between the two points is defined as follows:

$$\begin{aligned} q(u,t) = \sqrt{1 + t^2 - 2tu},\,\ \quad 0 \le q \le 2. \end{aligned}$$

(3)

The unitless substitution parameters $\{u, t, q\}$ greatly simplify the notation and formulation of all integrals in the spherical approximation. Spherical geometry usually suits well BVPs of physical geodesy transforming various gravitational parameters: local data are observed on the Earth’s surface, along aircraft trajectories, and satellite orbits, i.e., the geometry of sampling points and respective boundaries can be approximated using a sphere. Higher-order approximations can be applied, such as the geocentric biaxial ellipsoid, e.g., (Novák and Šprlák 2018), but they are more important for solving global problems not considered in this study.

2.2 Gravitational field, observables, and data characteristics

Let us consider only the static gravity field of the uniformly rotating and rigid Earth. Such a vector field can be decomposed into the gravitational and centrifugal fields. The latter field can easily be modelled. Assuming a conservative and irrotational gravitational field, then it can be represented anywhere in 3-D space by a scalar function of 3-D position called geopotential V [m$^{2}$ s$^{-2}$]. The geopotential is a harmonic function in mass-free space, i.e.,

$$\begin{aligned} {\textrm{div}}\ {\textrm{grad}}\ V(r,\Omega ) = 0\, \end{aligned}$$

(4)

and regular at infinity

$$\begin{aligned} \lim _{r \rightarrow \infty } V(r,\Omega ) = 0. \end{aligned}$$

(5)

Laplace’s condition in Eq. (4) allows for the geopotential to be represented by the spherical harmonic series (Heiskanen and Moritz 1967, Sect. 2–14)

$$\begin{aligned} V(r,\Omega ) = \sum _{n=0}^{\infty } \sum _{m=-n}^n t^n(r)\ Y_{nm}(\Omega )\ V_{nm}\, \end{aligned}$$

(6)

with numerical coefficients $V_{nm}$ of the geopotential and spherical harmonic functions $Y_{nm}$ of degree n and order m.

Assuming the geopotential is continuously known at the mean geocentric sphere of radius R, Dirichlet’s BVP (Kellogg 1929, pp. 240–242) is formed that can be solved for the mass-free exterior of the mean sphere by the spherical Poisson integral (Heiskanen and Moritz 1967, Eq. 1–89)

$$\begin{aligned} V(r,\Omega ) = \int _{\sigma } V(R,\Omega ')\ K(r,\Omega ,R,\Omega ')\ {\textrm{d}}\sigma (\Omega ')\, \end{aligned}$$

(7)

where $\textrm{d}\sigma$ is the $4 \pi$-normalized infinitesimal surface element, i.e., $\cos \varphi '\ {\textrm{d} \varphi '}\ {\textrm{d} \lambda '}/(4\pi )$, of a unit sphere. The kernel function K, known as the spherical Poisson function, can be conveniently formulated using the unitless substitution parameters u and t, see Eqs. (1) and (2),

$$\begin{aligned} K(t,u) = \sum _{n=3}^{nx}\ t^{n+1}\ (2n+1)\ P_n(u)\, \end{aligned}$$

(8)

with the Legendre polynomial $P_n$. Continuity, harmonicity, and regularity of the geopotential guarantee that the respective solution exists, is unique, and stable, see (Hörmander 1961).

Values of the geopotential are not directly observable. Its differences can be estimated by combining levelled height differences with surface gravity, e.g., (Vaníček and Krakiwsky 1987, Sect. 16.4) or by applying the theory of relativity when measuring time dilation in space (Chou et al. 2010). The geopotential is often estimated from measured values of its functionals observed at discrete points. Leaving out position parameters, they include the first-order geopotential gradients $V_a$ [m s$^{-2}$]

$$\begin{aligned} \text {grad}\ V = \frac{\partial {V}}{\partial a}\ {\textbf{e}}_a = V_a\ {\textbf{e}}_a,\,\ a = x, y, z\, \end{aligned}$$

(9)

and the second-order geopotential gradients $V_{ab}$ [s$^{-2}$]

$$\begin{aligned} \text {grad}\ \text {grad}\ V = \frac{\partial {V_a}}{\partial b}\ {\textbf{e}}_{a} \otimes {\textbf{e}}_{b} = V_{ab}\ {\textbf{e}}_{a} \otimes {\textbf{e}}_{b},\,\ b = x, y, z.\nonumber \\ \end{aligned}$$

(10)

Vectors are entered in bold lower-case letters and matrices (tensors) in bold upper-case letters. The third-order geopotential gradients $V_{abc}$ [m$^{-1}$ s$^{-2}$] are also considered as a foreseen type of observables

$$\begin{aligned} \text {grad}\ \text {grad}\ \text {grad}\ V= & {} \frac{\partial {V_{ab}}}{\partial c}\ {\textbf{e}}_{a} \otimes {\textbf{e}}_{b}\otimes {\textbf{e}}_{c} \nonumber \\= & {} V_{abc}\ {\textbf{e}}_{a} \otimes {\textbf{e}}_{b} \otimes {\textbf{e}}_{c},\,\ c = x, y, z. \end{aligned}$$

(11)

The symbols ${\textbf{e}}_a, {\textbf{e}}_b, {\textbf{e}}_c$ represent unit basis vectors defined in the local Cartesian system. The differential operators needed to formulate components of the geopotential gradient tensors in Eqs. (9)–(11) in the spherical coordinates can be found, e.g., in (Casotto and Fantino 2009). The structure of the second- and third-order geopotential gradient tensors in the Cartesian coordinate system is depicted in Fig. 2.

Fig. 2

Second- and third-order geopotential gradient tensors (unique gradients are blue)

Introducing the normal gravity potential generated by a rotating equipotential ellipsoid (Moritz 2000), the disturbing potential T represents orders of magnitude smaller differences between the real and normal gravity potentials (note also that the centrifugal components in both gravity fields cancel each other). Then, we define our observables in terms of the disturbing gradients $T_{\mu }$ with $\mu = \{a, ab, abc\}$ that are obtained from observed geopotential gradients by reduction for respective normal potential gradients. They can be computed by analytic formulas, e.g., (Claessens 2019).

From Eqs. (9)–(11), it follows that numerical values of the disturbing gradients decrease substantially as their order increases. If one uses the spherical coordinates, see Sect. 2, then the gradient operators of the order i include terms $r^{-i}$ with the radial distance r of the point from the origin of the coordinate system. In order to keep numerical values of the disturbing potential and its gradients at the same order of magnitude, the disturbing gradients are scaled by $R^i$. The scaled gradients $T^*_{\mu }$ are defined as follows:

$$\begin{aligned} T^*_{\mu } = R^i\ T_{\mu },\,\ i = 1, 2, 3\ {\textrm{for}}\ \mu = a, ab, abc. \end{aligned}$$

(12)

Scaled disturbing gradients $T^*_{\mu }$ have the same physical dimension [m$^{2}$ s$^{-2}$] as the disturbing potential. Values of the disturbing potential are at the order of $10^3$ m$^{2}$ s$^{-2}$ for the geometry of problems typical for physical geodesy, i.e., at the surface of the Earth and in its neighbourhood. First-order disturbing gradients are multiplied by the radius $R = 6.371 \times 10^6$ m, second-order disturbing gradients by $R^2 = 4.059 \times 10^{13}$ m$^2$, and third-order gradients by $R^3 = 2.586 \times 10^{20}$ m$^3$. The orders of magnitudes illustrate difficulties associated with the observability of higher-order gradients, when it comes to keeping their signal-to-noise ratio at an acceptable level.

Although the number of the disturbing gradients for the increasing order i grows with $i^3$, the number of independent disturbing gradients is only $(2 i + 1)$, i.e., 3, 5, 7 for $i = \{1,2,3\}$. The number of unique disturbing gradients is then the sum of the number of independent disturbing gradients and the number of respective Laplace conditions, i.e., 3, 6, 10, see Fig. 2, with unique gradients indicated in blue. The unique disturbing gradients for each order i in the form of three vectors denoted as ${\textbf{t}}^*_i$ will represent input values in our mathematical models. Components of the vectors ${\textbf{t}}^*_i$ in the local Cartesian system are shown, respectively, in Tables 1,  2, and 3, see their first columns.

As the disturbing potential T is estimated from measured values of its gradients $T_{\mu }$, it cannot fully be recovered (as integration requires integration constants). To make solutions to all BVPs formulated for different disturbing gradients consistent, the harmonic series representation of the disturbing potential, see Eq. (6), will be limited by the minimum degree $n = 3$ as solutions to some BVPs considered in this study exclude harmonic terms up to the degree 2. Note that the harmonic terms of degrees 0 and 1 can be eliminated by a properly defined normal field. Also, observed gradient data are limited to a certain maximum degree, either due to filtering of raw data (in order to remove a high-frequency observation noise present namely in data collected by moving sensors) or by their spatial resolution. In our study, the maximum degree in Eq. (6) is generally set to nx. The spherical harmonic representation of the degree-limited disturbing potential can be then written as follows:

$$\begin{aligned} T(r,\Omega ) = \sum _{n=3}^{nx} \sum _{m=-n}^n A_{nm}(r,\Omega )\ T_{nm}\, \end{aligned}$$

(13)

with solid harmonics $A_{nm}$. The spectral limitation, justified by spectral properties of measured gradient data, is a well-known regularization method that allows to represent involved operations, such as differentiation or downward continuation, by means of regular kernels and discretized surface integrals. The spectral limitation is also beneficial for least-square solutions to over-determined BVPs. The maximum degree nx used in processing of a particular gradient data set will be estimated by numerical experiments.

Table 1 Unique first-order disturbing gradients ${\textbf{t}}^*_1$ (first column), gradient groups ${\textbf{s}}^*_1$ (first row), and the matrix ${\textbf{U}}_1$

Table 2 Unique second-order disturbing gradients ${\textbf{t}}^*_2$ (first column), gradient groups ${\textbf{s}}^*_2$ (first row), and the matrix ${\textbf{U}}_2$

Table 3 Unique third-order gradients ${\textbf{t}}^*_3$ (first column), gradient groups ${\textbf{s}}^*_3$ (first row), and the matrix ${\textbf{U}}_3$

The section concludes with a short discussion on observability of the geopotential gradients defined (after reduction for the normal field effect) in Eqs. (9)–(11) that is important for understanding the applicability of the discussed BVPs. Noise characteristics of gradient data observed by various techniques are then important for respective stochastic models. Gravimetry as the most typical observation method in physical geodesy provides first-order geopotential gradients (Torge 1989). Their values are sampled on the Earth’s surface, by sensors on board aircraft and satellites. The accuracy of surface vertical gradients can reach 10$^{-8}$ m s$^{-2}$ or 1 ppb relatively (Sasagawa et al. 1995) that makes them the most accurate gradient data available. However, their spatial distribution is always limited. Surface values of the second-order geopotential gradients were first measured by Eötvös (1896).

Renaissance of second-order gradient observations occurred at the beginning of the 21st century, when suitable airborne sensors were designed, e.g., (Dransfield and Christensen 2013). The most significant progress in observing second-order gradients happened in 2009, when the European Space Agency launched the Gravity field and steady-state Ocean Circulation Explorer (Rummel 2010). Until 2013, the GOCE mission provided abundant observation material covering almost the entire Earth’s surface. The relative accuracy of its second-order gradient data was at the level of 1 % (Drinkwater et al. 2003). First attempts to measure third-order gradients were made relatively recently. Rosi et al. (2015) proposed an observation method based on the principle of atomic interferometry. Successful observations of third-order geopotential gradients in space, as proposed by (Brieden et al. 2010), would counterbalance the attenuation of the gravitational field with the increasing distance from the gravitating masses.

3 Deterministic models

In this section, we focus on formulation of integral formulas and integral equations that are (or could be) used to process scaled gradient data defined by Eq. (12). They represent deterministic models that are used as a basis for the formulation of corresponding stochastic models in Sect. 4.

Two types of mathematical models are formulated. If the unknown disturbing potential is on the left-hand side of the equation, the models are labelled as integral formulas. They transform the measured scaled disturbing gradients into the unknown disturbing potential. However, unique disturbing gradients for each order must be combined first to be representable by easily determinable kernel functions. The requirement of using the gradient groups reduces the number of available observations involved for the particular mathematical model and may increase their noise level relatively to that of the individual gradients. Also, if a particular gradient group should be transformed into the unknown disturbing potential, all gradients involved in the gradient group must be available.

If the unknown disturbing potential is on the right-hand side of the equation and under the integral sign, the respective mathematical models are designated as integral equations. In this case, scaled values of the measured disturbing gradients are expressed as surface integrals of the disturbing potential. This form of the mathematical model counteracts the effect of integration as an inverse step of differentiation, i.e., integral equations act as differentiators and mathematical models take the form of integro-differential equations. This property is counterbalanced by the fact that each disturbing gradient can be used independently to recover the unknown disturbing potential.

3.1 Integral formulas

The integral formulas are derived to solve for the unknown disturbing potential on the mean sphere from scaled values of its gradients observed in mass-free space outside the mean sphere. One can generally transform any higher-order gradient to any lower-order gradient, e.g., second-order gradients observed with GOCE can be transformed to first-order gradients that can be compared to surface gravity, e.g., (Kern and Haagmans 2005). However, mathematical models estimating the disturbing potential (zero-order gradient) from its first-, second-, and third-order gradients are only considered below.

BVPs for the unknown harmonic disturbing potential are formulated and their solutions represented by surface integrals with easily determinable kernel functions if boundary values can be expressed by solid spherical harmonics (Zerilli 1970). This means that the unique disturbing gradients for each order must be linearly combined. Recalling for each order a respective vector of the unique scaled disturbing gradients ${\textbf{t}}^*_i$, a vector of the scaled gradient groups ${\textbf{s}}^*_i$ can be written as follows:

$$\begin{aligned} {\textbf{s}}^*_i = {\textbf{U}}_i\ {\textbf{t}}^*_i,\,\ i = 1, 2, 3. \end{aligned}$$

(14)

Components of the gradient group vectors ${\textbf{s}}^*_i$ and matrices ${\textbf{U}}_i$ for the three considered orders are found in Tables 1,  2, and 3. A particular gradient group $T^*_{ij}$ is obtained by multiplying unique gradients with expressions in the column under the respective gradient group. For example, the group $T^*_{22}$ can easily be formulated using Table 2:

$$\begin{aligned} T^*_{22} = \left( T^*_{xx} - T^*_{yy} \right) \cos 2 \alpha ' - 2 T^*_{xy}\ \sin 2 \alpha '. \end{aligned}$$

(15)

The matrices ${\textbf{U}}_i$ contain goniometric functions of the azimuth $\alpha '$ between the integration point $(R,\Omega ')$ and the computation point $(r,\Omega )$, see Fig. 1, and their multiples for $i > 1$, see “Appendix A”. The gradient groups for each order can easily be formed using Eq. (14) and Tables 1,  2, and 3.

The spherical Poisson integral formula of Eq. (7) represents the basis for all integrals formulas presented below. Parameters, defining geocentric positions to which individual functions refer, will be omitted in the following equations as no confusion may arise. The gravimetric BVP for the first-order disturbing gradients $T^*_a$ was formulated by (Grafarend 2001). Two integral formulas can be formulated for two components of the first-order gradient group vector ${\textbf{s}}^*_1$, see Table 1,

$$\begin{aligned} T = \int _\sigma T^*_{10}\ K_{10}\ {\textrm{d}}\sigma = \int _\sigma T^*_{11}\ K_{11}\ {\textrm{d}}\sigma . \end{aligned}$$

(16)

The disturbing potential at the left-hand side of Eq. (16) is referred to the computation point outside the mean sphere, and the scaled first-order gradient groups under the two integrals are referred to the integration point at the mean sphere. The kernel functions $K_{10}$ and $K_{11}$ are both isotropic and unitless, see Eq. (20). If all three unique first-order disturbing gradients are measured, the problem of Eq. (16) for the noisy gradient data is over-determined and some suitable estimation method must be applied. The least-squares solution of the reduced problem in Eq. (16) can be sought (van Gelderen and Rummel 2001). As discussed in Sect. 2.2, the input gradient data are spectrally limited. Restricting the mathematical model to a finite dimensional space, the use of a least-squares estimator based on the discretized surface integral is justified. The least-squares estimator will be completed for a stochastic model in Sect. 4.

The gradiometric BVP (van Gelderen and Rummel 2001) transforms the second-order disturbing gradients to the disturbing potential. Six unique second-order gradients $T^*_{ab}$ stored in the vector ${\textbf{t}}^*_2$ are combined to form three second-order gradient groups in the vector ${\textbf{s}}^*_2$ that are representable by solid harmonics. Three integral formulas can be then formulated as follows (Martinec 2003):

$$\begin{aligned} T = \int _\sigma T^*_{20}\ K_{20}\ {\textrm{d}}\sigma = \int _\sigma T^*_{21}\ K_{21}\ {\textrm{d}}\sigma = \int _\sigma T^*_{22}\ K_{22}\ {\textrm{d}}\sigma \, \nonumber \\ \end{aligned}$$

(17)

with the kernel functions $K_{20}$, $K_{21}$, and $K_{22}$ that are also isotropic and unitless, see Eq. (20). Again, the solution of the reduced over-determined problem in Eq. (17) applied to noisy gradient data requires some estimation method with an associated stochastic model.

Finally, the curvature BVP transforms the third-order disturbing gradients $T^*_{abc}$ into the disturbing potential. Ten unique third-order gradients in the vector ${\textbf{t}}^*_3$ can be arranged into four third-order gradient groups in the vector ${\textbf{s}}^*_3$ for which the following integral formulas are derived (Šprlák and Novák 2016)

$$\begin{aligned} T= & {} \int _\sigma T^*_{30}\ K_{30}\ {\textrm{d}}\sigma = \int _\sigma T^*_{31}\ K_{31}\ {\textrm{d}}\sigma \nonumber \\= & {} \int _\sigma T^*_{32} K_{32}\, {\textrm{d}}\sigma = \int _\sigma T^*_{33}\ K_{33}\ {\textrm{d}}\sigma \, \end{aligned}$$

(18)

with the isotropic and unitless kernel functions $K_{30}$, $K_{31}$, $K_{32}$ and $K_{33}$, see Eq. (20). The mathematical model in Eq. (18) represents again a reduced over-determined problem.

The nine integral formulas in Eqs. (16)–(18) can be generalized as follows:

$$\begin{aligned} T = \int _\sigma T^*_{ij}\ K_{ij}\ {\textrm{d}}\sigma , \,\ i = 1, 2, 3\ {\textrm{and}}\ 0 \le j \le i. \end{aligned}$$

(19)

The spectral form of the kernel functions $K_{ij}$ can be expressed using the series of Legendre functions (no normalization is applied in contrast with spherical harmonic representations of the disturbing potential and its gradients)

$$\begin{aligned} K_{ij}(t,u)= & {} \sum _{n=3}^{nx}\ t^{n+1}\ (2n+1)\ \frac{(n-j)!}{(n+i)!}\ P_{nj}(u),\,\nonumber \\ i= & {} 1, 2, 3\, {\textrm{and}}\, 0 \le j \le i\, \end{aligned}$$

(20)

with the associated Legendre functions $P_{nj}$. The index j represents the order of the gradient group defined in the horizontal coordinates (x, y) of the local coordinate frame. The integral formulas with $j=\{1,2,3\}$ do not contain the respective terms of the harmonic degree $n=\{0,1,2\}$ in the spherical harmonic representation of the geopotential, see Eq. (6). Thus, the spectral constraint $n \ge 3$ is applied in the harmonic series of Eq. (13). The kernel functions in Eq. (20) can be also formulated using analytic (closed-form) expressions, see (Novák et al. 2017). However, they are not presented herein as spectrally limited gradient data are only considered in this study.

The kernel function $K_{10}$ is known in geodesy as extended Hotine’s function (Hotine 1969, p. 321)

$$\begin{aligned} K_{10}(t,u) = \sum _{n=3}^{nx}\ t^{n+1}\ \frac{2 n + 1}{n + 1}\ P_{n}(u). \end{aligned}$$

(21)

Its slightly modified version known as Stokes’s function (Stokes 1849) that transforms anomalous gravity into the disturbing potential with $t = 1$ is probably still the most frequently used Green’s function in physical geodesy. To provide an example of the mathematical model in Eq. (19) for the higher-order gradients, the transformation of the second-order gradient group $T^*_{22}$ in Eq. (15) involves the following kernel function

$$\begin{aligned} K_{22}(t,u) = \sum _{n=3}^{nx}\ t^{n+1}\ \frac{2 n + 1}{(n+2)\ (n+1)\ n\ (n-1)}\ P_{n2}(u).\nonumber \\ \end{aligned}$$

(22)

Theoretically, each of the nine integral formulas in Eq. (19) provides the same solution for the unknown disturbing potential T. This will change after discretization of their integration domains. Moreover, observation errors in the measured gradient data will propagate differently through the nine integral formulas. This issue is explored in Sect. 4.1.1.

3.2 Integral equations

Alternatively, the integral transform of the disturbing potential to its gradients can be formulated by differentiating both sides of the spherical Poisson integral equation. The sought disturbing potential on the mean sphere remains under the integral sign, and the mathematical model takes the form of the integral equations. In fact, the integral transforms and integral equations represent the inverse of one another. Products of the corresponding integral kernels provide the Poisson kernel function from which both mathematical models originate.

Recalling unique scaled first-order disturbing gradients forming the vector ${\textbf{t}}^*_1$, the following vector-valued integral equation can be derived (Jekeli 2007):

$$\begin{aligned} {\textbf{t}}^*_1 = \int _\sigma T\ {\textbf{h}}_1\ {\textrm{d}}\sigma . \end{aligned}$$

(23)

Components of the vector-valued kernel function ${\textbf{h}}_1$, which are unitless and anisotropic except for $H_z$, are represented by combinations of the isotropic functions

$$\begin{aligned} f_{ij}(t,u)= & {} \frac{1}{\alpha _j}\ \sum _{n=3}^{nx}\ t^{n+1+i}\ (2n+1)\ \frac{(n+i)!}{(n+j)!}\ P_{nj}(u)\,\nonumber \\ i= & {} 1, 2, 3\,\ 0 \le j \le i,\,\ \alpha _j = 1, 1, 2, 4\, \end{aligned}$$

(24)

with sine and cosine of the azimuth $\alpha$ between the computation point $(r,\Omega )$ and the integration point $(R,\Omega ')$, see Fig. 1, and their multiples for $i > 1$, see “Appendix A”. This combination can formerly be written as follows:

$$\begin{aligned} {\textbf{h}}_1 = {\textbf{V}}_1\ {\textbf{f}}_1. \end{aligned}$$

(25)

Components of all structures in Eq. (25) are found in Table 4. The first-order disturbing gradients ${\textbf{t}}^*_1$ at the left-hand side of Eq. (23) are related to the observation point outside the mean sphere, the disturbing potential under the integral is defined on the mean sphere, and the vector-valued kernel function ${\textbf{h}}_1$ refers to these two points. Since the sought disturbing potential is under the integral, the integral equation, known in mathematics as the Fredholm integral equation of the first kind, must be solved. If, after discretizing the integration domain, the number of observed gradients on the left-hand side exceeds that of the sought values of the disturbing potential, the problem is over-determined.

Table 4 Components of the vectors ${\textbf{h}}_1$ (first column) and ${\textbf{f}}_1$ (first row) and the matrix ${\textbf{V}}_1$

Integral transforms of the disturbing potential T into the unique scaled second-order disturbing gradients can be formulated as follows (Bölling and Grafarend 2005):

$$\begin{aligned} {\textbf{t}}^*_2 = \int _\sigma T\ {\textbf{h}}_2\ {\textrm{d}}\sigma . \end{aligned}$$

(26)

Only six out of the nine second-order gradients are unique. Moreover, only five of them are independent in the mass-free space as Laplace’s condition applies to three diagonal terms of the second-order gradient tensor. Components of the vector-valued kernel function ${\textbf{h}}_2$ are unitless and, with except of the kernel function $H_{zz}$, also anisotropic. However, they can be formulated using three isotropic functions $f_{ij}$ defined already by Eq. (24)

$$\begin{aligned} {\textbf{h}}_2 = {\textbf{V}}_2\ {\textbf{f}}_2. \end{aligned}$$

(27)

Components of all structures in Eq. (27) are given in Table 5.

Table 5 Components of the vectors ${\textbf{h}}_2$ (first column) and ${\textbf{f}}_2$ (first row) and the matrix ${\textbf{V}}_2$

Finally, the integral transforms of the disturbing potential T into the unique scaled third-order disturbing gradients, see Eqs. (11) and (12), read as follows (Šprlák and Novák 2015):

$$\begin{aligned} {\textbf{t}}^*_3 = \int _\sigma T\ {\textbf{h}}_3\ {\textrm{d}}\sigma . \end{aligned}$$

(28)

Out of the 27 third-order disturbing gradients, only ten are unique, and only seven are independent as three Laplace’s conditions apply in the mass-free space. The components of the vector-valued kernel function ${\textbf{h}}_3$ read as follows:

$$\begin{aligned} {\textbf{h}}_3 = {\textbf{V}}_3\ {\textbf{f}}_3. \end{aligned}$$

(29)

Components of all structures in Eq. (29) are found in Table 6. The same properties apply as for the disturbing gradients of the order one and two above.

Table 6 Components of the vectors ${\textbf{h}}_3$ (first column) and ${\textbf{f}}_3$ (first row) and the matrix ${\textbf{V}}_3$

The integral equations of Eqs. (23), (26), and (28) for the unique disturbing gradients of the order i can be generalized as follows:

$$\begin{aligned} {\textbf{t}}^*_i = \int _\sigma T\ {\textbf{h}}_i\ {\textrm{d}}\sigma = \int _\sigma T \left( {\textbf{V}}_i\ {\textbf{f}}_i \right) \ {\textrm{d}}\sigma , \,\ i = 1, 2, 3. \end{aligned}$$

(30)

In theory, Eq. (30) represents 19 different integral equations that provide the same solution of the disturbing potential T. However, gradient errors will propagate differently by discretized integral equations when individual gradients are contaminated by the observation noise. This issue is investigated in Sect. 4.1.2.

As in the case of integral transforms discussed in the previous section, one example of the mathematical model in Eq.  (30) is provided. The solution for the horizontal third-order gradient $T^*_{xxx}$, see Table 6, reads

$$\begin{aligned} T^*_{xxx} = \int _\sigma T \left( \cos 3 \alpha \ f_{33} - 3 \cos \alpha \ f_{31} \right) {\textrm{d}}\sigma \, \end{aligned}$$

(31)

with the isotropic functions, see Eq. (24),

$$\begin{aligned} f_{31}(t,u) = \sum _{n=3}^{nx}\ t^{n+4}\ (2n+1)\ (n+3)\ (n+2)\ P_{n1}(u)\, \end{aligned}$$

(32)

and

$$\begin{aligned} f_{33}(t,u) = \frac{1}{4}\ \sum _{n=3}^{nx}\ t^{n+4}\ (2n+1)\ P_{n3}(u). \end{aligned}$$

(33)

Recall that the solution for the disturbing potential T does not include the spherical harmonics of the first three harmonic degrees as it was previously explained.

4 Uncertainties in integral formulas and integral equations

Having defined in Sect. 3 mathematical models that relate the unknown disturbing potential with its scaled gradients or gradient groups (assumed to be obtainable from measured geopotential gradients), a question of uncertainties in estimated values of the disturbing potential due to the propagation of observation errors, and numerical and software implementation of the mathematical models arises. How large are the uncertainties of the estimated values if input gradient data with specific stochastic properties are applied? How do specific numerical and software implementations of the mathematical models affect the accuracy of their solution?

The following outlines possible methods that can be used in attempting to answer these questions. Some of them are implemented and more closely investigated. While some methods apply mathematical modelling (formal errors), other methods rely on results estimated using synthetic gradient data (closed-loop tests) or knowledge of independent reference values (external accuracy).

4.1 Propagation of formal errors

In this section, the integral formulas and integral equations presented in Sect. 3 are modified into practical estimators that can be implemented in software and applied to processing of discrete observations of the disturbing gradients. Subsequently, mathematical models are formulated that allow the propagation of their stochastic parameters into the uncertainties associated with the estimated values of the disturbing potential.

The error variance–covariance matrix (EVM), generally denoted herein as $\textbf{C}$, contains the noise variances (mean quadratic errors) and covariances associated with measured gradient data or estimates of the disturbing potential. As gradients of the normal geopotential can be computed analytically everywhere outside the reference ellipsoid using a set of four defining coefficients (Claessens 2019), the EVM of the measured geopotential gradients represents variances and covariances of their noise. For one sampling point, their dimensions would be $3 \times 3$, $6 \times 6$, and $10 \times 10$ for the unique disturbing gradients of the order 1, 2, and 3, respectively.

4.1.1 Propagation of the gradient noise by integral formulas

We start with the nine integrals formulas for the disturbing gradient groups described by Eq. (19). The gradient groups, which represent input values (pseudo-observables) for the integral transforms, are computed from the unique disturbing gradients for each order considered in this study, see Eq. (14). Applying the well-known covariance law, the EVM of the input unique disturbing gradients ${\textbf{C}}_{{\textbf{t}}^*_i}$ is transformed as follows:

$$\begin{aligned} {\textbf{C}}_{{\textbf{s}}^*_i} = {\textbf{U}}_i\ {\textbf{C}}_{{\textbf{t}}^*_i}\ {\textbf{U}}^T_i,\,\ i = 1, 2, 3. \end{aligned}$$

(34)

Note that the EVMs of the gradient groups ${\textbf{C}}_{{\textbf{s}}^*_i}$ are always fully populated, i.e., subsequent numerical solutions can be challenging (Klees et al. 2019). Thus, combining the gradients implies an increase in the noise variances and non-zero noise covariances. Geocentric positions of the computation and integration points, which would also affect the evaluation of the matrices ${\textbf{U}}_i$, are assumed to be error-free in this study.

Observed values of the disturbing gradients, especially in the case of surface and near-surface (aerial) data, are often limited to small geographical areas (hundreds by hundreds squared kilometres), i.e., they do not have the expected global coverage. Such local gradient data cannot be used for recovery of the full disturbing potential. Fortunately, there is a solution based on the combination of local gradient data with global gravitational models (GGMs). GGMs provide the reference (low-frequency or long-wavelength) component of the disturbing potential and local gradient data are used for recovery of the corresponding residual (high-frequency or short-wavelength) component.

The form of the solution will also depend on the location of points where the sought disturbing potential is being recovered. If the geoid is computed, then the disturbing potential is estimated at the mean sea level, i.e., inside topography under the continents. In this case, the GGM cannot be used as well as the apparatus of integral transforms that both depend on the harmonic disturbing potential. Appropriate measures must be applied (harmonization of the solution domain). But even in the case of recovering values of the height anomaly from the disturbing potential at the Earth’s surface, the GGM may fail due to divergence of the harmonic series within the Brillouin sphere circumscribing the Earth’s body. However, these issues are considered beyond the scope of this study.

The generalized integral transform of Eq. (19) for the disturbing gradient group of the particular order i with $0 \le j \le i$ can be then modified as follows:

$$\begin{aligned} T= & {} T^l + T^h \approx \int _{\sigma } T^{*l}_{ij}\ K_{ij}\ \textrm{d}\sigma + \int _{\sigma _o} T^{*h}_{ij}\ K^h_{ij}\ \textrm{d}\sigma , \nonumber \\{} & {} \sigma _o \subset \sigma \, \end{aligned}$$

(35)

with the global integration domain $\sigma$ and its sub-domain $\sigma _o$ where local gradient data are available. The reference component of the disturbing potential $T^l$, represented by the first integral on the right-hand side of Eq. (35), is evaluated using numerical coefficients $T_{nm}$ in the harmonic series representation of the disturbing potential up to the harmonic degree $max < nx$ on the mean sphere, see Eq. (13),

$$\begin{aligned} T^l = \sum _{n=3}^{max} \sum _{m=-n}^n A_{nm}\ T_{nm} = {\textbf{a}} \cdot {\mathbf {t_n}}\, \end{aligned}$$

(36)

where the vectors $\textbf{a}$ and $\mathbf {t_n}$ contain, respectively, solid harmonics and numerical coefficients of the disturbing potential. The vector of the reference values of the disturbing potential then reads

$$\begin{aligned} {\textbf{t}}^l = {\textbf{A}}\ {\mathbf {t_n}}. \end{aligned}$$

(37)

The residual component of the disturbing potential $T^h$ in Eq. (35) is evaluated using local gradient data $T^{*}_{\mu }$ reduced for the reference component synthesized from the GGM

$$\begin{aligned} T^{*l}_{\mu } = \sum _{n=3}^{max} \sum _{m=-n}^n \textrm{a}_{\mu }\left( A_{nm} \right) \ T_{nm} = {\textbf{a}}_{\mu } \cdot {\mathbf{t_n}},\,\ \mu = a, ab, abc\, \nonumber \\ \end{aligned}$$

(38)

with the operator $\textrm{a}_{\mu }$ transforming the n-degree term in the harmonic series of the disturbing potential T into the respective term of its scaled gradient $T^*_{\mu }$. The unique residual gradients then form the residual gradient groups

$$\begin{aligned} {\textbf{s}}^{*h}_{i} = {\textbf{U}}_i\ ({\textbf{t}}^{*}_i - {\textbf{t}}^{*l}_i),\,\ i = 1, 2,3\, \end{aligned}$$

(39)

that are convolved with the residual kernel function defined as follows:

$$\begin{aligned} K^h_{ij}{} & {} = \sum _{n=max+1}^{nx} t^{n+1}\ (2n+1)\ \frac{(n-j)!}{(n+i)!}\ P_{nj}(u)\,\nonumber \\ i= & {} 1, 2,3\ {\textrm{and}}\ 0 \le j \le i. \end{aligned}$$

(40)

The maximum degree nx should correspond to the spectral content of the local gradient data which is limited by their spatial sampling and raw signal preprocessing (namely noise filtering).

The discrete integral transform of the residual disturbing gradients then reads for one computation point (parameters indicating positions are used)

$$\begin{aligned} T^h(r,\Omega )= & {} \int _{\sigma _o} T^{*h}_{ij}(R,\Omega ')\ K^h_{ij}(t,u)\ \textrm{d}\sigma (\Omega ')\nonumber \\\approx & {} \sum _p T^{*h}_{ij}(R,\Omega _p)\ K^h_{ij}(t,u_p)\ \Delta \sigma (\Omega _p) = {\textbf{k}} \cdot {\textbf{s}}^{*h}_i\,\nonumber \\ \end{aligned}$$

(41)

with the kernel function vector $\textbf{k}$ and the data vector ${\textbf{s}}^{*h}_i$ containing scaled residual disturbing gradient groups $T^{*h}_{ij}$. Numerical mathematics provides a number of dicretization schemes, but quadrature rules are often used in geodesy (Lehmann 1997). Numerical errors due to the discretization of the surface integrals are beyond the scope of this study. The integral transforms have no singularities as long as the gradients are observed outside the mean sphere, i.e., for $r > R$. The spatial convolution in Eq. (41) can be also formulated and solved alternatively in the frequency domain, e.g., (Haagmans et al. 1993). The solution for the full vector of the estimated residual gradients reads

$$\begin{aligned} {\textbf{T}}^h = {\textbf{K}}\ {\textbf{s}}^{*h}_i = {\textbf{K}}\ {\textbf{U}}_i\ ({\textbf{t}}^{*}_i - {\textbf{t}}^{*l}_i),\,\ i = 1, 2,3\, \end{aligned}$$

(42)

with the design matrix of the problem ${\textbf{K}}$.

There is one more modification of the integral transforms that can be applied. If the reference component $T^l$ is evaluated (for whatever reason) using a low-degree part of the GGM, e.g., only up to some degree $mx < max$, the so-called far-zone contribution of the residual disturbing potential can be computed using a weighted harmonic series of the remaining harmonic coefficients, i.e., for $mx + 1 < n \le max$. Far-zone contributions have been formulated originally for the first-order vertical disturbing gradient $T_{10}$ that is known in geodesy as the gravity disturbance. They can easily be formulated for other vertical gradients of the disturbing potential, i.e., the second- and third-order vertical disturbing gradients $T^*_{20}$ and $T^*_{30}$. To demonstrate their principle, the first-order vertical disturbing gradient and the corresponding integral formula, known in geodesy as Hotine’s integral transform, can be used (note the scaling)

$$\begin{aligned}{} & {} \int _{\sigma -\sigma _o} T^*_{10}\ K_{10}\ \textrm{d} \sigma \nonumber \\{} & {} \approx \frac{R}{2} \sum _{n=mx+1}^{max} (n+1)\ t^n(r)\ Q_n(t,u_0)\ T_n(\Omega )\, \end{aligned}$$

(43)

with Laplace’s coefficients $T_n$ of the disturbing potential (Heiskanen and Moritz 1967, Eq. 2-152). The spectral weights $Q_n$, originally developed for the Stokes integral formula (Molodensky et al. 1962), can be easily computed for the domain $\sigma _o$ defined as a spherical cap of the radius $\psi _o$ ($u_o=\cos \psi _o$) centred at the computation point

$$\begin{aligned} Q_n(t,u_o) = \int _{-1}^{u_o} K^b_{10}(t,u)\ P_n(u)\ \textrm{d}u\, \end{aligned}$$

(44)

with the degree-limited kernel function $K^b_{10}$

$$\begin{aligned} K^b_{10}(t,u) = \sum _{n=mx+1}^{max} t^{n+1}\ \frac{2 n + 1}{n + 1}\ P_{n}(u). \end{aligned}$$

(45)

Truncation coefficients $Q_n$ have been also formulated for some other gradient data, e.g., (Tenzer et al. 2009) or (Eshagh and Ghorbannia 2014). Far-zone effects are discussed in the context of integral-based solutions to geodetic BVPs for completeness; however, they were not applied in the numerical experiments reported in Sect. 5.

Combining the two estimators in Eqs. (37) and (42), one obtains for the unknown vector $\textbf{t}$ with components representing estimates (with a hat) of the disturbing potential

$$\begin{aligned} \hat{\textbf{t}}= & {} {\textbf{A}}\ {\textbf{t}}_n + {\textbf{K}}\ {\textbf{s}}^{*h}_i = {\textbf{A}}\ {\textbf{t}}_n + {\textbf{K}}\ {\textbf{U}}_i\ ( {\textbf{t}}^{*}_i - {\textbf{A}}_{\mu }\ {\textbf{t}}_n)\nonumber \\= & {} ({\textbf{A}} - {\textbf{K}}\ {\textbf{U}}_i\ {\textbf{A}}_{\mu })\ {\textbf{t}}_n + {\textbf{K}}\ {\textbf{U}}_i\ {\textbf{t}}^*_i,\, \ i = 1, 2,3. \end{aligned}$$

(46)

Denoting the EVMs of the harmonic geopotential coefficients and observed gradient data as ${\textbf{C}}_{{\textbf{t}}_n}$ and ${\textbf{C}}_{{\textbf{t}}^{*}_i}$, respectively, then applying the covariance law (assuming there are no correlations between the noise of local surface gradient data and satellite-only GGM) yields the EVM of the estimated values of the disturbing potential

$$\begin{aligned} \textbf{C}_{\hat{\textbf{t}}}{} & {} = ({\textbf{A}} - {\textbf{K}}\ {\textbf{U}}_i\ {\textbf{A}}_{\mu })\ {\textbf{C}}_{{\textbf{t}}_n}\ ({\textbf{A}} - {\textbf{K}}\ {\textbf{U}}_i\ {\textbf{A}}_{\mu })^T + {\textbf{K}}\ {\textbf{U}}_i\ {\textbf{C}}_{{\textbf{t}}^*_i}\ {\textbf{U}}^t_i\ {\textbf{K}}^T. \nonumber \\ \end{aligned}$$

(47)

Since no matrix inversion is required, evaluating Eq. (47) numerically is not difficult. However, computations can be memory demanding depending on the spatial resolution and extent of the local gradient data, as well as on the maximum degree of the applied GGM.

Assuming the EVM of the local residual gradient data can be written as ${\textbf{C}}_{{\textbf{t}}^*_i} = \sigma ^2_{0,t^*_i} {\textbf{I}}$ and the EVM of the harmonic coefficients as ${\textbf{C}}_{{\textbf{t}}_n} = \sigma ^2_{0,t_n} {\textbf{Q}}$, then

$$\begin{aligned} \textbf{C}_{\hat{\textbf{t}}}{} & {} = \sigma ^2_{0,t_n}\ ({\textbf{A}} - {\textbf{K}}\ {\textbf{U}}_i\ {\textbf{A}}_{\mu })\ {\textbf{Q}}\ ({\textbf{A}} - {\textbf{K}}\ {\textbf{U}}_i\ {\textbf{A}}_{\mu })^T \nonumber \\ {}{} & {} \quad + \sigma ^2_{0,t^*_i}\ {\textbf{K}}\ {\textbf{U}}_i\ {\textbf{U}}^T_i\ {\textbf{K}}^T\, \end{aligned}$$

(48)

with the unitless variance factors $\sigma ^2_{0,t^*_i}$ and $\sigma ^2_{0,t_n}$, unit matrix ${\textbf{I}}$, and the co-factor matrix ${\textbf{Q}}$ of the harmonic coefficients (if the full EVM of the GGM is available).

4.1.2 Propagation of the gradient noise by integral equations

In the case of integral equations, see Sect. 3.2, the gradient data noise propagates differently. The discretized integral equations for one value of the particular disturbing gradient $T^*_{\mu }$ of the order i, with $\mu = \{a,ab,abc\}$ for $i=1,2,3$, can be written as follows:

$$\begin{aligned} T^*_{\mu }(r,\Omega )= & {} \int _\sigma T(R,\Omega ')\ H_{\mu }(t,u)\ {\textrm{d}}\sigma \nonumber \\\approx & {} \sum _p\ T(R,\Omega _p)\ H_{\mu }(t,u_p)\ \Delta \sigma (\Omega _p) = {\textbf{b}} \cdot {\textbf{t}}\, \nonumber \\ \end{aligned}$$

(49)

with the design vector of the mathematical model $\textbf{b}$, vector $\textbf{t}$ with unknown values of the disturbing potential on the mean sphere, and scaled disturbing gradients $T^*_{\mu }$ observed outside the mean sphere. The mathematical model of Eq. (49) is linear, but its inverse must be solved in order to estimate the unknown vector $\textbf{t}$. Assuming the random noise in the observed gradients, the standard solution is sought using an estimator that minimizes the quadratic norm of the vector of residuals, which represent unknown errors of the observed disturbing gradients. Unlike the integral formulas, one needs at least as many observed gradients as there are unknown values of the disturbing potential under the integral sign. However, the number of observed gradients usually exceeds the number of the unknown values and an over-determined model is solved.

If observed values of the disturbing gradients are available only locally, the integral equations in Eq. (49) can be modified as in the case of integral formulas in Sect. 4.1.1, i.e.,

$$\begin{aligned} T^*_{\mu } - T^{*l}_{\mu } \approx \int _{\sigma _o} T^h\ H^h_{\mu }\ {\textrm{d}}\sigma ,\,\ \sigma _o \subset \sigma . \end{aligned}$$

(50)

The reference gradients $T^{*l}_{\mu }$ are estimated by GGM, see Eq. (38), and only the residual disturbing potential $T^h$ is recovered from the local disturbing gradient data. Equation (50) written using the matrix form reads

$$\begin{aligned} {\textbf{t}}^*_{\mu } - {\textbf{A}}_{\mu }\ {\textbf{t}}_n = {\textbf{B}}\ {\textbf{t}}^h. \end{aligned}$$

(51)

Defining the matrix ${\textbf{N}} = {{\,\textrm{diag}\,}}({\textbf{I}},\ - {\textbf{A}}_{\mu })$ and input data vector ${\textbf{l}} = [\ {\textbf{t}}^*_{\mu }\ \ {\textbf{t}}_n\ ]^T$ with the block-diagonal ${\mathbf{C_l}} = {{\,\textrm{diag}\,}}({\textbf{C}}_{{\textbf{t}}^*_{\mu }}, {\textbf{C}}_{{\textbf{t}}_n})$, then

$$\begin{aligned} {\textbf{N}}\ {\textbf{l}} = {\textbf{B}}\ {\textbf{t}}^h. \end{aligned}$$

(52)

The solution for the residual disturbing potential reads

$$\begin{aligned} \hat{\textbf{t}}^h = [ {\textbf{B}}^T\ ({\textbf{N}}\ {\mathbf{C_l}}\ {\textbf{N}}^T)^{-1}\ {\textbf{B}} ]^{-1}\ {\textbf{B}}^T\ ({\textbf{N}}\ {\mathbf{C_l}}\ {\textbf{N}}^T)^{-1}\ {\textbf{N}}\ {\textbf{l}}. \end{aligned}$$

(53)

The least-squares solution provided by Eq. (53) yields directly the EVM of the estimated values of the residual disturbing potential, i.e.,

$$\begin{aligned} {\textbf{C}}_{\hat{\textbf{t}}^h} = [ {\textbf{B}}^T\ ({\textbf{N}}\ {\mathbf{C_l}}\ {\textbf{N}}^T)^{-1}\ {\textbf{B}} ]^{-1}. \end{aligned}$$

(54)

The total disturbing potential would then include the reference part computed from the GGM

$$\begin{aligned} {\mathbf{C_{\hat{t}}}} = {\textbf{C}}_{{\textbf{t}}^l} + {\textbf{C}}_{{\textbf{t}}^h} = {\textbf{A}}\ {\textbf{C}}_{{\textbf{t}}_n} {\textbf{A}}^T + [ {\textbf{B}}^T\ ({\textbf{N}}\ {\mathbf{C_l}}\ {\textbf{N}}^T)^{-1}\ {\textbf{B}} ]^{-1}. \nonumber \\ \end{aligned}$$

(55)

The system of normal equations in Eq. (53) provides the least-squares solution to the system of discretized Fredholm’s integral equations of the first kind. To evaluate its solution numerically can be difficult as the coefficient matrix of the normal equations is generally ill-conditioned, i.e., its condition number can be very large. Thus, estimates of the unknown disturbing potential will be very sensitive to errors in the measured gradient data. The design of the problem, i.e., properties of the design matrix $\textbf{B}$, and the EVMs of the observed disturbing gradients ${\textbf{C}}_{{\textbf{t}}^*_{\mu }}$ and harmonic coefficients ${\textbf{C}}_{{\textbf{t}}_n}$, will play an important role in this respect.

To obtain a solution, the system of normal equations in Eq. (53) must be often regularized. Different methods have been proposed for solving such ill-conditioned systems, which are usually categorized as direct and iterative methods; see, e.g., Bouman (1998) or Eshagh (2011b). Tikhonov’s regularization (Tikhonov 1963) adds a small positive value $\kappa$, known as the regularization parameter, to all diagonal elements of the coefficient matrix of the normal equations. The regularized solution is biased, but the bias can be estimated. The regularized solution then reads

$$\begin{aligned} \hat{\textbf{T}}^h_{\kappa }= & {} [ {\textbf{B}}^T\ ({\textbf{N}}\ {\mathbf{C_l}}\ {\textbf{N}}^T)^{-1}\ {\textbf{B}} + \kappa \ \textbf{I} ]^{-1}\ {\textbf{B}}^T\ ({\textbf{N}}\ {\mathbf{C_l}}\ {\textbf{N}}^T)^{-1}\ {\textbf{N}}\ {\textbf{l}}\nonumber \\= & {} {\textbf{M}}^{-1}_{\kappa }\ {\textbf{B}}^T\ ({\textbf{N}}\ {\mathbf{C_l}}\ {\textbf{N}}^T)^{-1}\ {\textbf{N}}\ {\textbf{l}}. \end{aligned}$$

(56)

The introduction of the small regularization term $\kappa$ causes a small error (bias) which is approximated using the regularized solution (Xu et al. 2006)

$$\begin{aligned} \beta _{\kappa } \approx - \kappa ^2\ {\textbf{M}}^{-1}_{\kappa }\ \hat{\textbf{T}}^h_{\kappa }\, \end{aligned}$$

(57)

where

$$\begin{aligned} {\textbf{M}}^{-1}_{\kappa } = {\textbf{B}}^T\ ({\textbf{N}}\ {\mathbf{C_l}}\ {\textbf{N}}^T)^{-1}\ {\textbf{B}} + \kappa \ \textbf{I}. \end{aligned}$$

(58)

Note that the regularization affects also the estimate of the respective EVM

$$\begin{aligned} {\textbf{C}}_{\hat{\textbf{T}}^h_{\kappa }} = {\textbf{M}}^{-1}_{\kappa }\ {\textbf{B}}^T\ ({\textbf{N}}\ {\mathbf{C_l}}\ {\textbf{N}}^T)^{-1}\ {\textbf{B}}\ {\textbf{M}}^{-1}_{\kappa }. \end{aligned}$$

(59)

4.2 Closed-loop tests and synthetic data

Closed-loop tests are particularly popular in physical geodesy because they allow for uncertainty estimation in a well-controlled environment. The prize one has to pay for this advantage is the artificial nature of synthetic gradient data and their noise which can never fully replicate characteristics of real data. However, some statistics can be used to simulate gradient data and their noise as close as possible to reality. Numerical errors related to the particular implementation of the mathematical model (such as errors associated with particular integration techniques, truncation of integration domains, or replacement of integral solution by truncated harmonic series) can also be separated. This scenario has been used many times and (Novák et al. 2001) is just one example.

Input gradient data for this method are represented by the GGM, either based on real data analysis or some empirical rules such as that of Kaula (1966). The method is also advantageous in the sense that basic properties of gradient data are guaranteed, i.e., the gravitational field is by definition harmonic and regular at infinity. The synthesis of the disturbing gradients from the GGM (Fantino and Casotto 2009) can generally be written as follows, see also Eq. (38):

$$\begin{aligned} T_{\mu } = \sum _{n=3}^{max}\ \sum _{m=-n}^{n} \textrm{a}_{\mu }\left( t^{n+i}\ Y_{nm} \right) \ T_{nm} = {\textbf{a}}_{\mu } \cdot {\textbf{t}}_n\, \end{aligned}$$

(60)

with $\textrm{a}_{\mu }$ representing the differential operator that must be applied to the disturbing potential T to derive its particular gradient. Since the surface spherical harmonics $Y_{nm}$ are analytic functions of the 2-D position, the corresponding series representations can be formulated for all gradients of the disturbing potential T applied in this study. Their non-singular expressions can be found in (Petrovskaya and Vershkov 2006; Eshagh 2009) and (Hamáčková et al. 2016), respectively.

The situation is a bit more complicated in the case of the gradient groups, which must be estimated by combing individual gradients synthesized from the GGM. Adding the observation noise can destroy these properties (as it is often the case in reality). Current GGMs contain formal errors and in some cases even their complete EVMs. In the case of the formal variances, their propagation is relatively simple

$$\begin{aligned} \sigma ^2_{T_{\mu }} = \sum _{n=3}^{max}\ \sum _{m=-n}^{n} [\ \textrm{a}_{\mu }\left( t^{n+i}\ Y_{nm} \right) \ ]^2\ \sigma ^2_{T_{nm}}. \end{aligned}$$

(61)

In the case of the full EVM, the covariance law is applied.

In general, any of the quantities discussed above can be synthesized from the GGM represented by the spherical harmonic series. The harmonic series represents the gravitational parameters in mass-free space (there is a corresponding mass model). The harmonic series allows the estimation of both the input gradient data and reference values of the disturbing potential, so that estimated values of the disturbing potential can directly be compared with their reference counterparts.

The harmonic series representation is a convenient method to generate disturbing gradients (or disturbing gradient groups) arbitrarily distributed in 3-D space with various spectral properties mimicking those of real or expected gradient data. When polluted by the noise, the formal error propagation can also be performed which can be separated from the implementation errors of the estimated solution. Although this method cannot be used for the rigorous noise propagation, it offers some interesting insights into properties of the integral formulas and integral equations, and their respective solutions.

4.3 Independent reference values

Finally, there is a method that can be used to validate the results and estimate their external accuracy through independent reference values, ideally provided along with their uncertainties. In the case of the mathematical models for estimation of the disturbing potential from measured values of its gradients, there are some independent reference values that can be used, namely GNSS/levelling points where both levelled heights and geocentric positions were measured. Levelled height differences, if corrected for surface gravity, provide normal heights. Geocentric Cartesian coordinates of the same points provided by GNSS can be transformed into geodetic coordinates that represent two-parametric curvilinear coordinates defined at the reference ellipsoid. One component of these coordinates is the geodetic height defined as an Euclidean distance of a surface point above the reference ellipsoid measured along the ellipsoidal normal. By subtracting the normal and geodetic heights, we obtain the so-called height anomaly, which can be converted to the disturbing potential at a surface point using the Bruns formula (Heiskanen and Moritz 1967, Eq. 2-144). Thus, completely independent reference values of the disturbing potential $T_\textrm{ref}$ are available at selected points on the Earth’s surface.

Mathematically, the validation of the estimated values of the disturbing potential $\hat{T}$ can be done using a simple relationship

$$\begin{aligned} \delta T = \hat{T} - T_\textrm{ref}. \end{aligned}$$

(62)

Considering a sample of n reference values $T_\textrm{ref}$, the mean value and variance of the differences $\delta T$ can be computed as follows:

$$\begin{aligned} \mu _{\delta T} = \frac{1}{n}\ \sum _i^n \delta T_i,\, \quad \sigma ^2_{\delta T} = \frac{1}{n}\ \sum _i^n \delta T^2_i. \end{aligned}$$

(63)

A sample of the estimated differences can be then tested for significant deviations from its expected statistical characteristics, e.g., zero mean and normal distribution of the differences. Given the accuracy of the reference values (the accuracy of both GNSS-based geodetic heights and levelled normal heights is at the level of 0.01 m that yields an uncertainty better than 0.02 m in the height anomaly and 0.2 m$^2$ s$^{-2}$ in the disturbing potential), the sample variance can be interpreted.

This simple analysis allows, in addition to providing values of the basic statistics, also to study the spatial properties of the differences and above all to interpret their non-random spatial behaviour (systematic errors in levelling, common to this type of geodetic observations, are often detected). In addition to using the point values of the disturbing potential, their differences between two points can also be used. These values are observable at the Earth’s surface by combining levelled height differences and surface gravity data (Jekeli 2000). Alternatively, successful experiments have already been carried out with the measurement of gravitational potential differences between two points on the Earth’s surface using atomic clocks (van Camp et al. 2021).

Basic statical tests include the zero mean test ("the mean difference does not significantly deviate from zero", i.e., "the solution is not biased") and the test for the normality of their distribution ("the differences are randomly distributed"). Given that these tests are rather standard in geodesy, interested readers can consult available textbooks, e.g., (Vaníček and Krakiwsky 1987, Chap. 13). Assuming the reference values to be error-free, the differences in Eq. (62) can be tested against the formal error $\sigma _{\hat{T}}$ estimated using the stochastic model, i.e., the hypothesis

$$\begin{aligned} |\delta T| \le z_{\alpha }\ \sigma _{\hat{T}}\, \end{aligned}$$

(64)

is tested for the selected value of the significance level $\alpha$ (e.g., $z_{\alpha } \approx 2$ for $\alpha = 0.05$).

5 Examples of the gradient noise propagation

In this section, the noise of the disturbing gradients and disturbing gradient groups is discussed and its realistic magnitude is assessed. It is then used to test the noise propagation by some stochastic models discussed in this study. Moreover, several examples of closed-loop testing and external accuracy estimation are also provided.

5.1 Assessing the gradient noise

For the investigation of the stochastic models and especially for their numerical implementation, several assumptions about the observation noise of the disturbing gradient data are adopted: 1-the noise of the disturbing gradients is a zero-mean Gaussian random variable, and 2-the noise of the disturbing gradients is spatially independent.

The noise characteristics of the first-order disturbing gradients and their respective gradient groups $T^*_{10}$ and $T^*_{11}$ are discussed first. Note that $T^*_{10} = T^*_z$ (gravity disturbance) is still the most widely available and most accurate gravity field information collected at, above and even below the Earth’s surface. The magnitude of their observation noise will largely depend on used instrumentation and observation technique (surface, marine, aerial or satellite platforms). While the accuracy of some reference gravity data measured typically by free-fall devices can be very high (relatively up to 1 ppb), the observational noise (or rather uncertainty caused partially by inaccurate positioning of gravity points) of national gravity surveys, providing values of the scaled disturbing gradients $T^*_z$, is typically at the level of 1 m$^2$ s$^{-2}$. The noise of the first-order gradient group $T^*_{11}$ is then approximately twice as large.

Surface gravity represents the most accurate and detailed data as static sensors located right at the gravitating masses can be deployed. Gradient data from moving sensors must be reduced for kinematic acceleration; moreover, they may suffer from less accurate positioning (kinematic GNSS), especially in the vertical direction. The accuracy of aerial and satellite gradient data is at least one-order of magnitude worse; moreover, observed gradient data must be filtered to a certain measurement bandwidth (only some wavelengths of a highly attenuated gravitational signal can be recovered).

To date, (almost) globally distributed observations of the second-order gradients have only been provided by the gradiometer on board the GOCE satellite. They contain rather complicated errors depending on characteristics of accelerometers. The accelerometers are highly sensitive only within the so-called measurement bandwidth limited by the frequencies between $5 \times 10^{-3}$ and 0.1 Hz (Rummel et al. 2011). Inside this bandwidth, signals provided by the accelerometers show a white noise behaviour. The gradient noise also includes drifting biases of the accelerometers and small periodical variations caused by non-uniform rotation of the GOCE satellite. Both can be modelled in the observation equation. Thus, the white noise assumption adopted above can be justified.

In the case of the third-order gradients, no relevant data are currently available. Their noise can be only hypothesized based on the characteristics of currently available accelerometers assembled into a specific observation platform. Three accelerometers, aligned with a local vertical direction $\Omega$ and separated by the distances $\Delta r_{12} = \Delta r_{23} = \Delta r$ and $\Delta r_{13} = 2 \Delta r$, observe the first-order vertical gradient of the geopotential $V_z$. The second-order vertical gradient $V_{zz}$ can approximately be computed in the mid-point $r_2$ as their difference divided by the respective separation, e.g.,

$$\begin{aligned} V_{zz}(r_2,\Omega ) \approx \frac{V_z(r_1,\Omega ) - V_z(r_3,\Omega )}{2 \Delta r}. \end{aligned}$$

(65)

The third-order vertical gradient $V_{zzz}$ can be computed by combining observations of all accelerometers

$$\begin{aligned} V_{zzz}(r_2,\Omega ) = \frac{V_z(r_1,\Omega ) - 2 V_z(r_2,\Omega ) + V_z(r_3,\Omega )}{\Delta r^2}. \end{aligned}$$

(66)

Assumptions important for further analyses include: 1-accelerometers have identical performance, 2-observed accelerations are uncorrelated, 3-position errors are ignored, and 4-orientation of the instrument baseline is aligned with the local vertical. In fact, the position and orientation of the observation platform in space realize the local Cartesian coordinate system to which measured gradients are related.

Since the noise level of each accelerometer is defined by the same variance $\sigma ^2_{V_z}$ [m$^2$ s$^{-4}$], then its propagation through Eqs. (65) and (66) yields

$$\begin{aligned} \sigma ^2_{V_{zz}}= & {} \frac{1}{2}\ \frac{\sigma ^2_{V_z}}{\Delta r^2}\ [\textrm{s}^{-4}]\, \end{aligned}$$

(67)

$$\begin{aligned} \sigma ^2_{V_{zzz}}= & {} 6\ \frac{\sigma ^2_{V_z}}{\Delta r^4}\ [\textrm{m}^{-2}\ \textrm{s}^{-4}]. \end{aligned}$$

(68)

Since the normal gradients can be computed analytically, Eq. (68) also represents, after using the scale $R^6$, the variances of the respective disturbing gradient $T^*_{zzz}$. The experiment design proposed by Šprlák et al. (2016) is based on a satellite orbiting at the mean elevation of $2.5 \times 10^5$ m (GOCE was at approximately $2.2 \times 10^5$ m) with three accelerometers separated from each other by $\Delta r = 1$ m and sampling data at 1 Hz. This design provides the magnitude of the standard deviation of the scaled third-order vertical gradient data as $2.5 \times 10^2$ m$^2$ s$^{-2}$. The analysis of the third-order gradient data then yields the noise ratio 1 : 1 : 3 : 10 for the gradient groups $T^*_{30}:T^*_{31}:T^*_{32}:T^*_{33}$ (Šprlák et al. 2016).

Table 7 Dilution of precision [unitless] vs. grid resolution [arc-deg] for transformation of gradients

Fig. 3

Structure of the normalized matrix $\textbf{C}$ for integral transforms of the first-order vertical disturbing gradient $T_z$ [unitless]

Synthetic disturbing gradients computed from the GGM can be contaminated by the Gaussian noise $\varepsilon _{T^*_{\mu }}$ with the zero mean and the standard deviation $\sigma _{T^*_{\mu }}$. Its values for different gradient data must be chosen realistically, although some of the gradients discussed here are not yet observable. Such noisy gradient data then read

$$\begin{aligned} T^{*\varepsilon }_{\mu } = T^*_{\mu } + \varepsilon _{T^*_{\mu }}\, \end{aligned}$$

(69)

with the EVM represented as follows:

$$\begin{aligned} {\textbf{C}}_{{\textbf{T}}^*_{\mu }} = \sigma _{T^*_{\mu }}^2\ {\textbf{I}}. \end{aligned}$$

(70)

The noise magnitudes of the scaled first-, second-, and third-order disturbing gradients are estimated to be approximately one, two and three in units of the geopotential.

Fig. 4

Structure of the normalized matrix $\textbf{C}$ for integral transforms of the second-order vertical disturbing gradient $T_{zz}$ [unitless]

Fig. 5

Degree-limited kernel functions for integral transforms of the vertical disturbing gradients $T_z$, $T_{zz}$, and $T_{zzz}$ [unitless]

5.2 Propagating gradient noise estimates

In this subsection, gradient noise characteristics, described in the previous subsection, are used to test the noise propagation and uncertainty estimation. Three options discussed in Sect. 4 are tested including formal error estimation, closed-loop testing, and external validation. Given the number of possible observables (19 gradients and 9 gradient groups), only selected examples are presented. Their main purpose is to demonstrate how these tools can be used in practice.

Fig. 6

Errors propagated by integral formulas from the vertical disturbing gradients $T_z$, $T_{zz}$, and $T_{zzz}$ into the geoid height [m]

Fig. 7

Degree-dependent errors propagated by integral formulas from the vertical disturbing gradients $T_z$, $T_{zz}$, and $T_{zzz}$ into the geoid height [m]

Fig. 8

Errors propagated by integral equations from the vertical disturbing gradients $T_z$, $T_{zz}$, and $T_{zzz}$ at 250 km into the geoid height [m]

5.2.1 Formal error estimation

Formal error propagation through integral formulas and integral equations is discussed in Sect. 4.1. In the case of integral formulas, the mathematical model reads as follows, see Eq. (47),

$$\begin{aligned} {\textbf{C}}_{\hat{\textbf{t}}}{} & {} = ({\textbf{A}} - {\textbf{K}}\ {\textbf{U}}_i\ {\textbf{A}}_{\mu })\ {\textbf{C}}_{{\textbf{t}}_n}\ ({\textbf{A}} - {\textbf{K}}\ {\textbf{U}}_i\ {\textbf{A}}_{\mu })^T \nonumber \\ {}{} & {} \quad + {\textbf{K}}\ {\textbf{U}}_i\ {\textbf{C}}_{{\textbf{t}}^*_{\mu }}\ {\textbf{U}}^T_i\ {\textbf{K}}^T\, \end{aligned}$$

(71)

and for the integral equations, see Eq. (55),

$$\begin{aligned} \textbf{C}_{\hat{\textbf{t}}} = {\textbf{A}}\ {\textbf{C}}_{{\textbf{t}}_n} {\textbf{A}}^T + [{\textbf{B}}^T\ ({\textbf{N}}\ {\mathbf{C_l}}\ {\textbf{N}}^T)^{-1}\ {\textbf{B}}]^{-1}. \end{aligned}$$

(72)

This apparatus can be used to propagate the gradient noise with different levels of complexity (white or coloured noise). Generally, the noise of local gradient data is spatially correlated, i.e., their EVMs are fully populated. Surface vertical gradient data $T_z$ (disturbing gravity) are derived from measured gravity differences (relative gravimetry) between points of a gravity network with geocentric positions estimated by GNSS. Such data can be adjusted using closed-loop conditions in exactly the same way as gravity-corrected levelled height differences. A fully populated EVM of the gradient data is then available and either Eqs. (71) or (72) could be applied.

In the absence of reliable information on gradient noise correlations, only noise variance estimates are used. Considering the second-order disturbing gradients $T^*_{ab}$, see Eqs. (10) and (12), a unique noise variance must be assigned to each of them. For example, the disturbing gradients $T_{xx}, T_{yy}, T_{zz}$ and $T_{xz}$ derived from GOCE observations are more accurate than $T_{xy}$ and $T_{yz}$ within their measurement bandwidth. There is also a significant difference among the more accurate disturbing gradients with $T_{xx}$ and $T_{yy}$ being approximately twice as accurate as $T_{zz}$ and $T_{xz}$. The matrix ${\textbf{C}}_{{\textbf{t}}^*_{\mu }}$ then contains only the noise variances on the main diagonal.

Fig. 9

Scaled second-order disturbing gradient $T^*_{xx}$ [m$^2$ s$^{-2}$]

Fig. 10

Scaled second-order disturbing gradient $T^*_{yy}$ [m$^2$ s$^{-2}$]

Fig. 11

Scaled second-order disturbing gradient $T^*_{xy}$ [m$^2$ s$^{-2}$]

Fig. 12

Scaled second-order disturbing gradient $T^*_{xz}$ [m$^2$ s$^{-2}$]

Fig. 13

Scaled second-order disturbing gradient $T^*_{yz}$ [m$^2$ s$^{-2}$]

Fig. 14

Scaled second-order disturbing gradient $T^*_{zz}$ [m$^2$ s$^{-2}$]

The most simple case involves the global vertical gradient data with ${\textbf{C}}_{{\textbf{t}}^*_{\mu }} = \sigma _0^2\ \textbf{I}$ that yields for the integral transforms

$$\begin{aligned} \textbf{C}_{\hat{\textbf{T}}}= \sigma _0^2\ {\textbf{K}}\ {\textbf{K}}^T\, \end{aligned}$$

(73)

and for the integral equations

$$\begin{aligned} \textbf{C}_{\hat{\textbf{T}}}= \sigma _0^2\ \left( {\textbf{B}}^T\ {\textbf{B}} \right) ^{-1}. \end{aligned}$$

(74)

This apparatus can be used to design studies indicating optimal (with respect to some selected criteria) solutions. In geodesy, it is often used in satellite positioning where the so-called dilution of precision (Langley 1999) is estimated only from the design of the experiment, i.e.,

$$\begin{aligned} {\textbf{C}} = {\textbf{K}}\ {\textbf{K}}^T = \left( {\textbf{B}}^T\ {\textbf{B}} \right) ^{-1}. \end{aligned}$$

(75)

The trace of the matrix ${\textbf{C}}$ can be evaluated and an optimum design of the observation experiment is then sought in terms of its minimum value. Table  7 includes values of the so-called dilution of precision computed for various designs of the observation experiment (in terms of angular resolutions of the gradient data). This approach can help in planning more complex designs of observation experiments including sensor characteristics and spatio-temporal data sampling, see, e.g., (Klokočník et al. 2008).

But also the information contained in the off-diagonal elements of the matrix ${\textbf{C}}$ as evaluated from Eq. (75) is interesting. Figures 3 and 4 present the structure of the matrix ${\textbf{K}}\ {\textbf{K}}^T$ in terms of normalized values of its elements for integral transformation of the first- and second-order vertical gradients $T_z$ and $T_{zz}$. The maximum degree of the harmonic series representing kernel functions was set to 180. Larger values of the off-diagonal elements for higher-order gradients indicate more significant correlations of the estimated noise caused by the behaviour of their respective kernel functions in the space domain, see Fig. 5. In case of the uncorrelated observation noise, the structure would correspond to that of the EVM of the estimated geopotential values.

These numerical tests explore the error propagation in the absence of actual gradient data. Based on the assumption the a priori variance factor is realistic, the behaviour of the discretized integral formulas related to the inversion of the vertical disturbing gradients $T_z$, $T_{zz}$, and $T_{zzz}$ is investigated. Indeed, the downward continuation is embedded within the integral kernels, as confirmed by the presence of the amplification factor $r/R > 1$, which significantly contributes to the kernel divergence. The challenge lies in estimating the disturbing potential (geoid height) from the disturbing gradients. However, for the purpose of studying error propagation properties of the integrals, neither real nor synthetic data are required.

To illustrate the propagation of gradient errors to the disturbing potential through integral formulas, the test area bounded by the latitudes 55 and 70 arc-deg N, and longitudes 5 and 30 arc-deg E is selected. Three integral formulas are used for estimating the unknown disturbing potential at the 1 arc-deg equiangular grid using the vertical disturbing gradients $T_z$, $T_{zz}$, and $T_{zzz}$. Given the inherent divergence of the integral kernels, their spectral representations are limited by the harmonic degrees 3-100. The choice of the maximum degree holds practical significance, as higher degrees lead to very diverging kernels, resulting in a substantial amplification of the gradient errors. Nevertheless, the maximum degree 100 warrants solutions for all three vertical gradients, i.e., error propagation characteristics across the three integral formulas can be compared.

For the gradient $T_z$, an error of 1 mGal is assumed, while corresponding error values of $1.6 \times 10^{-12}$ s$^{-2}$ and $2.4 \times 10^{-19}$ m$^2$ s$^{-2}$ are applied to the vertical disturbing gradients $T_{zz}$ and $T_{zzz}$, respectively. Square roots of the diagonal elements of the EVMs estimated from the three integral formulas are computed and subsequently divided by 9.8 m s$^{-2}$ to obtain the equivalent geoid height in metres. Figure 6 illustrates the propagated errors for the vertical disturbing gradients $T_z$, $T_{zz}$, and $T_{zzz}$ to the geoid height across the study area. Figure 6 also reveals a notable trend in the propagated errors: integral formulas involving the higher-order gradients propagate the data noise less than those involving the lower-order gradients. This phenomenon is attributed to downward continuation properties of the integral formulas.

Note that the integral kernels exhibit the asymptotic convergence, implying that their convergence extends only to a certain maximum degree. The key takeaway from Fig. 6 aligns with the behaviour observed at any maximum degree. However, the kernel associated with the gradient $T_z$ exhibits a greater divergence than the other two vertical disturbing gradients, leading to a significant increase in error, resulting in highly exaggerated and unrealistic errors for the geoid. This prompted us to limit the series form of the kernel functions at the degree 100 to obtain meaningful outcomes. But the investigations covered various maximum degrees, ensuring a comprehensive study and comparison. Yet, to illustrate the error behaviour effectively, the maximum degree of 100 was finally selected. At very high degrees, the geoid errors derived from the vertical disturbing gradients $T_{zz}$ and $T_{zzz}$ behave almost linearly.

It is evident that integral formulas for the higher-order disturbing gradients capture better higher frequencies of the disturbing potential. This characteristic is also reflected in their error propagation properties. In this context, an important consideration must be given to the choice of the a priori variance factor used for scaling EVMs. When the value of 1 is assumed for all gradients, it implies an error of 1 m s$^{-2}$ for the gradient $T_z$, 1 s$^{-2}$ for $T_{zz}$, and 1 m$^{-1}$ s$^{-2}$ for $T_{zzz}$. In this scenario, larger errors propagated from the input gradient $T_{zzz}$ would not be justified. The signal-to-noise ratio is a crucial factor, and for a fair comparison, the noise level should be selected in accordance with the signal magnitude.

Figure 7 shows that the average error propagated from the disturbing gradients $T_z$, $T_{zz}$, and $T_{zzz}$ can be linked to the maximum degree of the kernel function. The mean error reaches up to 1 m when $T_{z}$ is used over the test area when the kernel functions are limited to the maximum degree 120, while it reaches the 0.01 m level when $T_{zz}$ is applied, and it is even smaller for $T_{zzz}$. In this example, a rather complex scenario was encountered. This complexity arises from the inherent downward continuation properties of the integral transforms, which significantly influence the error propagation. It is important to note that when dealing with integral formulas characterized by such amplifying properties, the error propagation becomes less straightforward and manageable.

To illustrate the error propagation within the integral equations, we chose another test area bounded by the latitudes 40 and 80 arc-deg N, and longitudes 0 to 40 arc-deg E. The vertical disturbing gradients $T_z$, $T_{zz}$, and $T_{zzz}$ are synthesized at the equiangular 0.25 arc-deg grid using the EGM08 model (Pavlis et al. 2012) with the spherical harmonics up to the degree and order 360. The objective is to assess the error propagation from the vertical gradients into the disturbing potential (or equivalent geoid height) at the grid with the angular resolution of 0.5 arc-deg. Given that the system of equations obtained after discretizing the integral equations was found to be unstable, the Tikhonov regularization method (Tikhonov 1963) was applied with the regularization parameters estimated using the quasi-optimal estimation approach (Hansen 2007).

We considered the white noise at the level of about 10 % of the signal magnitude, which corresponds to the orders of 10$^{-5}$, 10$^{-10}$, and 10$^{-15}$. The estimated errors presented again in terms of the geoid height are shown in Fig. 8. The propagated errors behave in accordance with the scenario explained above. Furthermore, it is evident that the size, height, and resolution of the data area are significant for propagation of the gradient errors through the integral equations. The larger spatial resolution of the higher-order gradient data is justified due to the sharper shape of their kernel functions in the respective integral equation. Additionally, the larger data area leads to larger values of the propagated errors. Higher-order disturbing gradients are more localized in space, and the contribution of the long-wavelength part of their signal is considerably smaller than that of the shorter wavelengths.

5.2.2 Closed-loop testing

For the closed-loop tests, global grids of the second-order disturbing gradients are synthesized from the satellite-only global gravitational model GOCO06s (Kvas et al. 2021) computed up to the harmonic degree 300 using more than 1 billion observations to 19 satellites. Global equiangular grids of the second-order disturbing gradients with the angular resolution of 0.25 arc-deg (approximately 50 km half-wavelength at the equator) are computed using the singularity-free formulas in (Petrovskaya and Vershkov 2006). The grids contain 1,036,800 values for each of six unique second-order disturbing gradients at the mean orbital altitude of 250 km above the mean sphere, see Figs. 9, 10, 11, 12, 13 and 14. The disturbing gradients are scaled according to Eq. (12) with the squared radius of the mean sphere $R^2$. In the same way, reference values of the disturbing potential at the mean sphere are synthesized from GOCO06s on the same coordinate grid.

To test the integral formulas and their software implementation, noise-free gradient data are employed first, see Table 8. Gradient groups based on the global grids are formed according to Eq. (14). They are transformed by the integral formulas in Eq. (17) into estimates of the disturbing potential at the mean sphere and compared with the reference values of the disturbing potential. Their differences, originating from discrete numerical integration, are at the level of 0.01 m$^2$ s$^{-2}$, i.e., at the 1 mm level of the respective geoid height and 10 ppm relatively. Statistics of the differences obtained for all three second-order gradient groups are found in Table 9. Thus, one can conclude that the mathematical models are correctly formulated and implemented.

To test the sensitivity of the mathematical models to the observation errors in the gradient data, the scaled gradients at the mean orbital height are contaminated with Gaussian noise with the standard deviation of 40 m$^2$ s$^{-2}$, see Sect. 5.1. This value corresponds to the $10^{-11}$ s$^{-2}$ (or 10 mE) noise in unscaled gradient data. At the same time, this noise is relatively at the level of 10 % of the respective signal. Estimates of the disturbing potential are computed over a test area covering the Himalayas. This area is particularly interesting due to complexity of its gravity field. Values of the differences "estimated values—reference values" are found in Figs. 15, 16 and 17, and their statistics in Table 10. One can conclude that the noise of the estimated values of the disturbing potential reaches the magnitude of 1 m$^2$ s$^{-2}$, i.e., 0.1 m in terms of the geoid height. Note that the GOCO06s model includes also formal errors of the harmonic coefficients; however, they are not used in this study as they do not provide realistic estimates of the gradient noise.

Table 8 Scaled second-order disturbing gradients [$\times 10^4$ m$^2$ s$^{-2}$]

Table 9 Implementation errors for transformation of the gradient groups [m$^2$ s$^{-2}$]

Fig. 15

Differences “estimated–reference” for the gradient group $T^*_{20}$ [m$^2$ s$^{-2}$]

Fig. 16

Differences “estimated–reference” for the gradient group $T^*_{21}$ [m$^2$ s$^{-2}$]

Fig. 17

Differences “estimated–reference” for the gradient group $T^*_{22}$ [m$^2$ s$^{-2}$]

5.2.3 External validation

As an example of the external validation of the gradient data measured by satellites, the recent study of (Pitoňák et al. 2023) can be used. Second-order gradient data provided by the GOCE gradiometer are transformed into the disturbing potential at 1668 reference GNSS/levelling points in Norway. Figure 18 shows their distribution as well as the corresponding reference values of the height anomaly (surface values of the disturbing potential scaled by normal gravity at the telluroid). A global grid of the second-order gradients at the mean satellite orbit of $6.6 \times 10^6$ m is estimated by the so-called space-wise approach, see (Rummel et al. 1993) or (Reguzzoni and Tselfes 2006), with the equiangular resolution of 0.2 arc-deg. The gradient grid is then transformed into discrete values of the disturbing potential at the Earth’s surface using solutions to the gradiometric BVP, see Eq. (17), in terms of the external spherical harmonic series of the disturbing potential and its second-order gradients.

Table 10 Propagation of the 40 m$^2$ s$^{-2}$ white noise in transformation of the gradient groups [m$^2$ s$^{-2}$]

Geodetic heights are obtained by transformation of the geocentric Cartesian coordinates provided by GNSS. Normal heights are based on the common Nordic adjustment that takes into the account a vertical land uplift and refers to the Normaal Amsterdams Peil. Geodetic and normal heights of the reference points were transformed into the same tidal system before computing reference values of the disturbing potential. Estimated uncertainties of the geodetic and normal heights are 0.005 and 0.007 m, respectively (Kartverket 2020). Thus, the reference values of the disturbing potential have an uncertainty of 0.1 m$^2$ s$^{-2}$ (1 cm in terms of the geoid height).

Fig. 18

GNSS/levelling points in Norway and reference values of the height anomaly [m]

Estimated values of the disturbing potential are compared with the reference values, see Eq. (62). Biases and tilts in the estimated differences that originate from systematic errors of the geodetic and normal heights, and geodynamic effects such as the post-glacial rebound are removed using a corrector surfaces. Statistics of the estimated differences between the reference values of the disturbing potential at the GNSS/levelling points and its estimates obtained using the second-order vertical disturbing gradients $T^*_{zz}$ provide the zero mean difference, standard deviation of 1 m$^2$ s$^{-2}$ (or 0.1 m in terms of the geoid height), and extreme values in the range of ± 3 m$^2$ s$^{-2}$. Interestingly, the study of (Pitoňák et al. 2023) also contains results based on the other two second-order gradient groups, i.e., $T^*_{21}$ and $T^*_{22}$, including their spectral combinations, but without a significant effect on statistics of the estimated differences.

6 Conclusions

This contribution discusses mathematical models based on integral-based solutions to geodetic BVPs that transform gradients of the disturbing potential into the disturbing potential. A well-known representative of these models, often used in physical geodesy, is Hotine’s integral transform of surface disturbing gravity. Mathematical models for geopotential gradients up to the third order are considered reflecting data available today or in the foreseen future. Since integral formulas and integral equations represent only the deterministic solution of the problems, they must be completed for the stochastic component that allows for propagation of the observation noise. Stochastic models estimate uncertainties of the estimated values, thus enabling their assessment and quality testing.

Two types of the mathematical models solving the unknown disturbing potential from observed values of its gradients are discussed in the study. The first type of the mathematical models relies on solving spherical BVPs with the boundary values defined as groups of the disturbing gradients of up to the third order. The second type of the mathematical models employs the individual disturbing gradients; however, their solution has a form of Fredholm’s integral equation of the first kind. Both types of the mathematical models are modified for practical computations by discretizing involved surface integrals. This modification regularizes the solution to the Fredholm integral equation; however, further regularization may still be required, namely for higher-order geopotential gradients measured at satellite level.

Stochastic models for both integral formulas and integral equations are presented in this study. In the case of the integral formulas, the stochastic model takes the form of the well-known covariance law. In the case of the integral equations, the solution of over-determined problems can be formulated using the least-square principle (with regularization), which allows the EVM solution to be estimated. Based on the assessment of error characteristics of the disturbing gradients and their groups, respective EVMs are assembled and applied for stochastic modelling. Only selected numerical examples are presented in this study.

Moreover, other two approaches used for assessment of solutions to integral formulas and integral equations are discussed. Closed-loop tests take the advantage of validating mathematical formulations and their software implementation in a well-controlled environment based on synthetic gradient data. If independent reference values of the disturbing potential are available over the computation area, they can be used to estimate the external accuracy of the solution.

The text contributes to the topic of stochastic modelling in gravity field studies, which has recently been addressed by several authors. For a long time, the focus in physical geodesy has been on deterministic modelling, i.e., on estimating values of the unknown parameters. Stochastic modelling, which would handle stochastic properties of observed data and incorporate them into the solution, has been often neglected with the argument that stochastic properties of observed gradient data were largely unknown. This study attempts to fill this gap while reflecting new data types and respective developments in the methodology of gravity field modelling.

A Goniometric functions of the azimuth

In the article, the azimuths $\alpha$ and $\alpha '$ are used, see also (Šprlák and Novák 2016). The azimuth $\alpha$ is a signed angle at the point $\Omega$ measured clock-wise from the local meridian to the mean circle passing through the point $\Omega '$. Introducing two auxiliary parameters

$$\begin{aligned} \Delta \lambda = \lambda ' - \lambda ,\, \quad u' = (1 - u^2)^{-\frac{1}{2}}\, \end{aligned}$$

its goniometric functions can be evaluated as follows, see, e.g., (Winch and Roberts 1995):

$$\begin{aligned} \cos \alpha= & {} u'\ (\sin \varphi ' \cos \varphi - \cos \varphi ' \sin \varphi \cos \Delta \lambda )\, \end{aligned}$$

(76)

$$\begin{aligned} \sin \alpha= & {} u' \cos \varphi ' \sin \Delta \lambda . \end{aligned}$$

(77)

Analogously, goniometric functions of the azimuth at the point $\Omega '$ considered again clock-wise from the local meridian are defined (ibid):

$$\begin{aligned} \cos \alpha '= & {} u'\ (\sin \varphi \ \cos \varphi ' - \cos \varphi \ \sin \varphi ' \cos \Delta \lambda )\, \end{aligned}$$

(78)

$$\begin{aligned} \sin \alpha '= & {} - u' \cos \varphi \ \sin \Delta \lambda . \end{aligned}$$

(79)

Goniometric functions of the multiples of a general angle $\beta$ read (Abramowitz and Stegun 1972, p. 72)

$$\begin{aligned} \cos 2 \beta= & {} 2\ \cos ^2 \beta - 1\, \end{aligned}$$

(80)

$$\begin{aligned} \sin 2 \beta= & {} 2\ \cos \beta \ \sin \beta \,\end{aligned}$$

(81)

$$\begin{aligned} \cos 3 \beta= & {} \cos \beta \ (\cos ^2 \beta - 3 \sin ^2 \beta )\,\end{aligned}$$

(82)

$$\begin{aligned} \sin 3 \beta= & {} - \sin \beta \ (\sin ^2 \beta - 3 \cos ^2 \beta ). \end{aligned}$$

(83)