1 Introduction

Large-eddy simulation (LES) has been instrumental in the study of turbulence in the atmospheric boundary layer (ABL) (Moeng 1984; Andren et al. 1994; Albertson 1996). In LES, large-scale eddies are resolved, and the effects of the subgrid-scale (SGS) eddies are parametrized. The most widely used SGS parametrization is the Smagorinsky model, in which the model coefficients are derived from theoretical arguments and empirical formulations (Smagorinsky 1967). A significant disadvantage of the Smagorinsky model is that the SGS stresses are assumed to be universal, isotropic, and scale-invariant, which makes the model unsuitable for anisotropic flows such as ABL flows. To overcome the limitations of the Smagorinsky model, ad hoc wall damping functions, backscatter (Mason and Thomson 1992), and buoyancy corrections (Sullivan et al. 1994) have been proposed to account for the effects of wind shear and buoyancy.

Significant progress in SGS modelling was achieved with the introduction of the Germano identity (Germano et al. 1991). The Germano identity relates stresses at different scales and facilitates the calculation of the Smagorinsky coefficients without ad hoc formulations. This approach assumes scale-similarity, i.e., that the model coefficients do not vary with scale. However, scale-dependency is important in wall-bounded flows in which the grid scale approaches the local integral scale, such that the SGS stresses contribute significantly to the total stress. Scale-dependent models allow for more accurate modelling of SGS stresses and therefore can capture the flow physics in wall-bounded flows better than the Smagorinsky model (Meneveau and Katz 2000).

One class of scale-dependent models overcomes the limitation of scale similarity by calculating the model coefficients at different scales (Porté-Agel et al. 2000). This calculation is performed by using two so-called test filters. When calculating SGS constants with this method numerical instabilities can arise (Ghosal et al. 1995). To prevent this the model coefficients are averaged spatially (Porté-Agel et al. 2000) or in a Lagrangian way over fluid path-lines (Bou-Zeid et al. 2005). Planar averaging limits the coefficients to change only with height, while Lagrangian averaging allows for a three-dimensional variation of the SGS coefficients. For heterogeneous flows, such as flows over complex terrains or in extended wind farms, the three-dimensional variation of the model coefficient is necessary to model the flow physics accurately. It has been shown that the Lagrangian-averaged scale-dependent model (LASD) (Bou-Zeid et al. 2005) is a more suitable choice for such heterogeneous flows than SGS models that rely on planar averaging of the model coefficients.

A new class of SGS models that does not involve any additional filtering operations has recently been developed. In this approach, the minimum dissipation to balance the turbulence production at scales smaller than the grid scale is determined. These so-called minimum-dissipation models were initially developed for isotropic turbulence by Verstappen (2011). Further developments by Rozema et al. (2015) extended the approach to anisotropic turbulence. This model is known as the anisotropic minimum dissipation (AMD) model. Recently, Abkar and Moin (2017) incorporated buoyancy effects in the AMD model. The AMD model has been used successfully to model turbulent channel flows (Rozema et al. 2015), neutral ABL flow with passive scalars (Abkar et al. 2016), and the thermally-stratified ABL (Abkar and Moin 2017). The basic concept of the AMD model can be outlined as follows: the eddy viscosity in the minimum dissipation model is calculated by limiting the SGS eddies produced by the nonlinear advective terms in the Navier–Stokes equation from becoming dynamically significant. This argument does not involve any specific assumptions about the energy transfer between different scales, the energy spectrum, turbulent energy cascades, or phenomenological arguments (Verstappen 2011). The dynamically significant part of the motion is confined to large eddies by damping the velocity gradient with an eddy viscosity. The eddy viscosity is calculated such that the energy transferred from the large eddies to the SGS is dissipated at a rate that ensures that the production of SGS eddies by the non-linear terms in the Navier–Stokes equations becomes dynamically irrelevant.

To understand the performance of the different SGS models it is necessary to test them under different conditions. Therefore, we compare the performance of the standard Smagorinsky model (Smagorinsky 1967), the LASD model (Bou-Zeid et al. 2005; Stoll and Porté-Agel 2006, 2008), and the AMD model (Abkar and Moin 2017) for different atmospheric conditions. We analyze the first- and second-order turbulence statistics and the surface similarity for a neutral, stable, and unstable ABL. This provides more insight into the performance of two distinct classes of scale-dependent models (i.e., the LASD and the AMD model) for different atmospheric conditions.

The primary consideration in evaluating the performance of a SGS model is how accurately the model can capture the relevant flow physics. However, practical considerations can also play a role in the selection of an appropriate SGS model. The Smagorinsky model is by far the easiest to implement, but the limited accuracy of the Smagorinsky model is a significant drawback (Meneveau and Katz 2000). Scale-dependent models can capture the flow physics more accurately than the Smagorinsky model. While the LASD model (Bou-Zeid et al. 2005) has been used widely in the literature (Calaf et al. 2010; Wu and Porté-Agel 2011; Zhang et al. 2019; Gadde and Stevens 2019), the AMD model has only been developed relatively recently (Rozema et al. 2015; Abkar et al. 2016; Abkar and Moin 2017). While the LASD model has been shown to provide accurate predictions (Stevens et al. 2014), it has some practical drawbacks. It is challenging to implement, due to the required filtering operations and Lagrangian averaging procedure that are employed. Due to the additional filtering operations, the LASD model generates a computational overhead, and the numerical implementation of the Lagrangian averaging involves numerous interpolation operations, which requires MPI communication between multiple processors. Besides, the LASD model has an additional memory overhead due to the requirement to store the time histories of different quantities. These are all essential considerations for simulations performed on modern supercomputers. The AMD model, on the other hand, has low computational complexity and is straightforward to implement. Therefore, it is particularly interesting to see how the AMD model performs compared to the LASD model to assess whether it is a good alternative for the LASD model when considering large-scale simulations of ABL.

2 Large-Eddy Simulations

In LES, turbulent motions larger than the grid scale are resolved, and the SGS motions are parametrized. In a thermally stratified ABL, the Boussinesq approximation to model buoyancy leads to the following governing equations

$$\begin{aligned} \partial _{ i } {\widetilde{u}}_ i&=0, \end{aligned}$$
(1)
$$\begin{aligned} \partial _{ t }{\widetilde{u}}_ i + \partial _ j \left( {\widetilde{u}}_ i {\widetilde{u}}_ j \right)&=-\partial _{ i }{\widetilde{p}}-\partial _ j \tau _{ ij } + g\beta \left( {\widetilde{\theta }}-{\left\langle {\widetilde{\theta }}\right\rangle }\right) {\delta }_{ i3 }+f\varepsilon _{ ij3 }({\widetilde{u}}_ j -G_j), \end{aligned}$$
(2)
$$\begin{aligned} \partial _{ t }{\widetilde{\theta }} + {\widetilde{u}}_ j \partial _{ j }{\widetilde{\theta }}&=-\partial _{ j }q_ j , \end{aligned}$$
(3)

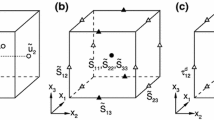
where the tilde represents spatial filtering, represents planar averaging, \({\widetilde{u}}_ i \) and \({\widetilde{\theta }}\) are the filtered velocity and potential temperature, respectively, \({\widetilde{p}}\) is the kinematic pressure, g is the acceleration due to gravity, \(\beta =1/\theta _ 0 \) is the buoyancy parameter with respect to the reference potential temperature \(\theta _ 0 \), \(\delta _{ ij }\) is the Kronecker delta, f is the Coriolis parameter, \(G_j=(U_g,V_g)\) is the geostrophic wind velocity, and \(\varepsilon _{ ijk }\) is the alternating unit tensor; \(\tau _{ ij }=\widetilde{u_{ i }u_{ j }}-{\widetilde{u}}_ i {\widetilde{u}}_ j \) is the traceless part of the SGS stress tensor and \(q_ j =\widetilde{u_ j \theta }-{\widetilde{u}}_ j {\widetilde{\theta }}\) is the SGS heat flux vector.

Wall-resolved LES are limited to moderate Reynolds numbers due to the very high computational cost (Piomelli 2008). Consequently, simulations of high Reynolds number ABL flows rely heavily on wall and SGS modelling. As it is impossible to resolve all the flow scales, an accurate representation of the SGS properties is crucial in these simulations (Sagaut 2006). It is common practice in LES to parametrize SGS stresses and fluxes using an eddy viscosity and an eddy diffusivity. Thus, the traceless part of the SGS stress and heat flux are modelled as

$$\begin{aligned} \tau _{ ij }-\frac{1}{3}\tau _ kk&= -2\nu _{T}{\widetilde{S}}_{ ij }\quad \,\,=-2(C_{s,\Updelta }\Updelta )^2|{\widetilde{S}}|{\widetilde{S}}_{ ij }, \end{aligned}$$
(4)
$$\begin{aligned} q_{ j }&= -\frac{\nu _{T}}{\text { Pr}_\text {sgs}}\partial _{ j }{\widetilde{\theta }}\,=-(D_{s,\Updelta }\Updelta )^2|{\widetilde{S}}|\partial _{ j }{\widetilde{\theta }}, \end{aligned}$$
(5)

where \({\widetilde{S}}_{ ij }=\frac{1}{2}\left( \partial _{ j }{\widetilde{u}}_ i +\partial _{ i }{\widetilde{u}}_ j \right) \) represents the filtered strain rate tensor, \(\nu _ T \) is the SGS eddy viscosity, and \({\textit{Pr}}_\text {sgs}\) is the SGS Prandtl number. Equations 4 and 5 are generally known as the Smagorinsky model (1963). In any SGS model, \(\nu _T\) and \({\textit{Pr}}_\text {sgs}\) are not known a priori. They are modelled by the mixing length approximation, which includes the strain rates calculated using the grid scale velocities, where the eddy viscosity is modelled as \(\nu _ T = (C_{s,\Updelta }\Updelta )^2|{\widetilde{S}}|\) with the Smagorinsky coefficient \(C_{s,\Updelta }\) at the grid scale \(\Updelta \), and \(|S|=\sqrt{2{\widetilde{S}}_{ ij }{\widetilde{S}}_ ij }\) is the strain-rate magnitude. The eddy diffusivity is modelled as \(\nu _{T}/\text {Pr}_\text {sgs}=(D_{s,\Updelta }\Updelta )^2|{\widetilde{S}}|\), where \(D_{s,\Updelta }\) is the Smagorinsky coefficient for the SGS heat flux. We emphasise that in the LASD and the AMD model, both \(C_{s,\Updelta }\) and \(D_{s,\Updelta }\) are dynamically calculated. However, in the Smagorinsky model \(C_{s,\Updelta }\) and \({\textit{Pr}}_\text {sgs}\) are chosen constants, and it is worth mentioning that the results obtained using the Smagorinsky model are sensitive to the choice of these constants (Shi et al. 2018).

2.1 Smagorinsky Model

For LES of ABL, the Smagorinsky coefficient \(C_{s,\Updelta }\) is determined using empirical formulations, field observations, and turbulence theory. Assuming the existence of in the turbulence spectrum inertial range spectrum, Lilly (1967) evaluated the Smagorinsky constant to be around 0.17 for homogeneous isotropic turbulence. To further account for the inhomogeneity of the flow, Moin and Kim (1982) used an ad hoc wall damping function in simulations of channel flows. This wall damping function was further modified by Mason and Thomson (1992) using phenomenological arguments to account for the scale-dependence of the SGS coefficients as

$$\begin{aligned} \frac{1}{(C_{s, \Updelta } \Updelta )^n} = \frac{1}{(C_{s0, \Updelta } \Updelta )^n} + \frac{1}{[\kappa (z+z_o)]^n}, \end{aligned}$$
(6)

where \(\kappa = 0.4\) is the von Kármán constant, \(C_{s0,\Updelta }\) is the mixing length away from the surface, \(n=2\) is the damping exponent, z is the distance from the surface, and \(z_0\) is the roughness length. In addition to \(C_{s,\Updelta }\), the value of the SGS Prandtl number \({\textit{Pr}}_\text {sgs}\) has to be specified when thermal stratification is included. Several stability corrections have been proposed to account for the effect of thermal stability. The value of \({\textit{Pr}}_\text {sgs}\) ranges from 0.44 for free convection, to 0.7 for neutral conditions, up to 1.0 for the critical Richardson number (Mason and Brown 1999). In our simulations we use \(C_{s0,\Updelta } = 0.17\) and \(\Pr _\text {sgs}=0.5\) when using the Smagorinsky model. The values were chosen by trial and error such that the results closely match the results of the dynamic models. We note here that Porté-Agel et al. (2000) used \(C_{s0,\Updelta }=0.17\) in the simulation of similar pressure-driven neutral ABLs. In addition, the wall damping function proposed by Mason and Thomson (1992) is applied, with a damping exponent \(n=2\).

2.2 Lagrangian-Averaged Scale-Dependent Model

A significant drawback of the Smagorinsky model is that the model coefficients have to be specified a priori. Besides, the use of an ad hoc wall damping function requires tuning of the constants on a case-by-case basis. Dynamic models overcome this limitation by computing the model coefficients based on the local flow properties (Germano et al. 1991). In a dynamic model, the model coefficients are calculated by relating stresses at two different scales by using the Germano identity. The filtering at two different filter sizes is known as test filtering. The stresses at these two different scales are equated by using the Smagorinsky approximation. The error due to the Smagorinsky approximation is then minimized by averaging over a plane (Porté-Agel et al. 2000), by dynamic localization (Ghosal et al. 1995), or averaging over fluid path lines (Meneveau et al. 1996). Inherent to the derivation of these models is the assumption of scale invariance. However, this assumption is inappropriate when the flow is anisotropic. In the LASD model, to break the scale invariance, a second test filter is used, and the process of error minimization is carried out over fluid path lines (Bou-Zeid et al. 2005). A similar process is employed for the calculations of the SGS heat flux. We refer to Bou-Zeid et al. (2005) and Stoll and Porté-Agel (2006, (2008) for a detailed derivation of the LASD model for neutral and thermally stratified conditions, respectively.

If two test filters of size \(2\Updelta \) and \(4\Updelta \) are used to relate stresses at two different scales, the scale-dependence parameters for the stresses \(\gamma \) and the heat flux \(\gamma _\theta \) are given by

$$\begin{aligned} \gamma =\frac{C_{s,4\Updelta }^2}{C_{s,2\Updelta }^2} ~~~ \text {and} ~~~ \gamma _\theta =\frac{D_{s,4\Updelta }^2}{D_{s,2\Updelta }^2}, \end{aligned}$$
(7)

where \(C_{s,2\Updelta }^2\) and \(C_{s,4\Updelta }^2\) are the calculated SGS coefficients for the filter sizes \(2\Updelta \) and \(4\Updelta \), respectively. Assuming that \(\gamma \) and \(\gamma _\theta \) are scale-invariant over the test-filter scale, i.e., \(\gamma ={C_{s,4\Updelta }^2}/{C_{s,2\Updelta }^2}={C_{s,2\Updelta }^2}/{C_{s,\Updelta }^2}\) and \(\gamma _\theta ={D_{s,4\Updelta }^2}/{D_{s,2\Updelta }^2}={D_{s,2\Updelta }^2}/{D_{s,\Updelta }^2}\), results in the model coefficients at grid scale \(\Updelta \)

$$\begin{aligned} C_{s,\Updelta }^2=\frac{C_{s,2\Updelta }^2}{\text {max}(\gamma ,0.125)}~~~ \text {and} ~~~ D_{s,\Updelta }^2=\frac{D_{s,2\Updelta }^2}{\text {max}(\gamma _\theta ,0.125)}. \end{aligned}$$
(8)

Technically, \(\gamma \) and \(\gamma _\theta \) can vary between 0 and \(\infty \). However, when \(\gamma \) approaches zero the \(C_{s,\Updelta }^2\) values become vary large, which causes numerical instabilities. Following Bou-Zeid et al. (2005) and Stoll and Porté-Agel (2008) we clip the \(\gamma \) and \(\gamma _\theta \) values to 0.125 to ensure numerical stability. This procedure does not impact the final statistics. It is worth mentioning here that the only tuning parameter used in this model is the Lagrangian averaging time scale, for which different choices are available (Meneveau et al. 1996). The time scale is chosen following (Bou-Zeid et al. 2005), i.e., \(T= 1.5\Updelta (L_{ij}M_{ij}/M_{ij}M_{ij})^{-1/8}\), where \(L_{ij}=\overline{{\widetilde{u}}_i{\widetilde{u}}_j}-\overline{{\widetilde{u}}_i}~\overline{{\widetilde{u}}_j}\), and \(M_{ij}=2\Updelta ^2[\overline{|{\widetilde{S}}|{\widetilde{S}}_{ij}}-4\gamma |\overline{{\widetilde{S}}|}~\overline{{\widetilde{S}}_{ij}}]\). We note that the Lagrangian time scale used in the LASD model works very well for most cases (Bou-Zeid et al. 2005).

2.3 Anisotropic Minimum Dissipation Model

In a minimum dissipation model, the main requirement is that the energy of the sub-filter scales in a filter box \(\Upomega _b\) does not increase. The upper bound for this energy is obtained from the Poincaré inequality, which is given by

$$\begin{aligned} \partial _{t}\int _{\Upomega _b}\frac{1}{2}{\tilde{u}}'_i{\tilde{u}}'_id\mathbf{x }\le {C_i}\partial _{t}\int _{\Upomega _b}\frac{1}{2}(\partial _{i}{{\tilde{u}}_j})(\partial _{j}{{\tilde{u}}_i})d\mathbf{x } \end{aligned}$$
(9)

where \(C_i\) is the modified Poincaré constant that controls the energy in the filter box. We refer to Abkar and Moin (2017) for a detailed description of the model.

In the model, the eddy viscosity and eddy diffusivity are given by

$$\begin{aligned} \nu _T = \frac{-({\hat{\partial }}_k{\widetilde{u}}_i)({\hat{\partial }}_k{\widetilde{u}}_j){\widetilde{S}}_{ij} + {\delta }_{i3}\beta ({\hat{\partial }}_k{\widetilde{u}}_i){\hat{\partial }}_k\left( {\tilde{\theta }}-\left\langle {\tilde{\theta }}\right\rangle \right) }{(\partial _l{\widetilde{u}}_m)(\partial _l{\widetilde{u}}_m)}, \end{aligned}$$
(10)

and

$$\begin{aligned} \nu _\theta =\frac{-({\hat{\partial }}_k{\widetilde{u}}_i)({\hat{\partial }}_k{\tilde{\theta }}){\hat{\partial }}_i{\tilde{\theta }}}{(\partial _l{\tilde{\theta }})(\partial _l{\tilde{\theta }})}, \end{aligned}$$
(11)

respectively, where \({\hat{\partial }}_i=\sqrt{C_i}{\delta }_i\partial _i\) (for i = 1, 2, 3) is the scaled gradient operator. The model constants are obtained based on the argument that in a filter box the energy of the SGS eddies does not increase with time. Essentially, in the filter box, the minimum dissipation required to balance the production of scales smaller than the grid scale is used to calculate the SGS coefficients (Verstappen 2011; Rozema et al. 2015; Abkar et al. 2016).

The value of the modified Poincaré constant depends on the used discretization method. It has been shown that \(C_i=1/12\) gives good results when a spectral method is used (Rozema et al. 2015; Abkar and Moin 2017). Rozema et al. (2015) find that for decaying turbulence simulations \(C_i=0.3\) provides good results, when a second-order central finite difference method is used. For a fourth-order method \(C_i=0.212\) works well. Abkar and Moin (2017) found that \(C_i=1/3\) works well for LES of thermally stratified boundary layers. We note here that Abkar and Moin (2017) used a code similar to ours, i.e., pseudo-spectral in the horizontal direction and second-order central difference in the vertical direction. Following them, we use \(C_i=1/12\) along the horizontal direction and \(C_i=1/3\) in the vertical direction throughout this study.

2.4 Numerical Method

We use a pseudo-spectral method and periodic boundary conditions in the horizontal directions and a second-order central difference scheme in the vertical direction. Time integration is performed using a second-order accurate Adams–Bashforth scheme. The aliasing errors resulting from the non-linear terms are prevented by using the 3/2 anti-aliasing rule (Canuto et al. 1988). Viscous terms are neglected as we consider very high-Reynolds-number flows. This method is based on work by Albertson and Parlange (1999). The computational domain is uniformly discretized with \(n_x\), \(n_y\), and \(n_z\) points, with grid sizes of \(\Updelta _{x} = L_x/n_x\), \(\Updelta _{y} = L_y/n_y\), and \(\Updelta _{z}=L_z/n_z\) in the streamwise, spanwise, and vertical directions, respectively, where \(L_x\), \(L_y\) and \(L_z\) are the dimensions of the computational domain in the streamwise, spanwise, and wall-normal direction. The computational planes are staggered in the vertical direction with the first vertical velocity plane at the ground. The first grid point for the streamwise and spanwise velocities and the potential temperature is located at \(\Updelta _z/2\) above the ground. Free-slip boundary conditions with zero vertical velocity are used at the top boundary.

The instantaneous shear stress and buoyancy flux at the surface, which form the boundary condition, are modelled with the Monin–Obukhov similarity theory (Moeng 1984) using the resolved velocities and temperature at the first grid point, i.e.

$$\begin{aligned} \tau _{xz|w}&=-{u_{*}^2}\cos (\alpha )=-\Bigg (\kappa \frac{{\sqrt{{\widetilde{u}}^2 + {\widetilde{v}}^2}}}{\ln (0.5\Updelta {z}/z_o)-\psi _{M}}\Bigg )^2\cos (\alpha ), \end{aligned}$$
(12)
$$\begin{aligned} \tau _{yz|w}&=-{u_{*}^2}\sin (\alpha )=-\Bigg (\kappa \frac{{\sqrt{{\widetilde{u}}^2 + {\widetilde{v}}^2}}}{\ln (0.5\Updelta {z}/z_o)-\psi _{M}}\Bigg )^2\sin (\alpha ), \end{aligned}$$
(13)

and

$$\begin{aligned} q_{*}&=\frac{u_{*}\kappa (\theta _s-{\tilde{\theta }})}{\text {ln}(0.5\Updelta {z}/z_{os})-\psi _{H}}, \end{aligned}$$
(14)

where \(\tau _{xz|w}\), \(\tau _{yz|w}\), and \(q_{*}\) are the instantaneous shear stress and buoyancy flux at the surface, respectively. Friction velocity is represented by \(u_*\), and \(z_0\) is the roughness length for momentum. Filtered velocities at the first grid level in the streamwise and spanwise directions are represented by \({\widetilde{u}}\) and \({\widetilde{v}}\) respectively and \(\alpha =\tan ^{-1}\left( {{\tilde{v}}}/{\tilde{u}}\right) \). Vertical grid size is denoted by \(\Updelta {z}\), \(\theta _s\) is the potential temperature at the surface, and \(z_{os}\) is the thermal surface roughness length. Stability corrections for momentum and temperature are denoted by \(\psi _M\) and \(\psi _H\), respectively. In classical works, the thermal surface roughness length is set to \(z_{os}=z_o/10\) (Brutsaert 1982). However, to facilitate easier comparison, we follow the reference cases (Sullivan et al. 1994; Beare et al. 2006), which use \(z_{os}=z_o\), in the present study. For the convective boundary layer we follow Brutsaert (1982) and set the stability corrections as follows

$$\begin{aligned} \psi _{M}&= 2\text {ln}\left[ \frac{1}{2}(1+\zeta )\right] + \text {ln}\left[ \frac{1}{2}(1+\zeta ^2)\right] -2\text {tan}^{-1}\left[ \zeta \right] +\pi /2, \end{aligned}$$
(15)
$$\begin{aligned} \psi _{H}&= 2\text {ln}\left[ \frac{1}{2}(1+\zeta ^{2})\right] , \end{aligned}$$
(16)

where \(\zeta =(1-16z/L)^{1/4}\) and \(L=-({u_*}^3\theta _{0})/({\kappa }gq_{*})\) is the Obukhov length. For the stable boundary layer we use the stability correction suggested by Beare et al. (2006)

$$\begin{aligned} \psi _{M}&= -4.8z/L, \end{aligned}$$
(17)
$$\begin{aligned} \psi _{H}&= -7.8z/L. \end{aligned}$$
(18)

In addition to the surface stresses, the vertical gradients of the velocity at \(z_1=\Updelta {z}/2\) are required for the calculation of SGS stress. They are given by the similarity relations

$$\begin{aligned} \left( \frac{\partial {{\tilde{u}}}}{\partial {z}}\right) _{\Updelta {z}/2}&= \frac{u_*\cos (\alpha )}{\kappa {\Updelta {z}/2}}, \end{aligned}$$
(19)
$$\begin{aligned} \left( \frac{\partial {{\tilde{v}}}}{\partial {z}}\right) _{\Updelta {z}/2}&= \frac{u_*\sin (\alpha )}{\kappa {\Updelta {z}/2}}. \end{aligned}$$
(20)

It is worth mentioning here that the surface similarity relations (Eqs. 12, 13, and 14) are defined for the mean stresses and fluxes. However, Moeng (1984) used this mean relation to calculate the ‘instantaneous’ stresses, which now is an established practice in the literature. However, this procedure also contributes to the logarithmic layer mismatch (Brasseur and Wei 2010; Yang et al. 2017). To reduce the effect, Albertson (1996) proposed calculating the mean gradients with the similarity theory and the fluctuations with finite differences. This technique has been used in our code. Furthermore, for the neutral boundary-layer cases, the correction proposed by Porté-Agel et al. (2000) is used to further reduce the effect of the log-layer mismatch.

To simplify the notation, the tilde representing the spatial filtering of the LES quantities is omitted hereafter.

3 Results and Discussion

Three canonical boundary layers with neutral, stable, and unstable temperature stratification are studied here. First, a mean pressure-driven neutral boundary layer is used to assess the performance of different models in truly neutral conditions. Second, we consider the Global Earth and Water Experiment (GEWEX) ABL Study (GABLS\(-1\)), which is a moderately stable stratified boundary layer (Beare et al. 2006). Finally, an unstable convective boundary layer with moderate capping inversion is considered (Moeng and Sullivan 1994).

3.1 Neutral Boundary Layer

We performed simulations of a neutral ABL over a rough homogeneous surface using the Smagorinsky, LASD, and AMD models. The Coriolis forces are neglected for this case, and the boundary layer is driven by an imposed pressure gradient \(1/\rho ({\nabla {p}})=-u_*^2/H\), where H is the domain height. The domain length L and width W are both set to \(2\pi {H}\). The domain is discretized with a grid of spacing \(\Updelta _{x} = \Updelta _{y} = 2\pi {\Updelta _{z}}\), where \(\Updelta _{x}\), \(\Updelta _{y}\), and \(\Updelta _z\) represent streamwise, spanwise, and vertical grid spacing, respectively. The computational domain is 1000 m in height and the vertical grid spacing is \(\Updelta _{x}, \Updelta _{y}=43.630\) m, \(\Updelta _{z}=6.944\) m. The roughness used to model the surface stresses is set to \(z_o/H = 10^{-4}\). The simulations are run until the flow has reached a statistically stationary state. The set-up considered here is the same as in Bou-Zeid et al. (2005).

Fig. 1
figure 1

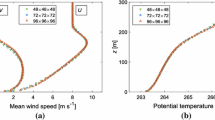
Planar-averaged vertical profiles for simulations of the neutral boundary layer. a Mean velocity profile on a semi-logarithmic plot. b Resolved (markers), SGS (lines), and total shear stress (black line) in the xz direction. The solid black line represents the total stress. c Vertical velocity variance and d non-dimensional velocity gradient \(\phi _{M}\). Results from Bou-Zeid et al. (2005) obtained with the LASI and the PASD models are also plotted for comparison

Full size image

The planar-averaged streamwise velocity component obtained from the simulations using the different SGS models is presented in Fig. 1a. This velocity profile is expected to follow the logarithmic law \(\left\langle {\overline{u}}\right\rangle \left( z\right) = \left( {u_*}/{\kappa }\right) \ln \left( {z}/{z_o}\right) \) in the surface layer, i.e., up to \(z/H \approx \) 0.1-0.2. The figure shows that the streamwise velocity profiles obtained from the AMD and the LASD models agree excellently with the logarithmic law in the surface layer. However, in agreement with previous studies (Porté-Agel et al. 2000; Bou-Zeid et al. 2005; Yang et al. 2017), the velocity profile obtained from the simulation with the Smagorinsky model shows a mismatch with the logarithmic profile.

The resolved and modelled SGS stresses obtained from the simulations with different SGS models are presented in Fig. 1b. The figure shows that the ratio of the resolved to modelled stresses increases with the distance from the surface. For the AMD and the Smagorinsky models, the resolved stresses increase smoothly with increasing height (Abkar et al. 2016). However, in agreement with Bou-Zeid et al. (2005), we find that the transition between the resolved and modelled stresses is very sharp in the LASD model. In all cases, the sum of the resolved and the modelled stresses follows the expected linear stress profile, which occurs at a steady state in the absence of Coriolis forces.

Fig. 2
figure 2

Normalized streamwise wavenumber spectra of the streamwise velocity at different heights using a the Smagorinsky model, b the LASD model, and c the AMD model

Full size image

Figure 1c shows the planar-averaged vertical velocity variance calculated as \({{\left\langle \overline{w'^2}\right\rangle }}=\left( {{\left\langle \overline{w^2}\right\rangle }} + {\left\langle {\overline{\tau }}_{zz}\right\rangle }\right) -{\left\langle {\overline{w}}\right\rangle }~{\left\langle {\overline{w}}\right\rangle }\). Further away from the surface the vertical velocity variance predicted by the LASD and the AMD model is nearly the same. However, in the surface layer (\(z/H \lesssim 0.1-0.2\)) there is a considerable difference in the variances obtained using the three models. The non-dimensional velocity gradient \(\phi _M\left( z\right) =\left( \kappa {z}/u_*\right) \partial {\left\langle {\overline{u}}\right\rangle }/\partial {z}\) is presented in Fig. 1d. Results from the Lagrangian-averaged scale-independent model (LASI) and planar-averaged scale-dependent model (PASD) from Bou-Zeid et al. (2005) are also included in the figure for better perspective. Higher \(\phi _M\) values near the surface are caused by the log-layer mismatch (Brasseur and Wei 2010) and the use of finite differences to calculate gradients. Close to the surface, \(\phi _M\) values predicted by the LASD and the AMD models are closer to the theoretical value of 1 than the ones predicted by the Smagorinsky, LASI, and PASD models. This shows that the simulations with the AMD and the LASD model capture the logarithmic law in the surface layer (\(z/H \lesssim \) 0.1–0.2) better than the Smagorinsky model. Furthermore, near the surface the values of \(\phi _M\) obtained from both the LASD and the AMD model are nearly equal, indicating a similar performance of the models.

To obtain further insight into the dissipation characteristics of the SGS models, we present the streamwise wavenumber spectra of the streamwise velocity component for various heights above the surface in Fig. 2. The spectra is defined as \(\int _0^{\infty }E_{11}(\kappa _1)d\kappa _1=\overline{u'u'}/2\), where \(E_{11}(\kappa _1)\) represents the spectral energy associated with wavenumber \(\kappa _1\) and \(u'\) represents streamwise velocity fluctuations. In the inertial subrange (for \(\kappa _1{z}>1\), where \(\kappa _{1}\) is the streamwise wavenumber and z is the distance from the surface) the turbulence is unaffected by the flow configuration, dissipation, or viscosity. The flow in the inertial subrange is nearly isotropic and the spectrum generally follows the Kolmogorov \(-5/3\) scaling (Monin and Yaglom 1971). Figure 2 shows that close to the surface the spectra obtained using the Smagorinsky model decay faster than \(\kappa ^{-5/3}\), while the LASD and AMD models accurately capture the Kolmogorov scaling. This indicates that the Smagorinsky model is too dissipative close to the surface. In the production range (\(\kappa _1{z}<1\)) the turbulence is affected by the flow configuration (Perry et al. 1986; Bou-Zeid et al. 2005). For a neutral ABL the production is expected to follow a \(\kappa ^{-1}\) scaling (Bou-Zeid et al. 2005). Figure 2 shows that the LASD and AMD model capture the \(\kappa ^{-1}\) scaling in the production range better than the Smagorinsky model. That the LASD and AMD model predict the spectra more accurately than the Smagorinsky model indicates that these scale-dependent models have better dissipation characteristics due to which the flow physics can be captured more accurately. A detailed comparison between the AMD and LASD model reveals that the LASD model captures the expected \(\kappa ^{-5/3}\) and \(\kappa ^{-1}\) laws in the production and inertial subranges slightly better than the AMD model.

Table 1 Details of the stable boundary layer simulations
Full size table

3.2 Stably Stratified Boundary Layer

In this section, we study the GABLS-1 inversion capped boundary layer with a constant cooling rate at the surface. The potential temperature is initialized with the two layer temperature profile given by Beare et al. (2006)

$$\begin{aligned} \theta (z) = \left\{ \begin{array}{ll} 265 \ \text {K}, &{}\quad 0 \ < z \ \le 100 \text { m}\\ 265 \ \text {K} + (z - 100) \times 0.01 \ [{\text {K m}}^{-1}],&{}\quad z > 100~\text {m}. \end{array}\right. \end{aligned}$$
(21)

The initial velocity is set to the geostrophic wind speed of 8 \(\text {m}~\text {s}^{-1}\) everywhere except at the surface. Turbulence is triggered by adding random perturbations. A random noise term of magnitude 3% the geostrophic wind speed is added to velocities below 50 m, and for the temperature a noise term with an amplitude of 0.1 K is added. The reference temperature \(\theta _0\) is set to 263.5 K. The Coriolis parameter \(f=1.39\times 10^{-4}\) \(\text {s}^{-1}\), which corresponds to latitude \(73^{\circ }\text {N}\), and the surface cooling rate is set to 0.25 \(\text {K h}^{-1}\). The simulations are performed in a computational domain of 400 m \(\times \) 400 m \(\times \) 400 m, which is discretized on an isotropic grid with a spacing of 2.08 m. Gravity waves are damped out by a Rayleigh damping layer with a strength of 0.0016 \(\text {s}^{-1}\) in the top 100 m of the computational domain (Klemp and Lilly 1978). The simulations were run for 9 \(\text {h}\) to ensure that quasi-equilibrium is reached. The statistics are gathered over the final hour. This is approximately equal to 400 large-eddy turnover times \(T=z_i/w_*\), where the velocity scale is \(w_*=(gq_*z_i/\theta _{\mathsf {0}})^{1/3}\) and \(z_i\) is the boundary-layer height.

Fig. 3
figure 3

Planar-averaged vertical profiles for the stable boundary layer simulations. a Streamwise and spanwise velocities, b potential temperature, c streamwise and spanwise momentum fluxes, and d the vertical heat flux

Full size image
Fig. 4
figure 4

Planar-averaged vertical profiles for the stable boundary layer simulations. a Normalized momentum flux, b horizontal velocity variance, c locally scaled momentum diffusivity and d locally scaled heat diffusivity. The experimental data by Nieuwstadt (1984) are given for comparison

Full size image

As theoretical results and experimental data are very limited, we also compare our results against the high-resolution results from Sullivan et al. (2016) and Beare et al. (2006). Even though these high-resolution simulations provide a useful reference, it is worth noting that these results still depend on the surface and SGS modelling. In Table 1 we compare various integral boundary layer properties obtained from our simulations with these high-resolution simulation results. We calculated the boundary-layer height \(z_i\) by determining the height where the mean stress falls below \(5\%\) of its surface value (Beare et al. 2006). We note that Sullivan et al. (2016) used a different method to determine the boundary-layer height. Therefore, to avoid confusion, any comparison to the boundary-layer height from their study is left out.

Beare et al. (2006) report that the time averaged buoyancy flux \(g\theta _{0}^{-1}\left\langle w\theta \right\rangle \) ranges from \(-3.5\times 10^{-3}\) to \(-5.5\times 10^{-3}\) \(\text {m}^2~\text {s}^{-3}\), which agrees well with the value of \(-3.8\times 10^{-3}\) \(\text {m}^2~\text {s}^{-3}\) that we find in our simulation with the LASD and AMD model. In addition, Beare et al. (2006) report that the mean momentum flux \(\sqrt{\left\langle \overline{u'w'}\right\rangle ^2+\left\langle \overline{v'w'}\right\rangle ^2}\) ranges from 0.06 to 0.08 \(\text {m}^2~\text {s}^{-2}\), which corresponds to a friction velocity of \(0.24-0.28\) \(\text {m s}^{-1}\). The mean momentum flux in our simulations varies between \(0.064-0.069\) \(\text {m}^2~\text {s}^{-2}\), which corresponds to a friction velocity range of 0.252–0.265 \(\text {m}~\text {s}^{-1}\). Hence, these values lie well within the range reported in the LES intercomparison study by Beare et al. (2006). A comparison of our simulation results with the high-resolution data presented by Beare et al. (2006) and Sullivan et al. (2016) shows that the AMD and LASD model provide more accurate predictions for the friction velocity, mean momentum fluxes, boundary-layer height, and the surface heat than the Smagorinsky model.

The surface-normal streamwise and spanwise velocity profiles are presented in Fig. 3a and reveal the pronounced super-geostrophic jet that is characteristic of the GABLS-1 case (Beare et al. 2006). The figure shows that the LASD and the AMD model results agree better with the high-resolution results of Sullivan et al. (2016) than the Smagorinsky model results. Figure 3b shows that the LASD and the AMD model results for the vertical temperature profile are closer to the high-resolution results by Sullivan et al. (2016) than the corresponding Smagorinsky model results. The planar-averaged vertical momentum and heat flux are presented in Fig. 3c, d. In agreement with the integral properties presented in Table 1, we find that the results obtained using the AMD and LASD model agree excellently. In contrast, the momentum and buoyancy fluxes due to which the velocity and temperature profiles are not accurately captured with the Smagorinsky model.

In Fig. 4a we compare the mean momentum flux obtained from the simulations with the theoretical model proposed by Nieuwstadt (1984). This model states that the normalized vertical momentum profile is given by:

$$\begin{aligned} \frac{\tau }{{\tau _0}}&=\left( 1-\frac{z}{z_i}\right) ^{3/2}, \end{aligned}$$
(22)

where the subscript 0 denotes the surface values and \(\tau =\sqrt{\left\langle \overline{u'w'}\right\rangle ^2 + \left\langle \overline{v'w'}\right\rangle ^2}\). The fluxes are calculated by adding the resolved fluxes \(\left( \left\langle \overline{u'w'}\right\rangle {\text { and }} \left\langle \overline{v'w'}\right\rangle \right) \) to the SGS fluxes (\(\left\langle {\overline{\tau }}_{xz}\right\rangle {\text { and }}\left\langle {\overline{\tau }}_{yz}\right\rangle )\). Nieuwstadt (1984) defined the boundary-layer height as the height where the turbulence is nearly zero. Therefore, only for this plot, the boundary-layer height is defined as the height where the turbulence is \(1\%\) of the surface values. Figure 4a shows that the mean momentum flux profiles obtained using all three SGS models agrees well with the theoretical prediction.

Figure 4b shows that the horizontal velocity variance \(\left( \left\langle \overline{u'^2}\right\rangle + \left\langle \overline{v'^2}\right\rangle \right) \) with \(\left\langle \overline{u'^2}\right\rangle = \left( \left\langle \overline{u^2}\right\rangle + \left\langle {{\overline{\tau }}_{xx}}\right\rangle - \left\langle {\overline{u}}\right\rangle \left\langle {\overline{u}}\right\rangle \right) \) and \(\left\langle \overline{v'^2}\right\rangle = \left( \left\langle \overline{v^2}\right\rangle + \left\langle {{\overline{\tau }}_{yy}}\right\rangle - \left\langle {\overline{v}}\right\rangle \left\langle {\overline{v}}\right\rangle \right) \) obtained using the three SGS models is similar. We note that the kinetic energy obtained using the LASD model shows a sharp peak at the first grid point above the surface. We believe this peak is related to the sharp transition between the resolved and modelled stresses in the LASD (see Fig. 1b).

To assess the effectiveness of the different models in capturing the surface-layer similarity profiles we plot the locally scaled momentum,

$$\begin{aligned} \phi _{KM}&=\frac{1}{\Lambda }\sqrt{\frac{\tau }{\left( \frac{\partial {\left\langle {\overline{u}}\right\rangle }}{\partial {z}}\right) ^2+\left( \frac{\partial {\left\langle {\overline{v}}\right\rangle }}{\partial {z}}\right) ^2}}, \end{aligned}$$
(23)

and the locally scaled heat diffusivity,

$$\begin{aligned} \phi _{KH}&=\frac{1}{\Lambda \tau ^{1/2}}\frac{-\left\langle \overline{w'\theta '}\right\rangle }{\frac{\partial {\left\langle {\overline{\theta }}\right\rangle }}{\partial {z}}}, \end{aligned}$$
(24)

where \(\Lambda =-\tau ^{3/2}/(\kappa {g}{\left\langle \overline{w'\theta '}\right\rangle })\) is the local Obukhov length (in Fig. 4c, d). Results obtained from two different models by Beare et al. (2006), i.e., the IMUK (University of Hannover) and NCAR (National Center for Atmospheric Research) are also included in the figures to provide a better perspective. The crosses in the Fig. 4c, d represent the mean values, and the shaded areas show the standard deviation from the observations of the stable boundary layer by Nieuwstadt (1984). According to the local scaling hypothesis of Nieuwstadt (1984), the quantities \(\phi _{KM}\) and \(\phi _{KH}\) can be expressed as a function of \(z/\Lambda \). We find that \(\phi _{KM}\) and \(\phi _{KH}\) reach a nearly constant value for large \(z/\Lambda \), which is known as the z-less stratification regime. Beare et al. (2006) report that the GABLS-1 boundary layer falls within the range of values (shaded region in Fig. 4c, d) found in Nieuwstadt (1984). Our results are consistent with the findings by Beare et al. (2006). The overlap of the results in the shaded region shows that the results fall within the limits of the observation at high \(z/\Lambda \), i.e. the z-less stratification limit. Our results are similar to the IMUK and NCAR results reported in the LES intercomparison of Beare et al. (2006). Overall, the results show that the LASD and the AMD models have similar performance, while the Smagorinsky model results are significantly different.

3.3 Unstably Stratified Boundary Layer

Following Moeng and Sullivan (1994), we performed simulations of an inversion-capped convective boundary layer in a computational domain of 5 km \(\times \) 5 \(\text {km}\) \(\times \) 2 \(\text {km}\) on a \(480^3\) grid. The boundary layer is driven by a constant geostrophic wind speed of 10 \(\text {m s}^{-1}\) and the Coriolis parameter \(f=10^{-4}\) \(\text {s}^{-1}\). The surface roughness lengths for momentum and heat are set to 0.16 m. The surface was heated at the bottom with a constant surface buoyancy flux of \(q_*=0.24\) \(\text {K m}~\text {s}^{-1}\). The reference potential temperature is set to \(\theta _\text {ref}=301.78\) K. The initial velocities are set to the geostrophic wind speed with randomly seeded uniform perturbations in the region \(0<z\le 937\) m to spin up turbulence. The potential temperature is initialized with a three-layered structure

$$\begin{aligned} \theta (z) =\left\{ \begin{array}{ll} 300 \ \text {K},&{} \quad 0< z \le 937~\text {m}\\ 300 \ \text {K} + \frac{8}{126}(z - 937) \ \text {K m}^{-1},&{} \quad 937~\text {m} < z \le 1063~\text {m}\\ 308 \ \text {K} + (z - 1063) \times 0.003 \ \text {K m}^{-1},&{} \quad z > 1063~\text {m}. \end{array}\right. \end{aligned}$$

The simulation reaches a quasi-stationary state in 10 large-eddy turnover times \(T=z_i/w_*\), where the convective velocity scale is \(w_*=(gq_*z_i/\theta _\text {ref})^{1/3}\) and the boundary-layer height \(z_i\) is defined as the height at which the buoyancy flux is minimum (Sullivan et al. 1994). The presented statistics are obtained from the time interval of 13T to 18T.

Table 2 Details of the unstably stratified boundary layer simulations
Full size table

Table 2 gives a summary of the simulation results, which are in good agreement with the results reported by Moeng and Sullivan (1994) and Abkar and Moin (2017). As these studies only provide results obtained on coarser grids, we also performed a high-resolution reference simulation on a \(960^3\) grid using the LASD model. It is worth noting that the integral boundary layer properties obtained by this high-resolution simulation can still depend on the surface and SGS modelling. Nevertheless, it provides a useful reference to judge the performance of the different SGS models. The results in Table 2 show that the AMD model predicts a lower friction velocity, surface Obukhov length, and boundary-layer height than the LASD and the Smagorinsky model. Furthermore, the results obtained with different SGS models agree reasonably well with our high-resolution results and the studies of Moeng and Sullivan (1994) and Abkar and Moin (2017). The results show that all the models predict values within an acceptable range and only minor variation is visible in the values of different quantities. Overall, all models perform well in predicting the friction velocity and boundary-layer height.

Figure 5a shows the variation of the planar-averaged horizontal wind speed \(u_\text {mag}=\sqrt{\left\langle {\overline{u}}\right\rangle ^2 + \left\langle {\overline{v}}\right\rangle ^2}\) normalized by the geostrophic wind velocity. In agreement with the lower friction velocity, the AMD model predicts a higher velocity in the boundary layer than the LASD or Smagorinsky model. Figure 5b shows that the variation of the potential temperature \(\left\langle {\overline{\theta }}\right\rangle /\theta _0\) with height predicted using the LASD and AMD model agrees excellently. Due to the intense turbulent mixing the velocity and temperature are almost constant in the mixed layer (0.1 \(< z/z_i < 0.9\)), which is a characteristic feature of convective boundary layers (Moeng and Sullivan 1994). Overall, the AMD model is as effective as the LASD model in predicting the velocity and temperature profiles.

Fig. 5
figure 5

Planar-averaged vertical profiles for the unstable boundary layer. a Mean velocity magnitude \(u_\text {mag}=\sqrt{\left\langle {\overline{u}}\right\rangle ^2+\left\langle {\overline{v}}\right\rangle ^2}\), b potential temperature, c vertical heat flux, and d variance of the potential temperature \({\langle \overline{\theta '^2} \rangle }/\theta _{*}^2\), where \(\theta _*=q_*/w_*\) compared to the observational data from the AMTEX experiment by Lenschow et al. (1980) and the high-resolution reference simulation

Full size image
Fig. 6
figure 6

Planar-averaged vertical profiles of the a horizontal and the b vertical velocity variance for the unstable boundary layer simulations compared to the AMTEX observational data by Lenschow et al. (1980) and the high-resolution reference simulation. The planar-averaged vertical profiles for the c non-dimensional velocity gradient \(\phi _{M}\), and d non-dimensional temperature gradient \(\phi _{H}\)

Full size image

Figure 5c compares the vertical profiles of the horizontally averaged vertical heat flux \(\left\langle \overline{w'\theta '}\right\rangle \). We observe that the heat flux decreases linearly over the boundary layer and reaches a minimum at the inversion height. The depth of the entrainment zone is defined as the region where \(\left\langle \overline{w'\theta '}\right\rangle \) is negative. The Smagorinsky and the LASD model results show a wider entrainment region than the AMD results. This means that there is more turbulent mixing at the inversion height when the Smagorinsky and LASD model are used. In an unstable boundary layer the profile of the temperature fluctuations is expected to show a sharp maximum at the inversion height, where the entrainment flux becomes negative (Lenschow et al. 1980).

Figure 5d compares the temperature variance as a function of height obtained with the different models against the Air Mass Transformation Experiment (AMTEX) observational data by Lenschow et al. (1980). The profiles show a sharp peak in the temperature variance at the inversion height. The origin of this peak is described by Sullivan et al. (1998), and a sharper peak corresponds to a smaller vertical extent of the entrainment zone. The AMD and LASD model results agree excellently and show a sharper peak than the Smagorinsky model results. The figure shows that the temperature variance obtained from the high-resolution reference simulation has an even sharper peak. This means that, for a given grid resolution, the Smagorinsky model strongly underestimates the temperature variance at the inversion layer when compared to the results of the LASD and AMD models. Therefore, we conclude that the LASD and the AMD model provide better predictions than the Smagorinsky model.

The vertical profiles of the horizontal velocity variance obtained using the three SGS models are compared in Fig. 6a. Although the results are nearly the same near the surface, there is a significant difference around the capping inversion \(z/z_i\approx 1\). This difference is a consequence of the different depth of the entrainment zone, which we discussed above. Furthermore, the AMD model agrees better with the high-resolution reference data than the LASD and the Smagorinsky model results. Figure 6b shows that temperature profiles obtained using the LASD and AMD agree better with the high-resolution reference data than the corresponding Smagorinsky model results.

To assess the effectiveness of the model in capturing the surface-layer similarity profiles, we plot the non-dimensional shear,

$$\begin{aligned} \phi _M&=\left( \frac{\kappa {z}}{u_*}\right) \frac{\partial {u}}{\partial {z}}, \end{aligned}$$
(25)

and the non-dimensional temperature gradient,

$$\begin{aligned} \phi _H&=\left( \frac{\kappa {z}}{\theta _*}\right) \frac{\partial {\theta }}{\partial {z}}, \end{aligned}$$
(26)

where \(\theta _*=q_*/u_*\). The vertical profiles of \(\phi _M\) and \(\phi _H\) are compared with the empirical formulations proposed by Brutsaert (1982) in Fig. 6c, d. The empirical similarity profiles, which are applicable close to the surface (\(-z/L<1.5\)) are \(\phi _M = (1-16\zeta )^{-1/4}\) and \(\phi _H =(1-16\zeta )^{-1/2}\). Figure 6c shows that both the LASD and the AMD model results are relatively similar when compared to the Smagorinksy model results. The deviation in the results from the empirical formulation is expected. This is similar to the deviation of the \(\phi _M\) values from the theoretical value of 1 in the case of the neutral boundary layer, observed in Fig. 1d. Furthermore, we also observe the log-layer mismatch in the plots of non-dimensional shear. Figure 6d shows that the results from the different models agree equally well with the similarity profile. This is consistent with the observation of a similar temperature profile for all models (see Fig. 5b). For both quantities, \(\phi _M\) and \(\phi _H\), we observe minor differences between the results obtained with the LASD and the AMD models.

4 Discussion and Conclusions

In summary, we compared the performance of the Smagorinsky, the AMD (Rozema et al. 2015; Abkar et al. 2016; Abkar and Moin 2017), and the LASD models (Bou-Zeid et al. 2005; Stoll and Porté-Agel 2006, 2008) for neutral, stable, and unstable conditions. For neutral conditions, we find that the LASD and the AMD models capture the logarithmic velocity profile and the streamwise wavenumber spectra of the streamwise velocity more accurately than the Smagorinsky model. For the stably stratified GABLS-1 boundary layer, we compared the results obtained using the different models with the higher resolution results of Sullivan et al. (2016) and Beare et al. (2006). A comparison with these high-resolution results reveals that, on a relatively coarse grid, the LASD and the AMD models provide better predictions than the Smagorinsky model. Also for the unstably stratified boundary layer we find that the AMD and the LASD model results obtained on a relatively coarse grid agree better with the high-resolution reference than the corresponding Smagorinsky model results. Furthermore, for turbulence characteristics such as the horizontal and vertical velocity variances, temperature variances, non-dimensional shear, and temperature gradients, the results obtained with the LASD and the AMD models are nearly the same, while the Smagorinsky model results are significantly different.

From all the above, we conclude that, with a given grid resolution, the LASD and the AMD models capture the flow physics better than the Smagorinsky model. While the LASD model (Bou-Zeid et al. 2005) has been successfully used for about 15 years (Stoll and Porté-Agel 2006; Calaf et al. 2010; Wu and Porté-Agel 2011; Stevens et al. 2014; Gadde and Stevens 2019) the AMD model was only developed recently (Rozema et al. 2015; Abkar et al. 2016; Abkar and Moin 2017). Here we show, using a one-to-one comparison, that the LASD and AMD models provide similar results for neutral, stable, and unstable test cases. Both the AMD and LASD models provide three-dimensional variation of the SGS coefficients, which is essential when considering heterogeneous flows, such as flows over complex terrains or in extended wind farms. An inspection of the streamwise wavenumber spectra of the streamwise velocity suggests that the LASD model predicts the velocity spectra in the inertial and production ranges slightly better than the AMD model.

Our results suggest that the AMD model is nearly as good as the LASD model in simulations of horizontally homogeneous atmospheric boundary layers. In simulations of neutral boundary layers, the AMD model provides similar dissipation characteristics as the LASD model, which is established by a similar turbulence spectrum. The performance analysis of different sub-grid models on three grid sizes \(240^3\), \(480^3\), and \(960^3\) reveals that the computational overhead of the AMD model compared to the Smagorinsky model is \(11.3\%\) (\(240^3\)), \(9.8\%\) (\(480^3\)), \(11.3\%\) (\(960^3\)), while the corresponding numbers for the LASD model are \(29.5\%\) (\(240^3\)), \(33.8\%\) (\(480^3\)), \(34.5\%\) (\(960^3\)), respectively. The numbers show that the computational overhead of the LASD model is higher than the AMD model and increases slowly with grid size due to increased MPI communication related to the interpolations in the Lagrangian model calculations. Furthermore, we emphasise that the Lagrangian averaging in the LASD model requires the storage of time histories of various terms in the model, which requires at least 8 additional three-dimensional arrays and numerous two-dimensional temporary arrays.

As indicated in the Introduction, we emphasize that the AMD model has several practical advantages and is more straightforward to implement than the LASD model. The reason is that the AMD model does not require filter operations or Lagrangian tracking of fluid parcels, which are required in the LASD model. The computational and memory overheads are essential considerations for simulations performed on modern supercomputers. Therefore, we conclude that the AMD model is an attractive alternative to the LASD model when considering large-scale LES of turbulent boundary layers. We have shown here that the results obtained with the AMD model are almost as good as the LASD model results. However, AMD model results depend on the modified Poincaré constant, which requires tuning in complex flow scenarios such as flow over cubes (urban boundary layer) or wind farms, while the LASD model is tuning free. In the future, it would be beneficial to study the performance of these models in the aforementioned complex flow scenarios.