1 Introduction

It is well-established that the atmospheric boundary layer can be divided vertically into essentially three parts (Holton 2004; Marshall and Plumb 2016). The lowest layer—the laminar sublayer—has a thickness of only a few millimetres and is of no relevance for the transfer of wind energy since therein all physical processes are controlled by molecular motion. Above it is the Prandtl (surface) layer, whose vertical extent is about 20–100 m (depending on the thermal stratification of the air) and where turbulence is fully developed, but the influence of the Earth’s rotation may be ignored. The upper layer, which typically covers 90% of the atmospheric boundary layer, having a vertical extent ranging from about 20–100 m to heights in excess of 1000 m, is the Ekman layer, in which the airflow is driven by a three-way balance between frictional effects, pressure gradients and the influence of the Coriolis force. Above the Ekman layer, in the free atmosphere, the small-scale flow is more or less non-turbulent and geostrophic, being controlled by the balance between the pressure gradient and the Coriolis force (since curvature effects are negligible). However, the Earth’s curvature has to be accounted for in studies based on synoptic scales by also including the centrifugal force, thus obtaining a gradient wind balance rather than merely the geostrophic balance (Holton 2004).

The vertical component, w, of the velocity vector (u, v, w) is typically much smaller than the zonal and meridional velocity components u and v, the characteristic numerical values for the magnitudes of the horizontal and vertical components of the wind velocity being 10 m s\(^{-1}\) and 0.1 m s\(^{-1}\), respectively (Zdunkowski and Bott 2003). Since in the Prandtl layer the airflow does not change direction with height, with a logarithmic profile commonly used to describe the vertical distribution of the horizontal mean wind speed under neutral conditions (Holton 2004), the main changes of wind direction in the boundary layer occur in the Ekman layer. Our aim here is to present a qualitative study of this motion. In non-equatorial regions of the Northern Hemisphere, the governing equations for mesoscale steady flow in the Ekman layer are conventionally taken to be

$$\begin{aligned} f(u-u_g)= & {} \frac{\mathrm{d}}{\mathrm{d}z}\left( K\,\frac{\mathrm{d}v}{\mathrm{d}z}\right) , \end{aligned}$$
(1)
$$\begin{aligned} f(v-v_g)= & {} -\,\frac{\mathrm{d}}{\mathrm{d}z}\left( K\,\frac{\mathrm{d}u}{\mathrm{d}z}\right) , \end{aligned}$$
(2)

where (u, v) is the horizontal z-dependent mean wind velocity, with zonal component u and meridional component v, \(u_g\) and \(v_g\) are the corresponding constant geostrophic wind components, while \(K=K(z)\) is the eddy viscosity; here z is the height above the Prandtl layer (Brown 1974; Pielke 2002; Holton 2004). We have written \(f=2{\Omega }\sin \theta \), the Coriolis parameter at the fixed latitude \(\theta \), in the Northern Hemisphere, where \({\Omega } \approx 7.29 \times 10^{-5}\) s\(^{-1}\) is the angular speed of rotation of the Earth and \(\theta \in (0,\uppi /2]\) is the angle of latitude in right-handed rotating spherical coordinates (with \(\theta =0\) corresponding to the Equator and \(\theta =\uppi /2\) to the North Pole). We invoke the traditional boundary conditions for the system (1)–(2) as

$$\begin{aligned}&u=v=0 \quad \text {at}\quad z=0, \end{aligned}$$
(3)
$$\begin{aligned}&u \rightarrow u_g \quad \text {and}\quad v \rightarrow v_g\quad \text {for}\quad z \rightarrow \infty , \end{aligned}$$
(4)

since, by virtue of the frictional properties of the flow below the Ekman layer, we impose the no-slip condition at the bottom \(z=0\) of the layer, while at the top of the Ekman layer the horizontal components of the velocity must be in geostrophic balance. Classical Ekman theory assumes a constant eddy viscosity K, but field data show that this is an extreme simplification. Although a number of other significant assumptions are required to derive (1)–(2), since, e.g., stratification and spherical geometry effects are ignored and the geostrophic velocity is assumed to be height-independent (i.e. a barotropic atmosphere), the system (1)–(2) is commonly used in meteorology. In this study, we limit ourselves to steady motions, the aim being to emphasize the role played by the vertical variation of the eddy viscosity. There is little doubt that temporal variations need to be included at some stage, but we regard this as a future extension of the current work, although any time dependence on K could be added as a parametric dependence if we use (1) and (2) as the relevant model equations. Note also that the time variation in the atmosphere is usually slow enough (the primary changes over land being driven by the diurnal cycle) for the main characteristics of the steady-state setting to prevail (Mason and Thomson 2015). A discussion of time-dependent Ekman layers can be found in Lewis and Belcher (2004) and Momen and Bou-Zeid (2017).

For constant eddy viscosity we have the solution

$$\begin{aligned} \left\{ \begin{array}{l} u(z)=u_g - \mathrm{e}^{-\gamma z}[u_g \cos (\gamma z)+v_g \sin (\gamma z)],\\ v(z)=v_g + \mathrm{e}^{-\gamma z}[u_g\sin (\gamma z) -v_g\cos (\gamma z)], \end{array}\right. \end{aligned}$$
(5)

of (1)–(4), where

$$\begin{aligned} \gamma =\sqrt{\frac{f}{2K}}, \end{aligned}$$

showing a turning of the horizontal ageostrophic velocity \((u-u_g,v-v_g)\) to the right with increasing height, with an ageostrophic speed decreasing upwards since, using complex notation,

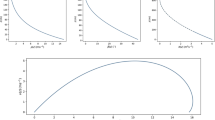
$$\begin{aligned}{}[u(z)-u_g]+\mathrm{i}[v(z)-v_g]=- \mathrm{e}^{-(1+\mathrm{i})\gamma z}\{u_g+\mathrm{i}v_g\}; \end{aligned}$$

note also that in the classical Ekman spiral (5) the rotation speed of the current (\(\gamma \)) is equal to the exponential decay rate. Values appropriate for mid-latitude flows are \(K= 5\) m\(^2\) s\(^{-1}\), with horizontal geostrophic velocity components \(u_g\) and \(v_g\) of the order of 5 m s\(^{-1}\) (Etling 2008). Even though the classical Ekman flow (5) is rarely observed in the mid-latitude atmospheric boundary layer (Holton 2004), certain polar regions, isolated and little affected by atmospheric perturbations, frequently feature a steady-state, barotropic atmospheric boundary layer with a wind pattern that often produces the classical Ekman-spiral structure on summer nights (Grachev et. al. 2005; Ryman et al. 2016). It is of interest to note that in these polar regions the eddy viscosity mainly ranges between 0.004 and 0.06 m\(^2\) s\(^{-1}\), i.e., at least two orders of magnitude smaller than the values encountered at mid-latitudes. Furthermore, the scarcity of field evidence for the ideal Ekman airflow at mid-latitudes is probably due to the inadequacy of the assumption of a constant eddy viscosity—in reality K typically varies rapidly with height near the base of the Ekman layer (Holton 2004). We observe that there appears to be no generally accepted view on the behaviour of this variation, other than the fact that K has to be determined by a combination of dimensional considerations and empirical measurements, a process beset by the technical challenges inherent in parameter estimations in meteorology (Mason and Thomson 2015). The available explicit solutions for a non-constant eddy viscosity are very scarce, being apparently restricted to linear and exponentially decaying profiles only (Madsen 1977; Miles 1994) or quadratic and cubic polynomials (Nieuwstadt 1983; Giometto et. al. 2017), so that for other types of non-constant eddy viscosity we have to rely on case-by-case approximations and numerical simulations. Several types of eddy-viscosity profiles have been determined as being relevant in specific physical contexts and these present quite different monotonicity properties: some increase with height, others decrease, and a few are not even monotonic (see Table 1 and Fig. 1 for examples of eddy viscosities suggested by field data, discussed in Berger and Grisogno (1998), Grisogno (1995), Tan (2001) and Parmhed et al. (2005)). We also note that in some models the eddy viscosity K(z) is taken to be constant above a certain height, with a non-constant polynomial profile below: linear in Estoque (1963), quadratic in Yang (1957), and cubic in O’Brien (1970). In addition, numerical simulations for profiles obtained by multiplying together a polynomial and a height-dependent function are discussed in Grisogno (2011), Large et al. (1994), and Marlatt et al. (2012), while Chai et al. (2004) provide field evidence for a function K(z) with multiple local extrema and inflexion points in the lower part of the Ekman layer.

Table 1 Some physically relevant height-dependent eddy viscosities over the first 1500 m in the Ekman layer (above this they remain practically constant)
Full size table
Fig. 1
figure 1

Profiles of the eddy viscosities listed in Table 1

Full size image

The previous considerations motivate the study of the governing equations (1)–(4) for an arbitrary height-dependent eddy viscosity K. We aim to present some general observations about this problem, with examples, which will help to clarify the effects of various choices for the model taken for K(z). This will also provide a framework for testing the relevance and usefulness of different types of model for K(z). Despite the significant variations in the different models used for the eddy viscosity, all the existing Ekman-type solutions retain two of the fundamental properties of the classical Ekman flow: the horizontal ageostrophic velocity spirals to the right (in the Northern Hemisphere) and the ageostropic speed decreases with height. This raises two important questions: (i) are these two features universally valid? (ii) what effect does the choice of K(z) have on the details of the Ekman flow? We answer the first question in the affirmative by pursuing an in-depth qualitative study of the governing equations (1)–(4) and provide information that helps to clarify the answer to the second question. Our aim is, primarily, to show that the features covered by question (i) hold whenever \(K: [0,\infty ) \rightarrow [k_-,k_+]\) is a continuous and bounded function with \(K(z) \rightarrow k^*\) as \(z \rightarrow \infty \), at a rate faster than quadratic (see Eq. 17 below), for some \(k^*\in [k_-,k_+]\); here \(k_\pm ,\,k^*>0\) are positive constants. This prescription on K(z) admits profiles that are non-monotonic (see Sect. 4). The system (1)–(2) is linear, yet we have made the remarkable discovery that the details for the Ekman flow are best developed by transforming it, using polar coordinates, into a nonlinear system. This aspect of the problem underlines the technically intricate nature of the dynamics of Ekman-type solutions with height-dependent eddy viscosities. We also present some explicit examples of particular choices for the eddy viscosity, K(z), which demonstrate the effect of a viscosity that initially increases, or decreases, above the bottom of the Ekman layer.

2 Existence of Ekman-Type Solutions

Given a continuous and bounded function \(K: [0,\infty ) \rightarrow [k_-,k_+]\) with \(K(z) \rightarrow k^*\) as \(z \rightarrow \infty \) for some \(k^*\in [k_-,k_+]\), by performing the implicit change of variables

$$\begin{aligned} s=\xi (z)= \int _0^z \frac{1}{K(s)}\,\mathrm{d}s,\quad s \in [0,\infty ), \end{aligned}$$
(6)

we transform the governing equations (1)–(2) to the second-order linear differential equation

$$\begin{aligned} {\Psi }''(s) = \mathrm{i}\,\alpha (s)\,{\Psi }(s),\quad s>0, \end{aligned}$$
(7)

for the complex-valued function

$$\begin{aligned} {\Psi }(s)=U(s)+\mathrm{i}V(s) \end{aligned}$$
(8)

with

$$\begin{aligned} U(s)&= u(z)-u_g ,\end{aligned}$$
(9a)
$$\begin{aligned} V(s)&= v(z)-v_g , \end{aligned}$$
(9b)

for \(s=\xi (z) \ge 0\), where

$$\begin{aligned} \alpha (s)=f\,K(z) \quad \text {for}\quad s=\xi (z) \ge 0, \end{aligned}$$
(10)

and the prime denotes differentiation with respect to the s variable (here and throughout the paper). The boundary conditions (3)–(4) are transformed into the equivalent form

$$\begin{aligned}&{\Psi }=-(u_g + \mathrm{i}v_g)\quad \text {at}\quad s=0, \end{aligned}$$
(11)
$$\begin{aligned}&{\Psi } \rightarrow 0 \quad \text {for}\quad s \rightarrow \infty . \end{aligned}$$
(12)

Note that by differentiation we infer from (10) and (6) that the function \(s \mapsto \alpha (s)\) mirrors any monotonicity properties of the function \(z \mapsto K(z)\).

To investigate the qualitative behaviour of the solutions to (7), let us denote by \({\Psi }_\pm \) the two solutions of (7) with the following property:

$$\begin{aligned} {\Psi }_\pm (s) \sim \mathrm{e}^{\mp (1+\mathrm{i})\lambda _0 s},\quad {\Psi }_\pm '(s) \sim \mp (1+\mathrm{i})\lambda _0 \mathrm{e}^{ \mp (1+\mathrm{i}) \lambda _0 s} \quad \text {as}\quad s \rightarrow \infty , \end{aligned}$$
(13)

where

$$\begin{aligned} \lambda _0=\sqrt{\frac{k^*f}{2}} >0. \end{aligned}$$

At great heights, due to (13), these solutions represent spirals, a decaying one turning to the right (\({\Psi }_+\)) and a growing one turning to the left (\({\Psi }_-\)), as \(s>0\) increases. Since the Wronskian bilinear form, defined by

$$\begin{aligned} \begin{vmatrix} {\Psi }_+&\quad {\Psi }_- \\ {\Psi }_+'&\quad {\Psi }_-' \end{vmatrix}={\Psi }_+{\Psi }_-'-{\Psi }_+'{\Psi }_-, \end{aligned}$$

is constant for all \(s>0\) and can be evaluated as \(2(1+\mathrm{i})\lambda _0 \ne 0\) in the limit \(s \rightarrow \infty \), we infer that the solutions \({\Psi }_\pm \) of (7) are linearly independent. Consequently the general solution \({\Psi }\) of (7) is a linear superposition of these two solutions:

$$\begin{aligned} {\Psi }(s)=c_1 \,{\Psi }_+(s) + c_2 \,{\Psi }_-(s),\quad s \ge 0, \end{aligned}$$

for some constants \(c_1,\,c_2 \in {{\mathbb {C}}}\). This shows that \({\Psi }_+\) is the physically relevant solution, generalizing the classical Ekman solution for the atmosphere. We observe that the solution \({\Psi }(s)\) is, in general, unstable: unless \(c_2= 0\), at great heights (\(s \rightarrow \infty \)), the term \(c_2\, {\Psi }_-(s)\) starts to play a role, triggering a significant departure from the dynamics of the Ekman spiral, even if this might be hardly noticeable at low altitudes. This, we suggest, explains why it is often difficult to observe the Ekman flow pattern.

It is not clear, on the basis of the presentation above, that \({\Psi }_\pm \) exist for everyK(z) (as specified). To establish their existence one can proceed as follows. Setting

$$\begin{aligned} {\Psi }(s)={\Psi }_+(s) \,\mathrm{e}^{(1+\mathrm{i})\lambda _0 s},\quad s \ge 0, \end{aligned}$$

from (13) we obtain \({\Psi } \rightarrow 1\) and \({\Psi }' \rightarrow 0\) as \(s \rightarrow \infty \), while (7) yields

$$\begin{aligned} {\Psi }'' - 2(1+\mathrm{i})\lambda _0 {\Psi }'=\mathrm{i}(\alpha -2\lambda _0^2){\Psi },\quad s>0. \end{aligned}$$

We obtain the Volterra integral equation

$$\begin{aligned} {\Psi }(s)=1 + \int _s^\infty D(t-s)\, q(t)\,{\Psi }(t)\,\mathrm{d}t,\quad s \ge 0, \end{aligned}$$
(14)

where

$$\begin{aligned} q(s)=\alpha (s)-2\lambda _0^2,\quad D(s)= \mathrm{i}\int _0^s \mathrm{e}^{-2(1+\mathrm{i})\lambda _0 t}\mathrm{d}t=\frac{\mathrm{e}^{-2(1+\mathrm{i})\lambda _0 s}-1}{2(\mathrm{i}-1)\lambda _0},\quad s > 0. \end{aligned}$$

Given a positive continuous function \(\alpha : [0,\infty ) \rightarrow (0,\infty )\) such that

$$\begin{aligned} \int _0^\infty s |\alpha (s)-2\lambda _0^2|\,\mathrm{d}s < \infty , \end{aligned}$$
(15)

the existence of a unique continuous solution \({\Psi }\) to (14) follows due to the convergence of the iterative process: for \(s \ge 0\) we have

$$\begin{aligned} {\Psi }(s)=1 + \sum _{n=1}^\infty \int _{s \le s_1 \le \cdots \le s_n} D(s_1-s)\cdots D(s_n-s_{n-1}) q(s_1)\cdots q(s_n)\,\mathrm{d}s_1 \cdots \mathrm{d}s_n, \end{aligned}$$

and there exists a constant \(m>0\) such that

$$\begin{aligned} |{\Psi }(s)-1| +|{\Psi }'(s)| \le m \int _s^\infty (1+t)|q(t)|\,\mathrm{d}t,\quad s \ge 0; \end{aligned}$$

see the discussions of the forward-scattering problem in Deift and Trubowitz (1979), Drazin and Johnson (1989) and Constantin (2011). We now define \({\Psi }_+(s)={\Psi }(s) \,\mathrm{e}^{-(1+\mathrm{i})\lambda _0 s}\) for \(s \ge 0\) and note that \({\Psi }_+\) solves (7) on \((0,\infty )\) and has the required asymptotic behaviour as \(s \rightarrow \infty \). A similar procedure establishes the existence of the solution \({\Psi }_-\) with the asymptotic behaviour specified in (13).

Note that, due to (6), we can recast (15) as

$$\begin{aligned} \int _0^\infty \left| 1- \frac{k^*}{K(z)}\right| \,\left( \int _0^z \frac{1}{K(s)}\,\mathrm{d}s\right) \,\mathrm{d}z < \infty . \end{aligned}$$
(16)

Since \(K(z) \in [k_-,k_+]\) ensures

$$\begin{aligned} \frac{z}{k_+} \le \int _0^z \frac{1}{K(s)}\,\mathrm{d}s \le \frac{z}{k_-}, \quad z \ge 0, \end{aligned}$$

as well as

$$\begin{aligned} \left| 1- \frac{k^*}{K(z)}\right| = \frac{|K(z)- k^*|}{K(z)} \le \frac{|K(z)- k^*|}{k_-}, \quad z \ge 0, \end{aligned}$$

we see that (16) holds if there exist constants \(a, \,b>0\) and \(\varepsilon >0\) such that

$$\begin{aligned} |K(z)- k^*| \le \frac{a}{1+ b z^{2+\varepsilon }},\quad z \ge 0. \end{aligned}$$
(17)

This is the only constraint required on K(z), which is otherwise continuous and bounded.

3 Qualitative Features of the Ekman-Type Solutions

The main issue of interest is to elucidate the behaviour of the physically relevant solution \({\Psi }_+\), whose existence was established in Sect. 2. We prove two general results, namely that the ageostrophic horizontal vector (U, V) rotates clockwise (see Sect. 3.2) and its speed \(\sqrt{U^2+V^2}\) is strictly decreasing with increasing height (see Sect. 3.3) for every \(K(z)>0\) satisfying (17).

3.1 Polar Coordinates

It is convenient to introduce polar coordinates. We denote the wind speed by

$$\begin{aligned} M=\sqrt{U^2+V^2} \ge 0 \end{aligned}$$

and let \(\tau \) with \(\tau (0) \in (-\uppi ,\uppi ]\) be such that

$$\begin{aligned} U(s)&= M(s)\,\cos [\tau (s)], \end{aligned}$$
(18a)
$$\begin{aligned} V(s)&= M(s)\,\sin [\tau (s)]. \end{aligned}$$
(18b)

Then M is differentiable whenever \(M \ne 0\) and

$$\begin{aligned} U'&= M'\cos (\tau ) -M\tau '\sin (\tau ) ,\end{aligned}$$
(19a)
$$\begin{aligned} V'&= M'\sin (\tau ) +M\tau '\cos (\tau ), \end{aligned}$$
(19b)

while

$$\begin{aligned} U''&= M''\cos (\tau ) - 2M'\tau '\sin (\tau ) - M\tau ''\,\sin (\tau ) - M (\tau ')^2\cos (\tau ) , \end{aligned}$$
(20a)
$$\begin{aligned} V''&= M''\sin (\tau ) + 2M'\tau '\cos (\tau ) + M\tau ''\,\cos (\tau ) -M (\tau ')^2\sin (\tau ) , \end{aligned}$$
(20b)

so that (7) is replaced by the pair of real equations

$$\begin{aligned}&M''\cos (\tau ) - 2M'\tau '\sin (\tau ) - M\tau ''\,\sin (\tau ) - M (\tau ')^2\cos (\tau ) =-\alpha M \sin (\tau ) ,\\&M''\sin (\tau ) + 2M'\tau '\cos (\tau ) + M\tau ''\,\cos (\tau ) - M (\tau ')^2\sin (\tau ) = \alpha M \cos (\tau ) . \end{aligned}$$

In the above system, multiply the first equation by \(\cos (\tau )\) and add to the second equation multiplied by \(\sin (\tau )\), and then multiply the first equation by \(-M\sin (\tau )\) and add to the second equation multiplied by \(M\cos (\tau )\) to obtain the nonlinear system

$$\begin{aligned}&M'' - M (\tau ')^2 =0,\end{aligned}$$
(21a)
$$\begin{aligned}&(M^2\tau ')' = \alpha M^2 , \end{aligned}$$
(21b)

which is equivalent to (7) on the intervals where \(M \ne 0\). On the other hand, writing

$$\begin{aligned} u_g+\mathrm{i}v_g=M_g\,\mathrm{e}^{\mathrm{i}\tau _g} \end{aligned}$$

with \(M_g>0\) and \(\tau _g \in (-\uppi ,\uppi ]\), the boundary conditions (11)–(12) can be written as

$$\begin{aligned}&M(0)=M_g,\end{aligned}$$
(22a)
$$\begin{aligned}&\tau (0)=\tau _g+\uppi \in (0,2\uppi ]. \end{aligned}$$
(22b)

The classical Ekman spiral, for which \(z=Ks\) and \(\alpha (s)=fK=\text {constant}\), corresponds to the solution

$$\begin{aligned}&M(s)=M_g\,\mathrm{e}^{-\gamma Ks}, \end{aligned}$$
(23a)
$$\begin{aligned}&\tau (s)=\tau _g-\gamma Ks+\uppi , \end{aligned}$$
(23b)

of the system (21) with the boundary conditions (22).

3.2 Monotonicity of the Ageostrophic Speed

We claim that, if \(M_+=|{\Psi }_+|\), then \(M_+(s)>0\) and \(M_+'(s)<0\) for all \(s > 0\). Let us first show that \(M_+(0)>0\). Indeed, multiplying (7), evaluated for \({\Psi }={\Psi }_+\), by \(\overline{{\Psi }_+}\), an integration yields

$$\begin{aligned} -{\Psi }_+'(0)\,\overline{{\Psi }_+(0)}= \int _0^\infty |{\Psi }_+'(s)|^2\,\mathrm{d}s + \mathrm{i}\int _0^\infty \alpha (s)\,|{\Psi }_+(s)|^2\,\mathrm{d}s, \end{aligned}$$

where the overbar denotes the complex conjugate. This shows that \({\Psi }_+(0)=0\) forces \({\Psi }_+ \equiv 0\), in contradiction to the asymptotic behaviour of \({\Psi }_+\).

We now claim that the closed set \(\{s \in (0,\infty ):\ M_+(s)=0\}\) has at most one point, otherwise its open complement, consisting of an, at most, countable disjoint union of open intervals, contains an interval (a, b) with \(M_+(a)=M_+(b)=0\) and \(M_+(s)>0\) for all \(s \in (a,b)\). This is impossible since \(M_+\) is differentiable on (a, b) and convex, given that (21) yields

$$\begin{aligned} (M_+M_+')'=(M_+')^2 + M_+^2(\tau ')^2 \ge 0. \end{aligned}$$
(24)

Let us now rule out the possibility that \(M_+(s^*)=0\) for some \(s^*>0\), with \(M_+(s)>0\) for \(s \in [0,s^*) \cup (s^*,\infty )\). In this case \(M_+\) would be differentiable on \((s^*,\infty )\), and (24) would hold on this interval. But a convex function \(M_+^2: (s^*,\infty ) \rightarrow (0,\infty )\) with \(M_+(s^*)=0\) fails to satisfy \(\lim \nolimits _{s \rightarrow \infty } M_+^2(s)=0\), and proves that \(M_+(s)>0\) for all \(s \ge 0\). Thus \(M_+\) is differentiable on \((0,\infty )\) and (24) holds on this interval, so that \(\lim \nolimits _{s \rightarrow \infty } \{M_+(s)M_+'(s)\}=0\) (which follows from Eq. 13) yields \(M_+'(s)<0\) for all \(s > 0\).

3.3 Rotation of the Horizontal Ageostrophic Flow

We now show that if \({\Psi }_+(s)=M_+(s)\,\mathrm{e}^{i\tau _+(s)}\) with \(\tau _+ \in (-\uppi ,\uppi ]\), then \(\tau _+'(s)<0\) for \(s \ge 0\), that is, the horizontal ageostrophic vector (U, V) rotates clockwise with increasing height, for any choice of K(z) satisfying (17).

Let us first prove that \(\tau _+'\) has at most one zero in \([0,\infty )\). Indeed, if \(b>a \ge 0\) were points with \(\tau _+'(a)=\tau _+'(b)=0\), then integration of (21b) yields \(0=\int _a^b \alpha (s)d_+^2(s)\,\mathrm{d}s\), which is impossible since \(\alpha >0\) and \(M_+>0\) on \([0,\infty )\), as shown in Sect. 3.2.

Let us now rule out the existence of a unique \(s_0 \ge 0\) with \(\tau _+'(s_0)=0\). Under this hypothesis, (21b) yields \(M_+^2(s)\tau _+'(s) > 0\) for \(s > s_0\) and, moreover,

$$\begin{aligned} M_+^2(s)\tau _+'(s) \ge M_+^2(s^*)\tau _+'(s^*)> 0,\quad s \ge s^*>s_0. \end{aligned}$$

Denoting \(A=M_+^2(s^*)\tau _+'(s^*) > 0\), the previous relation and (21a) yield

$$\begin{aligned} 2M_+'M_+'' = 2 M_+' M_+ (\tau _+')^2 \le 2A^2\,\frac{M_+'}{M_+^3},\quad s \ge s^*, \end{aligned}$$

since in Sect. 3.2 we showed that \(M_+'<0\). By integrating the above inequality on the interval \([s^*,s]\) we obtain

$$\begin{aligned}{}[M_+'(s)]^2 - [M_+'(s^*)]^2 \le A^2 \left\{ \frac{1}{M_+^2(s^*)} - \frac{1}{M_+^2(s)} \right\} ,\quad s > s^*, \end{aligned}$$

and this leads to a contradiction in the limit \(s \uparrow \infty \) since \(\lim \nolimits _{s \rightarrow \infty } M_+(s)=0\) [from (13)] shows that the left side remains bounded while the right side becomes unbounded (and negative). We conclude that \(\tau _+'\) does not vanish in \([0,\infty )\). Repeating the above reasoning we can also rule out the possibility \(\tau _+'(0) \ge 0\), and therefore \(\tau _+'(s)<0\) for all \(s \ge 0\).

3.4 The Top of the Ekman Layer

Above a specific height, designated as the top of the Ekman layer, the flow is very nearly geostrophic. Given that

$$\begin{aligned} u+\mathrm{i}v=u_g+\mathrm{i}v_g + M\,\mathrm{e}^{\mathrm{i}\tau } \end{aligned}$$

vanishes at the bottom \(z=0\) of the Ekman layer and \(M'(s)<0\) for \(s>0\), as shown in Sect. 3.2, it is reasonable to define the height \({\mathfrak {E}}\) of the Ekman layer as that corresponding to the uniquely determined value of \(s>0\) for which \(\tau (s)=\tau _g\), since this is the lowest height at which the wind is close to geostrophic, and above this level the ageostrophic wind decays with increasing height. The fact that \({\mathfrak {E}}\) is uniquely determined is a consequence of (22) in combination with the fact that \(\tau '(s)<0\) for \(s>0\), as shown in Sect. 3.3. In particular, (23) shows that \({\mathfrak {E}}=\uppi /\gamma =\uppi \sqrt{2K/f}\) for the classical Ekman spiral (Holton 2004). In particular, for constant viscosity \(K = 0.01\) m\(^2\,\)s\(^{-1}\), the predicted thickness of the Ekman layer at Dome C on the Antarctic Plateau, located at 75\(^\circ \)S, would be about 37 m, which is in accordance with the measurements reported in Ryman et al. (2016). The corresponding prediction for an Ekman flow at about 30\(^\circ \)N, with constant eddy viscosity \(K = 5\) m\(^2\,\)s\(^{-1}\), puts the thickness of the Ekman layer at about 1175 m.

3.5 The Deflection Angle

The angle between the flow near the bottom of the layer and the geostrophic wind vector is of considerable interest; to investigate this we first introduce the angle \(\beta \) between the wind vector at any height and that of the geostrophic vector,

$$\begin{aligned} \beta (s) =\text {arg}\left( \frac{u(s)+\mathrm{i}v(s)}{u_g+\mathrm{i}v_g}\right) =\text {arg}\left( 1+ \frac{M(s)}{M_g}\,\mathrm{e}^{\mathrm{i}[\tau (s)-\tau _g]}\right) ,\quad s>0. \end{aligned}$$
(25)

Thus

$$\begin{aligned} \tan [\beta (s)]=\frac{M(s)\,\sin [\tau (s)-\tau _g]}{M(s)\,\cos [\tau (s)-\tau _g] +M_g},\quad s>0. \end{aligned}$$
(26)

Using l’Hospital’s rule, this is readily evaluated for \(s \rightarrow 0\) (which corresponds to the bottom of the layer) to give

$$\begin{aligned} \beta (0) = \arctan \left[ \frac{M_g \tau '(0)}{M'(0)}\right] , \end{aligned}$$
(27)

where the prime denotes the derivative with respect to s. We note in passing that the direction of the flow near the bottom of the layer is obtained from

$$\begin{aligned} \lim _{z \rightarrow 0} \frac{v(z)}{u(z)}=\frac{ (\mathrm{d}v/\mathrm{d}z) }{ (\mathrm{d}u/\mathrm{d}z)}\Big |_{z=0}, \end{aligned}$$

which is the tangent of the angle associated with the direction of the viscous stress that maintains the no-slip boundary condition. (This is precisely the counterpart of the familiar result in oceanography where the surface wind produces a stress that deflects and drives the Ekman spiral in the near-surface ocean layer.) In the case of the classical Ekman spiral, we see that the solution (23) used in (27) gives \(\beta (0)=45^\circ \), while \(\beta (s) \in (0,45^\circ )\) in the Ekman layer, based on the considerations presented in Sects. 3.2 and 3.3. However, the angle \(\beta (0)\) that is observed is often rather smaller than 45\(^\circ \) (Etling 2008). Field data analysis shows that angles within the range 32\(^\circ \)–37\(^\circ \) are frequent (Grisogno 2011), with values as low as 15\(^\circ \)–25\(^\circ \) reported at the nearly flat Høvsøre testing site for wind turbines in western Denmark, located at an average height of about 2 m above sea level, where the ground is covered mostly by grass, crops and a few shrubs (Peña et al. 2016). On the other hand, measurements performed on the Tibetan Plateau, on a ruderal-covered pasturing area 4200 m above the mean sea level, yielded angles in excess of 50\(^\circ \) (Zhang et al. 2003). These data suggest that a height-dependent eddy viscosity is important. We will return to this issue, via a number of examples (Sect. 4), but first we derive a general property of the angle \(\beta (s)\).

Fig. 2
figure 2

Visualisation of a classical Ekman spiral at 30\(^\circ \)N, with vertical extent from 50 m to 1225 m, and with geostrophic velocity at a speed of 5 m s\(^{-1}\) in the x-direction above it. This atmospheric setting corresponds to low pressure to the north and high pressure to the south, with constant eddy viscosity \(K = 10\) m\(^2\) s\(^{-1}\). The qualitative features (decay with depth and spiralling to the right) are independent of the eddy viscosity profile, in contrast to quantitative aspects (the thickness of the Ekman layer and the deflection angle)

Full size image

From (26), given that \(M_g>M(s)>0\) for \(s>0\), we find by direct differentiation that the sign of \(\beta '(s)\) equals that of the expression

$$\begin{aligned} M_g M(s)\tau '(s) \,\left\{ \frac{M(s)}{M_g} + \frac{M'(s)}{M(s)\tau '(s)} \,\sin [\tau (s)-\tau _g] + \cos [\tau (s)-\tau _g] \right\} , \end{aligned}$$

which is negative throughout the Ekman layer. This is so because, within the layer, we have \(0<\tau (s)-\tau _g<\uppi \), while M(s) and \(\tau (s)\) are both strictly decreasing, with \(M(0)=M_g\); thus we see that

$$\begin{aligned} \frac{M'(s)}{M(s)\tau '(s)}\sin [\tau (s)-\tau _g]>0\ \text {and}\ \frac{M(s)}{M_g} + \cos [\tau (s)-\tau _g]> 1+\cos [\tau (s)-\tau _g] >0. \end{aligned}$$

This shows, as we move upwards through the Ekman layer, that the angle \(\beta (s)\) between the wind vector at any level and the geostrophic wind vector aloft decreases, i.e. the Ekman spiral rotates to the right in the Northern Hemisphere. The classical structure of the Ekman spiral in the atmosphere is depicted in Fig. 2. Note that, since the pressure is lower to the left of a geostrophic wind vector in the Northern Hemisphere (Mak 2011), the fact that \(\tan [\beta (s)]>0\) throughout the Ekman layer means that the flow has an ageostrophic component from high towards low pressure, while the geostrophic flow aloft moves parallel to the isobars (Vallis 2006).

4 Examples

We have seen that the equivalent formulations, (7) and (21), of the governing equations (1)–(2), for flows in the atmospheric boundary layer, enable us to produce some general results. But, quite significantly, they also provide a basis for testing various choices of variable eddy viscosity and, furthermore, they lay the foundations for the construction of explicit solutions. Indeed, either of the approaches that we have presented provides a systematic method for extending the choice of the eddy-viscosity function, opening the way to new theoretical observations on the nature of Ekman flows. We now illustrate these ideas by presenting a few examples.

4.1 Bessel-Type Solutions

We consider the case of an eddy viscosity that varies linearly with height in the lower part of the Ekman layer, and constant thereafter; that is, there is some \(z_0>0\) such that

$$\begin{aligned} K(z)=\left\{ \begin{array}{ll} a +bz,&{}\quad 0 \le z \le z_0,\\ a+bz_0,&{}\quad z > z_0, \end{array}\right. \end{aligned}$$
(28)

for constants \(a>0\) and \(b \in {{\mathbb {R}}}\) with \(a+bz_0>0\). From (6) and (10), we see that

$$\begin{aligned} \alpha (s)=\left\{ \begin{array}{ll} af\,\mathrm{e}^{bs},&{}\quad 0 \le s \le s_0,\\ af\,\mathrm{e}^{bs_0},&{}\quad s > s_0, \end{array}\right. \end{aligned}$$
(29)

where \(s_0=b^{-1}\ln [1+(b/a)z_0]>0\). The physically relevant solution (i.e. approaching the geostrophic background flow upwards) of (7) is clearly given by

$$\begin{aligned} {\Psi }_+(s)=\exp \left\{ -(1+ \mathrm{i})s \sqrt{\tfrac{af}{2}\,\mathrm{e}^{b s_0}}\right\} ,\quad s > s_0. \end{aligned}$$

For the solution in the lower part of the layer, \(s \in [0,s_0]\), we set

$$\begin{aligned} {\Psi }(s)={ \Phi }(x) \quad \text {with}\quad x=\mathrm{e}^{b s/2}, \end{aligned}$$

which transforms (7) into the Bessel equation

$$\begin{aligned} x^2\,\frac{\mathrm{d}^2 { \Phi }}{\mathrm{d}x^2} + x\,\frac{\mathrm{d} { \Phi }}{\mathrm{d}x}- \frac{4\mathrm{i}af}{b^2}\,x^2\,{ \Phi }=0. \end{aligned}$$
(30)

The general solution of Eq. 30 can be expressed as a linear combination of the (complex valued) Bessel functions of the first (\(J_0\)) and second (\(Y_0\)) kind, of order zero. Let us suppose, for the purposes of this introductory example, that the eddy viscosity decreases (upwards) to its constant value \(a+bz_0\), and so we take \(b<0\); we could, similarly, examine the case where the eddy viscosity increases upwards (these two options—initially increasing or decreasing viscosity—are discussed more fully in Example 4.3, below). Because \(Y_0\) increases as \(x=\mathrm{e}^{sb/2}=\sqrt{1+(a/b)\,z}\) decreases, a solution that approaches geostrophic balance is impossible unless this term is absent; thus we obtain the solution

$$\begin{aligned} { \Phi }(x) =c\,J_0\left( \frac{2\sqrt{af}}{|b|}\,x\, \mathrm{e}^{-\mathrm{i}\tfrac{\uppi }{4}} \right) ,\quad x>0, \end{aligned}$$
(31)

where c is an arbitrary complex constant. This example is simply an adaptation, to the atmosphere, of the solution found by Madsen (1977) in the oceanographic context.

Fig. 3
figure 3

Depiction of the properties of the Bessel-type solution, (31), for a deflection angle close to 50.5\(^\circ \) (solid curves), plotted against az / b. The classical, constant-viscosity case (\(b = 0\)) Ekman flow is also shown (dashed curves) and then the plot is for \(a = b\), i.e. original, non-dimensional z. Left-hand plot: ageostrophic wind speed (normalised); right-hand plot: relative deflection angle

Full size image

It is useful to note that this representation, (31), of a solution for variable eddy viscosity contains valuable information. So, for example, for \(2\sqrt{af}/|b| \approx 1.69\), the deflection of the flow near the bottom of the layer, relative to the direction of the geostrophic flow, can be as large as about \(55^\circ \); the classical \(45^\circ \) is approached for larger values of this parameter. Correspondingly (in the Northern Hemisphere) the wind rotates to the right and its speed relative to the ambient state tends to zero, for increasing height through the layer. This property of solution (31) is shown in Fig. 3, demonstrating that the familiar Ekman structure is recovered; specifically, we plot the ratio of the wind speed at any height to that at the bottom of the Ekman layer, and the deflection angle relative to the wind direction at the bottom, both against a normalized (non-dimensional) depth in the form az / b. More pronounced differences between the classical results and these Bessel-based ones will become evident when both are plotted against z (which is non-dimensional) for various a, b and f (which do not need to be specified for the plots shown here). The foregoing description of the flow properties is obtained simply by computing the real and imaginary parts of \({ \Phi }\) and its derivative.

4.2 Extended Bessel-Type Solution

A solution based on the properties of the Bessel function can be readily extended. To see how this works in outline, we first make the choice \(\alpha (s)=a+b\,\mathrm{e}^{-\lambda s}\) for positive constants a and \(\lambda \), and \(b \in {{\mathbb {R}}}\). We see that

$$\begin{aligned} K(z)=\frac{\alpha (s)}{f} \quad \text {where}\quad z=\frac{b}{f\lambda } + \frac{a}{f}\,s - \frac{b}{f\lambda }\,\mathrm{e}^{-\lambda s} , \end{aligned}$$

which gives the behaviour of K(z) as

$$\begin{aligned} K(0)=\frac{a+b}{f} \quad \text {with}\quad K(z) \rightarrow \frac{a}{f} \quad \text {for}\quad z \rightarrow \infty . \end{aligned}$$

In order to recover the physically realistic solution, we require \(a/f>0\) and \((a+b)/f>0\). This admits solutions for which either the eddy viscosity decreases upwards (\(b>0\)) or increases upwards (\(b<0\)). We set

$$\begin{aligned} {\Psi }(s)={ \Phi }(x) \quad \text {with}\quad x=\frac{\sqrt{2|b|}}{\lambda }\,[1-\mathrm{i}\,\text {sgn}(b)]\,\mathrm{e}^{-\lambda s/2}, \end{aligned}$$

which transforms (7) into the general Bessel equation

$$\begin{aligned} x^2\,\frac{\mathrm{d}^2{ \Phi }}{\mathrm{d}x^2}+ x\,\frac{\mathrm{d}{ \Phi }}{\mathrm{d}x} +(x^2- \nu ^2)\,{ \Phi }=0, \end{aligned}$$
(32)

where \(\nu =\sqrt{2a}\,(1+\mathrm{i})/\lambda \). Equation 32 possesses (complex valued) solutions based on the Bessel functions of order \(\nu \), namely, \(J_\nu \) and \(Y_\nu \) (Abramowitz and Stegun 1964). However, as \(z \rightarrow \infty \) (and so \(x \rightarrow 0\)), we must discard the solution \(Y_\nu \) (which diverges as \(x \rightarrow 0\)) if we seek a solution of (32) that approaches geostrophic balance at high altitude; we may therefore follow a similar route to that described in the preceding example, but now using \(J_\nu \). As before, for decreasing K, we may have a deflection of the ageostropic wind direction in excess of \(45^\circ \) to the right (Northern Hemisphere), the maximum possible angle varying with \(\nu \). On the other hand, for K increasing with height (but bounded), the deflection angle can be less than \(45^\circ \): as \(|\nu |\) increases, so the angle decreases e.g., using the Maple mathematical package, at \(|\nu |=10\) the deflection angle is about \(30^\circ \). In all cases, as \(|b|/\lambda \) increases, so the deflection angle approaches the classical result: \(45^\circ \), this limit corresponding to \(\lambda \rightarrow 0\), which recovers constant K.

4.3 Asymptotic Solution Near the Bottom of the Layer

The results obtained in the two preceding examples, and the discussion in Sect. 3.5, suggest that the initial deflection of the Ekman spiral (i.e. on \(z = 0\)) is governed by the behaviour of the eddy viscosity in the lowest most regions of the layer; this possibility can be explored directly, albeit via an asymptotic approximation. We examine the solution (cf. (1)–(2) and (8)–(9)) of

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}z}\,\left\{ K(z)\,\frac{\mathrm{d} {\Psi }}{\mathrm{d}z}\right\} =\mathrm{i}f{\Psi },\quad {\Psi }=U+\mathrm{i}V, \end{aligned}$$

with

$$\begin{aligned} K(z)=a+bz,\quad 0 \le z \le z_0, \end{aligned}$$

in some small neighbourhood of the bottom of the layer, and the choice of K(z) is otherwise arbitrary; we construct the associated asymptotic solution valid as \(z \rightarrow 0\) for \(a>0\) and \(b \in {\mathbb R}\), with \(a+bz_0>0\). This choice of eddy viscosity enables us to identify the behaviour at the bottom of the layer and so determine its effect on the flow properties. Thus we obtain

$$\begin{aligned} b\,\frac{\mathrm{d} {\Psi }}{\mathrm{d}z} + (a+bz)\,\frac{\mathrm{d}^2 {\Psi }}{\mathrm{d}z^2}=\mathrm{i}f{\Psi }, \end{aligned}$$

and so

$$\begin{aligned} b\,\frac{\mathrm{d} {\Psi }}{\mathrm{d}z} + a\,\frac{\mathrm{d}^2 {\Psi }}{\mathrm{d}z^2} \sim \mathrm{i}f{\Psi } \quad \text {as}\quad z \rightarrow 0; \end{aligned}$$
(33)

this asymptotic approximation makes no assumptions about the relative sizes of the terms in \({\Psi }\). We seek a solution of (33) in the form \({\Psi }(z)=c\,\mathrm{e}^{(\alpha + i\beta )z}\) (for \(\alpha \) and \(\beta \) real, and c an arbitrary complex constant) because, although we want the solution only as \(z \rightarrow 0\), this specification enables us to impose the condition that the solution of interest must be such that the velocity field can approach geostrophic balance away from \(z = 0\) (i.e. \(|{\Psi }(z)|\) decreases as z increases) . We find that the required solution corresponds to the choice

$$\begin{aligned} \beta = -\frac{1}{\sqrt{2}}\, \frac{|b|}{2a},\sqrt{-1+\sqrt{\gamma ^2+1}} \quad \text {and}\quad \alpha =-\frac{b}{2a}+ \frac{f}{2a\beta } \quad \text {where}\quad \gamma =\frac{4af}{b^2}; \end{aligned}$$

the direction of the geostrophic flow is determined from

$$\begin{aligned} (U+\mathrm{i}V)\Big |_{z=0} ={\Psi }(0), \end{aligned}$$

and that near the bottom of the layer is obtained from

$$\begin{aligned} \left( \frac{\mathrm{d}U}{\mathrm{d}z} + \mathrm{i} \frac{\mathrm{d}V}{\mathrm{d}z}\right) \Big |_{z=0} =\frac{\mathrm{d}{\Psi }}{\mathrm{d}z}(0). \end{aligned}$$

In the Northern Hemisphere (\(f>0\)), this shows that the deflection of the flow varies from 90\(^\circ \) (\(\gamma =0\)) to 45\(^\circ \) (\(\gamma \rightarrow \infty \)) for K decreasing away from the bottom (\(b<0\)), and from zero to 45\(^\circ \) for K increasing. (Note that \(\gamma \rightarrow \infty \) corresponds to \(|b|\rightarrow 0\), the constant-viscosity case.)

This asymptotic property extends the results obtained in the two preceding examples (and also that given in the next example) by emphasising the behaviour of the solution at the bottom of the layer. The apparent inconsistency with Example 4.1 arises because there we used K linear in z throughout a bounded, and non-zero, domain; here we used only the value of K, and its derivative, on \(z = 0\). These calculations, in isolation, suggest that, for suitable choices of K(z), it is possible to obtain solutions for which the angle of deflection of the wind relative to that of the applied stress (required to maintain the no-slip condition) can take any value (to the right in the Northern Hemisphere) between zero (i.e. parallel) and \(\uppi /2\). However, we should be more circumspect. Combining these asymptotic results (appropriate on \(z = 0\)) with those based on more complete prescriptions for K(z) (in Example 4.1, Example 4.2 and also in Example 4.4 below) indicate that the particular choice of K(z) throughout the Ekman layer does affect the deflection angle. Indeed, we conjecture that the form of K(z) above \(z = 0\) restricts the deflection angle from the extremes predicted from the behaviour on \(z = 0\) alone.

4.4 Solutions in Terms of Hypergeometric Functions

Explicit solutions are also available when we choose an exponential variation of the eddy viscosity in the lower part of the layer, and then constant above that; we set

$$\begin{aligned} K(z)=\left\{ \begin{array}{ll} a(\mathrm{e}^{-bz}-c),&{}\quad 0 \le z \le z_0,\\ a(\mathrm{e}^{-bz_0}-c),&{}\quad z>z_0, \end{array}\right. \end{aligned}$$
(34)

where a, b and c are positive constants, with \(k^*=a(\mathrm{e}^{-bz_0}-c)>0\); this exponential form corresponds to that used by Miles (1994). We introduce the change of variable defined by

$$\begin{aligned} s=\int _0^z \frac{\mathrm{d}t}{K(t)}=-\frac{1}{abc}\,\ln \left[ \frac{\mathrm{e}^{-bz}-c}{(1-c)\mathrm{e}^{-bz}} \right] \end{aligned}$$

and then set

$$\begin{aligned} \zeta =(1-c)\mathrm{e}^{-abc s}, \end{aligned}$$

which, with \({\Psi }(s)={ \Phi }(\zeta )\), gives the hypergeometric equation

$$\begin{aligned} \frac{\mathrm{d}^2 { \Phi }}{\mathrm{d} \zeta ^2} + \frac{1}{\zeta }\,\frac{\mathrm{d} { \Phi }}{\mathrm{d} \zeta } - \frac{\mathrm{i}f}{ab^2c}\,\frac{1}{\zeta (1-\zeta )}\,{ \Phi }=0, \quad 1-c>\zeta > 1-c \mathrm{e}^{bz_0}, \end{aligned}$$
(35)

for which

$$\begin{aligned} \alpha (s)=acf\,\frac{(1-c)\mathrm{e}^{-abc s}}{1-(1-c)\mathrm{e}^{-abc s}}=acf\,\frac{\zeta }{1-\zeta }. \end{aligned}$$

If we denote

$$\begin{aligned} \beta =\frac{1+\mathrm{i}}{b}\,\sqrt{\frac{f}{2ac}} \quad \text {and}\quad \gamma =-\beta , \end{aligned}$$

then the physically relevant solution of (35) is

$$\begin{aligned} { \Phi }(\zeta )=c\,{\mathfrak {F}}(\beta ,\gamma ;1;\zeta ), \end{aligned}$$

where c is an arbitrary (complex) constant and \({\mathfrak {F}}\) is Gauss’ hypergeometric function (Abramowitz and Stegun 1964).

The details of the solution follow similar lines to those noted in the Examples 4.1 and 4.2, based on the Bessel function. So here, for example, we find that for \(b^{-1}\sqrt{f/(2ac)} \approx 0.774\), the deflection angle is about 65\(^\circ \) (and approaches the classical 45\(^\circ \) as this parameter is increased), and the rotation and approach to ambient conditions at higher altitude are also repeated.

4.5 Solutions Related to Fuchsian Equations

The procedures described in Sects. 4.1, 4.2 and 4.4 show that explicit solutions can be constructed, based on special functions, by choosing \(\alpha (\zeta )\) to correspond to singular points of a second-order, ordinary differential equation. For example, another class of explicit solutions is available by choosing

$$\begin{aligned} \alpha (s)=\frac{\xi (\xi +1)}{(\xi -1)(\xi -r)} \quad \text {with}\quad \xi =\mathrm{e}^{-s} \in (0,1). \end{aligned}$$
(36)

This hinges on the fact that any Fuchsian equation with four singular points can be reduced to the Heun equation

$$\begin{aligned} \frac{\mathrm{d}^2 w}{\mathrm{d} \xi ^2} + \left( \frac{g_3}{\xi } + \frac{g_4}{\xi -1} + \frac{g_1+g_2-g_3-g_4+1}{\xi -r}\right) \, \frac{\mathrm{d} w}{\mathrm{d} \xi } + \frac{g_1g_2 \xi -g_5}{\xi (\xi -1)(\xi -r)}\,w=0, \end{aligned}$$

just as any Fuchsian equation with three singular points can be reduced to the Gauss hypergeometric equation (Maier 2007); here \(g_1,\,g_2,\, g_3,\, g_4 \in {{\mathbb {C}}}\) and \(r \in {{\mathbb {C}}} \setminus \{0,1\}\) are free parameters. The development of this solution is quite involved, so the details are not presented here; in the context of this general approach to Ekman spirals in the atmosphere, it is sufficient to note that other explicit solutions do exist (the details of which are readily examined by computation).

4.6 Another Method to Generate Explicit Solutions

In order to initiate this alternative approach, we note that the elimination of \(\tau \) between Eqs. 21a and 21b produces an expression for \(\alpha (s)\),

$$\begin{aligned} \alpha (s)=-\,\frac{3M'(s)M''(s)+M(s)M'''(s)}{2 M(s)\sqrt{M(s)M''(s)}},\quad s >0, \end{aligned}$$
(37)

where the prime denotes the derivative with respect to s. This result can be used to find solutions by first choosing M(s), so that \(\alpha (s)\) is determined directly, and then integrating to obtain \(\tau (s)\) from (21) i.e. from \(\tau '=-\sqrt{M''/M}\). We are concerned only with those solutions that steadily approach the ambient state (the geostrophic balance) at higher altitudes. The most straightforward way to accomplish this is to restrict ourselves to bounded intervals, and then it suffices to select M(s) as any convex, strictly decreasing function, chosen to ensure that (37) produces a positive expression for \(\alpha \). We present two solutions that show how this method can be employed.

4.6.1 Exponential Decay of the Ageostrophic Velocity with Height

Set

$$\begin{aligned} M(s)=\mathrm{e}^{-as-\tfrac{a^2}{4}\,s^2},\quad 0 \le s \le s_0, \end{aligned}$$
(38)

with \(a>0\) and \(s_0>0\); then we find that

$$\begin{aligned} \alpha (s)=\frac{a^2(2+as) (a^2+4a^3s+a^4 s^2)}{2\sqrt{2+4as+a^2s^2}},\quad 0 \le s \le s_0, \end{aligned}$$
(39)

and we simply take \(\alpha (s)=\alpha (s_0)\) for \(s > s_0\). On the interval \((s_0,\infty )\) the differential equation (7) for \({\Psi }\) has constant coefficients, while on \((0,s_0)\) the physically relevant solution (i.e. decaying as the height increases) is

$$\begin{aligned} {\Psi }_+(s)=\mathrm{e}^{-as-\tfrac{a^2}{4}\,s^2 + \mathrm{i} \tau _+(s)},\quad 0 \le s \le s_0. \end{aligned}$$
(40)

The function \(\tau _+(s)\) is obtained by integrating

$$\begin{aligned} \frac{\mathrm{d}\tau _+}{\mathrm{d} s}=- \frac{a}{2}\sqrt{2+4as+a^2\,s^2} ,\quad 0< s < s_0, \end{aligned}$$

to give

$$\begin{aligned} \tau _+(s)= \frac{1}{2} \ln \left( 2+as+\sqrt{2+4as+a^2s^2}\right) - \frac{2+as}{4}\sqrt{2 +4as+a^2s^2} , \end{aligned}$$
(41)

for \(0 \le s \le s_0\). The connection with the physical variable, z, is obtained from the definitions (6) and (10),

$$\begin{aligned} \frac{\mathrm{d} s}{\mathrm{d} z}=\frac{1}{K(z)}=\frac{f}{\alpha (s)}= \frac{2f\sqrt{2+4as+a^2\,s^2}}{a^2(2+as)(1+4as+a^2\,s^2)} ,\quad 0< s < s_0, \end{aligned}$$

which determines z(s) by quadrature. This slight complication here is avoided in the next example, but at the expense of a very simple variation of eddy viscosity with height and an associated simple flow structure.

4.6.2 Slow Decay of the Ageostrophic Velocity with Height

Now we simply take

$$\begin{aligned} M(s)=\left\{ \begin{array}{ll} \frac{b}{1+as},&{}\quad 0 \le s \le s_0,\\ \frac{b}{1+as_0},&{}\quad s>s_0, \end{array}\right. \end{aligned}$$

with \(a>0\), \(b>0\) and \(s_0>0\); it follows directly that

$$\begin{aligned} \alpha (s)=\left\{ \begin{array}{ll} \frac{3\sqrt{2}\,a^2}{(1+as)^2},&{}\quad 0 \le s \le s_0,\\ \frac{3\sqrt{2}\,a^2}{(1+as_0)^2},&{}\quad s>s_0, \end{array}\right. \end{aligned}$$

and

$$\begin{aligned} \tau (s)=-\sqrt{2}\,\ln (1+as),\quad 0 \le s \le s_0. \end{aligned}$$

We obtain

$$\begin{aligned} \frac{\mathrm{d}s}{\mathrm{d}z}=\frac{f}{3\sqrt{2}\,a^2}\,(1+as)^2,\quad 0 \le s \le s_0, \end{aligned}$$

and then

$$\begin{aligned} K(z)=\frac{3\sqrt{2}\,a^2}{f}\,\left( 1- \frac{f}{3\sqrt{2}\,a^2}\,z\right) ^2,\quad 0 \le z \le \frac{3\sqrt{2}\,a^2}{f}\,\frac{s_0}{1+as_0}. \end{aligned}$$

The horizontal velocity \((U,\,V)\) rotates and decreases linearly, so that geostrophic balance is approached at higher altitudes:

$$\begin{aligned} \left\{ \begin{array}{l} U(z)=b\left( 1- \displaystyle \frac{f}{3\sqrt{2}\,a^2}\,z\right) \,\cos \left[ \sqrt{2}\ln \left( 1-\frac{f}{3\sqrt{2}\,a^2}\,z\right) \right] ,\\ V(z)=-b\left( 1- \displaystyle \frac{f}{3\sqrt{2}\,a^2}\,z\right) \,\sin \left[ \sqrt{2}\ln \left( 1-\frac{f}{3\sqrt{2}\,a^2}\,z\right) \right] . \end{array}\right. \end{aligned}$$

These two examples, based on the choice of M(s), which then leads to the determination of \(\alpha (s)\) and \(\tau (s)\), and those presented earlier that led directly to the construction of \({\Psi }=U+\hbox {i}V\), show the potential of these ideas. There are clearly many opportunities for future investigation as other, possibly more sophisticated, choices are made.

5 Discussion

This general approach to the classical problem of the atmospheric Ekman flow has significantly extended and enhanced what is currently known. Most importantly, we have shown, for any eddy viscosity that is bounded and tends to a constant finite value at high altitude, that the decay and spiralling of the flow upwards is an enduring property. The spiral is clockwise in the Northern Hemisphere; the corresponding result is anticlockwise in the Southern Hemisphere, although we have not discussed this case explicitly here: it simply requires a change of sign in places. All previous work on this problem, starting from the seminal model proposed by Ekman, has been driven by a few explicit examples; these have provided the basis for conjecture, but we have proved that the familiar flow structure is always present. The overall picture of the classical Ekman spiral is unaltered by the details of the varying eddy viscosity, which is slightly surprising. We might have expected that viscosity profiles with a number of local maxima and minima, for example, would produce a significant distortion of the familiar structure of the flow; this is not the case.

The ideas and techniques that have been described here can be used to investigate these flows further. So, for example, the procedures that we have developed enable models for the variation of eddy viscosity with height to be checked, tested or invented. This is essentially because explicit solutions can be constructed in one of two ways: either directly from the classical formulation (based on the Ekman model in the f-plane approximation), written in complex form, or from the reformulation of this method using a polar-coordinate transformation. This latter approach helps to explain why the underlying structure of this problem, with variable viscosity, is so involved. We have provided a number of examples in each case, a small number of which are new. One particular result that we have obtained, both from explicit, exact solutions, and from an asymptotic analysis valid near the bottom of the Ekman layer, is that angles of deflection other than the usual 45\(^\circ \) are possible, and we are able to give some guidance as to whether the deflection is initially above or below this value. And all that we have presented is only the start of a detailed investigation. A number of different avenues can be explored because it is clear that we have barely scratched the surface; so, for example, we might investigate how stratification and baroclinicity modulate the solutions described here.

One obvious route to follow is the hunt for other exact solutions, most easily accomplished by choosing suitable ageostrophic-wind-speed functions M(s); this leads directly to the corresponding variable eddy viscosity and the fully detailed flow structure. A case is made in some of the literature, and we have alluded to this earlier, that time dependence needs further investigation, although we note that we can always accommodate significant time variation simply by superimposing a parametric time dependence on the solutions described here. A more fundamental issue is the use of the classical Ekman equations; these do not capture the effects of the Earth’s curvature, so a more comprehensive study, along the lines developed here, but based on the full Navier–Stokes equation, in rotating, spherical coordinates, is worth pursuing; a preliminary discussion of Ekman-type flows in a rotating, spherical coordinate system, can be found in Constantin and Johnson (2018). Our work, we submit, has enhanced our understanding of the classical Ekman flow, in the presence of variable eddy viscosity, to the extent that a number of new results and methods have been introduced. Finally, we note that all that we have described here is equally applicable to the corresponding oceanic flow model in the f-plane approximation, for wind-driven currents in the upper layer of the oceans; see Vallis (2006) and Marshall and Plumb (2016) for a theoretical discussion, and Röhrs and Christensen (2015) for recent field data.