1 Introduction

It can be said that ambiguous and fuzzy situation exists in every subject related to the real world. Evaluation problems often share a common characteristic of ambiguous information. The real world contains uncertainties as well as precise information. In daily life, it is impossible to define everything with 0 and 1 and to place it under certain values such as black-white, right-wrong, or good-bad. Furthermore, even if individuals use the exact words when expressing an opinion, their meanings can differ significantly as each has a different subjective perception. In other words, people can soften the definite limits by adding value and meaning to the information (Akram et al. 2022a). Reaching a correct and precise result by analyzing ambiguous and imprecise information can be achieved with fuzzy logic, which emerges as opposed to classical logic (Zadeh 1965). Existing methods are not as effective as fuzzy sets in handling numerical values, as the latter can mitigate the impact of sharp boundaries through their fuzzy nature (Peng and Luo 2021).

Fuzzy set theory was first introduced by Zadeh (1965). The fuzzy set is an extension of the characteristic function in classical sets and is characterized by a belonging function. Here, the Decision-Makers (DMs) can determine the membership degree in the range of [0, 1]. Elements have a certain degree of membership in that set. It has a definition that enables the inclusion of variable real-life judgments into calculations. The interest in fuzzy logic is growing gradually (Entemann 2002; Jana and Mahanta 2023; Pan et al. 2023a). In addition to engineering, fuzzy logic is used in many fields, such as artificial intelligence, computer, robotics, and space technologies. The increased interest in fuzzy logic also shows itself in scientific studies (Lima et al. 2021; Hentout et al. 2023).

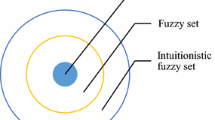
After fuzzy sets were defined, Intuitionistic Fuzzy Sets (IFS) were introduced by K.T. Atanassov (1986) as a generalization of fuzzy sets. While classical fuzzy sets are represented by membership degree only, IFSs are characterized by membership and non-membership degrees of all objects in the universe, and their sum is always in the range of [0, 1] (Atanassov 2012). IFS cannot be defined when the sum of the membership and non-membership grades is greater than 1. Therefore, to address this deficiency, the Pythagorean Fuzzy Set (PFS) was developed by Yager (2013) to generalize the IFS concept. While the sum of membership degrees in IFS is in the range of [0, 1], in PFS, the sum of the squares of the degrees of membership and non-membership falls into the range of [0, 1]. This shows that PFS includes IFS (Zhang and Xu 2014).

They are both commonly used in decision-making applications, yet they have some differences in their definition and properties. PFSs are defined based on the Pythagorean theorem, which allows the representation of uncertainty in terms of distance. PFS has attracted the attention of many experts and researchers in a short time and has been applied to decision-making problems in many different fields (Joshi 2019; Liu et al. 2020), such as technological innovation risk evaluation (Liang et al. 2015), investment decision (Aghamohagheghi et al. 2019), assessment on emergency response capabilities (Du et al. 2017), transportation problem applications (Saikia et al. 2023), renewable energy resource evaluation (Geetha et al. 2022) and technology provider selection (Zhou and Chen 2022). It has been observed that there are cases where the square sum of membership and non-membership degrees is greater than 1. IFS or PFS could not explain and solve these problems (Zhou and Chen 2022). Senapati and Yager (2020) proposed the Fermatean Fuzzy Set (FFS) in this direction.

Senapati and Yager (2020) conducted an analysis of the interrelationships among FFS, IFS, and PFS. They observed that IFS is a specific instance or special case within the broader framework of PFS, and, conversely, FFS is an extension or generalization of PFS. The limit of squares sums of the membership and non-membership degrees determined by the PFS has been expanded by defining the FFS (Senapati and Yager 2020). In FFS, the cubic sum of membership and non-membership values of an object are in the range of [0, 1] (Akram et al. 2022a). FFS theory plays an important role in various fields, as it is an advantageous and powerful concept for dealing with uncertain information (Liu et al. 2019a).

The main aim of Fuzzy Logic based approaches is soften the impacts of sharp borders. Therefore, FFS by providing a cubic sum of membership and non-membership values is seemed to be promising to handle vagueness better than IFS and PFS (Senapati and Yager 2019a). In literature, FFSs are seemed to be more flexible for capturing uncertainty of information (Keshavarz-Ghorabaee et al. 2020). The primary objective of methodologies rooted in Fuzzy Logic is the mitigation of the rigidity associated with distinct boundaries (Zadeh 1976). In this context, FFSs exhibit promise by presenting a cubic summation of membership and non-membership values. This feature positions FFS as a potentially superior approach for managing vagueness when compared to IFSs and PFSs, as indicated by the work of Senapati and Yager (2019a). Notably, within the academic discourse, FFSs are recognized for their heightened flexibility in capturing the nuances of uncertain information, as highlighted in the scholarly contributions of Keshavarz-Ghorabaee et al. (2020).

FFSs, being a relatively nascent concept within the realm of fuzzy logic, is presently undergoing a phase of initial development. Despite its emergent status, the field has witnessed a notable surge in research activity in recent years. Substantive contributions have been made in both conceptual and analytical domains. One pivotal facet of this exploration involves the development of innovative FFS operators, encompassing union, intersection, and negation (Akram et al. 2022c). These operators are meticulously crafted to accommodate the extended range of membership values intrinsic to FFSs. Concurrently, scholars are delving into the application of FFSs in decision-making realms, encompassing Multi-Criteria Decision Making (MCDM) and Group Decision Making (GDM) (Keshavarz-Ghorabaee et al. 2020; Akram et al. 2022a). This line of inquiry seeks to distinguish the potential of FFSs in enhancing the difficulties of decision-making processes. Furthermore, researchers are actively investigating the utilization of FFSs in pattern recognition applications, ranging from image recognition to data clustering (Ashraf et al. 2023). This exploration is poised to elucidate the adaptability and efficacy of FFSs across diverse recognition scenarios. In parallel, there is a concerted effort to scrutinize the mathematical properties of FFSs, particularly their ordering and aggregation characteristics (Chang et al. 2023; Fahmi et al. 2023b). Such analytical endeavors aim to unravel the inherent traits and capabilities of FFSs, contributing to a deeper understanding of this emerging fuzzy logic paradigm. Collectively, this research trajectory underscores the vibrant academic landscape surrounding FFSs and its potential to significantly impact various facets of fuzzy logic applications.

Despite the pivotal role and significant advantages that FFS hold in handling uncertain information, the current literature lacks a thorough analysis of key areas and applications. This deficiency extends to research gaps and outcomes, hindering a nuanced understanding of FFS. This gap in comprehensive analysis impedes the full realization of FFS's potential and calls for a more robust exploration of its foundational aspects and practical applications. Addressing this gap is crucial for advancing the theoretical foundation and facilitating future advancements in the field. In light of this deficiency in the existing literature, the objective of this review is to address the gap by formulating the following research questions (RQs):

  • RQ1: What are the current publication trends in FFSs literature?

    • RQ1.1: How has the interest in FFSs evolved over time?

    • RQ1.2: Are there specific journals or regions that dominate the publication landscape?

  • RQ2: What practical applications have been explored using FFSs, and what methodologies have been employed in these applications?

  • RQ3: How do different applied methods with FFSs contribute to solving real-world problems in various domains?

  • RQ4: What are the existing extensions of FFSs, and how do they enhance the expressive power of the original model?

  • RQ5: In what ways have these extensions addressed limitations or shortcomings in the application of FFSs?

  • RQ6: How do different aggregation operators (AOs) impact the performance and outcomes of FFSs in decision-making scenarios?

  • RQ7: How have linguistic sets been effectively incorporated into FFSs, and what role do they play in enhancing the interpretability of the model?

  • RQ8: How does FFSs compare with PFS and IFS in terms of representation and computational efficiency?

  • RQ9: What thematic patterns emerge from the literature on FFSs, and are there specific thematic clusters or trends that indicate the evolving nature of FFSs research?

  • RQ10: What are the current gaps and limitations in the existing literature on FFSs and what future research directions can be identified to address these gaps?

In summary, this comprehensive review aims to fill crucial gaps in the existing literature on FFSs. The articulated RQs span diverse dimensions, including publication trends, practical applications, methodological contributions, extensions and their impact, linguistic set incorporation, comparative analyses with other fuzzy set models, thematic patterns, and identification of current gaps. By addressing these inquiries, the review aspires to provide a nuanced understanding of the current state of FFS research, uncover emerging trends, and offer valuable insights to guide future explorations. The outputs of RQs will be leading contributions of this paper. The essential contributions can be summarized as follows:

  • Descriptive Analysis and Publication Trends (RQ1): Providing a comprehensive descriptive analysis to elucidate the current landscape of FFSs literature, unveiling the evolution of interest in FFS over time.

  • Methodological Contributions and FFS Applications (RQ2-RQ7): Exploring integrated FFSs technics, AOs, extensions, linguistic sets, practical applications and analyzing their role and effectiveness.

  • Comparative Analysis and Thematic Exploration (RQ8-RQ9): Conducting a comparative analysis of FFS with PFSs and IFSs in terms of representation and computational efficiency and uncovering thematic patterns in the literature on FFS and identifying specific clusters or trends indicative of the evolving nature of FFS research.

  • Identification of Gaps and Future Directions (RQ10): Identifying current gaps and limitations in the existing literature on FFSs and proposing future research directions to address the identified gaps.

The rest of the paper is structured as follows. The next Materials and Methods section explains the review methodology, Section 3, Literature Review, provide the detailed review to answer RQs 1 to 8. The following Section 4, Thematic Analysis, will give the thematic analysis conducted based on the bibliometric data gathered from the reviewed material. Section 5, Gaps and Future Directions will provide the current gaps and limitations based on thematic analysis and review results with future research directions and potential future RQs. Finally, Section 6 provides the conclusions.

2 Materials and methods

In pursuit of addressing the RQs, this review adopts a Systematic Literature Review (SLR) approach, aligning with contemporary studies that underscore the efficacy of such a methodology (Zhu et al. 2021; Siti-Dina et al. 2023; Saulick et al. 2023). For that purpose, we followed a protocol developed specifically for SLR which is Scientific Procedures and Rationales for Systematic Literature Reviews protocol (SPAR-4-SLR) (Paul et al. 2021). This protocol, comprising three stages and six sub-stages sequenced as assembling, arranging, and assessing, serves as a comprehensive framework for systematically conducting literature reviews (Paul et al. 2021). The initial stage involves the identification and acquisition of pertinent literature not yet synthesized. Subsequently, the arranging stage entails the organization and purification of literature currently under synthesis. The final stage, assessing, encompasses the evaluation and reporting of literature that has been synthesized. Adhering to the SPAR-4-SLR protocol positions our systematic literature review to provide state-of-the-art insights and stimulating agendas for advancing knowledge within the domain. Crucially, the utilization of this protocol ensures that our insights and agendas are thoroughly justified through logical and pragmatic rationales and transparently reported in accordance with the specified stages and sub-stages (Kumar et al. 2023).

2.1 Assembling

In the initial phase of the review, termed assembling, two distinct sub-stages unfold: identification and acquisition. The identification sub-stage serves as a preparatory phase, involving the comprehensive recognition of all activities pertinent to the study's objectives. This preparatory step is critical for the effective execution of the proposed methodological design. The focus during the identification sub-stage is primarily on discerning suitable keywords that possess the capability to encapsulate all relevant aspects, laying the groundwork for the subsequent stages of the review.

In the phase of selecting keywords, given our exclusive focus on FFSs, we opted for the key term "Fermatean Fuzzy". A preliminary search using this keyword on Google Scholar yielded a comprehensive collection of studies related to the topic. Subsequently, to ensure a thorough exploration of FFS-related literature, we chose to proceed exclusively with the "Fermatean Fuzzy" keyword. Regarding the selection of databases for our review, Scopus and Web of Science (WoS) were identified as mutually comprehensive platforms to capture the entirety of relevant literature on FFSs.

During the identification stage, crucial decisions were made regarding source type and quality. Prioritizing conceptual and empirical “articles” in “journals” was essential to avoid redundancy found in reviews and to ensure the inclusion of research subjected to rigorous peer scrutiny. This deliberate focus on articles within journals, as opposed to editorials, notes, books, book chapters, and conference proceedings, aligns with the goal of maintaining a corpus of the highest quality research. Given the global proliferation of predatory journals, which compromise promised quality, a meticulous quality check on journals was conducted before their final consideration (Grudniewicz et al. 2019). Drawing from established practices (Mohammadi and Sakhteh 2023; Kocak et al. 2023), our approach involved reviewing articles exclusively from the first and second quartiles (Q1 and Q2) of the WoS and Scopus databases, affirming our commitment to selecting high-quality journals relevant to FFS-centric research. This methodological rigor enhances the robustness and credibility of our literature review.

Subsequently, the acquisition sub-stage ensued, marking the initiation of activities pertaining to the search mechanism and material procurement. On November 27, 2023, a search syntax employing the identified keyword "Fermatean Fuzzy" in the search functions of WoS and Scopus resulted in the retrieval of 470 documents. We are aware that same studies can be in both Scopus and WoS search, in the following phase the arrangement will be perfomed to narrow down the list. To ensure comprehensiveness, the review period was intentionally left open, allowing for the inclusion of all pertinent articles within the scope of the review corpus.

2.2 Arranging

Moving to the second stage, namely arranging, this phase is characterized by two activity-based substages: organization and purification. The initial set of 470 documents obtained in the preceding stage necessitates systematic sorting and filtering to isolate articles aligning with the research objectives of the current review.

Within the organization activity, essential criteria were established for extraction. Specifically, the selection of source type "journal," document type "article," and language "English" was chosen. This meticulous curation process resulted in the selection of source type "journal" and document type “article", yielding a refined pool of 421 documents. Notably, 49 documents, spanning conference proceedings, books, editorials, and notes, were excluded from the original 470, streamlining the corpus. The rationale behind selecting "journal" as the source type is rooted in the preference for peer-reviewed scholarly works, ensuring a higher level of scrutiny and quality in the included literature (Kumar et al. 2022a, b). Similarly, the choice of document type "article" further refines the selection, prioritizing in-depth research contributions over other document types such as conference proceedings, books, editorials, and notes.

Subsequently, a language filter was applied to further enhance the reliability of this SLR. This additional refinement led to a final selection of 420 documents, with only one document not in the English language. This rigorous organization and purification process ensures that the ensuing analysis is grounded in a focused and linguistically consistent body of literature.

The subsequent phase, termed "purification," is contingent on the systematic elimination of duplicated documents identified in both Scopus and WoS. In the penultimate substage of the arranging activity, a judicious decision was made to exclusively include journals assessed within the esteemed Q1 and Q2 lists of Scopus and WoS (Mohammadi and Sakhteh 2023; Kocak et al. 2023). Initially, the removal of duplicate works resulted in a refined corpus comprising 265 documents. The removal of duplicates in both databases resulted in the exclusion of 155 documents from the initial pool of 420, thereby streamlining the corpus. Subsequently, an additional curation step involved the exclusion of Q3 and Q4 journals, leading to a further reduction to 152 documents. In the final purification step, a meticulous process of abstract reading and keyword verification was undertaken following the four-eye principle, culminating in the ultimate refinement of the corpus to a robust selection of 135 documents. This stringent purification process ensures the inclusion of high-quality, non-redundant literature, thereby fortifying the reliability and scholarly integrity of the SLR. During the four-eye principle reading process, the following criteria are utilized:

  • Generic articles not having any Fermatean Fuzzy Number (FFN) sets, operations, or operators.

  • Articles do not address any specific use of FFS operations and extensions.

Figure 1 furnishes a descriptive summary of the extracted review corpus, encompassing 135 articles.

Fig. 1
figure 1

Protocol for reviewing FFS literature

Full size image

2.3 Assessing

The third stage, namely assessing, encompasses activities focused on evaluation and reporting, with a primary emphasis on scrutinizing the descriptive analysis of current publication trends, methodological contributions, FFS applications, thematic exploration, and the identification of gaps and future directions.

In terms of evaluation, a meticulous examination was undertaken on the 135 articles extracted in accordance with the review protocol. To address RQ1, a bibliometric analysis was conducted utilizing the BibliometrixFootnote 1 analysis tool, specifically Biblioshiny. This analysis tool facilitated a comprehensive exploration of publication trends, shedding light on the evolution of interest and identifying dominant journals or regions.

Addressing RQ2 to 8 involved the utilization of content analysis. This method involved a thorough examination of each article, and pertinent data were meticulously compiled into Excel sheets to address the specific inquiries posed by each research question. This approach enabled a nuanced understanding of practical applications, extensions, AOs, linguistic sets, and comparative analyses with other fuzzy set models.

Subsequently, to tackle RQ9, a thematic analysis was conducted using Biblioshiny, aiming to generate thematic maps and evaluation figures (Aria and Cuccurullo 2017). These maps illuminated the areas predominantly focused on in the current literature, offering insights into both prominent and less-explored facets.

Furthermore, the detailed examination and discussion of thematic maps aimed to address RQ10, where potential research areas were derived. By discerning patterns and thematic concentrations, this stage contributes to identifying gaps in the literature and proposes future research directions within the realm of FFSs.

In the reporting phase, this investigation adopts a methodology akin to previous SLRs (Kumar et al. 2020; Paul et al. 2021; Goyal et al. 2021) by articulating its results through a blend of figures, such as network visualizations, tables containing metrics, and narrative descriptions.

3 Literature review

In this literature review section, our primary objective is to comprehensively assess 135 articles, offering insights to address RQ 1–8 within the domain of FFSs. To achieve this, each subsection is meticulously organized to review these articles in alignment with the specific requirements of the research questions. The initial focus centers on a descriptive bibliometric analysis, providing an overview of trends and the current state-of-the-art in FFS publications (RQ1). Subsequently, the studies are categorized into five distinct subsections to address various dimensions of FFS research. The first subsection classifies studies based on their applied methods in FFS, addressing RQ2 and RQ3. The second subsection delves into FFS extensions, providing insights into RQ4 and RQ5. The third subsection explores the AOs employed in the FFS literature, aligning with RQ6. Following this, the fourth subsection focuses on linguistic sets, contributing to the understanding of RQ7 in the context of FFS applications. Finally, the fifth subsection presents a comparative analysis between FFSs, IFSs, and PFSs, elucidating RQ8.

3.1 Descriptive analysis

In conducting the descriptive analysis to capture the trend in FFSs publications, the initial focal point is the presentation of Fig. 2, illustrating the distribution of articles on a yearly basis. Notably, the inclusion of Early Access articles from 2024 has been omitted from the figure, strategically opted to foster a clearer representation of the increasing trend in FFS publications.

Fig. 2
figure 2

Year wise distribution of the FFSs studies (2023 studies up to November 27, 2023)

Full size image

The evolving interest in FFSs is vividly reflected in the dynamic publication trends observed over recent years. Beginning with a modest representation in 2019 and 2020, the subsequent years, particularly 2022 and 2023, witnessed a substantial surge in scholarly contributions. This escalating trajectory not only underscores the growing significance of FFS but also signifies a heightened interest and engagement within the academic community. It's worth mentioning that the inclusion of Early Access articles from 2024 further emphasizes the ongoing momentum in FFS research, despite the year being incomplete at the time of this analysis. This escalating trajectory underscores the growing significance and scholarly activity surrounding FFSs. Figure 3, generated through the Bibliometrix tool, offers a visual representation of the most influential sources within the FFS literature.

Fig. 3
figure 3

Most relevant sources in FFS literature

Full size image

Analyzing the most relevant sources in FFSs literature, it becomes evident that certain journals play a prominent role in disseminating research on this topic. Notably, "Engineering Applications of Artificial Intelligence" and "Expert Systems with Applications" stand out as leading contributors, each with 11 articles. Additionally, journals such as "Granular Computing" and "Soft Computing" demonstrate significant influence, each publishing 8 articles. This distribution highlights the key journals shaping the landscape of FFS research and underscores the importance of these platforms in fostering scholarly discussions.

Figure 4 offers a preliminary insight into the current trends within FFSs literature, presenting a list of the most relevant words. This pre-overview, obtained through the Bibliometrix software, serves as a concise snapshot, laying the groundwork for a more detailed exploration through thematic analysis.

Fig. 4
figure 4

Most relevant word from FFS literature

Full size image

This most relevant words list, derived through the Bibliometrix tool and primarily based on author keywords, provides a succinct overview of the current trends in FFS literature. Notably, the recurring appearance of terms such as "fermatean fuzzy set" and "fermatean fuzzy sets" underscores their centrality, collectively accounting for a significant portion of occurrences. Furthermore, the prominence of keywords like "MCDM" and "decision-making" highlights a strong thematic connection between FFSs and decision science. Terms like "TOPSIS," "interval-valued fermatean fuzzy sets," "score function," and "uncertainty" further enrich the contextual landscape, shedding light on key aspects within the current literature. This preliminary insight serves as a foundation for more in-depth exploration through thematic analysis, affirming the integral role of FFSs in the realms of decision-making and uncertainty modeling.

With this preliminary bibliometric analysis offering a snapshot of the current trends in FFSs literature, we transition into a more detailed exploration of methodological contributions and FFS applications. The forthcoming subsections are intricately designed to provide a comprehensive analysis, specifically addressing RQ2 to RQ8.

3.2 Applied methods in FFS

FFS theory introduces a new approach to uncertainty in decision-making. Currently, researchers are exploring the potential of FFS and applying it to various decision-making problems. Most of the FFS studies that have been conducted so far have focused on MCDM problems. FFSs provide a nuanced way of modeling uncertainties and imprecisions, which can be particularly useful in decision-making scenarios where precise information is hard to come by. To address RQ2 and RQ3, this review mentions the MCDM methods discussed in the FFS field. It has been observed that about two-thirds of the studies on MCDM problems use single/hybrid MCDM methods. Meanwhile, other studies have presented several FFS applications based on distance measures and AOs to better understand the decision problem. These studies are detailed in the following sections.

3.2.1 MCDM methods used in FFS

Table 1 summarizes the several MCDM methods implied in the FFS literature. This table shows that the TOPSIS method, which is one of the most popular MCDM methods, is the most frequently implied technique in the FFS studies. The FFS-TOPSIS approach measures the degree of membership and non-membership in the evaluation process, considering the uncertainties in the problem. FFS-TOPSIS can determine the distance between each evaluated item and the PIS and NIS, making it a method attaining more data than additional MCDM methods (Senapati and Yager 2020).

Table 1 MCDM methods used in FFS studies
Full size table

The second prevalent MCDM technique in FFS literature is the CRITIC method. Using this method, it is possible to cope with the problems related to fuzzy sets and obtain more accurate results by avoiding subjectivity using the CRITIC method (Saraji et al. 2021). The third most common techniques are CODAS, COPRAS, DEMATEL and SWARA with their use in seven articles. Using the CODAS method helps to combine the two distance measures and reduce the possibility of instability in the solution by providing a more rational analysis and greater flexibility between distance-based methods (Biswas et al. 2021). COPRAS stands out with its ability to simultaneously describe the ratios to both ideal and anti-ideal solutions (Akram et al. 2022e). DEMATEL is particularly useful in analyzing complex systems and representing interrelationships visually, while SWARA provides a systematic and transparent approach to weight assessment, which reduces subjectivity and enables efficient decision-making (Gonzales et al. 2022a). CoCoSo and MULTIMOORA are the fourth most used methods with their use in six articles. CoCoSo has minimal impact on the results in case the alternatives change and supports the precision of the decision-making system (Lai et al. 2022). MULTIMOORA is a powerful tool that evaluates all objectives, considers all interactions between alternatives and objectives simultaneously (Rani and Mishra 2021). When the fifth most common MCDM methods in FFS studies are examined, the methods appeared as WASPAS and AHP. It has been observed that the use of AHP increased in 2023. AHP is a method used by practitioners in various fields in the literature due to its compatibility with hierarchical decision structures and its ability to make precise pairwise comparisons effectively. On the other hand, while ANP offers advantages in addressing interdependencies and feedback loops, it has not yet been used with FFSs. ANP's emphasis on network structures may be overly complex for decision scenarios where hierarchical representation is sufficient. The inherent adaptability and simplicity of AHP, together with its compatibility with FFSs, make it a well-suited method for decision modeling in scenarios where a more complex network structure is not a prerequisite.

Among other MCDM methods, MEREC, ELECTRE, MARCOS, EDAS, ARAS, MABAC, BWM, FUCOM, PROMETHEE, VIKOR and TODIM are used in more than one of the reviewed FFS studies. Each of the other MCDM methods, such as WPM, SMART, SAW, DEA, BRAW, LOPCOW, ITARA, QFD, MAIRCA and WINGS are used in only one study. Using these methods with FFS aims to get more flexible, reliable, and accurate results by closing the deficiencies in traditional approaches (Kao et al. 2022).

3.2.2 Integrated MCDM methods used in FFS

Each MCDM method has its advantages and disadvantages. Concerning these benefits and limitations from a single MCDM technique, most studies preferred using integrated MCDM methods to eliminate these restraints. Studies using the integrated MCDM method in FFS literature are shown in Table 2.

Table 2 Integrated MCDM methods used in FFS studies
Full size table

The most common methods in the FFS literature, in terms of integration, are the combinations of CRITIC-COPRAS, CRITIC-CODAS, SWARA-COPRAS and MEREC-MULTIMOORA. There exist two studies for both integrated methods. The rest of the integrated MCDM methods were used in only one study.

The use of integrated MCDM techniques empowers DMs to make more informed and reliable decisions by capitalizing on the strengths of multiple approaches and considering a wider range of factors, ultimately leading to enhanced decision quality and effectiveness. integrated MCDM techniques provide a means to handle the complexities and uncertainties inherent in real-world decision problems. The integration of diverse methods can enhance decision robustness and improve the accuracy of results, as it reduces the reliance on a single technique and accounts for various aspects and dimensions of the problem at hand (Lee and Chang 2018).

Taking all these factors into consideration, it has been substantiated in the academic literature that the FFS technique offers convenience and suitability in the utilization of both individual and integrated MCDM methodologies. The literature supports the notion that FFS is well-aligned with the requirements and complexities associated with decision-making processes, as it effectively accommodates the use of diverse MCDM techniques. The following Fig. 5 gives the divisions of studies according to their MCDM methodology.

Fig. 5
figure 5

Single MCDM methods vs. integrated methods in reviewed FFS literature

Full size image

3.2.3 Validation of the MCDM methods in FFS

The literature on FFS demonstrates a wide usage of various MCDM techniques. Several factors, including effort, accuracy, and computation time, are considered when selecting these techniques. Comparative analysis is frequently employed to compare the same application using different methods, thereby providing insights into the validity and effectiveness of the utilized approaches (Chakraborty and Saha 2022). This approach allows for a comprehensive evaluation and interpretation of the results derived from different MCDM methods, aiding in the determination of their suitability for specific decision-making scenarios.

Another important analysis is the sensitivity analysis (Yagmahan and Yılmaz 2023). This analysis plays an important role in checking the robustness and accuracy of decision results and applicability (Chowdhury and Paul 2020). Integrating sensitivity analysis with MCDM results enables the assessment of the responsiveness of the obtained outcomes when criteria importance undergoes changes. By examining the sensitivity of the results, researchers gain a deeper understanding of the stability and robustness of the decision-making outcomes, thereby contributing to the advancement of knowledge in the field. Moreover, the incorporation of sensitivity analysis provides crucial guidance for further research endeavors, facilitating the exploration of new avenues and the refinement of decision-making models and methodologies.

In FFS literature, it was observed that sensitivity analysis or comparative analysis were incorporated in 90% (122 articles) of the reviewed studies. Among these, 37% (50 articles) specifically focused on comparative analysis, comparing the performance of diverse MCDM techniques, different fuzzy extensions or AOs. However, it is noteworthy that in 9% of the articles (13 articles), neither comparative analysis nor sensitivity analysis was conducted. The absence of such analyses raises concerns regarding the robustness of the reported results. Incorporating comparative analysis and sensitivity analysis is vital to ensure the reliability and validity of findings in FFS research, warranting further attention in future studies.

3.2.4 Advantages and limitations of MCDM methods in FFS

Qualitative features in MCDM problems depend on the judgment of the DM. Evaluations are often based on inappropriate data or personal judgments given the uncertainty of a person's opinion, leading to inappropriate and biased decisions (Alsalem et al. 2022). FFS-MCDM techniques offer a suitable framework for evaluating available alternatives and selecting the optimal choice, particularly in decision-making scenarios where criteria involve subjective perceptions. These techniques bring forth distinct advantages, including their flexibility and effectiveness in managing uncertainty, conflicting criteria, and diverse preferences of DMs (Senapati and Yager 2020). By employing FFS-MCDM techniques, DMs gain the ability to interpret results intuitively and make more informed decisions.

In this section, we delve into a comprehensive interpretation of the advantages and limitations of the five most widely employed MCDM techniques in the FFS literature. This detailed analysis sheds light on the specific strengths and weaknesses of these techniques, providing valuable insights for researchers and practitioners alike. By understanding these nuances, DMs can effectively leverage the advantages offered by FFS-MCDM techniques, while also being aware of the potential limitations inherent in their application.

Upon examining the MCDM methods utilized in the FFS literature, it becomes evident that the most frequently employed approach is TOPSIS. The FFS-TOPSIS method offers distinct advantages, particularly in addressing the inherent uncertainties encountered in decision-making problems (Liu et al. 2019b; Yang et al. 2022). This method exhibits flexibility in handling conflicting criteria and varying levels of criterion importance. Notably, FFS-TOPSIS demonstrates remarkable robustness to errors and generates more stable outputs that are less susceptible to uncertainties. It excels in complex problem domains or situations where data availability is limited (Yang et al. 2022). The prominence of FFS-TOPSIS in the literature underscores its efficacy in dealing with the complexities and challenges associated with decision-making scenarios, making it a valuable tool for researchers and practitioners alike.

In addition to its notable advantages, the FFS-TOPSIS method is not without its limitations. One limitation is the relatively higher time consumption associated with the application of FFS-TOPSIS compared to the classical TOPSIS method. Furthermore, a challenge arises from the fact that experts may not be familiar with FFS concepts, as it is a relatively new approach in addition to fuzzy concepts. To address these challenges, a potential avenue for improvement lies in the development of user-friendly software tools that automate FFS-TOPSIS calculations. Such tools would enhance accessibility and streamline the application of the method in practice. Additionally, conducting comparisons between FFS-TOPSIS and other MCDM methods, as well as integrating it with different MCDM approaches, can contribute to a better understanding of its strengths and weaknesses, ultimately bolstering its effectiveness. By acknowledging these limitations and actively seeking solutions, researchers can pave the way for the refinement and wider adoption of the FFS-TOPSIS method, harnessing its benefits while mitigating potential drawbacks.

Another widely used method in the FFS literature is the CRITIC method. In addition to effectively handling uncertainties, this method exhibits flexibility by accommodating both multi-criteria and multi-option MCDM scenarios. Notably, the CRITIC method evaluates optimal criteria weights by considering individual contrast intensity and conflict between criteria, thereby yielding more accurate results (Saraji et al. 2021).

The third most used methods are emerged as CODAS, COPRAS, DEMATEL and SWARA. The prominent advantage of FFS-CODAS method lies in its ability to process data sets with missing or incomplete values. This method employs a combination of customizable distance measures tailored to the specific requirements of the application, enabling the handling of such data effectively (Simic et al. 2022a). Moreover, the FFS-CODAS method demonstrates flexibility and applicability across various types of data, while also offering ease of use as a notable advantage.

However, it is important to note a gap in the FFS-CODAS method related to standardization. Different researchers have employed various variations of the method, leading to difficulties in comparing results across different studies (Biswas et al. 2021; Akram et al. 2022d; Simic et al. 2022a). To establish the FFS-CODAS method as a reliable MCDM approach, further research is required to determine its effectiveness and practicality. Addressing the standardization issue is a crucial aspect that needs attention in future studies, enabling a more coherent and comparable evaluation of results obtained using the FFS-CODAS method.

The FFS-COPRAS approach has been found valuable for addressing quantitative and qualitative decision-making practices with many conflicting indicators (Rani et al. 2022a). The method offers a flexible and reliable way to deal with uncertain MCDM problems and inconsistent information. FFS-COPRAS considers both non-useful and useful type indicators. Considering both indicators in complex proportions contains more accurate information. It also makes data easier to read and results more accurate. Besides its advantages, it will be important to mention its limitations. In the FFS-COPRAS method, it is assumed that all criteria are interdependent. However, in realistic situations, there are interrelationships between criteria.

Moving on to the FFS-DEMATEL, this method is a powerful approach that can handle a wider range of intrapersonal and interpersonal uncertainties when making decisions. This method provides greater flexibility to experts when evaluating criteria in uncertain environments, allowing them to make better and more informed decisions (Gonzales et al. 2022a). Another method, FFS-SWARA, boasts impressive efficiency without requiring extensive comparison or calculation. This method is useful because it provides a more logical computation of weights and accurately determines the relative importance of criteria, while also effectively handling uncertainties and inaccuracies in the information regarding the weights of criteria (Ayyildiz 2022).

To ensure logical, flexible, and reliable results, decision-making models need to be capable of evaluating uncertain and complex information. FFS-MCDM methods have been designed and implemented with a focus on meeting these requirements (Aydin 2021). The integration of FFS-MCDM techniques with various MCDM approaches in future studies holds promise for their application in diverse fields. Additionally, conducting comparative analyses among different FFS-MCDM methods in the future can offer valuable guidance in selecting the most suitable method for specific decision-making contexts.

By acknowledging the necessity of handling uncertainty and complexity, FFS-MCDM methods strive to provide robust and adaptable solutions (Senapati and Yager 2020). Future research endeavors that explore the integration of FFS-MCDM techniques with other methodologies would expand their applicability and effectiveness across different domains. Furthermore, comparative assessments between various FFS-MCDM methods will enable researchers and DMs to make informed choices, considering the specific characteristics and requirements of their decision-making problems.

3.2.5 Non-MCDM methods used in MCDM problems

In addition to MCDM methods, the literature on FFS reveals the utilization of distance measures and AOs as alternative approaches to address MCDM problems. These techniques have been observed to play a significant role in the FFS literature, offering additional tools for tackling MCDM challenges.

Chakraborty and Saha (2022) used FF Hamy mean AOs, one of the most adaptable operators for dealing with complex and inconsistent data. Mondal et al. (2023) proposed a three-way multi-attribute decision-making model. FFS soft AOs were utilized by researchers (Zeb et al. 2022; Ali and Ansari 2022; Akram et al. 2022a) in their respective applications. The importance of Hamacher AOs and their application to Multiple Attribute Decision-Making (MADM)/ Multiple Attribute Group Decision-Making (MAGDM) problems are significant. Some studies proposed Hamacher AOs and their desirable qualities to solve the MADM problems (Shahzadi et al. 2021a, b; Hadi et al. 2021; Jan et al. 2021).

Shit and Ghorai (2021), used Dombi AOs for MADM problem in the field of education. Verma (2021) proposed a MAGDM approach based on new AOs under FF linguistic, while Wang et al. (2019) used Archimedean Bonferroni mean AOs to solve MCDM problems. Simic et al. (2023) proposed FF hybrid AOs for optimizing material selection and Ruan and Chen (2023) introduced the probability and interval values into hesitant FFSs.

Distance measures are also utilized in FFS area (Deng and Wang 2021, 2022; Ganie 2022). In the literature, it is seen that there are few studies on the FF entropy measure. Since it is the most useful measure in fuzzy set theory, it should be adopted in FFS studies. Apart from these studies, it has been seen that another study adopts the maximum-average approach and offers an application in the field of health (Ejegwa et al. 2022).

In addition to traditional MCDM methods, the literature on FFS highlights the significance of non-MCDM approaches, such as distance measures and AOs, in addressing complex decision-making challenges. These alternative techniques offer distinct benefits and expand the range of tools available in the FFS domain. The utilization of FF Hamy mean AOs, Dombi AOs, and other specialized AOs demonstrates their adaptability and effectiveness in handling diverse data scenarios. Furthermore, the exploration of FF entropy measure and maximum-average approach in FFS studies signify the potential for further advancements in the field. In the following sections, a more detailed analysis of the AOs will be provided, shedding light on their applications and insights gained. These investigations will contribute to a deeper understanding of the benefits and limitations of non-MCDM methods within the FFS framework, ultimately enhancing decision-making processes in various domains.

3.2.6 Application areas in the integrated FFS literature

To address RQ3, a rigorous examination of FFS integrated methods was undertaken, culminating in the creation of a table delineating application areas and objectives. This table, derived from meticulous evaluations by the authors, briefly encapsulates the focal points of FFS applications, substantiated by relevant references, thereby providing a nuanced perspective on the diverse domains where FFS demonstrates applicability (Table 3).

Table 3 FFS integrated methodologies’ application areas and their objectives
Full size table

3.3 The extensions of FFS

The FFS is also extended with existing fuzzy approaches to fortify its benefits while dealing with ambiguous information. This section provides an in-depth exploration of RQ4 and RQ5 by examining various extensions of FFS that have been proposed in the literature. By discussing the advantages and disadvantages of each extension, this analysis aims to shed light on how FFS can be further developed and improved to meet the needs of different applications and scenarios.

The following targets are aimed to reach by having an extended FFS approach (Wang et al. 2019; Akram et al. 2022c):

  • Employing the FFS in qualitative environments with semantic form,

  • Managing the membership and non-membership that are not fully defined but represented by interval form,

  • Coping with cubic sets, bipolar fuzzy sets, or hesitant fuzzy sets,

  • Handling the insufficiency of the parameterized by combining soft set,

  • Managing the estimations by fusing with the rough set.

Table 4 reveals that a significant portion of the FFS literature utilizes ordinary FFS, with a considerable number of studies also integrating MCDM techniques. While these extensions have demonstrated effectiveness in tackling diverse problems, the evolving and complex nature of decision-making environments demands further considerations. The limitations associated with these approaches will be discussed in subsequent sections. Moreover, future research endeavors will continue to explore FFS extensions, incorporating new mathematical models and tools, such as complex FFS and rough FFS, to enhance decision-making processes.

Table 4 Extensions of FFS
Full size table

3.3.1 Advantages and limitations of the extensions of FFS

FFS extensions are introduced to develop new decision-making methods or to improve the performance of existing methods. Extensions listed in Table 4 are also investigated to reveal their drawbacks and benefits. Here Table 5 summarizes them.

Table 5 Advantages and Limitations of the Extensions of FFS
Full size table

3.4 Fermatean fuzzy AOs

Aggregation methods are valuable for unifying and combining the various assessments in the form of FFSs. They are useful during the decision-making processes in which DMs explicit their valuation through the FFS in decision-making problems. Many addition operators used to make decisions are founded on geometric mean, arithmetic mean, and integrals (Peng and Dai 2020). To achieve robust and meaningful outcomes, selecting appropriate AOs is essential for tailoring FFSs to specific decision contexts. In this section, to address RQ6, AOs in FFS literature are introduced, and their properties, advantages, and limitations are explained.

3.4.1 Algebraic AOs

In MCDM problems, aggregation issues are elucidated through scoring techniques such as the weighted addition operator. Classic weighted aggregation methods are usually known as a weighted average, weighted geometric, or simple aggregation weighting. Other common addition operators can be specified as the ordered weighted average or the ordered weighted geometric operator.

Senapati and Yager (2019a) developed a series of FF AOs, such as the FF weighted average AOs and FF weighted geometric AOs and applied them in MCDM problems. Liu et al. (2019a) proposed FFLWA, FFLWG under an FF linguistic environment. Verma (2021) also proposed FFLWA, FFLWG, the FFL-ordered weighted averaging, the FFL-ordered weighted geometric, the FFL-hybrid averaging, and the FFL-hybrid geometric operators under FF linguistic environment for a MADGM problem and aggregated four DMs evaluations. Rani and Mishra (2022) used Interval-valued FF weighted geometric AOs. FF soft AOs such as FF soft weighted averaging, FF soft ordered weighted averaging, FF soft weighted geometric and FF soft ordered weighted geometric AOs are proposed by Zeb et al. (2022). Liu et al. (2022) utilized Interval-valued Hesitant FF weighted AOs and Lai et al. (2022) Hesitant FF weighted averaging AOs for a GDM problem consisting of three DMs. To address limitations in FF weighted average and FF weighted geometric AOs, recently, Simic et al. (2023) proposed FF hybrid weighted arithmetic geometric and FF hybrid ordered weighted arithmetic geometric AOs.

3.4.2 Hamacher AOs

Jan et al. (2021) proposed FF Hamacher weighted average, FF Hamacher ordered weighted average, FF Hamacher hybrid weighted average AOs for MADM problems and present an application in disaster management with three DMs. Shahzadi et al. (2021a) proposed Hamacher interactive hybrid weighted averaging AOs under FF numbers. It is stated that recommended operators have inefficiency, constraint, monotony, homogeneity characteristics and shear invariance. They are flexible and powerful operators that appropriately describe imprecise information in complex situations. In real-world circumstances, DMs frequently consider diverse criteria prioritization. Then, FF Hamacher prioritized AOs are suggested by Jan et al. (2021) to cope with this situation. Niu et al. (2022) presented Fermatean Cubic Fuzzy Sets Hamacher weighted averaging AOs under a Fermatean Cubic Fuzzy Environment. Ruan and Chen (2023) proposed probabilistic interval-valued hesitant FF Hamacher weighted averaging and geometric AOs in reducing carbon emissions of manufacturers in the supply chain.

3.4.3 Yager AOs

Combining the important features of FFS with the Yager operator, six new operators are proposed: FF Yager weighted average, FF Yager ordered weighted average, FF Yager hybrid weighted average, FF Yager weighted geometric, FF Yager ordered weighted geometric and FF Yager hybrid weighted geometric AOs (Garg et al. 2020). These AOs show more accurate outcomes when they are implied in real-life FFS-integrated MCDM problems.

3.4.4 Hamy mean AOs

The Hamy mean AOs are one of the popular operators included in IFSs (Xu 2020) and PFSs (Wei et al. 2019) implementations. It is an adaptive and comprehensive approach to deal with complex and inconsistent data, with its main advantage being that these operators consider the interrelationships between fuzzy numbers. Therefore, it has been applied to the FFS environment (Chakraborty and Saha 2022). It has been seen that three studies are using this operator in the FFS literature, and it is predicted that it will increase in the future.

3.4.5 Einstein AOs

Einstein AOs are a simple and creative approach to tackling decision-making problems. In the FFS literature, some Einstein AOs have been established as an improvement of algebraic operators like FF Einstein weighted averaging, FF Einstein ordered weighted averaging, generalized FF Einstein weighted averaging, and generalized FF Einstein ordered weighted averaging operators (Akram et al. 2020).

3.4.6 Dombi AOs

Dombi AOs, developed by Dombi (1982), provide a flexible concatenation operator thanks to its flexible parameter, which is the main advantage of these operators. It is aimed to create a more sensitive structure by using Dombi AOs on FFSs. Shit and Ghorai (2021) proposed FF Dombi weighted averaging operator, FF Dombi ordered weighted averaging operator, FF Dombi weighted geometric operator, and FF Dombi ordered weighted geometric operator.

3.4.7 Power AOs

Power AOs use a nonlinear weighted average aggregation tool that allows the input arguments to support each other (Peng and Selvachandran 2019). In the FFS literature, two studies proposed FF weighted power average operator and FF weighted power geometric operators with algebraic AOs (Luo and Liu 2022).

3.4.8 Aczel-Alsina AOs

Rong et al. (2022) proposed cubic FF Aczel-Alsina AOs in the selection of the old chain logistics distribution center. They aimed to flexibly integrate the cubic FF information. This presented operator can directly combine cubic FF information, but it is a limitation that it does not consider how the evaluation criteria are related to each other.

3.4.9 Schweizer–Sklar AOs

Schweizer–Sklar AOs are flexible operators to aggregate information. Wei et al. (2022) proposed FF Schweizer–Sklar weighted averaging operator, FF Schweizer–Sklar weighted geometric operator for green supplier selection problem based on four DMs.

3.4.10 Maclaurin symmetric mean AOs

These operators can capture interrelationships between multi-input criteria via variable parameters. In this way, they make the decision-making processes more realistic. Liu et al. (2022) proposed a new FF Archimedean copula-based Maclaurin symmetric mean operator based on three DMs for renewable energy source selection.

3.4.11 Frank AOs

These operators compensate for the lack of algebraic operations by providing more flexibility and robustness in the information aggregation process and can model decision-making problems more appropriately; hence they are introduced by Tan et al. (2022) for combining FF information.

3.4.12 Heronian mean AOs

The Heronian mean AO is an aggregation approach developed to deal with exact numeric values and is an important operator as it can capture the correlations of the combined arguments. Rani et al. (2022b) proposed FF weighted generalized geometric Heronian mean AO and presented an application on food waste treatment technology selection. Mishra et al. (2023b) applied interval-valued FF Heronian mean AOs to evaluate urban climate change policy alternatives for transportation.

3.4.13 Bonferroni mean AOs

This operator differs from other classical tools such as arithmetic, geometric, and harmonic in that it reflects the interrelationship between any arguments. In this way, it appears as a useful operator in decision-making applications. Wang et al. (2019) and Chakraborty and Saha (2023) proposed Archimedean Bonferroni mean AOs in Hesitant FF environment.

Upon examination of the FFS literature, it becomes apparent that a diverse range of 13 different AOs are employed within the FF environment. However, it is noteworthy that these operators may overlook the flexibility of the information aggregation process. To advance the field of FFS, future studies would greatly benefit from placing increased emphasis on the development and exploration of innovative operators. The subsequent sub-section will delve into the limitations and benefits associated with these AOs, shedding light on areas for further improvement and advancement within the realm of FFS.

3.4.14 Advantages and limitations of the fermatean fuzzy AOs

The effectiveness of AOs in integrating information within the context of FFS is well-established. Table 6 presents a comprehensive overview of FFS aggregation operators, offering insights into their properties, advantages, and limitations. This valuable resource serves as a guide for selecting the most suitable FFS addition operator when addressing decision-making problems.

Table 6 Properties, Advantages and Limitations of the Fermatean Fuzzy AOs
Full size table

3.5 FF linguistic sets

Linguistic variables play a significant role in managing the complexity and difficulty of the data collection process, particularly in decision-making scenarios (Akram et al. 2022e). FFLSs are a recent extension of the FFSs and fuzzy linguistic approach, designed to manage comparative linguistic expressions. In this section, linguistic sets used in decision-making problems in the FFS literature are examined and detailed to answer RQ6. Figure 6 provides an overview of the most used FFLSs in the FFS literature, which can serve as a useful reference for researchers and practitioners seeking to leverage the power of linguistic sets in their decision-making efforts.

Fig. 6
figure 6

Most commonly used FFLSs

Full size image

Within the literature on FFS, several researchers have proposed different linguistic scales for decision-making purposes. The most commonly employed linguistic scale is the 9-point scale, as indicated by studies (Keshavarz-Ghorabaee et al. 2020; Verma 2021; Gul et al. 2021; Biswas et al. 2021; Simic et al. 2022a; Akram et al. 2022e; Ayyildiz 2022; Kao et al. 2022; Chakraborty and Saha 2022, 2023; Erdogan and Ayyildiz 2022; Bouraima et al. 2023; Gao et al. 2024; Yang et al. 2024). Additionally, the 5-point linguistic scale has been utilized in various papers (Wang et al. 2019; Akram et al. 2020; Gonzales et al. 2022a; Simic et al. 2022b; Kirisci et al. 2022; Karuppiah et al. 2022; Ilieva and Yankova 2022; Mateen et al. 2023; Karuppiah and Sankaranarayanan 2023; Moktadir and Ren 2023a; Golui et al. 2024). Some authors opted for a 7-point linguistic scale for FFS applications, as evidenced by studies mentioned (Liu et al. 2019a, b; Akram et al. 2022c; Aro et al. 2022; Gonzales et al. 2022b; Chen et al. 2022; Zeng et al. 2023a; Deveci et al. 2023b; Görçün et al. 2023b). Furthermore, a 10-point linguistic scale was employed by Ruan and Chen (2023), Rao and Sujatha (2023), Chang et al. (2023), Rani et al. (2022b) and Mishra et al. (2022b), while Tan et al. (2022) and Wei et al. (2022) utilized an 11-point linguistic scale. Notably, Simic et al. (2022a) employed a combination of scales, using a 5-point scale to distinguish experts, a 7-point scale to evaluate criteria importance, and a 9-point scale to assess alternatives. Kirisci et al. (2022) applied a 5-point scale to calculate the weights of experts and criteria, and a 10-point scale was used to evaluate alternatives.

Linguistic sets play a crucial role in decision-making by providing a means to express and quantify subjective judgments and preferences. They enable DMs to describe and evaluate criteria, alternatives, and expert opinions using linguistic terms rather than precise numerical values. Linguistic sets bridge the gap between qualitative and quantitative assessments, allowing for a more intuitive and human-centric approach to decision-making (Herrera-Viedma et al. 2021). By incorporating linguistic sets, DMs can capture the nuances and uncertainties inherent in complex decision problems, leading to more accurate and meaningful results.

The utilization of proposed linguistic scales in decision-making problems serves the purpose of determining expert weights, evaluating criteria, and assessing alternatives (Akram et al. 2022d). The selection of a FF language scale depends on the specific decision-making context and the desired level of granularity for criteria evaluation. While scales such as the 9-point, 10-point, or 11-point provide greater detail and expressive capability, they can become time-consuming when dealing with a large number of criteria (Herrera-Viedma et al. 2021). On the other hand, the 5-point scale offers ease of use and is suitable for simpler decision-making scenarios, although it may lack the ability to differentiate adequately between different preference levels. In this regard, the 7-point scale strikes a balance between other scales, offering a practical compromise between detail and simplicity. The choice of an appropriate Fermatean fuzzy language scale should be based on the specific requirements of the decision-making problem at hand, taking into consideration the trade-offs between level of detail and computational complexity.

3.6 FFS comparison with IFS and PFS

In decision-making, choosing the appropriate type of fuzzy set is critical and requires careful analysis of the specific application and nature of the data. Different types of fuzzy sets, such as IFS, PFS, and FFS, offer distinct advantages and disadvantages depending on the problem at hand. Therefore, it is essential to consider the technical concepts of FFS and compare the different types of fuzzy sets to determine the most suitable one. To address RQ8, this section provides an overview of the comparison between FFS, IFS and PFS.

Table 7 provides a comprehensive comparison of IFS, PFS, and FFS, highlighting their respective strengths and weaknesses. In the existing literature, numerous studies employing integrated FFS methods have conducted comparisons between their proposed FFS-based approaches and the IF and PF approaches. These comparative analyses have consistently highlighted the advantages of FFS, particularly in domains characterized by significant uncertainty, such as risk assessment. Making the right choice of fuzzy set can significantly impact the accuracy and effectiveness of decision-making processes. Therefore, DMs should thoroughly evaluate their options and select the most appropriate fuzzy set for their specific needs.

Table 7 IFS, PFS and FFS comparison
Full size table

4 Thematic analysis

In addressing RQs 1 to 8, this section now turns its focus to respond to RQ9 through a thematic analysis facilitated by the Bibliometrix tool. Designed as an open-source R-tool, Bibliometrix serves as a robust instrument for comprehensive science mapping analysis, offering a suite of tools tailored for quantitative research in bibliometrics and scientometrics (Aria and Cuccurullo 2017). This analysis adheres to a recommended workflow, employing bibliometric methodologies to gather valuable insights from the vast landscape of FFS literature. Thematic maps, a product of this analytical process, are generated by scrutinizing co-occurrence networks of keywords, authors, or journals. Leveraging various algorithms and statistical methods, these maps unveil clusters of related items, painting a vivid picture of the thematic landscape in a visual format. By interpreting these maps, this section endeavors to discern research trends, identify hot topics, and shed light on emerging areas within the realm of FFS (Aras and Büyüközkan 2023).

In this analytical pursuit, thematic maps derived from both author keywords and titles are presented, each offering distinct lenses through which to understand the key themes in FFS literature. The decision to juxtapose these maps stems from the recognition that author keywords and titles encapsulate the nuanced perspectives of researchers. Author keywords, selected with precision, serve as deliberate indicators of core themes and research contributions, providing a direct reflection of authors' intended concentrations. In contrast, article titles, while also reflective of main themes, may adopt a more encompassing approach for broader appeal.

The comparative analysis of these thematic maps unfolds as a methodical exploration. Thematic maps based on author keywords often reveal a higher degree of consistency and repetition, signifying recurring core concepts across diverse articles. This consistency underscores the thematic depth and emphasis on specific dimensions within FFS research. Conversely, titles exhibit a propensity for variation in wording, capturing a broader spectrum of perspectives and emphasizing different facets of the research. This divergence in titles mirrors the diversity of thought and approaches encapsulated within the broader discourse on FFSs. Together, this comparative examination not only enriches our understanding of prevalent themes but also highlights the multifaceted nature of how FFS literature is framed and presented by its contributors. The maps are provided in the following page in Figure 7 and 8.

Fig. 7
figure 7

Thematic map derived from author keyword via Bibliometrix tool

Full size image
Fig. 8
figure 8

Thematic map derived from Titles of the FFS publications via Bibliometrix tool

Full size image

The interpretation of thematic maps hinges on two key metrics: centrality and density. Centrality illuminates the importance of a theme by assessing its connections within the network—high centrality denotes a pivotal theme with widespread connections, while low centrality signifies more specialized or peripheral concepts. Density gauges the cohesion among themes, indicating the degree of interconnectedness—high density reflects closely related themes forming cohesive clusters, while low density suggests diverse or distinct subfields. Analyzing both metrics concurrently unveils nuanced insights; high centrality coupled with high density highlights central themes tightly interconnected, high centrality with low density points to central themes with specialized subtopics, low centrality with high density indicates related but not necessarily central themes, and low centrality with low density suggests isolated or less interconnected themes. This comprehensive approach facilitates the identification of hub and peripheral themes, providing a holistic understanding of the thematic composition within a research field.

The identified Basic Themes, namely "fermatean fuzzy sets" and "MCDM," stand out with high centrality in the thematic analysis of FFS literature. Positioned strategically in the fourth quadrant, these Basic Themes signify their foundational importance and specialized focus within the broader FFS discourse. "Fermatean fuzzy sets" represent the core conceptualization, while "MCDM" underscores the integral role of Multiple Criteria Decision Making methodologies in the context of FFS (Senapati and Yager 2019a; Aydin 2021; Akram et al. 2022a; Narayanamoorthy et al. 2022).

On the other hand, Motor Themes, characterized by their high centrality and cohesive influence, emerge as pivotal contributors to the thematic landscape. Themes like "decision-making," "uncertainty," and “covid-19” stand out as central elements with specialized subtopics, underscoring their foundational role in FFS research. The former acknowledges the contemporary context of decision-making amidst the challenges posed by the COVID-19 pandemic, showcasing the adaptability of FFS in addressing real-world scenarios (Garg et al. 2020; Akram et al. 2020; Alsattar et al. 2022). The second group, featuring "aggregation operators" and "MADM," further reinforces the Motor Themes category. Positioned in the first quadrant, these themes exhibit high centrality and cohesive influence, indicating their pivotal roles in the overall thematic landscape. "Aggregation operators" and "MADM" are essential components that contribute to the robustness and applicability of FFS models, showcasing their influence in decision-making scenarios (Aydemir and Gunduz 2020; Garg et al. 2020; Hadi et al. 2021; Akram et al. 2022c, e; Chakraborty and Saha 2023).

The thematic analysis further unveils Niche Themes within the FFS literature, revealing distinctive elements that contribute to the nuanced understanding of the field. The first group encompasses "Pythagorean fuzzy set" and "transportation," positioned in a manner that distinguishes them as themes with a specialized focus. These Niche Themes occupy spaces in the thematic map that suggest their relevance in specific subtopics within FFS research. "Pythagorean fuzzy set" and "transportation" contribute to the diversity of topics explored in the literature, demonstrating their specialized roles within the broader thematic landscape (Akram et al. 2022f, g; Saikia et al. 2023). In the second group, "regret theory" emerges as another Niche Theme, reflecting a specialized area of investigation with a unique focus. Positioned strategically on the thematic map, this theme indicates its importance in addressing specific aspects of regret theory within the context of FFS (Niu et al. 2022; Fahmi et al. 2023a). As a Niche Theme, "regret theory" contributes to the depth and diversity of perspectives within the FFS literature. A third group, intriguingly positioned in the middle ground between Emerging and Niche Themes, includes "SWARA" and "2-Tuple linguistic fuzzy set." (Akram and Niaz 2022; Akram et al. 2022c; Akram and Bibi 2023) These themes are represented by smaller squares on the map, underscoring their status as distinctive but potentially evolving concepts. Placed at the intersection of Emerging and Niche Themes, "SWARA" and "2-Tuple linguistic fuzzy set" signify areas of exploration that are gaining attention but may still be in the early stages of development within the FFS literature.

Within the emerging trends of FFS literature, two distinct groups stand out, providing valuable insights into the evolving facets of the field. The first small group centers around "distance measure," positioning itself as an emerging theme with unique characteristics (Deng and Wang 2022; Ganie 2022; Kirisci 2023). This theme suggests a growing interest and exploration within the FFS literature, indicating an emerging discourse around the measurement of distances within the context of FFSs. In the second small group, strategically positioned between Basic Themes and Emerging Themes, "fermatean fuzzy number" takes center stage (Senapati and Yager 2019a; Fahmi et al. 2023a, b). This theme signifies a nuanced exploration that bridges foundational concepts with emerging perspectives. Its placement suggests that "fermatean fuzzy number" is gaining recognition as a concept of interest within the evolving landscape of FFS literature.

The analysis of the thematic map based on Titles provides a distinct perspective on the thematic landscape of FFS literature, emphasizing application areas and specific topics that researchers have prioritized in their studies. In this context, the inclusion of "fermatean fuzzy sets" and "fuzzy" themes within the Motor Themes section aligns logically with the foundational nature of these concepts, signifying their recurring prominence across various studies. The thematic emphasis on application areas becomes particularly pronounced in the Motor Themes section. This clustering suggests a concerted effort within the FFS literature to explore and apply FFSs in practical contexts related to waste management, risk assessment, and supply chain optimization (Aro et al. 2022; Alkan and Kahraman 2022; Saha et al. 2023; Deliktaş et al. 2023; Farid et al. 2023). The inclusion of these application areas underscores the versatility and adaptability of FFS models in addressing real-world challenges. Moving to the Basic Themes, the thematic focus extends to critical topics such as Covid-19, environmental studies, and sustainability studies in industries. This thematic clustering reflects a broader exploration of FFSs in contexts related to global challenges, public health, and environmental sustainability (Saraji et al. 2021; Baranidharan et al. 2022; Farid et al. 2023). It indicates a recognition within the literature of the potential of FFS models to contribute to decision-making processes in complex and dynamic scenarios. In the thematic analysis, "healthcare" and "assessment of barriers and challenges" emerge prominently as part of the Emerging Themes. The recognition of these themes highlights ongoing exploration and growing interest in applying FFS models to healthcare contexts and understanding the barriers and challenges associated with their implementation. Such explorations contribute to the depth and specificity of FFS research, showcasing its relevance in addressing sector-specific complexities.

In this section, our exploration delves deeper into the thematic landscape of FFS literature, moving beyond the descriptive analysis provided by relevant words. By interpreting thematic maps derived from author keywords and titles, we aim to uncover nuanced insights that go beyond surface-level trends. Building on this thematic understanding, the subsequent section will address RQ10, focusing on identifying gaps and proposing future directions in FFS research.

5 Gaps and future directions

Within the thematic analysis, several emerging themes have surfaced, contributing to the evolving landscape of FFS literature. These themes encompass diverse areas such as distance measure calculation with FFS, computations involving FFNs, the extension of FFS with the 2-Tuple linguistic model, and the application of FFS in healthcare, particularly in the assessment of challenges and barriers.

Distance measure calculation, a pivotal aspect in this thematic exploration, serves as a practical tool for quantifying the deviation between two sets or variables (Zeng et al. 2023b). This process holds significance as it constitutes a core step in various decision-making methods. In the context of MCDM, distance measures play a crucial role in evaluating and comparing alternatives. They enable DMs to assess alternatives based on their proximity to an ideal solution or their distance from undesirable outcomes. The calculation of distances between alternatives and reference points empowers DMs to identify the most suitable options according to their preferences and constraints. Accordingly based on the review some potential future RQs (FRQs) are generated based on the emerging themes:

  • FRQ1: What adaptations or modifications are needed in existing distance measures to effectively integrate FFSs, and how can these modifications enhance the precision and applicability of FF decision-making methods?

  • FRQ2: How can FFSs be tailored to address the unique challenges posed by distance measures in medical diagnosis, ensuring accurate and reliable outcomes in fuzzy decision-making frameworks?

  • FRQ3: In extending FFSs with the 2-Tuple linguistic model, what specific linguistic representations and methodologies prove most effective in addressing vagueness and uncertainty in decision-making scenarios?

  • FRQ4: How can FFSs be optimally applied in healthcare decision-making to overcome challenges and barriers, and what specific insights can be derived from such applications for broader interdisciplinary contexts?

This section delineates potential avenues for future research identified through the interpretation of thematic maps. Additionally, it systematically explores and presents the identified gaps corresponding to each RQs from 2 to 8 in a coherent and interconnected manner.

5.1 From the perspective of applied MCDM methods in FFS

The TOPSIS and CRITIC methods are the most frequently used methods in the literature. Generally, FFS integration to the existing MCDM methods targets the following key benefits (Keshavarz-Ghorabaee et al. 2020; Gul 2021; Aro et al. 2022; Simic et al. 2022a; Narayanamoorthy et al. 2022):

  1. o

    Improved accuracy,

  2. o

    More flexibility,

  3. o

    Enhanced transparency,

  4. o

    Faster decision-making.

These four main aims are valid for all FFS-MCDM integration. The FFS integration enables to handle decision-making problems with multiple criteria and imprecise information. However, there are still some gaps in the literature.

First, in the literature there is a lack of comparative studies that compare the performance of different integrated MCDM methods with FFS. This results in a difficulty for evaluating the effectiveness and suitability of these novel integrated methods.

Second, there is a lack of consideration for dynamic decision-making. Most of the case studies focus on static decision making, in which the decision-making is based on predetermined information. But, in today’s world, under constantly changing conditions, the flexibility in decision-making become prominent for effectiveness and resilience (Keshavarz-Ghorabaee et al. 2018; Peng et al. 2023). Thus, future research areas for FFS MCDM integration should address these needs.

The third one is the limited applicability. As stated in the previous sub-section, most of the numerical studies are based on hypothetical decision-making problems. There is a lack to prove the effectiveness of FFS-MCDM integration in real world scenarios. Most of the existing studies use a small number of datasets or synthetic datasets, which may not be representative of real-world scenarios. Accordingly, future researchers should focus to adapt hypothetical decision-making problems to the real-world changing environments. In this context, dynamic decision-making models may also help to ameliorate real world applications. In light of the identified understudied areas within FFS literature, here are our proposed FRQs:

FRQ5: How does the performance of integrated MCDM methods with FFS compare across different decision-making scenarios, and what criteria can be established to effectively evaluate the efficacy and suitability of these integrated approaches?

FRQ6: In the context of FFS integrated with MCDM, how can dynamic decision-making considerations be incorporated to enhance flexibility and adaptability under constantly changing conditions, ensuring the effectiveness and resilience of decision-making processes in real-world applications?

5.2 From the perspective of FFS Extensions

The FFS extensions are generated to create more flexible and transparent decision-making environments (Lai et al. 2022). In the literature ordinary FFS are highly studied. Considering the new emergence of the FFS subject, it is normal that most of the studies concentrate on ordinary FFS; however, ordinary FFS also has some drawbacks to be addressed such as precise value of membership and non-membership. In real-world decision problems, the hesitancy for assigning a membership or non-membership value also should be represented during decision-making (Deng and Wang 2021; Ilieva and Yankova 2022). Consequently, future researchers should focus on interval-valued FFS or hesitant-FFS to address these gaps in the literature.

Furthermore, linguistic decision-making can also be a prominent solution to obtain flexible and transparent decision-making process. The interpretability of the results with linguistic variables may also facilitates understanding and exposition of the results. Hence, linguistic extension for FFS is also a critical area for future studies. In light of the identified understudied areas within FFS literature, here are our proposed FRQ:

FRQ7: How can future research enhance decision-making processes by integrating interval-valued Fermatean Fuzzy Sets or hesitant-FFS, along with linguistic extensions, to address challenges related to precise values in real-world scenarios?

5.3 From the perspective of AOs

AOs are essential for FFS decision-making frameworks. They help to combine the information without any other techniques are involved. Various AOs are generated as mentioned in Sect. 4.2; yet some literature gaps still exist.

Majority of existing literature concentrates on AOs that work under static environments (Biswas et al. 2021; Simic et al. 2022c; Niu et al. 2022; Chen et al. 2022; Lai et al. 2022; Mishra et al. 2022b). As aforementioned the need for dynamic decision-making is crucial to better reflect the real-world problems (Peng et al. 2023). So, future studies may focus on generating dynamic AOs where the degree of membership may change over time, and dynamic aggregation operators may be necessary to account for these changes.

Finally, there is a gap for GDM approaches in FFS area. The GDM approach is a very prominent approach to reach an unbiased, objective decision-making process. AOs plays an important role to combine different opinions coming from multiple group members. There exist limited studies focusing on GDM approaches. For future studies researchers may address this lack of GDM approaches in FFS area. In light of the identified understudied areas within FFS literature, here are our proposed FRQ:

FRQ8: How can future research advance FFS decision-making frameworks by developing dynamic AOs that accommodate changes in the degree of membership over time, addressing the current literature gap in dynamic environments?

5.4 From the perspective of linguistic sets

Making decisions and evaluations in the light of linguistic variables provides a much easier decision-making process for DMs. Working with linguistic sets that the DM feels comfortable with is an important factor for the efficiency and accuracy of the decision-making process (Herrera-Viedma et al. 2021). In the FFS literature, there exist limited propositions for use of different linguistic sets.

First, there is a lack of comparative studies where each case uses different granulated linguistic sets. This gap prevents to compare the efficiency of various linguistic sets. Future researchers may address this gap and try to generate use of various linguistic sets by concerning the linguistic uncertainty.

The linguistic uncertainty is also a critical point in linguistic sets. Although FFS linguistic sets have been proposed to handle linguistic information, most of the existing literature has focused on modeling the degree of membership to a linguistic term and has not considered linguistic uncertainty or vagueness. This is an important limitation, as linguistic uncertainty can arise due to ambiguity, imprecision, or context-dependence of linguistic terms (Herrera-Viedma et al. 2021).

Finally, GDM approach is also noticeable for the perspective of linguistic sets. As aforementioned, GDM is based on combining individual DM assessments or reaching a consensus which is acceptable for every DM. During this process, DMs with various backgrounds and experiences try to make their evaluations for a certain subject. This variety of background and experience may complicate the decision-making process. Accordingly, future researchers should focus on diminishing this complexity by generating integration of different granulated linguistic sets in FFS environment. For that purpose, maybe integration of 2TL Model’s Linguistic Hierarchy Approach (Espinilla et al. 2011) to FFS environment can be a valuable proposition. In light of the identified understudied areas within FFS literature, here are our proposed FRQ:

FRQ9: How can future research address the existing gaps in FFS literature regarding linguistic sets, considering linguistic uncertainty, and fostering efficient GDM by integrating diverse granulated linguistic sets, potentially exploring the integration of the 2-Tuple Linguistic Model's Linguistic Hierarchy Approach in the FFS environment?

Summarizing understudied areas in FFS literature, the table below, curated by the authors, serves as a concise reference for future research. Complementing proposed FRQs, these identified areas offer a focused starting point for further scholarly exploration (Table 8).

Table 8 Summary of understudied areas in FFS literature providing a basis for future research directions
Full size table

6 Conclusions

The theory of FFS holds significant significance across diverse domains, offering a valuable framework for handling uncertain and ambiguous information. However, despite its advantages, there has been a lack of comprehensive analysis concerning key areas, applications, research gaps, and outcomes related to FFS. Consequently, this study aims to address this gap by conducting a systematic analysis of existing literature on FFS. The primary objectives are to assess current trends, identify research gaps within the field of FFS, and contribute to the development of a future research agenda in this area.

Since the family of IFSs and the family of q-rung orthopair fuzzy sets exhibit isomorphism, the exploration of individual variations within the IFS concept can be readily transformed into an analogous method employing FFSs, and vice versa (Peng and Luo 2021). Consequently, the interchangeability between IFSs and FFSs allows for a seamless translation of methodologies. It has been observed in the reviewed literature that these techniques, which can easily transition between each other, also exhibit certain advantages and weaknesses when compared to one another. In many articles, it has been noted in the discussions that FFS, particularly, better captures uncertainty compared to the mentioned IFS and PFS methods. Additionally, as seen in the surveyed literature, techniques that allow for seamless transitions between these methods possess specific strengths and weaknesses relative to one another. FFS, in particular, has been highlighted in the comments of several articles for its superior reflection of uncertainty compared to IFS and PFS methods (Akram et al. 2022a; Chakraborty and Saha 2023; Fahmi et al. 2023a).

This study adopts a SLR approach to delineate future research areas in the FFS domain. Commencing with a descriptive bibliometric analysis, we illuminate current trends in FFS literature. The subsequent review, guided by specific RQs detailed in the Introduction section, navigates through integrated methodologies and their applications (RQs 2–3), FFS extensions (RQs 4–5), AOs for FFS (RQ 6), FFS linguistic sets (RQ 7), and the comparative analysis with IFS and PFS (RQ 8). Employing the Bibliometrix tool, we conduct a thematic analysis to address RQ 9, revealing salient themes. Building on these themes, we define future directions and identify gaps in the FFS literature, answering RQ 10 comprehensively.

The exploration of FFS in this study uncovers pivotal research avenues, paving the way for the evolution of fuzzy decision-making methods. The formulated FRQs accentuate the necessity for nuanced modifications in existing distance measures to seamlessly integrate FFS, bolstering precision and applicability. A focal point emerges in the tailored application of FFS in medical diagnosis, ensuring accuracy within the complex landscape of fuzzy decision-making frameworks. The extension of FFS with the 2-Tuple linguistic model introduces FRQs probing the most effective linguistic representations and methodologies to navigate vagueness and uncertainty. A critical consideration is the optimal application of FFS in healthcare decision-making, offering insights to surmount challenges and barriers, with broader implications for interdisciplinary contexts. These future directions serve as a comprehensive inference from the thematic analysis, while additional FRQs are defined for each perspective explored in the review of FFS literature, encompassing AOs for dynamic decision-making and the integration of interval-valued and linguistic values under FFS for more precise decision-making.

Despite its significant contributions, this study is not without limitations. The research scope is confined to databases such as WoS and Scopus, potentially excluding relevant studies from other databases. The Q1 and Q2 journals from these databases are used to review. Furthermore, the inclusion criteria are limited to articles, excluding conference papers, books, and theses. The study's scope is also constrained to English-language publications. These limitations should be acknowledged when interpreting the findings.

The formulated FRQs generated in this study encourage researchers to contemplate the generalization of FFSs for effective adaptation to real-world applications with extensive datasets. Additionally, emphasizing specific application areas and crafting FFS-based solutions tailored to these domains could prove valuable for practical, real-world implementations. Moreover, the swift growth of studies in the FFS field, as evident in Fig. 2, underscores the imperative for employing methods like PageRank analysis in upcoming research to conduct more intricate analyses.