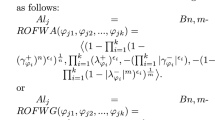Multiattribute decision-making under Fermatean fuzzy bipolar soft framework

Abstract

Fermatean fuzzy set theory is emerging as a novel mathematical tool to handle uncertainties in different domains of real world. Fermatean fuzzy sets were presented in order that uncertain information from quite general real-world decision-making situations could be mathematically tractable. To that purpose, these sets are more flexible and reliable than intuitionistic and Pythagorean fuzzy sets. This paper presents a novel hybrid model, namely, the Fermatean fuzzy bipolar soft set (FFBSS, in short) model as a general extension of two powerful existing models, that is, fuzzy bipolar soft set and Pythagorean fuzzy bipolar soft set models. Some fundamental properties of the proposed FFBSS model, namely, subset-hood, equal FFBSSs, relative null and relative absolute FFBSSs, restricted intersection and union, extended intersection and union, AND operation and OR operation are investigated along with numerical examples. In addition, certain basic operations, including Fermatean fuzzy weighted average and score function of FFBSSs are proposed. Furthermore, two applications of FFBSS are explored to deal with different multiattribute decision-making situations, that is, selection of best surgeon robot and analysis of most affected country due to COVID-19 (‘CO’ stands for corona, ‘VI’ for virus, ‘D’ for disease, and ‘19’ stands for its year of emergence, that is, 2019). The proposed methodology is supported by an algorithm. At the end, a comparison analysis of the proposed hybrid model with some existing models, including Pythagorean fuzzy bipolar soft sets is provided.

1 Introduction

In the last few decades, several researchers and decision-makers have been introduced different mathematical tools (that is, models and their hybrid structures) to cope with fuzziness and uncertainty in different domains of real-life, including physical sciences, medical sciences and engineering. Zadeh (1965) was the first who initiated a magical tool to deal with ambiguity and uncertainty, namely, fuzzy set (FS) theory. FS theory has shown meaningful applications in several real-world problems. Many multiattribute decision-making (MADM) problems have been solved by FS theory (see Chen and Jong 1997; Chen and Niou 2011; Chen et al. 2009; Chen and Wang 2010; Lin et al. 2006). In a FS $\eta$, for any object $\vartheta$ of the universe, it has one membership degree, i.e., ${0\le {\eta (\vartheta )}\le 1}$, which could not always be fit to solve some MADM problems.

For handling this critical situation, Atanassov (1986) proposed intuitionistic fuzzy set (IFS) model which is the natural generalization of FS theory. Several fruitful researches based on IFS theory have been completed in different domains of science (Chen and Randyanto 2013; Chen et al. 2016; Liu et al. 2020; Zeng et al. 2019; Zhang 2020; Zou et al. 2020). In an IFS, all the objects of the universe are characterized by both the membership and nonmembership degrees, whose sum is always bounded by 1. However, if their sum is greater than one, then the IFS will no longer be able to tackle such situation. Therefore, to remove this deficiency, a novel concept was developed by Yager (2013a, 2013b), namely, the Pythagorean fuzzy set (PFS) as a generalization of IFS. It is a very efficient mathematical tool for handling the vagueness and imprecision in data.

After the production of PFS model, it has gained a lot of attention from many experts and researchers of the domain. For instance, Yager and Abbasov (2013) discussed about the connection among the Pythagorean membership grades (PMGs) and complex numbers. Zhang and Xu (2014) originated a generalized Pythagorean fuzzy TOPSIS(that is, Technique for Order of Preference by Similarity to Ideal Solution) model to tackle different MADM situations involving Pythagorean fuzzy information. Moreover, it has rich potential applications in many field, such as service quality of domestic airline, decision-making and so on. But, in several problems, PFS approach could not be accepted. For instance, consider an experts team were invited to give their opinion on the army training institutes, and they were divided into two groups. The first group of experts expresses the degree of membership as 0.9, while the second group of experts expresses the degree of nonmembership as 0.8. It is clearly seen that ${{0.9}^2}+ {{0.8}^2}$ is greater than one. This situation could not be illustrated by the IFS and PFS.

To tackle this complexity, Senapati and Yager (2020) originated the notion of Fermatean fuzzy sets (FFSs) as an extension of the IFSs and PFSs. In a FFS, cubic sum of membership and nonmembership values of an object bounded by 1. Currently, FFS theory is playing a vital role in various domains because it is a strong concept to deal with imprecise and vague information in Fermatean fuzzy environment. To illustrate this claim, suppose that some old men are enduing their opinion to youngsters about the society, half group of old men is giving a degree to traditional society as 0.77 and the other half is giving a degree to modern society as 0.87. It can be readily seen that ${{0.77}}+ {{0.87}}\nleq 1$ and ${{0.77}^2}+ {{0.87}^2}\nleq 1$ but ${{0.77}^3}+ {{0.87}^3}\le 1$. Thus, FFS model is more flexible than IFSs and PFSs (see Fig. 1).

Till today, a number of researches have been done which are purely based on FFSs. For instance, Liu et al. (2019b) originated the notion of Fermatean fuzzy linguistic term set (FFLTS). Senapati and Yager (2019b) discussed some new operations over Fermatean fuzzy numbers. The concept of decision-making analysis based on Fermatean fuzzy Yager aggregation operators (with application in COVID-19 testing facility) was studied by the Garg et al. (2020). Yang et al. (2020) discussed the differential Calculus of Fermatean fuzzy functions. Shahzadi and Akram (2021) developed a novel decision-making concept to select an antivirus mask under Fermatean fuzzy soft information. In addition, Akram et al. (2020b) proposed a novel decision-making framework for the selection of an effective sanitizer to reduce COVID-19 under Fermatean fuzzy environment. Liu et al. (2019a) proposed the concept of distance measure for Fermatean fuzzy linguistic term sets based on linguistic scale function which is illustrated by the TODIM and TOPSIS methods.

Traditional mathematical tools such as FS, IFS, and interval set theories are not considered to be very effective mathematical tools for dealing with uncertainty and vagueness in some certain situations. The reason for these difficulties is, possibly, the inadequacy of the parameterization tool in these theories. Therefore, to remove this deficiency, Molodtsov (1999) introduced the notion of soft set theory which is different from all the existing theories, including FSs and IFSs. Molodtsov also mentioned that soft sets can be combined with existing models dealing with uncertainty to make a hybrid model which acquire the characteristics of all those models by which it is combined. The soft set theory has been used in many fields, including engineering and solved several real-world problems. Maji et al. (2001) offered certain applications of soft sets in decision-making. Ali et al. (2009) discussed several properties of soft set (see also Ali and Shabir 2010).

A wide variety of human decision-making is relying on two sided information, that is, negative side and positive side. For example, in Chinese medicine, Yin and Yang are the two sides. Yin is the positive side, while Yang is the negative side of a system. Motivated by these concerns, Zhang (1994) developed an idea of bipolar fuzzy set model. Like bipolar extension of fuzzy set theory, Shabir and Naz (2013) proposed the concept of bipolar soft set (BSS) as bipolar extension of soft sets. The idea behind the production of BSSs is the existence of parameters having opposite meanings in a decision-making situation. Afterwards, Naz and Shabir (2014) presented the concept of fuzzy BSS and its applications in decision-making. Akram and Ali (2020) developed two novel hybrid models, namely, Pythagorean fuzzy BSSs and rough Pythagorean fuzzy BSSs, and solved some MADM problems. Later on, Akram et al. (2020a) presented two novel MADM models, m-polar fuzzy BSSs and rough m-polar fuzzy BSS. For better understanding about the advantages and limitations of the literature, the readers are suggested to Table 1.

Table 1 Summary of the primary studies

The motivation of the proposed theory can be elaborated as follows:

• The supreme tendency of FFSs to address the inexact human decision make it more feasible and accurate to model two dimensional (i.e., membership and nonmembership) information in more wider space as compared to IFSs and PFSs.

• FFSs are inefficient to depict the bipolarity of parameters involved in a dataset. In a similar manner, Bipolar soft model is not capable to tackle data in Fermatean fuzzy environment. Therefore, there is a need of such hybrid model which have characteristics of both these models.

• The MADM based on FFSs show that the variation in nonmembership values will definitely affect the membership values of the objects.

• Till today two powerful extensions of the bipolar soft set theory have been introduced, namely, fuzzy BSSs (Naz and Shabir 2014) and Pythagorean fuzzy BSSs (Akram and Ali 2020). There is a deficiency in these model, that is, greater values of membership and nonmembership evaluations cannot be taken. Therefore, they can not applied in a situation where datasets contain evaluations in Fermatean fuzzy environment. Thus, there is a necessity of a novel model which not only remove this drawback of existing models but also a generalization of the existing models.

• Inspired by the existing theories of FFSs and BSSs, we present a more generalized model for MADM to cover the deficiencies and imperfections of the existing models. Our proposed model has ability to deal with data in both Fermatean fuzzy and bipolar soft environments.

With these settings, in this paper, a novel hybrid model, namely, FFBSSs is developed as an extension of Pythagorean fuzzy BSS model. Some fundamental properties of the proposed FFBSS model are investigated along with numerical examples. Also, certain basic operations, including Fermatean fuzzy weighted average and score function of FFBSSs are studied. Furthermore, two applications of FFBSSs are explored to deal with different MADM situations. The proposed methodology is supported by an algorithm. In the end, a comparison analysis of the proposed hybrid model with some existing models is provided. For other fruitful notions not explained in the paper, the reader are suggested to Akram and Ali (2021), Akram et al. (2019), Aydemir and Gunduz (2020), Chen and Han (2018), Dutta (2021), Feng et al. (2010), Kumar and Chen (2021a), Kumar and Chen (2021b), Senapti and Yager (2019a), Zhang (2017), Zhang (2020), Akram et al. (2021), Peng et al. (2015), Naz et al. (2018) and Zhang et al. (2020).

The main contributions of this paper are:

• The main objective of this study is to broaden the literature by proposing a new powerful model called Fermatean fuzzy bipolar soft set or FFBSS model by combining the FFSs and BSSs.

• We have proposed some fundamental properties of the developed FFBSS model, including Fermatean fuzzy weighted average and score function. Moreover, we have investigated these properties via numerical examples.

• The proposed MADM strategy is explained with the help of two applications in the field of medical.

• Further, we have spotlighted the merits of our proposed technique to describe its significance and authenticity as compared to some existing decision-making methods.

The rest of the paper is structured as follows. In Sect. 2, we first review the definitions of Fermatean fuzzy soft sets and BSSs, and then present a novel hybrid model called FFBSSs. We also investigate some basic properties of the developed model. In Sect. 3, we explore two applications of our proposed hybrid model to solve MADM problems. In Sect. 4, we study a comparison of the developed model with some existing models. Section 5 provides conclusion and future directions.

2 Fermatean fuzzy bipolar soft sets

This section first retrieves the notions of Fermatean fuzzy soft sets and BSSs, and then presents a novel concept of Fermatean fuzzy bipolar soft set model along with its basic properties.

Definition 1

(Shahzadi and Akram 2021) Let ${\mathcal {V}}$ be a universe of discourse and G be a universe of parameters. Let ${\mathcal {F}}({\mathcal {V}})$ denotes the set of all Fermatean fuzzy subsets of ${\mathcal {V}}$ and $L\subseteq G$. Then, a pair (R, L) is referred as a Fermatean fuzzy soft set (FFSS) on ${\mathcal {V}}$, if R is a function given by $R: L\rightarrow {\mathcal {F}}({\mathcal {V}})$.

Consider $\vartheta \in {\mathcal {V}}$ and $l\in L$, then R(l) is a FFS on ${\mathcal {V}}$, which is defined by

$$\begin{aligned} R(l)=\{\langle \vartheta ,(\eta ^+_R(l)(\vartheta ), \eta ^-_R(l)(\vartheta ))\rangle ~|~\vartheta \in {\mathcal {V}}\}, \end{aligned}$$

where the functions $\eta ^+_R(l)(\vartheta ): L \rightarrow [0,1]$ and $\eta ^-_R(l)(\vartheta ): L \rightarrow [0,1]$ indicate the degrees of membership and nonmembership of the element $\vartheta \in {\mathcal {V}}$, respectively. For simplicity, we consider $F=(\eta _R^+,\eta _R^-)$, a Fermatean fuzzy number (FFN).

Definition 2

(Shabir and Naz 2013) Let ${\mathcal {V}}$ be a universe of discourse and G be the universe of parameters. For every ${\mathcal {B}}\subseteq G$, a triplet $(f,g,{\mathcal {B}})$ is said to be a bipolar soft set or BSS on ${\mathcal {V}}$, where f and g are functions defined as

$$\begin{aligned} f:{\mathcal {B}}\rightarrow \mathcal {P}({\mathcal {V}}) \quad \text{and}\quad g:\lnot {\mathcal {B}}\rightarrow \mathcal {P}({\mathcal {V}}), \end{aligned}$$

such that $f(\vartheta ) \cap g(\lnot \vartheta ) = \emptyset$, $\forall ~\vartheta \in {\mathcal {B}},~\lnot \vartheta \in \lnot {\mathcal {B}}$.

Notice that $\lnot {\mathcal {B}} (\text{Not}~ {\mathcal {B}})$ is the set containing attributes opposite to those contained in ${\mathcal {B}}$.

Fig. 1

Membership grades related to IFSs, PFSs and FFSs (Senapati and Yager 2019b)

The main concept of this study is given in the following definition:

Definition 3

Let ${\mathcal {V}}$ be a universe of discourse and G be a universe of parameters. For any $L\subseteq G$, a triplet (P, Q, L) is referred as a Fermatean fuzzy bipolar soft set or FFBSS over ${\mathcal {V}}$, if the mappings of P and Q are defined as: $P:L\rightarrow {\mathcal {F}}({\mathcal {V}})$ and $Q:\lnot L\rightarrow {\mathcal {F}}({\mathcal {V}})$ with the following conditions:

$$\begin{aligned} 0\le&{(\eta ^+_P(l)(\vartheta ))^3}+{(\zeta ^+_Q(\lnot l)(\vartheta ))^3} \le 1, \end{aligned}$$

(1)

$$\begin{aligned} 0\le&{(\eta ^-_P(l)(\vartheta ))^3}+{(\zeta ^-_Q(\lnot l)(\vartheta ))^3} \le 1, \end{aligned}$$

(2)

for all $l\in L, ~\lnot l\in \lnot L$, and $\vartheta \in {\mathcal {V}}$ where $\lnot L$ represents the ‘Not set of L’, and $\eta ^+_P(l)(\vartheta ),~\eta ^-_P(l)(\vartheta ), ~\zeta ^+_Q(\lnot l)(\vartheta ),~\zeta ^-_Q(\lnot l)(\vartheta )\in [0,1]$. Clearly, $\eta ^+_P(l)(\vartheta )$ and $\zeta ^+_Q(\lnot l)(\vartheta )$ are the membership values with respect to P and Q, respectively.

Similarly, $\eta ^-_P(l)(\vartheta )$ and $\zeta ^-_Q(\lnot l)(\vartheta )$ are the nonmembership values.

Consequently, a FFBSS on ${\mathcal {V}}$ is the combination of two parameterized FFSs on ${\mathcal {V}}$, which satisfy the inequalities (1) and (2). For any $l\in L$, P(l) and $Q(\lnot l)$ are considered as the collections of l-approximate and $\lnot l$-approximate elements of the FFBSS (P, Q, L), respectively. To explain this novel concept, we give an illustrative example below:

Example 1

Let ${\mathcal {V}}=\{\vartheta _1,\vartheta _2,\ldots ,\vartheta _5\}$ be the set of five employees having different office expertise and let $G=\{l_1=\text{{computer expert}}, ~l_2=\text{{time management skills}}, l_3=\text{{good communication skills}},~l_4=\text{{honest}},l_5=\text{{work ethics}}\}$ be the collection of parameters (qualities) for the candidates $\vartheta _i\in {\mathcal {V}},~i=1,2,\ldots ,5$. Let the “Not set of G” be $\lnot G=\{\lnot l_1=\text{{computer inexpert}},~\lnot l_2=\text{{servitude}},~\lnot l_3=\text{{hush communication skills}},~\lnot l_4= \text{{dishonest}},\lnot l_5=\text{{negligent performance}}\}$. For $L=\{l_1=\text{{computer expert}}, ~l_2=\text{{time management skills}},l_5=\text{{work ethic}}\}\subseteq G$, we define a FFBSS (P, Q, L), which describe qualities and dis-qualities of the candidates whom are selected for a particular project. Thus, a FFBSS (P, Q, L) is given by

$$\begin{aligned} P(l_1)=\bigl \{&(\vartheta _1,0.5,0.9), (\vartheta _2,0.7,0.8), (\vartheta _3,0.7,0.9), \\ {}&(\vartheta _4,0.5,0.6), (\vartheta _5,0.9,0.6)\bigr \},\\ P(l_2)=\bigl \{&(\vartheta _1,0.3,0.8), (\vartheta _2,0.6,0.5), (\vartheta _3,0.9,0.5), \\ {}&(\vartheta _4,0.5,0.8), (\vartheta _5,0.5,0.6)\bigr \},\\ P(l_5)=\bigl \{&(\vartheta _1,0.7,0.4), (\vartheta _2,0.6,0.5), (\vartheta _3,0.7,0.9), \\ {}&(\vartheta _4,0.6,0.8), (\vartheta _5,0.2,0.5)\bigr \},\end{aligned}$$

$$\begin{aligned} Q(\lnot l_1)=\bigl \{&(\vartheta _1,0.5,0.1), (\vartheta _2,0.1,0.2), (\vartheta _3,0.2,0.0), \\ {}&(\vartheta _4,0.3,0.6), (\vartheta _5,0.2,0.6)\bigr \},\\ Q(\lnot l_2)=\bigl \{&(\vartheta _1,0.6,0.2), (\vartheta _2,0.1,0.5), (\vartheta _3,0.1,0.5), \\ {}&(\vartheta _4,0.3,0.6), (\vartheta _5,0.4,0.4)\bigr \},\\ Q(\lnot l_5)=\bigl \{&(\vartheta _1,0.3,0.4), (\vartheta _2,0.5,0.5), (\vartheta _3,0.2,0.0), \\ {}&(\vartheta _4,0.3,0.2), (\vartheta _5,0.8,0.4)\bigr \}. \end{aligned}$$

The FFBSS (P, Q, L) can be represented in tabular form given below(see Table 2).

The FFBSS (P, Q, L) on ${\mathcal {V}}$, given by Table 2 can also be represented by Tables 3 and 4.

Now we discuss some basic operations on FFBSSs and illustrate them via corresponding examples.

Table 2 Table for the FFBSS (P, Q, L)

Definition 4

Let $\gamma _1=(P_1,Q_1,L_1)$ and $\gamma _2=(P_2,Q_2,L_2)$ be two FFBSSs over the universe ${\mathcal {V}}$, then $\gamma _1$ is said to be Fermatean fuzzy bipolar soft subset of $\gamma _2$, represented by $\gamma _1\widetilde{\subseteq }\gamma _2$, if

• 1. $L_1\subseteq L_2$,

• 2. $P_1(l)\subseteq P_2(l)$ (i.e., $\eta ^+_{P_1}(l)(\vartheta )\le \eta ^+_{P_2}(l)(\vartheta ),~\eta ^-_{P_1}(l)(\vartheta )\ge \eta ^-_{P_2}(l)(\vartheta )$) and $Q_1(\lnot l)\supseteq Q_2(\lnot l)$ (that is, $\zeta ^+_{Q_2}(\lnot l)(\vartheta )\le \zeta ^+_{Q_1}(\lnot l)(\vartheta ),~\zeta ^-_{Q_2}(\lnot l)(\vartheta )\ge \zeta ^-_{Q_1}(\lnot l)(\vartheta )$) for all $l\in L$, $\lnot l\in \lnot L$ and $\vartheta \in {\mathcal {V}}$.

Note that if $\gamma _2$ is a Fermatean fuzzy bipolar soft subset of $\gamma _1$, then $\gamma _1$ is referred to as a Fermatean fuzzy bipolar soft super-set of $\gamma _2$ and is written as $\gamma _2\widetilde{\subseteq }\gamma _1$.

Table 3 Tabular representation for the parameters L

Table 4 Tabular representation for the “Not set of parameters” $\lnot L$

Example 2

Consider FFBSS (P, Q, L) on ${\mathcal {V}}$ as defined in Example 1, and $L_1=\{l_1=\text{{computer expert}},~l_2=\text{{time management skill}}\}\subseteq L$, we define a FFBSS $(P_1,Q_1,L_1)$, which is represented by Table 5.

From the Definition 4, one can easily verify that $(P_1,Q_1,L_1)\widetilde{\subset } (P,Q,L)$.

The following definition gives the notion of equal FFBSSs.

Table 5 Table for the FFBSS $(P_1, Q_1, L_1)$

Definition 5

Suppose $\gamma _1=(P_1,Q_1,L_1)$ and $\gamma _2= (P_2,Q_2,L_2)$ are two FFBSSs over the universe of discourse ${\mathcal {V}}$. Then, $\gamma _1$ and $\gamma _2$ are said to be equal FFBSSs, if $\gamma _1\widetilde{\subseteq }\gamma _2$ and $\gamma _2\widetilde{\subseteq }\gamma _1$.

Now we provide the concept of complementarity of FFBSSs in the following definition:

Definition 6

Let $\gamma =(P,Q,L)$ be a FFBSS over the universe of discourse ${\mathcal {V}}$. Then, its complement is denoted as $\gamma ^c=(P^c,Q^c,L)$ over ${\mathcal {V}}$, where $P^c:L\rightarrow [0,1]$ and $Q^c:\lnot L\rightarrow [0,1]$ are the mappings which are respectively defined as $P^c(l)(\vartheta )= (\eta ^-_P(l)(\vartheta ),\eta ^+_P(l)(\vartheta ))$ and $Q^c(\lnot l)(\vartheta )= (\zeta ^-_Q(\lnot l)(\vartheta ),\zeta ^+_Q(\lnot l)(\vartheta ))$ for all $l\in L$, $\lnot l\in \lnot L$ and $\vartheta \in {\mathcal {V}}$.

This useful notion illustrates via following example:

Example 3

Suppose $\gamma =(P,Q,L)$ is the FFBSS on the universe ${\mathcal {V}}$ as discussed in Example 1. Then, from Definition 6, its complement $\gamma ^c=(P^c,Q^c,L)$ is given by Table 6.

In the following, two novel notions, namely, relative null FFBSS and relative absolute FFBSS are provided.

Table 6 Table for the complement of FFBSS (P, Q, L)

Definition 7

A FFBSS over ${\mathcal {V}}$ is called a relative null FFBSS and is denoted by $(\Phi ,V,L)$, if $\Phi (l)(\vartheta )=(\eta ^+_{\Phi }(l)(\vartheta ) =0,\eta ^-_{\Phi }(l)(\vartheta )=1)$ and $V(\lnot l)(\vartheta )=(1,0)$ for all $l\in L,~\lnot l\in \lnot L,~\vartheta \in {\mathcal {V}}$.

Now we give some useful algebraic properties and operations of FFBSSs with illustrative examples.

Definition 8

A FFBSS over ${\mathcal {V}}$ is defined as a relative absolute FFBSS and is denoted by $(V,\Phi ,L)$, if $V(l)(\vartheta )=(\eta ^+_V(l)(\vartheta )=1,\eta ^-_V(l)(\vartheta )=0)$ and $\Phi (\lnot l)(\vartheta )=(0,1)$, $\forall ~l\in L,~\lnot l\in \lnot L,~\vartheta \in {\mathcal {V}}$.

Definition 9

Let $\gamma _1=(P_1,Q_1,L_1)$ and $\gamma _2=(P_2,Q_2, L_2)$ be two FFBSSs on ${\mathcal {V}}$. Then, the extended union of $\gamma _1$ and $\gamma _2$, represented by $\gamma _1\widetilde{\cup }_{\mathcal {E}}\gamma _2$, is again a FFBSS $((P_1\Cup P_2), (Q_1\Cap Q_2), L_1\cup L_2)$ on ${\mathcal {V}}$, which is defined as follows:

$$\begin{aligned} (P_1\Cup P_2)(l)= {\left\{ \begin{array}{ll} P_1(l),&{} \text{if}\ l\in L_1-L_2,\\ P_2(l),&{}\text{if}\ l\in L_2-L_1,\\ P_1(l)\underline{\cup }P_2(l)&{}\text{if}\ l\in L_1\cap L_2. \end{array}\right. } \end{aligned}$$

$$\begin{aligned} (Q_1\Cap Q_2)(\lnot l)= {\left\{ \begin{array}{ll} Q_1(\lnot l), &{}\text{if}\ neg l\in (\lnot L_1)-(\lnot L_2),\\ Q_2(\lnot l), &{}\text{if}\ \lnot k\in (\lnot L_2)-(\lnot L_1),\\ Q_1(\lnot l)\overline{\cap }Q_2(\lnot l)&{}\text{if}\ \lnot l\in (\lnot L_1)\cap (\lnot L_2), \end{array}\right. } \end{aligned}$$

where

$$\begin{aligned} P_1(l)\underline{\cup }P_2(l)=&\big \{\big \langle \vartheta ,\big (\eta ^+_{P_1}(l_i)(\vartheta )\vee \eta ^+_{P_2}(l_j)(\vartheta ),\\ {}&~\eta ^-_{P_1}(l_i)(\vartheta )\wedge \eta ^-_{P_2}(l_j)(\vartheta )\big )\big \rangle ~|~\vartheta \in {\mathcal {V}}\big \},\\ Q_1(\lnot l)\overline{\cap }Q_2(\lnot l)=&\big \{\big \langle \vartheta ,\big (\zeta ^+_{Q_1}(\lnot l_i)(\vartheta )\wedge \zeta ^+_{Q_2}(\lnot l_j)(\vartheta ),\\ {}&~\zeta ^-_{Q_1}(\lnot l_i)(\vartheta )\vee \zeta ^-_{Q_2}(\lnot l_j)(\vartheta )\big )\big \rangle ~|~\vartheta \in {\mathcal {V}}\big \}. \end{aligned}$$

Note that ‘$\vee$’ and ‘$\wedge$’ serve as maximum and minimum, respectively.

Definition 10

Let $\gamma _1=(P_1,Q_1,L_1)$ and $\gamma _2=(P_2,Q_2, L_2)$ be two FFBSSs on ${\mathcal {V}}$. Then, the restricted union of $\gamma _1$ and $\gamma _2$, represented by $\gamma _1\widetilde{\cup }_{\mathcal {R}}\gamma _2$, is again a FFBSS $((P_1\Cup P_2), (Q_1\Cap Q_2), L_1\cap L_2)$ on ${\mathcal {V}}$, where $(P_1\Cup P_2)(l)=P_1(l)\underline{\cup }P_2(l)$ for all $l\in L_1\cap L_2$ and $(Q_1\Cap Q_2)(\lnot l)=Q_1(\lnot l)\overline{\cap }Q_2(\lnot l)$ for all $\lnot l\in (\lnot L_1)\cap (\lnot L_2)$, and with the conditions $L_1\cap L_2\ne \emptyset$, $(\lnot L_1)\cap (\lnot L_2)\ne \emptyset$.

Definition 11

Let $\gamma _1=(P_1,Q_1,L_1)$ and $\gamma _2=(P_2,Q_2, L_2)$ be two FFBSSs on ${\mathcal {V}}$. Then, the extended intersection of $\gamma _1$ and $\gamma _2$, represented by $\gamma _1\widetilde{\cap }_{\mathcal {E}}\gamma _2$, is again a FFBSS $((P_1\Cap P_2), (Q_1\Cup Q_2), L_1\cup L_2)$ on ${\mathcal {V}}$, which is defined as follows:

$$\begin{aligned} (P_1\Cap P_2)(l)= {\left\{ \begin{array}{ll} P_1(l), &{}\text{if}\ l\in L_1-L_2,\\ P_2(l), &{}\text{if}\ l\in L_2-L_1,\\ P_1(l)\overline{\cap }P_2(l),&{}\text{if}\ l\in L_1\cap L_2. \end{array}\right. } \end{aligned}$$

$$\begin{aligned} (Q_1\Cup Q_2)(\lnot l)= {\left\{ \begin{array}{ll} Q_1(\lnot l), &{}\text{if}\ \lnot l\in (\lnot L_1)-(\lnot L_2),\\ Q_2(\lnot l), &{}\text{if}\ \lnot l\in (\lnot L_2)-(\lnot L_1),\\ Q_1(\lnot l)\underline{\cup }Q_2(\lnot l)&{}\text{if}\ \lnot l\in (\lnot L_1)\cap (\lnot L_2). \end{array}\right. } \end{aligned}$$

where

$$\begin{aligned} P_1(l)\overline{\cap }P_2(l)=&\big \{\big \langle \vartheta ,\big (\eta ^+_{P_1}(l_i)(\vartheta )\wedge \eta ^+_{P_2}(l_j)(\vartheta ),\\ {}&~\eta ^-_{P_1}(l_i)(\vartheta )\vee \eta ^-_{P_2}(l_j)(\vartheta )\big )\big \rangle ~|~\vartheta \in {\mathcal {V}}\big \},\\ Q_1(\lnot l)\underline{\cup }Q_2(\lnot l)=&\big \{\big \langle \vartheta ,\big (\zeta ^+_{Q_1}(\lnot l_i)(\vartheta )\vee \zeta ^+_{Q_2}(\lnot l_j)(\vartheta ),\\ {}&~\zeta ^-_{Q_1}(\lnot l_i)(\vartheta )\wedge \zeta ^-_{Q_2}(\lnot l_j)(\vartheta )\big )\big \rangle ~|~\vartheta \in {\mathcal {V}}\big \}. \end{aligned}$$

Definition 12

Let $\gamma _1=(P_1,Q_1,L_1)$ and $\gamma _2=(P_2,Q_2, L_2)$ be FFBSSs on ${\mathcal {V}}$. Then, the restricted intersection of $\gamma _1$ and $\gamma _2$, represented by $\gamma _1\widetilde{\cap }_{\mathcal {R}}\gamma _2$, is again a FFBSS $((P_1\Cap P_2), (Q_1\Cup Q_2), L_1\cap L_2)$ on ${\mathcal {V}}$, where $(P_1\Cap P_2)(l)=P_1(l)\overline{\cap }P_2(l)$ for all $l\in L_1\cap L_2$ and $(Q_1\Cup Q_2)(\lnot l)=Q_1(\lnot l)\underline{\cup }Q_2(\lnot l)$ for all $\lnot l\in (\lnot L_1)\cap (\lnot L_2)$, and with the conditions $L_1\cap L_2\ne \emptyset$, $(\lnot L_1)\cap (\lnot L_2)\ne \emptyset$.

Example 4

Let $\gamma =(P,Q,L)$ be the FFBSS on the universe of discourse ${\mathcal {V}}$ as discussed in Example  1. Take another FFBSS $\gamma _1=(P_1,Q_1,L_1)$ over ${\mathcal {V}}$, with $L_1=\{l_1,l_3,l_5\}$ provided by Table 7. Then, the extended union $\gamma \widetilde{\cup }_{\mathcal {E}}\gamma _1$ and the extended intersection $\gamma \cap _{\mathcal {E}}\gamma _1$ of FFBSSs are respectively provided by Tables 8 and 9. In the following, Tables 10 and 11 provide the tabular arrangements of the restricted intersection and union, respectively.

Table 7 Table for the FFBSS $(P_1, Q_1, L_1)$

Table 8 Table for the extended union $\gamma \widetilde{\cup }_{\mathcal {E}}\gamma _1$

Table 9 Table for the extended intersection $\gamma \widetilde{\cap }_{\mathcal {E}}\gamma _1$

Table 10 Table for the restricted intersection $\gamma \widetilde{\cap }_{\mathcal {R}}\gamma _1$

Table 11 Table for the restricted union $\gamma \widetilde{\cup }_{\mathcal {R}}\gamma _1$

Definition 13

Let $\gamma _1=(P_1,Q_1,L_1)$ and $\gamma _2=(P_2,Q_2, L_2)$ be two FFBSSs on the universe ${\mathcal {V}}$. Then the ”And operation” on $\gamma _1$ and $\gamma _2$ denoted by $\gamma _1\barwedge \gamma _2=(P,Q,L_1\times L_2)$, is defined as

$$\begin{aligned} P(l_i,l_j)(\vartheta )=&\big (\eta ^+_{P_1}(l_i)(\vartheta )\wedge \eta ^+_{P_2}(l_j)(\vartheta ),\\ {}&~\eta ^-_{P_1}(l_i)(\vartheta )\vee \eta ^-_{P_2}(l_j)(\vartheta )\big ),\\ Q(\lnot l_i,\lnot l_j)(\vartheta )=&\big (\zeta ^+_{Q_1}(\lnot l_i)(\vartheta )\vee \zeta ^+_{Q_2}(\lnot l_j)(\vartheta ),\\ {}&~\zeta ^-_{Q_1}(\lnot l_i)(\vartheta )\wedge \zeta ^-_{Q_2}(\lnot l_j)(\vartheta )\big ), \end{aligned}$$

for all $(l_i,l_j)\in L_1\times L_2,~(\lnot l_i,\lnot l_j)\in \lnot L_1\times \lnot L_2$, and $\vartheta \in {\mathcal {V}}$.

Definition 14

Let $\gamma _1=(P_1,Q_1,L_1)$ and $\gamma _2=(P_2,Q_2, L_2)$ be two FFBSSs over ${\mathcal {V}}$. Then the “OR operation” on $\gamma _1$ and $\gamma _2$ denoted as $\gamma _1\veebar \gamma _2=(P,Q,L_1\times L_2)$, is defined by

$$\begin{aligned} P(l_i,l_j)(\vartheta )=&\big (\eta ^+_{P_1}(l_i)(\vartheta )\vee \eta ^+_{P_2}(l_j)(\vartheta ),\\ {}&~\eta ^-_{P_1}(l_i)(\vartheta )\wedge \eta ^-_{P_2}(l_j)(\vartheta )\big ),\\ Q(\lnot l_i,\lnot l_j)(\vartheta )=&\big (\zeta ^+_{Q_1}(\lnot l_i)(\vartheta )\wedge \zeta ^+_{Q_2}(\lnot l_j)(\vartheta ),\\ {}&~\zeta ^-_{Q_1}(\lnot l_i)(\vartheta )\vee \zeta ^-_{Q_2}(\lnot l_j)(\vartheta )\big ). \end{aligned}$$

For all $(l_i,l_j)\in L_1\times L_2,~(\lnot l_i,\lnot l_j)\in \lnot L_1\times \lnot L_2$, and $\vartheta \in {\mathcal {V}}$.

Example 5

Let ${\mathcal {V}}=\{\vartheta _1,\vartheta _2,\ldots ,\vartheta _5\}$ be the collection of five candidates and let $\gamma _1=(P_1, Q_1, L_1)$ and $\gamma _2=(P_2,Q_2,L_2)$ be two FFBSSs over ${\mathcal {V}}$, where $L_1=\{l_2=\text{{time management skills}},~l_3=\text{{good communication skills}}\}, L_2=\{l_4=\text{{honest}}\}\subseteq G$ are the set of parameters, which are respectively displayed in Tables 12 and 13 given below.

Then, the “And” and “OR” operations between FFBSSs $(P_1,Q_1,L_1)$ and $(P_2,Q_2,L_2)$ are given by Tables 14 and 15, respectively.

The following lemma provides a connection between the extended union and restricted intersection of FFBSSs.

Table 12 Table for the FFBSS $(P_1, Q_1, L_1)$

Table 13 Table for the FFBSS $(P_2, Q_2, L_2)$

Table 14 Table for the And operation between FFBSS $\gamma _1$ and $\gamma _2$

Table 15 Table for the OR operation between FFBSS $\gamma _1$ and $\gamma _2$

Lemma 1

Let $\gamma _1=(P_1,Q_1,L_1)$ and $\gamma _2=(P_2,Q_2,L_2)$ be two FFBSSs on ${\mathcal {V}}$. Then

• 1. $\gamma _1\widetilde{\cup }_{\mathcal {E}}\gamma _2$ is the smallest FFBSS over ${\mathcal {V}}$ which contains both $\gamma _1$ and $\gamma _2$.

• 2. $\gamma _1\widetilde{\cap }_{\mathcal {R}}\gamma _2$ is the biggest FFBSS over ${\mathcal {V}}$ which is contained in both $\gamma _1$ and $\gamma _2$.

Proof

Its proof directly followed from Definitions 9 and 12.

Now two important definitions of score function and Fermatean fuzzy weighted average operator of FFBSSs are provided which support presented MADM methodology.

Definition 15

Let $F=(\eta _F^+,\eta _F^-)$ be an arbitrary FFN. Then, the score function of F is given as

$$\begin{aligned} s(F)=(\eta _F^+)^3-(\eta _F^-)^3. \end{aligned}$$

(3)

Definition 16

Let $F_1,F_2,\ldots ,F_n$ be a family of FFNs and every $F_j=(\eta ^+_{F_j},\eta ^-_{F_j})$ be related with an significant weight $w_j (j=1,2,\ldots ,n)$ with $\sum _{j=1}^{n} w_j=1$, satisfying $0\le w_j\le 1$, then the Fermatean fuzzy weighted average (FFWA) operator is defined as:

$$\begin{aligned} H(F_{1},F_{2},\ldots ,F_{n})=\left( \sum \limits _{j=1}^{n}w_j\eta _{F_j}^+,\sum \limits _{j=1}^{n}w_j\eta _{F_j}^-\right) . \end{aligned}$$

(4)

3 Applications

In the following, we provide a novel MADM algorithm based on FFBSSs, their score functions and FFWA operator discussed in the previous section. Algorithm: Selection of an appropriate object using FFBSS,

• 1. Input: ${\mathcal {V}}=\{\vartheta _1,\vartheta _2,\ldots ,\vartheta _n\}$, a universe containing n elements, $L\subseteq G$, a set of m parameters, a FFBSS (P, Q, L), where Fermatean fuzzy bipolar soft decision matrix with respect to FFBSS (P, Q, L) is given by

  $$\begin{aligned} F&=\big \langle (F_{ji})_{n\times m},(\lnot F_{ji})_{n\times m}\big \rangle \\ {}&=\big \langle (\eta _{ji}^+,\eta _{ji}^-)_{n\times m},(\zeta _{ji}^+,\zeta _{ji}^-)_{n\times m}\big \rangle . \end{aligned}$$

• 2. Insert weights $w_i$ with $\sum _{i=1}^m w_i=1$ for each parameter $l_i\in L$, where $i=1,2,\ldots ,m$.

• 3. From the Definition 16 of FFWA operator, compute the FFNs $(F_j)$ and $(\lnot F_j)$ for all $\vartheta _j\in {\mathcal {V}}$ where

  $$\begin{aligned} F_i&=H(F_{j1},F_{j2},\ldots ,F_{jm})\\ {}&=\left( \sum \limits _{i=1}^{m}w_i\eta _{ji}^+,\sum \limits _{i=1}^{m}w_i\eta _{ij}^-\right) ,\\ \lnot F_j&=H(\lnot F_{j1},\lnot F_{j2},\ldots ,\lnot F_{jm})\\ {}&=\left( \sum \limits _{i=1}^{m}w_i\zeta _{ji}^+,\sum \limits _{i=1}^{m}w_i\zeta _{ji}^-\right) , \end{aligned}$$

  where $\lnot F_j$ denotes the Fermatean membership values of the alternatives based upon the “Not set of parameters”.

• 4. Using Equation (3), determine the score function $s(F_j)$ and $s(\lnot F_j)$ of every object $\vartheta _j\in {\mathcal {V}}$.

• 5. Output: Find $s(F_t)=\max _{j}\{s(F_j)-s(\lnot F_j)\}$ and select the corresponding optimal object $\vartheta _t$ having highest score value.

To better understand the implication of the above Algorithm its flowchart diagram is given in the following Fig. 2.

Fig. 2

Flowchart diagram

3.1 Selection of a surgeon robot

When we talk about robots doing humans tasks, we often talk about the future, but robotic surgery is a reality. At the end of nineteenth century, when the PUMA 560 (Programmable Universal Machine for Assembly or Programmable Universal Manipulation Arm 560) robotic surgical arm was employed by Kwoh et al. (1988) in a delicate neurosurgical biopsy, a non-laparoscopic surgery, the first recorded use of a robot-assisted surgical technique took place. Robotic surgery helps doctors to perform certain types of complicated cases more accurately. To treat a wide variety of conditions, hospitals have rapidly adopted surgeon robots in the United States and Europe. The term “robotic” usually misguides people. Robots do not execute surgery, your surgeon conducts surgery with da Vinci (surgeon robot) via instruments that the surgeon guides through a console. The robotic surgery system translates your surgeon’s hand gestures at the computer in real-time, bending and rotating the instruments while conducting the operation. The tiny wrested types of equipment move like a human hand, but with an excellent motion range. The surgeon robot vision system also delivers highly magnified, three dimensional (3D) high-definition views of the surgical area. The instrument size makes it possible for surgeons to operate with one or a few small incisions. Surgeons who utilize the robotic system can easily see that for several techniques, it improves the control and flexibility during the operation and permits them to better see the location, as compared to other traditional procedures.

Suppose a hospital wants to select the best surgeon robot to assist the surgeons in critical surgeries. This critical task is given to the team of three senior doctors. Let ${\mathcal {V}}=\{\vartheta _1,\vartheta _2,\vartheta _3,\ldots ,\vartheta _{15}\}$ be the set of 15 surgeon robots under consideration, and $G=\{l_1=\text{great accuracy},l_2=\text{high agility},l_3=\text{leadership},l_4=\text{ambidextrous},l_5=\text{stereoscopic vision},l_6=\text{automation}\}$ be the criteria for judgment of surgeon robots. Then $\lnot G=\{l_1=\text{inaccuracy}, ~l_2=\text{low agility}, ~l_3=\text{non-leadership},~ l_4=\text{ambilevous}, ~l_5=\text{stereobling},~l_6=\text{manual work}\}$. Now the team of expert doctors of the hospital decide to evaluate each surgeon robot, according to the chosen subset $L=\{l_1,l_2,l_3\}$ of parameters. All the information about the surgeon robots with respect to important parameters is provided in the form of a FFBSS (P, Q, L) which truly illustrate the “qualities(requirements) of the surgeon robots” displayed by the Table 16.

Table 16 Table for the FFBSS (P, Q, L)

In comparison to the value of each criterion $l_i~(i=1,2,3)$, committee provides the corresponding weights as

$$\begin{aligned} w_1=0.1,\quad w_2=0.3,\quad w_3=0.4. \end{aligned}$$

Using Definition 16 of FFWA operator,

$$\begin{aligned} F_1&=\left( \sum \limits _{i=1}^{3}w_i\eta _{1i}^+,\sum \limits _{i=1}^{3}w_i\eta _{1i}^-\right) ,\\&=\big (w_1\eta _{11}^+ +w_2\eta _{12}^+ +w_3\eta _{13}^+,~w_1\eta _{11}^- +w_2\eta _{12}^- +w_3\eta _{13}^-\big ),\\&=(0.1\times 0.6+0.3\times 0.5+0.4\times 0.9,~0.1\times 0.7\\&\quad +0.3\times 0.8+0.4\times 0.3),\\&=(0.57,0.4). \end{aligned}$$

Similarly,

$$\begin{aligned} F_2&=(0.4,0.16),\quad F_3=(0.5,0.58),\\ F_4&=(0.48,0.48),\quad F_5=(0.6,0.3),\\ F_6&=(0.68,0.5),\quad F_7=(0.67,0.5),\\ F_8&=(0.57,0.45),\quad F_9=(0.37,0.34),\\ F_{10}&=(0.66,0.59),\quad F_{11}=(0.42,0.47),\\ F_{12}&=(0.68,0.46),\quad F_{13}=(0.54,0.4),\\ F_{14}&=(0.51,0.25),\quad F_{15}=(0.65,0.49). \end{aligned}$$

and

$$\begin{aligned} \lnot F_1&=\left( \sum \limits _{i=1}^{3}w_i\zeta _{1i}^+,\sum \limits _{i=1}^{3}w_i\zeta _{1i}^-\right) ,\\&=\big (w_1\zeta _{11}^+ +w_2\zeta _{12}^+ +w_3\zeta _{13}^+,~w_1\zeta _{11}^- +w_2\zeta _{12}^- +w_3\zeta _{13}^-\big ),\\&=(0.1\times 0.3+0.3\times 0.4+0.4\times 0.1,~0.1\times 0.2\\&\quad +0.3\times 0.2+0.4\times 0.6),\\&=(0.19,0.32). \end{aligned}$$

Similarly,

$$\begin{aligned} \lnot F_2&=(0.28,0.15),\quad \lnot F_3=(0.28,0.15),\\ \lnot F_4&=(0.28,0.18),\quad \lnot F_5=(0.16,0.49),\\ \lnot F_6&=(0.12,0.16),\quad \lnot F_7=(0.12,0.24),\\ \lnot F_8&=(0.16,0.3),\quad \lnot F_9=(0.35,0.38),\\ \lnot F_{10}&=(0.14,0.09),\quad \lnot F_{11}=(0.34,0.33),\\ \lnot F_{12}&=(0.11,0.26),\quad \lnot F_{13}=(0.18,0.37),\\ \lnot F_{14}&=(0.19,0.3),\quad \lnot F_{15}=(0.15,0.27). \end{aligned}$$

By Definition 15, we have

$$\begin{aligned} s(F_1)&=0.121193,\quad s(F_2)=0.059904,\\ s(F_3)&=-0.070112,\quad s(F_4)=0,\\ s(F_5)&=0.189,\quad s(F_6)=0.189432,\\ s(F_7)&=0.175363, \quad s(F_8)=0.094068,\\ s(F_9)&=0.011349,\quad s(F_{10})=0.082117,\\ s(F_{11})&=-0.029735,\quad s(F_{12})=0.217096,\\ s(F_{13})&=0.093464,\quad s(F_{14})=0.117026,\\ s(F_{15})&=0.156976. \end{aligned}$$

$$\begin{aligned} s(\lnot F_1)&=-0.025909,\quad s(\lnot F_2)=-0.055188,\\ s(\lnot F_3)&=0.018577,\quad s(\lnot F_4)=0.01612,\\ s(\lnot F_5)&=-0.113553,\quad s(\lnot F_6)=-0.00236,\\ s(\lnot F_7)&=-0.012096,\quad s(\lnot F_8)=-0.022904,\\ s(\lnot F_9)&=-0.011997,\quad s(\lnot F_{10})=0.002015,\\ s(\lnot F_{11})&=0.003367,\quad s(\lnot F_{12})=-0.016245,\\ s(\lnot F_{13})&=-0.044821,\quad s(\lnot F_{14})=0.020141,\\ s(\lnot F_{15})&=-0.016308. \end{aligned}$$

Now the final scores are computed as:

$$\begin{aligned} s(F_1)-s(\lnot F_1)&= 0.147102,\\s(F_2)-s(\lnot F_2)&=0.115092,\\s(F_3)-s(\lnot F_3)&=-0.051535,\\s(F_4)-s(\lnot F_4)&=-0.01612,\\s(F_5)-s(\lnot F_5)&=0.302553,\\s(F_6)-s(\lnot F_6)&=0.1918,\\s(F_7)-s(\lnot F_7)&=0.187859,\\s(F_8)-s(\lnot F_8)&=0.117972,\\s(F_9)-s(\lnot F_9)&=0.023346,\\s(F_{10})-s(\lnot F_{10})&=0.080102,\\s(F_{11})-s(\lnot F_{11})&=-0.033102,\\s(F_{12})-s(\lnot F_{12})&=0.233341,\\s(F_{13})-s(\lnot F_{13})&=0.138285,\\s(F_{14})-s(\lnot F_{14})&=0.137167,\\s(F_{15})-s(\lnot F_{15})&=0.173284. \end{aligned}$$

Clearly, $\vartheta _5$ is the decision object. Thus, the team will choose $\vartheta _5$ as the best surgeon robot.

Now, we use our methodology to another practical application.

3.2 Evaluation of the most affected country due to COVID-19

Among all dangerous viruses, coronavirus is the most malignant virus. It has plunged the world into a “crisis like no other”. COVID-19, being a novel viral disease affecting humans for the first time in the large scale. The COVID-19 pandemic, which had firstly detected in China in the end of 2019, has infected people in 188 countries. the spreading rate of this virus was exponential region-wise but now its rate is decreasing. Currently, the infected countries are banning gatherings of people to decrease the spreading rate of this virus. Several countries are locking their population and enforcing strict quarantine to decrease the spread of the damage of this highly contagious disease. With the emergence of COVID-19, it has paralyzed every domain of life like education system, economies, industries etc. The developing countries are sure to hit to be hard, due to this virus. Till date, around 100 million people infected from which 55.4 million recovered while 2.16 million died with this virus. Now different countries invented the vaccine of this deadly virus, including China, USA. Our main goal is to develop an application for the evaluation of the most affected country due to COVID-19 pandemic. Here we select few prevailed countries whose fields are mostly disturbed.

Suppose there is a set of fifteen countries ${\mathcal {V}}=\{\vartheta _1, \vartheta _2, \ldots , \vartheta _{15}\}$ and let $G=\{l_1, l_2,\ldots ,l_6\}$ be a collection of parameters(affected fields) under consideration. For $i= 1,2,\ldots , 6,$ the parameters $l_i$ stand for “education”, “health”, “global economy”, “employment”, “transport” and “trade”, respectively. Let the ‘Not set of G’ be $\lnot G=\{\lnot l_1=\text{illiterateness}, \lnot l_2=\text{illness}, \lnot l_3=\text{internet market},\lnot l_4=\text{unemployment},\lnot l_5=\text{stagnation},\lnot l_6=\text{dissuation}\}$. Each country is evaluated with respect to a favorable subset $L=\{l_1, l_2, l_3\}$ with respect to the opinions of different experts. The FFBSS (P, Q, L) describes the “impact of affected fields on selected countries” to evaluate the most affected country, which is given by the Table 17 below.

Table 17 Table for the FFBSS (P, Q, L)

For each parameter $l_i~(i=1,2,3)$, experts provide the following weights to parameters regarding their significance:

$$\begin{aligned} w_1=0.4,\quad w_2=0.2,\quad w_3=0.5. \end{aligned}$$

Using the Definition 16 of FFWA operator,

$$\begin{aligned} F_1&=\left( \sum \limits _{i=1}^{3}w_i\eta _{1i}^+,\sum \limits _{i=1}^{3}w_i\eta _{1i}^-\right) ,\\&=\big (w_1\eta _{11}^+ +w_2\eta _{12}^+ +w_3\eta _{13}^+,~w_1\eta _{11}^- +w_2\eta _{12}^- +w_3\eta _{13}^-\big ),\\&=(0.4\times 0.9+0.2\times 0.8+0.5\times 0.9,~0.4\times 0.8\\&\quad + 0.2\times 0.7+0.5\times 0.7),\\&=(0.97,0.6). \end{aligned}$$

Similarly,

$$\begin{aligned} F_2&=(0.8,0.89),\quad F_3=(0.8,0.87),\\ F_4&=(0.65,0.6),\quad F_5=(0.4,0.69),\\ F_6&=(0.59,0.72),\quad F_7=(0.6,0.78),\\ F_8&=(0.72,0.77),\quad F_9=(0.7,0.8),\\ F_{10}&=(0.75,0.69),\quad F_{11}=(0.87,0.77),\\ F_{12}&=(0.17,0.6),\quad F_{13}=(0.95,0.78),\\ F_{14}&=(0.57,0.6),\quad F_{15}=(0.97,0.76). \end{aligned}$$

Now

$$\begin{aligned} \lnot F_1&=\left( \sum \limits _{i=1}^{3}w_i\zeta _{1i}^+,\sum \limits _{i=1}^{3}w_i\zeta _{1i}^-\right) ,\\&=\big (w_1\zeta _{11}^+ +w_2\zeta _{12}^+ +w_3\zeta _{13}^+,~w_1\zeta _{11}^- +w_2\zeta _{12}^- +w_3\zeta _{13}^-\big ),\\&=(0.4\times 0.1+0.2\times 0.2+0.5\times 0.0,~0.4\times 0.2\\&\quad +0.2\times 0.3+0.5\times 0.3),\\&=(0.08,0.29). \end{aligned}$$

Similarly,

$$\begin{aligned} \lnot F_2&=(0.17,0.21),\quad \lnot F_3=(0.16,0.12),\\ \lnot F_4&=(0.3,0.3),\quad \lnot F_5=(0.56,0.37),\\ \lnot F_6&=(0.49,0.33),\quad \lnot F_7=(0.42,0.32),\\ \lnot F_8&=(0.36,0.1),\quad \lnot F_9=(0.45,0.25),\\ \lnot F_{10}&=(0.26,0.34),\quad \lnot F_{11}=(0.14,0.29),\\ \lnot F_{12}&=(0.65,0.5),\quad \lnot F_{13}=(0.11,0.31),\\ \lnot F_{14}&=(0.48,0.4),\quad \lnot F_{15}=(0.18,0.25). \end{aligned}$$

By Definition  15, we have

$$\begin{aligned} s(F_1)&=0.696673,\quad s(F_2)=-0.192969,\\ s(F_3)&=-0.146503,\quad s(F_4)=0.058525,\\ s(F_5)&=-0.264509,\quad s(F_6)=-0.167869,\\ s(F_7)&=-0.224505,\quad s(F_8)=-0.083285,\\ s(F_9)&=-0.169,\quad s(F_{10})=0.218414,\\ s(F_{11})&=0.20197,\quad s(F_{12})=-0.211087,\\ s(F_{13})&=0.382823,\quad s(F_{14})=-0.041788,\\ s(F_{15})&=0.473697. \end{aligned}$$

$$\begin{aligned} s(\lnot F_1)&=-0.023877,\quad s(\lnot F_2)=0.004348,\\ s(\lnot F_3)&=-0.002368,\quad s(\lnot F_4)=0,\\ s(\lnot F_5)&=0.124963,\quad s(\lnot F_6)=0.081712,\\ s(\lnot F_7)&=0.04132,\quad s(\lnot F_8)=0.045656,\\ s(\lnot F_9)&=0.0755,\quad s(\lnot F_{10})=-0.021728,\\ s(\lnot F_{11})&=-0.021645,\quad s(\lnot F_{12})=0.149625,\\ s(\lnot F_{13})&=-0.031437,\quad s(\lnot F_{14})=0.046592,\\ s(\lnot F_{15})&=-0.009793. \end{aligned}$$

Now the final scores are computed as:

$$\begin{aligned} s(F_1)-s(\lnot F_1)&= 0.72055,\\ s(F_2)-s(\lnot F_2)&=0.197317,\\ s(F_3)-s(\lnot F_3)&=-0.144135,\\ s(F_4)-s(\lnot F_4)&=0.058625,\\ s(F_5)-s(\lnot F_5)&=-0.139540,\\ s(F_6)-s(\lnot F_6)&=-0.249581,\\ s(F_7)-s(\lnot F_7)&=-0.183185,\\ s(F_8)-s(\lnot F_8)&=-0.128941,\\ s(F_9)-s(\lnot F_9)&=-0.2445,\\ s(F_{10})-s(\lnot F_{10})&=-0.1209,\\ s(F_{11})-s(\lnot F_{11})&=0.196686,\\ s(F_{12})-s(\lnot F_{12})&=-0.360712,\\ s(F_{13})-s(\lnot F_{13})&=0.351386,\\ s(F_{14})-s(\lnot F_{14})&=-0.004804,\\ s(F_{15})-s(\lnot F_{15})&=0.463904. \end{aligned}$$

Clearly, $\vartheta _1$ is the most affected country due to coronavirus.

4 Sensitivity analysis

To show the reliability and feasibility of the proposed FFBSS model, in this section, we discuss its merits, limitations and comparison with Pythagorean fuzzy BSS or PFBSS model (Akram and Ali 2020).

• Merits of the proposed model In the last few decades, a rapid progress in the uncertain modeling to tackle vague information is the evidence of this worthy topic. The wish to produce novel uncertain models and their hybridization is a limitless procedure due to the occurrence of numerous real-world decision-making uncertain problems. Undoubtedly, BSS model and its fuzzy and Pythagorean fuzzy versions are emerging as very useful mathematical tools. Nowadays, a more general model is needed which contains the characteristics of existing models (that is, more than one). Motivated by this thriving trend, a novel hybridization called FFBSSs is proposed which can handle the real data in Fermatean fuzzy bipolar soft environment. The presented FFBSS model is more feasible and reliable to handle uncertain information in different MADM situations. Especially, when the under consideration information containing parameters having opposite meanings in decision-making procedure. One can readily see that existing decision-making methods, that is, FFBSSs cannot consider the nonmembership degrees of objects under consideration in a MADM situation while PFBSSs cannot deal with the membership and nonmembership values whose sum of their squares is greater than 1. However, our proposed FFBSS model has ability to tackle both fuzzy and Pythagorean fuzzy bipolar soft information.

  Table 18 Comparison table for the Application 1(Selection of an employee) in Akram and Ali (2020)

  Table 19 Comparison table for the Application 2 (Selection of a house) in Akram and Ali (2020)

  Table 20 Comparison between rankings results of PFBSSs and proposed model on the Application 1 in Akram and Ali (2020).

  Table 21 Comparison between rankings results of PFBSSs and proposed model on the Application 2 in Akram and Ali (2020)

• Comparative analysis with existing models Many fruitful soft computing hybrid models such as FFBSSs (Naz and Shabir 2014), Pythagorean fuzzy BSSs (Akram and Ali 2020) and m-polar fuzzy BSSs (Akram et al. 2020a) have been proposed in the literature to tackle different kinds of uncertainties in several MADM problems. But the above-mentioned models contain some flaws in their structure like both FFBSS and m-polar fuzzy BSS models only consider membership values of objects regarding favorable parameters and PFBSSs only consider the membership and nonmembership values whose sum of their squares is less than 1. The invention of two powerful models, namely, intuitionistic fuzzy sets and Pythagorean fuzzy sets is enough to prove the significance of nonmembership part in several decision-making processes. Fermatean fuzzy sets are emerging as an efficient tool to deal with uncertain information as compared to intuitionistic and Pythagorean fuzzy sets. In view of this fact, FFBSSs are presented in this study to deal with Fermatean fuzzy bipolar soft information. Note that existing MADM approach based on Pythagorean fuzzy BSSs (Akram and Ali 2020) cannot be applied for dealing with proposed applications in Sect. 3 but developed MADM method based on FFBSSs can be used to solve MADM applications in Akram and Ali (2020). Thus, we have applied our proposed decision-making method on the datasets of Applications 1 and 2 in Akram and Ali (2020). One can easily see the significance of the developed FFBSS model by its comparison with PFBSS model (Akram and Ali 2020) which is displayed in Tables 18, 19, 20 and 21. Clearly, ranking order and optimal decision objects are similar. Therefore, our developed MADM method is more feasible and reliable than existing Pythagorean fuzzy BSSs.

• Limitations The major limitation of the proposed hybrid model is the existence of two sets of parameters, membership and nonmembership scores of alternatives with respect to these two sets of parameters, because in many MADM problems, the computational speed may be obtuse due to several parameters. It is a common drawback in several existing hybrid models which can be easily overcome with the appropriate coding of the algorithms using software such as MAPLE and MATLAB. Another deficiency of the proposed FFBSS model is that the rank of the alternatives may vary when new parameters (or alternatives) added or any existing parameters (or alternatives) removed in a provided MADM problem. The principal cause behind this occurrence is the autonomous behavior of parameters and alternatives.

5 Conclusion

Senapati and Yager (2020) have established a potential tool, namely, the FFS, to describe the uncertain information in different real-world decision-making situations more effectively as compared to fuzzy, intuitionistic fuzzy and Pythagorean fuzzy theories. In this paper, we have combined FFS with BSS and have presented a powerful hybrid model called FFBSSs as natural extension of Pythagorean fuzzy BSSs. We have discussed some fundamental properties of FFBSSs, namely, subset-hood, equal FFBSSs, relative null and relative absolute FFBSSs, restricted intersection and union, extended intersection and union, AND operation and OR operation. Our new hybrid model characterizes uncertain information more accurately and precisely than certain existing hybrid models like Pythagorean fuzzy BSSs. With the help of essential functions, like Fermatean fuzzy weighted average and score function of FFBSSs, we have constructed two applications of FFBSS to tackle different MADM situations. Further, we have designed an algorithm to support our proposed approach. At the end, we have compared our developed model with some existing hybrid models. In the future, we will try to extend our research work to (1) Interval-valued FFBSSs, (2) Fuzzy parameterized FFBSSs, and (3) q-rung orthopair fuzzy BSSs.