The Hybrid Incidence Susceptible-Transmissible-Removed Model for Pandemics

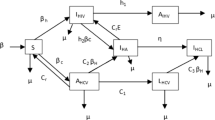
Abstract

The susceptible-transmissible-removed (STR) model is a deterministic compartment model, based on the susceptible-infected-removed (SIR) prototype. The STR replaces 2 SIR assumptions. SIR assumes that the emigration rate (due to death or recovery) is directly proportional to the infected compartment’s size. The STR replaces this assumption with the biologically appropriate assumption that the emigration rate is the same as the immigration rate one infected period ago. This results in a unique delay differential equation epidemic model with the delay equal to the infected period. Hamer’s mass action law for epidemiology is modified to resemble its chemistry precursor—the law of mass action. Constructing the model for an isolated population that exists on a surface bounded by the extent of the population’s movements permits compartment density to replace compartment size. The STR reduces to a SIR model in a timescale that negates the delay—the transmissible timescale. This establishes that the SIR model applies to an isolated population in the disease’s transmissible timescale. Cyclical social interactions will define a rhythmic timescale. It is demonstrated that the geometric mean maps transmissible timescale properties to their rhythmic timescale equivalents. This mapping defines the hybrid incidence (HI). The model validation demonstrates that the HI-STR can be constructed directly from the disease’s transmission dynamics. The basic reproduction number (${\mathcal{R}}_0$) is an epidemic impact property. The HI-STR model predicts that ${\mathcal{R}}_0 \propto \root \mathfrak{B} \of {\rho_n}$ where $\rho_n$ is the population density, and ${\mathfrak{B}}$ is the ratio of time increments in the transmissible- and rhythmic timescales. The model is validated by experimentally verifying the relationship. ${\mathcal{R}}_0$’s dependence on $\rho_n$ is demonstrated for droplet-spread SARS in Asian cities, aerosol-spread measles in Europe and non-airborne Ebola in Africa.

1 Introduction

The modelling of infectious disease dates from Bernoulli’s eighteenth century statistical model and En’ko’s compartment-model in the nineteenth century (Foppa 2017). In this manuscript, the models will arbitrarily be introduced as deterministic or stochastic. The deterministic models will either be ordinary differential equation (ODE), partial differential equation (PDE) or delay differential equation (DDE) compartment models. These deterministic compartment models’ numerical simulation will not be discussed. Under stochastic models, cellular automata (CA) are introduced as a subcategory of stochastic models because the distinction between the model and the numerical method is not obvious.

The ODE deterministic theory describing the propogation of an infectious disease as presented by Kermack and McKendrick (1927, 1991a, b, c) is the convergence of the basic reproduction number concepts of Böckh (1886), Kuczynski (1928), Dublin and Lotka (1925); Hamer (1906)’s mass action incidence; and the compartment models of En’ko (1989), Ross and Hudson (1917).

Böckh’s contribution is from demography (Dietz 1993; Heesterbeek 2002). See Perasso (2018), Heesterbeek and Dietz (1993) for discussions on Kuczynski’s and Lotka (1925)’s contributions, respectively. Hamer’s mass action incidence is based on a chemistry precursor (Heesterbeek 2005) – the law of mass action (Waage and Gulberg 1986). En’ko’s compartment model was published in Russian in 1889 (Dietz 1988). It predates Ross and Hudson’s compartment model of 1917 (Heesterbeek and Dietz 1993).

The 2 ODE compartment model prototypes classify all individuals in a closed population as either susceptible, infected or removed. Removed can either mean recovered (assumed immune) or dead. In the susceptible-infected-removed (SIR) model, all three compartments are used and individuals move in one direction only—from susceptible to infected to removed. The susceptible-infected-susceptible (SIS) model only uses 2 of these compartments and individuals are able to return to the susceptible compartment upon resolution of infection. Since then, an analytic solution for the SIR model has been found (Harko et al. 2014), standard incidence introduced (Hethcote 2000; Brauer et al. 2019) and pragmatic problems like herd immunity (Thompson et al. 2020) and vaccination threshold (Tuite and Fisman 2013) solved.

At least 2 layers of complexity have since been added. The basic ODE models assume an homogenous population—every infected-susceptible pair has the same probability of successful pathogen transmission over a fixed interaction period. Diekmann et al. define a next generation matrix (NGM) on a heterogenous population (Diekmann et al. 1990, 2013; Diekmann and Heesterbeek 2000). This NGM predicts the secondary infections due to the current infected population. They then show that ${\mathcal{R}}_0$ is the dominant eigenvalue of this NGM. Van den Driessche et al. propose that an heterogenous population can be approximated as the superposition of N homogenous population compartments (van den Driessche and Watmough 2002; Brauer et al. 2008). The NGM calculates ${\mathcal{R}}_0$ for this system of equations.

Secondly, additional compartments allow more realistic simulation of the dynamics of each disease (Hethcote 2000; Ivorra et al. 2020; Baccini et al. 2021; Leontitsis et al. 2021; Rǎdulescu et al. 2020; Giordano et al. 2020). One such model is the susceptible-exposed-infective-removed (SEIR) model (Liu 1993; Greenhalgh 1997; Korobeinikov and Maini 2005). The incubation period effectively subdivides the infected compartment into an asymptomatic, non-infectious, exposed compartment and an infectious compartment (van den Driessche 2017).

Conventional DDE compartment models are an alternative to the exposed compartment of ODE models (Huang et al. 2010; Li and Liu 2014). These DDE compartment models simulate a biologically appropriate constant incubation period. In contrast, the exposed compartment in the SEIR and SEIRS models implies an exponential distribution of incubation time (Huang et al. 2010; Arino and van den Driessche 2006). The delay from infection to infectious is typically included with the force of infection term as $\beta I(t-\tau )S(t)$ or $\beta I(t)S(t-\tau ).$ Hethcote et al. introduced alternative delay models (Arino and van den Driessche 2006; Hethcote and Tudor 1980; Hethcote et al. 1981a, b, 1989; Hethcote and van den Driessche 1995).

The homogenous mixing and large population assumptions reduce epidemic simulation to ODE models (Nåsell 2002; Diekmann et al. 2013). The assumption that the rate at which migrants enter a compartment is directly proportional to the size of compartment they exit is inconsistent with the biology (Bailey 1956a, b; Lloyd 2001; Krylova and Earn 2013).

PDE models allow the simulation of spatial spread. The spatial spread model commonly used is diffusion (Brauer et al. 2008; Diekmann and Heesterbeek 2000; Plank et al. 2009; Chalub and Souza 2011). Although diffusions models are described for rabies in foxes (Källén et al. 1985; Brauer et al. 2008) and the mosquito-vector West Nile fever in birds (Lin and Zhu 2017; Brauer et al. 2008), the statistical mechanical derivation of Fick’s law of diffusion requires random movement (Gillespie and Seitaridou 2012). Given non-random human-vector movement (Kurashima et al. 2018; Mollison 1977; Mansilla and Gutierrez 2001), the conditions under which the diffusion model is appropriate are not obvious. Furthermore, the diffusion model is not the only spatial spread model (Chen et al. 2014; Schneckenreither et al. 2008; Mollison 1977; Diekmann 1978; Bosch et al. 1988) nor the most general (Diekmann et al. 2013; Diekmann 1978; Mollison 1991).

The large number of discrete events assumed by the deterministic models result in continuous differentiable functions (Nåsell 2002). Stochastic models are a complement able to simulate small populations (e.g. early in the epidemic) and assign probabilities to outlier events (Bartlett 1964; Chowell et al. 2009; Brauer et al. 2019; Allen 2010). In 1760, Bernoulli used a statistical model to predict the effect of vaccination (Dietz and Heesterbeek 2002; Bailey 1975). Farr fitted bell-shaped curves to epidemics—attempting to identify empiric laws that describe their episodic nature (Bailey 1975). M’Kendrick constructed a spatial stochastic model on a two dimensional lattice (M’Kendrick 1925; Andersson and Britton 2000) but it was the Reed-Frost and Greenwood (Greenwood 1931) binomial chain models that became popular (Allen 2010; Bailey 1975). Both of these models assume long incubation periods with comparatively negligible infectious periods. A time increment equates to the incubation period and all infections occur at the end of this period. These assumptions result in asynchronous generations of pathogen hosts. Biologically, the model is consistent with seasonal procreation where the female dies after producing multiple offspring at that time ($e.g.$ spawning salmon). The conditions under which these models simulate epidemics most appropriately are not obvious. (Gani and Jerwood 1971) recognised these binomial chain models as examples of discrete time Markov chains (Gagniuc 2017; Allen and Burgin 2000). Continuous time Markov chains extrapolate the model to continuous time, discrete state variables (Allen 2017, 2010; Allen and Burgin 2000). This also represents a long latent period, branching process but the latent period is variable. Finally, continuous time, continuous state variables are simulated with stochastic differential equations (Allen 2017, 2010; Allen and Burgin 2000; Cai et al. 2019; Gray et al. 2011) with the variance of a Gaussian distribution (Osthus et al. 2017).

Cellular automata (CA) arose to study the complex phenomena that evolve when simple rules are applied on a regular lattice (Neumann 1966; Codd 1968; Sarkar 2000; Toffoli and Margolus 1987; Wolfram 1983). CA have been applied to computational fluid dynamics (CFD), economics, biology, ecology, physics and chemistry (Li et al. 2018; Menshutina et al. 2020). Schneckenreither et al. classify epidemic CA as lattice gas cellular automata (LGCA) or stochastic cellular automata (SCA) (Schneckenreither et al. 2008). The terms LGCA and the lattice Boltzmann method (LBM) are from CFD (Frisch et al. 1986; Wolf-Gladrow 2000) where the appropriate 2-step rules of stream and redistribute are shown to simulate the macroscopic, incompressible Navier-Stokes (NS) equations (Guo et al. 2000; He and Luo 1997). Similarly, Boccara and Cheong applied LGCA to epidemics by constructing a 2-step rule of streaming and redistribution of states S,I and R on a regular lattice (Boccara and Cheong 1992, 1993; Boccara et al. 1994). Schneckenreither et al. describe the LGCA spatial spread model as diffusion and classically simulates individuals occupying a cell. Mansilla and Gutierrez construct a spatial spread CA that can be tuned between the LGCA extreme of diffusion and perfect mixing (Mansilla and Gutierrez 2001).

In contrast, SCA redistributes cell states based on that cell’s previous state and adjacent cells’ proximity and previous states (White et al. 2007, 2009). The simulation does not model migration between cells but is intended to allow individuals within a cell to make contact with individuals in adjacent cells. States are represented as a ratio. Schneckenreither et al. refers to this spatial spread model as contact spread (Schneckenreither et al. 2008). Redistribution of compartments is based on the probabilities of changing compartment upon contact. The probabilistic cellular automata (PCA) model combines the contact spread of the SCA model with the LGCA’s integer cell occupants (Schimit and Monteiro 2009; Pereira and Schimit 2018). In the PCA model, the integer is 1. Holka et al.’s PCA model simulates a whole country and superimposes daily commutes (Holko et al. 2016)—migration is a LGCA feature. The SCA model has been extended to include uncertainty using a Markov chain Monte Carlo method with coupled Beta and Dirichlet distributions (Osthus et al. 2017; Wang et al. 2020; Zhou et al. 2020),.

Of note, in the CFD CA analogy, a Chapman-Enskog expansion is performed on the LGCA and LBM to derive the PDEs that describe the macroscopic phenomena (Guo et al. 2000; He and Luo 1997; Chapman et al. 1990). In contrast, the mean field approximation used on epidemic CAs necessarily describe population level ODEs (Berec 2002; Boccara and Cheong 1992, 1993; Boccara et al. 1994). Thus the population level spatial spread models described by the epidemic CAs are not obvious. In the CFD analogy, the CAs’ time- and space increments are tuned to achieve the appropriate viscosity—given that the viscocity in the CA-derived NS equations is a function of the time and space increments (Guo et al. 2000; He and Luo 1997). Without epidemiology CA derived PDEs, it is not obvious whether similar constraints pertain to the discretisation of these CAs.

This manuscript derives a DDE model where the delay is not due to the incubation period and is not an alternative to the exposed compartment. The delay addresses the assumption that the rate at which individuals leave the infectious compartment is proportional to the size of that compartment.

The conventional, ODE model concepts and properties are explored before deriving the susceptible-transmissible-removed (STR) model. The deterministic SIR model (Kermack and McKendrick 1991a, b, c; Kermack et al. 1927) assumes that individuals move between three compartments—susceptible (S), infected-infectious (I) and removed-recovered (R)—during an epidemic. S(t), I(t) and R(t) refer to the size of their respective compartments. There is no delay from infection to being infectious in the SIR model. R’s individuals can either be dead or recovered (assumed immune). The ODE model describing the movement between these compartments is (Chowell et al. 2009)

$$\begin{aligned} {\dot{S}}(t)= & {} -\frac{\xi (t)}{N} S(t)I(t)\nonumber \\ {\dot{I}}(t)= & {} \frac{\xi (t)}{N}S(t)I(t) - \alpha I( t) \nonumber \\ {\dot{R}}(t)= & {} \alpha I(t) \end{aligned}$$

(1)

where $S(t)+I(t) +R(t) =N$—the constant population size. The rate of new infection is proportional to S(t)I(t). This corresponds to the rate at which individuals leave S. The rate of recovery is directly proportional to I(t).

In Model (1), the rate of recovery is directly proportional to I(t). This has no biological interpretation. Biologically, an infection lasts for a fixed period ($T_I$). Individuals leave I at the same rate at which they entered it one $T_I$ ago.

Hethcote (2008), refers to $\xi (t)$ as the horizontal transmission incidence and it is usually treated as a constant ($\xi$). Epidemiologically, incidence is the number of new cases of a disease per unit time as a proportion of the susceptible population. At $t\gtrapprox t_0$, when $S\approx N$ and no individuals leave I,

$$\begin{aligned} \xi (t_0)= \frac{{\dot{I}}(t_0)}{S(t_0)}=-\frac{{\dot{S}}(t_0)}{S(t_0)} =\frac{{\dot{I}}(t_0)}{N}. \end{aligned}$$

(2)

There are two $\xi$s in epidemiology. The conventional mass action $\xi$ assumes that interactions are completely random. Further, N is so large that, early in the epidemic, all interactions are with susceptible individuals. Here, $\xi =\beta N.$

Hethcote (2000) and Brauer et al. (2019) argue that individuals have regular close contacts that are of similar count whether in a tribe, a village or a metropolis. Furthermore, as a generalisation, interactions only occur with these close contacts. This second $\xi$ is the standard incidence. $\xi =\beta_{si}$ is a constant for standard incidence. Although standard incidence is usually used for sexually transmitted diseases; Anderson demonstrates experimentally that, for airborne diseases, $0.03\le \nu \le 0.07$ in $\xi = \beta N^{\nu }$ (Anderson and May 1982, 1992).

The basic reproduction number (${\mathcal{R}}_0$) is a demographic concept (Dietz 1993; Heesterbeek 2002) that has been repurposed as an epidemic impact property. It represents the number of new infections produced by an infected individual directly. A straightforward ${\mathcal{R}}_0$ (Brauer et al. 2019) derivation exists for the SIR model. Consider I of Model (1).

$$\begin{aligned} {\dot{I}}(t) = \bigg (\frac{\xi S(t)}{N}-\alpha \bigg )I(t)> 0 \iff \frac{\xi S(t)}{N} -\alpha> 0 \iff \frac{\xi }{\alpha }\frac{S(t)}{N } >1. \end{aligned}$$

Define

$$\begin{aligned} {\mathcal{R}}_0 :{=} \frac{\xi }{\alpha }. \end{aligned}$$

(3)

For a completely susceptible population (at $t=0$), $S(0) \approx N.$ Then

$$\begin{aligned} {\mathcal{R}}_0> 1 \iff {\dot{I}}(t) > 0 \end{aligned}$$

(4)

implies that I grows indefinitely when ${\mathcal{R}}_0 > 1.$ Biologically, $\alpha$ is interpreted as the infection frequency.

2 A Boundaried, Delayed Differential Equation, SIR-Like Model

Define a host as an individual harbouring a pathogen that has the capacity to cause a disease. If the pathogen can be transmitted to a new host, the disease is infectious. The disease can only be transmitted to a new host if the host makes sufficient contact with a susceptible individual or potential host.

There is a delay from becoming infected to being infectious. Thus the infectious period $(T_i)$ is shorter than $T_I.$ In the SIR model this delay is negligible. $T_i$ and $T_I$ are biologically defined and limited by either recovery or death. Interventions like vaccination or medication either shorten $T_I$ or reduce the case fatality rate (CFR). The CFR is the ratio of those infected that die.

A host’s ability to transmit a disease can also be limited behaviourally and technologically. An example of the former is isolation in chicken pox. When the vesicular rash appears, the diagnosis is obvious and the caregiver isolates the host. The pharmacological treatment of tuberculosis (TB) is an example of technological transmission restriction. TB treatment results in non-infectious hosts. The transmissible period ($\varDelta {\overline{\tau }}$) will therefore be defined as the weighted average of the biological, behavioural and technological restrictions that limit the period during which a host has the opportunity to transmit a disease.

Define an isolated community as a subset of individuals that only interact with other members of that subset. The isolation can be due to a physical boundary like a mountain range or a wall; a cultural barrier like a tribal taboo or language; or a legal barrier prohibiting social interaction.

Let an isolated community of large population size ($N({\mathbf {x}},t)$) exist on a boundaried surface $\delta A({\mathbf {x}})$, where ${\mathbf {x}}$ is a central measure of $\delta A$, at time t. Natural births and deaths are neglected. Let the susceptible population in this community be $S({\mathbf {x}},t)$. Let the density of susceptible individuals be $s({\mathbf {x}},t)=\frac{ S({\mathbf {x}},t)}{\delta A}$. Similarly, let population density be $\rho_n({\mathbf {x}})= \frac{ N({\mathbf {x}})}{\delta A}$ at ${\mathbf {x}},\;\forall \,t$. Then for $N({\mathbf {x}})=\int_{\delta A}\rho_n({\mathbf {x}}) d{\mathbf {A}}$,

$$\begin{aligned} S(\mathbf {x,t})= & {} \int_{\delta A} s({\mathbf {x}},t) d{\mathbf {A}} \iff \frac{S({\mathbf {x}},t)}{N({\mathbf {x}},t)} = \frac{\int_{\delta A}s({\mathbf {x}},t) d{\mathbf {A}}}{\int_{\delta A}\rho_n({\mathbf {x}},t) d{\mathbf {A}}} \nonumber \\\iff & {} \int_{\delta A}s({\mathbf {x}},t) d{\mathbf {A}} = S({\mathbf {x}},t) \int_{\delta A}\frac{ \rho_n({\mathbf {x}},t) }{N({\mathbf {x}},t)}d{\mathbf {A}} \end{aligned}$$

(5)

where $N({\mathbf {x}},t)$ and $\rho_n({\mathbf {x}},t)$ are assumed positive constants in time because natural births and deaths are not significant in this time frame. Let

$$\begin{aligned} {\mathcal{M}} := \frac{1}{N({\mathbf {x}})}\int_{\delta A} \rho_n({\mathbf {x}}) d{\mathbf {A}}=1, \end{aligned}$$

(6)

by the definition of properties of $\rho_n$ and N above. For arbitrary scalar variable $\varphi$, (5) is

$$\begin{aligned} \int_{\delta A}s({\mathbf {x}},t) d{\mathbf {A}} = {\mathcal{M}}S = \int \frac{\partial S }{\partial \varphi } {\mathcal{M}} d\varphi \end{aligned}$$

(7)

because ${\mathcal{M}}$ is a constant. Substituting (6) back into (7),

$$\begin{aligned} \int_{\delta A}s({\mathbf {x}},t) d{\mathbf {A}}= & {} \int \int_{\delta A} \frac{\partial S}{\partial \varphi } \,\frac{\rho_n}{N}d{\mathbf {A}} \,d\varphi = \int_{\delta A}\frac{\rho_n}{N} \int \frac{\partial S}{\partial \varphi } d\varphi \,d{\mathbf {A}} \nonumber \\= & {} \int_{\delta A} S({\mathbf {x}},t)\frac{\rho_n({\mathbf {x}})}{N({\mathbf {x}})}d{\mathbf {A}} \end{aligned}$$

(8)

$$\begin{aligned} \iff s({\mathbf {x}},t)= & {} \frac{S({\mathbf {x}},t)}{N({\mathbf {x}},t)} \rho_n({\mathbf {x}},t). \end{aligned}$$

(9)

Similarly, for the transmissible compartment (T) and transmission-capable host population density ($\tau ({\mathbf {x}},t)$),

$$\begin{aligned} T({\mathbf {x}},t) = \int_{\delta A} \tau ({\mathbf {x}},t) d{\mathbf {A}} \iff \tau ({\mathbf {x}},t) = \frac{T({\mathbf {x}},t)}{N({\mathbf {x}})} \rho_n({\mathbf {x}}) . \end{aligned}$$

(10)

Define sufficient contact between two individuals as sufficient proximity, and duration of that proximity, to allow pathogens to be transmitted from host to potential host within that period. An interaction is necessarily spatial and of sufficient contact.

The position vector will be omitted because only one community is considered further. Let the probability density function, P(t), of an interaction at t be proportional to the product of the transmission-capable host density and the potential host density as for the law of mass action (Ferner and Aronson 2016). Then

$$\begin{aligned} P(t) = \eta \mu \kappa ({\mathbf {x}})\, s(t)\tau (t) \end{aligned}$$

(11)

where $\eta$ is an infectious disease-specific variable that reflects avidity (cumulative binding strength), $\mu$ is a function of mode of transmission (aerosol spread has a higher $\mu$ than droplet spread) and $\kappa ({\mathbf {x}})$ is a function of social behaviour (higher for a culture that greets by kissing compared to bowing). By definition,

$$\begin{aligned} 0\le \int_{\varDelta t}P(t)dt \le 1. \end{aligned}$$

An example of increased $\eta$ resulting in higher probability of transmission has been demonstrated for the $\alpha$ and $\beta$ variants of SARS-CoV2 in reference (Ramanathan et al. 2021). In corona virus disease 2019 (COVID19), it is necessary that the SARS-CoV2 spike protein binds to the luminal angiotensin converting enzyme 2 (ACE2) receptor for transmission. The authors propose that the increased transmissibility of the $\alpha$ and $\beta$ variants may be due to increased spike protein density, increased furin cleavage accessibility or increased spike protein-ACE2 receptor binding affinity. Affinity is the binding strength of one spike protein-ACE2 receptor combination. Avidity is the cumulative binding effect. In this case, avidity would be a function of the spike protein density, affinity and the concentration of virus particles. The authors demonstrate that the greater affinity of the $\alpha$ and $\beta$ variants are consistent with the increased transmissibility (probability of transmission) of these variants.

The 4 recognised respiratory virus modes of transmission are direct contact, indirect contact (fomite), droplet and aerosol (Leung 2021). Although the distinction between droplet and aerosol spread is recognised, a consensus metric for distinguishing between them does not exist. In principle droplets are larger, heavier and travel a shorter distance. Aerosols form a suspension in the air and are displaced, dispersed and diluted by ventilation and convection currents (Wells 1934). Influenza is an airborne disease (droplet and aerosol). Nguyen-Van-Tam et al. expose a control group and an intervention group to influenza. Droplet- and direct contact spread are negated in the intervention group. They demonstrate that, for influenza, droplet- and direct contact spread make negligible contributions to disease propagation. This and a proof of concept study were conducted in closed rooms. The infection rate (secondary attack rate) between this study and the proof of concept study differed significantly. The difference is ascribed to the ventilation rate of 4 L/s per person confined to the rooms of the main study diluting the aerosol (Nguyen-Van-Tam et al. 2020). Given that both aerosol and droplet spread occur in influenza, they have demonstrated (at least for influenza and barring an additional mode of spread) that aerosol spread has a higher transmission probability than droplet spread. This is the effect of $\mu$ in (11).

It is assumed that cultures are location specific. $\kappa ({\mathbf {x}})$ can be interpreted as culture-specific, short-term, socially-acceptable, casual proximity—to distinguish it from population density. Casual contact is the collection of interaction types that exclude the intimate interactions typically occurring within families. For example, an acceptable distance from a stranger in Hong Kong is $\gtrapprox 1,1\text {m}$ while in the USA this distance is $\lessapprox 1\text {m}$ (Sorokowska et al. 2017). Hong Kong has a much higher population density at 6677 per km$^2$ compared to the USA at 34 per km$^2.$ Despite this difference in population density, ${\mathcal{R}}_0$ for 2009 influenza epidemic is consistently higher for the USA (Biggerstaff et al. 2014). The difference in culturally acceptable personal space may explain part of the anomaly.

In a population of size N, the possible unique interactions are the sum of an arithmetic series $\left ( \frac{N(N-1)}{2}\right )$. For $N \gg 1$, this approximates to $\frac{N^2}{2}$. Each interaction represents a transmission opportunity. Then the maximum transmission opportunities $\big ( \psi (N)\big )$ approximate as

$$\begin{aligned} \psi (N) \lessapprox \frac{N^2}{2}. \end{aligned}$$

(12)

The maximum possible direct secondary transmissions due to a single host is $N-1$ but this is limited by $\varDelta {\overline{\tau }}$. Similarly, the maximum possible secondary transmissions over $\varDelta {{\overline{\tau }}}$ are

$$\begin{aligned} \psi (N)\int_{\varDelta {\overline{\tau }}}P(t) dt \lessapprox \frac{N^2}{2}\int_{\varDelta {\overline{\tau }}}P(t)dt. \end{aligned}$$

(13)

Substituting (9), (10) and (11) into (13), the transmissions produced over a primary host’s $\varDelta {{\overline{\tau }}}$ are

$$\begin{aligned} \int_{t_0}^{t_0+\varDelta {\overline{\tau }}} {\dot{T}}(t_0)dt= & {} \int_{t_0}^{t_0 + \varDelta {\overline{\tau }}} \eta \mu \kappa \frac{N^2}{2} s(t_0)\tau (t_0) dt \nonumber \\= & {} \int_{t_0}^{t_0 + \varDelta {\overline{\tau }}} \frac{\eta \mu \kappa }{2} \rho_n^2 S(t_0)T(t_0) dt \nonumber \\= & {} \int_{t_0}^{t_0 + \varDelta {\overline{\tau }}} \beta_A\rho_n^2 S(t_0)T(t_0) dt \end{aligned}$$

(14)

where $\beta_A = \frac{1}{2}\eta \mu \kappa$.

For interval $\varDelta t > \varDelta {\overline{\tau }}$, the Heaviside step function is used and emphasises the discrete underlying processes. The equivalent of (14) over this $\varDelta t$ is

$$\begin{aligned} \int_{\varDelta t} {\dot{T}}(t_0)\,dt = \int_{\varDelta t } [u(t_0)-u(t_0+\varDelta {\overline{\tau }})]\; \beta_A \rho_n^2 \;S(t_0)\,T(t_0) \,dt. \end{aligned}$$

(15)

Thus (14) is formulated over interval $\varDelta {\overline{\tau }}$ or an arbitrary period $\varDelta t >\varDelta {{\overline{\tau }}}$ (15).

As for the SIR model, the rate at which individuals leave S is the same as the rate at which they enter T. Restated, ${\dot{S}}(t) =-{\dot{T}}(t).$ Then from (14)

$$\begin{aligned} {\dot{S}}(t) = -\beta_A\rho_n^2S(t)T(t). \end{aligned}$$

(16)

For an interval greater than $\varDelta {\overline{\tau }}$ (15), the Heaviside version of (14), is required.

Redefine the removed compartment as consisting of hosts no longer transmission capable by virtue of recovery, death, behavioural adaptation or technological intervention. An individual is infected at $t_0$. That host remains transmission-capable for $\varDelta {\overline{\tau }}$. Thus the rate at which hosts enter R is the same as the rate at which they entered T one $\varDelta {\overline{\tau }}$ ago (Brauer et al. 2019). Restated,

$$\begin{aligned} {\dot{R}}(t) = {\dot{T}}(t-\varDelta {\overline{\tau }}). \end{aligned}$$

(17)

The SIR model proposes that ${\dot{I}}(t)$ is the difference between S’s rate of decrease and R’s rate of increase. Similarly, substituting (16) and (17) to determine ${\dot{T}}(t)$, the system of DDEs describing the movement between compartments $S,\,T$ and R are

$$\begin{aligned} {\dot{S}}(t)= & {} -\beta_A\rho_n^2 ({\mathbf {x}})\;S(t)\,T(t) \nonumber \\ {\dot{T}}(t)= & {} \beta_A\rho_n^2 ({\mathbf {x}})\;S(t)\,T(t) - {\dot{T}}( t-\varDelta {\overline{\tau }})\nonumber \\ {\dot{R}}(t)= & {} {\dot{T}}(t-\varDelta {\overline{\tau }}). \end{aligned}$$

(18)

Model (18) is the boundaried DDE version of Model (1) and is designated the STR model. The derivation of this model on a surface has incorporated population density.

Assume that the homogenous solution to $T({\mathbf {x}},t)$ is exponential such that

$$\begin{aligned} T({\mathbf {x}},t) = A({\mathbf {x}})e^{r({\mathbf {x}})t}. \end{aligned}$$

(19)

Equation (19) is the real, homogenous solution to the linearised STR (18) (Smith 2010)(See Appendix). Substituting (19) into the delay term of Model (18)’s T,

$$\begin{aligned} \frac{\partial }{\partial t} T({\mathbf {x}},t-\varDelta {\overline{\tau }}) = A({\mathbf {x}})r({\mathbf {x}})e^{-r({\mathbf {x}})\varDelta {\overline{\tau }}}e^{r({\mathbf {x}})t} = \alpha T({\mathbf {x}},t) \end{aligned}$$

(20)

where

$$\begin{aligned} \alpha ({\mathbf {x}},t) = {}_{\tau }\alpha \, u(\varDelta {\overline{\tau }}) \end{aligned}$$

(21)

and ${}_{\tau }\alpha ({\mathbf {x}}) = r({\mathbf {x}})e^{-r({\mathbf {x}})\varDelta {\overline{\tau }}}$. The subscript $\tau$ is for transmissible. Substituting (20) into Model (18), reduces the latter to an ODE-like model,

$$\begin{aligned} {\dot{S}}(t)= & {} -\beta_A\rho_n^2({\mathbf {x}}) \;S(t)\,T(t) \nonumber \\ {\dot{T}}(t)= & {} \beta_A\rho_n^2 ({\mathbf {x}})\;S(t)\,T(t) - \alpha ({\mathbf {x}}) \,T( t)\nonumber \\ {\dot{R}}(t)= & {} \alpha ({\mathbf {x}}) \,T( t). \end{aligned}$$

(22)

Comparing Models (22) and (1), the horizontal transmission incidence (Hethcote 2008) is

$$\begin{aligned} \xi ({\mathbf {x}}) = \beta_A\rho_n^2({\mathbf {x}})\,N({\mathbf {x}}). \end{aligned}$$

(23)

Applying the definition of ${\mathcal{R}}_0$ for the SIR model from Section 1’s (3) (Brauer et al. 2019), STR Model (22)’s basic reproduction number is

$$\begin{aligned} {}_{\tau }{\mathcal{R}}_0 ({\mathbf {x}})=\frac{\xi ({\mathbf {x}})}{\alpha ({\mathbf {x}},t \ge \varDelta {\overline{\tau }})} \end{aligned}$$

(24)

and undefined for $t< \varDelta {\overline{\tau }}$.

$\xi$’s derivation for Models (18) and (22) differs from Brauer et al.’s (Brauer et al. 2019) mass action $\xi$ derivation. Brauer et al. assume that a host has $\beta N$ transmission-capable interaction per unit time. They then multiply this by the chance that such an interaction is with a susceptible individual $\big (\frac{S}{N}\big )$. This product is ${\dot{S}}(t)$. Consequently, $\xi = \beta N$ for mass action incidence. Thus only the potential direct secondary transmissions are considered. In contrast, (14)’s $\xi$ calculates the average transmissions over all potential interactions on N over $\varDelta {\overline{\tau }}$. This includes indirect secondary transmissions. Thus, in principle,

$$\begin{aligned} {\mathcal{R}}_0 \le {}_{\tau }{\mathcal{R}}_0. \end{aligned}$$

Comparing the STR’s ${}_{\tau }{\mathcal{R}}_0$ to ${\mathcal{R}}_0$ for mass action incidence $(\xi =\beta N)$ and the standard incidence $(\xi = \beta_{si})$,

$$\begin{aligned} \frac{\beta_A\rho_n^2({\mathbf {x}})N({\mathbf {x}})}{\alpha (t>\varDelta {\overline{\tau }})} = {}_{\tau }{\mathcal{R}}_0({\mathbf {x}}) \ge {\mathcal{R}}_0 = \frac{\beta N}{\alpha } \;\; \text {or} \;\; \frac{\beta_{is}}{\alpha }. \end{aligned}$$

(25)

3 Biological Derivation of a Continuous Basic Reproduction Number

A transmissible timescale is derived that converts the STR model (18) into an ODE model. A rhythmic timescale is then defined and mass action-, standard- and hybrid incidence (HI) derived in the rhythmic timescale.

3.1 Defining the Transmissible Timescale

STR Model (18)’s coefficients are derived, in part, from (14). Equation (14)’s Heaviside version (15) emphasises the finite transmissible period.

For timescale $1:\varDelta t < 1:\varDelta {\overline{\tau }},$ (15) should be used to derive a Heaviside version of (16). Thus timescale $1:\varDelta t < 1: \varDelta {\overline{\tau }}$ introduces a step function (15) in the STR Model (18)’s $\xi .$ Conversely, $1: \varDelta t > 1:\varDelta {\overline{\tau }}$ introduces a step function in ODE-like Model (22)’s $\alpha .$

Thus timescale

$$\begin{aligned} 1:\varDelta t = 1:\varDelta {\overline{\tau }}. \end{aligned}$$

transforms (22) into an ODE model similar to Model (1). This $\varDelta {{\overline{\tau }}}$-based timescale is the transmissible timescale. ${}_{\tau }\alpha$ and ${}_{\tau }{\mathcal{R}}_0$ are then the transmissible timescale infection frequency and basic reproduction number, respectively.

3.2 Defining the Rhythmic Timescale

Consider a host infected by chickenpox (Varicella Zoster). The host becomes infectious after 14 days. There is an additional 2-3 days (the prodrome) before the vesicular rash appears, the diagnosis is obvious and the host is isolated.

This host’s routine may include sleeping from 10 PM to 6 AM, public transport between 7:30 and 8AM, and from 5:30 to 6PM; classroom from 8AM to 5PM; a cafeteria at 1PM; and family time from 6PM to 10PM. Comparing this routine with (11), a diurnal variation exists to the probability of a successful interaction. Selecting a timescale of 1 : 1 day masks this variation. Restated,

$$\begin{aligned} \int_{t_0+k\varDelta t}^{t_0+ (k+1)\varDelta t} P(t) dt = p_{daily} \qquad \forall \;\varDelta t = 1\, \text {day}, k \in {\mathbb {N}} \end{aligned}$$

Similarly, weekly, monthly and annual activities are periodic. Thus multiple timescales may exist that result in constant integrals of (11) over a time unit in that timescale.

A rhythmic timescale

$$\begin{aligned} 1:\varDelta t = 1:\delta t \end{aligned}$$

is defined for periodic host transmission opportunity. Assuming a periodic transmission opportunity, $\exists \;\delta t\in {\mathbb {R}}$ such that $\forall \,t_0 \in {\mathbb {R}}$

$$\begin{aligned} p = \int_{t_0}^{t_0+\delta t}P(t)dt = \int_{\delta t}P(t)dt. \end{aligned}$$

(26)

The constant, p, represents the probability of an event on $\psi (N)\; \text {over} \; \delta t.$ Successful interactions are then independent events with probability p on $\psi (N).$

3.3 The Rhythmic Timescale Mass Action-, Standard- and Hybrid Incidence ${\mathcal{R}}_0$

Let the time increments in the transmissible timescale be an integer multiple of the increments in the rhythmic timescale. Then

$$\begin{aligned} \varDelta {\overline{\tau }} \approx {\mathfrak{B}}\delta t \qquad \text {where} \qquad {\mathfrak{B}}\in {\mathbb {N}}. \end{aligned}$$

(27)

${\mathfrak{B}}$ is necessary to transform between the transmissible- and rhythmic timescales.

3.3.1 Mass Action Incidence, Basic Reproduction Number in Rhythmic Timescale

The mass action incidence formulation assumes that all host interactions are random and that $S\approx N$ for several $\delta t$ early in the epidemic. By definition, ${}_{\tau }{\mathcal{R}}_0$ is the number of secondary hosts produced by a primary host over $\varDelta {\overline{\tau }}.$ At $t=t_0$ the only host is the primary host and the number of secondary hosts over $\varDelta {\overline{\tau }}$ are necessarily ${}_{\tau }{\mathcal{R}}_0.$ This can be restated as

$$\begin{aligned} {}_{\tau }{\mathcal{R}}_0 = \int_{\varDelta t = \varDelta {\overline{\tau }}}{\dot{T}}(t_0) dt. \end{aligned}$$

(28)

At the equivalent $t= \varDelta {\overline{\tau }}$ in any timescale, (28) is true. From (2), in 1 time unit of the transmissible timescale,

$$\begin{aligned} \xi (t_0) = \frac{{}_{\tau }{\mathcal{R}}_0}{N\times 1}. \end{aligned}$$

From (26) the primary host will infect $pS \approx pN$ individuals over $\delta t$. Applying (2), over 1 time unit of the rhythmic timescale,

$$\begin{aligned} {}_{\varrho }\xi (t_0) = \frac{pN}{N \times 1} \end{aligned}$$

where ${}_{\varrho }\xi (t_0)$ is the rhythmic timescale $\xi$ at $t_0$. Because mass action incidence assumes $S\approx N$ for several $\delta t$, there are ${\mathfrak{B}}pN$ transmissions over ${\mathfrak{B}}\delta t =\varDelta {\overline{\tau }}$. From (28), ${\mathfrak{B}}pN = {}_{\tau }{\mathcal{R}}_0$. Therefore, after ${\mathfrak{B}}$ time units in the rhythmic timescale,

$$\begin{aligned} \int_{t_0}^{t_0 +{\mathfrak{B}}}{}_{\varrho }\xi (t) dt= & {} \sum_{{\mathfrak{B}}}\frac{pN}{N \times 1} = \frac{{\mathfrak{B}}pN}{N} ={\mathfrak{B}}\,{}_{\varrho }\xi (t_0)\\= & {} \frac{{}_{\tau }{\mathcal{R}}_0}{N} = \xi (t_0). \end{aligned}$$

Therefore, the rhythmic timescale $\xi$ is the arithmetic mean of the transmissible timescale $\xi$. Restated

$$\begin{aligned} {}_{\varrho }\xi (t_0) =\frac{\xi (t_0)}{{\mathfrak{B}}}. \end{aligned}$$

(29)

From (21), for $0< t < \varDelta {\overline{\tau }}$, $\alpha = 0$ and, consequently, ${}_{\varrho }{\mathcal{R}}_0$ is undefined. ${}_{\tau }{\mathcal{R}}_0$ is the number of secondary hosts originating over the primary host’s $\varDelta {\overline{\tau }}$ in a completely susceptible population. Therefore either ${\mathcal{R}}_0$ is timescale invariant or ${\mathcal{R}}_0 \ge 1$ or ${\mathcal{R}}_0 < 1$ (4) should be timescale invariant.

Define a non-zero rhythmic timescale $\alpha$ as

$$\begin{aligned} {}_{\varrho }\alpha :{=} \frac{{}_{\tau }\alpha }{{\mathfrak{B}}}. \end{aligned}$$

(30)

Then, from (3), one can use (29) and (30) to derive a rhythmic timescale ${\mathcal{R}}_0$:

$$\begin{aligned} {}_{\varrho }{\mathcal{R}}_0 =\frac{{}_{\varrho }\xi (t_0)}{{}_{\varrho }\alpha } = \frac{\xi (t_0)}{{}_{\tau }\alpha } ={}_{\tau }{\mathcal{R}}_0 \end{aligned}$$

that preserves ${\mathcal{R}}_0$ and the property ${\mathcal{R}}_0 \ge 1$ or ${\mathcal{R}}_0 < 1$. The resultant mass action incidence, STR model in the rhythmic timescale is then

$$\begin{aligned} {\dot{S}}(t)= & {} -\frac{ \beta }{{\mathfrak{B}}}\; S(t)\, T(t)\\ {\dot{T}}(t)= & {} \frac{ \beta }{{\mathfrak{B}}}\;S(t)\,T(t) - \frac{{}_{\tau }\alpha }{{\mathfrak{B}}}\, T(t)\\ {\dot{R}}(t)= & {} \frac{{}_{\tau }\alpha }{{\mathfrak{B}}}\, T(t). \end{aligned}$$

3.3.2 Standard Incidence Basic Reproduction Number in the Rhythmic Timescale

Hethcote’s standard incidence assumes that interactions are non-random. One only interacts with close contacts, $N_c\ll N$ (Hethcote 2008). Hethcote (2000), Anderson and May (1982, 1992) provide experimental evidence to support the argument.

From Sect. 3.2 and (26), the new transmissions over $\delta t$ occur with probability p. Transmission occurring in subsequent $\delta t$ are independent events. Early in the epidemic, the new entrants to T equate to ${\dot{T}}(t).$

Table 1 Changes in the SI compartments per $\delta t$ in the standard incidence model

Table 1 provides the compartment sizes, at $\delta t$ intervals, before primary host removal ($\jmath \delta t \le \varDelta {\overline{\tau }}$).

From (2) and the definition of incidence,

$$\begin{aligned} \xi (t\approx t_0) = -\frac{{\dot{S}}(t)}{S(t)} = \frac{{\dot{T}}(t\approx t_0)}{S(t\approx t_0)}. \end{aligned}$$

(31)

Substituting terms from Table 1 into (31), without loss of generality,

$$\begin{aligned} \xi (t\approx t_0) = -\frac{{\dot{S}}(t)}{S(t)} = \chi \qquad \text {where} \;\chi = p \;\;\text {or} \; \;\frac{p}{1-p}\qquad \iff S(t) =S_0e^{-\chi t} . \end{aligned}$$

In the rhythmic timescale ($1:\delta t$), over one time unit,

$$\begin{aligned} {}_{\varrho }\xi = \frac{S_0e^{-\chi } -S_0}{S_0 \times 1} \iff e^{-\chi } = {}_{\varrho }\xi + 1. \end{aligned}$$

(32)

After ${\mathfrak{B}}$ time units in this rhythmic timescale, S(t) is $S_0e^{-\chi {\mathfrak{B}}}$. ${\mathfrak{B}}$ time units in the rhythmic timescale is only one time unit in the transmissible timescale. Substituting (32) at $t_0$ over $\varDelta {\overline{\tau }}$ into the discrete version of (2),

$$\begin{aligned} {}_{\tau }\xi = \frac{S_0e^{-\chi {\mathfrak{B}}} -S_0}{S_0 \times 1} = ({}_{\varrho }\xi + 1)^{{\mathfrak{B}}} -1 \iff \root \mathfrak{B} \of {{}_{\tau }\xi + 1} = {}_{\varrho }\xi +1. \end{aligned}$$

Performing the binomial expansion,

$$\begin{aligned} \sum_{k=0}^{{\mathfrak{B}}} {{\mathfrak{B}}\atopwithdelims ()k} {}_{\varrho }\xi^{k} = {}_{\tau }\xi +1 \iff {}_{\tau }\xi = \sum_{k=1}^{{\mathfrak{B}}} {{\mathfrak{B}}\atopwithdelims ()k} {}_{\varrho }\xi^{k} . \end{aligned}$$

For ${}_{\varrho }\xi \gg 1$ and ${}_{\tau }\xi \gg 1$,

$$\begin{aligned} {}_{\varrho }\xi \lessapprox \root \mathfrak{B} \of { {}_{\tau }\xi } . \end{aligned}$$

(33)

As for the transmissible timescale mass action incidence in Section 3.3.1, from (21), $\alpha = 0$ in the rhythmic timescale. Consequently, ${\mathcal{R}}_0$ is undefined. Define

$$\begin{aligned} {}_{\tau }\alpha :{=} \sum_{k=1}^{{\mathfrak{B}}} {{\mathfrak{B}}\atopwithdelims ()k} {}_{\varrho }\alpha^{k} \Longrightarrow {}_{\varrho }\alpha \lessapprox \root \mathfrak{B} \of {{}_{\tau }\alpha } = \root \frac{\varDelta t}{\delta t} \of {\alpha (t>\varDelta {\overline{\tau }})} \quad 0\le t < \varDelta {\overline{\tau }} \end{aligned}$$

(34)

for ${}_{\varrho }\alpha \gg 1$ and ${}_{\tau }\alpha \gg 1$. Substituting (33) and (34) into (3),

$$\begin{aligned} {}_{\varrho }{\mathcal{R}}_0 \lessapprox \root \mathfrak{B} \of {\frac{ {}_{\tau }\xi }{{}_{\tau }\alpha }} = \root \mathfrak{B} \of {{}_{\tau }{\mathcal{R}}_0} \end{aligned}$$

(35)

and the property of ${\mathcal{R}}_0 < 1 \;\text {or} > 1$ (4) is preserved across timescales.

The standard incidence, STR in the rhythmic timescale is approximately

$$\begin{aligned} {\dot{S}}(t)= & {} -\root \mathfrak{B} \of {\beta_{si} }\;\frac{S(t)\,T(t)}{N({\mathbf {x}})} \\ {\dot{T}}(t)= & {} \root \mathfrak{B} \of {\beta_{si} }\;\frac{S(t)\,T(t)}{N({\mathbf {x}})} - \root \mathfrak{B} \of {{}_{\tau }\alpha }\;T(t) \\ {\dot{R}}(t)= & {} \root \mathfrak{B} \of {{}_{\tau }\alpha }\;I(t). \end{aligned}$$

3.3.3 Hybrid Incidence Basic Reproduction Number in the Rhythmic Timescale

Section 2 derives an N-dependent $\xi$ (23). Substituting (23) into (33),

$$\begin{aligned} {}_{\varrho }\xi = \root \mathfrak{B} \of {\beta_A\rho_n^2N} \end{aligned}$$

(36)

ensures the geometric decrease in S. As in (34),

$$\begin{aligned} {}_{\varrho }\alpha :{=} \frac{1}{{\mathfrak{B}}}\root \mathfrak{B} \of {{}_{\tau }\alpha }. \end{aligned}$$

From (35) and (25), the property ${\mathcal{R}}_0 <1$ or ${\mathcal{R}}_0>1$ (4) is preserved by

$$\begin{aligned} {}_{\varrho }{\mathcal{R}}_0({\mathbf {x}}) \approx \root \mathfrak{B} \of {{}_{\tau }{\mathcal{R}}_0} \ge \root \mathfrak{B} \of {{\mathcal{R}}_0}. \end{aligned}$$

(37)

The HI, STR in the rhythmic timescale is then approximately

$$\begin{aligned} {\dot{S}}(t)= & {} -\root \mathfrak{B} \of {\beta_A\rho_n^2N}\;\frac{S(t)\,T(t)}{N({\mathbf {x}})}\\ {\dot{T}}(t)= & {} \root \mathfrak{B} \of {\beta_A\rho_n^2N}\;\frac{S(t)\,T(t)}{N({\mathbf {x}})} - \root \mathfrak{B} \of {{}_{\tau }\alpha }\;I(t)\\ {\dot{R}}(t)= & {} \root \mathfrak{B} \of {{}_{\tau }\alpha }\;I(t). \end{aligned}$$

4 Hybrid Incidence, STR Validation in the 1 : 1 Day Timescale

The HI-STR’s predicted relationship between ${}_{\varrho }{\mathcal{R}}_0$ and $\rho_n$ is demonstrated for a droplet spread, an aerosol spread and a non-airborne disease. Published central measures (mode, median or mean) will represent ${}_{\varrho }{\mathcal{R}}_0$ ranges.

4.1 SARS (SARS-CoV)

Severe acute respiratory syndrome (SARS) was caused by SARS Coronavirus (SARS-CoV) in the Far East Asia in 2002 (Cheng et al. 2007; Christian et al. 2004). Transmission was primarily droplet spread (Christian et al. 2004). 22% may have required hospitalisation (Lau et al. 2004). Symptom onset marked infectiousness (Zeng et al. 2009). The incubation mode was 4 days (Lessler et al. 2009; Donnelly et al. 2003). Symptom onset to self-isolation is unknown. Symptom onset to hospitalisation mode was 0.5 to 2.5 days (Donnelly et al. 2003; Anderson et al. 2004). This is summarised in Table 2.

Table 2 Transmission dynamics for SARS—removal refers to removal from society

The unknown non-hospitalised $\varDelta {\overline{\tau }}$ is assumed the same as for the hospitalised. $\varDelta {\overline{\tau }} = 1.5$ days (Anderson et al. 2004). $\delta t = 1 \;\text{day}$. Substituting the resultant ${\mathfrak{B}} = 1.5$ into (37).

$$\begin{aligned} {}_{\varrho }{\mathcal{R}}_0 = \root \mathfrak{B} \of {{}_{\tau }{\mathcal{R}}_0} \;= & {} \;\root \mathfrak{B} \of {\frac{\beta_A \rho_n^2 N}{\alpha (t>\varDelta {\overline{\tau }})}} = \root \mathfrak{B} \of {\frac{\beta_AN}{{}_{\tau }\alpha }} \times \rho_n^{\frac{2.0}{1.5}}\nonumber \\ \iff \ln ({}_{\varrho }{\mathcal{R}}_0)= & {} \ln (\varGamma ) + 1.3 \ln (\rho_n) \end{aligned}$$

(38)

(where $\varGamma = \root \mathfrak{B} \of {\beta_A N / {}_{\tau }\alpha }$). SARS’ ${}_{\varrho }{\mathcal{R}}_0$’s theoretical dependence on $\rho_n$ is (38).

Table 3 2002/2003 SARS epidemic’s population density and basic reproduction number

Toronto and 4 Asian cities’ experimental ${}_{\varrho }{\mathcal{R}}_0$ (Chowell et al. 2004a; Tuan et al. 2007; Zhang et al. 2004) and $\rho_n$ (Statistics Canada. 2017 2017; Hong Kong Government 2003; Central Population and Housing Census Steering Committee 2010; Taipei City Government 2020) are presented in Table 3. The natural logarithms are plotted in Fig. 1. The experimental gradient of 1.35 should be compared with (38).

Fig. 1

Experimental depiction of the predicted linear $\ln ({}_{\varrho }{\mathcal{R}}_0)$ to $\ln (\rho_n)$ relationship

The SARS-CoV validation uses retrospective ${}_{\varrho }{\mathcal{R}}_0$ on a cross-section of (mostly Asian) cities during the course of one droplet-spread epidemic.

4.2 Measles (Rubeola)

Measles incubates for 10–12 days (Lessler et al. 2009). The prodrome of non-specific (Moss and Griffin 2012), but debilitating, symptoms heralds the infectious (Klinkenberg and Nishiura 2011) period. The pathognomonic morbilliform rash ends the 2-4 day prodrome.

Table 4 Population density and historical measles ${}_p{\mathcal{R}}_0$ for Measles in Europe

Fig. 2

Predicted linear relationship between $\ln ({}_{\varrho }{\mathcal{R}}_0)$ and $\ln (\rho_n)$for measles in Europe

Conjecturing isolation at day 3 of the prodrome, $\varDelta {\overline{\tau }}$ is 3 days; $\delta t =1$ day and ${\mathfrak{B}}=3.$ Substituting the latter into (37), for measles:

$$\begin{aligned} \ln ({}_{\varrho }{\mathcal{R}}_0) = \ln (\varGamma ) + 0.66 \ln (\rho_n). \end{aligned}$$

(39)

Table 4 documents the experimental ${}_{\varrho }{\mathcal{R}}_0$ for 5 countries at 8 historical periods Guerra et al. (2017). Figure 2 demonstrates the linear relationship predicted by (39).

Several experimental ${}_{\varrho }{\mathcal{R}}_0$ methods across multiple, historical, European measles epidemics have validated the STR for aerosol-spread infections. The increased $R^2$ is likely due to the several methods used by several investigators to calculate ${\mathcal{R}}_0$ for measles. The STR model applies to isolated communities. Although regions within countries may be treated as sufficiently isolated, it may be that countries are insufficiently isolated in Europe.

4.3 Ebola (EBOV)

Ebola disease is caused by 1 of 7 Ebola virus species in the genus Ebolavirus of the family filoviridae (Feldmann et al. 2020; Weppelmann et al. 2016; Jacob et al. 2020). Ebola disease has a high CFR (Colebunders and Borchert 2000; Chowell and Nishiura 2014; Althaus 2014; Feldmann et al. 2003) and is not airborne. Bodily fluid transmission is by blood, urine, faeces, vomit, breast milk, saliva and sexual contact (Jacob et al. 2020).

Ebola virus disease is the ebola disease caused by the Zaire species (EVOD). CFR is 43-89% (Jacob et al. 2020; Colebunders and Borchert 2000; Chowell and Nishiura 2014) and $\delta t$ is 1 day. The infected are categorised as

• asymptomatic,

• symptomatic and quarantined (hospital or an ebola treatment unit) (Jacob et al. 2020),

• symptomatic and isolated at home (Chowell and Nishiura 2014; Weppelmann et al. 2016).

The median incubation period—6-12 days (Feldmann et al. 2003, 2020; Weppelmann et al. 2016; Chowell and Nishiura 2014; Althaus 2014; Jacob et al. 2020; Velásquez et al. 2015; Van Kerkhove et al. 2015).

Table 5 Population density and Ebola ${}_{\varrho }{\mathcal{R}}_0$ for African countries

Kerkhove et al.’s median time from symptom onset to hospitalisation is 4 days (Van Kerkhove et al. 2015). Hospitalisation has been demonstrated to reduce transmission (Agua-Agum et al. 2016).

Fig. 3

Experimental linear relationship between $\ln ({}_{\varrho }{\mathcal{R}}_0)$ and $\ln (\rho_n)$ for Ebola in Africa

The end of $\varDelta {\overline{\tau }}$ is the weighted average of the time to hospitalisation and the time to isolation. These periods are assumed the same. The median time to hospitalisation is $\varDelta {\overline{\tau }} =4$ days (Van Kerkhove et al. 2015). Substituting $\delta t$ and $\varDelta {\overline{\tau }}$ into (37),

$$\begin{aligned} \ln ({}_{\varrho }{\mathcal{R}}_0) = \ln (\varGamma ) + 0.50 \ln (\rho_n). \end{aligned}$$

(40)

The Democratic Republic of Congo (DRC) outbreak in 1995 differs from the 2000 Uganda outbreak and the 2014 outbreak (Chowell et al. 2004b; Legrand et al. 2007). Chowell et al. (2004b) shows a shortened infectious period and Legrand (Legrand et al. 2007) demonstrates more transmission at funerals in the DRC. The DRC outbreak is omitted. Table 5 summarises ${}_{\varrho }{\mathcal{R}}_0$ for Guinea, Sierra Leone, Liberia (Althaus 2014) and Uganda (Legrand et al. 2007) . Equation (40)’s predicted linear relationship is demonstrated experimentally in Fig. 3.

The non-airborne Ebola validation has been performed using retrospective ${}_{\varrho }{\mathcal{R}}_0$ data for multiple African countries.

5 Discussion

The transmissible timescale is based on the period that a host is able to transmit disease. This period ends with either host demise, recovery, behavioural modification or technological intervention.

The rhythmic timescale is a consequence of the host’s cyclical transmission opportunity. The sleep-wake cycle is the origin of the periodic transmission opportunity of the childhood infectious diseases. For childhood infectious diseases the diurnal periodicity corresponds to the period of experimental data collection.

Hybrid incidence lies between the extremum of completely random interactions (mass action incidence) and completely non-random interactions (standard incidence). The geometric mean converts the basic reproduction number, infection frequency and horizontal transmission incidence between the transmissible- and rhythmic timescales under special circumstances.

The HI-STR model can predict the basic reproduction number for sufficiently isolated communities. The prediction is based on transmission dynamics, population-size and -density. It reduces to an ODE model in the transmissible timescale. The resultant localised basic reproductive numbers facilitate differentiated control measures and resource allocation. The isolated community idealisation has imposed a significant constraint on the discretisation of a surface. Experiential construction of isolated communities is necessary until an objective measure of sufficient isolation is derived.

The geographical constraints of the SIR model were not obvious. The HI-STR has established that the SIR model applies to sufficiently isolated populations. The HI-STR model effectively recognises a pandemic as a collection of epidemics of the same kind at multiple locations and stages of temporal propagation.

6 Conclusion

A boundaried, DDE SIR-like model—the STR model—is constructed. The hybrid incidence (HI) STR model in the rhythmic timescale predicts the basic reproduction number (${\mathcal{R}}_0$)’s dependence on population density. The model has been validated for multiple transmission modes where one host-vector predominates. The HI-STR allows a priori determination of localised ${\mathcal{R}}_0$s by adjusting for local population-size and -density. This permits localised mitigation strategies, resource allocation and temporal resource redistribution. Cultural similarity is required to transfer adjusted ${\mathcal{R}}_0$s.

For models simulating only one host type transmitting a disease, the transmissible timescale masks the HI-STR model’s delays. The geometric mean converts the horizontal transmission incidence and infection frequency between the transmissible- and rhythmic timescales.

7 Recommendation

The HI-STR allows geographical risk stratification based on population-size and -density. The impact is not obvious. It is conceivable that a high ${\mathfrak{B}}$ diminishes the significance of geographical stratification.

The isolated community idealisation simplifies the reduction of the HI-STR model to an ODE model. The resultant ODEs prohibit the modelling of spatial spread. A surface STR model with partial differential equations will simplify surface discretisation, simulate population mobility and predict a pandemic’s wave-like spatial propagation.

The model has been validated for infectious diseases with a diurnal variation in transmission opportunity. The sexually transmitted diseases’ (STDs’) cyclical transmission opportunities have a low frequency. The STDs thus provide an opportunity to validate the model in (non-diurnal) timescales that mask their longer transmission opportunity period.

Appendix: Solution for Linearised STR Model

A real solution to the linearised STR model is derived. Smith (2010) and Diekmann et al. (1995) provide comprehensive coverage.

Consider the system of DDEs (18). Early in the disease, one can make the approximation $N \approx S$ reducing the system to the linear DDE system

$$\begin{aligned} \begin{pmatrix} {\dot{S}}\\ {\dot{T}}\\ {\dot{R}} \end{pmatrix} = \begin{bmatrix} 0 &{} -\xi &{} 0 \\ 0 &{} \xi &{} 0 \\ 0 &{} 0 &{} 0 \end{bmatrix} \quad \begin{pmatrix} S(t)\\ T(t)\\ R(t) \end{pmatrix} + \begin{bmatrix} 0 &{} 0 &{} 0\\ 0 &{} -1 &{} 0\\ 0 &{} 1 &{} 0 \end{bmatrix} \quad \begin{pmatrix} {\dot{S}}(t-\varDelta {{\overline{\tau }}})\\ {\dot{T}}(t-\varDelta {{\overline{\tau }}}) \\ {\dot{R}}(t-\varDelta {{\overline{\tau }}}) \end{pmatrix} \end{aligned}$$

which (for ${\mathbf {z}}\;\in \;{\mathbb {R}}^3$) is of the form

$$\begin{aligned} \dot{{\mathbf {z}}} = A{\mathbf {z}}(t) + B \dot{{\mathbf {z}}}(t-\tau ). \end{aligned}$$

(41)

Refer to Kuang for analysis of this first order real scalar linear neutral delay equation (Kuang 1993). Only the transmissible compartment is considered further. For

$$\begin{aligned} {\dot{z}}_2 = \xi z_2(t) - {\dot{z}}_2(t-\tau ) \end{aligned}$$

(42)

Let $z_2(t) = e^{\lambda t}$ where $\lambda \in {\mathbb {C}}$. Substituting this into (42),

$$\begin{aligned} \lambda e^{\lambda t} = \xi e^{\lambda t} - \lambda e^{\lambda (t-\tau )} = \xi e^{\lambda t} - \lambda e^{\lambda t}e^{-\lambda \tau }\; \iff \; e^{\lambda t} (\xi - \lambda - \lambda e^{-\lambda \tau }) =0 \end{aligned}$$

(43)

and the roots of the characteristic equation

$$\begin{aligned} \xi -\lambda (1 + e^{-\lambda \tau }) = 0 \end{aligned}$$

are the solutions to $\lambda$. Let the real part of $\lambda$ be x and the imaginary part be y then on the complex plane,

$$\begin{aligned} \xi = x + x e^{ - x\tau }\cos (y\tau ) - y e^{-x}\sin (y\tau ) \nonumber \\ 0 = y + x e^{-x\tau } \sin (y\tau ) + ye^{-x} \cos (y\tau ) \nonumber \\ \begin{pmatrix} \xi \\ 0 \end{pmatrix} = \bigg [ I + e^{-\tau x}R(\tau y)\bigg ] \begin{pmatrix} x\\ y \end{pmatrix} \end{aligned}$$

(44)

where I is the identity matrix $\begin{bmatrix} 1 &{} 0 \\ 0&{} 1\end{bmatrix}$ and $R(\tau y) = \begin{bmatrix}\cos (\tau y) &{} -\sin (\tau y) \\ \sin (\tau y) &{} \cos (\tau y) \end{bmatrix}$ is the rotation matrix. Note that a positive real solutions exist. At $y =0$, for $x > 0$. $0< e^{-x}< 1$ and therefore $\frac{\xi }{2}< x < \xi$. Given that (biologically) $\xi >0$, for $y =0$, all the terms in $R(\tau y)>0$ and $e^{-\tau x} >0 \Rightarrow x \nleq 0.$