Efficient algorithm for 3D bimodulus structures

Abstract

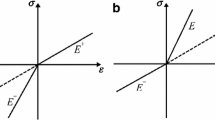
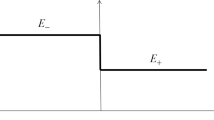
The bimodulus material is a classical model to describe the elastic behavior of materials with tension–compression asymmetry. Due to the inherently nonlinear properties of bimodular materials, traditional iteration methods suffer from low convergence efficiency and poor adaptability for large-scale structures in engineering. In this paper, a novel 3D algorithm is established by complementing the three shear moduli of the constitutive equation in principal stress coordinates. In contrast to the existing 3D shear modulus constructed based on experience, in this paper the shear modulus is derived theoretically through a limit process. Then, a theoretically self-consistent complemented algorithm is established and implemented in ABAQUS via UMAT; its good stability and convergence efficiency are verified by using benchmark examples. Numerical analysis shows that the calculation error for bimodulus structures using the traditional linear elastic theory is large, which is not in line with reality.

Appendices

Appendix A

1.1 Deduction of the constitutive equation Eq. (3)

The direction cosines obey the following relationships:

$$\left\{ {\begin{array}{*{20}l} {l_{1}^{2} + l_{2}^{2} + l_{3}^{2} { = }1,} \hfill & {l_{1} m_{1} + l_{2} m_{2} + l_{3} m_{3} = 0,} \hfill \\ {m_{1}^{2} + m_{2}^{2} + m_{3}^{2} = 1,} \hfill & {l_{1} n_{1} + l_{2} n_{2} + l_{3} n_{3} = 0,} \hfill \\ {n_{1}^{2} + n_{2}^{2} + n_{3}^{2} = 1,} \hfill & {m_{1} n_{1} + m_{2} n_{2} + m_{3} n_{3} = 0,} \hfill \\ {l_{1}^{2} + m_{1}^{2} + n_{1}^{2} { = }1,} \hfill & {l_{1} l_{2} + m_{1} m_{2} + n_{1} n_{2} = 0,} \hfill \\ {l_{2}^{2} + m_{2}^{2} + n_{2}^{2} { = }1,} \hfill & {l_{1} l_{3} + m_{1} m_{3} + n_{1} n_{3} = 0,} \hfill \\ {l_{3}^{2} + m_{3}^{2} + n_{3}^{2} { = }1,} \hfill & {l_{2} l_{3} + m_{2} m_{3} + n_{2} n_{3} = 0.} \hfill \\ \end{array} } \right.$$

(A.1)

The strain components in one coordinate system are given as

$$\left\{ \begin{aligned} \varepsilon_{x} \;\; = l_{1}^{2} \varepsilon_{\alpha } + m_{1}^{2} \varepsilon_{\beta } + n_{1}^{2} \varepsilon_{\gamma } \;\;,\;\;\;\gamma_{xy} = 2(l_{1} l_{2} \varepsilon_{\alpha } + m_{1} m_{2} \varepsilon_{\beta } + n_{1} n_{2} \varepsilon_{\gamma } ), \hfill \\ \varepsilon_{y} \;\; = l_{2}^{2} \varepsilon_{\alpha } + m_{2}^{2} \varepsilon_{\beta } + n_{2}^{2} \varepsilon_{\gamma } \;\;,\;\;\;\gamma_{yz} = 2(l_{2} l_{3} \varepsilon_{\alpha } + m_{2} m_{3} \varepsilon_{\beta } + n_{2} n_{3} \varepsilon_{\gamma } ), \hfill \\ \varepsilon_{z} \;\; = l_{3}^{2} \varepsilon_{\alpha } + m_{3}^{2} \varepsilon_{\beta } + n_{3}^{2} \varepsilon_{\gamma } \;\;,\;\;\;\gamma_{xz} = 2(l_{1} l_{3} \varepsilon_{\alpha } + m_{1} m_{3} \varepsilon_{\beta } + n_{1} n_{3} \varepsilon_{\gamma } ). \hfill \\ \end{aligned} \right.$$

(A.2)

Substitution of Eq. (1) into the constitutive Eq. (A.2) yields

$$\begin{aligned} \varepsilon_{x} & = l_{1}^{2} \varepsilon_{\alpha } + m_{1}^{2} \varepsilon_{\beta } + n_{1}^{2} \varepsilon_{\gamma } \\ & = l_{1}^{2} \left( {a_{11} \sigma_{\alpha } + a_{12} \sigma_{\beta } + a_{13} \sigma_{\gamma } } \right) + m_{1}^{2} \left( {a_{21} \sigma_{\alpha } + a_{22} \sigma_{\beta } + a_{23} \sigma_{\gamma } } \right) + n_{1}^{2} \left( {a_{31} \sigma_{\alpha } + a_{32} \sigma_{\beta } + a_{33} \sigma_{\gamma } } \right) \\ & = \left( {a_{11} l_{1}^{2} + a_{21} m_{1}^{2} + a_{31} n_{1}^{2} } \right)\sigma_{\alpha } + \left( {a_{12} l_{1}^{2} + a_{22} m_{1}^{2} + a_{32} n_{1}^{2} } \right)\sigma_{\beta } + \left( {a_{13} l_{1}^{2} + a_{23} m_{1}^{2} + a_{33} n_{1}^{2} } \right)\sigma_{\gamma } \\ & = a_{11} \left( {l_{1}^{2} \sigma_{\alpha } + m_{1}^{2} \sigma_{\beta } + n_{1}^{2} \sigma_{\gamma } } \right) + a_{22} \left( {l_{1}^{2} \sigma_{\alpha } + m_{1}^{2} \sigma_{\beta } + n_{1}^{2} \sigma_{\gamma } } \right) + a_{33} \left( {l_{1}^{2} \sigma_{\alpha } + m_{1}^{2} \sigma_{\beta } + n_{1}^{2} \sigma_{\gamma } } \right) \\ & \quad - \left[ {l_{1}^{2} \left( {a_{22} + a_{33} } \right)\sigma_{\alpha } + m_{1}^{2} \left( {a_{11} + a_{33} } \right)\sigma_{\beta } + n_{1}^{2} \left( {a_{11} + a_{22} } \right)\sigma_{\gamma } } \right] \\ & \quad + \left[ {\left( {a_{21} m_{1}^{2} + a_{31} n_{1}^{2} } \right)\sigma_{\alpha } + \left( {a_{12} l_{1}^{2} + a_{32} n_{1}^{2} } \right)\sigma_{\beta } + \left( {a_{13} l_{1}^{2} + a_{23} m_{1}^{2} } \right)\sigma_{\gamma } } \right] \\ & = \left( {a_{11} + a_{22} + a_{33} } \right)\sigma_{x} - \left( {a_{11} + a_{22} + a_{33} } \right)\left( {l_{1}^{2} \sigma_{\alpha } + m_{1}^{2} \sigma_{\beta } + n_{1}^{2} \sigma_{\gamma } } \right) + a_{11} l_{1}^{2} \sigma_{\alpha } + a_{22} m_{1}^{2} \sigma_{\beta } + a_{33} n_{1}^{2} \sigma_{\gamma } \\ & \quad + \left[ {\left( {m_{1}^{2} + n_{1}^{2} } \right)a_{21} \sigma_{\alpha } + \left( {l_{1}^{2} + n_{1}^{2} } \right)a_{12} \sigma_{\beta } + \left( {l_{1}^{2} + m_{1}^{2} } \right)a_{13} \sigma_{\gamma } } \right] \\ & = a_{11} l_{1}^{2} \sigma_{\alpha } + a_{22} m_{1}^{2} \sigma_{\beta } + a_{33} n_{1}^{2} \sigma_{\gamma } - a_{21} l_{1}^{2} \sigma_{\alpha } - a_{12} m_{1}^{2} \sigma_{\beta } - a_{13} n_{1}^{2} \sigma_{\gamma } + a_{21} \sigma_{\alpha } + a_{12} \sigma_{\beta } + a_{13} \sigma_{\gamma } \\ & = \left( {a_{11} - a_{21} } \right)l_{1}^{2} \sigma_{\alpha } + \left( {a_{22} - a_{12} } \right)m_{1}^{2} \sigma_{\beta } + \left( {a_{33} - a_{13} } \right)n_{1}^{2} \sigma_{\gamma } + a_{21} \sigma_{\alpha } + a_{12} \sigma_{\beta } + a_{13} \sigma_{\gamma } \\ & = \frac{{l_{1}^{2} \sigma_{\alpha } }}{{2G_{\alpha } }} + \frac{{m_{1}^{2} \sigma_{\beta } }}{{2G_{\beta } }} + \frac{{n_{1}^{2} \sigma_{\gamma } }}{{2G_{\gamma } }} + a_{21} \sigma_{\alpha } + a_{12} \sigma_{\beta } + a_{13} \sigma_{\gamma } , \\ \end{aligned}$$

$$\begin{aligned} \gamma_{xy} & = 2\left( {l_{1} l_{2} \varepsilon_{\alpha } + m_{1} m_{2} \varepsilon_{\beta } + n_{1} n_{2} \varepsilon_{\gamma } } \right) \\ & = 2\left[ {l_{1} l_{2} \left( {a_{11} \sigma_{\alpha } { + }a_{12} \sigma_{\beta } { + }a_{13} \sigma_{\gamma } } \right) + m_{1} m_{2} \left( {a_{21} \sigma_{\alpha } + a_{22} \sigma_{\beta } { + }a_{23} \sigma_{\gamma } } \right) + n_{1} n_{2} \left( {a_{31} \sigma_{\alpha } { + }a_{32} \sigma_{\beta } + a_{33} \sigma_{\gamma } } \right)} \right] \\ & = 2\left[ {\left( {a_{11} l_{1} l_{2} { + }a_{21} m_{1} m_{2} { + }a_{31} n_{1} n_{2} } \right)\sigma_{\alpha } + \left( {a_{12} l_{1} l_{2} + a_{22} m_{1} m_{2} { + }a_{32} n_{1} n_{2} } \right)\sigma_{\beta } + \left( {a_{13} l_{1} l_{2} { + }a_{23} m_{1} m_{2} + a_{33} n_{1} n_{2} } \right)\sigma_{\gamma } } \right] \\ & { = }\,2\left\{ \begin{aligned} & a_{11} \left( {l_{1} l_{2} \sigma_{\alpha } + m_{1} m_{2} \sigma_{\beta } + n_{1} n_{2} \sigma_{\gamma } } \right) + a_{22} \left( {l_{1} l_{2} \sigma_{\alpha } + m_{1} m_{2} \sigma_{\beta } + n_{1} n_{2} \sigma_{\gamma } } \right) \hfill \\ &+ a_{33} \left( {l_{1} l_{2} \sigma_{\alpha } + m_{1} m_{2} \sigma_{\beta } + n_{1} n_{2} \sigma_{\gamma } } \right) \hfill \\ &- \left[ {l_{1} l_{2} (a_{22} + a_{33} )\sigma_{\alpha } + m_{1} m_{2} (a_{11} + a_{33} )\sigma_{\beta } + n_{1} n_{2} (a_{11} + a_{22} )\sigma_{\gamma } } \right] \hfill \\ &{ + }\left[ {(a_{21} m_{1} m_{2} + a_{31} n_{1} n_{2} )\sigma_{\alpha } + (a_{12} l_{1} l_{2} + a_{32} n_{1} n_{2} )\sigma_{\beta } + (a_{13} l_{1} l_{2} + a_{23} m_{1} m_{2} )\sigma_{\gamma } } \right] \hfill \\ \end{aligned} \right\} \\ & = 2\left\{ \begin{aligned} & (a_{11} + a_{22} + a_{33} )\tau_{xy} - (a_{11} + a_{22} + a_{33} )(l_{1} l_{2} \sigma_{\alpha } + m_{1} m_{2} \sigma_{\beta } + n_{1} n_{2} \sigma_{\gamma } ) \hfill \\& + a_{11} l_{1} l_{2} \sigma_{\alpha } + a_{22} m_{1} m_{2} \sigma_{\beta } + a_{33} n_{1} n_{2} \sigma_{\gamma } \hfill \\& { + }\left[ {(m_{1} m_{2} + n_{1} n_{2} )a_{21} \sigma_{\alpha } + (l_{1} l_{2} + n_{1} n_{2} )a_{12} \sigma_{\beta } + (l_{1} l_{2} + m_{1} m_{2} )a_{13} \sigma_{\gamma } } \right] \hfill \\ \end{aligned} \right\} \\ & = 2\left( {a_{11} l_{1} l_{2} \sigma_{\alpha } + a_{22} m_{1} m_{2} \sigma_{\beta } + a_{33} n_{1} n_{2} \sigma_{\gamma } - a_{21} l_{1} l_{2} \sigma_{\alpha } - a_{12} m_{1} m_{2} \sigma_{\beta } - a_{13} n_{1} n_{2} \sigma_{\gamma } } \right) \\ & = 2(a_{11} - a_{21} )l_{1} l_{2} \sigma_{\alpha } + 2(a_{22} - a_{12} )m_{1} m_{2} \sigma_{\beta } + 2(a_{33} - a_{13} )n_{1} n_{2} \sigma_{\gamma } \\ & = \frac{{l_{1} l_{2} \sigma_{\alpha } }}{{G_{\alpha } }} + \frac{{m_{1} m_{2} \sigma_{\beta } }}{{G_{\beta } }} + \frac{{n_{1} n_{2} \sigma_{\gamma } }}{{G_{\gamma } }}. \\ \end{aligned}$$

Similarly, the remaining equations can be obtained in the same way.

Appendix B

2.1 The ratios $l_{2} /m_{1}$, $m_{3} /n_{2}$, and $n_{1} /l_{3}$

Note that the direction cosines satisfy the following equations:

$$\begin{array}{*{20}l} {l_{1} m_{1} + l_{2} m_{2} + l_{3} m_{3} = 0,} \hfill \\ {l_{1} n_{1} + l_{2} n_{2} + l_{3} n_{3} = 0,} \hfill \\ {m_{1} n_{1} + m_{2} n_{2} + m_{3} n_{3} = 0} \hfill \\ {l_{1} l_{2} + m_{1} m_{2} + n_{1} n_{2} = 0,} \hfill \\ {l_{1} l_{3} + m_{1} m_{3} + n_{1} n_{3} = 0,} \hfill \\ {l_{2} l_{3} + m_{2} m_{3} + n_{2} n_{3} = 0.} \hfill \\ \end{array}$$

(B.1)

When l₁, m₂, n₃ → 1; l₂, l₃, m₁, m₃, n₁, n₂ → 0, we have

$$\begin{array}{*{20}l} {m_{1} + l_{2} + l_{3} m_{3} = 0,} \hfill & {\left( a \right)} \hfill \\ {n_{1} + l_{2} n_{2} + l_{3} = 0,} \hfill & {\left( b \right)} \hfill \\ {m_{1} n_{1} + n_{2} + m_{3} = 0,} \hfill & {\left( c \right)} \hfill \\ {l_{2} + m_{1} + n_{1} n_{2} = 0,} \hfill & {\left( d \right)} \hfill \\ {l_{3} + m_{1} m_{3} + n_{1} = 0,} \hfill & {\left( e \right)} \hfill \\ {l_{2} l_{3} + m_{3} + n_{2} = 0.} \hfill & {\left( f \right)} \hfill \\ \end{array}$$

(B.2)

From Eqs. (a) and (d) in (B.2), we have

$$l_{3} m_{3} = n_{1} n_{2} \;\;\;\; \Rightarrow \;\;\;m_{3} /n_{2} = n_{1} /l_{3},$$

(B.3)

and from Eqs (b) (c) in (B.2), it is obvious that

$$l_{2} n_{2} = m_{1} m_{3} \;\;\; \Rightarrow \;\;\;l_{2} /m_{1} = m_{3} /n_{2} .$$

(B.4)

Similarly, from Eqs. (e) and (f) in (B.2), one has

$$l_{2} l_{3} = m_{1} n_{1} \;\;\; \Rightarrow l_{2} /m_{1} = n_{1} /l_{3} .$$

(B.5)

Combining Eqs. (B.3)–(B.5) and letting $\mathop {\lim }\limits_{\begin{subarray}{l} \;\;\;\;\;\;\;l_{1} ,m_{2} ,n_{3} \to 1 \\ l_{2} ,l_{3,} m_{1} ,m_{3} ,n_{1} ,n_{2} \to 0 \end{subarray} } l_{2} /m_{1} = k$, we have

$$\mathop {\lim }\limits_{\begin{subarray}{l} \;\;\;\;\;\;\;l_{1} ,m_{2} ,n_{3} \to 1 \\ l_{2} ,l_{3,} m_{1} ,m_{3} ,n_{1} ,n_{2} \to 0 \end{subarray} } l_{2} /m_{1} = m_{3} /n_{2} = n_{1} /l_{3} = k.$$

(B.6)

From Eqs. (B.3) to (B.6), it can be seen that the three shear moduli have similar form to k. Consider

$$\begin{array}{*{20}l} {l_{1}^{2} + l_{2}^{2} + l_{3}^{2} { = }1,} \hfill & {\left( {a'} \right)} \hfill \\ {m_{1}^{2} + m_{2}^{2} + m_{3}^{2} = 1,} \hfill & {\left( {b'} \right)} \hfill \\ {n_{1}^{2} + n_{2}^{2} + n_{3}^{2} = 1,} \hfill & {\left( {c'} \right)} \hfill \\ {l_{1}^{2} + m_{1}^{2} + n_{1}^{2} { = }1,} \hfill & {\left( {d'} \right)} \hfill \\ {l_{2}^{2} + m_{2}^{2} + n_{2}^{2} { = }1,} \hfill & {\left( {e'} \right)} \hfill \\ {l_{3}^{2} + m_{3}^{2} + n_{3}^{2} { = }1.} \hfill & {\left( {f'} \right)} \hfill \\ \end{array}$$

(B.7)

Equations (a′) and (d′) give

$$l_{2}^{2} + l_{3}^{2} = m_{1}^{2} + n_{1}^{2} .$$

Substitution of Eq. (B.6) into the above equation yields

$$(k^{2} - 1)m_{1}^{2} = (k^{2} - 1)l_{3}^{2} .$$

Thus

$$k^{2} = 1\,or\,m_{1}^{2} = l_{3}^{2} .$$

(B.8)

Similarly, from Eqs. (b′) and (e′), we have

$$k^{2} = 1\,or\,m_{1}^{2} = n_{2}^{2}$$

(B.9)

and from Eqs. (c′) and (f′)

$$k^{2} = 1\,or\,l_{3}^{2} = n_{2}^{2} .$$

(B.10)

Combining Eqs. (a′) and (e′) and taking the limits, we obtain

$$l_{3}^{2} = n_{2}^{2} .$$

(B.11)

Similarly, from Eqs. (a′) and (f),

$$l_{2}^{2} = m_{3}^{2},$$

(B.12)

and from Eqs. (b′) and (d′) and from Eqs. (b′) and (f′),

$$n_{1}^{2} = m_{3}^{2} ,$$

(B.13)

$$m_{1}^{2} = l_{3}^{2} .$$

(B.14)

Also, from Eqs. (c′) and (d′) and from Eqs. (c′) and (e′), one has

$$m_{1}^{2} = n_{2}^{2} ,$$

(B.15)

$$n_{1}^{2} = l_{2}^{2} .$$

(B.16)

Considering Eq. (B.6), Eqs. (B.8)–(B.16) yield

$$\begin{aligned} m_{1}^{2} = l_{3}^{2} = n_{2}^{2} , \hfill \\ l_{2}^{2} = n_{1}^{2} = m_{3}^{2} . \hfill \\ \end{aligned}$$

(B.17)

It can be seen from the above formula that the direction cosines have the same signs (positive or negative) or different signs at the same time. l₃, m₁, and n₂ are infinitesimally small quantities of the same order, as are l₂, n₁, and m₃. In addition, the limit can be obtained as

$$\begin{aligned} \mathop {\lim }\limits_{\begin{subarray}{l} \;\;\;\;\;\;\;l_{1} ,m_{2} ,n_{3} \to 1 \\ l_{2} ,l_{3,} m_{1} ,m_{3} ,n_{1} ,n_{2} \to 0 \end{subarray} } \tau_{xy} & = \mathop {\lim }\limits_{\begin{subarray}{l} \;\;\;\;\;\;\;l_{1} ,m_{2} ,n_{3} \to 1 \\ l_{2} ,l_{3,} m_{1} ,m_{3} ,n_{1} ,n_{2} \to 0 \end{subarray} } l_{1} l_{2} \sigma_{\alpha } + m_{1} m_{2} \sigma_{\beta } + n_{1} n_{2} \sigma_{\gamma } \\ & = \mathop {\lim }\limits_{\begin{subarray}{l} \;\;\;\;\;\;\;l_{1} ,m_{2} ,n_{3} \to 1 \\ l_{2} ,l_{3,} m_{1} ,m_{3} ,n_{1} ,n_{2} \to 0 \end{subarray} } l_{2} \sigma_{\alpha } + m_{1} \sigma_{\beta } + n_{1} n_{2} \sigma_{\gamma } \\ & { = }\mathop {\lim }\limits_{\begin{subarray}{l} \;\;\;\;\;\;\;l_{1} ,m_{2} ,n_{3} \to 1 \\ l_{2} ,l_{3,} m_{1} ,m_{3} ,n_{1} ,n_{2} \to 0 \end{subarray} } l_{2} \sigma_{\alpha } + m_{1} \sigma_{\beta } . \\ \end{aligned}$$

(B.18)

As the shear stress is zero on the principal stress surface, i.e.,

$$\tau_{\alpha \beta } = l_{1} m_{1} \sigma_{x} + l_{2} m_{2} \sigma_{y} + l_{3} m_{3} \sigma_{z} + (l_{1} m_{2} + l_{2} m_{1} )\tau_{xy} + (l_{2} m_{3} + l_{3} m_{2} )\tau_{yz} + (l_{1} m_{3} + l_{3} m_{3} )\tau_{zx} { = }0,$$

(B.19)

$$\begin{aligned} & \mathop {\lim }\limits_{\begin{subarray}{l} \;\;\;\;\;\;\;l_{1} ,m_{2} ,n_{3} \to 1 \\ l_{2} ,l_{3,} m_{1} ,m_{3} ,n_{1} ,n_{2} \to 0 \end{subarray} } l_{1} m_{1} \sigma_{x} + l_{2} m_{2} \sigma_{y} + l_{3} m_{3} \sigma_{z} + (l_{1} m_{2} + l_{2} m_{1} )\tau_{xy} + (l_{2} m_{3} + l_{3} m_{2} )\tau_{yz} + (l_{1} m_{3} + l_{3} m_{3} )\tau_{zx} \\ & { = }\mathop {\lim }\limits_{\begin{subarray}{l} \;\;\;\;\;\;\;l_{1} ,m_{2} ,n_{3} \to 1 \\ l_{2} ,l_{3,} m_{1} ,m_{3} ,n_{1} ,n_{2} \to 0 \end{subarray} } m_{1} \sigma_{x} + l_{2} \sigma_{y} + l_{3} m_{3} \sigma_{z} + (1 + l_{2} m_{1} )\tau_{xy} + (l_{2} m_{3} + l_{3} )\tau_{yz} + (m_{3} + l_{3} m_{3} )\tau_{zx} \\ & = \mathop {\lim }\limits_{\begin{subarray}{l} \;\;\;\;\;\;\;l_{1} ,m_{2} ,n_{3} \to 1 \\ l_{2} ,l_{3,} m_{1} ,m_{3} ,n_{1} ,n_{2} \to 0 \end{subarray} } m_{1} \sigma_{\alpha } + l_{2} \sigma_{\beta } + l_{3} m_{3} \sigma_{\gamma } + \tau_{xy} + l_{3} \tau_{yz} + m_{3} \tau_{xz} \\ & = \mathop {\lim }\limits_{\begin{subarray}{l} \;\;\;\;\;\;\;l_{1} ,m_{2} ,n_{3} \to 1 \\ l_{2} ,l_{3,} m_{1} ,m_{3} ,n_{1} ,n_{2} \to 0 \end{subarray} } m_{1} \sigma_{\alpha } + l_{2} \sigma_{\beta } + l_{3} m_{3} \sigma_{\gamma } + \tau_{xy} \\ & { = }\mathop {\lim }\limits_{\begin{subarray}{l} \;\;\;\;\;\;\;l_{1} ,m_{2} ,n_{3} \to 1 \\ l_{2} ,l_{3,} m_{1} ,m_{3} ,n_{1} ,n_{2} \to 0 \end{subarray} } m_{1} \sigma_{\alpha } + l_{2} \sigma_{\beta } + \tau_{xy} { = }0. \\ \end{aligned}$$

(B.20)

Then, it can be obtained from Eqs. (B.19) and (B.20) that

$$\mathop {\lim }\limits_{\begin{subarray}{l} \;\;\;\;\;\;\;l_{1} ,m_{2} ,n_{3} \to 1 \\ l_{2} ,l_{3,} m_{1} ,m_{3} ,n_{1} ,n_{2} \to 0 \end{subarray} } m_{1} \sigma_{\alpha } + l_{2} \sigma_{\beta } = - \tau_{xy}.$$

(B.21)

Combining Eqs. (B.18) and (B.21) yields

$$l_{2} \sigma_{\alpha } + m_{1} \sigma_{\beta } = - m_{1} \sigma_{\alpha } - l_{2} \sigma_{\beta } .$$

Therefore, we have

$$(l_{2} + m_{1} )(\sigma_{\alpha } + \sigma_{\beta } ) = 0.$$

(B.22)

Since the above equation is true for any magnitude principal stresses $\sigma_{\alpha }$ and $\sigma_{\beta }$, one has$\mathop {\lim }\limits_{\begin{subarray}{l} \;\;\;\;\;\;\;l_{1} ,m_{2} ,n_{3} \to 1 \\ l_{2} ,l_{3,} m_{1} ,m_{3} ,n_{1} ,n_{2} \to 0 \end{subarray} } l_{2} + m_{1} = 0,$which leads to

$$\mathop {\lim }\limits_{\begin{subarray}{l} \;\;\;\;\;\;\;l_{1} ,m_{2} ,n_{3} \to 1 \\ l_{2} ,l_{3,} m_{1} ,m_{3} ,n_{1} ,n_{2} \to 0 \end{subarray} } l_{2} /m_{1} = - 1.$$

(B.23)

In the same way, we have

$$\mathop {\lim }\limits_{\begin{subarray}{l} \;\;\;\;\;\;\;l_{1} ,m_{2} ,n_{3} \to 1 \\ l_{2} ,l_{3,} m_{1} ,m_{3} ,n_{1} ,n_{2} \to 0 \end{subarray} } m_{3} /n_{2} = l_{3} /n_{1} = - 1.$$

(B.24)