1 Introduction

Since the seminal work of Bendsøe and Kikuchi [1], structural topology optimization has been developed rapidly and used widely in industrial designs [2, 3]. Most, if not all, of the studies on topology optimization have been focusing on the optimization problems with fixed loads. However, the design-dependent load problems, such as the problems with pressure loads, in which both the locations and directions of loads depend on the design process, are also important and considerable. It is necessary and important to establish relevant and efficient topology optimization methods for structures with pressure loads.

The main challenge of such problems is how to accurately track pressure boundary during the design process. To solve this challenge, a direct idea is to use the boundary-based topology optimization methods, such as the level set method [4,5,6,7,8,9,10]. These kinds of methods provide an implicit description of material boundaries and also enable easier extraction of their geometric information (normal direction and curvature), and thus, are particularly suitable for structural boundary/interface-related design problems. However, the density-based topology optimization methods, such as the solid isotropic material with penalization (SIMP) method [11], are the most important, most mature, and most widely used method in topology optimization. It is very important and necessary to develop efficient topology optimization methods for structures with pressure loads, under the frame of density-based topology optimization method. However, there is no implicit (explicit) boundary in density-based methods [12,13,14,15,16], which makes the handling of design-dependent pressure loads difficult. Nevertheless, many researchers have proposed various pressure boundary tracking methods according to element density [17,18,19,20,21,22,23,24,25,26,27,28,29]. In these methods, the approximate density curve is used to approximately replace the pressure boundary; however, it is more or less inaccurate [21] for the recognition of pressure boundary because the beginning and end locations for the search procedure must be provided in the iso-density curves and there are gray elements in the density-based methods.

In fact, the method without pressure boundary recognition process is promising and effective for solving problems with pressure loads related to design. There are also some papers on this aspect. Chen and Kikuchi [30] simulated pressure loading by approximating it as an equivalent thermal load that is penalized with the design and a "dryness coefficient" to identify fluid and solid regions. Sigmund and Clausen [31] used a mixed displacement–pressure (u-p) formulation based on shear and bulk moduli to transmit the pressure load from boundaries to the evolving surface, and a similar method was presented by Bruggi and Cinquini [32]. Based on the bi-directional evolutionary structural optimization (BESO) method, Picelli et al. [33, 34] used Laplace’s equation and the steady-state incompressible Navier–Stokes equations to control the static fluid domain and the fluid flow domain, respectively, and constructed the corresponding fluid–structure coupling equations to solve the design-dependent pressure load problem. Kumar et al. [35, 36] modeled the design-dependent pressure loads on structures and compliant mechanisms using Darcy's law coupled with a "drainage" term.

It is easy to determine where the fluid is located when the topology is clear. However, there are gray elements in the SIMP method, and the boundary is not very clear, thus it is difficult to accurately define the fluid under the SIMP framework. So, it is necessary to establish a method to determine the area where the fluid is located based on the SIMP method.

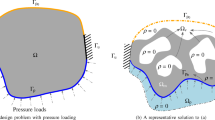
In this paper, we propose a thermal-solid–fluid method for topology optimization of structures with design-dependent pressure loads. The voids between the solid structure (may evolve in the topology optimization process) and the loading boundary are referred to as the open voids (the voids between the blue boundary and the yellow boundary in Fig. 1), and the other voids occurring in the topology optimization process is referred to as closed voids (such as the voids inside the structure or those between the structure and other boundaries of the initial design domain). The open voids are filled with an incompressible hydrostatic fluid, and the pressure load can be transferred through the fluid without any need for structure loading surface recognition. The topology optimization problem is equivalently transferred into a multi-material topology optimization problem with solid phase material and virtual fluid phase. The N-VTM [37,38,39] is used to distinguish the enclosed and open voids by the temperature difference between the enclosed (with higher temperature) and open (with lower temperature) voids. Therefore, the distribution of three materials is described by a thermal-solid–fluid interpolation. Finally, considering that the fluid is an incompressible material, which leads to the failure of the standard finite element method (FEM), the mixed displacement–pressure formulation (mixed form) is used to model this solid–fluid problem.

Fig. 1
figure 1

Topology optimization with design-dependent pressure boundary: a initial design domain; b structure topology in optimization process

Full size image

The remainder of this paper is organized as follows. In Sect. 2, the thermal-solid–fluid method proposed in this paper is introduced. In Sect. 3, the topology optimization model is introduced, and the sensitivity of objective function and constraint function is derived. In Sect. 4, several examples are given to verify the effectiveness of the method proposed in this paper. Section 5 concludes and discusses the advantages and disadvantages of this method.

2 Thermal-Solid–Fluid Method

2.1 General Idea

In this method, the incompressible fluid is used to transfer pressure load, which involves two problems: one is how to distribute three materials, the other is to solve the finite element problem with incompressible material.

For the first problem, a thermal-solid–fluid interpolation consisting of the density variable \(\overline{\mu }\) and temperature variable \(\overline{T}\) is used to distribute three materials, as shown in Fig. 2. For the second problem, the incompressible finite element problem can be solved by the mixed form.

Fig. 2
figure 2

General idea of thermal-solid–fluid interpolation

Full size image

2.2 Thermal-Solid–Fluid Interpolation

In this section, an interpolation function is constructed to describe the distribution of the three materials. It is easy to define solid structure through partial differential equation (PDE) filtering and Heaviside projection, the details of which can be found in Appendix. The rest is to distinguish between fluid and void. In this method, fluid always appears either outside or inside the structure; in other words, it is only necessary to distinguish between enclosed and open voids of the structure. A temperature field is applied to the design domain, where the solid areas are treated as the thermal insulation material, and other areas are filled with the self-heating highly thermally conductive material. The temperature of the enclosed void is high and the temperature of the open void is low by solving a nonlinear thermal problem. Therefore, enclosed and open voids of the structure are distinguished. Finally, the thermal-solid–fluid interpolation is constructed, and the definitions of three materials are shown in Eq. (1).

As shown in Fig. 2, the part in the dashed box shows the final distribution of three materials. The blue, black, and white parts represent fluid, solid, and void, respectively.

Three materials are specifically expressed as follows

$$ \begin{gathered} {\text{Solid:}}\quad \overline{\mu } \hfill \\ {\text{Fluid:}}\quad (1 - \overline{\mu })(1 - \overline{T}) \hfill \\ {\text{Void:}}\;{\kern 1pt} \quad (1 - \overline{\mu })\overline{T} \hfill \\ \end{gathered} $$
(1)

where \(\mu\) represents the initial density field; \(\tilde{\mu }\) and \(\overline{\mu }\) can be obtained through PDE filtering and Heaviside projection of variable \(\mu\), which is described in Appendix; \(T\) and \(\overline{T}\) can be obtained through the N-VTM and Heaviside projection of variable \(\overline{\mu }\).

The interpolation functions for element material properties are described as follows

$$ \begin{gathered} K(\overline{\mu },\overline{T}) = \overline{\mu }^{p} K_{{{\text{solid}}}} + (1 - \overline{\mu }^{p} )\left( {(1 - \overline{T}^{p} )K_{{{\text{fluid}}}} + \overline{T}^{p} K_{{{\text{void}}}} } \right) \hfill \\ G(\overline{\mu },\overline{T}) = \overline{\mu }^{p} G_{{{\text{solid}}}} + (1 - \overline{\mu }^{p} )\left( {(1 - \overline{T}^{p} )G_{{{\text{fluid}}}} + \overline{T}^{p} G_{{{\text{void}}}} } \right) \hfill \\ \end{gathered} $$
(2)

where p is the penalty factor; \(K_{{{\text{solid}}}}\), \(K_{{{\text{fluid}}}}\) and \(K_{{{\text{void}}}}\) represent the bulk moduli of solid, fluid, and void, respectively;\(G_{{{\text{solid}}}}\), \(G_{{{\text{fluid}}}}\) and \(G_{{{\text{void}}}}\) represent the shear moduli of solid, fluid, and void, respectively.

2.3 N-VTM

Based on the above analysis, distinguishing between void and fluid is equivalent to distinguishing between enclosed and open voids of structure. Now the N-VTM (the basic idea is shown in Fig. 3) [37,38,39] is introduced to identify the enclosed and open voids of structure. As shown in Fig. 3, the solid areas are treated as the thermal insulation material, which has low (near-zero) heat conductivity, while other areas are filled with the self-heating highly thermally conductive material, and a nonlinear thermal problem is described as follows

$$ \left\{ {\begin{array}{*{20}l} {\nabla (k\nabla T) + Q(T) = 0,} \hfill & {{\text{in}}\;\Omega } \hfill \\ {T = 0,} \hfill & {{\text{on}}\;\partial \Omega } \hfill \\ \end{array} } \right. $$
(3)
Fig. 3
figure 3

Identification between open and enclosed voids: a the general idea of N-VTM; b temperature distribution after N-VTM

Full size image

Here Q is a temperature-dependent heat source defined as

$$ Q = \frac{q}{{1 + {\text{e}}^{\alpha (T - 1)} }} $$
(4)

where \(\alpha\) is a positive number, which determines the sharpness of Q.

In Eqs. (3) and (4), k and q are defined as

$$ \left\{ {\begin{array}{*{20}c} {k = (k_{{{\text{min}}}} - 1)\overline{\mu } + 1} \\ {q = (1 - \overline{\mu })q_{0} \;\;\;\quad } \\ \end{array} } \right. $$
(5)

where \(k_{\min }\) is a small positive number; and \(q_{0}\) is a proportional parameter, which is defined as

$$ q_{0} = \frac{\lambda }{{\max (\tilde{y})}} $$
(6)

where \(\lambda\) is a positive number from 0.02 to 0.2; and \(\tilde{y}\) is obtained by solving the following linear partial differential equation

$$ \left\{ {\begin{array}{*{20}l} {\nabla^{2} \tilde{y} + 1 = 0,} \hfill & {{\text{in}}\;\Omega } \hfill \\ {\tilde{y} = 0,} \hfill & {{\text{on}}\;\partial \Omega } \hfill \\ \end{array} } \right. $$
(7)

this linear equation is design-independent, and thus it requires to be solved only one time for a given optimization problem.

Finally, the temperature field of the design domain is obtained, as shown in Fig. 3a, with high temperature in the enclosed void (red region), and low temperature in the open void (blue region). And then the 0–1 temperature field \(\overline{T}\) is obtained through the Heaviside function mentioned in Appendix. The temperature distribution is shown in Fig. 3b.

2.4 Numerical Solution of Three Materials: Mixed Form

As mentioned before, the incompressible fluid was used to transfer the pressure, leading to the failure of the standard FEM for elastic problems. So the mixed form is chosen to solve this problem.

The mixed form can be derived by introducing the pressure variable \(p = K{\varvec{m}}^{\text{T}} {{\varvec{\varepsilon}}}\), which can be separated from the equivalent integral weak form of the equilibrium conditions in the standard FEM form. More details can be found from [31, 40].

In the weak form, the equilibrium conditions for the mixed form can be written as follows

$$ \int_{\Omega } {{\updelta }{{\varvec{\varepsilon}}}^{\text{T}} {\varvec{D}}_{d} {{\varvec{\varepsilon}}}} {\text{d}}\Omega - \int_{\Omega } {{\updelta }{{\varvec{\varepsilon}}}^{\text{T}} {\varvec{m}}p} {\text{d}}\Omega - \int_{\Omega } {{\updelta }{\varvec{u}}^{\text{T}} {\varvec{f}}} {\text{d}}\Omega - \int_{{\Gamma_{f} }} {{\updelta }{\varvec{u}}^{\text{T}} {\varvec{T}}} {\text{d}}\Gamma = 0 $$
(8)

Here, \({\varvec{m}} = \{ 1,1,1,0,0,0\}^{\text{T}}\) in 3D, \({\varvec{m}} = \{ 1,1,0\}^{\text{T}}\) in 2D, \({\varvec{D}}_{d} = 2G\left( {{\varvec{I}}_{0} - \tfrac{1}{3}{\varvec{mm}}^{\text{T}} } \right)\) in 3D, \({\varvec{D}}_{d} = 2G\left( {{\varvec{I}}_{0} - \tfrac{1}{2}{\varvec{mm}}^{\text{T}} } \right)\) in 2D, and \({\varvec{I}}_{0}\) is a diagonal matrix with the entries \(\tfrac{1}{2}\{ 2,2,2,1,1,1\}^{\text{T}}\) in 3D and \(\tfrac{1}{2}\{ 2,2,1\}^{\text{T}}\) in 2D.

Since the pressure variable is separated as an independent variable, another equation is needed. It is noted that \(p/K = {\varvec{m}}^{\text{T}} {{\varvec{\varepsilon}}}\) is satisfied for isotropic material, and the weak form of \(p/K = {\varvec{m}}^{\text{T}} {{\varvec{\varepsilon}}}\) can be written as

$$ \int_{\Omega } {{\updelta }p\, (p/K - {\varvec{m}}^{\text{T}} {{\varvec{\varepsilon}}}){\text{d}}\Omega } = 0 $$
(9)

After discretization of the weak forms (8) and (9), the mixed-form linear system to be solved has the format

$$ \left[ {\begin{array}{*{20}c} {\varvec{K}} & {\varvec{C}} \\ {{\varvec{C}}^{{\text{T}}} } & { - {\varvec{D}}} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varvec{U}} \\ {\varvec{P}} \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\varvec{F}} \\ {\mathbf{0}} \\ \end{array} } \right\} $$
(10)

where

$$ \left. \begin{gathered} {\varvec{K}} = \sum\limits_{e} {{\varvec{K}}_{e} } = \sum\limits_{e} {\int_{{\Omega_{e} }} {{\varvec{B}}^{\text{T}} {\varvec{D}}_{d} {\varvec{B}}} {\text{d}}\Omega } \quad \hfill \\ {\varvec{C}} = \sum\limits_{e} {{\varvec{C}}_{e} } = \sum\limits_{e} {\int_{{\Omega_{e} }} {{\varvec{B}}^{\text{T}} {\varvec{mN}}_{p} } {\text{d}}\Omega } \hfill \\ {\varvec{D}} = \sum\limits_{e} {{\varvec{D}}_{e} } = \sum\limits_{e} {\int_{{\Omega_{e} }} {{\varvec{N}}_{p}^{\text{T}} \frac{1}{K}{\varvec{N}}_{p} } {\text{d}}\Omega } \hfill \\ {\varvec{F}} = \sum\limits_{e} {{\varvec{F}}_{e} = } \sum\limits_{e} {(\int_{{\Omega_{e} }} {{\varvec{N}}_{u}^{\text{T}} {\varvec{f}}} {\text{d}}\Omega } + \int_{{\Gamma_{f,e} }} {{\varvec{N}}_{u}^{\text{T}} {\varvec{T}}} {\text{d}}\Gamma ) \hfill \\ \end{gathered} \right\} $$
(11)

where \({\varvec{N}}_{u}\) and \({\varvec{N}}_{p}\) are the displacement shape function matrix and pressure shape function matrix, respectively.

C is the \({\varvec{P}} - {\varvec{F}}_{v - s} ({\text{pressure}} - {\text{force}})\) matrix. The external load \({\varvec{F}}\) can be divided into \({\varvec{F}}_{v - s}\) and \({\varvec{F}}_{d - s}\). \({\varvec{F}}_{v - s}\) and \({\varvec{F}}_{d - s}\) cause the volume strain and deviatoric strain of the structure, respectively. The relationship between \({\varvec{F}}_{v - s}\) and its corresponding element pressure is \({\varvec{CP = F}}_{v - s}\).

D is the \({\varvec{P}} - {\varvec{V}}_{p} ({\text{pressure}} - {\text{volume}})\) matrix. The unit of \({\varvec{DP}}\) is \(\text{m}^{3}\), which corresponds to the volume. The work done under pressure \({\varvec{P}}\) is equivalent to the work done by the external load \({\varvec{F}}_{v - s}\) (\({\varvec{P}}^{\text {T}} {\varvec{V}}_{p} = {\varvec{P}}^{\text {T}} {\varvec{DP}} = {\varvec{U}}^{\text {T}} {\varvec{F}}_{v - s}\)). Therefore, the relationship between the volume \({\varvec{V}}_{p}\) and the element pressure \({\varvec{P}}\) is \({\varvec{V}}_{p} = {\varvec{DP}}\).

3 Topology Optimization Model and Sensitivity Analysis

3.1 Topology Optimization Model

A minimum compliance topology optimization problem is considered in the paper. It is noted that the objective function contains the strain energy of fluid domain that shouldn’t be included. However, because of the incompressibility of fluid, the strain energy stored in the fluid domain is negligible compared to the solid domain. The volume of the solid material is constrained in this problem. The topology optimization model is as follows

$$ \begin{aligned} {\text{find}}\! : & \quad {{\varvec{\mu}}} = \left\{ {\mu_{1} ,\mu_{2} , \ldots ,\mu_{N} } \right\}^{\text{T}} \\ \min\! : & \quad W({{\varvec{\mu}}}) = \frac{1}{2}{\varvec{F}}^{\text{T}} {\varvec{U}} \\ {\text{s.t}}\!: & \quad \left[ {\begin{array}{*{20}c} {\varvec{K}} & {\varvec{C}} \\ {{\varvec{C}}^{{\text{T}}} } & { - {\varvec{D}}} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varvec{U}} \\ {\varvec{P}} \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\varvec{F}} \\ {\mathbf{0}} \\ \end{array} } \right\} \\ & \quad g_{V} = \sum\limits_{e = 1}^{N} {v_{e} \overline{\mu }_{e} (\mu_{e} )} /\sum\limits_{e = 1}^{N} {v_{e} } - f_{0} \le 0 \\ & \quad 0 < \mu_{\min } \le \mu_{e} \le 1,\quad e = 1,2, \ldots N \\ \end{aligned} $$
(12)

where \(v_{e}\) is the volume of elements, \(N\) is the number of elements, and \(\mu_{\min }\) is the minimum value of design variables to avoid matrix singularity in the mixed form.

3.2 Sensitivity of Objective Function

Based on the theory of mixed from, the stress can be written as \({{\varvec{\upsigma}}} = {\varvec{m}}p + {\varvec{D}}_{{{d}}} {{\varvec{\varepsilon}}}\), then the objective function can be written as

$$ W = \frac{1}{2}{\varvec{F}}^{\text {T}} {\varvec{U}} = \frac{1}{2}{{\varvec{\varepsilon}}}^{\text {T}} {{\varvec{\upsigma}}} = \frac{1}{2}\left( {{{\varvec{\varepsilon}}}^{\text{T}} {\varvec{m}}p + {{\varvec{\varepsilon}}}^{\text {T}} {\varvec{D}}_{d}{{\varvec{\varepsilon}}}} \right) $$
(13)

and the discrete form of Eq. (13) is as follows

$$ W = \frac{1}{2}\left( {{\varvec{U}}^{\text T} {\varvec{B}}^{\text {T}} {\varvec{mN}}_{p} {\varvec{P}} + {\varvec{U}}^{\text {T}} {\varvec{B}}^{\text {T}} {\varvec{D}}_{d} {\varvec{BU}}} \right)\, = \frac{1}{2}\left( {{\varvec{U}}^{\text {T}} {\varvec{CP}} + {\varvec{U}}^{\text {T}} {\varvec{KU}}} \right) $$
(14)

Taking the derivative with respect to a design variable, we get

$$ \frac{\partial W}{{\partial \mu }} = \frac{1}{2}\left( {{\varvec{U}}^{\text{T}} \frac{{\partial {\varvec{K}}}}{\partial \mu }{\varvec{U}} + 2{\varvec{U}}^{\text{T}} {\varvec{K}}\frac{{\partial {\varvec{U}}}}{\partial \mu } + \frac{{\partial {\varvec{U}}^{\text{T}} }}{\partial \mu }{\varvec{CP}} + {\varvec{U}}^{\text{T}} {\varvec{C}}\frac{{\partial {\varvec{P}}}}{\partial \mu }} \right) $$
(15)

note that the state equation in Eq. (12) can be written as

$$ \left\{ {\begin{array}{*{20}c} {{\varvec{KU}} + {\varvec{CP}} = {\varvec{F}}} \\ {{\varvec{C}}^{\text{T}} {\varvec{U}} - {\varvec{DP}} = 0} \\ \end{array} } \right. $$
(16)

The derivative of Eq. (16) for the design variables \(\mu\) is described as follows

$$ \left\{ {\begin{array}{*{20}l} {\frac{{\partial {\varvec{K}}}}{\partial \mu }{\varvec{U}} + {\varvec{K}}\frac{{\partial {\varvec{U}}}}{\partial \mu } + {\varvec{C}}\frac{{\partial {\varvec{P}}}}{\partial \mu } = 0} \hfill \\ {{\varvec{C}}^{\text{T}} \frac{{\partial {\varvec{U}}}}{\partial \mu } - \frac{{\partial {\varvec{D}}}}{\partial \mu }{\varvec{P}} - {\varvec{D}}\frac{{\partial {\varvec{P}}}}{\partial \mu } = 0} \hfill \\ \end{array} } \right. $$
(17)

Substituting Eq. (17) into Eq. (16) and paying attention to the symmetry, the sensitivity of the objective function can be written as

$$ \frac{\partial W}{{\partial \mu }} = - \frac{1}{2}{\varvec{U}}^{\text{T}} \frac{{\partial {\varvec{K}}}}{\partial \mu }{\varvec{U}} + \frac{1}{2}{\varvec{P}}^{\text{T}} \frac{{\partial {\mathbf{D}}}}{\partial \mu }{\varvec{P}} $$
(18)

in the above formulation, the two derivations of design variables can be obtained by the chain rule, as shown below

$$ \begin{gathered} \frac{{\partial {\varvec{K}}}}{\partial \mu } = {\varvec{KE}}\left( {\frac{\partial G}{{\partial \overline{\mu }}}\frac{{\partial \overline{\mu }}}{{\partial \tilde{\mu }}}\frac{{\partial \tilde{\mu }}}{\partial \mu } + \frac{\partial G}{{\partial \overline{T} }}\frac{{\partial \overline{T} }}{\partial T}\frac{\partial T}{{\partial \overline{\mu }}}\frac{{\partial \overline{\mu }}}{{\partial \tilde{\mu }}}\frac{{\partial \tilde{\mu }}}{\partial \mu }} \right) \hfill \\ \frac{{\partial {\varvec{D}}}}{\partial \mu } = - \frac{{{\varvec{DE}}}}{{K^{2} }}\left( {\frac{\partial K}{{\partial \overline{\mu }}}\frac{{\partial \overline{\mu }}}{{\partial \tilde{\mu }}}\frac{{\partial \tilde{\mu }}}{\partial \mu } + \frac{\partial K}{{\partial \overline{T} }}\frac{{\partial \overline{T} }}{\partial T}\frac{\partial T}{{\partial \overline{\mu }}}\frac{{\partial \overline{\mu }}}{{\partial \tilde{\mu }}}\frac{{\partial \tilde{\mu }}}{\partial \mu }} \right) \hfill \\ \end{gathered} $$
(19)

where \({\varvec{KE}}\) is part of \({\varvec{K}}\) that has nothing to do with \(G\), and \({\varvec{DE}}\) is part of \({\varvec{D}}\) that has nothing to do with \(K\). \(K\) and \(G\) is the interpolated bulk and shear moduli, respectively (see Eq. (2)). The parts in parentheses can be obtained through PDE filtering, Heaviside projection, and the N-VTM described before.

3.3 Sensitivity of Constraint Function

Material consumption is only considered in this paper, and the constraint function can be written as

$$ g_{V} = {{\sum\limits_{e = 1}^{N} {v_{e} \overline{\mu }_{e} (\mu_{e} )} } \mathord{\left/ {\vphantom {{\sum\limits_{e = 1}^{N} {v_{e} \overline{\mu }_{e} (\mu_{e} )} } {\sum\limits_{e = 1}^{N} {v_{e} } - f_{0} \le 0,}}} \right. \kern-\nulldelimiterspace} {\sum\limits_{e = 1}^{N} {v_{e} } - f_{0} \le 0}} $$
(20)

Taking the derivative with respect to a design variable, one has

$$ \frac{{{\text{d}}g_{V} }}{{{\text{d}}\mu }} = \frac{{{\text{d}}\overline{\mu }}}{{{\text{d}}\tilde{\mu }}}\frac{{{\text{d}}\tilde{\mu }}}{{{\text{d}}\mu }} $$
(21)

here, it can be obtained by deriving the PDE filtering and Heaviside projection function.

So far, all sensitivity information has been obtained. The optimization algorithm MMA [41, 42] is used in this paper.

4 Numerical Examples

Some two-dimensional calculation examples are given below to verify the effectiveness of the thermal-solid–fluid method. Some optimization parameters in the following examples are the same. The threshold parameters \(\eta_{1}\) and \(\eta_{2}\) in the projection process are both 0.5, and the sharpness parameters \(\beta_{1}\), \(\beta_{2}\) and \(\alpha\) in the N-VTM double every 50 steps (or at convergence), increasing from 1 to 128. Any changes to the above parameters will be discussed in detail. In addition, \(k_{\min }\) and \(\lambda\) in the N-VTM do not change during the optimization process, and their values are 10−9 and 0.1, respectively. The filter radius will be specifically introduced in each example. The given bulk modulus and shear modulus of the solid material are 0.83 and 0.38, respectively, which is equivalent to the case where the elastic modulus is 1 and Poisson's ratio is 0.3. \(K_{{{\text{void}}}}\), \(G_{{{\text{void}}}}\), and \(G_{{{\text{fluid}}}}\) are set to 10−9, and \(K_{{{\text{fluid}}}}\) will be discussed below in detail.

4.1 Arch-Like Structure

As shown in Fig. 4a, the minimum compliance problem similar to the arch-like structure under the external static pressure load on the three sides is considered. Since we know the result of this optimization problem, the feasibility and effectiveness of the method proposed in this article can be preliminarily verified in this example. In this example, the design domain is discretized by 24,000 (200 × 120) square elements, the three sides are under uniform pressure, and the total force is 1. The volume fraction, the filter radius \(R\), and \(K_{{{\text{fluid}}}}\) are set to 0.3, 6, and 1, respectively. The Poisson's ratio of fluid material can be calculated as 0.5, which meets the requirements of the incompressible property.

Fig. 4
figure 4

Topology optimization of arch-like structure: a design domain of arch-like structure; b optimization process of arch-like structure with structure topologies and temperature field

Full size image

As shown in Fig. 4b, this method converges quickly. In particular, the objective function tends to be stable after the 20th iteration, and the structure topology changes little after the 20th iteration. Observing the temperature field in Fig. 4b, the area with high temperature is always inside the structure, so the fluid and void can be well distinguished, which shows the successful application of N-VTM. So the feasibility and effectiveness of our method are verified preliminarily.

4.2 Piston

In this example, we discuss the influence of \(K_{{{\text{fluid}}}}\) on structure topology, which provides a reference for the selection of parameters in the subsequent examples. The \(K_{{{\text{fluid}}}}\) selected in this example can ensure the incompressibility of the fluid.

The design domain of this example is divided into 360 × 120 grids, and the volume fraction and the filter radius \(R\) are set to 0.3 and 6, respectively. The displacement boundary conditions are shown in Fig. 5. The top surface bears a uniformly distributed load, and the total load is 1 N.

Fig. 5
figure 5

Design domain of piston

Full size image

Figure 6 shows the optimized topologies of the method in this paper and the optimized topologies in [31], respectively. The common point of the two methods is that they both use the mixed form. The difference is that in this paper, only one design variable is used to describe the topology; while in [31], two design variables are used. The \(K_{{{\text{fluid}}}}\) in [31] is taken as 10, while \(f_{{{\text{fluid}}}}\) in Fig. 6b represents the volume fraction of fluid. It can be found that the volume of fluid is constrained in [31], but when \(f_{{{\text{fluid}}}}\) becomes larger, the fluid will exist inside the structure, and the topology is similar to the last two topologies, which are the worst two results in this example using this method. In addition, the \(f_{{{\text{fluid}}}}\) corresponding to the optimal topology is usually unknown, and it is inappropriate to optimize the result by adjusting \(f_{{{\text{fluid}}}}\). However, in this method, there is no need to limit the volume of the fluid, and the appropriate volume fraction of fluid can be automatically optimized by selecting the appropriate \(K_{{{\text{fluid}}}}\).

Fig. 6
figure 6

Influence of \(K_{{{\text{fluid}}}}\) on compliance and optimized topologies of piston: a optimized topologies of this method with different \(K_{{{\text{fluid}}}}\); b optimized topology in [31]

Full size image

It can be seen from Fig. 6a that when \(K_{{{\text{fluid}}}}\) is less than 10, the optimized structure has smaller compliance and better performance. However, if \(K_{{{\text{fluid}}}}\) is too small, the optimization result will tend to be load-independent. In addition, compliance increases significantly when \(K_{{{\text{fluid}}}}\) increases. In the optimization process, the temperature inside the structure is not sufficiently high due to greater bulk modulus and gray elements, which will lead to the existence of fluid inside the structure. In the later stage of optimization, the fluid no longer exists inside the structure because of clearer projection, which results in greater compliance. In order to avoid the two problems above, \(K_{{{\text{fluid}}}}\) must be appropriate. According to the example and experience, the range of \(K_{{{\text{fluid}}}}\) is chosen from 1 to 10.

4.3 Underwater Structures

Three examples with different boundary conditions are shown in Fig. 7. The design domain is discretized by 64,000 (400 × 160) square elements. and only 1/4 of the entire structure is considered. The volume fraction is 0.25, and the filter radius \(R\) and \(K_{{{\text{fluid}}}}\) are set to 6 and 10, respectively. The load per unit area is 1 N.

Fig. 7
figure 7

Design domain and optimized topologies of underwater structures: a original design domain; b design domain with fixed supports; c design domain with roller supports; d optimized topology of the original design, \(W = 1.27 \times 10^{6}\); f optimized topology of design with fixed supports, \(W = 3.1 \times 10^{4}\); g optimized topology of design with roller supports, \(W = 3.4 \times 10^{4}\)

Full size image

The last three figures in Fig. 7 show that boundary conditions have a great impact on the structure. For similar structures, the performance of the structure can be improved by adding supports in the design. In this example, the structural stiffness is increased approximately 40 times by adding supports, which is a very good phenomenon. In fact, adding supports is also in line with the engineering practice. This problem has also been studied by Ibhadode et al. [28], Li et al. [27], and Du and Olhoff [18]. In addition, the results of these examples fully demonstrate the effectiveness of our method.

4.4 Pressurized Chamber

The description of this problem is shown in Fig. 8a. The design domain is discretized by 60,000 (300 × 200) square elements. The channel part and the black part of the design domain are non-designable domains. The filter radius \(R\) and \(K_{{{\text{fluid}}}}\) are set to 6 and 10, respectively, and the volume fraction is set to 0.3. In this example, the fluid should be distributed inside the structure. So the zero thermal boundary conditions in N-VTM should be applied inside the design domain, and the fluid will appear inside the structure.

Fig. 8
figure 8

Topology optimization of the pressure chamber: a design domain of pressure chamber; b optimized topology of the pressure chamber in this method; c Hammer and Olhoff [17] (SIMP); d Chen and Kikuchi [30] (SIMP); e Zhang et al. [23] (SIMP); f Picelli et al. [33] (BESO); g Picelli et al. [43] (LSM); h Neofytou et al. [9] (LSM)

Full size image

Figure 8b shows the optimized topology in this method, which is very similar to the first three results based on the SIMP method in Fig. 8. These results show that the top structural member appears to be thicker with solid covering the area on top of the horizontal fluid region, and the support at the right-hand side corner is thinner. However, the result of this method shows a clearer topology, without small features such as those in Fig. 8c, and the result has few gray elements. Besides, the topological clarity is equivalent to that of the last three results based on discrete methods or boundary-based methods in Fig. 8. The topology shown in the last three figures of Fig. 8 is relatively uniform as a whole, not as thick on the left and thin on the right as in the SIMP-based method. These differences are possibly due to the slightly different shape of the pressure region used in these examples.

In general, this method shows similar effects to discrete methods or boundary-based methods (e.g., LSM), while retaining some characteristics of the SIMP method.

5 Conclusion

In this paper, based on the MMA optimization algorithm, solid, fluid, and void are distinguished by the thermal-solid–fluid method, and incompressible fluid is used to transfer the pressure load by solving the mixed form, and the topology optimization with design-dependent pressure load is realized. In this method, we have realized the automatic distribution of fluid, which well distinguishes the area where the fluid appears. Then, the feasibility and effectiveness of the method are verified by four examples: the arch-like structure, the piston, the underwater structures, and the pressurized chamber. Good results can be obtained for a variety of design-dependent pressure load topology optimization, which has a guiding effect on practical applications. However, this method still has some problems, for example, the numerical instability caused by the mixed form and the N-VTM.

The research in this paper currently only considers two-dimensional topology optimization problems, and further studies are still needed on three-dimensional topology optimization problems, better finite element methods to replace the mixed form, and improving the algorithm to make it more efficient and stable.