Abstract
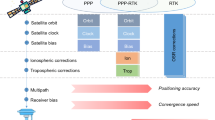
PPP-RTK is Precise Point Positioning (PPP) using corrections from a ground reference network, which enables single-receiver users with integer ambiguity resolution thereby improving its performance. However, most of the PPP-RTK studies are investigated and evaluated in a static situation or a post-processing mode because of the complexity of implementation in real-time practical applications. Moreover, although PPP-RTK achieves a faster convergence than PPP, it typically needs 30 s or even longer to derive high-accuracy results. We have implemented a real-time PPP-RTK approach based on undifferenced observations and State-Space Representation corrections with a fast convergence of less than 30 s to support autonomous driving of inland waterway vessels. The PPP-RTK performances and their feasibility to support autonomous driving have been evaluated and validated in a real-time inland waterway navigation. It proves the PPP-RTK approach can realize a precise positioning of less than 10 cm in horizontal with a rapid convergence. The convergence time is within 10 s after a normal bridge passing and less than 30 s after a complicated bridge passing. Moreover, the PPP-RTK approach can be extended to outside of the GNSS station network. Even if the location is 100 km away from the border of the GNSS station network, the PPP-RTK convergence time after a bridge passing is also normally less than 30 s. We have realized the first automated entry into a waterway lock for a vessel supported by PPP-RTK and taken the first step toward autonomous driving of inland vessels based on PPP-RTK.
Similar content being viewed by others
Explore related subjects
Find the latest articles, discoveries, and news in related topics.Avoid common mistakes on your manuscript.
Introduction
Global Navigation Satellite System (GNSS) code-based positioning is not adequate for accurate navigation of large vessels, especially in the case of limited maneuvering space. Real-Time Kinematic positioning (RTK) is a phase-based and widely applied relative precise positioning technique (Teunissen et al. 2014). Network RTK (NRTK) generates RTK corrections enabling the users to determine their position with centimeter accuracy in real-time using a shipborne GNSS receiver (Fotopoulos and Cannon 2001). It has been evaluated that the NRTK could provide accurate positioning in real-time from 5 to 10 cm in the fairway of Gothenburg, Sweden (Alissa et al. 2021). In Germany, an efficient navigation assistance function has been developed based on NRTK, aiming the reduction in risk of collisions in inland waterway transportation (Hesselbarth et al. 2020).
However, NRTK has some drawbacks, especially in the applications of inland waterway: (1) It needs a bi-directional communication link between the user and NRTK service provider, as the service provider needs to generate correction data based on the position received from the user, and then send the data back to the user. (2) It needs to compute correction data for each user. As the number of users increases, the computational pressure on service providers also increases, which is not capable of serving a huge number of autonomous-driving users in the future. (3) Last but not the least, NRTK correction data are encoded and transmitted as Observation Space Representation (OSR). Its size changes instantly depending on the number of visible GNSS satellites, and the data rate can therefore sometimes reach 1000 byte/s. However, the net capacity of modern maritime communication system Very High Frequency (VHF) Data Exchange System (VDES) for transmitting the NRTK correction data is only 650 byte/s, which cannot support multi-constellation NRTK positioning service for inland vessels (Alissa et al. 2021).
Although Precise Point Positioning (PPP) with only one single GNSS receiver can derive high accuracy solutions (Malys and Jensen 1990; Zumberge et al. 1997), the long convergence time of 5–30 min does not align with the requirements of real-time kinematic applications (Xia et al. 2019; An et al. 2020). Then, PPP-RTK is emerging to eliminate both issues of PPP and RTK (Wübbena et al. 2005; Teunissen and Khodabandeh 2015). PPP-RTK is based on precise satellite orbit, clock, signal biases and optional atmospheric products which are estimated from a GNSS ground station network. These products typically represented as State-Space Representation (SSR) information and broadcasted to PPP-RTK users. Currently, PPP-RTK can realize Ambiguity Resolution (AR) with the calibration of satellite phase bias products (Laurichesse et al. 2014), and different PPP-RTK methods have been proposed (Zhang et al. 2019; Aggrey and Bisnath 2019). The fusion of multi-constellation GNSS reduces the PPP-RTK convergence time to several minutes (Nadarajah et al. 2018; Li et al. 2020), which can be further shortened if precise atmospheric products are introduced (Geng et al. 2011; Li and Zhang 2014; Zha et al. 2021). All the PPP-RTK methods mentioned above are mostly investigated in a static scenario. Although the PPP-RTK has also been analyzed in dynamic scenarios for the vehicle (Geng et al. 2019; Gu et al. 2022; Li et al. 2022a, b) and inland waterway navigation (Lass and Ziebold 2021), it needs 30 s or even longer to achieve high accuracy results. Moreover, because of the complexity of implementation in a real-time practical application, PPP-RTK is mostly studied in a post-processing mode.
With regards to the real-time PPP-RTK positioning services (Li et al. 2022a, b), Japan has established the Centimeter Level Augmentation Service (CLAS) based on the Quasi-Zenith Satellite System (QZSS). Because this takes place via satellites, there is a time lag of 10 to 20 s until the augmentation information is created and transmitted. Thus, the augmentation service may not take place in time and would be utilized in an auxiliary way for driving on public roads. (https://qzss.go.jp/en/overview/services/sv06_clas.html). For the commercial PPP-RTK services, Trimble constructed CenterPoint-RTX service which can reduce the PPP-RTK convergence time to less than 1 min in North America and Europe. (https://positioningservices.trimble.com/services/rtx/centerpoint-rtx/). PointPerfect is an advanced GNSS augmentation service designed by Ublox to achieve accurate and immediately positioning. The positioning results with 3–6 cm horizontal accuracy can be obtained within 30 s. However, these commercial augmentation services are mainly evaluated in a static scenario (Nardo et al. 2015; Hohensinn et al. 2022) and rare studied for support autonomous driving.
The goal of this study is implementing a real-time PPP-RTK approach based on undifferenced GNSS observations with a fast convergence of a few seconds to support autonomous driving of inland vessels. We will evaluate how PPP-RTK performs in a real-time kinematic application and validate the feasibility of PPP-RTK when it supports a driver assistance system. In the following section, we will describe the PPP-RTK approach based on the real-time SSR corrections. Then, outline the measurement campaigns and data processing strategies, followed by the analysis of the PPP-RTK accuracy and convergence in inland waterway navigation. Finally, the conclusions are drawn.
Real-time kinematic PPP-RTK approach
This section will describe the PPP-RTK approach applied in a real-time kinematic scenario. It firstly describes GNSS observation equations, followed by the Kalman filter; then introduces AR to improve the PPP-RTK performance; finally, presents the workflow of PPP-RTK.
Observation equations
Observation equations of GNSS code, phase measurements and SSR atmospheric products from a satellite \(i\) to a receiver can be expressed as
in which \({P}_{1}^{i}\), \({P}_{2}^{i}\) and \({L}_{1}^{i}\), \({L}_{2}^{i}\) indicate GNSS code and phase measurements, respectively. Subscripts 1, 2 are two frequency bands, e.g., GPS L1, L2 or Galileo E1, E5a. \({\rho }^{i}\) means the geometric distance between the phase centers of satellite and receiver antennas. \(d\widetilde{t}\) is the receiver clock offset plus the receiver code bias of \({P}_{1}^{i}\). \({m}^{i}\) indicates the global mapping function (Böhm et al. 2006) of zenith tropospheric delay \(T\). \(I\) stands for the ionospheric delay, and \(g={\left({f}_{2}/{f}_{1}\right)}^{2}\) where \(f\) is the frequency of signals. \({\delta b}_{2}\) is the receiver differential code bias of \({P}_{2}^{i}\) with respect to \({P}_{1}^{i}\). \({S}_{P1}^{i}\), \({S}_{P2}^{i}\) and \({S}_{L1}^{i}\), \({S}_{L2}^{i}\) are SSR clock corrections plus satellite signal biases. \(\lambda\) is the corresponding wavelength. \({\widetilde{n}}_{1}^{i}\) and \({\widetilde{n}}_{2}^{i}\) represent the estimated phase ambiguities and are expressed as
where \({\delta h}_{1}\) and \({\delta h}_{2}\) are receiver phase biases; \({n}_{1}^{i}\) and \({n}_{2}^{i}\) are integer ambiguities. In addition to the code and phase measurements, we are receiving real-time SSR tropospheric and ionospheric products, named as \({S}_{T}^{i}\) and \({S}_{I}^{i}\), which are represented as a multi-state model and calculated according to the receiver position (Wübbena et al. 2020). They are seen as pseudo observations and added to the PPP-RTK observation equations. \(\varepsilon\) means the observation noise. Last but not the least, phase-windup (Wu et al. 1991) has been corrected in (1). The relativistic effect of Shapiro delay is about 1.5 ~ 2.5 cm in this case, and the solid earth tides correction is 4 ~ 6 cm in this region (McCarthy and Petit 2004). They are both considered, while the ocean tide corrections are less than 1 cm and ignored.
Reformulate (1) to a matrix format as
in which \(\left[ {\begin{array}{*{20}c} {P_{1}^{^{\prime}i} } & {P_{2}^{^{\prime}i} } & {\begin{array}{*{20}c} {L_{1}^{^{\prime}i} } & {L_{2}^{^{\prime}i} } \\ \end{array} } \\ \end{array} } \right]^{{\text{T}}}\) can be interpreted as observed minus computed observations and expressed as
In (3), \(\left[\begin{array}{ccc}{C}_{x}^{i}& {C}_{y}^{i}& {C}_{y}^{i}\end{array}\right]\) denotes the coefficients of \(\left[\begin{array}{ccc}dx& dy& dz\end{array}\right]\). Equation (3) is the basic observation equation for a given satellite used in PPP-RTK, and a Kalman filter is applied to solve the PPP-RTK observation equations.
Kalman filter
Prediction
Assuming we observe \(l\) satellites, the Kalman filter predicting model derives the state vector \({\mathbf{X}}_{k}\) at epoch \(\mathrm{k}\) from \({\mathbf{X}}_{k-1}\) according to
with
\({{\varvec{F}}}_{k}\) is a unit matrix and \({{\varvec{W}}}_{k}\) is the process noise which follows a zero mean multivariate normal distribution with a variance of \({{\varvec{Q}}}_{k}\). When the sampling interval is 1 s, it can be set as
In a kinematic scenario, PPP-RTK starts by performing code-based Single Point Positioning (SPP) to get an initial receiver position and clock offset at each epoch. The process noise of the SPP position and receiver clock offset are set as 52 and 1002 m2, which are relatively large and loose just in case some large errors may exist in SPP solutions under a harsh environment. It has been researched that the stability of differential code bias \({\delta b}_{2}\) within one day is normally less than 0.3 ns (0.09 m/day) (Li et al. 2018). Thus, setting the process noise of \({\delta b}_{2}\) as 0.0012 m2 per second is also relative loose and reasonable. The process noises of troposphere and ionosphere are set as 0.0012 and 0.012 m2 with a sampling rate of 1 Hz. The process noise of ambiguities is set as 0.0012 cycle2 due to the fact that the estimated float ambiguities in (2) are contaminated by the receiver signal biases between code and phase measurements. The corresponding covariance matrix of the predicted state vector is derived by
Update
At epoch k, an observation vector \({\mathbf{Z}}_{k}\) of the state vector \({\mathbf{x}}_{k}\) is formulated as
For a specific satellite \(\begin{array}{*{20}c} {i \in \left( {1,2, \ldots ,l} \right) {\mathbf{Z}}_{k}^{i} = \left[ {\begin{array}{*{20}c} {P_{1}^{^{\prime}i} } & {P_{2}^{^{\prime}i} } & {\begin{array}{*{20}c} {L_{1}^{^{\prime}i} } & {L_{2}^{^{\prime}i} } & {\begin{array}{*{20}c} {S_{T}^{^{\prime}i} } & {S_{I}^{^{\prime}i} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right]^{{\text{T}}} } \\ \end{array}\). \({\mathbf{H}}_{k}\) is the design matrix at epoch \(k\) and constructed according to (3). \({\mathbf{R}}_{k}\) is a diagonal matrix with the diagonal elements as the observational noise. The observation noises of code and phase measurements for GPS and Galileo are set as 0.6 m and 0.01 cycle. Because the SSR tropospheric and ionospheric products are precisely calculated based on a local GNSS station network, the corresponding noises are set as 0.01 m and 0.05 m.
The solution of Kalman filter without AR in the updating phase is derived by
with
The corresponding covariance matrix of state vector is
Ambiguity resolution
The float ambiguity vector \(\widetilde{{\varvec{n}}}\) and its covariance matrix \({{\varvec{P}}}_{\widetilde{\mathbf{n}}\widetilde{\mathbf{n}}}\) can be extracted from the solutions \({{\varvec{X}}}_{k|k}\) and \({\mathbf{P}}_{k|k}\). As mentioned before, the receiver signal biases \({\delta h}_{1}\) and \({\delta h}_{2}\) have an influence on the estimated ambiguities. The influence can be eliminated by differencing the ambiguities between two satellites. Before that, we need to select a pivot satellite for each GNSS constellation to construct single-differenced ambiguities between two satellites. The satellite with the minimum variance instead of the highest elevation is chosen as the pivot satellite.
Assuming the pivot satellite is p, the single-differenced ambiguities between two satellites are expressed as
with
in which \(\Delta\) is the single-difference operator between two satellites and \({\varvec{M}}\) is the matrix expression of the operator \(\Delta\). Considering a rapid AR, we further construct the wide-lane ambiguities as
with
where \(\nabla\) is the operator to construct wide-lane ambiguities, and \(\mathbf{N}\) is the matrix expression of the operator \(\nabla\).
From (1), it can be seen that SSR ionospheric products and code measurements contribute the estimation of the ionospheric delay. Normally, the ionospheric delay can be determined at an accuracy of several centimeters with one or several epochs data. Assuming the residual ionospheric error is 5 cm, its effects on GPS \({\widetilde{n}}_{1}\) ambiguity is \(0.05/0.19=0.26\) cycles and on GPS \({\widetilde{n}}_{2}\) ambiguity is \(0.05\times {\left({f}_{1}/{f}_{2}\right)}^{2}/0.24=0.34\) cycles, while on the ambiguity of \({\widetilde{n}}_{1}-{\widetilde{n}}_{2}\) is only \(0.26-0.34=-0.08\) cycles. That means the wide-lane ambiguity of \({\widetilde{n}}_{1}-{\widetilde{n}}_{2}\) is significantly less affected by the residual ionospheric errors, and can be faster resolved to integers compared to \({\widetilde{\mathrm{n}}}_{1}\) and \({\widetilde{\mathrm{n}}}_{2}\). That’s the reason why we construct and resolve the wide-lane ambiguities.
The constructed single-differenced wide-lane ambiguities between two satellites \(\nabla \Delta \widetilde{\mathbf{n}}\) are essential integers, its variance and covariance matrix is derived according to (15) as
Then, \(\nabla \Delta \widetilde{\mathbf{n}}\) and \({\mathbf{Q}}_{\nabla \Delta \widetilde{\mathbf{n}}}\) are as input parameters of the Modified Least-squares Ambiguity Decorrelation Adjustment (MLAMBDA) for resolving the integer ambiguities (Chang et al. 2005; Teunissen 1994). Both the full and partial AR are implemented. In partial AR, at most 3 satellites for each GNSS are discarded, at least 6 GPS and Galileo satellites are retained. The ratio test of fixed failure rate is used for ambiguity validation (Verhagen and Teunissen 2013), where the fix failure rate is set as 1%. Once the ambiguities are successfully resolved to an integer vector \(\nabla \Delta n\), the fixed ambiguities will be seen as tight constraints and added to (9), which will be solved again to get the solution with AR.
Instead of directly utilizing the single-differenced observations between two satellites, we apply undifferenced observations in Kalman filter and construct the single-differenced wide-lane ambiguities between two satellites in the stage of ambiguity resolution. It stems from two considerations: (1) The observation noise of undifferenced observation is definitely lower than that of the single-differenced observation, which will benefit the estimation of Kalman filter and reduce the observation residuals. (2) It has more freedom to select and switch the pivot satellites. For example, in a harsh environment where some GNSS signals are interrupted, the pivot satellite may have some small cycle slips or minor errors which are not detected and excluded in the stage of cycle-slip or residual detection. Then all the formed single-differenced ambiguities with respect to this pivot satellite will contain some biases, consequently, the AR will fail. If the PPP-RTK is based on single-differenced observations between two satellites, we have to change the pivot satellite, reconstruct the single-differenced observations between two satellites and solve the Kalman filter again. However, if the PPP-RTK is based on undifferenced observations, it does not need to solve the Kalman filter equation again. We just need to select another pivot satellite from the estimated state vector, and calculate a new set of single-differenced ambiguities between two satellites, then directly try to resolve the new set of ambiguities to integers.
Workflow
The PPP-RTK system supporting autonomous driving of inland vessels includes 4 segments, as illustrated in Fig. 1: Reference stations, PPP-RTK service center, PPP-RTK unit and driver assistance system with display unit. The reference stations construct a GNSS station network. PPP-RTK service center in this case is Satellite Positioning Service of the German Land Survey (SAPOS), which collects observation data from the network and generates SSR corrections in real time. Considering the time-variant nature of different error sources, it provides low-rate and high-rate corrections: the low-rate corrections consist of satellite orbit, clock, signal biases and atmospheric model with an updating interval of 30 s; the high-rate corrections refer to the satellite high-rate clock corrections with an updating interval of 5 s. These SSR corrections are compressed as SSRZ format (Wübbena et al. 2020) for saving bandwidth and broadcasted to the users through VDES in maritime or cellular network.
The PPP-RTK unit is the main topic we focus on in this paper, which contributes to the autonomous driving of inland vessels and comprises five submodules:
-
1.
Onboard GNSS receivers. They are the hardware we installed on the vessel to receive the GNSS observations.
-
2.
GNSS data preprocessing. It mainly includes the cycle slip detection and large errors detection (Blewitt 1990); if cycle slips or large errors are detected, reset the ambiguity parameters or remove the corresponding measurements.
-
3.
Decoding corrections. This submodule decodes the received SSR corrections, calculates precise satellite orbit and clocks, calibrates the measurements based on the signal biases products and computes the ionospheric and tropospheric delays based on the decoded atmospheric model parameters.
-
4.
Kalman filter. It is mainly composed of constructing GNSS observation equation, predicting state vector, update the state vector based on the measurements and solve the Kalman filter equation. Then, detect large residuals. If a large error is detected, remove the corresponding measurement and reupdate the state vector until no large residuals exist.
-
5.
Ambiguity resolution. Try to fully or partially resolve the single-differenced wide-lane ambiguities between two satellites to integers based on MLAMBDA; if the ambiguities are successfully resolved to integers, then derive the fixed solution otherwise float solution.
Finally, the driver assistance system steers the vessel according to the PPP-RTK solutions and displays the position of the vessel on a precise map.
Measurement campaign and data processing strategies
To comprehensively evaluate and analyze the PPP-RTK performances, we have conducted 2 measurement campaigns located inside and outside the GNSS station network, as shown in Fig. 2.
Measurement campaign 1 (M1): A geodetic GNSS antenna connected with a JAVAD Delta receiver was mounted on the bow of a research vessel “MS BINGEN” which is 4 m wide and 14 m long. The Positioning, Navigation and Timing (PNT) unit, installed in the vessel and shown in Fig. 3, computes PPP-RTK solutions in real time. The measurement campaign was carried out on 17th of November, 2021 in Koblenz, Germany. The real-time SSR corrections received from SAPOS were generated based on 18 reference stations. Furthermore, an RTK reference station was also setup so as to calculate a reference solution of the shipborne receiver by using RTKLib (Takasu and Yasuda 2009) in a post-processing RTK mode.
Measurement campaign 2 (M2): It was conducted on 23rd of February, 2022 in Strasbourg, France. As shown in Fig. 3, a GNSS antenna was mounted on a large vessel “Victor Hugo” which is 83 m long and 9.5 m wide. The location is roughly 200 km away from the center and 100 km away from the boundary of the GNSS station network. This measurement campaign achieved the first automatic entry into a waterway lock for the vessel with the support of PPP-RTK. Instead of setting up an RTK base station, a static station, named as ENTZ, from European Reference Frame Permanent GNSS Network (EPN) is selected for calculating the reference solutions of the shipborne receiver by using RTKLib in a post-processing RTK mode.
The real-time PPP-RTK solutions are calculated by RTFramework (Gewies et al. 2012) which is a software platform developed by the Institute of Communications and Navigation of German Aerospace Center (DLR) for real-time GNSS data processing. The RTK solutions are post-processed by RTKLib using the final orbit and clock products from the Center for Orbit Determination in Europe (CODE). The SSR orbit and clocks applied by PPP-RTK are determined based on a station network of regional scale, while CODE estimates the orbit and clocks in a global scale. As a result, there is a mean offset between PPP-RTK and RTK solutions. This offset is calculated by averaging the positioning differences between PPP-RTK and RTK solutions and removed in the comparison analysis. The processing strategies of PPP-RTK and RTK are listed in Table 1.
PPP-RTK performances and analysis
In inland waterway applications, the PPP-RTK performance in horizontal is more important and practical than that in vertical, thus horizontal positioning performances are mainly analyzed. The convergence time is defined as the positioning errors starting lower than 10 cm and retaining within 10 cm in the sequential 10 s. Moreover, because the PPP-RTK approach estimates the atmospheric delays based on the SSR atmospheric corrections, the PPP-RTK approach could be applied to outside of the GNSS station network. Therefore, the PPP-RTK performances inside and outside of the GNSS station network are both evaluated.
PPP-RTK performances inside of the network
The trajectory of M1 is illustrated in Fig. 4, where the vessel started moving from a waterway lock at 11:21, then crossed 7 bridges, and finally ended in a harbor at 15:30. The PPP-RTK positioning errors with respect to RTK solutions and the corresponding distribution of the errors are presented in Fig. 5.
It is shown in Fig. 5 that the errors follow a normal distribution. 97.2% and 96.0% of the PPP-RTK errors are within ± 0.1 m at east and north components, respectively. Only 0.17% and 0.16% of the absolute PPP-RTK errors are larger than 0.2 m. Although the vertical positioning errors is not as good as those in horizontal and only 47.8% and 81.1% of the PPP-RTK errors in vertical are within ± 0.1 m and ± 0.2 m, the inland waterway applications mainly require a precise positioning in horizontal. Moreover, when the GNSS signals are significantly interfered by the infrastructure of the waterway the PPP-RTK is interrupted and initialized again. Consequently, there are some larger errors observed in Fig. 5. Therefore, passing the bridges and waterway locks are two challenging scenarios and mainly analyzed in the next.
Bridge passing
The PPP-RTK trajectories over different types of bridge passing are shown in Fig. 6. Although the bridges definitely block the GNSS signals, it also depends on the height and type of the bridges. Therefore, the bridges passing in this section are classified as three situations: A simple situation, a normal situation and a complicated situation. In the simple situation, bridges are relatively high or sufficient GNSS signals can be tracked during a passage. The PPP-RTK may not be interrupted but with some float solutions. In the normal situation, the GNSS signals are severely blocked by the bridges. Consequently, the solutions are interrupted by a few seconds because of the limited available satellites. The PPP-RTK solver has to initialize again after the passage. The initialization takes 9, 6, and 9 s after passing bridges 1, 3 and 4. In the complicated situation, the vessel continuously passes through two bridges within a short time. The GNSS signals are not only harshly blocked by the first bridge, but also somehow interfered by the second bridge after passing the first bridge. It takes 13 s to get the first fixed solution after passing bridge 5, and then after 3 s the AR fail in the subsequent 10 s. Thus, it totally requires 26 s to get a reliable fixed solution. The initialization takes 13 and 9 s after passing bridges 6 and 7, which are shorter than passing through bridge 5.
The RTK solutions are generated based on the nearby reference station, the longest baseline length from the base station to the rover receiver is about 15 km, and the processing strategies are listed in Table 1. The PPP-RTK positioning errors with respect to RTK solutions are plotted in Fig. 7. In the simple situation, most of the positioning errors are lower than 10 cm. As for the normal situation, the ambiguities are successfully resolved within 10 s after passing the bridge and the positioning errors are then less than 10 cm. Regarding the complicated situation, the PPP-RTK solutions are obviously biased by several decimeters in the initialization. It takes 26 and 13 s to get a reliable fixed solution with an accuracy of less than 10 cm for bridges 5 and 6, respectively. The convergence time, fixing rate of PPP-RTK and the horizontal precision of PPP-RTK fixed solutions during passing through these bridges are listed in Table 2. It demonstrates that in a simple and normal bridge passing, PPP-RTK is capable of achieving rapid convergence of less than 10 s with a positioning precision of less than 10 cm, and the fixing rate is more than 90%. Even for the complicated bridges passing, the initialization time is less than 30 s to reach precise positioning within 10 cm.
PPP-RTK positioning error with respect to RTK solutions during passing the 7 bridges: a simple situation (bridges 2 and 7), a normal situation (bridges 1, 3, 4) and a complicated situation (bridges 5, 6). In the legend, the green dotes (PPP-RTK & RTK fixed) mean both PPP-RTK and RTK solutions realized AR; the blue dots (PPP-RTK fixed & RTK float) indicate the PPP-RTK solutions achieved AR but RTK not; the orange dotes (PPP-RTK float & RTK fixed) illustrate the PPP-RTK solutions failed to realize AR but RTK solutions realized; the red dots (PPP-RTK & RTK float) mean both the PPP-RTK and RTK solutions did not realized AR
Waterway lock passing
Different phases of passing through a waterway lock and available satellites are shown in Fig. 8. In the phases 1 and 3, more than 11 GPS and Galileo satellites are available. The most challenging phase is phase 2 when the vessel is in the chamber. Regularly there are 9 GPS and Galileo satellites in this phase. However, the number of satellites decreases to 7 during the vessel crossing the lock gate in the chamber. The GNSS signals are severely interfered by the building indicated in Fig. 8. Consequently, the AR fails in 0.3% of the solutions and all of them exist at the junction of phases 2 and 3. Once the vessel passed the lock gate, the number of available satellites increases and the ambiguities are soon successfully resolved.
The comparison between PPP-RTK and RTK solutions is plotted in Fig. 9. The fixing rates of ambiguities for PPP-RTK and RTK are 99.7% and 97.3%, respectively. The standard deviations of the errors in east are 0.015 m, 0.025 m and 0.011 m for Phases 1, 2 and 3; in the north, they are 0.019 m, 0.022 m and 0.015 m. The standard deviation at Phase 2 is the worst, because the available satellites are relatively less than the other phases. To summarize, the available satellites undoubtedly affect the PPP-RTK performance, especially when the vessel passes through a lock gate in the lock chamber, the number of available satellites decreases, and fixed solutions are not expected to be obtained. Once the vessel passed through the lock gate, the ambiguities can be immediately resolved to integers and then derive PPP-RTK fixed solutions.
PPP-RTK performances outside of the network
The trajectory of M2 and position of RTK reference station are shown in Fig. 10. Because the location of the measurement campaign is far away from the SSR GNSS station network. We enlarge the observation noise of SSR tropospheric and ionospheric products from 0.01 m and 0.05 m to 0.04 m and 0.2 m, respectively. The PPP-RTK performances of bridges passing and waterway lock entering are analyzed in the next.
Bridges passing
The PPP-RTK performances over the bridges are plotted in Fig. 11. When the vessel is under the bridges, there is a solution gap of several seconds. The PPP-RTK has to initialize after crossing the bridges. The PPP-RTK positioning errors with respect to RTK solutions are shown in Fig. 12. The number of GPS and Galileo available satellites is less than 5 when the vessel is under the bridges. After passing through the bridges 1, 2, 3 and 4 from south to north, the convergence time is 16 s, 17 s, 67 s and 3 s, which are listed in Table 3. While it spends 9 s, 46 s, 16 s and 16 s for bridges 4, 3, 2 and 1 when the vessel moving from north to south. The convergence is a little bit longer than that of M1, because the bridges are wider and the structures are more complicated as those used in M1. Moreover, because bridge 3 is a suspension bridge, which has a more complicated structure than other bridges, it takes the longest time of convergence. The fixing rate of PPP-RTK solutions is 96.5%. Compared with RTK solutions, the positioning precision at 95% confidence level is 0.06 m when the vessel moving from south to north. When the vessel moving from north to south, the fixing rate is 93.5% and the positioning precision at 95% confidence level is 0.07 m.
PPP-RTK positioning errors in horizontal with respect to RTK solutions and the available satellites during passing the bridges, in which B1, B2, B3, B4 indicate Bridges1, 2, 3 and 4, respectively. The meaning of different colors in the panels of top two rows refers to Fig. 7
Waterway lock entering
The main purpose of this measurement is to assess the PPP-RTK performances when PPP-RTK supports a driver assistance system to steer a vessel automatically entering into a waterway lock. The driver assistance system steered the vessel following a straight line to enter into the waterway lock. Actually, the true trajectory of the vessel is not an absolute straight line because of the steering accuracy. The vessel tried to enter into the waterway lock three times. The trajectory of the vessel and also the perpendicular offsets with respect to the theoretical straight line are plotted in Fig. 13.
It is the most challenging for the vessel crossing the lock gate, where most of the solutions are float solutions. For the 1st entry into the waterway lock, PPP-RTK and RTK have comparable fixing rates, they are 94.3% and 94.8%. While for the 2nd and 3rd entries, the fixing rates of RTK are 95.1% and 90.7%, which are higher than the PPP-RTK fixing rates of 83.8% and 86.9%. Regarding the percentages of the perpendicular offsets within ± 10 cm for the three entries, they are 93.2%, 72.9%, 83.6% for PPP-RTK and 91.8%, 66.9%, 90.4% for RTK solutions. The percentage of the 2nd entry is the lowest no matter for PPP-RTK or RTK solutions. This is because the steering amplitude of the 2nd entry is larger than other times.
The discrepancies between PPP-RTK and RTK solutions for the 3 entries are presented in Fig. 14. There are large discrepancies during crossing the lock gate. Especially for the 2nd entry, the discrepancies are even larger than 0.5 m. Actually, the large errors are mainly from RTK float solutions. RTK solutions have obvious larger errors just before crossing the lock gate, which can be seen from the trajectory of RTK solutions in Fig. 13. The convergence time, fixing rate of PPP-RTK and horizontal precision at 95% confidence level after convergence for the three enteries of the waterway lock are listed in Table 4. The convergence time for the three entries is 13 s, 22 s and 9 s. After convergence, the horizontal precision of PPP-RTK is 0.05 m, 0.14 m and 0.07 m for the three entries, respectively. It proves that, PPP-RTK can realized a rapid convergence and achieve an accuracy of less than 10 cm for the 1st and 3rd entries after crossing the lock gate. Therefore, PPP-RTK can well support the driver assistance system with a high precision, this is also the first time that a vessel automatically enters into a waterway lock supported by PPP-RTK.
PPP-RTK positioning discrepancies in horizontal with respect to RTK solutions and available satellites during the three entries of the waterway lock. The meaning of different colors in the panels of top two rows refers to Fig. 7
Actually, we installed two GNSS antennas on the bow and stern of the long vessel, respectively. As an example, this manuscript just showed the PPP-RTK performances of the bow antenna. The PPP-RTK are running independently for the bow and stern GNSS antennas. When passing through a bridge, the GNSS signals of the bow antenna is blocked by the bridge, while the stern antenna is still in an open area and normally provides PPP-RTK services to the control system of the vessel. As a result, the control system of the vessel can continually get the PPP-RTK solutions from the two-antenna system when passing through a bridge. We are taking the first step of PPP-RTK for supporting autonomous driving of inland vessels. In the next step, we are going to implement the tight coupled PPP-RTK and IMU so as to provide continual positioning service and integrity information for autonomous driving even in a harsh environment.
Conclusions
Compared with RTK, PPP-RTK has more advantages and is more suitable for autonomous driving. By utilizing the state-of-the-art SSR corrections, we implemented a PPP-RTK approach with instant AR and rapid convergence. It has been proven that the convergence time is within 10 s after a normal bridging passing and less than 30 s after a complicated bridge passing. The standard deviation in horizontal is less than 0.03 m during the vessel passing through the waterway lock. In addition, this approach estimates the ionospheric and tropospheric delays based on a priori knowledge of SSR atmospheric model, thus the PPP-RTK approach can be extended to outside of the GNSS station network. Even the location is 100 km away from the border of the GNSS station network, the PPP-RTK convergence time after a bridge passing is also less than 30 s except for a very complicated suspension bridge, and more than 90% of the discrepancies between PPP-RTK and RTK are less than 10 cm during entering a waterway lock. The high-accuracy real-time PPP-RTK with rapid convergence has been well applied for accurate navigation in inland waterway. Finally, we realized a vessel automatically entering into a waterway lock supported by PPP-RTK solutions.
Data availability
All data generated during and analyzed during the current study are available from the corresponding author upon reasonable request.
References
Aggrey J, Bisnath S (2019) Improving GNSS PPP convergence: the case of atmospheric-constrained. Multi-GNSS PPP-AR Sensors 19(3):587. https://doi.org/10.3390/s19030587
Alissa S, Håkansson M, Henkel P, Mittmann U, Hüffmeier J, Rylander R (2021) Low bandwidth network-RTK correction dissemination for high accuracy maritime navigation. TransNav 15(1):171–179. https://doi.org/10.12716/1001.15.01.17
An X, Meng X, Jiang W (2020) Multi-constellation GNSS precise point positioning with multi-frequency raw observations and dual-frequency observations of ionospheric-free linear combination. Satell Navig 1:7. https://doi.org/10.1186/s43020-020-0009-x
Blewitt G (1990) An automatic editing algorithm for GPS data. Geophys Res Lett 17(3):199–202. https://doi.org/10.1029/GL017i003p00199
Böhm J, Niell A, Tregoning P, Schuh H (2006) Global mapping function (GMF): a new empirical mapping function based on numerical weather model data. Geophys Res Lett 33(7):1–4. https://doi.org/10.1029/2005GL025546
Chang XW, Yang X, Zhou T (2005) MLAMBDA: a modified LAMBDA method for integer least-squares estimation. J Geod 79(9):552–565. https://doi.org/10.1007/s00190-005-0004-x
Fotopoulos G, Cannon M (2001) An overview of multi-reference station methods for cm-level positioning. GPS Solutions 4:1–10. https://doi.org/10.1007/PL00012849
Geng J, Teferle FN, Meng X, Dodson AH (2011) Towards PPP-RTK: ambiguity resolution in real-time precise point positioning. Adv Space Res 47(10):1664–1673. https://doi.org/10.1016/j.asr.2010.03.030
Geng J, Guo J, Chang H, Li X (2019) Towards global instantaneous decimeter-level positioning using tightly-coupled multi-constellation and multi-frequency GNSS. J Geod 93(7):977–991. https://doi.org/10.1007/s00190-018-1219-y
Gewies S, Becker C, Noack T (2012) Deterministic framework for parallel real-time processing in GNSS applications. 2012 6th ESA Workshop on Satellite Navigation Technologies (Navitec 2012) & European Workshop on GNSS Signals and Signal Processing, Noordwijk, Netherlands, pp 1-6.
Gu S, Dai C, Mao F, Fang W (2022) Integration of multi-GNSS PPP-RTK/INS/vision with a cascading kalman filter for vehicle navigation in urban areas. Remote Sens 14(17):4337. https://doi.org/10.3390/rs14174337
Hesselbarth A, Medina D, Ziebold R, Sandler M, Hoppe M, Uhlemann M (2020) Enabling assistance functions for the safe navigation of inland waterways. IEEE Intell Transp Syst Mag 12(3):123–135. https://doi.org/10.1109/MITS.2020.2994103
Hohensinn R et al (2022) Low-cost GNSS and real-time PPP: assessing the precision of the u-blox ZED-F9P for kinematic monitoring applications. Remote Sens 14(20):5100. https://doi.org/10.3390/rs14205100
Lass C, Ziebold R (2021) Development of precise point positioning algorithm to support advanced driver assistant functions for inland vessel navigation. TransNav 15(14):781–789. https://doi.org/10.12716/1001.15.04.09
Laurichesse D, Mercier F, Berthias J, Broca P, Cerri L (2014) Integer ambiguity resolution on undifferenced GPS phase measurements and its application to PPP and satellite precise orbit determination. Navig 56(2):135–149. https://doi.org/10.1002/j.2161-4296.2009.tb01750.x
Li P, Zhang X (2014) Integrating GPS and GLONASS to accelerate convergence and initialization times of precise point positioning. GPS Solutions 18(3):461–471. https://doi.org/10.1007/s10291-013-0345-5
Li M, Yuan Y, Wang N, Liu T, Chen Y (2018) Estimation and analysis of the short-term variations of multi-GNSS receiver differential code biases using global ionosphere maps. J Geod 92(2):889–903. https://doi.org/10.1007/s00190-017-1101-3
Li P, Jiang X, Zhang X, Ge M, Schuh H (2020) GPS + Galileo + BeiDou precise point positioning with triple-frequency ambiguity resolution. GPS Solutions 24(3):78. https://doi.org/10.1007/s10291-020-00992-1
Li X, Huang J, Li X, Shen Z, Han J, Li L (2022a) Wang B (2022) Review of PPP–RTK: achievements, challenges, and opportunities. Satell Navig 3:28. https://doi.org/10.1186/s43020-022-00089-9
Li X, Qin Z, Shen Z, Li X, Zhou Y, Song B (2022b) A high-precision vehicle navigation system based on tightly coupled PPP-RTK/INS/ odometer integration. IEEE Trans Intell Transp Syst. https://doi.org/10.1109/TITS.2022.3219895
Malys S, Jensen PA (1990) Geodetic point positioning with GPS carrier beat phase data from the CASA UNO experiment. Geophys Res Lett 17(5):651–654
McCarthy DD, Petit G (2004) IERS Conventions (2003). International earth rotation and reference systems service (IERS), Germany, 2004.
Nadarajah N, Khodabandeh A, Wang K, Choudhury M, Teunissen PJG (2018) Multi-GNSS PPP-RTK: from large-to small-scale networks. Sensors 18(4):1078. https://doi.org/10.3390/s18041078
Nardo A et al (2015) Experiences with trimble CenterPoint RTX with fast convergence. Trimble TerraSat GmbH, Haringstrasse 19:85635
Takasu T, Yasuda A (2009) Development of the low-cost RTK-GPS receiver with an open source program package RTKLIB. IntI. Sym. on GPS/GNSS, Jeju, Korea, 2009.
Teunissen PJG (1994) The least-squares ambiguity decorrelation adjustment: a method for fast GPS integer ambiguity estimation. J Geod 70(1):65–82. https://doi.org/10.1007/BF00863419
Teunissen PJG, Khodabandeh A (2015) Review and principles of PPP-RTK methods. J Geod 89(3):217–240. https://doi.org/10.1007/s00190-014-0771-3
Teunissen PJG, Odolinski R, Odijk D (2014) Instantaneous BeiDou+ GPS RTK positioning with high cut-off elevation angles. J Geod 88(4):335–350. https://doi.org/10.1007/s00190-013-0686-4
Verhagen S, Teunissen PJG (2013) The ratio test for future GNSS ambiguity resolution. GPS Solutions 17(4):535–548. https://doi.org/10.1007/s10291-012-0299-z
Wu JT, Wu SC, Hajj G, Bertiger WI, Lichten SM (1991) Effects of antenna orientation on GPS carrier phase. In Proc. Astrodynamics 1991, Durango, CO, USA, Aug. 1991.
Wübbena G, Schmitz M, Bagge A (2005) PPP-RTK: precise point positioning using state-space representation in RTK networks. In Proc. ION GNSS 2005. Long Beach, CA, USA, Sep 2005:2584–2594
Wübbena G, Perschke C, Wübbena J, Wübbena T, Schmitz M (2020) GNSS SSR real-time correction: The Geo++ SSRZ format and applications. In Proc. ION GNSS+ 2020, 2020, pp 55–98. https://doi.org/10.33012/2020.17552
Xia F, Ye S, Xia P, Zhao L, Jiang N, Chen D, Hu G (2019) Assessing the latest performance of Galileo-only PPP and the contribution of Galileo to Multi-GNSS PPP. Adv Space Res 63(9):2784–2795. https://doi.org/10.1016/j.asr.2018.06.008
Zha J, Zhang B, Liu T, Hou P (2021) Ionosphere-weighted undifferenced and uncombined PPP-RTK: theoretical models and experimental results. GPS Solutions 25:135. https://doi.org/10.1007/s10291-021-01169-0
Zhang B, Chen Y, Yuan Y (2019) PPP-RTK based on undifferenced and uncombined observations: theoretical and practical aspects. J Geod 93:1011–1024. https://doi.org/10.1007/s00190-018-1220-5
Zumberge JF, Heflin MB, Jefferson DC, Watkins MM, Webb FH (1997) Precise point positioning for the efficient and robust analysis of GPS data from large networks. J Geophys Res 102(B3):5005–5017. https://doi.org/10.1029/96JB03860
Acknowledgements
Thank all project partners within the project SCIPPPER, which are Argonics GmbH, ArgoNav GmbH, Alberding GmbH, Weatherdock AG, Federal Waterways Engineering and Research Institute (BAW) and the Federal Waterways and Shipping Administration for the fruitful collaboration within the project. The supports during the measurement activities from the crew of MS BINGEN and VICTOR_HUGO are acknowledged. We also thank SAPOS and GEO++ for the provision of the SSR correction data. This work was supported by the SCIPPPER project granted by German Federal Ministry of Economic Affairs and Climate Action Grant number 03SX470E). It was also partially funded by the German Federal Ministry for Digital and Transport (Grant number: VB18F1025B) and the European Commission (Grant number: 861377). Last but not the least, we acknowledge anonymous reviewers for their valuable, constructive and prompt comments.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
XA: Conceptualization, Methodology, Validation, Formal analysis, Visualization, Software, Data collection, Writing—original draft, Writing—review & editing. RZ: Conceptualization, Data collection, Supervision, Funding acquisition, Writing—review & editing. CL: Conceptualization, Data collection, Software, Writing—review & editing.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
An, X., Ziebold, R. & Lass, C. From RTK to PPP-RTK: towards real-time kinematic precise point positioning to support autonomous driving of inland waterway vessels. GPS Solut 27, 86 (2023). https://doi.org/10.1007/s10291-023-01428-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10291-023-01428-2