Introduction

Global navigation satellite system (GNSS) users mainly depended on American GPS or Russian GLONASS in the past. However, this has gradually changed with the emergence of Chinese BeiDou navigation satellite system (BDS) and European Galileo system. BDS-3 primary system was announced to provide global services on December 27, 2018 (http://en.beidou.gov.cn/). The constellation of BDS includes geostationary earth orbit (GEO) satellites, inclined geosynchronous orbit (IGSO) satellites, and medium earth orbit (MEO) satellites. By November, 2019, it had 5 BDS-2 GEO satellites, 7 BDS-2 IGSO satellites, 3 BDS-2 MEO satellites, and 19 BDS-3 satellites in normal operation (https://www.glonass-iac.ru/en/BEIDOU/). The European Galileo system is also planned to achieve its full capability around 2020, and it currently has 21 usable MEO satellites (https://www.gsc-europa.eu/system-status/Constellation-Information). As a result, the number of GNSS satellites used for positioning is approaching and will exceed 100, which brings both opportunities and challenges to Precise Point Positioning (PPP).

PPP is most characterized by its high efficiency in GNSS data processing and avoidance of nearby reference stations [1]. As an essential positioning technology, it could be widely used in various areas that require precise position information from GNSS, such as crustal deformation monitoring, intelligent transport, environmental monitoring, and precise agriculture [2,3,4,5]. PPP typically uses dual-frequency observations of the ionospheric-free (IF) linear combination from a GPS-only system [2, 6]. By combining GPS and GLONASS observations, the convergence time of PPP can be significantly shortened [7,8,9]. To further reduce initialization time and improve reliability, quad-constellation PPP based on the IF combination has also been studied with BDS-2 and few Galileo satellites [10, 11]. With the significant increase in Galileo satellites, the performance of multi-GNSS PPP with the current constellation requires further analysis.

Rather than using observations of the IF combination, PPP based on raw observations is more convenient for multi-frequency GNSS data processing. GPS and GLONASS satellites have the capability of transmitting dual-frequency signals, while with their modernization, 13 GPS satellites and 2 GLONASS satellites can currently transmit triple-frequency signals. Different from GPS and GLONASS, all BDS and Galileo satellites can transmit multi-frequency signals, e.g. BDS-2 B1, B2, B3 and Galileo E1, E5a, E5b, E5, E6. The linear combinations of triple-frequency or multi-frequency measurements have more advantages on integer ambiguity resolution and high-order ionosphere delay elimination for GNSS PPP, which have been studied in depth [12,13,14]. It has been proven that using raw observations is more adaptable for multi-frequency PPP [15]. The observations at each frequency are assumed to be independent, thus avoiding noise amplification in the linear combinations [16]. However, the combined quad-constellation PPP using raw observations of all available frequencies has not been studied. Therefore, to make best use of multi-frequency GNSS measurements, the potentials of multi-frequency and multi-constellation GNSS data processing must be fully explored.

To track, collate, and analyze all available GNSS signals, the International GNSS Service (IGS) [17] set up the multi-GNSS experiment (MGEX) [18]. IGS analysis centers (ACs) have gradually started to provide Multi-GNSS precise orbits and clock and multi-frequency differential code bias (DCB) products. These products guarantee high-precision PPP performance. We selected 96 MGEX stations with a global distribution to analyze PPP performance based on multi-frequency raw measurements and dual-frequency measurements of the IF combination. The PPP performance with current GNSS constellations was assessed. Considering the large orbit error of BDS GEO satellites, the 5 BDS-2 GEO satellites were excluded. Also, because most of the MGEX stations cannot completely track triple-frequency signals of BDS-3 satellites, only BDS-2 MEO and IGSO satellites are included in the following PPP data processing. The corresponding mathematical model is described in “Mathematical model” section. The experiment network and processing strategies follow in “Experimental network and processing strategy” section. “Results and discussions” section presents the results and comparison analysis, and conclusions are given in “Conclusions” section.

Mathematical model

PPP with multi-frequency raw observations

The observation equations for PPP based on raw multi-frequency measurements are formulated as follows:

$$\left\{ \begin{aligned} P_{1}^{sys,i} & = \rho^{i} + \delta s^{sys} + I_{1}^{i} + b_{1}^{sys} + b_{1}^{i} + \varepsilon \left( {P_{1}^{sys,i} } \right) \\ P_{k}^{sys,i} & = \rho^{i} + \delta s^{sys} + \frac{{f_{1}^{2} }}{{f_{k}^{2} }}I_{1}^{i} + b_{k}^{sys} + b_{k}^{i} + \varepsilon \left( {P_{k}^{sys,i} } \right) \\ L_{1}^{sys,i} & = \rho^{i} + \delta s^{sys} - I_{1}^{i} + N_{1}^{i} + h_{1}^{sys} + h_{1}^{i} + \varepsilon \left( {L_{1}^{sys,i} } \right) \\ L_{k}^{sys,i} & = \rho^{i} + \delta s^{sys} - \frac{{f_{1}^{2} }}{{f_{k}^{2} }}I_{1}^{i} + N_{k}^{i} + h_{k}^{sys} + h_{k}^{i} + \varepsilon \left( {L_{k}^{sys,i} } \right) \\ \end{aligned} \right.$$
(1)

where P and L denote code and carrier-phase measurements, respectively, the superscript sys indicates the GPS (G), GLONASS (R), BDS (C), or Galileo (E) system, and i is an index for the satellites belonging to the corresponding system; the subscript 1 is the reference frequency index for each system, e.g., L1 for GPS. k is the frequency index except for the reference frequency, such as L2, L5 for GPS; f1 and fk are the frequencies. \(\rho^{i}\) is the non-dispersive distance that includes the geometric distance, the satellite and receiver clock corrections, and the tropospheric delays; antenna phase center corrections have been applied to all code and carrier phase measurements to make \(\rho^{i}\) independent of frequency. \(\delta s\) represents the inter-system bias for GLONASS, BDS, and Galileo with respect to GPS, which is zero for GPS observation equations. \(I_{1}^{i}\) is the ionospheric delay on the reference frequency, and N represents the ambiguity parameter. In addition, \(b_{1}^{sys}\), \(b_{k}^{sys}\) and \(b_{1}^{i}\), \(b_{k}^{i}\) are the respective receiver and satellite code hardware delays on frequency 1 and k, and the corresponding phase hardware delays for the receiver and satellite are \(h_{1}^{sys}\), \(h_{k}^{sys}\) and \(h_{1}^{i}\), \(h_{k}^{i}\). \(\varepsilon\) denotes the observation noise.

In general, the precise satellite orbit, clock, and DCB products issued by IGS ACs are applied in PPP. Therefore, the satellite code hardware delay parameters are eliminated in Eq. (1). Considering the singularity between the phase hardware delays and ambiguity parameters, we merge them together. After linearization, the observation equations can be rewritten as

$$\left\{ \begin{aligned} P_{1}^{sys,i} & = {\mathbf{A}}^{i} {\mathbf{X}} + dt + B^{i} T + \delta s^{sys} + I_{1}^{i} + b_{1}^{sys} \\ P_{k}^{sys,i} & = {\mathbf{A}}^{i} {\mathbf{X}} + dt + B^{i} T + \delta s^{sys} + \frac{{f_{1}^{2} }}{{f_{k}^{2} }}I_{1}^{i} + b_{k}^{sys} \\ L_{1}^{sys,i} & = {\mathbf{A}}^{i} {\mathbf{X}} + dt + B^{i} T + \delta s^{sys} - I_{1}^{i} + \tilde{N}_{1}^{i} \\ L_{k}^{sys,i} & = {\mathbf{A}}^{i} {\mathbf{X}} + dt + B^{i} T + \delta s^{sys} - \frac{{f_{1}^{2} }}{{f_{k}^{2} }}I_{1}^{i} + \tilde{N}_{k}^{i} \\ \end{aligned} \right.,\quad {\mathbf{W}} = \left[ {\begin{array}{*{20}c} {{1 \mathord{\left/ {\vphantom {1 {\varepsilon \left( {P_{1}^{sys,i} } \right)^{2} }}} \right. \kern-0pt} {\varepsilon \left( {P_{1}^{sys,i} } \right)^{2} }}} \\ {{1 \mathord{\left/ {\vphantom {1 {\varepsilon \left( {P_{k}^{sys,i} } \right)^{2} }}} \right. \kern-0pt} {\varepsilon \left( {P_{k}^{sys,i} } \right)^{2} }}} \\ {{1 \mathord{\left/ {\vphantom {1 {\varepsilon \left( {L_{1}^{sys,i} } \right)^{2} }}} \right. \kern-0pt} {\varepsilon \left( {L_{1}^{sys,i} } \right)^{2} }}} \\ {{1 \mathord{\left/ {\vphantom {1 {\varepsilon \left( {L_{k}^{sys,i} } \right)^{2} }}} \right. \kern-0pt} {\varepsilon \left( {L_{k}^{sys,i} } \right)^{2} }}} \\ \end{array} } \right]$$
(2)

with

$$\left\{ \begin{aligned} \tilde{N}_{1}^{i} & = N_{1}^{i} { + }h_{1}^{sys} - h_{1}^{i} \\ \tilde{N}_{k}^{i} & = N_{k}^{i} { + }h_{k}^{sys} - h_{k}^{i} \\ \end{aligned} \right.$$
(3)

where Ai represents the coefficient matrix of the vector X, which includes the station coordinate parameters, W is the weighting matrix for the observations, dt is the receiver clock correction, and Bi is the coefficient for tropospheric zenith delay parameter T. To remove the singularity between the receiver clock and code hardware delay parameters, we employ the following constraints on Eq. (2):

$$\left\{ \begin{aligned} & b_{1}^{G} + b_{2}^{G} + b_{5}^{G} = 0 \\ & b_{1}^{R} + b_{2}^{R} = 0 \\ & b_{2}^{C} + b_{6}^{C} + b_{7}^{C} = 0 \\ & b_{1}^{E} + b_{5}^{E} { + }b_{6}^{E} + b_{7}^{E} { + }b_{8}^{E} = 0 \\ \end{aligned} \right.$$
(4)

where the subscript numbers are the frequency indexes for each system. Equation (2) is the basic observation equation for multi-constellation GNSS PPP with multi-frequency raw measurements.

To efficiently reduce the convergence time of PPP, we introduce initial ionospheric delay and employ temporal ionospheric constraints. A priori knowledge on ionospheric delay plays an important role in reducing the convergence time of PPP solutions. As an empirical standard model of the ionosphere, the International Reference Ionosphere (IRI)-2016 model can provide the vertical total electron content (VTEC) from the ground to a certain altitude for a given location and time [19]. The model is based on experimental evidence using all available ground and space data sources. The precision of VTEC derived from the IRI model is approximately 2 to 10 TEC Units (TECU), which has been deeply analyzed and well validated by various authors [20,21,22]. The initial ionospheric delay derived by IRI-2016 is

$$I_{1}^{i} { = }\frac{40.3}{{f_{1}^{2} }}F(z) \times VTEC_{IRI} ,\quad w{ = 1/}\sigma_{I}^{2}$$
(5)

where z is the zenith distance of the satellite at the receiver, F is the mapping function (as given in http://aiuws.unibe.ch/ionosphere/mslm.pdf) to convert \(VTEC_{IRI}\) derived from IRI to slant TEC (STEC), w is the weight, and \(\sigma_{I}\) denotes the a priori noise of the initial ionospheric delay, which is set as 1.28 m (approximately 8 TECU).

The temporal variation of ionospheric delay for a satellite–station pair can be modelled by a random walk process. Considering their temporal correlation, the line-of-sight ionospheric delays are imposed as the temporal constraint:

$$I_{1,t}^{i} = I_{1,t - 1}^{i} + \varepsilon_{t} , \, \varepsilon_{t} \sim N\left( {0,\sigma_{\varepsilon }^{2} } \right)$$
(6)

where t and t − 1 represent the current and previous epochs, respectively, and \(\varepsilon_{t}\) is the assumed variation of ionospheric delay from t − 1 to t, which is set to 0.25 TECU with a 30 s sampling interval.

The ionosphere is modulated by the solar and magnetic activity, which shows significant gradients in the North to South and West to East directions. Therefore, ionosphere spatial constraints can help to further reduce the convergence time. The ionospheric gradient parameters for a satellite are expressed as

$$I_{1}^{i} = F(z) \times \left( {a_{0} + a_{1} dL + a_{2} dL^{2} + a_{3} dB + a_{4} dB^{2} } \right),\quad w = 1/\sigma_{spatial}^{2}$$
(7)

where \(I_{1}^{i}\) is the slant ionospheric delay, dL and dB respectively represent the longitude and latitude difference between the ionospheric pierce point and station location; a0, a1, a2, a3, and a4 are the coefficients of the two second-order polynomials, which fit the horizontal gradients of east–westward and south–northward, respectively. The coefficients are simultaneously estimated with the slant ionospheric parameters. \(\sigma_{spatial}^{2}\) is the a priori noise of the ionospheric spatial constraints. The TEC gradients are correlated with the ionospheric activity; a high gradient value of up to 10 TECU/deg was found in the post-noon ionosphere [23], while a 2 TECU/deg gradient was suggested by Hernández-Pajares [24] under low solar activity.

The a priori ionospheric information and temporal and spatial constraints are seen as pseudo observations. These pseudo observations together with the basic observation of Eq. (2) are lumped into the normal equation and compose the complete mathematical model for multi-constellation GNSS PPP with multi-frequency raw measurements. The frequencies used by the raw observations are L1/L2/L5 for GPS, G1/G2 for GLONASS, B1/B2/B3 for BDS-2, and E1/E5a/E5b/E5/E6 for Galileo.

PPP with dual-frequency observations of the IF combination

The observation of dual-frequency IF linear combination can efficiently mitigate the first-order ionospheric delay. The observation equation is written as

$$\left\{ \begin{aligned} & P_{if}^{sys,i} = {\mathbf{A}}^{i} {\mathbf{X}} + dt + B^{i} T + \delta s^{sys} \\ & L_{if}^{sys,i} = {\mathbf{A}}^{i} {\mathbf{X}} + dt + B^{i} T + \delta s^{sys} + \tilde{N}_{if}^{i} \\ \end{aligned} \right. ,\quad {\mathbf{W}} = \left[ {\begin{array}{*{20}c} {{1 \mathord{\left/ {\vphantom {1 {\varepsilon \left( {P_{if}^{sys,i} } \right)^{2} }}} \right. \kern-0pt} {\varepsilon \left( {P_{if}^{sys,i} } \right)^{2} }}} \\ {{1 \mathord{\left/ {\vphantom {1 {\varepsilon \left( {L_{if}^{sys,i} } \right)^{2} }}} \right. \kern-0pt} {\varepsilon \left( {L_{if}^{sys,i} } \right)^{2} }}} \\ \end{array} } \right]$$
(8)

where the subscript if denotes the IF combination. Compared with the raw observation model, the observation equation based on IF linear combination is more simplified because it does not require the receiver DCB and ionospheric delay parameters. The two frequencies selected to form the IF combination are L1/L2 for GPS, G1/G2 for GLONASS, B1/B2 for BDS-2, and E1/E5a for Galileo.

Experimental network and processing strategy

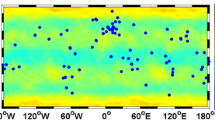
The globally distributed stations of the MGEX provide offline and real-time data of global and regional navigation satellite systems as well as various satellite-based augmentation systems. Therefore, MGEX is an ideal data source for multi-GNSS PPP. Data from 96 MGEX stations with a global distribution were collected, as shown in Fig. 1. All stations can track GPS, GLONASS, BDS-2, and Galileo signals. The observation period is GPS week 2057, which is from day of year (DOY) 160 to DOY 166 in 2019. The average number of visible satellites at an epoch varies from 19 to 37 in DOY 160, and 60% of the stations can track more than 30 GNSS satellites on average at an epoch. Because the current constellations of BDS and Galileo have more visible satellites in the Asia–Pacific and Europe regions, there are more observed satellites in the Eastern Hemisphere than in the Western Hemisphere.

Fig. 1
figure 1

Distribution of the 96 MGEX stations

Full size image

Data processing of the experimental network is based on the Positioning And Navigation Data Analysis (PANDA) platform. PANDA is widely used by Wuhan University in China, which is one of the IGS ACs, to generate precise multi-GNSS orbit and clock products. The observation time for each station is longer than 18 h. The detailed processing strategies are listed in Table 1. The reference coordinates of the stations are collected from the IGS weekly solution. The positioning errors are the differences between the estimated coordinates and reference coordinates. The convergence refers to the positioning errors reaching a certain level, which is usually defined as 0.1 m for the East (E), North (N), and Up (U) components. We also check the positioning errors of 20 sequential epochs. If the errors of all 20 epochs are within the limit, we consider that the position has converged in this epoch. To analyze the performance of PPP convergence, the daily data are divided into 12 two-hour sessions. Seven days’ data at 95 IGS stations are processed in two-hour sessions, totalling 7980 re-convergence sessions.

Table 1 Processing strategies in multi-constellation GNSS PPP
Full size table

Results and discussions

Carrier-phase and code residuals

The post-fit code and carrier-phase residuals can help us to detect whether the PPP model has other unmodeled errors. Normally, the residuals are elevation-dependent with a normal distribution. Figure 2 shows a scatter plot of the code residuals for GPS, GLONASS, BDS, and Galileo. The residuals are based on all observations of the 96 stations during the observation period. The residuals are illustrated with the elevation of the satellites above the local horizon for the stations. In this figure, one can clearly see the increase in observation noise at low elevations, which is a well-known phenomenon mainly caused by multipath effects and residual atmospheric delay. The noise amplifications of IF combination for GPS L1/L2, GLONASS G1/G2, BDS-2 B1/B2, and Galileo E1/E5a are 2.978, 2.958, 2.898, and 2.588, respectively. Thus, the IF observations show larger residuals compared with the raw observations. Code measurements of Galileo have the minimum noise, where the corresponding root mean squares (RMS) are 7.41 dm and 3.60 dm for the IF and raw observations, respectively. Although the satellite-induced code biases of the BDS-2 MEO and IGSO satellites have been calibrated, the residual BDS-2 code bias still contaminates the code measurements; it makes the RMS of BDS-2 raw/IF code residuals the largest among the four systems with corresponding RMS values of 16.45 dm and 8.26 dm for IF and raw code measurements, respectively. In addition, due to the influence of GLONASS inter-frequency code bias, the residuals of GLONASS are larger than those of GPS and Galileo.

Fig. 2
figure 2

Post-fit code residuals for the raw and IF observations; the color from blue to red indicates an increase in density. C1/C2… denote the code observations on different frequencies; PC12, PC27, and PC15 represent the observations of IF combination at frequencies 1, 2 and 2, 7 and 1, 5, respectively

Full size image

The post-fit carrier-phase residuals are shown in Fig. 3. Compared with the code residuals, the residuals of carrier-phase observations are significantly lower. The carrier-phase residuals are obviously decreased with an increase in satellite elevation, and the residuals of IF observations are approximately 2 to 4 times those of the raw observations. The number of BDS-2 MEO and IGSO satellites is significantly lower than in other systems; therefore. the samples of BDS carrier-phase residuals are less than those of GPS, GLONASS, and Galileo. The RMS values of the raw carrier-phase measurements for the four systems are at the same level, ranging from 0.40 to 0.63 cm. The IF carrier-phase residuals of BDS and Galileo are slightly larger than those of GPS and GLOANSS. This is possibly because the unprecise orbit, clock and PCO/PCV errors have little influence on the raw observations; while these errors are amplified in the IF combination.

Fig. 3
figure 3

Post-fit carrier-phase residuals of PPP based on raw observations and IF observations; the symbols and colors refer to the same as in Fig. 2

Full size image

Single-system PPP based on raw and IF observations

Compared with BDS-2 and Galileo, GPS and GLONASS have better global PPP performance. Therefore, we mainly consider PPP performance on a global scale for GPS and GLONASS. The reference coordinates were collected from the IGS weekly solution at GPS week 2057 on June, 2019.

Figure 4 shows the time series of the positioning accuracy of GPS PPP for the stations; the averaged convergence times for the 96 stations in the E, N, and U components are also plotted. Although GPS PPP based on dual-frequency raw observations must estimate more ionospheric parameters, it introduces a priori information and ionospheric temporal and spatial constraints. Also, because of the lower noise of raw observations, the convergence time is shortened by 2 to 3 min compared with the PPP with IF observations. With the additional L5 and C5 observations, the convergence time is further reduced; the corresponding convergence times for the E, N, and U components are 32, 9, and 34 min, respectively. Normally, GPS PPP can converge to 10 cm within 40 min regardless of whether raw observations or IF observations are used.

Fig. 4
figure 4

Time series of the position error for GPS PPP for the 96 stations at GPS week 2057. The orange dashed line indicates the averaged convergence time

Full size image

After convergence, the positioning accuracy for the stations are shown in Fig. 5. The RMS values for the E, N, and U components are all lower than 10 cm. It can be seen that the stations have comparable accuracy on a global scale. The positioning accuracy of PPP with dual-frequency raw observations is slighter higher than that of PPP based on IF observations. The mean RMS values for the E, N, and U components are respectively 2.47 cm, 1.79 cm, and 3.35 cm for PPP based on IF observations and 2.2 cm, 1.39 cm, and 3.14 cm for PPP based on dual-frequency raw observations, as listed in Table 2. The RMS value for the U component is the highest but is still lower than 4.0 cm on average. After adding GPS L5 signals, the mean RMS value is lower, but the improvement is limited.

Fig. 5
figure 5

3-D RMS of the GPS PPP results after convergence for the 96 stations during GPS week 2057

Full size image
Table 2 Averaged RMS values for E, N, and U components for different GPS PPP solutions
Full size table

The time series of positioning error for GONASS PPP are plotted in Fig. 6. Because only two GLONASS satellites have the capability of transmitting G3 signals, the G3 signal is not included in the data processing. Compared with GPS PPP, GLONASS has fewer available satellites. The positioning error of GLOANSS is larger than that of GPS. The convergence times of GLONASS PPP based on raw observations are 36, 22, and 41 min for the E, N, and U components, respectively, which is longer than that of GPS PPP based on dual-frequency raw observations. The PPP results based on IF observations converged slightly slower than those of PPP based on dual-frequency raw observations. The convergence times of GLONASS PPP with IF observations for the E, N, and U components are 39, 24, and 42 min, respectively. Therefore, GLONASS PPP using dual-frequency raw and IF observations have comparable convergence times on a global scale.

Fig. 6
figure 6

Time series of positioning error for GLONASS PPP for the 96 stations in GPS week 2057

Full size image

The corresponding positioning accuracy of GLONASS PPP after convergence for the stations is illustrated in Fig. 7 and Table 3. Generally, the U component has the longest convergence time and lowest accuracy compared with the E and N components. The positioning accuracy of GLOANSS PPP is lower than that of GPS, and the RMS value of GLONASS PPP based on raw observations is slightly lower than that of PPP using dual-frequency IF observations. The averaged RMS values for the stations at E, N, and U are 2.69, 1.81, and 3.82 cm for PPP based on raw observations, and 2.72, 2.09, and 4.03 cm for PPP with IF observations. Therefore, the GLONASS PPP results based on raw observations can be converged to 10 cm within 45 min for the E, N, and U components, and the positioning accuracy after convergence is lower than 3 cm in the E and N components and lower than 4 cm in the U component.

Fig. 7
figure 7

3-D RMS of the GLONASS PPP results after convergence for the 96 stations during GPS week 2057

Full size image
Table 3 Averaged RMS of E, N, and U components for different GLONASS PPP solutions
Full size table

Multi-constellation GNSS PPP

Figure 8 plots the results of multi-GNSS PPP based on IF observations and raw observations. Compared with the single-GNSS PPP, multi-GNSS PPP can efficiently shorten the convergence time to less than 15 min for the E and N components, while the convergence time for the U component is approximately 3 to 10 min longer than the E and N components. Moreover, the convergence time of PPP based on dual-frequency raw observations is 1 to 2 min shorter than that of PPP based on IF observations. Moreover, after introducing multi-frequency observations, the convergence time is slightly reduced again. It can be clearly seen that the positioning errors are smaller after convergence compared with those of single-GNSS PPP. In summary, combining the observations from multi-constellation GNSS observations can significantly reduce PPP convergence time.

Fig. 8
figure 8

Time series of the positioning error for Multi-GNSS PPP for the 96 stations in GPS week 2057

Full size image

The positioning accuracy for the stations is illustrated in Fig. 9. The mean RMS values of the E, N, and U components for different solutions are listed in Table 4. The 3-D RMS values of the stations are below 8 cm. The multi-GNSS PPP based on raw observations has a higher accuracy compared with that of multi-GNSS using dual-frequency IF observations. For some stations, the 3-D RMS value of the PPP results based on dual-frequency raw observations is larger than that of the PPP based on IF observations. The mean RMS values of the E, N, and U components for PPP based on dual-frequency raw observations are 2.01, 1.35, and 2.82 cm, respectively. They are lower than those of the dual-frequency IF PPP, which are 2.09, 1.50, and 2.94 cm, respectively. By introducing multi-frequency signals, the mean RMS values of the multi-frequency PPP are improved to 1.25, 1.06, and 2.37 cm, respectively. Currently, the PCO values at the receiver ends for BDS and Galileo satellites are unknown in data processing, so we use the values of GPS PCO as substitutes. Although it may not be precise, the multi-GNSS can improve the positioning accuracy after reducing the weights of BDS and Galileo observations. Therefore, the additional observations from multi-GNSS and multi-frequency not only improve accuracy but also reduce convergence time.

Fig. 9
figure 9

3-D RMS of the multi-GNSS PPP results after convergence for the 96 stations during GPS week 2057

Full size image
Table 4 Averaged RMS values for the E, N, and U components for different multi-GNSS PPP solutions
Full size table

Conclusions

GNSS satellites are increasingly becoming available for providing global PPP services, and MGEX stations can receive more than 40 GNSS satellites at an epoch. Based on the globally distributed MGEX stations, we assessed the performance of multi-GNSS PPP based on raw and IF observations. The results showed that the code measurements of Galileo have the lowest residuals compared with those of GPS and BDS. Currently, because there are no available PCO and PCV values for the Galileo and BDS satellites, the GPS PCO/PCV values were used as substitutes. Due to the relatively large orbit, clock and PCO/PCV errors of BDS and Galileo satellites, the phase residuals of dual-frequency IF combination of Galileo and BDS are larger than those of GPS and GLONASS. By reducing the weights of the BDS and Galileo observations, multi-frequency and multi-constellation GNSS PPP based on raw observations achieved better performance than single-GNSS PPP. The fusion of multi-constellation and multi-frequency GNSS observations can significantly shorten convergence time, which was reduced from approximately 40 min for GPS PPP to less than 20 min for multi-GNSS PPP. After convergence, the positioning accuracy of multi-GNSS PPP was improved by 0.5 to 1.0 cm compared with GPS or GLONASS PPP. The positioning accuracy of Multi-GNSS could be further improved with the precise BDS and Galileo orbits, clock and PCO/PCV products in the future.