Derivative-free separable quadratic modeling and cubic regularization for unconstrained optimization

Abstract

We present a derivative-free separable quadratic modeling and cubic regularization technique for solving smooth unconstrained minimization problems. The derivative-free approach is mainly concerned with building a quadratic model that could be generated by numerical interpolation or using a minimum Frobenius norm approach, when the number of points available does not allow to build a complete quadratic model. This model plays a key role to generate an approximated gradient vector and Hessian matrix of the objective function at every iteration. We add a specialized cubic regularization strategy to minimize the quadratic model at each iteration, that makes use of separability. We discuss convergence results, including worst case complexity, of the proposed schemes to first-order stationary points. Some preliminary numerical results are presented to illustrate the robustness of the specialized separable cubic algorithm.

1 Introduction

We consider unconstrained minimization problems of the form

$$\begin{aligned} \min _{x\in \mathbb {R}^{n}} f(x), \end{aligned}$$

(1)

where the objective function $f: \mathbb {R}^{n} \rightarrow \mathbb {R}$ is continuously differentiable in $\mathbb {R}^{n}$. However, we assume that the derivatives of f are not available and that cannot be easily approximated by finite difference methods. This situation frequently arises when f must be evaluated through black-box simulation packages, and each function evaluation may be costly and/or contaminated with noise (Conn et al. 2009b).

Recently (Brás et al. 2020; Martínez and Raydan 2015, 2017), in a derivative-based context, several separable models combined with either a variable-norm trust-region strategy or with a cubic regularization scheme were proposed for solving (1), and their standard asymptotic convergence results were established. The main idea of these separable model approaches is to minimize a quadratic (or a cubic) model at each iteration, in which the quadratic part is the second-order Taylor approximation of the objective function. With a suitable change of variables, based on the Schur factorization, the solution of these subproblems is trivialized and an adequate choice of the norm at each iteration permits the employment of a trust-region reduction procedure that ensures the fulfillment of global convergence to second-order stationary points (Brás et al. 2020; Martínez and Raydan 2015). In that case, the separable model method with a trust-region strategy has the same asymptotic convergence properties as the trust-region Newton method. Later in Martínez and Raydan (2017), starting with the same modeling introduced in Martínez and Raydan (2015), the trust-region scheme was replaced with a separable cubic regularization strategy. Adding convenient regularization terms, the standard asymptotic convergence results were retained, and moreover the complexity of the cubic strategy for finding approximate first-order stationary points became $O(\varepsilon ^{-3/2})$. For the separable cubic regularization approach used in Martínez and Raydan (2017), complexity results with respect to second-order stationarity were also established. We note that regularization procedures serve to the same purpose and are strongly related to trust-region schemes, with the advantage of possessing improved worst-case complexity (WCC) bounds; see, e.g., (Bellavia et al. 2021; Birgin et al. 2017; Cartis et al. 2011a, b; Cartis and Scheinberg 2018; Grapiglia et al. 2015; Karas et al. 2015; Lu et al. 2012; Martínez 2017; Nesterov and Polyak 2006; Xu et al. 2020).

However, as previously mentioned, the separable cubic approaches developed in Brás et al. (2020), Martínez and Raydan (2015), Martínez and Raydan (2017) are based on the availability of the exact gradient vector and the exact Hessian matrix at every iteration. When exact derivatives are not available, quadratic models which are based only on the objective function values, computed at sample points, can be obtained retaining good quality of approximation of the gradient and the Hessian of the objective function. These derivative-free models can be constructed by means of polynomial interpolation or regression or by any other approximation technique. These models are called, depending on their accuracy, fully-linear or fully-quadratic; see (Conn et al. 2008a, b, 2009b) for details.

Fully-linear and fully-quadratic models are the basis for derivative-free optimization trust-region methods (Conn et al. 2009a, b; Scheinberg and Toint 2010) and have also been successfully used in the definition of a search step for unconstrained directional direct search algorithms (Custódio et al. 2010). In the latter, minimum Frobenious norm approaches are adopted, when the number of points available does not allow the computation of a determined interpolation model.

This state of affairs motivated us to develop a derivative-free separable version of the regularized method introduced in Martínez and Raydan (2017). This means that we will start with a derivative-free quadratic model, which can be obtained by different schemes, to obtain an approximated gradient vector and Hessian matrix per iteration, and then we will add the separable regularization cubic terms associated with an adaptive regularization parameter to guarantee convergence to stationary points.

The paper is organized as follows. In Sect. 2 we present the main ideas behind the derivative-based separable modeling approaches. Section 3 revises several derivative-free schemes for building quadratic models. In Sect. 4 we describe our proposed derivative-free separable cubic regularization strategy, and discuss the associated convergence properties. Section 5 reports numerical results to give further insight into the proposed approach. Finally, in Sect. 6 we present some concluding remarks.

Throughout, unless otherwise specified, we will use the Euclidean norm $\Vert x\Vert = (x^{\top } x)^{1/2}$ on $\mathbb {R}^{n}$, where the inner product $x^{\top } x = \sum _{i=1}^{n} x_i^2$. For a given $\widetilde{\Delta } >0$ we will denote the closed ball $B(x;\widetilde{\Delta }) = \{ y\in \mathbb {R}^{n}\, |\,\Vert y-x\Vert \le \widetilde{\Delta } \}$.

2 Separable cubic modeling

In the standard derivative-based quadratic modeling approach, for solving (1), a quadratic model of f(x) around $x_k$ is constructed by defining the model of the objective function as

$$\begin{aligned} m_k(s) \; = \; f_k + g_k^{\top } s + \frac{1}{2}s^{\top }H_ks, \end{aligned}$$

(2)

where $f_k=f(x_k)$, $g_k = \nabla f(x_k)$ is the gradient vector at $x_k$, and $H_k$ is either the Hessian of f at $x_k$, $\nabla ^2 f(x_k)$, or a symmetric approximation of it. The step $s_k$ is the minimizer of $m_k(s)$.

In Martínez and Raydan (2015), instead of using the standard quadratic model associated with Newton’s method, the equivalent separable quadratic model

$$\begin{aligned} {m}_k^S(y) \; = \; f_k + (Q_k^{\top } g_k)^{\top } y + \frac{1}{2}y^{\top } D_k y \end{aligned}$$

(3)

was considered to approximate the objective function f around the iterate $x_k$. In (3), the change of variables $y = Q_k^{\top } s$ is used, where the spectral (or Schur) factorization of $H_k$:

$$\begin{aligned} H_k \; = \; Q_k D_k Q_k^{\top }, \end{aligned}$$

(4)

is computed at every iteration. In (4), $Q_k$ is an orthogonal $n\times n$ matrix whose columns are the eigenvectors of $H_k$, and $D_k$ is a real diagonal $n\times n$ matrix whose diagonal entries are the eigenvalues of $H_k$. Let us note that since $H_k$ is symmetric then (4) is well-defined for all k. We also note that (3) may be non-convex, i.e., some of the diagonal entries of $D_k$ could be negative.

For the separable regularization counterpart in Martínez and Raydan (2017), the model (3) is kept and a cubic regularization term is added:

$$\begin{aligned} {m}_k^{SR}(y) \; = \; f_k + (Q_k^{\top } g_k)^{\top } y + \frac{1}{2}y^{\top } D_k y + \sigma _k \frac{1}{6}\sum _{i=1}^n | y_i |^3, \end{aligned}$$

(5)

where $\sigma _k\ge 0$ is dynamically obtained. Note that a 1/6 factor is included in the last term of (5) to simplify derivative expressions. Notice also that, since $D_k$ is a diagonal matrix, models (3) and (5) are indeed separable.

As a consequence, at every iteration k the subproblem

$$\begin{aligned} \min _{y\in \mathbb {R}^{n}} {m}_k^{SR}(y) \end{aligned}$$

is solved to compute the vector $y_k$, and then the step will be recovered as $s_k\; = \; Q_k y_k$.

The gradient of the model ${m}_k^{SR}(y)$, given by (5), can be written as follows:

$$\begin{aligned} \nabla {m}_k^{SR}(y) \; = \; Q_k^{\top } g_k + D_k y + \frac{\sigma _k}{2} \widehat{u}_k, \end{aligned}$$

where the i-th entry of the n-dimensional vector $\widehat{u}_k$ is equal to $|\textit{y}_i|\textit{y}_i$. Similarly, the Hessian of (5) is given by

$$\begin{aligned} \nabla ^2 {m}_k^{SR}(y) \; = \; D_k + \sigma _k\,\text{ diag }(|y_i|). \end{aligned}$$

To solve $\nabla {m}_k^{SR}(y) = 0$, and find the critical points, we only need to independently minimize n one-dimensional special functions. These special one-variable functions are of the following form

$$\begin{aligned} h(z) \; = \; c_0 + c_1 z + c_2 z^2 + c_3|z|^3. \end{aligned}$$

The details on how to find the global minimizer of h(z) are fully described in (Martínez and Raydan 2017, Sect. 3).

In the next section, we will describe several derivative-free alternatives to compute a model of type (2), to be incorporated in the separable regularized model (5).

3 Fully-linear and fully-quadratic derivative-free models

Interpolation or regression based models are commonly used in derivative-free optimization as surrogates of the objective function. In particular, quadratic interpolation models are used as replacement of Taylor models in derivative-free trust-region approaches (Conn et al. 2009a; Scheinberg and Toint 2010).

The terminology fully-linear and fully-quadratic, to describe a derivative-free model that retains Taylor-like bounds, was first proposed in Conn et al. (2009b). Definitions 3.1 and 3.2 provide a slightly modified version of it, suited for the present work. Throughout this section, $\Delta _{max}$ is a given positive constant that represents an upper bound on the radii of the regions in which the models are built.

Assumption 3.1

Let f be a continuously differentiable function with Lipschitz continuous gradient (with constant $L_g$).

Definition 3.1

(Conn et al. 2009b, Definition 6.1) Let a function $f: \mathbb {R}^n\rightarrow \mathbb {R}$, that satisfies Assumption 3.1, be given. A set of model functions $M=\{m: \mathbb {R}^n\rightarrow \mathbb {R}, \, m \in C^1 \}$ is called a fully-linear class of models if:

• 1. There exist positive constants $\kappa _{ef}$ and $\kappa _{eg}$ such that for any $x\in \mathbb {R}^n$ and $\widetilde{\Delta } \in (0,\Delta _{max}]$ there exists a model function m(s) in M, with Lipschitz continuous gradient, and such that

  • the error between the gradient of the model and the gradient of the function satisfies

    $$\begin{aligned} { \Vert \nabla f(x+s) - \nabla m(s)\Vert \le \kappa _{eg} \, \widetilde{\Delta }, \quad \forall s \in B(0;\widetilde{\Delta }),} \end{aligned}$$

    (6)

    and

  • the error between the model and the function satisfies

    $$\begin{aligned} { |f(x+s) - m(s) | \le \kappa _{ef} \, \widetilde{\Delta }^2, \quad \forall s \in B(0;\widetilde{\Delta }).} \end{aligned}$$

  Such a model m is called fully-linear on $B(x; \widetilde{\Delta })$.

• 2. For this class M there exists an algorithm, which we will call a ‘model-improvement’ algorithm, that in a finite, uniformly bounded (with respect to x and $\widetilde{\Delta }$) number of steps can

  • either establish that a given model $m\in M$ is fully-linear on $B(x;\widetilde{\Delta })$ (we will say that a certificate has been provided),

  • or find a model $m \in M$ that is fully-linear on $B(x;\widetilde{\Delta })$.

For fully-quadratic models, stronger assumptions on the smoothness of the objective function are required.

Assumption 3.2

Let f be a twice continuously differentiable function with Lipschitz continuous Hessian (with constant $L_H$).

Definition 3.2

(Conn et al. 2009b, Definition 6.2) Let a function $f: \mathbb {R}^n\rightarrow \mathbb {R}$, that satisfies Assumption 3.2, be given. A set of model functions $M=\{m: \mathbb {R}^n\rightarrow \mathbb {R}, \, m \in C^2 \}$ is called a fully-quadratic class of models if:

• 1. There exist positive constants $\kappa _{ef}$, $\kappa _{eg}$, and $\kappa _{eh}$ such that for any $x\in \mathbb {R}^n$ and $\widetilde{\Delta } \in (0,\Delta _{max}]$ there exists a model function m(s) in M, with Lipschitz continuous Hessian, and such that

  • the error between the Hessian of the model and the Hessian of the function satisfies

    $$\begin{aligned} { \Vert \nabla ^2 f(x+s) - \nabla ^2 m(s)\Vert \le \kappa _{eh} \, \widetilde{\Delta }, \quad \forall s \in B(0;\widetilde{\Delta }),} \end{aligned}$$

    (7)

  • the error between the gradient of the model and the gradient of the function satisfies

    $$\begin{aligned} { \Vert \nabla f(x+s) - \nabla m(s)\Vert \le \kappa _{eg} \, \widetilde{\Delta }^2, \quad \forall s \in B(0;\widetilde{\Delta }),} \end{aligned}$$

    (8)

    and

  • the error between the model and the function satisfies

    $$\begin{aligned} { | f(x+s) - m(s) | \le \kappa _{ef} \, \widetilde{\Delta }^3, \quad \forall s \in B(0;\widetilde{\Delta }).} \end{aligned}$$

  Such a model m is called fully-quadratic on $B(x; \widetilde{\Delta })$.

• 2. For this class M there exists an algorithm, which we will call a ‘model-improvement’ algorithm, that in a finite, uniformly bounded (with respect to x and $\widetilde{\Delta }$) number of steps can

  • either establish that a given model $m\in M$ is fully-quadratic on $B(x; \widetilde{\Delta })$ (we will say that a certificate has been provided),

  • or find a model $m \in M$ that is fully-quadratic on $B(x;\widetilde{\Delta })$.

Algorithms for model certification or for improving the quality of a given model can be found in Conn et al. (2009b). This quality is directly related to the geometry of the sample set used in its computation (Conn et al. 2008a, b). However, some practical approaches have reported good numerical results related to implementations that do not consider a strict geometry control (Bandeira et al. 2012; Fasano et al. 2009).

4 Derivative-free separable cubic regularization approach

In a derivative-free optimization setting, instead of (2), we will consider the following quadratic model

$$\begin{aligned} \tilde{m}_k(s) \; = \; f_k + \tilde{g}_k^{\top } s + \frac{1}{2}s^{\top }\tilde{H}_ks, \end{aligned}$$

where $\tilde{g}_k=\nabla \tilde{m}_k(x_k)$ and $\tilde{H}_k= \nabla ^2 \tilde{m}_k(x_k)$ are good quality approximations of $g_k$ and $H_k$, respectively, built using interpolation or a minimum Frobenius norm approach (see Chapters 3 and 5 in Conn et al. (2009b)). Hence, analogous to the discussion in Sect. 2, by using the change of variables $y = \tilde{Q}_k^{\top } s$, where $\tilde{H}_k= \tilde{Q}_k \tilde{D}_k \tilde{Q}_k^{\top }$, with $\tilde{Q}_k$ an orthogonal $n\times n$ matrix whose columns are the eigenvectors of $\tilde{H}_k$, and $\tilde{D}_k$ is a real diagonal $n\times n$ matrix whose diagonal entries are the eigenvalues of $\tilde{H}_k$, the equivalent separable quadratic model

$$\begin{aligned} \tilde{m}_k^S(y) \; = \; f_k + (\tilde{Q}_k^{\top } \tilde{g}_k)^{\top } y + \frac{1}{2}y^{\top } \tilde{D}_k y \end{aligned}$$

(9)

is used for the approximation of the objective function f around the iterate $x_k$. We then regularize (9) by adding a cubic or a quadratic term, depending on having been able to compute a fully-quadratic or a fully-linear model, respectively:

$$\begin{aligned} \tilde{m}_k^{SR}(y) \; = \; f_k + (\tilde{Q}_k^{\top } \tilde{g}_k)^{\top } y + \frac{1}{2}y^{\top } \tilde{D}_k y + \sigma _k \frac{1}{p!}\sum _{i=1}^n | y_i |^p, \end{aligned}$$

where $p\in \{2,3\}$ and $\sigma _k\ge 0$ is dynamically obtained.

As a consequence, at every iteration k the subproblem

$$\begin{aligned} \min _{y\in \mathbb {R}^{n}} \tilde{m}_k^{SR}(y) \; \text{ subject } \text{ to } \; \frac{\xi }{\sigma _k} \le \Vert y \Vert _\infty \le \Delta , \end{aligned}$$

(10)

is solved to compute the vector $y_k$, and then the step will be recovered as $s_k \; = \; \tilde{Q}_k y_k$.

The constraint $\Vert y \Vert _\infty \le \Delta$, where $\Delta >0$ is a fixed given parameter for all k, is necessary to ensure the existence of a solution of problem (10) in some cases. Indeed, since some diagonal entries of $\tilde{D}_k$ might be negative, for $p=2$ the existence of an unconstrained minimizer of the objective function in (10) is not guaranteed. In the case of $p=3$ and any $\sigma _k>0$, the existence of an unconstrained minimizer of the same function is guaranteed. Nevertheless, if some diagonal entries of $\tilde{D}_k$ are negative, and $\sigma _k$ is still close to zero, imposing the constraint $\Vert y \Vert _\infty \le \Delta$ prevents the obtained vector y from being too large, and therefore avoids unnecessary numerical difficulties when solving (10).

The additional constraint $\Vert y \Vert _\infty \ge \frac{\xi }{\sigma _k}$ relates the stepsize with the regularization parameter and is required to establish WCC results. A similar strategy has been used in Cartis and Scheinberg (2018) when building models using a probabilistic approach. As we will see in Section 4, this additional lower bound does not prohibit the iterative process to drive the first-order stationarity measure below any given small positive threshold.

In this case, by solving n one-dimensional independent minimization problems in the closed intervals $[-\Delta , -\xi /\sigma ]$ and $[\xi /\sigma , \Delta ]$, we are being more demanding than the original constraint. These one-variable functions are of the form

$$\begin{aligned} h(z) \; = \; c_0 + c_1 z + c_2 z^2 + c_3|z|^3. \end{aligned}$$

The details on how to find the global minimizer of h(z) on the closed and bounded intervals $[-\Delta , -\xi /\sigma ]$ and $[\xi /\sigma , \Delta ]$, for $\Delta >0$ and $\xi /\sigma >0$, are similar to the ones described in (Martínez and Raydan 2017, Sect.  3). A practical approach for the resolution of (10) will be suggested and tested in Sect. 5.

The following algorithm is an adaptation of Algorithm 2.1 in Martínez and Raydan (2017), for the derivative-free case.

If (12) is fulfilled, define $s_k= s_{trial}$, $x_{k+1} = x_k+ s_k$, update $k \leftarrow k+1$ and go to Step 1. Otherwise set $\sigma _{new} = \eta \sigma _k$, update $\sigma _k \leftarrow \sigma _{new}$, and go to Step 2.

Remark 4.1

The upper bound constraint in (11) does not affect the separability nature of Step 3, since it can be equivalently replaced by $|(\tilde{Q}_k^{\top } s)_i| \le \Delta$ for all i. However, the lower bound in (11) affects the separability of Step 3. Two strategies have been developed to impose the lower bound constraint in (11) while maintaining the separability approach. These strategies will be described in Sect. 5.

In the following subsections, the convergence and worst-case behavior of Algorithm 1 will be analyzed independently for the fully-linear and fully-quadratic cases.

4.1 Fully-linear approach

This subsection will be devoted to the analysis of the WCC of Algorithm 1 when fully-linear models are used. For that, we need the following technical lemma.

Lemma 4.1

(Nesterov 2004, Lemma 1.2.3) Let Assumption 3.1 hold. Then, we have

$$\begin{aligned} \left| f(x+s) - f(x) - \nabla f(x)^{\top } s \right| \le \frac{L_g}{2} \Vert s\Vert ^2. \end{aligned}$$

(13)

As it is common in nonlinear optimization, we assume that the norm of the Hessian of each model is bounded.

Assumption 4.1

Assume that the norm of the Hessian of the model is bounded, i.e.,

$$\begin{aligned} \Vert \tilde{H}_k\Vert \le \kappa _{\tilde{H}}, \quad \forall k \ge 0 \end{aligned}$$

(14)

for some $\kappa _{\tilde{H}} > 0$.

We also assume that the trial point provides decrease to the current model, i.e., that for $p=2$ the value of the objective function of (11) at $s_{trial}$ is less than or equal to its value at $s = 0$.

Assumption 4.2

Assume that

$$\begin{aligned} \tilde{g}_k^{\top } s_{trial}+ \frac{1}{2} s_{trial}^{\top } \tilde{H}_ks_{trial}+ \frac{\sigma _k }{2}\sum _{i=1}^n [\tilde{Q}_k^{\top } s_{trial}]_i^2 \le 0. \end{aligned}$$

(15)

Clearly, (15) holds if $s_{trial}$ is a global solution of (11) for $p=2$. Hence, taking advantage of our separability approach, the vector $s_{trial}$ obtained at Step 3 of Algorithm 1 satisfies (15).

In the following lemma, we will derive an upper bound on the number of function evaluations required to satisfy the sufficient decrease condition (12), which in turn guarantees that every iteration of Algorithm 1 is well-defined. Moreover, we also obtain an upper bound for the regularization parameter.

Lemma 4.2

Let Assumptions 3.1, 4.1, and 4.2 hold and assume that at Step 2 of Algorithm 1 a fully-linear model is always used. In order to satisfy condition (12), with $p=2$, Algorithm 1 needs at most

(16)

function evaluations, not accounting for the ones required for model computation. In addition, the maximum value of $\sigma _k$ for which (12) is satisfied, is given by

$$\begin{aligned} \sigma _{max}= \max \left\{ \sigma _{small}, 2\eta \left( \alpha + \frac{L_g}{2} + \kappa _{eg} + \frac{\kappa _{{\tilde{H}}}}{2}\right) \right\} . \end{aligned}$$

(17)

Proof

First, we will show that if

$$\begin{aligned} \sigma _k \; \ge \; 2\left( \alpha + \frac{L_g}{2} + \kappa _{eg} + \frac{\kappa _{\tilde{H}}}{2}\right) \end{aligned}$$

(18)

then the sufficient decrease condition (12) of Algorithm 1 is satisfied for $p=2$.

In view of (15), we have

$$\begin{aligned} f(x_k+ s_{trial}) - f(x_k)&\le f(x_k+ s_{trial}) - f(x_k) - \tilde{g}_k^{\top } s_{trial}- \frac{1}{2} s_{trial}^{\top } \tilde{H}_ks_{trial}\\&\quad {-} \frac{\sigma _k }{2}\sum _{i{=}1}^n [\tilde{Q}_k^{\top } s_{trial}]_i^2 \\&{\le } | f(x_k{+} s_{trial}) {-} f(x_k) {-} \nabla f(x_k)^{\top } s_{trial}|\\&\quad {+} |(\nabla f(x_k) - \tilde{g}_k)^{\top }s_{trial}| \\&\quad + \left| \frac{1}{2} s_{trial}^{\top } \tilde{H}_ks_{trial}\right| - \frac{\sigma _k }{2}\sum _{i=1}^n [\tilde{Q}_k^{\top } s_{trial}]_i^2. \end{aligned}$$

Thus, by using (6), (13), (14), and $\Vert s_{trial}\Vert \ge \frac{\xi }{\sigma _k}$ (due to Step 3 of Algorithm 1), we obtain

$$\begin{aligned} f(x_k+ s_{trial}) - f(x_k)&\le \frac{L_g}{2}\Vert s_{trial}\Vert ^2 \kappa _{eg} \frac{\xi }{\sigma _k}\Vert s_{trial}\Vert \\&\quad {+} \frac{\kappa _{\tilde{H}}}{2}\Vert s_{trial}\Vert ^2 {-} \frac{\sigma _k }{2}\sum _{i=1}^n [\tilde{Q}_k^{\top } s_{trial}]_i^2 \\&\le \left( \frac{L_g}{2} + \kappa _{eg} + \frac{\kappa _{\tilde{H}}}{2}\right) \Vert s_{trial}\Vert ^2 - \frac{\sigma _k }{2}\sum _{i=1}^n [\tilde{Q}_k^{\top } s_{trial}]_i^2 \\&= \; \left( \frac{L_g}{2} + \kappa _{eg} + \frac{\kappa _{\tilde{H}}}{2} - \frac{\sigma _k}{2}\right) \sum _{i=1}^n [\tilde{Q}_k^{\top } s_{trial}]_i^2 \\ {}&\le -\alpha \sum _{i=1}^n[\tilde{Q}_k^{\top } s_{trial}]_i^2, \end{aligned}$$

where the equality in the third line follows from the fact that $\tilde{Q}$ is an orthogonal $n\times n$ matrix and so $\Vert s_{trial}\Vert ^2= \Vert \tilde{Q}_k^{\top } s_{trial}\Vert ^2 = \sum _{i=1}^n[\tilde{Q}_k^{\top } s_{trial}]_i^2$, and the last inequality holds due to (18).

Now, from the way $\sigma _k$ is updated at Step 4 of Algorithm 1, it can be easily seen that for the fulfillment of (12) with $p=2$ we need

$$\begin{aligned} \big \lceil \frac{{\text{ log }}\left( \left[ 2\left( { {\alpha }} + \frac{L_g}{2} + \kappa _{eg} + \frac{\kappa _{\tilde{H}}}{2}\right) \right] /\sigma _{small}\right) }{\text{ log } \eta } \big \rceil +1 \end{aligned}$$

function evaluations, and, additionally, the upper bound on $\sigma _k$ at (17) is derived from (18). $\square$

The following assumption, which holds for global solutions of subproblem (11) (with $p=2$), is central in establishing our WCC results. For similar assumptions required to obtain worst-case complexity bounds see (Birgin et al. 2017; Martínez 2017).

Assumption 4.3

Assume that, for all $k\ge 0$,

$$\begin{aligned}&\Vert \tilde{Q}_k^{\top } s_{trial}\Vert _\infty \; = \; \frac{\xi }{\sigma _k}, \text{ or } \Vert \tilde{Q}_k^{\top } s_{trial}\Vert _\infty \; = \; \Delta , \nonumber \\ \text{ or }&\left\| \nabla _s\left[ \tilde{g}_k^{\top } s + \frac{1}{2} s^{\top } \tilde{H}_ks + \frac{\sigma _k}{2}\sum _{i=1}^n [\tilde{Q}_k^{\top } s]_i^2\right] _{s=s_{trial}}\right\| \le \beta _1 \Vert s_{trial}\Vert , \end{aligned}$$

(19)

for some $\beta _1 > 0$.

Under this assumption, we are able to prove that, when the trial point is not on the boundary of the feasible region of (11) (with $p=2$), then the norm of the gradient of the objective function at the new point is of the same order as the norm of the trial point.

Lemma 4.3

Let Assumptions 3.1, 4.1, 4.2, and 4.3 hold. Then, we have

$$\begin{aligned} \Vert \tilde{Q}_k^{\top } s_{trial}\Vert _\infty \; = \; \frac{\xi }{\sigma _k} \text{ or } \Vert \tilde{Q}_k^{\top } s_{trial}\Vert _\infty \; = \; \Delta , \end{aligned}$$

(20)

or

$$\begin{aligned} \Vert \nabla f(x_k+ s_{trial}) \Vert \le \kappa _1 \Vert s_{trial}\Vert , \end{aligned}$$

where $\kappa _1 = L_g + \kappa _{eg} + \kappa _{\tilde{H}} + \sigma _{max} + \beta _1$, and $\sigma _{max}$ was defined in Lemma 4.2.

Proof

Assume that none of the equalities at (20) hold. We have $\nabla _s \tilde{m}_k^{SR}(s_{trial}) = \tilde{g}_k+ \tilde{H}_ks_{trial}+ r(s_{trial})$, where

$$\begin{aligned} r(s_{trial}) \; = \; \sigma _k\tilde{Q}_k \left( [\tilde{Q}_k^{\top } s_{trial}]_1, \ldots , [\tilde{Q}_k^{\top } s_{trial}]_n\right) ^{\top }. \end{aligned}$$

Now, by using Assumption 3.1, (14), and (6), we have

$$\begin{aligned} \left\| \nabla f(x_k{+} s_{trial}) {-} \nabla _s \tilde{m}_k^{SR}(s_{trial})\right\|&{=} \left\| \nabla f(x_k{+} s_{trial}) {-} \left( \tilde{g}_k{+} \tilde{H}_ks_{trial}{+} r(s_{trial})\right) \right\| \; \\&\le \left\| \nabla f(x_k+ s_{trial}) {-} \nabla f(x_k) \right\| {+} \left\| \nabla f(x_k) {-} \tilde{g}_k\right\| \\&\quad {+} \left\| \tilde{H}_ks_{trial}\right\| {+} \left\| r(s_{trial})\right\| \\&\le \left( L_g + \kappa _{eg} + \kappa _{\tilde{H}} + \sigma _{max}\right) \Vert s_{trial}\Vert . \end{aligned}$$

Therefore, in view of (19), we have

$$\begin{aligned} \Vert \nabla f(x_k+ s_{trial}) \Vert&\le \Vert \nabla f(x_k+ s_{trial}) - \nabla _s \tilde{m}_k^{SR}(s_{trial})\Vert + \Vert \nabla _s \tilde{m}_k^{SR}(s_{trial}) \Vert \\&\le \left( L_g + \kappa _{eg} + \kappa _{\tilde{H}} + \sigma _{max} + \beta _1\right) \Vert s_{trial}\Vert , \end{aligned}$$

which completes the proof. $\square$

Now, we have all the ingredients to derive an upper bound on the number of iterations required by Algorithm 1 to find a point at which the norm of the gradient is below some given positive threshold.

Theorem 4.1

Given $\epsilon > 0$, let Assumptions 3.1, 4.1, 4.2, and 4.3 hold. Let $\{x_k\}$ be the sequence of iterates generated by Algorithm 1, and $f_{min}\le f(x_0)$. Then the number of iterations such that $\Vert \nabla f(x_{k+1}) \Vert > \epsilon$ and $f(x_{k+1}) > f_{min}$ is bounded above by

$$\begin{aligned} \frac{f(x_0) - f_{min}}{\alpha \min \left\{ \left( \frac{\xi }{\sigma _{max}}\right) ^2 , (\frac{\epsilon }{\kappa _1})^{2} \right\} }, \end{aligned}$$

(21)

where $\sigma _{max}$ and $\kappa _1$ were defined in Lemmas 4.2 and 4.3, respectively.

Proof

In view of Lemma 4.3, we have

$$\begin{aligned} \Vert s_k\Vert \; \ge \; \min \left\{ \frac{\xi }{\sigma _k}, \Delta , \frac{\Vert \nabla f(x_{k+1}) \Vert }{\kappa _1} \right\} . \end{aligned}$$

Hence, since $\Vert \nabla f(x_{k+1}) \Vert > \epsilon$ and $\Delta > \frac{\xi }{\sigma _k}$, we obtain

$$\begin{aligned} \Vert s_k\Vert \; \ge \; \min \left\{ \frac{\xi }{\sigma _k} , \frac{\epsilon }{\kappa _1} \right\} \; \ge \; \min \left\{ \frac{\xi }{\sigma _{max}} , \frac{\epsilon }{\kappa _1} \right\} . \end{aligned}$$

On the other hand, due to the sufficient decrease condition (12), we obtain

$$\begin{aligned} f(x_{k+1})&\le f(x_k) - \alpha \sum _{i=1}^n [\tilde{Q}_k^{\top } s_k]_i^2 \\&= \; f(x_k) - \alpha \Vert \tilde{Q}_k^{\top } s_k\Vert ^2 \\&\le f(x_k) - \alpha \min \left\{ \left( \frac{\xi }{\sigma _{max}}\right) ^2 , \left( \frac{\epsilon }{\kappa _1}\right) ^{2} \right\} . \end{aligned}$$

By summing up these inequalities, for $0, 1, \ldots , k$, we obtain

$$\begin{aligned} k +1 \le \frac{f(x_0) - f_{min}}{\alpha \min \left\{ \left( \frac{\xi }{\sigma _{max}}\right) ^2, \left( \frac{\epsilon }{\kappa _1}\right) ^{2} \right\} }, \end{aligned}$$

which concludes the proof. $\square$

Since $\kappa _{eg} = \mathcal {O}(\sqrt{n})$ (see Chapter 2 in Conn et al. 2009b), we have $\kappa _1 = \mathcal {O}(\sqrt{n})$. Now, if $\xi$ is chosen such that $\frac{\xi }{\sigma _{max}} = \mathcal {O}( \frac{\epsilon }{\kappa _1})$, then the dependency of the upper bound given at (21) on n is $\mathcal {O}(n)$. Furthermore, for building a fully-linear model we need $\mathcal {O}(n)$ function evaluations. Combining these facts with Theorem 4.1, we can derive an upper bound on the number of function evaluations that Algorithm 1 needs for driving the first-order stationarity measure below some given positive threshold.

Corollary 4.1

Given $\epsilon > 0$, let Assumptions 3.1, 4.1, 4.2, and 4.3 hold. Let $\{x_k\}$ be the sequence of iterates generated by Algorithm 1 and assume that $\Vert \nabla f(x_{k+1}) \Vert > \epsilon$ and $f(x_{k+1}) > f_{min}$. Then, Algorithm 1 needs at most $\mathcal {O}\left( n^2 \epsilon ^{-2}\right)$ function evaluations for driving the norm of the gradient below $\epsilon$.

The complexity bound derived here matches the one derived in Garmanjani et al. (2016) for derivative-free trust-region optimization methods and for direct search methods in Vicente (2013); see also Dodangeh et al. (2016).

4.2 Fully-quadratic approach

In this subsection, we will analyze the WCC of Algorithm 1 when we build fully-quadratic models. The following lemma is essential for establishing such bounds.

Lemma 4.4

(Nesterov 2004, Lemma 1.2.4) Let Assumption 3.2 hold. Then, we have

$$\begin{aligned} \left| f(x+s) - f(x) - \nabla f(x)^{\top } s - \frac{1}{2} s^{\top } \nabla ^2 f(x) s \right| \le \frac{L_H}{6} \Vert s\Vert ^3, \end{aligned}$$

(22)

and

$$\begin{aligned} \left\| \nabla f(x+s) - \nabla f(x) - \nabla ^2 f(x) s \right\| \le \frac{L_H}{2} \Vert s\Vert ^2. \end{aligned}$$

(23)

Similarly to the fully-linear case, we assume that the trial point provides decrease to the current model, i.e., that for $p=3$ the value of the objective function of (11) at $s_{trial}$ is less than or equal to its value at $s = 0$.

Assumption 4.4

Assume that

$$\begin{aligned} \tilde{g}_k^{\top } s_{trial}+ \frac{1}{2} s_{trial}^{\top } \tilde{H}_ks_{trial}+ \frac{\sigma _k }{6}\sum _{i=1}^n |[\tilde{Q}_k^{\top } s_{trial}]_i|^3 \le 0. \end{aligned}$$

(24)

We note that (24) is clearly satisfied if $s_{trial}$ is a global solution of (11) when $p=3$. Therefore, taking advantage of our separability approach, the vector $s_{trial}$ obtained at Step 3 of Algorithm 1 satisfies (24).

With this assumption, we are able to obtain upper bounds on the number of function evaluations required to satisfy the sufficient decrease condition (12), and also on the regularization parameter.

Lemma 4.5

Let Assumptions 3.2 and 4.4 hold and assume that at Step 2 of Algorithm 1 a fully-quadratic model is always used. In order to satisfy condition (12), with $p=3$, Algorithm 1 needs at most

function evaluations, not considering the ones required for model computation. In addition, the maximum value of $\sigma _k$ for which (12) is satisfied, is given by

(25)

Proof

First, we will show that if

$$\begin{aligned} \sigma _k \; \ge \; 6\left( \alpha + \sqrt{n}\left( \frac{L_H}{6} + \kappa _{eg} + \frac{\kappa _{eh}}{2}\right) \right) \end{aligned}$$

(26)

then the sufficient decrease condition (12) of Algorithm 1 is satisfied, with $p=3$.

In view of (22), we have

$$\begin{aligned} f(x_k+ s_{trial}) - f(x_k)&\le \nabla f(x_k)^{\top } s_{trial}+ \frac{1}{2} s_{trial}^{\top } \nabla ^2 f(x_k) s_{trial}+ \frac{L_H}{6} \Vert s_{trial}\Vert ^3 \\&\le \tilde{g}_k^{\top } s_{trial}+ \frac{1}{2} s_{trial}^{\top } \tilde{H}_ks_{trial}+ \frac{L_H}{6} \Vert s_{trial}\Vert ^3 \\&\quad + |(\nabla f(x_k) - \tilde{g}_k)^{\top }s_{trial}| \\&\quad + \frac{1}{2} |s_{trial}^{\top } (\nabla ^2 f(x_k)- \tilde{H}_k)s_{trial}|. \end{aligned}$$

Thus, by using (7), (8), and since $\Vert s_{trial}\Vert \ge \frac{\epsilon }{\sigma _k}$ (due to Step 3 of Algorithm 1), we obtain

$$\begin{aligned} f(x_k+ s_{trial}) - f(x_k)&\le \tilde{g}_k^{\top } s_{trial}+ \frac{1}{2} s_{trial}^{\top } \tilde{H}_ks_{trial}+\frac{L_H}{6}\Vert s_{trial}\Vert ^3 \\&\quad + \kappa _{eg} (\frac{\xi }{\sigma _k})^2 \Vert s_{trial}\Vert + \frac{\kappa _{eh}}{2}\Vert s_{trial}\Vert ^3 \\&\le \tilde{g}_k^{\top } s_{trial}+ \frac{1}{2} s_{trial}^{\top } \tilde{H}_ks_{trial}{+} \left( \frac{L_H}{6} {+} \kappa _{eg} {+} \frac{\kappa _{eh}}{2}\right) \Vert s_{trial}\Vert ^3. \end{aligned}$$

Now, by applying (24), we have

$$\begin{aligned} f(x_k+ s_{trial}) - f(x_k) \le - \frac{\sigma _k }{6}\sum _{i=1}^n |[\tilde{Q}_k^{\top } s_{trial}]_i|^3 + \left( \frac{L_H}{6} + \kappa _{eg} + \frac{\kappa _{eh}}{2}\right) \Vert s_{trial}\Vert ^3, \end{aligned}$$

which, in view of the inequality $\Vert \cdot \Vert _3 \ge n^{-1/6} \Vert \cdot \Vert _2$ (see Theorem 16 on page 26 in Hardy et al. (1934)), leads to

$$\begin{aligned} f(x_k{+} s_{trial}) {-} f(x_k)&{\le } {-} \frac{\sigma _k }{6}\sum _{i{=}1}^n |[\tilde{Q}_k^{\top } s_{trial}]_i|^3 {+} \sqrt{n}\left( \frac{L_H}{6} {+} \kappa _{eg}{+} \frac{\kappa _{eh}}{2}\right) \Vert \tilde{Q}_k^{\top }s_{trial}\Vert _3^3 \\&= \; \left( \sqrt{n}\left( \frac{L_H}{6} + \kappa _{eg} + \frac{\kappa _{eh}}{2}\right) - \frac{\sigma _k }{6}\right) \sum _{i=1}^n |[\tilde{Q}_k^{\top } s_{trial}]_i|^3 \\&\le - \alpha \sum _{i=1}^n |[\tilde{Q}_k^{\top } s_{trial}]_i|^3, \end{aligned}$$

where the equality in the second line follows from the fact that, for any vector $w\in \mathbb {R}^{n}$, $\Vert w\Vert _3^3 = \sum _{i=1}^n |w_i|^3$ and so $\Vert \tilde{Q}_k^{\top } s_{trial}\Vert _3^3 = \sum _{i=1}^n |[\tilde{Q}_k^{\top } s_{trial}]_i|^3$, and the last inequality holds due to (26).

Now, from the way $\sigma _k$ is updated at Step 4 of Algorithm 1, it can easily be seen that for the fulfillment of (26) we need

$$\begin{aligned} \big \lceil \frac{\log \left( \left[ 6\left( \alpha + \sqrt{n}\left( \frac{L_H}{6} + \kappa _{eg} + \frac{\kappa _{eh}}{2}\right) \right) \right] /\sigma _{small}\right) }{\log \eta } \big \rceil +1 \end{aligned}$$

function evaluations, and, additionally, the upper bound on $\sigma _k$ at (25) is derived from (26). $\square$

The following assumption is quite similar to condition (14) given in Martínez and Raydan (2017), and it holds for global solutions of subproblem (11) (with $p=3$). For similar assumptions, required to obtain worst-case complexity bounds associated with cubic regularization, see (Bellavia et al. 2021; Birgin et al. 2017; Cartis et al. 2011b; Cartis and Scheinberg 2018; Martínez 2017; Xu et al. 2020).

Assumption 4.5

Assume that, for all $k\ge 0$,

$$\begin{aligned}&\Vert \tilde{Q}_k^{\top } s_{trial}\Vert _\infty \; = \; \frac{\xi }{\sigma _k}, \text{ or } \Vert \tilde{Q}_k^{\top } s_{trial}\Vert _\infty \; = \; \Delta , \nonumber \\&\quad \text{ or } \left\| \nabla _s\left[ \tilde{g}_k^{\top } s + \frac{1}{2} s^{\top } \tilde{H}_ks + \sum _{i=1}^n \frac{\sigma _k}{6} |[\tilde{Q}_k^{\top } s]_i|^3\right] _{s=s_{trial}}\right\| \le \beta _2 \Vert s_{trial}\Vert ^2, \end{aligned}$$

(27)

for some $\beta _2 > 0$.

Again, we are able to prove that, when the trial point is not on the boundary of the feasible region of (11) (with $p=3$), then the norm of the gradient of the function computed at the new point is of the order of the squared norm of the trial point.

Lemma 4.6

Let Assumptions 3.2, 4.4, and 4.5 hold. Then, we have

$$\begin{aligned} \Vert \tilde{Q}_k^{\top } s_{trial}\Vert _\infty \; = \; \frac{\xi }{\sigma _k} \text{ or } \Vert \tilde{Q}_k^{\top } s_{trial}\Vert _\infty \; = \; \Delta , \end{aligned}$$

(28)

or

$$\begin{aligned} \Vert \nabla f(x_k+ s_{trial}) \Vert \le \kappa _2 \Vert s_{trial}\Vert ^2, \end{aligned}$$

where $\kappa _2 = \frac{L_H}{2} + \kappa _{eg} + \kappa _{eh} + \frac{\sigma _{max}}{2} + \beta _2$, and $\sigma _{max}$ was defined in Lemma 4.5.

Proof

Assume that none of the equalities at (28) hold. We have $\nabla _s \tilde{m}_k^{SR}(s_{trial}) = \tilde{g}_k+ \tilde{H}_ks_{trial}+ r(s_{trial})$, where

$$\begin{aligned} r(s_{trial}) \; = \; \frac{\sigma _k }{2}\tilde{Q}_k \left( \text {sign}\left( [\tilde{Q}_k^{\top } s_{trial}]_1\right) [\tilde{Q}_k^{\top } s_{trial}]_1^2, \ldots , \text {sign}\left( [\tilde{Q}_k^{\top } s_{trial}]_n\right) \right. \\ \left. \times [\tilde{Q}_k^{\top } s_{trial}]_n^2\right) ^{\top }. \end{aligned}$$

Now, by using (23), (7), and (8), we have

$$\begin{aligned} \left\| \nabla f(x_k{+} s_{trial}) {-} \nabla _s \tilde{m}_k^{SR}(s_{trial})\right\|&{=} \left\| \nabla f(x_k{+} s_{trial}) {-} \left( \tilde{g}_k{+} \tilde{H}_ks_{trial}{+} r(s_{trial})\right) \right\| \; \\&{\le } \left\| \nabla f(x_k{+} s_{trial}) {-} \nabla f(x_k) {-} \nabla ^2 f(x_k)s_{trial}\right\| \\&\quad {+} \left\| \nabla f(x_k) {-} \tilde{g}_k\right\| {+} \left\| \left( \nabla ^2 f(x_k) {-} \tilde{H}_k\right) s_{trial}\right\| \\&\quad {+} \left\| r(s_{trial})\right\| \\&\le \left( \frac{L_H}{2} {+} \kappa _{eg} {+} \kappa _{eh} {+} \frac{\sigma _{max}}{2} \right) \Vert s_{trial}\Vert ^2. \end{aligned}$$

Therefore, in view of (27), we have

$$\begin{aligned} \Vert \nabla f(x_k+ s_{trial}) \Vert&\le \Vert \nabla f(x_k+ s_{trial}) - \nabla _s \tilde{m}_k^{SR}(s_{trial})\Vert + \Vert \nabla _s \tilde{m}_k^{SR}(s_{trial}) \Vert \\&\le \left( \frac{L_H}{2} + \kappa _{eg} + \kappa _{eh} + \frac{\sigma _{max}}{2} + \beta _2\right) \Vert s_{trial}\Vert ^2, \end{aligned}$$

which completes the proof. $\square$

Now, we have all the supporting results to establish the WCC bound of Algorithm 1 for the fully-quadratic case.

Theorem 4.2

Given $\epsilon > 0$, let Assumptions 3.2, 4.4, and 4.5 hold. Let $\{x_k\}$ be the sequence of iterates generated by Algorithm 1, and $f_{min}\le f(x_0)$. Then the number of iterations such that $\Vert \nabla f(x_{k+1}) \Vert > \epsilon$ and $f(x_{k+1}) > f_{min}$ is bounded above by

$$\begin{aligned} \frac{\sqrt{n}(f(x_0) - f_{min})}{\alpha \min \left\{ \left( \frac{\xi }{\sigma _{max}}\right) ^3 , (\frac{\epsilon }{\kappa _2})^{3/2} \right\} }, \end{aligned}$$

(29)

where $\sigma _{max}$ and $\kappa _2$ were defined in Lemmas 4.5 and 4.6, respectively.

Proof

In view of Lemma 4.6, we have

$$\begin{aligned} \Vert s_k\Vert \; \ge \; \min \left\{ \frac{\xi }{\sigma _k}, \Delta , \sqrt{\frac{\Vert \nabla f(x_{k+1}) \Vert }{\kappa _2}} \right\} . \end{aligned}$$

Hence, since $\Vert \nabla f(x_{k+1}) \Vert > \epsilon$ and $\Delta > \frac{\xi }{\sigma _k}$, we obtain

$$\begin{aligned} \Vert s_k\Vert \; \ge \; \min \left\{ \frac{\xi }{\sigma _k} , \sqrt{\frac{\epsilon }{\kappa _2}} \right\} \; \ge \; \min \left\{ \frac{\xi }{\sigma _{max}} , \sqrt{\frac{\epsilon }{\kappa _2}} \right\} . \end{aligned}$$

On the other hand, due to the sufficient decrease condition (12) and the inequality $\Vert \cdot \Vert _3 \ge n^{-1/6} \Vert \cdot \Vert _2$, we obtain

$$\begin{aligned} f(x_{k+1})&\le f(x_k) - \alpha \sum _{i=1}^n |[\tilde{Q}_k^{\top }s_k]_i|^3 \\&\le f(x_k) - \frac{\alpha \Vert \tilde{Q}_k^{\top } s_k\Vert ^3 }{\sqrt{n}}\\&\le f(x_k) - \frac{\alpha \min \left\{ \left( \frac{\xi }{\sigma _{max}}\right) ^3 , (\frac{\epsilon }{\kappa _2})^{3/2} \right\} }{\sqrt{n}}. \end{aligned}$$

By summing up these inequalities, for $0, 1, \ldots , k$, we obtain

$$\begin{aligned} k +1 \le \frac{\sqrt{n}(f(x_0) - f_{min})}{\alpha \min \left\{ \left( \frac{\xi }{\sigma _{max}}\right) ^3, (\frac{\epsilon }{\kappa _2})^{3/2} \right\} },\end{aligned}$$

which concludes the proof. $\square$

Similarly to what we saw before for the fully-linear case, since $\kappa _{eg} = \mathcal {O}(n)$ and $\kappa _{eh} = \mathcal {O}(n)$ (see Chapter 3 in Conn et al. (2009b)), we have $\kappa _2 = \mathcal {O}(n^{3/2})$. By choosing $\xi$ in a way such that $\frac{\xi }{\sigma _{max}} = \mathcal {O} (\sqrt{\frac{\epsilon }{\kappa _2}})$, the dependency of the upper bound given at (29) on n becomes of the order $\mathcal {O}(n^{11/4})$. Additionally, for building a fully-quadratic model we need $\mathcal {O}(n^2)$ function evaluations. Combining these facts with Theorem 4.2, we can establish a WCC bound for driving the first-order stationarity measure below some given positive threshold.

Corollary 4.2

Given $\epsilon > 0$, let Assumptions 3.2, 4.4, and 4.5 hold. Let $\{x_k\}$ be the sequence of iterates generated by Algorithm 1 and assume that $\Vert \nabla f(x_{k+1}) \Vert > \epsilon$ and $f(x_{k+1}) > f_{min}$. Then, Algorithm 1 needs at most $\mathcal {O}\left( n^{19/4} \epsilon ^{-3/2}\right)$ function evaluations for driving the norm of the gradient below $\epsilon$.

In terms of $\epsilon$, the derived complexity bound matches the one established in Cartis et al. (2012) for a derivative-free method with adaptive cubic regularization. The dependency of the bound derived here on n is worse than the one derived in Cartis et al. (2012). However, we have explicitly taken into account the dependency of the constants $\kappa _{eg}$ and $\kappa _{eh}$ on n.

5 Illustrative numerical experiments

In this section we illustrate the different options to build the quadratic models at Step 2 of Algorithm 1 and two different strategies to address the subproblems (10).

Model computation is a key issue for the success of Algorithm 1. However, in Derivative-free Optimization, saving in function evaluations by reusing previously evaluated points is a main concern. At each evaluation of a new point, the corresponding function value is stored in a list, of maximum size equal to $(n+1)(n+2)$, for possible future use in model computation. If new points need to be generated with the sole purpose of model computation, the center, ‘extreme’ points and ‘mid-points’ of the set defined by $x_k+\frac{1}{\sigma _k}[I\;\; -I]$ are considered. Inspired by the works of Bandeira et al. (2012), Fasano et al. (2009), no explicit control of geometry is kept (in fact, we also tried the approach suggested by Scheinberg and Toint (2010), but the results did not improve). If a new point is evaluated and the maximum number of points allowed in the list has been reached, then the point farther away from the current iterate will be replaced by the new one. Points are always selected in $B(x_k;\frac{1}{\sigma _k})$ for model computation. The option for a radius larger than $\frac{\xi }{\sigma _k}$, since in our numerical implementation $\xi =10^{-5}$, allows a better reuse of the function values previously computed, avoiding an excessive number of function evaluations just for model computation. Additionally, the definition of the radius as $\frac{1}{\sigma _k}$ ensures that if the regularization parameter increases, the size of the neighborhood in which the points are selected decreases, a mechanism that resembles the behavior of trust-region radius in derivative-based optimization.

Fully-linear and fully-quadratic models can be considered at all iterations, as well as hybrid versions, where depending on the number of points available for reuse inside $B(x_k;\frac{1}{\sigma _k})$ the option for a fully-linear or a fully-quadratic model is taken (thus, some iterations will use a fully-linear model and others a fully-quadratic model). Fully-quadratic models always require $(n+1)(n+2)/2$ points for computation. Fully-linear models are built using all the points available in $B(x_k;\frac{1}{\sigma _k})$, once that this number is at least $n+2$ and does not exceed $(n+1)(n+2)/2-1$. In this case, a minimum Frobenius norm approach is taken to solve the linear system that provides the model coefficients (see Conn et al. 2009b, Section 5.3).

Regarding the solution of subproblem (10), the imposed lower bound causes difficulties to the separability approach. Two strategies were considered to address it. In the first one, every one-dimensional problem considers the corresponding lower and upper bounds. This approach is not equivalent to the original formulation. It imposes a stronger condition since any vector y computed with this approach will satisfy $\Vert y\Vert _{\infty }\ge \frac{\xi }{\sigma _k}$, but there could be a vector y satisfying $\Vert y\Vert _{\infty }\ge \frac{\xi }{\sigma _k}$, which does not satisfy $|y_i|\ge \frac{\xi }{\sigma _k},\forall i\in \{1,\ldots ,n\}$. The second approach adopted disregards the lower bound condition, only considering $\Vert y\Vert _{\infty }\le \Delta$ when solving subproblem (10). After computing y, the lower bound condition is tested and, if not satisfied, $\max _{i=1,\ldots ,n} |y_i|$ is set equal to $\frac{\xi }{\sigma _k}$ to force the obtained vector y to also satisfy the lower bound constraint at (10).

Algorithm 1 was implemented in Matlab 2021a. The experiments were executed in a laptop computer with CPU Intel core i7 1.99 GHz, RAM memory of 16 GB, running Windows 10 64-bits. As test sets, we considered the smooth collection of 44 problems proposed in Moré and Wild (2009) and 111 unconstrained problems with 40 or less variables from OPM, a subset of the CUTEst collection (Gould et al. 2015). Computational codes for the problems and the proposed initial points can be found at https://www.mcs.anl.gov/~more/df and https://github.com/gratton7/OPM, respectively.

Parameters in Algorithm 1 were set to the following values: $\Delta =10$, for each iteration k, $\sigma _{small}=0.1$, $\eta =8$, and $\alpha =10^{-4}$. At each iteration, the process is initialized with the minimization of the quadratic model (9), with no regularization term, computed by selecting points in $B(x_k;1)$. In this case, no lower bound is considered when solving subproblem (10). If the sufficient decrease condition (12) is not satisfied by the computed solution, then the regularization process is initiated, considering $\sigma _k =\sigma _{small}$. This approach allows to take advantage of the local properties of the “pure” quadratic models. As stopping criteria we consider $\Vert \tilde{g}_k\Vert <\epsilon$, where $\epsilon =10^{-5}$, or a maximum of 1500 function evaluations.

Regarding model computation, four variants were tested, depending on using fully-linear or fully-quadratic models and also on the value of p in the sufficient decrease condition used to accept new points at Step 4 of Algorithm 1. Fully-quadratic variant always computes a fully-quadratic model, built using $(n+1)(n+2)/2$ points, with a cubic sufficient decrease condition ($p=3$). Fully-linear always computes a quadratic model, using $n+2$ points, under a minimum Frobenious norm approach. In this case, the sufficient decrease condition considers $p=2$. Hybrid versions compute fully-quadratic models, using $(n+1)(n+2)/2$ points or fully-linear minimum Frobenious norm models, with at least $n+2$ points and a maximum of $(n+1)(n+2)/2-1$ points (depending on the number of points available in $B(x_k;1/\sigma _k)$). In this case, variant Hybrid_p3 always uses a cubic sufficient decrease condition to accept new points, whereas variant Hybrid_p23 selects a quadratic or cubic sufficient decrease condition, depending on the type of model that could be computed at the current iteration ($p=2$ for fully-linear and $p=3$ for fully-quadratic).

Results are reported using data profiles (Moré and Wild 2009) and performance profiles (Dolan and Moré 2002). In a simplified way, a data profile provides the percentage of problems solved by a given algorithmic variant inside a given computational budget (expressed in sets of $n_p+1$ function evaluations, where $n_p$ denotes the dimension of problem p). Let $\mathcal {S}$ and $\mathcal {P}$ represent the set of solvers, associated to the different algorithmic variants considered, and the set of problems to be tested, respectively. If $h_{p,s}$ represents the number of function evaluations required by algorithm $s\in \mathcal {S}$ to solve problem $p\in \mathcal {P}$ (up to a certain accuracy), the data profile cumulative function is given by

$$\begin{aligned} d_s(\zeta ) \; = \; \frac{1}{|\mathcal {P}|} \left| \left\{ p\in \mathcal {P}:\frac{h_{p,s}}{n_p+1}\le \zeta \right\} \right| . \end{aligned}$$

(30)

With this purpose, a problem is considered to be solved to an accuracy level $\tau$ if the decrease obtained from the initial objective function value ($f(x_0) - f(x)$) is at least $1-\tau$ of the best decrease obtained for all the solvers considered ($f(x_0) - f_L$), meaning:

$$\begin{aligned} f(x_0) - f(x) \; \ge \; (1-\tau ) [ f(x_0) - f_L ]. \end{aligned}$$

(31)

In the numerical experiments reported, the accuracy level was set equal to $10^{-5}$.

Performance profiles allow to evaluate the efficiency and the robustness of a given algorithmic variant. Let $t_{p,s}$ be the number of function evaluations required by solver $s \in \mathcal {S}$ to solve problem $p \in \mathcal {P}$, according to the criterion (31). The cumulative distribution function, corresponding to the performance profile for solver $s \in \mathcal {S}$ is given by:

$$\begin{aligned} \rho _s(\varsigma )=\frac{1}{\mid \mathcal {P}\mid }\mid \{p\in \mathcal {P}:r_{p,s}\le \varsigma \}\mid , \end{aligned}$$

with $r_{p,s}=t_{p,s}/\min \{t_{p,\bar{s}}:\bar{s}\in \mathcal {S}\}$. Thus, the value of $\rho _s(1)$ represents the percentage of problems where solver s required the minimum number of function evaluations, meaning it was the most efficient solver. Large values of $\varsigma$ allow to evaluate the capability of the algorithmic variants to solve the complete collection.

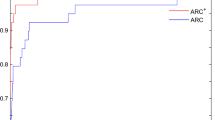
Figure 1 reports the results obtained when considering different strategies for building the quadratic models. In this case, the stricter approach is used for solving subproblem (10), always imposing the lower bound for each entry of the vector y at each one-dimensional minimization.

Fig. 1

Data and performance profiles comparing the use of different strategies for the computation of the quadratic models

It is clear that the hybrid version, that adequately adapts the sufficient decrease condition to the type of computed model, presents the best performance. The hybrid version that does not adapt the sufficient decrease condition is no better than the fully-linear approach. Even so, both are better than requiring the computation of a fully-quadratic model at every iteration.

For the best variant, namely the hybrid version that adapts the sufficient decrease condition, we considered the second approach to the solution of problem (10), where the lower bound constraint is initially ignored, being the computed solution y modified a posteriori, if it does not satisfy the lower bound constraint. We denote this variant by adding the word projection. Results are very similar and can be found in Fig. 2.

Fig. 2

Data and performance profiles comparing two different strategies to address the solution of subproblem (10)

It is worth mentioning that the modification of the final solution, which was obtained by ignoring the lower bound constraint, was required only in seven problems, with a maximum of three times in two of those seven problems.

6 Conclusions and final remarks

We present and analyze a derivative-free separable regularization approach for solving smooth unconstrained minimization problems. At each iteration we build a quadratic model of the objective function using only function evaluations. Several variants have been considered for this task, from a less expensive minimum Frobenius norm approach, to a more expensive fully-quadratic model, or a hybrid version that combines the previous approaches depending on the number of available useful points from previous iterations.

For each one of the variants, we add to the model either a separable quadratic or a separable cubic regularization term to guarantee convergence to stationary points. Moreover, for each option we present a WCC analysis and we establish that, for driving the norm of the gradient below $\epsilon >0$, the fully-quadratic and the minimum Frobenius norm regularized approaches need at most $\mathcal {O}\left( n^{19/4} \epsilon ^{-3/2}\right)$ or $\mathcal {O}\left( n^2 \epsilon ^{-2}\right)$ function evaluations, respectively.

The application of a convenient change of variables, based on the Schur factorization of the approximate Hessian matrices, trivializes the computation of the minimizer of the regularized models required at each iteration. In fact, the solution of the subproblem required at each iteration is reduced to the global minimization of n independent one-dimensional simple functions (a polynomial of degree 2 plus a term of the form $|z|^3$) on a closed and bounded set on the real line. It is worth noticing that, for the typical low-dimensions used in DFO, the $O(n^3)$ computational cost of Schur factorizations is insignificant, as compared to the cost associated with the function evaluations required to build the quadratic model. Nevertheless, in addition to its use in Brás et al. (2020), this separability approach can be extended to be efficiently applied in other large-scale scenarios, for example in inexact or probabilistic adaptive cubic regularization; see, e.g., (Bellavia et al. 2021; Cartis and Scheinberg 2018). We would like to point out that the global minimizers of the regularized models can also be obtained using some other tractable schemes that, instead of solving n independent one-dimensional problems, solve at each iteration only one problem in n variables; see, e.g., (Cartis et al. 2011a; Cristofari et al. 2019; Nesterov and Polyak 2006). These non-separable schemes, as well as our separable approach, require an $O(n^3)$ linear algebra computational cost.

We also present a variety of numerical experiments to add understanding and illustrate the behavior of all the different options considered for model computation. In general, we noticed that all the options show a robust performance. However, the worst behavior, concerning the required number of function evaluations, is consistently observed when using the fully-quadratic approach, and the best performance is observed when using the hybrid versions combined with a separable regularization term.

Concerning the worst case complexity (WCC) results obtained for the considered approaches, a few comments are in order. Even though these results are of a theoretical nature and in general pessimistic in relation to the practical behavior of the methods, it is interesting to analyze which of the two considered approaches produces a better WCC result. For that, it is convenient to use their leading terms, i.e., $n^{19/4} \epsilon ^{-3/2}$ for the one using the fully-quadratic model and $n^2 \epsilon ^{-2}$ for the one using the minimum Frobenius norm model. After some simple algebraic manipulations, we obtain that for the fully-quadratic approach to be better (that is, to require fewer function evaluations in the worst case), it must hold that $n < \epsilon ^{-2/11}$ or equivalently that $\epsilon < 1/n^{11/2}$. Therefore, if n is relatively small and $\epsilon$ is not very large (for example $n <9$ and $\epsilon \approx 10^{-5}$) then the combined scheme that is based on the fully-quadratic model has a better WCC result than the scheme based on the minimum Frobenius norm approach. In our numerical experiments, the average dimension was 8.8 and for our stopping criterion we fix $\epsilon = 10^{-5}$, and hence from the theoretical WCC point of view, the best option is the one based on the fully-quadratic model. However, in our computational experiments the worst practical performance is clearly associated with the combination that uses the fully-quadratic model. We also note that if we choose a more tolerant stopping criterion (say $\epsilon = 10^{-2}$), then for most of the same considered small-dimensional problems we have that $\epsilon > 1/n^{11/2}$, and so the scheme that uses the minimum Frobenius norm model exhibits simultaneously the best theoretical WCC result as well as the best practical performance.

Finally, for future work, it would be interesting to study the practical behavior and the WCC results of the proposed derivative-free approach in the case of convex functions.