A distributed lumped parameter model of blood flow with fluid-structure interaction

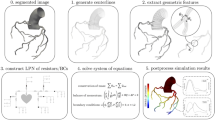
Abstract

A distributed lumped parameter (DLP) model of blood flow was recently developed that can be simulated in minutes while still incorporating complex sources of energy dissipation in blood vessels. The aim of this work was to extend the previous DLP modeling framework to include fluid–structure interactions (DLP-FSI). This was done by using a simple compliance term to calculate pressure that does not increase the simulation complexity of the original DLP models. Verification and validation studies found DLP-FSI simulations had good agreement compared to analytical solutions of the wave equations, experimental measurements of pulsatile flow in elastic tubes, and in vivo MRI measurements of thoracic aortic flow. This new development of DLP-FSI allows for significantly improved computational efficiency of FSI simulations compared to FSI approaches that solve the full 3D conservation of mass and momentum equations while also including the complex sources of energy dissipation occurring in cardiovascular flows that other simplified models neglect.

Appendix

1.1 Symmetry of forward vs. backward traveling waves

By considering the “convergence” of 0D models to 1D models it has previously been shown that the classical lumped parameter model dissipates forward traveling waves while amplifying backward traveling waves (Milišić and Quarteroni 2004). The analysis begins by assuming that the 1D linear system (Eq. 3) is replaced by a series of 0D models with length ${\Delta }x$. For the classical lumped parameter model this series of 0D models can be written as (Fig. 

Fig. 8

a. The numerical stencil for the finite difference approximation derived from the classical lumped parameter model and b. the numerical stencil for the finite difference approximation derived from the symmetric lumped parameter model

8)

$$\begin{array}{*{20}c} {C^{\prime}\frac{{dP_{i} }}{dt} = - \frac{1}{\Delta x} \left( {Q_{i + 1} - Q_{i} } \right)} \\ \end{array}$$

(44)

$$\begin{array}{*{20}c} {L^{\prime}\frac{{dQ_{i} }}{dt} = - R^{\prime}Q_{i} - \frac{1}{\Delta x} \left( {P_{i} - P_{i - 1} } \right),} \\ \end{array}$$

where C’, L’, and R’ are the vessel’s compliance, impedance, and resistance per unit length. This can be regarded as a first-order finite difference approximation of 1D linear system.

Utilizing the “water hammer” equations (Milišić and Quarteroni 2004; Parker 2009)

$$\begin{array}{*{20}c} {\left[ {\begin{array}{*{20}c} w \\ z \\ \end{array} } \right] = \frac{1}{2}\left[ {\begin{array}{*{20}c} 1 & {\sqrt {\frac{{L^{\prime}}}{{C^{\prime}}}} } \\ 1 & { - \sqrt {\frac{{L^{\prime}}}{{C^{\prime}}}} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} P \\ Q \\ \end{array} } \right],} \\ \end{array}$$

(45)

the 1D linear system can be rewritten as

$${\frac{{\partial w}}{{\partial t}} = - \frac{1}{{\sqrt {L^{\prime } C^{\prime } } }}\frac{{\partial w}}{{\partial x}} - \frac{{R^{\prime } }}{{2L^{\prime } }}\left( {w - z} \right)}$$

(46)

$$\frac{\partial z}{{\partial t}} = \frac{1}{{\sqrt {L^{\prime}C^{\prime}} }}\frac{\partial w}{{\partial x}} + \frac{{R^{\prime}}}{{2L^{\prime}}}\left( {w - z} \right),$$

where w and z are called the characteristic variables and physically represent the pressure of the forward and backwards traveling waves.

The finite difference scheme (Eq. 44) can similarly be rewritten for characteristic variables as

$${\frac{{\partial w_{i} }}{{\partial t}} = - \frac{1}{{\sqrt {L^{\prime } C^{\prime } } }}\frac{{\left( {w_{{i + 1}} - w_{{i - 1}} } \right)}}{{2\Delta x}} - \frac{{R^{\prime } }}{{2L^{\prime } }}\left( {w_{i} - z_{i} } \right) + \frac{{\Delta x}}{{2\sqrt {L^{\prime } C^{\prime } } }}\frac{{\left( {z_{{i + 1}} - 2z_{i} + z_{{i - 1}} } \right)}}{{\Delta x^{2} }}}$$

(47)

$$\frac{{\partial z_{i} }}{\partial t} = \frac{1}{{\sqrt {L^{\prime}C^{\prime}} }}\frac{{\left( {z_{i + 1} - z_{i - 1} } \right)}}{2\Delta x} + \frac{{R^{\prime}}}{{2L^{\prime}}}\left( {w_{i} - z_{i} } \right) - \frac{\Delta x}{{2\sqrt {L^{\prime}C^{\prime}} }}\frac{{\left( {w_{i + 1} - 2w_{i} + w_{i - 1} } \right)}}{{\Delta x^{2} }},$$

which correspond to a centered finite difference discretization of the characteristic system (Eq. 46) with the addition of two terms that scale with ${\Delta }x$, a dissipative term in the first equation and an anti-dissipative term in the second equation. This asymmetry indicates that the classical lumped parameter circuit artificially dampens forward traveling waves while amplifying backward traveling waves.

In our lumped parameter scheme the pressure drop between nodes is due to the average flow between those two nodes so a series of 0D models can be written as

$$\begin{array}{*{20}c} {\frac{{C^{\prime}}}{2}\frac{{dP_{i} }}{dt} = - \frac{1}{\Delta x} \left( {Q_{{i + \frac{1}{2}}} - Q_{i} } \right)} \\ \end{array}$$

(48)

$$\frac{{C^{\prime}}}{2}\frac{{dP_{i + 1} }}{dt} = - \frac{1}{\Delta x} \left( {Q_{i + 1} - Q_{{i + \frac{1}{2}}} } \right)$$

$$\begin{array}{*{20}c} {L^{\prime}\frac{{dQ_{{i + \frac{1}{2}}} }}{dt} = - R^{\prime}Q_{{i + \frac{1}{2}}} - \frac{1}{\Delta x} \left( {P_{i + 1} - P_{i} } \right),} \\ \end{array}$$

which correspond to a centered finite difference approximation of the 1D linear system where the average flowrate between nodes is defined at the segment midpoint. Recognizing that the lumped parameter model was derived by assuming linear interpolation of pressure between nodes ($P_{{i + \frac{1}{2}}} = \frac{1}{2}\left( {P_{i} + P_{i + 1} } \right)$, the system of Eqs. 48 can also be rewritten in terms of the characteristic variables (w and z)

$$\begin{array}{*{20}c} {\frac{{\partial w_{{i + \frac{1}{2}}} }}{\partial t} = - \frac{1}{{\sqrt {L^{\prime}C^{\prime}} }}\frac{{\left( {w_{i + 1} - w_{i} } \right)}}{\Delta x} - \frac{{R^{\prime}}}{{2L^{\prime}}}\left( {w_{{i + \frac{1}{2}}} - z_{{i + \frac{1}{2}}} } \right)} \\ \end{array}$$

(49)

$$\frac{{\partial z_{{i + \frac{1}{2}}} }}{\partial t} = \frac{1}{{\sqrt {L^{\prime}C^{\prime}} }}\frac{{\left( {z_{i + 1} - z_{i} } \right)}}{\Delta x} + \frac{{R^{\prime}}}{{2L^{\prime}}}\left( {w_{{i + \frac{1}{2}}} - z_{{i + \frac{1}{2}}} } \right),$$

which is a centered finite difference approximation of the characteristic equation (Eq. 46). Importantly, the system of Eqs. 49 does not contain the dissipative and antidissipative terms that resulted from the classical lumped parameter model (Eq. 47). This result indicates that our lumped parameter model does not asymmetrically treat forward and backward traveling waves. The asymmetry of the classical lumped parameter model is visually appreciated by looking at the numerical stencils of the finite difference approximations generated by the classical lumped parameter model (Eq. 44) and our symmetric lumped parameter model (Eq. 48).

1.2 Rigid-walled DLP model

The rigid wall DLP model used in the in vivo validation case was implemented as by enforcing mass conservation at vascular junctions

$$\begin{array}{*{20}c} {\Sigma \hat{Q}_{in} - \Sigma \hat{Q}_{out} = 0,} \\ \end{array}$$

(50)

and conserving momentum over each vascular junction

$$\begin{array}{*{20}c} {L\frac{{d\hat{Q}}}{dt} + R\hat{Q} = P_{1} - P_{2} } \\ \end{array}$$

(51)

where the impedance term L is calculated with Eq. 5 and the nonlinear resistance term R is calculated with Eq. 24. A schematic representation of the rigid DLP model would be similar to Fig. 3b, but without only the resistors and inductors.