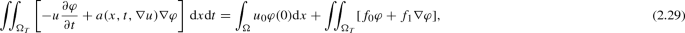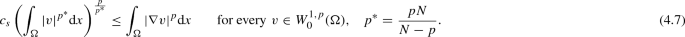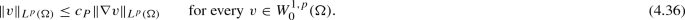Abstract
In this paper, we study a class of nonlinear parabolic problems including the p-Laplacian equation. The initial datum and the forcing term are allowed to be summable functions or Radon measures. We prove that these equations have surprising regularizing properties. Moreover, we study the behavior in time of these solutions proving that decay estimates hold true also for nonzero reaction terms. Finally, we study the autonomous case.
Similar content being viewed by others
1 Introduction
Let us consider the following nonlinear parabolic problem
where \(\Omega _T = \Omega \times (0,T) \), \(\Omega \) is an open bounded set of \({\mathbb {R}}^N\), \(N > 2\), \(T>0\) and \(\Gamma = \partial \Omega \times (0,T)\), with \(\partial \Omega \) regular.
Here the function \(a(x,t,\xi ): \Omega \times (0,T) \times {\mathbb {R}}^N \rightarrow {\mathbb {R}}^N\) is a Caratheodory functionFootnote 1 satisfying, for a.e. \((x,t) \in \Omega _{T} \) and for every \(\xi \) and \(\eta \in {\mathbb {R}}^N\) the following structure conditions
and
Notice that assumptions (1.2) and (1.3) are equivalent to require that (1.3) and the following coercivity condition hold true
We recall that under the previous structural assumptions, also in presence of only summable data \(f \in L^1(\Omega _T)\) and \(u_0 \in L^1(\Omega )\), there exists at least a solution u of (1.1) (see [7] and Definition 2.1). Generally, these solutions are not unique. To guarantee the uniqueness further requirements are needed even when the forcing term f is identically zero (see [1, 3,4,5, 11, 21, 28] and the references therein).
The model we have in mind is the p-Laplacian equation
which is widely studied since it appears in a lot of applicative problems modeling diffusive problems arising in various different contexts like, for example, fluid dynamics (non-Newtonian fluids), biology (evolution of biological species and populations), hydrology, glaciology etc. (see [29] and the references therein).
It is well known that in the absence of the forcing term f, i.e., when (1.6) becomes
a very strong regularization property appears: there exists a solution u of (1.7) which becomes “immediately bounded” also if the initial datum \(u_0\) is only a summable function (see [15] if \(N=1\), [9, 13, 14, 20, 29, 30] and the references therein). Moreover, this solution satisfies the following decay estimate
Indeed, also the following bound holds true
where c depends only on \(N, p, \alpha \) and \(|\Omega |\) (see [20]). This last estimate is noticeable different from (1.8) because it does not depend on the initial datum \(u_0\). Bounds like (1.9) (i.e., independent of \(u_0\)) are often referred in the literature as “universal estimates”. Notice that the value \(\frac{1}{p-2}\) is larger than the decay exponent that appears in (1.8) and consequently this last inequality is a better estimate for large values of t.
Finally, all the previous results remain true for problem (1.7) replaced by
when (1.2)–(1.4) are retained and also estimates (1.8)–(1.9) still hold true in this more general setting (see [10, 20]).
In addition, it is also unique the solution that has this regularizing property (see [21]) and it is also possible to show that if the summability of the initial datum increases, for example if \(u_0\) belongs to \(L^{r_0}(\Omega )\) with \(r_0>1\), then this higher summability influences the decay estimates (1.8) that becomes
(see [20]).
We point out that, although this equation is widely studied, it seems an open problem to understand what happens to these decay estimates and to this strong \(L^{\infty }\)-regularization property when f is not identically zero and the initial datum \(u_0\) belongs to \(L^1(\Omega )\).
Hence, this “open case” is the contempt of this paper.
We prove here that if f is a function satisfying
and
then there exists a solution of (1.1) which immediately increases its regularity reaching the same summability properties of the solution \(u^0\) (obtained by approximation) of the following problem
Hence, for every \(\varepsilon \in (0,T)\) we have
In particular, when \(f \equiv 0\) being \(u^0 \in L^{\infty }(\Omega _T)\) (indeed in this case \(u^0 \equiv 0\)) we obtain the \(L^{\infty }\)-regularization property recalled above for null data f. Notice that \(u^0\) belongs to \(L^{\infty }(\Omega _T)\) also when f is a function not identically zero satisfying (1.12) and
Thus, there exists a solution u of (1.1) that becomes immediately bounded also for sufficiently regular data f (i.e., satisfying (1.16)) even if \(u_0\) is only a summable function.
We point out that (1.15) holds true for every \(u_0 \in L^1(\Omega )\) and for every forcing term satisfying (1.12); hence also if f does not satisfy (1.16), an improvement in summability immediately appears and again u(t) immediately reaches the same summability of \(u^0\) (see Corollary 2.2 for further details). To our knowledge, this regularizing phenomenon is not known in the literature.
Moreover, we prove that the following estimate holds true for almost every \(t \in (0,T)\)
where \(C_i\), \(i=0,1\) are positive constants depending only on p, N and the coercivity constant \(\alpha \) defined in (1.5). Notice that the previous result includes, as particular cases, the decay estimates (1.8) and (1.9), since, as recalled above, when the forcing term f is identically zero also \(u^0\) is identically zero.
We notice that the previous estimate is rather surprising since it holds true for every choice of f and hence, also when the condition (1.16) is not satisfied and hence when generally both u(t) and \(u^0(t)\) are not in \(L^{\infty }(\Omega )\). Thus, the difference between these solutions u and \(u^0\) is bounded although it may happen that both these solutions are unbounded!
Indeed, we will show that there exists a global solution u of (1.1) (see Definition 2.2) satisfying the bound (1.17) for almost every \(t > 0\). This last result allows to describe the asymptotic behavior in time of u(t) and implies that
In other words, for t large the solution u(t) forgets its “initial value \(u_0\)” and has the same behavior of the solution \(u^0\) which satisfies a null condition.
In this paper, we also study the autonomous case:
and we prove that for every \(u_0 \in L^1(\Omega )\) and \(f \in L^1(\Omega )\) there exists a global solution u(t) of (1.1) that satisfies
where w is the solution (obtained by approximation) of the associate stationary problem
In other words, u(t) tends in the \(L^{\infty }(\Omega )\)-norm to the solution w of the nonlinear elliptic problem (1.18) even when both these solutions, u(t) and w, do not belong to \(L^{\infty }(\Omega )\)!
Finally, we investigate what happens to the results described above in the more general case of Radon measures as initial data which is an open problem even in the case of null function f. We complete our investigation considering the case of forcing term f Radon measure too and extending our study also to the semilinear case \(p=2\) being this last case not present in the literature (see [2, 8, 16, 23] and the references therein).
We show that most of the results remain true in this more general setting. In particular, the instantaneous regularizing property (1.15) holds true and the \(L^{\infty }\)-estimate (1.17) described above in the framework of measure data becomes
and
where \(C_{0}\) and \(C_1\) are the same positive constants in (1.17) (hence they depend only on N, p and \(\alpha \)), \(C_2\) is a positive constant depending only on N and \(\alpha \) and \(\sigma \) is a positive constant depending only on \(\alpha \), \(|\Omega |\) and N (see formula (4.52)).
The plan of the paper is the following: in Sect. 2 we state all our results. In Sect. 3, for the convenience of the reader, we recall some known results which we use in the proofs. Finally, Sect. 4 is devoted to the proofs of all the results.
2 Main results
We state here our results in all the details. We start considering the case of data in Lebesgue spaces and then (in Sect. 2.2) we will study what happens in the presence of measure data.
2.1 Data in Lebesgue spaces
Before enouncing our results, we recall what we mean by a solution of (1.1).
Definition 2.1
Assume that the data f and \(u_0\) satisfy
Then a measurable function \(u \in L^{\infty }(0,T;L^1(\Omega )) \cap L^1(0,T;W_0^{1,1}(\Omega ))\) is a solution of (1.1) if \(a(x,t,\nabla u) \in (L^1(\Omega _T))^N\) and
for every \(\varphi \in W^{1,\infty }(0,T;L^\infty (\Omega ))\cap L^\infty (0,T;W_0^{1,\infty }(\Omega ))\) satisfying \(\varphi (T)=0\).
We observe that under the structure conditions (1.2)–(1.4) and the assumption (2.1) on the data, there exists at least one solution of (1.1) (see [7]). As noticed above, these solutions (in absence of further requirements) are not unique.
One of the main results of this paper is the following \(L^\infty \)-estimate which describes the behavior in time of the distance between two solutions of (1.1) satisfying different initial data in \(L^1(\Omega )\) and that can be considered as a sort of “continuous dependence of the initial data” (see also Remark 2.1). The importance of this estimate relies not only in the estimate itself, which is rather surprising, but also in various interesting properties of the solutions that it implies and that we will explain below. In detail, let us consider the following nonlinear parabolic equation
(i.e., problem (1.1) with initial datum \(v_0\)) where
We have the following result
Theorem 2.1
Let (1.2)–(1.4) be satisfied. Assume (2.1) and (2.4). Then there exists at least a solution \(u \in C([0,T];L^1(\Omega ))\) of (1.1) and there is at least a solution \(v \in C([0,T];L^1(\Omega ))\) of (2.3) such that the following estimate holds
where \(C_{0}\) and \(C_1\) are positive constants depending only on N, p and \(\alpha \).
Moreover, u and v are obtained as the limit (a.e. in \(\Omega _T\)) of “classical” solutions of the approximating problems (respectively) (4.1) and (4.4).
Finally, if u and v are two solutions of, respectively (1.1) and (2.3), obtained as the limit (a.e. in \(\Omega _T\)) of solutions of the approximating problems (respectively) (4.1) and (4.4), then they satisfy (2.5).
As noticed in Introduction, estimate (2.5) is rather amazing since in general both the solution u and v are not bounded.
We observe that the previous result can be generalized to global solutions. To show the existence of these global solutions, let us assume
(where h is the function in (1.4)) and
The following result holds true.
Theorem 2.2
Let (1.2)–(1.4) and (2.6) be satisfied. Assume (2.7) and (2.4). Then there exists at least a global solution \(u \in C_{loc}([0,+\infty );L^1(\Omega ))\) of (1.1) and there is at least a global solution \(v \in C_{loc}([0,+\infty );L^1(\Omega ))\) of (2.3) such that the following estimate is satisfied
where \(C_{0}\) and \(C_1\) are the same constants in (2.5), hence positive constants depending only on N, p and \(\alpha \).
In particular, it results
Finally, u and v are obtained as limit of regular approximating solutions.
We recall that here by a global solution we mean the following.
Definition 2.2
A measurable function u is a global solution of (1.1) if it is a solution of (1.1) for every \(T>0\) arbitrarily fixed. We also denote a global solution of (1.1) as a solution of the following problem
Remark 2.1
We point out that the global solutions u and v constructed in Theorem 2.2 are obtained by approximation. We recall that the solutions in \(\Omega _T\) constructed by approximation are unique, i.e., if you change the approximation sequences of the data you always get (passing to the limit) the same solution named for this reason “solution obtained by approximation” (see [11]). Hence, the result of Theorem 2.2 is valid not only for the particular solutions constructed here but for all the solutions constructed by approximation. In particular, this implies that all the global solutions constructed by approximation have the same asymptotic behavior for \(t \rightarrow + \infty \) independently from the initial datum that they satisfy. In other words, the initial data do not influence the behavior for large value of t of all these solutions.
Moreover, a continuous dependence from the initial data holds true for all the solutions of problem (1.1) constructed by approximation.
In the autonomous case
the previous result imply the following.
Corollary 2.1
Let (1.2)–(1.4), (2.6), (2.7) and (2.11) be satisfied. Then there exists a global solution \(u \in C_{loc}([0,+\infty );L^1(\Omega ))\) of (1.1) (that is the unique solution constructed by approximation) such that
where w is the (unique) solution of the stationary problem (2.14) obtained by approximation. Moreover, the following estimate is satisfied
where \(C_{0}\) and \(C_1\) are the same constants in (2.5).
Here, by a solution w of
we mean a function \(w \in W_0^{1,1}(\Omega )\) such that \(a(x, \nabla w) \in (L^1(\Omega ))^N\) and
for every \(\varphi \in W^{1,\infty }_0(\Omega )\). Moreover, we say that w is a solution of (2.14) constructed by approximation if it is obtained as limit in \(L^1(\Omega )\) of the solutions \(w_n \in W_0^{1,p}(\Omega ) \cap L^{\infty }(\Omega )\) of the following approximating problems
where \(f_n \in L^{\infty }(\Omega )\) satisfies
Hence, in the autonomous case, whatever is the choice of the initial datum \(u_0\), the “corresponding” global solution of (1.1) which take \(u_0\) as initial datum and is obtained by approximation, converges (letting \(t \rightarrow +\infty \)) to the (unique) solution of the associate stationary problem (2.14) obtained by approximation. We show now that the estimates proved in the previous theorems allow to prove also interesting information on the regularity of the solutions of (1.1).
To this aim, let \(u^0\) be as in Introduction the (unique) solution of (1.1) constructed by approximation which assume zero initial datum. Thus, \(u^0\) solves (1.14) and is the a.e. limit in \(\Omega _T\) of the regular solutions \(u^0_n\) of the following approximating problems
where
Recall that under the assumptions of Theorem 2.2 (i.e., (1.2)–(1.4), (2.6) and f as in (2.7)) \(u^0\) has a global extension in \(\Omega \times (0,+\infty )\).
We notice explicitly that in all what follows the solution \(u^0\) can be replaced by any solution v of (2.3) (constructed by approximation) that satisfy a bounded initial condition.
Theorem 2.3
Assume (1.2)–(1.4) and (2.1). Let \(u^0\) be the solution of (1.14) defined above. Then there exists a solution \(u \in C([0,T];L^1(\Omega ))\) of (1.1) which in every set \(\Omega \times (\varepsilon ,T)\), \(\varepsilon \in (0,T)\), has the same summability properties of \(u^0\), i.e., for every \(\varepsilon \in (0,T)\)
where \(\delta \) and \(\nu \) belong to the set \([1,+\infty ]\). In particular, it results
Moreover, the following estimate holds true for every \(\varepsilon \in (0,T)\)
with \(C_0\) and \(C_1\) as in (2.5), and where (here and throughout the paper) we adopt the convention that \(\frac{1}{+\infty } = 0\) and we denote \(|\Omega |\) the measure of \(\Omega \). In particular, the following universal estimate is satisfied
Finally, u is obtained as the limit (a.e. in \(\Omega _T\)) of the approximating solutions \(u_n\) of problem (4.1) and under the further “global assumptions” (2.6) and (2.7) it can be extended to a global solution (denoted again u) satisfying the assert of Theorem 2.2.
Thus, thanks to the previous result, we can assert that, although the initial datum \(u_0\) is only a summable function, instantaneously the solution u reaches the same regularity of the solution \(u^0\) which satisfy a bounded initial datum condition. Moreover, for every \(\varepsilon >0\) arbitrarily fixed, it is possible to estimate the norm of u in every set \(\Omega \times (\varepsilon ,T)\) with a constant independent of \(u_0\). Universal estimates are known in the literature when \(f \equiv 0\) and in the framework of bounded solutions. Hence, estimate (2.21) allows to conclude that universal estimates remain true also for nonzero data f and for possibly unbounded solutions.
An immediate consequence of Theorem 2.3 is the following regularity result.
Corollary 2.2
Assume (1.2)–(1.4), \(u_0 \in L^1(\Omega )\) and \(f \in L^m(0,T;L^s(\Omega ))\) with m and s in \((1, + \infty ]\). Then there exists a solution \(u \in C([0,T];L^1(\Omega ))\) of (1.1) satisfying, for every \(\varepsilon >0\), the following regularity properties
where
Indeed, there is “an immediate improvement in regularity” also of the gradient of u if the datum f is not too irregular. In detail, it results:
Theorem 2.4
Let (1.2)–(1.4) be satisfied. Assume \(u_0 \in L^1(\Omega )\) and \(f \in L^m(0,T;L^s(\Omega ))\) with m and s in \((1, + \infty ]\) satisfying
Then there exists a solution u of (1.1) (which is the same solution that appears in Theorems 2.1 and 2.2 ) satisfying
for every \( 0< \varepsilon < T\) and verifying the following estimates for almost every \(t \in (0,T)\)
and
where \(c_0=c_0(T,|\Omega |, N, \alpha )\) and \(C_0\) and \(C_1\) are exactly the same constants that appear in (2.5). In particular, the following universal estimates hold true
Moreover, the solution u is obtained as the limit (a.e. in \(\Omega _T\)) of the approximating solutions \(u_n\) of (4.1). Finally, u is Hoelder continuous (of exponent \(\beta \) with respect to x and \(\frac{\beta }{p}\) with respect to t) in \({\overline{\Omega }}\times (\varepsilon ,T)\), for every \(0< \varepsilon < T\). In particular, it results
Remark 2.2
We notice that the previous result reveals that although the initial datum \(u_0\) is only in \(L^1(\Omega )\) there exists a solution u which becomes immediately bounded and whose gradient increases its summability too. Moreover, universal estimates, i.e., estimate which are not influenced at all by the initial datum \(u_0\) are satisfied both by the \(L^{\infty }\)-norm of u and by the \(L^p\)-norm of the gradient of u. To our knowledge these universal estimates are not known in the literature for nonzero data f.
Remark 2.3
We recall that it is well known that if f belongs to \(L^m(0,T;L^s(\Omega ))\) with m and s satisfying (2.22), also without any information on the initial datum \(u_0\), all the solution of (1.1) belonging to \(C(0,T;L^2(\Omega )) \cap L^p(0,T;W^{1,p}_0(\Omega ))\) are bounded (see [12] and the references therein). Moreover, the result has a local nature, i.e., if u is a local solution belonging to \(C_{loc}(0,T;L^2_{loc}(\Omega )) \cap L^p_{loc}(0,T;W^{1,p}_{loc}(\Omega ))\) and f is in \(L^m_{loc}(0,T;L^s_{loc}(\Omega ))\) (with m and s as before) then u is locally bounded (see [12, 17] and the references therein). The difference here with the classical \(L^{\infty }\)-theory is that the “starting regularity” \(C(0,T;L^2(\Omega )) \cap L^p(0,T;W^{1,p}_0(\Omega ))\) is not assumed since we do not know if solutions with \(L^1\)-initial data have such a regularity. Moreover, the \(L^\infty \)-estimates that we derive are completely different from the classical ones since they do not depend at all from the solution itself.
Indeed, even if the initial datum is only a summable function, it is sufficient that f belongs to the space \( L^{p'}(0,T;W^{-1,p'}(\Omega ))\) to have solutions that immediately belong to the energy space \( C((0,T);L^2(\Omega )) \cap L^p_{loc}(0,T;W_0^{1,p}(\Omega ))\) as the following result shows.
Theorem 2.5
Let (1.2)–(1.4) be satisfied. Assume \(u_0 \in L^1(\Omega )\) and \(f \in L^{p'}(0,T;W^{-1,p'}(\Omega ))\), i.e., \(f = f_0-\)div\((f_1)\), with \(f_i \in L^{p'}(\Omega _T)\), \(i=0,1\). Then there exists a solutionFootnote 2 u of (1.1) belonging to \(C([0,T];L^1(\Omega )) \cap C((0,T);L^2(\Omega )) \cap L^p_{loc}(0,T;W_0^{1,p}(\Omega ))\)Footnote 3 and satisfying the following estimates
where \(C_{\alpha } = \left[ \frac{2}{ p' \alpha ^{\frac{1}{p-1}}} (\max \{1,c_P \})^{p'}\right] ^{\frac{1}{2}} \), \(c_P\) is the Poincaré constant defined in (4.36) and \(c_0=\frac{p'}{\alpha } C_{\alpha }^2 + \frac{1}{ \alpha ^{p'}} (\max \{1,c_P \})^{p'}\).
In particular the following universal estimates hold true
where \(c_1 = \frac{C_{0}^2 p'}{\alpha }|\Omega |\). Finally, u is the same solution satisfying Theorems 2.1–2.3 and hence it is obtained as the limit (a.e. in \(\Omega _T\)) of the regular solution \(u_n\) of (4.1).
We prove now that under the assumptions of the previous theorem, the solutions that immediately regularize are unique. In detail we have the following result.
Theorem 2.6
Under the assumptions of Theorem 2.5 there exists only one solution u of (1.1) belonging to \(C([0,T];L^1(\Omega )) \cap C((0,T);L^2(\Omega )) \cap L^p_{loc}(0,T;W_0^{1,p}(\Omega ))\).
Moreover, if v is a solution of (2.3) with \(v_0 \in L^1(\Omega )\) and if u is a solution of (1.1) and if both u and v belong to \(C([0,T];L^1(\Omega )) \cap C((0,T);L^2(\Omega )) \cap L^p_{loc}(0,T;W_0^{1,p}(\Omega ))\) then the following estimate (“continuous dependence from the initial data”) holds true
where \(C_1\) is the same constant (depending only on N, p and \(\alpha \)) that appears in (2.5).
Remark 2.4
An immediate consequence of the previous result together with Theorem 2.5 (see also Remark 4.2) is that the solutions constructed by approximation are unique. We point out that it is well known in the literature that the solutions constructed by approximation are unique (and also in a more general setting) but here the proof of this result is completely different and shows that indeed the uniqueness holds in the set of the solutions that immediately increase their regularity. Thus, the “reason” of the uniqueness of the solutions constructed by approximation is their regularity \(C([0,T];L^1(\Omega )) \cap C((0,T);L^2(\Omega )) \cap L^p_{loc}(0,T;W_0^{1,p}(\Omega ))\).
We conclude this section showing (in the following subsection) that most of the previous results remain true in the more general framework of Radon measure data.
2.2 Measure data
Let us denote M(O) the set of (finite) Radon measures on O. As usual, if f is a Radon measure on O, we identify the measure f with the application \(\varphi \rightarrow \int _{O} \varphi {\text {d}}f\) defined on \(C({\overline{O}})\). If we assume
and
by a solution of (1.1) we mean the following
Definition 2.3
Under the assumptions (2.35) and (2.36) a function \(u \in L^1(0,T;W_0^{1,1}(\Omega ))\) is a solution of (1.1) if \(a(x,t,\nabla u) \in (L^1(\Omega _T))^N\) and
for every \(\varphi \in C^{\infty }(\overline{\Omega _T})\) which is zero in a neighborhood of \(\Gamma \cup (\Omega \times \{ T \})\).
As noticed above, here we investigate both the semilinear case \(p=2\) and the degenerate case \(p>2\). The singular case \(p < 2\) will be the subject of a forthcoming paper (see [26]).
We recall that if the data \(u_0\) and f are finite Radon measures and if the structure conditions (1.2)–(1.4) are satisfied with \(p \ge 2\), then there exists at least one solution of (1.1) (see [7]). We have the following results:
Theorem 2.7
Let (1.2)–(1.4) be satisfied with \(p \ge 2\). Assume (2.35), (2.36) and \(v_0\) in \(M(\Omega )\). Then there exist u and v solutions of, respectively, (1.1) and of (2.3) such that the following estimates hold true for almost every \(t \in (0,T)\)
and
where \(C_{0}\) and \(C_1\) are the same positive constants defined in (2.5), \(C_2\) is a positive constant depending only on N and \(\alpha \) and \(\sigma \) is a positive constant depending only on \(\alpha \), \(|\Omega |\) and N (see formula (4.52)).
Moreover, these solutions u and v are obtained as the limit (a.e. in \(\Omega _T\)) of “classical” solutions of the approximating problems (respectively) (4.46) and (4.49).
As already noticed in the case of \(L^1\)-data, the previous estimates are rather unexpected being the data only bounded Radon measures. We point out that in the particular case
choosing \(v_0=0\), by the previous Theorem it follows that there exists a solution u of (1.1) satisfying the following estimates for almost every \( t \in (0,T)\)
and
(being in this case \(v \equiv 0\)). To our knowledge, estimates (2.40) and (2.41) seem not known in literature and show that the \(L^{\infty }\)-regularization property, well known (when \(f \equiv 0\)) for \(L^1\)-initial data, appears also for measure initial data. Notice that if \(p>2\) by (2.40) it follows the universal estimate
and hence again, as in the case of initial data in Lebesgue spaces, the \(L^\infty \) norm of the solution can be estimate by quantity independent of the initial datum itself.
We show now that also in the case of measure data there exist global solutions (according to Definition 2.2) having the same asymptotic behavior in time. We point out that the proof of the existence of such global solutions is different from the previous case of \(L^1\)-data since now the solutions in \(\Omega _T\) (generally) do not belong to \(C([0,T];L^1(\Omega ))\). In detail, we have:
Theorem 2.8
Let (1.2)–(1.4) and (2.6) be satisfied with \(p \ge 2\). Assume (2.35) and \(v_0\) in \(M(\Omega )\). If (2.36) holds for every \(T>0\), then there exist a global solution u of (1.1) and a global solution v of (2.3) such that estimate (2.38) if \(p>2\) and (2.39) if \(p=2\) are satisfied for almost every \(t > 0\).
In particular, the limit (2.9) holds true, i.e.,
Corollary 2.3
(Autonomous case) Let (2.11), (1.2)–(1.4) and (2.6) be satisfied with \(p \ge 2\). Assume (2.35) and f in \( M(\Omega )\). Then there exists a global solution u of (1.1) such that for almost every \(t > 0\)
and
where \(C_{0}\) and \(C_1\) are the same positive constants defined in (2.5), \(C_{2}\) and \(\sigma \) are the same positive constants defined in (2.39) and w is a solution (constructed by approximation) of the associated stationary problem (2.14). In particular, it results
Here, by a solution w of the stationary problem (2.14) with datum f in \( M(\Omega )\) we mean a function \(w \in W_0^{1,1}(\Omega )\) such that \(a(x, \nabla w) \in (L^1(\Omega ))^N\) and
for every \(\varphi \in C^{\infty }_0(\Omega )\).
We point out that the assumptions of Corollary 2.3 guarantee the existence of a solution w of (2.14) (see [7]).
The following result shows that also in the case of measure initial data there exists at least a solution which “immediately” improves its regularity reaching the same regularity of the solutions verifying bounded initial data. In details, let us assume
and let v a solution of (2.3) obtained as limit (a.e. in \(\Omega _T\)) of \(v_n \in L^{\infty }(\Omega _T) \cap C([0,T];L^2(\Omega )) \cap L^p(0,T;W_0^{1,p}(\Omega ))\) solutions of
where
We recall that under the assumptions (1.2)–(1.4), there exists such a solution v (see [7]). Moreover, in this more general setting of measure, we do not know if the solutions of (2.3) obtained by approximation are unique. Anyway, we have the following regularity result:
Theorem 2.9
Let (1.2)–(1.4) be satisfied with \(p \ge 2\). Assume (2.45) and (2.35). If v is as above a solution of (2.3) constructed by approximation, then there exists a solution u of (1.1) having the same summability properties of v, i.e., for every \(\varepsilon \in (0,T)\) it results
where \(\delta \) and \(\nu \) belong to the set \([1,+\infty ]\). In particular, it results
Moreover, if \(p> 2\) the following estimate holds true for every \(\varepsilon \in (0,T)\)
with \(C_0\) and \(C_1\) as in (2.5) (positive constants depending only on p, N and \(\alpha \)). In particular, the following universal estimate holds
If otherwise \(p=2\), for every \(\varepsilon \in (0,T)\) it results
with \(C_2\) and \(\sigma \) as in (2.39). Finally, u is obtained by approximation.
Hence, an interesting consequence of the previous result is that if f is in \(L^m(0,T;L^s(\Omega ))\) with m and s satisfying (2.22) and \(u_0\) is in \(M(\Omega )\), then there exists a solution of (1.1) which immediately becomes bounded, despite the fact that the initial datum is only a Radon measure. The following result shows that, analogously to the case of summable initial data, also the gradient of the solution improves instantaneously its regularity.
Theorem 2.10
Let (1.2)–(1.4) be satisfied with \(p \ge 2\). Assume \(u_0 \in M(\Omega )\) and \(f \in L^m(0,T;L^s(\Omega ))\) with m and s in \((1,+\infty ]\) satisfying (2.22). Then there exists a solution u of (1.1) satisfying
for every \( 0< \varepsilon < T\). Moreover, for almost every \(t \in (0,T)\) the following estimates hold true
where
and
with \(c_0=c_0(T,|\Omega |, N, \alpha )\) as in (2.24) and \(C_i\) (\(i=0,1,2\)) and \(\sigma \) as in Theorem 2.7.
In particular, if \(p>2\) the universal estimates (2.26) and (2.27) are satisfied.
Finally u is Hoelder continuous in \({\overline{\Omega }} \times (\varepsilon ,T)\) and the regularity property (2.28) holds.
An immediate consequence of the previous theorem is the following interesting result.
Corollary 2.4
Let (1.2)–(1.4) be satisfied with \(p \ge 2\). Assume \(u_0 \in M(\Omega )\). Then there exists a solution u of (1.10) belonging to \(L^{\infty }(\varepsilon ,T;L^{\infty }(\Omega )) \cap L^p( \varepsilon , T;W_0^{1,p}(\Omega )) \cap C([\varepsilon ,T];L^2(\Omega ))\) and Holder continuous in \({\overline{\Omega }} \times (\varepsilon ,T)\), for every \(\varepsilon \in (0,T)\). Moreover, the following universal decay estimates hold if \(p>2\)
and the following exponential decay estimates are true if \(p=2\)
where \(C_3 = \frac{C_0^2|\Omega |}{2 \alpha } \), \(C_4= \frac{C_2 \sqrt{|\Omega |}}{\sqrt{2\alpha }} \) with \(C_0\), \(C_2\) and \(\sigma \) as in Theorem 2.7.
Indeed, although the initial data are only Radon measures, to have an immediate improvement in the regularity of the gradient of the solutions (again as in the case of summable initial data) it is sufficient that the data f belong to \(L^{p'}(0,T;W^{-1,p'}(\Omega ))\), as the following result clarify.
Theorem 2.11
Let (1.2)–(1.4) be satisfied with \(p \ge 2\). Assume \(u_0 \in M(\Omega )\) and \(f \in L^{p'}(0,T;W^{-1,p'}(\Omega ))\), i.e., \(f = f_0-\)div\((f_1)\), with \(f_i \in L^{p'}(\Omega _T)\), \(i=0,1\). Then there exists a solution u of (1.1) belonging to \(L^p_{loc}(0,T;W_0^{1,p}(\Omega )) \cap C_{loc}(0,T;L^2(\Omega ))\) and satisfying the following estimates
where
where \(C_{\alpha }\) and \(c_0\) as in Theorem 2.5.
In particular, if \(p>2\) the universal estimates (2.32) and (2.33) hold true.
Finally, u is obtained as the limit (a.e. in \(\Omega _T\)) of the regular solution \(u_n\) of (4.46).
3 Preliminary results
We recall here some known results about \(L^\infty \)-decay estimates proved in [20] that will be essential in the proofs of the outcomes presented here. We observe that in the theorems below only integral estimates are assumed (hence a priori the functions involved could not solve any partial differential equation). Moreover, the proofs of all the results stated in this section make use only of elementary tools (a Lemma on suitable continuous functions proved in [27] and a classical Lemma on nonnegative real numbers often used in the framework of boundedness). We point out that further developments and applications of regularity results proved simply by means of suitable integral inequalities can be found in [19,20,21,22,23,24,25,26].
In detail, let us define
We have:
Theorem 3.1
(Theorem 2.1 in [20]) Assume that
where \(\Omega \) is an open set of \({\mathbb {R}}^N\), \(N \ge 1\), \(0<T\le +\infty \) and
Suppose that u satisfies the following integral estimates for every \(k>0\)
where \(c_1\) and \(c_2\) are positive constants independent of k and
Then there exists a positive constant \(C_1\) (see formula (4.19) in [20]) depending only on N, \(c_1\), \(c_2\), r, \(r_0\), q and b such that
where
Moreover, if \(\Omega \) has finite measure we have universal bounds if \(b > r\) and exponential estimates if \(b=r\). More in detail we have the following results.
Theorem 3.2
(Theorem 2.2 in [20]) Let the assumptions of Theorem 3.1 hold true.
If \(\Omega \) has finite measure and \( b > r\) we have the following universal bound
where
and \(C_{\sharp } \), (see formula (4.19) in [20]), is a constant depending only on r, \(r_0\), q, b, \(c_1\), \(c_2\) and the measure of \(\Omega \).
Theorem 3.3
(Theorem 2.2 in [20]) Let the assumptions of Theorem 3.1 hold true.
If \(\Omega \) has finite measure and \( b = r\) the following exponential bound holds
where \(C_2\) is a positive constant depending only on N, \(c_1\), \(c_2\), r, \(r_0\), b and q, \(h_1\) is as in (3.8) and
4 Proofs of results
In this section, we prove all the results stated in Sect. 2.
4.1 Proof of Theorem 2.1
Let u be a solution u of (1.1) obtained as the a.e. limit in \(\Omega _T\) of the solutions \(u_n \in L^{\infty }(\Omega _T) \cap C([0,T];L^2(\Omega )) \cap L^p(0,T;W_0^{1,p}(\Omega ))\) of the following approximating problems
where the data \(u_{0,n}(x) \in L^{\infty }(\Omega )\) and \(f_n(x,t) \in L^{\infty }(\Omega _T)\) satisfy
(see [7]). Notice that being \(u_n\) in \( C([0,T];L^2(\Omega ))\) we can choose in (2.2) also test functions \(\varphi \) not satisfying \(\varphi (T)=0\) and in these last cases in the left-hand side of (2.2) will appear also the integral on \(\Omega \) of \(u_n(T)\varphi (T)\). Indeed, it results
(see again [7]) and
(see [28]). Analogously, let \(v \in C([0,T];L^1(\Omega )) \cap L^q(0,T;W_0^{1,q}(\Omega ))\) be a solution of (2.3) obtained as the a.e. limit in \(\Omega _T\) of the sequence \(v_n \in L^{\infty }(\Omega _T) \cap C([0,T];L^2(\Omega )) \cap L^p(0,T;W_0^{1,p}(\Omega ))\) solutions of the following approximating problems
where \(v_{0,n}(x) \in L^{\infty }(\Omega )\) satisfies
and with \(f_n\) the same approximating sequence defined in (4.3). Let k a positive constant arbitrarily fixed and \(G_k(s)\) the real function defined in (3.1). Choose \(G_k(u_n -v_n)\) as test function in (4.1) and in (4.4). Notice that these choices, together with the following ones can be made rigorous by means of the Steklov averaging process. Subtracting the equations obtained in this way we get for every \(0< t_1< t_2 < T\)
By (1.3) the previous estimate implies
and hence, thanks to the Sobolev inequalityFootnote 4 we obtain
Notice that the previous inequality is equivalent to require that the assumption (3.4) is satisfied by \(u_n-v_n\) with \(c_1 = 2 \alpha c_s \), \(r=2\), \(b=p\) and \(q=p^*\). Observe also that the previous choice of the coefficients r, b and q satisfies the condition (3.3) with \(r_0 = 1\). Moreover, it results \(b > r\). Hence to apply Theorem 3.2, we need to prove that also (3.5) is verified. To this aim, let \(\delta >1\) arbitrarily fixed and take as test function \(\varphi = \left\{ 1- \frac{1}{[1+|G_k(u_n -v_n)|]^\delta }\right\} \hbox { sign}(u_n -v_n)\) in both the problems (4.1) and (4.4); subtracting the equations obtained in this way we get for every \(0 \le t_0< t < T \)
from which, thanks to assumption (1.3), we obtain for every \(0 \le t_0< t < T\) and \(\delta > 1\)
Hence (letting \(\delta \rightarrow +\infty \)) we deduce
i.e., (3.5) is satisfied. Thus we can apply Theorem 3.2 obtaining the following universal estimate
where the positive constant \(C_{\sharp }\) depends only on N, p and \(\alpha \). Noticing that \(u_n - v_n\) converges a.e. to \(u-v\) in \(\Omega _T\) by the previous estimate we deduce
where \(C_0 = C_{\sharp }\). We observe that also the assumptions of Theorem 3.1 are satisfied and consequently also the following estimate holds true
where \(C_1\) is a positive constant depending only on N, p and \(\alpha \). Hence by (4.12) we obtain
By (4.11) and (4.13) it follows that estimate (2.5) holds true. \(\square \)
Remark 4.1
We notice that if in (4.1) we change the approximation of the initial datum \(u_0\), i.e., if we consider another approximation, as for example
where the data \(z_{0,n}(x) \in L^{\infty }(\Omega )\) satisfy
and \(f_n(x,t) \in L^{\infty }(\Omega _T)\) are as in (4.3) then by estimate (4.12) it follows that
and hence both these approximations will converge to the same solution u of (1.1). In other words, changing the approximation of the initial datum, the solution u that we obtain as a limit does not change. The uniqueness of the solutions obtained by approximation is a known result but here we obtain a different proof that make use of the “continuity estimate” (4.12) (or, equivalently, of (4.13)).
4.2 Proof of Theorem 2.2
Let \(T_0 > 0\) arbitrarily fixed. By Theorem 2.1 there exists a solution \(U_0 \in C([0,T_0];L^1(\Omega ))\) of
obtained as a.e. limit in \(\Omega \times (0,T_0)\) of regular solutions \(u_n \in L^{\infty }(\Omega _{T_0}) \cap C([0,T_0];L^2(\Omega )) \cap L^p(0,T_0;W_0^{1,p}(\Omega ))\) of the following approximating problems
where the data \(u_{0,n}(x) \in L^{\infty }(\Omega )\) are as in (4.2) and \(f^0_n(x,t) \in L^{\infty }(\Omega _{T_0})\) satisfy
With a similar construction and again by Theorem 2.1, we obtain a solution \(U_1 \) belonging to \(C([T_0,2T_0];L^1(\Omega ))\) of
obtained as a.e. limit in \(\Omega \times (T_0,2T_0)\) of regular solutions (that for sake of notation we denote again \(u_n\)) problems \(u_n \in L^{\infty }(\Omega \times (T_0,2T_0)) \cap C([T_0,2T_0];L^2(\Omega )) \cap L^p(T_0,2T_0;W_0^{1,p}(\Omega ))\) of the following approximating problems
where the data \(u_{1,n}(x) \in L^{\infty }(\Omega )\) are regular approximations of \(U_0(T_0)\) (hence satisfying similar converging properties in (4.2)) and \(f^1_n(x,t) \in L^{\infty }(\Omega \times (T_0,2T_0))\) satisfy
Iterating this process, we construct a sequence of solutions \(U_i \) in \(C([iT_0,(i+1)T_0];L^1(\Omega ))\) (\(i \in \mathbf{N}\)) of
obtained by approximation. We define \(u=U_i\) in \(\Omega \times [iT_0,(i+1)T_0]\), for every \(i \in \mathbf{N}\). By construction it follows that u is a global solution (according to Definition 2.2). In a similar way, using the same approximation of f defined above (i.e., \(f_n(x,t)=f_n^i(x,t)\) in \(\Omega \times (iT_0,(i+1)T_0)\) for every \(i \in \mathbf{N}\)) we construct a global solution v of (2.3). Now the assert follows by Theorem 2.1. \(\square \)
4.3 Proof of Corollary 2.1
Let w be the solution of the stationary problem (2.14) obtained as the limit in \(L^1(\Omega )\) of the solutions \(w_n \in W_0^{1,p}(\Omega ) \cap L^{\infty }(\Omega )\) of (2.15) where \(f_n \in L^{\infty }(\Omega )\) satisfy (2.16). Passing eventually to subsequences, we can assume that \(w_n\) converges a.e. in \(\Omega \) to w. We observe that \(w(x,t) \equiv w(x)\) is also a global solution (according to Definition 2.2) of the following problem
Moreover, the approximating functions \(w_n(x) \equiv w_n(x,t)\) are global solutions too but of the following problems
Let u be the global solution of (1.1) constructed in the proof of Theorem 2.2, i.e., u is the a.e. limit in \(\Omega _T\) (for every arbitrarily fixed \(T > 0\)) of the solutions \(u_n \in L^{\infty }(\Omega _T) \cap C([0,T];L^2(\Omega )) \cap L^p(0,T;W_0^{1,p}(\Omega ))\) of the following approximating problems
where the data \(u_{0,n}(x) \in L^{\infty }(\Omega )\) satisfy (4.2) and \(f_n\) is the same sequence chosen above in (4.23). Now the assert follows applying Theorem 2.1. \(\square \)
4.4 Proof of Theorem 2.3
Let \(u^0\) be (as in the statement of the theorem) the solution of (1.14) obtained as limit of the approximating solutions \(u^0_n\) of (2.17). Construct u as the solution in \(C([0,T];L^1(\Omega ))\) obtained as the limit (a.e. in \(\Omega _T\)) of the solutions of the approximating problems (4.1) where \(f_n\) is the same approximating sequence of f chosen in (2.17). Hence, by Theorem 2.1 (applied choosing \(v=u^0\)) we deduce that (2.5) holds true, i.e.,
from which it follows that for almost every \( (x,t) \in \Omega _T\)
Now the claims (2.19) and (2.20) gather by the previous estimate. \(\square \)
4.5 Proof of Corollary 2.2
The assertions follow by the results in Theorem 2.3 together with the regularity results (applied to \(u^0\)) in [6, 12, 18]. \(\square \)
4.6 Proof of Theorem 2.4
By Theorem 2.3 there exists a solution u of (1.1) which belongs to \(C([0,T];L^1(\Omega ))\) and satisfies (2.19) and (2.20). Moreover, u is obtained as the limit (a.e. in \(\Omega _T\)) of the approximating solution \(u_n \in L^{\infty }(\Omega _T) \cap C([0,T];L^2(\Omega )) \cap L^p(0,T;W_0^{1,p}(\Omega )) \) of (4.1). It is not restrictive to assume that the approximating sequence \(f_n\) satisfy
Since assumption (2.22) implies that \(u^0\) belongs to \(L^{\infty }(\Omega _T)\), it follows that for every \(\varepsilon \in (0,T)\) arbitrarily fixed, u belongs to \(L^{\infty }(\varepsilon ,T;L^{\infty }(\Omega ))\) and satisfies
By the previous estimate and recalling that \(u^0\) satisfies the classical \(L^\infty \)-estimate
(where \(c_0\) depends only on \(T, N, \alpha , p\) and \(|\Omega |\)) we conclude that estimate (2.24) holds true. We show now that also the gradient of u has an immediate improvement in regularity and satisfies estimate (2.25).
To this aim, take \(u_n\) as test function in (4.1). We deduce that for every \(0 < t \le T\)
Notice that we can estimate the right-hand side of the previous inequality as follows. Thanks to (2.24) we have
where A(t) is as in (2.24). Moreover, it results (thanks to (4.26))
Hence, using again estimate (2.24) we deduce
Thus by the previous inequalities we obtain
By (4.28)–(4.31) we conclude that
which implies the assertion (2.25).
We observe that from what proved above it follows that u belongs to \(C((0,T);L^2(\Omega ))\). As a matter of fact, the sequence \(u_n\) is a Cauchy sequence in \(C([0,T];L^1(\Omega ))\) and by (4.30) it is also equi-bounded in \([\varepsilon ,T] \times \Omega \) (by \(A(\varepsilon )\)) for every \(\varepsilon > 0\) arbitrarily fixed. Hence \(u_n\) is also a Cauchy sequence in \(C([\varepsilon ,T];L^2(\Omega ))\) for every \(\varepsilon > 0\) arbitrarily fixed and consequently u belongs to \(C([\varepsilon ,T];L^2(\Omega ))\) (for every \(\varepsilon > 0\) arbitrarily fixed), i.e., u is in \(C((0,T);L^2(\Omega ))\).
Now, observing that u belongs to \( L^{\infty }((\varepsilon ,T);L^{\infty }(\Omega ))\cap C((0,T);L^2(\Omega )) \cap L^p((\varepsilon ,T);W_0^{1,p}(\Omega ))\) (for every \(\varepsilon \in (0,T)\) arbitrarily fixed) the Hoelder continuity of u in \({\overline{\Omega }} \times (\varepsilon ,T)\) follows by the result in [13] (see also [12]). \(\square \)
4.7 Proof of Theorem 2.5
Since the datum f is in the dual space \(L^{p'}(0,T;W^{-1,p'}(\Omega ))\), we can construct a solution u of (1.1) as the a.e. limit in \(\Omega _T\) of the solutions \(u_n \in C([0,T];L^2(\Omega )) \cap L^p(0,T;W_0^{1,p}(\Omega )) \) of the approximating problems
where the sequence \(u_{0,n}\) satisfies (4.2) and, differently from the previous approximation problems (4.1) above, now it is not necessary to approximate also the datum f with more regular data \(f_n\). Hence now, differently from above, generally \(u_n\) doesn’t belong to \(L^{\infty }(\Omega _T)\). Anyway, the regularity of the approximating sequence \(u_n \) is enough to conclude (doing the same calculations in the proofs of Theorems 2.1 and 2.3 ) that also now (2.19) and (2.20) hold true with \(u^0\) the unique solution of (1.14) belonging to \(C([0,T];L^2(\Omega )) \cap L^p(0,T;W_0^{1,p}(\Omega ))\).
Thus, being \(u^0\) in \(L^{\infty }(0,T;L^2(\Omega ))\), by (2.19) and (2.20) it follows that u belongs to \(L^{\infty }(\varepsilon ,T;L^2(\Omega ))\) (for every positive \(\varepsilon \)) and verifies
where \(C_0\) and \(C_1\) are as in (2.5). Hence, to obtain an estimate for u by the previous inequality we need to estimate the norm \(\Vert u^0\Vert _{L^{\infty }(\varepsilon ,T;L^{2}(\Omega ))}\). To this aim taking \(u^0\) as test function in (1.14) and using (1.5) we deduce for every \( 0 < t \le T\)
We estimate now the right-hand side of the previous inequality. We have (using Young and PoincaréFootnote 5 inequalities)
where \({c}_P\) is the Poincaré constant defined in (4.36). By the previous two estimates, we deduce that for every \( 0 < t \le T\)
which implies
where \(C_{\alpha } = \left[ \frac{2}{ p' \alpha ^{\frac{1}{p-1}}} (\max \{1,c_P \})^{p'}\right] ^{\frac{1}{2}}\). By (4.39) and (4.34) it follows
and hence estimate (2.30) is proved.
We show now that also the gradient of u has an immediately improvement in regularity. To this aim, choose \(u_n\) as test function in (4.33). We obtain
Proceeding as in the proof of (4.40) we deduce that
Moreover, by reasoning exactly as in (4.37) we get
that is
from which the assert (2.31) follows. To conclude the proof it remains to show that u belongs also to \(C((0,T);L^2(\Omega )) \cap C([0,T];L^1(\Omega ))\). The regularity \(C((0,T);L^2(\Omega ))\) follows by the regularity \(L^p_{loc}(0,T;W_0^{1,p}(\Omega ))\) proved above together with the structure assumption (1.4). Finally, the regularity \(C([0,T];L^1(\Omega ))\) can be proved proceeding exactly as in the proof of Theorem 1.7 (first step) in [21] and hence we omit it. \(\square \)
Remark 4.2
We point out that the previous proof shows that under the assumptions of Theorem 2.5 every solution u constructed by approximation (i.e., as the limit of regular solutions \(u_n\) of (4.33)) immediately increases its regularity, since it belongs to \(C([0,T];L^1(\Omega )) \cap C((0,T);L^2(\Omega )) \cap L^p_{loc}(0,T;W_0^{1,p}(\Omega ))\). Moreover, it also satisfies all the estimates stated in Theorem 2.5.
4.8 Proof of Theorem 2.6
It is sufficient to prove estimate (2.34), since the uniqueness result immediately follows applying such an estimate to (eventually different) solutions belonging to \(C([0,T];L^1(\Omega )) \cap C((0,T);L^2(\Omega )) \cap L^p_{loc}(0,T;W_0^{1,p}(\Omega ))\) and satisfying the same initial datum \(u_0\). Hence, let u and v as in the statement of the theorem. Now the proof of (2.34) follows proceeding exactly as in the proof of estimate (4.12) (simply replacing \(u_n\) with u and \(v_n\) with v in the proof above) since the regularity on u and v is sufficient to repeat exactly the same calculation done before. \(\square \)
4.9 Proof of Theorem 2.7
Let u be a solution u of (1.1) obtained as the a.e. limit in \(\Omega _T\) of the solutions \(u_n \in L^{\infty }(\Omega _T) \cap C([0,T];L^2(\Omega )) \cap L^p(0,T;W_0^{1,p}(\Omega ))\) of the following approximating problems
where the data satisfy
(see [7]). We recall that also in the case of measure data it results
(see again [7]). Analogously, let \(v \in L^q(0,T;W_0^{1,q}(\Omega ))\) be a solution of (2.3) obtained as the a.e. limit in \(\Omega _T\) of the sequence \(v_n \in L^{\infty }(\Omega _T) \cap C([0,T];L^2(\Omega )) \cap L^p(0,T;W_0^{1,p}(\Omega ))\) solutions of the following approximating problems
where \(f_n\) is the same approximating sequence defined in (4.48) and \(v_{0,n}(x)\) satisfies
We also choose the approximating sequence \(u_{0,n}(x)\) verifying
Choosing \(G_k(u_n -v_n)\) (\(k>0\)) as test function in (4.46) and in (4.49) and proceeding exactly as in the proof of Theorem 2.1 we deduce that estimate (4.10) if \(p >2\) and (4.12) if \(p \ge 2\) hold true. Indeed, if \(p=2\), proceeding as in the proof of (4.10) but applying Theorem 3.3 (instead of Theorem 3.2) we deduce that also the following estimate holds
where \(C_{2}\) is a positive constant depending only on N and \(\alpha \) and \(\sigma \) is given by the following formula
Hence, by the previous estimates and (4.51) it follows that for almost every \( t \in (0,T)\)
and
which imply the claims. \(\square \)
Remark 4.3
We notice that the proof above shows that if u and v are two solutions of, respectively (1.1) and (2.3), obtained as the limit (a.e. in \(\Omega _T\)) of solutions of the approximating problems (respectively) (4.46) and (4.49) with the approximating data \(u_{0,n}\), \(v_{0,n}\) and \(f_{n}\) satisfying (4.47), (4.50) and (4.48), then if \(p>2\) it results
Moreover, if we also assume (4.51), then also estimate (2.38) holds true if \(p>2\) together with (2.39) if \(p=2\).
4.10 Proof of Theorem 2.8
We observe that in the case of data in \(L^1\), the construction of a global solution done in the proof of Theorem 2.2 above make use of the regularity \(C([0,T];L^1(\Omega ))\) of the solution, which now fails having only measure data. Hence, it is necessary to proceed in a different way. The proof proceeds by steps.
Step 1 The goal of this step is the construction of a global solution u of (1.1). To this aim, let us consider the following parabolic problems
where \(u_{0,n}\) satisfies (4.47) and \(f_n(x,t)\) belong to \( L^{\infty }_{loc}([0,+\infty );L^{\infty }(\Omega ))\) and satisfy
We recall that for every fixed \(n \in \mathbf{N}\), there exists a unique global solution \(u_n\) of (4.55) in \( L^{\infty }_{loc}([0,+\infty );L^{\infty }(\Omega )) \cap C_{loc}([0,+\infty ];L^2(\Omega )) \cap L^p_{loc}([0,+\infty );W_0^{1,p}(\Omega ))\). Moreover, for every arbitrarily fixed \(T>0\), there exists a subsequence of the sequence \(u_n\) converging a.e. in \(\Omega _T\) (indeed a stronger convergence holds) to a solution of our problem (1.1) in \(\Omega _T\) (see [7]). Hence, let \(T_1 > 0\) arbitrarily fixed. As said above, there exists a subsequence of \(u_n\), that we denote \(u^{(1)}_n\), such that
where \(u_1\) is a solution of our problem (1.1) in \(\Omega _{T_1}\). We recall that every term of the sequence \(u^{(1)}_n\) is a global solution, and thus it is also a solution in \(\Omega _{2T_1}\). Hence, again by the results in [7], there exists a subsequence of \(u^{(1)}_n\), that we denote \(u^{(2)}_n\), such that
where \(u_2\) is a solution of our problem (1.1) in \(\Omega _{2T_1}\).
Iterating this procedure, we define a function u in \(\Omega \times (0,+\infty )\) in the following way
where \(m \in \mathbf{N}\) is such that \(mT_0 > T\). We notice that the definition of u is well posed since (by construction) if \(h \in \mathbf{N}\) is such that \(hT_0 > T\) then it results
We point out that for every arbitrarily fixed \(T >0\)u solves (1.1) and hence is a global solution.
Step 2 We conclude here the proof of the theorem. Let v be the global solution constructed exactly as in the previous step but only changing the approximating sequence \(u_{0,n}\) with a sequence \(v_{0,n}\) satisfying (4.50) and (4.51) (hence we do not change the approximating sequence \(f_n\) of f). Let now \(T > 0\) arbitrarily fixed. Proceeding exactly as in the proof of Theorem 2.7 we deduce that estimate (2.38) if \(p >2\) and (2.39) if \(p = 2\) hold true. Hence the assertion follows by the arbitrariness of T. \(\square \)
4.11 Proof of Corollary 2.3
As just recalled above, under the assumptions of Corollary 2.3 there exists a solution w of the stationary problem (2.14). Moreover, w can be constructed as the a.e. limit in \(\Omega \) (indeed further convergences are true) of the solutions \(w_n\) of (2.15) with \(f_n\) satisfying
Let now u be the global solution of (1.1) constructed as in the proof of Theorem 2.8 but using the same approximation \(f_n\) of f done above to construct w (this is possible being f independent of the variable t). It is not restrictive to assume also that the approximation sequence \(u_{0,n}\) in (4.55) satisfies
Now the proof proceeds similarly at all to that of Corollary 2.1 and hence we omit it. \(\square \)
4.12 Proof of Theorem 2.9
The proof is similar at all to that of Theorem 2.3. Let v as in the statement of the theorem a solution of (2.3) constructed as the limit (a.e. in \(\Omega _T\)) of \(v_n\) solutions in \( L^{\infty }(\Omega _T) \cap C([0,T];L^2(\Omega )) \cap L^p(0,T;W_0^{1,p}(\Omega ))\) of (2.46) with \(f_n\) as in (2.47). By Theorem 2.7 and its proof we deduce that there exists a solution u of (1.1) satisfying (2.38) if \(p>2\) and (2.39) if \(p=2\). Consequently, it results for almost every \((x,t) \in \Omega _T\)
and
Now all the assertions are immediate consequences of the previous estimates. \(\square \)
4.13 Proof of Theorem 2.10
Let us choose \(v_0 = 0\) and \(v = u^0\), where \(u^0\) is, as above, the solution of (1.14) obtained as limit of the approximating solutions \(u^0_n\) of (2.17). We recall that \(u^0\) is bounded and satisfies the \(L^{\infty }\)-estimate (4.27). Hence, by Theorem 2.9 there exists a solution u (obtained by approximation) satisfying
and
Now the proof of the theorem proceeds exactly as that of Theorem 2.4 and hence we omit it. \(\square \)
4.14 Proof of Theorem 2.11
The proof follows closely the outline of the proof of Theorem 2.5 and hence we only describe the changes. Let \(u^0\) be the unique solution of (1.14) belonging to \( C([0,T];L^2(\Omega )) \cap L^p(0,T;W_0^{1,p}(\Omega ))\). Since the datum f is sufficiently regular, we can construct u by approximating only the initial datum \(u_0\). In detail, let u be the almost everywhere limit in \(\Omega _T\) of the solution \(u_n\) of (4.33) where we choose the sequence \(u_{0,n}\) satisfying (4.47) and the following bound
We point out that the regularity of \(u_n\) and \(u^0\) is enough to conclude (choosing \(G_k(u_n-u^0)\) as test functions in (4.33) and in (1.14) and proceeding exactly as in the proof Theorem 2.7) that estimates (4.53) and (4.54) hold true with \(v_n\) replaced by \(u^0\), i.e., it results
and
with \(C_0\) and \(C_1\) as in (2.5) and \(C_2\) and \(\sigma \) as in (2.39). Hence, by the previous estimates we deduce (proceeding as in the proof of Theorem 2.9) that for every \(\varepsilon \in (0,T)\) the following estimates hold
and
Hence, estimate (2.57) follows by the previous estimates recalling the \(L^{\infty }(\varepsilon ,T;L^{2}(\Omega ))\)-estimate (4.39) of \(u^0\).
Now the remaining estimate (2.58) on the gradient of u follows proceeding as in the proof of the bound (2.31) of Theorem 2.5, i.e., combining the \(L^{\infty }(\varepsilon ,T;L^2(\Omega ))\)-estimates above with (4.41) and (4.43). \(\square \)
Notes
i.e., It is continuous with respect to \(\xi \) for almost every \((x,t)\in \Omega _T\), and measurable with respect to (x, t) for every \(\xi \in {\mathbb {R}}^N\).
Here, similarly to Definition 2.1, by a solution of (1.1) we mean a measurable function \(u \in L^{\infty }(0,T;L^1(\Omega )) \cap L^1(0,T;W_0^{1,1}(\Omega ))\) such that \(a(x,t,\nabla u) \in (L^1(\Omega _T))^N\) and
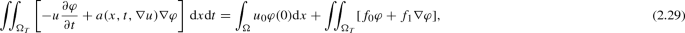
for every \(\varphi \in W^{1,\infty }(0,T;L^\infty (\Omega ))\cap L^\infty (0,T;W_0^{1,\infty }(\Omega ))\) satisfying \(\varphi (T)=0\).
By \(L^p_{loc}(0,T;W_0^{1,p}(\Omega ))\) we mean the space \(L^p_{loc}((0,T];W_0^{1,p}(\Omega ))\).
The Sobolev inequality: there exists a constant \(c_s\) depending only on N and p (\(N>2\)) such that
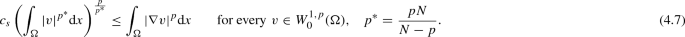
The Poincaré inequality: there exists a constant \(c_P\) depending only on \(\Omega \), N and p such that
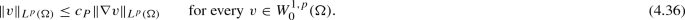
References
Andreu, F., Mazon, J.M., Segura De Leon, S., Toledo, J.: Existence and uniqueness for a a degenerate parabolic equation with \(L^1(\Omega )\) data. Trans. Am. Math. Soc. 351, 285–306 (1999)
Aronson, D.G., Serrin, J.: Local behavior of solutions of quasilinear parabolic equations. Arch. Ration. Mech. Anal. 25, 81–122 (1967)
Blanchard, D., Murat, F.: Renormalized solutions of nonlinear parabolic problems with \(L^1\) data, Existence and uniqueness. Proc. R. Soc. Edimburgh Sect. A 127, 1137–1152 (1997)
Blanchard, D., Murat, F., Redwane, H.: Existence and uniqueness of a renormalized solution for a fairly general class of nonlinear parabolic problems. J. Differ. Equ. 177, 331–374 (2001)
Blanchard, D., Redwane, H.: Renormalized solutions for a class of nonlinear evolution problems. J. Math. Pure Appl. 77, 117–151 (1998)
Boccardo, L., Dall’Aglio, A., Gallouet, T., Orsina, L.: Existence and regularity results for nonlinear parabolic equations. Adv. Math. Sci. Appl. 9, 1017–1031 (1999)
Boccardo, L., Gallouet, T.: Nonlinear elliptic and parabolic equations involving measure data. J. Funct. Anal. 87, 149–169 (1989)
Boccardo, L., Porzio, M.M., Primo, A.: Summability and existence results for nonlinear parabolic equations. Nonlinear Anal TMA 71, 978–990 (2009)
Bonforte, M., Grillo, G.: Super and ultracontractive bounds for doubly nonlinear evolution equations. Rev. Mat. Iberoamericana 22(1), 11–129 (2006)
Cipriani, F., Grillo, G.: Uniform bounds for solutions to quasilinear parabolic equations. J. Differ. Equ. 177, 209–234 (2001)
Dall’Aglio, A.: Approximated solutions of equations with \(L^1\) data. Application to the \(H\)-convergence of quasi-linear parabolic equations. Ann. Mat. Pura Appl. 170, 207–240 (1996)
Di Benedetto, E.: Degenerate Parabolic Equations. Springer, New York (1993)
Di Benedetto, E., Herrero, M.A.: On the Cauchy problem and initial traces for a degenerate parabolic equation. Trans. AMS 314, 187–224 (1989)
Herrero, M.A., Vazquez, J.L.: Asymptotic behaviour of the solutions of a strongly nonlinear parabolic problem. Ann. Fac. Sci. Toulose Math. (5) 3(2), 113–127 (1981)
Kalashnikov, A.S.: Cauchy’s problem in classes of increasing functions for certain quasi-linear degenerate parabolic equations of the second order. Differ. Uravneniya 9(4), 682–691 (1973)
Ladyženskaja, O., Solonnikov, V.A., Ural’ceva, N.N.: Linear and Quasilinear Equations of Parabolic Type. Translations of the American Mathematical Society. American Mathematical Society, Providence (1968)
Porzio, M.M.: \(L^\infty _{loc}\)-estimates for degenerate and singular parabolic equations. Nonlinear Anal Theory Methods Appl 17(11), 1093–1107 (1991)
Porzio, M.M.: Existence of solutions for some “noncoercive” parabolic equations. Discrete Continuous Dyn Syst 5(3), 553–568 (1999)
Porzio, M.M.: Local regularity results for some parabolic equations. Houston J. Math. 25(4), 769–792 (1999)
Porzio, M.M.: On decay estimates. J. Evol. Equ. 9(3), 561–591 (2009)
Porzio, M.M.: Existence, uniqueness and behavior of solutions for a class of nonlinear parabolic problems. Nonlinear Anal. TMA 74, 5359–5382 (2011)
Porzio, M.M.: On uniform and decay estimates for unbounded solutions of partial differential equations. J. Differ. Equ. 259, 6960–7011 (2015)
Porzio, M.M.: Regularity and time behavior of the solutions of linear and quasilinear parabolic equations. Adv. Differ. Equ. 23(5–6), 329–372 (2018)
Porzio, M.M.: A new approach to decay estimates. Application to a nonlinear and degenerate parabolic PDE. Rend. Lincei Mat. Appl. 29, 635–659 (2018)
Porzio, M.M.: Quasilinear parabolic and elliptic equations with singular potentials. In: Wood, D.R., de Gier, J., Praeger, C.E., Tao, T. (eds.) 2017 MATRIX Annals. MATRIX Book Series, vol 2. Springer, Cham (2019)
Porzio, M.M.: Regularity and time behavior of the solutions to weak monotone parabolic equations (preprint)
Porzio, M.M., Pozio, M.A.: Parabolic equations with non-linear, degenerate and space-time dependent operators. J. Evol. Equ. 8, 31–70 (2008)
Prignet, A.: Existence and uniqueness of “entropy” solutions of parabolic problems with \(L^1\) data. Nonlinear Anal. TMA 28(12), 1943–1954 (1997)
Vazquez, J.L.: Smoothing and Decay Estimates for Nonlinear Diffusion Equations. Oxford University Press, Oxford (2006)
Veron, L.: Effects regularisants des semi-groupes non linéaires dans des espaces de Banach. Ann. Fac. Sci. Toulose Math. (5) 1(2), 171–200 (1979)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Porzio, M.M. Asymptotic behavior and regularity properties of strongly nonlinear parabolic equations. Annali di Matematica 198, 1803–1833 (2019). https://doi.org/10.1007/s10231-019-00845-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10231-019-00845-w
Keywords
- Decay estimates
- Asymptotic behavior
- Regularity of solutions
- p-Laplacian equation
- Nonlinear degenerate parabolic equations
- Smoothing effect