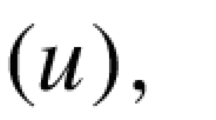Amann–Zehnder type results for p-Laplace problems

Abstract

The existence of a nontrivial solution is proved for a class of quasilinear elliptic equations involving, as principal part, either the p-Laplace operator or the operator related to the p-area functional, and a nonlinearity with p-linear growth at infinity. To this aim, Morse theory techniques are combined with critical groups estimates.

1 Introduction

In 1980, Amann and Zehnder [4] studied the asymptotically linear elliptic problem

$$\begin{aligned} \left\{ \begin{array}{ll} - \, \Delta u = g(u) &{} \qquad \text {in }\varOmega \,, \\ u=0 &{} \qquad \text {on }\partial \varOmega \,, \end{array} \right. \end{aligned}$$

(1.1)

where $\varOmega$ is a bounded domain in ${\mathbb {R}}^N$ with smooth boundary, $g:{\mathbb {R}}\rightarrow {\mathbb {R}}$ is a $C^1$-function such that $g(0)=0$ and there exists $\lambda \in {\mathbb {R}}$ such that

$$\begin{aligned} \lim _{|s|\rightarrow \infty } g'(s) = \lambda \,. \end{aligned}$$

They proved that problem (1.1) admits a nontrivial solution u, supposing that $\lambda$ is not an eigenvalue of $-\Delta$, the so-called nonresonance condition at infinity, and that there exists some eigenvalue of $-\Delta$ between $\lambda$ and $g'(0)$. The same result was obtained by Chang [9] in 1981, using Morse theory for manifolds with boundary, and by Lazer and Solimini [38] in 1988, combining mini–max characterization of the critical point and Morse index estimates. More precisely, the basic idea in [38] is to recognize that the energy functional associated with the asymptotically linear problem (1.1) has a saddle geometry, which implies that a suitable Poincaré polynomial is not trivial, and also to show that a certain critical group at zero is trivial, to ensure the existence of a solution $u \ne 0$ of (1.1).

In the present work, we are interested in finding nontrivial solutions u for the quasilinear elliptic problem

$$\begin{aligned} \left\{ \begin{array}{ll} - \, \mathrm {div}\,\left[ \left( \kappa ^2+ |\nabla u|^2\right) ^{\frac{p-2}{2}} \nabla u\right] = g(u) &{} \qquad \text {in }\varOmega \,, \\ u=0 &{} \qquad \text {on }\partial \varOmega \,, \end{array} \right. \end{aligned}$$

(1.2)

where $\varOmega$ is a bounded open subset of ${\mathbb {R}}^N$, $N\ge 1$, with $\partial \varOmega$ of class $C^{1,\alpha }$ for some $\alpha \in ]0,1]$, while $\kappa \ge 0$, $p >1$ are real numbers, and $g:{\mathbb {R}}\rightarrow {\mathbb {R}}$ is a $C^1$-function such that:

(a):

$g(0)=0$ and there exists $\lambda \in {\mathbb {R}}$ such that

$$\begin{aligned} \lim _{|s|\rightarrow \infty } \frac{g(s)}{|s|^{p-2}s} = \lambda \,. \end{aligned}$$

About the principal part of the equation, the reference cases are $\kappa =0$, which yields the p-Laplace operator, and $\kappa =1$, which yields the operator related to the p-area functional. In the case $p=2$ the value of $\kappa$ is irrelevant.

It is standard that weak solutions u of (1.2) correspond to critical points of the $C^1$-functional $f:W^{1,p}_0(\varOmega )\rightarrow {\mathbb {R}}$ defined as

$$\begin{aligned} f(u) = \int _{\varOmega } \varPsi _{p,\kappa }(\nabla u)\,{\text {d}}x - \int _{\varOmega } G(u)\,{\text {d}}x \,, \end{aligned}$$

(1.3)

where

$$\begin{aligned} \varPsi _{p,\kappa }(\xi ) = \frac{1}{p}\, \left[ \left( \kappa ^2 + |\xi |^2\right) ^{\frac{p}{2}} - \kappa ^p\right] \,, \qquad G(s)= \int _0^s g(t) {\text {d}}t. \end{aligned}$$

With reference to the approach of [38], when $p \ne 2$ the new difficulties that one has to face are related to both the main ingredients of the argument, namely to recognize a saddle structure, with a related information on a suitable Poincaré polynomial, and to provide an estimate of the critical groups at zero by some Hessian type notion.

Concerning the first aspect, the spectral properties of $-\Delta _p$ are not yet well understood. We say that the real number $\lambda$ is an eigenvalue of $-\Delta _p$ if the equation $-\Delta _p u = \lambda |u|^{p-2}u$ admits a nontrivial solution $u \in W^{1,p}_0(\varOmega )$ and we denote by $\sigma (-\Delta _p)$ the set of such eigenvalues. It is known that there exists a first eigenvalue $\lambda _1>0$, which is simple, and a second eigenvalue $\lambda _2 >\lambda _1$, both possessing several equivalent characterizations (see [5, 6, 22, 26, 40, 41]). Moreover, one can define in at least three different ways a diverging sequence $(\lambda _m)$ of eigenvalues of $-\Delta _p$ (see [13, 26, 43]), but it is not known if they agree for $m \ge 3$ and if the whole set $\sigma (-\Delta _p)$ is covered. Therefore, it is not standard to recognize a saddle type geometry for the energy functional associated with the quasilinear problem.

On the other hand, for functionals defined on Banach spaces, serious difficulties arise in extending Morse theory (see [10,11,12, 49, 50]). More precisely, by standard deformation results, which hold also in general Banach spaces, one can prove the so-called Morse relations, which can be written as

$$\begin{aligned} \sum _{m=0}^{\infty } C_m t^m = \sum _{m=0}^{\infty } \beta _m t^m + (1+t) Q(t)\,, \end{aligned}$$

where $(\beta _m)$ is the sequence of the Betti numbers of a pair of sublevels $(\{f\le b\},\{f < a\})$ and $(C_m)$ is a sequence related to the critical groups of the critical points u of f with $a\le f(u) \le b$ (see, e.g., the next Definition 2.1 and [11, Theorem I.4.3]). The problem, in the extension from Hilbert to Banach spaces, concerns the estimate of $(C_m)$, hence of critical groups, by the Hessian of f or some related concept. In a Hilbert setting, the classical Morse lemma and the generalized Morse lemma [30] provide a satisfactory answer. For Banach spaces, a similar general result is so far not known, also due to the lack of Fredholm properties of the second derivative of the functional.

The first difficulty has been overcome by the first two authors in [13] for a problem quite similar to (1.2). By generalizing from [11] the notion of homological linking, in [13, Theorem 3.6] an abstract result has been proved which allows to produce a pair of sublevels $(\{f\le b\},\{f < a\})$ with a nontrivial homology group. In order to describe its dimension in terms of $\lambda$ in the setting of problem (1.2), it is then convenient to set, whenever $m\ge 1$,

$$\begin{aligned} \lambda _m = \inf \left\{ \sup _A \mathcal {E}:\, A \subseteq M, A \text { is symmetric and Index } (A)\ge m \right\} \,, \end{aligned}$$

where

$$\begin{aligned} M = \left\{ u \in W^{1,p}_0(\varOmega ):\, \int _{\varOmega } |u|^p\,{\text {d}}x= 1\right\} \,,\qquad \mathcal {E}(u) = \int _{\varOmega } |\nabla u|^p \,{\text {d}}x \end{aligned}$$

and $\mathrm {Index}$ denotes the ${\mathbb {Z}}_2$-cohomological index of Fadell and Rabinowitz [27, 28]. For a matter of convenience, we also set $\lambda _0=-\infty$. It is well known that $(\lambda _m)$ is a nondecreasing divergent sequence. The arguments of [13] apply for any $p>1$.

For the second difficulty, the value of p becomes relevant. In [16] the first and the last author have proved, for $p>2$ and $\kappa >0$, an extension of the Morse Lemma and established a connection between the critical groups and the Morse index, taking advantage of the fact that, under suitable assumptions on g, the functional f is actually of class $C^2$ on $W^{1,p}_0(\varOmega )$ and that

$$\begin{aligned} \varPsi ''_{p,\kappa }(\eta )[\xi ]^2 \ge \nu _{p,\kappa }|\xi |^2 \qquad \text {with }\nu _{p,\kappa }>0\,. \end{aligned}$$

Related results in the line of Morse theory have been proved by the first and the last author, in the case $p>2$, in [17,18,19]. By means of the results of [19], an Amann–Zehnder type result has been proved in [13] for a problem quite similar to (1.2), provided that $p>2$.

In this work we are first of all interested in a corresponding result in the case $1<p<2$, which amounts to establish a relation between critical groups and Hessian type notions also in this case. Since our argument recovers also the case $p\ge 2$ with less assumptions on g, we provide an Amann–Zehnder type result for any $p>1$.

Let us point out that, if $1<p<2$, the functional f is not of class $C^2$ on $W^{1,p}_0(\varOmega )$. For $\kappa =0$, even the function $\varPsi _{p,\kappa }$ is not of class $C^2$ on ${\mathbb {R}}^N$.

If $\kappa >0$ or $p \ge 2$, let us denote by m(f, 0) the supremum of the dimensions of the linear subspaces where the quadratic form $Q_0:W^{1,2}_0(\varOmega ) \rightarrow {\mathbb {R}}$ defined as

$$\begin{aligned} Q_0(u) = {\left\{ \begin{array}{ll} \displaystyle { \kappa ^{p-2}\,\int _{\varOmega } |\nabla u|^2 \, {\text {d}}x - g'(0) \, \int _{\varOmega } u^2 \, {\text {d}}x} \quad &{}\text {if }\;\kappa>0 \text { or }p>2\,,\\ \displaystyle { \int _{\varOmega } |\nabla u|^2 \, {\text {d}}x - g'(0) \, \int _{\varOmega } u^2 \, {\text {d}}x} \quad &{}\text {if }\;\kappa =0 \text { and }p=2\,, \end{array}\right. } \end{aligned}$$

is negative definite. Let us also denote by $m^*(f,0)$ the supremum of the dimensions of the linear subspaces where the quadratic form $Q_0$ is negative semidefinite. If $\kappa =0$ and $1<p<2$, we set $m(f,0)=m^*(f,0)=0$.

Our first result is the following:

Theorem 1.1

Assume $1<p<\infty$, $\kappa \ge 0$ and hypothesis (a) on g. Suppose also that $\lambda \not \in \sigma (-\Delta _p)$ and denote by $m_{\infty }$ the integer such that $\lambda _{m_{\infty }}< \lambda < \lambda _{m_{\infty }+1}$.

If

$$\begin{aligned} m_{\infty } \not \in [m(f,0),m^*(f,0)]\,, \end{aligned}$$

then there exists a nontrivial solution u of (1.2).

It is easily seen that, if $p=2$, the assumption that there exists some eigenvalue of $-\Delta$ between $\lambda$ and $g'(0)$ is equivalent to $m_{\infty } \not \in [m(f,0),m^*(f,0)]$.

Differently from [13], we aim also to deal with the resonant case, namely $\lambda \in \sigma (-\Delta _p)$. This is not motivated by the pure wish of facing a more complicated situation. To our knowledge, nobody has so far excluded the possibility that $\sigma (-\Delta _p)=\{\lambda _1\}\cup [\lambda _2,+\infty [$. In such a case, the restriction $\lambda \not \in \sigma (-\Delta _p)$ would be quite severe. Taking into account Theorem 1.1, the next result has interest if $\lambda \in \sigma (-\Delta _p)$.

Theorem 1.2

Assume hypothesis (a) on g and one of the following:

$(b_-)$ :

we have

$$\begin{aligned} \lim _{|s|\rightarrow \infty } \left[ pG(s) - g(s)s\right] = -\infty \,; \end{aligned}$$

then we denote by $m_{\infty }$ the integer such that

$$\begin{aligned} \lambda _{m_{\infty }} < \lambda \le \lambda _{m_{\infty }+1}\,; \end{aligned}$$

$(b_+)$ :

we have

$$\begin{aligned} \lim _{|s|\rightarrow \infty } \left[ pG(s) - g(s)s\right] = +\infty \end{aligned}$$

and, moreover, either $1<p\le 2$ with $\kappa \ge 0$ or $p>2$ with $\kappa =0$; then we denote by $m_{\infty }$ the integer such that

$$\begin{aligned} \lambda _{m_{\infty }} \le \lambda < \lambda _{m_{\infty }+1}\,. \end{aligned}$$

If

$$\begin{aligned} m_{\infty } \not \in [m(f,0),m^*(f,0)]\,, \end{aligned}$$

then there exists a nontrivial solution u of (1.2).

Remark 1.3

Concerning the lower order term, examples of g satisfying (a) and $(b_+)$ or $(b_-)$ are given by

$$\begin{aligned} \begin{array}{ll} g(s) = \lambda (1+s^2)^{\frac{p-2}{2}}s + \mu (1+s^2)^{\frac{q-2}{2}}s &{}\quad \text {with }\;\mu \ne 0\text { and }0<q<p\le 2\,,\\ g(s) = \lambda |s|^{p-2}s + \mu |s|^{q-2} s &{}\quad \text {with }\;\mu \ne 0\text { and }2\le q<p\,, \end{array} \end{aligned}$$

so that, respectively,

$$\begin{aligned}&G(s) = \frac{\lambda }{p}\, \left[ \left( 1 + s^2\right) ^{\frac{p}{2}} - 1\right] + \frac{\mu }{q}\, \left[ \left( 1 + s^2\right) ^{\frac{q}{2}} - 1\right] \,, \\&G(s) = \frac{\lambda }{p}\,|s|^p + \frac{\mu }{q}\,|s|^q\,. \end{aligned}$$

Remark 1.4

Let $p=4$, so that

$$\begin{aligned} \varPsi _{p,\kappa }(\xi ) = \frac{1}{4}\,|\xi |^4 + \frac{1}{2}\,\kappa ^2 |\xi |^2\,, \end{aligned}$$

and let

$$\begin{aligned} g(s) = \lambda _m s^3 + \mu s \end{aligned}$$

with $m\ge 1$ and $\mu >0$, so that

$$\begin{aligned} \lim _{|s|\rightarrow \infty } \left[ 4G(s) - g(s)s\right] = +\infty \,, \end{aligned}$$

while

$$\begin{aligned} f(u) = \frac{1}{4} \int _\varOmega \left[ |\nabla u|^4 - \lambda _m |u|^4\right] \,{\text {d}}x + \frac{1}{2} \int _\varOmega \left[ \kappa ^2|\nabla u|^2 - \mu |u|^2\right] \,{\text {d}}x\,. \end{aligned}$$

It is clear that we cannot describe the geometry of the functional f, if we have no information concerning $\kappa ^2$ and $\mu$. For this reason in $(b_+)$ only the case $\kappa =0$ is considered, when $p>2$.

In Sect. 2 we state some results about the critical groups estimates for a large class of functionals including (1.3). We refer to Theorems 2.2, 2.3 and 2.4 for $k>0$ and to Theorems 2.6 and 2.7 for $k=0$ and $1<p<2$ (such results have been announced, without proof, in [15]). Moreover, in a more particular situation which is however enough for the proof of Theorems 1.1 and 1.2, we extend Theorem 2.2 to any $\kappa \ge 0$ and $1<p<\infty$ (see Theorem 2.8).

Sections 3, 4, 5 and 6 are devoted to the proof, by a finite-dimensional reduction introduced in a different setting in [37], of the results stated in Sect. 2, while Sect. 7 contains the proof of Theorems 1.1 and 1.2.

2 Critical groups estimates

In this section we consider a class of functionals including (1.3). More precisely, let $\varOmega$ be a bounded open subset of ${\mathbb {R}}^N$, $N\ge 1$, with $\partial \varOmega$ of class $C^{1,\alpha }$ for some $\alpha \in ]0,1]$, and let $f:W^{1,p}_0(\varOmega )\rightarrow {\mathbb {R}}$ be the functional defined as

$$\begin{aligned} f(u) = \int _{\varOmega } \varPsi (\nabla u)\,{\text {d}}x - \int _{\varOmega } G(x,u)\,{\text {d}}x \end{aligned}$$

(2.1)

where $G(x, s)= \int _0^s g(x, t) {\text {d}}t$. We assume that:

$(\varPsi _1)$ :

the function $\varPsi :{\mathbb {R}}^N\rightarrow {\mathbb {R}}$ is of class $C^1$ with $\varPsi (0)=0$ and $\nabla \varPsi (0)=0$; moreover, there exist $1<p<\infty$, $\kappa \ge 0$ and $0<\nu \le C$ such that the functions $\left( \varPsi -\nu \,\varPsi _{p,\kappa }\right)$ and $\left( C\,\varPsi _{p,\kappa }-\varPsi \right)$ are both convex; such a p is clearly unique;

$(\varPsi _2)$ :

if $\kappa =0$ and $1<p<2$, then $\varPsi$ is of class $C^2$ on ${\mathbb {R}}^N{\setminus }\{0\}$; otherwise, $\varPsi$ is of class $C^2$ on ${\mathbb {R}}^N$;

$(g_1)$ :

the function $g:\varOmega \times {\mathbb {R}}\rightarrow {\mathbb {R}}$ is such that $g(\cdot ,s)$ is measurable for every $s\in {\mathbb {R}}$ and $g(x,\cdot )$ is of class $C^1$ for a.e. $x\in \varOmega$; moreover, we suppose that:

• if $p < N$, there exist $C, q > 0$ such that $q \le p^* -1=\frac{Np}{N-p} - 1$ and

  $$\begin{aligned} |g(x,s)| \le C( 1+ |s|^{q}) \qquad \text {for\;a.e. }x\in \varOmega \text { and every }s\in {\mathbb {R}}\,; \end{aligned}$$

• if $p = N$, there exist $C, q > 0$ such that

  $$\begin{aligned} |g(x,s)| \le C( 1+ |s|^{q}) \qquad \text {for\;a.e. }x\in \varOmega \text { and every }s\in {\mathbb {R}}\,; \end{aligned}$$

• if $p > N$, for every $S>0$ there exists $C_S>0$ such that

  $$\begin{aligned} |g(x,s)|\le C_S \qquad \text {for\;a.e. }x\in \varOmega \text { and every }s\in {\mathbb {R}}\text { with }|s|\le S\,; \end{aligned}$$

$(g_2)$ :

for every $S>0$ there exists $\widehat{C}_S>0$ such that

$$\begin{aligned} |D_sg(x,s)|\le \widehat{C}_S \qquad \text {for\;a.e. }x\in \varOmega \text { and every }s\in {\mathbb {R}}\text { with }|s|\le S\,. \end{aligned}$$

From $(\varPsi _1)$ it follows that $\varPsi$ is strictly convex. Moreover, under these assumptions, it is easily seen that $f:W^{1,p}_0(\varOmega )\rightarrow {\mathbb {R}}$ is of class $C^1$, while it is of class $C^2$ if $p>\max \{N,2\}$. Finally, even in the case $g=0$, f is never of class $C^2$ for $1<p<2$ and is of class $C^2$ in the case $p=2$ iff $\varPsi$ is a quadratic form on ${\mathbb {R}}^N$ (see [1, Proposition 3.2]).

Now, let $u_0\in W^{1,p}_0(\varOmega )$ be a critical point of the functional f, namely a weak solution of

$$\begin{aligned} \left\{ \begin{array}{ll} - \, \mathrm {div}\,\left[ \nabla \varPsi (\nabla u)\right] = g(x,u) &{} \qquad \text {in }\;\varOmega \,, \\ u=0 &{} \qquad \text {on }\;\partial \varOmega \,. \end{array} \right. \end{aligned}$$

According to [25, 31, 39, 47, 48], $u_0 \in C^{1,\beta }(\overline{\varOmega })$ for some $\beta \in ]0,1]$ (see also the next Theorems 3.1 and 3.2).

Let us recall the first ingredient we need from [11, 23, 42].

Definition 2.1

Let ${\mathbb {G}}$ be an abelian group, $c=f(u_0)$ and $f^c= \left\{ u \in W^{1,p}_0(\varOmega ) : f(u) \le c \right\}$. The m-th critical group of f at $u_0$ with coefficients in ${\mathbb {G}}$ is defined by

$$\begin{aligned} C_m(f,u_0;{\mathbb {G}}) = H^m \left( f^{c}, f^{c}\setminus \{u_0\};{\mathbb {G}}\right) , \end{aligned}$$

where $H^*$ stands for Alexander–Spanier cohomology [46]. We will simply write $C_m(f,u_0)$, if no confusion can arise.

In general, it may happen that $C_m(f,u_0)$ is not finitely generated for some m and that $C_m(f,u_0)\ne \{0\}$ for infinitely many m’s. If, however, $u_0$ is an isolated critical point, under assumptions $(\varPsi _1)$ and $(g_1)$ it follows from [14, Theorem 1.1] and [3, Theorem 3.4] that $C_*(f,u_0)$ is of finite type.

The other ingredient is a notion of Morse index, which is not standard, as the functional f is not in general of class $C^2$.

In the case $\kappa >0$ and $1<p<\infty$, observe that

$$\begin{aligned}&\nu \,\min \left\{ (p-1),1\right\} \, (\kappa ^2+ |\eta |^2)^{\frac{p-2}{2}}\,|\xi |^2 \le \varPsi ''(\eta )[\xi ]^2 \\&\quad \le C\,\max \left\{ (p-1),1\right\} \, (\kappa ^2+ |\eta |^2)^{\frac{p-2}{2}}\,|\xi |^2 \qquad \text {for any }\eta , \xi \in {\mathbb {R}}^N\,, \end{aligned}$$

as $\left( \varPsi -\nu \,\varPsi _{p,\kappa }\right)$ and $\left( C\,\varPsi _{p,\kappa }-\varPsi \right)$ are both convex. Therefore, there exists $\tilde{\nu }>0$ such that

$$\begin{aligned} \tilde{\nu }\,|\xi |^2 \le \varPsi ''(\nabla u_0(x))\,[\xi ]^2 \le \dfrac{1}{\tilde{\nu }}\,|\xi |^2 \qquad \text {for any }x\in \varOmega \text { and }\xi \in {\mathbb {R}}^N\,, \end{aligned}$$

as $\nabla u_0$ is bounded. Moreover, $D_sg(x,u_0)\in L^{\infty }(\varOmega )$, as $u_0$ is bounded. Thus, we can define a smooth quadratic form $Q_{u_0}:W^{1,2}_0(\varOmega ) \rightarrow {\mathbb {R}}$ by

$$\begin{aligned} Q_{u_0}(v) = \int _{\varOmega }\varPsi ''(\nabla u_0)[\nabla v]^2\,{\text {d}}x - \int _{\varOmega } D_sg(x,u_0)v^2\,{\text {d}}x \end{aligned}$$

and define the Morse index of f at $u_0$ [denoted by $m(f,u_0)$] as the supremum of the dimensions of the linear subspaces of $W^{1,2}_0(\varOmega )$ where $Q_{u_0}$ is negative definite and the large Morse index of f at $u_0$ [denoted by $m^*(f,u_0)$] as the supremum of the dimensions of the linear subspaces of $W^{1,2}_0(\varOmega )$ where $Q_{u_0}$ is negative semidefinite. We clearly have $m(f,u_0)\le m^*(f,u_0)<+\infty$. Let us point out that $Q_{u_0}$ is well behaved on $W^{1,2}_0(\varOmega )$, while f is naturally defined on $W^{1,p}_0(\varOmega )$.

In the case $\kappa =0$ and $p>2$, we still have

$$\begin{aligned} \varPsi ''(\nabla u_0(x))\,[\xi ]^2 \le \dfrac{1}{\tilde{\nu }}\,|\xi |^2 \qquad \text {for any }x\in \varOmega \text { and }\xi \in {\mathbb {R}}^N\,, \end{aligned}$$

so that $Q_{u_0}:W^{1,2}_0(\varOmega ) \rightarrow {\mathbb {R}}$, $m(f,u_0)$ and $m^*(f,u_0)$ can be defined as before and $m(f,u_0)\le m^*(f,u_0)$. However, $m(f,u_0)$ and $m^*(f,u_0)$ might take the value $+\infty$.

Finally, in the case $\kappa =0$ and $1<p<2$ observe that

$$\begin{aligned} \frac{(p-1)\nu }{|\eta |^{2-p}}\,|\xi |^2 \le \varPsi ''(\eta )[\xi ]^2 \le \frac{C}{|\eta |^{2-p}}\,|\xi |^2 \qquad \text {for any }\eta , \xi \in {\mathbb {R}}^N\text { with }\eta \ne 0\,, \end{aligned}$$

whence

$$\begin{aligned} \varPsi ''(\nabla u_0(x))\,[\xi ]^2 \ge \tilde{\nu }\,|\xi |^2 \qquad \text {for any }x\in \varOmega \text { with }\nabla u_0(x)\ne 0 \text { and }\xi \in {\mathbb {R}}^N\,. \end{aligned}$$

Set

$$\begin{aligned} Z_{u_0}&=\left\{ x\in \varOmega :\,\, \nabla u_0(x) = 0\right\} \,,\\ X_{u_0}&= \left\{ v\in W^{1,2}_0(\varOmega ):\,\,\nabla v(x)=0\text { a.e. in }Z_{u_0}\text { and } \dfrac{|\nabla v|^2}{|\nabla u_0|^{2-p}}\in L^1(\varOmega {\setminus } Z_{u_0}) \right\} \,. \end{aligned}$$

Then

$$\begin{aligned} (v|w)_{u_0} = \int _{\varOmega {\setminus } Z_{u_0}} \varPsi ''(\nabla u_0)\,[\nabla v,\nabla w]\,{\text {d}}x \end{aligned}$$

is a scalar product on $X_{u_0}$ which makes $X_{u_0}$ a Hilbert space continuously embedded in $W^{1,2}_0(\varOmega )$. Moreover, we can define a smooth quadratic form $Q_{u_0}:X_{u_0}\rightarrow {\mathbb {R}}$ by

$$\begin{aligned} Q_{u_0}(v) = \int _{\varOmega {\setminus } Z_{u_0}} \varPsi ''(\nabla u_0)[\nabla v]^2\,{\text {d}}x - \int _{\varOmega } D_sg(x,u_0)v^2\,{\text {d}}x \end{aligned}$$

and denote again by $m(f,u_0)$ the supremum of the dimensions of the linear subspaces of $X_{u_0}$ where $Q_{u_0}$ is negative definite and by $m^*(f,u_0)$ the supremum of the dimensions of the linear subspaces of $X_{u_0}$ where $Q_{u_0}$ is negative semidefinite. Since the derivative of $Q_{u_0}$ is a compact perturbation of the Riesz isomorphism, we have $m(f,u_0)\le m^*(f,u_0)<+\infty$. For a sake of uniformity, let us set $X_{u_0}=W^{1,2}_0(\varOmega )$ when $\kappa >0$ and $1<p<\infty$.

Now we can state the results concerning the critical groups estimates for the functional (2.1).

Theorem 2.2

Let $\kappa >0$ and $1<p<\infty$. Let $u_0 \in W^{1,p}_0(\varOmega )$ be a critical point of the functional f defined in (2.1).

Then we have

$$\begin{aligned} C_m(f, u_0) = \{0\}\qquad \text {whenever }m < m(f,u_0)\text { or }m > m^*(f,u_0)\,. \end{aligned}$$

When the quadratic form $Q_{u_0}$ has no kernel, we can provide a complete description of the critical groups.

Theorem 2.3

Let $\kappa >0$ and $1<p<\infty$. Let $u_0 \in W^{1,p}_0(\varOmega )$ be a critical point of the functional f defined in (2.1) with $m(f,u_0)=m^*(f,u_0)$.

Then $u_0$ is an isolated critical point of f and we have

$$\begin{aligned} \left\{ \begin{array}{ll} C_m(f,u_0) \approx {\mathbb {G}}\quad &{}\text {if }\;m = m(f,u_0)\,,\\ C_m(f, u_0) = \{0\} \quad &{}\text {if }\;m \ne m(f,u_0)\,. \end{array} \right. \end{aligned}$$

If $u_0$ is an isolated critical point of f, then a sharper form of Theorem 2.2 can be proved. Taking into account Theorem 2.3, only the case $m(f,u_0)<m^*(f,u_0)$ is interesting.

Theorem 2.4

Let $\kappa >0$ and $1<p<\infty$. Let $u_0 \in W^{1,p}_0(\varOmega )$ be an isolated critical point of the functional f defined in (2.1) with $m(f,u_0)<m^*(f,u_0)$.

Then one and only one of the following facts holds:

(a):

we have

$$\begin{aligned} \left\{ \begin{array}{ll} C_m(f,u_0) \approx {\mathbb {G}}\quad &{}\text {if }\;m = m(f,u_0)\,,\\ C_m(f, u_0) = \{0\} \quad &{}\text {if }\;m \ne m(f,u_0)\,; \end{array} \right. \end{aligned}$$

(b):

we have

$$\begin{aligned} \left\{ \begin{array}{ll} C_m(f,u_0) \approx {\mathbb {G}}\quad &{}\text {if }\;m = m^*(f,u_0)\,,\\ C_m(f, u_0) = \{0\} \quad &{}\text {if }\;m \ne m^*(f,u_0)\,; \end{array} \right. \end{aligned}$$

(c):

we have

$$\begin{aligned} C_m(f, u_0) = \{0\}\qquad \text {whenever }m \le m(f,u_0)\text { or }m \ge m^*(f,u_0)\,. \end{aligned}$$

Remark 2.5

Since the value of $\kappa$ is irrelevant in the case $p=2$, Theorems 2.2, 2.3 and 2.4 cover also the case $\kappa =0$ with $p=2$.

In the case $\kappa =0$ and $p\ne 2$, we cannot provide such a complete description. Let us mention, however, that critical groups estimates have been obtained in [2] when $\varOmega$ is a ball centered at the origin, and the critical point $u_0$ is a positive and radial function such that $|\nabla u_0( x)|\ne 0$ for $x \ne 0$.

Apart from the radial case, if $p>2$ and g is subjected to assumptions that imply f to be of class $C^2$ on $W^{1,p}_0(\varOmega )$, it has been proved in [37, Theorem 3.1] that $C_m(f, u_0) = \{0\}$ whenever $m < m(f,u_0)$. On the contrary, there is no information, in general, when $p>2$ and $m > m^*(f,u_0)$.

In the case $1<p<2$, the situation turns out to be in some sense reversed. We will prove a result when $m > m^*(f,u_0)$, while we have no information, in general, when $m < m(f,u_0)$.

Theorem 2.6

Let $\kappa =0$ and $1<p<2$. Let $u_0 \in W^{1,p}_0(\varOmega )$ be a critical point of the functional f defined in (2.1).

Then we have

$$\begin{aligned} C_m(f, u_0) = \{0\}\qquad \text {whenever }m > m^*(f,u_0)\,. \end{aligned}$$

However, in the case $u_0=0$, we can provide an optimal result in the line of Theorem 2.3.

Theorem 2.7

Let $\kappa =0$ and $1<p<2$. Let 0 be a critical point of the functional f defined in (2.1).

Then, we have $m(f,0)=m^*(f,0)=0$ and 0 is a strict local minimum and an isolated critical point of f with

$$\begin{aligned} \left\{ \begin{array}{ll} C_m(f,0) \approx {\mathbb {G}}\quad &{}\text {if }\;m = 0\,,\\ C_m(f, 0) = \{0\} \quad &{}\text {if }\;m \ne 0\,. \end{array} \right. \end{aligned}$$

Finally, under more specific assumptions we can extend Theorem 2.2 to any $\kappa$ and p. This will be enough for the results stated in the Introduction.

Theorem 2.8

Let $\kappa \ge 0$ and $1<p<\infty$. Let 0 be an isolated critical point of the functional f defined in (2.1) and suppose that g is independent of x and satisfies assumption $(g_1)$ with $q<p^*-1$ in the case $p<N$.

Then, we have

$$\begin{aligned} C_m(f, 0) = \{0\}\qquad \text { whenever }m < m(f,0)\text { or }m > m^*(f,0)\,. \end{aligned}$$

3 Some auxiliary results

In the following, for any $q\in [1,\infty ]$ we will denote by $\Vert ~\Vert _q$ the usual norm in $L^q(\varOmega )$. We also set, for any $u\in C^{1,\alpha }(\overline{\varOmega })$,

$$\begin{aligned} \Vert u\Vert _{C^{1,\alpha }} = \sup _{\varOmega } |u| + \sup _{\varOmega } |\nabla u| + \sup _{\begin{array}{c} x,y\in \varOmega \\ x\ne y \end{array}} \dfrac{|\nabla u(x)-\nabla u(y)|}{|x-y|^{\alpha }}\,. \end{aligned}$$

Throughout this section, we assume that $\varOmega$ is a bounded open subset of ${\mathbb {R}}^N$ and we suppose that $\varPsi$ and g satisfy assumptions $(\varPsi _1)$, $(\varPsi _2)$ and $(g_1)$, without any further restriction on p and $\kappa$.

In the first part, we adapt to our setting some regularity results from [25, 31, 39, 47, 48].

Theorem 3.1

For every $u_0\in W^{1,p}_0(\varOmega )$, there exists $r>0$ such that, for any $u\in W^{1,p}_0(\varOmega )$ and $w\in W^{-1,\infty }(\varOmega )$ satisfying

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle { \int _\varOmega \left[ \nabla \varPsi (\nabla u)\cdot \nabla v - g(x,u)v\right] \,{\text {d}}x \le \langle w,v\rangle } \\ \qquad \qquad \qquad \qquad \text {for any }v\in W^{1,p}_0(\varOmega )\text { with } vu\ge 0\text { a.e. in }\varOmega \,,\\ \Vert \nabla u-\nabla u_0\Vert _p\le r\,, \end{array} \right. \end{aligned}$$

we have $u\in L^{\infty }(\varOmega )$ and

$$\begin{aligned} \Vert u\Vert _{\infty } \le C\left( \Vert w\Vert _{W^{-1,\infty }}\right) . \end{aligned}$$

Proof

We only sketch the proof in the case $1<p<N$. The case $p\ge N$ is similar and even simpler. Since $\left( \varPsi -\nu \varPsi _{p,\kappa }\right)$ is convex, we have

$$\begin{aligned} \nabla \varPsi (\xi )\cdot \xi = (\nabla \varPsi (\xi )-\nabla \varPsi (0))\cdot \xi \ge \nu \left( \kappa ^2 + |\xi |^2\right) ^{\frac{p-2}{2}}\,|\xi |^2 \qquad \text {for every }\xi \in {\mathbb {R}}^N\,. \end{aligned}$$

Then, the argument is the same of [31, Corollary 1.1]. We only have to remark that, for every $V_0 \in L^{N/p}(\varOmega )$ and $q<\infty$, there exists $r>0$ such that, for any $u\in W^{1,p}_0(\varOmega )$, $V \in L^{N/p}(\varOmega )$ and $w\in W^{-1,\infty }(\varOmega )$ satisfying

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle { \int _\varOmega \left[ \nabla \varPsi (\nabla u)\cdot \nabla v - V|u|^{p-2}u v\right] \,{\text {d}}x \le \langle w,v\rangle } \\ \qquad \qquad \qquad \qquad \text {for any }v\in W^{1,p}_0(\varOmega )\text { with } vu\ge 0\text { a.e. in }\varOmega \,,\\ \Vert V-V_0\Vert _{N/p}\le r\,, \end{array} \right. \end{aligned}$$

we have $u\in L^q(\varOmega )$ and

$$\begin{aligned} \Vert u\Vert _q \le C\left( q,\Vert u\Vert _{p^*},\Vert w\Vert _{W^{-1,\infty }}\right) \end{aligned}$$

(see, in particular, [31, Proposition 1.2 and Remark 1.1]). The key point is that, for any $\varepsilon >0$, there exist $r,\overline{k}$ such that

$$\begin{aligned} k\ge \overline{k}\quad \Longrightarrow \quad \int _{\{|V|>k\}} |V|^{N/p}\,{\text {d}}x \le \varepsilon \end{aligned}$$

whenever $\Vert V-V_0\Vert _{N/p}\le r$. After removing the dependence on V in [31, Proposition 1.2], hence on u in [31, Corollary 1.1], the argument is the same of [31]. $\square$

Theorem 3.2

Assume that $\partial \varOmega$ is of class $C^{1,\alpha }$ for some $\alpha \in ]0,1]$. Then, there exists $\beta \in ]0,1]$ such that any solution u of

$$\begin{aligned} \left\{ \begin{array}{ll} u\in W^{1,p}_0(\varOmega ),\\ - \, \mathrm {div}\,[\nabla \varPsi (\nabla u)] = w_0 - \mathrm {div}\,w_1 &{}\qquad \text {in }W^{-1,p'}(\varOmega )\,, \end{array} \right. \end{aligned}$$

with $w_0\in L^{\infty }(\varOmega )$ and $w_1\in C^{0,\alpha }(\overline{\varOmega };{\mathbb {R}}^N)$, belongs also to $C^{1,\beta }(\overline{\varOmega })$ and we have

$$\begin{aligned} \Vert u\Vert _{C^{1,\beta }} \le C\left( \Vert w_0\Vert _{\infty },\Vert w_1\Vert _{C^{0,\alpha }}\right) \,. \end{aligned}$$

Proof

Since $\varPsi$ is strictly convex and

$$\begin{aligned} \nabla \varPsi (\xi )\cdot \xi \ge \nu \left( \kappa ^2 + |\xi |^2\right) ^{\frac{p-2}{2}}\,|\xi |^2 \qquad \text {for every }\xi \in {\mathbb {R}}^N, \end{aligned}$$

it is standard that, for every $w_0\in L^{\infty }(\varOmega )$ and $w_1\in C^{0,\alpha }(\overline{\varOmega };{\mathbb {R}}^N)$, there exists one and only one $u\in W^{1,p}_0(\varOmega )\cap L^{\infty }(\varOmega )$ such that $- \, \mathrm {div}\,[\nabla \varPsi (\nabla u)] = w_0 - \mathrm {div}\,w_1$. Moreover, we have

$$\begin{aligned} \Vert u\Vert _{\infty } \le C\left( \Vert w_0\Vert _{\infty },\Vert w_1\Vert _{C^{0,\alpha }}\right) \end{aligned}$$

(see, e.g., [35, 36]).

Now, for every $N\ge 1$, fix a nonnegative smooth function $\varrho$ with compact support in the unit ball of ${\mathbb {R}}^N$ and unit integral. Then define, for every $\varPhi \in L^1_\mathrm{loc}({\mathbb {R}}^N)$ and $\varepsilon >0$,

$$\begin{aligned} (R_{\varepsilon }\varPhi )(\xi ) = \int \varrho (y) \varPhi (\xi -\varepsilon y) \,dy\,. \end{aligned}$$

It is easily seen that there exist $0<\check{\nu }(N,p)\le \check{C}(N,p)$ such that

$$\begin{aligned} \check{\nu } (1+|\xi |)^{p-2}&\le \int \varrho (y) (1+|\xi - t y|)^{p-2} \,{\text {d}}y \le \check{C} (1+|\xi |)^{p-2}\,, \\ \check{\nu } (1+|\xi |)^{p-2}&\le \int \varrho (y) (t+|\xi - y|)^{p-2} \,{\text {d}}y \le \check{C} (1+|\xi |)^{p-2}\,, \end{aligned}$$

for every $t\in [0,1]$ and $\xi \in {\mathbb {R}}^N$. Then, there exist $0<\hat{\nu }(N,p)\le \widehat{C}(N,p)$ such that

$$\begin{aligned} \hat{\nu } (\varepsilon +\kappa +|\xi |)^{p-2} \le \int \varrho (y) (\kappa +|\xi - \varepsilon y|)^{p-2} \,{\text {d}}y \le \widehat{C} (\varepsilon +\kappa +|\xi |)^{p-2}\,, \end{aligned}$$

for every $\kappa \ge 0$, $\varepsilon >0$ and $\xi \in {\mathbb {R}}^N$.

Observe that $\varPsi _{p,\kappa } \in W^{2,1}_\mathrm{loc}({\mathbb {R}}^N)$ and

$$\begin{aligned}&\frac{p-1}{2}\, \left( \kappa +|\eta |\right) ^{p-2}\,|\xi |^2\le \varPsi ''_{p,\kappa }(\eta )[\xi ]^2 \le \left( \kappa +|\eta |\right) ^{p-2}\,|\xi |^2 \\&\qquad \text {for every }\eta , \xi \in {\mathbb {R}}^N\text { with }\eta \ne 0. \end{aligned}$$

It follows that there exist $0<\tilde{\nu }(N,p)\le \widetilde{C}(N,p)$ such that

$$\begin{aligned} \tilde{\nu } (\varepsilon +\kappa +|\eta |)^{p-2} |\xi |^2 \le (R_{\varepsilon }\varPsi _{p,\kappa })''(\eta )[\xi ]^2 \le \widetilde{C} (\varepsilon +\kappa +|\eta |)^{p-2} |\xi |^2\,, \end{aligned}$$

for every $\kappa \ge 0$, $\varepsilon >0$ and $\xi ,\eta \in {\mathbb {R}}^N$. Since $\left( \varPsi -\nu \,\varPsi _{p,\kappa }\right)$ and $\left( C\,\varPsi _{p,\kappa }-\varPsi \right)$ are both convex, we infer that $R_{\varepsilon }\varPsi :{\mathbb {R}}^N\rightarrow {\mathbb {R}}$ is a smooth function satisfying

$$\begin{aligned} \nu \tilde{\nu } (\varepsilon +\kappa +|\eta |)^{p-2} |\xi |^2 \le (R_{\varepsilon }\varPsi )''(\eta )[\xi ]^2 \le C \widetilde{C} (\varepsilon +\kappa +|\eta |)^{p-2} |\xi |^2\,, \end{aligned}$$

(3.1)

for every $\varepsilon >0$ and $\xi ,\eta \in {\mathbb {R}}^N$.

Again, from the results of [35, 36], it follows that there exists one and only one $u_{\varepsilon }\in W^{1,p}_0(\varOmega )\cap L^{\infty }(\varOmega )$ such that $-\,\mathrm {div}\,[\nabla (R_{\varepsilon }\varPsi )(\nabla u_{\varepsilon })] = w_0 - \mathrm {div}\,w_1$. Moreover, we have

$$\begin{aligned} \Vert u_{\varepsilon }\Vert _{\infty } \le C\left( \Vert w_0\Vert _{\infty },\Vert w_1\Vert _{C^{0,\alpha }}\right) \end{aligned}$$

and the estimate is independent of $\varepsilon$ for, say, $0<\varepsilon \le 1$.

Then from (3.1) and [39, Theorem 1] we infer that $u_{\varepsilon }\in C^{1,\beta }(\overline{\varOmega })$ and

$$\begin{aligned} \Vert u_{\varepsilon }\Vert _{C^{1,\beta }} \le C\left( \Vert w_0\Vert _{\infty },\Vert w_1\Vert _{C^{0,\alpha }}\right) \end{aligned}$$

for some $\beta \in ]0,1]$, again with an estimate independent of $\varepsilon \in ]0,1]$.

Therefore, $(u_{\varepsilon })$ is convergent, as $\varepsilon \rightarrow 0$, to u in $C^1(\overline{\varOmega })$ and the assertion follows. $\square$

From (3.1) we also infer the next result.

Proposition 3.3

We have $\varPsi \in W^{2,q}_\mathrm{loc}({\mathbb {R}}^N)$ for some $q>N$, so that the map $\nabla \varPsi :{\mathbb {R}}^N\rightarrow {\mathbb {R}}^N$ is locally Hölder continuous.

Now let X be a reflexive Banach space. The next concept is taken from [8, 45].

Definition 3.4

Let $D \subseteq X$. A map $F:D \rightarrow X'$ is said to be of class $(S)_+$ if, for every sequence $(u_k)$ in D weakly convergent to u in X with

$$\begin{aligned} \limsup _k \,\langle F(u_k),u_k-u\rangle \le 0\,, \end{aligned}$$

we have $\Vert u_k-u\Vert \rightarrow 0$.

Proposition 3.5

Let $f:X\rightarrow {\mathbb {R}}$ be a function of class $C^1$and let C be a closed and convex subset of X. Assume that $f'$ is of class $(S)_+$ on C.

Then, the following facts hold:

(a):

f is sequentially lower semicontinuous on C with respect to the weak topology;

(b):

if $(u_k)$ is a sequence in C weakly convergent to u with

$$\begin{aligned} \limsup _k \,f(u_k) \le f(u)\,, \end{aligned}$$

we have $\Vert u_k-u\Vert \rightarrow 0$;

(c):

any bounded sequence $(u_k)$ in C, with $\Vert f'(u_k)\Vert \rightarrow 0$, admits a convergent subsequence.

Proof

Let $(u_k)$ be a sequence in C weakly convergent to u. To prove (a) we may assume, without loss of generality, that

$$\begin{aligned} \limsup _k\, f(u_k) \le f(u)\,. \end{aligned}$$

Let $t_k\in ]0,1[$ be such that

$$\begin{aligned} f(u_k) = f(u) + \langle f'(v_k),u_k-u\rangle \,, \qquad v_k=u+t_k(u_k-u)\,. \end{aligned}$$

Then, $(v_k)$ also is a sequence in C weakly convergent to u and

$$\begin{aligned} \limsup _k\,\langle f'(v_k),v_k-u\rangle = \limsup _k\,t_k\langle f'(v_k),u_k-u\rangle = \limsup _k\,t_k\left( f(u_k)-f(u)\right) \le 0 \,. \end{aligned}$$

Since $f'$ is of class $(S)_+$ on C, we infer that $\Vert v_k-u\Vert \rightarrow 0$, hence that

$$\begin{aligned} \lim _k f(u_k) = \lim _k \left[ f(u) + \langle f'(v_k),u_k-u\rangle \right] = f(u) \end{aligned}$$

and assertion (a) follows.

To prove (b), let $\tau _k\in \left]\frac{1}{2},1\right[$ be such that

$$\begin{aligned} f(u_k) - f\left( \frac{1}{2}\,u_k+\frac{1}{2}\,u\right) = \frac{1}{2}\,\langle f'(w_k),u_k-u\rangle \,, \qquad w_k = u+\tau _k(u_k-u)\,. \end{aligned}$$

Observe that $\left( \frac{1}{2}\,u_k+\frac{1}{2}\,u\right)$ also is a sequence in C weakly convergent to u, whence

$$\begin{aligned} \liminf _k f\left( \frac{1}{2}\,u_k+\frac{1}{2}\,u\right) \ge f(u)\,. \end{aligned}$$

It follows

$$\begin{aligned} \limsup _k\,\langle f'(w_k),u_k-u\rangle = \limsup _k\,2\left[ f(u_k)- f\left( \frac{1}{2}\,u_k+\frac{1}{2}\,u\right) \right] \le 0 \end{aligned}$$

whence, as before, $\Vert w_k-u\Vert \rightarrow 0$. Since $(\tau _k)$ is bounded away from 0, we conclude that $\Vert u_k-u\Vert \rightarrow 0$.

Finally, to prove (c) we may assume that $(u_k)$ is weakly convergent to some u, whence

$$\begin{aligned} \lim _k \,\langle f'(u_k),u_k-u\rangle = 0\,. \end{aligned}$$

Since $f'$ is of class $(S)_+$ on C, assertion (c) also follows. $\square$

We end the section with a result relating the minimality in the $C^1$-topology and that in the $W^{1,p}_0$-topology. When $W=W^{1,p}_0(\varOmega )$ and $\varPsi (\xi )=\frac{1}{p}|\xi |^p$, the next theorem has been proved in [29], which extends to the p-Laplacian the well-known result by Brezis and Nirenberg [7] for the case $p=2$ (see also [32] for $p>2$ and [34] in a nonsmooth setting).

Theorem 3.6

Assume that $\partial \varOmega$ of class $C^{1,\alpha }$ and that $u_0\in W^{1,p}_0(\varOmega )\cap C^{1,\alpha }(\overline{\varOmega })$ for some $\alpha \in ]0,1]$. Suppose also that $W^{1,p}_0(\varOmega )=V\oplus W$, where V is a finite-dimensional subspace of $W^{1,p}_0(\varOmega )$, W is closed in $W^{1,p}_0(\varOmega )$ and the projection $P_V:W^{1,p}_0(\varOmega )\rightarrow V$, associated with the direct sum decomposition, is continuous from the topology of $L^1(\varOmega )$ to that of V.

If $u_0$ is a strict local minimum for the functional f defined in (2.1) along $u_0+(W\cap C^1(\overline{\varOmega }))$ for the $C^1(\overline{\varOmega })$-topology, then $u_0$ is a strict local minimum of f along $u_0+W$ for the $W^{1,p}_0(\varOmega )$-topology.

Proof

Define a convex and coercive functional $h:W^{1,p}_0(\varOmega )\rightarrow {\mathbb {R}}$ by

$$\begin{aligned} h(u) = \int _{\varOmega }\bigl [ \varPsi (\nabla u) - \varPsi (\nabla u_0) - \nabla \varPsi (\nabla u_0)\cdot (\nabla u-\nabla u_0)\bigr ]\,{\text {d}}x \end{aligned}$$

and observe that $v_k \rightarrow u_0$ in $W^{1,p}_0(\varOmega )$ if and only if $h(v_k) \rightarrow 0$. Actually, if $v_k \rightarrow u_0$ in $W^{1,p}_0(\varOmega )$, it is clear that $h(v_k) \rightarrow 0$. Conversely, assume that $h(v_k) \rightarrow 0$. Since

$$\begin{aligned} \varPsi (\nabla v_k) - \varPsi (\nabla u_0) - \nabla \varPsi (\nabla u_0)\cdot (\nabla v_k-\nabla u_0) \rightarrow 0 \qquad \text {in }L^1(\varOmega ), \end{aligned}$$

up to a subsequence we have

$$\begin{aligned} \varPsi (\nabla v_k) - \varPsi (\nabla u_0) - \nabla \varPsi (\nabla u_0)\cdot (\nabla v_k-\nabla u_0) \rightarrow 0 \qquad \text {a.e. in }\varOmega , \end{aligned}$$

hence $\nabla v_k\rightarrow \nabla u_0$ a.e. in $\varOmega$ by the strict convexity of $\varPsi$. On the other hand,

$$\begin{aligned}&\varPsi (\nabla v_k) - \varPsi (\nabla u_0) - \nabla \varPsi (\nabla u_0)\cdot (\nabla v_k-\nabla u_0) \\&\quad \ge \dfrac{\nu }{p}\,|\nabla v_k|^p - \nabla \varPsi (\nabla u_0)\cdot \nabla v_k - z \qquad \text {a.e. in }\varOmega \end{aligned}$$

for some $z\in L^1(\varOmega )$. Therefore, $(\nabla v_k)$ is convergent to $\nabla u_0$ also weakly in $L^p(\varOmega )$. If we apply Fatou’s Lemma to the sequence

$$\begin{aligned} \left[ \varPsi (\nabla v_k) - \varPsi (\nabla u_0) - \nabla \varPsi (\nabla u_0)\cdot (\nabla v_k-\nabla u_0)\right] - \dfrac{\nu }{p}\,|\nabla v_k|^p + \nabla \varPsi (\nabla u_0)\cdot \nabla v_k + z \ge 0, \end{aligned}$$

we find that

$$\begin{aligned} \limsup _k \int _{\varOmega }|\nabla v_k|^p\,{\text {d}}x \le \int _{\varOmega }|\nabla u_0|^p\,{\text {d}}x, \end{aligned}$$

whence the convergence of $(v_k)$ to $u_0$ in $W^{1,p}_0(\varOmega )$.

Since h is of class $C^1$ with

$$\begin{aligned} \langle h'(u),u-u_0\rangle = \int _{\varOmega }\bigl ( \nabla \varPsi (\nabla u) - \nabla \varPsi (\nabla u_0)\bigr ) \cdot (\nabla u -\nabla u_0)\,{\text {d}}x>0 \qquad \text {for any }u\ne u_0, \end{aligned}$$

for every $r>0$ the set

$$\begin{aligned} \left\{ w\in W:\,\,h(u_0+w) = r\right\} \end{aligned}$$

is a $C^1$-hypersurface in W. Moreover, if r is small enough, the map $f'$ is of class $(S)_+$ on

$$\begin{aligned} \left\{ u\in W^{1,p}_0(\varOmega ):\,\,h(u_0+u)\le r\right\} . \end{aligned}$$

If $\varPsi =\varPsi _{p,0}$ with $1<p<N$, this is proved in [14, Theorem 1.2], while the general case follows from [3, Theorem 3.4]. From Proposition 3.5 we infer that $\{u\mapsto f(u_0+u)\}$ is weakly lower semicontinuous on

$$\begin{aligned} \left\{ u\in W^{1,p}_0(\varOmega ):\,\,h(u_0+u)\le r\right\} , \end{aligned}$$

hence on

$$\begin{aligned} \left\{ w\in W:\,\,h(u_0+w)\le r\right\} , \end{aligned}$$

which is weakly compact.

If we argue by contradiction, we find a sequence $(w_k)$ in W such that $w_k$ is a minimum of $\{w\mapsto f(u_0+w)\}$ on

$$\begin{aligned} \left\{ w\in W:\,\,h(u_0+w)\le r_k\right\} \end{aligned}$$

with $r_k\rightarrow 0$ and $w_k\ne 0$, in particular $f(u_0+w_k) \le f(u_0)$. Therefore, there exists $\lambda _k\ge 0$ such that

$$\begin{aligned} \langle f'(u_0+w_k) + \lambda _k h'(u_0+w_k),u\rangle =0 \qquad \text {for any }u\in W, \end{aligned}$$

namely

$$\begin{aligned}&\int _{\varOmega } \nabla \varPsi (\nabla (u_0+w_k))\cdot \nabla u\,{\text {d}}x \quad - \int _{\varOmega } g(x,u_0+w_k)u\,{\text {d}}x \\&\quad + \lambda _k \int _{\varOmega }\bigl ( \nabla \varPsi (\nabla (u_0+w_k)) - \nabla \varPsi (\nabla u_0)\bigr ) \cdot \nabla u\,{\text {d}}x = 0 \qquad \text {for any }u\in W\,, \end{aligned}$$

which is equivalent to

$$\begin{aligned}&\int _{\varOmega } \nabla \varPsi (\nabla (u_0+w_k))\cdot \nabla u\,{\text {d}}x - \dfrac{1}{1+\lambda _k}\,\int _{\varOmega } g(x,u_0+w_k)u\,{\text {d}}x \\&\quad = \dfrac{\lambda _k}{1+\lambda _k}\, \int _{\varOmega }\nabla \varPsi (\nabla u_0) \cdot \nabla u\,{\text {d}}x \qquad \text {for any }u\in W. \end{aligned}$$

It follows

$$\begin{aligned}&\int _{\varOmega } \nabla \varPsi (\nabla (u_0+w_k))\cdot \nabla u\,{\text {d}}x - \dfrac{1}{1+\lambda _k}\,\int _{\varOmega } g(x,u_0+w_k)u\,{\text {d}}x \\&\quad = \dfrac{\lambda _k}{1+\lambda _k}\, \int _{\varOmega }\nabla \varPsi (\nabla u_0) \cdot \nabla u\,{\text {d}}x + \int _{\varOmega }\nabla \varPsi (\nabla (u_0+w_k))\cdot \nabla P_Vu\,{\text {d}}x\\&\qquad - \dfrac{1}{1+\lambda _k}\,\int _{\varOmega } g(x,u_0+w_k)P_Vu\,{\text {d}}x \\&\qquad - \dfrac{\lambda _k}{1+\lambda _k}\, \int _{\varOmega }\nabla \varPsi (\nabla u_0) \cdot \nabla P_Vu\,{\text {d}}x \qquad \text {for any }u\in W^{1,p}_0(\varOmega ). \end{aligned}$$

Since $P_V$ is continuous from the topology of $L^1(\varOmega )$ to that of $W^{1,p}_0(\varOmega )$, we have

$$\begin{aligned}&\int _{\varOmega }\nabla \varPsi (\nabla (u_0+w_k))\cdot \nabla P_Vu\,{\text {d}}x - \dfrac{1}{1+\lambda _k}\,\int _{\varOmega } g(x,u_0+w_k)P_Vu\,{\text {d}}x \\&\quad - \dfrac{\lambda _k}{1+\lambda _k}\, \int _{\varOmega }\nabla \varPsi (\nabla u_0) \cdot \nabla P_Vu\,{\text {d}}x = \int _{\varOmega } z_k u\,{\text {d}}x \qquad \text {for any }u\in W^{1,p}_0(\varOmega ) \end{aligned}$$

with $(z_k)$ bounded in $L^{\infty }(\varOmega )$. It follows

$$\begin{aligned} - \, \mathrm {div}\,\left[ \nabla \varPsi (\nabla (u_0+w_k))\right] - \dfrac{1}{1+\lambda _k}\,g(x,u_0+w_k) = z_k - \mathrm {div}\,\left[ \dfrac{\lambda _k}{1+\lambda _k}\, \nabla \varPsi (\nabla u_0)\right] \end{aligned}$$

(3.2)

and $\nabla \varPsi (\nabla u_0)\in C^{0,\beta }(\overline{\varOmega };{\mathbb {R}}^N)$ for some $\beta \in ]0,1]$, by Proposition 3.3.

If $p<N$, from $(g_1)$ we infer that

$$\begin{aligned} \begin{aligned} \dfrac{1}{1+\lambda _k}\, [g(x,u_0+w_k) - g(x,0)] u&\le |g(x,u_0+w_k)-g(x,0)|\,|u| \\&=\frac{|g(x,u_0+w_k)-g(x,0)|}{|u_0+w_k|} \,(u_0+w_k) u \\&\le \frac{C(1+|u_0+w_k|^{p^*-1})}{|u_0+w_k|} \,(u_0+w_k)u \\&=C\frac{u_0+w_k}{|u_0+w_k|}\,u + C|u_0+w_k|^{p^*-2}(u_0+w_k)u \,, \end{aligned} \end{aligned}$$

whenever $u(u_0+w_k)\ge 0$ a.e. in $\varOmega$. It follows

$$\begin{aligned}&\int _{\varOmega }\nabla \varPsi (\nabla (u_0+w_k))\cdot \nabla u\,{\text {d}}x \quad - \int _{\varOmega } C|u_0+w_k|^{p^*-2}(u_0+w_k)u\,{\text {d}}x \\&\quad \le \int _{\varOmega } \left[ \dfrac{1}{1+\lambda _k}\, g(x,0) + \hat{z}_k+z_k\right] u\,{\text {d}}x + \dfrac{\lambda _k}{1+\lambda _k}\, \int _{\varOmega }\nabla \varPsi (\nabla u_0)\cdot \nabla u\,{\text {d}}x \\&\qquad \text {for any }u\in W^{1,p}_0(\varOmega ) \text { with }u(u_0+w_k)\ge 0\text { a.e. in }\varOmega \,, \end{aligned}$$

where

$$\begin{aligned} \hat{z}_k=\left\{ \begin{array}{ll} \displaystyle { C\frac{u_0+w_k}{|u_0+w_k|}} \quad &{}\text {where }\;u_0+w_k\ne 0\,,\\ 0 \quad &{}\text {where }\;u_0+w_k=0\,. \end{array} \right. \end{aligned}$$

From Theorem 3.1 it follows that $(u_0+w_k)$ is bounded in $L^\infty (\varOmega )$. Coming back to (3.2), from Theorem 3.2 we conclude that $(u_0+w_k)$ is bounded in $C^{1,\beta }(\overline{\varOmega })$ for some $\beta \in ]0,1]$. Then $(u_0+w_k)$ is convergent to $u_0$ in $C^1(\overline{\varOmega })$ and a contradiction follows.

If $p\ge N$, the argument is similar and even simpler. $\square$

4 Parametric minimization

Throughout this section, we assume that $\varOmega$ is a bounded open subset of ${\mathbb {R}}^N$ with $\partial \varOmega$ of class $C^{1,\alpha }$ for some $\alpha \in ]0,1]$ and that $\varPsi$ and g satisfy assumptions $(\varPsi _1)$, $(\varPsi _2)$, $(g_1)$ and $(g_2)$ with either $\kappa >0$ and $1<p<\infty$ or $\kappa =0$ and $1<p<2$.

Let $u_0$ denote a critical point of the functional f defined in (2.1). According to Theorems 3.1 and 3.2, we have $u_0 \in C^{1,\beta }(\overline{\varOmega })$ for some $\beta \in ]0,1]$.

Given a continuous function $\varPhi :{\mathbb {R}}^N\rightarrow {\mathbb {R}}$, for any $x,v \in {\mathbb {R}}^N$ we set

$$\begin{aligned}\underline{\varPhi }''(x)[v]^2 = \liminf _{\begin{array}{c} y\rightarrow x\\ t\rightarrow 0\\ w\rightarrow v \end{array}}\, \dfrac{\varPhi (y+t w)+\varPhi (y-t w)-2\varPhi (y)}{t^2}\,. \end{aligned}$$

Then, the function $\left\{ (x,v)\mapsto \underline{\varPhi }''(x)[v]^2\right\}$ is lower semicontinuous. If $\varPhi$ is convex, it is also clear that $\underline{\varPhi }''(x)[v]^2\in [0,+\infty ]$ and that $\underline{\varPhi }''(x)[0]^2=0$. In particular, it is easily seen that

$$\begin{aligned} \kappa =0\text { and }1<p<2\,\Longrightarrow \, \underline{\varPsi }''_{\,p,\kappa }(0)[\xi ]^2 = \left\{ \begin{array}{ll} 0 &{}\quad \text {if }\;\xi = 0\,,\\ +\infty &{}\quad \text {if }\;\xi \ne 0\,. \end{array} \right. \end{aligned}$$

Since $\left( \varPsi -\nu \,\varPsi _{p,\kappa }\right)$ is convex, we also have

$$\begin{aligned} \kappa =0\text { and }1<p<2\,\Longrightarrow \, \underline{\varPsi }''(0)[\xi ]^2 = \left\{ \begin{array}{ll} 0 &{}\quad \text {if }\;\xi = 0\,,\\ +\infty &{}\quad \text {if }\;\xi \ne 0\,, \end{array} \right. \end{aligned}$$

while $\underline{\varPsi }''(\eta )[\xi ]^2= \varPsi ''(\eta )[\xi ]^2$ in the other cases. In particular, the function $\left\{ \xi \mapsto \underline{\varPsi }''(\eta )[\xi ]^2\right\}$ is convex for any $\eta \in {\mathbb {R}}^N$:

Proposition 4.1

For every $u,v\in W^{1,p}_0(\varOmega )$, the function

$$\begin{aligned} \biggl \{(x,t) \mapsto (1-t) \underline{\varPsi }'' \bigl (\nabla u(x)+t(\nabla v(x)-\nabla u(x))\bigr ) \bigl [\nabla v(x)-\nabla u(x)\bigr ]^2 \biggr \} \end{aligned}$$

belongs to $L^1(\varOmega \times ]0,1[)$ and one has

$$\begin{aligned}&\int _\varOmega \varPsi (\nabla v)\,{\text {d}}x - \int _\varOmega \varPsi (\nabla u)\,{\text {d}}x - \int _\varOmega \nabla \varPsi (\nabla u) \cdot (\nabla v-\nabla u)\,{\text {d}}x \\&\quad = \int _0^1(1-t)\left\{ \int _\varOmega \underline{\varPsi }'' \bigl (\nabla u(x)+t(\nabla v(x)-\nabla u(x))\bigr ) \bigl [\nabla v(x)-\nabla u(x)\bigr ]^2\, {\text {d}}x\right\} \,{\text {d}}t. \end{aligned}$$

Proof

Let us treat the case $\kappa =0$ and $1<p<2$. The case $\kappa >0$ and $1<p<\infty$ is similar and even simpler. First of all, $\left\{ (\eta ,\xi )\mapsto \underline{\varPsi }''(\eta )[\xi ]^2\right\}$ is a Borel function, being lower semicontinuous. Moreover, we have

$$\begin{aligned} \underline{\varPsi }''(\eta )[\xi ]^2=\varPsi ''(\eta )[\xi ]^2 \le \frac{C}{|\eta |^{2-p}}\,|\xi |^2 \qquad \text {for any }\eta , \xi \in {\mathbb {R}}^N\text { with }\eta \ne 0. \end{aligned}$$

Therefore, for every $\eta ,\xi \in {\mathbb {R}}^N$, the function $\left\{ t\mapsto \varPsi (\eta +t(\xi -\eta ))\right\}$ belongs to $W^{2,1}_\mathrm{loc}({\mathbb {R}})$ and we have

$$\begin{aligned} \varPsi (\xi ) - \varPsi (\eta ) - \nabla \varPsi (\eta )\cdot (\xi -\eta ) = \int _0^1 (1-t)\underline{\varPsi }'' \bigl (\eta +t(\xi -\eta )\bigr ) \bigl [\xi -\eta \bigr ]^2\,{\text {d}}t. \end{aligned}$$

Then, given $u,v\in W^{1,p}_0(\varOmega )$, we have a.e. in $\varOmega$

$$\begin{aligned}&\varPsi (\nabla v(x)) - \varPsi (\nabla u(x)) - \nabla \varPsi (\nabla u(x)) \cdot (\nabla v(x)-\nabla u(x)) \\&\quad = \int _0^1 (1-t)\underline{\varPsi }'' \bigl (\nabla u(x)+t(\nabla v(x)-\nabla u(x))\bigr ) \bigl [\nabla v(x)-\nabla u(x)\bigr ]^2\,{\text {d}}t. \end{aligned}$$

By integrating over $\varOmega$ and applying Fubini’s theorem, the assertion follows. $\square$

Theorem 4.2

Let $(u_k)$ be a sequence in $W^{1,p}_0(\varOmega )\cap L^{\infty }(\varOmega )$ and $(v_k)$ a sequence in $W^{1,2}_0(\varOmega )$ such that $(u_k)$ is bounded in $L^{\infty }(\varOmega )$ and convergent to u in $W^{1,p}_0(\varOmega )$, while $(v_k)$ is weakly convergent to v in $W^{1,2}_0(\varOmega )$.

Then, we have

$$\begin{aligned}&\int _{\varOmega } \underline{\varPsi }''(\nabla u)[\nabla v]^2\,{\text {d}}x - \int _{\varOmega } D_sg(x,u)v^2\,{\text {d}}x \\&\quad \le \liminf _k \left( \int _{\varOmega } \underline{\varPsi }''(\nabla u_k)[\nabla v_k]^2\,{\text {d}}x - \int _{\varOmega } D_sg(x,u_k)v_k^2\,{\text {d}}x\right) \,. \end{aligned}$$

Proof

Since $(v_k)$ is convergent to v in $L^2(\varOmega )$, we clearly have

$$\begin{aligned} \int _{\varOmega } D_sg(x,u)v^2\,{\text {d}}x = \lim _k \int _{\varOmega } D_sg(x,u_k)v_k^2\,{\text {d}}x. \end{aligned}$$

Then, the assertion follows from the Theorem in [33]. $\square$

Proposition 4.3

There exists a direct sum decomposition

$$\begin{aligned} L^1(\varOmega ) = V \oplus \widetilde{W} \end{aligned}$$

such that:

(a):

$V\subseteq X_{u_0}\cap W^{1,p}_0(\varOmega )\cap L^{\infty }(\varOmega )$ with $\dim V = m^*(f,u_0)<+\infty$, while $\widetilde{W}$ is closed in $L^1(\varOmega )$;

(b):

we have

$$\begin{aligned}&\int _{\varOmega } \underline{\varPsi }''(\nabla u_0)[\nabla (v+w)]^2\,{\text {d}}x - \int _{\varOmega } D_sg(x,u_0)(v+w)^2\,{\text {d}}x \\&\quad =\int _{\varOmega } \underline{\varPsi }''(\nabla u_0)[\nabla v]^2\,{\text {d}}x - \int _{\varOmega } D_sg(x,u_0)v^2\,{\text {d}}x \\&\qquad +\, \int _{\varOmega } \underline{\varPsi }''(\nabla u_0)[\nabla w]^2\,{\text {d}}x - \int _{\varOmega } D_sg(x,u_0)w^2\,{\text {d}}x \\&\qquad \text {for any }v\in V\text { and } w\in \widetilde{W}\cap W^{1,2}_0(\varOmega ),\\&\qquad \int _{\varOmega } \underline{\varPsi }''(\nabla u_0)[\nabla v]^2\,{\text {d}}x - \int _{\varOmega } D_sg(x,u_0)v^2\,{\text {d}}x \le 0 \\&\qquad \text {for any }v\in V\,,\\&\qquad \int _{\varOmega } \underline{\varPsi }''(\nabla u_0)[\nabla w]^2\,{\text {d}}x - \int _{\varOmega } D_sg(x,u_0)w^2\,{\text {d}}x > 0 \\&\qquad \text {for any}\;w\in (\widetilde{W}\cap W^{1,2}_0(\varOmega )){\setminus }\{0\}\,. \end{aligned}$$

Proof

Let us treat in detail the case $\kappa =0$ and $1<p<2$. Since the derivative of the smooth quadratic form $Q_{u_0}:X_{u_0}\rightarrow {\mathbb {R}}$ is a compact perturbation of the Riesz isomorphism, it is standard that there exists a direct sum decomposition

$$\begin{aligned} X_{u_0} = V \oplus \widehat{W} \end{aligned}$$

such that $\dim V = m^*(f,u_0)<+\infty$,

$$\begin{aligned} \begin{array}{ll} \widehat{W} = \left\{ w\in X_{u_0}:\,\, \int _{\varOmega } vw\,{\text {d}}x = 0\quad \text {for any }v\in V\right\} ,&{}\\ Q_{u_0}(v+w) = Q_{u_0}(v) + Q_{u_0}(w) &{}\text {for any }v\in V\text { and }w\in \widehat{W},\\ Q_{u_0}(v) \le 0 &{} \text {for any }v\in V,\\ Q_{u_0}(w) > 0 &{} \text {for any }w\in \widehat{W}{\setminus }\{0\}. \end{array} \end{aligned}$$

Moreover, either $V=\{0\}$ or $V=\mathrm {span}\left\{ e_1,\ldots ,e_{m^*}\right\}$ and each $e_j\in X_{u_0}{\setminus }\{0\}$ is a solution of

$$\begin{aligned} \int _{\varOmega {\setminus } Z_{u_0}} \varPsi ''(\nabla u_0)[\nabla e_j,\nabla u]\,{\text {d}}x - \int _{\varOmega } D_sg(x,u_0)e_j u \,{\text {d}}x = \lambda _j \int _{\varOmega } e_j u\,{\text {d}}x \qquad \text {for any }u\in X_{u_0} \end{aligned}$$

for some $\lambda _j\le 0$ (which is possible only if $\Vert \nabla u_0\Vert _{\infty }>0$).

If $\varphi :{\mathbb {R}}\rightarrow {\mathbb {R}}$ is a nondecreasing Lipschitz function with $\varphi (0)=0$, then $\varphi (e_j)\in X_{u_0}$, whence

$$\begin{aligned} \int _{\varOmega {\setminus } Z_{u_0}} \varphi '(e_j)\varPsi ''(\nabla u_0)[\nabla e_j]^2\,{\text {d}}x - \int _{\varOmega } D_sg(x,u_0)e_j \varphi (e_j) \,{\text {d}}x = \lambda _j \int _{\varOmega } e_j \varphi (e_j)\,{\text {d}}x\le 0\,. \end{aligned}$$

On the other hand, we have

$$\begin{aligned} \varPsi ''(\nabla u_0(x))[\xi ]^2 \ge \frac{(p-1)\nu }{|\nabla u_0(x)|^{2-p}}\,|\xi |^2 \ge \frac{(p-1)\nu }{\Vert \nabla u_0\Vert _{\infty }^{2-p}}\,|\xi |^2 \\ \qquad \text {for any }x\in \varOmega {\setminus } Z_{u_0}\text { and }\xi \in {\mathbb {R}}^N\,, \end{aligned}$$

whence

$$\begin{aligned} \frac{(p-1)\nu }{\Vert \nabla u_0\Vert _{\infty }^{2-p}}\, \int _{\varOmega } \varphi '(e_j)|\nabla e_j|^2\,{\text {d}}x - \int _{\varOmega } D_sg(x,u_0)e_j \varphi (e_j) \,{\text {d}}x \le 0\,. \end{aligned}$$

Since $D_sg(x,u_0)\in L^{\infty }(\varOmega )$, it is standard (see, e.g., [35, 36]) that $e_j\in L^{\infty }(\varOmega )$, whence $V\subseteq X_{u_0}\cap L^{\infty }(\varOmega ) \subseteq W^{1,p}_0(\varOmega )$, as $p<2$.

If we set

$$\begin{aligned} \widetilde{W} = \left\{ w\in L^1(\varOmega ):\,\, \int _{\varOmega } vw\,{\text {d}}x = 0\quad \text {for any }v\in V\right\} \,, \end{aligned}$$

then $\widetilde{W}$ is a closed linear subspace of $L^1(\varOmega )$ and

$$\begin{aligned} L^1(\varOmega ) = V\oplus \widetilde{W}\,. \end{aligned}$$

Since

$$\begin{aligned} \begin{array}{ll} \int _{\varOmega } \underline{\varPsi }''(\nabla u_0)[\nabla u]^2\,{\text {d}}x - \int _{\varOmega } D_sg(x,u_0) u^2\,{\text {d}}x = Q_{u_0}(u) &{}\qquad \text {if }\;u\in X_{u_0}\,,\\ \int _{\varOmega } \underline{\varPsi }''(\nabla u_0)[\nabla u]^2\,{\text {d}}x - \int _{\varOmega } D_sg(x,u_0) u^2\,{\text {d}}x = +\infty &{}\qquad \text {if }\;u\in W^{1,2}_0(\varOmega ){\setminus } X_{u_0}\,, \end{array} \end{aligned}$$

the other assertions easily follow.

In the case $\kappa >0$, one has $X_{u_0}=W^{1,2}_0(\varOmega )$ and the adaptation of the previous argument is very simple if $1<p\le 2$. If $p>2$, one has to remark that $\varPsi ''(\nabla u_0)$ is continuous. By standard regularity results (see, e.g., [44, Theorem 7.6]) it follows that $e_j\in W^{1,p}_0(\varOmega )$, whence $V\subseteq W^{1,p}_0(\varOmega )$. $\square$

In the following, we consider a direct sum decomposition as in the previous proposition. In particular, the projection $\widetilde{P}_V:L^1(\varOmega )\rightarrow V$, associated with the direct sum decomposition, is continuous with respect to the $L^1$-topology. Since $V\subseteq W^{1,2}_0(\varOmega )\cap L^{\infty }(\varOmega )$ is finite dimensional, it is equivalent to consider the norm of $W^{1,2}_0(\varOmega )\cap L^{\infty }(\varOmega )$ on V.

Then, we set $W=\widetilde{W}\cap W^{1,p}_0(\varOmega )$, which is a closed linear subspace of $W^{1,p}_0(\varOmega )$, so that

$$\begin{aligned} W^{1,p}_0(\varOmega ) = V \oplus W \end{aligned}$$

and $P_V = \widetilde{P}_V\bigl |_{W^{1,p}_0}$ is $L^1$-continuous as well.

We also set, for any $r>0$,

$$\begin{aligned} B_r&=\left\{ u\in W^{1,p}_0(\varOmega ):\,\, \Vert \nabla u\Vert _p < r\right\} \,,\\ D_r&=\left\{ u\in W^{1,p}_0(\varOmega ):\,\, \Vert \nabla u\Vert _p\le r\right\} \,. \end{aligned}$$

Lemma 4.4

For any $M>0$, there exist $r,\delta >0$ such that, for every $u \in (u_0+D_r)\cap W^{1, \infty }(\varOmega )$ with $\Vert u\Vert _{\infty }+ \Vert \nabla u\Vert _{\infty } \le M$ and every $w \in \widetilde{W} \cap W^{1,2}_0(\varOmega )$, one has

$$\begin{aligned} \int _{\varOmega } \underline{\varPsi }''(\nabla u)[\nabla w]^2\,{\text {d}}x - \int _{\varOmega } D_sg(x,u) w^2\,{\text {d}}x \ge \delta \int _{\varOmega } |\nabla w|^2\,{\text {d}}x \,. \end{aligned}$$

Proof

Assume, for a contradiction, that there exist a sequence $(v_k)$ in $W^{1,p}_0(\varOmega )\cap W^{1,\infty }(\varOmega )$, strongly convergent to $u_0$ in $W^{1,p}_0(\varOmega )$ and bounded in $W^{1,\infty }(\varOmega )$, and a sequence $(w_k)$ in $\widetilde{W} \cap W^{1,2}_0(\varOmega )$ such that

$$\begin{aligned} \int _{\varOmega } \underline{\varPsi }''(\nabla v_k)[\nabla w_k]^2\,{\text {d}}x - \int _{\varOmega } D_sg(x,v_k) w_k^2\,{\text {d}}x < \frac{1}{k} \, \int _{\varOmega } |\nabla w_k|^2\,{\text {d}}x \,. \end{aligned}$$

(4.1)

Without loss of generality, we may assume that $\Vert \nabla w_k\Vert _2=1$. Then, up to a subsequence, $(w_k)$ is weakly convergent to some w in $W^{1,2}_0(\varOmega )$. In particular, $w\in \widetilde{W}$. From Theorem 4.2 we infer that

$$\begin{aligned} \int _{\varOmega } \underline{\varPsi }''(\nabla u_0)[\nabla w]^2\,{\text {d}}x - \int _{\varOmega } D_sg(x,u_0) w^2\,{\text {d}}x\le 0\,, \end{aligned}$$

whence $w=0$.

Coming back to (4.1), now we deduce that

$$\begin{aligned} \lim _k \int _{\varOmega } \underline{\varPsi }''(\nabla v_k)[\nabla w_k]^2\,{\text {d}}x =0\,. \end{aligned}$$

Since $(\nabla v_k)$ is bounded in $L^{\infty }(\varOmega )$, in both cases $\kappa =0$ with $1<p<2$ and $\kappa >0$ with $1<p<\infty$ we infer that $\nabla w_k\rightarrow 0$ in $L^2(\varOmega )$. Since $\Vert \nabla w_k\Vert _2=1$, a contradiction follows. $\square$

Theorem 4.5

There exist $M, r>0$ and $\beta \in ]0,1]$ such that:

(a):

the map $f'$ is of class $(S)_+$ on $u_0+D_{2r}$;

(b):

for every $v\in V\cap D_r$, the derivative of the functional

$$\begin{aligned} \begin{array}{ccc} W &{} \rightarrow &{} {\mathbb {R}}\\ w &{}\mapsto &{} f(u_0+v+w) \end{array} \end{aligned}$$

is of class $(S)_+$ on $W\cap D_r$; moreover, if w is a critical point of such a functional with $w\in D_r$, then $v+w\in C^{1,\beta }(\overline{\varOmega })$ and

$$\begin{aligned} \Vert v+w\Vert _{C^{1,\beta }} < M\,; \end{aligned}$$

finally, the functional $\left\{ w\mapsto f(u_0+v+w)\right\}$ is strictly convex on

$$\begin{aligned}&\bigl \{w\in W\cap D_r:\,\, (v+w)\in W^{1,\infty }(\varOmega ) \bigr . \\&\quad \bigl . \text {and }\Vert v+w\Vert _{\infty } + \Vert \nabla (v+w)\Vert _{\infty } \le M\bigr \}\,; \end{aligned}$$

(c):

$u_0$ is a strict local minimum of f along $u_0+W$ for the $W^{1,p}_0(\varOmega )$-topology.

Proof

As already observed in the proof of Theorem 3.6, there exists $r>0$ such that the map $f'$ is of class $(S)_+$ on $u_0+D_{2r}$. It follows that $\{w \mapsto f(u_0+v+w)\}$ is of class $(S)_+$ on $W\cap D_r$ for any $v\in V\cap D_r$. Moreover, if w is a critical point, we have

$$\begin{aligned} \langle f'(u_0+v+w),u-P_Vu\rangle = 0 \qquad \text {for any }u\in W^{1,p}_0(\varOmega )\,, \end{aligned}$$

whence

$$\begin{aligned} \langle f'(u_0+v+w),u\rangle = \langle f'(u_0+v+w),P_Vu\rangle \qquad \text {for any }u\in W^{1,p}_0(\varOmega )\,. \end{aligned}$$

Since $P_V$ is continuous from the topology of $L^1(\varOmega )$ to that of $W^{1,p}_0(\varOmega )$ and $f'$ is bounded on bounded sets, it follows that

$$\begin{aligned} \langle f'(u_0+v+w),P_Vu\rangle = \int _{\varOmega } z u\,{\text {d}}x \qquad \text {for any }u\in W^{1,p}_0(\varOmega ) \end{aligned}$$

with z uniformly bounded in $L^{\infty }(\varOmega )$ with respect to v and w, whence

$$\begin{aligned} \langle f'(u_0+v+w),u\rangle = \int _{\varOmega } z u\,{\text {d}}x \qquad \text {for any }u\in W^{1,p}_0(\varOmega )\,. \end{aligned}$$

From Theorems 3.1 and 3.2, possibly by decreasing r, we conclude that $u_0+v+w$, hence $v+w$, is uniformly bounded in $C^{1,\beta }(\overline{\varOmega })$.

Finally, again by decreasing r, we infer by Lemma 4.4 that

$$\begin{aligned} \int _{\varOmega } \underline{\varPsi }''(\nabla (u_0+u))[\nabla w]^2\,{\text {d}}x - \int _{\varOmega } D_sg(x,u_0+u) w^2\,{\text {d}}x \ge \delta \int _{\varOmega } |\nabla w|^2\,{\text {d}}x \end{aligned}$$

(4.2)

for every $u \in D_{2r}\cap W^{1, \infty }(\varOmega )$ with $\Vert u\Vert _{\infty }+ \Vert \nabla u\Vert _{\infty } \le M$ and every $w \in \widetilde{W} \cap W^{1,2}_0(\varOmega )$.

If $v\in V\cap D_r$, $t \in [0,1]$ and $w_0, w_1\in W\cap D_r$ with $(v+w_j)\in W^{1,\infty }(\varOmega )$ and

$$\begin{aligned} \Vert v+w_j\Vert _{\infty } + \Vert \nabla (v+w_j)\Vert _{\infty } \le M\,, \end{aligned}$$

we have $w_j\in W^{1,p}_0(\varOmega )\cap W^{1,2}(\varOmega )$, hence $w_j \in W^{1,2}_0(\varOmega )$, as $\partial \varOmega$ is smooth enough. By Proposition 4.1 and (4.2) we easily deduce that

$$\begin{aligned}&(1-t)f(u_0+v+w_0)+t f(u_0+v+w_1) \\&\quad \ge f(u_0+v+(1-t)w_0+tw_1) + \dfrac{\delta }{2}\,t(1-t)\, \int _{\varOmega } |\nabla w_1-\nabla w_0|^2\,{\text {d}}x\,. \end{aligned}$$

Therefore, $\left\{ w\mapsto f(u_0+v+w)\right\}$ is strictly convex.

In particular, the critical point $u_0$ is a strict local minimum of f along $u_0+(W\cap C^1(\overline{\varOmega }))$ for the $C^1(\overline{\varOmega })$-topology. From Theorem 3.6 we infer that $u_0$ is a strict local minimum of f along $u_0+W$ for the $W^{1,p}_0(\varOmega )$-topology. $\square$

Theorem 4.6

There exist $M, r>0$, $\beta \in ]0,1]$ and $\varrho \in ]0,r]$ such that, for every $v \in V\cap D_{\varrho }$, there exists one and only one $\overline{w} \in W \cap D_r$ such that

$$\begin{aligned} f(u_0 + v + \overline{w})\le f(u_0 + v + w) \qquad \text {for any }w \in W \cap D_r\,. \end{aligned}$$

Moreover, $v + \overline{w} \in C^{1,\beta }(\overline{\varOmega })$ with $\Vert v + \overline{w}\Vert _{C^{1,\beta }}\le M$, $\overline{w}\in B_r$ and $\overline{w}$ is the unique critical point of $\{w\mapsto f(u_0+v+w)\}$ in $W\cap D_r$.

Finally, if we set $\psi (v)=\overline{w}$, the map

$$\begin{aligned} \left\{ v\mapsto v+\psi (v)\right\} \end{aligned}$$

is continuous from $V\cap D_{\varrho }$ into $C^1(\overline{\varOmega })$, while the map $\psi$ is continuous from $V\cap D_{\varrho }$ into $W^{1,p}_0(\varOmega )\cap L^{\infty }(\varOmega )$. Moreover, $\psi (0)=0$.

In the case $\kappa >0$, the map $\psi$ is also of class $C^1$ from $V\cap B_{\varrho }$ into $W^{1,2}_0(\varOmega )$ and, for every $z\in V\cap B_{\varrho }$ and $v\in V$, we have that $\psi '(z)v$ is the minimum point of the functional

$$\begin{aligned} \biggl \{w\mapsto \dfrac{1}{2}\, \int _{\varOmega } \left\{ \varPsi ''(\nabla u)[\nabla w]^2 - D_sg(x,u) w^2\right\} \,{\text {d}}x \biggr . \\ \biggl . + \int _{\varOmega } \left\{ \varPsi ''(\nabla u)[\nabla v,\nabla w] - D_sg(x,u) v w\right\} \,{\text {d}}x \biggr \} \end{aligned}$$

on $\widetilde{W}\cap W^{1,2}_0(\varOmega )$, where $u=u_0+z+\psi (z)$. Moreover, $\psi '(0)=0$.

Proof

Let $M, r>0$ and $\beta \in ]0,1]$ be as in Theorem 4.5. In particular, we may suppose that $f(u_0)<f(u_0+w)$ for every $w\in W\cap D_r$ with $w\ne 0$. By Lemma 4.4 we may also assume that there exists $\delta >0$ such that

$$\begin{aligned} \int _{\varOmega } \underline{\varPsi }''(\nabla (u_0+u))[\nabla w]^2\,{\text {d}}x - \int _{\varOmega } D_sg(x,u_0+u) w^2\,{\text {d}}x \ge \delta \int _{\varOmega } |\nabla w|^2\,{\text {d}}x \end{aligned}$$

(4.3)

for every $u \in D_{2r}\cap C^{1,\beta }(\overline{\varOmega })$ with $\Vert u\Vert _{C^{1,\beta }} \le M$ and every $w \in \widetilde{W} \cap W^{1,2}_0(\varOmega )$.

We claim that there exists $\varrho \in ]0,r]$ such that

$$\begin{aligned} f(u_0+v)<f(u_0+v+w) \qquad \text {for any }v\in V\cap D_{\varrho }\, \text {and any }w\in W\text { with }\Vert \nabla w\Vert _p = r. \end{aligned}$$

By contradiction, let $(v_k)$ be a sequence in V with $v_k\rightarrow 0$ and let $(w_k)$ be a sequence in W with $\Vert \nabla w_k\Vert _p = r$ and $f(u_0+v_k)\ge f(u_0+v_k+w_k)$. Up to a subsequence, $(w_k)$ is weakly convergent to some $w\in W\cap D_r$. Then $(u_0+v_k+w_k)$ is weakly convergent to $u_0+w$ with

$$\begin{aligned} \limsup _k f(u_0+v_k+w_k) \le \lim _k f(u_0+v_k) = f(u_0) \le f(u_0+w)\,. \end{aligned}$$

Combining Proposition 3.5 with Theorem 4.5, we deduce that $(u_0+v_k+w_k)$ is strongly convergent to $u_0+w$, whence $f(u_0+w)=f(u_0)$ with $\Vert \nabla w\Vert _p = r$, and a contradiction follows.

Again from Proposition 3.5 and Theorem 4.5 we know that $\{w\mapsto f(u_0+v+w)\}$ is weakly lower semicontinuous on $W\cap D_r$ for any $v\in V\cap D_{\varrho }$. Therefore, there exists a minimum point $\overline{w}\in W\cap D_r$ and in fact $\overline{w} \in B_r$. In particular, we have

$$\begin{aligned} \langle f'(u_0 + v + \overline{w}),w\rangle = 0 \qquad \text {for any }w\in W\,. \end{aligned}$$

From Theorem 4.5 we infer that $v + \overline{w} \in C^{1,\beta }(\overline{\varOmega })$ with $\Vert v + \overline{w}\Vert _{C^{1,\beta }}\le M$. Since $\left\{ w\mapsto f(u_0+v+w)\right\}$ is strictly convex on

$$\begin{aligned} \left\{ w\in W\cap D_r:\,\, (v+w)\in W^{1,\infty }(\varOmega ) \text { and }\Vert v+w\Vert _{\infty } + \Vert \nabla (v+w)\Vert _{\infty } \le M\right\} \,, \end{aligned}$$

the minimum is unique. If $v=0$, then $\overline{w}=0$.

Finally, if we set $\psi (v)=\overline{w}$, the map $\left\{ v\mapsto v+\psi (v)\right\}$ is defined from $V\cap D_{\varrho }$ into

$$\begin{aligned} \left\{ u\in C^{1,\beta }(\overline{\varOmega }):\,\, \Vert u\Vert _{C^{1,\beta }}\le M\right\} \,, \end{aligned}$$

which is a compact subset of $C^1(\overline{\varOmega })$, and has closed graph, as f is continuous. Therefore, it is a continuous map. The continuity of $\psi$ follows.

In the case $\kappa >0$, the function $\varPsi$ is of class $C^2$ on ${\mathbb {R}}^N$. Therefore, there exists $C>0$ such that

$$\begin{aligned}&\left| \int _{\varOmega } \varPsi ''(\nabla (u_0+u)) [\nabla u_1,\nabla u_2]\,{\text {d}}x \right. \nonumber \\&\quad \left. - \int _{\varOmega } D_sg(x,u_0+u) u_1 u_2\,{\text {d}}x\right| \le C \,\Vert \nabla u_1\Vert _2 \,\Vert \nabla u_2\Vert _2 \end{aligned}$$

(4.4)

for every $u \in D_{2r}\cap C^{1,\beta }(\overline{\varOmega })$ with $\Vert u\Vert _{C^{1,\beta }} \le M$ and every $u_1, u_2 \in W^{1,2}_0(\varOmega )$. Moreover, we have

$$\begin{aligned}&\langle f'(u_0+v_1+\psi (v_1)),u\rangle - \langle f'(u_0+v_0+\psi (v_0)),u\rangle \nonumber \\&\quad = \int _0^1 \int _{\varOmega } \biggl \{\varPsi ''(\nabla \gamma _t) [\nabla (v_1-v_0+\psi (v_1)-\psi (v_0)),\nabla u] \biggr . \nonumber \\&\qquad -\, \biggl . D_sg(x,\gamma _t) (v_1-v_0+\psi (v_1)-\psi (v_0)) u\biggr \}\,{\text {d}}x\,{\text {d}}t \end{aligned}$$

(4.5)

for any $v_0, v_1\in V\cap D_{\varrho }$ and $u\in W^{1,2}_0(\varOmega )$, where

$$\begin{aligned} \gamma _t=u_0+v_0+\psi (v_0)+t(v_1-v_0+\psi (v_1)-\psi (v_0))\,. \end{aligned}$$

Now let $z\in V\cap B_{\varrho }$ and let $u=u_0+z+\psi (z)$. From (4.3) and (4.4) it follows that, for every $v\in V$, the functional

$$\begin{aligned}&\biggl \{w\mapsto \dfrac{1}{2}\, \int _{\varOmega } \left\{ \varPsi ''(\nabla u)[\nabla w]^2 - D_sg(x,u) w^2\right\} \,{\text {d}}x \biggr . \\&\quad \biggl . + \int _{\varOmega } \left\{ \varPsi ''(\nabla u)[\nabla v,\nabla w] - D_sg(x,u) v w\right\} \,{\text {d}}x \biggr \} \end{aligned}$$

admits one and only one minimum point $L_zv$ in $\widetilde{W}\cap W^{1,2}_0(\varOmega )$, which satisfies

$$\begin{aligned}&\int _{\varOmega } \left\{ \varPsi ''(\nabla u)[\nabla (L_zv),\nabla w] - D_sg(x,u) (L_zv) w\right\} \,{\text {d}}x \nonumber \\&\quad = - \int _{\varOmega } \left\{ \varPsi ''(\nabla u)[\nabla v,\nabla w] - D_sg(x,u) v w\right\} \,{\text {d}}x \quad \text {for any }w\in \widetilde{W}\cap W^{1,2}_0(\varOmega )\,. \end{aligned}$$

(4.6)

Moreover, the map $L_z:V\rightarrow W^{1,2}_0(\varOmega )$ is linear and continuous, as V is finite dimensional. Since $Q_{u_0}(v+w)=Q_{u_0}(v)+Q_{u_0}(w)$ for any $v\in V$ and $w\in \widetilde{W}\cap W^{1,2}_0(\varOmega )$, we also have $L_0=0$.

By (4.5), for every $v_0, v_1\in V\cap B_{\varrho }$ and $w\in \widetilde{W}\cap W^{1,2}_0(\varOmega )$, it holds

$$\begin{aligned} 0&= \langle f'(u_0+v_1+\psi (v_1)),w\rangle - \langle f'(u_0+v_0+\psi (v_0)),w\rangle \\&= \int _0^1 \int _{\varOmega } \biggl \{\varPsi ''(\nabla \gamma _t) [\nabla (v_1-v_0+\psi (v_1)-\psi (v_0)),\nabla w] \biggr . \\&\quad - \biggl . D_sg(x,\gamma _t) (v_1-v_0+\psi (v_1)-\psi (v_0)) w\biggr \}\,{\text {d}}x\,{\text {d}}t\,. \end{aligned}$$

Taking into account (4.6), we deduce that

$$\begin{aligned} \begin{aligned}&\int _0^1 \int _{\varOmega } \biggl \{ \varPsi ''(\nabla \gamma _t) [\nabla (\psi (v_1)-\psi (v_0)),\nabla w] - D_sg(x,\gamma _t) (\psi (v_1)-\psi (v_0)) w \biggr \}\,{\text {d}}x\,{\text {d}}t \\&\quad - \int _{\varOmega } \biggl \{\varPsi ''(\nabla u)[\nabla (L_z(v_1-v_0)),\nabla w] - D_sg(x,u) (L_z(v_1-v_0)) w\biggr \}\,{\text {d}}x \\&\quad = - \int _0^1 \int _{\varOmega } \biggl \{ \left[ \varPsi ''(\nabla \gamma _t) - \varPsi ''(\nabla u)\right] [\nabla (v_1-v_0),\nabla w] \\&\qquad -\, \left[ D_sg(x,\gamma _t) - D_sg(x,u)\right] (v_1-v_0) w\biggr \} \,{\text {d}}x\,{\text {d}}t\,. \end{aligned} \end{aligned}$$

It follows

$$\begin{aligned} \begin{aligned}&\int _0^1 \int _{\varOmega } \biggl \{ \varPsi ''(\nabla \gamma _t) [\nabla (\psi (v_1)-\psi (v_0)-L_z(v_1-v_0)),\nabla w] \\&\quad - D_sg(x,\gamma _t) (\psi (v_1)-\psi (v_0)-L_z(v_1-v_0)) w \biggr \}\,{\text {d}}x\,{\text {d}}t \\&\quad = - \int _0^1 \int _{\varOmega }\biggl \{ \left[ \varPsi ''(\nabla \gamma _t) - \varPsi ''(\nabla u)\right] [\nabla (L_z(v_1-v_0)),\nabla w] \\&\qquad -\, \left[ D_sg(x,\gamma _t) - D_sg(x,u)\right] (L_z(v_1-v_0)) w\biggr \}\,{\text {d}}x\,{\text {d}}t \\&\qquad -\, \int _0^1 \int _{\varOmega } \biggl \{ \left[ \varPsi ''(\nabla \gamma _t) - \varPsi ''(\nabla u)\right] [\nabla (v_1-v_0),\nabla w] \\&\qquad -\, \left[ D_sg(x,\gamma _t) - D_sg(x,u)\right] (v_1-v_0) w\biggr \}\,{\text {d}}x\,{\text {d}}t \,. \end{aligned} \end{aligned}$$

Since the map $\left\{ v\mapsto v+\psi (v)\right\}$ is continuous from $V\cap B_{\varrho }$ into $C^1(\overline{\varOmega })$, from (4.3) we infer that

$$\begin{aligned} \lim _{\begin{array}{c} (v_0,v_1)\rightarrow (z,z)\\ v_0\ne v_1 \end{array}}\, \dfrac{\Vert \nabla (\psi (v_1)-\psi (v_0)-L_z(v_1-v_0))\Vert _2}{ \Vert \nabla (v_1-v_0)\Vert _2} = 0\,. \end{aligned}$$

Therefore, $\psi$ is of class $C^1$ from $V\cap B_{\varrho }$ into $W^{1,2}_0(\varOmega )$ and $\psi '(z) = L_z$. $\square$

5 The finite-dimensional reduction

Throughout this section we keep the assumptions and the notations of Sect. 4. We also define the reduced functional $\varphi :V\cap B_{\varrho }\rightarrow {\mathbb {R}}$ as

$$\begin{aligned} \varphi (v) = f(u_0+v+\psi (v)) =\min \left\{ f(u_0+v+w):\,\,w\in W\cap D_r\right\} \,. \end{aligned}$$

Theorem 5.1

Let $\kappa >0$ with $1<p<\infty$ or $\kappa =0$ with $1<p<2$. Then the functional $\varphi$ is of class $C^1$ and

$$\begin{aligned} \langle \varphi '(z),v\rangle = \langle f'(u_0+z+\psi (z)),v\rangle \qquad \text {for any }z\in V\cap B_{\varrho }\text { and }v\in V\,. \end{aligned}$$

(5.1)

In particular, 0 is a critical point of $\varphi$. Moreover, we have

$$\begin{aligned} C_m(\varphi ,0) \approx C_m(f,u_0) \qquad \text {for any }m \ge 0\,. \end{aligned}$$

Finally, 0 is an isolated critical point of $\varphi$ if and only if $u_0$ is an isolated critical point of f.

Proof

For any $v_0, v_1\in V\cap B_{\varrho }$, we have

$$\begin{aligned} \varphi (v_1)&= f(u_0+v_1+\psi (v_1)) \\&= f(u_0+v_0+\psi (v_1)) + \langle f'(u_0+v_0+t(v_1-v_0)+\psi (v_1)),v_1-v_0\rangle \\&\ge f(u_0+v_0+\psi (v_0)) + \langle f'(u_0+v_0+t(v_1-v_0)+\psi (v_1)),v_1-v_0\rangle \\&= \varphi (v_0) + \langle f'(u_0+v_0+t(v_1-v_0)+\psi (v_1)),v_1-v_0\rangle \end{aligned}$$

for some $t\in ]0,1[$. Since $\psi$ is continuous from $V\cap B_{\varrho }$ into $W^{1,p}_0(\varOmega )$, it follows that

$$\begin{aligned} \liminf _{\begin{array}{c} (v_0,v_1)\rightarrow (z,z)\\ v_0\ne v_1 \end{array}}\, \dfrac{\varphi (v_1)-\varphi (v_0)- \langle f'(u_0+z+\psi (z)),v_1-v_0\rangle }{\Vert v_1-v_0\Vert } \ge 0\,. \end{aligned}$$

We also have

$$\begin{aligned} \varphi (v_1)&= f(u_0+v_1+\psi (v_1)) \le f(u_0+v_1+\psi (v_0)) \\&= f(u_0+v_0+\psi (v_0)) + \langle f'(u_0+v_0+t(v_1-v_0)+\psi (v_0)),v_1-v_0\rangle \\&= \varphi (v_0) + \langle f'(u_0+v_0+t(v_1-v_0)+\psi (v_0)),v_1-v_0\rangle \end{aligned}$$

for some $t\in ]0,1[$, whence

$$\begin{aligned} \limsup _{\begin{array}{c} (v_0,v_1)\rightarrow (z,z)\\ v_0\ne v_1 \end{array}}\, \dfrac{\varphi (v_1)-\varphi (v_0)- \langle f'(u_0+z+\psi (z)),v_1-v_0\rangle }{\Vert v_1-v_0\Vert } \le 0\,. \end{aligned}$$

Therefore, $\varphi$ is of class $C^1$ with

$$\begin{aligned} \langle \varphi '(z),v\rangle = \langle f'(u_0+z+\psi (z)),v\rangle \,. \end{aligned}$$

Since $\psi (0)=0$, we also have $\varphi '(0)=0$.

Now consider

$$\begin{aligned} Y = \left\{ u_0+ z + \psi (z):\,\, z \in V \cap B_{\varrho } \right\} \end{aligned}$$

endowed with the $W^{1,p}_0(\varOmega )$-topology. Since $\left\{ z\mapsto u_0+ z + \psi (z)\right\}$ is a homeomorphism from $V \cap B_{\varrho }$ onto Y which sends 0 into $u_0$, it is clear that

$$\begin{aligned} C_m(\varphi ,0) \approx C_m(f\bigl |_Y,u_0) \qquad \text {for any }m \ge 0\,. \end{aligned}$$

On the other hand, from Proposition 3.5 and Theorem 4.5 we see that the functional $\left\{ w\mapsto f(u_0+v+w)\right\}$ satisfies the Palais–Smale condition over $W\cap D_r$ for any $v\in V\cap B_{\varrho }$. Moreover, $\psi (v)$ is the unique critical point, in fact the minimum, of such a functional in $W\cap D_r$. Arguing as in the Second Deformation Lemma, it is possible to define a deformation

$$\begin{aligned} \mathcal {H}: \left( u_0+(V\cap B_{\varrho })+(W\cap D_r)\right) \times [0,1] \rightarrow \left( u_0+(V\cap B_{\varrho })+(W\cap D_r)\right) \end{aligned}$$

such that

$$\begin{aligned}&\mathcal {H}(u,t) - u \in W\,,\qquad f(\mathcal {H}(u,t)) \le f(u)\,,\\&\mathcal {H}(u,1) \in Y\,,\qquad \mathcal {H}(u,t)=u \qquad \text {if }u\in Y\,, \end{aligned}$$

whence

$$\begin{aligned} H^m(f^c,f^c{\setminus }\{u_0\}) \approx H^m(f^c\cap Y,(f^c\cap Y){\setminus }\{u_0\})\,. \end{aligned}$$

This is proved in [16, Theorem 5.4] in the case $p>2$, but the argument works also for $1<p\le 2$. See also [37, Theorem 4.7] in a nonsmooth setting.

Therefore, we have

$$\begin{aligned} C_m(\varphi ,0) \approx C_m(f\bigl |_Y,u_0) \approx C_m(f,u_0) \qquad \text {for any }m \ge 0\,. \end{aligned}$$

Since any critical point u of f in $u_0+(V\cap B_{\varrho })+(W\cap D_r)$ must be of the form $u=u_0+z+\psi (z)$ with $z\in V\cap B_{\varrho }$, from (5.1) we infer that 0 is isolated for $\varphi$ if and only if $u_0$ is isolated for f. $\square$

Theorem 5.2

Let $\kappa >0$ with $1<p<\infty$. Then, $\varphi$ is of class $C^2$ and

$$\begin{aligned} \varphi ''(z)[v]^2&= \int _{\varOmega }\biggl \{\varPsi ''(\nabla u)[\nabla (v+\psi '(z)v)]^2 - D_sg(x,u)(v+\psi '(z)v)^2\biggr \}\,{\text {d}}x \nonumber \\&\quad = \int _{\varOmega }\biggl \{\varPsi ''(\nabla u)[\nabla v]^2 - D_sg(x,u)v^2\biggr \}\,{\text {d}}x \nonumber \\&\qquad - \int _{\varOmega }\biggl \{\varPsi ''(\nabla u)[\nabla (\psi '(z)v)]^2 - D_sg(x,u)(\psi '(z)v)^2\biggr \}\,{\text {d}}x \nonumber \\&\qquad \text {for any }z\in V\cap B_{\varrho }\text { and }v\in V, \text {where }u=u_0+z+\psi (z)\,. \end{aligned}$$

(5.2)

In particular, we have

$$\begin{aligned} \varphi ''(0)[v]^2 = \int _{\varOmega }\biggl \{\varPsi ''(\nabla u_0)[\nabla v]^2 - D_sg(x,u_0)v^2\biggr \}\,{\text {d}}x \qquad \text {for any }v\in V\,. \end{aligned}$$

Proof

By Theorem 4.6, the map $\psi$ is of class $C^1$ from $V\cap B_{\varrho }$ into $W^{1,2}_0(\varOmega )$ with $\psi (0)=0$ and $\psi '(0)=0$. For any $z\in V\cap B_{\varrho }$, let $L_z:V \rightarrow V'$ be the linear map defined by

$$\begin{aligned} \langle L_zv_1,v_2\rangle&= \int _{\varOmega } \biggl \{\varPsi ''(\nabla u) [\nabla v_1,\nabla v_2] - D_sg(x,u) v_1 v_2\biggr \}\,{\text {d}}x\nonumber \\&\quad + \int _{\varOmega } \biggl \{\varPsi ''(\nabla u) [\nabla (\psi '(z)v_1),\nabla v_2] - D_sg(x,u) (\psi '(z)v_1) v_2\biggr \}\,{\text {d}}x \,, \end{aligned}$$

(5.3)

where $u=u_0+z+\psi (z)$. By (4.5), for every $v_0, v_1\in V\cap B_{\varrho }$ and $v\in V$, we have

$$\begin{aligned} \langle \varphi '(v_1),v\rangle - \langle \varphi '(v_0),v\rangle&= \langle f'(u_0+v_1+\psi (v_1)),v\rangle - \langle f'(u_0+v_0+\psi (v_0)),v\rangle \\&= \int _0^1 \int _{\varOmega } \biggl \{\varPsi ''(\nabla \gamma _t) [\nabla (v_1-v_0+\psi (v_1)-\psi (v_0)),\nabla v] \biggr . \\&\quad - \biggl . D_sg(x,\gamma _t) (v_1-v_0+\psi (v_1)-\psi (v_0)) v\biggr \}\,{\text {d}}x\,{\text {d}}t\,, \end{aligned}$$

where $\gamma _t=u_0+v_0+\psi (v_0)+t(v_1-v_0+\psi (v_1)-\psi (v_0))$. Taking into account (5.3), we deduce that

$$\begin{aligned} \begin{aligned}&\langle \varphi '(v_1),v\rangle - \langle \varphi '(v_0),v\rangle - \langle L_z(v_1-v_0),v\rangle \\&\quad = \int _0^1 \int _{\varOmega } \biggl \{\varPsi ''(\nabla \gamma _t) [\nabla (v_1-v_0+\psi (v_1)-\psi (v_0)),\nabla v] \biggr . \\&\qquad -\, \biggl . D_sg(x,\gamma _t) (v_1-v_0+\psi (v_1)-\psi (v_0)) v\biggr \}\,{\text {d}}x\,{\text {d}}t \\&\qquad -\, \int _{\varOmega } \biggl \{\varPsi ''(\nabla u) [\nabla (v_1-v_0),\nabla v] - D_sg(x,u) (v_1-v_0) v\biggr \}\,{\text {d}}x \\&\qquad -\, \int _{\varOmega } \biggl \{\varPsi ''(\nabla u) [\nabla (\psi '(z)(v_1-v_0)),\nabla v] - D_sg(x,u) (\psi '(z)(v_1-v_0)) v\biggr \}\,{\text {d}}x \,. \end{aligned} \end{aligned}$$

It follows

$$\begin{aligned} \begin{aligned}&\langle \varphi '(v_1),v\rangle - \langle \varphi '(v_0),v\rangle - \langle L_z(v_1-v_0),v\rangle \\&\quad = \int _0^1 \int _{\varOmega } \biggl \{ \left[ \varPsi ''(\nabla \gamma _t) - \varPsi ''(u)\right] [\nabla (v_1-v_0),\nabla v] \biggr . \\&\qquad -\, \biggl . \left[ D_sg(x,\gamma _t) - D_sg(x,u)\right] (v_1-v_0) v\biggr \}\,{\text {d}}x\,{\text {d}}t \\&\qquad +\, \int _0^1 \int _{\varOmega } \biggl \{\varPsi ''(\nabla \gamma _t) [\nabla (\psi (v_1)-\psi (v_0)-\psi '(z)(v_1-v_0)),\nabla v] \biggr . \\&\qquad -\, \biggl . D_sg(x,\gamma _t) (\psi (v_1)-\psi (v_0)-\psi '(z)(v_1-v_0)) v \biggr \}\,{\text {d}}x\,{\text {d}}t \\&\qquad +\, \int _0^1 \int _{\varOmega } \biggl \{ \left[ \varPsi ''(\nabla \gamma _t) - \varPsi ''(u)\right] [\nabla (\psi '(z)(v_1-v_0)),\nabla v] \biggr . \\&\qquad -\, \biggl . \left[ D_sg(x,\gamma _t) - D_sg(x,u)\right] (\psi '(z)(v_1-v_0)) v \biggr \}\,{\text {d}}x\,{\text {d}}t \,. \end{aligned} \end{aligned}$$

Since the map $\left\{ v\mapsto v+\psi (v)\right\}$ is continuous from $V\cap B_{\varrho }$ into $C^1(\overline{\varOmega })$, we infer that

$$\begin{aligned} \lim _{\begin{array}{c} (v_0,v_1)\rightarrow (z,z)\\ v_0\ne v_1 \end{array}}\, \dfrac{\langle \varphi '(v_1),v\rangle - \langle \varphi '(v_0),v\rangle - \langle L_z(v_1-v_0),v\rangle }{ \Vert \nabla (v_1-v_0)\Vert _2} = 0 \qquad \text {for any }v\in V\,. \end{aligned}$$

Therefore, $\varphi$ is of class $C^2$ and

$$\begin{aligned} \varphi ''(z)[v_1,v_2] =&\int _{\varOmega } \biggl \{\varPsi ''(\nabla u) [\nabla v_1,\nabla v_2] - D_sg(x,u) v_1 v_2\biggr \}\,{\text {d}}x \\&+ \int _{\varOmega } \biggl \{\varPsi ''(\nabla u) [\nabla (\psi '(z)v_1),\nabla v_2)] - D_sg(x,u) (\psi '(z)v_1) v_2\biggr \}\,{\text {d}}x. \end{aligned}$$

By Theorem 4.6, we also have

$$\begin{aligned}&\int _{\varOmega } \left\{ \varPsi ''(\nabla u)[\nabla (\psi '(z)v),\nabla w] - D_sg(x,u) (\psi '(z)v) w \right\} \,{\text {d}}x \\&\quad = - \int _{\varOmega } \left\{ \varPsi ''(\nabla u)[\nabla v,\nabla w] - D_sg(x,u) v w \right\} \,{\text {d}}x \\&\qquad \text {for any }v\in V\text { and } w\in \widetilde{W}\cap W^{1,2}_0(\varOmega ), \end{aligned}$$

whence (5.2).

Since $\psi (0)=0$ and $\psi '(0)=0$, the formula for $\varphi ''(0)$ follows. $\square$

6 Proof of the results of Sect. 2

Proof of Theorems 2.6, 2.7, 2.2, 2.3 and 2.4

From Theorem 5.1 we know that

$$\begin{aligned} C_m(f,u_0) \approx C_m(\varphi ,0) \qquad \text {for any }m \ge 0\,. \end{aligned}$$

Since the critical groups are defined using Alexander–Spanier cohomology, it is clear that $C_m(\varphi ,0)=\{0\}$ whenever $m > \dim V = m^*(f,u_0)$, both in the case $\kappa >0$ with $1<p<\infty$ and in the case $\kappa =0$ with $1<p<2$.

In the particular case $u_0=0$ with $\kappa =0$ and $1<p<2$, we clearly have $Z_{u_0}=\varOmega$ and $X_{u_0}=\{0\}$, whence $m(f,0)=m^*(f,0)=0$, $V=\{0\}$ and $W=W^{1,p}_0(\varOmega )$. From Theorem 4.6 it follows that 0 is a strict local minimum and an isolated critical point of f. By the excision property, it follows

$$\begin{aligned} C_m(f,0) \approx H^m \left( \{0\},\emptyset \right) , \end{aligned}$$

whence

$$\begin{aligned} \left\{ \begin{array}{ll} C_m(f,0) \approx {\mathbb {G}}\quad &{}\text {if }\,m = 0,\\ C_m(f, 0) = \{0\} \quad &{}\text {if }\,m \ne 0. \end{array} \right. \end{aligned}$$

Now assume that $\kappa >0$ with $1<p<\infty$. From Theorem 5.2 and Proposition 4.3 we infer that $\varphi$ is of class $C^2$ with

$$\begin{aligned} \varphi ''(0)[v]^2 = Q_{u_0}(v) \le 0 \qquad \text {for any }v\in V. \end{aligned}$$

Let $V_-$ be a subspace of $X_{u_0}=W^{1,2}_0(\varOmega )$ of dimension $m(f,u_0)$ such that $Q_{u_0}$ is negative definite on $V_-$. Then it is easily seen that $Q_{u_0}$ is negative definite also on $P_V(V_-)$, which has the same dimension of $V_-$. Therefore, we may assume, without loss of generality, that $V_- \subseteq V$ and we have

$$\begin{aligned} \varphi ''(0)[v]^2 = Q_{u_0}(v) < 0 \qquad \text {for any }v\in V_-{\setminus } \{0\}. \end{aligned}$$

It follows (see, e.g., [37, Theorem 3.1]) that $C_m(\varphi ,0)=\{0\}$ whenever $m<\dim V_-=m(f,u_0)$. The proof of Theorems 2.6, 2.7 and 2.2 is complete.

If $m(f,u_0)=m^*(f,u_0)$, we have $V_-=V$. Then 0 is a nondegenerate critical point of $\varphi$ with Morse index $\dim V=m(f,u_0)$. It follows that 0 is an isolated critical point of $\varphi$ and

$$\begin{aligned} C_m(f,u_0) \approx C_m(\varphi ,0) \approx \delta _{m, m(f,u_0)} {\mathbb {G}}. \end{aligned}$$

Moreover, $u_0$ is an isolated critical point of f by Theorem 5.1 and hence Theorem 2.3 follows.

Finally, assume that $u_0$ is an isolated critical point of f with $m(f,u_0)<m^*(f,u_0)$. By Theorem 5.1 we infer that 0 is an isolated critical point of $\varphi$ and Theorem 2.4 follows from [42, Corollary 8.4]. $\square$

Proof of Theorem 2.8

By Theorem 2.2, Remark 2.5 and Theorem 2.7, we have only to treat the case $\kappa =0$ with $p > 2$, so that

$$\begin{aligned} Q_{u_0}(v) = Q_0(v) = - \int _\varOmega g'(0)v^2\,{\text {d}}x \qquad \forall v\in W^{1,2}_0(\varOmega ). \end{aligned}$$

If $g'(0)=0$, we have $m(f,0)=0$, $m^*(f,0)=+\infty$ and the assertion is obvious.

If $g'(0)<0$, we have $m(f,0)=m^*(f,0)=0$. On the other hand, it is easily seen that

$$\begin{aligned} f:W^{1,p}_0(\varOmega )\cap C^1(\overline{\varOmega })\rightarrow {\mathbb {R}}\end{aligned}$$

is strictly convex in a neighborhood of 0 for the $C^1(\overline{\varOmega })$-topology. In particular, 0 is a strict local minimum for the $C^1(\overline{\varOmega })$-topology. From Theorem 3.6 we infer that 0 is a strict local minimum of

$$\begin{aligned} f:W^{1,p}_0(\varOmega )\rightarrow {\mathbb {R}}\end{aligned}$$

for the $W^{1,p}_0(\varOmega )$-topology. By the excision property we have

$$\begin{aligned} C_m(f,0) \approx H^m \left( \{0\},\emptyset \right) \end{aligned}$$

and the assertion follows.

If $g'(0)>0$, we have $m(f,0)=m^*(f,0)=+\infty$. If $p>N$, the functional f is of class $C^2$ on $W^{1,p}_0(\varOmega )$ with

$$\begin{aligned} f''(0)(v)^2 = - \int _\varOmega g'(0)v^2\,{\text {d}}x \qquad \forall v\in W^{1,p}_0(\varOmega ). \end{aligned}$$

From [37, Theorem 3.1] we infer that $C_m(f,0)=\{0\}$ for any m and the assertion follows.

If $p\le N$, recall that

$$\begin{aligned} |g(s)| \le C( 1+ |s|^{q}) \end{aligned}$$

with $q<p^*-1$ if $p<N$, and consider a $C^\infty$-function $\vartheta :{\mathbb {R}}\rightarrow [0,1]$ with $\vartheta (s)=1$ for $|s|\le 1$ and $\vartheta (s)=0$ for $|s|\ge 2$. Then define, for every $t\in [0,1]$, a $C^1$-functional $f_t:W^{1,p}_0(\varOmega )\rightarrow {\mathbb {R}}$ as

$$\begin{aligned} f_t(u) = \int _{\varOmega } \varPsi (\nabla u)\,{\text {d}}x - \int _{\varOmega } G_t(u)\,{\text {d}}x, \end{aligned}$$

where

$$\begin{aligned} g_t(s) = g(\vartheta (ts)s),\qquad G_t(s) = \int _0^s g_t(\sigma )\,d\sigma . \end{aligned}$$

For any $t\in ]0,1]$ the functional $f_t$ is of class $C^2$ with

$$\begin{aligned} f_t''(0)(v)^2 = - \int _\varOmega g'(0)v^2\,{\text {d}}x \qquad \forall v\in W^{1,p}_0(\varOmega ). \end{aligned}$$

Again from [37, Theorem 3.1] we infer that $C_m(f_t,0)=\{0\}$ for any $t\in ]0,1]$ and any m.

Let $r>0$ be such that 0 is the unique critical point of $f_0=f$ in

$$\begin{aligned} D_r =\left\{ u\in W^{1,p}_0(\varOmega ):\,\, \Vert \nabla u\Vert _p\le r\right\} \end{aligned}$$

and such that the assertion of Theorem 3.1 holds for

$$\begin{aligned} \hat{g}(s) = C|s|^{q-1}s. \end{aligned}$$

Then the map $\left\{ t\mapsto f_t\right\}$ is continuous from [0, 1] into $C^1(D_r)$. Moreover from [3, Theorem 3.5] we infer that $f_t'$ is of class $(S)_+$, so that $f_t$ satisfies the Palais–Smale condition over $D_r$, for any $t\in [0,1]$.

We claim that there exists $\overline{t}\in ]0,1]$ such that 0 is the unique critical point of $f_t$ in $D_r$ whenever $0\le t\le \overline{t}$. Assume, for a contradiction, that $t_k\rightarrow 0$ and $u_k\in D_r{\setminus }\{0\}$ is a critical point of $f_{t_k}$. Then, for every $v\in W^{1,p}_0(\varOmega )$ with $v u_k\ge 0$, we have

$$\begin{aligned} \begin{aligned} \int _\varOmega \nabla \varPsi (\nabla u_k)\cdot \nabla v\,{\text {d}}x&= \int _\varOmega g_{t_k}(u_k)v\,{\text {d}}x\\&\le \int _{\{u_k\ne 0\}} |g(\vartheta (t_ku_k)u_k)|\,|v|\,{\text {d}}x\\&= \int _{\{u_k\ne 0\}} \frac{|g(\vartheta (t_ku_k)u_k)|}{|u_k|} \,u_kv\,{\text {d}}x\\&\le \int _{\{u_k\ne 0\}} \frac{C(1+|u_k|^q)}{|u_k|} \,u_kv\,{\text {d}}x \\&= \int _{\{u_k\ne 0\}} C\frac{u_k}{|u_k|}\,v\,{\text {d}}x + \int _{\varOmega } C|u_k|^{q-1}u_kv\,{\text {d}}x. \end{aligned} \end{aligned}$$

It follows

$$\begin{aligned} \int _\varOmega \left[ \nabla \varPsi (\nabla u_k)\cdot \nabla v - \hat{g}(u_k)v\right] \,{\text {d}}x \le \langle \hat{w}_k,v\rangle , \end{aligned}$$

where

$$\begin{aligned} \hat{w}_k=\left\{ \begin{array}{ll} \displaystyle { C\frac{u_k}{|u_k|}} &{}\quad \text {where }\;u_k\ne 0,\\ 0 \quad &{}\text {where }\;u_k=0. \end{array} \right. \end{aligned}$$

From Theorem 3.1 we infer that $(u_k)$ is bounded in $L^\infty (\varOmega )$, so that $\vartheta (t_ku_k)=1$ eventually as $k\rightarrow \infty$. Then $u_k$ is a critical point of f and a contradiction follows.

From [21, Theorem 5.2] we deduce that $C_m(f,0)\approx C_m(f_{\overline{t}},0)$ (for related results, see also [11, Theorem I.5.6], [14, Theorem 3.1] and [42, Theorem 8.8]) and the assertion follows. $\square$

7 Proof of the main results

In this last section we prove the main results stated in the Introduction. Let us recall some variants of the results of [13] suited for our purposes. We start with a saddle theorem, where linear subspaces are substituted by symmetric cones.

Theorem 7.1

Let X be a real Banach space and let $X_-, X_+$ be two symmetric cones in X such that $X_+$ is closed in X, $X_- \cap X_+ = \{0\}$ and such that

$$\begin{aligned} \mathrm {Index}(X_-{\setminus }\{0\}) = \mathrm {Index}(X{\setminus } X_+) < +\infty . \end{aligned}$$

Let $r>0$ and let

$$\begin{aligned} D_-=\left\{ u\in X_-:\,\Vert u\Vert \le r\right\} , \qquad S_-=\left\{ u\in X_-:\,\Vert u\Vert = r\right\} . \end{aligned}$$

Let $f:X\rightarrow {\mathbb {R}}$ be a function of class $C^1$ such that

$$\begin{aligned}&\inf _{X_+} f>-\infty \,,\qquad \sup _{D_-} f< +\infty \,,\\&\quad \text {if }X_-\ne \{0\}, \text { we have } f(u) < \inf _{X_+} f\text { whenever }u\in S_-. \end{aligned}$$

Set

$$\begin{aligned} a= \inf _{X_+} f,\qquad b= \sup _{D_-} f,\qquad m= \mathrm {Index}(X_-{\setminus }\{0\}) \end{aligned}$$

and assume that every sequence $(u_n)$ in X, with

$$\begin{aligned} f(u_n)\rightarrow c\in [a,b] \text { and } (1+\Vert u_n\Vert )\Vert f'(u_n)\Vert \rightarrow 0, \end{aligned}$$

admits a convergent subsequence (Cerami–Palais–Smale condition) and that $f^{-1}([a,b])$ contains a finite number of critical points.

Then, there exists a critical point u of f with $a\le f(u)\le b$ and $C_m(f,u)\ne \{0\}$.

Proof

From [24, Theorems 2.7 and 2.8] we infer that $(D_-,S_-)$ links $X_+$ cohomologically in dimension m over ${\mathbb {Z}}_2$. According to [20, Remark 4.4], the Cerami–Palais–Smale condition is just the usual Palais–Smale condition with respect to an auxiliary distance function. Then the assertion follows from [23, Theorem 5.2, Remark 5.3 and Theorem 7.5]. $\square$

Theorem 7.2

Let $(\lambda _m)$ be defined as in the Introduction and let $m\ge 0$ be such that $\lambda _m<\lambda _{m+1}$. If we set

$$\begin{aligned} \begin{array}{ll} \left\{ \begin{array}{lll} X_- &{}= &{}\displaystyle {\left\{ u\in W^{1,p}_0(\varOmega ):\,\, \int _\varOmega |\nabla u|^p\,dx \le \lambda _m \int _\varOmega |u|^p\,{\text {d}}x\right\} } \\ X_+ &{}= &{}\displaystyle {\left\{ u\in W^{1,p}_0(\varOmega ):\,\, \int _\varOmega |\nabla u|^p\,{\text {d}}x \ge \lambda _{m+1} \int _\varOmega |u|^p\,{\text {d}}x\right\} } \end{array} \right. &{}\qquad \text {if }\;m\ge 1\,,\\ \left\{ \begin{array}{lll} X_- &{}= &{}\displaystyle {\left\{ 0\right\} } \\ X_+ &{}= &{} W^{1,p}_0(\varOmega ) \end{array} \right.&\qquad \text {if }\;m=0, \end{array} \end{aligned}$$

then $X_-, X_+$ are two closed symmetric cones in $W^{1,p}_0(\varOmega )$ such that $X_- \cap X_+ = \{0\}$ and such that

$$\begin{aligned} \mathrm {Index}(X_-{\setminus }\{0\}) = \mathrm {Index}(W^{1,p}_0(\varOmega ){\setminus } X_+) = m. \end{aligned}$$

Proof

If $m\ge 1$, the result is contained in [24, Theorem 3.2]. The case $m=0$ is obvious. $\square$

Now let $f:W^{1,p}_0(\varOmega )\rightarrow {\mathbb {R}}$ be the $C^1$-functional defined in (1.3) by setting

$$\begin{aligned} f(u) = \int _{\varOmega } \varPsi _{p,\kappa }(\nabla u)\,{\text {d}}x - \int _{\varOmega } G(u)\,{\text {d}}x. \end{aligned}$$

Proof of Theorem 1.1

Let us show that f satisfies the Cerami–Palais–Smale condition. Let $(u_n)$ be a sequence in $W^{1,p}_0(\varOmega )$ with $f(u_n)$ bounded and $(1+\Vert u_n\Vert )\Vert f'(u_n)\Vert \rightarrow 0$, so that

$$\begin{aligned} \lim _n \,\langle f'(u_n),v-u_n\rangle = 0 \qquad \forall v\in W^{1,p}_0(\varOmega )\,. \end{aligned}$$

(7.1)

First of all, let us show that $(u_n)$ is bounded in $W^{1,p}_0(\varOmega )$. By contradiction, assume that $\Vert u_n\Vert \rightarrow \infty$ and set $z_n = \frac{u_n}{\Vert u_n\Vert }$. Up to a subsequence, $z_n$ is convergent to some z weakly in $W^{1,p}_0(\varOmega )$, strongly in $L^p(\varOmega )$ and a.e. in $\varOmega$. Since $\langle f'(u_n),z-z_n\rangle \rightarrow 0$, dividing by $\Vert u_n \Vert ^{p-1}$ and taking into account (a), we get

$$\begin{aligned} \lim _n \int _{\varOmega } \left( \frac{\kappa ^2}{\Vert u_n\Vert ^2}+ |\nabla z_n|^2\right) ^{\frac{p-2}{2}} \nabla z_n \cdot \nabla (z - z_n) \, {\text {d}}x = 0 \,. \end{aligned}$$

By the convexity of $\varPsi _{p,\kappa }$, it follows

$$\begin{aligned} \limsup _n \int _\varOmega |\nabla z_n|^p\,{\text {d}}x \le \limsup _n \int _\varOmega \left( \frac{\kappa ^2}{\Vert u_n\Vert ^2} + |\nabla z_n|^2\right) ^{\frac{p}{2}}\,{\text {d}}x \\ \le \lim _n \int _\varOmega \left( \frac{\kappa ^2}{\Vert u_n\Vert ^2} + |\nabla z|^2\right) ^{\frac{p}{2}}\,{\text {d}}x = \int _\varOmega |\nabla z|^p\,{\text {d}}x, \end{aligned}$$

so that $z_n \rightarrow z$ strongly in $W^{1,p}_0(\varOmega )$ and $z\ne 0$.

Given $v \in W^{1,p}_0(\varOmega )$, we also have $\langle f'(u_n),v\rangle \rightarrow 0$ whence, dividing again by $\Vert u_n \Vert ^{p-1}$,

$$\begin{aligned} \lim _n \int _{\varOmega } \left[ \left( \frac{\kappa ^2}{\Vert u_n\Vert ^2}+ |\nabla z_n|^2\right) ^{\frac{p-2}{2}} \nabla z_n \cdot \nabla v - \frac{g(\Vert u_n\Vert z_n)}{\Vert u_n\Vert ^{p-1}}\,v\right] \, {\text {d}}x = 0. \end{aligned}$$

Taking again into account (a), we get

$$\begin{aligned} \int _{\varOmega } |\nabla z|^{p-2} \nabla z \cdot \nabla v \, {\text {d}}x = \lambda \, \int _{\varOmega } |z|^{p-2} z v \,{\text {d}}x \qquad \forall v \in W^{1,p}_0(\varOmega ), \end{aligned}$$

which contradicts the assumption that $\lambda \not \in \sigma (-\Delta _p)$. Therefore, $(u_n)$ is bounded in $W^{1,p}_0(\varOmega )$, hence convergent, up to a subsequence, to some u weakly in $W^{1,p}_0(\varOmega )$.

According to [3, Theorem 3.5], the operator $f'$ is of class $(S)_+$. From (7.1) we infer that $(u_n)$ is strongly convergent to u in $W^{1,p}_0(\varOmega )$.

Now define $X_-, X_+$ according to Theorem 7.2 with $m=m_\infty$, so that $X_-, X_+$ are two symmetric cones in $W^{1,p}_0(\varOmega )$ satisfying the assumptions of Theorem 7.1 with $\mathrm {Index}(X_-{\setminus }\{0\}) = m_\infty$. Let us treat the case $m_\infty \ge 1$. The case $m_\infty = 0$ is similar and simpler. If

$$\begin{aligned} \lambda _{m_\infty }< \alpha '< \alpha ''< \lambda< \beta '< \beta '' < \lambda _{m_\infty +1}, \end{aligned}$$

taking into account assumption (a) we infer that there exists $C>0$ such that

$$\begin{aligned}&\frac{\beta ''}{p\lambda _{m_\infty +1}} \,|\xi |^p - C&\le \varPsi _{p,\kappa }(\xi )&\le \frac{\alpha '}{p\lambda _{m_\infty }}\,|\xi |^p +C&\qquad \forall \xi \in {\mathbb {R}}^N,\\&\frac{\alpha ''}{p}\,|s|^p - C&\le G(s)&\le \frac{\beta '}{p}\,|s|^p +C&\qquad \forall s\in {\mathbb {R}}. \end{aligned}$$

It easily follows that

$$\begin{aligned} \inf _{X_+} f >-\infty ,\qquad \lim _{\begin{array}{c} \Vert u\Vert \rightarrow \infty \\ u\in X_- \end{array}}\,f(u) = -\infty . \end{aligned}$$

In particular, there exists $r>0$ such that

$$\begin{aligned} \forall u \in S_-:\,\, f(u) < \inf _{X_+} f \end{aligned}$$

and, since f is bounded on bounded subsets, we also have $\sup \limits _{D_-} f < +\infty$.

If f has infinitely many critical points, we are done. Otherwise, from Theorem 7.1 we infer that there exists a critical point u of f with $C_{m_\infty }(f,u)\ne \{0\}$.

Since $m_{\infty } \not \in [m(f,0),m^*(f,0)]$, from Theorem 2.8 we deduce that $C_{m_\infty }(f,0) = \{0\}$. Therefore, $u\ne 0$ and the assertion follows. $\square$

In order to prove Theorem 1.2, we need an auxiliary result.

Proposition 7.3

Let $\gamma \in {\mathbb {R}}$ and $\Gamma :{\mathbb {R}}\rightarrow {\mathbb {R}}$ be a function of class $C^1$ such that

$$\begin{aligned}&\lim _{|s|\rightarrow \infty }\, \frac{\Gamma (s)}{|s|^p} = \gamma ,\\&\lim _{|s|\rightarrow \infty } \, \left[ p\Gamma (s) - s \Gamma '(s) \right] = +\infty . \end{aligned}$$

Then, we have

$$\begin{aligned} \lim _{|s|\rightarrow \infty }\, \left[ \Gamma (s) - \gamma |s|^p \right] = +\infty . \end{aligned}$$

Proof

Let $H(s)= \Gamma (s) -\gamma |s|^p$, so that

$$\begin{aligned}&\lim _{|s|\rightarrow \infty }\, \frac{H(s)}{|s|^p} = 0,\\&\lim _{|s|\rightarrow \infty } \, \left[ p H(s) - s H'(s) \right] = +\infty . \end{aligned}$$

For every $M >0$, there exists $\overline{s} >0$ such that $p H(s) - s H'(s) \ge pM$ for any $s \ge \overline{s}$. It follows

$$\begin{aligned} \biggl (\frac{H(s) - M}{s^p}\biggr )^\prime = \frac{s H'(s) - p H(s) + pM}{s^{p+1}} \le 0 \qquad \forall s \ge \overline{s}, \end{aligned}$$

which implies that

$$\begin{aligned} \frac{H(t)}{t^p} -\frac{M}{t^{p}} \le \frac{H(s)}{s^{p}} - \frac{M}{s^{p}} \qquad \text {whenever }t \ge s \ge \overline{s}\,. \end{aligned}$$

Passing to the limit as $t \rightarrow + \infty$, we get

$$\begin{aligned} 0 \le \frac{H(s)}{s^p} - \frac{M}{s^{p}} \qquad \forall s \ge \overline{s}, \end{aligned}$$

namely

$$\begin{aligned} H(s) \ge M \qquad \forall s \ge \overline{s}. \end{aligned}$$

Therefore,

$$\begin{aligned} \lim _{s\rightarrow +\infty }\,H(s) = +\infty . \end{aligned}$$

The limit as $s\rightarrow -\infty$ can be treated in a similar way. $\square$

Proof of Theorem 1.2

Assume $(b_-)$. Let us show that f satisfies the Cerami–Palais–Smale condition. Let $(u_n)$ be a sequence in $W^{1,p}_0(\varOmega )$ with $f(u_n)$ bounded and $(1+\Vert u_n\Vert )\Vert f'(u_n)\Vert \rightarrow 0$. First of all, let us show that $(u_n)$ is bounded in $W^{1,p}_0(\varOmega )$. By contradiction, assume that $\Vert u_n\Vert \rightarrow \infty$ and set $z_n = \frac{u_n}{\Vert u_n\Vert }$. Up to a subsequence, $z_n$ is convergent to some z weakly in $W^{1,p}_0(\varOmega )$, strongly in $L^p(\varOmega )$ and a.e. in $\varOmega$. As in the proof of Theorem 1.1, we infer that $z_n \rightarrow z$ strongly in $W^{1,p}_0(\varOmega )$ and $z\ne 0$.

We also have

$$\begin{aligned} \limsup _n \left| p f(u_n) - \langle f'(u_n),u_n\rangle \right| <+\infty . \end{aligned}$$

Since

$$\begin{aligned} p \varPsi _{p,\kappa }(\xi ) - \nabla \varPsi _{p,\kappa }(\xi )\cdot \xi = \kappa ^2 \left( \kappa ^2+|\xi |^2\right) ^{\frac{p-2}{2}} - \kappa ^p \end{aligned}$$

is bounded from below, we infer that

$$\begin{aligned} \liminf _n \int _\varOmega \left[ pG(u_n)-g(u_n)u_n\right] \,{\text {d}}x > -\infty . \end{aligned}$$

On the other hand, there exists $C>0$ such that

$$\begin{aligned} pG(s) - g(s)s \le C \qquad \forall s\in {\mathbb {R}}\end{aligned}$$

whence, by Fatou’s lemma,

$$\begin{aligned} \int _\varOmega \left\{ \limsup _n \left[ pG(u_n)-g(u_n)u_n\right] \right\} \,{\text {d}}x > -\infty . \end{aligned}$$

Since we have

$$\begin{aligned} \lim _n\left[ pG(u_n(x))-g(u_n(x))u_n(x)\right] = -\infty \qquad \text {for a.e. }x\in \varOmega \text { with }z(x)\ne 0, \end{aligned}$$

we infer that $z=0$ a.e. in $\varOmega$ and a contradiction follows.

We conclude that the sequence $(u_n)$ is bounded, hence convergent, up to a subsequence, to some u weakly in $W^{1,p}_0(\varOmega )$. As in the proof of Theorem 1.1, we get that $(u_n)$ is strongly convergent to u in $W^{1,p}_0(\varOmega )$.

Now let

$$\begin{aligned} \lambda _{m_{\infty }} < \lambda \le \lambda _{m_{\infty }+1} \end{aligned}$$

and define $X_-, X_+$ as in the proof of Theorem 1.1.

We have

$$\begin{aligned} \varPsi _{p,\kappa }(\xi ) \ge \frac{1}{p}\,|\xi |^p - \frac{1}{p}\,\kappa ^p \qquad \forall \xi \in {\mathbb {R}}^N \end{aligned}$$

and, by Proposition 7.3,

$$\begin{aligned} \lim _{|s|\rightarrow \infty }\, \left[ G(s)-\frac{\lambda }{p}\,|s|^p\right] = -\infty . \end{aligned}$$

Therefore, there exists $C>0$ such that

$$\begin{aligned} G(s) \le \frac{\lambda }{p}\,|s|^p + C \qquad \forall s\in {\mathbb {R}}. \end{aligned}$$

It easily follows that $\inf \limits _{X_+} f > -\infty$ and we conclude as in the proof of Theorem 1.1.

Now assume $(b_+)$, so that

$$\begin{aligned} \lambda _{m_{\infty }} \le \lambda < \lambda _{m_{\infty }+1} \end{aligned}$$

and either $1<p\le 2$ with $\kappa \ge 0$ or $p>2$ with $\kappa =0$. It follows that

$$\begin{aligned} p \varPsi _{p,\kappa }(\xi ) - \nabla \varPsi _{p,\kappa }(\xi )\cdot \xi \end{aligned}$$

is even bounded and the Cerami–Palais–Smale condition can be proved as in the previous case.

Now let us show that

$$\begin{aligned} \lim _{\begin{array}{c} \Vert u\Vert \rightarrow \infty \\ u\in X_- \end{array}}\,f(u) = -\infty . \end{aligned}$$

(7.2)

Let $u_n\in X_-$ with $\Vert u_n\Vert \rightarrow \infty$ and let $z_n = \frac{u_n}{\Vert u_n\Vert }$. Up to a subsequence, $(z_n)$ is convergent to some z weakly in $W^{1,p}_0(\varOmega )$, strongly in $L^p(\varOmega )$ and a.e. in $\varOmega$. Since $z_n\in X_-$, we also have $z\ne 0$. From Proposition 7.3 we infer that

$$\begin{aligned} \lim _{|s|\rightarrow \infty }\, \left[ G(s)-\frac{\lambda }{p}\,|s|^p\right] = +\infty . \end{aligned}$$

In particular, there exists $C>0$ such that

$$\begin{aligned} G(s) \ge \frac{\lambda }{p}\,|s|^p - C \qquad \forall s\in {\mathbb {R}}. \end{aligned}$$

From Fatou’s lemma we infer that

$$\begin{aligned} \lim _n\, \int _\varOmega \left[ G(u_n)-\frac{\lambda }{p}\,|u_n|^p\right] \,{\text {d}}x = +\infty . \end{aligned}$$

Since

$$\begin{aligned} \varPsi _{p,\kappa }(\xi ) \le \frac{1}{p}\,|\xi |^p \qquad \forall \xi \in {\mathbb {R}}^N, \end{aligned}$$

it follows that

$$\begin{aligned} f(u_n) \le \frac{1}{p}\, \int _{\varOmega } \left[ |\nabla u_n|^p - {\lambda } |u_n|^p \right] \,{\text {d}}x - \int _{\varOmega } \left[ G(u_n) - \frac{\lambda }{p} |u_n|^p \right] \,{\text {d}}x, \end{aligned}$$

whence (7.2). Now we conclude as in the proof of Theorem 1.1. $\square$