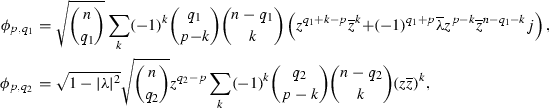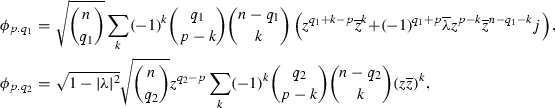Classification of homogeneous minimal immersions from $S^2$ to ${\mathbb {H}}P^n$

Abstract

In this paper we determine all homogeneous minimal immersions of 2-spheres in quaternionic projective spaces ${\mathbb {H}}P^n$.

1 Introduction

In 1990 Ohnita (cf. [13]) gave a series of homogeneous minimal 2-spheres $\left\{ \phi _{n,\alpha }\right\}$ of constant curvature in quaternionic projective spaces ${\mathbb {H}}P^n$ and conjectured that $\left\{ \phi _{n,\alpha }\right\}$ exhaust all proper minimal isometric immersions of $S^2$ in ${\mathbb {H}}P^n$. Recently, we get a classification theorem of linearly full unramified conformal minimal immersions of constant curvature from $S^2$ to ${\mathbb {H}}P^2$ (cf. [8]), which verifies that in the case $n=2$, $\left\{ \phi _{n,\alpha }\right\}$ exhaust all linearly full unramified minimal isometric immersions of constant curvature from $S^2$ to ${\mathbb {H}}P^2$. In [10], we determine all conformal minimal immersions of 2-spheres in ${\mathbb {H}}P^n$ with parallel second fundamental form (implies that it is of constant curvature). In this paper, we determine all homogeneous (stronger than the condition of unramified with constant curvature) minimal 2-spheres in ${\mathbb {H}}P^n$ (see Theorem 5.5) and solve completely Ohnita’s conjecture for n odd. Indeed, in this case, we find homogeneous minimal 2-spheres not in the series $\left\{ \phi _{n,\alpha }\right\}$. When n is even, the series $\left\{ \phi _{n,\alpha }\right\}$ gives all homogeneous minimal 2-spheres, but it is unknown whether there are any proper non-homogeneous minimal isometric immersions.

In this paper we mainly combine the methods of harmonic sequences and moving frames to study homogeneous harmonic maps from $S^2$ to ${\mathbb {H}}P^n$.

Our arrangement is as follows.

In the second section of this paper, firstly we give the definition of quaternionic projective space ${\mathbb {H}}P^{n}$ as the totally geodesic submanifold in $G(2,2n+2)$, then we give some fundamental results concerning G(k, N) from the viewpoint of harmonic sequences by moving frames, and at last we give some brief description of Veronese sequence and the rigidity theorem in ${\mathbb {C}}P^N$. In the third section, we simply introduce homogeneous harmonic maps from $S^2$ to G(k, N) and give an important property. In the fourth section, we determine all reducible harmonic maps of constant curvature from $S^2$ to ${\mathbb {H}}P^n$, which represent the homogeneous ones completely. In the last section, we determine all irreducible homogeneous harmonic maps from $S^2$ to ${\mathbb {H}}P^n$ by mathematical induction. Finally we obtain the classification Theorem 5.5.

2 Preliminaries

For any $N=1,2,\ldots ,$ let $\left\langle , \right\rangle$ denote the standard Hermitian inner product on ${\mathbb {C}}^{N}$ defined by $\left\langle z, w\right\rangle = z_1\overline{w}_1 +\cdots + z_N\overline{w}_N$ where $z=(z_1, \ldots , z_N)^T, w=(w_1, \ldots , w_N)^T\in {{\mathbb {C}}}^N$ and $^{-}$ denotes complex conjugation. Let ${\mathbb {H}}$ denote the division ring of quaternions. Let j be a unit quaternion with $j^2=-1$. Then we have an identification of ${{\mathbb {C}}}^2$ with ${\mathbb {H}}$ given by making $(a,b)\in {{\mathbb {C}}}^2$ correspond to $a+bj\in {\mathbb {H}}$; let $n \in \left\{ 1,2,\ldots \right\}$, we have a corresponding identification of ${{\mathbb {C}}}^{2n+2}$ with ${{\mathbb {H}}}^{n+1}$. For any $a+bj\in {\mathbb {H}}$, the left multiplication by j is given by $j(a+bj)=-\overline{b}+\overline{a}j$; the conjugation is given by $\overline{a+bj}=\overline{a}-bj$; and the positive definite inner product is given by $\left\langle x, y\right\rangle _{{\mathbb {H}}}=Re(x\overline{y})$ for any $x,y\in {\mathbb {H}}$.

Let ${\mathbf {J}}:{{\mathbb {C}}}^{2n+2} \rightarrow {{\mathbb {C}}}^{2n+2}$ be the conjugate linear map given by left multiplication by j, i.e.,

$$\begin{aligned} {{\mathbf {J}}}(z_1, z_2, \ldots , z_{2n+1}, z_{2n+2})^T= (-{\bar{z}}_2, {\bar{z}}_1, \ldots , -{\bar{z}}_{2n+2}, {\bar{z}}_{2n+1})^T. \end{aligned}$$

Then ${{\mathbf {J}}}^2=-id$ where id denotes the identity map on ${{\mathbb {C}}}^{2n+2}$. In fact, for any $v\in {{\mathbb {C}}}^{2n+2}$,

$$\begin{aligned} {{\mathbf {J}}}v=J_{n+1} {\bar{v}}, \end{aligned}$$

where $J_{n+1}=diag \underbrace{\left\{ \left( \begin{array} {lr} 0 &{} -1 \\ 1 &{} 0 \\ \end{array}\right) , \ldots , \left( \begin{array} {lr} 0 &{} -1 \\ 1 &{} 0 \\ \end{array}\right) \right\} }_{n+1}$.

Let $G(2,2n+2)$ denote the Grassmann manifold of all complex 2-dimensional subspaces of ${{\mathbb {C}}}^{2n+2}$ with its standard Kähler structure. The quaternionic projective spaces ${\mathbb {H}}P^{n}$ are the set of all one-dimensional quaternionic subspaces of ${{\mathbb {H}}}^{n+1}$. Throughout the above we shall regard ${\mathbb {H}}P^{n}$ as the totally geodesic submanifold of $G(2,2n+2)$ given by

$$\begin{aligned} {\mathbb {H}}P^{n}=\left\{ V\in {G(2,2n+2)}: {{\mathbf {J}}}V=V\right\} . \end{aligned}$$

Let $Sp(n+1)=\left\{ g\in GL(n+1;{\mathbb {H}}), \ g^*g=I_{n+1}\right\}$ be the symplectic isometry group of ${\mathbb {H}}P^{n}$. The explicit description is that the following diagram commutes:

where $i_1,i_2$ are inclusions and $\pi _1,\pi _2$ are projections, and $i_1(g)=E$, for $1\le a,b\le n+1$

$$\begin{aligned} {\left\{ \begin{array}{ll} E_{2b-1}^{2a-1}=A_{b}^{a},\quad E_{2b}^{2a-1}=-\overline{B}_{b}^{a},\\ E_{2b-1}^{2a}=B_{b}^{a},\quad E_{2b}^{2a}=\overline{A}_{b}^{a}, \end{array}\right. }\ \end{aligned}$$

where $A=(A_{b}^{a}),\ B=(B_{b}^{a})\in M_{n+1}({\mathbb {C}}),\ g=A+\overline{B}j\in Sp(n+1)$;

$$\begin{aligned} \pi _1(g)=g\cdot \left[ (1,0,\ldots ,0)^T\right] \in {\mathbb {H}}P^{n}; \end{aligned}$$

$$\begin{aligned} \pi _2(E)=E\cdot \left[ \begin{pmatrix}1,0,0,\ldots ,0\\ 0,1,0,\ldots ,0\end{pmatrix}^T\right] \in G(2,2n+2); \end{aligned}$$

$$\begin{aligned} i_2\left( \left[ (z_1+\overline{z}_2j,~\ldots ,~z_{2n+1}+\overline{z}_{2n+2}j)^T\right] \right) = \left[ \begin{pmatrix}z_1,~z_2,~\ldots ,~z_{2n+1},~z_{2n+2}\\ -\overline{z}_2,~\overline{z}_1,~\ldots ,~-\overline{z}_{2n+2},~\overline{z}_{2n+1}\end{pmatrix}^T\right] . \end{aligned}$$

Here we consider $G(2,2n+2)$ as the set of all Hermitian orthogonal projections from ${\mathbb {C}}^{2n+2}$ onto 2-dimensional complex subspaces, i.e.,

$$\begin{aligned} G(2,2n+2)=\left\{ \varphi \in M_{2n+2}({\mathbb {C}}) |\varphi ^2=\varphi ,\varphi ^{*}=\varphi ,\text {tr}\varphi =2\right\} . \end{aligned}$$

Let $\tau :G(2,2n+2)\rightarrow U(2n+2)$ be the Cartan embedding, which is defined by $\tau (\varphi )=2\varphi -I\in U(2n+2)$. We take the bi-invariant metric $\mathrm{d}s_{U(2n+2)}^2=\frac{1}{8}\text {tr}\omega \omega ^{*}$ on $U(2n+2)$; then the metric on $G(2,2n+2)$ induced by $\tau$ is given by

$$\begin{aligned} \mathrm{d}s_{G(2,2n+2)}^2=\frac{1}{2}\text {tr}\mathrm{d}\varphi \mathrm{d}\varphi , \end{aligned}$$

where $\omega$ is the Maurer–Cartan form of $U(2n+2)$.

Then the metric induced by $i_2$ is twice as much as the standard metric of constant Q-sectional curvature 4 on ${\mathbb {H}}P^{n}$.

Thus we regard the harmonic map from $S^2$ to ${\mathbb {H}}P^{n}$ as the one from $S^2$ to $G(2,2n+2)$.

For any $g\in Sp(n+1)$, the action of g on ${\mathbb {H}}P^{n}$ induces an action of E on ${\mathbb {C}}P^{2n+1}$, where $E\in U(2n+2)$ which commutes with ${{\mathbf {J}}}$. Then

$$\begin{aligned} Sp(n+1)=\left\{ E\in U(2n+2), \ E\circ {{\mathbf {J}}}={{\mathbf {J}}} \circ E\right\} =\left\{ E\in U(2n+2), \ E J_{n+1} E^{T}=J_{n+1}\right\} . \end{aligned}$$

In the following, we deal with the symplectic isometry of ${\mathbb {H}}P^{n}$ through the corresponding symplectic isometry of ${\mathbb {C}}P^{2n+1}$.

Next, we simply introduce harmonic maps and harmonic sequences in G(k, N) (cf. [4, 5]) and calculate some corresponding geometric quantities.

Let M be a simply connected domain in the unit sphere $S^2$ and let $(z,\overline{z})$ be complex coordinates on M. We take the metric $\mathrm{d}s^2_M=\mathrm{d}z\mathrm{d}\overline{z}$ on M. Denote

$$\begin{aligned} \partial =\frac{\partial }{\partial z}, \quad \overline{\partial }=\frac{\partial }{\partial \overline{z}}. \end{aligned}$$

We consider the complex Grassmann manifold G(k, N) as the set of Hermitian orthogonal projections from ${{\mathbb {C}}}^N$ onto a k-dimensional subspace in ${{\mathbb {C}}}^N$. Then $\phi :S^2\rightarrow G(k,N)$ is a Hermitian orthogonal projection onto a k-dimensional subbundle $\underline{\phi }$ of the trivial bundle ${\underline{{\mathbb {C}}}}^N=M\times {{\mathbb {C}}}^N$ given by setting the fiber of $\underline{\phi }$ at x, ${\underline{\phi }}_x$, equal to $\phi (x)$ for all $x\in M$. For any two orthogonal subbundles $\underline{\phi }, \underline{\psi }$ of ${\underline{{\mathbb {C}}}}^N$, define vector bundle morphisms over any coordinate chart, and $A'_{\phi , \psi }, A''_{\phi , \psi }: \underline{\phi } \rightarrow \underline{\psi }$ is called the $\partial {'}$- and $\partial {''}$-second fundamental forms of $\underline{\phi }$ in $\underline{\phi } \oplus \underline{\psi }$ by $A'_{\phi , \psi }(v)=\pi _{\psi }(\partial v), \quad A''_{\phi , \psi }(v)=\pi _{\psi }(\overline{\partial } v)$ for $v\in C^{\infty }(\underline{\phi })$ . Here $\pi _{\psi }$ denotes orthogonal projection onto $\underline{\psi }$ and $C^{\infty }(\underline{\phi })$ denotes the vector space of smooth sections of $\underline{\phi }$. Although these morphisms are only defined on coordinate charts, all the constructions we will do involve their images which are globally defined independent of choice of local coordinate. In particular $A'_{\phi }=A'_{\phi , \phi ^{\perp }}, A''_{\phi }=A''_{\phi , \phi ^{\perp }}$ are called the second fundamental forms of $\underline{\phi }$ in ${\underline{{\mathbb {C}}}}^N$.

Let $\phi : S^2 \rightarrow G(k,N)$ be a smooth harmonic map. Then from $\phi$ two harmonic sequences (cf. [4]) are derived as follows:

$$\begin{aligned} \underline{\phi }= & {} \underline{\phi }_{0}\mathop {\longrightarrow }\limits ^{A'_{\phi _0}}\underline{\phi }_1\mathop {\longrightarrow }\limits ^{A'_{\phi _1}}\cdots \mathop {\longrightarrow }\limits ^{A'_{\phi _{\alpha -1}}}\underline{\phi }_ {\alpha }\mathop {\longrightarrow }\limits ^{A'_{\phi _{\alpha }}}\cdots , \end{aligned}$$

(2.1)

$$\begin{aligned} \underline{\phi }= & {} \underline{\phi }_{0}\mathop {\longrightarrow }\limits ^{A''_{\phi _0}}\underline{\phi }_{-1}\mathop {\longrightarrow }\limits ^{A''_{\phi _{-1}}}\cdots \mathop {\longrightarrow }\limits ^{A''_{\phi _{-\alpha +1}}} \underline{\phi }_{-\alpha }\mathop {\longrightarrow }\limits ^{A''_{\phi _{-\alpha }}}\cdots , \end{aligned}$$

(2.2)

where $\underline{\phi }_ {\alpha } = {\underline{Im}} A'_{\phi _{\alpha -1}}$ and $\underline{\phi }_ {-\alpha } = {\underline{Im}} A''_{\phi _{-\alpha +1}}$ are harmonic subbundles of ${\underline{{\mathbb {C}}}}^N$ (i.e., represent harmonic maps), respectively, $\alpha =1,2,\ldots$.

We assume that $\phi$ is a linearly full harmonic map from $S^2$ to G(k, N); here linearly full means that $\underline{\phi }$ cannot be contained in any proper trivial subbundle ${\underline{{\mathbb {C}}}}^m$ of ${\underline{{\mathbb {C}}}}^N$ ($m< N$). We know that several consecutive harmonic maps in (2.1) are not mutually orthogonal generally. So it is meaningful to define the isotropy order of $\phi$ (cf. [4], §3A) to be the greatest integer r such that $\underline{\phi }_i \perp \underline{\phi }_j$ $\forall i,j \in \mathbb {Z}$ with $0< |i-j| \le r$; if $r=\infty$, then $\phi$ is said to be strongly isotropic. Now we consider a special harmonic sequence.

Suppose that $\phi : S^2 \rightarrow G(k,N)$ is a linearly full harmonic map having isotropy order at least 2. Then $\phi$ belongs to the following harmonic sequence:

$$\begin{aligned} 0\mathop {\longleftarrow }\limits ^{A''_{\phi _{-{\alpha }_0}}}\underline{\phi }_{-{\alpha }_0} \mathop {\longleftarrow }\limits ^{A''_{\phi _{-{\alpha }_0-1}}}\ldots \mathop {\longleftarrow }\limits ^{A''_{\phi _{-1}}}\underline{\phi }_{-1} \mathop {\longleftarrow }\limits ^{A''_{\phi }}\underline{\phi }_0=\underline{\phi } \mathop {\longrightarrow }\limits ^{A'_{\phi }}\underline{\phi }_1 \mathop {\longrightarrow }\limits ^{A'_{\phi _1}}\ldots \mathop {\longrightarrow }\limits ^{A'_{\phi _{{\beta }_0-1}}}\underline{\phi }_{{\beta }_0} \mathop {\longrightarrow }\limits ^{A'_{\phi _{{\beta }_0}}} 0,\quad \end{aligned}$$

(2.3)

where for $\alpha =-{\alpha }_0+1,\ldots ,{\beta }_0-1$, $\underline{\phi }_{\alpha -1}, \underline{\phi }_{\alpha }, \underline{\phi }_{\alpha +1}$ are mutually orthogonal.

Denote $k_\alpha =$ rank $\underline{\phi }_{\alpha }$ ($\alpha =-{\alpha }_0, \ldots , \beta _0$).

For the harmonic sequence (2.3) we choose the unit vectors $\left\{ \ldots ,e_{-1}, e_1, \ldots \right\}$ of ${\underline{{\mathbb {C}}}}^N$ such that $e_1,\ldots ,e_{k_0}$ locally span subbundle $\underline{\phi }_{0}$,  $e_{k_0+\ldots +k_{\alpha -1}+1}, \ldots , e_{k_0+\ldots +k_{\alpha -1}+k_{\alpha }}$ locally span subbundle $\underline{\phi }_{\alpha }$  ($\alpha =1, \ldots , \beta _0$),  $e_{-1},\ldots ,e_{-k_{-1}}$ locally span subbundle $\underline{\phi }_{-1}$,  $e_{-k_{-1}-\ldots -k_{\alpha +1}-1}, \ldots , and e_{-k_{-1}-\ldots -k_{\alpha +1}-k_{\alpha }}$ locally span subbundle $\underline{\phi }_{\alpha }$ ($\alpha =-2, \ldots , -\alpha _0$). Let $W_0=(e_1, \ldots , e_{k_0})$ be an $(N\times k_0)$-matrix, $W_{\alpha }=(e_{k_0+\ldots +k_{\alpha -1}+1}, \ldots , e_{k_0+\ldots +k_{\alpha -1}+k_{\alpha }})$ be an $\left( N\times k_{\alpha }\right)$-matrix for $\alpha =1, \ldots , \alpha _0$ and let $W_{-1}=(e_{-1},\ldots ,e_{-k_{-1}})$ be an $(N\times k_{-1})$-matrix, $W_{\alpha }=(e_{-k_{-1}-\ldots -k_{\alpha +1}-1}, \ldots , e_{-k_{-1}-\ldots -k_{\alpha +1}-k_{\alpha }})$ be an $\left( N\times k_{\alpha }\right)$-matrix for $\alpha =-2, \ldots , -\alpha _0$. Since $\underline{\phi }_{\alpha -1}, \underline{\phi }_{\alpha }, \underline{\phi }_{\alpha +1}$ are mutually orthogonal, we can extend

$\left\{ W_{\alpha -1},W_{\alpha },W_{\alpha +1}\right\}$ into the local unitary frame with respect to $\phi _{\alpha }$. Then we have

$$\begin{aligned} \phi _{\alpha }= & {} W_{\alpha }W^*_{\alpha }, \end{aligned}$$

(2.4)

$$\begin{aligned} W^*_{\alpha }W_{\alpha }= & {} I_{k_{\alpha }\times k_{\alpha }}, \quad W^*_{\alpha }W_{\alpha +1} =0,\quad W^*_{\alpha } W_{\alpha -1}=0. \end{aligned}$$

(2.5)

By (2.5), a straightforward computation shows

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial W_{\alpha } = W_{\alpha +1} \Omega _{\alpha } + W_{\alpha } \Psi _{\alpha },\\ \overline{\partial }W_{\alpha } =-W_{\alpha -1} \Omega ^*_ {\alpha -1}- W_{\alpha }\Psi ^*_{\alpha }, \end{array}\right. } \end{aligned}$$

(2.6)

where $\Omega _{\alpha }$ is a $\left( k_{\alpha +1} \times k_{\alpha }\right)$-matrix and $\Psi _{\alpha }$ is a $\left( k_{\alpha }\times k_{\alpha }\right)$-matrix for $\alpha =-{\alpha }_0+1,\ldots ,{\beta }_0-1$.

It is very evident that integrability conditions for (2.6) are

$$\begin{aligned} \overline{\partial } \Omega _{\alpha }= & {} \Psi ^*_{\alpha +1} \Omega _ {\alpha }- \Omega _ {\alpha } \Psi ^*_{\alpha },\\ \overline{\partial }\Psi _{\alpha }+\partial \Psi ^*_{\alpha }= & {} \Omega ^*_{\alpha }\Omega _{\alpha }+\Psi ^*_{\alpha }\Psi _{\alpha }- \Omega _{\alpha -1}\Omega ^*_{\alpha -1}-\Psi _{\alpha }\Psi ^*_{\alpha }. \end{aligned}$$

From (2.6) we have $A'_{\phi _{\alpha }}(W_{\alpha })=W_{\alpha +1} \Omega _{\alpha }$ and $A''_{\phi _{\alpha +1}}(W_{\alpha +1})=-W_{\alpha } \Omega ^*_{\alpha }$, which implies

$$\begin{aligned} \left| A'_{\phi _{\alpha }}\right| ^2= & {} \text {sup}\left\{ \frac{\left| A'_{\phi _{\alpha }}(W_{\alpha })\right| ^2}{\left| W_{\alpha }\right| ^2}:W_{\alpha }\in \underline{\phi }_{\alpha }\text {with}\quad W_{\alpha }\ne 0\right\} \\= & {} \text {sup}\left\{ \frac{\text {tr}(A'_{\phi _{\alpha }}(W_{\alpha }))(A'_{\phi _{\alpha }}(W_{\alpha }))^*}{\text {tr}W_{\alpha }W^*_{\alpha }}:W_{\alpha }\in \underline{\phi }_{\alpha }\text {with}\quad W_{\alpha }\ne 0\right\} \\= & {} \text {tr} (\Omega _{\alpha } \Omega ^*_{\alpha })\\= & {} \left| A''_{\phi _{\alpha +1}}\right| ^2. \end{aligned}$$

Set $L_{\alpha } =\text {tr} (\Omega _{\alpha } \Omega ^*_{\alpha })=\left| A'_{\phi _{\alpha }}\right| ^2=\left| A''_{\phi _{\alpha +1}}\right| ^2.$ Then the metric induced by $\phi _{\alpha }$ is given by

$$\begin{aligned} \mathrm{d}s^2_{\alpha } = (L_{\alpha -1}+L_{\alpha })\mathrm{d}z\mathrm{d}\overline{z}. \end{aligned}$$

(2.7)

The Laplacian $\triangle _{\alpha }$ and the curvature $K_{\alpha }$ of $\mathrm{d}s^2_{\alpha }$ are given by

$$\begin{aligned} \triangle _{\alpha }= \frac{4}{L_{\alpha -1} + L_{\alpha }} \partial \overline{\partial }, \quad \ K_{\alpha }=-\frac{2}{L_{\alpha -1}+ L_{\alpha }} \partial \overline{\partial } \log (L_{\alpha -1}+L_{\alpha }). \end{aligned}$$

(2.8)

In particular, let $\psi :S^2 \rightarrow {\mathbb {C}}P^N$ be a linearly full harmonic map. Eells and Wood’s result (cf. [6]) shows that the following sequence in ${\mathbb {C}}P^N$ is uniquely determined by $\psi$

$$\begin{aligned} 0\mathop {\longleftarrow }\limits ^{A_0''} \underline{\psi } _0^{(N)} \mathop {\longrightarrow }\limits ^{A_0'}\cdots \mathop {\longrightarrow }\limits ^{A_{i-1}'} \underline{\psi } =\underline{\psi }_i^{(N)} \mathop {\longrightarrow }\limits ^{A_i'} \cdots \mathop {\longrightarrow }\limits ^{A_{N-1}'} \underline{\psi } _N ^{(N)} \mathop {\longrightarrow }\limits ^{A_N'} 0, \end{aligned}$$

(2.9)

for some $i =0, 1, \ldots ,N$, and here $A_0''$, $A_j'$ denote $A_{\psi _0^{(N)}}''$, $A_{\psi _j^{(N)}}'$, respectively, $(j=0, \ldots , N)$.

Let $f_0^{(N)}$ be a holomorphic section of ${\underline{\psi }}^{(N)}_0$, i.e., $\overline{\partial } f_0 ^{(N)} = 0$, and let $f_i^{(N)}$ be a local section of ${\underline{\psi }}^{(N)}_i$ such that

$$\begin{aligned} f_i ^{(N)} = \psi ^{(N)\perp }_{i-1} ( \partial f_{i-1} ^{(N)} ) \end{aligned}$$

for $i=1, \ldots ,N$. Then we have some formulas as follows (cf. [3]):

$$\begin{aligned} \partial f_i ^{(N)}= & {} f_{i+1}^{(N)} + \partial \log |f_i ^{(N)}|^2 f_i ^{(N)}, \ i= 0,\ldots , N-1, \end{aligned}$$

(2.10)

$$\begin{aligned} \overline{\partial } f_i^{(N)}= & {} - l_{i-1} ^{(N)} f_{i-1} ^{(N)}, \ i = 1, \ldots , N, \end{aligned}$$

(2.11)

$$\begin{aligned} \partial \overline{\partial } \log |f_i ^{(N)}|^2= & {} l_i^{(N)}-l_{i-1}^{(N)}, \end{aligned}$$

(2.12)

$$\begin{aligned} \partial \overline{\partial } \log l_i^{(N)}= & {} l_{i+1} ^{(N)}- 2 l_i^{(N)} + l_{i-1}^{(N)}, \ i =0, \ldots , N-1, \end{aligned}$$

(2.13)

where $l_i ^{(N)}= |f_{i+1}^{(N)}|^2/ |f_i^{(N)}|^2$ for $i =0, \ldots , N$, and $l_{-1} ^{(N)}= l_N^{(N)}=0$.

For convenience, we denote $\underline{f}_i^{(N)}=\underline{\psi }_i^{(N)}$ for $i=0, 1, \ldots , N$.

In the following, we give a definition of the unramified harmonic map as follows:

Definition 2.1

If $\det (\Omega _\alpha \Omega ^*_\alpha ) \mathrm{d}z^{k_{\alpha +1}} \mathrm{d}\overline{z} ^{k_{\alpha +1}}\ne 0$ everywhere on $S^2$ in (2.3) for some $\alpha =-\alpha _0+1, \ldots , \beta _0-1$ , we say that $\phi _\alpha : S^2 \rightarrow G(k_\alpha ,N)$ is unramified. If $\det (\Omega _\alpha \Omega ^*_\alpha ) \mathrm{d}z^{k_{\alpha +1}} \mathrm{d}\overline{z} ^{k_{\alpha +1}}\ne 0$ everywhere on $S^2$ in (2.3) for each $\alpha =-\alpha _0+1, \ldots , \beta _0-1$, we say that the harmonic sequence (2.3) is totally unramified. In this case we also say that each map $\phi _\alpha$ in (2.3) is totally unramified.

Here $\mathrm{d}z^{k_{\alpha +1}} \mathrm{d}\overline{z} ^{k_{\alpha +1}} =\frac{1}{2}\left( \mathrm{d}z^{k_{\alpha +1}}\otimes \mathrm{d}\overline{z} ^{k_{\alpha +1}} +\mathrm{d}\overline{z} ^{k_{\alpha +1}}\otimes \mathrm{d}z^{k_{\alpha +1}}\right)$ and the quantity $\det (\Omega _\alpha \Omega ^*_\alpha ) \mathrm{d}z^{k_{\alpha +1}} \mathrm{d}\overline{z} ^{k_{\alpha +1}}$ is independent of choice of local coordinate. In the case $k=1$, the above definition is in accordance with that in $\S 3$ of [3].

Now recall ([4], §3A) that a harmonic map $\phi : S^2 \rightarrow G(k,N)$ in (2.1) (resp. (2.2)) is said to be $\partial '$ -irreducible (resp. $\partial ''$ -irreducible) if rank $\underline{\phi }$=rank $\underline{\phi }_1$ (resp. rank $\underline{\phi }$=rank $\underline{\phi }_{-1}$) and $\partial '$ -reducible (resp. $\partial ''$ -reducible) otherwise. We assume that $\phi _{\alpha }$ in (2.3) is $\partial '$-irreducible, then $|\det \Omega _{\alpha }|^2 \mathrm{d}z^{k_\alpha } \mathrm{d}\overline{z} ^{k_\alpha }$ is a well-defined invariant and has only isolated zeros on $S^2$. Under this condition, it can be checked that (cf. [11])

$$\begin{aligned} \partial \overline{\partial }\log {|\det \Omega _{\alpha }|^2}= L_{\alpha -1}-2L_{\alpha }+L_{\alpha +1}, \end{aligned}$$

(2.14)

which is in accordance with (2.13) in the case $k=1$. Furthermore if $\phi _{\alpha }$ is $\partial '$-irreducible and unramified, then $|\det \Omega _{\alpha }|^2 \mathrm{d}z^{k_\alpha } \mathrm{d}\overline{z} ^{k_\alpha }$ is a well-defined invariant and has no zeros on $S^2$. It follows from (2.14) that (cf. [11])

$$\begin{aligned} \delta _{\alpha -1} - 2\delta _\alpha + \delta _{\alpha +1} = - 2 k_\alpha , \end{aligned}$$

(2.15)

where $\delta _\alpha =\frac{1}{2\pi \sqrt{-1}} \int _{S^2} L_\alpha \mathrm{d} \overline{z} \wedge \mathrm{d}z$.

At last, we review the rigidity theorem of conformal minimal immersions with constant curvature from $S^2$ to ${\mathbb {C}}P^N$.

The Veronese sequence. Let $f_i^{(N)}=\left( f_{i,0},\ldots , f_{i,N}\right) ^T$ for each $i=0,\ldots ,N$. Let $f_{i,p}$ be given for $i,p=0,1,\ldots ,N$ as follows

$$\begin{aligned} f_{i,p}=\frac{i!}{(1+z\overline{z})^i}\sqrt{N \atopwithdelims ()p}z^{p-i} \sum _k (-1)^k {p \atopwithdelims ()i-k} {N-p \atopwithdelims ()k} (z\overline{z})^k. \end{aligned}$$

(2.16)

Such a map $\phi _i^{(N)} =[f_i^{(N)}]:S^2 \rightarrow {\mathbb {C}}P^N$ is a conformal minimal immersion with constant curvature $\frac{4}{N+2i(N-i)}$ and constant Kähler angle $\theta _i ^{(N)}$ given by

$$\begin{aligned}\left( \tan \frac{\theta _i^{(N)}}{2}\right) ^2=\frac{i(N-i+1)}{(i+1)(N-i)}.\end{aligned}$$

Such a harmonic sequence $\phi _0^{(N)},\ldots , \phi _N ^{(N)} :S^2 \rightarrow {\mathbb {C}}P^N$ is called the Veronese sequence. We always denote it by $V _0^{(N)},\ldots , V _N ^{(N)} :S^2 \rightarrow {\mathbb {C}}P^N$.

Bolton et al. proved that (cf. [3]) if $\psi$ is a linearly full conformal minimal 2-sphere of constant curvature immersed in ${\mathbb {C}}P^N$, then, up to a holomorphic isometry of ${\mathbb {C}}P^N$, $\psi$ is an element of the Veronese sequence (i.e., a Veronese surface).

3 Homogeneous harmonic maps from $S^2$ to G(k, N)

An immersion $\phi :S^2\rightarrow G(k,N)$ is said to be homogeneous, if for any two points $p,q\in S^2$ there exist an isometry $\sigma$ of $S^2$ and a holomorphic isometry u of G(k, N) such that $\sigma (p)=q$ and the following diagram communicates

i.e.,

$$\begin{aligned} \phi \circ \sigma =u\circ \phi . \end{aligned}$$

(3.1)

Here we can identify $\sigma$ (resp. u) with an element of SU(2) (resp. U(N)) (cf. [7]). All such u form a subgroup G of U(N) and G acts transitively on $\phi (S^2)$. It is known that such 2-spheres in G(k, N) have constant curvature, but they are non-minimal in general. Let the complex coordinate z on $S^2\simeq {\mathbb {C}}P^1$ be given by two complex variables $z_0$ and $z_1$, i.e., $z=[(z_0,z_1)^T]=[(1,\frac{z_1}{z_0})^T]$ (for computation convenience $z=\frac{z_1}{z_0}$) and let

$$\begin{aligned} SU(2)=\left\{ g= \begin{pmatrix} a&{}-\overline{b}\\ b&{}\overline{a} \end{pmatrix}; a,b\in {\mathbb {C}}, |a|^2+|b|^2=1 \right\} . \end{aligned}$$

(3.2)

Then $\sigma$ is given by

$$\begin{aligned} \sigma (z)=g^*z=[(\overline{a}z_0+\overline{b}z_1,~-bz_0+az_1)^T]. \end{aligned}$$

(3.3)

In particular, if $\phi$ is harmonic and satisfies (3.1), then it is called a homogeneous harmonic map from $S^2$ to G(k, N). In the following we give a property of homogeneous harmonic map.

Lemma 3.1

Let $\phi :S^2\rightarrow G(k,N)$ be a homogeneous harmonic map that belongs to the harmonic sequence (2.3), then for each $\alpha =-\alpha _0,\ldots ,\beta _0$ the harmonic map $\phi _{\alpha }:S^2\rightarrow G(k_{\alpha },N)$ is homogeneous. This time the harmonic sequence (2.3) is said to be a homogeneous harmonic sequence.

Proof

Since $\phi _0$ in (2.3) is homogeneous, it follows from (3.1) that

$$\begin{aligned} \phi _0\circ \sigma =u\circ \phi _0. \end{aligned}$$

(3.4)

Set $\underline{\phi }_0=$ span$\left\{ e_1,\ldots ,e_{k_0}\right\}$, where $e_1,\ldots ,e_{k_0}$ are unit orthogonal vectors of ${\mathbb {C}}^N$. Then from $\underline{\phi }_1=A_{{\phi }_0}'(\underline{\phi }_0)$ we get $\underline{\phi }_1=$ span$\left\{ v_{k_0+1},\ldots ,v_{k_0+k_1}\right\}$; for each $i=1,\ldots ,k_0$, $v_{k_0+i}$ is given by

$$\begin{aligned} v_{k_0+i}=\partial {e_i}-\sum _{s=1}^{k_0}\left\langle \partial {e_i} , e_s \right\rangle e_s, \end{aligned}$$

(3.5)

since there may exist some i such that $v_{k_0+i}=0$, we exclude all zero vectors, so here $k_1\le k_0$.

Set $u\in U(N)$. By (3.5) a straightforward computation shows

$$\begin{aligned} \begin{aligned} \partial {(ue_i)}-\sum _{s=1}^{k_0}\left\langle \partial {(ue_i)} , e_s \right\rangle e_s&=(\partial {u}e_i+u\partial {e_i})-\sum _{s=1}^{k_0}\left\langle \partial {u}e_i+u\partial {e_i} , e_s \right\rangle e_s\\&=u\left( \partial {e_i}-\sum _{s=1}^{k_0}\left\langle \partial {e_i} , e_s \right\rangle e_s\right) \\&=uv_{k_0+i}, \end{aligned} \end{aligned}$$

(3.6)

which implies

$$\begin{aligned} A_{{\phi }_0}'(u\circ \underline{\phi }_0)=u\circ A_{{\phi }_0}'(\underline{\phi }_0)=u\circ \underline{\phi }_1. \end{aligned}$$

(3.7)

On the other hand, from (3.3) $\phi _0\circ \sigma =\phi _0(w)$, where $w=\frac{-b+az}{\overline{a}+\overline{b}z}$. Since $\frac{\partial {\phi _0}}{\partial {z}}=\frac{\partial {\phi _0}}{\partial {w}}\frac{\partial {w}}{\partial {z}}$, then

$$\begin{aligned} A_{{\phi }_0}'(\underline{\phi }_0\circ \sigma )=A_{{\phi }_0}'(\underline{\phi }_0)\circ \sigma =\underline{\phi }_1\circ \sigma . \end{aligned}$$

(3.8)

It follows from (3.4), (3.7) and (3.8) that

$$\begin{aligned} \underline{\phi }_1\circ \sigma =u\circ \underline{\phi }_1 \end{aligned}$$

(3.9)

which verifies that $\phi _1$ is homogeneous.

The other cases of $\phi _{\alpha }$ are similar to the above. Thus we get the conclusion. $\square$

In the case $k=1$, Veronese sequence is the standard homogeneous harmonic sequence in ${\mathbb {C}}P^{N-1}$ (cf. [2]). In the case $k=2$, if $\phi$ is a homogeneous harmonic map from $S^2$ to ${\mathbb {H}}P^n$, then u is an element of $Sp(n+1)\subset U(2n+2)$ in (3.1).

4 Reducible homogeneous harmonic maps from $S^2$ to ${\mathbb {H}}P^n$

Let $\phi :S^2 \rightarrow {\mathbb {H}}P^n$ be a linearly full harmonic map of isotropy order r. If $\phi$ has finite isotropy order, then $r=2s$ for $1\le s\le n$ by ([1], Proposition 3.2 and Lemma 3.10); if $\phi$ is strongly isotropic, then $r=\infty$. If $\phi _0:S^2 \rightarrow {\mathbb {H}}P^n$ is a reducible linearly full harmonic map, then by ([1], Proposition 3.7) we know that $\phi _0$ is a quaternionic mixed pair or a quaternionic Frenet pair.

Definition 4.1

([1])

• 1. A map $\phi :M \rightarrow {\mathbb {H}}P^n$ is called a quaternionic mixed pair if $\underline{\phi }=\underline{f}\oplus {{\mathbf {J}}}\underline{f}$ where $f:M\rightarrow {\mathbb {C}}P^{2n+1}$ is holomorphic and $G'(f)\perp {{\mathbf {J}}}\underline{f}$. Here $G'(f)=\underline{Im}A_f'$.

• 2. A map $\phi :M \rightarrow {\mathbb {H}}P^n$ is called a quaternionic Frenet pair if $\underline{\phi }=G^{(r-1)}(h)\oplus G^{(r)}(h)$ for some integer r, with $1\le r\le n+1$ and holomorphic map $h:M\rightarrow {\mathbb {C}}P^{2n+1}$ with $G^{(2r-1)}(h)={{\mathbf {J}}}\underline{h}$. Here $~G^{(0)}(h)=\underline{h}, ~G^{(i)}(h)=G'(G^{(i-1)}(h))$.

In the following we discuss these two types in the case of constant curvature.

If $\phi _0$ is a linearly full quaternionic Frenet pair, then

$$\begin{aligned} \underline{\phi }_0=\underline{f}_n^{(2n+1)} \oplus \underline{f}_{n+1}^{(2n+1)}, \end{aligned}$$

(4.1)

where $\underline{f}_0^{(2n+1)}, \ldots , \underline{f}_{2n+1}^{(2n+1)}:S^2 \rightarrow {\mathbb {C}}P^{2n+1}$ is a harmonic sequence with the linearly full totally ${\mathbf {J}}$-isotropic map $\underline{f}_0^{(2n+1)}$.

Firstly we recall ([1], §3) that a full holomorphic map $\underline{f}_0^{(2n+1)} : S^2 \rightarrow CP^{2n+1}$ satisfying ${\underline{f}}_{2n+1}^{(2n+1)}={{\mathbf {J}}}\underline{f}_0^{(2n+1)}$ is said to be totally ${\mathbf {J}}$ -isotropic; this generates a harmonic sequence

$$\begin{aligned} 0\mathop {\longleftarrow }\limits ^{A_0''} {\underline{f}} _0^{(2n+1)} \mathop {\longrightarrow }\limits ^{A_0'}\cdots \mathop {\longrightarrow }\limits ^{A_{n-1}'} {\underline{f}}_{n}^{(2n+1)} \mathop {\longrightarrow }\limits ^{A_{n}'} {\underline{f}}_{n+1}^{(2n+1)} \mathop {\longrightarrow }\limits ^{A_{n+1}'} \cdots \mathop {\longrightarrow }\limits ^{A_{2n}'} {\underline{f}}_{2n+1}^{(2n+1)} \mathop {\longrightarrow }\limits ^{A_{2n+1}'} 0. \end{aligned}$$

From the harmonic sequence, $f_{2n+1-i}^{(2n+1)}={\mathbf {J}} f_i^{(2n+1)}$ for all i so that:

$$\begin{aligned} l_j^{(2n+1)}=l_{2n+1-j}^{(2n+1)}, \end{aligned}$$

(4.2)

and set ${\mathbf {J}} f_0^{(2n+1)}=\tau _{2n+1} f_{2n+1}^{(2n+1)}$ , then

$$\begin{aligned} |\tau _{2n+1}|^2=\frac{|f_0^{(2n+1)}|^2}{|f_{2n+1}^{(2n+1)}|^2},\quad {\mathbf {J}} f_j^{(2n+1)}=\tau _{2n+1-j} f_{2n+1-j}^{(2n+1)}, \end{aligned}$$

(4.3)

where $\tau _{2n+1-j}=(-1)^j \tau _{2n+1} \frac{|f_{2n+1}^{(2n+1)}|^2}{|f_{2n+1-j}^{(2n+1)}|^2}$ for each $j=0, \ldots , 2n+1$.

Obviously $\phi _0$ belongs to the following harmonic sequence (cf. [4])

$$\begin{aligned} 0\mathop {\longleftarrow }\limits ^{A_0''} {{\underline{f}}_0^{(2n+1)}} \mathop {\longleftarrow }\limits ^{A_1''} \cdots \mathop {\longleftarrow }\limits ^{A_{n-1}''} {{\underline{f}}_{n-1}^{(2n+1)}} \mathop {\longleftarrow }\limits ^{A_{\phi _0}''} \underline{\phi }_0 \mathop {\longrightarrow }\limits ^{A_{\phi _0}'} {\underline{f}}_{n+2}^{(2n+1)} \mathop {\longrightarrow }\limits ^{A_{n+2}'} \cdots \mathop {\longrightarrow }\limits ^{A_{2n}'} {\underline{f}}_{2n+1}^{(2n+1)} \mathop {\longrightarrow }\limits ^{A_{2n+1}'} 0. \end{aligned}$$

(4.4)

Then we give the following proposition without proof:

Proposition 4.2

([9], Proposition 3.1) Let $\phi _0:S^2 \rightarrow {\mathbb {H}}P^n$ be a linearly full quaternionic Frenet pair of constant curvature $K_0$. Denote the isotropy order of $\phi _0$ by r. Then $K_0=\frac{2}{n(n+2)}$, $r=\infty$, and up to a symplectic isometry of ${\mathbb {H}}P^n$,

$$\begin{aligned} \underline{\phi }_0=U\underline{V}_n^{(2n+1)}\oplus U\underline{V}_{n+1}^{(2n+1)} \end{aligned}$$

for some $U\in G_{2n+2}\triangleq \bigg \{U\in U(2n+2), \ UW_{n+1} U^{T}=J_{n+1}\bigg \}$,

where $W_{n+1}=\mathrm{antidiag} \underbrace{\left\{ \left( \begin{array} {lr} 0 &{} -1 \\ 1 &{} 0 \\ \end{array}\right) , \ldots , \left( \begin{array} {lr} 0 &{} -1 \\ 1 &{} 0 \\ \end{array}\right) \right\} }_{n+1}$.

Remark 4.3

Since both $\underline{V}_n^{(2n+1)}$ and $\underline{V}_{n+1}^{(2n+1)}$ are Veronese surfaces in ${\mathbb {C}}P^{2n+1}$. It is easy to check that such $\phi _0$ is SU(2)-equivalent, so $\phi _0$ is homogeneous. Thus all linearly full homogeneous quaternionic Frenet pairs are given by Proposition 4.2.

If $\phi _0$ is a linearly full quaternionic mixed pair, then

$$\begin{aligned} \underline{\phi }_0=\underline{f}_{0}^{(m)}\oplus {\mathbf {J}} \underline{f}_{0}^{(m)}, \end{aligned}$$

(4.5)

where $\underline{f}_0^{(m)} :S^2 \rightarrow {\mathbb {C}}P^{m} \subseteq {\mathbb {C}}P^{2n+1}$ ($n\le m\le 2n+1$) is holomorphic and ${\underline{f}}_1^{(m)} \perp {{\mathbf {J}}}{\underline{f}_0^{(m)}}$.

Obviously $\phi _0$ belongs to the following harmonic sequence

$$\begin{aligned} 0\mathop {\longleftarrow }\limits ^{A_{Jm}''} {\mathbf {J}}{{\underline{f}}_m^{(m)}} \mathop {\longleftarrow }\limits ^{A_{J(m-1)}''} \cdots \mathop {\longleftarrow }\limits ^{A_{J1}''} {\mathbf {J}}{{\underline{f}}_1^{(m)}} \mathop {\longleftarrow }\limits ^{A_{\phi ^0}''} \underline{\phi }_0 \mathop {\longrightarrow }\limits ^{A_{\phi ^0}'} {\underline{f}}_1^{(m)} \mathop {\longrightarrow }\limits ^{A_1'} \cdots \mathop {\longrightarrow }\limits ^{A_{m-1}'} {\underline{f}}_m^{(m)} \mathop {\longrightarrow }\limits ^{A_m'} 0, \end{aligned}$$

(4.6)

where $A_{Ji}''$ represents $A_{{\mathbf {J}}{{f}_i^{(m)}}}''$ for each $i=1,\ldots ,m$.

So the induced metric by $\phi _0$ is given by

$$\begin{aligned} \mathrm{d}s_0^2=2l_0^{(m)} \mathrm{d}z \mathrm{d}\overline{z}, \end{aligned}$$

(4.7)

where $l_0^{(m)} \mathrm{d}z \mathrm{d}\overline{z}$ is the induced metric by the map $\underline{f}_0^{(m)}$.

Then we prove

Proposition 4.4

Let $\phi _0:S^2 \rightarrow {\mathbb {H}}P^n$ be a linearly full homogeneous quaternionic mixed pair. Denote the isotropy order and Gaussian curvature of $\phi _0$ by r and $K_0$, respectively. Then up to a symplectic isometry of ${\mathbb {H}}P^n$, $\phi _0$ belongs to one of the following minimal immersions.

• 1. $\phi _0=U\underline{V}_0^{(2n+1)}\oplus U\underline{V}_{2n+1}^{(2n+1)}$ for some $U\in G_{2n+2}$, where $K_0=\frac{2}{2n+1}$, $r=2n$;

• 2. $\phi _0=\underline{V}_0^{(n)}$ with $K_0=\frac{2}{n}$, $r=\infty$;

• 3. $n=2t+1~(t>0)$ and $\phi _0=\left[ \left( \phi _{0,0},\ldots ,\phi _{0,n}\right) ^T\right]$, for $q_1=0,\ldots ,t$, $q_2=t+1,\ldots ,n$, $\phi _{0,q_1}$, $\phi _{0,q_2}$ are given by

  $$\begin{aligned} \phi _{0,q_1}=\sqrt{{n\atopwithdelims ()q_1}}z^{q_1}+(-1)^{q_1}\overline{\lambda }\sqrt{{n\atopwithdelims ()n-q_1}}\overline{z}^{n-q_1}j, ~\phi _{0,q_2}=\sqrt{1-|\lambda |^2}\sqrt{{n\atopwithdelims ()q_2}}z^{q_2}, \end{aligned}$$

  where $\lambda$ is a complex parameter satisfying $0<|\lambda |^2<1$ and $K_0=\frac{2}{n}$, $r=n-1$.

Proof

Let $\phi _0:S^2 \rightarrow {\mathbb {H}}P^n$ be a linearly full quaternionic mixed pair. Since $\phi _0$ is homogeneous, we know that there exists a matrix $u\in Sp(n+1)\subset SU(2n+2)$ such that

$$\begin{aligned} u\circ f_0^{(m)}=f_0^{(m)}\circ \sigma . \end{aligned}$$

(4.8)

By (4.7) we get that $K_0=\frac{2}{m}$, and up to a holomorphic isometry of $CP^{2n+1}$, $\underline{f}_0^{(m)}$ is a Veronese surface. We can choose a complex coordinate z on ${\mathbb {C}}=S^2 {\setminus } \left\{ pt\right\}$ so that $f_0^{(m)}=UV_0^{(m)}$, where $U \in U(2n+2)$ and $V_0^{(m)}$ has the standard expression given in (2.16) (adding zeros to $V_0^{(m)}$ such that $V_0^{(m)}\in {\mathbb {C}}^{2n+2}$). A straightforward computation shows

$$\begin{aligned} V_0^{(m)}\circ \sigma (z_0,~z_1)=\begin{pmatrix} D_{m+1}&{}*\\ O&{}*\end{pmatrix}V_0^{(m)}(z_0,~z_1), \end{aligned}$$

(4.9)

where

$$\begin{aligned} D_{m+1}=\left( d_{ij}\right) _{0\le i,j\le m}, ~d_{ij}=\frac{\sqrt{m\atopwithdelims ()i}}{\sqrt{m\atopwithdelims ()j}}{m-i\atopwithdelims ()k}{i\atopwithdelims ()j-k} \overline{a}^{m-i-k}\overline{b}^{k}(-b)^{i-j+k}a^{j-k}.\quad \end{aligned}$$

(4.10)

Then we have

$$\begin{aligned} \overline{U}^T uU V_0^{(m)}(z_0,~z_1)=\begin{pmatrix} D_{m+1}&{}D_2 \\ O&{}D_4 \end{pmatrix}V_0^{(m)}(z_0,~z_1). \end{aligned}$$

(4.11)

By differentiating with respect to $z_0$ in the above formula, the matrices $\overline{U}^T uU$ and $\begin{pmatrix} D_{m+1}&{}D_2 \\ O&{}D_4 \end{pmatrix}$ have the same effect on all derivatives of $V_0^{(m)}(z_0,~z_1)$. Generally, $V_0^{(m)}(z_0,~z_1)$ is not full in ${\mathbb {C}}^{2n+2}$, so the two above matrixes are not identical. But the matrix $\overline{U}^T uU$ is still the type of the following matrix, i.e.,

$$\begin{aligned} \overline{U}^T uU =\begin{pmatrix} D_{m+1}&{}*\\ O&{}*\end{pmatrix}. \end{aligned}$$

(4.12)

Since $U\in U(2n+2)$ and $u\in Sp(n+1)\subset SU(2n+2)$, we get

$$\begin{aligned} \overline{U}^T uU =\begin{pmatrix} D_{m+1}&{}O \\ O&{}C_{2n+1-m} \end{pmatrix}, \end{aligned}$$

(4.13)

where $D_{m+1}\in U(m+1)$ and $C_{2n+1-m}\in U(2n+1-m)$.

Set $U^{T}J_{n+1}U=\overline{W}$. Then

$$\begin{aligned} W^{T}=-W, \ W^*W=I, \end{aligned}$$

(4.14)

where I is the identity matrix.

Since $u\in Sp(n+1)$, from (4.13) we have

$$\begin{aligned} \begin{pmatrix} \overline{D_{m+1}}&{}\quad O \\ O&{}\quad \overline{C_{2n+1-m}} \end{pmatrix} \overline{W} =\overline{W} \begin{pmatrix} {D_{m+1}}&{}\quad O \\ O&{}\quad {C_{2n+1-m}} \end{pmatrix}. \end{aligned}$$

(4.15)

Set $\overline{W}=\begin{pmatrix} W_{11}&{}W_{12} \\ W_{21}&{}W_{22} \end{pmatrix}$ with $W_{11}=\left( w_{kl}\right) _{0\le k,l\le m}$. Then (4.10) and (4.15) yield

$$\begin{aligned} {\left\{ \begin{array}{ll} w_{m-j,j}=(-1)^{m-j}w_{0m},~j=0,\ldots ,m\\ w_{kl}=0,~k+l\ne m \end{array}\right. } \end{aligned}$$

(4.16)

Case I . r is finite. It follows from the harmonic sequence (4.6) that $m\ge r+1$. Thus for each $1\le \alpha \le r$, we have ${\underline{f}}_{\alpha }^{(m)}\perp {{\mathbf {J}}}{\underline{f}_0^{(m)}}$, which are equivalent to the following equations

$$\begin{aligned} tr\left( V_{\alpha }^{(m)} {V_0^{(m)}}^{T} U^{T}J_{n+1}U\right) =0 \Leftrightarrow tr\left( V_{\alpha }^{(m)} {V_0^{(m)}}^{T} \overline{W}\right) =0,\ \alpha =1,\ldots ,r \end{aligned}$$

(4.17)

hold.

Set $V_{\alpha }^{(m)} {V_0^{(m)}}^{T}=\begin{pmatrix} V_{11}&{}O \\ O&{}O \end{pmatrix}$ with $V_{11}=\left( v_{ij}\right) _{0\le i,j\le m}$, then

$$\begin{aligned} v_{ij}=\frac{\alpha !}{(1+z\overline{z})^{\alpha }}\sqrt{{m\atopwithdelims ()i}{m\atopwithdelims ()j}}\sum _{k}(-1)^k {i\atopwithdelims ()\alpha -k}{m-i\atopwithdelims ()k}z^{i+j+k-\alpha }\overline{z}^{k}. \end{aligned}$$

(4.18)

Since r is finite, we know $w_{0m}\ne 0$. From (4.16) and (4.18), we get

$$\begin{aligned} tr\left( V_{m-1}^{(m)} {V_0^{(m)}}^{T} \overline{W}\right) =0,\ tr\left( V_{m}^{(m)} {V_0^{(m)}}^{T} \overline{W}\right) \ne 0, \end{aligned}$$

(4.19)

which implies that ${\underline{f}}_{m-1}^{(m)}$ is perpendicular to ${{\mathbf {J}}}{\underline{f}_0^{(m)}}$, but ${\underline{f}}_{m}^{(m)}$ is not perpendicular to ${{\mathbf {J}}}{\underline{f}_0^{(m)}}$ by (4.17).

Hence we have

$$\begin{aligned} m=r+1. \end{aligned}$$

(4.20)

Let $r=2s$. It follows from (4.16) that

$$\begin{aligned} W_{11}=w_{m0}W_{s+1}. \end{aligned}$$

(4.21)

Then the corresponding $\overline{W}$ is given by

$$\begin{aligned} \overline{W}=\begin{pmatrix} w_{m0}W_{s+1}&{}W_{12} \\ W_{21}&{}W_{22} \end{pmatrix}, \end{aligned}$$

(4.22)

where $W_{21}$ is a $(2n+1-m)\times (m+1)$-matrix.

Define a set

$$\begin{aligned} G_W\triangleq \left\{ U\in U(2n+2), \ UWU^{T}=J_{n+1}\right\} . \end{aligned}$$

For a given W, the following can be easily checked

• (i) $\forall \ A\in Sp(n+1), \ U\in G_W$, we have that $AU\in G_W$;

• (ii) $\forall \ U, V \in G_W, \ \exists \ A=UV^* \in Sp(n+1) \ s.t. \ U=AV$.

In the following, in order to get the explicit expression of $\phi _0$, we discuss W, respectively, by the two cases that n is an even or odd.

Case I.1. n is an even, i.e., $n=2t~(t>0)$.

In this case, since $m>n$, i.e., $m+1>2n+1-m$, then from (4.14) and (4.22) we know $W_{21}=O$, i.e.,

$$\begin{aligned} {W}=\begin{pmatrix} W_{s+1}&{}O \\ O&{}W_{22} \end{pmatrix}, \end{aligned}$$

(4.23)

where $W_{22}\in U(2n+1-m)$.

Now we claim that $m=2n+1~(s=n)$. Otherwise if $m<2n+1$, then $s<n$, and for any given W, we can choose proper $U\in G_W$ such that ${{\mathbf {J}}} UV_0^{(m)}=-UV_{m}^{(m)}$, and then up to $Sp(n+1)$,

$$\begin{aligned} \underline{\phi }_0=U\underline{V}_0^{(m)}\oplus U\underline{V}_{m}^{(m)}. \end{aligned}$$

Obviously $\phi _0$ has image in ${\mathbb {H}}P^{s}$ , so it is not linearly full. It contradicts our assumption that $\phi _0$ is linearly full.

Furthermore we get $K_0=\frac{2}{2n+1}$, $W=W_{n+1}$ and $G_W=G_{2n+2}$. Then the proof of Proposition 4.2(see ([9], Proposition 3.1)) gives that up to $Sp(n+1)$,

$$\begin{aligned} \underline{\phi }_0=U\underline{V}_0^{(2n+1)}\oplus U\underline{V}_{2n+1}^{(2n+1)}, \end{aligned}$$

where $U\in G_{2n+2}$.

Obviously it belongs to case (1) with $K_0=\frac{2}{2n+1},~r=2n$.

Case I.2. n is an odd, i.e., $n=2t+1~(t>0)$.

In this case, if $m>n$, then by the same discussion as

Case I.1, we conclude that $m=2n+1$, and up to $Sp(n+1)$, the corresponding $\phi _0$ belongs to case (1) with $K_0=\frac{2}{2n+1},~r=2n$.

If $m=n$, then the corresponding $W_{21}$ in (4.22) is a $(n+1)\times (n+1)$-matrix. If $|w_{n0}|^2=0$, then $W_{11}=O$, which implies $f_m^{(m)}\perp {{\mathbf {J}}}{f_0^{(m)}}$, so $\phi _0$ is strongly isotropic. It contradicts our assumption that the isotropy order r is finite. If $|w_{n0}|^2=1$, then the corresponding $\phi _0$ is not linearly full.

Now we assume $0<|w_{n0}|^2<1$. Denote $w_{n0}$ by $\lambda$. Then we get the type of $\overline{W}=U^{T}J_{n+1}U\in U(2n+2)$ as follows:

(4.24)

where $0<|\lambda |^2<1$.

From $\overline{W}\overline{U}^T = U^T J_{n+1}$, the corresponding $U=\left[ e_1,e_2,\ldots ,e_{2n+1},e_{2n+2}\right] ^T$ satisfy

$$\begin{aligned} e_{2\alpha }=\overline{W}\overline{e}_{2\alpha -1},\quad \alpha =1,\ldots ,n+1, \end{aligned}$$

(4.25)

where $e_i$ are unit column vectors in ${\mathbb {C}}^{2n+2}$.

Generally, suppose $\{e_1,e_2,\ldots ,e_{2\alpha -3},e_{2\alpha -2}=\overline{W}\overline{e}_{2\alpha -3}\}~(\alpha \ge 2)$ are mutually orthogonal, we choose a unit column vector $e_{2\alpha -1}{\in } {\mathbb {C}}^{2n+2}$ such that $\{e_1,e_2,\ldots ,e_{2\alpha -3},e_{2\alpha -2},e_{2\alpha -1}\}$ are mutually orthogonal. Set $e_{2\alpha }=\overline{W}\overline{e}_{2\alpha -1}$, then

$$\begin{aligned} \left\langle e_{2\alpha },~e_{2\alpha -1}\right\rangle =e_{2\alpha -1}^TW^Te_{2\alpha -1}=-tr(e_{2\alpha -1}e_{2\alpha -1}^TW)=0, \end{aligned}$$

and for any $2\le \beta \le \alpha$,

$$\begin{aligned}&\left\langle e_{2\alpha },~e_{2\beta -3}\right\rangle ={e}_{2\alpha -1}^TW^Te_{2\beta -3} =-{e}_{2\alpha -1}^TWe_{2\beta -3} =-{e}_{2\alpha -1}^T\overline{e}_{2\beta -2}\\&\quad =-\left\langle e_{2\alpha -1},~e_{2\beta -2}\right\rangle =0, \end{aligned}$$

$$\begin{aligned} \left\langle e_{2\alpha },~e_{2\beta -2}\right\rangle ={e}_{2\alpha -1}^TW^T\overline{W}\overline{e}_{2\beta -3} ={e}_{2\alpha -1}^T\overline{e}_{2\beta -3} =\left\langle e_{2\alpha -1},~e_{2\beta -3}\right\rangle =0. \end{aligned}$$

Thus $\{e_1,e_2,\ldots ,e_{2\alpha -3},e_{2\alpha -2},e_{2\alpha -1},e_{2\alpha }\}$ are mutually orthogonal.

Without loss of generality, in this case for $p=0,\ldots ,t$ we choose

$$\begin{aligned} e_{2p+1}=\left( \underbrace{0,\ldots ,0}_{p},1,0,\ldots ,0\right) ^T, \end{aligned}$$

(4.26)

then the corresponding $e_{2p+2}$ is given by

$$\begin{aligned} e_{2p+2}=\overline{W}\overline{e}_{2p+1}=\left( \underbrace{0,\ldots ,0}_{n-p},(-1)^p\lambda ,0,\ldots ,0,-w_{p+1,n+2},\ldots ,-w_{p+1,2n+2}\right) ^T. \end{aligned}$$

(4.27)

Observing (4.26) and (4.27), we find $\left\{ e_1,e_2,\ldots ,e_{2t+1},e_{2t+2}\right\}$ are mutually orthogonal.

Next for $q=t+1,\ldots ,n$ we successively choose

$$\begin{aligned}&e_{2q+1}\nonumber \\&=\left( \underbrace{0,\ldots ,0}_{q},\sqrt{1-|\lambda |^2},0,\ldots ,0,(-1)^{n-q}\frac{\overline{\lambda }w_{n+1-q,n+2}}{\sqrt{1-|\lambda |^2}},\ldots ,(-1)^{n-q}\frac{\overline{\lambda }w_{n+1-q,2n+2}}{\sqrt{1-|\lambda |^2}}\right) ^T\nonumber \\ \end{aligned}$$

(4.28)

then the corresponding $e_{2q+2}$ is given by

$$\begin{aligned} e_{2q+2}=\left( \underbrace{0,\ldots ,0}_{n+1},*\right) ^T. \end{aligned}$$

(4.29)

From (4.26)-(4.29) we obtain the type of the corresponding U; furthermore, we have

$$\begin{aligned} UV_0^{(n)}=\left( \ldots ,\sqrt{{n \atopwithdelims ()p}}z^p,(-1)^p\lambda \sqrt{{n \atopwithdelims ()n-p}}z^{n-p},\ldots ,\sqrt{1-|\lambda |^2}\sqrt{{n \atopwithdelims ()q}}z^q,0,\ldots \right) ^T, \end{aligned}$$

(4.30)

where $p=0,\ldots ,t$ and $q=t+1,\ldots ,n$.

So the corresponding $\phi _0$ belongs to case (3) with $K_0=\frac{2}{n}$, $r=n-1$.

Case II. $r=\infty$. In this case, it follows from ([9], Proposition 3.2) that up to $Sp(n+1)$,

$$\begin{aligned} \phi _0=U\underline{V}_0^{(n)}\oplus {{\mathbf {J}}}U\underline{V}_0^{(n)} \end{aligned}$$

with $K_0=\frac{2}{n}$ for some $U\in G_{2n+2}$.

For convenience, we choose

$$\begin{aligned} U=\begin{pmatrix} 1 &{} 0 &{} \cdots &{} 0 &{} 0 &{} 0 &{} \cdots &{} 0 &{} 0 \\ 0 &{} 0 &{} \cdots &{} 0 &{} 0 &{} 0 &{} \cdots &{} 0 &{} (-1)^0 \\ 0 &{} 1 &{} \cdots &{} 0 &{} 0 &{} 0 &{} \cdots &{} 0 &{} 0\\ 0 &{} 0 &{} \cdots &{} 0 &{} 0 &{} 0 &{} \cdots &{} (-1)^{1} &{} 0 \\ \vdots &{} \vdots &{} \ddots &{} \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots &{} \vdots \\ 0 &{} 0 &{} \cdots &{} 0 &{} 0 &{} (-1)^{n-1} &{} \cdots &{} 0 &{} 0\\ 0 &{} 0 &{} \cdots &{} 1 &{} 0 &{} 0 &{} \cdots &{} 0 &{} 0\\ 0 &{} 0 &{} \cdots &{} 0 &{} (-1)^n &{} 0 &{} \cdots &{} 0 &{} 0 \end{pmatrix}\in G_{2n+2}. \end{aligned}$$

A straightforward calculation shows

$$\begin{aligned} U{V}_0^n= & {} \left[ (1,0,\sqrt{2}z,0,\ldots ,z^n,0)^T\right] ,\\ {{\mathbf {J}}}U{V}_0^n= & {} \left[ (0,1,0,\sqrt{2}\overline{z},\ldots ,0,\overline{z}^n)^T\right] , \end{aligned}$$

which implies

$$\begin{aligned} \phi _0=\left[ (1,\sqrt{2}z,\ldots ,z^n)^T\right] :S^2\rightarrow {\mathbb {C}}P^n\hookrightarrow {\mathbb {H}}P^n. \end{aligned}$$

Hence, in this case, up to $Sp(n+1)$, $\phi _0$ is the composition of ${V}_0^{(n)}$ with the totally geodesic inclusion of ${\mathbb {C}}P^n$ in ${\mathbb {H}}P^n$ and belongs to case (2) with $K_0=\frac{2}{n},~r=\infty$.

In summary we get the conclusion. $\square$

Remark 4.5

We conjecture that all linearly full quaternionic mixed pairs of constant curvature are given by Proposition 4.4.

5 Irreducible homogeneous harmonic maps from $S^2$ to ${\mathbb {H}}P^n$

Now, we consider the irreducible harmonic maps $\phi : S^2 \rightarrow {\mathbb {H}}P^{n}$ of isotropy order r. In the following we consider the two cases of finite isotropy order or strongly isotropic.

At first we consider the case of finite isotropy order, i.e., $r=2s~(s=1,\ldots ,n-1)$. Here we exclude the case of $s=n$, as if $r=2n$, then the corresponding $\phi$ is reducible by ([1], Lemma 3.10). We state the following lemma by ([1], Theorem 4.7):

Lemma 5.1

([1]) Let $\phi : S^2 \rightarrow {\mathbb {H}}P^n$ be an irreducible harmonic map of finite isotropy order r, where $r=2s~(s=1,\ldots ,n-1)$. Then there is a unique sequence of harmonic maps $\phi ^i:S^2 \rightarrow G(2,2n+2)~(i=0,1,\ldots ,2l)$ where $l=1,\ldots ,n-s$ such that

• (i) $\underline{\phi }^0=\underline{f}_0^{(m)} \oplus {\mathbf {J}} \underline{f}_0^{(m)}$ for some holomorphic map $\underline{f}_0^{(m)} :S^2 \rightarrow {\mathbb {C}}P^{m} \subseteq {\mathbb {C}}P^{2n+1}$ ($n\le m\le 2n+1$) satisfying ${\underline{f}}_p^{(m)} \perp {{\mathbf {J}}}{\underline{f}_0^{(m)}}$ for $1\le p\le 2l+2s$ but ${\underline{f}}_p^{(m)} \not \perp {{\mathbf {J}}}{\underline{f}_0^{(m)}}$ for $p=2l+2s+1$, that is, $\phi ^0$ is a quaternionic mixed pair of isotropy order $2l+2s$;

• (ii) $\phi ^{2l}=\phi$;

• (iii) for $k=0,1,\ldots ,l-1$, $\phi ^{2k+1}$ is obtained from $\phi ^{2k}$ by forward replacement of some holomorphic subbundle of $\underline{\phi }^{2k}$ not equal to the image of the first $\partial '$-return map of $\phi ^{2k}$. Then the inverse of this transformation is given by ([1], Proposition 4.6(a)) and is given by backward replacement of the image of the first $\partial ''$-return map;

• (iv) for $k=0,1,\ldots ,l-1$, $\phi ^{2k+2}$ is obtained from $\phi ^{2k+1}$ by backward replacement of $\underline{\beta }_k^{\perp } \cap \underline{\phi }^{2k+1}$ where $\underline{\beta }_k$ is the unique holomorphic subbundle of $\underline{\phi }^{2k+1}$ not equal to the image of the first $\partial '$-return map of $\phi ^{2k+1}$ such that $\underline{Im}(A_{\phi ^{2k+1}}' \mid _{\underline{\beta }_k}) \perp {\mathbf {J}} \underline{\beta }_k$. In fact, it is the operation in ([1], Proposition 4.5(b)) with $\underline{\beta }_k^{\perp } \cap \underline{\phi }^{2k+1}$ equal to the antiholomorphic subbundle $\beta$ in ([1], Proposition 4.5(b)). Then the inverse of this transformation is given by ([1], Proposition 4.5(a)) and is given by forward replacement of the image of the first $\partial '$-return map.

  Furthermore,

• (v) for $k=0,1,\ldots ,l-1$, $\phi ^{2k}:S^2 \rightarrow {\mathbb {H}}P^n$ is a quaternionic harmonic map;

• (vi) for $k=0,1,\ldots ,l-1$, $\phi ^{2k+1}:S^2 \rightarrow G(2,2n+2)$ satisfies $G^{''}(\phi ^{2k+1})={\mathbf {J}} \phi ^{2k+1}$;

• (vii) for $i=0,1,\ldots ,2l$, the isotropy order of $\phi ^i$ is $2l+2s-i$.

Let $\phi : S^2 \rightarrow {\mathbb {H}}P^n$ be a linearly full irreducible homogeneous harmonic map of finite isotropy order. By Lemma 5.1 we know the construction of harmonic maps is reversible. Then for $i=0,1,\ldots ,2l-1$ the corresponding harmonic map $\phi ^i$ is obtained by the direct sum of two line bundles of the harmonic maps in the harmonic sequence of $\phi ^{i+1}$. They are all homogeneous. Moreover each harmonic map in the harmonic sequence generated by $\phi ^i$ is also homogeneous by Lemma 3.1. In the following we use Lemma 5.1 to determine all irreducible homogeneous harmonic maps $\phi$ of finite isotropy order.

In (i) of Lemma 5.1 $\phi ^0$ belongs to the harmonic sequence as follows:

$$\begin{aligned} 0\mathop {\longleftarrow }\limits ^{A_{Jm}''} {{\mathbf {J}}}{\underline{f}_m^{(m)}} \mathop {\longleftarrow }\limits ^{A_{J(m-1)}''} \cdots \mathop {\longleftarrow }\limits ^{A_{J1}''} {{\mathbf {J}}}{\underline{f}_1^{(m)}} \mathop {\longleftarrow }\limits ^{A_{\phi ^0}''} \underline{\phi }^0 \mathop {\longrightarrow }\limits ^{A_{\phi ^0}'} {\underline{f}}_1^{(m)} \mathop {\longrightarrow }\limits ^{A_1'} \cdots \mathop {\longrightarrow }\limits ^{A_{m-1}'} {\underline{f}}_{m}^{(m)} \mathop {\longrightarrow }\limits ^{A_{m}'} 0, \end{aligned}$$

(5.1)

where $\underline{\phi }^0 ={\underline{f}}_0^{(m)} \oplus {{\mathbf {J}}}{\underline{f}_0^{(m)}}$. In fact we find $m=2n+1~(2l+2s=2n)$ or $m=n=2t+1~(2l+2s=n-1)$ by Proposition 4.4. At this time the isotropy order of $\phi ^0$ is $m-1$.

By (iii) of Lemma 5.1 and (5.1), there exists a local section $V_0=x_0 f_0^{(m)}+ {\mathbf {J}} f_0^{(m)}$ such that $\underline{V}_0$ is an antiholomorphic subbundle of $\underline{\phi }^0$, and $\phi ^1$ is obtained from $\phi ^0$ by forward replacement of $\underline{V}_0^{\perp }$, i.e.,

$$\begin{aligned} \underline{\phi }^1=\underline{V}_0 \oplus {\underline{f}}_1^{(m)}, \end{aligned}$$

(5.2)

where $x_0$ is a smooth function on $S^2$ expect at some isolated points, and here $\underline{V}_0$ denotes the line bundle generated by $V_0$.

Since $\underline{V}_0$ is an antiholomorphic subbundle of $\underline{\phi }^0$, then we get $\pi _{\phi ^0}(\partial V_0)\in \underline{V}_0$, which implies the equation

$$\begin{aligned} \partial x_0 + x_0 \partial \log |f_0^{(2n+1)}|^2=0 \end{aligned}$$

(5.3)

holds.

Then ${\phi }^1$ with isotropy order $m-2$ belongs to the harmonic sequence as follows:

$$\begin{aligned} 0\mathop {\longleftarrow }\limits ^{A_{Jm}''} {{\mathbf {J}}}{\underline{f}_m^{(m)}} \mathop {\longleftarrow }\limits ^{A_{J(m-1)}''} \cdots \mathop {\longleftarrow }\limits ^{A_{J2}''} {{\mathbf {J}}}{\underline{f}_2^{(m)}} \mathop {\longleftarrow }\limits ^{A_{\phi _{0}^1}''} \underline{\phi }_{0}^1 \mathop {\longrightarrow }\limits ^{A_{\phi _0^1}'} \underline{\phi }_1^1 \mathop {\longrightarrow }\limits ^{A_{\phi _1^1}'} {\underline{f}}_2^{(m)} \mathop {\longrightarrow }\limits ^{A_2'} \cdots \mathop {\longrightarrow }\limits ^{A_{m-1}'} {\underline{f}}_{m}^{(m)} \mathop {\longrightarrow }\limits ^{A_{m}'} 0, \end{aligned}$$

(5.4)

where $\underline{\phi }_0^1 ={\mathbf {J}} \underline{\phi }^1$ and $\underline{\phi }_{1}^1 = \underline{\phi }^1$.

Since $\phi _0^1$ is homogeneous, it has constant curvature. Next we compute the geometric quantities of $\phi _0^1$ to determine its explicit expression. We choose the following orthogonal unit vectors in ${\mathbb {C}}^{2n+2}$

$$\begin{aligned} e_1=\frac{{{\mathbf {J}}}V_0}{|V_0|}, e_2=\frac{{{\mathbf {J}}}f_1^{(m)}}{|f_1^{(m)}|}, e_3=\frac{V_0}{|V_0|}, e_4=\frac{f_1^{(m)}}{|f_1^{(m)}|},e_5=\frac{f_2^{(m)}}{|f_2^{(m)}|},e_{-1}=\frac{{{\mathbf {J}}}f_2^{(m)}}{|f_2^{(m)}|}, \end{aligned}$$

(5.5)

and extend them into the local unitary frame with respect to $\phi _0^1$.

Set $W_0=(e_1, e_2)$, $W_1=(e_3, e_4)$, $W_2=(e_5)$, $W_{-1}=(e_{-1})$, then by (2.6) we get

$$\begin{aligned} \Omega _0= \begin{pmatrix} \lambda _0&{}t_0 \\ \mu _0&{}0 \end{pmatrix},\ \Omega _1= \begin{pmatrix} 0&\frac{|f_2^{(m)}|}{|f_1^{(m)}|} \end{pmatrix},\ \Omega _{-1}= \begin{pmatrix} 0\\ -\frac{|f_2^{(m)}|}{|f_1^{(m)}|} \end{pmatrix}, \end{aligned}$$

(5.6)

where $\lambda _0=\frac{\partial \overline{x}_0-\overline{x}_0\partial \log |f_0^{(m)}|^2 }{|x_0|^2+1}$, $\mu _0=t_0=-\frac{|f_1^{(m)}|}{|V_0|}$ with $|V_0|^2=(|x_0|^2+1)|f_0^{(m)}|^2$.

A straightforward computation shows

$$\begin{aligned} |det\Omega _0|^2\mathrm{d}z^2\mathrm{d}\overline{z}^2= & {} \frac{1}{(|x_0|^2+1)^2} l_0^{(m)}l_0^{(m)} \mathrm{d}z^2\mathrm{d}\overline{z}^2, \end{aligned}$$

(5.7)

$$\begin{aligned} L_0= & {} \lambda _0\overline{\lambda }_0+\mu _0\overline{\mu }_0+t_0\overline{t}_0, \end{aligned}$$

(5.8)

$$\begin{aligned} L_{1}= & {} L_{-1}=l_{1}^{(m)}. \end{aligned}$$

(5.9)

We claim that $\frac{1}{(|x_0|^2+1)^2}$ has no zeros on $S^2$. Otherwise if $z=z_0$ is a zero point of $\frac{1}{(|x_0|^2+1)^2}$, then rank$\ \Omega _0|_{z=z_0}=1$ by (5.6), which implies that $\phi _0^1$ is not homogeneous. It is a contradiction.

So $|det\Omega _0|^2\mathrm{d}z^2\mathrm{d}\overline{z}^2\ne 0$ everywhere on $S^2$. It follows from (2.15) that

$$\begin{aligned} \delta _1-2\delta _0+\delta _{-1}=-4, \end{aligned}$$

(5.10)

where $\delta _{\alpha }=\frac{1}{2\pi \sqrt{-1}} \int _{S^2} L_\alpha d \overline{z} \wedge \mathrm{d}z$ ($\alpha =-1,0,1$).

Since all harmonic maps in the harmonic sequence (5.4) have constant curvature, then we can choose a complex coordinate z on ${\mathbb {C}}=S^2 {\setminus } \left\{ pt\right\}$ so that the induced metric $\mathrm{d}s_{\phi _0^1}^2=(L_0+L_{-1}) \mathrm{d}z \mathrm{d}\overline{z}$ by $\phi _0^1$ is given by

$$\begin{aligned} \mathrm{d}s_{\phi _0^1}^2 = \frac{4m-2}{(1+z\overline{z})^2}\mathrm{d}z\mathrm{d}\overline{z}, \end{aligned}$$

(5.11)

and from ([3], §3) we get

$$\begin{aligned} l_i ^{(m)}=\frac{(i+1)(m-i)}{(1+z\overline{z})^2},\quad \delta _i ^{(m)}= (i+1)(m-i),\quad i=0,\ldots ,m-1. \end{aligned}$$

(5.12)

It follows from (5.9) and (5.12) that

$$\begin{aligned} L_{-1}=\frac{\delta _{-1}}{(1+z\overline{z})^2}. \end{aligned}$$

(5.13)

Analyzing (5.11) and (5.13), we find for $i=-1,0,1$,

$$\begin{aligned} L_{i}=\frac{\delta _{i}}{(1+z\overline{z})^2}. \end{aligned}$$

(5.14)

Using (5.7), (5.9), (5.10), (5.12), (5.14) and (2.14), we obtain

$$\begin{aligned} \partial \overline{\partial } \log (|x_0|^2+1)=0. \end{aligned}$$

(5.15)

It follows from (5.7) that $|x_0|^2+1$ is globally defined on ${\mathbb {C}}$ and has a positive constant limit $c_1$ as $z\rightarrow \infty$. Thus from (5.15)

$$\begin{aligned} |x_0|^2=c_1-1. \end{aligned}$$

(5.16)

In view of (5.3) we have $\overline{\partial }(\overline{x}_0|f_0^{(m)}|^2)=0$, which implies

$$\begin{aligned} \overline{x}_0=\frac{h(z)}{|f_0^{(m)}|^2}=\frac{h(z)}{(1+z\overline{z})^m}, \end{aligned}$$

(5.17)

where h(z) is a holomorphic function on ${\mathbb {C}}$.

It follows from (5.16) and (5.17) that

$$\begin{aligned} |h(z)|^2=(c_1-1)(1+z\overline{z})^{2m}. \end{aligned}$$

(5.18)

Now we claim that $c_1=1$. Otherwise if $c_1\ne 1$, then the holomorphic function h(z) includes the factor such as $(1+z\overline{z})$, which is impossible. So $x_0=0$ and

$$\begin{aligned} \underline{\phi }^1={{\mathbf {J}}}\underline{f}_0^{(m)} \oplus {\underline{f}}_1^{(m)}. \end{aligned}$$

(5.19)

By (iv) of Lemma 5.1, (5.4) and (5.19), there exists a local section $V=y_1 f_1^{(m)} + {{\mathbf {J}}}{f}_0^{(m)}$ such that $\underline{\beta }^{\perp } \cap \underline{\phi }^1=\underline{V}$ is an antiholomorphic subbundle of $\underline{\phi }^1$, and $\phi ^2$ is obtained from $\phi ^1$ by backward replacement of $\underline{V}$, i.e.,

$$\begin{aligned} \underline{\phi }^2=\underline{X} \oplus {\mathbf {J}} \underline{X}, \end{aligned}$$

(5.20)

where $X=\frac{1}{|f_1^{(m)}|^2} f_1^{(m)}- \frac{\overline{y}_1}{|{f}_0^{(m)}|^2} {{\mathbf {J}}}{f}_0^{(m)}$ and $y_1$ is a smooth function on $S^2$ expect at some isolated points.

By the properties of the harmonic sequence (5.4), we know $\pi _{(\phi ^1)^{\perp }}(\overline{\partial } V)={\mathbf {J}} \underline{X}$, which implies $y_1=0$ by a straightforward computation. So

$$\begin{aligned} \underline{\phi }^2=\underline{f}_1^{(m)} \oplus {\mathbf {J}} \underline{f}_1^{(m)}. \end{aligned}$$

(5.21)

Then ${\phi }^2$ with isotropy order $m-3$ belongs to the harmonic sequence as follows:

$$\begin{aligned} 0\mathop {\longleftarrow }\limits ^{A_{Jm}''} \cdots \mathop {\longleftarrow }\limits ^{A_{J3}''} {{\mathbf {J}} \underline{f}_3^{(m)}} \mathop {\longleftarrow }\limits ^{A_{\phi _{-1}^2}''} \underline{\phi }_{-1}^2 \mathop {\longleftarrow }\limits ^{A_{\phi _0^2}''} \underline{\phi }_0^2 \mathop {\longrightarrow }\limits ^{A_{\phi _0^2}'} \underline{\phi }_1^2 \mathop {\longrightarrow }\limits ^{A_{\phi _1^2}'} {\underline{f}}_3^{(m)} \mathop {\longrightarrow }\limits ^{A_3'} \cdots \mathop {\longrightarrow }\limits ^{A_{m}'} 0, \end{aligned}$$

(5.22)

where $\underline{\phi }_0^2 =\underline{\phi }^2$, $\underline{\phi }_1^2={\mathbf {J}} \underline{f}_0^{(m)} \oplus {\underline{f}}_2^{(m)}$ and $\underline{\phi }_{-1}^2={\mathbf {J}} \underline{\phi }_1^2$.

Now we prove

Proposition 5.2

Let $\phi :S^2 \rightarrow {\mathbb {H}}P^n$ be a linearly full irreducible homogeneous harmonic map of finite isotropy order r with constant curvature K. Then up to a symplectic isometry of ${\mathbb {H}}P^n$, $\phi$ is one of the following:

• (1) For some $p=1,\ldots ,n-1$, $\phi =U\underline{V}_p^{(2n+1)}\oplus U\underline{V}_{2n+1-p}^{(2n+1)}$ with some $U\in G_{2n+2}$, where $K=\frac{2}{2p(2n+1-p)+2n+1}$, $r=2n-2p$;

• (2) $n=2t+1~(t>0)$ and for some $p=1,\ldots ,t-1$, $\phi =\left[ \left( \phi _{p,0},\ldots ,\phi _{p,n}\right) ^T\right]$, for $q_1=0,\ldots ,t$, $q_2=t+1,\ldots ,n$, $\phi _{p,q_1}$, $\phi _{p,q_2}$ are given by

  

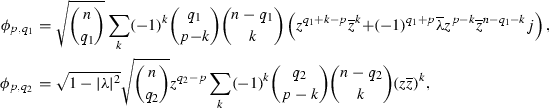
  where $\lambda$ is a complex parameter satisfying $0<|\lambda |^2<1$ and $K=\frac{2}{2p(n-p)+n}$, $r=n-1-2p$.

Proof

In Lemma 5.1 we add the condition of homogeneous. For any $0\le k\le \frac{m-3}{2}$ we prove

$$\begin{aligned} \underline{\phi }^{2k+1}= {\mathbf {J}} \underline{f}_k^{(m)}\oplus \underline{f}_{k+1}^{(m)},\ \underline{\phi }^{2k+2}=\underline{f}_{k+1}^{(m)}\oplus {\mathbf {J}} \underline{f}_{k+1}^{(m)} \end{aligned}$$

(5.23)

hold by induction on k. If $k=0$, then

$$\begin{aligned} \underline{\phi }^{1}= {\mathbf {J}} \underline{f}_0^{(m)}\oplus \underline{f}_{1}^{(m)},\ \underline{\phi }^{2}=\underline{f}_1^{(m)}\oplus {\mathbf {J}} \underline{f}_1^{(m)} \end{aligned}$$

(5.24)

hold by (5.19) and (5.21).

Assume now that the assertion is correct for $0,\ldots ,k-1$. Consider the case of $k~(k<\frac{m-3}{2})$. By induction hypotheses we have

$$\begin{aligned} \underline{\phi }^{2k}=\underline{f}_{k}^{(m)}\oplus {\mathbf {J}} \underline{f}_{k}^{(m)}. \end{aligned}$$

(5.25)

Then ${\phi }^{2k}$ with isotropy order $m-1-2k~(\ge 4)$ belongs to the harmonic sequence as follows:

$$\begin{aligned} 0\mathop {\longleftarrow }\limits ^{A_{Jm}''} \cdots \mathop {\longleftarrow }\limits ^{A_{\phi _{-1}^{2k}}''} \underline{\phi }_{-1}^{2k} \mathop {\longleftarrow }\limits ^{A_{\phi _0^{2k}}''} \underline{\phi }_0^{2k} \mathop {\longrightarrow }\limits ^{A_{\phi _0^{2k}}'} \underline{\phi }_1^{2k} \mathop {\longrightarrow }\limits ^{A_{\phi _1^{2k}}'} \cdots \mathop {\longrightarrow }\limits ^{A_{\phi _{k-1}^{2k}}'} \underline{\phi }_k^{2k} \mathop {\longrightarrow }\limits ^{A_{\phi _k^{2k}}'} \underline{f}_{2k+1}^{(m)} \mathop {\longrightarrow }\limits ^{A_{2k+1}'} \cdots \mathop {\longrightarrow }\limits ^{A_{m}'} 0, \end{aligned}$$

(5.26)

where $\underline{\phi }_0^{2k} =\underline{\phi }^{2k}$, for $\alpha =1,\ldots ,k$, $\underline{\phi }_{\alpha }^{2k}={\mathbf {J}} \underline{f}_{k-\alpha }^{(m)} \oplus {\underline{f}}_{k+\alpha }^{(m)}$ and $\underline{\phi }_{-\alpha }^{2k}={\mathbf {J}} \underline{\phi }_{\alpha }^{2k}$.

By (iii) of Lemma 5.1 and (5.26), there exists a local section $V_0^{2k}=x_k f_k^{(m)}+ {\mathbf {J}} f_k^{(m)}$ such that $\underline{V}_0^{2k}$ is an antiholomorphic subbundle of $\underline{\phi }^{2k}$, and $\phi ^{2k+1}$ is obtained from $\phi ^{2k}$ by forward replacement of $(\underline{V}_0^{2k})^{\perp }\cap \underline{\phi }^{2k}={\mathbf {J}} \underline{V}_0^{2k}$, i.e.,

$$\begin{aligned} \underline{\phi }^{2k+1}=\underline{V}_0^{2k} \oplus \underline{V}_1^{2k}, \end{aligned}$$

(5.27)

where $\underline{V}_1^{2k}=\pi _{({\phi }^{2k})^{\perp }}({\partial } {\mathbf {J}} \underline{V}_0^{2k})$, i.e., ${V}_1^{2k}=\overline{x}_k l_{k-1}^{(m)} {\mathbf {J}} f_{k-1}^{(m)}+f_{k+1}^{(m)}$, $x_k$ is a smooth function on $S^2$ expect at some isolated points, and here $\underline{V}_0^{2k}$ denotes a line bundle consists of $V_0^{2k}$.

Since $\underline{V}_0^{2k}$ is an antiholomorphic subbundle of $\underline{\phi }^{2k}$, then we get $\pi _{{\phi }^{2k}}(\partial V_0^{2k})\in \underline{V}_0^{2k}$, which implies the equation

$$\begin{aligned} \partial x_k + x_k \partial \log |f_k^{(m)}|^2=0 \end{aligned}$$

(5.28)

holds.

In fact ${\phi }^{2k+1}$ with isotropy order $m-2-2k~(\ge 3)$ belongs to the harmonic sequence as follows:

$$\begin{aligned} 0\mathop {\longleftarrow }\limits ^{A_{Jm}''} \cdots \mathop {\longleftarrow }\limits ^{A_{J2}''} \underline{\phi }_{-1}^{2k+1} \mathop {\longleftarrow }\limits ^{A_{\phi _{0}^1}''} \underline{\phi }_{0}^{2k+1} \mathop {\longrightarrow }\limits ^{A_{\phi _0^1}'} \underline{\phi }_1^{2k+1} \mathop {\longrightarrow }\limits ^{A_2'} \cdots \mathop {\longrightarrow }\limits ^{A_{\phi _0^1}'} \underline{\phi }_{k+1}^{2k+1} \mathop {\longrightarrow }\limits ^{A_{\phi _1^1}'} {\underline{f}}_{2k+2}^{(m)} \mathop {\longrightarrow }\limits ^{A_2'} \cdots \mathop {\longrightarrow }\limits ^{A_{m}'}0,\nonumber \\ \end{aligned}$$

(5.29)

where $\underline{\phi }_0^{2k+1} ={\mathbf {J}} \underline{\phi }^{2k+1}$, $\underline{\phi }_{1}^{2k+1} = \underline{\phi }^{2k+1}$, and for $\alpha =1,\ldots ,k$, $\underline{\phi }_{\alpha +1}^{2k+1}=\underline{W}_{\alpha }^{2k}\oplus \underline{V}_{\alpha +1}^{2k}$, $\underline{\phi }_{-\alpha }^{2k+1}={\mathbf {J}} \underline{\phi }_{\alpha +1}^{2k+1}$ with $\underline{W}_{\alpha }^{2k}=(\underline{V}_{\alpha }^{2k})^{\perp }\cap \underline{\phi }_{\alpha }^{2k}$, $\underline{V}_{\alpha +1}^{2k}=\pi _{({\phi }_{\alpha }^{2k})^\perp }(\partial V_{\alpha }^{2k})$, but $\underline{V}_{k+1}^{2k}={\underline{f}}_{2k+1}^{(m)}$.

Since $\phi ^{2k+1}$ is homogeneous, it has constant curvature; moreover, all the harmonic maps in the harmonic sequence (5.29) are homogeneous and have constant curvature. Next we compute the geometric quantities of the corresponding harmonic maps to determine their explicit expressions. We choose the following unit vectors in ${\mathbb {C}}^{2n+2}$

$$\begin{aligned} {\left\{ \begin{array}{ll} e_1=\frac{{{\mathbf {J}}}V_{1}^{2k}}{|V_{1}^{2k}|}, e_2=\frac{{{\mathbf {J}}}V_{0}^{2k}}{|V_{0}^{2k}|}, e_3=\frac{V_{0}^{2k}}{|V_{0}^{2k}|},e_4=\frac{V_{1}^{2k}}{|V_{1}^{2k}|},\\ e_{2\alpha +3}=\frac{W_{\alpha }^{2k}}{|W_{\alpha }^{2k}|},e_{2\alpha +4}=\frac{V_{\alpha +1}^{2k}}{|V_{\alpha +1}^{2k}|}, \text {for} ~\alpha =1,\ldots ,k,\\ e_{2k+5}=\frac{{f}_{2k+1}^{(m)}}{|{f}_{2k+1}^{(m)}|}. \end{array}\right. } \end{aligned}$$

(5.30)

Set $W_{\alpha }=(e_{2\alpha +1}, e_{2\alpha +2})$, for $\alpha =0,1,\ldots ,k+1$, and $W_{k+2}=e_{2k+5}$, $W_{-1}={\mathbf {J}} W_{2}$.

Since for each $\alpha =0,1,\ldots ,k$ the harmonic map $\phi _{\alpha }^{2k+1}$ is irreducible and the isotropy order $\ge 3$, then $W_{\alpha -1},W_{\alpha },W_{\alpha +1}$ are orthogonal and it is suitable to extend them into the local unitary frame with respect to $\phi _{\alpha }^{2k+1}$. By (2.6) we get

$$\begin{aligned} \Omega _0^{2k+1}= \begin{pmatrix} \lambda _0&{}t_0 \\ 0 &{} \mu _0 \end{pmatrix}, \end{aligned}$$

(5.31)

where $\lambda _0=\mu _0=-\frac{|x_k|^2l_{k-1}^{(m)}|f_k^{(m)}|^2+|f_{k+1}^{(m)}|^2}{|V_0^{2k}||V_1^{2k}|}$, $t_0=\frac{\partial \overline{x}_k-\overline{x}_k\partial \log |f_k^{(m)}|^2 }{|x_k|^2+1}$ with $|V_0^{2k}|^2=(|x_k|^2+1)|f_k^{(m)}|^2$ and $|V_1^{2k}|^2=|x_k|^2l_{k-1}^{(m)}|f_k^{(m)}|^2+|f_{k+1}^{(m)}|^2$.

A straightforward computation shows

$$\begin{aligned} |det\Omega _0^{2k+1}|^2\mathrm{d}z^2\mathrm{d}\overline{z}^2= & {} \left( \frac{|x_k|^2l_{k-1}^{(m)}+l_{k}^{(m)}}{|x_k|^2+1}\right) ^2\mathrm{d}z^2\mathrm{d}\overline{z}^2, \end{aligned}$$

(5.32)

$$\begin{aligned} L_{1}^{2k+1}= & {} L_{-1}^{2k+1}, \end{aligned}$$

(5.33)

$$\begin{aligned} L_{k+1}^{2k+1}= & {} l_{2k+1}^{(m)}. \end{aligned}$$

(5.34)

For each $\alpha =0,1,\ldots ,k$ the harmonic map $\phi _{\alpha }^{2k+1}$ is irreducible and homogeneous, so $|det\Omega _\alpha |^2\mathrm{d}z^2\mathrm{d}\overline{z}^2\ne 0$ everywhere on $S^2$. It follows from (2.15) that

$$\begin{aligned} \delta _{\alpha -1}^{2k+1}-2\delta _{\alpha }^{2k+1}+\delta _{\alpha +1}^{2k+1}=-4, \end{aligned}$$

(5.35)

where $\delta _{\alpha }^{2k+1}=\frac{1}{2\pi \sqrt{-1}} \int _{S^2} L_{\alpha }^{2k+1} d \overline{z} \wedge \mathrm{d}z$ ($\alpha =0,1,\ldots ,k$).

Since all the harmonic maps in the harmonic sequence (5.29) have constant curvature, then we can choose a complex coordinate z on ${\mathbb {C}}=S^2 {\setminus } \left\{ pt\right\}$ such that for $\alpha =0,1,\ldots ,k+1$ the induced metric $\mathrm{d}s_{\phi _{\alpha }^{2k+1}}^2=(L_{\alpha -1}^{2k+1}+L_{\alpha }^{2k+1}) \mathrm{d}z \mathrm{d}\overline{z}$ by $\phi _{\alpha }^{2k+1}$ is given by

$$\begin{aligned} \mathrm{d}s_{\phi _{\alpha }^{2k+1}}^2 = \frac{\delta _{\alpha -1}^{2k+1}+\delta _{\alpha }^{2k+1}}{(1+z\overline{z})^2}\mathrm{d}z\mathrm{d}\overline{z}, \end{aligned}$$

(5.36)

and from ([3], §3) we get

$$\begin{aligned} l_i ^{(m)}=\frac{(i+1)(m-i)}{(1+z\overline{z})^2},\quad \delta _i ^{(m)}= (i+1)(m-i),\quad i=0,\ldots ,m-1. \end{aligned}$$

(5.37)

It follows from (5.34) and (5.37) that

$$\begin{aligned} L_{k+1}^{2k+1}=\frac{\delta _{k+1}^{2k+1}}{(1+z\overline{z})^2}. \end{aligned}$$

(5.38)

Analyzing (5.35), (5.36) and (5.38), we find for $\alpha =-1,0,1,\ldots ,k$,

$$\begin{aligned} L_{\alpha }^{2k+1}=\frac{\delta _{\alpha }^{2k+1}}{(1+z\overline{z})^2}. \end{aligned}$$

(5.39)

Using (5.32), (5.33), (5.35), (5.37), (5.39)and (2.14), we obtain

$$\begin{aligned} \partial \overline{\partial } \log \left[ \frac{k(m-k+1)|x_k|^2+(k+1)(m-k)}{|x_k|^2+1}\right] =0. \end{aligned}$$

(5.40)

Since $\frac{k(m-k+1)|x_k|^2+(k+1)(m-k)}{|x_k|^2+1}$ is globally defined on ${\mathbb {C}}$ and has a positive constant limit $c_1$ as $z\rightarrow \infty$. Thus from (5.40)

$$\begin{aligned} \frac{k(m-k+1)|x_k|^2+(k+1)(m-k)}{|x_k|^2+1}=c_1. \end{aligned}$$

(5.41)

It follows from $k(m-k+1)\ne (k+1)(m-k)$ that

$$\begin{aligned} |x_k|^2=c, \end{aligned}$$

(5.42)

where c is a constant.

In view of (5.28) we have $\overline{\partial }(\overline{x}_k|f_k^{(m)}|^2)=0$, which implies

$$\begin{aligned} \overline{x}_k=\frac{h_k(z)}{|f_k^{(m)}|^2}=\frac{h_k(z)}{(1+z\overline{z})^{m-2k}}, \end{aligned}$$

(5.43)

where $h_k(z)$ is a holomorphic function on ${\mathbb {C}}$.

It follows from (5.42) and (5.43) that

$$\begin{aligned} |h_k(z)|^2=c(1+z\overline{z})^{2m-4k}. \end{aligned}$$

(5.44)

Now we claim that $c=0$. Otherwise if $c\ne 0$, then the holomorphic function $h_k(z)$ includes the factor such as $(1+z\overline{z})$, which is impossible. So $x_k=0$ and

$$\begin{aligned} \underline{\phi }^{2k+1}={{\mathbf {J}}}\underline{f}_k^{(m)} \oplus {\underline{f}}_{k+1}^{(m)}. \end{aligned}$$

(5.45)

By (iv) of Lemma 5.1, (5.29) and (5.45), there exists a local section $V^{2k+1}=y_{k+1} f_{k+1}^{(m)} + {{\mathbf {J}}}{f}_k^{(m)}$ such that $\underline{\beta }^{\perp } \cap \underline{\phi }^{2k+1}=\underline{V}^{2k+1}$ is an antiholomorphic subbundle of $\underline{\phi }^{2k+1}$, and $\phi ^{2k+2}$ is obtained from $\phi ^{2k+1}$ by backward replacement of $\underline{V}^{2k+1}$, i.e.,

$$\begin{aligned} \underline{\phi }^{2k+2}=\underline{X}^{2k+1} \oplus {\mathbf {J}} \underline{X}^{2k+1}, \end{aligned}$$

(5.46)

where $X^{2k+1}=\frac{1}{|f_{k+1}^{(m)}|^2} f_{k+1}^{(m)}- \frac{\overline{y}_{k+1}}{|{f}_k^{(m)}|^2} {{\mathbf {J}}}{f}_k^{(m)}$ and $y_{k+1}$ is a smooth function on $S^2$ expect at some isolated points.

By the properties of the harmonic sequence (5.29) we know $\pi _{({\phi }^{2k+1})^{\perp }}(\overline{\partial } V^{2k+1})={\mathbf {J}} \underline{X}^{2k+1}$, which implies $y_{k+1}=0$ by a straightforward computation. So

$$\begin{aligned} \underline{\phi }^{2k+2}=\underline{f}_{k+1}^{(m)} \oplus {\mathbf {J}} \underline{f}_{k+1}^{(m)}, \end{aligned}$$

(5.47)

and the isotropy order of ${\phi }^{2k+2}$ is $m-3-2k~(\ge 2)$.

Hence it verifies (5.23) by (5.45) and (5.47).

In fact in the harmonic sequence (5.1), ${\phi }^0$ only belongs to case (1) or (3) of Proposition 4.4 by Proposition 4.4. Thus the conclusion follows from (5.23). $\square$

At last we consider the case of strongly isotropic. Let $\phi :S^2 \rightarrow {\mathbb {H}}P^n$ be a linearly full irreducible strongly isotropic harmonic map, then $\phi$ must belong to the following harmonic sequence:

$$\begin{aligned} 0{\longleftarrow } \cdots \mathop {\longleftarrow }\limits ^{A_{\phi _{-\alpha }^0}''} \underline{\phi }_{-\alpha }^0 \mathop {\longleftarrow }\limits ^{A_{\phi _{-(\alpha -1)}^0}''} \cdots \mathop {\longleftarrow }\limits ^{A_{\phi _0^0}''} \underline{\phi }_0^0 =\underline{\phi } \mathop {\longrightarrow }\limits ^{A_{\phi _0^0}'} \cdots \mathop {\longrightarrow }\limits ^{A_{\phi _{\alpha -1}^0}'} \underline{\phi }_{\alpha }^0 \mathop {\longrightarrow }\limits ^{A_{\phi _{\alpha }^0}'} \underline{\phi }_{\alpha +1}^0 \mathop {\longrightarrow }\limits ^{A_{\phi _{\alpha +1}^0}'} \cdots {\longrightarrow } 0, \end{aligned}$$

(5.48)

where for $\beta =1,\ldots$, $\underline{\phi }_{-\beta }^0={\mathbf {J}} \underline{\phi }_{\beta }^0$ and for $\beta =1,\ldots ,\alpha$, rank $\underline{\phi }_{\beta }^0=2$; for $\beta =\alpha +1,\ldots$, rank $\underline{\phi }_{\beta }^0=0$ or 1.

We give a corresponding Lemma as follows.

Lemma 5.3

Let $\phi :S^2 \rightarrow {\mathbb {H}}P^n$ be a linearly full irreducible strongly isotropic harmonic map, then from $\phi$ by $2\alpha -1$ steps of proper forward or backward replacements, we get the harmonic map $\phi ^{2\alpha -1}:S^2 \rightarrow G(2,2n+2)$, which is strongly isotropic and belongs to the following harmonic sequence:

$$\begin{aligned} 0\mathop {\longleftarrow }\limits ^{A_{Jm}''} \cdots \mathop {\longleftarrow }\limits ^{A_{Js}''} {\mathbf {J}}{{\underline{f}}_s^{(m)}} \mathop {\longleftarrow }\limits ^{A_{\phi _{-1}^{2\alpha -1}}''} \underline{\phi }_{-1}^{2\alpha -1} \mathop {\longleftarrow }\limits ^{A_{\phi _0^{2\alpha -1}}''} \underline{\phi }_0^{2\alpha -1} \mathop {\longrightarrow }\limits ^{A_{\phi _0^{2\alpha -1}}'} {\underline{f}}_s^{(m)} \mathop {\longrightarrow }\limits ^{A_s'} \cdots \mathop {\longrightarrow }\limits ^{A_{m-1}'} {\underline{f}}_m^{(m)} \mathop {\longrightarrow }\limits ^{A_m'} 0, \nonumber \\ \end{aligned}$$

(5.49)

where $\underline{\phi }_0^{2\alpha -1} =\underline{\phi }^{2\alpha -1}$, $\underline{\phi }_{-1}^{2\alpha -1} ={\mathbf {J}} \underline{\phi }^{2\alpha -1}$ with $f_i^{(m)}, {\mathbf {J}} f_i^{(m)}:S^2 \rightarrow {\mathbb {C}}P^m\subseteq {\mathbb {C}}P^{2n+1}$ and $A_{Ji}''$ denotes $A_{{\mathbf {J}} f_i^{(m)}}''$ ($i=0, \ldots , m$).

Furthermore, let $\underline{\beta }$ be the holomorphic line subbundle of $\underline{\phi }^{2\alpha -1}$ defined by $\underline{Ker} A_{\phi ^{2\alpha -1}}'$. Let $\phi ^{2\alpha }$ be obtained from $\phi ^{2\alpha -1}$ by backward replacement of $\underline{\alpha }=\underline{\beta }^{\perp } \cap \underline{\phi }^{2\alpha -1}$. Then $\phi ^{2\alpha }$ is quaternionic. Moreover, $\phi ^{2\alpha }$ is a quaternionic mixed pair or a quaternionic Frenet pair.

Proof

In the harmonic sequence (5.48), if rank $\underline{\phi }_{\alpha +1}^0=1$, let $\underline{\gamma }$ be the holomorphic line subbundle of $\underline{\phi }_{\alpha }^0$ defined by $\underline{Ker} A_{{\phi }_{\alpha }^0}'$, then ${\phi }_{\alpha -1}^1$ obtained from ${\phi }_{\alpha }^0$ by backward replacement of $\underline{\gamma }^{\perp } \cap \underline{\phi }_{\alpha }^0$ belongs to the following harmonic sequences

$$\begin{aligned} 0{\longleftarrow } \cdots \mathop {\longleftarrow }\limits ^{A_{\phi _{-\alpha }^1}''} \underline{\phi }_{-\alpha }^1 \mathop {\longleftarrow }\limits ^{A_{\phi _{-(\alpha -1)}^1}''} \cdots \mathop {\longleftarrow }\limits ^{A_{\phi _0^1}''} \underline{\phi }_0^1 \mathop {\longrightarrow }\limits ^{A_{\phi _0^1}'} \cdots \mathop {\longrightarrow }\limits ^{A_{\phi _{\alpha -2}^1}'} \underline{\phi }_{\alpha -1}^1 \mathop {\longrightarrow }\limits ^{A_{\phi _{\alpha -1}^1}'} \underline{\phi }_{\alpha }^1 \mathop {\longrightarrow }\limits ^{A_{\phi _{\alpha }^1}'} \cdots {\longrightarrow } 0, \nonumber \\ \end{aligned}$$

(5.50)

where for $\beta =1,\ldots$, $\underline{\phi }_{-\beta }^1={\mathbf {J}} \underline{\phi }_{\beta -1}^1$ and for $\beta =0,\ldots ,\alpha -1$, rank $\underline{\phi }_{\beta }^1=2$; for $\beta =\alpha ,\ldots$, rank $\underline{\phi }_{\beta }^1=1$.

Reusing the above methods we will get the wanted harmonic sequence (5.49) from (5.50) by $2\alpha -2$ steps of backward replacements.

If rank $\underline{\phi }_{\alpha +1}^0=0$, let $\underline{\gamma }$ be any holomorphic line subbundle of $\underline{\phi }_0^0$, then $\underline{\phi }_0^0=\underline{\gamma } \oplus {\mathbf {J}} \underline{\gamma }$; using ([1], Lemma 4.1) we get a new harmonic sequence which is just (5.50). Similarly we can get (5.49).

The rest follows from ([8], Lemma 3.3). $\square$

Let $\phi :S^2 \rightarrow {\mathbb {H}}P^n$ be an irreducible strongly isotropic homogeneous harmonic map, then from Lemma 5.3 we know the corresponding harmonic map $\phi ^{2\alpha }$ is also homogeneous and strongly isotropic. Through Proposition 4.2 and 4.4 we get $\phi ^{2\alpha }$ is given by

$$\begin{aligned} \underline{\phi }^{2\alpha }=\underline{f}_{n}^{(2n+1)}\oplus \underline{f}_{n+1}^{(2n+1)}, \text {or} ~\underline{\phi }^{2\alpha }=\underline{f}_{0}^{(n)}\oplus {\mathbf {J}} \underline{f}_{0}^{(n)}, \end{aligned}$$

(5.51)

where ${f}_{n}^{(2n+1)}=U{V}_{n}^{(2n+1)}$ and ${f}_{0}^{(n)}=U{V}_{0}^{(n)}$ with $U\in G_{2n+2}$.

In the following we discuss the above two cases, respectively, to prove the following Proposition.

Proposition 5.4

Let $\phi :S^2 \rightarrow {\mathbb {H}}P^n$ be a linearly full irreducible strongly isotropic homogeneous harmonic map with constant curvature K. Then up to a symplectic isometry of ${\mathbb {H}}P^n$, for some $p=1,\ldots ,\left[ \frac{n}{2}\right]$, $\phi$ is given by

$$\begin{aligned} \underline{\phi }=\underline{V}_p^{(n)} \end{aligned}$$

with $K=\frac{2}{2p(n-p)+n}$. Here $\left[ \frac{n}{2}\right]$ denotes the maximal integer which is not more than $\frac{n}{2}$.

Proof

Case I. $\underline{\phi }^{2\alpha }=\underline{f}_{n}^{(2n+1)}\oplus \underline{f}_{n+1}^{(2n+1)}$. Obviously ${\phi }^{2\alpha }$ belongs to the harmonic sequence (4.4). In (5.49) we choose a local section $V=x_n f_n^{(2n+1)}+f_{n+1}^{(2n+1)}$ such that

$$\begin{aligned} \underline{\phi }^{2\alpha -1}=\underline{V} \oplus {\underline{f}}_{n+2}^{(2n+1)}, \end{aligned}$$

(5.52)

where $x_n$ is a smooth function on $S^2$ expect at some isolated points and $x_n\ne 0$.

This time ${\phi }^{2\alpha -1}$ belongs to the harmonic sequence as follows:

$$\begin{aligned} 0\mathop {\longleftarrow }\limits ^{A_{{m}}''} \cdots \mathop {\longleftarrow }\limits ^{A_{n-2}''} {{\underline{f}}_{n-2}^{(2n+1)}} \mathop {\longleftarrow }\limits ^{A_{\phi _{0}^{2\alpha -1}}''} \underline{\phi }_{0}^{2\alpha -1} \mathop {\longrightarrow }\limits ^{A_{\phi _0^{2\alpha -1}}'} \underline{\phi }_1^{2\alpha -1} \mathop {\longrightarrow }\limits ^{A_{\phi _1^{2\alpha -1}}'} {\underline{f}}_{n+3}^{(2n+1)} \mathop {\longrightarrow }\limits ^{A_{n+3}'} \cdots \mathop {\longrightarrow }\limits ^{A_{2n+1}'} 0,\nonumber \\ \end{aligned}$$

(5.53)

where $\underline{\phi }_{0}^{2\alpha -1}={\mathbf {J}} \underline{\phi }^{2\alpha -1}$ and $\underline{\phi }_1^{2\alpha -1}=\underline{\phi }^{2\alpha -1}$.

Since $A_{\phi ^{2\alpha -1}}'(\underline{\phi }^{2\alpha -1})={\underline{f}}_{n+3}^{(2n+1)}$, then we get by (5.52)

$$\begin{aligned} \pi _{({\phi }^{2\alpha -1})^\perp }(\partial V)={\underline{f}}_{n+3}^{(2n+1)}, \end{aligned}$$

(5.54)

which is equivalent to the equation

$$\begin{aligned} \partial {x_n}-x_n^2+x_n\partial \log l_n^{(2n+1)}=0, \end{aligned}$$

(5.55)

hold. From (5.53) we choose a local unitary frame with respect to ${\phi }_{0}^{2\alpha -1}$ in ${\mathbb {C}}^{2n+2}$ as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} e_1=\frac{{{\mathbf {J}}}V}{|V|}, \quad e_2=\frac{{{\mathbf {J}}}f_{n+2}^{(2n+1)}}{|f_{n+2}^{(2n+1)}|},\quad e_3=\frac{V}{|V|}, \quad e_4=\frac{f_{n+2}^{(2n+1)}}{|f_{n+2}^{(2n+1)}|},\\ e_{2\alpha -1}=\frac{f_{n+\alpha }^{(2n+1)}}{|f_{n+\alpha }^{(2n+1)}|},e_{2\alpha }=\frac{f_{n+1-\alpha }^{(2n+1)}}{|f_{n+1-\alpha }^{(2n+1)}|}, \text {for} ~\alpha =3,\ldots ,n+1. \end{array}\right. } \end{aligned}$$

(5.56)

Set $W_0=(e_1, e_2)$, $W_1=(e_3, e_4)$, $W_2=(e_5)$, $W_{-1}=(e_6)$, then by (2.6) we get

$$\begin{aligned} \Omega _0= \begin{pmatrix} \lambda _0&{}t_0 \\ \mu _0&{}0 \end{pmatrix},\ \Omega _1= \begin{pmatrix} 0&\frac{|f_{n+3}^{(2n+1)}|}{|f_{n+2}^{(2n+1)}|} \end{pmatrix},\ \Omega _{-1}= \begin{pmatrix} 0\\ (-1)^{n-1}\frac{|f_{n-1}^{(2n+1)}|}{|f_{n-2}^{(2n+1)}|} \end{pmatrix}, \end{aligned}$$

(5.57)

where $\lambda _0=\frac{\partial \overline{x}_n-l_n^{(2n+1)}\tau _{n+1}|f_{n+1}^{(2n+1)}|^2}{|V|^2}$, $t_0=-\frac{\overline{x}_nl_{n+1}^{(2n+1)}\tau _{n}|f_n^{(2n+1)}|^2}{|f_{n+2}^{(2n+1)}||V|}$, $\mu _0=-\frac{\overline{x}_nl_{n-1}^{(2n+1)}\tau _{n+2}|f_{n+2}^{(2n+1)}|}{|V|}$ with $|V|^2=(|x_n|^2+l_n^{(2n+1)})|f_n^{(2n+1)}|^2$ and $\tau _{i}~(i=n,n+1,n+2)$ is given by (4.3).

A straightforward computation shows

$$\begin{aligned} |det\Omega _0|^2\mathrm{d}z^2\mathrm{d}\overline{z}^2= & {} \frac{|x_n|^4}{(|x_n|^2+l_n^{(2n+1)})^2} l_{n+1}^{(2n+1)}l_{n-1}^{(2n+1)} \mathrm{d}z^2\mathrm{d}\overline{z}^2, \end{aligned}$$

(5.58)

$$\begin{aligned} L_{1}=L_{-1}= & {} l_{n+2}^{(2n+1)}. \end{aligned}$$

(5.59)

Since $\phi _0^{2\alpha -1}$ is irreducible and homogeneous, so $|det\Omega _0|^2\mathrm{d}z^2\mathrm{d}\overline{z}^2\ne 0$ everywhere on $S^2$. It follows from (2.15) that

$$\begin{aligned} \delta _{-1}-2\delta _{0}+\delta _{1}=-4, \end{aligned}$$

(5.60)

where $\delta _{i}=\frac{1}{2\pi \sqrt{-1}} \int _{S^2} L_{i} d \overline{z} \wedge \mathrm{d}z$ ($i=-1,0,1$).

Since all the harmonic maps in the harmonic sequence (5.53) have constant curvature, then we can choose a complex coordinate z on ${\mathbb {C}}=S^2 {\setminus } \left\{ pt\right\}$ such that the induced metric $\mathrm{d}s_{\phi _{0}^{2\alpha -1}}^2=(L_{-1}+L_{0}) \mathrm{d}z \mathrm{d}\overline{z}$ by $\phi _{0}^{2\alpha -1}$ is given by

$$\begin{aligned} \mathrm{d}s_{\phi _{0}^{2\alpha -1}}^2 = \frac{\delta _{-1}+\delta _{0}}{(1+z\overline{z})^2}\mathrm{d}z\mathrm{d}\overline{z}, \end{aligned}$$

(5.61)

and from ([3], §3) we get

$$\begin{aligned} l_i ^{(2n+1)}{=}\frac{(i+1)(2n+1-i)}{(1{+}z\overline{z})^2},\quad \delta _i ^{(2n+1)}{=} (i+1)(2n+1-i),\quad i=0,\ldots ,2n.\qquad \end{aligned}$$

(5.62)

It follows from (5.59) and (5.62) that

$$\begin{aligned} L_{-1}=\frac{\delta _{-1}}{(1+z\overline{z})^2}. \end{aligned}$$

(5.63)

Analyzing (5.61) and (5.63) we find for $i=-1,0,1$,

$$\begin{aligned} L_{i}=\frac{\delta _{i}}{(1+z\overline{z})^2}. \end{aligned}$$

(5.64)

Using (5.58), (5.59), (5.60), (5.62), (5.64) and (2.14), we obtain

$$\begin{aligned} \partial \overline{\partial } \log \left[ \frac{|x_n|^2}{|x_n|^2+l_n ^{(2n+1)}}\right] =0. \end{aligned}$$

(5.65)

Since $\frac{|x_n|^2}{|x_n|^2+l_n ^{(2n+1)}}$ is globally defined on ${\mathbb {C}}$ and has a positive constant limit $c_1$ as $z\rightarrow \infty$. Thus from (5.65)

$$\begin{aligned} \frac{|x_n|^2}{|x_n|^2+l_n ^{(2n+1)}}=c_1. \end{aligned}$$

(5.66)

It follows from (5.62) and (5.66) that

$$\begin{aligned} x_n=\frac{c}{1+z\overline{z}}, \end{aligned}$$

(5.67)

where c is a constant.

In view of (5.55) and (5.67) we have $c=0$. Then $x_n=0$, which contradicts the fact that $x_n\ne 0$. So this case does not occur.

Case II. $\underline{\phi }^{2\alpha }=\underline{f}_{0}^{(n)}\oplus {\mathbf {J}} \underline{f}_{0}^{(n)}$. It follows from the proof of Proposition 5.2 that for $k=1,\ldots ,n-1$, $\underline{\phi }^{2\alpha -2k}$ is given by

$$\begin{aligned} \underline{\phi }^{2\alpha -2k}=\underline{f}_{k}^{(n)}\oplus {\mathbf {J}} \underline{f}_{k}^{(n)}, \end{aligned}$$

(5.68)

where ${f}_{k}^{(n)}=U{V}_{k}^{(n)}$ with $U\in G_{2n+2}$ and the corresponding constant curvature $K=\frac{2}{2k(n-k)+n}$.

Hence we get the conclusion. $\square$

By Proposition 4.2, 4.4, 5.2 and 5.4, we obtain a classification of homogeneous minimal 2-spheres in quaternionic projective space ${\mathbb {H}}P^n$ as follows:

Theorem 5.5

Let $\phi :S^2 \rightarrow {\mathbb {H}}P^n$ be a linearly full homogeneous harmonic map of isotropy order r with constant curvature K. Then up to a symplectic isometry of ${\mathbb {H}}P^n$, $\phi$ is one of the following:

• (1) For some $p=0,1,\ldots ,n$, $\phi$ is given by

  $$\begin{aligned} \underline{\phi }=U\underline{V}_p^{(2n+1)}\oplus U\underline{V}_{2n+1-p}^{(2n+1)},~U\in G_{2n+2} \end{aligned}$$

  with $K=\frac{2}{2p(2n+1-p)+2n+1}$ and $r=2n-2p$ $\left( K=\frac{2}{n(n+2)},~r=+\infty ~\text {when}~ p=n\right)$;

• (2) For some $p=0,1,\ldots ,\left[ \frac{n}{2}\right]$, $\phi$ is given by

  $$\begin{aligned} \underline{\phi }=\underline{V}_p^{(n)} \end{aligned}$$

  with $K=\frac{2}{2p(n-p)+n}$ and $r=+\infty$;

• (3) $n=2t+1~(t>0)$ and for some $p=0,1,\ldots ,t-1$, $\phi =\left[ \left( \phi _{p,0},\ldots ,\phi _{p,n}\right) ^T\right]$, for $q_1=0,\ldots ,t$, $q_2=t+1,\ldots ,n$, $\phi _{p,q_1}$, $\phi _{p,q_2}$ are given by

  

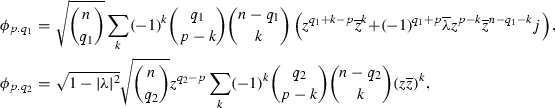
  where $\lambda$ is a complex parameter satisfying $0<|\lambda |^2<1$ and $K=\frac{2}{2p(n-p)+n}$, $r=n-1-2p$.

Remark 5.6

• (a) Case (1) is just the series of SU(2)-equivariant minimal 2-spheres in ${\mathbb {H}}P^n$ given by ([13], Proposition 7.1).

• (b) Case (2) is contained in totally geodesic submanifold ${\mathbb {C}}P^n\subset {\mathbb {H}}P^n$. In this case, since there exists a Sp(n) matrix which transforms $\underline{V}_p^{(n)}$ into $\underline{V}_{n-p}^{(n)}$, then $\underline{V}_p^{(n)}$ and $\underline{V}_{n-p}^{(n)}$ are congruent in ${\mathbb {H}}P^n$ (but they are not congruent in ${\mathbb {C}}P^n$). So here we omit the cases of $p>\left[ \frac{n}{2}\right]$.

• (c) Case (3) is not totally geodesic and exists only when n is odd. In this case, for some $p=t,\ldots ,2t~(=n-1)$, $\phi$ is given by

  $$\begin{aligned} \underline{\phi }=\underline{f}_{p}^{(n)}\oplus {\mathbf {J}} \underline{f}_{p}^{(n)}, \end{aligned}$$

  where ${f}_{p}^{(n)}=U{V}_{p}^{(n)}$ and U is given by (4.26)–(4.29). A straightforward computation shows that these $\phi$ are homogeneous but non-minimal in ${\mathbb {H}}P^n$. So we obtain the conclusion that a homogeneous 2-sphere in ${\mathbb {H}}P^n$ may be non-minimal.

Theorem 5.5 gives all homogeneous minimal 2-spheres in ${\mathbb {H}}P^n$ and shows that they contain those given by ([13], Proposition 7.1.), even more than those in the case of n is odd. Of course a natural problem that how to decide all homogeneous (non-minimal) 2-sphere in ${\mathbb {H}}P^n$ deserves further consideration.