Heterogeneity and uncertainty in a multistate framework

Abstract

This research develops the scheme proposed in the paper Pollard [J Inst Actuar 96(2): 251–264, 1970], which is based on a two-state model for the analysis of 1-year mortality, but the results are also valid for the probabilities related to other types of insurance events such as disablement and accidents. We extend the Pollard’s original scheme into time-discrete models with more states (active-invalid-dead) together with further investigation into multi-year time horizon. Additionally, hypotheses for real-valued individual frailty are assumed in the models. As the baseline probabilistic structure, we have adopted a traditional three-state model in a Markov context. We focus on an insurance portfolio. Our outputs of interest are based on the probability distributions of the annual payouts for term insurance policies providing lump sum benefits both in case of death and in case of permanent disability. The analysis of the probability distributions allows us to assess the risk profile of the insurance portfolio, and thus to suggest appropriate actions in terms of premiums and capital allocation. In this regards, we adopt the percentile principle.

1 Introduction

The use of multistate models and, in particular, of Markov structures to represent the biometric features of insurance products in the area of insurance of the person can be dated back to the seminal contribution by Hoem (1969). Later contributions to life insurance and related fields, based on multistate models, are given by Amsler (1988), Hoem (1988) and Waters (1984).

Moving to actuarial textbooks which present the actuarial structure of life and health insurance contracts in terms of multistate models, we quote (Haberman and Pitacco 1999; Norberg 2002) and, as specifically regards long-term care insurance, Denuit et al. (2019). Health insurance, and, more specifically disability insurance are presented by Pitacco (2014). The value of disability insurance from an economic perspective is addressed for example by Chandra and Samwick (2009).

As noted by Pitacco (2019), heterogeneity of a population in respect of mortality (and disability) is due to differences among the individuals, which are caused by various risk factors. Some risk factors are observable, while others are unobservable. The set of observable risk factors clearly depends on the type of population addressed. It follows that the scientific and technical literature dealing with heterogeneity modelling is manifold.

The long-term and multi-year characteristics of the life insurance contracts and of many health insurance contracts imply difficulties in expressing the impact of unobservable heterogeneity on the individual risk profile. The early contributions to this topic must be credited to Beard (1959) (in the actuarial context) and Vaupel et al. (1979) (in the demographic context).

Among the features which heavily affect the risk profile of an insurance portfolio, uncertainty in the parameters of the stochastic models should be carefully considered. This topic has raised great interest in the insurance field; see, for example, Cairns (2000). Parameter uncertainty has a significant impact on the risk profile of a life annuity portfolio or a pension plan; see Pitacco et al. (2009) and references therein. As regards uncertainty in the assessment of probabilities (of death in particular) an interesting model has been proposed by Olivieri and Pitacco (2009), while a simple quantification is proposed by Olivieri and Pitacco (2015). The latter is here adopted to express uncertainty in the assessment of probabilities of disablement.

The main contribution of the present paper consists in implementing a stochastic approach to the assessment of the annual payouts of a portfolio of life insurance policies also providing lump sum benefits in the case of permanent disability. The “shift” from deterministic to stochastic approach has been realized as follows.

• 1. Referring to a two-state, 1-year setting, interesting generalizations of the classical binomial model have been proposed by Pollard (1970), where the presence of both observable heterogeneity and uncertainty is allowed. In line with generalization proposed by Valente (2017), we have defined the following general settings:

  • (a) by adding appropriate probability distributions to quantify the uncertainty;

  • (b) by allowing for unobservable heterogeneity.

• 2. In our model, we have assumed, as the “baseline” setting, a three-state model with a Markov structure. This structure has been adopted, in absence of uncertainty, for homogeneous portfolios as well as for portfolios with observable heterogeneity. The presence of either uncertainty or unobservable heterogeneity calls for more general settings: the resulting structure we have defined consists of Markov processes conditional on the outcomes of the unknown quantities which express uncertainty or unobservable heterogeneity.

• 3. We have applied the model, structured as described under 1(a), 1(b) and 2, to a portfolio of multi-year policies providing death and permanent disability benefits. In line with the need for stochastic assessments, we have calculated, via stochastic simulation, the (empirical) distributions of the payouts for benefits paid in case of death in the active state, in case of death in the disability state, and in case of disablement. The results achieved provides a clear picture of the risk profile of the portfolio throughout time.

The remainder of the paper is organized as follows. Starting from the classical multistate model with a Markov structure, described in Sect. 2, a generalized portfolio model embedding possible uncertainty and unobservable heterogeneity has been built-up and described in Sect. 3. Then, in Sect. 4 the generalized model is implemented to perform assessment of the portfolio risk profile; a number of numerical results are presented and discussed.

Finally, suggestions for future research work are provided in the concluding Sect. 5.

2 A three-state model

In this Section an implementation of the Markov model described above is proposed. A time-discrete framework is assumed, with the year as the time unit.

2.1 Application to an insurance cover

We consider an insurance cover providing lump sum benefits in case of death and in case of disablement causing a permanent disability.

The state space is

$$\begin{aligned} \mathcal{L}={\left\{ a, i, d \right\} } \end{aligned}$$

(1)

where:

• ${{a}}=\text {active (or healthy)}$;

• ${{i}}=\text {disabled (or invalid)}$;

• ${{d}}=\text {dead}$.

Benefits are assumed to be paid at the end of the year in which a relevant event occurs. The benefit amounts are as follows:

• $B_1$ if the individual dies in the year, being in the active state, that is, if the transition $a\rightarrow d$ occurs;

• $B_2$ if a disablement occurs and the individual is alive at the end of the year, that is, if the transition $a\rightarrow i$ occurs;

• $B_3$ if a disablement occurs and the individual dies before the end of the year, that is, if the transitions $a\rightarrow i\rightarrow d$ occur.

Because of the benefit structure we have defined, the set of transitions is as follows:

$$\begin{aligned} \mathcal{T} = \{(a,i), (a,d), (i,d)\} \end{aligned}$$

(2)

We disregard recovery. The above setting can represent a simple insurance package. Assuming $B_3 > B_1$, we indeed recognize the structure of a term insurance policy with a basic death benefit $B_1$, supplementary benefit in case of death because of accident given by $B_3 - B_1$, and benefit $B_2$ in the case of disablement leading to permanent disability, provided the individual is alive at the end of the year.

2.2 The basic Markov structure

We describe the probabilistic structure required by the three-state model defined above. We adopt the Hamza notation (commonly used in the actuarial framework; see for example Haberman and Pitacco 1999).

For an active individual age x, we define the following probabilities:

• $p_x^{aa} =$ probability of being active at age $x+1$;

• $q_x^{aa} =$ probability of dying within 1 year, the death occurring in state active (a);

• $p_x^{ai} =$ probability of being disabled at age $x+1$;

• $q_x^{ai} =$ probability of dying within 1 year, the death occurring in state disability (i);

• $p_x^{a}=$ probability of being alive at age $x+1$;

• $q_x^{a}=$ probability of dying within 1 year [the state of time at death being either active (a) or invalid (i)];

• $w_x=$ probability of becoming disabled within 1 year.

Obvious relations hold among the above probabilities (see, for example, Pitacco 2014); in particular:

$$\begin{aligned} p_x^{aa}+p_x^{ai}= & {} p_x^{a};\\ q_x^{aa}+q_x^{ai}= & {} q_x^{a};\\ p_x^{a}+q_x^{a}= & {} 1;\\ p_x^{ai}+q_x^{ai}= & {} w_x. \end{aligned}$$

Given the definition of the benefit structure, disablement and death constitute two exit causes. Hence, probabilities related to individuals in state invalid (at the beginning of the year) are not relevant.

We note that the probability $q_x^{ai}$ refers to an event consisting of two transitions, that is, $a\rightarrow i$ and $i\rightarrow d$. The following approximation is frequently adopted in the actuarial practice (see, for example, Pitacco 2014):

$$\begin{aligned} q_x^{ai} \approx w_x \frac{q_x^{i}}{2} \end{aligned}$$

(3)

where $q_x^{i}$ generically denotes the mortality of disabled people. The following approximation, which will be useful in the following, can then be derived:

$$\begin{aligned} w_x \left( 1 - \frac{q_x^{i}}{2}\right) \approx p_x^{ai} \end{aligned}$$

(4)

The three-state Markov model we have described constitutes the baseline setting to define the portfolio stochastic structure. A first (trivial) generalization is required if the insurance portfolio is split, thanks to observable risk factors, into subportfolios, each one consisting of homogeneous risks. The generalization consists in assigning different probabilities to individuals belonging to different subportfolios.

We note that, given the benefit structure as defined in Sect. 2.1, our three-state model can be interpreted, as a model with three causes of “decrement”, all the causes implying that the individual leaves the portfolio:

• 1. transition $a \rightarrow d$, implying benefit $B_1$;

• 2. transition $a \rightarrow i$, implying benefit $B_2$;

• 3. transitions $a \rightarrow i \rightarrow d$, implying benefit $B_3$.

2.3 Allowing for frailty or uncertainty

Lack of information might imply a (more or less significant) margin of vagueness in assigning the above probabilities. In particular, this may be caused by:

• heterogeneity due to unobservable risk factors, which implies individual frailty;

• uncertainty in stating the same probability for all the individuals belonging to the portfolio (or to a subportfolio).

Our modelling choice consists in representing the vagueness, in both the above situations, by considering the probabilities as random quantities and assigning to these quantities four-parameter beta distributions.

Numerical values of the probabilities will be determined via stochastic simulation. One or more assumptions and one or more set of probabilities are needed according to the portfolio structure: see Sect. 3.1.

3 The insurance portfolio

3.1 Portfolio structures

In this Section we define, in stochastic terms, a set of portfolio structures, each one labelled as “case”.

Generally speaking, uncertainty and frailty might affect all the probabilities involved in the calculations. Here, we only focus on the probabilities of disablement (see below). More details will be provided in Sect. 4, when defining a specific insurance portfolio. In all the cases, we assume that the portfolio initially consists of n individuals, all aged $x_0$. Each individual risk is covered by a m-year insurance policy.

The age-patterns of mortality are described by the first Heligman–Pollard law which, in terms of the mortality odds, is given by the following expression:

$$\begin{aligned} \frac{q_x}{1-q_x} = {A^{(x+B)^C}} + {D \, \mathrm{e}^{-E(\ln x - \ln F)^2}} + {G \, H^x} \end{aligned}$$

(5)

We note that the first term represents infant mortality, the second term represents young-adult hump, the third term represents adult-old mortality (see Heligman and Pollard 1980). A given set of parameters is assumed for the mortality of active people, that is for the probabilities $q_x^{aa}$. The parameters are specified in Table 1 (see Sect. 4.3) and have been chosen to reflect the mortality experience in portfolios of standard risks. For the mortality of disabled people we assume:

$$\begin{aligned} q_x^{i} = (1 + \mu ) \, q_x^{aa} \end{aligned}$$

(6)

that is, a multiplicative model expressing extra mortality, assuming that $\mu$ can represent an average increase in mortality for the members of the group.

Table 1 Parameters of the first Heligman–Pollard law

Probability of disablement is assumed constant over the whole age range involved. More precisely, we have adopted the approximation (4), assuming a constant w.

In the case of frailty or uncertainty, the probability of disablement is a random quantity, denoted with W. From the outcome of W, the same approximation for $p_x^{ai}$ is applied.

3.1.1 Case 1

The insurance portfolio consists of one homogeneous group; all individuals have the same known probability of disablement, w.

Summarizing: homogeneity, no uncertainty.

3.1.2 Case 2

A heterogeneous portfolio, thanks to observable heterogeneity, is arranged in r subportfolios, with given sizes $n_1,n_2, \ldots , n_r$, such that $\sum _{j=1}^{r}{n_j}=n$. Each subportfolio includes individuals with the same probability of disablement. Probability of disablements are $w_1< w_2< \cdots < w_r$. We define the average probability of disablement as follows:

$$\begin{aligned} \overline{w}=\sum _{j=1}^{r}{\frac{n_j}{n} \, w_{j}} \end{aligned}$$

(7)

and assume that $\overline{w} = w$, that is the probability of disablement in Case 1.

Summarizing: observable heterogeneity, deterministic group sizes, no uncertainty.

3.1.3 Case 3

The insurance portfolio consists of one homogeneous group; all individuals have the same unknown probability of disablement, W. Hence, W is a random variable with probability distribution $\mathrm{Beta}(\alpha ,\beta ,\gamma ,\delta )$. We note that $\alpha ,\, \beta$ are the shape parameters, whereas $\gamma$ is the lower bound and $\delta$ is the upper bound, so that $\left( \gamma ,\delta \right]$ is the interval of possible outcomes.

Summarizing: homogeneity, uncertainty.

3.1.4 Case 4

The insurance portfolio consists of one heterogeneous group; all individuals have unknown probability of disablement. Let $W^{(i)}$ denote the random variable expressing the probability of disablement for the individual i, $i=1,2,\ldots ,n$. All the $W^{(i)}$ have the same probability distribution $\mathrm{Beta}(\alpha ,\beta ,\gamma ,\delta )$. This case represents the situation of individual frailty. Thus, each individual may have a different probability of disablement, but this probability is unknown.

Summarizing: unobservable heterogeneity, continuous frailty modelling.

3.1.5 Case 5

A heterogeneous portfolio, thanks to observable risk factors, is arranged in r subportfolios. However, the sizes of the subportfolios, $N_1,N_2, \ldots , N_r$, are random because of unobservable individual heterogeneity, and the vector

$$\begin{aligned} {\underline{N}=(N_1,N_2,\ldots ,N_{r})} \end{aligned}$$

has multinomial distribution with parameters $(n,f_1,f_2,\ldots ,f_{r})$, such that $n=N_1+N_2+\cdots +N_{r}$ and $f_1+f_2+\cdots +f_{r}=1$. The probabilities of disablement within each subportfolio $w_j$ are given, and such that $w_1< w_2< \cdots < w_r$. This multinomial scheme can represent in a discrete framework the individual frailty, thus providing an approximation of the continuous frailty model as defined by Case 4.

Summarizing: unobservable heterogeneity, discrete frailty modelling.

3.1.6 Case 6

A heterogeneous portfolio, thanks to observable risk factors, is arranged in r subportfolios, each with known size, that is, $n_1,n_2, \ldots , n_r$. All individuals in the subportfolio j have the same unknown probability of disablement, $W_j$. Hence, $W_j$ is a random variable with probability distribution $\mathrm{Beta}(\alpha _j,\beta _j,\gamma _j,\delta _j)$, $j=1\ldots ,r$.

Summarizing: observable heterogeneity, uncertainty.

3.2 Outflows

3.2.1 Benefits

The benefit structure has already been defined in Sect. 2.1. The benefit amounts are the same for all the individuals belonging to the portfolio.

3.2.2 Annual payouts

The benefits define the insurer’s annual payouts.

• $X_h(t) =$ annual random payout at time t for benefits $B_h$; $h=1,2,3$.

where $t=1,2,\ldots ,m$, with m the common term of all the individual policies. $X(t)=x_{1(t)+}x_{2(t)+}x_{3(t)}$

Our main target is to quantify the payout randomness in terms of probability distributions for $t=1,2,\ldots ,m$.

3.3 Facing the annual payouts

Random payouts constitute the insurer’s liability, which must be met by appropriate assets. Hence, a calculation principle is needed, in order to summarize a sequence of random amounts in terms of deterministic quantities.

Usually, a share of the total amount meeting the liability, i.e. the premiums, is provided by the policyholders, while the remaining share, i.e. the capital allocated, is provided by the insurer.

3.3.1 Premiums

We only focus on natural premiums, which are defined as the annual expected costs to the insurer. Technical equilibrium in each policy year is then achieved. The natural premium arrangement is particularly interesting in the context of group insurance, when the employer acts as the sponsor of the scheme and then pays the premiums. In this case, the annual total premium amount paid by the employer is usually given by the sum of the individual natural premiums, and hence can vary according to the composition of the insured group.

3.3.2 Capital allocation

Capital allocation aims at insurer’s solvency. The assets provided by the premium collection plus the assets backing the shareholders’ capital must face, according to some specified principle, the insurer’s liabilities. Of course, a time horizon must be stated. In what follows, we will refer to a 1-year time horizon; actually, this choice is in line with both the current solvency logic and the natural premium arrangement that we are adopting.

3.3.3 The percentile principle

In what follows, we will determine, for each year, the amounts of assets facing, according to the percentile principle (that is, according to the Value at Risk logic), the random value of the payout for benefits falling due in that year.

Hence, we will not distinguish between assets financed by the premium collection and assets backing the shareholders’ capital.

In formal terms, according to the percentile principle, we have to find, for $t=1,2,\ldots ,m$, the amount A(t) such that:

$$\begin{aligned} \mathrm{Pr}\{ X(t) > A(t) \} = \epsilon \end{aligned}$$

(8)

where $\epsilon$ denotes an assigned (small) probability.

More in detail, we can state the following requirements. Find, for $t=1,2,\ldots ,m$ and $h=1,2,3$, the amounts $A_h(t)$ such that:

$$\begin{aligned} \mathrm{Pr}\{ X_h(t) > A_h(t) \} = \epsilon _h \end{aligned}$$

(9)

Requirements defined by conditions (9) can be interesting as they provide information about the specific impact of each type of benefit on the total requirement. From a product design perspective, a high impact might suggest a redesign of the insurance product and even the removal of a benefit, or at least the reduction in the related amount.

4 Stochastic analysis: Numerical results

4.1 Calculation procedures

Probability distributions of the random variables $X_1(t), X_2(t), X_3(t)$ (and then X(t)), for $t=1,2,\ldots , m$, must be determined. Calculations will be performed via simulation. Hence, simulated distributions of the variables $X_1(t), X_2(t), X_3(t)$ will be calculated.

4.2 An overall scheme

The structure of the simulation procedure depends, of course, on the type of portfolio and the relevant probabilistic structure. A first insight into the diverse procedure structures is provided by Fig.  1.

Fig. 1

Calculation procedures

4.2.1 Specific procedures: Cases 1 and 2

Portfolio structures labelled as Cases 1 and 2 require the simplest procedures. In the absence of both individual frailty and uncertainty, the probabilities involved in the three-state model are completely defined. In detail, one set of probabilities is given for the Case 1, more sets are required for the Case 2, where heterogeneous portfolio is split into homogeneous subportfolios. In these cases the simulation procedure is directly applied to each individual belonging to the portfolio; see step $\textcircled {a}$ in Fig. 1.

4.2.2 Specific procedures: Cases 3, 4 and 6

Uncertainty or frailty feature Cases 3, 4, and 6. Hence, the simulation procedure must start with the generation of (pseudo-)random numbers beta-distributed; see step $\textcircled {b}$ in Fig. 1. In detail:

• the presence of uncertainty in Case 3 calls for the simulation of the random variable W, whose outcome is applied to all the risks in the portfolio;

• the presence of individual frailty in Case 4 requires the simulation of the random variables $W^{(i)}$, $i=1,2,\ldots ,n$, all with the same beta distribution; then, the outcomes represent the individual frailty levels;

• Case 6 combines:

  • (i) observable heterogeneity, which allows us to split the portfolio into r homogeneous subportfolios, with sizes $n_1, n_2,\ldots ,n_r$;

  • (ii) uncertainty in disability rate which affects all individuals in each subportfolio.

  Hence, the simulation of random variables $W_j$, beta-distributed with $\mathrm{Beta}(\alpha _j,\beta _j,\gamma _j,\delta _j)$, $j=1,\ldots ,r$, is needed.

In all the above cases, step $\textcircled {a}$ then follows.

4.2.3 Specific procedures: Case 5

In Case 5 the sizes of the subportfolios are random. So the first step in the calculation procedure consists in simulating the subportfolio sizes according to a multinomial distribution with parameters $n, f_1, f_2, \ldots , f_r$; see step $\textcircled {c}$ in Fig. 1.

An alternative procedure to determine the values of the parameters $f_1, f_2, \ldots , f_r$ is the following one.

• Split the range of outcomes, $\delta -\gamma$, of the random variable W, with distribution $\mathrm{Beta}(\alpha ,\beta ,\gamma ,\delta )$, into r subintervals, each with size $s = (\delta -\gamma ) / r$.

• Let f(w) denote the probability density function of the beta distribution; calculate, for $j=1,2,\ldots ,r$, the following probabilities:

  $$\begin{aligned} f_j = \mathrm{Pr}\{ (j-1)\,s < W \le j \,s \} = \int _{(j-1)\,s}^{j \,s} f(w)\,\mathrm{d}w \end{aligned}$$

  (10)

• Calculate the conditional expected value related to each subinterval, and set:

  $$\begin{aligned} w_j = \mathbb {E}(W | (j-1)\,s < W \le j \,s) = \frac{1}{f_j}\int _{(j-1)\,s}^{j \,s} w\,f(w)\,\mathrm{d}w \end{aligned}$$

  (11)

• Finally, the subportfolio sizes are simulated according to the multinomial distribution with parameters $n,f_1, f_2, \ldots , f_r$.

We note that, this way, a continuous-frailty setting can be approximated by adopting a discrete setting, for which the frailty levels are given by the quantities $w_j$, $j=1,2,\ldots ,r$ as defined by Eq. (11).

4.3 Defining the portfolio: input data

The numerical examples are based on the following input data.

4.3.1 General data

The following input data are used in all the Cases.

• Number of simulations 100,000 for each case.

• Portfolio initial size $n=10,000$.

• Insureds’ initial age $x_0 = 40$.

• Policy term $m=25$.

• Benefits $B_1=B_2=B_3=1000$ monetary units.

• Mortality of active people following the Heligman–Pollard law [see Eq. (5)], with the parameters suggested by Olivieri and Pitacco (2015) for mortality of assured people, given in Table 1.

• Mortality of disabled people according to the multiplicative model [see Eq. (6)], with $\mu = 0.30$. This percentage has been chosen to represent an average increase in mortality experienced in disability insurance.

• In all the Cases in which uncertainty in probability of disablement is accounted for, the beta distribution $\mathrm{Beta}(\alpha , \beta , \gamma , \delta )$ have been chosen to represent a reasonable range $(\gamma , \delta ]$ of possible outcomes, and reasonable concentration—dispersion via parameters $\alpha ,\, \beta$.

4.3.2 Case-specific data

Case 1 only requires the value w of the probability of disablement, assumed independent of the attained age:

• $w=0.02$

In Case 2 the portfolio is split into r subportfolios, with different given probabilities of disablement:

• $r=3$;

• subportfolio sizes and probabilities of disablement: see Table 2.

Table 2 Case 2—Subportfolio sizes and probabilities of disablement

Table 3 Case 5—Parameters of the multinomial distribution and probabilities of disablement

Table 4 Case 6—Subportfolio sizes and parameters of the beta distributions

Fig. 2

Case 1 versus Case 2, distribution of X(5)

Fig. 3

Case 1 versus Case 2, distribution of X(25)

Fig. 4

Case 1 versus Case 3, distribution of X(5)

Fig. 5

Case 1 versus Case 3, distribution of X(25)

Fig. 6

Case 1 versus Case 4, distribution of X(5)

Fig. 7

Case 1 versus Case 4, distribution of X(25)

Fig. 8

Case 4 versus Case 5, distribution of X(5)

Fig. 9

Case 4 versus Case 5, distribution of X(25)

Fig. 10

Case 2 versus Case 6, distribution of X(5)

Fig. 11

Case 2 versus Case 6, distribution of X(25)

Fig. 12

Case 3 versus Case 6, distribution of X(5)

Fig. 13

Case 3 versus Case 6, distribution of X(25)

Fig. 14

Percentiles for total payout X(1), Case 1 versus Case 3

Fig. 15

Percentiles for total payout X(5), Case 1 versus Case 3

Fig. 16

95% percentiles for $X(t),\, t=1,\ldots ,25$, Case 1

Fig. 17

95% percentiles for $X(t),\, t=1,\ldots ,25$, Case 3

Fig. 18

95% percentiles for $X(t),\, t=1,\ldots ,25$, Case 4

Fig. 19

Assets backing the liabilities/expected value

Case 3 represents the uncertainty situation in terms of probability of disablement W, following a beta distribution:

• $W \sim \mathrm{Beta}(2.2, 3.3, 0, 0.05)$.

Case 4 represents the situation of random individual frailty, $W^{(i)}$, following a beta distribution:

• $W^{(i)} \sim \mathrm{Beta}(2.2, 3.3, 0, 0.05)$, for $i=1,2,\ldots ,n$.

Case 5 requires the simulation of subportfolio random sizes, according to the multinomial distribution with probabilities $f_j$, and related probability of disablements $w_j$; see Table 3. We recall that the high number of subportfolios has been chosen aiming to approximate the individual frailty by adopting a discrete setting.

In Case 6 the portfolio is split into r subportfolios, with different random probability of disablement beta-distributed:

• $r=3$;

• parameters of the beta distributions: see Table 4.

We note that parameters have been chosen to obtain the same weighted mean, that is 2%, hence to achieve comparability.

4.4 Simulated distributions

Simulated distributions are plotted in the following figures (Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 and 13) aiming to compare in each figure the features of two diverse heterogeneity settings.

4.4.1 Case 1 versus Case 2

We assess the effect of splitting the portfolio into homogeneous subportfolios thanks to observable risk factors. We see that, in our multi-year, three-state framework, splitting the portfolio is not effective for all the distributions considered, unlike the 1-year, two-state framework (see for more details, Valente 2017). We note that, in both the cases, the setting is totally deterministic.

4.4.2 Case 1 versus Case 3

In both the cases the portfolio is not split into subportfolios. We analyze the impact of uncertainty in the assessment of the probability of disablement. We note that uncertainty in the probability of disablement affects, at the same time and to the same extent all the individuals in the portfolio. On the contrary, the frailty (see the next comparison) separately affects each individual determining a lower impact on the portfolio risk profile.

4.4.3 Case 1 versus Case 4

In Case 4 the portfolio is not split into subportfolios. Individual frailty is modelled as a continuous variable. Unlike the case of uncertainty, the presence of individual frailty does not heavily impact on the portfolio risk profile.

4.4.4 Case 4 versus Case 5

Frailty is modelled as a continuous or a discrete variable, respectively. Discrete modelling is realized via grouping with random group sizes. We note that, in terms of simulated distributions, results almost coincide. Thanks to this fact, discrete frailty modelling can be considered as an interesting practical alternative.

4.4.5 Case 2 versus Case 6

In both the cases, the portfolio is split into subportfolios. Case 2 is totally deterministic (see above), whereas in Case 6 uncertainty is allowed for and affects each subportfolio separately. Uncertainty heavily impacts on the portfolio risk profile.

4.4.6 Case 3 versus Case 6

We look at the effect of splitting the portfolio into homogeneous subportfolios due to the observable risk factors. Unlike previous comparison (see Case 1 versus Case 2) in both the cases, the settings consider uncertainty in the assessments of the probability of disablement. The impact is evident on Figs. 12 and 13: splitting the portfolio into homogeneous subportfolios lowers the dispersion.

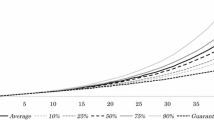
4.5 Assets required

In Figs. 14 and 15 the total amounts of assets facing the liabilities are shown for various percentiles, at time $t=1$ and $t=5$, respectively. We note that, because of the uncertainty effect, the assets required are much higher in Case 3 than in Case 1. In Figs. 16, 17 and 18 the assets required for the percentile 95% are displayed. We note that requirements of course decrease with time and then with decreasing portfolio size and hence the decreasing insurers liabilities. Finally, Fig. 19 shows the ratio between assets required (according to 95% percentile) and expected value of the total payout. We see, also from this perspective, the heavy impact of uncertainty in the probability of disablement.

5 Concluding remarks and outlook

Probability distributions of the annual payouts in an insurance portfolio constitute the main topic dealt with in the present paper. In particular, we have addressed a portfolio of term insurance policies providing lump sum benefits both in case of death and in case of permanent disability.

The analysis of probability distributions allows us to assess the riskiness inherent in the portfolio, and hence to suggest appropriate actions in terms of premiums and capital allocation. In this regard, we have adopted the percentile principle.

Among our achievements, we stress the impact of uncertainty and frailty on the risk profile of the portfolio, in particular in terms of assets to allocate in order to face the portfolio riskiness. Other significant results relate to the effect of splitting the portfolio into (more or less homogeneous) subportfolios.

The model we have proposed can be generalized in several ways, and can be implemented for other purposes. As regards possible generalizations:

• 1. the benefit structure can be extended, for example to include the payment of recurrent benefits such as disability annuities;

• 2. the multistate model can be extended from three to four states in order to represent diverse degrees of disability severity.

Numerical results obviously depend on modelling choices and parameter values. Specific implementations in particular aim at sensitivity analysis. For example:

• to assess the impact of the (initial) portfolio size and hence the diversification effect produced by risk pooling (as regards the random fluctuation risk);

• to assess the impact of a sudden jump in mortality and/or disability, thus according to the logic of stress testing.