Abstract
Scenario optimization is an approach to data-driven decision-making that has been introduced some fifteen years ago and has ever since then grown fast. Its most remarkable feature is that it blends the heuristic nature of data-driven methods with a rigorous theory that allows one to gain factual, reliable, insight in the solution. The usability of the scenario theory, however, has been restrained thus far by the obstacle that most results are standing on the assumption of convexity. With this paper, we aim to free the theory from this limitation. Specifically, we focus on the body of results that are known under the name of “wait-and-judge” and show that its fundamental achievements maintain their validity in a non-convex setup. While optimization is a major center of attention, this paper travels beyond it and into data-driven decision making. Adopting such a broad framework opens the door to building a new theory of truly vast applicability.
Similar content being viewed by others
1 Introduction
In a variety of applied fields that range from telecommunications to finance, from medicine to various branches of engineering, the role of data is growing more important every day. The main reason of this trend lies in the increasing complexity of the systems under consideration and the consequent inability of traditional modeling tools to keep adequate control on all the attendant descriptive issues. Data are therefore used to tailor otherwise general-purpose decision processes to the specific situation at hand. Along this approach, however, a major concern is that traditional model-based approaches leave way to more heuristic methods where data are often used without the necessary theoretical insight. It is in this context that the scenario approach has affirmed itself for its ability to address this concern thanks to a full-fledged theory able to rigorously characterize the reliability of the ensuing solutions (generalization theory).
1.1 The scenario approach
Let \(x \! \in \! \mathcal {X}\) be a vector of design variables. While in many problems \(\mathcal {X}= \mathbb {R}^{d}\), the Euclidean space with d components,Footnote 1 in the scenario theory \(\mathcal {X}\) can as well be infinite dimensional and, even more generally, it is not required to exhibit any specific structure. Hence, \(\mathcal {X}\) can be just thought of as any set. Further, let \(\delta \) be a parameter that describes the environment to which the decision is applied.Footnote 2 The interplay between x and \(\delta \) is formalized by the concept of appropriateness: we say that x is appropriate for \(\delta \) if a given user-chosen “satisfaction condition” is fulfilled. For example, in an investment the satisfaction condition can be that the reward is more than a given threshold and, in a medical application, that the patient is correctly classified as having, or not having, a given disease. The set of the values of x that are appropriate for a given \(\delta \) is denoted by \(\mathcal {X}_\delta \).Footnote 3 The reader is referred to the book [1] and the survey paper [2] for a more comprehensive description of these ingredients with reference to diverse practical problems.
In the scenario approach, it is assumed that the user has at her/his disposal a list \(\delta _1,\ldots ,\delta _N\) of observations of the variable \(\delta \) (each \(\delta _i\) is called a scenario),Footnote 4 which are used to make a design, i.e., to choose a value of x. Mathematically, \(\delta _1,\ldots ,\delta _N\) is described as an independent and identically distributed (i.i.d.) sample from a probability space \((\Delta ,\mathcal {D},\mathbb {P})\). The scenario approach recognizes that there is a substantial difference between positing the existence of an underlying generative mechanism given by \((\Delta ,\mathcal {D},\mathbb {P})\) and assuming that such a mechanism is known. Correspondingly, using the scenario method does not require any knowledge of \((\Delta ,\mathcal {D},\mathbb {P})\) (distribution-free perspective) and, yet, the existing generalization results by which one can exert control on the probability of inappropriateness are quite tight and informative. Expressed in other words, the scenario approach lets the data \(\delta _1,\ldots ,\delta _N\) speak in their double role of (i) building a decision; and (ii) ascertaining the ability of the solution to act appropriately on unseen, out-of-sample, \(\delta \)’s.
Before delving into the theory, it is also important to remind that the scenario approach is not one single algorithm, rather it is an entire body of methods: the map that goes from \(\delta _1,\ldots ,\delta _N\) into the decision can, e.g., be built by worst-case optimization, as well as by the minimization of various risk measures (for example, CVaR - Conditional Value at Risk); moreover, outliers can be discarded for the purpose of improving the optimization value and relaxed schemes are also part of the scenario approach. Among these methods, one of the simplest is robust scenario optimization, which operates as follows: given a cost function c(x), one is asked to perform its minimization under the constraint that the solution is appropriate for all the scenarios \(\delta _1,\ldots ,\delta _N\), viz.,
For example, in an investment problem one optimizes a given financial index under the constraint that a minimum reward is attained in the market conditions that have been observed in the past as \(\delta _i\)’s. Or, in a control problem, one minimizes, say, the settling time when tracking given reference signals while enforcing suitable appropriateness constraints (which express, e.g., that the closed-loop is stable) for the recorded list of operating conditions. The reader is referred to [3,4,5,6,7,8,9,10,11,12,13] for applications of this scheme to control design, to [14,15,16,17,18,19,20] for system identification problems and to [21,22,23,24,25,26,27] for studies in the machine learning domain.
After the robust scenario problem () has been solved, one obtains a solution \(x^*_N\) by which the cost \(c(x^*_N)\) can be evaluated. On the other hand, the actual level of appropriateness that the solution \(x^*_N\) achieves for new, out-of-sample, \(\delta \)’s remains unknown to the user.Footnote 5 To better formalize this idea, let us define, for any given \(x \in \mathcal {X}\), the risk of x as \(V(x) = \mathbb {P}\{ \delta \in \Delta \!: x \notin \mathcal {X}_\delta \}\).Footnote 6 Hence, V(x) quantifies the probability of drawing a new \(\delta \) for which x is not appropriate. One is interested in the risk met by the scenario solution \(x^*_N\), that is, \(V(x^*_N)\). However, this quantity is not directly computable, for its computation would require the knowledge of \(\mathbb {P}\), which is in general not available or, perhaps, just partly available. The beauty of the scenario approach is that it comes accompanied by a powerful generalization theory by which \(V(x^*_N)\) can be estimated without using any extra observations besides those employed to optimize.
The scenario risk theory has been developed – indeed not just for the robust scheme () but, rather, for the entire body of methods the scenario approach encompasses – by the work of many researchers in a series of publications, of which a selected sample is [28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47]. However, all these papers assume convexity or a technical, limiting, assumption called non-degeneracy, which applies broadly to convex problems only. The goal of this paper is to overcome this limitation. In the following section, we revise in particular the fundamental achievements obtained in [39] in relation to the scheme in () because this study forms the starting line of the new exploration in this paper.Footnote 7 We anticipate, on the other hand, that the findings of this paper travel well beyond the scheme in () and into a full-fledged decision theory that contains many scenario algorithms as particular cases, see Sect. 1.4 for a complete overview of the content of the present paper.
1.2 The results of [39] and their limitations
Consider problem () with N, the number of scenarios, replaced by m, which is a generic index that takes any possible integer value, including zero (\(m = 0,1,2,\ldots \)):
where \(\delta _1,\ldots ,\delta _m\) is an i.i.d. sample from \((\Delta ,\mathcal {D},\mathbb {P})\).Footnote 8 Hence, (2) is in fact a class of problems indexed by m, which contains () as a particular case achieved for \(m = N\). In [39] it is assumed that a solution to (2) exists for every m and for every choice of \(\delta _1,\ldots ,\delta _m\) and, in case of multiple minimizers, a solution \(x^*_m\) is singled out by a rule of preference in the domain \(\mathcal {X}\).Footnote 9
The following notion of complexity is central in the analysis of [39].
Definition 1
(support list and complexity – robust optimization) Given a list of scenarios \(\delta _1,\ldots ,\delta _m\), a support list is a sub-list, say \(\delta _{i_1},\ldots ,\delta _{i_k}\) with \(i_1< i_2< \cdots < i_k\),Footnote 10 such that:
-
i.
the solution to problem
$$\begin{aligned} \min _{x \in \mathcal {X}}{} & {} c(x) \nonumber \\ \text {subject to:}{} & {} x \in \bigcap _{j = 1,\ldots ,k} \mathcal {X}_{\delta _{i_j}} \end{aligned}$$(3)is the same as the solution to (1) (in other words, removing all scenarios but those in the sub-list does not change the solution);
-
ii.
\(\delta _{i_1},\ldots ,\delta _{i_k}\) is irreducible, that is, no element can be further removed from \(\delta _{i_1},\ldots ,\delta _{i_k}\) while leaving the solution unchanged.
For a given \(\delta _1,\ldots ,\delta _m\), there can be more than one selection of the indexes \(i_1,i_2,\ldots ,i_k\), possibly with different cardinality k, that give a support list. The minimal cardinality among all support lists is called the complexity and is denoted by \(s^*_m\).
The theoretical achievements of [39] are deeply grounded on the following assumption of non-degeneracy.
Assumption 1
(non-degeneracy - robust optimization) For any m, with probability 1, there exists a unique choice of indexes \(i_1< i_2< \cdots < i_k\) such that \(\delta _{i_1},\ldots ,\delta _{i_k}\) is a support list for \(\delta _1,\ldots ,\delta _m\).
Remark 1
(rapprochement with the definitions of [39]) Assumption 1 in this paper is stated differently from the non-degeneracy Assumption 2 in [39], but it is provably equivalent to it. Under non-degeneracy, it is an easy exercise to show that the notion of complexity as per Definition 1 of this paper coincides with that given in Definition 2 of [44]. This latter notion coincides with the concept in use in paper [39] without explicitly calling it “complexity”.
Note now that \(x^*_N\) and \(s^*_N\) depend on the list \(\delta _1,\ldots ,\delta _N\) and, as such, are random elements defined over the product probability space \((\Delta ^N,\mathcal {D}^N,\mathbb {P}^N)\) (the fact that the probability is a product is because the scenarios are drawn independently). The main result of [39] is then as follows.
Theorem 1
(Theorem 3 in [39]) Let \(\epsilon (k)\), \(k=0,1,\ldots ,N\), be any [0, 1]-valued function. Under the non-degeneracy Assumption 1, it holds that
where (\(\textsf {P}_N\) is the class of polynomials of order N and \( \textbf{1}_{A} \) is the indicator function of set A)
Theorem 1 sets a limit to the probability with which the risk \(V(x^*_N)\) exceeds a user-chosen function of the complexity. Even though this result provides a guarantee in terms of the probability \(\mathbb {P}\) (which appears as \(\mathbb {P}^N\) and, implicitly, in the definition of V(x)), a practical use of the theorem does not require any knowledge of \(\mathbb {P}\) (distribution-free result): one computes the complexity \(s^*_N\), substitutes it in function \(\epsilon (k)\) and obtains an upper bound to \(V(x^*_N)\) that holds with probability \(1 - \gamma ^*\) (this latter probability is called confidence).
In [39], an additional theorem is proven, which is a sort of converse to Theorem 1: given a user-chosen level \(1 - \beta \) of the confidence (normally, chosen to be very close to 1), this additional theorem returns a function \(\epsilon (k)\) that, when evaluated corresponding to the complexity, serves as a valid upper bound to the risk \(V(x^*_N)\) with confidence at least \(1-\beta \). The function \(\epsilon (k)\) is defined as follows. For any \(k=0,1,\ldots ,N-1\), consider the polynomial equation in the t variableFootnote 11
Equation (5) has one and only one solution t(k) in the interval (0, 1).Footnote 12 The function \(\epsilon (k)\) is then defined as
Theorem 2
(Theorem 4 in [39]) With \(\epsilon (k)\), \(k=0,1,\ldots ,N\), as defined in (6), under the non-degeneracy Assumption 1, it holds that
Figure 3 in Sect. 2.1 depicts the graph of function \(\epsilon (k)\) given in (6). See also [39] for more discussion and interpretation of these theorems.
An instance of a convex problem in which the support list is not unique: both sub-lists \(\delta _1, \delta _2\) and \(\delta _1, \delta _3\) return the same solution as that obtained with all three constraints. This happens because the boundary of the constraint corresponding to \(\delta _3\) goes through the solution that is obtained by only considering \(\delta _1\) and \(\delta _2\)
An instance of a non-convex problem. Sub-lists \(\delta _1, \delta _2\) and \(\delta _1, \delta _3\) return the same solution as that obtained with all three constraints (note that one of the two between \(\delta _2\) and \(\delta _3\) has to be kept in addition to \(\delta _1\) for, otherwise, the solution “falls” in \(\bar{x}\)). Nonetheless, the boundaries of the constraints do not accumulate at the solution
1.3 The role of convexity
We have said above that much of the theory on the scenario approach is rooted in an assumption of convexity. On the other hand, the results of [39] that we have revised in the previous section do not contain such an assumption, at least explicitly stated. Can we perhaps conclude from this that convexity is unimportant to the findings of [39]? Certainly not: convexity lingers on [39] as well, even though from behind the curtains, since non-degeneracy is a mild assumption in a convex setup only,Footnote 13 To understand this point, one has to note that, in a convex setup, a support list is associated to constraints that are all active at the solution. As a consequence, degeneracy corresponds to an anomalous accumulation of the constraints, see Fig. 1 for an example. On the contrary, in a non-convex problem the constraints associated to the scenarios in a support list need not be active, see Fig. 2, and degeneracy do not call for any anomalous accumulation of the constraints. Indeed, non-degeneracy is almost the norm in non-convex problems.Footnote 14 The interested reader is referred to [39] for more discussion on the concept of degeneracy.
1.4 The contribution of this paper
This paper aims at removing the assumption of non-degeneracy in the scenario approach, with profound implications on its applicability to non-convex optimization problems.
The next Sect. 2 presents two new theorems, Theorems 3 and 4, in the wake of Theorems 1 and 2 in Sect. 1.2. As compared to Theorems 1 and 2, the new results take two main departures: (i) they hold without non-degeneracy; (ii) they are stated in a very general and unitary setup called “scenario decision-making” that was first introduced in [44, Section 5]. Features (i) and (ii) open new doors to using the scenario results in vast territories that were previously precluded and that are partially explored in Sects. 3 and 4 of the present paper. Specifically, in Sect. 3, Theorems 3 and 4 are applied to the robust optimization setup of Sect. 1.2 showing that Theorems 1 and 2 maintain their validity without the Assumption 1 of non-degeneracy. This delivers results that naturally find their way into non-convex robust scenario optimization. The versatility of the results of Sect. 2 are further demonstrated in Sect. 4 where they are applied to schemes beyond robust optimization (more specifically, to optimization with constraints relaxation and CVaR optimization) and also for introducing a general approach able to cope with problems in which the solution may not exist.
Before moving to the technical results, we also feel it is important to spend some more words to say that the present paper is not meant to supersede the body of results that are known in the non-degenerate case. As said, the new theorems in the next section of this paper better the theorems of similar content in [39]. On the other hand, [39] also contains a slightly stronger theorem (Theorem 1 in [39]) that holds when the complexity is deterministically upper-bounded, which, in turn, implies the famous “Beta-result” (this is stated as Corollary 1 in [39]), a finding first established in [28]. Interestingly, the result in Theorem 1 of [39] ceases to be true without the non-degeneracy condition, a fact that is discussed in Sect. 3.2 of this paper. We further notice that also lower bounds to the risk hold when the problem is non-degenerate, so that the risk is in sandwich between two bounds which, provably, meet asymptotically for a number of data points that grows unbounded. This theory has been presented in [44]. Without the non-degeneracy assumption, the lower bounds become unattainable. All this shows that previous studies of the risk under the assumption of non-degeneracy have a value, and this value is well maintained after the findings of this paper.
2 A theory of scenario decision-making without non-degeneracy assumptions
To move towards a general theory of decision-making, we need first to introduce a formal setup that is more general than, and strictly contains, the robust framework of (). Let \(\mathcal {Z}\) be a generic set, which we interpret as the domain from which a decision z has to be chosen.Footnote 15 To each \(\delta \), there is associated a set \(\mathcal {Z}_\delta \subseteq \mathcal {Z}\) that contains the decisions that are appropriate for \(\delta \) (according to any given appropriateness criterion). For any \(m = 0,1,2,\ldots \), given a sample of i.i.d. scenarios \(\delta _1,\ldots ,\delta _m\) from \((\Delta ,\mathcal {D},\mathbb {P})\), we consider a map
that associates a decision to any list of m scenarios. The interpretation of \(M_m\) depends on the problem at hand; as we shall see, robust optimization defines one such map, and so do many other schemes, some of which will be discussed in later sections. The decision returned by \(M_m\) is normally denoted by \(z^*_m\), while, when we want to emphasize that \(z^*_m\) is selected by \(M_m\) corresponding to a sample \(\delta _1,\ldots , \delta _m\), we also use the notation \(M_m(\delta _1, \ldots , \delta _m)\). When \(m=0\), \(\delta _1,\ldots , \delta _m\) is meant to be the empty list and \(M_0\) returns the decision that is made when no scenarios are available.Footnote 16 The following property, borrowed from [44, Section 5], will play a fundamental role in our study.
Property 1
For any integers \(m \ge 0\) and \(n > 0\) and for any choiceFootnote 17 of \(\delta _1,\ldots ,\delta _m\) and \(\delta _{m+1}, \ldots , \delta _{m+n}\), the following three conditions hold:
-
(i)
if \(\delta _{i_1}, \ldots , \delta _{i_m}\) is a permutation of \(\delta _1, \ldots , \delta _m\), then it holds that \(M_m(\delta _1, \ldots , \delta _m) = M_m(\delta _{i_1}, \ldots , \delta _{i_m})\);
-
(ii)
if \(z^*_m \in \mathcal {Z}_{\delta _{m+i}}\) for all \(i=1,\ldots ,n\), then it holds that \(z^*_{m+n} \! = \! M_{m+n}(\delta _1,\ldots , \delta _{m+n}) \! = \! M_{m}(\delta _1, \ldots , \delta _m) \! = \! z^*_m\);
-
(iii)
if \(z^*_m \notin \mathcal {Z}_{\delta _{m+i}}\) for one or more \(i \in \{1,\ldots ,n\}\), then it holds that \(z^*_{m+n}= M_{m+n}(\delta _1,\ldots ,\delta _{m+n}) \ne M_{m}(\delta _1, \ldots , \delta _m) = z^*_m\).
Condition (i) is called permutation-invariance; (ii) requires that the decision does not change if additional scenarios are added for which the decision is already appropriate (confirmation under appropriateness); finally (iii) imposes that the process of selection reacts to getting exposed to additional scenarios for which the previous decision is not appropriate (responsiveness to inappropriateness). Conditions (ii) and (iii) are known as relations of consistency. In the following, we shall refer for short to the whole Property 1 as the “consistency property”, even though, strictly speaking, it also includes the additional condition of permutation invariance. It is easy to see that the robust optimization scheme of Sect. 1.2 readily fits into the frame of Property 1 (see Sect. 3 for details). On the other hand, we anticipate that (i)-(iii) do not imply that \(z^*_m \in \mathcal {Z}_{\delta _1} \cap \cdots \cap \mathcal {Z}_{\delta _m}\), an important feature that will allow us to later accommodate optimization schemes where some constraints are possibly violated for the purpose of improving the cost value (see Sect. 4 for details).
The following definition of risk generalizes the definition of risk that is in use for robust optimization.
Definition 2
(risk) For a given \(z \in \mathcal {Z}\), the risk of z is defined as \(V(z) = \mathbb {P}\{ \delta \in \Delta : z \notin \mathcal {Z}_\delta \}\).
The notion of support list and that of complexity now become as follows.
Definition 3
(support list and complexity) Given a list of scenarios \(\delta _1,\ldots ,\delta _m\), a support list is a sub-list, say \(\delta _{i_1},\ldots ,\delta _{i_k}\) with \(i_1< i_2< \cdots < i_k\),Footnote 18 such that:
-
i.
\(M_m(\delta _1, \ldots , \delta _m) = M_k(\delta _{i_1},\ldots ,\delta _{i_k})\);
-
ii.
\(\delta _{i_1},\ldots ,\delta _{i_k}\) is irreducible, that is, no element can be further removed from \(\delta _{i_1},\ldots ,\delta _{i_k}\) while leaving the decision unchanged.
For a given \(\delta _1,\ldots ,\delta _m\), there can be more than one selection of the indexes \(i_1,i_2,\ldots ,i_k\), possibly with different cardinality k, that give a support list. The minimal cardinality among all support lists is called the complexity and is denoted by \(s^*_m\).Footnote 19
Let N be the actual number of scenarios on which the decision is based. Note that, given \(\delta _1, \ldots , \delta _N\), \(s^*_N\) can be computed from its definition without any additional information on the mechanism by which scenarios are generated. In statistical terminology, \(s^*_N\) is a statistic of the scenarios. The following two theorems – which are presented and fully proved in this paper – are the main contributions of the present work.
Theorem 3
(decision theory) Assume that the maps \(M_m\) satisfy Property 1 and let \(\epsilon (k)\), \(k=0,1,\ldots ,N\), be any [0, 1]-valued function. For any \(\mathbb {P}\), it holds that
where (\(\textsf {P}_N\) is the class of polynomials of order N and \( \textbf{1}_{A} \) is the indicator function of set A)
Proof
see Sect. 5.1.
Theorem 4
(decision theory – choice of function \(\epsilon (k)\)) Assume that the maps \(M_m\) satisfy Property 1. With \(\epsilon (k)\), \(k=0,1,\ldots ,N\), as defined in (6), for any \(\mathbb {P}\) it holds that
Proof
see Sect. 5.2.
The interpretation of Theorems 3 and 4 is, mutatis mutandis, the same as that of Theorems 1 and 2. In particular, the complexity \(s^*_N\) (observable variable) is shown to carry fundamental information to estimate the risk \(V(z^*_N)\) (hidden variable). The novelty of Theorems 3 and 4 rests on their sheer generality: they address decision theory, not just optimization, and do not require any non-degeneracy assumption. The power of these new results will be demonstrated in the next few sections: Sect. 3 on non-convex robust optimization; Sect. 4.1 that presents optimization with constraint relaxation; Sect. 4.3, where the optimization of CVaR - Conditional Value at Risk - is discussed. It remains that this is only a partial and limited sample of problems to which the new theory of this paper can be applied.
2.1 On the practical use of Theorems 3 and 4
In many ways, of the two theorems, the one that plays the most prominent role in applications is Theorem 4, while Theorem 3 retains crucial theoretical value because of its generality. This claim is elaborated upon in this section, in which we will also clarify further practical facts that are not immediately obvious from a reading of the theorems.
We start by providing in Fig. 3 a visual representation of function \(\epsilon (k)\) given in (6) for various value of N and \(\beta \). It stands out that \(\epsilon (k)\) exhibits a modest dependence on the value of \(\beta \). Indeed, function \(\epsilon (k)\) takes a margin above the straight line k/N that depends logarithmically on \(\beta \) and, provably, this margin goes to zero uniformly in k as N increases, see [26]. Moreover, \(\epsilon (k)\) is a monotonically increasing function of k, so that over-bounding \(s^*_N\) (which is often easier than exactly computing it) and using this bound in \(\epsilon (k)\) leads to a valid, even though looser, evaluation of \(V(x^*_N)\).Footnote 20
As discussed in [39], while not fully optimized, function \(\epsilon (k)\) in (6) has a very little margin of improvement. Referring, e.g., to Figure 5 in [39], one observes that the function \(\bar{\epsilon }(k)\) in red (which is pretty close to \(\epsilon (k)\)) provides an impassable lower limit for \(\epsilon (k)\): any function \(\epsilon (k)\) that is smaller than \(\bar{\epsilon }(k)\) even for just one value of k is not a valid bound for the risk (in other words, counter-examples can be found that show that the level of confidence with one such function \(\epsilon (k)\) drops below \(1 - \beta \)). This fact highlights the tightness of the evaluations provided by Theorem 4. Interestingly enough, one can look at this same result from a different point of view. Say that an individual carries a particular interest for a given value \(\bar{k}\) and, in an attempt to improve \(\epsilon (\bar{k})\), s/he elevates the values of \(\epsilon (k)\) for \(k \ne \bar{k}\) while trying simultaneously to considerably reduce \(\epsilon (\bar{k})\). Nonetheless, owing to the above mentioned insurmountable limits, the computation of the confidence via Theorem 3 necessarily yields unsatisfactory results, even when the values of \(\epsilon (k)\) for k other than \(\bar{k}\) are significantly elevated (we express this fact that no “waterbed effect” holds: increasing function \(\epsilon (k)\) within a range of values k does not result in a corresponding reduction elsewhere). Finally, we mention in passing that these observations offer a practical approach to compute a valid upper bound for \(\gamma ^*\) in (7) (note that (7) is a semi-infinite optimization problem, an inherently difficult problem to solve): rename \(\tilde{\epsilon }(k)\) the function in use in Theorem 3; given a value of \(\beta \), compute function \(\epsilon (k)\) according to Theorem 4; if \(\epsilon (k) \le \tilde{\epsilon }(k), \forall k\), than \(\beta \) is a guaranteed upper bound for \(\gamma ^*\), in the opposite it is not; this fact offers an easy approach to search for a suitable upper bound for \(\gamma ^*\) through a bisection procedure (interestingly, in view of the foregoing discussion on the waterbed effect, having at convergence \(\epsilon (k) {\approx } \tilde{\epsilon }(k)\) for only some values k does not indicate conservatism in the evaluation).
2.2 A comparison with the results in [48]
The problem of evaluating the risk associated to scenario decisions without the assumption of non-degeneracy has been previously considered along a different line in [48], a paper whose authorship includes the two authors of the present contribution. Here, we feel advisable to compare our achievements in this paper with those obtained in [48].
The first observation is that the setup of [48] is definitely more stiff than the one of the present paper in that it only addresses robust decision problems (the decision need be appropriate for all scenarios). This clearly limits the applicability of the results in [48]. On the other hand, the setup of [48] is also more general in another sense: the consistency Property 1 of this paper is not assumed in [48]. Releasing this assumption allows for extra freedom that licenses the use of the theory in problems beyond those considered in the present contribution; for example, the problem in Appendix A of [48] does not satisfy the consistency Property 1. In terms of the achieved bounds, those in [48] are significantly looser than those presented in this paper. And, indeed, the tight bounds of this paper are not attainable in the setup of [48], showing that consistency embodies the relevant properties by which the most powerful risk theory of this paper can be established.Footnote 21 Considering that the consistency property holds in many problems (e.g., in all optimization problems, convex and non-convex), one sees that obtaining tight results under the condition of consistency is an important achievement of vast applicability. A final notice is that the new theory of this paper does not come for free and we anticipate that the derivations of the results are highly technical and, certainly, significantly more complex than those in [48]. This is the reason why we have preferred to postpone the derivations until Sect. 5.
3 Non-convex robust scenario optimization
Consider again the setup in Sect. 1.2. Letting \(\mathcal {Z}= \mathcal {X}\), problem (2) defines a map \(M^{\textrm{ro}}_m\) (superscript “ro” stands for robust optimization) from \(\delta _1,\ldots ,\delta _m\) to a decision \(z^*_m = x^*_m\). Define \(\mathcal {Z}_\delta = \mathcal {X}_\delta \), \(\forall \delta \in \Delta \). We want to prove that \(M^{\textrm{ro}}_m\) satisfies the consistency Property 1.
\(\diamond \) Consistency of \(M^{\textrm{ro}}_m\). Condition (i) is evidently true since the solution to (2) does not depend on the ordering of the constraints. Turn to (ii) and (iii). Suppose that the constraints \(x \in \mathcal {X}_{\delta _{m+i}}\), \(i=1,\ldots ,n\), are added to the original group of constraints \(x \in \mathcal {X}_{\delta _i}\), \(i=1,\ldots ,m\). If \(x^*_m \in \mathcal {X}_{\delta _{m+i}}\) for all \(i=1,\ldots ,n\), then \(x^*_m\) is feasible for the problem with \(m \! + \! n\) constraints. Hence, \(x^*_m\) remains optimal after adding the new n constraints, which gives \(x^*_{m+n} = x^*_m\).Footnote 22 This proves (ii). Suppose instead that \(x^*_m \notin \mathcal {X}_{\delta _{m+i}}\) for some i. Then, \(x^*_m\) is no longer feasible for the problem with \(m+n\) constraints, leading to \(x^*_{m+n} \ne x^*_m\) because the solution to (2) needs to be a feasible point. This shows the validity of (iii).
Let us further note that in the present context the notions of support list and that of complexity \(s^*_m\) given in Definition 3 coincide with those of Definition 1. In short, a support list corresponds to an irreducible sub-sample of constraints \(x \in \mathcal {X}_{\delta _{i_j}}\), \(j=1,\ldots ,k\), that, alone, suffice to return the same solution \(x^*_m\) as with all the constraints in place and the complexity is the cardinality of the smallest such support lists. Since we did not mention any non-degeneracy condition at the time we verified that \(M^{\textrm{ro}}_m\) satisfies the consistency property, by applying Theorems 3 and 4 to \(M^{\textrm{ro}}_m\) we are now in a position to unveil the deep-seated fact that the results in Theorems 1 and 2 remain valid even when the non-degeneracy Assumption 1 is dropped. This puts in our hands a powerful tool by which the scenario theory can be applied at large to non-convex robust scenario optimization. The resulting theorems are re-stated for easy reference.
Theorem 5
(robust optimization) Let \(\epsilon (k)\), \(k=0,1,\ldots ,N\), be any [0, 1]-valued function. For any \(\mathbb {P}\), it holds that
where \(\gamma ^*\) is given by (7).
Theorem 6
(robust optimization – choice of function \(\epsilon (k)\)) With \(\epsilon (k)\), \(k=0,1,\ldots ,N\), as defined in (6), for any \(\mathbb {P}\) it holds that
3.1 An example
Consider the robust scenario problem
where \(\delta _i = (\delta _{1,i},\delta _{2,i})\), \(i=1,\ldots ,N\), are independently drawn from \([0,1] \times [0,+\infty )\) according to a probability distribution \(\mathbb {P}\) given by the product of the uniform distribution over [0, 1] (\(\delta _1\) component) and the exponential distribution with mean equal to 0.1 (\(\delta _2\) component). In (8), each scenario constraint requires that the solution lies above a function with the shape of a reversed V whose vertex is \(\delta _i\) and the problem is clearly non-convex. See Fig. 4 for a realization of problem (8) with \(N=6\).
A realization of problem (8) with \(N=6\). The dashed region at bottom is the unfeasible domain. \(x^*_N\) violates the constraints whose vertex \(\delta \) lies in the greyed region
As it can be easily recognized (see Fig. 4 again), the risk of \(x^*_N = (x^*_{1,N},x^*_{2,N})\) is the probability that a new \(\delta \) falls in the region above the function \(\delta _2 = x^*_{2,N} + \vert x^*_{1,N}-\delta _1 \vert \), a probability that can be straightforwardly computed if one knows \(\mathbb {P}\).Footnote 23 Instead, computing the complexity is a bit more cumbersome, but it can be done exactly (without any approximation) by the following procedure. The first step is to isolate all the constraints that form the boundary of the feasibility region and to discard all the others. Indeed, a constraint set \(\mathcal {X}_{\delta _i}\) not involved in the boundary is completely dominated by another constraint set that is part of the boundary, which alone can replace \(\mathcal {X}_{\delta _i}\). It is perhaps also worth noticing that the constraints forming the boundary can be easily determined because they are those and only those whose vertex is within the feasibility domain of all other constraints. Next, one starts from \(x^*_N\) and scans all the remaining constraints (those forming the boundary) one by one, in the order they are found first moving leftward and then rightward (if only one constraint is active at \(x^*_N\), then the scanning only proceeds in one direction). Each time, one tries to remove the constraint under consideration and checks whether the solution changes or not after its removal. If it changes, then the constraint is kept; if instead the solution does not change, then the constraint is actually discarded and the list of the remaining constraints is updated correspondingly before moving to consider the next constraint. After completing the scanning of all constraints, one is left with a support list (because, by the very selection criterion, none of the remaining constraints can be further eliminated without changing the solution); provably, this support list is also minimal. As a matter of fact, call this support list L and, for the sake of contradiction, suppose that there is another support list \(L'\) with smaller cardinality; we show that this is impossible. In fact, scan again one by one all the constraints forming the boundary in the same order as before and continue until a discrepancy between L and \(L'\) is found, that is, the currently inspected constraint is in one support list but not in the other. Certainly, it cannot be that the constraint is in L but not in \(L'\) because this would generate a new solution, one that belongs to the infeasible domain for the constraint under scrutiny. Then, suppose the other possibility, the constraint is in \(L'\) but it is missing in L. If so, consider dropping this constraint from \(L'\) and substituting it with the next constraint found in the boundary. This operation does not increase the cardinality (either the cardinality remains the same or it drops by one, if the next constraint was already in \(L'\)) and preserves the solution (because the solution is preserved by L, which already lacks the dropped constraint). We have therefore proved that if L and \(L'\) agree till, say, the p-th constraint in the boundary, then they can be made to agree till the \((p+1)\)-th constraint without increasing the cardinality. Repeating the same process until all constraints have been considered, we re-generate L without increasing the cardinality, which shows that the cardinality of \(L'\) could not be lower than that of L.
In a computer-simulated experiment, we considered 500 instances of problem (8) with \(N=400\), each time re-drawing the scenarios independently of those in the other instances. For each instance, the solution \(x^*_N\) was recorded along with the risk \(V(x^*_N)\) and the complexity \(s^*_N\). Figure 5 displays the 500 pairs \((s^*_N,V(x^*_N))\) (black dots) along with function \(\epsilon (k)\) when \(\beta = 10^{-4}\) (blue squares). The values of \(s^*_N\) span the range \(\{1,2,\ldots ,9\}\) and the black dots lie all below the curve given by \(\epsilon (k)\). This is in agreement with Theorem 6 according to which one might expect that \(V(x^*_N) > \epsilon (s^*_N)\) only in one case out of \(10,\! 000\), at most. The figure also shows the function \(\epsilon (k)\) proposed in [48] to bound the risk (red diamonds). One can notice the significant improvement obtained by the bound of this paper.
3.2 On the traces of a deeper result that holds when the complexity is bounded
In this section, we go back to [39] to isolate a deeper result that holds when the complexity is upper bounded by a deterministic, known, quantity and see whether this result carries over to the present context in which the hypothesis of non-degeneracy is turned down. Although the impact on applications is minor because, quantitatively, this additional result takes a modest margin over the previous one, still the outcome of this investigation has a theoretical and conceptual value.
In [39], the following result – stronger than Theorem 3 in [39] (which is Theorem 1 in this paper) – is proven, still under the Assumption 1 of non-degeneracy.Footnote 24
Theorem 7
(Theorem 1 in [39] revisited) Assume that, for some integer d, it holds that \(s^*_m \le d\) with probability 1 for any m. Let \(\epsilon (k)\), \(k=0,1,\ldots ,d\), be any [0, 1]-valued function. Under the non-degeneracy Assumption 1, for any \(N\ge d\) it holds that
where (\(\textsf {C}^d[0,1]\) is the class of d-times continuously differentiable functions over [0, 1])
The reason why the thesis of this theorem is stronger than that in Theorem 3 in [39] is that the optimization problem (9) used to define \(\gamma ^*\) is less constrained than the corresponding optimization problem in Theorem 3 (\(\forall k=0,1,\ldots ,N\) is replaced by \(\forall k=0,1,\ldots ,d\)) and, moreover, optimization is conducted over the class of continuous functions \(\textsf {C}^d[0,1]\), which strictly contains the class of polynomials \(\textsf {P}_N\). As a consequence, the upper bound \(\gamma ^*\) to the confidence provided by this theorem is certainly not larger, and normally turns out to be strictly smaller, than that in Theorem 3.
Exploiting the extra strength provided by this theorem, in [39] the following corollary is further established.
Corollary 8
(Corollary 1 in [39]) Assume that, for some integer d, it holds that \(s^*_m \le d\) with probability 1 for any m. Let \(\epsilon \in [0,1]\). Under the non-degeneracy Assumption 1, for \(N\ge d\) it holds that
The right-hand side of (10) is a Beta distribution with degrees of freedom d and \(N \! - \! d \! + \! 1\), written as \(\mathcal{B}(d,N \! - \! d \! + \! 1)\). Hence, Corollary 8 states that the distribution of \(V(x^*_N)\) is dominated by a \(\mathcal{B}(d,N \! - \! d \! + \! 1)\) distribution. This result is obtained from Theorem 7 by showing that quantity \(\sum _{i=0}^{d-1} {N \atopwithdelims ()i} \epsilon ^i (1-\epsilon )^{N-i}\) attains the \(\inf \) of (9) when \(\epsilon (k) = \epsilon \) (constant) for all \(k = 0,1,\ldots ,d\). Moreover, this result is not improvable because the distribution of \(V(x^*_N)\) is exactly a \(\mathcal{B}(d,N \! - \! d \! + \! 1)\) for a full class of problems called fully-supported, see [28].
We now pose the question: does this result continue to hold if the non-degeneracy assumption is removed? Interestingly, the answer is negative: there are optimization problems such that condition \(s^*_m \le d\) holds with probability 1 for any m for which \(\mathcal{B}(d,N \! - \! d \! + \! 1)\) is not a valid bound to the distribution of \(V(x^*_N)\). The next example provides a counterexamples in the setting of non-convex optimization in \(\mathbb {R}^d\).
Example 1
(lyrebird tail example) Let \(\mathcal {X}\) be the closed disk of radius 10 in \(\mathbb {R}^2\).Footnote 25 The scenarios \(\delta _i\) are independently drawn from \(\Delta = [-1,0) \cup (0,1]\) according to a uniform probability. Moreover, we let
and \(c(x) = x_2\). Figure 6 depicts a realization of problem (2) for \(m = 5\). All sets \(\mathcal {X}_\delta \) are curvy lines that have the origin in common and, as soon as there are at least two \(\delta _i\) with the same sign, the origin becomes the only feasible point and therefore it is the solution to (2). For \(m \ge 3\), there must be at least two \(\delta _i\) with the same sign and these two \(\delta _i\) form a support list of minimal cardinality (one constraint alone does not suffice because it gives a solution that drops at level \(x_2 = -1\)). Thus, \(s^*_m = 2\) for any \(m \ge 3\), while, obviously, \(s^*_m \le 2\) for \(m \le 2\). Hence, 2 is a deterministic upper bound to the complexity. It is also readily seen that the non-degeneracy Assumption 1 does not hold since multiple support lists do exist, for example there are certaily at least two support lists for \(m \ge 4\) since one can find at least two couples of scenarios having the same sign.
A realization of problem (2). Any \(\delta _i\) sets a constraint having essential dimension 1 as represented by the solid, curvy, lines and all these constraints meet at the origin. The overall figure is reminiscent of the tail of a lyrebird
We now show that the conclusion of Corollary 8 is false in the present example. Take \(N=2\). In this case, two situations may occur: (a) \(\delta _1\) and \(\delta _2\) have opposite sign, in which case the solution \(x^*_N\) is not the origin and \(V(x^*_N) = 1\) (because \(x^*_N\) is infeasible for any other \(\delta \) but \(\delta _1\) and \(\delta _2\)); (b) \(\delta _1\) and \(\delta _2\) have the same sign, in which case the solution is \(x^*_N = (0,0)\) and \(V(x^*_N) = 0\) (because all constraints contain the origin). Since (a) and (b) occurs with probability 1/2 each (with respect to the draws of \(\delta _1\) and \(\delta _2\)), then the cumulative distribution function of \(V(x^*_N)\) is given by
On the other hand, should Corollary 8 hold, then \(\mathbb {P}^2 \{ V(x^*_N) \le \epsilon \}\) would approach 1 as \(\epsilon \rightarrow 1\) because a Beta distribution admits a density. Hence, the thesis of Corollary 8 is invalid in this case. (For a comparison of the cumulative distribution of a \(\mathcal{B}(2,1)\) – note that in our example we have \(d = 2\) and \(N \! - \! d \! + \! 1 = 1\) – and the actual cumulative distribution function of \(V(x^*_N)\), see Fig. 7).
Remark 2
(a digression into the convex setup) In this remark we show that even in a convex setup the thesis of Corollary 8 (that is, the property that the cumulative distribution function of the violation is lower-bounded by a \(\mathcal{B}(d,N \! - \! d \! + \! 1)\) distribution) ceases to be correct if the problem is degenerate. We mention this fact explicitly to burn off a fallacious belief to the contrary that has circulated in some research environments. This digression will also allow us to introduce open problems that we feel like sharing with the community.
A counterexample to the thesis of Corollary 8 in a convex setup can be easily derived from the lyrebird tail example by lifting the problem from \(\mathbb {R}^2\) into \(\mathbb {R}^3\). Let \(x = (x_1,x_2,x_3)\) be a generic point in \(\mathbb {R}^3\). Each \(\mathcal {X}_\delta \) has a triangular shape as follows. In the plane of \(x_1\), \(x_2\) consider the square with vertexes (1, 0), (0, 1), \((-1,0)\), \((0,-1)\) and, in this square, draw the segments parallel to the edges of the square that are obtained by intersecting the square with the \(+45\)-degree lines \(x_2 - x_1 = \delta + 1\) for \(\delta \in [-2,0)\) and with the \(-45\)-degree lines \(x_2 + x_1 = \delta - 1\) for \(\delta \in (0,2]\). Hence, \(\Delta = [-2,0) \cup (0,2]\), from which we assume that \(\delta \) is drawn uniformly. To build the triangular-shaped \(\mathcal {X}_\delta \), connect the end points of each segment with the point \((0,2,-1)\). The cost to be minimized is \(c(x) = x_2\). See Fig. 8 for a visualization of this problem with \(m = 3\). Applying the same arguments as done in the lyrebird tail example, the reader will not have difficulty in showing that also in the present case 2 is a deterministic upper bound to the complexity, while the cumulative distribution function of \(V(x^*_N)\) for \(N = 2\) is given by (11). Again, this is in violation of the thesis of Corollary 8.
A realization of the scenario program described in Remark 2
An aspect we want to further discuss in relation to this example relates to the existence of a nonempty interior of the feasibility domain. Let us start by observing that the treatment of [28] for convex problems assumes that the feasibility domain of any realization of the scenario problem has a nonempty interior (Assumption 1 in [28]). Under the existence of a nonempty interior (besides existence and uniqueness of the solution), Theorem 1 in [28] claims that the cumulative distribution function of \(V(x^*_N)\) is always dominated (also in the degenerate case) by a Beta distribution \(\mathcal{B}(\bar{d},N \! - \! \bar{d} \! + \! 1)\) (\(\bar{d}\) is the dimension of the optimization domain). Whether this claim preserves its validity without the assumption on the existence of a nonempty interior is at present an open problem. In fact, no theoretical result confirms this claim, while no counterexample is known that confutes its validity. In contrast, when the nonempty interior assumption is dropped, the example in this remark sets a final negative word on the possibility of dominating the cumulative distribution function of \(V(x^*_N)\) with a Beta distribution \(\mathcal{B}(d,N \! - \! d \! + \! 1)\), where d is an upper bound to the complexity strictly smaller than \(\bar{d}\).Footnote 26 Whether this conclusion maintains its validity in the presence of a nonempty interior of the feasibility domain is at present another open problem.Footnote 27
3.3 Ridge regularization
We just touch upon in this short section a point that would call for much closer attention in future publications: the use of regularization. Consider again the problem in (2), but this time with a two-norm regularization (ridge regularization) term
where \(\Vert x\Vert ^2_Q\) is short for \(x^T Q x\).Footnote 28 Adding \(\Vert x - x_0\Vert ^2_Q\) “attracts” the solution towards \(x_0\), while matrix Q determines stregth and direction of this action.
It is well recognized that regularization helps generalization. This idea finds an easy theoretical justification, and a ground for quantitative evaluation, within the theory of this paper. Indeed, suppose that Q is chosen very very large. Then, assuming \(x_0\) is an interior point of the feasibility region, the solution gets to a point close to \(x_0\) still inside the feasibility region; this is a point that remains the minimizer even in the absence of any scenarios. Hence, no matter how large the set of optimization variables is, the complexity becomes zero. On the opposite extreme of no regularization infinite Euclidean spaces, with a large amount of optimization variables it is common experience that the solution is supported by many constraints, resulting in a large complexity. In between, when Q increases starting at \(Q = 0\) and progressively assumes larger and larger values, one can expect a gradual (even though not necessarily monotonic) decrease of the complexity. By applying Theorems 5 and 6 to this context (of course, there is nothing special in considering \(c(x) + \Vert x - x_0\Vert ^2_Q\) instead of c(x) as the cost function of interest and, hence, Theorems 5 and 6 can well be applied), one can quantitatively ascertain the level of generalization achieved by the regularization as it grows mightier. Interestingly, one can also conceive to try out a (possibly large) number of \(Q_i\) matrices and a posteriori select the choice that provides the preferred balance in terms of quality of the minimizer (in any respect, as suggested by the problem at hand) and the corresponding risk (as evaluated by the theorems).Footnote 29
4 Other scenario optimization schemes
We first present an optimization scheme of wide applicability in which the constraints are relaxed under the payment of a regret and then CVaR (Conditional Value at Risk) optimization. This section contains also a discussion on the assumption of existence of the solution, and suggests a way to release it.
4.1 Scenario optimization with constraints relaxation
Robust optimization is a rigid scheme that often generates conservative solutions with an unsatisfactory cost value. To allow for more flexibility, optimization with constraint relaxation performs a trade-off between the cost and the satisfaction of the constraints. It comes with a tuning knob and robust optimization is recovered in the limit when the tuning knob goes to infinity.
Matters of convenience suggest that constraints are written in this section as \(f(x,\delta ) \le 0\), where, for any given \(\delta \), \(f(x,\delta )\) is a real-valued function of x. In other words, \(\mathcal {X}_{\delta } = \{x: \; f(x,\delta ) \le 0\}\). The reason for this choice is that function f is used to express the “regret” for violating a constraint: for a given \(\delta \), the regret for an infeasible x (for which \(f(x,\delta ) > 0\)) is \(f(x,\delta )\). In this set-up, we consider the following scenario optimization problem with penalty-based constraint relaxation:
Note that (13) has m additional optimization variables, namely, \(\xi _i\), \(i=1,\ldots ,m\). If \(\xi _i > 0\), the constraint \(f(x,\delta _i) \le 0\) is relaxed to \(f(x,\delta _i) \le \xi _i\) and this generates the regret \(\xi _i\). Hence, if a constraint is satisfied at optimum, then the corresponding \(\xi _i\) is set to its floor value zero and there is no regret, while constraint violation generates a regret that equals \(f(x^*_m,\delta _i)\). Parameter \(\rho \) is used to set a suitable trade-off between the original cost function and the extra cost paid for violating some constraints. When \(\rho \rightarrow \infty \), one goes back to the robust setup.
Because of the presence of the \(\xi _i\), problem (13) is never infeasible (given a \(x \in \mathcal {X}\), just take large enough values of the variables \(\xi _i\) to satisfy all inequalities \(f(x,\delta _i) \le \xi _i\)); we further assume that, for every m and for every choice of \(\delta _1,\ldots ,\delta _m\), the \(\min \) in (13) is attained in at least one point of the feasibility domain.Footnote 30 In case of multiple minimizers, a solution \(x^*_m\) is singled out by a rule of preference in the domain \(\mathcal {X}\).Footnote 31
Given N scenarios, solving (13) with \(m=N\) returns \(x^*_N\) and \(\xi ^*_{i,N}\), \(i=1,\ldots ,N\), from which one can empirically evaluate the probability of constraint violation by formula \((1/N) \sum _{i=1}^N \textbf{1}_{\xi ^*_{i,N} > 0} \) (\( \textbf{1}_{A} \) is the indicator function of set A). This empirical evaluation, however, is not a consistent estimate of the true probability of constraint violation. Nevertheless, by an application of the general theory of Sect. 2, we show here that the complexity can instead be used to accurately estimate the probability of constraint violation. This result may also be used to select a suitable value for the hyper-parameter \(\rho \): one tries out a set of values for \(\rho \) and compares the corresponding solutions in terms of cost (which is readily available as an outcome of the optimization problem) and probability of constraint violation (as given by the theory) to make a suitable selection. The same comment made in Footnote 29 applies to this context.
To apply the theory of Sect. 2, we have to frame the setup of this section into that of scenario decision making. It turns out that a convenient formalization amounts to consider as decision the value of \(x^*_m\) augmented with the number of variables \(\xi ^*_{m,i}\) that are positive (considering the actual value of \(\xi ^*_{m,i}\) is redundant for the goal we pursue here). Correspondingly, let \(\mathcal {Z}= \mathcal {X}\times \mathbb {N}\), with \(\mathbb {N} = \{0,1,\ldots \}\), and define \(z^*_m = (x^*_m,q^*_m)\) where \(q^*_m:= \# [ \xi ^*_{m,i} \! > \! 0, \; i=1,\ldots ,m ]\), the number of positive \(\xi ^*_{m,i}\), \(i=1,\ldots ,m\). The map from \(\delta _1,\ldots ,\delta _m\) to \(z^*_m\) is indicated with the symbol \(M^{\textrm{ocr}}_m\) (superscript “ocr” stands for optimization with contraint relaxation). Further, let \(\mathcal {Z}_\delta := \{ (x,q) \in \mathcal {Z}: \; f(x,\delta ) \le 0 \}\). With this definition we have \(V(z) = \mathbb {P}\{ \delta : \; z \notin \mathcal {Z}_\delta \} = \mathbb {P}\{ \delta : \; f(x,\delta ) > 0 \}\), where the last quantity is the probability of constraint violation (in the following indicated with V(x)), which is what we want to estimate. Hence, we shall apply the theory of scenario decision to upper bound \(V(z^*_N)\), which is the same as \(V(x^*_N)\).
We start with verifying that \(M^{\textrm{ocr}}_m\) satisfies the consistency Property 1.
\(\diamond \) Consistency of \(M^{\textrm{ocr}}_m\). Condition (i) follows from the fact that \(x^*_m\) and \(q^*_m\) in the definition of \(z^*_m\) do not depend on the ordering of the constraints. To verify (ii) and (iii), add new scenarios \(\delta _{m+1},\ldots ,\delta _{m+n}\) to the original sample \(\delta _1,\ldots ,\delta _m\) and suppose first that \(z^*_m \in \mathcal {Z}_{\delta _{m+i}}\) for all \(i=1,\ldots ,n\), which means that \(f(x^*_m,\delta _{m+i}) \le 0\) for all \(i=1,\ldots ,n\). Consider problem (13) with \(m \! + \! n\) in place of m. Since \(f(x^*_m,\delta _{m+i}) \le 0\) for all \(i=1,\ldots ,n\), augmenting the solution of (13) with \(\xi _i = 0\), \(i=m \! + \! 1,\ldots ,m \! + \! n\), gives a point \((x^*_m,\xi ^*_{m,1},\ldots ,\xi ^*_{m,m},0,\ldots ,0)\) that is feasible for problem (13) with \(m+n\) in place of m. It is claimed that this is indeed the optimal solution. As a matter of fact, if the optimal solution were a different one, say \((\bar{x}, \bar{\xi }_i, i=1,\ldots ,m \! + \! n)\), then one of the following two cases would hold:
-
(a)
\(c(\bar{x})+\rho \sum _{i=1}^{m+n} \bar{\xi }_i < c(x^*_m)+\rho \sum _{i=1}^{m} \xi ^*_{m,i}\). But then this would give \(c(\bar{x})+\rho \sum _{i=1}^m \bar{\xi }_i < c(x^*_m)+\rho \sum _{i=1}^{m} \xi ^*_{m,i}\) (because the dropped \(\bar{\xi }_i\), \(i=m \! + \! 1,\ldots ,m \! + \! n\), are non-negative), showing that in problem (13) \((\bar{x}, \bar{\xi }_i, i=1,\ldots ,m)\) would outperform the optimal solution \((x^*_m,\xi ^*_{m,i}, i=1,\ldots ,m)\), which is impossible;
-
(b)
\(c(\bar{x})+\rho \sum _{i=1}^{m+n} \bar{\xi }_i = c(x^*_m)+\rho \sum _{i=1}^{m} \xi ^*_{m,i}\) and \(\bar{x}\) ranks better than \(x^*_m\) according to the tie-break rule. But then \((\bar{x}, \bar{\xi }_i, i=1,\ldots ,m)\) would be feasible for (13) and would achieve \(c(\bar{x})+\rho \sum _{i=1}^{m} \bar{\xi }_i \le c(x^*_m)+\rho \sum _{i=1}^{m} \xi ^*_{m,i}\). Should this latter equation hold with inequality, we would have a contradiction similarly to (a). If instead equality holds, then \((\bar{x}, \bar{\xi }_i, i=1,\ldots ,m)\) would still be preferred to \((x^*_m,\xi ^*_{m,i}, i=1,\ldots ,m)\) in problem (13) because \(\bar{x}\) ranks better than \(x^*_m\), leading again to a contradiction.
Therefore, it remains proven that \(x^*_{m+n} = x^*_m\), \(\xi ^*_{m+n,i} = \xi ^*_{m,i}\) for \(i=1,\ldots ,m\) and \(\xi ^*_{m+n,i} = 0\) for \(i=m+1,\ldots ,m+n\). This gives \(z^*_{m+n} = (x^*_{m \! + \! n},q^*_{m \! + \! n}) = (x^*_m,q^*_m) = z^*_m\), which shows the validity of (ii).
Suppose instead that \(z^*_m \notin \mathcal {Z}_{\delta _{m+i}}\) for some i, i.e., \(f(x^*_m,\delta _{m+i}) > 0\) for some i. Then, if it happens that \(x^*_{m+n} = x^*_m\), then \(\xi ^*_{m+n,i} = \xi ^*_{m,i}\) for \(i=1,\ldots ,m\) and \(\xi ^*_{m+n,m+i} > 0\) for some i. Whence, \(q^*_{m+n} > q^*_m\), which implies that \(z^*_{m+n} \ne z^*_m\). If instead \(x^*_{m+n} \ne x^*_m\), this gives straightforwardly \(z^*_{m+n} \ne z^*_m\). This proves the validity of (iii).
We want next to make more explicit what the complexity is for the present problem of optimization with constraint relaxation. We first note that all \(\delta _i\)’s for which \(f(x^*_m,\delta _i) > 0\) (corresponding to \( \xi ^*_{m,i} > 0\)) must belong to any support list. Indeed, if not, at \(x^*_m\) there would be a deficiency of violated constraints so giving a value of q strictly lower than \(q^*_m\). Therefore, a support list of minimal cardinality must contain all \(\delta _i\)’s for which \(f(x^*_m,\delta _i) > 0\) and, in addition, a minimal amount of other \(\delta _i\)’s such that solving (13) with only the selected scenarios in place gives \(x^*_m\) as x component of the solution. The cardinality of one such support list is the complexity.
We now have the following theorems that are obtained from Theorems 3 and 4 tailored to the present context.
Theorem 9
(optimization with constraint relaxation) Let \(\epsilon (k)\), \(k=0,1,\ldots ,N\), be any [0, 1]-valued function. For any \(\mathbb {P}\), it holds that
where \(\gamma ^*\) is given by (7) and \(s^*_N\) is the number of \(\delta _i\)’s for which \(f(x^*_N,\delta _i) > 0\) (violated constraints) plus the cardinality of a minimal amount of additional \(\delta _i\)’s that, used in conjunction with those giving violation, returns \(x^*_N\) as x component of the solution.
Theorem 10
(optimization with constraint relaxation – choice of function \(\epsilon (k)\)) With \(\epsilon (k)\), \(k=0,1,\ldots ,N\), as defined in (6), for any \(\mathbb {P}\) it holds that
where \(s^*_N\) is defined as in the previous theorem.
Remark 3
(a further look at the results of this section) Theorem 9 allows one to evaluate the violation of the minimizer \(x^*_N\) of an optimization problem with relaxation. Note that, the general theory of Theorem 3 has not been directly applied to this context with the position \(z^*_N = x^*_N\). Instead, the optimization problem with relaxation has been lifted into a decision problem where \(z^*_N\) accounts not only for \(x^*_N\), but also for the number of scenarios corresponding to violated constraints. As one can easily verify, the technical reason for why \(x^*_N\) cannot be directly used as \(z^*_N\) is that the map from the scenarios to \(x^*_N\) is not consistent (think of how weird it would be if it were: then, the violation of \(x^*_N\) could be estimated from the complexity of just constructing \(x^*_N\), with no concern for how many scenarios are violated!). The last step in the derivation of Theorem 9 is the rapprochement of the risk of the decision \(z^*_N\) with the violation of \(x^*_N\). As a result of all this journey, the two main objects appearing in the statement of Theorem 9, namely \(x^*_N\) and \(s^*_N\), are not tied to each other by the same kinship that links \(z^*_N\) and \(s^*_N\) in Theorem 3. For this reason, looking at Theorem 9 as a particular case of Theorem 3 is inappropriate, while it is true that Theorem 3 is the support on which Theorem 9 builds.
4.2 Non-existence of the solution
Before moving to CVaR optimization, we revisit in this section the assumption that the solution always exists and introduce a general scheme to waive this condition while preserving the theoretical guarantees. This finds application not only when the solution does not exist because the problem is infeasible, it is also significant in relation to cases in which the optimization problem is tout court not defined for some value of m (so that the solution does not exist because no procedure has been introduced for its determination). As we shall see, one such case is in fact CVaR optimization, and this is the reason for having this section coming before that of CVaR.
Since the subject matter at stake here is relevant to a multitude of problems even beyond optimization, we prefer to address it at the most general level, that of scenario decision-making as per Sect. 2. Hence, we assume that \(M_m\) may not be defined for some choices of \(\delta _1,\ldots ,\delta _m\), in which case we say that the decision does not exist. In this context, we assume that conditions (i)-(iii) in the consistency Property 1 remain in force whenever the decision \(z^*_m\) exists.Footnote 32 Let \(\mathcal {Z}_{\textrm{aug}} = \mathcal {Z}\cup \left[ \bigcup _{m=0}^\infty \{\text {multisets containing } m \text { elements from } \Delta \} \right] \) (for \(m = 0\), the multiset is just the empty multiset) and define \(z_{\textrm{aug},m}^*= z^*_m\) whenever \(z^*_m\) exists and \(z_{\textrm{aug},m}^*\) to be the multiset \(\{\delta _1,\ldots ,\delta _m\}\) otherwise.Footnote 33 Moreover, let \(\mathcal {Z}_{\textrm{aug},\delta } = \mathcal {Z}_\delta \), which implies that any augmented decision of the type \(\{\delta _1,\ldots ,\delta _m\}\) is inappropriate for any \(\delta \). These definitions give a map \(M_{\textrm{aug},m}\) that always return a decision in \(\mathcal {Z}_{\textrm{aug}}\), along with a notion of appropriateness. We want to show that \(M_{\textrm{aug},m}\) satisfies the consistency Property 1.
\(\diamond \) Consistency of \(M_{\textrm{aug},m}\). Permutation invariance of \(M_{\textrm{aug},m}\) easily follows from the unordered structure of multisets and the fact that \(M_m\) is permutation invariant whenever a decision exists. When new scenarios \(\delta _{m+1},\ldots ,\delta _{m+n}\) are added, if \(z_{\textrm{aug},m}^*= z_m^*\), then the two conditions (ii) and (iii) in Property 1 for \(M_{\textrm{aug},m}\) follows from the validity of the same conditions for \(M_m\). Suppose instead that \(z_{\textrm{aug},m}^*= \{\delta _1,\ldots ,\delta _m\}\), in which case, certainly, \(z_{\textrm{aug},m}^*\) is inappropriate for all \(\delta _{m+1},\ldots ,\delta _{m+n}\). Then, either \(M_{m+n}(\delta _1,\ldots ,\delta _{m+n})\) exists, so that \(M_{\textrm{aug},m+n}(\delta _1,\ldots ,\delta _{m+n})\) is an element of \(\mathcal {Z}\) (in which case the augmented decision has changed), or \(M_{m+n}(\delta _1,\ldots ,\delta _{m+n})\) does not exist, which gives: \(M_{\textrm{aug},m+n}(\delta _1,\ldots ,\delta _{m+n}) = \{\delta _1,\ldots ,\delta _{m+n}\} \ne z_{\textrm{aug},m}^*\) (and, again, the augmented decision has changed). Since the augmented decision changes in both cases, condition (iii) (the only relevant one when \(z_{\textrm{aug},m}^*= \{\delta _1,\ldots ,\delta _m\}\)) is satisfied.
Having verified the consistency Property 1, Theorems 3 and 4 can be applied to \(M_{\textrm{aug},m}\) to upper bound \(\mathbb {P}^N \{V(z^*_{\textrm{aug},N}) > \epsilon (s^*_{\textrm{aug},N}) \}\), where we have that \(s_{\textrm{aug},N}^*= s_N^*\) if \(M_N(\delta _1,\ldots ,\delta _N)\) exists and \(s^*_N = N\) otherwise. The ensuing result can be cast back into an evaluation of the risk associated with the original decision \(z^*_N\) by further observing that
where the last equality is obtained by suppressing the second term and recalling that, when \(z^*_N\) exists, (a) it holds that \(z^*_{\textrm{aug},N} = z^*_N\) and \(s^*_{\textrm{aug},N} = s^*_N\) and (b) the two notions of risks for the augmented and the original decision coincide. We have obtained the following theorems.
Theorem 11
(decision theory with no assumption of existence of the solution) Assume that the maps \(M_m\) satisfy conditions (i)-(iii) in Property 1 whenever the decision \(z^*_m\) exists and let \(\epsilon (k)\), \(k=0,1,\ldots ,N\), be any [0, 1]-valued function. For any \(\mathbb {P}\), it holds that
where \(\gamma ^*\) is given by (7).
Theorem 12
(decision theory with no assumption of existence of the solution – choice of function \(\epsilon (k)\)) Assume that the maps \(M_m\) satisfy conditions (i)-(iii) in Property 1 whenever the decision \(z^*_m\) exists. With \(\epsilon (k)\), \(k=0,1,\ldots ,N\), as defined in (6), for any \(\mathbb {P}\) it holds that
4.3 Scenario conditional value at risk (CVaR)
Certain design problems come with no constraints and a cost function that depends on the uncertainty parameter \(\delta \), which we write \(c(x,\delta )\). For example, \(c(x,\delta )\) can be the return of a portfolio (with negative sign in front to make it a cost), in which case x is the vector containing the percentages of capital invested on various financial instruments and \(\delta \) describes the evolution of their value over the period of investment.Footnote 34
One way to deal with uncertain cost functions is by worst-case optimization, a well-known approach that plays a prominent role in various disciplines. In the scenario framework, worst-case optimization amounts to solve the following problem
and rewriting (14) in epigraphic form reveals that this is nothing but a special case of the robust approach dealt with in Sect. 3:
where h is an auxiliary optimization variable. In this context, the theory of Sect. 3 allows one to evaluate the probability of exceeding the largest empirical cost, that is, the probability with which \(c(x^*_N,\delta ) > h^*_N\), where \(x^*_N\) and \(h^*_N = \max _{i=1,\ldots ,N} c(x^*_N,\delta _i)\) are obtained from (15) with N in place of m.Footnote 35
Worst-case optimization is often undesirably conservative. Hence, one may want to move to Conditional Value at Risk (CVaR), which amounts to minimize the average cost over a worst-case tail (shortfall cases): for any given x, re-order the indexes \(1,\ldots ,m\) according to the value taken by \(c(x,\delta _i)\), from largest to smallest (in case of ties, maintain the initial order), and let \(1_m(x)\) be the first index, \(2_m(x)\) the second, etc.. Given an integer q (q is a user-chosen parameter that defines how many scenarios are included in the tail and averaged upon), for \(m \ge q\), CVaR consists in the following minimization problem
where we conveniently assume that a solution exists and, in case of ties, a minimizer \(x^{*,q}_m\) is selected according to a rule of preference in the domain \(\mathcal {X}\). When \(m < q\), CVaR is instead not defined. Note that problem (16) comes down to (14) when \(q = 1\); selecting larger values of q mitigates the conservatism inherent in the worst-case approach by the effect of averaging over q scenarios. Value \(h^{*,q}_m:= c(x^{*,q}_m,\delta _{q_m(x^{*,q}_m)})\) is the q-th largest empirical cost incurred by \(x^{*,q}_m\) and it is the tipping point that separates shortfalls from other cases. In what follows, we derive distribution-free results on the probability with which a new \(\delta \) incurs a cost in the shortfall range.
Start by defining \(M^{\textrm{CVaR},q}_{m}\), \(m \ge q\), as the map from the scenarios to the decision \(z^{*,q}_{m} = (x^{*,q}_m,h^{*,q}_m,v^{*,q}_m)\), where \(v^{*,q}_m:= \frac{1}{q} \sum _{j=1}^q c(x^{*,q}_m,\delta _{j_m(x^{*,q}_m)})\) is the CVaR value (hence, \(\mathcal {Z}= \mathcal {X}\times \mathbb {R}\times \mathbb {R}\)). It is then easy to verify that \(M^{\textrm{CVaR},q}_{m}\) satisfies conditions (i)-(iii) in the consistency Property 1 with \(\mathcal {Z}_\delta = \{ (x,h,v): \; c(x,\delta ) \le h \}\) whenever \(m \ge q\), an exercise that we pursue in the following.
\(\diamond \) \(M^{\textrm{CVaR},q}_{m}\) satisfies (i)-(iii) in Property1for \(m \ge q\). \(M^{\textrm{CVaR},q}_{m}\) is clearly permutation invariant, so that (i) is satisfied. When n new scenarios \(\delta _{m+1},\ldots ,\delta _{m+n}\) are added to the original sample \(\delta _1,\ldots ,\delta _m\), condition \(z^{*,q}_{m} \in \mathcal {Z}_{\delta _{m+i}}\), \(i=1,\ldots ,n\), implies that \(\frac{1}{q} \sum _{j=1}^q c(x^{*,q}_m,\delta _{j_{m+n}(x^{*,q}_m)}) = \frac{1}{q} \sum _{j=1}^q c(x^{*,q}_m,\delta _{j_{m}(x^{*,q}_m)})\) (that is, the average of the top q values at \(x = x^{*,q}_m\) remains unchanged). Since for any other x it holds that \(\frac{1}{q} \sum _{j=1}^q c(x,\delta _{j_{m+n}(x)}) \ge \frac{1}{q} \sum _{j=1}^q c(x,\delta _{j_{m}(x)})\) (strict inequality holds when, for an x other than the minimizer \(x^{*,q}_m\), it happens that a new \(\delta _{m+i}\) incurs a cost in the shortfall range), then \(x^{*,q}_m\) remains the optimal solution, and also \(h^{*,q}_m\) and \(v^{*,q}_m\) do not change (condition (ii)). If instead \(z^{*,q}_{m} \notin \mathcal {Z}_{\delta _{m+i}}\) for some i, then either the minimizer changes: \(x^{*,q}_m \ne x^{*,q}_{m+n}\) (and, therefore, the decision changes), or (if \(x^{*,q}_m = x^{*,q}_{m+n}\)), we have: \(v^{*,q}_{m+n} = \frac{1}{q} \sum _{j=1}^q c(x^{*,q}_{m+n},\delta _{j_{m+n}(x^{*,q}_{m+n})}) = \frac{1}{q} \sum _{j=1}^q c(x^{*,q}_m,\delta _{j_{m+n}(x^{*,q}_m)}) > v^{*,q}_m\) (and the decision changes in the v part). This shows the validity of condition (iii).
Since CVaR is not defined for \(m \le q\), we want to apply Theorems 11 and 12. Under the assumption that \(N \ge q\), CVaR certainly gives a solution, so that in the reformulation of Theorems 11 and 12 the specification “\(z^*_N\) exists” can be dropped. This gives the following theorems.
Theorem 13
(CVaR) Assume \(N \ge q\) and let \(\epsilon (k)\), \(k=0,1,\ldots ,N\), be any [0, 1]-valued function. For any \(\mathbb {P}\), it holds that
where \(\gamma ^*\) is given by (7), \(s^{*,q}_N\) is the complexity associated with \(M^{\textrm{CVaR},q}_{N}(\delta _1,\ldots ,\delta _N)\),Footnote 36 and \(V(x,h,v) = \mathbb {P}\{c(x,\delta ) > h\}\).
Theorem 14
(CVaR – choice of function \(\epsilon (k)\)) Assume \(N \ge q\). With \(\epsilon (k)\), \(k=0,1,\ldots ,N\), as defined in (6), for any \(\mathbb {P}\) it holds that
where \(s^{*,q}_N\) is the complexity associated with \(M^{\textrm{CVaR},q}_{N}(\delta _1,\ldots ,\delta _N)\) and \(V(x,h,v) = \mathbb {P}\{c(x,\delta ) > h\}\).
Remark 4
(“virtual” maps) We make here a remark that can be applied broadly to scenario decision making and not just to CVaR; our referring to CVaR is for the sake of concreteness. Say that, in CVaR, q is set at the value 10 and N is 100 and that, by this choice, the user means to regard as shortfalls the \(10\%\) worst cases. Later, as new observations come along, the user would like to increase q; for example, with 110 data points, s/he would like to take \(q = 11\) to keep the ratio q/(no. of data points) constant. This leads to a CVaR scheme in which q changes with m. However, as it is easily verified, this infringes the rules of consistency (for, increasing m by one unit may cause q to also increase and, thereby, the solution may change even when the solution with m observations is appropriate for the \((m \! + \! 1)\)-th observation). Do we have to conclude that the theory of this paper does not apply to this setup with a changing q? The answer to this question is indeed negative, for the reason explained in the following. The first thing to note is that, for any given N, the only “real” map is \(M^{\textrm{CVaR},q}_N\), it is this map that sets the decision and, thereby, determines the risk that is associated with it. All other maps \(M^{\textrm{CVaR},q}_m\) for \(m \ne N\) simply have no active role. What does the consistency property (which introduces dependencies across maps \(M_m\) for different values of m) enforce then? The answer is that it introduces an interrelation among objects of which one, map \(M_N\), is the only one that really operates, while all others, \(M_m\) for \(m \ne N\) to which \(M_N\) is linked by consistency, enforce additional constraints on \(M_N\). It is precisely these constraints that limit the behavior of map \(M_N\) so as to make the results of this paper valid. But now we see clearly that, given \(M_N\), to apply the theory it is enough that there exist “virtual” maps \(\tilde{M}_0, \tilde{M}_1, \ldots , \tilde{M}_{N-1}, \tilde{M}_{N+1}, \ldots \) that, augmented with \(M_N\), form a list \(\tilde{M}_0, \tilde{M}_1, \ldots , \tilde{M}_{N-1}, M_N, \tilde{M}_{N+1}, \ldots \) that satisfy the consistency property. This is, e.g., well true in our CVaR context because any given N has associated a value of q and this value of q can be kept constant when defining \(\tilde{M}^{\textrm{CVaR},q}_m\) for \(m \ne N\).
5 Proofs
5.1 Proof of Theorem 3
A comparison with [39]. Before delving into the proof, following a suggestion of a referee, we highlight its main differences with the proof of Theorem 3 in [39]. Similarly to Theorem 3 in [39], the initial step involves reformulating the probability \(\mathbb {P}^N \{ V(z^*_N) > \epsilon (s^*_N) \}\) in integral form, utilizing appropriate generalized distribution functions that are shown to satisfy certain conditions. The crucial difference rests in the fact that allowing for degeneracy introduces in the conditions more freedom to transfer probabilistic masses from one of these generalized distribution functions to another when increasing by 1 the number of data points. In technical terms this is captured by equation (21), which asserts that the difference distribution function that appears in the equation that follows (21) belongs to the negative cone. In contrast, under non-degeneracy as in [39], this difference distribution function is null, implying that one can work with generalized distribution functions that are singled-indexed by k. By this initial change the rest of the proof takes a major departure from that of Theorem 3 in [39] and in the present proof one needs to work with a Lagrangian that incorporates specific functionals tailored to the problem at hand.
In the derivations, it is convenient to associate to any list \(\delta _1,\ldots ,\delta _m\) a minimal support list which is defined by a unique choice of indexes \(i_1,i_2,\ldots ,i_k\). Such an association may become impossible if two or more \(\delta _i\)’s have the same value, which happens with non zero probability whenever \(\mathbb {P}\) has concentrated mass. This difficulty, however, can be easily circumvented by augmenting the original \(\delta \) with a real number \(\eta \) drawn independently of \(\delta \) and according to the uniform distribution \(\mathbb {U}\) over [0, 1]. Precisely, define \(\tilde{\Delta }= \Delta \times [0,1]\), \(\tilde{\mathcal {D}}= \mathcal {D}\otimes \mathcal {B}_{[0,1]}\) (\(\mathcal {B}_{[0,1]}\) is the \(\sigma \)-algebra of Borel sets in [0, 1]), \(\tilde{\mathbb {P}}= \mathbb {P}\times \mathbb {U}\), and let \(\tilde{\delta }= (\delta ,\eta )\) be an outcome from the probability space \((\tilde{\Delta },\tilde{\mathcal {D}},\tilde{\mathbb {P}})\). For any m, let \(\tilde{\delta }_i = (\delta _i,\eta _i)\), \(i=1,\ldots ,m\), be i.i.d. draws from \((\tilde{\Delta },\tilde{\mathcal {D}},\tilde{\mathbb {P}})\). Note that, owing to the \(\eta _i\)’s, the \(\tilde{\delta }_i\)’s are all distinct with probability 1, so that any rule that selects a minimal support list satisfies the requirement that this support list is defined by a unique choice of the indexes with probability 1. In the following, we consider the map \(\textsf{S}_m: \tilde{\Delta }^m \rightarrow \bigcup _{k=0}^m \tilde{\Delta }^k\) that selects from \(\tilde{\delta }_1,\ldots ,\tilde{\delta }_m\) the sub-list \(\tilde{\delta }_{i_1},\ldots ,\tilde{\delta }_{i_k}\), with \(i_1< \cdots < i_k\), by the following rule: the first components \(\delta _{i_1},\ldots ,\delta _{i_k}\) form a support list for \(\delta _1,\ldots ,\delta _m\) of minimal cardinality and, among the sub-lists that have this property, the rule favors the sub-list whose second components \(\eta _{i_1},\ldots ,\eta _{i_k}\) minimize \(\sum _{\ell =1}^k \eta _{i_\ell }\). Since the choice with minimal sum \(\sum _{\ell =1}^k \eta _{i_\ell }\) is unique with probability 1, \(\textsf{S}_m(\tilde{\delta }_1,\ldots ,\tilde{\delta }_m)\) is univocally defined except for a zero-probability set. This zero-probability set plays no role in the following derivations and, hence, \(\textsf{S}_m(\tilde{\delta }_1,\ldots ,\tilde{\delta }_m)\) can be arbitrarily specified over it.
With \(\textsf{S}_m\) in our hands, we shall be able to prove the assertion of the theorem with \(\tilde{\mathbb {P}}\) in place of \(\mathbb {P}\), viz. \(\tilde{\mathbb {P}}^N \{ V(z^*_N) > \epsilon (s^*_N) \} \le \gamma ^*\). On the other hand,
because the event in curly brackets does not depend on the second components of the \(\tilde{\delta }_i\)’s, and therefore the theorem will remain proven.
Start by noting that
where the last equality is true because \(\eta _1 \ne \eta _2 \ne \cdots \ne \eta _N\) holds with probability 1, which implies that sub-lists \(\tilde{\delta }_{i_1},\ldots ,\tilde{\delta }_{i_k}\) are all different from each other with probability 1 and, therefore, \(\textsf{S}_N(\tilde{\delta }_1,\ldots ,\tilde{\delta }_N) = \tilde{\delta }_{i_1},\ldots ,\tilde{\delta }_{i_k}\) holds for one and only one choice of the indexes with probability 1.
Now, for any fixed k, all the probabilities in the inner summation of (18) are equal. To see this, consider two choices of indexes \(i_1',i_2',\ldots ,i_k'\) and \(i_1'',i_2'',\ldots ,i_k''\) and let
and
We show that \(E''\) is obtained from \(E'\) by the permutation of \(\tilde{\delta }_1,\ldots ,\tilde{\delta }_N\) defined as follows: \(i_1' \rightarrow i_1''\), \(i_2' \rightarrow i_2''\), ..., \(i_k' \rightarrow i_k''\), and the other elements fill the holes while keeping the same order. Indeed, after permutation, \(z^*_N\) does not change because \(M_N\) is permutation invariant so that condition \(V(z^*_N) > \epsilon (k)\) for a point in \(E'\) implies \(V(z^*_N) > \epsilon (k)\) for the permuted point; moreover, \(\textsf{S}_N\) selects a sub-list depending on the values of the \(\tilde{\delta }_i\)’s and not on their positions so that, when \(\textsf{S}_N(\tilde{\delta }_1,\ldots ,\tilde{\delta }_N) = \tilde{\delta }_{i_1'},\ldots ,\tilde{\delta }_{i_k'}\), after permutation \(\textsf{S}_N\) returns \(\tilde{\delta }_{i_1''},\ldots ,\tilde{\delta }_{i_k''}\). Hence, a point of \(E'\) gives, after permutation, a point of \(E''\) and, since the opposite holds with the inverse permutation, it turns out that \(E''\) is a permutation of \(E'\). The fact that \(\tilde{\mathbb {P}}^N(E') = \tilde{\mathbb {P}}^N(E'')\) now follows because the \(\tilde{\delta }_i\)’s are i.i.d. draws.
Since all terms in the inner summation of (18) are equal, we can write
where \(F_{k,N}\) is a generalized distribution functionFootnote 37 defined as follows (for future use we introduce a definition that holds for a generic m, and not just for \(m=N\)): for all \(m = 0,1,\ldots \) and \(k=0,\ldots ,m\), let
Note that \(F_{k,m}(v) = 0\) for \(v < 0\) and \(F_{k,m}(v)\) is constant for \(v \ge 1\).
Next we show that Property 1 implies that the \(F_{k,m}\)’s satisfy conditions (a) and (b) below. Later, these conditions will be enforced when maximizing the right-hand side of (19) with the goal of finding an upper bound to \(\tilde{\mathbb {P}}^N \{ V(z^*_N) > \epsilon (s^*_N) \}\).
-
(a)
For \(m=0,1,\ldots \), it holds that
$$\begin{aligned} \sum _{k=0}^m {m \atopwithdelims ()k} \int _{[0,1]} \textrm{d}F_{k,m} = 1; \end{aligned}$$(20) -
(b)
For \(m=0,1,\ldots \) and \(k=0,\ldots ,m\), it holds that
$$\begin{aligned} \int _B \textrm{d}F_{k,m+1} - \int _B (1-v) \; \textrm{d}F_{k,m} \le 0, \end{aligned}$$(21)for any Borel set \(B \subseteq [0,1]\).
For any given B, the left-hand side of (21) returns a numerical value and, when B ranges over the Borel sets in [0, 1], the left-hand side of (21) defines a signed measure. Condition (21) means that this measure is in fact negative. Letting \(F^{(1-v)}_{k,m}(v):= \int _{(-\infty ,v]} (1-w) \; \textrm{d}F_{k,m}(w)\), condition (b) can also be rewritten as
where \(\mathcal {C}^-\) is the cone of negative generalized distribution functions (i.e., functions that are non-increasing and right continuous) with value zero for \(v<0\) and constant value for \(v \ge 1\).
-
Proof of (a): Along the same lines as in (18) and (19), we obtain
$$\begin{aligned} 1= & {} \sum _{k=0}^m \tilde{\mathbb {P}}^m \Big \{ \vert \textsf{S}_m(\tilde{\delta }_1,\ldots ,\tilde{\delta }_m)\vert = k \Big \} \nonumber \\= & {} \sum _{k=0}^m \tilde{\mathbb {P}}^m \left( \bigcup _{ \begin{array}{c} i_1< i_2< \cdots< i_k: \\ \{ i_1,\ldots ,i_k \} \subseteq \{1,\ldots ,m\} \end{array} } \Big \{ \textsf{S}_m(\tilde{\delta }_1,\ldots ,\tilde{\delta }_m) = \tilde{\delta }_{i_1},\ldots ,\tilde{\delta }_{i_k} \Big \} \right) \nonumber \\= & {} \sum _{k=0}^m \sum _{ \begin{array}{c} i_1< i_2< \cdots < i_k: \\ \{ i_1,\ldots ,i_k \} \subseteq \{1,\ldots ,m\} \end{array} } \tilde{\mathbb {P}}^m \Big \{ \textsf{S}_m(\tilde{\delta }_1,\ldots ,\tilde{\delta }_m) = \tilde{\delta }_{i_1},\ldots ,\tilde{\delta }_{i_k} \Big \} \nonumber \\= & {} \sum _{k=0}^m {m \atopwithdelims ()k} \tilde{\mathbb {P}}^m \Big \{ \textsf{S}_m(\tilde{\delta }_1,\ldots ,\tilde{\delta }_m) = \tilde{\delta }_1,\ldots ,\tilde{\delta }_k \Big \} \nonumber \\= & {} \sum _{k=0}^m {m \atopwithdelims ()k} \int _{[0,1]} \textrm{d}F_{k,m}. \end{aligned}$$\(\square \)
-
Proof of (b): for any given Borel set B in [0, 1], we have that
$$\begin{aligned} \int _B \textrm{d}F_{k,m+1} = \tilde{\mathbb {P}}^{m+1} \Big \{ \textsf{S}_{m+1}(\tilde{\delta }_1,\ldots ,\tilde{\delta }_{m+1}) = \tilde{\delta }_1,\ldots ,\tilde{\delta }_k \text { and } V(z^*_k) \in B \Big \}.\nonumber \\ \end{aligned}$$(22)Over the set where \(\textsf{S}_{m+1}(\tilde{\delta }_1,\ldots ,\tilde{\delta }_{m+1}) = \tilde{\delta }_1,\ldots ,\tilde{\delta }_k\) (which is part of the condition defining the set on the right-hand side of (22)), it must hold that \(z^*_k \in \mathcal {Z}_{\delta _{m+1}}\). As a matter of fact, if \(z^*_k \notin \mathcal {Z}_{\delta _{m+1}}\), then, by (iii) in Property 1, we would have \(z^*_k:= M_k(\delta _1,\ldots ,\delta _k) \ne M_{m+1}(\delta _1,\ldots ,\delta _k,\delta _{k+1},\ldots ,\delta _{m+1}) =: z^*_{m+1}\). This implies that \(\delta _1,\dots ,\delta _k\) is not a support list for \(\delta _1,\dots ,\delta _{m+1}\) and, therefore, that \(\textsf{S}_{m+1}(\tilde{\delta }_1,\ldots ,\tilde{\delta }_{m+1}) \ne \tilde{\delta }_1,\ldots ,\tilde{\delta }_k\), which is a contradiction.Footnote 38 Over the set where \(\textsf{S}_{m+1}(\tilde{\delta }_1,\ldots ,\tilde{\delta }_{m+1}) = \tilde{\delta }_1,\ldots ,\tilde{\delta }_k\) it must also hold that \(\textsf{S}_m(\tilde{\delta }_1,\ldots ,\tilde{\delta }_m) = \tilde{\delta }_1,\ldots ,\tilde{\delta }_k\). To show this, note first that it is not possible that \(z^*_m \ne z^*_k\). Indeed, by (ii) in Property 1, \(M_m(\delta _1,\ldots ,\delta _k,\delta _{k+1},\ldots ,\delta _m) =: z^*_m \ne z^*_k:= M_k(\delta _1,\ldots ,\delta _k)\) implies that \(z^*_k \notin \mathcal {Z}_{\delta _j}\) for some \(j \in \{k+1,\ldots ,m\}\) and, by (iii) in Property 1, this gives \(z^*_{m+1}:= M_{m+1}(\delta _1,\ldots ,\delta _k,\delta _{k+1},\ldots ,\delta _m,\delta _{m+1}) \ne M_k(\delta _1,\ldots ,\delta _k) =: z^*_k\), which is not possible given that \(\textsf{S}_{m+1}(\tilde{\delta }_1,\ldots ,\tilde{\delta }_{m+1}) = \tilde{\delta }_1,\ldots ,\tilde{\delta }_k\). Hence, it must be that \(z^*_m = z^*_k\) and this implies that \(\delta _1,\ldots ,\delta _k\) is a support list for \(\delta _1,\ldots ,\delta _m\) (note that the irreducibility of \(\delta _1,\ldots ,\delta _k\) – which is in the definition of support list – follows from the fact that \(\delta _1,\ldots ,\delta _k\) is a support list for \(\delta _1,\ldots ,\delta _{m+1}\)). To close the proof that \(\textsf{S}_m(\tilde{\delta }_1,\ldots ,\tilde{\delta }_m) = \tilde{\delta }_1,\ldots ,\tilde{\delta }_k\), suppose for the sake of contradiction that \(\textsf{S}_m(\tilde{\delta }_1,\ldots ,\tilde{\delta }_m) = \tilde{\delta }_{i_1},\ldots ,\tilde{\delta }_{i_h} \ne \tilde{\delta }_1,\ldots ,\tilde{\delta }_k\). This means that \(\delta _{i_1},\ldots ,\delta _{i_h}\) is another support list for \(\delta _1,\ldots ,\delta _m\) and that \(\tilde{\delta }_{i_1},\ldots ,\tilde{\delta }_{i_h}\) is preferred by \(\textsf{S}_m\) either because \(\tilde{\delta }_{i_1},\ldots ,\tilde{\delta }_{i_h}\) has smaller cardinality than \(\tilde{\delta }_1,\ldots ,\tilde{\delta }_k\) or because \(\tilde{\delta }_{i_1},\ldots ,\tilde{\delta }_{i_h}\) ranks better according to the \(\eta _i\)’s. If so, however, we would have \(M_h(\delta _{i_1},\ldots ,\delta _{i_h}) = z^*_m = z^*_k = z^*_{m+1}\), which means that \(\delta _{i_1},\ldots ,\delta _{i_h}\) would be a support list for \(\delta _1,\ldots ,\delta _{m+1}\) too. This gives a contradiction because \(\tilde{\delta }_{i_1},\ldots ,\tilde{\delta }_{i_h}\) would be preferred to \(\tilde{\delta }_1,\ldots ,\tilde{\delta }_k\) while, instead, \(\textsf{S}_{m+1}(\tilde{\delta }_1,\ldots ,\tilde{\delta }_{m+1}) = \tilde{\delta }_1,\ldots ,\tilde{\delta }_k\).Footnote 39 Summarizing, we have proven that \(\textsf{S}_{m+1}(\tilde{\delta }_1,\ldots ,\tilde{\delta }_{m+1}) = \tilde{\delta }_1,\ldots ,\tilde{\delta }_k\) implies that \(z^*_k \in \mathcal {Z}_{\delta _{m+1}}\) and that \(\textsf{S}_m(\tilde{\delta }_1,\ldots ,\tilde{\delta }_m) = \tilde{\delta }_1,\ldots ,\tilde{\delta }_k\), which yields
$$\begin{aligned}{} & {} { \tilde{\mathbb {P}}^{m+1} \Big \{ \textsf{S}_{m+1}(\tilde{\delta }_1,\ldots ,\tilde{\delta }_{m+1}) = \tilde{\delta }_1,\ldots ,\tilde{\delta }_k \text { and } V(z^*_k) \in B \Big \} } \nonumber \\{} & {} \quad \le \tilde{\mathbb {P}}^{m+1} \Big \{ z^*_k \in \mathcal {Z}_{\delta _{m+1}} \text { and } \textsf{S}_m(\tilde{\delta }_1,\ldots ,\tilde{\delta }_m) = \tilde{\delta }_1,\ldots ,\tilde{\delta }_k \text { and } V(z^*_k) \in B \Big \}, \nonumber \\ \end{aligned}$$(23)because the set on the left-hand side is included in the set on the right-hand side. Using (23) in (22) now gives (\( \textbf{1}_{A} \) is the indicator function of set A)
$$\begin{aligned}{} & {} {\int _B \textrm{d}F_{k,m+1}} \nonumber \\{} & {} \quad \le \tilde{\mathbb {P}}^{m+1} \Big \{ z^*_k \in \mathcal {Z}_{\delta _{m+1}} \text { and } \textsf{S}_m(\tilde{\delta }_1,\ldots ,\tilde{\delta }_m) = \tilde{\delta }_1,\ldots ,\tilde{\delta }_k \text { and } V(z^*_k) \in B \Big \} \nonumber \\{} & {} \quad = \int _{\tilde{\Delta }^{m+1}} \textbf{1}_{z^*_k \in \mathcal {Z}_{\delta _{m+1}}} \nonumber \\{} & {} \quad \quad {\cdot \textbf{1}_{\textsf{S}_m(\tilde{\delta }_1,\ldots ,\tilde{\delta }_m) = \tilde{\delta }_1,\ldots ,\tilde{\delta }_k} \cdot \textbf{1}_{V(z^*_k) \in B} } \; \textrm{d}\tilde{\mathbb {P}}^{m+1}(\tilde{\delta }_1,\ldots ,\tilde{\delta }_m,\tilde{\delta }_{m+1}) \nonumber \\{} & {} \quad = \int _{\tilde{\Delta }^m} \left( \int _{\tilde{\Delta }} \textbf{1}_{z^*_k \in \mathcal {Z}_{\delta _{m+1}}} \ \textrm{d}\tilde{\mathbb {P}}(\tilde{\delta }_{m+1}) \right) \nonumber \\{} & {} \quad \quad {\cdot \textbf{1}_{\textsf{S}_m(\tilde{\delta }_1,\ldots ,\tilde{\delta }_m) = \tilde{\delta }_1,\ldots ,\tilde{\delta }_k} \cdot \textbf{1}_{V(z^*_k) \in B} } \; \textrm{d}\tilde{\mathbb {P}}^m(\tilde{\delta }_1,\ldots ,\tilde{\delta }_m) \nonumber \\{} & {} \quad = {\int _{\tilde{\Delta }^m} \big ( 1-V(z^*_k) \big ) \cdot \textbf{1}_{V(z^*_k) \in B} \cdot \textbf{1}_{\textsf{S}_m(\tilde{\delta }_1,\ldots ,\tilde{\delta }_m) = \tilde{\delta }_1,\ldots ,\tilde{\delta }_k} \; \textrm{d}\tilde{\mathbb {P}}^m(\tilde{\delta }_1,\ldots ,\tilde{\delta }_m)} \nonumber \\{} & {} \quad = {\int _{\tilde{\Delta }^m} \big ( 1-V(z^*_k) \big ) \cdot \textbf{1}_{V(z^*_k) \in B} \; \textrm{d}{\tilde{\mathbb {Q}}}^m(\tilde{\delta }_1,\ldots ,\tilde{\delta }_m),} \end{aligned}$$(24)where measure \({\tilde{\mathbb {Q}}}^m\) is defined through relation
$$\begin{aligned} {{\tilde{\mathbb {Q}}}^m(A) = \int _A \textbf{1}_{\textsf{S}_m(\tilde{\delta }_1,\ldots ,\tilde{\delta }_m) = \tilde{\delta }_1,\ldots ,\tilde{\delta }_k} \; \textrm{d}\tilde{\mathbb {P}}^m(\tilde{\delta }_1,\ldots ,\tilde{\delta }_m), \quad \quad A \in \tilde{\mathcal {D}}^m,} \end{aligned}$$and the last equality in (24) is justified in view of [51, Theorem 1.29]. By a change of variables, the right-hand side of (24) can finally be rewritten as
$$\begin{aligned} {\int _{\mathbb {R}} (1-v) \cdot \textbf{1}_{v \in B} \; \textrm{d}F_{k,m} = \int _B (1-v) \; \textrm{d}F_{k,m}.} \end{aligned}$$This concludes the proof of (b).\(\square \)
We are now ready to upper-bound \(\tilde{\mathbb {P}}^N \left\{ V(z^*_N) > \epsilon (s^*_N) \right\} \) by taking the \(\sup \) of the right-hand side of (19) under conditions (a) and (b) (in addition to the fact that the \(F_{k,m}\)’s belong to the cone \(\mathcal {C}^+\) of generalized distribution functions with value zero for \(v<0\) and constant value for \(v \ge 1\)). This gives
where \(\gamma \) is defined as the value of the optimization problem
Problem () involves infinitely many constraints. On the other hand, as explained below, it is a fact that all constraints (26b) with \(m > N\) and all constraints (26c) with \(m > N-1\) are superfluous and can be removed without changing the optimal value of the problem. In formulas, this gives
To see this, first notice that the optimal value of () cannot be bigger than the optimal value of () because () has more constraints than (). On the other hand, for any feasible point of (), say \(\bar{F}_{k,m}\) for \(m=0,\ldots ,N\) and \(k=0,\ldots ,m\), we obtain a feasible point of () by letting: \(F_{k,m} = \bar{F}_{k,m}\) for \(m=0,\ldots ,N\) and \(k=0,\ldots ,m\); \(F_{k,m} = 0\) for \(m=N+1,N+2,\ldots \) and \(k=0,\ldots ,m-1\); and \(F_{m,m}\) be any generalized distribution function with unitary mass (e.g., a unitary concentrated mass in \(v=1\)) for \(m=N+1,N+2,\ldots \). This feasible point of () achieves the same cost value as \(\bar{F}_{k,m}\) in (). Hence, it is also true that the optimal value of () cannot be smaller than that of (), and therefore the two optimal values must coincide.
To evaluate \(\gamma \), we proceed by dualizing (). To this purpose, consider the Lagrangian:
which is a function of
-
\(F_{k,m} \in \mathcal {C}^+, \; \; m=0,\ldots ,N, \; \; k=0,\ldots ,m,\)
and the Lagrange multipliers
-
\(\lambda _m \in \mathbb {R}, \; \; m=0, \ldots , N\),
-
\(\mu ^+_{k,m} \in \textsf {C}^0_+[0,1], \; \; m=0,\ldots ,N-1, \; \; k=0,\ldots ,m\),
where \(\textsf {C}^0_+[0,1]\) is the set of positive and continuous functions over [0, 1].
We show below thatFootnote 40
where \(\gamma ^*\) is the value of the dual of problem ():
(note that, to keep the notation compact, in (30b) there appear various functions, for instance \(\mu ^+_{0,-1}\), that are not listed as optimization variables; however, these functions are all multiplied by an indicator function that is zero and they are therefore “phantoms” that play no role).
-
Proof of (A) in (29): The goal is to show that the class of linear functionals introduced in the Lagrangian is rich enough to enforce the constraints in problem () and, from this, that the conclusion follows. If the generalized distribution functions \({F_{k,m}}\) do not satisfy the constraints in (27b) and (27c), then \(\inf _{\{\lambda _m\}, \{\mu ^+_{k,m}\}} \mathfrak {L}\) is equal to \(-\infty \). This is plainly true for (27b) because, if for some m the term
$$\begin{aligned} \left( \sum _{k=0}^m {m \atopwithdelims ()k} \int _{[0,1]} \textrm{d}F_{k,m} - 1 \right) \end{aligned}$$in the right-hand side of (28) is not null, then \(\lambda _m\) can be taken any large with sign equal to that of that term, bringing \(\mathfrak {L}\) down to arbitrary large negative values. Likewise, if (27c) is not satisfied for a given pair (k, m), then the last term in the right-hand side of (28) can be made any large negative by selecting a suitable positive large continuous function \(\mu ^+_{k,m}\).Footnote 41 Hence, the search for \(\sup _{\{F_{k,m}\}}\) of \(\inf _{\{\lambda _m\}, \{\mu ^+_{k,m}\}} \mathfrak {L}\) can be restricted to the \(F_{k,m}\)’s in \(\mathcal {C}^+\) that satisfy (27b) and (27c) and, once (27b) and (27c) hold, \(\inf _{\{\lambda _m\}, \{\mu ^+_{k,m}\}} \mathfrak {L}\) is achieved by setting the second and third terms in the right-hand side of (28) to zero (e.g. by choosing \(\lambda _m = 0\) and \(\mu ^+_{k,m} = 0\) for all m and k). This leads to the conclusion that \(\sup _{\{F_{k,m}\}} \inf _{\{\lambda _m\}, \{\mu ^+_{k,m}\}} \mathfrak {L}\) equals \(\gamma \) of problem (). \(\square \)
-
Proof of (B) in (29): Let \(\tau > 0\) be a number smaller than \(1-\epsilon (k)\) for all k’s for which \(\epsilon (k) \ne 1\) ad smaller than \(\epsilon (k)\) for all k’s for which \(\epsilon (k) \ne 0\). Matters of convenience (as shown later) suggest to introduce a modified Lagrangian
$$\begin{aligned} \mathfrak {L}_\tau= & {} \sum _{k=0}^N {N \atopwithdelims ()k} \int _{[0,1]} \varphi _{k,\tau }(v) \; \textrm{d}F_{k,N} - \sum _{m=0}^N \lambda _m \left( \sum _{k=0}^m {m \atopwithdelims ()k} \int _{[0,1]} \textrm{d}F_{k,m} - 1 \right) \nonumber \\{} & {} - \sum _{m=0}^{N-1} \sum _{k=0}^m \int _{[0,1]} \mu ^+_{k,m}(v) \; \textrm{d}[ F_{k,m+1} - F^{(1-v)}_{k,m} ], \end{aligned}$$where \(\varphi _{k,\tau }\) is a continuous function over [0, 1] defined as follows: for all k for which \(\epsilon (k) \ne 1\) and \(\epsilon (k) \ne 0\), \(\varphi _{k,\tau }(v)\) is equal to 0 for \(v \in [0,\epsilon (k) - \tau ]\),Footnote 42 equal to 1 for \(v \in [\epsilon (k), 1]\), and with a linear slope connecting 0 to 1 in between; while \(\varphi _{k,\tau }(v)\) is identically zero when \(\epsilon (k) = 1\) and identically equal to 1 when \(\epsilon (k) = 0\). We show below the validity of the following relations:
 (31)
(31)Notice that the above relations imply the sought result that
$$\begin{aligned} \sup _{\{F_{k,m}\}} \inf _{\begin{array}{c} \{\lambda _m\} \\ \{\mu ^+_{k,m}\} \end{array}} \mathfrak {L} = \inf _{\begin{array}{c} \{\lambda _m\} \\ \{\mu ^+_{k,m}\} \end{array}} \sup _{\{F_{k,m}\}} \mathfrak {L} \end{aligned}$$because \(\inf _{\begin{array}{c} \{\lambda _m\} \\ \{\mu ^+_{k,m}\} \end{array}} \sup _{\{F_{k,m}\}} \mathfrak {L}\) is in sandwich between \(\sup _{\{F_{k,m}\}} \inf _{\begin{array}{c} \{\lambda _m\} \\ \{\mu ^+_{k,m}\} \end{array}} \mathfrak {L}\) and \(\inf _{\begin{array}{c} \{\lambda _m\} \\ \{\mu ^+_{k,m}\} \end{array}} \sup _{\{F_{k,m}\}} \mathfrak {L}_\tau \), two quantities that converge one onto the other as \(\tau \downarrow 0\). The two inequalities in (31) are justified as follows: the “\(\le \)” at the bottom of (31) is valid because relation “\(\sup \inf \le \inf \sup \)” is always true, while the “
 ” on the right follows from the fact that \(\varphi _{k,\tau }(v)\) in \(\mathfrak {L}_\tau \) is greater than or equal to \( \textbf{1}_{v \in (\epsilon (k),1]} \) in \(\mathfrak {L}\). What remains to show is thus the “\(=\)” at the top of (31) and the convergence “\(\downarrow _{\tau \downarrow 0}\)” on the left. We first show that $$\begin{aligned} \sup _{\{F_{k,m}\}} \inf _{\begin{array}{c} \{\lambda _m\} \\ \{\mu ^+_{k,m}\} \end{array}} \mathfrak {L}_\tau = \inf _{\begin{array}{c} \{\lambda _m\} \\ \{\mu ^+_{k,m}\} \end{array}} \sup _{\{F_{k,m}\}} \mathfrak {L}_\tau , \end{aligned}$$(32)
” on the right follows from the fact that \(\varphi _{k,\tau }(v)\) in \(\mathfrak {L}_\tau \) is greater than or equal to \( \textbf{1}_{v \in (\epsilon (k),1]} \) in \(\mathfrak {L}\). What remains to show is thus the “\(=\)” at the top of (31) and the convergence “\(\downarrow _{\tau \downarrow 0}\)” on the left. We first show that $$\begin{aligned} \sup _{\{F_{k,m}\}} \inf _{\begin{array}{c} \{\lambda _m\} \\ \{\mu ^+_{k,m}\} \end{array}} \mathfrak {L}_\tau = \inf _{\begin{array}{c} \{\lambda _m\} \\ \{\mu ^+_{k,m}\} \end{array}} \sup _{\{F_{k,m}\}} \mathfrak {L}_\tau , \end{aligned}$$(32)for which purpose we need to introduce a proper topological vector space, [52], as specified in the following.
-
Consider the vector space \(\mathcal{B}\mathcal{V}\) of functions \(F^{\mathcal{B}\mathcal{V}}\) of bounded variation, [51], that are right continuous with value zero for \(v < 0\) and constant value for \(v \ge 1\). Moreover, let \(\mathcal{L}\mathcal{F}\) be the vector space of linear functionals on \(\mathcal{B}\mathcal{V}\) of the form \(\int _{[0,1]} \mu (v) \; \textrm{d}F^{\mathcal{B}\mathcal{V}}\), where \(\mu \) is a continuous function (\(\mu \in \textsf {C}^0[0,1]\)). In \(\mathcal{B}\mathcal{V}\), introduce the weak topology induced by \(\mathcal{L}\mathcal{F}\), see [52, Section 3.8]. This weak topology makes \(\mathcal{B}\mathcal{V}\) into a locally convex topological vector space whose dual space coincides with \(\mathcal{L}\mathcal{F}\), see [52, Theorem 3.10].Footnote 43 By also considering the standard topology of \(\mathbb {R}\) generated by open intervals, the ambient space in which we are going to work is the topological vector space given by \(\mathbb {R}\times \mathbb {R}^{N+1} \times \mathcal{B}\mathcal{V}^{\frac{(N+1)N}{2}} =: \mathcal {S}\) equipped with the product topology. The interpretation of \(\mathcal {S}\) is that it is the codomain of an operator that maps \(F_{k,m}\), \(m=0,1,\ldots ,N\), \(k=,0,\ldots ,m\) into an element of \(\mathcal {S}\) according to the rule:
$$\begin{aligned}{} & {} { \big \{ F_{k,m} \big \}_{{\begin{array}{l}m=0,1,\ldots ,N \\ k=0,\ldots ,m \end{array}}} } \\\longrightarrow & {} \left\{ \begin{array}{ll} \sum _{k=0}^N {N \atopwithdelims ()k} \int _{[0,1]} \varphi _{k,\tau }(v) \ \textrm{d}F_{k,N} &{} \quad (\in \mathbb {R}) \\ \left\{ \sum _{k=0}^m {m \atopwithdelims ()k} \int _{[0,1]} \textrm{d}F_{k,m} - 1 \right\} _{m=0,1,\ldots ,N} &{} \quad (\in \mathbb {R}^{N+1}) \\ \big \{ F_{k,m+1} - F^{(1-v)}_{k,m} \big \}_{{\begin{array}{l}m=0,1,\ldots ,N-1 \\ k=0,\ldots ,m \end{array}}}&\quad (\in \mathcal{B}\mathcal{V}^{\frac{(N+1)N}{2}}) \end{array} \right. \end{aligned}$$(note that this operator returns various terms that are found in \(\mathfrak {L}_\tau \)). We next consider the image of this operator, that is, the range of points in \(\mathcal {S}\) that are reached as \(\{F_{k,m}\}\) varies in its domain \(\left( \mathcal {C}^+\right) ^{\frac{(N+2)(N+1)}{2}}\). This image is further enlarged by adding to each term \(F_{k,m+1} - F^{(1-v)}_{k,m}\) an arbitrary \(P_{k,m} \in \mathcal {C}^+\) (the reason for this will become clear shortly). The final set that is obtained as \(\{F_{k,m}\}\) and \(\{P_{k,m}\}\) vary over their domains is denoted by H:
$$\begin{aligned} H:= & {} \Big \{(w,\{r_m\},\big \{ Q^{\mathcal{B}\mathcal{V}}_{k,m} \big \}) \in \mathbb {R}\times \mathbb {R}^{N+1} \times \mathcal{B}\mathcal{V}^{\frac{(N+1)N}{2}}: \nonumber \\{} & {} \quad \quad \quad w = \sum _{k=0}^N {N \atopwithdelims ()k} \int _{[0,1]} \varphi _{k,\tau }(v) \ \textrm{d}F_{k,N}, \nonumber \\{} & {} \quad \quad \quad \{r_m\} = \left\{ \sum _{k=0}^m {m \atopwithdelims ()k} \int _{[0,1]} \textrm{d}F_{k,m} - 1 \right\} , \nonumber \\{} & {} \quad \quad \quad \big \{ Q^{\mathcal{B}\mathcal{V}}_{k,m} \big \} = \big \{F_{k,m+1} - F^{(1-v)}_{k,m} + P_{k,m} \big \}, \nonumber \\{} & {} \quad \text{ where, } \text{ for } \text{ all } m \text{ and } k, \ \ F_{k,m} \in \mathcal {C}^+, P_{k,m} \in \mathcal {C}^+ \Big \}. \end{aligned}$$(33)The closure of H in the topology of \(\mathcal {S}\) is denoted by \(\bar{H}\).Footnote 44 The following definitions refer to the restrictions of H and \(\bar{H}\) to the line where all \(r_m\), \(m=0,1,\ldots ,N\), and \(Q^{\mathcal{B}\mathcal{V}}_{k,m}\), \(m=0,1,\ldots ,N-1\), \(k=0,\ldots ,m\), are set to 0 (i.e., the zero element in \(\mathbb {R}\) and \(\mathcal{B}\mathcal{V}\), respectively): quantities
$$\begin{aligned} W:= & {} \sup \Big \{ v: \; (v,\{r_m = 0 \},\big \{ Q^{\mathcal{B}\mathcal{V}}_{k,m} = 0 \big \}) \in H \Big \} \\ \bar{W}:= & {} \sup \Big \{ v: \; (v,\{ r_m = 0 \}, \big \{ Q^{\mathcal{B}\mathcal{V}}_{k,m} = 0 \big \}) \in \bar{H} \Big \} \end{aligned}$$are called value and supervalue, respectively.Footnote 45 With this notation, we have
$$\begin{aligned} \sup _{\{F_{k,m}\}} \inf _{\begin{array}{c} \{\lambda _m\} \\ \{\mu ^+_{k,m}\} \end{array}} \mathfrak {L}_\tau = W \end{aligned}$$(this fact easily follows from an argument similar to the proof of equality (A) in (29) after noting that W in the present context plays the same role as \(\gamma \) in left-hand side of (29)). On the other hand, we also have
$$\begin{aligned} \inf _{\begin{array}{c} \{\lambda _m\} \\ \{\mu ^+_{k,m}\} \end{array}} \sup _{\{F_{k,m}\}} \mathfrak {L}_\tau = \bar{W}, \end{aligned}$$(34)a fact that can be proven by the Hahn-Banach theorem as shown below. After this, the proof of (32) will be closed by proving that \(W = \bar{W}\).
-
The argument to prove (34) is inspired by [53]. Note that \(\bar{H}\) is convex and closed and, for any \(\varepsilon > 0\), point \(s^\varepsilon := (\bar{W} + \varepsilon , \{ r_m = 0 \}, \{ Q^{\mathcal{B}\mathcal{V}}_{k,m} = 0 \}) \notin \bar{H}\). By an application of Hahn-Banach theorem (see [52, Theorem 3.4]), one can therefore find a linear continuous functional defined over \(\mathcal {S}\) that “separates” \(\bar{H}\) from \(s^\varepsilon \) in such a way that the functional computed at any point of \(\bar{H}\) is strictly smaller than the functional computed at \(s^\varepsilon \). A generic linear continuous functional defined over \(\mathcal {S}\) is written as
$$\begin{aligned} a \cdot w - \sum _{m=0}^N \lambda _m r_m - \sum _{m=0}^{N-1} \sum _{k=0}^m \int _{[0,1]} \mu _{k,m}(v) \; \textrm{d}Q^{\mathcal{B}\mathcal{V}}_{k,m}, \end{aligned}$$(35)where \(a,\lambda _m \in \mathbb {R}^{}\) and \(\mu _{k,m} \in \textsf {C}^0[0,1]\), and hence the separation condition yields
$$\begin{aligned}&a^\varepsilon \cdot w - \sum _{m=0}^N \lambda _m^\varepsilon r_m - \sum _{m=0}^{N-1} \sum _{k=0}^m \int _{[0,1]} \mu _{k,m}^\varepsilon (v) \; \textrm{d}Q^{\mathcal{B}\mathcal{V}}_{k,m} \nonumber \\&\quad < a^\varepsilon \cdot (\bar{W} + \varepsilon ), \quad \forall (w, \{ r_m\}, \{ Q^{\mathcal{B}\mathcal{V}}_{k,m} \}) \in \bar{H}, \end{aligned}$$(36)where \(a^\varepsilon , \lambda _m^\varepsilon , \mu _{k,m}^\varepsilon \) are specific choices of \(a, \lambda _m, \mu _{k,m}\) in (35). Specializing (36) to a point \((w,\{r_m = 0\},\{ Q^{\mathcal{B}\mathcal{V}}_{k,m} = 0 \})\) in \(\bar{H}\) yields \(a^\varepsilon \cdot w < a^\varepsilon \cdot (\bar{W} + \varepsilon )\), which implies \(a^\varepsilon > 0\). Moreover, noting that \(Q^{\mathcal{B}\mathcal{V}}_{k,m}\) contains \(P_{k,m}\), which is in \(\mathcal {C}^+\) (and, therefore, corresponds to a positive measure) and arbitrarily large, one concludes that \(\mu _{k,m}^\varepsilon \) must be non-negative for inequality (36) to hold over the whole \(\bar{H}\). To take notice of this fact, we write \(\mu _{k,m}^{\varepsilon , +}\) in place of \(\mu _{k,m}^\varepsilon \). Dividing by \(a^\varepsilon \), inequality (36) now gives
$$\begin{aligned}&w - \sum _{m=0}^N \frac{\lambda _m^\varepsilon }{a^\varepsilon } r_m - \sum _{m=0}^{N-1} \sum _{k=0}^m \int _{[0,1]} \frac{\mu _{k,m}^{\varepsilon ,+}(v)}{a^\varepsilon } \; \textrm{d}Q^{\mathcal{B}\mathcal{V}}_{k,m} \nonumber \\&\quad < \bar{W} + \varepsilon , \quad \forall (w, \{ r_m\}, \{ Q^{\mathcal{B}\mathcal{V}}_{k,m} \}) \in \bar{H}. \end{aligned}$$Given the arbitrariness of \(\varepsilon \) and restricting attention to \(H \subseteq \bar{H}\), one concludes that
$$\begin{aligned}&\inf _{\begin{array}{c} \{\lambda _m\} \\ \{\mu ^+_{k,m}\} \end{array}} \sup _{(w, \{ r_m\}, \{ Q^{\mathcal{B}\mathcal{V}}_{k,m} \}) \in H} \; \left\{ w - \sum _{m=0}^N \lambda _m r_m \right. \nonumber \\&\quad \quad \quad \quad \left. - \sum _{m=0}^{N-1} \sum _{k=0}^m \int _{[0,1]} \mu _{k,m}^+(v) \; \textrm{d}Q^{\mathcal{B}\mathcal{V}}_{k,m} \right\} \le \bar{W}. \end{aligned}$$(37)On the other hand, recalling the expression of w, \(r_m\), \(Q^{\mathcal{B}\mathcal{V}}_{k,m}\) in the definition of H given in (33), the left-hand side of (37) can be rewritten as
$$\begin{aligned} \inf _{\begin{array}{c} \{\lambda _m\} \\ \{\mu ^+_{k,m}\} \end{array}} \sup _{\{F_{k,m}\}, \{P_{k,m}\}} \; \left\{ \mathfrak {L}_\tau - \sum _{m=0}^{N-1} \sum _{k=0}^m \int _{[0,1]} \mu _{k,m}^+(v) \; \textrm{d}P_{k,m} \right\} , \end{aligned}$$which further becomes
$$\begin{aligned}&\inf _{\begin{array}{c} \{\lambda _m\} \\ \{\mu ^+_{k,m}\} \end{array}} \left\{ \sup _{\{F_{k,m}\}} \; \mathfrak {L}_\tau + \sup _{\{P_{k,m}\}} \left\{ - \sum _{m=0}^{N-1} \sum _{k=0}^m \int _{[0,1]} \mu _{k,m}^+(v) \; \textrm{d}P_{k,m} \right\} \right\} \nonumber \\&\quad = \inf _{\begin{array}{c} \{\lambda _m\} \\ \{\mu ^+_{k,m}\} \end{array}} \sup _{\{F_{k,m}\}} \; \mathfrak {L}_\tau , \end{aligned}$$(38)where in the last equality the second term has been suppressed because \(\sup _{\{P_{k,m}\}}\) is taken over non-positive quantities and \(P_{k,m} = 0\) is admissible. Altogether, (37) and (38) give the relation
$$\begin{aligned} \inf _{\begin{array}{c} \{\lambda _m\} \\ \{\mu ^+_{k,m}\} \end{array}} \sup _{\{F_{k,m}\}} \; \mathfrak {L}_\tau \le \bar{W}. \end{aligned}$$(39)To close the proof of (34), we show that strict inequality in (39) cannot hold. Indeed, in the opposite, there would exist a linear continuous functional of the form (35) that separates H from \(\bar{p}:= (\bar{W}, \{ r_m = 0 \}, \{ Q^{\mathcal{B}\mathcal{V}}_{k,m} = 0 \})\) in such a way that the value at \(\bar{p}\) is strictly larger than the value at any point of H. If we now consider the open set A obtained as counter-image of the reals greater than the value taken by this functional at \(\bar{p}\) minus a small enough margin, then A contains \(\bar{p}\), while A leaves out all H, contradicting the fact that \(\bar{p}\) is a contact point of H.Footnote 46
We now show that \(W = \bar{W}\), so closing the proof of (32). We start by constructing a sequence of neighborhoods of \(\bar{p} = (\bar{W}, \{ r_m = 0 \}, \{ Q^{\mathcal{B}\mathcal{V}}_{k,m} = 0 \})\) that exhibit asymptotic properties of interest. Consider a countable set of continuous functions \(g_1, g_2, \ldots \) dense in \(\textsf {C}^0[0,1]\) with respect to the \(\sup \) norm (e.g., polynomials with rational coefficients, see [54, Theorem 7.26]). For \(i=1,2,\ldots \), the neighborhoods of \(\bar{p}\) are defined as follows:
$$\begin{aligned} O_i:= & {} \Big \{(w,\{r_m\},\{ Q^{\mathcal{B}\mathcal{V}}_{k,m} \}) \text{ with } \vert w - \bar{W} \vert< 1/i; \ \vert r_m \vert< 1/i, \\{} & {} \quad m=0,1,\ldots ,N; \text{ and } \max _{j=1,\ldots ,i}\left| \int _{[0,1]} g_j(v) \; \textrm{d}Q^{\mathcal{B}\mathcal{V}}_{k,m} \right| < 1/i, \\{} & {} \quad m=0,1,\ldots ,N-1 \text{ and } k=0,\ldots ,m \Big \}. \end{aligned}$$Further, for any \(m=0,1,\ldots ,N\) and \(k=0,1,\ldots ,m\) consider sequences \(F^{i}_{k,m} \in \mathcal {C}^+\) and \(P^{i}_{k,m} \in \mathcal {C}^+\) indexed in i such that, for each \(i=1,2,\ldots \), the pair \((\{F^{i}_{k,m} \},\{P^{i}_{k,m}\})\) maps into a point of H that is also in \(O_i\) (such sequences certainly exist since \(\bar{p}\) is a contact point of H, see Footnote 46). For these sequences we have
$$\begin{aligned}&\lim _{i \rightarrow \infty } \sum _{k=0}^N {N \atopwithdelims ()k} \int _{[0,1]} \varphi _{k,\tau }(v) \; \textrm{d}F^{i}_{k,N} = \bar{W}; \end{aligned}$$(40)$$\begin{aligned}&\lim _{i \rightarrow \infty } \left[ \sum _{k=0}^m {m \atopwithdelims ()k} \int _{[0,1]} \textrm{d}F^{i}_{k,m} - 1 \right] = 0, \ \ \ m=0,1,\ldots ,N; \end{aligned}$$(41)$$\begin{aligned}&\lim _{i \rightarrow \infty } \int _{[0,1]} g_j(v) \; \textrm{d}[F^{i}_{k,m+1} - F^{(1-v),i}_{k,m} + P^{i}_{k,m}] = 0, \nonumber \\&\quad \forall g_j, \; j=1,2,\ldots , \ \ \ m=0,1,\ldots ,N-1, \ \ \ k=0,\ldots ,m. \end{aligned}$$(42)For given m and k, each \(F^{i}_{k,m} \in \mathcal {C}^+\) corresponds to a measure with all its mass in [0, 1]. Moreover, in view of (41), the \(F^{i}_{k,m}\)’s are uniformly bounded in i (i.e., \(F^{i}_{k,m}(v) \le C\), \(\forall v\), for all i, for some positive constant \(C < +\infty \)). Hence, by Helly’s theorem, [55, Theorem 2, Section 2, Chapter III], we conclude that there exists a sub-sequence of indexes \(i_h\) such that \(F^{i_h}_{k,m}\) has weak limit \(\bar{F}_{k,m} \in \mathcal {C}^+\). By repeating the same reasoning in a nested manner, we can further find a sub-sequence of the indexes \(i_h\) such that weak convergence also holds for another choice of m and k. Proceeding the same way for all choices of m and k, we conclude that there exists a sub-sequence of indexes (which, with a little abuse of notation, we still indicate as \(i_h\)) such that \(F^{i_h}_{k,m}\) has weak limit \(\bar{F}_{k,m} \in \mathcal {C}^+\), \(\forall \; m,k\). This gives
$$\begin{aligned} \int _{[0,1]} f(v) \; \textrm{d}\bar{F}_{k,m} = \lim _{i_h \rightarrow \infty } \int _{[0,1]} f(v) \; \textrm{d}F^{i_h}_{k,m}, \quad \forall \; m,k, \end{aligned}$$(43)for any continuous function \(f \in \textsf {C}^0[0,1]\). Since \(\varphi _{k,\tau }\), as well as the constant function equal to 1, are continuous, (43) together with (40) and (41) yield
$$\begin{aligned} \sum _{k=0}^N {N \atopwithdelims ()k} \int _{[0,1]} \varphi _{k,\tau }(v) \; \textrm{d}\bar{F}_{k,N} = \bar{W} \end{aligned}$$(44)and
$$\begin{aligned} \sum _{k=0}^m {m \atopwithdelims ()k} \int _{[0,1]} \textrm{d}\bar{F}_{k,m} - 1 = 0, \quad m=0,1,\ldots ,N. \end{aligned}$$(45)Turn now to consider (42), from which we have
$$\begin{aligned} \lim _{i_h \rightarrow \infty } \int _{[0,1]} g_j(v) \; \textrm{d}[F^{i_h}_{k,m+1} - F^{(1-v),i_h}_{k,m}] = - \lim _{i_h \rightarrow \infty } \int _{[0,1]} g_j(v) \; \textrm{d}P^{i_h}_{k,m}, \nonumber \\ \end{aligned}$$(46)where the limit in (42) restricted to the sub-sequence \(i_h\) can be broken up in the two limits in (46) because the left-hand side of (46) exists due to the weak convergence of generalized distribution functions \(F^{i_h}_{k,m}\).Footnote 47 For the functions \(g_j\) that are non-negative (i.e., \(g_j(v) \ge 0\), \(\forall v\)), which we henceforth write as \(g^+_j\) to help interpretation, (46) gives
$$\begin{aligned} \lim _{i_h \rightarrow \infty } \int _{[0,1]} g^+_j(v) \; \textrm{d}[F^{i_h}_{k,m+1} - F^{(1-v),i_h}_{k,m}] \le 0. \end{aligned}$$(47)Taking now any non-negative function \(f^+\) in \(\textsf {C}^0[0,1]\) and noting that \(f^+\) can be arbitrarily approximated in the \(\sup \) norm by a function \(g^+_j\),Footnote 48 weak convergence of \(F^{i_h}_{k,m}\) to \(\bar{F}_{k,m}\) used in (47) yields
$$\begin{aligned} \int _{[0,1]} f^+(v) \; \textrm{d}[\bar{F}_{k,m+1} - \bar{F}^{(1-v)}_{k,m}] \le 0, \end{aligned}$$from which \(\bar{F}_{k,m+1} - \bar{F}^{(1-v)}_{k,m}\) is in \(\mathcal {C}^-\) (recall Footnote 41). If we now choose \(\bar{P}_{k,m} = -[\bar{F}_{k,m+1} - \bar{F}^{(1-v)}_{k,m}]\) (which is in \(\mathcal {C}^+\)), then, also in the light of (44) and (45), one sees that \((\{\bar{F}_{k,m} \},\{\bar{P}_{k,m}\})\) maps into the point \((\bar{W},\{r_m = 0 \},\big \{ Q^{\mathcal{B}\mathcal{V}}_{k,m} = 0 \big \})\), which proves that this point is in H. Hence, it holds that \(W = \bar{W}\) and equation (32) remains proven.
-
We next show that
$$\begin{aligned} \lim _{\tau \downarrow 0} \; \sup _{\{F_{k,m}\}} \inf _{\begin{array}{c} \{\lambda _m\} \\ \{\mu ^+_{k,m}\} \end{array}} \mathfrak {L}_\tau = \sup _{\{F_{k,m}\}} \inf _{\begin{array}{c} \{\lambda _m\} \\ \{\mu ^+_{k,m}\} \end{array}} \mathfrak {L} \end{aligned}$$(48)(in the sense that the limit on the left exists and it equals the expression on the right), which is the only relation in (31) that is still unproven, so concluding the proof of (B) in (29).
-
Notice that, in both sides of (48), the \(\inf \) operator sends the value to \(-\infty \) whenever the constraints in (27b) or (27c) are not satisfied by \(\{ F_{k,m}\}\): hence, (27b) and (27c) must be satisfied and are always assumed from now on. Under (27b) and (27c), \(\inf \) is attained for \(\lambda _m = 0\) and \(\mu ^+_{k,m} = 0\) for all m and k, and (48) is therefore rewritten as
$$\begin{aligned}{} & {} { \lim _{\tau \downarrow 0} \; \sup _{\{F_{k,m}\}} \sum _{k=0}^N {N \atopwithdelims ()k} \int _{[0,1]} \varphi _{k,\tau }(v) \; \textrm{d}F_{k,N} } \nonumber \\= & {} \sup _{\{F_{k,m}\}} \sum _{k=0}^N {N \atopwithdelims ()k} \int _{[0,1]} \textbf{1}_{v \in (\epsilon (k),1]} \; \textrm{d}F_{k,N}. \end{aligned}$$(49)Note that \(\lim _{\tau \downarrow 0}\) on the left certainly exists because, by the very definition of \(\varphi _{k,\tau }\), the quantity under the sign of limit is decreasing as \(\tau \downarrow 0\) and is lower bounded by 0. To show the validity of (49), we discretize \(\tau \) into \(\tau _i\), \(i=1,2,\ldots \), \(\tau _i \downarrow 0\), and consider a sequence \(\{ \breve{F}^{i}_{k,m} \}\), \(i=1,2,\ldots \) (with \(\breve{F}^{i}_{k,m} \in \mathcal {C}^+\) satisfying (27b) and (27c) for any i), such that
$$\begin{aligned} \lim _{i\rightarrow \infty } \sum _{k=0}^N {N \atopwithdelims ()k} \int _{[0,1]} \varphi _{k,\tau _i}(v) \; \textrm{d}\breve{F}^{i}_{k,N} \end{aligned}$$equals the left-hand side of (49) (for this to hold, \(\breve{F}^{i}_{k,m}\) must achieve a progressively closer and closer approximation of \(\sup _{\{F_{k,m}\}}\) in the left-hand side of (49) as i increases); then, we construct from \(\{ \breve{F}^{i}_{k,m} \}\) a new sequence \(\{ \tilde{F}^{i}_{k,m} \}\), \(i=1,2,\ldots \) (still in \(\mathcal {C}^+\) and satisfying (27b) and (27c)), such that,Footnote 49
$$\begin{aligned}&\lim _{i\rightarrow \infty } \sum _{k=0}^N {N \atopwithdelims ()k} \int _{[0,1]} \varphi _{k,\tau _i}(v) \; \textrm{d}\breve{F}^{i}_{k,N} \nonumber \\&\quad \le \liminf _{i\rightarrow \infty } \sum _{k=0}^N {N \atopwithdelims ()k} \int _{[0,1]} \textbf{1}_{v \in (\epsilon (k),1]} \; \textrm{d}\tilde{F}^{i}_{k,N}. \end{aligned}$$(50)This shows that the left-hand side of (49) (which is equal to the left-hand side of (50)) has value no bigger than the right-hand side of (49) (because the right-hand side of (50) is clearly no bigger than the right-hand side of (49)). Since, on the other hand, the left-hand side of (49) cannot be smaller than the right-hand side of (49) because \(\varphi _{k,\tau }(v) \ge \textbf{1}_{v \in (\epsilon (k),1]} \), \(\forall v\), relation (49) remains proven. The construction of \(\{ \tilde{F}^{i}_{k,m} \}\) is in three steps:
- Step 1.:
-
[construction of \(\{ \check{F}^{i}_{k,m} \}\)] For all k for which \(\epsilon (k) \ne 1\) and for all m, move the mass of \(\breve{F}^{i}_{k,m}\) contained in the interval \((\epsilon (k)-\tau _i,\epsilon (k)]\) into a concentrated mass in point \(\epsilon (k)+\tau _i\)Footnote 50; let \(\check{F}^{i}_{k,m}\) be the resulting generalized distribution functions.
- Step 2.:
-
[construction of \(\{ \hat{F}^{i}_{k,m} \}\)] The mass shift in Step 1 can lead to generalized distribution functions \(\check{F}^{i}_{k,m}\) that violate condition (27c) in \(\epsilon (k)+\tau _i\); the new generalized distribution functions \(\hat{F}^{i}_{k,m}\) restore the validity of this condition. For all k for which \(\epsilon (k) = 1\) (so that no mass shift has been performed in Step 1), let \(\hat{F}^{i}_{k,m} = \check{F}^{i}_{k,m}\), for all \(m = k, \ldots , N\). For all other k’s, let \(\hat{F}^{i}_{k,k} = \check{F}^{i}_{k,k}\); then, verify sequentially for \(m = k, \ldots , N-1\) whether the condition
$$\begin{aligned} \Delta \check{F}^{i}_{k,m+1}(\epsilon (k)+\tau _i) - (1-(\epsilon (k)+\tau _i)) \; \Delta \hat{F}^{i}_{k,m}(\epsilon (k)+\tau _i) \le 0 \end{aligned}$$is satisfied (\(\Delta F(\bar{v})\) stands for the jump in \(\bar{v}\), i.e., \(F(\bar{v}) - \lim _{v \uparrow \bar{v}} F(v)\)); if yes, let \(\hat{F}^{i}_{k,m+1} = \check{F}^{i}_{k,m+1}\), otherwise trim the jump \(\Delta \check{F}^{i}_{k,m+1}(\epsilon (k)+\tau _i)\) to the value \((1-(\epsilon (k)+\tau _i)) \; \Delta \hat{F}^{i}_{k,m}(\epsilon (k)+\tau _i)\) and define \(\hat{F}^{i}_{k,m+1}\) as the trimmed version of \(\check{F}^{i}_{k,m+1}\).
- Step 3.:
-
[construction of \(\{ \tilde{F}^{i}_{k,m} \}\)] The trimming operation in Step 2 may have unbalanced some equalities in (27b), i.e., it may be that
$$\begin{aligned} \sum _{k=0}^m {m \atopwithdelims ()k} \int _{[0,1]} \textrm{d}\hat{F}^{i}_{k,m} < 1 \end{aligned}$$for some m. If so, re-gain balance by adding to \(\hat{F}^{i}_{m,m}\) a suitable mass (e.g., concentrated in \(v=1\)), while leaving all other \(\hat{F}^{i}_{k,m}\), \(k \ne m\), unaltered. The so-obtained generalized distribution functions are \(\tilde{F}^{i}_{k,m}\). Note that this operation preserves the validity of condition \(\tilde{F}^{i}_{m,m+1} - \tilde{F}^{(1-v),i}_{m,m} \in \mathcal {C}^-\), so that \(\{ \tilde{F}^{i}_{k,m} \}\) satisfies (27c) besides (27b).
Since \(\varphi _{k,\tau _i}(v)\) is non-decreasing in v, the mass shift in Step 1 can only increase \(\sum _{k=0}^N {N \atopwithdelims ()k} \int _{[0,1]} \varphi _{k,\tau _i}(v) \; \textrm{d}\breve{F}^{i}_{k,N}\); moreover, as \(\tau _i \downarrow 0\), any trimming and re-balancing in Steps 2 and 3 involve vanishing masses. Therefore,
$$\begin{aligned}&\lim _{i\rightarrow \infty } \sum _{k=0}^N {N \atopwithdelims ()k} \int _{[0,1]} \varphi _{k,\tau _i}(v) \; \textrm{d}\breve{F}^{i}_{k,N} \nonumber \\&\quad \le \liminf _{i\rightarrow \infty } \sum _{k=0}^N {N \atopwithdelims ()k} \int _{[0,1]} \varphi _{k,\tau _i}(v) \; \textrm{d}\tilde{F}^{i}_{k,N}. \end{aligned}$$(51)On the other hand, by construction, \(\varphi _{k,\tau _i}(v) = \textbf{1}_{v \in (\epsilon (k),1]} \) if \(\epsilon (k) = 1\), while, for \(\epsilon (k) \ne 1\), \(\varphi _{k,\tau _i}(v) \ne \textbf{1}_{v \in (\epsilon (k),1]} \) only occurs on the interval \((\epsilon (k)-\tau _i,\epsilon (k)]\) where \(\tilde{F}^{i}_{k,N}\) has no mass by construction. Hence,
$$\begin{aligned} \sum _{k=0}^N {N \atopwithdelims ()k} \int _{[0,1]} \varphi _{k,\tau _i}(v) \; \textrm{d}\tilde{F}^{i}_{k,N} = \sum _{k=0}^N {N \atopwithdelims ()k} \int _{[0,1]} \textbf{1}_{v \in (\epsilon (k),1]} \; \textrm{d}\tilde{F}^{i}_{k,N}, \end{aligned}$$
This concludes the proof of (B) in (29).\(\square \)
-
-
Proof of (C) in (29): First note that the Lagrangian can be rewritten as follows (in the second last term we have used the change of running index \(j = m \! + \! 1\))
$$\begin{aligned} \mathfrak {L}= & {} \sum _{m=0}^N \sum _{k=0}^m \int _{[0,1]} {m \atopwithdelims ()k} \textbf{1}_{v \in (\epsilon (k),1]} \textbf{1}_{m=N} \; \textrm{d}F_{k,m} \\{} & {} - \sum _{m=0}^N \sum _{k=0}^m \int _{[0,1]} \lambda _m {m \atopwithdelims ()k} \; \textrm{d}F_{k,m} \nonumber \\{} & {} + \sum _{m=0}^N \lambda _m - \sum _{j=0}^{N} \sum _{k=0}^j \int _{[0,1]} \mu ^+_{k,j-1}(v) \textbf{1}_{j \ne k} \; \textrm{d}F_{k,j} \nonumber \\{} & {} + \sum _{m=0}^{N} \sum _{k=0}^m \int _{[0,1]} \mu ^+_{k,m}(v) \cdot (1-v) \textbf{1}_{m \ne N} \; \textrm{d}F_{k,m}. \end{aligned}$$By renaming j as m in the second last term and re-arranging the summations \(\sum _{m=0}^{N} \sum _{k=0}^m\) as \(\sum _{k=0}^N \sum _{m=k}^{N}\), we then obtain:
$$\begin{aligned} \mathfrak {L}= & {} \sum _{m=0}^N \lambda _m + \sum _{k=0}^N \sum _{m=k}^N \int _{[0,1]} \Bigg [ {m \atopwithdelims ()k} \textbf{1}_{v \in (\epsilon (k),1]} \textbf{1}_{m=N} + (1-v) \mu ^+_{k,m}(v) \textbf{1}_{m \ne N} \nonumber \\{} & {} - \lambda _m {m \atopwithdelims ()k} - \mu ^+_{k,m-1}(v) \textbf{1}_{m \ne k} \Bigg ] \; \textrm{d}F_{k,m}. \end{aligned}$$(52)Now, if for some pair (k, m) the constraint in (30b) is not satisfied for a given \(v = \bar{v}\), then \(\sup _{\{F_{k,m}\}} \mathfrak {L}\) can be sent to \(+\infty \) by choosing \(F_{k,m}\) that has an arbitrarily large mass concentrated in \(\bar{v}\). Hence, the \(\inf _{\{\lambda _m\}, \{\mu ^+_{k,m}\}}\) of \(\sup _{\{F_{k,m}\}} \mathfrak {L}\) is attained at \(\lambda _m\)’s and \(\mu ^+_{k,m}\)’s satisfying (30b) and, once (30b) holds, \(\sup _{\{F_{k,m}\}} \mathfrak {L}\) is achieved by setting the second term in the right-hand side of (52) to zero (e.g., choose \(F_{k,m}=0\), for all k and m). This leads to the conclusion that \(\inf _{\{\lambda _m\}, \{\mu ^+_{k,m}\}} \sup _{\{F_{k,m}\}} \mathfrak {L}\) equals \(\gamma ^*\) of problem (). \(\square \)
Next we want to evaluate \(\gamma ^*\) of problem (). For a better visualization of the constraints in (30b), we write them more explicitly in groups indexed by k as follows:

For any given \(k \in \{0,\ldots ,N\}\), consider the corresponding set of inequalities and multiply both sides of the first inequality by \((1-v)^0\), both sides of the second inequality by \((1-v)^1\), and so on till the last inequality, which is multiplied by \((1-v)^{N-k}\). Then, summing side-by-side the so-obtained inequalities, and noting that all functions \(\mu ^+_{k,m}(v)\) cancel out, one obtains that the constraints in (53) imply the following inequalities:
We next show that the optimal value of problem () equals the optimal value of an optimization problem with the same cost function as problem () and the constraints (54), viz.
Since the constraints in () are implied by those present in () (as shown before), the optimal value of () is not bigger than the optimal value of (). The opposite inequality that the optimal value of () is not bigger than the optimal value of () is proven by showing that for any feasible point of () one can find a feasible point of () that attains the same value. This requires the following derivation.
-
Consider a feasible point \(\lambda _0,\ldots ,\lambda _N\) of (). Evaluating the constraints (55b) for \(k=0,\ldots ,N\) at \(v = 1\), one sees that \(\lambda _m \ge 0\) for \(m=0, \ldots , N\). To find the sought feasible point of (), consider the same \(\lambda _m\) as those for the feasible point of () and complement them with the following functions \(\mu ^+_{k,m}\) for \(k=0,\ldots ,N-1\) and \(m = k,\ldots , N-1\). The functions \(\mu ^+_{k,m}\) are first defined over [0, 1) and then extended to the closed interval [0, 1]. Over [0, 1), consider the inequalities in (53) for \(k=0,\ldots ,N-1\), \(m = k, \ldots , N-1\) and take \(\mu ^+_{k,m}(v)\) such that these inequalities are satisfied with equality, starting from top and then proceeding downwards. This gives
$$\begin{aligned} \mu ^+_{k,k}(v)= & {} \frac{\lambda _k {k \atopwithdelims ()k}}{1-v}, \nonumber \\ \mu ^+_{k,k+1}(v)= & {} \frac{\lambda _{k+1} {k+1 \atopwithdelims ()k}}{1-v} + \frac{\lambda _k {k \atopwithdelims ()k}}{(1-v)^2} \nonumber \\&\vdots&\\ \mu ^+_{k,N-1}(v)= & {} \sum _{j=k}^{N-1}\frac{\lambda _j {j \atopwithdelims ()k}}{(1-v)^{N-j}}. \nonumber \end{aligned}$$(56)Since \(\lambda _m \ge 0\), the obtained \(\mu ^+_{m,k}(v)\)’s are all positive and, moreover, are continuous over [0, 1). We show that choice (56) satisfies over [0, 1) the remaining inequalities (those in (53) for \(k=0,\ldots ,N\) and \(m = N\)). For \(k=0,\ldots ,N-1\) and \(m = N\), substituting \(\mu ^+_{k,N-1}(v) = \sum _{j=k}^{N-1}\frac{\lambda _j {j \atopwithdelims ()k}}{(1-v)^{N-j}}\) gives
$$\begin{aligned} {N \atopwithdelims ()k} \textbf{1}_{v \in (\epsilon (k),1]} \le \sum _{j=k}^{N} \lambda _j {j \atopwithdelims ()k} \frac{1}{(1-v)^{N-j}}, \end{aligned}$$(57)while for \(k=N\) and \(m = N\), we have
$$\begin{aligned} {N \atopwithdelims ()N} \textbf{1}_{v \in (\epsilon (N),1]} \le \lambda _N {N \atopwithdelims ()N}. \end{aligned}$$(58)Equations (57) and (58) are satisfied because they coincide with (55b). As for \(v = 1\), note that functions \(\mu ^+_{m,k}\) defined in (56) tend to infinity when \(v \rightarrow 1\). This poses a problem of existence for \(v = 1\), which, however, can be easily circumvented by truncating the functions \(\mu ^+_{m,k}\) in the interval \(v \in [1 \! - \! \rho ,1]\) at their value \(\mu ^+_{k,m}(1 \! - \! \rho )\) to obtain
$$\begin{aligned} \mu ^{+,\rho }_{k,m}(v) = {\left\{ \begin{array}{ll} \mu ^+_{k,m}(v) &{} v < 1-\rho \\ \mu ^+_{k,m}(1 \! - \! \rho ) &{} v \ge 1-\rho , \end{array}\right. } \end{aligned}$$and noting that all the inequalities are satisfied over [0, 1] if \(\rho \) is chosen small enough.
Summarizing the results so far achieved, we have
where \(\gamma ^*\) is given by (). The proof of the theorem is concluded by recognizing that () is equivalent to (7) by defining \(t:=1-v\) and \(\xi (t):= \sum _{m=0}^N \lambda _m t^m\) (which for different values of the \(\lambda _m\)’s spans the whole class \(\textsf {P}_N\) of polynomials of order N) and noticing that \(\xi (1) = \sum _{m=0}^N \lambda _m\) and that \(\frac{1}{k!} \frac{\textrm{d}^{k}}{\textrm{d}t^{k}} \xi (t) = \sum _{m=k}^N \lambda _m {m \atopwithdelims ()k} t^{m-k}\).\(\square \)
5.2 Proof of Theorem 4
The proof is obtained from Theorem 3 by showing that the specific choice of \(\epsilon (k)\) given in the statement of Theorem 4 yields \(\gamma ^*\le \beta \). Consider thus (7) and take \(\xi (t) = \frac{\beta }{N} \sum _{m=0}^{N-1} t^m\). This gives \(\frac{1}{k!} \frac{\textrm{d}^{k}}{\textrm{d}t^{k}} \xi (t) = \frac{\beta }{N} \sum _{m=k}^{N-1} {m \atopwithdelims ()k} t^{m-k}\) for \(k=0,1,\ldots ,N-1\) and \(\frac{1}{N!} \frac{\textrm{d}^{N}}{\textrm{d}t^{N}} \xi (t) = 0\). This choice of \(\xi (t)\) is feasible for (7) because the constraint for \(k=N\) becomes \(0 \le 0\) (recall that \(\epsilon (N) = 1\) so that the indicator function is 1 over an empty set), while the constraints for \(k=0,\ldots ,N-1\) are satisfied in view of the definition of \(\epsilon (k)\) in (5) and (6): for \(t = 1-\epsilon (k)\), equation (5) implies that the constraints hold with equality, while the monotonicity property noted in Footnote 12 implies the satisfaction of the constraints for all other values of \(t \in [0,1]\). Given the feasibility of \(\xi (t)\), we then have \(\gamma ^*\le \xi (1) = \beta \) and this concludes the proof. \(\square \)
Notes
x can, e.g., be the d-dimensional vector that contains the parameters of a controller, or those of a regression model or a predictor, or it may describe how the wealth is distributed on d assets (portfolio) in an investment problem.
For example, in an investment problem, \(\delta \) describes the evolution of the market in the investment period and in a medical application it describes the clinical condition of a patient.
So, in an investment problem, \(\mathcal {X}_\delta \) contains the portfolios resulting in a reward above the threshold when the market condition is \(\delta \) and, in a medical application, \(\mathcal {X}_\delta \) is the set of parameters for which a predictor correctly classifies a given patient \(\delta \) as being sick or healthy on the ground of a clinical test.
We prefer to speak of “list” rather than “set” to emphasize the existence of a positional ordering (hence, we can refer to the first, or the second, element in the list); the list can contain repeated elements, for instance \(\delta _2\) and \(\delta _3\) can have the same value.
Despite that the solution is appropriate for all the scenarios, one cannot exclude that it is inappropriate for other \(\delta \)’s, possibly covering a set that has large probability to occur.
It is assumed that the set \(\{ \delta \in \Delta \!: x \notin \mathcal {X}_\delta \}\) is measurable. Measurability is also tacitly assumed elsewhere throughout this paper.
The presentation of the results in [39] will somehow delay the description of the novel contribution of this paper. However, we feel this line of narration is strictly needed for a precise comprehension of the content of the present paper.
When \(m=0\), it is meant that (2) becomes \(\min _{x \in \mathcal {X}} c(x)\), optimization without constraints.
This is just a total ordering in \(\mathcal {X}\).
k can as well be zero, in which case the support list is the empty list.
The equation (32) in [39] (the equivalent to equation (5) here) is slightly different from (5) as it has \(N+1\) at the denominator and the summation arrives at N; however, it is not difficult to prove that Theorem 2 in [39] holds true with the equation (32) substituted by the equation (5) given here.
The fact that the solution is unique is readily seen because (5) is equivalent to
$$\begin{aligned} \frac{\beta }{N} \sum _{m=k}^{N-1} \frac{{m \atopwithdelims ()k}}{{N \atopwithdelims ()k}}\frac{1}{t^{N-m}} = 1,\end{aligned}$$whose left-hand side is a continuous and strictly decreasing function that takes value no bigger than \(\beta \) for \(t=1\) and goes to \(+\infty \) as \(t \rightarrow 0\).
This fact has been well recognized in [39, Section 8] to which the reader is referred for a more ample discussion than that provided here.
The terminology non-degenerate was aptly coined in a convex setup; however, in a non-convex setup “degeneracy” appears to be an inappropriate word to indicate a situation that is in fact the norm. We keep this terminology here because this facilitates a comparison with other contributions.
We use z instead of x because in various cases we have to recast an optimization problem into the framework of decisions by adding new variables to the original optimization variable x; in these cases, it is convenient to have available two distinct symbols, x and z.
In the robust optimization setup, this corresponds to unconstrained optimization.
Conditions (i)-(iii) might be softened to requiring that they hold with probability 1 and all results would maintain their validity. We do not pursue this straightforward generalization here.
k can as well be zero, in which case the support list is the empty list.
When the smallest support list is the empty list, then \(s^*_m = 0\). In view of condition (ii) of Property 1, this happens when the decision with no scenarios is already appropriate for all the scenarios.
When the problem is convex, a support list only contains \(\delta _i\)’s corresponding to active constraints and the computation of a bound for the complexity is further simplified.
In case of multiple minimizers, \(x^*_m\) ranks first according to the rule of preference because it already ranked first in the larger feasibility set before the new constraints were added.
This probability is given by \(\int _0^1 \int _{\max \{0,x^*_{2,N} + \vert \delta _1-x^*_{1,N} \vert \}}^{+\infty } 10 \ \textrm{e}^{-10 \delta _2} \; \textrm{d}\delta _2 \; \textrm{d}\delta _1\). In this simulation example, we illustrate how the risk distributes as a function of the complexity and are therefore interested in computing the risk using \(\mathbb {P}\). Obviously, this operation has no sense in real applications where \(\mathbb {P}\) is unknown.
In [39], Theorem 1 is stated for the particular setup in which \(\mathcal {X}= \mathbb {R}^d\), c(x) is convex and \(\mathcal {X}_\delta \) are convex sets for any \(\delta \). In this convex setup, it is proven that the complexity is certainly bounded by d and only this latter fact is used in the subsequent part of the proof; in other words, no mention is made in the proof of, e.g., the fact that c(x) is convex or that \(\mathcal {X}= \mathbb {R}^d\) other than for establishing that the complexity is bounded by d. As a consequence, the proof in [39] carries over to prove Theorem 7 in this section, in which the complexity is explicitly assumed to be bounded by d, without any mention to convexity.
The only reason for not just taking \(\mathbb {R}^2\) is to allow for the existence of a solution when a linear cost is considered (as is done below) and there are no constraints (\(m = 0\)).
We say “when the nonempty interior assumption is dropped” because our counterexample does not satisfy this assumption: any two \(\mathcal {X}_\delta \)’s corresponding to segments with the same inclination (either \(+45\) or \(-45\) degrees) have only the point \((0,2,-1)\) in common, so violating the nonempty interior assumption.
Instead, the conclusion is certainly valid in a non-convex setup where the assumption on the existence of a nonempty interior becomes void: just add to any constraint a ball corresponding to a large value of the cost without altering the remaining part of the constraint. For example, in the lyrebird tail example, one can add a small ball centered at point (0, 1).
While we refer to ridge regularization in finite Euclidean spaces for concreteness, nothing in the present section depends crucially on this choice, and the same reasoning can be applied to any other type of regularization process.
In this process of multiple evaluations, the user has to pay attention to the fact that each single evaluation may fail to be correct with probability \(\beta \); hence, all evaluations, and thereby the evaluation for the selection that has been made, are simultaneously guaranteed with confidence \(1 - M \beta \), where M is the total number of evaluations. This is not a big concern since confidence is cheap.
While feasible, the solution can still not exist because it “drifts” to infinity.
Note that it is enough to break the tie on x because, at optimum, it must be that \(f(x,\delta _i) = \xi _i\) so that, once the tie on x is broken, then the \(\xi _i\) variables are unambiguously determined.
More explicitly, if \(M_m(\delta _1,\ldots ,\delta _m) = z^*_m\), and the arguments are permuted, then \(M_m\) again returns \(z^*_m\). Moreover, if new scenarios are added for which \(z^*_m\) is appropriate, then \(z^*_m\) is confirmed, i.e., \(M_{m+n}(\delta _1,\ldots ,\delta _{m+n}) = z^*_m\), whereas having one or more new scenarios for which \(z^*_m\) is not appropriate leads to a change, giving either a new decision or that the decision no longer exists.
A multiset is simply a set with repetitions, that is, it has no ordering but two elements in it can coincide. The reason why \(z_{\textrm{aug},m}^*\) is not simply defined as the list \((\delta _1,\ldots ,\delta _m)\) is that a list has an ordering, which would lead to a definition of \(M_{\textrm{aug},m}\) that is not permutation invariant. Note also that, since we want to distinguish whether a z comes from \(\mathcal {Z}\) or from \(\bigcup _{m=0}^\infty \{\text {multisets containing } m \text { elements from } \Delta \}\), we require that \(\mathcal {Z}\) and \(\bigcup _{m=0}^\infty \{\text {multisets containing } m \text { elements from } \Delta \}\) do not have any element in common. If this is not the case (for example \(\mathcal {Z}= \mathbb {R}\) and \(\Delta = \mathbb {R}\) so that \(\mathcal {Z}\) and the \(\{\text {multisets containing } m \text { elements from } \Delta \}\) coincide for \(m = 1\)), we simply add an identification flag (the same for all elements) to all elements in \(\Delta \). \(\mathcal {Z}_{\textrm{aug}}\) is called the “augmented” decision domain.
In [35], the problem of estimating the probability of exceeding any empirical cost (not just the largest) is studied under a non-degeneracy condition. The results of [35] can be carried over to the present framework in which the non-degeneracy assumption is dropped, but we do not pursue this generalization here.
The complexity cannot be smaller than q. Generally, \(s^{*,q}_N > q\) because more that q scenarios are needed for the solution \(x^{*,q}_N\) to remain in its initial location; this is not dissimilar from worst-case optimization, which is a particular case of CVaR obtained for \(q = 1\). Moreover, in case functions \(c(x,\delta )\) are convex in x for any \(\delta \), then it is easily seen that the search for scenarios to be included in a support list can be restricted to the \(\delta _i\)’s for which \(c(x,\delta _i)\) takes value \(h^{*,q}_N\) or higher at \(x^{*,q}_N\).
That is, \(F_{k,N}\) is non-decreasing and right continuous, but does not necessarily end up in 1.
To be precise, we should have specified that the last argument holds with probability 1. The specification “with probability 1” is needed because, as pointed out at the time when \(\textsf{S}_m\) was introduced, \(\textsf{S}_m\) can be arbitrarily defined when \(\sum _{\ell =1}^k \eta _{i_\ell }\) is minimized by more than one choice of the indexes, an event that occurs with probability zero. Since specifying the exception of probability zero sets is immaterial in so far as a probability is computed, we shall omit to explicitly indicate such exceptions in later junctures.
The reader may have noticed that the specific rule by which \(\textsf{S}_m\) selects a sub-list (i.e., by minimizing \(\sum _{\ell = 1}^k \eta _{i_\ell }\)) does not play any role in the derivation. However, what indeed matters is that this rule only refers to the object to be selected and not to the list from which the object is selected. If, for example, the rule were: “if m is odd, then do this; and if m is even, then do that”, then the last sentence “This gives a contradiction because \(\tilde{\delta }_{i_1},\ldots ,\tilde{\delta }_{i_h}\) would be preferred to \(\tilde{\delta }_1,\ldots ,\tilde{\delta }_k\) while, instead, \(\textsf{S}_{m+1}(\tilde{\delta }_1,\ldots ,\tilde{\delta }_{m+1}) = \tilde{\delta }_1,\ldots ,\tilde{\delta }_k\)” would not be correct owing to the fact that the selection rule changes when moving from m to \(m+1\).
In various parts of this paper from here onward, the set of generalized distribution functions \(F_{k,m} \in \mathcal {C}^+, \; m=0,\ldots ,N, \; \; k=0,\ldots ,m,\) is indicated by the notation \(\{F_{k,m}\}\), where the range of variability for m and k and the fact that \(F_{k,m} \in \mathcal {C}^+\) are suppressed for brevity. Similar notations apply to \(\lambda _m\), \(\mu ^+_{k,m}\) and other collections alike.
For a formal proof of this intuitive fact, suppose that \(F_{k,m+1} - F^{(1-v)}_{k,m} \notin \mathcal {C}^-\). Then, there are reals \(a < b\) such that \(F_{k,m+1}(b) - F^{(1-v)}_{k,m}(b) > F_{k,m+1}(a) - F^{(1-v)}_{k,m}(a)\) with \(b \in [0,1]\) (note that when \(b=0\), a will be negative; this accommodates a positive jump at 0 of \(F_{k,m+1} - F^{(1-v)}_{k,m}\)). This gives \(\int _{\mathbb {R}} \textbf{1}_{v \in (a,b]} \; \textrm{d}[F_{k,m+1} - F^{(1-v)}_{k,m}] > 0\). Now, approximate \( \textbf{1}_{v \in (a,b]} \) with continuous, positive, functions \(f_n\) which equals 1 on \([a+\frac{1}{n},b]\), 0 on \((-\infty ,a] \cup [b+\frac{1}{n},+\infty )\) and with linear slopes connecting 0 to 1 on both sides. When \(n \rightarrow +\infty \), \(f_n \rightarrow \textbf{1}_{v \in (a,b]} \) pointwise, and
$$\begin{aligned} \int _{\mathbb {R}} f_n(v) \; \textrm{d}[F_{k,m+1} - F^{(1-v)}_{k,m}] \rightarrow \int _{\mathbb {R}} \textbf{1}_{v \in (a,b]} \; \textrm{d}[F_{k,m+1} - F^{(1-v)}_{k,m}] \end{aligned}$$by dominated convergence. Whence, there exists a \(\bar{n}\) large enough such that \(\int _{\mathbb {R}} f_{\bar{n}}(v) \; \textrm{d}[F_{k,m+1} - F^{(1-v)}_{k,m}] > 0\), which yields \(\int _{[0,1]} f_{\bar{n}}(v) \; \textrm{d}[F_{k,m+1} - F^{(1-v)}_{k,m}] > 0\), because integration is with respect to a measure that has no mass outside [0, 1]. Function \(\mu ^+_{k,m}\) is now defined as the restriction of \(f_{\bar{n}}\) to [0, 1] with an arbitrary re-scaling to make the integral arbitrarily large.
Note that interval \([0,\epsilon (k) - \tau ]\) is non-empty owing to condition \(\tau < \epsilon (k)\); condition \(\tau < 1-\epsilon (k)\) will be used in a subsequent juncture.
For the applicability of Theorem 3.10, one needs that \(\mathcal{L}\mathcal{F}\) “separates” \(\mathcal{B}\mathcal{V}\), a fact that follows from Footnote 41.
The closure \(\bar{H}\) is formed by all contact points of H, where a point is of contact if any neighborhood of the point contains at least one point in H; clearly, any point \(h \in H\) also belongs to \(\bar{H}\).
Note that, in the definition of W, \(\sup \) is taken over a nonempty set. As a matter of fact, owing to (20) and (21), the maps \(M_m\) that satisfy Property 1 give rise to generalized distribution functions \(F_{k,m}\) for which one obtaines \(r_m = 0\) for all m and \(Q^{\mathcal{B}\mathcal{V}}_{k,m} = 0\) for all m and k by the choice \(P_{k,m} = -( F_{k,m+1} - F^{(1-v)}_{k,m})\). It is also worth noticing that \(\bar{W}\) (and hence W too) is finite and no bigger than 1. In fact, by the definition of H, every point in H satisfies \(w \le r_N+1\). On the other hand, if it were that \(\bar{W} > 1\), then there would exist a contact point of H such that \(w > 1\) and \(r_N = 0\), which is in contradiction with the fact that \(w \le r_N+1\) for all points in H.
\(\bar{p}\) is a contact point of H because \(\bar{W}\) is defined via a \(\sup \) operation over contact points and, therefore, any neighborhood of \(\bar{p}\) is also a neighborhood of a contact point \((w,\{r_m = 0 \}\big \{ Q^{\mathcal{B}\mathcal{V}}_{k,m} = 0 \big \})\) with w close enough to \(\bar{W}\), so that the neighborhood must contain a point of H.
Indeed, \(\int _{[0,1]} g_j(v) \; \textrm{d}[F^{i_h}_{k,m+1} - F^{(1-v),i_h}_{k,m}]\) can be rewritten as \(\int _{[0,1]} g_j(v) \; \textrm{d}F^{i_h}_{k,m+1} - \int _{[0,1]} g_j(v) (1-v) \; \textrm{d}F^{i_h}_{k,m}\) and the two terms have limits because \(g_j(v)\) and \(g_j(v)(1-v)\) are continuous functions.
Note that function \(f^+(v)\) can be zero for some v, so that an approximant, however close, might as well take negative values, against the requirement that the approximant is a non-negative \(g^+_j\). Nonetheless, any \(\varepsilon \)-close approximant of \(f^+(v)+\varepsilon \) is non-negative and it is also a \(2\varepsilon \)-close approximant of \(f^+(v)\).
This is to say that \(\breve{F}^{i}_{k,m}\) is flattened on \((\epsilon (k)-\tau _i,\epsilon (k)]\) and a jump \(\breve{F}^{i}_{k,m}(\epsilon (k))-\breve{F}^{i}_{k,m}(\epsilon (k)-\tau _i)\) is added in \(\epsilon (k)+\tau _i\). Note also that \(\epsilon (k)+\tau _i \in [0,1]\) because \(\tau _i < 1 - \epsilon (k)\) (see the very beginning of the proof of (B) in (29)).
References
Campi, M.C., Garatti, S.: Introduction to the Scenario Approach. MOS-SIAM Series on Optimization, Philadelphia (2018)
Campi, M.C., Carè, A., Garatti, S.: The scenario approach: a tool at the service of data-driven decision making. Annu. Rev. Control. 52, 1–17 (2021)
Calafiore, G.C., Campi, M.C.: The scenario approach to robust control design. IEEE Trans. Autom. Control 51(5), 742–753 (2006)
Campi, M.C., Garatti, S., Prandini, M.: The scenario approach for systems and control design. Annu. Rev. Control. 33(2), 149–157 (2009)
Garatti, S., Campi, M.C.: Modulating robustness in control design: principles and algorithms. IEEE Control. Syst. 33(2), 36–51 (2013)
Schildbach, G., Fagiano, L., Frei, C., Morari, M.: The scenario approach for stochastic model predictive control with bounds on closed-loop constraint violations. Automatica 50(12), 3009–3018 (2014)
Grammatico, S., Zhang, X., Margellos, K., Goulart, P.J., Lygeros, J.: A scenario approach for non-convex control design. IEEE Trans. Autom. Control 61(2), 334–345 (2016)
Sutter, T., Mohajerin Esfahani, P., Lygeros, J.: Approximation of constrained average cost Markov control processes. In: Proceedings of the 53rd IEEE Conference on Decision and Control, Los Angeles, CA, USA, pp. 6597–6602 (2014)
Alamo, T., Tempo, R., Luque, A., Ramirez, D.R.: Randomized methods for design of uncertain systems: sample complexity and sequential algorithms. Automatica 51, 160–172 (2015)
Nasir, H.A., Caré, A., Weyer, E.: A scenario-based stochastic MPC approach for problems with normal and rare operations with an application to rivers. IEEE Trans. Control Syst. Technol. 27(4), 1397–1410 (2019)
Deori, L., Garatti, S., Prandini, M.: A randomized relaxation method to ensure feasibility in stochastic control of linear systems subject to state and input constraints. Automatica 115, 108854 (2020)
Geng, X., Xie, L.: Data-driven decision making in power systems with probabilistic guarantees: theory and applications of chance-constrained optimization. Annu. Rev. Control. 47, 341–363 (2019)
Falsone, A., Deori, L., Ioli, D., Garatti, S., Prandini, M.: Optimal disturbance compensation for constrained linear systems operating in stationary conditions: a scenario-based approach. Automatica 110, 108537 (2019)
Welsh, J.S., Rojas, C.R.: A scenario based approach to robust experiment design. In: Proceedings of the 15th IFAC Symposium on System Identification, Saint-Malo, France (2009)
Campi, M.C., Calafiore, G., Garatti, S.: Interval predictor models: identification and reliability. Automatica 45(2), 382–392 (2009)
Welsh, J.S., Kong, H.: Robust experiment design through randomisation with chance constraints. In: Proceedings of the 18th IFAC World Congress, Milan, Italy (2011)
Crespo, L.G., Kenny, S.P., Giesy, D.P.: Random predictor models for rigorous uncertainty quantification. Int. J. Uncertain. Quantif. 5(5), 469–489 (2015)
Crespo, L.G., Kenny, S.P., Giesy, D.P.: Interval predictor models with a linear parameter dependency. J. Verif. Valid. Uncertain. Quantif. 1(2), 1–10 (2016)
Garatti, S., Campi, M.C., Carè, A.: On a class of interval predictor models with universal reliability. Automatica 110, 108542 (2019)
Rocchetta, R., Crespo, L.G., Kenny, S.P.: A scenario optimization approach to reliability-based design. Reliab. Eng. Syst. Saf. 196, 107900 (2020)
Campi, M.C.: Classification with guaranteed probability of error. Mach. Learn. 80, 63–84 (2010)
Campi, M.C., Carè, A.: Random convex programs with \(l_1\)-regularization: sparsity and generalization. SIAM J. Control. Optim. 51(5), 3532–3557 (2013)
Margellos, K., Prandini, M., Lygeros, J.: On the connection between compression learning and scenario based single-stage and cascading optimization problems. IEEE Trans. Autom. Control 60(10), 2716–2721 (2015)
Caré, A., Ramponi, F.A., Campi, M.C.: A new classification algorithm with guaranteed sensitivity and specificity for medical applications. IEEE Control Syst. Lett. 2(3), 393–398 (2018)
Crespo, L.G., Colbert, B.K., Kenny, S.P., Giesy, D.P.: On the quantification of aleatory and epistemic uncertainty using sliced-normal distributions. Syst. Control Lett. 134 (2019)
Campi, M.C., Garatti, S.: A theory of the risk for optimization with relaxation and its application to support vector machines. J. Mach. Learn. Res. 22(288), 1–38 (2021)
Fele, F., Margellos, K.: Probably approximately correct Nash equilibrium learning. IEEE Trans. Autom. Control 66(9), 4238–4245 (2021)
Campi, M.C., Garatti, S.: The exact feasibility of randomized solutions of uncertain convex programs. SIAM J. Optim. 19(3), 1211–1230 (2008)
Luedtke, J., Ahmed, S.: A sample approximation approach for optimization with probabilistic constraints. SIAM J. Optim. 19(2), 674–699 (2008)
Alamo, T., Tempo, R., Camacho, E.F.: A randomized strategy for probabilistic solutions of uncertain feasibility and optimization problems. IEEE Trans. Autom. Control 54(11), 2545–2559 (2009)
Campi, M.C., Garatti, S.: A sampling-and-discarding approach to chance-constrained optimization: feasibility and optimality. J. Optim. Theory Appl. 148(2), 257–280 (2011)
Schildbach, G., Fagiano, L., Morari, M.: Randomized solutions to convex programs with multiple chance constraints. SIAM J. Optim. 23(4), 2479–2501 (2013)
Carè, A., Garatti, S., Campi, M.C.: FAST—fast algorithm for the scenario technique. Oper. Res. 62(3), 662–671 (2014)
Margellos, K., Goulart, P.J., Lygeros, J.: On the road between robust optimization and the scenario approach for chance constrained optimization problems. IEEE Trans. Autom. Control 59(8), 2258–2263 (2014)
Carè, A., Garatti, S., Campi, M.C.: Scenario min-max optimization and the risk of empirical costs. SIAM J. Optim. 25(4), 2061–2080 (2015)
Mohajerin Esfahani, P., Sutter, T., Lygeros, J.: Performance bounds for the scenario approach and an extension to a class of non-convex programs. IEEE Trans. Autom. Control 60(1), 46–58 (2015)
Zhang, X., Grammatico, S., Schildbach, G., Goulart, P.J., Lygeros, J.: On the sample size of random convex programs with structured dependence on the uncertainty. Automatica 60, 182–188 (2015)
Caré, A., Garatti, S., Campi, M.C.: A coverage theory for least squares. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 79(5), 1367–1389 (2017)
Campi, M.C., Garatti, S.: Wait-and-judge scenario optimization. Math. Program. 167(1), 155–189 (2018)
Mohajerin Esfahani, P., Sutter, T., Kuhn, D., Lygeros, J.: From infinite to finite programs: explicit error bounds with applications to approximate dynamic programming. SIAM J. Optim. 28(3), 1968–1998 (2018)
Picallo, M., Dörfler, F.: Sieving out unnecessary constraints in scenario optimization with an application to power systems. In: Proceedings of the 58th IEEE Conference on Decision and Control (CDC), pp. 6100–6105 (2019)
Assif, M., Chatterjee, D., Banavar, R.: Scenario approach for minmax optimization with emphasis on the nonconvex case: positive results and caveats. SIAM J. Optim. 30(2), 1119–1143 (2020)
Shang, C., You, F.: A posteriori probabilistic bounds of convex scenario programs with validation tests. IEEE Trans. Autom. Control 66(9), 4015–4028 (2021)
Garatti, S., Campi, M.C.: Risk and complexity in scenario optimization. Math. Program. 191(1), 243–279 (2022)
Romao, L., Margellos, K., Papachristodoulou, A.: On the exact feasibility of convex scenario programs with discarded constraints. IEEE Trans. Autom. Control 68(4), 1986–2001 (2023)
Falsone, A., Margellos, K., Zizzo, J., Prandini, M., Garatti, S.: On the sensitivity of linear resource sharing problems to the arrival of new agents. IEEE Trans. Autom. Control 68(1), 272–284 (2023)
Garatti, S., Carè, A., Campi, M.C.: Complexity is an effective observable to tune early stopping in scenario optimization. IEEE Trans. Autom. Control 68(2), 928–942 (2023)
Campi, M.C., Garatti, S., Ramponi, F.A.: A general scenario theory for nonconvex optimization and decision making. IEEE Trans. Autom. Control 63(12), 4067–4078 (2018)
Ramponi, F.A., Campi, M.C.: Expected shortfall: heuristics and certificates. Eur. J. Oper. Res. 267(3), 1003–1013 (2017)
Arici, G., Campi, M.C., Carè, A., Dalai, M., Ramponi, F.A.: A theory of the risk for empirical CVaR with application to portfolio selection. J. Syst. Sci. Complex. 34(5), 1879–1894 (2021)
Rudin, W.: Real and Complex Analysis. McGraw-Hill, Singapore (1987)
Rudin, W.: Functional Analysis. McGraw-Hill, New York (1991)
Anderson, E.J., Nash, P.: Linear Programming in Infinite-dimensional Spaces: Theory and Applications. Wiley, New York (1987)
Rudin, W.: Principle of Mathematical Analysis. McGraw-Hill, Singapore (1976)
Shiryaev, A.N.: Probability. Springer, New York (1996)
Funding
Open access funding provided by Politecnico di Milano within the CRUI-CARE Agreement. The research presented in this article has been partly supported by MUR under the PRIN 2022 project “The Scenario Approach for Control and Non-Convex Design” (project number D53D23001440006) and by FAIR (Future Artificial Intelligence Research) project, funded by the NextGenerationEU program within the PNRR-PE-AI scheme (M4C2, Investment 1.3, Line on Artificial Intelligence).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have no financial or non-financial interests that are directly or indirectly related to this work.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Garatti, S., Campi, M.C. Non-convex scenario optimization. Math. Program. (2024). https://doi.org/10.1007/s10107-024-02074-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10107-024-02074-3
Keywords
- Data-driven Optimization
- Scenario approach
- Non-convex optimization
- Probabilistic constraints
- Statistical learning



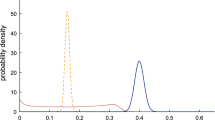









 ” on the right follows from the fact that
” on the right follows from the fact that