Estimation of uncertainty from duplicate measurements: new quantification procedure in the case of concentration-dependent precision

Abstract

In many analytical measurements, the analyte concentration in test samples can vary considerably. In such cases, the standard deviation (SD) quantifying measurement imprecision should be expressed as a function of the concentration, c: ${s}_{c}=\sqrt{{\mathrm{s}}_{0}^{2}+{ s}_{r}^{2}{c}^{2}}$, where s₀ represents a non-zero SD at zero concentration and s_r represents a near-constant relative SD at very high concentrations. In the case of SD repeatability, these parameters can be estimated from the differences of duplicated results measured on routine test samples. Datasets with a high number of duplicate results can be obtained within internal quality control. Most procedures recommended for this estimation are based on statistically demanding weighted regression.

This article proposes a statistically less demanding procedure. The s₀ and s_r parameters are estimated from selected subsets of absolute and relative differences of duplicates measured at low to medium concentrations and high to medium concentrations, respectively. The estimates are obtained by iterative calculations from the root mean square of the differences with a correction for the influence of the second parameter. This procedure was verified on Monte Carlo simulated datasets. The variability of the parameter estimates obtained by this proposed procedure may be similar or slightly worse than that of the estimates obtained by the best regression procedure, but better than the variability of the estimates obtained by other tested regression procedures. However, a selection of the duplicates from an inappropriate concentration range may cause a substantial increase in variability of the estimates obtained.

Introduction

The concept of uncertainty is now widely accepted in analytical chemistry. According to the international vocabulary of metrology [9], “a measurement result is generally expressed as a single measured quantity value and a measurement uncertainty”. The measurement uncertainty is reported as an estimate generalized for the entire class of specified samples analyzed by the relevant validated method. The uncertainty values in a given laboratory are estimated on the basis of information from internal method development and validation studies or internal quality control (IQC) results or information from other sources [5]. The standard uncertainty is expressed as standard deviation (SD). The reliability of the SD estimate improves with the number of results, n, from which the estimate has been obtained, more precisely with the degrees of freedom. For example, in the case of normally distributed results, n should be higher than 50 in order for the relative SD of the experimental standard deviation to fall below 10 %. A high number of results suitable for estimation can be relatively easily accumulated within IQC.

Note 1. This relative SD was calculated using the variance of SD estimate obtained from n values originated from a normal population with a standard deviation of σ. The variance is approximately $\frac{{\sigma^{2} }}{{2\left( {n - 1} \right)}}$ [15].

One way to perform internal quality control is by duplicate analysis of selected routine test samples. The duplicate test portions are randomly placed in the order of the test samples in the analytical run. The absolute values of the differences of duplicated results are plotted in control charts. The time series of differences provides information on the dispersion of measurement results under repeatability conditions. Variability caused by the nuances of the matrix of tested samples of the specified type is also captured [5, 14, 23].

The estimation of measurement uncertainty is often complicated by wide variability in the analyte concentration in the test samples. There may be a need to process the results of duplicate analyses of test samples of a given specification, whose analyte concentration varies within several orders of magnitude. See, e.g., papers evaluating the differences of duplicated results obtained in analyses of environmental samples [7, 18, 20], or in analyses in clinical laboratories [11], or in analyses of contaminants in food [5]. In such cases, it must be taken into account that the uncertainty, expressed as SD or its multiples, varies significantly with the level of the measurand. For the upper part of the concentration range, it usually makes sense to estimate a single relative uncertainty [5, 13]. At the same time, it may be appropriate to estimate a constant absolute uncertainty for the low concentrations [13]. However, for the entire range, from the limit of detection (LOD) to the maximum measured concentrations of the analyte, it is advisable to look for an algebraic relationship describing how SD or uncertainty varies with concentration. Thompson uses the term "uncertainty function" for this dependence [19, 24].

Estimating constant SDs

The difference, d_i, between a pair of concentrations, c_i1, c_i2, obtained by the duplicate measurement on the i-th sample

$${d}_{i}={c}_{i1}-{c}_{i2}$$

(1)

is equal to the difference between the random errors of those duplicated results. If all measured samples are similar, particularly in their matrix and analyte concentration, the random errors in the measurement can be supposed to have the same probability distribution. The SD of this distribution is estimated as a measure of measurement imprecision. This estimate, s, can be computed from a set of such d_i differences. Two procedures of estimation were used in this work.

First, it was the frequently used method with the sum of squared differences recommended in a number of publications, e.g. [2, 3, 8, 25]:

$$s=\sqrt{\frac{\sum {d}_{i}^{2}}{2n}}$$

(2)

The procedure was also given in articles by Hyslop and White [7] and by Thompson and Howarth [21].

Note 2. Equation (2) is the same as pooling the SD estimates obtained from n duplicate results (each estimate calculated from two results of a duplicate using the equation for sample standard deviation).

Secondly, the median estimation procedure was applied

$$s=1.0484\widetilde{\left|d\right|}$$

(3)

where $\widetilde{\left|d\right|}$ is the median of the absolute values of d_i. This function is not valid if the distribution of d_i values is not normal. Since the median is a robust statistic, the estimated s value is not unduly affected by outliers.

There are also other procedures suggested to estimate s from a set of d_i values [7, 21].

In this article, Eqs. (2) and (3) were used only in the calculations of estimates obtained by regression procedures. These estimates served mainly for comparison with those obtained by the proposed procedure. Equation (3) was applied because Thompson and his colleagues mainly used the median procedure in their papers [18, 20, 21, 22]. Equation (2) was applied because the equations for estimating by our proposed procedure are based on the sum of squared differences, just like Eq. (2). Equation (2) corresponds to the definition relation for standard deviation (see e.g. [3 or 4]), while the calculation according to Eq. (3) is only an alternative estimation procedure. The estimates obtained by Eq. (3) have therefore greater variability.

Note 3. Based on SD estimates from duplicate results generated by Monte Carlo at n = 20 and a number of estimates of 10 000, we found that the variance of SD estimates calculated according to Eq. (2) was approximately 0.025 times the chosen value of σ². This correspond to the relationship ${\sigma }^{2}/\left(2n\right)$ for this variance (see [15] p. 133]). The variance of SD estimates calculated by Eq. (3) was about 2.5 times greater.

Estimating constant RSDs

If the differences d_i were obtained by duplicate measurements of samples with an identical matrix but with different concentrations of the analyte, and if the concentration range of the measured samples was sufficiently distant from the LOD, the SD can usually be assumed to increase proportionally with the concentration. In this case, the proportionality constant represents the RSD characterizing the precision of the measurement. Again, its value can be estimated using Eqs. (2) and (3), but the differences d_i in these mathematical relationships must be replaced by relative differences, d_ri. These are the differences between the concentration values measured in duplicate divided by the concentration means [5, 7, 11, 17], ${\overline{c} }_{i}$:

$${\overline{c} }_{i}=\left({c}_{i1}+{c}_{i2}\right)/2$$

(4)

$${d}_{ri}={d}_{i}/{\overline{c} }_{i}$$

(5)

Continuous functions expressing the dependence of the SD on the concentration

If the relationship between the SD characterizing the measurement precision and the analyte concentration, c, is studied over a wide range of concentrations from levels close to the LOD to concentrations significantly higher, it should be taken into account that the SD value at very low concentrations cannot be zero and therefore the RSD cannot be constant at the bottom of the concentration range. Based on a literature study as well as statistical processing rich sets of duplicated analytical results Thompson [18] recommended two adequate mathematical models of the SD increasing with the analyte concentration, s_c:

$${s}_{c}={s}_{0}+{s}_{r}c$$

(6)

$${s}_{c}^{2}={s}_{0}^{2}+{s}_{r}^{2}{c}^{2}$$

(7)

Both equations had been previously published by Zitter and God [27]. They describe the dependence of SD on the concentration by a continuous function with two parameters. The parameter s₀ represents a non-zero SD at zero concentration and s_r represents a near-constant RSD at very high concentrations, the so-called asymptotic RSD. Equation (6) calculates the total standard deviation s_c as the sum of two individual standard deviations—the linear model; Eq. (7) calculates ${s}_{c}^{2}$, i.e., the total variance, as the sum of two individual variance components—the variance model. These relationships were also recommended by the Eurachem/CITAC guide [5] and Jiménez-Chacón and Alvarez-Prieto [10] to express changes in uncertainty with concentration; the authors of paper [10] based their recommendation on the processing of many sets of empirical analytical data.

Thompson stated in paper [18] that both models showed similar results, but the s_r estimates obtained by the variance model appeared to be closer to the true value. In particular, this model was theoretically more correct than the linear, since independent uncertainties should be combined as variances and not as standard deviations. On the other hand, the linear model was more user-friendly. In subsequent papers [19, 24], Thompson and his co-worker promoted only the variance model. This function was recommended as a general expression of the relationship between the standard uncertainty and the analyte concentration, which compactly specified the behavior of analytical systems, the so-called “uncertainty function”.

In the case of the variance model (Fig. 1), it can be seen that the plotted curve expressing the function s_c = f(c) can be divided into three parts [5]: (i) the range of very low concentrations where the curve can be approximated by the straight line ${s}_{c}={s}_{0}$, since ${s}_{0}^{2}\gg {s}_{r}^{2}{c}^{2}$; (ii) the range of very high concentrations where the curve can be approximated by the straight line ${s}_{c}={s}_{r}$ c, since ${s}_{0}^{2}\ll {s}_{r}^{2}{c}^{2}$; (iii) the range of intermediate concentrations where both variance components affect the total variance value because ${s}_{0}^{2}\approx {s}_{r}^{2}{c}^{2}$.

Fig. 1

Standard deviation, s_c, and relative standard deviation, s_c/c, as functions of the analyte concentration, c, in the case of variance model (see Eq. (7)) with s₀ = 0.15 cu and s_r = 0.07; c_E = s₀/ s_r = 2.14 cu

Estimating s ₀ and s _r from duplicated results

A procedure that processes duplicated results for estimating the parameters of a mathematical model expressing the relationship between SD and concentration for a wide concentration range starting at zero was proposed by Thomson and Howarth [21, 22]. These authors [6] tested the procedure robustness by processing data that they had simulated by Monte Carlo technique. This procedure was applied to process large sets of duplicated results obtained by routine analyses [18, 20].

The d_i differences and corresponding ${\overline{c} }_{i}$ means of all processed duplicates were arranged in increasing order of concentration. The sorted data were divided into subgroups with some equal number of the duplicated results, n > 10. In each subgroup, the SD was estimated using the median method (Eq. (3)) and the median or mean of the ${\overline{c} }_{i}$ values was also calculated. From the SD vs. concentration pairs obtained, the s₀ and s_r parameters of the investigated models of s_c = f(c) were estimated using regression procedures. As the uncertainty of SD estimates increased with concentration, i.e., due to heteroscedasticity of the data, weighted regression was necessary. In the case of the variance model, iterative nonlinear weighted regression was used [18, 20].

Jiménez-Chacón and Alvarez-Prieto [10] also estimated the parameters of the linear and variance models using various regression methods, but not from duplicated results. They estimated the parameters of the variance model by linear regression because they processed SD squares and concentration squares. Consequently, the parameters were also estimated as squares, i.e., ${s}_{0}^{2}$ and ${s}_{r}^{2}$. They found that the weighted least squares method, WLS, or robust regression method was appropriate for this task. Linear regression of SD squares vs concentration squares was also recommended in guide [5] but using the method of ordinary least squares, OLS.

It should be admitted that some of the estimation procedures used are quite complex, especially weighted regression, and may annoy those users who are not well-qualified statisticians.

The idea of a newly proposed estimating procedure

If the variance model with the parameters s₀ and s_r fits a large set of duplicated results covering a wide concentration range starting at zero, essentially each parameter can be estimated separately: the value of s₀ from a proportion of the results measured at very low concentrations, where ${s}_{c}\approx {s}_{0}$, and s_r from a proportion of the results measured at very high concentrations, where RSD ≈ s_r. However, it would be advisable to use all available results, including those in the range of intermediate concentrations (Fig. 1). At such concentrations, the values of the two terms on the right side of Eq. (7) are comparable, and therefore none of them can be omitted in these estimations. When estimating a given parameter, the effect of the interfering term could be eliminated by correction. However, to quantify it, it is necessary to know an estimate of the second parameter. This means that unbiased estimates of both parameters could be achieved by successive approximations—an iterative process.

A similar but much simpler procedure for estimating s₀ and s_r from duplicates over a wide concentration range has previously been recommended in Nordtest NT TR 537 [13]. The parameters s₀ and s_r are estimated from the duplicates for low and high concentrations, respectively, by Eq. (2), without any correction, i.e., assuming constant absolute and relative uncertainty. However, if the concentration range starts at zero and is sufficiently wide, this assumption is not satisfied for at least one parameter. This must cause a systematic overestimation of the parameter estimate which depends on several factors and may be unacceptably high and which is not indicated by anything (see below).

Derivation of equations for estimation of s ₀ and s _r and their application

Both parameters of the variance model (Eq. (7)) should be estimated from a set of n duplicated results that have been measured on a large set of samples with a similar matrix but with a wide concentration range starting at a level near LOD. First, it is necessary to calculate ${\overline{c} }_{i}$ mean concentrations (Eq. (4)), their reciprocals, $1/{\overline{c} }_{i}$, d_i differences (Eq. (1)) and d_ri relative differences (Eq. (5)) from the duplicated results. The obtained set of values of these four quantities shall be arranged in an increasing order of concentration. The estimates of s₀ and s_r should be calculated from the data measured at concentrations where ${s}_{0}^{2}$ and ${s}_{r}^{2}{c}^{2}$, respectively, represent the dominated or at least comparable variance component (Eq. (7)) compared to the second component. It means that the arranged set must be divided into two subsets, one suitable for estimating s₀ from the first n₀ data belonging to the lower concentrations and the other suitable for estimating s_r from the last n_r data belonging to the higher concentrations; both subsets may overlap.

From a given d_i difference an individual i-th estimate of ${s}_{c}^{2}$ can be calculated:

$${s}_{i}^{2}={d}_{i}^{2}/2$$

(8)

and then an individual i-th very unreliably estimate of either ${s}_{0}^{2}$ or ${s}_{r}^{2}$ could be obtained if an estimate of the second parameter was known:

$${s}_{0i}^{2}={s}_{i}^{2}-{s}_{r}^{2}{\overline{c} }_{i}^{2}=\frac{{d}_{i}^{2}}{2}-{s}_{r}^{2}{\overline{c} }_{i}^{2}$$

(9)

$$s_{{ri}}^{2} = \frac{{s_{{ci}}^{2} - s_{0}^{2} }}{{\bar{c}_{i}^{2} }} = \frac{{\left( {d_{i} /2} \right)^{2} }}{{\bar{c}_{i}^{2} }} - \frac{{s_{0}^{2} }}{{\bar{c}_{i}^{2} }} = \frac{{d_{{ri}}^{2} }}{2} - \frac{{s_{0}^{2} }}{{\bar{c}_{i}^{2} }}$$

(10)

The n₀ individual estimates of ${s}_{0i}^{2}$ or, respectively, n_r individual estimates of ${s}_{ri}^{2}$ can be pooled to obtain a more reliable estimate of ${s}_{0}^{2}$ or ${s}_{r}^{2}$:

$${s}_{0}^{2}=\frac{\sum {s}_{0i}^{2}}{{n}_{0}}=\frac{\sum {d}_{i}^{2}}{2{n}_{0}}-{s}_{r}^{2}\cdot \frac{\sum {\overline{c} }_{i}^{2}}{{n}_{0}}$$

(11)

$$s_{r}^{2} = \frac{{\sum s_{{ri}}^{2} }}{{n_{r} }} = \frac{{\sum d_{{ri}}^{2} }}{{2n_{r} }} - s_{0}^{2} \cdot \frac{{\sum \left( {1/\bar{c}_{i} } \right)^{2} }}{{n_{r} }}$$

(12)

The final equations to estimate s₀ and s_r are:

$${s}_{0}=\sqrt{\frac{\sum_{1}^{{n}_{0}}{d}_{i}^{2}}{2{n}_{0}}-{s}_{r}^{2}\cdot \frac{\sum_{1}^{{n}_{0}}{\overline{c} }_{i}^{2}}{{n}_{0}}}$$

(13)

$$s_{r} = \sqrt {\frac{{\mathop \sum \nolimits_{{n + 1 - n_{r} }}^{n} d_{{ri}}^{2} }}{{2n_{r} }} - s_{0}^{2} \cdot \frac{{\mathop \sum \nolimits_{{n + 1 - n_{r} }}^{n} \left( {1/\bar{c}_{i} } \right)^{2} }}{{n_{r} }}}$$

(14)

At the beginning of the calculations, no estimate of the parameters is known. To calculate an estimate, e.g., s_r according to Eq. (14), we need some rough estimate of s₀. Such an estimate can be calculated by Eq. (2). Then the estimations of s_r and s₀ can be repeated alternately according to Eqs. (14) and (13) until two consecutive approximations are almost the same.

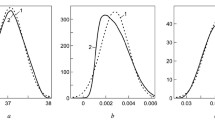
Figure 2, as an instructional example, shows the plots of the dependence of |d_i| and |d_ri| against concentration for a dataset used to estimate s₀ and s_r. The points used in both estimations are highlighted; the data and calculations, see Electronic Supplementary Material 2, ESM_2.xlsx, Sheet 5. From the obtained estimates, dependencies, √2s_c and √2s_c/c (i.e., standard deviations of d_i and d_ri) on concentration were calculated, which are shown in the plots. In the plots, the so-called equivalence concentration, c_E, is indicated as an important characteristic. It is the concentration at which both components of variance are equal, so ${c}_{\rm E}={s}_{0}/{s}_{r}$. Differences from ranges with concentrations lower and higher than c_E are suitable for estimating s₀ and s_r, respectively.

Fig. 2

Absolute values of differences, |d_i|, (a) and relative differences, |d_ri|, (b) of duplicates with respect to mean concentration,${\overline{c} }_{i}$; for the data, see Sheet 5 in ESM_2.xlsx; n₀ and n_r denote the number of points applied in estimating s₀ and s_r, respectively (green +); unused points (blue ×). The red curves display the concentration dependence of √2s_c and √2s_c/c; s_c was calculated from the estimated s_r and s₀ values; c_E denotes the equivalence concentration (▪)

The objectives of this paper

The main goals are:

• a) to verify the trueness of the parameter estimates obtained by the proposed procedure from pairs of large sets of duplicated results simulated in parallel by Monte Carlo technique with chosen values of s₀ and s_r, and with a wide concentration range and various types of probability distributions of concentration;

• b) to examine the trueness and precision of the parameter estimates obtained by the proposed procedure from repeatedly simulated sets of duplicates with a number accessible within IQC; simultaneously to estimate the parameters by regression procedures; to compare the estimates obtained by both approaches;

• c) on the basis of the results obtained, to specify the proposed procedure in order to reduce the subjectivity of decision-making in the choice of the duplicate differences intended for estimating s₀ and s_r.

Procedures and methods

Datasets of duplicated results

To verify the proposed procedure for estimating the parameters of the variance model, datasets of duplicated results were simulated using Monte Carlo method with these chosen parameter values: s₀ = 0.15 concentration unit, cu, and s_r = 0.07.

Note 4. The stated values of s₀ and s_r were not chosen fully at random; their choice was based on the estimates that had been obtained in processing a set of empirical data. This processing and the obtained results were not included in this theoretical work.

First, it was necessary to generate sets of true concentrations, μ_i, of measured samples with selected types of their distribution and selected numbers of values, n. The true concentrations could not be negative, the lowest values were to be located around the LOD, i.e., 3s₀ = 0.45 cu, and the highest values were to reach about 20 LOD, i.e., ca. 10 cu, or a bit higher, see Electronic Supplementary Material 1, ESM_1.pdf, Text S2.

The selected distributions were (the distribution parameters are given in brackets): uniform (a = 0, b = 10), normal (µ = 6, σ = 1.5), log-normal (µ = 0, σ = 0.7) and exponential (λ = 1/2.35). Further information on these distributions is provided in Table S1 and also in Fig. S1 (see ESM_1.pdf), on which their probability density functions, PDF, are plotted. For each type of distribution, two datasets of the true concentrations with n = 20 000 were simulated. Furthermore, for the uniform and also exponential distributions, 10 sets of true concentrations with n = 200 were simulated.

Using these simulated true concentrations sets, corresponding sets of duplicately measured concentrations c_i1 and c_i2 were generated. The duplicated results were obtained by adding random errors to the values μ_i

$${c}_{i1}= {\mu }_{i}+{\varepsilon }_{i1}+{\eta }_{i1}{\mu }_{i}$$

(15)

$${c}_{i2}= {\mu }_{i}+{\varepsilon }_{i2}+{\eta }_{i2}{\mu }_{i}$$

(16)

where ε_i1, ε_i2, and η_i1, η_i2 represent the random absolute and relative errors, respectively, of the i-th duplicate measurement. These errors were simulated as independent values drawn at random from two normal distributions with zero means and the chosen variances ${\mathrm{s}}_{0}^{2}$ for the absolute errors and ${s}_{r}^{2}$ for the relative errors. For each dataset, the means ${\overline{c} }_{i}$ and the differences d_i were computed from the pairs of c_i1 and c_i2 (Eqs. (1) and (4)).

In the case of the datasets with n = 20 000, where two sets were simulated for each type of the chosen probability distributions, it was possible to obtain two pairs of s₀ and s_r estimates for each distribution type. For the first series of the simulated sets of the true concentrations μ_i and means ${\overline{c} }_{i}$, some descriptive statistics were computed that characterized the individual types of the chosen concentration distributions; these statistics are summarized in Table S1 (see ESM_1.pdf). For the datasets with n = 200, it was possible to obtain 10 estimates of s₀ or s_r with the uniform and exponential concentration distributions.

The simulations of all datasets were performed by Microsoft Excel Professional version 2007. Other calculations were also made by this program, unless otherwise stated.

Estimating s ₀ and s _r by the proposed procedure

Processing all simulated datasets

First, the values of ${\overline{c} }_{i}$ (Eq. (4)), $1/{\overline{c} }_{i}$, d_i (Eq. (1)) and d_ri (Eq. (5)) were calculated from all duplicated results of the processed dataset. The obtained values were arranged in ascending order of ${\overline{c} }_{i}$. In the case of the datasets with n = 200, all negative values of ${\overline{c} }_{i}$ that appeared were replaced with a positive value much smaller than s₀, used 0.001 cu. There were only a few negative values individual sets, a maximum of 2 and 6 in the uniformly and exponentially distributed datasets, respectively.

Note 5. For the itself calculation, this substitution of negative values is not necessary. This was done because, when studying the data in the graphs, there were problems with negative values when using a logarithmic scale on the concentration axis.

Then the estimates of s₀ and s_r could be computed by Eqs. (13) and (14), but first it was necessary to choose appropriate values of n₀ and n_r, i.e., to divide each dataset into two subsets suitable for the estimations of s₀ and s_r (see above).

When deciding on this matter, it is recommended to approach each dataset individually, after examining the relevant plots of dependence of $\left|{d}_{i}\right|$ and $\left|{d}_{ri}\right|$ values on ${\overline{c} }_{i}$ (see Fig. 2 and calculation examples in Sheets 2 and 4 in ESM_2.xlsx). When processing the datasets simulated with n = 20 000, the number of points in the plot was too high, so the plots were confusing, incomprehensible, and therefore it was impossible to make decisions based on them. So, in almost all cases, the first choice was n₀ = n_r. Subsequently, other values of n₀ and n_r, either higher or lower, were tested to increase or decrease, respectively, the number of suitable values or the number of values unsuitable for estimation. The higher number of variants used indicates the difficulty of selecting suitable values of n₀ and n_r. Also, when processing datasets with n = 200, the individual plot approach was not used, since all 10 sets simulated with a given concentration distribution had to be processed by the same chosen variant of the procedure. With an individual approach, subjective decision-making in selecting differences for estimation would have influenced the variability of the estimates obtained. The first variants were selected according to the results found on the sets with n = 20 000. The variants were then adjusted to reduce the proportion of unsuitable differences included. However, in some case, deliberately higher proportions of differences not suitable for estimation were used.

The sequential estimations of s₀ and s_r started by calculating a rough s₀ estimate from n₀ differences according to Eq. (2), irrespective of whether the differences showed a concentration trend. For this rough estimation we omitted the correction term from Eq. (13). The estimation could also have started by calculating a rough s_r estimate. The first s_r estimate was then calculated according to Eq. (14) and the first s₀ estimate according to Eq. (13). This was followed by a sequence of alternate calculations of the s_r and s₀ estimates (Eqs. (14) and (13)). The estimating process was terminated when the difference between two successive estimates was practically negligible, i.e., < 0.5 % of the true value. In this paper, the estimates thus obtained are called final estimates. Due to the position in the estimate sequence, the rough, i.e., the uncorrected estimates of parameters are referred to as zeroth estimates. Sequential estimates can be seen in Table S2 in ESM_1.pdf or Sheets 3 and 5 in ESM_2.xlsx in the case of the datasets with n = 20 000 or n = 200, respectively.

In the case of datasets, with n = 20 000 with the exponential, log-normal, uniform, and normal distribution of concentrations, estimates were obtained by 1, 2, 3, and 4, respectively, variants of the proposed procedure. These variants differed in the chosen values of n₀ and n_r. The chosen subsets of the duplicates with n₀ and n_r values were formed by dividing the entire set of n differences without overlapping, so that there was a concentration boundary between these subsets The estimates of s₀ and s_r are summarized in Table S4 (see ESM_1.pdf), they are expressed in percentages of the true values of the parameters. The table shows the zeroth and final estimates obtained by the used variants from pairs of datasets simulated in parallel for each type of concentration distribution.

Table S3 in ESM_1.pdf shows for each pair of parallel estimates the mean, the difference, both statistics are given for the final and zeroth estimates. The table also shows the number of iterations needed to obtain the final estimates (without the zeroth step), boundary concentration and other statistics.

The datasets with n = 200 were also processed by several variants of the proposed procedure. The s₀ and s_r estimates obtained from the uniformly and exponentially distributed datasets are summarized in Tables S5 and S6 (see ESM_1.pdf), respectively. Statistics characterizing the sets of the estimates obtained by the variants used are given in Tables 1 and 2. These variants differed in the choice of the n₀ and n_r values. They were denoted by n₀/n_r or the concentration boundary, e.g., c = 2.6, between the non-overlapping subsets. The chosen variant was always followed when processing all ten datasets with the given distribution. The final estimates were usually obtained after three consecutive estimates of the pair s₀ and s_r, in worse cases up to five consecutive estimates were needed.

Table 1 Statistical characteristics of the sets of the final s₀ and s_r estimates obtained by different variants of the proposed procedure and regression procedures from the 10 datasets with 200 duplicates simulated with the uniform concentration distribution; the variants of proposed procedure are denoted by either border concentration c or by the ratio of the number of differences used to estimate s₀ and s_r, Mean of the parameter estimates, for s₀ expressed in cu; RME and RSD—relative mean error and relative standard deviation expressed in percentages of the true values; P-value—probability value of the t-test assessing the significance of the RME; V/V_R—ratio of the variance of an investigated estimate set, V, and the corresponding reference variance, V_R, i.e., the variance of the estimate set obtained by the RMS WLS procedure

Table 2 Statistical characteristics of the sets of the final s₀ and s_r estimates obtained by different variants of the proposed procedure and regression procedures from the 10 datasets with 200 duplicates simulated with the exponential concentration distribution; the variants of proposed procedure are denoted by the ratio of the number of differences used to estimate s₀ and s_r, Mean of the parameter estimates, for s₀ expressed in cu; RME and RSD – relative mean error and relative standard deviation expressed in percentages of the true values; P-value – probability value of the t-test assessing the significance of the RME; V/V_R—ratio of the variance of an investigated estimate set, V, and the corresponding reference variance, V_R, i.e., the variance of the estimate set obtained by the RMS WLS procedure

Objective approach to the processing of datasets

ESM_2.xlsx gives 2 examples of estimating s₀ and s_r where the subjectivity of decision-making was limited in the selection of subsets for estimating both parameters. This procedure using objective decision criteria, equivalence concentration and correction proportion, was applied for processing datasets 3 and 9, n = 200 with uniform and exponential distribution, respectively. These sets were chosen because when processed by the 100/100 and 100/140 variants, extremely underestimated estimates of s₀ and s_r, respectively, were obtained (see Tables S5 and S6 in ESM_1.pdf).

The estimation process starts by examining the plots of the dependence of $\left|{d}_{i}\right|$ and $\left|{d}_{ri}\right|$ values on ${\overline{c} }_{i}$ for the processed dataset. Arranging the points in these plots can show whether the variation model is appropriate for a given dataset at all, and it can also reveal potential outliers. At the beginning of the process, only these plots allow us to define those concentration ranges with differences suitable for estimating s₀ and s_r, i.e., choosing n₀ and n_r. Somewhere in the bend of the dependence of $\left|{d}_{i}\right|$ or $\left|{d}_{ri}\right|$ on concentration the equivalence concentration lies (see Fig. 2, c_E = 2.14 cu). The upper and lower concentration limits of the subsets of those differences suitable for estimating s₀ and s_r, respectively, should be above and below the equivalence concentration so that the two subsets overlap. Due to the large random dispersion of values plotted on the y-axis, it can be difficult to distinguish the beginning of the bend from random fluctuations. In addition, on the plots with $\left|{d}_{i}\right|,$ the bend is not very pronounced.

If we want to avoid looking for both concentration limits using plots alone, it is possible to find preliminary s₀ and s_r estimates in advance and calculate a preliminary estimate of c_E from them. For this estimation of s₀ and s_r, only those d_i and d_ri differences that are from concentration ranges where $\left|{d}_{i}\right|$ and $\left|{d}_{ri}\right|$ values appear to be trendless should be used. When processing a large dataset, it should be possible to select at least 10 to 20 differences from both the concentration range around LOD and the high concentration range. The preliminary estimates of s₀ and s_r shall be calculated by Eq. (2), i.e., without the correction term. From these, a preliminary estimate of c_E can be obtained. Slightly above and below c_E, it is then possible to choose the upper limit and lower limit of the concentration ranges with d_i and d_ri differences useable for estimating s₀ and s_r, respectively (see Sheets S3 and S5 in ESM_2.xlsx).

It should be emphasized that both these preliminary estimates and the zeroth estimates shall be calculated according to Eq. (2). In the former case, the use of this equation is fully justified, so the estimates obtained will be essentially unbiased. However, they could be estimated with a large random error, since a small number of differences have been used. In the latter case, the estimates calculated without correction will be greatly overestimated. Their variability may be low, since a higher number of differences have been used. The preliminary estimates can be advantageously used instead of the zeroth estimates at the beginning of sequential estimation of s₀ and s_r. Of course. when calculating the correction proportions, see below and Text S5 in ESM_1.pdf, only zeroth estimates must be used, not preliminary ones.

After selecting the n₀ and n_r values, a first attempt can be made to estimate s₀ and s_r using Eqs. (13) and (14) according to the proposed iterative procedure. If the estimates obtained are real numbers, i.e., the resulting values under the square root are not negative, it is possible to continue with subsequent checks. It is necessary to check that (i) the correction proportions are not too high—less than 50 % is recommended, (ii) the upper and lower concentration limits are, respectively, above and below the newly found c_E value.

A high correction proportion or even a negative value under the square root points out the inclusion of a large proportion of the differences unsuitable for estimating the parameter. For subsequent estimation, it is necessary to reduce the n₀ or n_r value. On the other hand, if the upper concentration limit for differences d_i or the lower concentration limit for differences the d_ri is not above or below the newly determined c_E, respectively, this means that not all suitable differences have been used in estimating the parameter. A low value of the correction proportion, e.g., less than 10%, also points to the same issue. The number of differences included in the calculation of the parameter should then be increased. It would also be advisable to increase the number of included differences if their number is significantly less than half of the total number of differences and the correction proportion is sufficiently below 50 %. Adjusting the number of differences included may be followed by another iterative estimation of s₀ and s_r with further review of the newly obtained estimates.

Estimating s ₀ and s _r by the regression procedures

The datasets with n = 200 were also processed by regression methods. The sets of ${\overline{c} }_{i}$ and |d_i| paired values, arranged in increasing order of concentration, were divided into 10 segments with 20 pairs. For each segment with 20 values of ${\overline{c} }_{i}$ and |d_i|, the mean concentration and SD were calculated. The SD values were calculated by two procedures: using the root mean squares of the differences (Eq. (2)), referred to as the RMS procedure, and using the median of |d_i| (Eq. (3)), referred to as the MAD procedure. In this way, for each simulated dataset, two tables with 10 pairs of concentration means and SDs were derived. From the squares of these two variables, the values of ${s}_{0}^{2}$ and ${s}_{r}^{2}$ of the variance model were estimated. Since a linear relationship was assumed between the squares of the mean concentrations and SDs, the linear regression could be used [10]. The estimations of the parameters were calculated by two regression procedures, firstly by OLS and secondly by WLS with weights 1/${s}_{c}^{4}$.

Note 6. The weight is inversely proportional to the variance of the dependent variable [16], i.e., to the variance of ${s}_{c}^{2}$, and directly proportional to the number of the differences used to the SD estimation, n_i. In the case of a variable normally distributed with standard deviation σ, the variance of the estimate σ² is equal to 2σ⁴/(n-1) or 2σ⁴(n-1)/n², see [1]. Consequently, the weighs are inversely proportional to ${s}_{c}^{4}$. The n_i values are the same for all segments, n_i = 20; this constant value does not influence the estimate values. In the OLS regression the n_i values are ignored. If they are also ignored in the WLS regression, a comparison of the precision of the two kinds of estimates will show the advantage of the WLS regression only with respect to the heteroscedasticity.

The ${s}_{c}^{4}$ values were calculated from the concentration means for each segment according to Eq. (7) with the values of ${s}_{0}^{2}$ and ${s}_{r}^{2}$ that had just been estimated. The first input values were the estimates of ${s}_{0}^{2}$ and ${s}_{r}^{2}$ calculated using OLS. The weighted regression, was calculated iteratively until the estimates expressed to 6 decimal places stopped changing. Using the regression procedures, four different parameter estimates were obtained for each simulated dataset with n = 200. The results obtained from the datasets distributed uniformly and exponentially are summarized in Tables S5 and S6 (see ESM_1.pdf), respectively; the statistics characterizing the sets of these estimates are given in Tables 1 and 2. The procedures and results obtained are labeled according to the combination of the SD calculation used and the regression method: RMS OLS, MAD OLS, RMS WLS and MAD WLS.

Statistical treatment of the estimates

Assessing the estimate trueness and precision

The quality of the s₀ and s_r estimates obtained by the above-mentioned procedures was assessed for their precision and trueness, the estimates computed from the tens of datasets with n = 200 and from the couples of datasets with n = 20 000 were investigated separately. The trueness was evaluated on the basis of the relative mean error, RME, as a measure of bias. The estimate of RME was computed as the deviation of the arithmetic mean of the set of estimates from the true parameter value; it was expressed in percentages of the true parameter value. At the same time, the statistical significance of the RME estimates was monitored. In the case of the estimates from the datasets with n = 20.000, the RME values were compared with the half-widths of the 95 % confidence intervals calculated by multiplying the differences between the two parallel estimates by a coefficient of 6.4 [3] (see Table S3 in ESM_1.pdf). In the case of the estimates from the datasets with n = 200, the t-test was applied. The results are given as the p-values of that test (see Tables 1 and 2).

The precision of the estimates was evaluated according to two measures of variability: RSD values and relative differences between two parallel estimates were used as these measures for the estimates obtained from the datasets with n = 200 and n = 20 000, respectively. Both quantities were expressed relatively to the true values of the parameters. The variances, V, of the sets of the estimates obtained from the datasets with n = 200 by the individual procedures or their variants were compared with the variances of the corresponding sets of the estimates obtained by the RMS WLS procedure, V_R. The variances of the RMS WLS procedure were taken as reference values because this procedure proved to be the best estimation procedure. The V/V_R ratio was used as a quantitative indicator (see Tables 1 and 2); it was not understood as an F-test; some of the stated sets were not distributed normally.

In order for the variants of the proposed procedure to be assessed, it was appropriate to considered not only the final s₀ and s_r estimates, but also the zeroth estimates – calculated without the correction. The values of the zeroth estimates obtained from the datasets with n = 20 000 are summarized in Table S4 (see ESM_1.pdf); the means and differences of all pairs of the parallel zeroth estimates are shown in Table S3 (see ESM_1.pdf). Table 3 summarizes statistics calculated from the two sets of the10 zeroth estimates of s₀ and s_r obtained from the datasets with n = 200 and with the uniform and exponential distribution. These are the relative means, RM_Z, and relative standard deviations, RSD_Z, of the sets of estimates, both quantities are expressed in percentages of the true parameter values; the ratios of the variances of the final and zeroth estimates, V_F/V_Z, are also given. The RM_Z value provides information about the overestimation of the zeroth estimate, i.e., information about the size of the correction needed. The V_F/V_Z ratio informs how the imprecision of the estimate increased due to the correction (it was again not understood as an F-test).

Table 3 Statistics of the sets of the zeroth estimates that were obtained by the used variants of the proposed procedure from the datasets simulated with n = 200; the variants are denoted by either border concentration c or by the ratio of the number of differences used to estimate s₀ and s_r, RM_Z and RSD_Z – relative mean and relative standard deviation of the zeroth estimates expressed in percentages of the true parameter values; ACP – average correction proportion in percentages of the sum of ${d}_{i}^{2}$ or ${d}_{ri}^{2}$; V_F/V_Z – ratio between the variances of the final and zeroth parameter estimates (the statistics for the final estimates see Tables 1 and 2)

Correction proportion from the sum of squared differences: its purpose and calculation

In Eqs. (13) and (14) for estimating s₀ and s_r there are two subtracted terms under the square root. The relative variability of the parameter estimated by first or second equation depends on the variability of these two terms, and also on the value of the difference between the two terms, actually on the ratio of their values. If the value of the correction term is small with respect to the value of the first term, i.e., the term with the sum of squared differences, the value of this difference will be significantly larger than if both terms have practically the same value. It means, in the second case, even if the two terms had little relative variability, the resulting estimate would have high relative variability. It follows that the inclusion of too large proportion of d_i or d_ri differences unsuitable for estimating a given parameter causes a higher level of variability in the final estimates of the parameters. This was documented by the estimates obtained from simulated datasets, see Text S5 in ESM_1.pdf. After obtaining an estimate of, e.g., s₀ from a given set of differences, it would therefore be appropriate to compare the values of both terms under the square root in Eq. (13) and assess whether it would not be appropriate to reduce the number of included differences from the range of higher concentrations and thus reduce the value of the correction term. This would reduce the relative variability of the estimate obtained, i.e., the probability of a large error in the estimate.

From Eqs. (11) and (12) it is possible to derive indicators comparing the values of the two terms, which are here called correction proportions, P_cor, from the sum of squares of the differences. These indicators can be calculated from the differences and mean concentrations of duplicates, as well as possibly from the final and zeroth estimates of the parameters, s₀ and s_r symbols are denoted by subscripts F and Z, respectively:

$${\text{In calculating }}s_{0} { }P_{{{\text{cor}}}} = \frac{{2s_{r}^{2} \sum \overline{c}_{i}^{2} }}{{\sum d_{i}^{2} { }}} = 1 - \frac{{s_{0F}^{2} }}{{s_{0Z}^{2} }}$$

(17)

$${\text{In calculating }}s_{r} P_{{{\text{cor}}}} = \frac{{2s_{0}^{2} \sum 1/\overline{c}_{i}^{2} }}{{\sum d_{ri}^{2} { }}} = 1 - \frac{{s_{rF}^{2} }}{{s_{rZ}^{2} }}$$

(18)

In text S5 in ESM_1.pdf, the correction proportions for estimates obtained from the simulated datasets are presented and discussed. The individual P_cor values for all estimates obtained from the datasets with n = 20 000 and the average correction proportions for the pairs of the parallel estimates are given in Tables S4 and S3 (see ESM_1.pdf), respectively. For the estimates from the 10 datasets with n = 200 and with the uniform and exponential distributions, the individual P_cor values are given in Tables S10 and S11 (see ESM_1.pdf) and the average correction proportions for the sets of 10 estimates obtained by a particular variant of the procedure are given in Table 3.

Other statistical procedures used

In one exponentially distributed dataset with n = 200, there was an extremely outlying d_i difference identified (dataset no. 2. plotted in Fig. 4c, d; its parameter estimates see Tab. S6 in ESM_1.pdf). The consequences of excluding this outlier were studied. Table 4 summarizes the differences between the estimates obtained by all the procedures investigated, with and without the outlier.

Table 4 Differences between the pairs of the s₀ and s_r estimates obtained by the investigated procedures from the dataset displayed in Fig. 4c, d when the estimates were calculated with and without the highlighted outlier; the differences are expressed in percentages of the true parameter values; a positive difference represents decreasing in the parameter estimate after excluding the outlier (the estimates with outlier included—see the results from dataset no. 2 in Table S6 in ESM_1.pdf)

Furthermore, the sets with tens of s₀ or s_r estimates, which were obtained using the different procedures from the datasets with n = 200, were checked on their homogeneity and normality. The relationships between some random variables were investigated using Spearman′s rank correlation coefficient. Information on these procedures is provided in Text S1.1 in ESM_1.pdf.

Results and their discussion

The estimates of s ₀ and s _r obtained from the datasets with n = 20 000

The text dealing with the full processing of results and their discussion has been included in ESM_1.pdf, see Text S3. The text is too extensive and most of the issues addressed in it, including the resulting conclusions, reappear when processing the results obtained on datasets with n = 200, see the next subchapter.

This subchapter summarizes the conclusions obtained from processing datasets simulated with the four types concentration distribution by variants of the proposed procedure.

The means calculated from the pairs of parameter estimates did not deviate significantly from the true values within the variability evaluated on the bases of the differences between these estimate pairs. The variability of estimates obtained in the cases of uniform, exponential, and log-normal distributions was acceptable, a few percent or tenths of percent of the true value. The variability of estimates in the case of processing sets with normal distribution was too high, about 10 % or even tens of percent. The high variability was related to the inclusion of a large number of differences less suitable or even unsuitable for estimating the parameter. In these cases, the zeroth, i.e., uncorrected, estimates were considerably higher than the final estimates obtained with the correction. An indicator that draws attention to the high variability of a given estimate, i.e., the high probability of a large random error of the estimate, may be the correction proportion see above and Text S5 in ESM_1.pdf. Of course, higher variability may also be due to the fact that a small number of differences, albeit suitable, were used in the estimation. This is the case where only hundreds of differences instead of thousands were used to estimate them. The high variability was then reflected not only in the final estimate, but also in the zeroth estimate.

Pairs of random errors of s₀ and s_r estimates obtained when processing all the simulated sets by different variants of the proposed procedure showed a negative correlation. In these iterative calculations, where the previous estimate of one parameter is used to correct in the estimation of the other parameter, a higher positive estimation error of one parameter causes a higher negative estimation error for the other parameter, and vice versa.

When processing a given dataset of duplicates, the possibility of including a sufficiently large proportion of differences suitable for estimating s₀ or s_r is determined by the concentration distribution of that set. So, for example, the datasets simulated with the chosen normal distribution had only 0,5 % of the differences suitable for estimating s₀. They did not provide an opportunity to obtain an estimate of this parameter with low variability. The datasets with the chosen log-normal distribution had a relatively low proportion of differences suitable for s_r estimation, 14 %. Datasets with these concentration distributions were not included in the subsequent study of datasets with n = 200.

The estimates of s ₀ and s _r obtained from the datasets with n = 200

This subchapter deals with the s₀ and s_r estimates obtained from the datasets of 200 duplicated results simulated 10 times with the uniform and exponential distribution of concentrations. Such large duplicate datasets can be considered achievable within IQC. The estimates were obtained by the chosen variants of the proposed procedure being verified as well as by four variants of the regression procedure, for comparison. The procedures used were compared mainly on the basis of the variability of the estimates obtained.

Checking homogeneity and normality of the estimate sets

First, the sets of the s₀ and s_r estimates were investigated for their skewness, kurtosis and normality, and the presence of outliers. A complete evaluation is given in ESM_1.pdf (see Text S4, Fig. S2 and Tables S7 and S8). The inner and outer fences in the box plots identified outliers only in the s₀ estimate sets, especially when the estimates were obtained by the RMS OLS procedure. Among the estimate sets obtained by the proposed procedure, outliers were found only in the set obtained by the variant 100/100 from uniformly distributed datasets: minimum—extreme outlier and 2nd minimum—mild outlier. No outlier was identified in the s_r estimates sets. The Grubbs tests identified outliers essentially in accordance with the fences. In the case of the s₀ estimate sets obtained by the variant 100/100 from the uniformly distributed datasets and by the RMS OLS procedure from the uniformly as well as the exponentially distributed datasets, significant coefficients of skewness and kurtosis were identified. Among all the estimate sets investigated; the normality test identified only two sets violating the normality assumptions. Both sets were obtained by the proposed procedure: the s₀ estimate sets obtained by variants c = 2.6 and 100/100 from the uniformly distributed datasets. Only in the second case of estimates, the departures from normality were also identified by the previous tests. The study showed that it can be assumed that most of the monitored sets of estimates obtained by the proposed procedure and procedures RMS WLS and MAD WLS are distributed normally or very similarly.

It should be noted that a prerequisite for using the F-test is the normality of the tested sets. When using the t-test, due to the central limit theorem, this test can be used even for the average of values with a non-normal distribution if their number is high enough.

The estimates obtained by the proposed procedure

From the datasets distributed uniformly, the parameter estimates were obtained by four variants of the proposed procedure. These variants differed in the chosen n₀ and n_r values. First, the datasets were divided into two non-overlapping subsets according to concentration boundaries in two ways. These following two boundaries were selected: ${\overline{c} }_{i}$ equal to 2.6 cu and 4 cu. The average n₀ and n_r values were 53 and 147, respectively, in the former case and 83 and 117 in the latter case. Table 1 shows that at 2.6 cu and 4 cu, the RSD values for the s₀ estimates were 21 % and 11 %, respectively, and for the s_r estimates 5.1 % and 8.4 %. In the third variant, two overlapping subsets were selected with n₀ = 85 and n_r = 150. It was assumed that these higher numbers of processed d_i differences could provide lower variability in estimates of both parameters at the same time. However, the RSD values obtained were somewhat worse than expected: 16 % for s₀ and 7.3 % for s_r. As a matter of interest, the variant with n₀ = n_r = 100 was tried. As expected, the RSD value of the s₀ estimates achieved in this case was excessively high: 30 %.

Only 21 % of all d_i differences in the datasets processed were from the concentration range where s₀² > ${s}_{r}^{2}{c}^{2}$. For the variants marked c = 2.6, c = 4, 85/150 and 100/100, the s₀ estimates were computed from d_i differences in concentration ranges where the ${s}_{r}^{2}{c}^{2}$ component was up to 1.5, 3.5, 4 and 5.5 times higher than s₀² and the average correction proportions represented 37.3 %, 56.5 %, 58.8 % a 63.2 %, respectively (see Table 3). In the first case, this meant that all the differences applied were suitable for estimating s₀. This corresponds to a low overestimation of the mean of the zeroth estimates, the RM_Z amounts to only 114 % (see Table 3). Despite this, the RSD value of the final estimates was relatively high, 21 %. However, this must have been mainly due to the higher variability of the sum of ${d}_{i}^{2}$, not due to a high correction, since the RSD value for the zeroth estimates was already high, 17 %. It is true that the number of differences processed was the lowest, the average of n₀ was equal to 53. However, this does not seem to justify such a high variability of the zeroth estimates. In the other three cases, a certain proportion of differences less suitable or even inappropriate was always used. The estimates obtained by the 100/100 variant, i.e., the variant with the highest proportion of inappropriate differences, had the highest mean of the zeroth estimates, 164 %, and the highest correction proportion. This correction was associated with a high increase in variability (see the highest V_F/V_Z ratio, 4.8, Table 3) and the set of the final estimates had the highest RSD value (Tables 1). This high variability in the estimates was due to the two outlying minima, one of which was an extreme outlier (see above); the s₀ estimates were 21.8 % and 70.8 % of the true value (see Fig. S2 and Table S5 in ESM_1.pdf). The distribution of this set was identified as non-normal by all tests used. When the extreme minimum was excluded from the set, the RSD value dropped to 17.5 %, a value comparable to the values for the sets obtained by the other variants.

When estimating the s_r values, all d_ri differences used were from concentration ranges where ${s}_{r}^{2}{c}^{2}$ > s₀²; the RSD values for the sets of these estimates did not exceed 9% (see Table 1). The means of the zeroth estimates of s_r were only moderately overestimated, < 8 %, the average correction proportions were low, maximum 15.2 %, and the V_F/V_Z ratios were low, < 2 % (see Table 3).

The RME values, as indicators of the estimate bias, were more favorable for the s_r estimates, the absolute values of RME < 1.9 %, than for the s₀ estimates, the RME values from -4.7 % to -9 %; no value was significant (see the p-values in Table 1).

In the case of the datasets distributed exponentially, the results were also obtained by four variants of the proposed procedure. Values of n₀ and n_r equal to 100 were chosen as the first variant, because this division was successfully used when processing the large sets distributed exponentially (see Text S3.2 and Table S3 in ESM_1.pdf). The RSD value obtained for the s₀ estimates was 8.2 %, which was better than the RSD values for the estimates from the uniformly distributed datasets. However, the variability in the s_r estimates, RSD = 11.0 %, was worse than the variability of the estimates from the uniformly distributed sets (compare Tables 1 and 2). The n_r value was therefore increased to 120, but the variability of the s_r estimates did not improve, RSD = 12.2 %. Further changes of the n₀ and n_r values were made, the increase in the n_r value caused a deterioration in the s_r variability: with n₀ = 110, n_r = 90 and n₀ = 100, n_r = 140 the RSD values were 10.6 % and 17.0 %, respectively. The RSD values for the s₀ estimates remained almost the same: 8.6 %; and 8.0 %. In this context, it should be emphasized that three of the four variants used differed in the n_r values but not in n₀, n₀ = 100. This meant that these three variants repeatedly computed the s₀ estimates from exactly the same subsets of d_i differences and ${\overline{c} }_{i}$ values; the calculations of these estimates differed only in the values of the s_r estimate in Eq. (14).

In the datasets simulated with the exponential distribution, 60 % of d_i differences were from the concentration range where s₀² > ${s}_{r}^{2}{c}^{2}$. This meant that when n₀ was chosen equal to 100 or 110, only suitable differences were used to estimate s_0. The overestimation of the means of zeroth estimates was low, ≤ 10 %, so the average correction proportions were small, < 20 %, and the correction practically did not change the variability of the estimates, the V_F/V_Z ratios were approximately 1 (see Table 3). On the other hand, with the chosen n_r values equal to 100, 120 and 140, a certain proportion of the differences used in the s_r estimations always came from the concentration range where s₀² > ${s}_{r}^{2}{c}^{2}$ and the s₀² component was up to 1.7 times, 3.2 times and 6.5 times larger, respectively. In the second and third cases, the average correction proportions were 47.0 % and 58.3 %, respectively, (see Table 3), i.e., differences less suitable or even unsuitable for estimating s_r accounted for a substantial part of all d_ri differences included in the calculation. The estimate set obtained by the 100/140 variant, i.e., with the highest correction proportion, had the highest variability of the final estimates (see Table 2, RSD = 17 %, or the box plot in Fig. S2d in ESM_1.pdf). This set contains the most outlying value, the minimum, of all s_r estimate sets and this set is also the most skewed; both these phenomena are not significant (see Table S8 in ESM_1.pdf). This set also has the highest V_F/V_Z ratio, 2.8 (see Table 3).

For the parameter estimate sets obtained by the proposed procedure, the RME values were low. The highest absolute RME values were below 1.4 % and 3.8 % for s₀ and s_r, respectively; the p-values of the t-tests did not indicate statistical significance of the RME values (see Table 2).

The evaluation of the s₀ and s_r estimates obtained by the different variants of the proposed procedure from the datasets with uniform and exponential distribution confirmed that the higher included proportion of differences that are less suitable and unsuitable for estimating the parameter leads to a higher variability in the estimates obtained. A positive correlation was proved between the correction proportion and the RSD of estimates. Furthermore, it was proved that due to the large variability of the individual values of the correction proportion, its high overestimation or, on the contrary, underestimation will result in a large negative or positive error in the parameter estimation, respectively. These issues are documented in detail and discussed in ESM_1.pdf (see Text S5 and Tables S9, S10 and S11). Thus, when estimating parameters, a high value of the correction proportion indicates the inclusion of a large proportion of differences unsuitable for estimation as well as the risk of a large negative estimate error.

The estimates obtained by the regression procedure

The sets of s₀ and s_r estimates from the datasets with the uniform and exponential distribution were also obtained by the four variants of the regression procedure. These estimates were mainly used for a comparison with those obtained by the proposed procedure.

No RME value of these estimate sets differed statistically significantly from zero (see the p-values of the t-test in Tables 1 and 2). However, as in the previous assessments (se subchapter 3.2.2), the variability of the estimates was a more important assessing factor than their bias. The results presented unequivocally show that of the four regression procedures used, the RMS WLS procedure provided the best estimates. The s₀ and s_r estimate sets obtained by this procedure from both types of datasets had acceptable RME values. A worse RME value, -2.7 %, was found for the s₀ estimate set from the uniformly distributed datasets. The RSD values show that the RMS WLS procedure estimated the parameters with lower variability than the other regression procedures (see Tables 1 and 2 and Fig. S2 in ESM_1.pdf). The highest RSD value of the sets obtained by this procedure, 15.8 %, was again found for the s₀ estimates from the uniformly distributed datasets.

When the s₀ and s_r estimates were calculated using the MAD WLS procedure, the indicators evaluating their quality turned out to be substantially worse. This was rather surprising because the random measurement errors were simulated with a normal distribution (see above) and the MAD estimation of SD was proposed just for this type of distribution. The RSD values were worse in all four cases and the RME values were worse in three cases, except for the above-mentioned case of the s₀ estimates obtained from the uniformly distributed datasets.

Using the OLS method, the quality of the estimates obtained was even worse. For example, the RSD values for the s₀ estimates increased to several tens of percentage, especially in the case of the uniformly distributed datasets. The parameter estimates obtained by the MAD OLS procedure from this type of datasets had the highest RSD values, 76 % and 20 % for s₀ and s_r, respectively.

Based on the RSD values of the estimate sets obtained by the regression methods tested, the best estimates were provided by the RMS WLS procedure, then the MAD WLS, and finally the RMS OLS and MAD OLS procedures. A similar assessment of the regression procedures was obtained on the basis of the results of the t-tests evaluating the statistical significance of the s₀² and ${s}_{r}^{2}$ estimates (see Text S6 and Table S12 in ESM_1.pdf).

The plots of $\left|{{\varvec{d}}}_{{\varvec{i}}}\right|$ or $\left|{{\varvec{d}}}_{{\varvec{r}}{\varvec{i}}}\right|$ against ${\overline{{\varvec{c}}} }_{{\varvec{i}}}$

Figure 3 shows several examples of these plots for the datasets with the uniformly distributed concentrations. Figure 3a, b depict the plots with the $\left|{d}_{i}\right|$ and $\left|{d}_{ri}\right|$ values for a representative dataset. Based on the s₀ and s_r estimates in Table S5 (ESM_1.pdf), dataset no. 5 was unequivocally selected as representative. The curves were calculated from the estimates obtained by the RMS WLS procedure and the proposed procedure (variant c = 4). Both curves are nearly identical to the curve calculated from the true values. The following plot (see Fig. 3c) displays the values for a dataset where, in the range with concentrations less than 3 cu, the $\left|{d}_{i}\right|$ values have lower variability than the values in the reference plot in Fig. 3a. This absence of higher $\left|{d}_{i}\right|$ values could explain why the s₀ estimates obtained by the variants of the proposed procedure as well as by the RMS WLS procedure are underestimated (see the estimates from dataset no. 6 in Table S5 in ESM_1.pdf). Similarly, the plot in Fig. 3d shows an absence of high $\left|{d}_{ri}\right|$ values at concentrations above 7 cu in comparison with the reference plot in Fig. 3b. All s_r estimates obtained from this dataset are underestimated (see the estimates from dataset no. 10 in Table S5 in ESM_1.pdf). These two examples show that deviations of the estimates from the true parameter values can also be caused by random changes in the variability of the simulated duplicate concentrations.

Fig. 3

Plots of the absolute differences, |d_i|, and absolute relative differences, |d_ri|, of the duplicates against the mean concentration,${\overline{c} }_{i}$, (blue ×) for the uniformly distributed datasets a and b no. 5; c no. 6; and d no. 10 (the s₀ and s_r estimates obtained from these datasets see Table S5 in ESM_1.pdf). The three curves depicted in the plots express the dependences between the standard deviations of the d_i and d_ri values and the concentration; these standard differences equal √2s_c and √2s_c/c, respectively; s_c was calculated by Eq. (7) substituting for s₀ and s_r: (black □) true values; (green ○) estimates obtained by the RMS WLS procedure; (red ∆) estimates obtained by proposed procedure—variant c = 4

Figure 4a, b depict the plots for a representative example selected from the datasets exponentially distributed, see the estimates obtained from dataset no. 8 in Table S6 in ESM_1.pdf. The proposed estimates were calculated using the 100/100 variant. A comparison of the plots in Figs. 3a and 4a reveals differences between the point arrangements in the case of the datasets distributed uniformly and exponentially. The points for the exponentially distributed datasets are mainly cumulated in the range with lower concentration values (ca. c < 4 cu). Thus, the number of d_i differences suitable for estimating s₀ is higher than in the case of the uniformly distributed datasets, while the number of d_ri differences suitable for estimating of s_r is lower. This might explain the lower variability of the s₀ estimates obtained from the exponentially distributed datasets than from the datasets distributed uniformly, which applies to the estimates calculated by all procedures, and also the higher variability of the s_r estimates from the exponentially distributed datasets, this only applies to the estimates calculated by the variants of the proposed procedure (see Tables 1 and 2).

Fig. 4

Plots of the absolute differences, |d_i|, and absolute relative differences, |d_ri|, of the duplicates against the mean concentration,${\overline{c} }_{i}$, (blue ×) for the exponentially distributed datasets a and b no. 8; c and d no. 2 (the s₀ and s_r estimates obtained from these datasets see Table S6 in ESM_1.pdf); (blue ●) outlier. The three curves depicted in the plots express the dependences between the standard deviations of the d_i and d_ri values and the concentration; these standard differences equal √2s_c and √2s_c/c, respectively; s_c, was calculated by Eq. (7) substituting for s₀ and s_r: (black □) true values; (green ○) estimates obtained by the RMS WLS procedure; (red ∆) estimates obtained by proposed procedure—variant 100/100

Figure 4c depicts a plot for a dataset with the exponential distribution, where there is a point that appears to be an outlier—the point with the highest concentration and the highest $\left|{d}_{i}\right|$ value. However, the plot in Fig. 4d shows that the corresponding $\left|{d}_{ri}\right|$ value does not look extremely high compared to the other $\left|{d}_{ri}\right|$ values from the concentration range with nearly constant RSD. These plots depicts dataset no. 2. The estimates obtained from it are given in Table S6 in ESM_1.pdf. It is interesting to compare the parameter estimates calculated by the investigated procedures from this dataset with and without this critical point (see Table 4).

When a regression procedure based on the RMS estimation was used the above-mentioned d_i difference caused an overestimation of the s_c estimate for the segment with the highest concentrations. Thus, the resulting s_r estimate was also overestimated, especially in the case of the OLS regression. After excluding the critical point, the s_r estimates obtained by the procedures RMS OLS and RMS WLS improved considerably; they decreased from 125 % to 93 % and 109 % to 98 % of the true value, respectively. Moreover, in the case of the RMS OLS procedure, the substantial reduction in the s_r estimate was associated with an enormous improvement in the s₀ estimate, from 33 % to 92 %. The new s₀ estimate was significant as opposed to the original (see Table S12 in ESM_1.pdf). Since the MAD method provides robust estimates, after that exclusion, the s_r estimates obtained by the MAD OLS and MAD WLS procedures changed only slightly, they increased by 4 % and 1 %, respectively. The s_r estimates obtained by the four variants of the proposed procedure were acceptable both before and after the exclusion. After the exclusion, the estimates decreased by less than 2.5 % of the true value. This suggests that the proposed procedure was robust against such a type of d_i outliers since the d_ri values were processed, while the RMS WLS procedure proved to be less robust in this case, even though it generally gave better parameter estimates.

Comparing the estimates obtained by the newly proposed and regression procedures

The s₀ or s_r estimate sets obtained by the proposed and regression procedures from the datasets simulated with the uniform and exponential concentration distributions were compared according to variability. Tables 1 and 2 show that the RSD values of the s₀ and s_r estimates obtained by the RMS WLS procedure, the best regression procedure, are either as good as or better than the RSD values of the estimates obtained by the variants of the proposed procedure (see also the box plots on Fig. S2 in ESM_1.pdf). At the same time, the RMS WLS procedure has been shown to provide such estimates reliably, while in the case of the proposed procedure there is a risk of unsuitable choice of n₀ or n_r values, which will cause an unnecessary increase in the estimate variability. Only in the case of s_r estimates from the exponentially distributed datasets, the estimates obtained by all variants of the proposed procedure had substantially higher variability than those obtained by the RMS WLS procedure. The lowest RSD value of the s_r estimates achieved by the variants of the proposed procedure was about 11 %, the variants 100/90 and 100/100, while in the case of the RMS WLS procedure, the RSD value was only about 6 %.

In some cases, the variances of sets of the s₀ and s_r estimates obtained by variants of the proposed procedure were much greater than the variances of the estimates obtained by the RMS WLS procedure, e.g., more than three times (see Tables 1 and 2). However, a value of the V/V_R ratio greater than 4.03, which is the critical value for a two-sided F-test at α = 0.05, was found only once, for the s_r estimate set obtained by the variant 100/140 from the exponentially distributed datasets. Its value was 7.8 (see Table 2). In this calculation, the average correction proportion was 58.3 % (see Table 3). At the limit of significance was the V/V_R ratio for the s_r estimates obtained by the variant 100/120, its value was 4.0. For s₀ estimates, the highest V/V_R ratio, 3.7, was found for the set obtained by the variant 100/100 from the uniformly distributed datasets (see Table 1). In this calculation, the average correction proportion was the largest, 63.2 % (see Table3). This set of estimates was non-normally distributed and had two outlying minima (see Fig. S2a and Table S7 in ESM_1.pdf).

The parameter estimates obtained by regression procedures other than the RMS WLS procedure had generally higher variability than those obtained by the variants of the proposed procedure (see Tables 1 and 2 and Fig. S2 in ESM_1.pdf). Only in the case of s_r estimates obtained from the exponentially distributed datasets, the RSD values of the estimates obtained by both procedures were mostly comparable. However, the estimate sets obtained by the variants, where extremely high proportions of differences unsuitable for estimation were intentionally included, had higher RSD values than those obtained using the MAD WLS procedure. These were the two sets of estimates calculated with the maximum average correction proportions mentioned above, i.e., the estimates of s_r and s₀ from the exponential and uniform concentration distribution by the 100/140 and 100/100 variants, respectively.

The parameter estimate sets obtained by the different variants of estimating procedures were also compared by Spearman′s correlation coefficients (see Tables S14 and S15 in ESM_1.pdf). Cases were found where two series of the s₀ or s_r estimates obtained from a given set of simulated datasets by two compared procedures correlated significantly positively, the critical value was 0.65 [26]. Of course, such a correlation coefficient may occur if two compared series of estimates were obtained by similar procedures, e.g., by two variants of the proposed procedure or by the RMS WLS and RMS OLS procedures. As the main objective of this paper was to evaluate the proposed procedure, particular attention was paid to significant correlation coefficients related to the pairs of estimates obtained by a variant of the proposed procedure and the RMS WLS procedure, as the best of the tested procedures.

When studying the uniformly distributed datasets, significant correlations were found between the estimates obtained by the RMS WLS procedure and the proposed procedure for the following estimate sets: the s_r estimates computed by all four variants of the proposed procedure, the correlation coefficients were from 0.71 to 0.88, and also the s₀ estimates computed by the variant c = 2.6, the coefficient was 0.84. These estimates were calculated only from differences suitable for estimating the parameter in question. Table 3 shows that the values of the average correction proportions for these estimate sets were low: for the s_r estimate sets the maximum value was 15.2 % and for the set of s₀ estimates the value was 37.3 %. The remaining sets of s₀ estimates with insignificant correlation coefficients, their values from − 0.02 to − 0.31, were calculated from differences with a high proportion of values less suitable or unsuitable for estimating—the average correction proportions for the estimations were from 56.5 % to 63.2 %.

In the case of the exponentially distributed datasets, all sets of s₀ estimates obtained by the proposed and the RMS WLS procedure were significantly correlated, with coefficients ranging from 0.71 to 0.79. Again, these estimates were calculated only from suitable differences, the average correction proportions for these sets of estimates being less than 20 %. The s_r estimate sets obtained by the proposed procedure variants did not correlate with those obtained by the RMS WLS procedure—the coefficient values ranged from 0.19 to 0.45. The variability of these s_r estimates was higher than that obtained by the RMS WLS procedure, the V/V_R ratio was greater than 3. For the 100/120 and 100/140 variants, V/V_R was 4 and 7.8, respectively, and the average correction proportion was also high, at 47.0 % and in particular 58.3 %. However, the average correction proportion values for the 110/90 and 100/100 variants were acceptable, 30.3 % and 35.9 %, respectively.

Significant correlations between the sets of estimates obtained by the RMS WLS procedure and the proposed procedure were only found when the average correction proportions were low. However, this condition may not be sufficient. In cases where the proposed procedure and the RMS WLS procedure provided the sets of correlated estimates which additionally had comparable variances and insignificant biases, it can be stated that both procedures provided very similar estimates.

The results found showed that the proposed procedure can provide as good estimates as the RMS WLS procedure. However, the RMS WLS procedure provides parameter estimates with a low level of variability reliably, whereas in the case of the proposed procedure, a particularly improper choice of n₀ or n_r may result in unnecessarily high variability in the estimates obtained. Moreover, the results indicated that an appropriate selection of differences does not in itself guarantee the achievement of the variability of estimates ensured by the RMS WLS procedure. The results showed, at least for the estimation of s_r, that with a low proportion of differences suitable for estimating, the estimates obtained by the proposed procedure may not have as low variability as those obtained by the RMS WLS procedure. The RMS WLS procedure and regression procedures generally provide the single best estimate of the pair s₀ and s_r achievable by the chosen procedure from the processed dataset, while the proposed procedure allows the user to obtain one of the possible pairs of s₀ and s_r estimates that match well the dataset. To estimate a given parameter, they use all differences in the processed dataset, not just a certain part of them. On the other hand, the RMS WLS calculation is statistically more complex than the calculation of the proposed procedure, especially the iterative calculation of WLS regression, and places great demands on the user's knowledge. In the range with very high concentrations, the proposed procedure proved to be more robust against outlying d_i differences than the RMS WLS procedure.

Comparison of the simple Nordtest procedure [13] and the proposed procedure

As mentioned above (see Introduction), the simple procedure proposed in Nordest NT TR 537 [13] has a major defect. If the duplicate differences are distributed from zero over a wide range of concentrations, the variance of absolute or relative differences, or both, is not constant, although the estimation according to Eq. (2) requires a constant variance of the differences processed. This leads to an overestimation of estimate of the corresponding parameter. It can be documented, e.g., by the so-called zero estimates, which were calculated from the sets with n = 20 000 (see Text S3.2 and Table S3 in ESM_1.pdf). These were estimated in the same way as prescribed by the simple procedure—from two non-overlapping parts of the entire set of differences. Table 5 shows these estimates for different concentration distributions of differences and for differently chosen boundary concentrations between the subsets of differences at the calculation of s₀ and s_r. No results for the normal distribution are included in the table, since all differences in this set can legitimately be used to estimate s_r according to Eq. (2), except for a few outliers. It can be seen that one of the s₀ and s_r estimates tends to be somewhat more overestimated, the values for the higher estimates from the pairs are in the range of 125 % to 167 % of the true values. The minimum was an estimate of s₀ from the uniformly distributed set, the maximum was an estimate of s_r from the exponentially distributed set, in both cases the sets were divided in the same way, n₀ = n_r = 10 000. It is obvious that the overestimation is influenced by the distribution of the concentration of the measured duplicates—exceptionally unfavorably if the duplicates are accumulated mainly in the middle part of the concentration range. The overestimation also depends on the choice of subsets, which is given by a somewhat subjective decision of the solver. Thus, it may be the case that the relative errors of both parameters will be comparable. Such an overestimation will be smaller than when the overestimation is mainly reflected in the estimation of one parameter. Thus, with a favorable concentration distribution of differences and at the same time with a random selection of suitable subsets of differences, the estimation errors could be relatively small and possibly acceptable in terms of the use of estimated parameters. Otherwise, the error of the estimate may well be unacceptably high. However, the simple procedure does not address the question of the magnitude of the estimation error caused by the unjustified use of Eq. (2).

Table 5 Zeroth s₀ and s_r estimates obtained by different variants of the proposed procedure from pairs of datasets with 20 000 simulated duplicate differences (d_i—absolute, d_ri—relative) with selected concentration distributions; Estimation—the mean of two estimates calculated by ${s}_{0}=\sqrt{\sum {d}_{i}^{2}/2{n}_{0}}$ and ${s}_{r}=\sqrt{\sum {d}_{ri}^{2}/2{n}_{r}}$, expressed in percentages of the true parameter values; n₀ and n_r—numbers of duplicates for calculation of s₀ and s_r; c – concentration at the boundary between the subsets of the n₀ and n_r duplicate differences

The proposed procedure starts in the same way as the simple procedure above. However, the selected subsets of differences should overlap in order to make the most of the information provided by the dataset. Equation (2) is used only for the preliminary estimate and for the zeroth estimate of one parameter at the beginning of the iterative calculation. Iterative calculations with correction achieve steady values of unbiased estimates. In addition, the procedure is complicated by the selection of subsets of differences, as appropriate as possible for estimating the parameters, in order to obtain estimates with low variability. The price of non-biased estimates is the complexity of the procedure.

Conclusions

Equation (7) may form the basis for expressing the measurement uncertainty of an analyte in a specific type of samples by a given method over the entire measurement range by a single uncertainty function. A new procedure has been proposed to estimate the parameters of this equation for repeatability SD from duplicated results measured on routine samples of a specific matrix and with a wide concentration range starting around LOD. The proposed procedure does not use regression, so it could serve as an alternative to previously proposed regression procedures, which, due to the heteroscedasticity of the processed data, require the use of statistically demanding weighted regression. The s₀ and s_r parameters are estimated from selected subsets of differences from the lower and respectively upper parts of the concentration range of the entire processed data set. Equations (13) and (14) derived for estimating individual parameters are based on the root mean square of the absolute and relative differences with a subtracted correction term eliminating the influence of the second parameter. By using sequential iterative steps, unbiased estimates are achieved. Comparison of estimates obtained by different procedures from Monte Carlo simulated datasets showed that the proposed procedure can provide estimates with variability comparable to those obtained by the best tested regression procedure. However, this is conditioned by (i) an appropriate choice of the difference subsets, which is dependent on the user's decision, but also (ii) by a sufficiently large proportion of differences suitable for estimation of each parameter in the processed data set, which is given by the concentration distribution of the processed data set. The appropriateness of the choice of these subsets can be assessed according to the correction proportion and equivalence concentration, but these can only be determined from parameter estimates. Therefore, after the first attempt at estimation of the parameters, it may turn out that it is necessary to repeat the estimation with a better choice. From this point of view, the proposed procedure is complicated, it requires a heuristic approach of the user.

The proposed procedure was tested only on Monte Carlo simulated datasets. Its real possibilities will become apparent if it is applied to empirical datasets. The procedure should therefore be further tested by processing empirical datasets with duplicated results. The estimates thus obtained should be compared with those obtained by the RMS WLS procedure.