Dynamic response of a graded cracked half-plane with embedded sources

Abstract

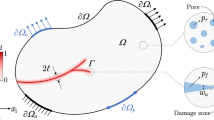
In this work, an efficient boundary integral equation method is developed based on an analytically derived Green’s function for the graded half-plane with buried point sources. The problem under investigation is the dynamic field which develops in an elastic, isotropic, and graded half-plane with an embedded, inclined Griffith crack as it is enveloped by time-harmonic waves radiating from buried monopoles and dipoles. Following numerical verification, the methodology is used to perform a series of parametric studies to investigate the dependence of the displacement and stress concentration wave fields on the following key parameters: (a) the material gradient which exhibits a quadratic type of variation with depth; (b) the type and characteristics of the source; (c) the position and geometrical configuration of the embedded geological crack, and (d) the dynamic interaction phenomena between the propagating wave in the material, the crack, and the free surface of the geological continuum.

Appendix: Half-plane monopole and dipole Green’s functions

For completeness purposes, we present here the derivation of Green’s functions in the half-plane with point force and moment sources.

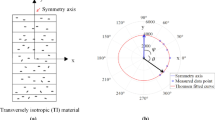
Recall that the inhomogeneity function is $h(x)=(ax_2+1)^2$, $a\le 0$, defined in $R^2_-=\{x_2<0\}$, the stiffness tensor is $C_{jkpq}(x)=\mu (x)(\delta _{jk}\delta _{pq}+\delta _{jp}\delta _{kq}+\delta _{jq}\delta _{kp})$, $\mu (x)=\mu _0h(x)$, Poisson’s ratio is fixed at a value of $\nu =0.25$, and density $\rho (x)=\rho _0h(x)$

We now expand the earlier derivation given in [73] for Green’s function of a half-plane with a point force source. Consider the dynamic equilibrium equation and boundary conditions in the half-plane $R^2_-$. We denote Green’s function as $G=G^0(x,\xi ,\omega )$ if $e_0=1, e_s=0$ and $G=G^s(x,\xi ,\omega )$ if $e_0=0, e_s=1, s=1,2$ satisfying the equation

$$\begin{aligned} L^{a}(G)=(C_{ikpq}(x)G_{ip,q})_{,j}+\rho (x)\omega ^2G_{jk} =-(e_0\delta (x-\xi )+e_s\delta _{,s}(x-\xi ))\varepsilon _{jk}, \end{aligned}$$

(A.1)

and boundary conditions with

$$\begin{aligned} T^{a}_{ij}(G)= C_{i2pq}G_{jp,q}=0, \hbox { on } x_2=0, \ \ G\rightarrow 0, \hbox { for } x_2\rightarrow -\infty . \end{aligned}$$

(A.2)

In the above, $x, \xi \in R^2_{-}$, $\varepsilon =\varepsilon _{jk}$ is the unit tensor, $\delta$ is Dirac’s delta function, and Green’s tensor G satisfies the Sommerfeld’s radiation condition along lines parallel to $\{x_2=0\}$. The Green’s function with upper index 0 corresponds to the case of a point force source, while with upper index s corresponds the case of sources of the dipoles type.

For example, in reference to the case of Eq. (2), $u_i=G^0_{ij}f_{0j}+G^s_{ij}f_{sj}$.

Let the matrix-valued function u be a solution of Eq. (A.1), i.e.,

$$\begin{aligned} L^{a}(u)=-(e_)\delta (x-\xi )+e_s\delta _{,s}(x-\xi ))\varepsilon , \ \ \hbox {for} \ \ x, \xi \in R^2_{-}, \end{aligned}$$

while w is a smooth matrix-valued function introduced so that the traction-free surface boundary condition can be satisfied,

$$\begin{aligned}&L^{a}(w)=0, \ \ \hbox {for} \ \ x, \xi \in R^2_{-}, \end{aligned}$$

(A.3)

$$\begin{aligned}&T^{a}(w)=-T^{a}(u), \ \ \hbox {on} \ \ x_2=0. \end{aligned}$$

(A.4)

Here, superscript a in the operators corresponds to the degree of inhomogeneity. The problem under consideration is linear, so by using superposition principle, the complete Green’s function is simply $G=u+w$.

The fundamental solution u can be expressed as in [74] in the following form in order to transform the partial differential equation (A.1) with variable coefficients to one with constant coefficients,

$$\begin{aligned} u(x,\xi ,\omega )=h^{-1/2}(\xi )U(x,\xi ,\omega )h^{-1/2}(x). \end{aligned}$$

(A.5)

Here U is a solution for the corresponding homogeneous material case

$$\begin{aligned} L^0(U)=-(\mathbf {f_0}\delta (x-\xi )+\mathbf {f_s}\delta _{,s}(x-\xi ))\varepsilon , \ \ \hbox {with}\ \ x,\xi \in R^2. \end{aligned}$$

The matrix-valued function $U=e_0U^0+e_1U^1+e_2U^2$ in $R^2$ corresponding to the homogeneous case is available in [75] as

$$\begin{aligned}&U^0_{jk}=\frac{i}{4\mu _0} \left[ \delta _{jk}H^{(1)}_0(k_2r)\right. \left. +\frac{1}{k^2_2}\partial ^2_{jk}\left( H^{(1)}_0(k_2r)-H^{(1)}_0(k_1r)\right) \right] , \hbox { if } \mathbf {f_0}=1, \mathbf {f_s}=0, \end{aligned}$$

(A.6)

$$\begin{aligned}&U^s_{jk,s}=\frac{i}{4\mu _0} \left[ \delta _{jk}H^{(1)}_0(k_2r)\right. \left. +\frac{1}{k^2_2}\partial ^2_{jk}\left( H^{(1)}_0(k_2r)-H^{(1)}_0(k_1r)\right) \right] _{,s}, \hbox { if } \mathbf {f_0}=0, \mathbf {f_s}=1. \end{aligned}$$

(A.7)

In the above, $r=\sqrt{(x_1-\xi _1)^2+(x_2-\xi _2)^2}$, $k_1=\sqrt{\frac{\rho _0}{3\mu _0}}\omega$, and $k_2=\sqrt{\frac{\rho _0}{\mu _0}}\omega$ are wavenumbers, and $H^{(1)}_0(z)$ is the Bessel function of third kind (or Hankel function), zero order (see [76]).

A general solution $w^s$ of Eq. (A.3) is in the form

$$\begin{aligned} w^s(x,\xi ,\omega )=h^{-1/2}(x)W^s(x,\xi ,\omega ),\quad s=0,1,2, \end{aligned}$$

where $W^s=\{W^s_{jk}\}$ is defined by the inverse Fourier transform with respect to $\phi$ as

$$\begin{aligned} W^s_{jk}=\frac{1}{2\pi }\int _RK^s_{jk}e^{i\phi x_1}\hbox {d}\phi , \end{aligned}$$

with a kernel function $K^s_{jk}$ depending on $e^{\beta _j x_2}$, $\phi , \omega , a$, and parameter $\beta _j=\sqrt{\phi ^2-k_j^2}$.

The kernel matrix function ${K^s_{jk}}$ is found in the form $K={K^s_{jk}}=\sum ^2_{m=1}C^{ks}_m\nu ^m_je^{\beta _mx_2}$, and constants $C^{ks}_m$ will be determined from the boundary condition (A.4), where

$$\begin{aligned} \nu ^1=\left( \begin{array}{l}\phi \\ -i\beta _1\end{array}\right) , \nu ^2=\left( \begin{array}{l} i\beta _2 \\ \phi \end{array}\right) . \end{aligned}$$

The traction field corresponding to the displacement field $w^s$ on $x_2=0$ is

$$\begin{aligned} \begin{array}{l} T^s_{1k}=\frac{1}{2\pi }\displaystyle \int \limits _R\mu _0\left[ \phi (-a+2\beta _1)C^{ks}_1\right. \left. +i(-a\beta _2+2\phi ^2-k^2_2)C^{ks}_2\right] e^{i\phi x_1}\hbox {d}\phi , \\ \\ T^s_{2k}=\frac{1}{2\pi }\displaystyle \int \limits _R\mu _0\left[ i(3a\beta _1-2\phi ^2+k^2_2)C^{ks}_1\right. \left. +\phi (-3a+2\beta _2)C^{ks}_2\right] e^{i\phi x_1}\hbox {d}\phi . \end{array} \end{aligned}$$

(A.8)

Employing Eqs. (A.5)–(A.7) for u and for U, respectively, we obtain

$$\begin{aligned} T^a_{jk}(u^s)=\frac{i}{2\pi }\int _RD^s_{jk}e^{i\phi x_1}\hbox {d}\phi , \end{aligned}$$

(A.9)

and the matrix components $D^s_{jk}$ are given as follows:

$$\begin{aligned}&\begin{array}{l} D^0_{11}=\frac{h^{-1/2}(\xi )}{2k^2_2} \left[ \left( -a\beta _2-2\phi ^2+k^2_2\right) e^{\xi _2\beta _2}+\phi ^2\left( \frac{a}{\beta _1}+2\right) e^{\xi _2\beta _1}\right] , \\ D^0_{21}=\frac{i\phi h^{-1/2}(\xi )}{2k^2_2\beta _1}\left[ \beta _1\left( -3a-2\beta _2\right) e^{\xi _2\beta _2}\right. \left. +\left( 3a\beta _1+2\phi ^2-k^2_2\right) e^{\xi _2\beta _1}\right] , \\ D^0_{12}=\frac{i\phi h^{-1/2}(\xi )}{2k^2_2\beta _2}\left[ \left( -a\beta _2-2\phi ^2+k^2_2\right) e^{\xi _2\beta _2}\right. \left. +\beta _2\left( a+2\beta _1\right) e^{\xi _2\beta _1}\right] , \\ D^0_{22}=\frac{i\phi h^{-1/2}(\xi )}{2k^2_2}\left[ \phi ^2\left( \frac{3a}{\beta _2}+2\right) e^{\xi _2\beta _2}+\left( -3a\beta _1-2\phi ^2+k^2_2\right) e^{\xi _2\beta _1}\right] . \end{array} \\&\begin{array}{l} \displaystyle D^1_{11}=\frac{i\phi h^{-1/2}(\xi )}{2k^2_2} \left[ \left( \frac{-a}{\beta _2}(k_2^2-\phi ^2)+k^2_2-2\phi ^2\right) e^{\xi _2\beta _2}\right. \left. +\left( \frac{-a\phi ^2}{\beta _1}+2\phi ^2\right) e^{\xi _2\beta _1}\right] , \\ D^1_{21}=\frac{-\phi ^2 h^{-1/2}(\xi )}{2k^2_2}\left[ \left( -3a+3\beta _2+i\phi \right) e^{\xi _2\beta _2}+\left( 3a-i\phi -3\beta _1\right) e^{\xi _2\beta _1}\right] , \\ D^1_{12}=\frac{-\phi ^2 h^{-1/2}(\xi )}{2k^2_2}\left[ \left( -a+2\beta _2+\frac{k^2_2}{\beta _2}\right) e^{\xi _2\beta _2}+\left( a-2\beta _1\right) e^{\xi _2\beta _1}\right] , \\ D^1_{22}=\frac{i\phi h^{-1/2}(\xi )}{2k^2_2}\left[ \left( \frac{-3ak_2^2}{\beta _2}-3a\beta _2-\phi ^2+3(k_2^2+\beta _2^2)\right) e^{\xi _2\beta _2}+\left( 3a\beta _1-3\beta _1^2+\phi ^2\right) e^{\xi _2\beta _1}\right] . \end{array} \\&\begin{array}{l} D^2_{11}=\frac{ h^{-1/2}(\xi )}{2k^2_2} \left[ \left( -a(k_2^2-\phi ^2)+\beta _2(k_2^2-2\phi ^2)\right) e^{\xi _2\beta _2} +\left( -\phi ^2(a-2\beta _1)\right) e^{\xi _2\beta _1}\right] , \\ D^2_{21}=\frac{i\phi h^{-1/2}(\xi )}{2k^2_2}\left[ \left( -3a\beta _2-3\beta ^2_2+k_2^2-\phi ^2\right) e^{\xi _2\beta _2} +\left( 3\beta ^2_1+3a\beta _1-\phi ^2\right) e^{\xi _2\beta _1}\right] , \\ D^2_{12}=\frac{i\phi h^{-1/2}(\xi )}{2k^2_2}\left[ \left( -a\beta _2+k_2^2+2\beta _2^2\right) e^{\xi _2\beta _2} +\left( a\beta _1-2\beta _1^2\right) e^{\xi _2\beta _1}\right] , \\ D^2_{22}=\frac{h^{-1/2}(\xi )}{2k^2_2}\left[ \left( -3a(k_2^2+\beta ^2_2+\beta _2(3k_2^2-\phi ^2) +3\beta _2^3)\right) e^{\xi _2\beta _2}+\left( 3a\beta _1-3\beta _1^3+\phi ^2\beta _1\right) e^{\xi _2\beta _1}\right] . \end{array} \end{aligned}$$

Using the boundary condition (A.4) we can find $C^{ks}_m=\Delta ^{a}_{mk}/\Delta ^{a}$, where the sub-determinants $\Delta ^{a}_{mk}$ are given as:

$$\begin{aligned} \begin{array}{l} \Delta ^{as}_{11}=\left| \begin{array}{ll} -D^s_{11} &{} i\mu _0(-a\beta _2+2\phi ^2-k^2_2) \\ -D^s_{21} &{} \mu _0\phi (-3a+2\beta _2) \end{array}\right| ,\ \ \Delta ^{as}_{21}=\left| \begin{array}{ll} \mu _0\phi (-a+2\beta _1) &{} -D^s_{11} \\ i\mu _0(3a\beta _1-2\phi ^2+k^2_2) &{} -D^s_{21} \end{array}\right| , \\ \\ \Delta ^{as}_{12}=\left| \begin{array}{ll} \mu _0\phi (-a+2\beta _1) &{} -D^s_{12} \\ i\mu _0(3a\beta _1-2\phi ^2+k^2_2) &{} -D^s_{22} \end{array}\right| , \ \ \Delta ^{as}_{22}=\left| \begin{array}{ll} -D^s_{12} &{} i\mu _0(-a\beta _2+2\phi ^2-k^2_2) \\ -D^s_{22} &{} \mu _0\phi (-3a+2\beta _2) \end{array}\right| \end{array} \end{aligned}$$

and

$$\begin{aligned} \Delta ^{a}=\frac{\mu ^2_0}{4\pi ^2}\left| \begin{array}{ll} \phi (-a+2\beta _1) &{} i(-a\beta _2+2\phi ^2-k^2_2) \\ i(3a\beta _1-2\phi ^2+k^2_2) &{} \phi (-3a+2\beta _2) \end{array}\right| . \end{aligned}$$

Note that by setting the inhomogeneity parameter $a=0$ we recover the homogeneous half-plane Green’s function for $e_0=1, e_s=0$ given in [77].

For the case $e_0=0, e_s\ne 0$ there are no published results even for the homogeneous case $a=0$.