Simplified models for determining the response of an isotropic, continuously nonhomogeneous half-plane to a moving distributed line load

Abstract

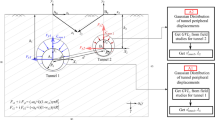
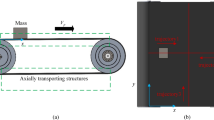
The problem of a vertical distributed line load moving with constant speed on the surface of an isotropic half-plane with shear modulus varying continuously with depth has been very recently solved analytically by the authors in an exact manner. The same problem is solved here also analytically under various reasonably simplified assumptions that effectively reduce the coupled system of the two governing partial differential equations of motion into an uncoupled one. The assumptions are zero horizontal displacement, or zero horizontal normal stress, or zero horizontal normal stress plus zero derivative of the horizontal displacement with respect to the vertical coordinate. The method of complex Fourier series involving the horizontal coordinate and the time is used to reduce the uncoupled two partial differential equations to ordinary ones with variable coefficients, which are solved by the method of Frobenius in closed form. Comparison of the approximate solutions corresponding to the aforementioned simplified assumptions against the ‘exact’ solution by means of parametric studies serves to assess the degree of their accuracy for both cases of the shear modulus increasing and decreasing with depth.

Appendices

Appendix A

First simplified model results for the case of shear modulus decreasing with depth:

$$\begin{aligned}&\zeta =\varXi e^{-az},\quad \varXi =1-\left( {{G_\infty }/{G_0 }} \right) ,\quad {G_0 }/{G_\infty }=\delta >1,\nonumber \\&G\left( \zeta \right) =G_\infty \left( {1+\delta \zeta } \right) . \end{aligned}$$

(A.1)

Governing equations of motion

$$\begin{aligned}&\left( {1-k_v } \right) \left( {1+\delta \zeta } \right) W_n^{\prime } +k_v \delta W_n =0, \end{aligned}$$

(A.2)

$$\begin{aligned}&\zeta ^{2}\left( {1+\delta \zeta } \right) W_n^{{\prime }{\prime }} +\zeta \left( {1+2\delta \zeta } \right) W_n^{\prime } +k_v \left[ {\theta -\beta \left( {1+\delta \zeta } \right) } \right] W_n =0. \end{aligned}$$

(A.3)

Boundary conditions

$$\begin{aligned}&\left[ {-\left( {1+\delta \zeta } \right) \zeta \,W_n^{\prime } } \right] _{\zeta =\varXi } =-\frac{F_n k_v }{aG_\infty }, \end{aligned}$$

(A.4)

$$\begin{aligned}&\left[ {W_n } \right] _{\zeta =\varXi } =0. \end{aligned}$$

(A.5)

Solution of (A.3) satisfying (A.4):

$$\begin{aligned}&W_n \left( \zeta \right) ={A}\sum \limits _{r=0}^\infty a_r \zeta ^{r+m}, \end{aligned}$$

(A.6)

$$\begin{aligned}&m=\sqrt{k_v \left( {\beta -\theta } \right) },\,\,\,a_0 =1, \end{aligned}$$

(A.7)

$$\begin{aligned}&\left[ {\left( {r+m} \right) \left( {r+m-1} \right) +\left( {r+m} \right) +k_v \left( {\theta -\beta } \right) } \right] a_r =-\delta \left[ \left( {r+m-1} \right) \left( {r+m-2} \right) \nonumber \right. \\&\quad \left. +2\left( {r+m-1} \right) -k_v \beta \right] a_{r-1}, \end{aligned}$$

(A.8)

$$\begin{aligned}&A=-\frac{F_n k_v }{aG_\infty \left( {1+\delta \varXi } \right) \varXi \mathop \sum \nolimits _{r=0}^\infty \left( {r+m} \right) \,a_r \varXi ^{r+m-1}}, \end{aligned}$$

(A.9)

$$\begin{aligned}&\varSigma _{zz}^n =-\left( {1/{k_v }} \right) aG_\infty \left( {1+\delta \zeta } \right) \zeta W_n^{\prime }. \end{aligned}$$

(A.10)

Equations (A.2) and (A.5) are not satisfied, while condition (22)$_{1}$ is satisfied since $u=0$ everywhere.

Appendix B

Second simplified model results for the case of shear modulus decreasing with depth:

$$\begin{aligned}&\zeta =\varXi e^{-az},\quad \varXi =1-\left( {{G_\infty }/{G_0 }} \right) ,\quad {G_0 }/{G_\infty }=\delta >1, \nonumber \\&G\left( \zeta \right) =G_\infty \left( {1+\delta \zeta } \right) . \end{aligned}$$

(B.1)

Governing equations of motion:

$$\begin{aligned}&\left( {1+\delta \zeta } \right) \zeta ^{2}\,U_n^{{\prime }{\prime }} +\zeta \left( {1+2\delta \zeta } \right) \,U_n^{\prime } +\left[ {\frac{\beta \left( {1+\delta \zeta } \right) }{1-2k_v }+\theta } \right] U_n +i\gamma \delta \zeta W_n =0, \end{aligned}$$

(B.2)

$$\begin{aligned}&\left( {1+\delta \zeta } \right) \zeta ^{2}\left( {3-2k_v } \right) \,W_n^{{\prime }{\prime }} +\left[ {\left( {1+\delta \zeta } \right) \left( {3-2\,k_v } \right) \zeta +4\left( {1-k_v } \right) \delta \zeta ^{2}} \right] \,W_n^{\prime } +\left( {\theta -\beta -\delta \beta \zeta } \right) W_n =0.\nonumber \\ \end{aligned}$$

(B.3)

Boundary conditions:

$$\begin{aligned}&-4G_\infty \left( {1-k_v } \right) \left[ {\left( {1+\delta \zeta } \right) \alpha \zeta W_n^{\prime } } \right] _{\zeta =\varXi } =-F_n, \end{aligned}$$

(B.4)

$$\begin{aligned}&\left[ {\zeta \,U_n^{\prime } +i\gamma W_n } \right] _{\zeta =\varXi } =0. \end{aligned}$$

(B.5)

Solution of (B.3) satisfying (B.4):

$$\begin{aligned}&W_n \left( \zeta \right) =A\sum \limits _{r=0}^\infty a_r \zeta ^{r+m}, \end{aligned}$$

(B.6)

$$\begin{aligned}&m=\sqrt{\frac{\beta -\theta }{3-2k_v }},\quad a_0 =1, \end{aligned}$$

(B.7)

$$\begin{aligned}&\left[ {\left( {3-2k_v } \right) \left( {r+m} \right) \left( {r+m-1} \right) +\left( {3-2k_v } \right) \left( {r+m} \right) +\left( {\theta -\beta } \right) } \right] a_r \nonumber \\&\quad =-\delta \left[ {\left( {3-2k_v } \right) \left( {r+m-1} \right) \left( {r+m-2} \right) +\left( {7-6k_v } \right) \left( {r+m-1} \right) -\beta } \right] \,a_{r-1}, \end{aligned}$$

(B.8)

$$\begin{aligned}&A=\frac{F_n }{a\,G_\infty \left( {1-k_v } \right) \left[ {4\left( {1+\delta \varXi } \right) \varXi } \right] \mathop \sum \nolimits _{r=0}^\infty \left( {r+m} \right) \,a_r \varXi ^{r+m-1}}, \end{aligned}$$

(B.9)

$$\begin{aligned}&\varSigma _{zz}^n =-4a\left( {1-k_v } \right) G_\infty \zeta \left( {1+\delta \zeta } \right) W_n^{\prime }. \end{aligned}$$

(B.10)

Equations (B.2) and hence (22)$_{1}$ are satisfied as in the increasing shear modulus with depth case. However, Eq. (B.5) may or may not be satisfied.

Appendix C

Third simplified model results for the case of shear modulus decreasing with depth:

$$\begin{aligned}&\zeta =\varXi e^{-az},\quad \varXi =1-\left( {{G_\infty }/{G_0 }} \right) ,\quad {G_0 }/{G_\infty }=\delta >1, \nonumber \\&G\left( \zeta \right) =G_\infty \left( {1+\delta \zeta } \right) . \end{aligned}$$

(C.1)

Governing equations of motion:

$$\begin{aligned}&i\gamma \delta \zeta \left( {1-2k_v } \right) W_n +\left[ {\beta \left( {1+\delta \zeta } \right) +\left( {1-2k_v } \right) \theta } \right] U_n =0, \end{aligned}$$

(C.2)

$$\begin{aligned}&2\left( {1+\delta \zeta } \right) \zeta ^{2}W_n^{{\prime }{\prime }} +2\zeta \left( {1+2\delta \zeta } \right) W_n^{\prime } +\frac{1}{2\left( {1-k_v } \right) }\left[ {\theta -\beta \left( {1+\delta \zeta } \right) } \right] W_n =0. \end{aligned}$$

(C.3)

Boundary conditions:

$$\begin{aligned}&-4G_\infty a\left( {1-k_v } \right) \left[ {\left( {1+\delta \zeta } \right) \zeta \,W_n^{\prime } } \right] _{\zeta =\varXi } =-F_n, \end{aligned}$$

(C.4)

$$\begin{aligned}&\left[ {W_n } \right] _{\zeta =\varXi } =0. \end{aligned}$$

(C.5)

Solution of (C.3) satisfying (C.4):

$$\begin{aligned}&W_n \left( \zeta \right) ={A}\sum \limits _{r=0}^\infty a_r \zeta ^{r+m}, \end{aligned}$$

(C.6)

$$\begin{aligned}&m=\frac{1}{2}\sqrt{\frac{\beta -\theta }{1-k_v }},\,\,a_0 =1, \end{aligned}$$

(C.7)

$$\begin{aligned}&\left[ {2\left( {r+m} \right) \left( {r+m-1} \right) +2\left( {r+m} \right) +\frac{1}{2\left( {1-k_v } \right) }\left( {\theta -\beta } \right) } \right] a_r \nonumber \\&\quad =-\delta \left[ {2\left( {r+m-1} \right) \left( {r+m-2} \right) +4\left( {r+m-1} \right) -\frac{1}{2\left( {1-k_v } \right) }\beta } \right] a_{r-1}, \end{aligned}$$

(C.8)

$$\begin{aligned}&A=\frac{F_n }{aG_\infty \left( {1-k_v } \right) 4\left( {1+\delta \varXi } \right) \varXi \mathop \sum \nolimits _{r=0}^\infty \left( {r+m} \right) \,a_r \varXi ^{r+m-1}}, \end{aligned}$$

(C.9)

$$\begin{aligned}&\varSigma _{zz}^n =-4a\left( {1-k_v } \right) G_\infty \zeta \left( {1+\delta \zeta } \right) W_n^{\prime }. \end{aligned}$$

(C.10)

Equation (C.2) and hence (22)$_{1}$ are satisfied as in the increasing shear modulus with depth case. However, Eq. (C.5) is not satisfied.