1 Introduction

Although the Saint-Venant’s torsion of cylindrical bars is a classical one in the field of elasticity, there has recently been growing interest in the context of non-homogeneous, anisotropic and piezoelectric barssee [1,2,3,4,5,6,7,8,9,10]. It must be mentioned that several papers deal also with the problem of uniform torsion of non-homogeneous and/or anisotropic bars such as [11,12,13,14,15,16,17,18,19,20,21].

Application of piezoelectric materials and structures has been increasing recently. Sensors and actuators are examples of active components made of piezoelectric materials which are used widely in smart structures. These structural components are often subjected to mechanical loading. The torsional deformation of these structural members is an important task. The Saint-Venant’s theory of uniform torsion for homogeneous piezoelectric bars has been analyzed in [7,8,9,10, 22]. Bisegna’s papers use the Prandtl’s stress function and electric displacement potential function formulation for simply connected cross section. The work of Davi [22] obtained a coupled boundary-value problem for the torsion function and for the electric potential function from a constrained three-dimensional static problem by the application of the usual assumptions of the Saint-Venant theory. Rovenski et al. [9, 10] give a torsion function and electric potential function formulation of the Saint-Venant torsional problem for monoclinic homogeneous piezoelectric beams. In these papers [9, 10], a coupled Neumann problem is derived for the torsion function and electric potential function, where the exact and numerical solutions for elliptical and rectangular cross sections are presented. Ecsedi and Baksa [23] give a formulation of the Saint-Venant torsional problem for homogeneous monoclinic piezoelectric beams in terms of Prandtl’s stress function and electric displacement potential function. The Prandtl’s stress function and electric displacement potential function satisfy a coupled Dirichlet problem in the multiply connected cross section. A direct and a variational formulation are developed in the paper by Ecsedi and Baksa [23]. In another paper [24], a variational formulation is presented for the solution of Saint-Venant’s torsion problem of homogeneous linear piezoelectric monoclinic beams. The variational formulation presented in [24] uses the torsion function and electric potential function as independent quantities of the considered variational functional defined in [24], and examples illustrate the application of the presented variational functional. Rovenski and Abramovich [25] apply a linear analysis to piezoelectric beams with non-homogeneous cross section that consist of various monoclinic (piezoelectric and elastic) materials. They give the solution procedure for extension, bending, torsion and shear.

The developed method is illustrated by numerical examples. Nodargi and Bisegna [26] presented a solution of the relaxed Saint-Venant problem for general anisotropic piezoelectric beams under the assumption of material homogeneity along the beam axis. The method of the developed solution is based on the observation that the strain field, the electric field, the stress field and the electric displacement field are mostly linear functions of the axial coordinate, see [26]. It must be mentioned that in [26] the solution of the Saint-Venant problem for a general anisotropic homogeneous cylinder with circular cross section has been derived in closed form. Hassani and Fae [27] dealt with a circular bar which is coated by a piezoelectric layer and subjected to Saint-Venant torsional loading. The considered circular bar is weakened by a Volterra-type screw dislocation. Talebanpour and Hematiyan [28] presented an approximate analytical method for the torsional analysis of hollow piezoelectric bars which is based on the Prandtl stress function and on the electric displacement potential function formulation. The paper by Ecsedi and Baksa [29] deals with the Saint-Venant torsion of a radially non-homogeneous hollow and solid circular cylinder made of orthotropic piezoelectric material. All material constants have only radial dependence.

In this paper, the torsional deformation of an orthotropic piezoelectric elliptical bar is studied. The shape of the orthotropic piezoelectric elliptical cross section which does not warp under the applied torque is determined. The size of the orthotropic solid piezoelectric cross section which has the maximum torsional rigidity for given cross-sectional area is also specified.

2 Formulation of the Saint-Venant torsion problem for elliptical cross section

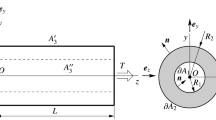
Let \(B=A\times (0,L)\) be a right elliptical cylindrical body of length L made of orthotropic linearly piezoelectric material with axial poling.

Fig. 1
figure 1

Orthotropic piezoelectric elliptical cylinder.

Full size image

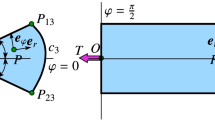
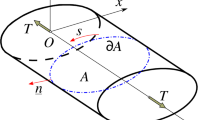
The governing equations of uniform torsion of unelectroded orthotropic piezoelectric elliptical bar are formulated in Cartesian coordinates \(x,\,y,\,z\). The origin of the coordinate system O is the center of the left end cross section of the bar as shown in Fig. 1. The equation of the boundary contour of elliptical cross section A (see Fig. 2) is

$$\begin{aligned} \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} - 1 = 0 \qquad (x,y) \in \partial A, \end{aligned}$$
(1)

where \(\partial A\) denotes the boundary curve of the cross section A. The normal vector \({{\varvec{n}}}\) to the boundary curve \(\partial A\) can be represented as [18, 20]

$$\begin{aligned} {\varvec{n}}=n_{x} {\varvec{e}}_{x} + n_{y}{\varvec{e}}_{y},\quad n_{x} =\frac{x}{a^{2}}, \quad n_{y}=\frac{y}{b^{2}} \quad (x,y) \in \partial A. \end{aligned}$$
(2)

The principal directions of orthotropy are assumed to be coincide with \(x,\, y\) and z directions, and the material of the piezoelectric beam is homogeneous.

Fig. 2
figure 2

Solid elliptical cross section

Full size image

The analytical solution of the Saint-Venant’s torsional problem originates from the next displacement and electric potential hypothesis

$$\begin{aligned} u=-\vartheta yz, \quad v=\vartheta xz, \quad w=\vartheta \omega (x,y), \quad \varphi = \vartheta \phi (x,y), \end{aligned}$$
(3)

where \(u,\,v,\,w\) are the displacements in \(x,\,y\) and z direction, \(\vartheta \) is the rate of twist with respect to axial coordinate z, \(\omega =\omega (x,y)\) is the torsion function, \(\varphi =\varphi (x,y)\) is the electric potential function [9, 10]. Application of the strain-displacement and electric field-electric potential relationships (Rovenski et al. [9, 10]) gives

$$\begin{aligned} \varepsilon _{x}&= \varepsilon _{y}=\varepsilon _{z}=\gamma _{xy}=0, \end{aligned}$$
(4)
$$\begin{aligned} \gamma _{xz}&=\vartheta \left( \frac{\partial \omega }{\partial x}-y\right) ,\quad \gamma _{yz}=\vartheta \left( \frac{\partial \omega }{\partial y}+x\right) , \end{aligned}$$
(5)
$$\begin{aligned} E_{x}&=-\vartheta \frac{\partial \phi }{\partial x},\quad E_{y}=-\vartheta \frac{\partial \phi }{\partial y},\quad E_{z}=0. \end{aligned}$$
(6)

In Eq. (4) \(\varepsilon _{x}\), \(\varepsilon _{y}\) and \(\varepsilon _{z}\) are the longitudinal strains, \(\gamma _{xy}\), \(\gamma _{yz}\) and \(\gamma _{xz}\) are the shearing strains, and in Eq. (6) \(E_{x}\), \(E_{y}\) and \(E_{z}\) are the components of the electric field vector \({\varvec{E}}\). In the present problem, the mechanical equilibrium and Gauss equation can be written in the form

$$\begin{aligned} \frac{\partial \tau _{xz}}{\partial x} + \frac{\partial \tau _{yz}}{\partial y} = 0 , \qquad \frac{\partial D_{x}}{\partial x} + \frac{\partial D_{y}}{\partial y} = 0 \quad (x,y)\in A, \end{aligned}$$
(7)

where \(\tau _{xz}=\tau _{xz}(x,y)\) and \(\tau _{yz}=\tau _{yz}(x,y)\) are the shearing stresses and \(D_{x}=D_{x}(x,y)\) and \(D_{y}=D_{y}(x,y)\) are the components of the electric displacement vector. Here, we note that (Rovenski et al. [9, 10])

$$\begin{aligned} \sigma _{x}=\sigma _{y}=\sigma _{z} =\tau _{xy}=0 \quad \text {and}\quad D_{z}=0 \qquad (x,y,z)\in A\times (0,L). \end{aligned}$$
(8)

In Eq. (8) \(\sigma _{x}\), \(\sigma _{y}\) and \(\sigma _{z}\) are the normal stresses, \(\tau _{xy}\) is shearing stress and \(D_{z}\) is the axial component of the electric displacement vector \({\varvec{D}}\). The mantle of the beam is stress and charge-free; that is, we have

$$\begin{aligned} \tau _{xz} n_{x} + \tau _{yz} n_{y}=0, \quad D_{x} n_{x} + D_{y} n_{y} = 0 \quad (x,y)\in \partial A. \end{aligned}$$
(9)

Here we note that the Saint-Venant torsion of a piezoelectric beam can be considered as a mixed type three-dimensional boundary-value problem whose boundary conditions are as follows:

$$\begin{aligned}&u=0,\quad v=0,\quad \sigma _{z}=0, \quad D_{z}=0, \quad z=0\quad (x,y)\in A, \end{aligned}$$
(10)
$$\begin{aligned}&u=-\vartheta L y, \quad v=\vartheta L x, \quad \sigma _{z}=0, \quad D_{z}=0, \quad z=L \quad (x,y)\in A, \end{aligned}$$
(11)
$$\begin{aligned}&\sigma _{x}n_{x}+\tau _{xy}n_{y} = 0,\quad \tau _{yx}n_{x} + \sigma _{y}n_{y}=0, \nonumber \\&\tau _{xz}n_{x} + \tau _{yz}n_{y} = 0, \quad (x,y,z)\in (0,L)\times \partial A, \end{aligned}$$
(12)
$$\begin{aligned}&D_{x}n_{x} + D_{y}n_{y}=0\quad (x,y,z)\in (0,L)\times \partial A. \end{aligned}$$
(13)

The applied mechanical torque T in terms of \(\tau _{xz}\) and \(\tau _{yz}\) can be computed as

$$\begin{aligned} T=\int \limits _{A} \left( x\tau _{yz} - y \tau _{xz}\right) \, \mathrm{d} A. \end{aligned}$$
(14)

Bai and Shield [30] by use of Eqs. (7)\(_{1}\), (9)\(_{1}\) and Eq. (14) proved that

$$\begin{aligned} T=2\int \limits _{A} x \tau _{yz}\,\mathrm{d} A = -2\int \limits _{A} y\tau _{xz} \,\mathrm{d} A. \end{aligned}$$
(15)

The torsional rigidity \(S_{M}\) of the orthotropic piezoelectric bar poling in direction of axis z is defined by

$$\begin{aligned} S_{M}=\frac{T}{\vartheta }. \end{aligned}$$
(16)

The shearing stresses \(\tau _{xz}\), \(\tau _{yz}\) and electric displacements \(D_{x}\) , \(D_{y}\) according to the constitutive equations of linear orthotropic piezoelectric bars can be written as

$$\begin{aligned} \tau _{xz}&=A_{55}\gamma _{xz} + e_{15}\frac{\partial \varphi }{\partial x}, \qquad \tau _{yz}=A_{44}\gamma _{yz} + e_{24}\frac{\partial \varphi }{\partial y}, \end{aligned}$$
(17)
$$\begin{aligned} D_{x}&= e_{15}\gamma _{xz} - \kappa _{11}\frac{\partial \varphi }{\partial x}, \quad D_{y} = e_{24}\gamma _{yz} - \kappa _{22}\frac{\partial \varphi }{\partial y}. \end{aligned}$$
(18)

Substitution of Eqs. (17) and (18) into Eq. (7)\(_{1,2}\) gives the following results:

$$\begin{aligned}&A_{55}\frac{\partial ^{2} \omega }{\partial x^{2}} + A_{44} \frac{\partial ^{2} \omega }{\partial y^{2}} + e_{15}\frac{\partial ^{2} \phi }{\partial x^{2}} + e_{24}\frac{\partial ^{2} \phi }{\partial y^{2}} = 0 \qquad (x,y)\in A, \end{aligned}$$
(19)
$$\begin{aligned}&e_{15}\frac{\partial ^{2} \omega }{\partial x^{2}} + e_{24} \frac{\partial ^{2} \omega }{\partial y^{2}} - \kappa _{11}\frac{\partial ^{2} \phi }{\partial x^{2}} - \kappa _{22}\frac{\partial ^{2} \phi }{\partial y^{2}} = 0 \qquad (x,y)\in A. \end{aligned}$$
(20)

For an elliptical cross section, the boundary condition formulated in Eq. (9)\(_{1,2}\) is as follows:

$$\begin{aligned}&\frac{x}{a^{2}}A_{55}\left( \frac{\partial \omega }{\partial x} - y \right) + \frac{y}{b^{2}}A_{44}\left( \frac{\partial \omega }{\partial y} + x \right) + \frac{x}{a^{2}} e _{15}\frac{\partial \phi }{\partial x} + \frac{y}{b^{2}} e_{24}\frac{\partial \phi }{\partial y} = 0 \quad (x,y)\in \partial A, \end{aligned}$$
(21)
$$\begin{aligned}&\frac{x}{a^{2}}e_{15}\left( \frac{\partial \omega }{\partial x} - y \right) + \frac{y}{b^{2}}e_{24}\left( \frac{\partial \omega }{\partial y} + x \right) - \frac{x}{a^{2}} \kappa _{11}\frac{\partial \phi }{\partial x} - \frac{y}{b^{2}} \kappa _{22}\frac{\partial \phi }{\partial y} = 0 \quad (x,y)\in \partial A. \end{aligned}$$
(22)

The standard results from the theory of linear second-order partial differential equation show that the classical (strong) solution to the boundary value problem given by Eqs. (19–22) is unique in two constants. This means that if \(\omega =\omega (x,y)\) and \(\phi =\phi (x,y)\) are a solution, then

$$\begin{aligned} \widetilde{\omega }(x,y) = \omega (x,y)+K_{\omega } \quad \text {and} \quad \widetilde{\phi }(x,y) = \phi (x,y) + K_{\phi } \end{aligned}$$
(23)

are also a solution for arbitrary values of the constants \(K_{\omega }\) and \(K_{\phi }\). The following theorem is valid.

Theorem 1

The solution of Saint-Venant’s torsional boundary-value problem formulated by Eqs. (19–22) is

$$\begin{aligned} \omega (x,y)=C_{\omega } xy + K_{\omega }, \qquad \phi (x,y) = C_{\phi } xy + K_{\phi } \qquad (x,y)\in A \cup \partial A, \end{aligned}$$
(24)

where

$$\begin{aligned}&C_{\omega } = \frac{ b^{4}(A_{55}\kappa _{11}+e_{15}^{2}) -a^{4}(A_{44}\kappa _{22} + e_{24}^{2}) + a^{2}b^{2} (A_{55}\kappa _{22} - A_{44}\kappa _{11}) }{ b^{4}(A_{55}\kappa _{11}+e_{15}^{2}) + a^{4}(A_{44}\kappa _{22} + e_{24}^{2}) + a^{2}b^{2}(A_{44}\kappa _{11} + A_{55}\kappa _{22}+2e_{24}e_{25}) }, \end{aligned}$$
(25)
$$\begin{aligned}&C_{\phi } = - \frac{ 2a^{2}b^{2}(A_{44}e_{15}-A_{55}e_{24}) }{ b^{4}(A_{55}\kappa _{11}+e_{15}^{2}) + a^{4}(A_{44}\kappa _{22} + e_{24}^{2}) + a^{2}b^{2}(A_{44}\kappa _{11} + A_{55}\kappa _{22}+2e_{24}e_{25}) } \end{aligned}$$
(26)

and \(K_{\omega }\) and \(K_{\phi }\) are arbitrary real constants.

A direct substitution of Eq. (24)\(_{1,2}\) into Eqs. (19–22) shows that the functions given by Eq. (24)\(_{1,2}\) with arbitrary constants \(K_{\omega }\) and \(K_{\phi }\) satisfy the torsional boundary-value problem formulated in Eqs. (19–22). In the following, we define \(K_{\omega }=0\) and \(K_{\phi }=0\) according to the statement formulated by Eq. (23).

Substitution of Eq. (24) into the formulae of shearing stresses given by Eq. (17), we obtain

$$\begin{aligned} {\begin{matrix} \tau _{xz} &{}= \vartheta \left[ A_{55}(C_{\omega }-1) + e_{15}C_{\phi }\right] y, \\ \tau _{yz} &{}= \vartheta \left[ A_{44}(C_{\omega }+1) + e_{24}C_{\phi }\right] x. \end{matrix}} \end{aligned}$$
(27)

From Eq. (18) and the expression of \(\omega =\omega (x,y)\) and \(\phi =\phi (x,y)\), it follows that

$$\begin{aligned} {\begin{matrix} D_{x} &{}= \vartheta \left[ e_{15}(C_{\omega }-1) - \kappa _{11} C_{\phi }\right] y, \\ D_{y} &{}= \vartheta \left[ e_{24}(C_{\omega }+1) - \kappa _{22} C_{\phi }\right] x. \end{matrix}} \end{aligned}$$
(28)

The connection of applied torque T and \(\vartheta \) in the present case can be formulated as

$$\begin{aligned} T= 2 \int \limits _{A} x \tau _{yz} \,\mathrm{d} A = \vartheta \left[ (C_{\omega }+1)A_{44} + e_{24}C_{\phi } \right] \frac{a^{3}b}{2}\pi . \end{aligned}$$
(29)

According to the definition of the torsional rigidity \(S_{M}\), we have

$$\begin{aligned} S_{M}=\frac{1}{2}\left[ (C_{\omega }+1)A_{44} + e_{24} C_{\phi }\right] a^{3} b \pi = \frac{a^{2}}{2} \left[ (C_{\omega }+1)A_{44} + e_{24}C_{\phi }\right] A. \end{aligned}$$
(30)

In Eq. (30), A is the area of the elliptical cross section, that is

$$\begin{aligned} A=ab\pi . \end{aligned}$$
(31)

3 Elliptical cross section which does not warp

For the non-warping elliptical cross section, we have \(C_{\omega }=0\), that is

$$\begin{aligned} (A_{55}\kappa _{11} + e_{15}^{2}) q^{4} + (A_{55}\kappa _{22}-A_{44}\kappa _{11})q^{2} - (A_{44}\kappa _{22} + e_{24}^{2}) = 0, \end{aligned}$$
(32)

where

$$\begin{aligned} q=\frac{b}{a} \end{aligned}$$
(33)

is the ratio of the major and minor axes of elliptical cross section. Since Eq. (32) is a second-order algebraic equation for \(q^{2}\) and

$$\begin{aligned} A_{44}\kappa _{22} + e_{24}^{2} \ge 0, \end{aligned}$$
(34)

we have there exists a positive real root of Eq. (32) for q which is

$$\begin{aligned}&q=\frac{b}{a}=\left\{ \frac{A_{44}\kappa _{11}-A_{55}\kappa _{22}}{2(A_{55}\kappa _{11}+e_{15}^{2})}+ \frac{\sqrt{ A_{55}^{2} \kappa _{22}^{2} + 2 A_{44}A_{55}\kappa _{11}\kappa _{22} + A_{44}^{2} \kappa _{11}^{2} + 4 A_{55}\kappa _{11}e_{24}^{2} + 4 A_{44}\kappa _{22}e_{15}^{2} + 4 e_{15}^{2}e_{24}^{2} }}{2(A_{55}\kappa _{11}+e_{15}^{2})} \right\} ^{0.5}. \end{aligned}$$
(35)

In the Appendix of this paper, we give a proof that Eq. (33) has only a one positive real root in every possible case. Here, we note that for the elastic homogeneous orthotropic cross section \(e_{15}=e_{24} = 0\) and from Eq. (35) we get Chen’s result \(q=\frac{b}{a}=\sqrt{\frac{A_{44}}{A_{55}}}\) [14].

4 Elliptical cross section with maximum torsional rigidity

Next, we consider an elliptical cross section whose area A is a given value. For this cross section

$$\begin{aligned} b=\frac{A}{a\pi } \end{aligned}$$
(36)

and

$$\begin{aligned}&C_{\omega }{(a)}= \frac{ A^{4}(A_{55}\kappa _{11}+e_{15}^{2}) + A^{2}a^{4}\pi ^{2}(A_{55}\kappa _{22}-A_{44}\kappa _{11}) - a^{8} \pi ^{4}(A_{44}\kappa _{22} + e_{24}^{2}) }{ A^{4}(A_{55}\kappa _{11}+e_{15}^{2}) + A^{2}a^{4}\pi ^{2} (A_{44}\kappa _{11}+A_{55}\kappa _{22}+2e_{15}e_{24}) + a^{8} \pi ^{4}(A_{44}\kappa _{22} + e_{24}^{2}) }, \end{aligned}$$
(37)
$$\begin{aligned}&C_{\phi }(a)=\frac{2A^{2}a^{4}\pi ^{2} (A_{55}e_{24}-A_{44}e_{15})}{ A^{4}(A_{55}\kappa _{11}+e_{15}^{2}) + A^{2}a^{4}\pi ^{2}(A_{44}\kappa _{11}+A_{55}\kappa _{22} +2e_{15}e_{24}) + a^{8} \pi ^{4}(A_{44}\kappa _{22} + e_{24}^{2}) }. \end{aligned}$$
(38)

The aim is to determine the size of the orthotropic piezoelectric cross section whose torsional rigidity is the maximum for the given cross-sectional area A. Application of formula (30) leads to the result

$$\begin{aligned} S_{M}(a)=\frac{a^{2}}{2}\left[ A_{44}(C_{\omega }{(a)}+1), + e_{24}C_{\phi }(a)\right] A. \end{aligned}$$
(39)

Formula (39) gives the dependence of the torsional rigidity from the semi-axis a \((0< a <\infty )\), for fixed cross-sectional are A. In order to obtain

$$\begin{aligned} \widetilde{S}_{M}=\underset{a\rightarrow \infty }{\mathrm {lim}}\, S_{M}(a), \end{aligned}$$
(40)

we reformulate the expressions of \(S_{M}(a)\) in the form

$$\begin{aligned} S_{M}(a) = \frac{ a^{6}A^{3}(A_{44}A_{55} \kappa _{22}+A_{55}e_{24}^{2}) \pi ^{2} + a^{2} A^{5}(A_{44}A_{55}\kappa _{11} + A_{44}e_{15}^{2}) }{ a^{8}(A_{44}\kappa _{22}+e_{24}^{2})\pi ^{4} + a^{4}A^{2}(A_{44}\kappa _{11}+A_{55}\kappa _{22}+2e_{15}e_{24})\pi ^{2}+A^{4}(A_{55}\kappa _{11} + e_{15}^{2}) }. \end{aligned}$$
(41)

It is evident for prescribed A that

$$\begin{aligned} S_{M}(0)=0, \qquad \underset{a\rightarrow \infty }{\mathrm {lim}\, S_{M}(a)} = 0 \quad \text {and}\quad S_{M}>0 \quad \text {for}\quad 0<a<\infty . \end{aligned}$$
(42)

From Eq. (42), it follows that the function \(S=S(a)\) has at least one positive maximum in the interval \(0<a<\infty \), that is

$$\begin{aligned} S_{M}(a) \le \underset{a}{\max } \,S_{M}(a)=S_{M}(\widetilde{a}) \quad \text {for} \quad 0<a<\infty . \end{aligned}$$
(43)

The electrical torsional rigidity \(S_{E}\) is defined by the next equation:

$$\begin{aligned} S_{E} =\frac{1}{\vartheta }\int \limits _{A}(xD_{y}(x,y) - y D_{x}(x,y))\, \mathrm{d} A. \end{aligned}$$
(44)

By the use of [30] formula for Eqs. (7)\(_{1}\) and (9)\(_{1}\), we can write

$$\begin{aligned} S_{E}=\frac{2}{\vartheta }\int \limits _{A} x D_{y} (x,y)\,\mathrm{d} A. \end{aligned}$$
(45)

Substitution of Eq. (28) into Eq. (45) gives

$$\begin{aligned} S_{E}=2\int \limits _{A}\left[ e_{24}(C_{\omega }+1) - \kappa _{22}C_{\phi }\right] x^{2} \mathrm{d} A = \frac{a^{2}}{2}\left[ e_{24}(C_{\omega }+1) - \kappa _{22}C_{\phi }\right] A. \end{aligned}$$
(46)

For a given cross-sectional area A, \(S_{E}\) as a function of a can be represented as

$$\begin{aligned} S_{E}(a) = a^{2}A\frac{ A^{4}(A_{55}\kappa _{11} + e_{15}^{2}) e_{24} + a^{4}A^{2}(A_{44}\kappa _{22}+ e_{24}^{2}) e_{15}\pi ^{2} }{ A^{4}(A_{55}\kappa _{11} + e_{15}^{2}) + a^{4} A^{2}(A_{44}\kappa _{11}+A_{55}\kappa _{22}+2e_{15}e_{24})\pi ^{2} + a^{8} (A_{44}\kappa _{22}+e_{24}^{2})\pi ^{4} }. \end{aligned}$$
(47)

The function \(S_{E}=S_{E}(a)\) has the properties

$$\begin{aligned} S_{E}(0)=0,\quad \underset{a\rightarrow \infty }{\lim } S_{E}(a)=0 \quad \text {and} \quad S_{E}(a)> 0 \quad \text {for}\quad 0<a<\infty . \end{aligned}$$
(48)

According to Eq. (48), we have the function \(S_{E}=S_{E}(a)\) has at least one positive maximum in the interval \(0<a<\infty \), that is,

$$\begin{aligned} S_{E}(a) = \underset{a}{\max }S_{E}(a) = S_{E}(\hat{a}) \quad \text {for} \quad 0< a <\infty . \end{aligned}$$
(49)

5 Prandtl’s stress function and electric displacement potential function

The expression of shearing stresses and electric displacements in terms of Prandtl’s stress function \(U=U(x,y)\) and electric displacement potential function \(F=F(x,y)\) can be represented as [7, 8, 23]

$$\begin{aligned}&\tau _{xz}=\vartheta \frac{\partial U}{\partial y}, \quad \tau _{yz}=-\vartheta \frac{\partial U}{\partial x} \qquad (x,y) \in A\cup \partial A, \end{aligned}$$
(50)
$$\begin{aligned}&D_{x}=\vartheta \frac{\partial F}{\partial y}, \quad D_{y}=-\vartheta \frac{\partial F}{\partial x} \qquad (x,y) \in A\cup \partial A. \end{aligned}$$
(51)

Prandtl’s stress function and electric displacement potential function satisfy the homogeneous boundary conditions

$$\begin{aligned} U(x,y)=0,\qquad F(x,y)=0 \qquad \text {on}\quad \partial A. \end{aligned}$$
(52)

The determination of the Prandtl stress function \(U=U(x,y)\) and the electric displacement potential function \(F=F(x,y)\) is based on the system of partial differential equations given by Eqs. (53) and (54):

$$\begin{aligned} \begin{aligned} \frac{\partial U}{\partial y}&=\left[ A_{55}\left( C_{\omega }-1\right) + e_{15} C_{\phi } \right] y, \\ -\frac{\partial U}{\partial x}&= \left[ A_{44}\left( C_{\omega }+1\right) + e_{24}C_{\phi } \right] x, \end{aligned} \end{aligned}$$
(53)
$$\begin{aligned} \begin{aligned} \frac{\partial F}{\partial y}&=\left[ e_{15}\left( C_{\omega }-1\right) - \kappa _{11} C_{\phi } \right] y, \\ -\frac{\partial F}{\partial x}&= \left[ e_{24}\left( C_{\omega }+1\right) - \kappa _{22}C_{\phi } \right] x. \end{aligned} \end{aligned}$$
(54)

In the following, we deal with the non-warping elliptical cross section, that is

$$\begin{aligned}&C_{\omega }=0, \qquad a=\alpha , \qquad b=\beta =q\alpha , \end{aligned}$$
(55)
$$\begin{aligned}&C_{\phi }=-\frac{2q^{2}(A_{44}e_{15}-A_{55}e_{24})}{A_{44}\kappa + e_{24}^{2}+q^{2}(A_{44}\kappa _{11}+A_{55}\kappa _{22}+2e_{15}e_{24})+q^{4}(A_{55} \kappa _{11}+e_{15}^{2})}. \end{aligned}$$
(56)

Equation (56) shows that for non-warping cross section the electric potential function \(\varphi =\varphi (x,y)\) does not depend on \(\alpha \).

A detailed calculation based on Eqs. (53) and (45) gives

$$\begin{aligned}&U(x,y)=K_{U}\left( 1-\frac{x^{2}}{\alpha ^{2}} - \frac{y^{2}}{q^{2}\alpha ^{2}}\right) , \qquad \nonumber \\&\quad F(x,y)=K_{F}\left( 1-\frac{x^{2}}{\alpha ^{2}} - \frac{y^{2}}{q^{2}\alpha ^{2}}\right) \qquad (x,y) \in A \cup \partial A, \end{aligned}$$
(57)

where

$$\begin{aligned}&K_{U}=\frac{\alpha ^{2}}{2}\left[ A_{44}- \frac{2q^{2}(A_{44}e_{15}e_{24}-A_{55}e_{24}^{2})}{A_{44}\kappa _{22}+e_{24}^{2}+q^{2}(A_{44}\kappa _{11}+A_{55}\kappa _{22}+2e_{15}e_{24}) + q^{4}(A_{55}\kappa _{11}+e_{15}^{2})} \right] , \end{aligned}$$
(58)
$$\begin{aligned}&K_{F}=\frac{\alpha ^{2}}{2}\left[ e_{24}- \frac{2q^{2}(A_{44}e_{15}\kappa _{22}-A_{55}e_{24}\kappa _{22})}{A_{44}\kappa _{22}+e_{24}^{2}+q^{2}(A_{44}\kappa _{11}+A_{55}\kappa _{22}+2e_{15}e_{24}) + q^{4}(A_{55}\kappa _{11}+e_{15}^{2})} \right] . \end{aligned}$$
(59)

It is known that [7, 8, 23] the torsional rigidity \(S_{M}\) and the electric torsional rigidity \(S_{E}\) in terms of \(U=U(x,y)\) and \(F=F(x,y)\) can be computed as

$$\begin{aligned} S_{M} =2\int \limits _{A}U\,\mathrm{d} A,\qquad S_{E}=2\int \limits _{A}F\,\mathrm{d} A. \end{aligned}$$
(60)

A simple calculation gives

$$\begin{aligned} S_{M}=K_{U}q\alpha ^{2} \pi , \qquad S_{E}=K_{F}q\alpha ^{2} \pi . \end{aligned}$$
(61)

6 Illustration of the theoretical results by numerical example

In this section, a numerical example is presented to illustrate the theoretical results of Sects. 3, 4 and 5.

The following data are used:

$$\begin{aligned} {\begin{matrix} A_{44} &{}=1.56\times 10^{10}\,\mathrm {Pa}, \qquad A_{55}={ 2.56}\times 10^{10}\,\mathrm {Pa}, \\ e_{15} &{}=13\,\mathrm {C/m^{2}}, \qquad \qquad e_{24} = 12 \,\mathrm {C/m^{2}}, \\ \kappa _{11} &{}= {6.43}\times 10^{-9} \,\mathrm {C/Vm}, \qquad \kappa _{22} = 7.024\times 10^{-9}\,\mathrm {C/Vm}, \\ A &{}= 0.003\,356\,72\,\mathrm {m^{2}}. \end{matrix}} \end{aligned}$$
(62)

Application of formulae (34) and (55) gives

$$\begin{aligned} q={ 0.872\,226\,81}, \;\; \alpha =0.035\,\mathrm {m},\;\; \beta ={0.030\,527\,93\,}\mathrm {m} \end{aligned}$$
(63)

for the non-warping cross section

$$\begin{aligned} C_{\omega }=0\quad \text {and}\quad C_{\phi }=1.770\,642\,18 { \times 10^{8}}\,\mathrm {V/m}. \end{aligned}$$
(64)
Fig. 3
figure 3

The plot of \(S_{M}(a)\) as a function of half major axis of elliptical cross section

Full size image

The plot of \(S_{M}(a)\) for the prescribed cross-sectional area is shown in Fig. 3. A detailed computation gives

$$\begin{aligned} {\begin{matrix} \max \limits _{a} S(a) &{}{}= S(\widetilde{a}) = 36\,645.483\,62\,\mathrm {Nm^{2},} \\ \widetilde{a}&{}{}=0.036\,859\,15\,\mathrm {m}, \end{matrix}} \end{aligned}$$
(65)
$$\begin{aligned} S(\alpha )=36\,441.993\,78\,\mathrm {Nm^{2}}. \end{aligned}$$
(66)
Fig. 4
figure 4

The graph of function \(S_{E}=S_{E}(a)\) for given cross-sectional area

Full size image

The numerical results (65) and (66) support the validity of the statement that for given cross-sectional area the non-warping cross section does not have the maximum value of torsional rigidity.

The graph of function \(S_{E}=S_{E}(a)\) for given cross-sectional area is shown in Fig. 4. By a detailed computation, we can derive the next results:

$$\begin{aligned} \max \limits _{a}S_{E}(a)&=S_{E}(\hat{a}) = 0.000\,022\,217\,637 \, \mathrm {Cm^{2}}, \end{aligned}$$
(67)
$$\begin{aligned} \hat{a}&=0.033\,404\,757 \, \mathrm {m}, \end{aligned}$$
(68)
$$\begin{aligned} S_{E}(\alpha )&= 0.000\,022\,211\,487\,\mathrm {Cm^{2}}. \end{aligned}$$
(69)

Application of formula (61) gives

$$\begin{aligned} S_{M}(\alpha )&= K_{U} q\alpha ^{2} \pi = 36\,441.993\,81 \,\mathrm {Nm^{2}}, \end{aligned}$$
(70)
$$\begin{aligned} S_{E}(\alpha )&= K_{F}q\alpha ^{2}\pi = 0.000\,022\,114\,873 \,\mathrm {Cm^{2}}. \end{aligned}$$
(71)

7 Conclusions

The Saint-Venant torsion of a solid elliptical cylinder made of orthotropic homogeneous axially poling piezoelectric material is considered. The shape of the elliptical cross section which does not warp under the action of applied torque is determined. The size of the orthotropic homogeneous piezoelectric cross section which has the maximum torsional rigidity for given cross-sectional area are also calculated.