Non-uniform torsion of functionally graded anisotropic bar of an elliptical cross section

Abstract

An analytical solution is given to the problem of non-uniform torsion of an elliptical cylinder made of functionally graded anisotropic linear elastic material. The material moduli of the considered anisotropic non-homogeneous elastic bar are smooth functions of the axial coordinate. The contour of the elliptical cross section depends on the elastic constants. This dependence provides the zero warping property of the considered elliptical cross section. The obtained stress field is independent of the axial coordinate as in the case of Saint-Venant’s torsion problem, but the rate of twist depends on the axial coordinate.

1 Introduction

Functionally graded materials (FGMs) are a new generation of engineered materials that have emerged from the need to optimize material performance [1, 6, 15]. In a homogeneous material, the properties are constant, whereas in an FGM, the material properties vary continuously with position, usually in one coordinate direction. Functionally graded linearly elastic structures can be considered as non-homogeneous elastic bodies whose material moduli are smooth functions of the position coordinates. The books by Lekhnitskii [9] and Lomakin [10] give the solutions to many linearly elastic problems for non-homogneous bodies.

Analytical solutions for the Saint-Venant torsion and flexure of FG bars have been given by Rooney and Ferrai, they assumed that the elastic moduli are smooth functions of the cross-sectional coordinates [12]. Horgan and Chan [7] have investigated the Saint-Venant’s torsion problem of functionally graded isotropic linearly elastic bars. The special case of the circular rod with shear modulus depending on the radial coordinate was analysed by Horgan and Chan [7]. Analytical solutions to the problem of non-uniform torsion of a circular cylinder made of functionally graded material with the material moduli smooth functions of the axial coordinate only have been presented by Batra [2]. The paper [2] deals with isotropic, transversely isotropic, compressible and incompressible materials. The aim of this paper is to give an analytical solution to the non-uniform torsion problem of an elliptical cylinder made of functionally graded anisotropic linearly elastic materials. The material moduli of the considered anisotropic non-homogeneous bar are smooth functions of the axial coordinate. The contour of the elliptical cross section is assumed to be dependent on elastic constants. The stress boundary condition on the cylindrical boundary surface determines the dependence of the boundary contour from the material constants under the condition of zero axial displacement. The considered torsion problem is not of Saint-Venant type since the rate of twist depends on the axial coordinate.

2 Formulation of the non-uniform torsion problem

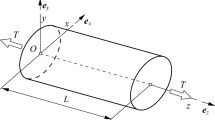
Consider a non-homogeneous anisotropic elastic bar of uniform cross section which is bounded by a cylindrical surface and two planes normal to the side surface. The Oz axis is directed parallel to the generators of the cylindrical surface and the plane Oxy is chosen to coincide with the “lower” ends of the bar. The ”upper” end cross section has the coordinate $z=L> 0$ (Fig.  1). The bar is not subjected to body forces and it is free from external forces on its lateral surface. There are no normal stresses on the end cross sections. The in-plane displacements of the cross sections at $z=0$ and at $z=L$ are prescribed.

Fig. 1

Non-uniform torsion of functionally graded anisotropic elliptical cylindrical bar

The material of the considered bar is linearly elastic, non-homogeneous and anisotropic. The material properties are smooth functions of the axial coordinate z. This means that each cross section is made of one material, but the material of one cross section is different from that of its adjoining one. The assumed form of the anisotropy and z dependence of material properties are given as [9, 11, 13]:

$$\begin{aligned} \sigma _{x}= & {} g(z)(c_{11}\varepsilon _{x}+c_{12}\varepsilon _{y}+c_{13}\varepsilon _{z}+c_{16}\gamma _{xy}), \end{aligned}$$

(1)

$$\begin{aligned} \sigma _{y}= & {} g(z)(c_{12}\varepsilon _{x}+c_{22}\varepsilon _{y}+c_{23}\varepsilon _{z}+c_{26}\gamma _{xy}), \end{aligned}$$

(2)

$$\begin{aligned} \sigma _{z}= & {} g(z)(c_{13}\varepsilon _{x}+c_{23}\varepsilon _{y}+c_{33}\varepsilon _{z}+c_{36}\gamma _{xy}), \end{aligned}$$

(3)

$$\begin{aligned} \tau _{yz}= & {} g(z)(c_{44}\gamma _{yz}+c_{45}\gamma _{xz}), \end{aligned}$$

(4)

$$\begin{aligned} \tau _{xz}= & {} g(z)(c_{45}\gamma _{yz}+c_{55}\gamma _{xz}), \end{aligned}$$

(5)

$$\begin{aligned} \tau _{xy}= & {} g(z)(c_{16}\varepsilon _{x}+c_{26}\varepsilon _{y}+c_{36}\varepsilon _{z}+c_{66}\gamma _{xy}). \end{aligned}$$

(6)

The non-homogeneity which appears in the axial direction is described by the smooth function $g=g(z)$. The stiffness coefficients $c_{ij}$ ($i, j=1,...,6$) are constants, their units are [force]/[length]$^{{2}}$ and g is unit-free. In Eq. (1) $\varepsilon _{x}$, $\varepsilon _{y}$, $\varepsilon _{z}$ are normal strains, $\gamma _{yz}$, $\gamma _{xz}$, $\gamma _{xy }$are shearing strains, $\sigma _{x}$, $\sigma _{y},\sigma _{z}$ are normal stresses and $\tau _{yz}$, $\tau _{xz}$, $\tau _{xy}$ are shearing stresses. From Eqs. (1–6) can be read that there exists a plane of symmetry of elasticity. The plane of symmetry of elasticity is the plane Oxy, thus the non-homogeneous monoclinic system is considered [7, 11, 13]. From the positivity of strain energy density it follows that [7, 11] the Hooke’s matrix

$$\begin{aligned} {\mathbf {C}}=\left( {\begin{array}{cccccc} c_{11} &{}\quad {c}_{12}&{}\quad {c}_{13} &{}\quad 0 &{}\quad 0&{}\quad {c}_{16} \\ c_{12}&{}\quad {c}_{22} &{}\quad c_{23}&{}\quad 0&{}\quad 0 &{} \quad c_{26} \\ c_{13}&{}\quad c_{23} &{}\quad c_{33} &{}\quad 0&{}\quad 0&{}\quad {c}_{36} \\ 0&{}\quad 0&{}\quad 0&{}\quad c_{44}&{}\quad {c}_{45} &{}\quad 0 \\ 0&{} \quad 0&{}\quad 0&{}\quad {c}_{45}&{}\quad {c}_{55} &{}\quad 0 \\ c_{16}&{}\quad { c}_{26} &{}\quad c_{36}&{}\quad 0&{}\quad 0 &{}\quad c_{66} \\ \end{array}} \right) \end{aligned}$$

(7)

is a positive definite matrix and $g(z) > 0$, $(0\le z\le L)$. Let the boundary curve $\partial A$ of the cross section A (Fig. 1) be given by the equation

$$\begin{aligned} c_{44}x^{2}-2c_{45}xy+c_{55}y^{2}=k(x,y)\in \partial A, \end{aligned}$$

(8)

where k is an arbitrary positive real number. Units of k is [force] and from the positive definitness of matrix C it follows that

$$\begin{aligned} c_{44}>0,c_{55}>0,\quad { c}_{44}c_{55}-(c_{45})^{2}>0. \end{aligned}$$

(9)

This latter inequalities assures that the points whose x and y coordinates satisfy Eq. (8) are on an ellipse. The centre of the boundary ellipse is the origin of the cross-sectional coordinate system Oxy. The non-uniform torsion problem for the functionally graded cylinder whose cross section is given by Eq. (8) is defined by the next mixed type boundary conditions

$$\begin{aligned}&\sigma _{x}n_{x}+\tau _{xy}n_{y}=\tau _{xy}n_{x}+\sigma _{y}n_{y}=\tau _{xz}n_{x}+\tau _{yz}n_{y}=0 \,\,\, {\mathrm{on }}\, \partial A {\times (0,}L{),} \end{aligned}$$

(10)

$$\begin{aligned}&\sigma _{z}\left( x,y,0 \right) =\sigma _{z}\left( x,y,L \right) =0, \quad u\left( x,y,0 \right) =v\left( x,y,0 \right) =0,\nonumber \\&u(x,y,L)=-\varTheta y, \quad v(x,y,L)=\varTheta x. \end{aligned}$$

(11)

In Eq. (10) $n_{x}\,\mathrm{and}\, n_{y}$ are the components of the unit normal vector of boundary curve $\partial A$ and in Eqs. (11)$_{{3}}$ and (11)$_{{4}} \varTheta$ is a given constant.

Assumed form of the displacement field of the twisted anisotropic non-homogeneous bar is as follows

$$\begin{aligned} \mathrm{u}=- \varPhi \left( z \right) \mathrm{y},\,\mathrm{v}= \varPhi \left( z \right) \mathrm{x},\quad w=0\,\left( x,y \right) \in A \, \mathrm{and }\, 0 \le z{ \le } L{,} \end{aligned}$$

(12)

where $\varPhi =\varPhi (z)$ is an unknown function with the boundary conditions

$$\begin{aligned} \varPhi (0)=0, \quad \varPhi (L)=\varTheta . \end{aligned}$$

(13)

Application of the strain-displacement relationships of the linearized theory of elasticity gives the result [9, 14]:

$$\begin{aligned} \varepsilon _{x}= & {} \frac{\partial u}{\partial x}=0,\quad { \varepsilon }_{y}=\frac{\partial v}{\partial y}=0,\quad { \varepsilon }_{z}=\frac{\partial w}{\partial z}=0, \quad \gamma _{xy}=\frac{\partial v}{\partial x}+\frac{\partial u}{\partial y}=0, \end{aligned}$$

(14)

$$\begin{aligned} \gamma _{xz}= & {} \frac{\partial u}{\partial z}+\frac{\partial w}{\partial x}=-\frac{d\varPhi }{dz}y,\quad \gamma _{yz}=\frac{\partial v}{\partial z}+\frac{\partial w}{\partial x}=\frac{d\varPhi }{dz}x. \end{aligned}$$

(15)

Combination of Eqs. (1–6) with Eqs. (14) and (15) yields

$$\begin{aligned} \sigma _{x}= & {} \sigma _{y}=\sigma _{z}=\tau _{xy}=0, \end{aligned}$$

(16)

$$\begin{aligned} \tau _{yz}= & {} g(z)\frac{\mathrm{d}\varPhi }{\mathrm{d}z}(c_{44}x-c_{45}y), \quad \tau _{xz}=g(z)\frac{\mathrm{d}\varPhi }{\mathrm{d}z}(c_{45}x-c_{55}y). \end{aligned}$$

(17)

Starting from Eqs. (16), (17) and using the equations of equilibrium [14]

$$\begin{aligned}&\frac{\partial \sigma _{x}}{\partial x}+\frac{\partial \tau _{xy}}{\partial y}+\frac{\partial \tau _{xz}}{\partial z}=0\,(x,y)\in A \, \mathrm{and }\,0<z{<}L{,} \end{aligned}$$

(18)

$$\begin{aligned}&\frac{\partial \tau _{xy}}{\partial x}+\frac{\partial \sigma _{y}}{\partial y}+\frac{\partial \tau _{yz}}{\partial z}=0(x,y)\in A \, \mathrm{and }\, 0\,<z{<}L{,} \end{aligned}$$

(19)

$$\begin{aligned}&\frac{\partial \tau _{xz}}{\partial x}+\frac{\partial \tau _{yz}}{\partial y}+\frac{\partial \sigma _{z}}{\partial z}=0\,(x,y)\in A\, \mathrm{and}\, 0<z{<}L{.} \end{aligned}$$

(20)

and stress boundary conditions formulated by Eq. (10) we get

$$\begin{aligned}&\frac{\mathrm{d}}{\mathrm{d}z}\left( g(z)\frac{\mathrm{d}\varPhi }{\mathrm{d}z} \right) =0\,\,0<z<L, \end{aligned}$$

(21)

$$\begin{aligned}&\tau _{xz}n_{x}+\tau _{yz}n_{y}=g(z)\frac{\mathrm{d}\varPhi }{\mathrm{d}z}\left[ (c_{45}x-c_{55}y)\frac{\mathrm{d}y}{\mathrm{d}s}-(c_{44}x-c_{45}y)\frac{\mathrm{d}x}{\mathrm{d}s} \right] =0 \,\, \mathrm{on} \, \partial A. \end{aligned}$$

(22)

Here, we have used

$$\begin{aligned} n_{x}=\frac{\mathrm{d}y}{\mathrm{d}s},\, n_{y}=-\frac{\mathrm{d}x}{\mathrm{d}s}\,\mathrm{on}\, \partial A , \end{aligned}$$

(23)

where $x=x(s), y=y(s)$ are the equation of the boundary curve $\partial A$ and s is an arc-length defined on curve $\partial A$ (Fig. 1). From Eqs. (22), we obtain

$$\begin{aligned}&\left[ \left( c_{45}x-c_{55}y \right) \frac{\mathrm{d}y}{\mathrm{d}s}-\left( c_{44}x-c_{45}y \right) \frac{\mathrm{d}x}{\mathrm{d}s} \right] \nonumber \\&\quad = -\frac{\mathrm{d}}{\mathrm{d}s}\left( c_{44}x^{2}-2c_{45}xy+c_{55}y^{2} \right) =-\frac{\mathrm{d}k}{\mathrm{d}s}=0\,\, \mathrm{on}\, \partial A, \end{aligned}$$

(24)

thus all the boundary conditions on the cylindrical surface are satisfied if the contour of elliptical cross section is given by Eq. (8).

3 Computation of cross-sectional shear forces and torque

The bending moments $M_{x}=M_{x}(z)\, \mathrm{and}\, M_{y}=M_{y}(z)$ are equal to zero, whereas we have $\sigma _{z}=0$ in all points of the elliptical cylinder. The shear forces are obtained from

$$\begin{aligned} V_{y}(z)=\frac{\mathrm{d}M_{x}}{\mathrm{d}z},\quad V_{x}(z)=\frac{\mathrm{d}M_{y}}{\mathrm{d}z}. \end{aligned}$$

(25)

From equation (25) it follows that $V_{x}(z)=V_{y}(z)=0, 0\le z\le L.$ Integration of Eq. (21) under the boundary condition (13) gives

$$\begin{aligned} \varPhi (z)=\varTheta \frac{\int _0^z \frac{\mathrm{d}\zeta }{g(\zeta )} }{\int _0^L \frac{\mathrm{d}\zeta }{g(\zeta )}}. \end{aligned}$$

(26)

Here, we note

$$\begin{aligned} H=g(z)\frac{\mathrm{d}\varPhi }{\mathrm{d}z}=\frac{\varTheta }{\int _0^L \frac{\mathrm{d}\zeta }{g(\zeta )} }=\mathrm{constant.} \end{aligned}$$

(27)

It is easy to see that the shearing stresses are independent of the axial coordinate z because we have

$$\begin{aligned} \tau _{xz}= & {} g\left( z \right) \frac{\mathrm{d}\varPhi }{\mathrm{d}z}\left( c_{45}x-c_{55}y \right) =H\left( c_{45}x-c_{55}y \right) ,\nonumber \\ \tau _{yz}= & {} g\left( z \right) \frac{\mathrm{d}\varPhi }{\mathrm{d}z}\left( c_{44}x-c_{45}y \right) =H(c_{44}x-c_{45}y). \end{aligned}$$

(28)

The torque T in an arbitrary cross section, according to Eq. (28) can be computed as

$$\begin{aligned} T=\int _A \left( x\tau _{yz}(x,y,z)-y\tau _{xz}(x,y,z)\mathrm{d}A \right) =H\int _A \left( c_{44}x^{2}-2c_{45}xy+c_{55}y^{2} \right) \mathrm{d}A. \end{aligned}$$

(29)

A detailed computation, which is given in the Appendix, leads to the result

$$\begin{aligned} T=\frac{\pi }{2}\frac{k^{2}H}{\sqrt{c_{44}c_{55}-(c_{45})^{2}} }. \end{aligned}$$

(30)

If

$$\begin{aligned} c_{44}=c_{55}=c,\, c_{45}=0, \quad k=R^{2}c, \end{aligned}$$

(31)

then the Batra’s solution for isotropic circular cylinder is recovered [2]. The shear modulus of the isotropic functionally graded circular cylinder is $\mu (z)=cg(z)$ and the radius of the circular boundary is $R=\sqrt{k/c}$.

The stress field which is independent of the axial coordinate z, its expression in terms of applied torque T is as follows:

$$\begin{aligned} \tau _{xz} =\frac{2T}{k^{2}\pi }\sqrt{c_{44} c_{55} -(c_{45} )^{2}} (c_{45} x-c_{55} y),\,\,\,\, \tau _{yz}=\frac{2T}{k^{2}\pi }\sqrt{c_{44}c_{55}-(c_{45})^{2}} (c_{44}x-c_{45}y). \end{aligned}$$

(32)

The rate of twist $\vartheta$ depends on the axial coordinate z as

$$\begin{aligned} \vartheta =\frac{\mathrm{d}\varPhi }{\mathrm{d}z}=\frac{2T}{\pi k^{2}}\frac{\sqrt{c_{44}c_{55}-(c_{45})^{2}} }{g(z)}, \quad 0\le z\le L \end{aligned}$$

(33)

and the expression of the rotation of cross sections in the terms of applied torque is

$$\begin{aligned} \varPhi (z)=\frac{2T}{\pi k^{2}}\sqrt{c_{44}c_{55}-(c_{45})^{2}} \int _0^z \frac{\mathrm{d}\zeta }{g(\zeta )} , \quad 0\le z\le L. \end{aligned}$$

(34)

The derived formulas are valid for homogeneous anisotropic elliptical cylinder when

$$\begin{aligned} g(z)=1, \quad 0\le z\le L. \end{aligned}$$

(35)

In this case, the considered torsion problem is Saint-Venant’s torsion (uniform torsion) since the rate of twist

$$\begin{aligned} \vartheta =\frac{\mathrm{d}\varPhi (z)}{\mathrm{d}z}=\frac{\varTheta }{L}=\mathrm{constant},\quad 0 \le z{\le } L. \end{aligned}$$

(36)

For homogeneous anisotropic elliptical cylinder, the torsional rigidity S of the cross section is defined according to the Saint-Venant’s theory of uniform torsion as [9, 14]

$$\begin{aligned} S=\frac{T}{\vartheta }. \end{aligned}$$

(37)

In the present case from Eqs. (33) and (35), we get

$$\begin{aligned} S=\frac{k^{2}\pi }{2\sqrt{c_{44}c_{55}-c_{45}^{2}} }. \end{aligned}$$

(38)

We remark that, the elliptical anisotropic homogeneous cross section whose boundary contour is given by Eq. (8) does not warp. The non-warping quality of anisotropic cross section in the framework of Saint-Venant’ theory of torsion was analysed in papers by Chen [3], Chen and Wei [4], Ecsedi [5], and Horgan [8]. From Eq. (8) it follows that, the equation of the contour of homogeneous orthotropic non-warping elliptical cross section in the case Saint-Venant torsion is

$$\begin{aligned} \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1, \,\, \mathrm{where}\,\, \frac{b^{2}}{a^{2}} =\frac{c_{44}}{c_{55}},\quad { c}_{45}=0\,\, \mathrm{and}\,\, g(z)=1, \qquad 0\le z\le L. \end{aligned}$$

(39)

Equation (39) was derived at first by Chen [3].

4 Conclusions

By use of an assumed form of the displacement field, an analytical solution is given to the problem of non-uniform torsion of an elliptical cylinder made of functionally graded linearly elastic anisotropic material. The material moduli are smooth functions of the axial coordinate. The contour of the elliptical cross section depends on the elastic constants. This dependence provides zero warping property of the considered elliptical cross section. The obtained stress field is independent of the axial coordinate as in the case of Saint-Venant’s torsion problem. Since the rate of twist depends on the axial coordinate the torsional problem analysed is not of Saint-Venant type.

Appendix A. Computation of the area integral appearing in formula (29)

Introducing new variables instead of x and y by the equations

$$\begin{aligned} {x}=\xi \cos \alpha -{\eta }\sin {\alpha },\quad {y}={\xi }\sin {\alpha }+{\eta }\cos {\alpha }, \end{aligned}$$

(A.1)

where

$$\begin{aligned} \tan {2{\upalpha }}=\frac{2c_{45}}{c_{55}-c_{44}}, \end{aligned}$$

(A.2)

we get

$$\begin{aligned} I=\int _A {\left( c_{44}x^{2}-2c_{45}xy+c_{55}y^{2} \right) \mathrm{d}A} =\int _A^{'} {(c_{1}\xi ^{2}+c_{2}\eta ^{2})} \mathrm{d}\xi \mathrm{d}\eta . \end{aligned}$$

(A.3)

Here

$$\begin{aligned} c_{1}= & {} \frac{1}{2}\left[ c_{44}+c_{55}-\sqrt{(c_{44}-c_{55})^{2}+4(c_{45})^{2}} \right] , \end{aligned}$$

(A.4)

$$\begin{aligned} c_{2}= & {} \frac{1}{2}\left[ c_{44}+c_{55}+\sqrt{(c_{44}-c_{55})^{2}+4(c_{45})^{2}} \right] \end{aligned}$$

(A.5)

and

$$\begin{aligned} A^{'}=\left\{ (\xi ,\eta ) \right. \vert \left. 0\le c_{1}\xi ^{2}+c_{2}\eta ^{2}\le k \right\} . \end{aligned}$$

(A.6)

We transform $\xi$ and $\eta$ to t and ${\phi }$ by use of the equations

$$\begin{aligned} {\xi }=\sqrt{\frac{k}{c_{1}}} {t}\cos {\phi },\quad {\eta }=\sqrt{\frac{k}{c_{2}}} {t}\sin {\phi }, \end{aligned}$$

(A.7)

where $0\le t\le 1$ and $0\le {\phi } \le 2\pi$. The determinant of the Jacobi matrix J is

$$\begin{aligned} \mathrm{det}\, {\mathbf {J}}=\mathrm{det}\, \left[ \frac{\partial (\xi ,\eta )}{\partial (t,\varphi )} \right] =\frac{kt}{\sqrt{c_{1}c_{2}} }. \end{aligned}$$

(A.8)

The expression of the area element in terms of t and ${\phi }$ is as follows:

$$\begin{aligned} \mathrm{d}\xi \mathrm{d}\eta =\vert \mathrm{det}\, {\mathbf {J}}\vert \mathrm{d}t\mathrm{d}{\phi }=\frac{kt}{\sqrt{c_{1}c_{2}} }\mathrm{d}t\mathrm{d}{\phi }. \end{aligned}$$

(A.9)

The combination of Eqs. (A.3), (A.7) with (A.9) gives

$$\begin{aligned} I=\frac{k^{2}}{\sqrt{c_{1}c_{2}} }\int _0^{2\pi } \left( \int _0^1 t^{3}\mathrm{d}t\right) \mathrm{d}\phi =\frac{k^{2}\pi }{2\sqrt{c_{1}c_{2}} }. \end{aligned}$$

(A.10)

From (A.4) and (A.5) it follows that

$$\begin{aligned} \sqrt{c_{1}c_{2}} =\sqrt{c_{44}c_{55}-(c_{45})^{2}} , \end{aligned}$$

(A.11)

that is

$$\begin{aligned} I=\frac{k^{2}\pi }{2\sqrt{c_{44}c_{55}-(c_{45})^{2}} }, \end{aligned}$$

(A.12)

which shows the validity of formula (30).