1 Introduction

The Saint-Venant torsion problem for elastic bars has been addressed by engineers for the last 150 years. The uniform torsion was described by the rigorous theory developed by Saint-Venant [1, 2]. According to the Saint-Venant’s theory of uniform torsion only two shearing stresses appear nonzero, the axis of the bar remains straight and the cross-sectional warping does not depend on the position of the cross section. These conditions are valid for anisotropic bars if the one plane of elastic symmetry is orthogonal to the axis of bar [3,4,5,6,7,8].

The Saint-Venant torsion of anisotropic linearly elastic bars has been a subject of several studies. Books by Lekhnitskii [3, 4], Sarkisyan [5, 6], Rand and Rovenski [7], Milne-Thomson [9] give the detailed analyses of Saint-Venant torsion of anisotropic and of orthotropic bars. In these books, both the Prandtl’ stress function and torsion function formulations are presented. The warping properties of twisted functionally graded Cartesian anisotropic linearly elastic bars are treated by Horgan [10]. Some important properties of torsion of Cartesian anisotropic bar for elliptical cross section have been studied in paper by Ecsedi and Baksa [11]. Paper [12] deals with the Saint-Venant’s torsion of elastic cylindrical orthotropic solid elliptical cross section. By the use of principle of minimum of potential energy and principle of minimum of complementary energy, approximate analytical solutions are derived for the torsion function and for the Prandtl’s stress function in paper by Ecsedi and Baksa [12].

Papers [13,14,15,16] present the formulation of uniform torsion and some analytical solutions for the cylindrical orthotropic elastic bars. The Saint-Venant torsion of the compound cylindrical orthotropic bar is studied in paper [17]. Analytical solution is given for the uniform torsion of the cylindrical orthotropic annular wedge-shaped bar whose curved boundary segments are strengthened by thin isotropic elastic shells (Ecsedi and Baksa [17]). The paper [18] deals with the Saint-Venant torsion of elastic cylindrical orthotropic composite bar whose cross section is a sector of a solid circle. An analytical method is presented to obtain the Prandtl’s stress function and the torsion function of the composite cross section made of two different cylindrical orthotropic materials.

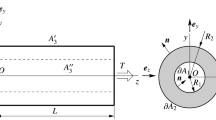
The present paper addresses the Saint-Venant torsion for cylindrical orthotropic homogeneous linearly elastic bars, whose cross section is bounded by two straight lines and a curved arc. The geometry of the boundary curve of solid cross section depends on the shear moduli of the cylindrical orthotropic bar. The cross section of the considered bar has an axis of symmetry (Fig. 1). The polar coordinate system \(Or\varphi {z}\) is positioned at the left and cross section of the bar as shown in Fig. 1. The unit vector in radial direction is \({\varvec{e}}_{r}\), in circumferential direction the unit vector is denoted by \({\varvec{e}}_{\varphi }\), and the unit vector in axial direction of the bar is \({\varvec{e}}_{z}\). The cross section of the bar is bounded by two straight lines \(c_{1}\) and \(c_{2}\) and a curved arc \(c_{3}\).

Fig. 1
figure 1

Saint-Venant torsion of cylindrically orthotropic bar

Full size image

The geometry of the cross section depends on the material properties of cylindrical orthotropic elastic material. The principle directions of cylindrical orthotropy at point P are given by the unit vectors \({\varvec{e}}_{r}\), \({\varvec{e}}_{\varphi }\) and \({\varvec{e}}_{z}\), and the shear moduli are [3,4,5,6]

$$\begin{aligned} A_{44}=G_{\varphi z}, \quad A_{55} = G_{rz}, \quad A_{66}=G_{r\varphi }. \end{aligned}$$
(1)

Let

$$\begin{aligned} \beta =\sqrt{\frac{G_{rz}}{G_{\varphi z}}} \end{aligned}$$
(2)

The positions of boundary line segments \(c_{1}\) and \(c_{2}\) are given by the angle \(\alpha \) (Fig. 1)

$$\begin{aligned} \alpha =\frac{\pi }{6\beta } \end{aligned}$$
(3)

and the equation of curved boundary curve \(c_{3}\) is

$$\begin{aligned} R(\varphi )=\frac{a}{\cos \beta \varphi }, \qquad -\alpha \le \varphi \le \alpha . \end{aligned}$$
(4)

Since \(\alpha <\pi /2\), we have

$$\begin{aligned} \beta >\frac{1}{3}. \end{aligned}$$
(5)

The shape of boundary curve segment \(c_{3}\) as a function of \(\beta \) is shown in Fig. 2.

Fig. 2
figure 2

Shape of boundary curve \(c_{3}\)

Full size image

2 Governing equations

The torsion function is denoted by \(\omega =\omega (r,\varphi )\), the Prandtl’s stress function of the considered triangle-like shape cross section is \(U=U(r,\varphi )\). The rate of twist is represented by \(\vartheta \), and the applied torque is T. The torsional rigidity S is defined as

$$\begin{aligned} S=\frac{T}{\vartheta }. \end{aligned}$$
(6)

It is known that the Saint-Venant torsion of cylindrical orthotropic homogeneous linearly elastic bar leads to the following boundary value problem for the torsion function

$$\begin{aligned}&G_{rz}\left( \frac{\partial ^{2} {\omega }}{\partial {r}^{2}} + \frac{1}{r}\frac{\partial {\omega }}{\partial {r}}\right) +\frac{G_{\varphi {z}}}{r^{2}}\frac{\partial ^{2} {\omega }}{\partial {\varphi }^{2}} = 0 \quad (r,\varphi ) \in A, \end{aligned}$$
(7)
$$\begin{aligned}&G_{rz} n_{r}\frac{\partial {\omega }}{\partial {r}} + G_{\varphi z} n_{\varphi }\left( \frac{1}{r}\frac{\partial {\omega }}{\partial {\varphi }} + r \right) =0 \quad (r,\varphi ) \in \partial A. \end{aligned}$$
(8)

In Eqs. (7), (8), A denotes the cross section, \(\partial A\) is the boundary curve of A; \(n_{r}\) and \(n_{\varphi }\) are the component of the boundary normal vector \({\varvec{n}}=n_{r}{\varvec{e}}_{r} + n_{\varphi }{\varvec{e}}_{\varphi }\) [4,5,6,7]. The solution of Saint-Venant uniform torsion in terms of Prandtl’s stress function obtained from the following Dirichlet type boundary value problem

$$\begin{aligned}&\frac{\partial ^{2} {U}}{\partial {r}^{2}} + \frac{1}{r}\frac{\partial {U}}{\partial {r}} + \frac{G_{\varphi {z}}}{r^{2} G_{rz}} \frac{\partial ^{2} {U}}{\partial {\varphi }^{2}} = -2 G_{\varphi {z}} \quad (r,\varphi ) \in A, \end{aligned}$$
(9)
$$\begin{aligned}&U=0 \quad (r,\varphi ) \in \partial A. \end{aligned}$$
(10)

Knowing solutions of boundary value problems given by Eqs. (7), (8) and Eqs. (9), (10) the shearing stresses \(\tau _{rz}=\tau _{rz}(r,\varphi )\) and \(\tau _{\varphi z}=\tau _{\varphi z}(r,\varphi )\) can be computed from formulae (11) and (12)

$$\begin{aligned}&\tau _{rz}=\vartheta G_{rz}\frac{\partial {\omega }}{\partial {r}} =\frac{\vartheta }{r}\frac{\partial {U}}{\partial {\varphi }} \end{aligned}$$
(11)
$$\begin{aligned}&\tau _{\varphi z} = \vartheta G_{\varphi z} \left( \frac{1}{r}\frac{\partial {\omega }}{\partial {\varphi }}+r\right) =-\vartheta \frac{\partial {U}}{\partial {r}}. \end{aligned}$$
(12)

The torsional rigidity of the cross section can be obtained by the use of Eq. (13) or Eq. (14)

$$\begin{aligned}&S=G_{\varphi z} \int \limits _{A} \left( \frac{\partial {\omega }}{\partial {\varphi }}+r^{2}\right) \,\mathrm{d} {A} =G_{\varphi z} \int \limits _{\varphi =-\alpha }^{\alpha } \left( \int \limits _{r=0}^{R(\varphi )} \left( \frac{\partial {\omega }}{\partial {\varphi }} + r^{2}\right) \, \mathrm{d} {r} \right) \,\mathrm{d} {\varphi }, \end{aligned}$$
(13)
$$\begin{aligned}&S=2\int \limits _{A} U \,\mathrm{d} {A} = 2 \int \limits _{\varphi =-\alpha }^{\alpha } \left( \int \limits _{r=0}^{R(\varphi )}rU(r,\varphi )\, \mathrm{d} {r}\right) \,\mathrm{d} {\varphi }. \end{aligned}$$
(14)

3 Solution of the Saint-Venant torsion by Prandtl’s stress function

We shall try to solve the Dirichlet type boundary value problem formulated in Eqs. (9) and (10) by supposing that the stress function \(U=U(r,\varphi )\) is given by as

$$\begin{aligned} U(r,\varphi ) = C r^{2} \left( \sin ^{2}\beta \varphi - \frac{1}{3} \cos ^{2}\beta \varphi \right) \left( r \cos \beta \varphi - a\right) \qquad (r,\varphi )\in A\cup \partial A. \end{aligned}$$
(15)

for some computable constant C. The form of the function \(U=U(r,\varphi )\) is suggested by the homogeneous boundary condition (10). After some simple calculations from Eq. (9), it follows that

$$\begin{aligned} C=\frac{3 G_{\varphi z}}{2 a}, \end{aligned}$$
(16)

that is,

$$\begin{aligned} U(r,\varphi )&= \frac{3 G_{\varphi z}}{2 a} r^{2} \left( \sin ^{2}\beta \varphi - \frac{1}{3}\cos ^{2}\beta \varphi \right) \left( r\cos \beta \varphi - a \right) \nonumber \\&\quad (r,\varphi ) \in A\cup \partial A. \end{aligned}$$
(17)

The shearing stresses can be computed by the application of formulae (11) and (12). We have

$$\begin{aligned}&\tau _{rz}(r,\varphi )= \frac{\vartheta G_{\varphi z}}{2a}r\beta \sin \beta \varphi \left[ 12r\cos ^{2}\beta \varphi -8a\cos \beta \varphi - 3r \right] , \end{aligned}$$
(18)
$$\begin{aligned}&\tau _{\varphi z}(r,\varphi ) = \frac{\vartheta G_{\varphi z}r}{2a} \left[ -9r\cos \beta \varphi + 12r\cos ^{3}\beta \varphi +6a - 8a\cos ^{2}\beta \varphi \right] . \end{aligned}$$
(19)

From the formula (14), we obtain for the torsional rigidity

$$\begin{aligned} S=\frac{G_{\varphi z}a^{4}}{10\beta }\left( \tan \frac{\pi }{6} -\tan ^{3}\frac{\pi }{6}\right) = 0.03846001795 \frac{G_{\varphi z}}{\beta } a^{4}. \end{aligned}$$
(20)

Equation (20) for \(\beta =1\) \((G_{rz}=G_{\varphi z})\) gives the expression of torsional rigidity of isotropic equilateral triangle cross section [8]. The shearing stresses \(\tau _{rz}\) and \(\tau _{\varphi z}\) are zero at point P(2a/3, 0), i.e.,

$$\begin{aligned} \tau _{rz}\left( \frac{2a}{3},0\right) = \tau _{\varphi z}\left( \frac{2a}{3},0\right) = 0 \end{aligned}$$
(21)

independently of the value of \(\beta \).

The torsional rigidity of the cross section in terms of cross-sectional area

$$\begin{aligned} A=\frac{a^{2}}{\beta \sqrt{3}} \end{aligned}$$
(22)

can be expressed as

$$\begin{aligned} S=\frac{\sqrt{3}}{15}\sqrt{G_{rz}G_{\varphi z}} A^{2}. \end{aligned}$$
(23)

4 Solution of the Saint-Venant torsion by torsion function

To obtain the torsion function \(\omega =\omega (r,\varphi )\), the following equations will be used

$$\begin{aligned} \frac{\partial {\omega }}{\partial {r}} = \frac{1}{rG_{rz}} \frac{\partial {U}}{\partial {\varphi }}, \qquad \frac{\partial {\omega }}{\partial {\varphi }}= - \frac{r}{G_{\varphi z}} \frac{\partial {U}}{\partial {r}} - r^{2} \qquad (r,\varphi ) \in A\cup \partial A. \end{aligned}$$
(24)

The validity of these equations follows from the formulae (11) and (12). Solution of the system of partial differential equations (29) for \(\omega =\omega (r,\varphi )\) is as follows

$$\begin{aligned} \omega (r,\varphi )&= \frac{1}{2a\beta } \left[ r^{2}(4r \cos ^{2}\beta \varphi - 4 a \cos \beta \varphi -r)\sin \beta \varphi \right] \nonumber \\&\quad +c (r,\varphi )\in A\cup \partial A, \end{aligned}$$
(25)

By substitution of the expression of torsion function \(\omega =\omega (r,\varphi )\) into Eqs. (7) and (8), it can be pointed out that the function given by Eq. (25) is a solution of the Neumann type boundary value problem formulated in Eqs. (7) and (8). In the checking computation it is used that, the components of the boundary curve normal vector are

$$\begin{aligned}&n_{r} = 0, \quad n_{\varphi }=1 \qquad \text {on}\quad c_{1}, \end{aligned}$$
(26)
$$\begin{aligned}&n_{r} = 0, \quad n_{\varphi }=-1 \qquad \text {on}\quad c_{2}, \end{aligned}$$
(27)
$$\begin{aligned}&n_{r} = 1, \quad n_{\varphi }=-\tan \varphi \qquad \text {on}\quad c_{3}. \end{aligned}$$
(28)

A rigid body like translational motion of the bar in direction of axis z is described by c. We note that the warping of the cross section depends on only one material parameter \(\beta \).

5 Numerical example

The following data are used in the numerical example:

$$\begin{aligned}&G_{\varphi z}=5\times 10^{8}\,\mathrm{Pa}, \qquad G_{rz} = 8\times 10^{8}\,\mathrm{Pa}, \\&a=0.05\,\mathrm{m},\qquad \vartheta =2.5\times 10^{-2}\,1/\mathrm{m} \end{aligned}$$

The contour lines of the Prandtl’s stress function are shown in Fig. 3.

Fig. 3
figure 3

Contour lines of the stress function

Full size image

In Fig. 4, the contour lines of torsion function for \(c=0\) are given.

Fig. 4
figure 4

Contour lines of torsion function, \(c=0\)

Full size image

The radial shearing stress on the boundary line segment \(c_{1}\) is shown in Fig. 5 as a function of the radial coordinate r.

Fig. 5
figure 5

Plot of the radial shearing stress on the boundary curve segment \(c_{1}\)

Full size image

The circumferential shearing stress as a function of r at \(\varphi =0\) is illustrated in Fig. 6.

Fig. 6
figure 6

Graph of the circumferential shearing stresses as a function of r at \(\varphi =0\)

Full size image

In Fig. 7, the plots of torsion function are shown for five different values of radial coordinates \((r=\frac{a}{8},\,\frac{a}{4},\,\frac{a}{2},\,\frac{3a}{4},\,a)\) \(-\alpha \le \varphi \le \alpha \). Application of formula (20) gives the following result for the torsional rigidity

$$\begin{aligned} S=1893.997579\,\mathrm{Nm}^{2}. \end{aligned}$$
(29)

The contour lines of resultant shearing stress

$$\begin{aligned} \tau (r,\varphi ) = \sqrt{\tau _{rz}^{2} + \tau _{\varphi z}^{2}} \qquad (r,\varphi )\in A\cup \partial A \end{aligned}$$
(30)

are shown in Fig. 8.

Fig. 7
figure 7

Illustration of the torsion function for five different values of r as a function of \(\varphi \)

Full size image

The expressions of the \(\tau (r,\varphi )\) in terms of T at \(r=a\), \(\varphi =0\) and \(r=\frac{a}{\sqrt{3}}\), \(\varphi =\pm \frac{\pi }{6\beta }\) are as follows

$$\begin{aligned} \tau (a,0) = \frac{15}{2}\sqrt{3}\beta \frac{T}{a^{3}}, \qquad \tau \left( \frac{a}{\sqrt{3}},\pm \frac{\pi }{6\beta }\right) = \beta \tau (a,0). \end{aligned}$$
(31)

It is known that for \(\beta =1\)

$$\begin{aligned} \tau (a,0)=\tau \left( \frac{a}{\sqrt{3}},\pm \frac{\pi }{6}\right) . \end{aligned}$$
(32)
Fig. 8
figure 8

Contour lines of the resultant shearing stresses

Full size image

6 Conclusions

The object of this paper is the Saint-Venant torsion of cylindrical orthotropic homogeneous linearly elastic bar with solid cross section. The cross section of the considered bar is bounded by two straight lines and a curved arc. The geometry of the boundary curve of cross section depends on the shear moduli of the cylindrical orthotropic material. Closed-form solutions were derived for the Prandtl’s stress function, torsion function, shearing stresses and torsional rigidity. An example illustrates the application of the obtained formulae.