A four-variable global–local shear deformation theory for the analysis of deep curved laminated composite beams

Abstract

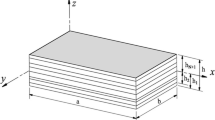
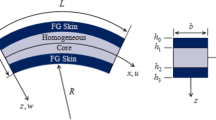
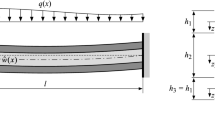
A precise global–local shear deformation theory is developed for the prediction of static and dynamic behaviors of thin and thick layered curved beams. The effect of deepness is considered in the derivation of the proposed beam theory. Variations of the shear stress along the thickness direction of the curved beam are approximated by using a global parabolic shear stress function which is locally refined at each layer. The zero conditions of shear stresses on the boundary surfaces of the curved beam are exactly satisfied, and no shear correction coefficient is needed. One of the important features of the present theory is that it has only four unknown field variables, which is only one more than the first-order shear deformation theory. A displacement-based finite element model is employed for solving the governing equations. For validation, the results obtained from static and free vibration tests are compared with the results of three-dimensional (3D) finite element analysis, classical theories, and other advanced shear deformation beam theories. The obtained numerical results show that the present model can precisely predict static and free vibration responses of both shallow and deep composite beams with arbitrary boundary and layup conditions.

Appendices

Appendix A: Material coordinate transformation

$$\begin{aligned} Q_{11}^{(i)}= & {} c_{11}^{(i)} \cos ^{4}\theta +2(c_{12}^{(i)} +2c_{66}^{(i)} )\cos ^{2}\theta \sin ^{2}\theta +C_{22}^{(i)} \sin ^{4}\theta , \end{aligned}$$

(A.1)

$$\begin{aligned} Q_{12}^{(i)}= & {} c_{12}^{(i)} \cos ^{4}\theta +(c_{11}^{(i)} +c_{22}^{(i)} -4c_{66}^{(i)} )\cos ^{2}\theta \sin ^{2}\theta +c_{12}^{(i)} \sin ^{4}\theta , \end{aligned}$$

(A.2)

$$\begin{aligned} Q_{13}^{(i)}= & {} c_{13}^{(i)} \cos ^{2}\theta +c_{23}^{(i)} \sin ^{2}\theta , \end{aligned}$$

(A.3)

$$\begin{aligned} Q_{16}^{(i)}= & {} \left( c_{11}^{(i)} -c_{12}^{(i)} -2c_{66}^{(i)} \right) \cos ^{3}\theta \sin \theta +\left( 2c_{66}^{(i)} +c_{12}^{(i)} -c_{22}^{(i)} \right) \cos \theta \sin ^{3}\theta , \end{aligned}$$

(A.4)

$$\begin{aligned} Q_{26}^{(i)}= & {} \left( c_{12}^{(i)} -c_{22}^{(i)} +2c_{66}^{(i)} \right) \cos ^{3}\theta \sin \theta +\left( c_{11}^{(i)} -c_{12}^{(i)} -2c_{66}^{(i)} \right) \cos \theta \sin ^{3}\theta , \end{aligned}$$

(A.5)

$$\begin{aligned} Q_{36}^{(i)}= & {} \left( c_{13}^{(i)} -c_{23}^{(i)} \right) \cos \theta \sin \theta , \end{aligned}$$

(A.6)

$$\begin{aligned} Q_{22}^{(i)}= & {} c_{22}^{(i)} \cos ^{4}\theta +2\left( c_{12}^{(i)} +2c_{66}^{(i)} \right) \cos ^{2}\theta \sin ^{2}\theta +C_{11}^{(i)} \sin ^{4}\theta , \end{aligned}$$

(A.7)

$$\begin{aligned} Q_{23}^{(i)}= & {} c_{23}^{(i)} \cos ^{2}\theta +c_{13}^{(i)} \sin ^{2}\theta , \end{aligned}$$

(A.8)

$$\begin{aligned} Q_{33}^{(i)}= & {} c_{33}^{(i)} , \end{aligned}$$

(A.9)

$$\begin{aligned} Q_{44}^{(i)}= & {} c_{44}^{(i)} \cos ^{2}\theta +c_{55}^{(i)} \sin ^{2}\theta , \end{aligned}$$

(A.10)

$$\begin{aligned} Q_{45}^{(i)}= & {} \left( c_{55}^{(i)} -c_{44}^{(i)} \right) \cos \theta \sin \theta , \end{aligned}$$

(A.11)

$$\begin{aligned} Q_{55}^{(i)}= & {} c_{55}^{(i)} \cos ^{2}\theta +c_{44}^{(i)} \sin ^{2}\theta , \end{aligned}$$

(A.12)

$$\begin{aligned} Q_{66}^{(i)}= & {} \left( c_{11}^{(i)} +c_{22}^{(i)} -2c_{12}^{(i)} -2c_{66}^{(i)} \right) \cos ^{2}\theta \sin ^{2}\theta +c_{66}^{(i)} \left( \cos ^{4}\theta +\sin ^{4}\theta \right) \end{aligned}$$

(A.13)

where $\theta$ is the fiber orientation of the ith composite layer (i.e., the angle from s-direction to the 1-direction).

Appendix B: Euler’s differential equation

A first-order differential equation can be written in the following standard form:

$$\begin{aligned} \frac{\partial y}{\partial z}+p(z)y=g\left( z \right) \end{aligned}$$

(B.1)

where y(z) is an unknown function to be determined and p(z) and g(z) are continuous functions of z. The above type of differential equations is called Euler’s equation. The solution of the above equation is given by:

$$\begin{aligned} y(z)=\frac{1}{\mu (z)}\left( {y_{0} +\int {\mu (z)g\left( z \right) \,\mathrm{d}z} } \right) , \end{aligned}$$

(B.2)

where $\mu (z)=\exp ^{\int {p\left( z \right) \,\mathrm{d}z} }$, and $y_{0}$ is a constant that must be determined by applying the boundary condition.

Appendix C: Calculation of shear and radial stresses from equilibrium equations

In the absence of body forces, the equilibrium equations for a curved beam in the polar coordinate system ($\bar{{r}}$, $\theta$) can be written as follows [31]:

$$\begin{aligned} \frac{\partial \sigma _{\overline{{rr}}} }{\partial \bar{{r}}}+\frac{1}{\bar{{r}}}\frac{\partial \sigma _{\bar{{r}}\theta } }{\partial \theta }+\frac{\left( \sigma _{\overline{{rr}}} -\sigma _{\theta \theta }\right) }{\partial \bar{{r}}}=0, \end{aligned}$$

(C.1.1)

$$\begin{aligned} \frac{\partial \sigma _{\bar{{r}}\theta } }{\partial \bar{{r}}}+\frac{1}{\bar{{r}}}\frac{\partial \sigma _{\theta \theta } }{\partial \theta }+\frac{2\sigma _{\bar{{r}}\theta } }{\bar{{r}}}=0. \end{aligned}$$

(C.1.2)

Note that the s- and r-coordinates are related to polar coordinates ($\bar{{r}}$, $\uptheta )$ as follows:

$$\begin{aligned} r= & {} \bar{{r}}-R\end{aligned}$$

(C.2.1)

$$\begin{aligned} s= & {} R\theta . \end{aligned}$$

(C.2.2)

Equation (C.1.2) can be rewritten as follows:

$$\begin{aligned} \frac{\partial \sigma _{\bar{{r}}\theta } }{\partial \bar{{r}}}+\frac{2\sigma _{\bar{{r}}\theta } }{\bar{{r}}}=-\frac{1}{\bar{{r}}}\frac{\partial \sigma _{\theta \theta } }{\partial \theta }. \end{aligned}$$

(C.3)

The solution of the above Euler’s differential equation with considering the coordinate transformation relations (C.2) can be written as:

$$\begin{aligned} \sigma _{sr} =\frac{1}{(R+r)^{2}}\left[ {-\frac{1}{(R-h/2)^{2}}-\int _0^r {(R+r)R\frac{\partial \sigma _{ss} }{\partial s}\mathrm{d}r} } \right] . \end{aligned}$$

(C.4)

Similarly, Eq. (C.1.1) can be rewritten in the following form:

$$\begin{aligned} \frac{\partial \sigma _{\overline{{rr}}} }{\partial \bar{{r}}}+\frac{\sigma _{\overline{{rr}}} }{\partial \bar{{r}}}=\frac{\sigma _{\theta \theta } }{\partial \bar{{r}}}-\frac{1}{\bar{{r}}}\frac{\partial \sigma _{\bar{{r}}\theta } }{\partial \theta }. \end{aligned}$$

(C.5)

After solving the above Euler’s differential equation, the following expression is obtained for the normal stress:

$$\begin{aligned} \sigma _{rr} =\frac{1}{(R+r)}\left[ {-\frac{1}{(R-h/2)}+\int _0^r {\left( \sigma _{ss} -R\frac{\partial \sigma _{sr} }{\partial s}\right) \mathrm{d}r} } \right] . \end{aligned}$$

(C.6)