Vibrational behavior investigation of axially functionally graded cylindrical shells under moving pressure

Abstract

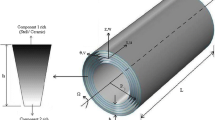
The current work presents an analytical procedure for the free vibration characteristics and dynamic response of an axisymmetric cylindrical shell that has finite length and it is made of functionally graded materials. The shell is subjected to a moving internal pressure. The material properties are assumed to vary along the axial direction according to an exponential law. The equations of motion are extracted based on the classical shell theory using Hamilton’s principle. These equations, which are a system of coupled partial differential equations with variable coefficients, are solved analytically to find the natural frequencies and the responses of the structure. A sensitivity analysis is performed, and the effects of different parameters on the results are studied. The results are compared with the results available in the literature. Also, the results of the free vibration problem are compared with those of the finite element method.

Appendix A

Before solving Eq. (18), it is necessary to compute the non-homogenous part of the equation. The load distribution can be defined using the Heaviside step function Eq. (20). So the right-hand side of Eq. (18b) can be written as:

$$\begin{aligned} \frac{2R}{L}\int _0^L {P\left( {x,t} \right) \exp \left( -\frac{nx}{L}\right) \sin (k_m x)\mathrm{d}x} =\frac{2R}{L}\int _0^{v.t} {q. \exp \left( -\frac{nx}{L}\right) \sin (k_m x)\mathrm{d}x} =f_6 (t). \end{aligned}$$

(A.1)

Therefore, Eqs. (18) are:

$$\begin{aligned}&-A_2 k_m^2 u_m +A_4 k_m w_m +A_5 \ddot{u}_m =0, \end{aligned}$$

(A.2)

$$\begin{aligned}&-A_6 k_m u_m +(A_7 -A_8 k_m^2 +A_{10} k_m^4 ) w_m +(A_5 -A_{12} k_m^2 ) \ddot{w}_m =f_6 (t). \end{aligned}$$

(A.3)

To solve Eqs. (A.2, A.3), one can use the Laplace transform for a solution. By assuming the zero initial conditions, one can write:

$$\begin{aligned}&-A_2 k_m^2 \bar{{u}}_m +A_4 k_m \bar{{w}}_m +A_5 s^{2}\bar{{u}}_m =0; \ \bar{{u}}_m (s)=\mathrm{Laplace}(u_m (t)); \ \bar{{w}}_m (s)=\mathrm{Laplace}(w_m (t)), \end{aligned}$$

(A.4)

$$\begin{aligned}&-A_6 k_m \bar{{u}}_m +(A_7 -A_8 k_m^2 +A_{10} k_m^4 ) \bar{{w}}_m +(A_5 -A_{12} k_m^2 ) s^{2} \bar{{w}}_m =\bar{{f}}_6 ; \ \bar{{f}}_6 (s)=\mathrm{Laplace}(f_6 (t)). \end{aligned}$$

(A.5)

Solving the algebraic equations (A.4, A.5) results in the displacements $\bar{{u}}_m ,\bar{{w}}_m$ in the Laplace domain. By applying the inverse Laplace, one can find the values $u_m (t), w_m (t)$. Now the solution can be found using Eq. (16). We performed the calculations using the mathematical software Maple 15. The mentioned formulation is correct when $t \,{<}\, L/V$ or before departure of the wavefront from the tube. When the wavefront arrived at the end of the shell or depart it, i.e., $t \,{\ge }\, L/V$, the pressure distribution is $P(x,t) \,{=}\,q$. For this case, the right-hand side of Eq. (A.3) is not a function of time and it is a constant so Eq. (A.5) is as follows:

$$\begin{aligned} -A_6 k_m \bar{{u}}_m +\left( A_7 -A_8 k_m^2 +A_{10} k_m^4\right) \bar{{w}}_m +\left( A_5 -A_{12} k_m^2\right) s^{2} \bar{{w}}_m =\frac{f_6 }{s}. \end{aligned}$$

(A.6)

Similar to Eqs. (A.4, A.5), one can solve Eqs. (A.4, A.6). Note that we have two sets of solutions: a solution for $t < L/V$ which is named as $y_{1}$ and one after the departure from the tube, e.g., $y_{2}$. The total solution is defined as:

$$\begin{aligned} Y= y_{1}\cdot (1-H(t-L/V))+ y_{2}\cdot (H(t-L/V)). \end{aligned}$$

(A.7)