Isogeometric hyperelastic shell analysis with out-of-plane deformation mapping

Abstract

We derive a hyperelastic shell formulation based on the Kirchhoff–Love shell theory and isogeometric discretization, where we take into account the out-of-plane deformation mapping. Accounting for that mapping affects the curvature term. It also affects the accuracy in calculating the deformed-configuration out-of-plane position, and consequently the nonlinear response of the material. In fluid–structure interaction analysis, when the fluid is inside a shell structure, the shell midsurface is what it would know. We also propose, as an alternative, shifting the “midsurface” location in the shell analysis to the inner surface, which is the surface that the fluid should really see. Furthermore, in performing the integrations over the undeformed configuration, we take into account the curvature effects, and consequently integration volume does not change as we shift the “midsurface” location. We present test computations with pressurized cylindrical and spherical shells, with Neo-Hookean and Fung’s models, for the compressible- and incompressible-material cases, and for two different locations of the “midsurface.” We also present test computation with a pressurized Y-shaped tube, intended to be a simplified artery model and serving as an example of cases with somewhat more complex geometry.

1 Introduction

A shell formulation based on the Kirchhoff–Love shell theory and isogeometric discretization was introduced in [1,2,3]. It has the advantage of not requiring rotational degrees of freedom. Extension to general hyperelastic material can be found in [4]. The formulation has been successfully used in computation of a good number of challenging problems, including wind-turbine fluid–structure interaction (FSI) [3, 5,6,7,8,9], bioinspired flapping-wing aerodynamics [10], bioprosthetic heart valves [11,12,13,14,15], fatigue and damage [16,17,18,19,20,21], and design [22, 23].

In this article, we start with the formulation from [4] and derive, based on the Kirchhoff–Love shell theory and isogeometric discretization, a hyperelastic shell formulation that takes into account the out-of-plane deformation mapping. Accounting for that mapping affects the curvature term. It also affects the accuracy in calculating the deformed-configuration out-of-plane position, and consequently the nonlinear response of the material. We are extending the range of applicability of Kirchhoff–Love shell theory to the situations where the Kirchhoff–Love shell kinematics is still valid, yet the thickness or the curvature change is significant enough to make a difference in the response. Fung’s model has different versions. In the version used in [12], the first invariant of the Cauchy–Green deformation tensor appears in a squared form. In the version we use in this article, it appears without being squared, and this version has been used in a number of arterial FSI computations [24,25,26,27,28,29,30,31] with the continuum model.

In FSI analysis, when the fluid is inside a shell structure, the shell midsurface is what it would know. That would be physically wrong, especially when the thickness is significant, because the inner surface is the one that the fluid should really see. In this article we also propose, as an alternative, shifting the “midsurface” location in the shell analysis to the inner surface. Furthermore, in performing the integrations over the undeformed configuration, we take into account the curvature effects, and consequently integration volume does not change as we shift the “midsurface” location.

To evaluate the performance of the shell formulation presented, we do test computations with pressurized cylindrical and spherical shells, with Neo-Hookean and Fung’s models, for the compressible- and incompressible-material cases, and for two different locations of the “midsurface.” We compare the results to near-analytical reference solutions. We also do test computation with a pressurized Y-shaped tube, intended to be a simplified artery model. This serves as an example of cases with somewhat more complex geometry.

In Sect. 2 we provide the governing equations. The hyperelastic shell model is presented in Sect. 3. Test computations with the cylindrical and spherical geometries and Y-shaped tube are presented in Sect. 4, and the concluding remarks in Sect. 5. In the Appendix, we provide some derivations used in Sect. 3, and the constitutive laws.

2 Governing equations

Let ${\varOmega }_t\subset {\mathbb {R}}^{n_{\mathrm {sd}}}$ be the spatial domain with boundary ${\varGamma }_{t}$ at time $t \in (0,T)$, where ${n_{\mathrm {sd}}}$ is the number of space dimensions. The subscript t indicates the time-dependence of the domain. The equations governing the structural mechanics are then written, on ${\varOmega }_t$ and $\forall t \in (0,T)$, as

$$\begin{aligned} \rho \left( \frac{\mathrm {d}^2 {\mathbf {y}}}{\mathrm {d}t^2} - {\mathbf {f}}\right) - \pmb {\nabla }\cdot \pmb {\sigma }= {\mathbf {0}}, \end{aligned}$$

(1)

where $\rho$, ${\mathbf {y}}$, ${\mathbf {f}}$ and $\pmb {\sigma }$ are the density, displacement, body force and Cauchy stress tensor. The essential and natural boundary conditions are represented as ${\mathbf {y}}= {\mathbf {g}}$ on $\left( {\varGamma }_t\right) _\mathrm {g}$ and ${\mathbf {n}}\cdot \pmb {\sigma }= {\mathbf {h}}$ on $\left( {\varGamma }_t\right) _\mathrm {h}$, where ${\mathbf {n}}$ is the unit normal vector, and ${\mathbf {g}}$ and ${\mathbf {h}}$ are given functions. The Cauchy stress tensor can be obtained from

$$\begin{aligned} \pmb {\sigma }&= J^{-1} {\mathbf {F}}{\mathbf {S}}{\mathbf {F}}^T, \end{aligned}$$

(2)

where ${\mathbf {F}}$ and $J$ are the deformation gradient tensor and its determinant, and ${\mathbf {S}}$ is the second Piola–Kirchhoff stress tensor. It is obtained from the strain-energy density function $\varphi$ as follows:

$$\begin{aligned} {\mathbf {S}}&\equiv \frac{\partial \varphi }{\partial {\mathbf {E}}}, \end{aligned}$$

(3)

where ${\mathbf {E}}$ is the the Green–Lagrange strain tensor:

$$\begin{aligned} {\mathbf {E}}&= \frac{1}{2}\left( {\mathbf {C}}- {\mathbf {I}}\right) , \end{aligned}$$

(4)

${\mathbf {C}}$ is the Cauchy–Green deformation tensor:

$$\begin{aligned} {\mathbf {C}}&\equiv {\mathbf {F}}^T \cdot {\mathbf {F}}, \end{aligned}$$

(5)

and ${\mathbf {I}}$ is the identity tensor. From Eqs. (3) and (4),

$$\begin{aligned} {\mathbf {S}}= 2\frac{\partial \varphi }{\partial {\mathbf {C}}}. \end{aligned}$$

(6)

3 Hyperelastic shell model

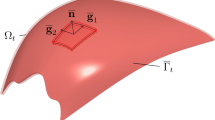
We split the domain as ${\varOmega }_t = \overline{{\varGamma }}_t\times \left( h_\mathrm {th}\right) _t$, where $\overline{{\varGamma }}_t$ represents the midsurface of the domain, which is parametrized by ${n_{\mathrm {pd}}}= {n_{\mathrm {sd}}}- 1$, where ${n_{\mathrm {pd}}}$ is the number of parametric dimensions. With the position $\overline{{\mathbf {x}}} \in \overline{{\varGamma }}_t$, we define a natural coordinate system:

$$\begin{aligned} \overline{{\mathbf {g}}}_\alpha&\equiv \frac{\partial \overline{{\mathbf {x}}}}{\partial \xi ^\alpha } \end{aligned}$$

(7)

$$\begin{aligned}&= \overline{{\mathbf {x}}}_{,\alpha }, \end{aligned}$$

(8)

where $\alpha = 1, \ldots , {n_{\mathrm {pd}}}$, and the third direction is based on

$$\begin{aligned} {\mathbf {n}}&\equiv \overline{{\mathbf {g}}}_3 \end{aligned}$$

(9)

$$\begin{aligned}&= \frac{\overline{{\mathbf {g}}}_1 \times \overline{{\mathbf {g}}}_2}{\left\| \overline{{\mathbf {g}}}_1 \times \overline{{\mathbf {g}}}_2\right\| }. \end{aligned}$$

(10)

The components of the metric tensor are

$$\begin{aligned} \overline{g}_{\alpha \beta } = \overline{{\mathbf {g}}}_{\alpha } \cdot \overline{{\mathbf {g}}}_{\beta }, \end{aligned}$$

(11)

and this is known as the first fundamental form. Similarly, we define the components of the metric tensor for the contravariant basis vectors as

$$\begin{aligned} \overline{g}^{\alpha \beta } = \overline{{\mathbf {g}}}^{\alpha } \cdot \overline{{\mathbf {g}}}^{\beta }, \end{aligned}$$

(12)

and obtain the tensor components and contravariant basis vectors from

$$\begin{aligned} \left[ \overline{g}^{\alpha \beta } \right]&= \left[ \overline{g}_{\alpha \beta } \right] ^{-1} \end{aligned}$$

(13)

and

$$\begin{aligned} \overline{{\mathbf {g}}}^\alpha&= \overline{g}^{\alpha \beta } \overline{{\mathbf {g}}}_\beta . \end{aligned}$$

(14)

We define

$$\begin{aligned} \overline{\pmb {{\varGamma }}}_{\alpha \beta }&= \frac{\partial ^2 \overline{{\mathbf {x}}}}{\partial \xi ^\alpha \partial \xi ^\beta }, \end{aligned}$$

(15)

and with that, components of the covariant curvature tensor are

$$\begin{aligned} \overline{b}_{\alpha \beta }&= \overline{\pmb {{\varGamma }}}_{\alpha \beta }\cdot {\mathbf {n}}\end{aligned}$$

(16)

$$\begin{aligned}&= \overline{{\mathbf {g}}}_{\beta , \alpha }\cdot {\mathbf {n}}, \end{aligned}$$

(17)

and this is known as the second fundamental form.

A position ${\mathbf {x}} \in {\varOmega }_t$ is represented as

$$\begin{aligned} {\mathbf {x}}&= \overline{{\mathbf {x}}} + {\mathbf {n}}\xi ^3, \end{aligned}$$

(18)

where $-1 \le \xi ^\alpha \le 1$ and $\xi ^3 \in \left( h_\mathrm {th}\right) _t$. The basis vectors are represented as

$$\begin{aligned} {\mathbf {g}}_{\alpha }&\equiv {\mathbf {x}}_{, \alpha } \end{aligned}$$

(19)

$$\begin{aligned}&= \overline{{\mathbf {g}}}_\alpha + {{\mathbf {n}}}_{,\alpha } \xi ^3 \end{aligned}$$

(20)

$$\begin{aligned}&= \overline{{\mathbf {g}}}_\alpha -\overline{b}_{\alpha \gamma } \overline{{\mathbf {g}}}^\gamma \xi ^3. \end{aligned}$$

(21)

See Appendix A.1 for the lines between Eqs. (20) and (21). Because ${\mathbf {g}}_\alpha$ and $\overline{{\mathbf {g}}}_\alpha$ are on parallel planes (from the Kirchhoff–Love shell theory),

$$\begin{aligned} {\mathbf {g}}_3&= \overline{{\mathbf {g}}}_3. \end{aligned}$$

(22)

With that, the metric tensor components in 3D space are

$$\begin{aligned} g_{\alpha \beta }&= \overline{g}_{\alpha \beta } - 2 \overline{b}_{\alpha \beta } \xi ^3 + \overline{b}_{\alpha \gamma } \overline{g}^{\gamma \delta } \overline{b}_{\beta \delta } \left( \xi ^3\right) ^2, \end{aligned}$$

(23)

$$\begin{aligned} g_{\alpha 3}&= 0, \end{aligned}$$

(24)

$$\begin{aligned} g_{3 \alpha }&= 0, \end{aligned}$$

(25)

$$\begin{aligned} g_{3 3}&= 1. \end{aligned}$$

(26)

Remark 1

The quadratic term may be omitted. However, if the metric tensor is obtained from the basis vectors, the term will automatically be included.

We now provide similar definitions and derivations for the undeformed configuration. We start with the basis vectors:

$$\begin{aligned} \overline{{\mathbf {G}}}_\alpha&= \frac{\partial \overline{{\mathbf {X}}}}{\partial \xi _0^\alpha } \end{aligned}$$

(27)

$$\begin{aligned}&= \overline{{\mathbf {X}}}_{,\alpha }, \end{aligned}$$

(28)

and

$$\begin{aligned} {\mathbf {N}}&\equiv \overline{{\mathbf {G}}}_3 \end{aligned}$$

(29)

$$\begin{aligned}&= \frac{\overline{{\mathbf {G}}}_1 \times \overline{{\mathbf {G}}}_2}{\left\| \overline{{\mathbf {G}}}_1 \times \overline{{\mathbf {G}}}_2\right\| }. \end{aligned}$$

(30)

A position ${\mathbf {X}} \in {\varOmega }_0$ is expressed as

$$\begin{aligned} {\mathbf {X}}&= \overline{{\mathbf {X}}} + {\mathbf {N}} \xi ^3_0, \end{aligned}$$

(31)

where $-1 \le \xi ^\alpha _0 \le 1$ and $\xi ^3_0 \in \left( h_\mathrm {th}\right) _0$. The basis vectors are represented as

$$\begin{aligned} {\mathbf {G}}_\alpha&= {\mathbf {X}}_{,\alpha } \end{aligned}$$

(32)

$$\begin{aligned}&= \overline{{\mathbf {G}}}_\alpha + {\mathbf {N}}_{, \alpha } \xi ^3_0 \end{aligned}$$

(33)

$$\begin{aligned}&= \overline{{\mathbf {G}}}_\alpha - \overline{B}_{\alpha \gamma } \overline{{\mathbf {G}}}^\gamma \xi ^3_0, \end{aligned}$$

(34)

$$\begin{aligned} {\mathbf {G}}_3&= \overline{{\mathbf {G}}}_3. \end{aligned}$$

(35)

The metric tensor components in 3D space are

$$\begin{aligned} G_{\alpha \beta }&= \overline{G}_{\alpha \beta } - 2 \overline{B}_{\alpha \beta } \xi ^3_0 + \overline{B}_{\alpha \gamma } \overline{G}^{\gamma \delta } \overline{B}_{\beta \delta } \left( \xi ^3_0\right) ^2 , \end{aligned}$$

(36)

$$\begin{aligned} G_{3 \alpha }&= 0, \end{aligned}$$

(37)

$$\begin{aligned} G_{\alpha 3}&= 0, \end{aligned}$$

(38)

$$\begin{aligned} G_{3 3}&= 1, \end{aligned}$$

(39)

and $\overline{B}_{\alpha \beta }$ is the second fundamental form for the midsurface of the undeformed configuration. On the midsurface the parametric coordinates indicate the same material points, and therefore, $\xi ^\alpha = \xi ^\alpha _0$. In the third direction, however, because of the normalization, the coordinates may not be the same. The relationship is

$$\begin{aligned} \frac{\mathrm {d}\xi ^3}{\mathrm {d}\xi ^3_0}&= \lambda _3, \end{aligned}$$

(40)

where $\lambda _3$ is the stretch in the third direction.

3.1 Kinematics

We obtain ${\mathbf {F}}$ from the following relationship:

$$\begin{aligned} {\mathbf {g}}_{\alpha } \mathrm {d}\xi ^{\alpha }_0 + {\mathbf {g}}_{3}\lambda _3 \mathrm {d}\xi ^3_0&= {\mathbf {F}} \cdot \left( {\mathbf {G}}_\alpha \mathrm {d}\xi ^\alpha _0 + {\mathbf {G}}_3 \mathrm {d}\xi ^3_0 \right) . \end{aligned}$$

(41)

This means that

$$\begin{aligned} {\mathbf {g}}_{\alpha }&= {\mathbf {F}}\cdot {\mathbf {G}}_{\alpha }, \end{aligned}$$

(42)

$$\begin{aligned} \lambda _3 {\mathbf {g}}_{3}&= {\mathbf {F}}\cdot {\mathbf {G}}_{3}. \end{aligned}$$

(43)

Then we can write ${\mathbf {F}}$ as

$$\begin{aligned} {\mathbf {F}}&= {\mathbf {g}}_\alpha {\mathbf {G}}^\alpha + \lambda _3 {\mathbf {g}}_3 {\mathbf {G}}^3, \end{aligned}$$

(44)

and J as

$$\begin{aligned} J&= \frac{1}{ {\mathbf {G}}_3 \cdot \left( {\mathbf {G}}_1 \times {\mathbf {G}}_2 \right) } \left( {\mathbf {F}}\cdot {\mathbf {G}}_3 \right) \cdot \left( \left( {\mathbf {F}}\cdot {\mathbf {G}}_1 \right) \times \left( {\mathbf {F}}\cdot {\mathbf {G}}_2 \right) \right) \end{aligned}$$

(45)

$$\begin{aligned}&= \lambda _3 \frac{\left( {\mathbf {g}}_1 \times {\mathbf {g}}_2 \right) \cdot {\mathbf {n}}}{\left( {\mathbf {G}}_1 \times {\mathbf {G}}_2\right) \cdot {\mathbf {N}}} \end{aligned}$$

(46)

$$\begin{aligned}&= \lambda _3 \frac{\left\| {\mathbf {g}}_1 \times {\mathbf {g}}_2 \right\| }{\left\| {\mathbf {G}}_1 \times {\mathbf {G}}_2\right\| }. \end{aligned}$$

(47)

From Eq. (5), we can write ${\mathbf {C}}$ as

$$\begin{aligned} {\mathbf {C}}&= \left( {\mathbf {G}}^\alpha {\mathbf {g}}_\alpha + \lambda _3 {\mathbf {G}}^3 {\mathbf {g}}_3 \right) \cdot \left( {\mathbf {g}}_\beta {\mathbf {G}}^\beta + \lambda _3 {\mathbf {g}}_3 {\mathbf {G}}^3 \right) \end{aligned}$$

(48)

$$\begin{aligned}&= g_{\alpha \beta } {\mathbf {G}}^\alpha {\mathbf {G}}^\beta + \lambda _3^2 {\mathbf {G}}^3 {\mathbf {G}}^3, \end{aligned}$$

(49)

and the determinant of ${\mathbf {C}}$ gives the square of J:

$$\begin{aligned} J^2&= \det {\mathbf {C}}\end{aligned}$$

(50)

$$\begin{aligned}&=\frac{A^2}{A_0^2} \lambda _3^2, \end{aligned}$$

(51)

$$\begin{aligned} A^2&=\det \left[ g_{\alpha \beta }\right] , \end{aligned}$$

(52)

$$\begin{aligned} A_0^2&=\det \left[ G_{\alpha \beta } \right] . \end{aligned}$$

(53)

From Eq. (4), we can write ${\mathbf {E}}$ as

$$\begin{aligned} {\mathbf {E}}&= \frac{1}{2}\left( {\mathbf {C}}- \left( G_{\alpha \beta } {\mathbf {G}}^\alpha {\mathbf {G}}^\beta + {\mathbf {G}}^3 {\mathbf {G}}^3\right) \right) \end{aligned}$$

(54)

$$\begin{aligned}&= \frac{1}{2}\left( g_{\alpha \beta } - G_{\alpha \beta }\right) {\mathbf {G}}^\alpha {\mathbf {G}}^\beta + \frac{1}{2}\left( \lambda _3^2 - 1\right) {\mathbf {G}}^3 {\mathbf {G}}^3. \end{aligned}$$

(55)

The covariant components of the in-plane strain tensor are

$$\begin{aligned} E_{\alpha \beta }&= \frac{1}{2}\left( g_{\alpha \beta } - G_{\alpha \beta }\right) \end{aligned}$$

(56)

$$\begin{aligned}&= \underbrace{\frac{1}{2}\left( \overline{g}_{\alpha \beta } -\overline{G}_{\alpha \beta }\right) }_{\overline{\varepsilon }_{\alpha \beta }} + \left( - \overline{b}_{\alpha \beta } \xi ^3 + \overline{B}_{\alpha \beta } \xi ^3_0 \right) \nonumber \\&\quad + \frac{1}{2}\left( \overline{b}_{\alpha \gamma } \overline{g}^{\gamma \delta } \overline{b}_{\beta \delta } \left( \xi ^3\right) ^2 - \overline{B}_{\alpha \gamma } \overline{G}^{\gamma \delta } \overline{B}_{\beta \delta } \left( \xi ^3_0\right) ^2 \right) . \end{aligned}$$

(57)

We write $\xi ^3\left( \xi _0^3\right)$ as $\xi ^3\left( \xi _0^3\right) = \hat{\lambda _3} \left( \xi _0^3\right) \xi _0^3$. From the Taylor expansion of $\hat{\lambda _3}$ around $\xi _0^3 = 0$, we obtain

$$\begin{aligned} \xi ^3&= \overline{\lambda _3} \xi ^3_0 + \frac{\mathrm {d}\hat{\lambda _3} }{\mathrm {d}\xi ^3_0} \left( \xi ^3_0\right) ^2 +{\mathcal {O}}\left( \left( \xi _0^3\right) ^3\right) . \end{aligned}$$

(58)

We note that $\overline{\lambda _3}$ is the stretch at $\xi _0^3 = 0$, which is $\hat{\lambda _3}\left( 0\right)$. With that,

$$\begin{aligned}&E_{\alpha \beta } = \overline{\varepsilon }_{\alpha \beta } + \left( - \overline{b}_{\alpha \beta } \xi ^3 + \overline{B}_{\alpha \beta } \xi ^3_0 \right) + \frac{1}{2} \nonumber \\&\quad \left( \overline{b}_{\alpha \gamma } \overline{g}^{\gamma \delta } \overline{b}_{\beta \delta } \overline{\lambda _3}^2 - \overline{B}_{\alpha \gamma } \overline{G}^{\gamma \delta } \overline{B}_{\beta \delta } \right) \left( \xi ^3_0\right) ^2 + {\mathcal {O}}\left( \left( \xi _0^3\right) ^3\right) \end{aligned}$$

(59)

$$\begin{aligned}&= \overline{\varepsilon }_{\alpha \beta } + \left( - \overline{b}_{\alpha \beta } \xi ^3 + \overline{B}_{\alpha \beta } \xi ^3_0 \right) +{\mathcal {O}}\left( \left( \xi _0^3\right) ^2\right) . \end{aligned}$$

(60)

3.2 Constitutive equations

The total differential of the second Piola–Kirchhoff stress tensor is

$$\begin{aligned} \mathrm {d}{\mathbf {S}}&= \frac{\partial {\mathbf {S}}}{\partial {\mathbf {E}}}: \mathrm {d}{\mathbf {E}}\end{aligned}$$

(61)

$$\begin{aligned}&= \frac{\partial S^{IJ}}{\partial E_{KL}} {\mathbf {G}}_{I}{\mathbf {G}}_{J} {\mathbf {G}}_{K} {\mathbf {G}}_{L} : \mathrm {d}E_{M N} {\mathbf {G}}^{M} {\mathbf {G}}^{N} \end{aligned}$$

(62)

$$\begin{aligned}&= {\mathbb {C}}^{IJKL} {\mathbf {G}}_{I}{\mathbf {G}}_{J} \mathrm {d}E_{K L}, \end{aligned}$$

(63)

where $I, J, K, L, M, N = 1, \ldots , {n_{\mathrm {sd}}}$. From Eq. (4), the following expression can be used:

$$\begin{aligned} {\mathbb {C}}^{IJKL}&= 2 \frac{\partial S^{IJ}}{\partial C_{KL}}. \end{aligned}$$

(64)

For shells,

$$\begin{aligned} \mathrm {d}S^{IJ} = {\mathbb {C}}^{IJ\gamma \delta } \mathrm {d}E_{\gamma \delta } + {\mathbb {C}}^{IJ 33} \mathrm {d}E_{33}, \end{aligned}$$

(65)

because $\mathrm {d}E_{3\alpha } = \mathrm {d}E_{\alpha 3} = 0$. From Eq. (65), we can write

$$\begin{aligned} \mathrm {d}S^{33} = {\mathbb {C}}^{33\gamma \delta } \mathrm {d}E_{\gamma \delta } + {\mathbb {C}}^{33 33} \mathrm {d}E_{33}, \end{aligned}$$

(66)

and from Eqs. (4) and (66), we can write

$$\begin{aligned} \mathrm {d}S^{33} = \frac{1}{2}{\mathbb {C}}^{33\gamma \delta } \mathrm {d}C_{\gamma \delta } + \frac{1}{2}{\mathbb {C}}^{33 33} \mathrm {d}C_{33}. \end{aligned}$$

(67)

From the plane stress condition $S^{33} = 0$, $\mathrm {d}S^{33} = 0$, and consequently

$$\begin{aligned} \mathrm {d}E_{33}&= - \frac{{\mathbb {C}}^{33\gamma \delta }}{{\mathbb {C}}^{33 33}} \mathrm {d}E_{\gamma \delta }, \end{aligned}$$

(68)

which makes

$$\begin{aligned} \mathrm {d}S^{\alpha \beta }&= {\mathbb {C}}^{\alpha \beta \gamma \delta } \mathrm {d}E_{\gamma \delta } - \frac{ {\mathbb {C}}^{\alpha \beta 33} {\mathbb {C}}^{33\gamma \delta } }{{\mathbb {C}}^{33 33}} \mathrm {d}E_{\gamma \delta }, \end{aligned}$$

(69)

and therefore we introduce

$$\begin{aligned} \hat{{\mathbb {C}}}^{\alpha \beta \gamma \delta }&= {\mathbb {C}}^{\alpha \beta \gamma \delta } - \frac{{\mathbb {C}}^{\alpha \beta 3 3 }{\mathbb {C}}^{33\gamma \delta }}{{\mathbb {C}}^{33 33}}. \end{aligned}$$

(70)

In computing $C_{33}$, we have different methods for incompressible and compressible materials. In the case of incompressible material, from Eq. (49) we can write $C_{33} = \lambda _3^2$. Because $J = 1$,

$$\begin{aligned} \lambda _3&= \frac{1}{A / A_0}, \end{aligned}$$

(71)

and therefore

$$\begin{aligned} C_{33}&= \frac{A_0^2}{A^2}. \end{aligned}$$

(72)

In the case of compressible material, as can be found in [32], $C_{33}$ can be calculated by Newton–Raphson iterations that would make $S^{33} = 0$. Because $C_{\gamma \delta }$ does not change during the iterations, the iteration increment is

$$\begin{aligned} \varDelta C_{33}^i&= - \frac{\left( S^{33}\right) ^i}{\left( \mathrm {d}S^{33}/ \mathrm {d}C_{33} \right) ^i}. \end{aligned}$$

(73)

From Eq. (67) and remembering that $\mathrm {d}C_{\gamma \delta } = 0$ during the iterations,

$$\begin{aligned} \varDelta C_{33}^i&= - 2 \frac{\left( S^{33}\right) ^i}{\left( {\mathbb {C}}^{3333}\right) ^i}. \end{aligned}$$

(74)

The update takes place as

$$\begin{aligned} C_{33}^{i+1}&= C_{33}^i + \varDelta C_{33}^i, \end{aligned}$$

(75)

where superscript i is the iteration counter, and as the initial guess we have the following three options:

$$\begin{aligned} C_{33}^{0}&= 1, \end{aligned}$$

(76)

$$\begin{aligned} C_{33}^{0}&= \frac{A^2_0}{A^2}, \end{aligned}$$

(77)

$$\begin{aligned} C_{33}^{0}&= \frac{1}{2} g_{\alpha \beta } G^{\alpha \beta }. \end{aligned}$$

(78)

The option given by Eq. (78) comes from the constitutive law for zero bulk modulus. To preclude $C_{33}$ being negative, we introduce an alternative update method based on the logarithm of $C_{33}$:

$$\begin{aligned} \ln C_{33}^{i+1}&= \ln C_{33}^{i} + \frac{\mathrm {d}\ln C_{33}}{\mathrm {d}C_{33}} \varDelta C_{33}^{i}\end{aligned}$$

(79)

$$\begin{aligned}&= \ln C_{33}^{i} + \frac{\varDelta C_{33}^{i}}{C_{33}^i}. \end{aligned}$$

(80)

3.3 Variational formulation

The variation of the in-plane components of the Green–Lagrange tensor is

$$\begin{aligned} \delta E_{\alpha \beta }&= \delta \overline{\varepsilon }_{\alpha \beta } - \delta \overline{b}_{\alpha \beta } \xi ^3 + \overline{b}_{\alpha \beta } \delta \xi ^3. \end{aligned}$$

(81)

The variation of $\xi ^3$ can be dropped (see Appendix B), and we obtain

$$\begin{aligned} \delta E_{\alpha \beta }&= \delta \overline{\varepsilon }_{\alpha \beta } + \underbrace{ \left( - \delta \overline{b}_{\alpha \beta } \right) }_{ \delta \overline{\kappa }_{\alpha \beta } } \xi ^3. \end{aligned}$$

(82)

With that,

$$\begin{aligned} \delta W_{\mathrm {int}}&= -\int _{{\varOmega }_0} \delta {\mathbf {E}}: {\mathbf {S}}\mathrm {d}{\varOmega }\end{aligned}$$

(83)

$$\begin{aligned}&= -\int _{\overline{{\varGamma }}_0} \int _{(h_\mathrm {th})_0} \delta \overline{\varepsilon }_{\alpha \beta } {{\mathbf {G}}}^{\alpha } {{\mathbf {G}}}^{\beta } : S^{\gamma \delta } {\mathbf {G}}_{\gamma } {\mathbf {G}}_{\delta } \frac{A_0}{\overline{A}_0} \mathrm {d}\xi ^3 \mathrm {d}{\varGamma }\nonumber \\&\quad - \int _{\overline{{\varGamma }}_0} \int _{(h_\mathrm {th})_0} \xi ^3 \delta \overline{\kappa }_{\alpha \beta } {{\mathbf {G}}}^{\alpha } {{\mathbf {G}}}^{\beta } : S^{\gamma \delta } {\mathbf {G}}_{\gamma } {\mathbf {G}}_{\delta } \frac{A_0}{\overline{A}_0} \mathrm {d}\xi ^3 \mathrm {d}{\varGamma }, \end{aligned}$$

(84)

which means

$$\begin{aligned} \delta W_{\mathrm {int}}&= -\int _{\overline{{\varGamma }}_0} \delta \overline{\varepsilon }_{\alpha \beta } \int _{(h_\mathrm {th})_0} S^{\alpha \beta } \frac{A_0}{\overline{A}_0} \mathrm {d}\xi ^3 \mathrm {d}{\varGamma }\nonumber \\&\quad - \int _{\overline{{\varGamma }}_0} \delta \overline{\kappa }_{\alpha \beta } \int _{(h_\mathrm {th})_0} \xi ^3 S^{\alpha \beta } \frac{A_0}{\overline{A}_0} \mathrm {d}\xi ^3 \mathrm {d}{\varGamma }. \end{aligned}$$

(85)

Remark 2

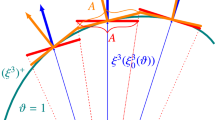
Evaluation of ${\mathbf {S}}$ requires a material point correspondence in the third direction. We take that into account by integrating Eq. (40) with the 4th order Runge–Kutta method, and $\lambda _3$ can be obtained from the constitutive law given in Sect. 4.1. Figure 1 illustrates the deformation mapping. In general, stretch at a convex side is less than the stretch at the concave side, which results in a nonuniform $\lambda _3$.

Now we derive what we need:

$$\begin{aligned} \delta \overline{\varepsilon }_{\alpha \beta }&= \frac{1}{2}\left( \delta \overline{{\mathbf {g}}}_\alpha \cdot \overline{{\mathbf {g}}}_\beta + \overline{{\mathbf {g}}}_\alpha \cdot \delta \overline{{\mathbf {g}}}_\beta \right) \end{aligned}$$

(86)

$$\begin{aligned}&= \frac{1}{2}\left( \frac{\partial \delta \overline{{\mathbf {x}}}}{\partial \xi ^\alpha } \cdot \overline{{\mathbf {g}}}_\beta + \overline{{\mathbf {g}}}_\alpha \cdot \frac{\partial \delta \overline{{\mathbf {x}}}}{\partial \xi ^\beta } \right) , \end{aligned}$$

(87)

$$\begin{aligned} \delta \overline{\kappa }_{\alpha \beta }&= - \frac{\partial \delta \overline{{\mathbf {g}}}_\alpha }{\partial \xi ^\beta } \cdot {\mathbf {n}} - \frac{\partial \overline{{\mathbf {g}}}_\alpha }{\partial \xi ^\beta } \cdot \delta {\mathbf {n}} \end{aligned}$$

(88)

$$\begin{aligned}&= - \delta \overline{\pmb {{\varGamma }}}_{\alpha \beta } \cdot {\mathbf {n}} + \overline{\pmb {{\varGamma }}}_{\alpha \beta } \cdot \overline{{\mathbf {g}}}^\gamma \left( {\mathbf {n}}\cdot \delta \overline{{\mathbf {g}}}_\gamma \right) \end{aligned}$$

(89)

$$\begin{aligned}&= - \left( \delta \overline{\pmb {{\varGamma }}}_{\alpha \beta } - \left( \overline{\pmb {{\varGamma }}}_{\alpha \beta } \cdot \overline{{\mathbf {g}}}^\gamma \right) \delta \overline{{\mathbf {g}}}_\gamma \right) \cdot {\mathbf {n}}, \end{aligned}$$

(90)

where

$$\begin{aligned} \delta \overline{\pmb {{\varGamma }}}_{\alpha \beta }&= \delta \overline{{\mathbf {x}}}_{,\alpha \beta }, \end{aligned}$$

(91)

and the variation of the normal vector (see Appendix A.2) is

$$\begin{aligned} \delta {\mathbf {n}}&= - \overline{{\mathbf {g}}}^\gamma \left( {\mathbf {n}}\cdot \delta \overline{{\mathbf {g}}}_\gamma \right) . \end{aligned}$$

(92)

Fig. 1

Deformation mapping from the undeformed configuration to the current configuration. Mapping of the integration points (5 in this case) is included in the sketch, and calculation of the kth integration point in the current configuration is shown

Fig. 2

Pressurized cylinder. Neo-Hookean model. Reference solutions. Midsurface model (top) and inner-surface model (bottom)

Fig. 3

Pressurized cylinder. Fung’s model. Reference solutions. Midsurface model (top) and inner-surface model (bottom). Note that the pressure scale is logarithmic

Fig. 4

Pressurized cylinder. Fung’s model. Reference solutions. Midsurface model. Two more Poisson’s ratios beyond those in Fig. 3

Fig. 5

Pressurized cylinder. Neo-Hookean model ($\nu = 0.45$). Midsurface model (top), inner-surface model (middle), and continuum model (bottom). Solid curve is the reference solution

Fig. 6

Pressurized cylinder. Neo-Hookean model ($\nu =0.49$). Midsurface model (top), inner-surface model (middle), and continuum model (bottom). Solid curve is the reference solution

Fig. 7

Pressurized cylinder. Neo-Hookean model (incompressible). Midsurface model (top), and inner-surface model (bottom). Solid curve is the reference solution

Fig. 8

Pressurized cylinder. Fung’s model ($\nu =0.45$). Midsurface model (top), inner-surface model (middle), and continuum model (bottom). Solid curve is the reference solution

Fig. 9

Pressurized cylinder. Fung’s model ($\nu =0.49$). Midsurface model (top), inner-surface model (middle), and continuum model (bottom). Solid curve is the reference solution

Fig. 10

Pressurized cylinder. Fung’s model (incompressible). Midsurface model (top), and inner-surface model (bottom). Solid curve is the reference solution

Fig. 11

Pressurized cylinder. Fung’s model. Incompressible-material case. Midsurface model. Solutions from the shell models with and without the out-of-plane deformation mapping

Fig. 12

Pressurized sphere. Neo-Hookean model. Reference solutions. Midsurface model (top) and inner-surface model (bottom)

Fig. 13

Pressurized sphere. Fung’s model. Reference solutions. Midsurface model (top) and inner-surface model (bottom). Note that the pressure scale is logarithmic

3.4 Linearization for the Newton–Raphson iterations

The linearization for the Newton–Raphson iterations is done as

$$\begin{aligned}&\delta _a \delta _b W_{\mathrm {int}}= -\int _{\overline{{\varGamma }}_0} \delta _a \delta _b \overline{\varepsilon }_{\alpha \beta } \int _{(h_\mathrm {th})_0} S^{\alpha \beta } \frac{A_0}{\overline{A}_0} \mathrm {d}\xi ^3 \mathrm {d}{\varGamma }\nonumber \\&\quad - \int _{\overline{{\varGamma }}_0} \delta _a \delta _b \overline{\kappa }_{\alpha \beta } \int _{(h_\mathrm {th})_0} \xi ^3 S^{\alpha \beta } \frac{A_0}{\overline{A}_0} \mathrm {d}\xi ^3 \mathrm {d}{\varGamma }\nonumber \\&\quad -\int _{\overline{{\varGamma }}_0} \delta _a \overline{\varepsilon }_{\alpha \beta } \int _{(h_\mathrm {th})_0} \hat{{\mathbb {C}}}^{\alpha \beta \gamma \delta } \frac{A_0}{\overline{A}_0} \mathrm {d}\xi ^3 \delta _b \overline{\varepsilon }_{\gamma \delta } \mathrm {d}{\varGamma }\nonumber \\&\quad -\int _{\overline{{\varGamma }}_0} \delta _a \overline{\varepsilon }_{\alpha \beta } \int _{(h_\mathrm {th})_0} \hat{{\mathbb {C}}}^{\alpha \beta \gamma \delta } \xi ^3 \frac{A_0}{\overline{A}_0} \mathrm {d}\xi ^3 \delta _b \overline{\kappa }_{\gamma \delta } \mathrm {d}{\varGamma }\nonumber \\&\quad -\int _{\overline{{\varGamma }}_0} \delta _a \overline{\kappa }_{\gamma \delta } \int _{(h_\mathrm {th})_0} \hat{{\mathbb {C}}}^{\alpha \beta \gamma \delta } \xi ^3 \frac{A_0}{\overline{A}_0} \mathrm {d}\xi ^3 \delta _b \overline{\varepsilon }_{\gamma \delta } \mathrm {d}{\varGamma }\nonumber \\&\quad -\int _{\overline{{\varGamma }}_0} \delta _a \overline{\kappa }_{\gamma \delta } \int _{(h_\mathrm {th})_0} \hat{{\mathbb {C}}}^{\alpha \beta \gamma \delta } \left( \xi ^3\right) ^2 \frac{A_0}{\overline{A}_0} \mathrm {d}\xi ^3 \delta _b \overline{\kappa }_{\gamma \delta } \mathrm {d}{\varGamma }. \end{aligned}$$

(93)

The variation with subscript a is associated with the variational formulation, and the variation with subscript b is associated with the iteration linearization. Again, the variation of $\xi ^3$ is dropped.

In this part too, we derive what we need:

$$\begin{aligned} \delta _b \delta _a \overline{\varepsilon }_{\alpha \beta }&= \frac{1}{2}\left( \frac{\partial \delta _a \overline{{\mathbf {x}}}}{\partial \xi ^\alpha } \cdot \frac{\partial \delta _b \overline{{\mathbf {x}}}}{\partial \xi ^\beta } + \frac{\partial \delta _b \overline{{\mathbf {x}}}}{\partial \xi ^\alpha } \cdot \frac{\partial \delta _a \overline{{\mathbf {x}}}}{\partial \xi ^\beta } \right) , \end{aligned}$$

(94)

$$\begin{aligned} \delta _a \delta _b \overline{\kappa }_{\alpha \beta }&= - \left( \delta _a \overline{\pmb {{\varGamma }}}_{\alpha \beta } - \left( \overline{\pmb {{\varGamma }}}_{\alpha \beta } \cdot \overline{{\mathbf {g}}}^\gamma \right) \frac{\partial \delta _a \overline{{\mathbf {x}}}}{\partial \xi ^\gamma } \right) \cdot \delta _b {\mathbf {n}}\nonumber \\&\quad + \delta _b \left( \overline{\pmb {{\varGamma }}}_{\alpha \beta } \cdot \overline{{\mathbf {g}}}^\gamma \right) \delta _a \overline{{\mathbf {g}}}_\gamma \cdot {\mathbf {n}}\end{aligned}$$

(95)

$$\begin{aligned}&= - \left( \delta _a \overline{\pmb {{\varGamma }}}_{\alpha \beta } - \left( \overline{\pmb {{\varGamma }}}_{\alpha \beta } \cdot \overline{{\mathbf {g}}}^\gamma \right) \frac{\partial \delta _a \overline{{\mathbf {x}}}}{\partial \xi ^\gamma } \right) \cdot \delta _b {\mathbf {n}}\nonumber \\&\quad + \left( \delta _b \overline{\pmb {{\varGamma }}}_{\alpha \beta } \cdot \overline{{\mathbf {g}}}^\gamma + \overline{\pmb {{\varGamma }}}_{\alpha \beta } \cdot \delta _b \overline{{\mathbf {g}}}^\gamma \right) \delta _a \overline{{\mathbf {g}}}_\gamma \cdot {\mathbf {n}}\end{aligned}$$

(96)

$$\begin{aligned}&= \left( \delta _a \overline{\pmb {{\varGamma }}}_{\alpha \beta } - \left( \overline{\pmb {{\varGamma }}}_{\alpha \beta } \cdot \overline{{\mathbf {g}}}^\gamma \right) \frac{\partial \delta _a \overline{{\mathbf {x}}}}{\partial \xi ^\gamma } \right) \cdot \overline{{\mathbf {g}}}^\gamma \left( {\mathbf {n}}\cdot \delta _b \overline{{\mathbf {g}}}_\gamma \right) \nonumber \\&\quad + \delta _a \overline{{\mathbf {g}}}_\gamma \cdot {\mathbf {n}}\left( \overline{{\mathbf {g}}}^\gamma \cdot \delta _b \overline{\pmb {{\varGamma }}}_{\alpha \beta } - \overline{\pmb {{\varGamma }}}_{\alpha \beta } \cdot \overline{{\mathbf {g}}}^{\delta } \overline{{\mathbf {g}}}^{\gamma } \cdot \delta _b \overline{{\mathbf {g}}}_\delta \right) \end{aligned}$$

(97)

$$\begin{aligned}&= \left( \delta _a \overline{\pmb {{\varGamma }}}_{\alpha \beta } - \left( \overline{\pmb {{\varGamma }}}_{\alpha \beta } \cdot \overline{{\mathbf {g}}}^\gamma \right) \frac{\partial \delta _a \overline{{\mathbf {x}}}}{\partial \xi ^\gamma } \right) \cdot \overline{{\mathbf {g}}}^\gamma \left( {\mathbf {n}}\cdot \delta _b \overline{{\mathbf {g}}}_\gamma \right) \nonumber \\&\quad + \left( \delta _b \overline{\pmb {{\varGamma }}}_{\alpha \beta } - \left( \overline{\pmb {{\varGamma }}}_{\alpha \beta } \cdot \overline{{\mathbf {g}}}^{\delta } \right) \frac{\partial \delta _b \overline{{\mathbf {x}}}}{\partial \xi ^\delta } \right) \cdot \overline{{\mathbf {g}}}^\gamma \left( {\mathbf {n}}\cdot \delta _a \overline{{\mathbf {g}}}_\gamma \right) . \end{aligned}$$

(98)

Here, we used

$$\begin{aligned} \delta \overline{{\mathbf {g}}}^\gamma&= - \overline{{\mathbf {g}}}^{\delta }\overline{{\mathbf {g}}}^{\gamma } \cdot \delta \overline{{\mathbf {g}}}_\delta , \end{aligned}$$

(99)

and the proof for this can be found in Appendix C.

4 Test problems

We test the formulation given in Sect. 3 by using pressurized cylindrical and spherical shells, with Neo-Hookean and Fung’s models, for the compressible- and incompressible-material cases, and for two different locations of the “midsurface.” For the compressible-material cases, we include tests with the continuum model. We compare the results to near-analytical reference solutions. We also do test computation with a pressurized Y-shaped tube.

4.1 Constitutive models

We test two constitutive models: neo-Hookean and Fung’s. The elastic-energy density functions are

$$\begin{aligned} \varphi _\mathrm {NH} \left( {\mathbf {C}}\right)&= \frac{1}{2} \mu \left( \mathrm {tr}{\mathbf {C}}- {n_{\mathrm {sd}}}\right) , \end{aligned}$$

(100)

$$\begin{aligned} \varphi _\mathrm {F} \left( {\mathbf {C}}\right)&= D_1 \left( e^{\left( D_2 \mathrm {tr}{\mathbf {C}}- {n_{\mathrm {sd}}}\right) } - 1 \right) , \end{aligned}$$

(101)

where $\mu$ is the shear modulus, and $D_1$ and $D_2$ are the coefficients of the Fung’s model.

For incompressible material, we use

$$\begin{aligned} \varphi _\mathrm {NHI} \left( {\mathbf {C}}\right)&= \varphi _\mathrm {NH} \left( {\mathbf {C}}\right) + p \left( J- 1 \right) , \end{aligned}$$

(102)

$$\begin{aligned} \varphi _\mathrm {FI} \left( {\mathbf {C}}\right)&= \varphi _\mathrm {F} \left( {\mathbf {C}}\right) + p \left( J- 1 \right) , \end{aligned}$$

(103)

where p is the pressure, which can be eliminated by the plane stress condition.

For compressible material, we use

$$\begin{aligned} \varphi _\mathrm {NHR} \left( {\mathbf {C}}\right)&= \varphi _\mathrm {NH} \left( J^{-\frac{2}{{n_{\mathrm {sd}}}}}{\mathbf {C}}\right) + \varphi _\mathrm {vol}\left( J\right) , \end{aligned}$$

(104)

$$\begin{aligned} \varphi _\mathrm {FR} \left( {\mathbf {C}}\right)&= \varphi _\mathrm {F} \left( J^{-\frac{2}{{n_{\mathrm {sd}}}}}{\mathbf {C}}\right) + \varphi _\mathrm {vol}\left( J\right) , \end{aligned}$$

(105)

where

$$\begin{aligned} \varphi _\mathrm {vol} \left( J\right)&=\frac{1}{2}\kappa \left( \frac{1}{2}\left( J^2-1\right) - \ln J\right) , \end{aligned}$$

(106)

and $\kappa$ is the bulk modulus.

4.2 Test computations

The pressure, applied at $r = r_p$, is normalized by the shear modulus (at the zero-stress state):

$$\begin{aligned} p^*&= \frac{p}{\mu } \end{aligned}$$

(107)

for the neo-Hookean model,

$$\begin{aligned} p^*&= \frac{p}{2 D_1 D_2} \end{aligned}$$

(108)

for the Fung’s model, and we use $D_2 = 8.365$. We determine the bulk modulus from the Poisson’s ratio $\nu$ as follows:

$$\begin{aligned} \kappa = \frac{2 \mu \left( 1 + \nu \right) }{3 \left( 1 - 2 \nu \right) } \end{aligned}$$

(109)

for the neo-Hookean model, and

$$\begin{aligned} \kappa = \frac{4 D_1 D_2 \left( 1 + \nu \right) }{3 \left( 1 - 2 \nu \right) } \end{aligned}$$

(110)

for the Fung’s model.

How to deal with pressure acting on the inner surface is not easy because the midsurface is the geometry we are using in the computation. Here we propose two ways. In the first one, “midsurface model,” the pressure is applied on the midsurface of the current configuration. In the second one,“inner-surface model,” the structure “midsurface” is moved to the inner surface and the pressure is applied there.

Remark 3

In applying the pressure, the midsurface model is physically wrong, especially when the thickness is significant. The inner-surface model will have larger absolute value for $\xi ^3$, which would lead to larger discretization errors.

In the test cases, we use the inner and outer radii $R_\mathrm {I}$ and $R_\mathrm {O}$, and the thickness $H = R_\mathrm {O} - R_\mathrm {I}$. The condition used here is $\frac{H}{2 R_\mathrm {I}} = 0.1$, which is slightly thinner than most arteries. To have a reference solution to compare the results to, we provide in Appendix D the second Piola–Kirchhoff stress tensor expressed in terms of the principal stretches. The results are compared by inspecting pressure as a function of stretch. The stretch is $\overline{\lambda _1} \equiv \frac{r_p}{\overline{R}}$ for the midsurface model, where $r_p = \overline{r}$, and $\overline{\lambda _1} \equiv \frac{r_p}{R_\mathrm {I}}$ for the inner-surface model, where $r_p = r_\mathrm {I}$. In the computations, we increase the pressure gradually in obtaining the solution and calculate the stretch. In obtaining the reference solutions, we use numerical integrations, which are explained in the following subsections.

Fig. 14

Pressurized sphere. Fung’s model. Reference solutions. Midsurface model. Two more Poisson’s ratios beyond those in Fig. 13

4.2.1 Pressurized cylinder

We use orthogonal basis vectors: the first basis vector is in the radial direction, the second one is in the cylinder axis direction, and the third one is normal to the surface. The force equilibrium gives the following relationship:

$$\begin{aligned} p 2 r_p&= 2 \int _{r_\mathrm {I}}^{r_\mathrm {O}} \sigma _{11} \mathrm {d}x_3\end{aligned}$$

(111)

$$\begin{aligned}&= 2 \int _{r_\mathrm {I}}^{r_\mathrm {O}} J^{-1} \lambda _1^2 S_{11} \mathrm {d}x_3\end{aligned}$$

(112)

$$\begin{aligned}&= 2 \int _{R_\mathrm {I}}^{R_\mathrm {O}} J^{-1} \lambda _1^2 S_{11} \lambda _3 \mathrm {d}X_3\end{aligned}$$

(113)

$$\begin{aligned}&= 2 \int _{R_\mathrm {I}}^{R_\mathrm {O}} \frac{\lambda _1}{\lambda _2} S_{11} \mathrm {d}X_3. \end{aligned}$$

(114)

Because the cylinder height does not change, $\lambda _2= 1$, and we obtain

$$\begin{aligned} p&= \frac{1}{r_p} \int _{R_\mathrm {I}}^{R_\mathrm {O}} \lambda _1 S_{11} \mathrm {d}X_3. \end{aligned}$$

(115)

See Appendix D.1 for $S_{11}$. Figures 2 and 3 show the reference solutions for the neo-Hookean and Fung’s models.

Fig. 15

Pressurized sphere. Cubic T-spline mesh used in the computations. Red circles represent the control points

Fig. 16

Pressurized sphere. Neo-Hookean model ($\nu =0.45$). Midsurface model (top), inner-surface model (middle), and continuum model (bottom). Solid curve is the reference solution

Fig. 17

Pressurized sphere. Neo-Hookean model ($\nu =0.49$). Midsurface model (top), inner-surface model (middle), and continuum model (bottom). Solid curve is the reference solution

Fig. 18

Pressurized sphere. Neo-Hookean model (incompressible). Midsurface model (top), and inner-surface model (bottom). Solid curve is the reference solution

Fig. 19

Pressurized sphere. Fung’s model ($\nu =0.45$). Midsurface model (top), inner-surface model (middle), and continuum model (bottom). Solid curve is the reference solution

Fig. 20

Pressurized sphere. Fung’s model ($\nu =0.49$). Midsurface model (top), inner-surface model (middle), and continuum model (bottom). Solid curve is the reference solution

Fig. 21

Pressurized sphere. Fung’s model (incompressible). Midsurface model (top), and inner-surface model (bottom). Solid curve is the reference solution

Fig. 22

Pressurized sphere. Fung’s model. Incompressible-material case. Midsurface model. Solutions from the shell models with and without the out-of-plane deformation mapping

Remark 4

For the Fung’s model, to show convergence to incompressible-material response with increasing Poisson’s ratio, for the midsurface model we add Fig. 4, with two more Poisson’s ratios beyond those in Fig. 3.

We compute, in 2D, with uniform, periodic cubic B-splines with 8 elements. For comparison purposes, we also compute with the continuum model, using 128 uniform, periodic cubic B-spline elements in the circumferential direction, and 1 element in the radial direction.

Figures 5, 6 and 7 show the solutions for the neo-Hookean model, and Figs. 8, 9 and 10 for the Fung’s model. Figures 5, 8 and 6, 9 show, for $\nu = 0.45$ and 0.49, the solutions from the midsurface, inner-surface and continuum models. Figures 7, 10 show, for incompressible material, the solutions from the midsurface and inner-surface models.

Remark 5

To compare the solutions from the shell models with and without the out-of-plane deformation mapping, we use near-analytical solutions to represent the shell-model solutions (see Appendix E). We do this for the incompressible-material case, with the midsurface model. To have some sense of scale for the difference between the solutions, we include in the comparison the solution we get when we use 1-point $\xi ^3$ integration in the model without the out-of-plane deformation mapping. Figure 11 shows the comparison for the Fung’s model. For the neo-Hookean model, there is no visible difference between the solutions. However, we note that the curvature changes are very small in this test problem.

Fig. 23

Pressurized Y-shaped tube. Undeformed configuration. The end diameters are 20, 14 and $10~\mathrm {mm}$

Fig. 24

Pressurized Y-shaped tube. Cubic T-splines mesh used in the computation. Red circles represent the control points

Fig. 25

Pressurized Y-shaped tube. Maximum principal curvature for the undeformed configuration

Fig. 26

Pressurized Y-shaped tube. Thickness distribution for the undeformed configuration

Fig. 27

Pressurized Y-shaped tube. Maximum principal curvature for the deformed configuration

Fig. 28

Pressurized Y-shaped tube. Thickness distribution for the deformed configuration

4.2.2 Pressurized sphere

We use orthogonal basis vectors: the first two vectors are on the surface, and the third vector is normal to the surface. The force equilibrium gives the following relationship:

$$\begin{aligned} p \pi r_p^2&= \int _{r_\mathrm {I}}^{r_\mathrm {O}} 2 \pi x_3 \sigma _{11} \mathrm {d}x_3 \end{aligned}$$

(116)

$$\begin{aligned}&= \int _{r_\mathrm {I}}^{r_\mathrm {O}} 2 \pi J^{-1} \lambda _1^2 x_3 S_{11} \mathrm {d}x_3 \end{aligned}$$

(117)

$$\begin{aligned}&= \int _{R_\mathrm {I}}^{R_\mathrm {O}} 2 \pi J^{-1} \lambda _1^2 \underbrace{\lambda _1 X_3}_{x_3} S_{11} \lambda _3 \mathrm {d}X_3 \end{aligned}$$

(118)

$$\begin{aligned}&= \int _{R_\mathrm {I}}^{R_\mathrm {O}} 2 \pi \frac{ \lambda _1^2}{\lambda _2} X_3 S_{11} \mathrm {d}X_3. \end{aligned}$$

(119)

Because of the symmetry between the two basis vector directions on the surface, $\lambda _1 = \lambda _2$, and we obtain

$$\begin{aligned} p&= \frac{2}{r_p^2}\int _{R_\mathrm {I}}^{R_\mathrm {O}} X_3 \lambda _1 S_{11} \mathrm {d}X_3. \end{aligned}$$

(120)

See Appendix D.2 for $S_{11}$. Figures 12 and 13 show the reference solutions for the neo-Hookean and Fung’s models.

Remark 6

For the Fung’s model, to show convergence to incompressible-material response with increasing Poisson’s ratio, for the midsurface model we add Fig. 14, with two more Poisson’s ratios beyond those in Fig. 13.

We compute, in 3D, with a cubic T-spline mesh, which consists of 296 control points and 534 Bézier elements (see Fig. 15). For comparison purposes, we also compute with the continuum model, which is extruded in the thickness direction with 1 element.

Remark 7

The number of elements used in the integration is the number of Bézier elements, which is 534 in this case. The mesh was generated by a commercial software, Rhinoceros with the T-splines plug-in. It actually has, in the finite element sense, 294 elements.

Figures 16, 17 and 18 show the solutions for the neo-Hookean model, and Figs. 19, 20 and 21 for the Fung’s model. Figures  16, 19 and 17, 20 show, for $\nu = 0.45$ and 0.49, the solutions from the midsurface, inner-surface and continuum models. Figures 18, 21 show, for incompressible material, the solutions from the midsurface and inner-surface models.

Remark 8

In the same way described in Remark 5 for the pressurized cylinder, we compare the solutions from the shell models with and without the out-of-plane deformation mapping. Figure 22 shows the comparison for the Fung’s model. For the neo-Hookean model there is no visible difference between the solutions. We again note that the curvature changes are very small in the test problem.

4.2.3 Pressurized Y-shaped tube

The undeformed configuration of the tube is shown in Fig. 23. The end diameters of the tube are 20, 14 and 10 $\mathrm {mm}$. Figure 24 shows the cubic T-splines mesh used in the computation. The number of control points and elements are 1,295 and 1,296. Figure 25 shows the maximum principal curvature for the undeformed configuration. We use the incompressible-material Fung’s model with $D_1 = 2.6447{\times }10^3~\mathrm {Pa}$ and $D_2 = 8.365$. The “midsurface” location in the shell analysis is the inner surface, and the pressure applied is $12.3{\times }10^3$ $\mathrm {Pa}$. The thickness distribution for the undeformed configuration is shown in Fig. 26. This smooth thickness distribution is outcome of solving the Laplace’s equation over the inner surface of the tube, with Dirichlet boundary conditions at the tube ends, where the value specified is 0.146 times the end diameter. Figures 27 and 28 show the maximum principal curvature and thickness distribution for the deformed configuration.

5 Concluding remarks

We have presented a hyperelastic shell formulation based on the Kirchhoff–Love shell theory and isogeometric discretization. The formulation takes into account the out-of-plane deformation mapping. Accounting for that mapping affects the curvature term. It also affects the accuracy in calculating the deformed-configuration out-of-plane position, and consequently the nonlinear response of the material. In FSI analysis, when the fluid is inside a shell structure, the shell midsurface is what it would know. That would be physically wrong, especially when the thickness is significant, because the inner surface is the one that the fluid should really see. For that reason, in this article we also proposed, as an alternative, shifting the “midsurface” location in the shell analysis to the inner surface. The way we perform the integrations over the undeformed configuration takes into account the curvature effects, and consequently integration volume does not change if we shift the “midsurface” location. We presented test computations with pressurized cylindrical and spherical shells, with Neo-Hookean and Fung’s models, for the compressible- and incompressible-material cases, and for two different locations of the “midsurface.” We compared the results to near-analytical reference solutions, and in all cases we see a good match. We also presented test computation with a pressurized Y-shaped tube, intended to be a simplified artery model and serving as an example of cases with somewhat more complex geometry.

Appendices

Appendix A: Derivative and variation of the normal vector in the shell model

1.1 A.1 Derivative of the normal vector

Derivative of the normal vector with respect to $\xi ^\alpha$ can be obtained as follows:

$$\begin{aligned} \overline{{\mathbf {n}}}_{,\alpha }&= \frac{\partial }{\partial \xi ^\alpha }\left( \frac{\overline{{\mathbf {g}}}_1\times \overline{{\mathbf {g}}}_2}{\left( \overline{{\mathbf {g}}}_1\times \overline{{\mathbf {g}}}_2\right) \cdot {\mathbf {n}}} \right) \end{aligned}$$

(121)

$$\begin{aligned}&= \left( {\mathbf {I}}- {\mathbf {n}}{\mathbf {n}}\right) \cdot \frac{\overline{{\mathbf {g}}}_{1,\alpha }\times \overline{{\mathbf {g}}}_2 + \overline{{\mathbf {g}}}_1\times \overline{{\mathbf {g}}}_{2,\alpha }}{\left( \overline{{\mathbf {g}}}_1\times \overline{{\mathbf {g}}}_2\right) \cdot {\mathbf {n}}} \end{aligned}$$

(122)

$$\begin{aligned}&= \left( {\mathbf {I}}- {\mathbf {n}}{\mathbf {n}}\right) \cdot \frac{ \overline{{\mathbf {g}}}_{1,\alpha }\times \left( {\mathbf {n}}\times \overline{{\mathbf {g}}}^1\right) + \overline{{\mathbf {g}}}_{2,\alpha }\times \left( {\mathbf {n}}\times \overline{{\mathbf {g}}}^2\right) }{\left( \overline{{\mathbf {g}}}^1\times \overline{{\mathbf {g}}}^2\right) \cdot {\mathbf {n}}{\left( \overline{{\mathbf {g}}}_1\times \overline{{\mathbf {g}}}_2\right) \cdot {\mathbf {n}}}} \end{aligned}$$

(123)

$$\begin{aligned}&= \left( {\mathbf {I}}- {\mathbf {n}}{\mathbf {n}}\right) \cdot \left( \overline{{\mathbf {g}}}_{\beta ,\alpha }\times \left( {\mathbf {n}}\times \overline{{\mathbf {g}}}^\beta \right) \right) \end{aligned}$$

(124)

$$\begin{aligned}&= \left( {\mathbf {I}}- {\mathbf {n}}{\mathbf {n}}\right) \cdot \left( \left( \overline{{\mathbf {g}}}_{\beta ,\alpha } \cdot \overline{{\mathbf {g}}}^\beta \right) {\mathbf {n}}- \left( \overline{{\mathbf {g}}}_{\beta ,\alpha } \cdot {\mathbf {n}}\right) \overline{{\mathbf {g}}}^\beta \right) \end{aligned}$$

(125)

$$\begin{aligned}&= -\left( \overline{{\mathbf {g}}}_{\beta , \alpha } \cdot {\mathbf {n}}\right) \overline{{\mathbf {g}}}^{\beta } + {\mathbf {n}}\underbrace{\left( {\mathbf {n}}\cdot \overline{{\mathbf {g}}}^\beta \right) }_{=0} \left( \overline{{\mathbf {g}}}_{\beta , \alpha } \cdot {\mathbf {n}}\right) \end{aligned}$$

(126)

$$\begin{aligned}&= -\overline{{\mathbf {g}}}^{\beta } \overline{{\mathbf {g}}}_{\beta , \alpha } \cdot {\mathbf {n}}\end{aligned}$$

(127)

$$\begin{aligned}&= -\overline{{\mathbf {g}}}^{\beta } \overline{b}_{\alpha \beta }. \end{aligned}$$

(128)

In the derivation, we used the following relationships, which generally hold:

$$\begin{aligned} {\mathbf {g}}_1&= \frac{{\mathbf {g}}^2 \times {\mathbf {g}}^3}{\left( {\mathbf {g}}^1\times {\mathbf {g}}^2\right) \cdot {\mathbf {g}}^3}, \end{aligned}$$

(129)

$$\begin{aligned} {\mathbf {g}}_2&= \frac{{\mathbf {g}}^3 \times {\mathbf {g}}^1}{\left( {\mathbf {g}}^1\times {\mathbf {g}}^2\right) \cdot {\mathbf {g}}^3}, \end{aligned}$$

(130)

$$\begin{aligned} \left( {\mathbf {g}}^1 \times {\mathbf {g}}^2\right) \cdot {\mathbf {g}}^3&= \left( \left( {\mathbf {g}}_1 \times {\mathbf {g}}_2\right) \cdot {\mathbf {g}}_3 \right) ^{-1}. \end{aligned}$$

(131)

1.2 A.2 Variation of the normal vector

From the steps given by Eqs. (121)–(127), the variation of the normal vector can be written as

$$\begin{aligned} \delta {\mathbf {n}}&= - \overline{{\mathbf {g}}}^{\beta } \delta \overline{{\mathbf {g}}}_{\beta } \cdot {\mathbf {n}}. \end{aligned}$$

(132)

Appendix B: Variation of $\xi ^3$ is a second-order term

Taking the variation of both sides of Eq. (58), we obtain

$$\begin{aligned} \delta \xi ^3&= \delta \overline{\lambda _3} \xi ^3_0 + \delta \frac{\mathrm {d}\hat{\lambda _3} }{\mathrm {d}\xi ^3_0} \left( \xi ^3_0\right) ^2 +{\mathcal {O}}\left( \left( \xi _0^3\right) ^3\right) . \end{aligned}$$

(133)

For a representative value of the variation, we take the average over the thickness:

$$\begin{aligned} \overline{ \delta \xi ^3}&\equiv \frac{1}{(h_\mathrm {th})_0} \int _{- (h_\mathrm {th})_0/2 }^{ (h_\mathrm {th})_0/2 } \delta \xi ^3 \mathrm {d}\xi ^3_0 \end{aligned}$$

(134)

$$\begin{aligned}&= \frac{1}{(h_\mathrm {th})_0} \left( \frac{2}{3} \delta \frac{\mathrm {d}\hat{\lambda _3} }{\mathrm {d}\xi ^3_0} \left( \frac{(h_\mathrm {th})_0}{2}\right) ^3 +{\mathcal {O}}\left( (h_\mathrm {th})_0^5\right) \right) \end{aligned}$$

(135)

$$\begin{aligned}&= \frac{1}{12} \delta \frac{\mathrm {d}\hat{\lambda _3} }{\mathrm {d}\xi ^3_0} (h_\mathrm {th})_0^2 +{\mathcal {O}}\left( (h_\mathrm {th})_0^4\right) . \end{aligned}$$

(136)

Thus, the variation of $\xi ^3$ is a second-order term.

Appendix C: Variation of the contravariant basis vector

Here we show that $\delta {\mathbf {g}}^\gamma$ can be expressed as

$$\begin{aligned} \delta {\mathbf {g}}^\gamma&= - {\mathbf {g}}^\delta {\mathbf {g}}^\gamma \cdot \delta {\mathbf {g}}_{\delta }. \end{aligned}$$

(137)

We start with the transformation from the contravariant basis vectors to the covariant basis vectors:

$$\begin{aligned} {\mathbf {g}}_{\alpha }&= g_{\alpha \delta } {\mathbf {g}}^{\delta }. \end{aligned}$$

(138)

We take the variation of both sides:

$$\begin{aligned} \delta {\mathbf {g}}_{\alpha }&= \delta g_{\alpha \delta } {\mathbf {g}}^{\delta } + g_{\alpha \delta } \delta {\mathbf {g}}^{\delta }, \end{aligned}$$

(139)

and from that obtain

$$\begin{aligned} g_{\alpha \delta } \delta {\mathbf {g}}^{\delta }&= \delta {\mathbf {g}}_{\alpha } - \delta g_{\alpha \delta } {\mathbf {g}}^{\delta }. \end{aligned}$$

(140)

From that and Eq. (11), we obtain

$$\begin{aligned} g_{\alpha \delta } \delta {\mathbf {g}}^{\delta }&= \delta {\mathbf {g}}_{\alpha } - \left( \delta {\mathbf {g}}_\alpha \cdot {\mathbf {g}}_{\delta } + {\mathbf {g}}_\alpha \cdot \delta {\mathbf {g}}_{\delta } \right) {\mathbf {g}}^{\delta } \end{aligned}$$

(141)

$$\begin{aligned}&= \delta {\mathbf {g}}_{\alpha } - \delta {\mathbf {g}}_\alpha \cdot \underbrace{ {\mathbf {g}}_{\delta } {\mathbf {g}}^{\delta } }_{={\mathbf {I}}} - {\mathbf {g}}_\alpha \cdot \delta {\mathbf {g}}_{\delta } {\mathbf {g}}^{\delta } \end{aligned}$$

(142)

$$\begin{aligned}&= \delta {\mathbf {g}}_{\alpha } - \delta {\mathbf {g}}_\alpha - {\mathbf {g}}_\alpha \cdot \delta {\mathbf {g}}_{\delta } {\mathbf {g}}^{\delta } \end{aligned}$$

(143)

$$\begin{aligned}&= - {\mathbf {g}}_\alpha \cdot \delta {\mathbf {g}}_{\delta } {\mathbf {g}}^{\delta }. \end{aligned}$$

(144)

Multiplying both sides with $g^{\gamma \alpha }$, we obtain

$$\begin{aligned} \underbrace{ g^{\gamma \alpha } g_{\alpha \delta } }_{=\delta ^\gamma _\delta } \delta {\mathbf {g}}^{\delta }&= - \underbrace{ g^{\gamma \alpha } {\mathbf {g}}_\alpha }_{={\mathbf {g}}^\gamma } \cdot \delta {\mathbf {g}}_{\delta } {\mathbf {g}}^{\delta }. \end{aligned}$$

(145)

Thus,

$$\begin{aligned} \delta {\mathbf {g}}^{\gamma }&= - {\mathbf {g}}^{\gamma } \cdot \delta {\mathbf {g}}_{\delta } {\mathbf {g}}^{\delta } \end{aligned}$$

(146)

$$\begin{aligned}&= - {\mathbf {g}}^{\delta } {\mathbf {g}}^{\gamma } \cdot \delta {\mathbf {g}}_{\delta }. \end{aligned}$$

(147)

Appendix D: Constitutive law: second Piola–Kirchhoff tensor

$$\begin{aligned} \left( S_\mathrm {NHI}\right) _{11}&= \mu \left( 1 - \frac{\lambda _3^2}{\lambda _1^2}\right) ,\end{aligned}$$

(148)

$$\begin{aligned} \left( S_\mathrm {NHR}\right) _{11}&= \mu J^{-\frac{2}{3}} \left( 1 - \frac{\lambda _1 + \lambda _2 + \lambda _3}{3 \lambda _1^2}\right) \nonumber \\ \quad&+ \frac{1}{2 \lambda _1^2}\kappa \left( J^2-1 \right) ,\end{aligned}$$

(149)

$$\begin{aligned} \left( S_\mathrm {FI}\right) _{11}&= 2 D_1 D_2 e^{\left( D_2 \left( \left( \lambda _1 + \lambda _2 + \lambda _3 \right) -3\right) \right) } \left( 1 - \frac{\lambda _3^2}{\lambda _1^2}\right) ,\end{aligned}$$

(150)

$$\begin{aligned} \left( S_\mathrm {FR}\right) _{11}&= 2 D_1 D_2 e^{\left( D_2 \left( J^{\frac{-2}{3}}\left( \lambda _1 + \lambda _2 + \lambda _3 \right) -3\right) \right) } J^{-\frac{2}{3}} \nonumber \\&\quad \left( 1 - \frac{\lambda _1 + \lambda _2 + \lambda _3}{3 \lambda _1^2}\right) + \frac{1}{2 \lambda _1^2}\kappa \left( J^2-1 \right) . \end{aligned}$$

(151)

1.1 D.1 Cylinder

$$\begin{aligned} \left( S_\mathrm {NHI}\right) _{11}&= \mu \left( 1 - \lambda _1^{-4}\right) ,\end{aligned}$$

(152)

$$\begin{aligned} \left( S_\mathrm {NHR}\right) _{11}&= \mu \left( \lambda _1 \lambda _3\right) ^{-\frac{2}{3}} \left( 1 - \frac{\lambda _1 + \lambda _3 + 1}{3 \lambda _1^2}\right) \nonumber \\&\quad + \frac{1}{2}\kappa \left( \lambda _3^2 - \lambda _1^{-2} \right) ,\end{aligned}$$

(153)

$$\begin{aligned} \left( S_\mathrm {FI}\right) _{11}&= 2 D_1 D_2 e^{\left( D_2 \left( \left( \lambda _1 + \lambda _1^{-1} +1 \right) -3\right) \right) } \left( 1 - \lambda _1^{-4}\right) ,\end{aligned}$$

(154)

$$\begin{aligned} \left( S_\mathrm {FR}\right) _{11}&= 2 D_1 D_2 e^{\left( D_2 \left( J^{\frac{-2}{3}}\left( \lambda _1 + \lambda _3 +1 \right) -3\right) \right) } \left( \lambda _1 \lambda _3\right) ^{-\frac{2}{3}}\nonumber \\&\quad \left( 1 - \frac{\lambda _1 + \lambda _3 + 1}{3 \lambda _1^2}\right) + \frac{1}{2}\kappa \left( \lambda _3^2 - \lambda _1^{-2} \right) . \end{aligned}$$

(155)

1.2 D.2 Sphere

$$\begin{aligned} \left( S_\mathrm {NHI}\right) _{11}&= \mu \left( 1 - \frac{1}{\lambda _1^6}\right) ,\end{aligned}$$

(156)

$$\begin{aligned} \left( S_\mathrm {NHR}\right) _{11}&= \mu \left( \lambda _1^2 \lambda _3\right) ^{-\frac{2}{3}} \left( 1 - \frac{2 \lambda _1 + \lambda _3}{3 \lambda _1^2}\right) \nonumber \\&\quad + \frac{1}{2 }\kappa \left( \lambda _3^2 -\lambda _1^{-2} \right) ,\end{aligned}$$

(157)

$$\begin{aligned} \left( S_\mathrm {FI}\right) _{11}&= 2 D_1 D_2 e^{\left( D_2 \left( \left( 2 \lambda _1 + \lambda _1^{-2} \right) -3\right) \right) } \left( 1 - \frac{1}{\lambda _1^6}\right) ,\end{aligned}$$

(158)

$$\begin{aligned} \left( S_\mathrm {FR}\right) _{11}&= 2 D_1 D_2 e^{\left( D_2 \left( \left( \lambda _1^2 \lambda _3\right) ^{-\frac{2}{3}} \left( 2 \lambda _1 + \lambda _3 \right) -3\right) \right) } \left( \lambda _1^2 \lambda _3\right) ^{-\frac{2}{3}} \nonumber \\&\quad \left( 1 - \frac{2 \lambda _1 + \lambda _3}{3 \lambda _1^2}\right) + \frac{1}{2 }\kappa \left( \lambda _3^2 -\lambda _1^{-2} \right) . \end{aligned}$$

(159)

Appendix E: Representation of the shell-model solutions with the near-analytical reference solutions

Consider the following relationship between the stress tensor and stress vector at a cross-sectional surface:

$$\begin{aligned} {\mathbf {h}}_0 = {\mathbf {F}}{\mathbf {S}}\cdot {\mathbf {n}}_0, \end{aligned}$$

(160)

where ${\mathbf {h}}_0$ and ${\mathbf {n}}_0$ are the stress and unit normal vectors on the reference configuration. Integrating this over $\left( h_\mathrm {th}\right) _0$, we get

$$\begin{aligned} \int _{\left( h_\mathrm {th}\right) _0} {\mathbf {h}}_0 \mathrm {d}\xi ^3_0&= \int _{\left( h_\mathrm {th}\right) _0} {\mathbf {F}}{\mathbf {S}}\cdot {\mathbf {n}}_0 \mathrm {d}\xi ^3_0. \end{aligned}$$

(161)

Combining this with Eq. (44), we obtain

$$\begin{aligned} \int _{\left( h_\mathrm {th}\right) _0} {\mathbf {h}}_0 \mathrm {d}\xi ^3_0 = \int _{\left( h_\mathrm {th}\right) _0} \left( {\mathbf {g}}_\alpha {\mathbf {G}}^\alpha + \lambda _3 {\mathbf {g}}_3 {\mathbf {G}}^3 \right) \cdot {\mathbf {S}}\cdot {\mathbf {n}}_0 \mathrm {d}\xi ^3_0, \end{aligned}$$

(162)

and because ${\mathbf {G}}^3 \cdot {\mathbf {S}}$ = ${\mathbf {0}}$ in the Kirchhoff–Love shell theory, we get

$$\begin{aligned} \int _{\left( h_\mathrm {th}\right) _0} {\mathbf {h}}_0 \mathrm {d}\xi ^3_0 = \int _{\left( h_\mathrm {th}\right) _0} {\mathbf {g}}_\alpha {\mathbf {G}}^\alpha \cdot S^{\delta \beta } {\mathbf {G}}_{\delta } {\mathbf {G}}_{\beta } \cdot {\mathbf {n}}_0 \mathrm {d}\xi ^3_0. \end{aligned}$$

(163)

Using the relationship ${\mathbf {G}}^\alpha \cdot {\mathbf {G}}_\delta = \delta ^\alpha _\delta$, we obtain

$$\begin{aligned} \int _{\left( h_\mathrm {th}\right) _0} {\mathbf {h}}_0 \mathrm {d}\xi ^3_0 = \int _{\left( h_\mathrm {th}\right) _0} S^{\alpha \beta } {\mathbf {g}}_\alpha {\mathbf {G}}_{\beta } \cdot {\mathbf {n}}_0 \mathrm {d}\xi ^3_0. \end{aligned}$$

(164)

Combining this with Eq. (21), we obtain

$$\begin{aligned} \int _{\left( h_\mathrm {th}\right) _0} {\mathbf {h}}_0 \mathrm {d}\xi ^3_0 = \int _{\left( h_\mathrm {th}\right) _0} S^{\alpha \beta } \left( \overline{{\mathbf {g}}}_\alpha -\overline{b}_{\alpha \gamma } \overline{{\mathbf {g}}}^\gamma \xi ^3 \right) {\mathbf {G}}_{\beta } \cdot {\mathbf {n}}_0 \mathrm {d}\xi ^3_0, \end{aligned}$$

(165)

and taking the midsurface quantities out of the integration, we get

$$\begin{aligned} \int _{\left( h_\mathrm {th}\right) _0} {\mathbf {h}}_0 \mathrm {d}\xi ^3_0&= \overline{{\mathbf {g}}}_\alpha \int _{\left( h_\mathrm {th}\right) _0} S^{\alpha \beta } {\mathbf {G}}_{\beta } \cdot {\mathbf {n}}_0 \mathrm {d}\xi ^3_0 \nonumber \\&\quad -\overline{b}_{\alpha \gamma } \overline{{\mathbf {g}}}^\gamma \int _{\left( h_\mathrm {th}\right) _0} \xi ^3 S^{\alpha \beta } {\mathbf {G}}_{\beta } \cdot {\mathbf {n}}_0 \mathrm {d}\xi ^3_0. \end{aligned}$$

(166)

For the model without the out-of-plane deformation mapping, the approximation is

$$\begin{aligned} \int _{\left( h_\mathrm {th}\right) _0} {\mathbf {h}}_0 \mathrm {d}\xi ^3_0&\approx \overline{{\mathbf {g}}}_\alpha \int _{\left( h_\mathrm {th}\right) _0} \left. S^{\alpha \beta } \right| _{\xi ^3 = \xi _0^3} \mathrm {d}\xi ^3_0 \left( \overline{{\mathbf {G}}}_{\beta } \cdot {\mathbf {n}}_0 \right) \nonumber \\&\quad -\overline{b}_{\alpha \gamma } \overline{{\mathbf {g}}}^\gamma \int _{\left( h_\mathrm {th}\right) _0} \xi ^3_0 \left. S^{\alpha \beta } \right| _{\xi ^3 = \xi _0^3} \mathrm {d}\xi ^3_0 \left( \overline{{\mathbf {G}}}_{\beta } \cdot {\mathbf {n}}_0 \right) . \end{aligned}$$

(167)

When using 1-point $\xi ^3$ integration in the model without the out-of-plane deformation mapping, the approximation becomes

$$\begin{aligned} \int _{\left( h_\mathrm {th}\right) _0} {\mathbf {h}}_0 \mathrm {d}\xi ^3_0&\approx \overline{{\mathbf {g}}}_\alpha \left. S^{\alpha \beta } \right| _{\xi ^3 = \xi _0^3 =0} \left( \overline{{\mathbf {G}}}_\beta \cdot {\mathbf {n}}_0 \right) \left( h_\mathrm {th}\right) _0 \nonumber \\&\quad - \overline{b}_{\alpha \kappa } \overline{{\mathbf {g}}}^{\kappa } \frac{\left( h_\mathrm {th}\right) _0^3}{12} \left. \frac{\partial S^{\alpha \beta } }{\partial E_{\gamma \delta }} \frac{\partial E_{\gamma \delta }}{ \partial \xi ^3_0} \right| _{\xi ^3 = \xi _0^3 = 0} \left( \overline{{\mathbf {G}}}_\beta \cdot {\mathbf {n}}_0 \right) . \end{aligned}$$

(168)

Substituting Eqs. (23) and (36) into Eq. (56), omit the quadratic terms, and taking derivative with respect to $\xi ^3_0$, we obtain

$$\begin{aligned} \frac{\partial E_{\gamma \delta }}{\partial \xi ^3_0}&=-\left( \overline{b}_{\gamma \delta } - \overline{B}_{\gamma \delta }\right) . \end{aligned}$$

(169)

Using Eqs. (69) and (70), we obtain

$$\begin{aligned}&\int _{\left( h_\mathrm {th}\right) _0} {\mathbf {h}}_0 \mathrm {d}\xi ^3_0 \approx \overline{{\mathbf {g}}}_\alpha \left. S^{\alpha \beta } \right| _{\xi ^3 = \xi _0^3 =0} \left( \overline{{\mathbf {G}}}_\beta \cdot {\mathbf {n}}_0 \right) \left( h_\mathrm {th}\right) _0 \nonumber \\&\quad + \overline{b}_{\alpha \kappa } \overline{{\mathbf {g}}}^{\kappa } \frac{\left( h_\mathrm {th}\right) _0^3}{12} \left. \hat{{\mathbb {C}}}^{\alpha \beta \gamma \delta } \right| _{\xi ^3 = \xi _0^3 = 0} \left( \overline{b}_{\gamma \delta }- \overline{B}_{\gamma \delta }\right) \left( \overline{{\mathbf {G}}}_\beta \cdot {\mathbf {n}}_0 \right) . \end{aligned}$$

(170)

1.1 E.1 Cylinder

For the model without the out-of-plane deformation mapping, Eq. (115) is approximated as

$$\begin{aligned} p&= \frac{1}{r_p} \overline{\lambda _1}\int _{R_\mathrm {I}}^{R_\mathrm {O}} \left. {S}_{11}\right| _{x_3=X_3+\overline{r}-\overline{R}} \mathrm {d}X_3 \nonumber \\&\quad + \frac{1}{r_p} \int _{R_\mathrm {I}}^{R_\mathrm {O}} \left. \frac{X_3-\overline{R}}{\overline{R}} {S}_{11}\right| _{x_3=X_3+\overline{r}-\overline{R}} \mathrm {d}X_3. \end{aligned}$$

(171)

When using 1-point $\xi ^3$ integration in the model without the out-of-plane deformation mapping, the approximation becomes

$$\begin{aligned} p&= \frac{1}{r_p} \overline{\lambda _1} \left. {S}_{11} \right| _{x_3=\overline{r},~X_3=\overline{R}} H \nonumber \\&\quad +\frac{1}{r_p} \left. {\hat{{\mathbb {C}}}}_{1111} \right| _{x_3=\overline{r},~X_3=\overline{R}} \frac{\overline{\lambda _1} - 1}{\overline{R}^2}\frac{H^3}{12}. \end{aligned}$$

(172)

1.2 E.2 Sphere

For the model without the out-of-plane deformation mapping, Eq. (120) is approximated as

$$\begin{aligned} p&= \frac{2}{r_p^2} \overline{R} \overline{\lambda _1}\int _{R_\mathrm {I}}^{R_\mathrm {O}} \left. S_{11}\right| _{x_3=X_3 + \overline{r} -\overline{R}} \mathrm {d}X_3 \nonumber \\&\quad + \frac{2}{r_p^2} \overline{R} \int _{R_\mathrm {I}}^{R_\mathrm {O}}\frac{X_3 - \overline{R}}{\overline{R}} \left. S_{11}\right| _{x_3=X_3 + \overline{r} -\overline{R}} \mathrm {d}X_3. \end{aligned}$$

(173)

We note that Eq. (173) has been obtained after also neglecting the volume change in the thickness direction (see [4]). When using 1-point $\xi ^3$ integration in the model without the out-of-plane deformation mapping, the approximation becomes

$$\begin{aligned} p&= \frac{2}{r_p^2} \overline{R} \overline{\lambda _1} \left. S_{11} \right| _{x_3=\overline{r},~X_3=\overline{R}} H \nonumber \\&\quad +\frac{2}{r_p^2} \overline{R} \left( \left. {\hat{{\mathbb {C}}}}_{1111} \right| _{x_3=\overline{r},~X_3=\overline{R}} + \left. {\hat{{\mathbb {C}}}}_{1122} \right| _{x_3=\overline{r},~X_3=\overline{R}} \right) \nonumber \\&\quad \times \frac{\overline{\lambda _1} - 1}{\overline{R}^2}\frac{H^3}{12}. \end{aligned}$$

(174)